Abstract
Bayesian optimization algorithms are widely used for solving problems with a high computational complexity in terms of objective function evaluation. The efficiency of Bayesian optimization is strongly dependent on the quality of the surrogate models of an objective function, which are built and refined at each iteration. The quality of surrogate models, and hence the performance of an optimization algorithm, can be greatly improved by selecting the appropriate hyperparameter values of the approximation algorithm. The common approach to finding good hyperparameter values for each iteration of Bayesian optimization is to build surrogate models with different hyperparameter values and choose the best one based on some estimation of the approximation error, for example, a cross-validation score. Building multiple surrogate models for each iteration of Bayesian optimization is computationally demanding and significantly increases the time required to solve an optimization problem. This paper suggests a new approach, called exploratory landscape validation, to find good hyperparameter values with less computational effort. Exploratory landscape validation metrics can be used to predict the best hyperparameter values, which can improve both the quality of the solutions found by Bayesian optimization and the time needed to solve problems.
Keywords:
Bayesian optimization; Gaussian process; surrogate modeling; hyperparameter tuning; exploratory landscape analysis; exploratory landscape validation; variability map of objective function MSC:
90C26; 90C56; 90C59
1. Introduction
Continuous optimization problems with high computational complexity in terms of objective functions arise in many fields of engineering, material design, automatic machine learning, and others [1]. In real-world optimization problems, evaluating the value of an objective function requires time-consuming computational experiments or simulations. The time needed to solve an optimization problem is primarily defined by the total number of objective function evaluations performed by the optimization algorithm. When solving computationally expensive optimization problems, the main termination criterion for the algorithm is the maximum number of objective evaluations, which is usually called the computational budget [2].
Problems with a limited computational budget are best solved by optimization algorithms that utilize surrogate models of the objective function [2]. The most promising candidates for objective evaluation are identified by refining and exploring surrogate models at every optimization iteration. Hence, both the quality of surrogate models and the parameters of the model exploration procedure can have an impact on the optimization algorithm’s efficiency. Many studies have focused on tuning the parameters of the model exploration procedure, specifically the type and the parameters of the acquisition function, as well as the parameters of the algorithm for optimizing it [3,4]. This article focuses on ways to improve the efficiency of optimization algorithms by increasing the quality of surrogate models.
Surrogate models are usually built by approximation algorithms with tunable hyperparameters. Numerous studies have been conducted to find the best hyperparameter values that maximize the accuracy of surrogate models and, hence, the optimization algorithm’s efficiency [5,6,7]. The process of finding such hyperparameter values is called hyperparameter tuning. Here are some examples of hyperparameters being tuned for different types of surrogate models:
- Degree of polynomial regression models;
- Size of the hidden layer for models based on neural networks;
- Kernel type and parameters for models based on Gaussian process (GP) regression;
- Number of trees and tree depth for models based on random forest regression.
This article considers the tuning of kernel parameters for models based on GP regression, which includes, for example, the scale mixture parameter of the rational quadratic kernel or the parameter of the Matern kernel [8].
In order to perform hyperparameter tuning, the hyperparameter efficiency metric is defined based on the quality estimate of a surrogate model built with a given hyperparameter vector. The model quality is usually measured on a test sample of points using some error approximation metric, such as mean absolute error, mean squared error, score, etc. [9,10]. In cases of a strict computational budget, maintaining a separate test sample by evaluating a costly objective function is not sufficient. To increase the reliability of hyperparameter efficiency estimates, resampling procedures are used, which involve the building of multiple models for each hyperparameter vector, for example, the well-known cross-validation procedure [10]. Using cross-validation for hyperparameter efficiency estimation significantly increases the computational cost of hyperparameter tuning. This article introduces a new approach for estimating hyperparameter efficiency called exploratory landscape validation, along with new efficiency metrics that require less computational effort, and that, in some cases, outperform cross-validation in terms of solution quality. One of the metrics is based on a so-called ranking preservation indicator [11], calculated on an extended training sample. Another metric is evaluated by comparing the variability maps of an objective function [12] constructed for a training sample and a surrogate model.
Much of the recent research on the parameter tuning of optimization algorithms, which also includes the hyperparameter tuning of surrogate models, has focused on using exploratory landscape analysis (ELA) algorithms to estimate the characteristic features of optimization problems [13,14,15]. The hyperparameter prediction process is based on the following idea. Given the ELA feature vectors, which incorporate the specifics of problems, and the best hyperparameter values found for those problems, a machine learning (ML) algorithm is used to build a tuning model to predict the best hyperparameter values or the best approximation algorithm [12,16,17]. According to such an ELA-ML approach, the tuning model is then used to identify hyperparameter values that are reasonably effective when solving similar problems based on the feature vectors of those problems. In [16], for example, the authors constructed tuning models that are based on different classification algorithms to predict the best surrogate modelling algorithm using the ELA features of the problem. Despite the fact that additional computational effort is required to collect the training data and build a tuning model, the increase in efficiency of the optimization algorithm outweighs the computational costs in a long-term perspective. This article also explores the benefits of using tuning models that are built using the proposed metrics for finding effective hyperparameter values.
The rest of the article is organized in the following way. Section 2 presents a statement for a global continuous optimization problem, describes the canonical form of the Bayesian optimization algorithm, and formalizes the hyperparameter tuning and prediction problems. In Section 3, a new approach to the quality estimation of surrogate models, called landscape validation, is introduced, and includes a variety of criteria for selecting and predicting the best hyperparameter values. Section 4 starts with the general setup for computational experiments, followed by a description of the experiments performed with the hyperparameter tuning and hyperparameter prediction approaches based on the proposed hyperparameter efficiency metrics; then, the experimental results are discussed.
2. Bayesian Optimization with Hyperparameter Tuning and Prediction
The following statement of the continuous global optimization problem is considered:
where is the vector of continuous variables of size ; is a scalar objective function; is a convex region of the permissible variables’ values; is the vector of the variables’ values for which the objective function has the minimal value . It is assumed that the region is formed by the set of inequalities , where and are the lower and upper bounds of the -th variable, respectively. The problem (1) is referred to as the base optimization problem.
Due to the high computational complexity of the objective function, the total number of objective evaluations allowed for solving the problem (1) is limited to , which is called the computational budget of the problem. When solving computationally expensive base problems, common practice is to build and explore surrogate models of the objective function . By using a surrogate model , promising areas of the search region can be located approximately without utilizing the budget . The algorithm for building surrogate models usually has tunable hyperparameters, the vector of the values of which is denoted as .
In this section, the Bayesian optimization algorithm is described and the problem statements for hyperparameter tuning and hyperparameter prediction for the surrogate modeling algorithm are formulated. The aim of this section is to outline and formalize common approaches for solving computationally expensive optimization problems, on the basis of which, new approaches to the hyperparameter efficiency estimation will be presented in the next section.
2.1. Bayesian Optimization Algorithm
In contrast to other surrogate-based optimization algorithms, Bayesian optimization algorithms use surrogate models that are based on Gaussian process (GP) approximation. In GP models, each point of the search region is associated with a normal distribution of the predicted objective values , where is the mean and is the standard deviation of values. Having the probability distribution over allows for selection of promising points for the objective function evaluation based on both predicted objective values and uncertainty estimates of those predictions. Formally, promising point selection is defined as the maximization problem of a so-called acquisition function. Hence, the tunable parameters of a Bayesian optimization algorithm include the type and parameters of the acquisition function, as well as the hyperparameters of the GP approximation algorithm, which are the type and parameters of a covariance function, also referred to as a kernel [5].
The Bayesian optimization algorithm includes the following steps (Figure 1):
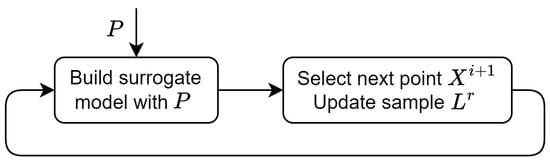
Figure 1.
Bayesian optimization with fixed hyperparameter values.
- Generate the initial sample for training the first GP model, where is the initial sample size. Points are chosen either randomly or according to one of the designs of the experiment algorithm, e.g., the Latin hypercube sampling (LHS) algorithm [18];
- Perform iterations , where as follows:
- Build the surrogate model using the current training sample and the vector of the hyperparameter values;
- Select the next point for the objective function evaluation by optimizing an acquisition function, e.g., by minimizing the lower confidence bound (LCB) [19] function as follows:where is a tunable parameter;
- Evaluate the objective function for point to obtain the corresponding value and extend the training sample .
- The point that has the minimal corresponding objective value is considered as the solution of the base problem (1).
Although the formal optimality of the best-found point is not guaranteed in any sense, the same notation as in the problem definition (1) is used for simplicity. The rest of the article focuses on ways to improve the optimization algorithm’s efficiency by tuning the GP hyperparameters.
2.2. Hyperparameter Tuning for a Bayesian Optimization Algorithm
The efficiency of Bayesian optimization can be improved by selecting, at each iteration, the vector that is the best for the training sample according to the hyperparameter efficiency metric . Given the set of allowed hyperparameter values , the best vector is found by solving the following hyperparameter optimization problem at step 2a (Figure 2):
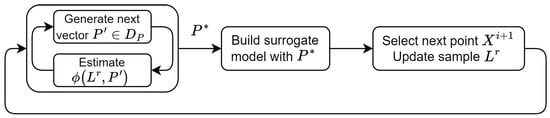
Figure 2.
Bayesian optimization with hyperparameter tuning.
The hyperparameter efficiency metric is commonly defined based on approximation accuracy metrics, e.g., mean squared error, on a test sample.
In most cases, the size of sample in Bayesian optimization is already not sufficient for the search space dimension due to a very limited budget . Since it would not be practical either to split sample into train and test parts or to spend the budget on collecting and updating a separate test sample, the cross-validation procedure is used to estimate the average accuracy of the surrogate models built with the given vector . The corresponding hyperparameter efficiency metric is calculated as follows:
where is the total number of cross-validation folds, is the coefficient of determination, is the test sample for the -th fold, and are the known and predicted objective values at the -th fold correspondingly, and is the mean of the known objective values at the -th fold.
Using the metric when solving the problem (3) requires building as many GP models for each vector as there are cross-validation iterations. Since building a GP model has complexity, where is the training sample size, the hyperparameter tuning process may become time consuming and unprofitable. In this article, it is proposed to develop new hyperparameter efficiency metrics that reduce the computational complexity of solving the problem (3) while maintaining the accuracy of solutions comparable to the metric .
2.3. Hyperparameter Prediction for a Bayesian Optimization Algorithm
Solving the problem (3) from scratch at each iteration of the Bayesian optimization is a straightforward but time-consuming approach to hyperparameter tuning. Modern approaches to parameter tuning or the selection of optimization algorithms involve combining ELA and ML to predict the most efficient algorithm or parameters for solving the base problem (1) [16,17]. The ELA-ML approach relies on the assumption that the best optimization algorithm or parameter values for solving similar optimization problems will also be nearly identical. The similarity of optimization problems can be estimated by a similarity measure between the corresponding ELA feature vectors.
Although many of the known ELA-ML approaches are developed for the best optimization algorithm selection, the same idea can be adapted for hyperparameter tuning the following way. The process of solving the problem (3) is divided into separate phases as is shown in Figure 3.
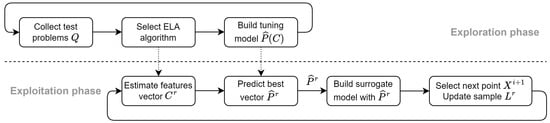
Figure 3.
Bayesian optimization with hyperparameter prediction.
Exploration phase—before solving the base problem (1):
- Define a representative set of test optimization problems , where is the number of test problems;
- Generate random training samples of different sizes , where is the number of samples for each problem ;
- For each sample , calculate the vector of ELA features and find the vector that is the best according to some metric by solving the problem (3);
- Build a tuning model using the set of known pairs , the total number of which is .
Exploitation phase—at step 2a of the Bayesian optimization algorithm:
- Calculate the vector of features using the current training sample ;
- Predict the best hyperparameter values using the tuning model built at step 4 of the exploration stage;
- Build the surrogate model using the current training sample and the vector of the predicted hyperparameter values.
The efficiency of hyperparameter prediction is generally defined by the set , the feature vector , and the metric . The exploration phase involves most of the computational expenses of solving the problem (3), which makes it practical to apply even costly metrics, such as the metric . As illustrated in Figure 3, the test problems set can be refined and extended permanently, even during the exploitation phase. New metrics are proposed in Section 3 to speed up the quality estimation of surrogate models for hyperparameter tuning and prediction. The efficiency of hyperparameter prediction with the metric and with the proposed new metrics will be examined in Section 4. The scope of the article does not include formation of a representative set of the test problems, or identification of the most suitable vector of ELA features.
3. Exploratory Landscape Validation
This section presents new metrics for estimating the efficiency of vector on a given sample . The new metrics evaluate not only the approximation accuracy of the surrogate models, as the metric does, but also certain properties of them that could be crucial for the optimization algorithm’s performance. Since the metrics are developed on the basis of an ELA algorithm, namely the variability map (VM) algorithm [12], we refer to them as exploratory landscape validation (ELV) metrics.
There are known metrics for estimating the quality of surrogate models that are not based on approximation accuracy and can, hence, be considered ELV metrics. For example, the ranking preservation (RP) metric [11], which we will refer to as , estimates the level of preservation of comparative relations between pairs of objective values approximated by the given surrogate model. According to the authors, the metric is calculated using an independent test sample of points, that is not practical to collect in the context of a strict budget for objective function evaluations. At the same time, when using interpolating approximation algorithms, such as GP, the metric value calculated for the training sample will be close to the maximum possible value. To be able to use the metric for hyperparameter tuning, an algorithm for generating an extended training sample is introduced in this paper. The proposed metrics, which are based on extended samples , are referred to as and . The metric is unique in the sense that it estimates the quality of surrogate models by directly comparing the VMs of those models with the VM of the training sample.
Section 3.1 starts with an improved algorithm for building a VM, followed by a discussion of VM quality assessment. Next, in Section 3.2, an algorithm for constructing an extended variability map (EVM) from a VM is suggested to enhance the reliability of landscape validation by extending the training sample. Based on that, new EVM-based landscape validation metrics and are proposed and explained in Section 3.3. Thus, the proposed ELV approach consists of the process of building VMs, extending VMs, and calculating values of one of the suggested metrics based on an extended training sample when solving the problem (3).
3.1. Variability Map of an Objective Function
VMs were first proposed to estimate ELA features of the function based on a given sample [12]. A VM is built by collecting a set of triples from the sample , where is the total number of triples. Each triple is composed of points that are neighboring in space. The triples for each point of sample are collected from all of its neighboring points. Two points are considered neighbors if the distance between them is less than the maximum distance between pairs of the closest points in sample , taken with some correction factor. Using the corresponding objective values of the collected triples, the pair of increment values is calculated. The values characterize increments of the objective function between pairs of points and respectively. The set of increment values then forms the VM and can be visually represented as a cloud of points on the plane , as shown in Figure 4.
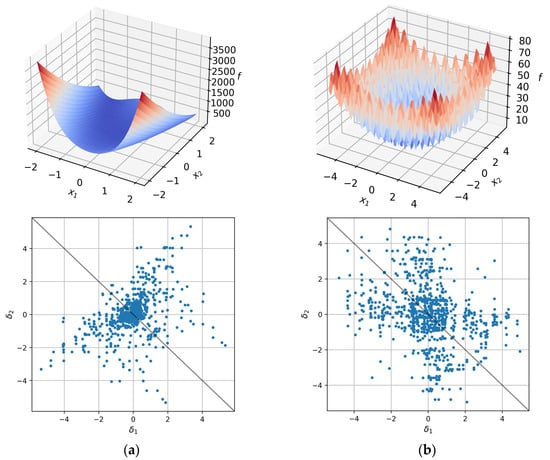
Figure 4.
Landscape plots and corresponding VMs for (a) Rosenbrock and (b) Rastrigin test optimization functions. VM’s increment values are represented by blue dots.
In cases where sample is irregular, such as when point density varies a great deal, using a max–min distance estimate for triple collecting, as suggested in [12], may not be a sustainable strategy. We propose a new algorithm for VM building based on angular ranges, which works better with irregular samples as well.
The new algorithm consists of the steps listed below:
- Select a random point from sample and find the closest point :where is the Euclidean distance between the points;
- Find all the points that satisfy the conditions:where is the mean distance from -th point to all the other points, is the angle formed by , , points in the space. The first condition is a quick check that reduces the number of points for which the angle needs to be calculated;
- For each angle range from the set of ranges , that is formed by splitting the range into three equal ranges, do the following:
- find a point that has the minimal distance in that angle range:
- extend the set of triples with a new one ;
- increase the distances and by a factor of 2 so that the other points are considered if is randomly selected in the next iterations.
- If the maximum number of triples is not reached, move to step 1.
The presented algorithm has several tunable parameters. The set of angle ranges is formed by splitting the range of allowed angles into three equal ranges. It is recommended to use a lower bound of at least 90 degrees as triples with smaller angles may not be informative for landscape analysis purposes [12]. At the same time the angle formed by a triple of points in the space is limited to 180 degrees. The number of splits determines the maximum number of triples to be collected for each considered point. It is recommended to increase the number of splits for bigger dimensions . Both the lower bound of the allowed angle range and the number of splits are tunable parameters of the algorithm. The maximum number of triples is another parameter of the algorithm that is usually set as the multiple of the total number of points , e.g., by multiplying by the number of angle ranges. Increasing the distance between the points in step 3c helps to avoid selecting the same points for the next triples. It is recommended to multiply the distance between and at least by 1.5 and completely remove from the neighbors (e.g., by setting the corresponding distance value to infinity).
In Figure 5, the difference between the old and the new algorithm for collecting VM triples based on an irregular sample of points is illustrated. The training sample of size is represented by black dots in the space with dimension . The points of the collected triples are connected by multicolor lines. It can be seen from the figure that the new algorithm provides better “coverage” of the space with the same number of triples. In Figure 5b, triples form connections between more distant points and fill the gaps in space caused by an irregular sample structure. The new algorithm generates triples with a lesser number of shared pairs of points, which is better for the landscape validation algorithm, further described below, and which is based on extended training samples.
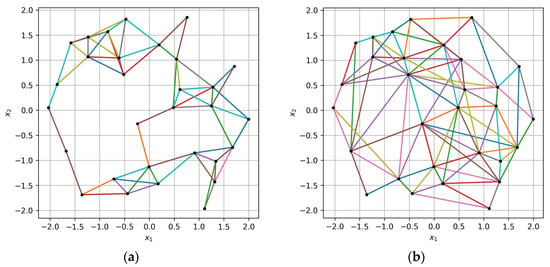
Figure 5.
Triples of points collected (a) based on the max–min distance between the points and (b) with the proposed algorithm based on angular ranges. Black dots represent the training sample points in space (), and multicolor lines connect the points of the collected triples.
The quality of a VM-building algorithm can be formally measured by the average distance between the points of the triples and average angles formed by those points. Formalizing the “coverage” quality and analyzing the connection between the quality of the VM and the efficiency of hyperparameter tuning or prediction is beyond the scope of this article.
3.2. Extended Variability Map of an Objective Function
A training sample-based landscape validation is not suitable for interpolation techniques like GP; at the same time, it is not practical to evaluate an expensive objective function for additional points in such cases. We propose the following method for extending the training sample using an extended version of a VM, built on that sample.
- Collect the set of triples as it was described in Section 3.1;
- For each triple , where , perform the following steps:
- split the vector into three parts by the points and , so that the points are arranged in the given order on the same line in space, where for the new points ;
- calculate the approximate objective values for the new points , respectively, using a linear interpolation between the known points ;
- update the training sample ;
- update the extended set of triples ;
- repeat steps a-d for the vector .
The set of triples and the corresponding increment values form the extended variability map (EVM). The EVM is based on an extended training sample , which includes the new points linearly interpolated between the points of triples . The examples of the original training sample and the extended sample , built with the proposed algorithm, are shown in Figure 6. It is clear from Figure 6b that the new points are placed along the triples of the original sample presented in Figure 6a.
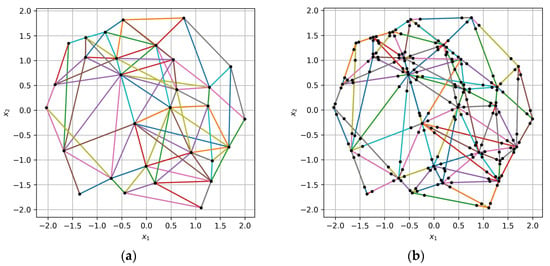
Figure 6.
The points and triples of the (a) original and (b) extended samples. Black dots represent points of the original and the extended training samples in space (), and multicolor lines connect the points of the collected triples.
Note that the set of triples does not include the original set , while the sample also includes the points from . It is recommended to locate the new points , closer to the points , e.g., by making logarithmic steps when splitting the vector , since it may positively affect the accuracy of landscape validation. The closer the new points are to the original ones, the stronger the requirements for the surrogate model to preserve comparative relations between pairs of those points.
In Figure 7, the VM of the original sample and the EMV of the extended sample can be seen. Since the new points are linearly interpolated, the additional points of the EVM (Figure 7b) are located on the diagonals and .
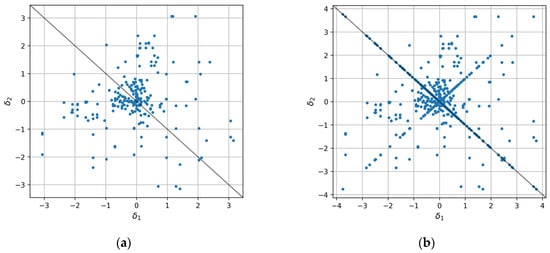
Figure 7.
VM plots for the (a) original and (b) extended samples. VM’s increment values are represented by blue dots.
3.3. Landscape Validation Metrics
To measure the landscape consistency between a surrogate model and the original sample using the extended training sample , the value of metric is calculated the following way:
- Build a surrogate model using the training sample and the vector of hyperparameter values;
- Using the model , calculate values for all the points of the extended sample , where . The corresponding values form the sample ;
- Given the samples and , that have the common values, calculate the ranking preservation metric:where is the result of the comparison of and values with the possible outcomes: less, equal, more.
Note that includes both the original values from L and the linearly interpolated values . The value of the metric in the range measures the ratio of pairwise comparisons of objective values that are preserved by the model .
Figure 8 shows an example of models with different levels of ranking preservation. The training sample points are shown in black, while the predicted model values are shown in blue. The highest level of ranking preservation is achieved for Model 1, shown in Figure 8a, as for any pair of points , in the given range the ranking preservation condition is met. Model 2 in Figure 8b is violating the rankings near the edge points of the training sample. Although Model 1 preserves the ranking better, both Model 1 and Model 2 will have the highest value of the metric when estimated based on the training sample only.
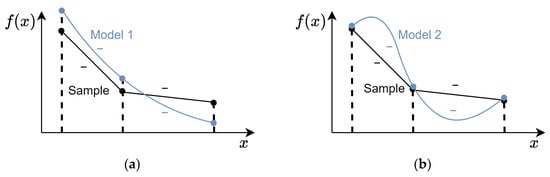
Figure 8.
Example of models with (a) high and (b) low ranking preservation levels, .
Figure 9 illustrates the idea of using the extended training sample to identify the level of ranking preservation. Although Model 2, shown in Figure 9b, has a better accuracy on the training sample, the violation of extra point ranking indicates that the model may not be suitable for optimization purposes. Although the metrics and are correlated, they are not identical, meaning that models with similar accuracy may preserve the landscape of the training sample differently.
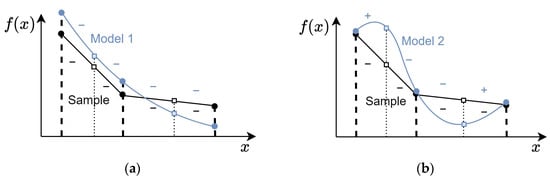
Figure 9.
Example of models with (a) high and (b) low ranking preservation levels for the extended training sample,
We propose another landscape validation metric , called the angular divergence (AD) of the EVM. The metric is based on the extended sample , the extended set of triples and the corresponding increment values . Instead of directly measuring the consistency of the model’s landscape using the original sample , it measures the consistency of the corresponding EVMs in the following way:
- Build a surrogate model using the training sample and the vector of hyperparameter values;
- Using the model , calculate values for all the points of the extended sample , where . The calculated values form the sample ;
- For all the triples from , calculate the increment values using the sample ;
- Assuming each pair of the increment values correspond to the vector in the space, and each pair of the values —to the vector , calculate the angular divergence metric based on the cosine similarity of the vectors and :where is a dot product of the corresponding vectors.
The metric is calculated as an average angle of rotation of EVM points around the central point of the plane. The rotation angle is determined by the model’s ability to preserve the ratio between the and values, and not the absolute magnitude of those values. In Figure 10, the example of the AD calculation of a single triple for models with different levels of ranking preservation is shown. Model 1, presented in Figure 10a, preserves the signs of the increment values, so the angle between the EVM points that correspond to the sample and the model is relatively small. Model 2, shown in Figure 10b, alters the sign of the second increment value, hence the angular divergence for the corresponding EVM point is around 90 degrees. The signs of both increments are altered by Model 3 shown in Figure 10c, which results in an even larger angular divergence. Figure 11 illustrates the angular divergence for the whole EVMs built for GP models with different values of the Matern kernel parameter. The extended sample increments are shown in black points, while the increments calculated for the models are shown in blue. The value of the metric of the first model shown in Figure 11a is lower than for the second model shown in Figure 11b (13 and 19 degrees on average, correspondingly).
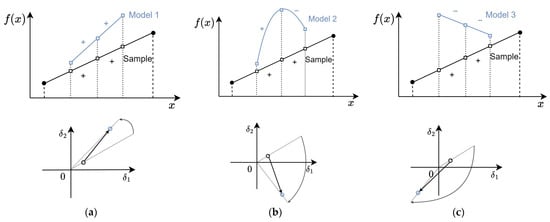
Figure 10.
Example of angular divergence of a single triple and the corresponding point on a VM for models with (a) high, (b) medium, and (c) low ranking preservation levels, .
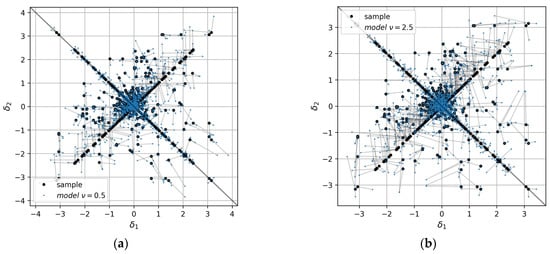
Figure 11.
EVMs of GP models with Matern kernel parameter (a) and (b) .
4. Computational Experiment
In this section, the results of computational experiments performed with the proposed landscape validation metrics are presented. The baseline is set by estimating the Bayesian optimization efficiency with fixed hyperparameter values. In the first experiment, the efficiency of Bayesian optimization with hyperparameter tuning based on different landscape validation metrics is estimated. The second experiment evaluates the efficiency of the hyperparameter prediction approach based on ELA-ML approach with different landscape validation metrics.
4.1. General Setup
The Bayesian optimization efficiency is estimated on the set of optimization problems that are based on the BBOB set of 24 test functions, that are widely used for optimization efficiency studies [20]. The BBOB set is accessed by using Python interface of the IOHexperimenter package [21]. Each function in the BBOB set is available for arbitrary dimensions and the numbers of so-called instances obtained by a random shift in space. The set of test optimization problems is composed of BBOB test functions that have dimensions and the fixed instance number. Hence the total number of test problems is .
To solve test problems , an open Python implementation of the Bayesian optimization algorithm in the ByesOpt package is used [22]. The surrogate models are built using the Matern kernel, which has a tunable parameter with a recommended value of specified in the package. The set of allowed values is fixed to for hyperparameter tuning and prediction. By default, the package uses the LCB acquisition function with to select the next point for objective evaluation [22].
The set of ELA features is used to categorize the test problems for hyperparameter prediction. The vector includes 41 features evaluated by the pFlacco package [23] and 43 features based on VM [12]. Only ELA features that are based on a fixed sample of points are used since additional objective evaluations are not permissible with a fixed computational budget. The ELA features that require cell mapping of the search space are also excluded. Due to the exponential growth of the total number of cells with the dimension , the sample sizes will not be sufficient for cell mapping feature calculation.
In the following sections, the method of solving the tuning problem (3) is referred to as a strategy of the Bayesian optimization algorithm. The efficiency of the following strategies is analyzed:
- Fixed vector —no hyperparameter tuning;
- Hyperparameter tuning with the considered metrics:
- -
- metric with 5 folds (see Equation (4) in Section 2.2);
- -
- metric (see Equation (8) in Section 3.3);
- -
- metric (see Equation (9) in Section 3.3).
- Predicted vector (see Section 2.3);
- The metrics and will be referred to as and respectively, to simplify the experiment description.
In the experiments, the efficiency of the Bayesian optimization algorithm with a given strategy is measured by the solution’s quality and by the computational cost of solving a test problem. The solution’s quality is determined by the best objective value found during the run. The computational cost is assessed by estimating the average time required to solve a test problem, which includes the time spent on building surrogate models and calculating values of the selected metric. Since test problems are used, the time spent on objective evaluation is negligible. The time required to build a tuning model is not taken into account when using the hyperparameter prediction strategy. The experiments were performed on a computer with an Intel E5-2643 processor.
4.2. Bayesian Optimization with Hyperparameter Tuning
To compare the efficiency of Bayesian optimization with fixed hyperparameter values and hyperparameter tuning, the experiment with the following steps is performed.
- For each problem with the objective function , generate the number of random initial samples , each sample of size ;
- Using each initial sample , perform iterations of the Bayesian optimization algorithm, as described in Section 2.1;
- Using each initial sample , perform iterations of the Bayesian optimization algorithm with hyperparameter tuning, as described in Section 2.2, with each of the following metrics: and . The best hyperparameter values are selected from the set ;
- Estimate the average of the best objective values found in 10 random runs with fixed hyperparameter values in step 2 and with hyperparameter tuning based on the metrics and in step 3:where is the best objective value found for the problem in the -th run;
- For each problem select the metric with which the best objective value was found on average.
In the described experiment, each of the 72 test optimization problems was solved using 10 random initial samples and four different strategies with the computational budget −2880 runs of the Bayesian optimization algorithm in total.
4.3. Bayesian Optimization with Hyperparameter Prediction
The experiment aims to measure the efficiency of using the hyperparameter prediction approach based on the ELA-ML framework by performing the following steps for each optimization problem , . The experiment is split into exploration and exploitation phases as it is described in Section 2.3.
Exploration phase—evaluate ELA features, find the best hyperparameter values:
- Remove problems from the set that are based on the same BBOB function as the current problem , including those with different dimensions , so that the remaining problems compose the set ;
- For each problem generate the random samples with different sizes . Within the given range, 20 sample sizes are chosen and 15 random samples of each size are generated in ;
- For each sample calculate the vector of ELA features Ck,s, where and find the best hyperparameter values by solving the problem (3) with the set of allowed values . As the hyperparameter efficiency metric use the metric , which showed the best performance for the problem in Section 4.2;
- Use the set of pairs as a training sample to build a tuning model by using the random forest classifier implemented in the scikit-learn package [24].
Exploitation phase—use the tuning model for hyperparameter prediction:
- For the current problem , generate the number of random initial samples , each sample of size ;
- Using each initial sample perform iterations of the Bayesian optimization algorithm with hyperparameter prediction by using the tuning model , as described for the exploitation phase in Section 2.3;
- Estimate the average of the best objective values found in 10 random runs with hyperparameter prediction.
Each tuning model is built using 20,700 pairs of observations, all of which are collected for problems based on different BBOB functions. The experiment is structured in such a way that it is comparable to the cross-validation procedure. Each problem is excluded from the exploration phase to build a tuning model and is solved during the exploitation phase with the hyperparameter values predicted by that model. The hyperparameter values are predicted based on the ELA features similarity between the problem and the set of problems analyzed during the exploration phase. In our case, the accuracy of hyperparameter prediction for a particular problem depends, among other factors, on the presence of BBOB functions with a similar landscape in the set .
4.4. Experimental Results
The results of the first experiment are summarized in Table 1. For each problem , the best strategy is selected that provides the best value . For each considered strategy, the table shows the number of problems where the best result was found while using that strategy. It should be noted that for certain test problems, such as with the linear slope objective function, multiple strategies were able to find the optimal solution.

Table 1.
The number of best-solved problems with the fixed hyperparameter value and the hyperparameter tuning approach using different metrics.
With the fixed hyperparameter values, the number of best-solved problems is the lowest, as expected. Using the proposed metrics for hyperparameter tuning leads to the best results on a wider range of problems. Based on the results, it can be assumed that different problems require different approaches to hyperparameter tuning, i.e., different metrics.
Table 2 summarizes the results of the second experiment in the same manner. On top of that, the average of the best-found values and the average time required to solve a test problem are provided. Since the scale of objective values of the test problems vary a great deal, the best-found values were normed to the range , so that 0 and 1 correspond to the best and worst values found for the problem in all the runs with different strategies.

Table 2.
The experimental results with the fixed hyperparameter value, the hyperparameter tuning approach using different metrics and the hyperparameter prediction approach.
It is evident that the proposed hyperparameter prediction approach provides the best results for a larger number of problems. The metric that requires cross-validation of the surrogate models is the most time-consuming but also the most accurate metric. However, with the proposed metrics and the results of comparable quality can be found with over 50% less effort. By using the hyperparameter prediction strategy, the problems can be solved with even less time (up to 70%), while the quality of the results is about 5% better than for the most accurate metric .
When benchmarking optimization algorithms, average efficiency estimates are often not sufficient for making informed conclusions. Figure 12 presents the experimental results in the form of so-called performance profiles [25]. The performance profile of each strategy is constructed by calculating the number of test problems with a better value for all possible values . As a result, the performance profile plot shows the number of test problems as a function of the quality of the solution. For example, the two most effective strategies for finding near-best values use the fixed vector and hyperparameter tuning with the metric . Figure 13 presents the same performance profiles for all the algorithm runs with random initial samples (10 random runs for each of the 72 problems).
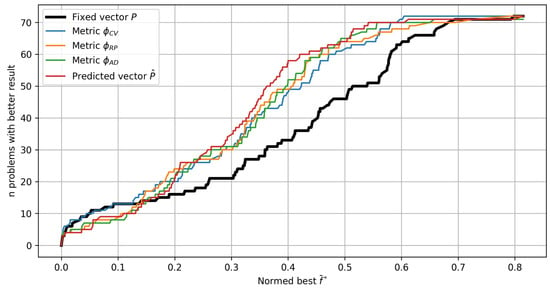
Figure 12.
Performance profile plots for different strategies of Bayesian optimization: the number of test problems solved with better values .
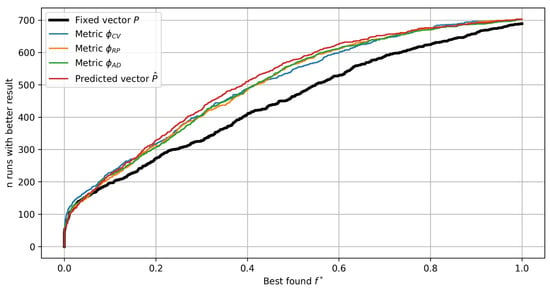
Figure 13.
Performance profile plots for different strategies of Bayesian optimization: the number of runs with better values .
In Figure 14 the performance profile plots are shown for the number of test problems as a function of the time required to solve a problem. It can be clearly seen that the plot has «jumping» segments due to the time difference between solving the problems of different dimensions . The computational complexity grows with the problem dimension slower for the metric than for the metric . The hyperparameter prediction strategy is relatively expensive for smaller dimensions due to the computational costs involved in estimating the features vector and evaluating the tuning model . Using the fixed vector and selecting hyperparameter values with the metric are obviously the strategies with the best and the worst time efficiency, respectively. Figure 15 presents the same performance profiles for all the algorithm runs with random initial samples (10 random runs for each of the 72 problems).
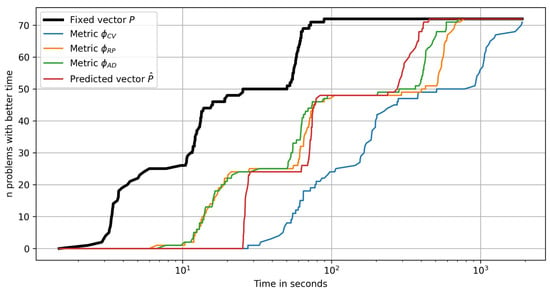
Figure 14.
Performance profile plots for different Bayesian optimization strategies: the number of test problems solved in less time.
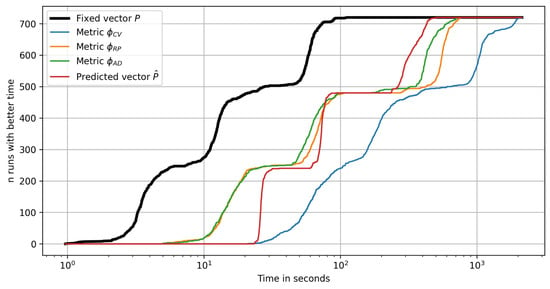
Figure 15.
Performance profile plots for different Bayesian optimization strategies: the number of runs completed in less time.
5. Discussion
The presented exploratory landscape validation approach enables the finding pf effective hyperparameter values without relying on approximation accuracy estimations of surrogate models. In cases of limited computational budget and hence relatively small training samples, landscape validation metrics provide a faster way to estimate the efficiency of hyperparameter values. The presented metrics summarize the essential differences between the landscapes of surrogate models and training samples, that are generally characterized by ELA features. The study, however, has the following potential limitations. The experiments were performed with test optimization problems, but the applicability of the proposed metrics is mainly determined by the computational complexity of objective evaluation and hence the computational budget. In the event of a higher complexity of objective evaluation and relatively small budget, the computational impact even of the cross-validation metric may become negligible. On the other hand, if the budget is large enough, the increase in the optimization algorithm’s efficiency may not be sufficient to justify the computational cost of hyperparameter tuning with any of the considered metrics. Analyzing applicability conditions for different tuning strategies when solving practical optimization problems could be the focus of future research. It is also promising to explore other ways of estimating the level of landscape feature preservation by surrogate models based on the known ELA methods, for example, by direct comparison of ELA feature vectors. Landscape validation can be based on various ways of measuring the differences between the variability maps of samples and surrogate models.
It was shown that landscape validation metrics can be used to both find and predict the best hyperparameter values during Bayesian optimization. Another potential extension of this work is to analyze the efficiency of hyperparameter prediction with different ELA algorithms and approximation algorithms used for building a tuning model. The efficiency of hyperparameter prediction is also affected by the level of similarity between the problems being solved at exploration and exploitation phases, which is difficult to formalize. One possible approach would be to use the ELA features of the test problem set to define the region of allowed feature values for the exploitation-phase problems. If the new problem has unrelated feature values, then the efficiency of the predicted hyperparameter values cannot be guaranteed; therefore, the default hyperparameter values should be used for that problem. In such cases, the test problem set should be refined to keep it representative of the problems solved during the exploitation phase.
6. Conclusions
The article considers different approaches to improving the efficiency of Bayesian optimization algorithms by selecting the best hyperparameter values of the surrogate modeling algorithm. The optimal vector of hyperparameter values is found based on a hyperparameter efficiency metric, which defines the way of measuring the quality of a surrogate model built with different vectors. The hyperparameter tuning problem is being solved at each iteration of Bayesian optimization, so using computationally demanding metrics may lead to a significant increase in the time spent solving the problem.
When solving computationally expensive optimization problems, the number of objective evaluations allowed is relatively small, as well as the size of the training sample for building a surrogate model. The commonly used efficiency metric for such cases is the cross-validation score, which requires building multiple surrogate models on different subsets of the training sample. In this article, a new approach is introduced called exploratory landscape validation (ELV), which includes the proposed hyperparameter efficiency metrics to assess the quality of surrogate models without considering the approximation error estimates. The experiments showed that hyperparameter tuning with the new metrics can provide solutions of comparable quality with less than half the time required when using the cross-validation metric. The experimental results also indicate that different metrics provide the best solutions for different optimization problems.
Another way of reducing the costs of hyperparameter tuning is to build a model that predicts the best hyperparameter values during Bayesian optimization based on ELA features estimated from the training sample. The hyperparameter prediction approach is based on collecting a test set of problems, estimating the ELA features of those problems, finding the best hyperparameter values according to an efficiency metric, and building a tuning model. In general, each optimization problem has its own best-suited efficiency metric for hyperparameter tuning. In the computational experiment, the tuning models are built to predict the hyperparameter values that are most effective according to the metrics chosen individually for each test optimization problem. With the suggested hyperparameter prediction approach and individual efficiency metrics, better-quality solutions were found in less than 70% of the time needed by a hyperparameter tuning approach based on cross-validation score. Even though additional computational expenses are required to create a tuning model, they are insignificant when compared to potential permanent improvement in the optimization algorithm’s efficiency.
Author Contributions
Conceptualization, A.K. and T.A.; methodology, A.K.; software, T.A.; validation, T.A.; formal analysis, T.A.; investigation, T.A.; writing—original draft preparation, T.A.; writing—review and editing, T.A.; visualization, T.A.; supervision, A.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The source code and the results of the computational experiments are openly available at https://github.com/agataleh/boela_bench (accessed on 6 January 2024).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alizadeh, R.; Allen, J.K.; Mistree, F. Managing computational complexity using surrogate models: A critical review. Res. Eng. Des. 2020, 31, 275–298. [Google Scholar] [CrossRef]
- Palar, P.S.; Liem, R.P.; Zuhal, L.R.; Shimoyama, K. On the use of surrogate models in engineering design optimization and exploration: The key issues. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; Association for Computing Machinery: New York, NY, USA; pp. 1592–1602. [Google Scholar]
- Jariego Perez, L.C.; Garrido Merchan, E.C. Towards Automatic Bayesian Optimization: A first step involving acquisition functions. In Proceedings of the 19th Conference of the Spanish Association for Artificial Intelligence, Advances in Artificial Intelligence, Malaga, Spain, 22–24 September 2021; Springer: Cham, Switzerland; pp. 160–169. [Google Scholar]
- Gan, W.; Ji, Z.; Liang, Y. Acquisition functions in Bayesian optimization. In Proceedings of the 2nd International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE), Zhuhai, China, 24–26 September 2021; IEEE: Piscataway Township, NJ, USA; pp. 129–135. [Google Scholar]
- Palar, P.S.; Parussini, L.; Bregant, L.; Shimoyama, K.; Zuhal, L.R. On kernel functions for bi-fidelity Gaussian process regressions. Struct. Struct. Multidiscip. Multidiscip. Optim. Optim. 2023, 66, 37. [Google Scholar] [CrossRef]
- Yu, H.; Tan, Y.; Sun, C.; Zeng, J. A comparison of quality measures for model selection in surrogate-assisted evolutionary algorithm. Soft Comput. Comput. 2019, 23, 12417–12436. [Google Scholar] [CrossRef]
- Bischl, B.; Binder, M.; Lang, M.; Pielok, T.; Richter, J.; Coors, S.; Thomas, J.; Ullmann, T.; Becker, M.; Boulesteix, A.L.; et al. Hyperparameter optimization: Foundations, algorithms, best practices, and open challenges. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2023, 13, e1484. [Google Scholar] [CrossRef]
- Williams, C.K.I.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 4, pp. 83–89. [Google Scholar]
- Bhosekar, A.; Ierapetritou, M. Advances in surrogate based modeling, feasibility analysis, and optimization: A review. Comput. Comput. Chem. Chem. Eng. Eng. 2018, 108, 250–267. [Google Scholar] [CrossRef]
- Garbo, A.; German, B.J. Performance assessment of a cross-validation sampling strategy with active surrogate model selection. Struct. Multidiscip. Optim. 2019, 59, 2257–2272. [Google Scholar] [CrossRef]
- Diaz-Manriquez, A.; Toscano, G.; Coello Coello, C.A. Comparison of metamodeling techniques in evolutionary algorithms. Soft Comput. 2017, 21, 5647–5663. [Google Scholar] [CrossRef]
- Agasiev, T.A. Characteristic feature analysis of continuous optimization problems based on Variability Map of objective function for optimization algorithm configuration. Open Comput. Sci. 2020, 10, 97–111. [Google Scholar] [CrossRef]
- Škvorc, U.; Eftimov, T.; Korošec, P. Understanding the problem space in single-objective numerical optimization using exploratory landscape analysis. Appl. Soft Comput. 2020, 90, 106138. [Google Scholar] [CrossRef]
- Renau, Q.; Doerr, C.; Dreo, J.; Doerr, B. Exploratory landscape analysis is strongly sensitive to the sampling strategy. In Proceedings of the 16th International Conference on Parallel Problem Solving from Nature, Leiden, The Netherlands, 5–9 September 2020; Springer: Cham, Switzerland; pp. 139–153. [Google Scholar]
- Kerschke, P.; Preuss, M. Exploratory landscape analysis. In Proceedings of the Companion Conference on Genetic and Evolutionary Computation, Lisbon, Portugal, 15–19 July 2023; Association for Computing Machinery: New York, NY, USA; pp. 990–1007. [Google Scholar]
- Saini, B.S.; López-Ibáñez, M.; Miettinen, K. Automatic surrogate modelling technique selection based on features of optimization problems. In Proceedings of the Genetic and Evolutionary Computation Conference Companion, Prague, Czech Republic, 13–17 July 2019; Association for Computing Machinery: New York, NY, USA; pp. 1765–1772. [Google Scholar]
- Kerschke, P.; Trautmann, H. Automated algorithm selection on continuous black-box problems by combining exploratory landscape analysis and machine learning. Evol. Comput. 2019, 27, 99–127. [Google Scholar] [CrossRef] [PubMed]
- Viana, F.A.; Venter, G.; Balabanov, V. An algorithm for fast optimal Latin hypercube design of experiments. Int. J. Numer. Methods Eng. 2010, 82, 135–156. [Google Scholar] [CrossRef]
- Wang, X.; Jin, Y.; Schmitt, S.; Olhofer, M. Recent advances in Bayesian optimization. ACM Comput. Surv. 2023, 55, 1–36. [Google Scholar] [CrossRef]
- Varelas, K.; El Hara, O.A.; Brockhoff, D.; Hansen, N.; Nguyen, D.M.; Tušar, T.; Auger, A. Benchmarking large-scale continuous optimizers: The bbob-largescale testbed, a COCO software guide and beyond. Appl. Soft Comput. 2020, 97, 106737. [Google Scholar] [CrossRef]
- de Nobel, J.; Ye, F.; Vermetten, D.; Wang, H.; Doerr, C.; Bäck, T. Iohexperimenter: Benchmarking platform for iterative optimization heuristics. Evol. Comput. 2023, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Nogueira, F. Bayesian Optimization: Open Source Constrained Global Optimization Tool for Python. 2014. Available online: https://github.com/bayesian-optimization/BayesianOptimization (accessed on 6 December 2023).
- Prager, R.P.; Trautmann, H. Pflacco: Feature-Based Landscape Analysis of Continuous and Constrained Optimization Problems in Python. Evol. Comput. 2023, 1–25. [Google Scholar] [CrossRef] [PubMed]
- Hao, J.; Ho, T.K. Machine learning made easy: A review of scikit-learn package in python programming language. J. Educ. Behav. Stat. 2019, 44, 348–361. [Google Scholar] [CrossRef]
- Moré, J.J.; Wild, S.M. Benchmarking derivative-free optimization algorithms. SIAM J. Optim. 2009, 20, 172–191. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).