On Unicyclic Graphs with Minimum Graovac–Ghorbani Index

Abstract

In discrete mathematics, graph theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects. Chemical graph theory is concerned with non-trivial applications of graph theory to the solution of molecular problems. Its main goal is to use numerical invariants to reduce the topological structure of a molecule to a single number that characterizes its properties. Topological indices are numerical invariants associated with the chemical constitution, for the purpose of the correlation of chemical structures with various physical properties, chemical reactivity, or biological activity. They have found important application in predicting the behavior of chemical substances. The Graovac–Ghorbani ($AB{C}_{GG}$) index is a topological descriptor that has improved predictive potential compared to analogous descriptors. It is used to model both the boiling point and melting point of molecules and is applied in the pharmaceutical industry. In the recent years, the number of publications on its mathematical properties has increased. The aim of this work is to partially solve an open problem, namely to find the structure of unicyclic graphs that minimize the $AB{C}_{GG}$ index. We characterize unicyclic graphs with even girth that minimize the $AB{C}_{GG}$ index, while we also present partial results for odd girths. As an auxiliary result, we compare the $AB{C}_{GG}$ indices of paths and cycles with an odd number of vertices.

1. Introduction

Let G be a simple connected undirected graph of order $n=\left|V\right(G\left)\right|$ and size $m=\left|E\right(G\left)\right|$. The degree $d\left(v\right)$ of a vertex $v\in V\left(G\right)$ is the number of vertices adjacent to v. We write $d_G\left(v\right)$ if we want to emphasize the graph G in which the degree of a vertex v is considered. The distance $d(u,v)$ between the vertices u and v is defined as the number of edges on the shortest path connecting u and v. In chemical graph theory, a graph is used to represent a molecule by considering the atoms as the vertices of the graph and the molecular bonds as the edges.

Molecular descriptors can be defined as mathematical representations of molecular properties generated by algorithms. The numerical values of molecular descriptors are used to quantitatively describe the physical and chemical information of molecules. Topological descriptors are molecular descriptors [1] that serve as a tool for the compact and effective description of structural formulas used to study and predict the structure-property correlation of organic compounds [2,3,4]. Countless applications of topological indices have been reported, most of which are related to the study of medical and pharmacological issues.

The best known topological index seems to be the Randić connectivity index [5], which has numerous applications in chemistry and pharmacology, with a profound mathematical background. A quite successful descendant of the Randić index is the atom–bond connectivity ($ABC\left(G\right)$) index introduced by Estrada et al. in 1998 [6], as follows

$$ABC\left(G\right)=\sum _{uv\in E\left(G\right)}\sqrt{\frac{d\left(u\right)+d\left(v\right)-2}{d\left(u\right)d\left(v\right)}}.$$

According to Furtula [7], the $ABC$ index is one of the best degree–based molecular descriptors.

In 2010, Graovac and Ghorbani defined a new version of the atom-bond connectivity index, a distance-based topological descriptor known as the Graovac–Ghorbani ($AB{C}_{GG}$) index [8]. It is defined as

$$AB{C}_{GG}\left(G\right)=\sum _{uv\in E\left(G\right)}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}},$$

(1)

where $n_u$ is the number of vertices that are closer to the vertex u than to vertex v, and $n_v$ is the number of vertices that are closer to v than to u. It was pointed out in [7] that the $AB{C}_{GG}$ index provides significantly better correlations than the atom–bond connectivity index for certain physico-chemical properties. In recent years, the mathematical properties of the $AB{C}_{GG}$ index [9,10,11,12,13,14] have been intensively studied in the literature. Recently, a survey of the $AB{C}_{GG}$ index was presented in [15], which included a complete bibliography for future research. Its recentness and the current knowledge on the $AB{C}_{GG}$ index suggest that there are many opportunities for further research into its properties.

For many types of graphs, extreme values of the $AB{C}_{GG}$ index are unknown. In 2013, Das et al. [16] found maximum values of the $AB{C}_{GG}$ index for unicyclic graphs, while the problem of finding minimum values for the same class of graphs has remained open. Throughout this paper, we investigate the properties of the $AB{C}_{GG}$ index in unicyclic graphs. We characterize unicyclic graphs with even girth that minimize the $AB{C}_{GG}$ index, while we present partial results for odd girth. As an auxiliary result, we compare the $AB{C}_{GG}$ indices of paths and cycles with an odd number of vertices. Our study is significant because it partially solves an open problem regarding the $AB{C}_{GG}$ index of unicyclic graphs using new mathematical results related to this quantity, which can be applied to other types of graphs.

2. Preliminaries

We present two lemmas related to summands in the definition (1) of the $AB{C}_{GG}$ index.

Lemma 1.

Let $f:{\mathbb{N}}^2\to \mathbb{R}$ be a function defined by $f(x,y)=\sqrt{\frac{x+y-2}{xy}}.$ Then

(i) 

$f(x,y)=f(y,x)\ge 0$, $\forall (x,y)\in {\mathbb{N}}^2$;

(ii) 

$f(x,1)<1$, $\forall x\in \mathbb{N}$, $f(2,1)=\sqrt{1/2}$ and $f(x,1)$ is a strictly increasing function of x;

(iii) 

For $x\ge 2$ and $y\ge 2$ it holds $f(x,y)\le \sqrt{1/2}$ and f is a decreasing function, i.e., $\forall (x,y),(x^{\prime },y^{\prime })\in {\mathbb{N}}^2$ it holds

$$(x\le x^{\prime }andy\le y^{\prime })\Rightarrow f(x,y)\ge f(x^{\prime },y^{\prime });$$

(iv) 

For $x\ge 2$, $y\ge 2$, $t\in \mathbb{N}$ and $y>t$ it holds $f(x,y)\ge f(x+t,y-t)$ if and only if $y-x\ge t$.

Proof. 

Let $g:{\mathbb{N}}^2\to \mathbb{R}$ be a function defined by $g(x,y)=\frac{x+y-2}{xy}.$ Then, $f(x,y)=\sqrt{g(x,y)}$, i.e., f is monotonic transformation of g (if g increases (decrases), then f increases (decreases)). Notice that g (f) is a symmetric function. It is easy to prove that claims $\left(i\right)$ and $\left(ii\right)$ hold for g, and consequently for (f). $\left(iii\right)$ Let $r,t\in {\mathbb{N}}_0$ and $x,y\ge 2$. Then

$$\begin{array}{cc}\hfill g(x,y)-g(x+t,y+r)& =\frac{x+y-2}{xy}-\frac{x+t+y+r-2}{(x+t)(y+r)}\hfill \\ \hfill & =\frac{rx(x-2)+ty(y-2)+tr(x+y-2)}{xy(x+t)(y+r)}\hfill \\ \hfill & \ge 0.\hfill \end{array}$$

Therefore, $f(x,y)\ge f(x+t,y+r)$ and $f(2,2)=1/\sqrt{2}$. $\left(iv\right)$ Let $t\in \mathbb{N}$, $x,y\ge 2$ and $y>t$. Then,

$$\begin{array}{cc}\hfill g(x,y)-g(x+t,y-t)& =\frac{x+y-2}{xy}-\frac{x+t+y-t-2}{(x+t)(y-t)}\hfill \\ \hfill & =\frac{t(x+y-2)(y-x-t)}{xy(x+t)(y-t)}.\hfill \end{array}$$

We conclude that g decreases if and only if $y\ge x+t$. Therefore, $f(x,y)\ge f(x+t,y-t)$ if and only if $y\ge x+t$. □

Throughout this paper, for $uv\in E\left(G\right)$ and the numbers $n_u$ and $n_v$ defined as in (1), $f(n_u,n_v)$ is called the gg-value of $uv$.

Lemma 2.

For $n\ge 5$, we have

$$2\sqrt{\frac{n-3}{n-2}}>\sqrt{\frac{n-2}{n-1}}+\sqrt{\frac{1}{2}}.$$

(2)

Proof. 

Cases $n=5$ and $n=6$ can be checked directly. Let $n\ge 7$. Both sides of inequality (2) are increasing functions of n. For $n\ge 7$, we have $2\sqrt{\frac{n-3}{n-2}}\ge 1.7889$ and $\sqrt{\frac{1}{2}}+\sqrt{\frac{n-2}{n-1}}<\sqrt{\frac{1}{2}}+1=1.7071$. Therefore,

$$\underset{n\ge 7}{min}2\sqrt{\frac{n-3}{n-2}}>\underset{n\ge 7}{sup}\left(\sqrt{\frac{1}{2}}+\sqrt{\frac{n-2}{n-1}}\right)$$

and this completes the proof. □

3. Main Results

Paths and cycles are fundamental concepts in graph theory, often considered as subgraphs of other graphs [17]. A path graph $P_n$ is a graph whose vertices can be listed in the order $1,2,\dots ,n$, so that the edges are $\{i,i+1\}$ for $i=1,\dots ,n-1$. The cycle graph $C_n$ is derived from $P_n$ by connecting vertices 1 and n using an edge. A unicyclic graph G is a connected graph with exactly one cycle. This implies $\left|E\right(G\left)\right|=n$. We now compare the $AB{C}_{GG}$ indices for paths and cycles.

3.1. Graovac–Ghorbani Index of Paths and Cycles

In 2014, Rostami and Sohrabi-Haghighat found trees that minimize the $AB{C}_{GG}$ index.

Theorem 1

([18]). The path $P_n$ is the $n-$vertex tree with the minimum Graovac–Ghorbani index.

The Graovac–Ghorbani index of a path $P_n$ is given by the following formula:

$$AB{C}_{GG}\left(P_n\right)=\sum _{i=1}^{n-1}\sqrt{\frac{n-2}{i(n-i)}},$$

which can be written as

$$AB{C}_{GG}\left(P_n\right)=\left\{\begin{array}{c}2·{\displaystyle \sum _{i=1}^{\frac{n-1}{2}}}\sqrt{\frac{n-2}{i(n-i)}}, \mathrm{for} n \mathrm{odd},\hfill \\ 2·{\displaystyle \sum _{i=1}^{\frac{n}{2}-1}}\sqrt{\frac{n-2}{i(n-i)}}+\frac{2\sqrt{n-2}}{n}, \mathrm{for} n \mathrm{even}.\hfill \end{array}\right.$$

From part $\left(iv\right)$ of Lemma 1, we can observe that the gg-values of the edges in $P_n$ decrease as we move from pendant edges to the central one (ones). For an even n, the smallest gg-value is obtained for a single central edge and is equal to $f(n/2,n/2)=2\frac{\sqrt{n-2}}{n}$, while for n odd, we have two central edges with the smallest gg-value $f((n-1)/2,(n+1)/2)=2\sqrt{\frac{n-2}{n^2-1}}$.

In a cycle graph $C_n$, all edges have the same gg-value. For n even, this is $\sqrt{\frac{n-2}{\frac{n^2}{4}}}=\frac{2}{n}$, while for n odd, we have $\sqrt{\frac{n-3}{\frac{{(n-1)}^2}{4}}}=\frac{2\sqrt{n-3}}{n-1}$. Therefore,

$$AB{C}_{GG}\left(C_n\right)=\left\{\begin{array}{c}2\sqrt{n-2}, \mathrm{for} n\mathrm{even},\hfill \\ \frac{2n\sqrt{n-3}}{n-1}, \mathrm{for} n \mathrm{odd}.\hfill \end{array}\right.$$

In [10], Dimitrov et al. investigated the $AB{C}_{GG}$ index of bipartite graphs. As an auxiliary result, they established that $AB{C}_{GG}\left(P_n\right)>AB{C}_{GG}\left(C_n\right)$ for all even $n\ge 8$, while for $n\in \{4,6\}$, it holds $AB{C}_{GG}\left(P_n\right)<AB{C}_{GG}\left(C_n\right)$. Here, we examine the case where n is odd. For this purpose, we need several auxiliary results.

Lemma 3.

For $n\ge 3$ and $i=1,\dots ,\lfloor \frac{n}{2}\rfloor$ it holds

$$2\sqrt{\frac{n-2}{i(n-i)}}>\sqrt{\frac{n-1+i}{i}}·2\sqrt{\frac{n-3}{n(n-2)}}.$$

(3)

Proof. 

Let us prove that $4\frac{n-2}{i(n-i)}>\frac{n-1+i}{i}·\frac{4(n-3)}{n(n-2)}$, that is

$$n{(n-2)}^2>(n-3)(n-i)(n+i-1).$$

(4)

By expanding and simplifying both sides of (4), we obtain $n>i(i-1)(3-n)$, which holds for any $n\ge 3$. Therefore, the inequality (4) and consequently (by taking square roots) (3) holds. □

Lemma 4.

For odd $n\ge 11$ it holds

$$\sum _{i=1}^{\frac{n-1}{2}}\sqrt{\frac{n-1+i}{i}}>n.$$

(5)

Proof. 

Numerical calculations show that for n odd, $11\le n\le 23$ inequality holds. Let $n\ge 25$. Then, $n=2t+1$, $t\ge 12$ and inequality (5) can be written as

$$\sum _{i=1}^t\sqrt{\frac{2t+i}{i}}>2t+1.$$

(6)

It is easy to see that $\sqrt{\frac{2t+i}{i}}$ is a decreasing function of i. Therefore, all summands in (6) are decreasing and the last one is equal to $\sqrt{3}$. Next, we notice that $\sqrt{\frac{2t+i}{i}}<2\iff 2t/3<i\le t$. Similarly, $\sqrt{\frac{2t+i}{i}}<3\iff i>t/4$. Bearing in mind that $i\in \mathbb{N}$, we have

$$\begin{array}{cc}\hfill \sqrt{3}\le \sqrt{\frac{2t+i}{i}}<2,& \mathrm{for}⌊2t/3⌋<i\le t,\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill 2\le \sqrt{\frac{2t+i}{i}}<3& \mathrm{for}⌊t/4⌋<i\le ⌊2t/3⌋,\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill \sqrt{\frac{2t+i}{i}}\ge 3,& \mathrm{for}1\le i\le ⌊t/4⌋.\hfill \end{array}$$

(9)

Let $t=k\left(\mathrm{mod}3\right)$, $k\in \{0,1,2\}$ and $t=l\left(\mathrm{mod}4\right)$, $l\in \{0,1,2,3\}$. Then, $⌊2t/3⌋=2(t-k)/3$, $⌊t/4⌋=(t-l)/4$ and inequalities (7)–(9) imply

$$\begin{array}{cc}\hfill \sum _{i=1}^t\sqrt{\frac{2t+i}{i}}& >\left(t-\frac{2(t-k)}{3}\right)\sqrt{3}+\left(\frac{2(t-k)}{3}-\frac{t-l}{4}\right)2+\frac{t-l}{4}3\hfill \\ \hfill & =2t+\frac{(4\sqrt{3}-5)t-8(2-\sqrt{3})k-3l}{12}.\hfill \end{array}$$

(10)

Notice that (10) is larger than $2t+1$ if and only if

$$(4\sqrt{3}-5)t-8(2-\sqrt{3})k-3l>12.$$

(11)

If we analyze the inequality (11) for each of the 12 possible pairs $(k,l)$, we come to the conclusion that it holds for $t\ge 12$. The results are summarized in Table 1 and the proof is complete. □

Table 1. Values of t for $k\in \{0,1,2,3\}$ and $l\in \{0,1,2\}$ in the proof of Lemma 4.

$(\mathit{k},\mathit{l})$	t	$(\mathit{k},\mathit{l})$	t	$(\mathit{k},\mathit{l})$	t
$(0,0)$	$12,24,36,48,\dots$	$(1,0)$	$16,28,40,52,\dots$	$(2,0)$	$20,32,44,56,\dots$
$(0,1)$	$21,33,45,57\dots$	$(1,1)$	$13,25,37,49,\dots$	$(2,1)$	$17,29,41,53,\dots$
$(0,2)$	$18,30,42,54,\dots$	$(1,2)$	$22,34,46,58,\dots$	$(2,2)$	$14,26,38,50,\dots$
$(0,3)$	$15,27,39,51,\dots$	$(1,3)$	$19,31,43,55,\dots$	$(2,3)$	$23,35,47,59,\dots$

Now, we are ready to prove the main result.

Theorem 2.

For $4\le n\le 7$ it holds $AB{C}_{GG}\left(P_n\right)<AB{C}_{GG}\left(C_n\right)$, while for $n=3$ and for $n\ge 8$ we have $AB{C}_{GG}\left(P_n\right)>AB{C}_{GG}\left(C_n\right)$.

Proof. 

As we mentioned above, for n even, $n\ge 4$ inequalities were proven in [10]. For $n=3$, $AB{C}_{GG}\left(C_3\right)=0<\sqrt{2}=AB{C}_{GG}\left(P_3\right)$. Inequality $AB{C}_{GG}\left(P_n\right)<AB{C}_{GG}\left(C_n\right)$ can be checked directly for $n\in \{5,7,9\}$. Let $n\ge 11$, n odd. From Lemmas 3 and 4, it follows that

$$\begin{array}{cc}\hfill AB{C}_{GG}\left(P_n\right)& =2\sum _{i=1}^{\frac{n-1}{2}}\sqrt{\frac{n-2}{i(n-i)}}\hfill \\ \hfill & >\sum _{i=1}^{\frac{n-1}{2}}\sqrt{\frac{n+i-1}{i}}·2\sqrt{\frac{n-3}{n(n-2)}}\hfill \\ \hfill & >\sum _{i=1}^{\frac{n-1}{2}}\sqrt{\frac{n+i-1}{i}}·2\sqrt{\frac{n-3}{{(n-1)}^2}}\hfill \\ \hfill & >2n\frac{\sqrt{n-3}}{n-1}=AB{C}_{GG}\left(C_n\right).\hfill \end{array}$$

□

Graovac–Ghorbani indices of $P_n$ and $C_n$ for some n are presented in Table 2.

Table 2. Numerical values of Graovac–Ghorbani indices of $P_n$ and $C_n$, $3\le n\le 12$.

n	${\mathit{ABC}}_{\mathit{GG}}\left({\mathit{P}}_{\mathit{n}}\right)$	${\mathit{ABC}}_{\mathit{GG}}\left({\mathit{C}}_{\mathit{n}}\right)$	n	${\mathit{ABC}}_{\mathit{GG}}\left({\mathit{P}}_{\mathit{n}}\right)$	${\mathit{ABC}}_{\mathit{GG}}\left({\mathit{C}}_{\mathit{n}}\right)$
3	$1.4142$	0	8	$5.1431$	$4.8990$
4	$2.3401$	$2.8284$	9	$5.7155$	$5.5114$
5	$3.1463$	$3.5356$	10	$6.2546$	$5.6569$
6	$3.8697$	4	11	$6.7657$	$6.2225$
7	$4.5310$	$4.6667$	12	$7.2524$	$6.3246$

3.2. Unicyclic Graphs

As we mentioned in the introduction, unicyclic graphs maximizing the $AB{C}_{GG}$ index were found in [16]. To the best of our knowledge, the problem of minimizing the $AB{C}_{GG}$ index for unicyclic graphs has not been solved in general. By studying the $AB{C}_{GG}$ index of bipartite graphs. Dimitrov et al. [10] characterized unicyclic graphs with an even number of vertices and even girth in a non-explicit way that minimized the $AB{C}_{GG}$ index. By $C_n^{\prime }$ we denote a unicyclic $n-$vertex graph consisting of a cycle $C_{n-1}$ with a pendant vertex, and by $C_n^{″}$ we denote a graph with an odd number of vertices n comprised of two even cycles $C_{n-1}$ and $C_4$ that have three common vertices and two common edges.

Theorem 3

([10]). Among all bipartite graphs on $n\ge 8$ vertices, the minimum Graovac–Ghorbani index is attained by the cycle $C_n$ for even n, by $C_n^{\prime }$ for odd $n\le 15$, and by $C_n^{″}$ for odd $n\ge 17$. For $n<8$, the graph that minimizes the Graovac–-Ghorbani index is the path $P_n$ on n vertices. Furthermore, these are the unique graphs with these properties.

If we restrict ourselves to bipartite unicyclic graphs with an even number n of vertices, $n\ge 8$, then a direct consequence of Theorem 3 states that for such n, the cycle $C_n$ is a unicyclic graph with even girth and minimal $AB{C}_{GG}$ index.

Pendant edge-moving transformation of a connected graph G. Let $a\ge b\ge 1$ and let G be a connected graph with an induced path (induced subgraph that is a path) $P_{a+b+1}$, in which only one internal vertex has a degree of at least 3. Let a be the number of vertices of $P_{a+b+1}$ on one side of w, and b the number of vertices on the other side, see Figure 1. By moving a pendant vertex from the $b-$side of a path to its $a-$side, we perform a so-called pendant edge-moving transformation of G.

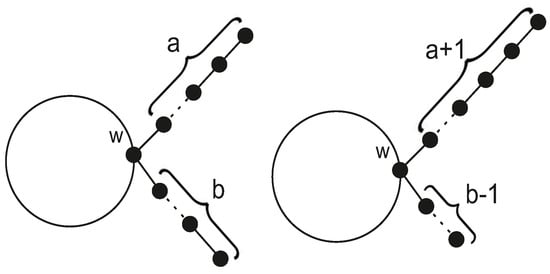
Figure 1. Pendant edge-moving transformation of a connected graph.

In [18], Rostami and Sohrabi-Haghighat proved the following lemma for trees. We generalize it to connected graphs.

Lemma 5.

Let G be a connected $n-$vertex graph that allows the pendant edge-moving transformation, and let $G_1$ be the resulting graph. Then

$$AB{C}_{GG}\left(G_1\right)<AB{C}_{GG}\left(G\right).$$

Proof. 

Let $a\ge b\ge 1$ and let $P_{a+b+1}$ be an induced path of G with a single internal vertex w, such that $d_G\left(w\right)\ge 3$. Then, w is a cut-vertex in both G and $G_1$. Let $H:=(G\setminus P_{a+b+1})+w$. Then, $H=(G_1\setminus P_{a+b+1})+w$ and the pendant edge-moving transformation preserves the gg-values of the edges in H. We have

$$AB{C}_{GG}\left(G\right)=\sum _{uv\in E\left(H\right)}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}+\sum _{i=1}^a\sqrt{\frac{n-2}{i(n-i)}}+\sum _{j=1}^b\sqrt{\frac{n-2}{j(n-j)}}.$$

Similarly,

$$AB{C}_{GG}\left(G_1\right)=\sum _{uv\in E\left(H\right)}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}+\sum _{i=1}^{a+1}\sqrt{\frac{n-2}{i(n-i)}}+\sum _{j=1}^{b-1}\sqrt{\frac{n-2}{j(n-j)}}.$$

We obtain

$$\begin{array}{cc}\hfill AB{C}_{GG}\left(G\right)-AB{C}_{GG}\left(G_1\right)& =\sqrt{\frac{n-2}{b(n-b)}}+\sqrt{\frac{n-2}{(a+1)(n-a-1)}}\hfill \\ \hfill & =f(b,n-b)-f(a+1,n-a-1).\hfill \end{array}$$

If we take $t=a-b+1$, then $n-b\ge b+t$ and from Lemma 1$\left(iv\right)$ we obtain

$$\begin{array}{cc}\hfill AB{C}_{GG}\left(G\right)-AB{C}_{GG}\left(G_1\right)& =f(b,n-b)-f(a+1,n-a-1)\hfill \\ \hfill & =f(b,n-b)-f(b+t,n-b-t)>0.\hfill \end{array}$$

□

For $s\in \mathbb{N}$, $s\ge 3$, we denote by $C(r_1,r_2,\dots ,r_s)$ an $n-$vertex unicyclic graph consisting of a cycle $C_s$, $|V\left(C_s\right)|=\{v_1,v_2,\dots ,v_s\}$ and paths $P_{r_i}$, $r_i\ge 1$, such that $v_i$ is an end vertex of $P_{r_i}$, $i=1,\dots ,s$. The vertices $v_1,\dots ,v_s$ are positioned clockwise on $C_s$, see Figure 2. Consequently, $n=r_1+\cdots +r_s$.

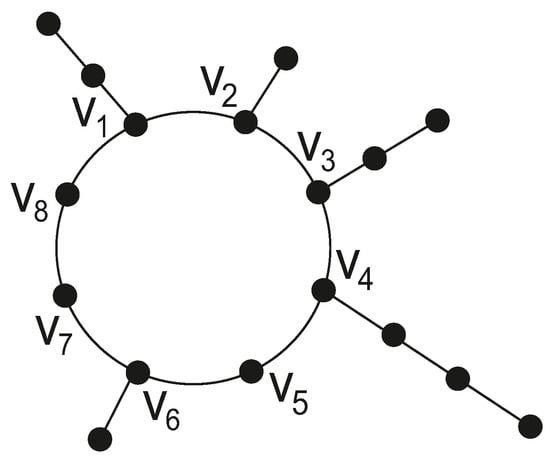
Figure 2. The unicyclic graph $C(3,2,3,4,1,2,1,1)$.

Theorem 4.

Let G be a unicyclic graph with a cycle $C_s$, $s\ge 3$, $V\left(C_s\right)=\{v_1,\dots ,v_s\}$, and let $T_{r_i}$ be an $r_i-$vertex tree in G containing $v_i$, $i=1,\dots ,s$. Then

$$AB{C}_{GG}\left(G\right)\ge AB{C}_{GG}\left(C(r_1,\dots ,r_s)\right).$$

Proof. 

We repeatedly apply a pendant-edge moving transformation to G; i.e., to each $T_{r_i}$, $i=1,\dots ,s$, we perform a sequence of pendant-edge moving transformations until we obtain a path $P_{r_i}$. These transformations preserve the unicyclic property of G, while Lemma 5 implies a reduction in the $AB{C}_{GG}$ index. □

Due to Theorem 4, unicyclic graphs with minimal $AB{C}_{GG}$ index belong to the class of graphs $C(r_1,r_2,\dots ,r_s)$. Due to a different behavior, $n-$vertex unicyclic graphs of girth 3 are considered separately.

The calculations show that among all unicyclic graphs with $3\le n\le 5$ vertices, the graph $C(n-2,1,1)$ has the smallest $AB{C}_{GG}$ index.

Theorem 5.

Let $n\ge 6$ and let G be an $n-$vertex unicyclic graph of girth 3. Then

$$AB{C}_{GG}\left(G\right)>AB{C}_{GG}\left(C_n\right).$$

Proof. 

The cases $n=6$ and $n=7$ can be tested directly. Let $n\ge 8$. From Theorem 4, it follows for every unicyclic graph G of girth 3 with trees $T_{r_i}$, $i=1,2,3$ that $AB{C}_{GG}\left(G\right)\ge AB{C}_{GG}\left(C(r_1,r_2,r_3)\right)$. Therefore, we only focus on the graphs $C(r_1,r_2,r_3)$. Without loss of generality, we assume $r_1\ge r_2\ge r_3\ge 1$. We consider three cases:

Case 1: $r_2=1$. Then, $r_1=n-2$ and $r_3=1$. According to Lemma 2 and Theorem 2, we have

$$\begin{array}{cc}\hfill AB{C}_{GG}\left(C(n-2,1,1)\right)& =\sum _{i=1}^{n-3}\sqrt{\frac{n-2}{i(n-i)}}+2\sqrt{\frac{n-3}{n-2}}+0\hfill \\ \hfill & >\sum _{i=1}^{n-3}\sqrt{\frac{n-2}{i(n-i)}}+\sqrt{\frac{1}{2}}+\sqrt{\frac{n-2}{n-1}}\hfill \\ \hfill & =AB{C}_{GG}\left(P_n\right)>AB{C}_{GG}\left(C_n\right).\hfill \end{array}$$

Case 2: $r_2\ge 2$ and $r_3=1$. Then, $r_1+r_2=n-1$. Notice that the gg-value of the edge $v_1{v}_2$ is equal to $f(r_1,r_2)=\sqrt{\frac{r_1+r_2-2}{r_1{r}_2}}$, and for $j=1,2$, the gg-value of the edge $v_j{v}_3$ is $f(r_j,1)=\sqrt{\frac{r_j-1}{r_j}}$. By applying Theorem 2 and parts $\left(ii\right)$ and $\left(iii\right)$ of Lemma 1, we obtain

$$\begin{array}{cc}\hfill AB{C}_{GG}\left(C(r_1,r_2,1)\right)& =\sum _{i=1}^{r_1-1}\sqrt{\frac{n-2}{i(n-i)}}+\sum _{i=1}^{r_2-1}\sqrt{\frac{n-2}{i(n-i)}}\hfill \\ \hfill & +\sqrt{\frac{r_1-1}{r_1}}+\sqrt{\frac{r_2-1}{r_2}}+\sqrt{\frac{r_1+r_2-2}{r_1{r}_2}}\hfill \\ \hfill & >\sum _{i=1}^{r_1-1}\sqrt{\frac{n-2}{i(n-i)}}+\sum _{i=1}^{r_2-1}\sqrt{\frac{n-2}{i(n-i)}}+2\sqrt{\frac{1}{2}}\hfill \\ \hfill & >\sum _{i=1}^{r_1-1}\sqrt{\frac{n-2}{i(n-i)}}+\sum _{i=1}^{r_2-1}\sqrt{\frac{n-2}{i(n-i)}}\hfill \\ \hfill & +\sqrt{\frac{n-2}{r_1(n-r_1)}}+\sqrt{\frac{n-2}{r_2(n-r_2)}}\hfill \\ \hfill & =AB{C}_{GG}\left(P_n\right)>AB{C}_{GG}\left(C_n\right).\hfill \end{array}$$

Case 3: $r_3\ge 2$. Since $r_1\ge r_2\ge r_3$ and $r_1+r_2+r_3=n$, we have $r_3\le \lfloor n/3\rfloor$ and $r_2\le \lfloor n/2\rfloor -1$. From Lemma 1$\left(iii\right)$, we have $f(r_1,r_2)>f(r_1,r_2+r_3)=f(r_1,n-r_1)$, $f(r_2,r_3)>f(r_2,r_3+r_1)=f(r_2,n-r_2)$ and $f(r_1,r_3)>f(r_1+r_2,r_3)=f(r_3,n-r_3)$. This and the part $\left(iv\right)$ of Lemma 1 imply

$$\begin{array}{cc}\hfill AB{C}_{GG}\left(C(r_1,r_2,r_3)\right)& =\sum _{i=1}^{r_1-1}\sqrt{\frac{n-2}{i(n-i)}}+\sum _{i=1}^{r_2-1}\sqrt{\frac{n-2}{i(n-i)}}+\sum _{i=1}^{r_3-1}\sqrt{\frac{n-2}{i(n-i)}}\hfill \\ \hfill & +\sqrt{\frac{r_1+r_2-2}{r_1{r}_2}}+\sqrt{\frac{r_1+r_3-2}{r_1{r}_3}}+\sqrt{\frac{r_2+r_3-2}{r_2{r}_3}}\hfill \\ \hfill & >\sum _{i=1}^{r_1}\sqrt{\frac{n-2}{i(n-i)}}+\sum _{i=1}^{r_2}\sqrt{\frac{n-2}{i(n-i)}}+\sum _{i=1}^{r_3}\sqrt{\frac{n-2}{i(n-i)}}\hfill \\ \hfill & >\sum _{i=1}^{r_1}\sqrt{\frac{n-2}{i(n-i)}}+\sum _{i=1}^{r_2}\sqrt{\frac{n-2}{i(n-i)}}+(r_3-1)\sqrt{\frac{n-2}{r_3(n-r_3)}}\hfill \\ \hfill & \ge \sum _{i=1}^{r_1}\sqrt{\frac{n-2}{i(n-i)}}+\sum _{i=1}^{r_2}\sqrt{\frac{n-2}{i(n-i)}}+(r_3-1)\sqrt{\frac{n-2}{r_2(n-r_2)}}\hfill \\ \hfill & >AB{C}_{GG}\left(P_n\right).\hfill \end{array}$$

The last inequality holds since $f(r_2,n-r_2)>f(x,n-x)$, $x=r_2+1,\dots ,\lfloor n/2\rfloor$. Application of Theorem 2 results in $AB{C}_{GG}\left(C(r_1,r_2,r_3)\right)>AB{C}_{GG}\left(C_n\right)$ and the proof is complete. □

Next, we find the smallest gg-values of the edges of a cycle $C_s$, $s\ge 4$ in any unicyclic $n-$vertex graph G.

Lemma 6.

Let $n\in \mathbb{N}$, $n\ge 4$ and let G be a unicyclic graph with cycle $C_s$, $s\ge 4$. Then we have for each edge $e=uv\in E\left(C_s\right)$

$$\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\ge \left\{\begin{array}{}\mathrm{(12)}& 2\frac{\sqrt{n-2}}{n}, \mathrm{for} n\mathrm{even} \mathrm{and} s\mathrm{even},\hfill \mathrm{(13)}& 2\sqrt{\frac{n-3}{n(n-2)}}, \mathrm{for} n\mathrm{even} \mathrm{and} s\mathrm{odd},\hfill \mathrm{(14)}& 2\frac{\sqrt{n-3}}{n-1}, \mathrm{for} n\mathrm{odd} \mathrm{and} s\mathrm{odd},\hfill \mathrm{(15)}& 2\sqrt{\frac{n-2}{n^2-1}}, \mathrm{for} n\mathrm{odd} \mathrm{and} s\mathrm{even}.\hfill \end{array}\right.$$

The equality is given if $s=n$, i.e., the edge e belongs to $C_n$, or if $s=n-1$, i.e., the edge e belongs to a cycle in $C_n^{\prime }$. The graphs $C_n$ and $C_n^{\prime }$ are unique unicyclic graphs containing the maximum number of cycle edges with the smallest gg-values.

Proof. 

• Case 1: n and s are even. For each edge $e=uv\in E\left(C_s\right)$, $s\ge 4$ we have $n_u,n_v\ge 2$, $n_u+n_v=n$ and the largest value of the product $n_u{n}_v$ is obtained for $n_u=n_v=n/2$. Therefore, $\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\ge \sqrt{\frac{n-2}{\frac{n^2}{4}}}=2\frac{\sqrt{n-2}}{n}$, which is a gg-value of an arbitrary edge of $C_n$.
• Case 2: n is even and s is odd. Then, $s\ge 5$ and at least one vertex of G does not lie on a cycle $C_s$. For $e=uv\in E\left(C_s\right)$, we have $n_u,n_v\ge 2$ and $n_u+n_v=t\le n-1$, since there is at least one vertex that is equidistant from u and v. (For $t=n-1$, such a vertex is unique and belongs to $C_s$). If t is odd, then $n_u{n}_v\le \frac{t-1}{2}·\frac{t+1}{2}$, so $\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\ge 2\sqrt{\frac{t-2}{t^2-1}}$. Note that $\frac{4(t-2)}{t^2-1}$ is a decreasing function of odd $t\ge 5$ and reaches its minimum value for $t=n-1$. (If $t=3$, then $n_u=1$ and $n_v=2$, which implies $s=3$.) Therefore, $\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\ge 2\sqrt{\frac{n-3}{n(n-2)}}$. If t is even, then $4\le t\le n-2$ and $n_u{n}_v\le \frac{t^2}{2}$, so $\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\ge \sqrt{\frac{t-2}{\frac{t^2}{4}}}$. Function $\frac{t-2}{\frac{t^2}{4}}$ is a decreasing function of even $t\ge 4$. It follows that $2\sqrt{\frac{t-2}{t^2}}\ge 2\sqrt{\frac{n-4}{{(n-2)}^2}}$. However, $2\sqrt{\frac{n-4}{{(n-2)}^2}}\ge 2\sqrt{\frac{n-3}{n(n-2)}}$ for every (even) $n\ge 6$. Therefore, $\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\ge 2\sqrt{\frac{n-3}{n(n-2)}}$.
  Let w be the vertex on a cycle for which $d_G\left(w\right)\ge 3$ (such a vertex exists since at least one vertex of G is not on a cycle). Then, there is a single edge $f\in E\left(C_s\right)$ whose end vertices are equidistant from w. Since a tree attached to w exists, we conclude that the gg-value of f is greater than $2\sqrt{\frac{n-3}{n(n-2)}}$ and there exists at least one pendant edge in G having gg-value $\sqrt{\frac{n-2}{n-1}}>2\sqrt{\frac{n-3}{n(n-2)}}$. Therefore, G contains at least 2 edges with a non-minimal gg-value. We conclude that the maximum number of cycle edges with the smallest gg-value is $n-2$ and they belong to $G=C_n^{\prime }$.
• Case 3: n and s are odd. Then, $s\ge 5$ and for a cycle edge $e=uv$, we have $n_u,n_v\ge 2$, $n_u+n_v=t\le n-1$. Similarly to in Case 2, if t is odd, then $n_u{n}_v\le \frac{t-1}{2}·\frac{t+1}{2}$ and $\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\ge 2\sqrt{\frac{t-2}{t^2-1}}\ge 2\sqrt{\frac{n-4}{{(n-2)}^2-1}}$, since $t\le n-2$. It follows that $2\sqrt{\frac{n-4}{{(n-2)}^2-1}}\ge 2\frac{\sqrt{n-3}}{n-1}$. If t is even, then $4\le t\le n-1$, $n_u{n}_v\le \frac{t^2}{2}$ and $\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\ge \sqrt{\frac{t-2}{\frac{t^2}{4}}}\ge 2\frac{\sqrt{n-3}}{n-1}$. Cycle $C_n$ is the unique graph in which all edges have the smallest gg-value.
• Case 4: n is odd and s is even. Then, $s\ge 4$ and for any cycle edge in G, we have $n_u,n_v\ge 2$ and $n_u+n_v=n$. It follows that $\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\ge 2\sqrt{\frac{n-2}{\frac{n-1}{2}·\frac{n+1}{2}}}=2\sqrt{\frac{n-2}{n^2-1}}$. In $C_n^{\prime }$, all cycle edges have the smallest gg-value. □

In the following, we compare gg-values of edges in an arbitrary $n-$vertex tree with the smallest gg-values of cycle edges in an $n-$vertex unicyclic graph G.

Lemma 7.

Let $n,i\in \mathbb{N}$, $n\ge 4$ and $i\le \lfloor n/2\rfloor$. Then

$$\sqrt{\frac{n-2}{i(n-i)}}\ge \left\{\begin{array}{c}2\frac{\sqrt{n-2}}{n}, \mathrm{for} n \mathrm{even},\hfill \\ 2\sqrt{\frac{n-2}{n^2-1}}, \mathrm{for} n \mathrm{odd}.\hfill \end{array}\right.$$

(16)

and for $n\ge 5$, it holds

$$\sqrt{\frac{n-2}{i(n-i)}}<\left\{\begin{array}{}\mathrm{(17)}& 2\sqrt{\frac{n-3}{n(n-2)}}\iff \left(i>\frac{n-\sqrt{n-1}}{2}\mathrm{and}\right. n \mathrm{even},\hfill \mathrm{(18)}& 2\frac{\sqrt{n-3}}{n-1}\iff \left(i>\frac{n-\sqrt{n-2}}{2}\mathrm{and}\right. n \mathrm{odd}.\hfill \end{array}\right.$$

Proof. 

We have $f(i,n-i)=\sqrt{\frac{n-2}{i(n-i)}}$ and from Lemma 1$\left(iv\right)$, by taking $t=1$ we obtain

$$f(1,n-1)>f(2,n-2)>\cdots >f(\lfloor n/2\rfloor ,\lceil n/2\rceil )=\left\{\begin{array}{c}2\frac{\sqrt{n-2}}{n}, \mathrm{for} n \mathrm{even},\hfill \\ 2\sqrt{\frac{n-2}{n^2-1}}, \mathrm{for} n \mathrm{odd}\hfill \end{array}\right.$$

and the inequality (16) is proven.

To prove (17), notice that $\frac{n-2}{i(n-i)}<4\frac{n-3}{n(n-2)}$ is equivalent to

$$4i^2-4ni+\frac{n{(n-2)}^2}{n-3}<0,$$

which is a quadratic inequality of variable i. Its solutions are integers i from the interval $\left(\frac{n-\sqrt{n-1}}{2},\frac{n}{2}\right]$. Therefore, (17) holds. Similarly, we note that $\frac{n-2}{i(n-i)}<4\frac{n-3}{{(n-1)}^2}$ is equivalent to

$$4i^2-4ni+\frac{(n-2){(n-1)}^2}{n-3}<0,$$

which gives integer solutions i from $\left(\frac{n-\sqrt{n-2}}{2},\frac{n-1}{2}\right]$ and we have proven (18). □

We are ready to characterize unicyclic graphs with even girth that minimize the Graovac–Ghorbani index.

Theorem 6.

For $n\ge 4$, let G be an $n-$vertex unicyclic graph of even girth. Then

$$AB{C}_{GG}\left(G\right)\ge \left\{\begin{array}{c}AB{C}_{GG}\left(C_n\right),\mathrm{for} n \mathrm{even},\hfill \\ AB{C}_{GG}\left(C_n^{\prime }\right),\mathrm{for} n \mathrm{odd}.\hfill \end{array}\right.$$

(19)

Proof. 

Let us consider the case where n is even. The inequality (12) from Lemma 6 implies that the gg-value of each edge of a cycle in G is greater than or equal to the gg-value of $C_n$, which is equal to $\frac{2}{n}\sqrt{n-2}$. Moreover, inequality (16) from Lemma 7 implies that the gg-value of each edge of a tree in G (if any) is greater than or equal to the gg-value of $C_n$.

For n odd, the inequality (15) from Lemma 6 implies that the gg-value of each edge of a cycle in G is greater than or equal to the gg-value of a cycle edge in $C_n^{\prime }$, which is equal to $2\sqrt{\frac{n-2}{n^2-1}}$. The inequality (16) from Lemma 7 implies that the gg-value of each edge of a tree in G (which exists) is greater than or equal to the gg-value of a cycle edge $C_n^{\prime }$. Since $C_n^{\prime }$ contains a single pendant edge, we obtain

$$\begin{array}{cc}\hfill AB{C}_{GG}\left(G\right)& =\sum _{uv\in E\left(C_s\right)}f(n_u,n_v)+\sum _{uv\notin E\left(C_s\right)}f(n_u,n_v)\hfill \\ \hfill & \ge 2s\sqrt{\frac{n-2}{n^2-1}}+2(n-s-1)\sqrt{\frac{n-2}{n^2-1}}+\sqrt{\frac{n-2}{n-1}}\hfill \\ \hfill & =2(n-1)\sqrt{\frac{n-2}{n^2-1}}+\sqrt{\frac{n-2}{n-1}}\hfill \\ \hfill & =AB{C}_{GG}\left(C_n^{\prime }\right)\hfill \end{array}$$

and the inequality (19) is proven. □

Lemma 8.

For odd $n\ge 5$, it holds $AB{C}_{GG}\left(C_n^{\prime }\right)>AB{C}_{GG}\left(C_n\right)$.

Proof. 

A simple calculation shows that the inequality holds for $n=5,7$. Let $n\ge 9$. The Lemma 3 implies

$$\sqrt{\frac{n-2}{n-1}}>\frac{\sqrt{n}}{2}·\frac{2\sqrt{n-3}}{n-1}.$$

Therefore,

$$\begin{array}{cc}\hfill AB{C}_{GG}\left(C_n^{\prime }\right)& =\sqrt{\frac{n-2}{n-1}}+(n-1)\frac{2\sqrt{n-2}}{\sqrt{n^2-1}}\hfill \\ \hfill & =\sqrt{\frac{n-2}{n-1}}+\frac{2(n-1)}{\sqrt{n+1}}·\sqrt{\frac{n-2}{n-1}}\hfill \\ \hfill & =\sqrt{\frac{n-2}{n-1}}\left(\frac{2(n-1)}{\sqrt{n+1}}+1\right)\hfill \\ \hfill & >\frac{\sqrt{n}}{2}\left(\frac{2(n-1)}{\sqrt{n+1}}+1\right)\frac{2\sqrt{n-3}}{n-1}.\hfill \end{array}$$

Since $AB{C}_{GG}\left(C_n\right)=\frac{2n\sqrt{n-3}}{n-1}$, it is sufficient to prove the inequality

$$\frac{\sqrt{n}}{2}\left(\frac{2(n-1)}{\sqrt{n+1}}+1\right)>n,$$

which is equivalent to

$$\frac{\sqrt{n}(n-3)}{\sqrt{n+1}+2}>\frac{2n}{\sqrt{n+1}+\sqrt{n}}.$$

(20)

For $n\ge 9$, we have $\sqrt{n}(n-3)\ge 2n$ and for $n\ge 5$, it holds $\sqrt{n+1}+\sqrt{n}>\sqrt{n+1}+2$. Therefore, the inequality (20) holds and this completes the proof. □

Corollary 1.

Let $n\ge 4$ and let G be an $n-$vertex unicyclic graph of girth $s\ge 4$, s is even. Then

$$AB{C}_{GG}\left(G\right)\ge AB{C}_{GG}\left(C_n\right).$$

Proof. 

The result follows directly from Theorem 6 and Lemma 8. □

We continue our studies by examining unicyclic graphs G with odd girth s, where $s\ge 5$. We say that the edge of a tree in G (if any) is gg-small if its gg-value $\sqrt{\frac{n-2}{i(n-i)}}$ satisfies the inequality (17) (if n is even) or the inequality (18) (if n is odd).

Theorem 7.

Let $n\ge 5$ and let G be an $n-$vertex unicyclic graph of odd girth $s\ge 5$ with zero gg-small edges. Then

$$AB{C}_{GG}\left(G\right)\ge \left\{\begin{array}{c}AB{C}_{GG}\left(C_n\right),\mathrm{for} n \mathrm{odd},\hfill \\ AB{C}_{GG}\left(C_n^{\prime }\right),\mathrm{for} n \mathrm{even}.\hfill \end{array}\right.$$

Proof. 

• Case 1: n is odd. If $e=uv\in E\left(C_s\right)$, then, from the inequality (14) of Lemma 6, we have $f(n_u,n_v)\ge 2\frac{\sqrt{n-3}}{n-1}$. Let $e=uv\notin E\left(C_s\right)$. The assumption of zero gg-small edges in G means that the reversed inequality in (18) holds; i.e., $f(n_u,n_v)\ge 2\frac{\sqrt{n-3}}{n-1}$. We conclude $AB{C}_{GG}\left(G\right)\ge AB{C}_{GG}\left(C_n\right)$.
• Case 2: n is even. Then, G contains at least one vertex that is not on the cycle. Consequently, it contains at least one pendant edge and for at least one cycle edge $f=wz$ there are $p\ge 2$ vertices equidistant from u and v. We have $n_w+n_z=t=n-p$. Note that p and t have the same parity and $t\le n-2$ if t is even, while $t\le n-3$ if t is odd. We omit the details and refer to Case 2 of Lemma 6 to conclude that $f(n_w,n_z)\ge f(n/2-1,n/2-1)$$=2\sqrt{\frac{n-4}{{(n-2)}^2}}$. The above considerations in combination with the inequality (13) and the reversed inequality in (17) result in

  $$\begin{array}{cc}\hfill AB{C}_{GG}\left(G\right)& =\sum _{uv\in E\left(C_s\right)}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}+\sum _{uv\notin E\left(C_s\right)}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\hfill \\ \hfill & \ge 2\sqrt{\frac{n-4}{{(n-2)}^2}}+2(s-1)\sqrt{\frac{n-3}{n(n-2)}}\hfill \\ \hfill & +2(n-s-1)\sqrt{\frac{n-3}{n(n-2)}}+\sqrt{\frac{n-2}{n-1}}\hfill \\ \hfill & =2\sqrt{\frac{n-4}{{(n-2)}^2}}+2(n-2)\sqrt{\frac{n-3}{n(n-2)}}+\sqrt{\frac{n-2}{n-1}}\hfill \\ \hfill & =AB{C}_{GG}\left(C_n^{\prime }\right).\hfill \end{array}$$
  □

Lemma 9.

For even $n\ge 6$, it holds $AB{C}_{GG}\left(C_n^{\prime }\right)>AB{C}_{GG}\left(C_n\right)$.

Proof. 

The proof follows directly from the inequalities

$$\sqrt{\frac{n-2}{n-1}}>2\sqrt{\frac{n-4}{{(n-2)}^2}}\ge 2\sqrt{\frac{n-3}{n(n-2)}}>2\frac{\sqrt{n-2}}{n}.$$

□

Corollary 2.

Let $n\ge 5$ and let G be an $n-$vertex unicyclic graph of odd girth $s\ge 5$ with zero gg-small edges. Then

$$AB{C}_{GG}\left(G\right)\ge AB{C}_{GG}\left(C_n\right).$$

Proof. 

The result follows directly from Theorem 7 and Lemma 9. □

Now, we focus on graphs with odd girth $s\ge 5$ that contain gg-small edges. Note that pendant edge-moving transformations of such graphs also contain gg-small edges. Therefore, we consider $C(r_1,\dots ,r_s)$ with gg-small edges.

Lemma 10.

There exist at most two paths $P_{r_k}$ and $P_{r_l}$, $k\ne l$, $k,l\in \{1,\dots ,s\}$ in $C(r_1,\dots ,r_s)$, which contain gg-small edges.

Proof. 

If $C(r_1,\dots ,r_s)$ contains paths, then the maximum number of vertices that are not on a cycle $C_s$ is equal to $n-5$. Suppose that there are at least three paths in $C(r_1,\dots ,r_s)$ that contain gg-small edges. Then, the number of vertices on these paths is at least $3i$, where, according to Lemma 7, $i>\frac{n-\sqrt{n-2}}{2}$ if n is odd, and $i>\frac{n-\sqrt{n-1}}{2}$ if n is even. In both cases, we show that $3i>n-5$. For n odd, $3\frac{n-\sqrt{n-2}}{2}>n-5$ can be written as $n+10>3\sqrt{n-2}$, while for n even, $3\frac{n-\sqrt{n-1}}{2}>n-5$ can be written as $n+10>3\sqrt{n-1}$. Both inequalities are valid for every $n\ge 5$, and we obtain a contradiction. □

Theorem 8.

If $C(r_1,\dots ,r_s)$ contains two disjoint paths with gg-small edges, then

$$AB{C}_{GG}\left(C(r_1,\dots ,r_s)\right)>\left\{\begin{array}{c}AB{C}_{GG}\left(C_n\right),\mathrm{for} n \mathrm{odd},\hfill \\ AB{C}_{GG}\left(C_n^{\prime }\right),\mathrm{for} n \mathrm{even}.\hfill \end{array}\right.$$

Proof. 

For the sake of simplicity, we use the notation $H:=C(r_1,\dots ,r_s)$. Let us consider a graph $H_1=C(r_1,\dots ,r_5)$. Then, $H_1$ contains the maximum number of vertices that do not lie on a cycle (it is $n-5$), and it consequently has the maximum number of gg-small edges. Let $S_1$ and S be the set of gg-small edges in $H_1$ and H, respectively. Then, $\left|S\right|\le |S_1]$.

Case 1: n is odd. For $9\le n\le 27$, at most one path in $H_1$ contains gg-small edges, so we assume $n\ge 29$. Let us calculate $|S_1|$. For simplicity, we assume that the paths in $H_1$ are balanced, i.e., each contains $(n-5)/2$ edges (moving a pendant vertex from a path P to a path Q in $H_1$ decreases the number of gg-small edges of P by one, while simultaneously increasing the number of gg-small edges in Q by one). Then, from the inequality (18) of Lemma 7, the number of gg-small edges on each path in $H_1$ is equal to the number of integers i satisfying the condition $\frac{n-\sqrt{n-2}}{2}<i\le \frac{n-5}{2}$. If $\frac{n-\sqrt{n-2}}{2}$ is an integer, then the number of gg-small edges on both paths is

$$\left|S_1\right|=2\left(\frac{n-5}{2}-\frac{n-\sqrt{n-2}}{2}\right)=\sqrt{n-2}-5.$$

From Lemma 3, we know

$$\begin{array}{cc}\hfill 2\left(\sqrt{\frac{n-2}{n-1}}+\sqrt{\frac{1}{2}}\right)& >\left(\sqrt{n}+\sqrt{\frac{n+1}{2}}\right)·2\sqrt{\frac{n-3}{n(n-2)}}\hfill \\ \hfill & >\left(\sqrt{n}+\sqrt{\frac{n+1}{2}}\right)·2\frac{\sqrt{n-3}}{n-1}.\hfill \end{array}$$

(21)

Notice that $\sqrt{2n}+\sqrt{n+1}>\sqrt{2n-4}-\sqrt{2}$, for each $n\ge 2$. By dividing this inequality by $\sqrt{2}$, we obtain

$$\sqrt{n}+\sqrt{\frac{n+1}{2}}>4+\sqrt{n-2}-5=4+|S_1|\ge 4+|S|.$$

(22)

By inserting (22) into (21), we obtain

$$2\left(\sqrt{\frac{n-2}{n-1}}+\sqrt{\frac{1}{2}}\right)>(4+|S\left|\right)·2\frac{\sqrt{n-3}}{n-1}.$$

(23)

The above inequality shows that sum of the four largest gg-values on paths in H is greater than $4+\left|S\right|$ gg-values of $C_n$.

If $\frac{n-\sqrt{n-2}}{2}\notin \mathbb{N}$, then the number of gg-small edges on both paths in $H_1$ is

$$\begin{array}{cc}\hfill |S_1|& =2\left(\frac{n-5}{2}-⌈\frac{n-\sqrt{n-2}}{2}⌉+1\right)\hfill \\ \hfill & <2\left(\frac{n-5}{2}-\frac{n-\sqrt{n-2}}{2}+1\right)\hfill \\ \hfill & =\sqrt{n-2}-3.\hfill \end{array}$$

It is easy to see that $\sqrt{2n}+\sqrt{n+1}>\sqrt{2n-4}+\sqrt{2}$ for each for $n\ge 2$, that is

$$\sqrt{n}+\sqrt{\frac{n+1}{2}}>4+\sqrt{n-2}-3>4+|S_1|\ge 4+|S|.$$

(24)

Combining (24) with (21), we obtain (23). We conclude that for n odd, we have $\left|S\right|<\sqrt{n-2}-3$. From (23) and from Lemmas 6 and 7, we obtain

$$\begin{array}{cc}\hfill AB{C}_{GG}\left(H\right)& =\sum _{uv\in E\left(C_s\right)}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}+\sum _{uv\notin (E\left(C_s\right)\cup S)}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\hfill \\ \hfill & +\sum _{uv\in S}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\hfill \\ \hfill & >2s\frac{\sqrt{n-3}}{n-1}+2(n-s-|S|-4)\frac{\sqrt{n-3}}{n-1}+(4+|S\left|\right)·2\frac{\sqrt{n-3}}{n-1}\hfill \\ \hfill & =2n\frac{\sqrt{n-3}}{n-1}=AB{C}_{GG}\left(C_n\right).\hfill \end{array}$$

Case 2: n is even. For $8\le n\le 36$, at most one path in $H_1$ contains gg-small edges, so let $n\ge 38$. Similarly to Case 1, we consider $H_1$ with balanced paths. Then, one path contains $(n-4)/2$ edges and the other one contains $(n-6)/2$ edges. Note that $\frac{n-\sqrt{n-1}}{2}\notin \mathbb{N}$. Therefore, on one path, the number of gg-small edges is equal to the number of integers i that satisfy $⌈\frac{n-\sqrt{n-1}}{2}⌉\le i\le \frac{n-4}{2}$, while on the other path, this is the number of integers i that satisfies $⌈\frac{n-\sqrt{n-1}}{2}⌉\le i\le \frac{n-6}{2}$. We have

$$\left|S_1\right|=2\left(\frac{n-6}{2}-⌈\frac{n-\sqrt{n-1}}{2}⌉+1\right)+1<\sqrt{n-1}-3.$$

From Lemma 3, we have

$$\sqrt{\frac{n-2}{n-1}}+2\sqrt{\frac{1}{2}}>\left(\frac{\sqrt{n}}{2}+\sqrt{\frac{n+1}{2}}\right)·2\sqrt{\frac{n-3}{n(n-2)}}.$$

(25)

Since for each $n\ge 2$ it holds $\sqrt{n}+\sqrt{2n+2}>2\sqrt{n-1}$, combining this with (25) gives

$$\left(\sqrt{\frac{n-2}{n-1}}+2\sqrt{\frac{1}{2}}\right)>(3+|S\left|\right)·2\sqrt{\frac{n-3}{n(n-2)}}.$$

(26)

From (26) and from Lemmas 6 and 7, we obtain

$$\begin{array}{cc}\hfill AB{C}_{GG}\left(H\right)& =\sum _{uv\in E\left(C_s\right)}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}+\sum _{uv\notin (E\left(C_s\right)\cup S)}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\hfill \\ \hfill & +\sum _{uv\in S}\sqrt{\frac{n_u+n_v-2}{n_u{n}_v}}\hfill \\ \hfill & >2\sqrt{\frac{n-4}{{(n-2)}^2}}+2(s-1)\sqrt{\frac{n-3}{n(n-2)}}+\sqrt{\frac{n-2}{n-1}}\hfill \\ \hfill & +2(n-s-|S|-4)2\sqrt{\frac{n-3}{n(n-2)}}+(3+|S\left|\right)·2\sqrt{\frac{n-3}{n(n-2)}}\hfill \\ \hfill & =2\sqrt{\frac{n-4}{{(n-2)}^2}}+2(n-2)\sqrt{\frac{n-3}{n(n-2)}}+\sqrt{\frac{n-2}{n-1}}\hfill \\ \hfill & =AB{C}_{GG}\left(C_n^{\prime }\right).\hfill \end{array}$$

□

Corollary 3.

If a pendant edge-moving transformation of an unicyclic graph G with odd girth $s\ge 5$ yields $C(r_1,\dots ,r_s)$ with gg-small edges on two disjoint paths $P_{r_k}$ and $P_{r_l}$, then $AB{C}_{GG}\left(G\right)>AB{C}_{GG}\left(C_n\right)$.

Proof. 

Theorems 4, 8 and Lemma 9 give

$$AB{C}_{GG}\left(G\right)\ge AB{C}_{GG}\left(C(r_1,\dots ,r_s)\right)>AB{C}_{GG}\left(C_n^{\prime }\right)>AB{C}_{GG}\left(C_n\right).$$

□

Now, a single type of unicyclic graph with an odd girth remains to be investigated. This is a graph with gg-small edges whose pendant edge-moving transformation gives $C(r_1,\dots ,r_s)$ with gg-small edges on a single path. Numerical experiments indicate that many such graphs have an $AB{C}_{GG}$ index larger than $AB{C}_{GG}\left(C_n\right)$. However, at this moment, we are not able to provide a general proof of this conjecture, so we leave this for future research.

4. Conclusions

In this study, we investigated the Graovac–Ghorbani index for unicyclic graphs. As an auxiliary result, we first showed that for every $n\ge 8$ the $AB{C}_{GG}$ index of the cycle $C_n$ is larger than the $AB{C}_{GG}$ index of the path $P_n$. We characterized unicyclic graphs of even girth with the smallest $AB{C}_{GG}$ index using pendant edge-moving transformation. For unicyclic graphs with odd girth, we offer a conjecture based on an analysis of a large number of cases.

Conjecture 1.

Let G be an $n-$vertex unicyclic graph with an odd girth $s\ge 5$. Then

$$AB{C}_{GG}\left(G\right)\ge AB{C}_{GG}\left(C_n\right).$$