A Parametric Six-Step Method for Second-Order IVPs with Oscillating Solutions

Abstract

In this paper, we develop an explicit symmetric six-step method for the numerical solution of second-order initial value problems (IVPs) with oscillating solutions. The proposed method is phase-fitted and incorporates a free coefficient as a parameter to optimize its performance. By exploring a wide range of values for this parameter, we computationally determine the periodicity interval. The objective of this procedure is to identify the range of the parameter’s values for which the method remains stable. Based on the output from the periodicity interval analysis, we then aim to define the optimal values for the parameter by numerically solving three initial value problems. The results guided us in identifying these optimal values and confirm the high efficiency of the new method. The method’s efficiency is further validated for the chosen optimal parameter value for specific oscillatory problems, where it is compared with well-known phase-fitted methods.

1. Introduction

This paper focuses on the numerical solution of the initial value problem (IVP) characterized by the following form:

$$y^{″}\left(t\right)=f(t,y),y\left(t_0\right)=y_0,y^{\prime }\left(t_0\right)=y_0^{\prime },$$

(1)

whose solutions display a notable oscillatory nature. This kind of problem is commonly encountered across a wide spectrum of scientific disciplines, such as quantum mechanical scattering problems, celestial mechanics, and elsewhere.

Several authors have derived numerical methods of a single step, such as Runge–Kutta or Runge–Kutta–Nyström, which are based on properties such as phase lag or trigonometric/exponential fitting (see [1,2,3,4,5,6]), while others use these properties for the development of multistep methods (see [7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]). All of these methods incorporate frequency-dependent coefficients and demonstrate high efficiency in numerical solution of second-order IVPs with oscillating solutions.

In the context of linear multistep methods, many researchers have developed optimized approaches based on phase lag properties. For the numerical solution of oscillatory IVPs, Chawla and Rao [25] introduced a three-stage, two-step P-stable method of the sixth order with minimal phase lag. Henrici [26] proposed a four-step symmetric method, also of the sixth order. Van de Vyver [28] developed an optimized Numerov-type method with zero phase lag and amplification error. Panopoulos et al. [29] constructed an eighth-order method with zero phase lag, achieving high accuracy. Williams and Simos [24] presented a family of two-step P-stable, phase-fitted methods, while Simos [21] introduced a class of dissipative Numerov-type methods with a high phase-lag order. Anastassi and Simos [30] developed an eight-step symmetric multistep method with phase lag of the infinite order, designed to solve the Schrödinger equation and related problems numerically. Additionally, Simos [22] created an explicit four-step phase-fitted and amplification-fitted method for first-order IVPs with oscillatory solutions, followed by an implicit five-step version for the same problem class in [23].

In this research work, a new explicit parametric symmetric linear six-step method is produced. The new method is of the sixth algebraic order with zero phase lag and is used for the numerical solution of oscillatory problems. The approach of this study is based on the procedure of Anastassi and Simos [12] for the derivation of a linear four-step method, and it should be considered as a technique which gives the opportunity to choose an appropriate value for the free parameter in order to numerically solve an IVP, depending on whether it needs a fast low accurate solution or a solution of high accuracy.

In particular, in Section 2, the basic theory of linear multistep methods is provided. In Section 3, the development of the new parametric method is presented, as well as the local truncation error and periodicity analysis for the new method. Furthermore, in Section 4, the results of the application to three well-known problems are demonstrated. Finally, the conclusions of this research article are presented in Section 5.

2. Theory of Linear Multistep Methods

The linear k-step method for the numerical integration of the initial value problem (1) is of the form

$$\sum _{i=0}^k{a}_i{y}_{n+i}=h^2\sum _{i=0}^k{b}_{i}f(t_{n+i},y_{n+i}).$$

(2)

The general method (2) is known to be associated with the linear difference operator, which is given from the expression

$$L\left(t\right)=\sum _{i=0}^k{a}_{i}y(t+ih)-h^2\sum _{i=0}^k{b}_i{y}^{″}(t+ih),$$

(3)

where $y\in C^2$.

Definition 1.

The multistep method (2) is said to be of algebraic order p if the associated linear operator L in Equation (3) vanishes for any linear combination of linearly independent functions $1,t,t^2,\dots ,t^{p+1}$.

At this point, we consider the scalar test equation

$${\displaystyle \frac{d^{2}y\left(t\right)}{d{t}^2}}=-{\omega }^{2}y\left(t\right),\omega \in {\mathbb{R}}^{+}.$$

(4)

By applying a 2k-step symmetric method to Equation (4), the difference equation below is produced:

$$A_k\left(v\right)y_{n+k}+\dots +A_1\left(v\right)y_{n+1}+A_0\left(v\right)y_n+A_1\left(v\right)y_{n-1}+\dots +A_k\left(v\right)y_{n-k},$$

(5)

where $A_0,A_1,\dots ,A_k$ are polynomials in v of the form $A_i\left(v\right)=a_i+b_i{v}^2,i=0\left(1\right)k$ and $v=\omega h$.

The characteristic equation which is associated with (5) is

$$A_k\left(v\right)s^k+\dots +A_1\left(v\right)s+A_0\left(v\right)y_n+A_1\left(v\right)s^{-1}+\dots +A_k\left(v\right)s^{-k}=0.$$

(6)

The following definitions are derived from Lambert and Watson [31]:

Definition 2.

A symmetric 2k-step method with a characteristic equation of the form (6) has an interval of periodicity $(0,s_0^2)$; if $\forall s<s_0$, the characteristic roots should satisfy the following conditions:

• ${\lambda }_0=e^{I\varphi \left(s\right)},{\lambda }_1=e^{-I\varphi \left(s\right)}$ and $|{\lambda }_i|\le 1,i=2\left(1\right)m-1$,
• where $s=\omega h$, and $\varphi \left(s\right)$ is a real function of s.

Definition 3.

For any method corresponding to the characteristic Equation (6), the phase lag is defined as the term $t=v-\varphi \left(v\right)$.

• If the quantity $t=O\left(v^{q+1}\right)$ as $v\to 0$, the order of phase lag is q, where the characteristic roots are of the form ${\lambda }_0=e^{I\varphi \left(v\right)},{\lambda }_1=e^{-I\varphi \left(v\right)},v=\omega h$ and satisfy the conditions of Definition 2.

Theorem 1.

The symmetric 2k-step method with the characteristic equation given by (6) has a phase lag q and a phase lag constant c given by

$$-c{v}^{q+2}+O\left(v^{q+4}\right)={\displaystyle \frac{2A_k\left(v\right)\cos \left(kv\right)+\dots +2A_j\left(v\right)\cos \left(jv\right)+\dots +A_0\left(v\right)}{2k^2{A}_k\left(v\right)+\dots +2j^2{A}_j\left(v\right)+\dots +2A_1\left(v\right)}}.$$

(7)

3. Development of the New Symmetric Method

This section outlines the derivation approach for an explicit symmetric linear six-step method featuring frequency-dependent coefficients.

With this objective in mind, we examine the following scheme:

$$y_3=-y_{-3}-a_2(y_2+y_{-2})-a_1(y_1+y_{-1})+h^2\left(b_2(f_2+f_{-2})+b_1(f_1+f_{-1})+b_0{f}_0\right).$$

(8)

The linear method we are about to formulate is of the sixth algebraic order and incorporates a variable coefficient as a parameter. This coefficient will be utilized to explore both accuracy and the interval of periodicity. If we apply the six-step method (8) on the scalar Equation (4), we generate the polynomials $A_k\left(v\right)|k=0\left(1\right)2$, with $v=\omega h$, where $\omega$ represents the primary frequency of the problem and h denotes the integration step size. Subsequently, using Theorem (1), we derive the expression for the method’s phase lag (PL).

$$PL={\displaystyle \frac{2\cos \left(3v\right)+2\left(b_2{v}^2+a_2\right)\cos \left(2v\right)+2\left(b_1{v}^2+a_1\right)\cos \left(v\right)+b_0{v}^2}{18+8b_2{v}^2+8a_2+2b_1{v}^2+2a_1}}.$$

(9)

To attain both zero phase lag and the highest achievable algebraic order p for Method (8), the following conditions must be satisfied:

$$PL=0.$$

(10)

$$L\left(t^i\right)=0,i=0,1,\dots ,p+1.$$

(11)

Upon solving the aforementioned system, we obtain the expressions for the method’s coefficients.

$$\begin{array}{ccc}\hfill a_1& =& -1-a_2,\hfill \\ \hfill K& =& v^2\left({\left(\cos \left(v\right)\right)}^2+1-2\cos \left(v\right)\right),\hfill \\ \hfill b_0& =& (-144{\left(\cos \left(v\right)\right)}^3+144\cos \left(v\right)+36\cos \left(v\right)a_2-112\cos \left(v\right)v^2\hfill \\ & & -72a_2{\left(\cos \left(v\right)\right)}^2+36a_2+32v^2-3v^2{a}_2-57\cos \left(v\right)v^2{a}_2\hfill \\ & & -64v^2{\left(\cos \left(v\right)\right)}^2+6v^2{a}_2{\left(\cos \left(v\right)\right)}^2)/12K,\hfill \\ \hfill b_1& =& (80v^2{\left(\cos \left(v\right)\right)}^2+16v^2+96{\left(\cos \left(v\right)\right)}^3-96\cos \left(v\right)-24\cos \left(v\right)a_2\hfill \\ & & +48a_2{\left(\cos \left(v\right)\right)}^2-24a_2+21v^2{a}_2+15v^2{a}_2{\left(\cos \left(v\right)\right)}^2)/12K,\hfill \\ \hfill b_2& =& -(48{\left(\cos \left(v\right)\right)}^3-48\cos \left(v\right)-12\cos \left(v\right)a_2+80\cos \left(v\right)v^2\hfill \\ & & +24a_2{\left(\cos \left(v\right)\right)}^2-12a_2-32v^2+3v^2{a}_2+15\cos \left(v\right)v^2{a}_2)/24K.\hfill \end{array}$$

(12)

As $v\to 0$, instead of using the above expressions, we use the Taylor series expansions.

$$\begin{array}{ccc}\hfill b_0& =& {\displaystyle \frac{52}{15}}+{\displaystyle \frac{37}{40}}{a}_2+\left(-{\displaystyle \frac{118}{315}}+{\displaystyle \frac{53}{3360}}{a}_2\right)v^2+\left({\displaystyle \frac{197}{9450}}+{\displaystyle \frac{11}{33600}}{a}_2\right)v^4\hfill \\ & & +\left(-{\displaystyle \frac{13}{69300}}-{\displaystyle \frac{19}{8870400}}{a}_2\right)v^6+\left({\displaystyle \frac{5267}{972972000}}-{\displaystyle \frac{6427}{10378368000}}{a}_2\right)v^8\hfill \\ & & +\left(-{\displaystyle \frac{589}{40864824000}}-{\displaystyle \frac{11509}{290594304000}}{a}_2\right)v^{10}\hfill \\ & & +\left(-{\displaystyle \frac{449}{308756448000}}-{\displaystyle \frac{56369}{29640619008000}}{a}_2\right)v^{12}\hfill \\ & & +\left(-{\displaystyle \frac{1723}{15506914752000}}-{\displaystyle \frac{3011933}{37845142349414400}}{a}_2\right)v^{14},\hfill \\ \hfill b_1& =& {\displaystyle \frac{4}{5}}+{\displaystyle \frac{29}{30}}{a}_2+\left({\displaystyle \frac{236}{945}}-{\displaystyle \frac{53}{5040}}{a}_2\right)v^2+\left(-{\displaystyle \frac{11}{50400}}{a}_2-{\displaystyle \frac{197}{14175}}\right)v^4\hfill \\ & & +\left({\displaystyle \frac{13}{103950}}+{\displaystyle \frac{19}{13305600}}{a}_2\right)v^6+\left(-{\displaystyle \frac{5267}{1459458000}}+{\displaystyle \frac{6427}{15567552000}}{a}_2\right)v^8\hfill \\ & & +\left({\displaystyle \frac{589}{61297236000}}+{\displaystyle \frac{11509}{435891456000}}{a}_2\right)v^{10}\hfill \\ & & +\left({\displaystyle \frac{449}{463134672000}}+{\displaystyle \frac{56369}{44460928512000}}{a}_2\right)v^{12}\hfill \\ & & +\left({\displaystyle \frac{1723}{23260372128000}}+{\displaystyle \frac{3011933}{56767713524121600}}{a}_2\right)v^{14},\hfill \\ \hfill b_2& =& {\displaystyle \frac{22}{15}}+{\displaystyle \frac{17}{240}}{a}_2+\left({\displaystyle \frac{53}{20160}}{a}_2-{\displaystyle \frac{59}{945}}\right)v^2+\left({\displaystyle \frac{197}{56700}}+{\displaystyle \frac{11}{201600}}{a}_2\right)v^4\hfill \\ & & +\left(-{\displaystyle \frac{13}{415800}}-{\displaystyle \frac{19}{53222400}}{a}_2\right)v^6+\left(-{\displaystyle \frac{6427}{62270208000}}{a}_2+{\displaystyle \frac{5267}{5837832000}}\right)v^8\hfill \\ & & +\left(-{\displaystyle \frac{589}{245188944000}}-{\displaystyle \frac{11509}{1743565824000}}{a}_2\right)v^{10}\hfill \\ & & +\left(-{\displaystyle \frac{449}{1852538688000}}-{\displaystyle \frac{56369}{177843714048000}}{a}_2\right)v^{12}\hfill \\ & & +\left(-{\displaystyle \frac{1723}{93041488512000}}-{\displaystyle \frac{3011933}{227070854096486400}}{a}_2\right)v^{14}.\hfill \end{array}$$

(13)

Local Truncation Error and Periodicity Analysis

Using Expression (13) into Method (8), we derive the principal error for the test Equation (4). This error arises from the Taylor series expansion of the difference between both sides of Equation (8), and its expression is as follows:

$$PLTE={\displaystyle \frac{3776-159a_2}{60480}}\left(y^{\left(8\right)}\left(t\right)+y^{\left(6\right)}\left(t\right){\omega }^2\right)h^8.$$

(14)

At this point, we computationally determine the interval of periodicity. Following the application of Method (8) using the coefficients outlined in (12) to address Test Problem (4), we calculate the characteristic equation for the new parametric method as defined in Equation (6). The characteristic equation obtained is expressed as follows:

$${\lambda }^6+B_2{\lambda }^5+B_1{\lambda }^4+B_0{\lambda }^3+B_1{\lambda }^2+B_2\lambda +1=0,$$

(15)

where

$$\begin{array}{ccc}\hfill B_0& =& -{\displaystyle \frac{1}{12}}{\displaystyle \frac{\left(64{\left(\cos \left(s\right)\right)}^2-6a_2{\left(\cos \left(s\right)\right)}^2+57\cos \left(s\right)a_2-32+3a_2+112\cos \left(s\right)\right)s^2}{{\left(\cos \left(s\right)-1\right)}^2}}\hfill \\ & & -{\displaystyle \frac{1}{12}}{\displaystyle \frac{144{\left(\cos \left(s\right)\right)}^3-144\cos \left(s\right)-36a_2+72a_2{\left(\cos \left(s\right)\right)}^2-36\cos \left(s\right)a_2}{{\left(\cos \left(s\right)-1\right)}^2}},\hfill \\ \hfill B_1& =& {\displaystyle \frac{1}{12}}{\displaystyle \frac{\left(15a_2{\left(\cos \left(s\right)\right)}^2+80{\left(\cos \left(s\right)\right)}^2+21a_2+16\right)s^2}{{\left(\cos \left(s\right)-1\right)}^2}}\hfill \\ & & +{\displaystyle \frac{1}{12}}{\displaystyle \frac{96{\left(\cos \left(s\right)\right)}^3+36a_2{\left(\cos \left(s\right)\right)}^2-36a_2-12{\left(\cos \left(s\right)\right)}^2-72\cos \left(s\right)-12}{{\left(\cos \left(s\right)-1\right)}^2}},\hfill \\ \hfill B_2& =& -{\displaystyle \frac{1}{24}}{\displaystyle \frac{\left(15\cos \left(s\right)a_2+3a_2+80\cos \left(s\right)-32\right)s^2}{{\left(\cos \left(s\right)-1\right)}^2}}\hfill \\ & & -{\displaystyle \frac{1}{24}}{\displaystyle \frac{48{\left(\cos \left(s\right)\right)}^3+36\cos \left(s\right)a_2-36a_2-48\cos \left(s\right)}{{\left(\cos \left(s\right)-1\right)}^2}},\hfill \\ \hfill s& =& \omega h.\hfill \end{array}$$

We perform computational analysis on the characteristic Equation (15) over a broad spectrum of coefficient values, $a_2$. In this process, we ascertain the periodicity interval by assessing the conditions stipulated in Definition 2 for the set $\left\{\widehat{s}\right|{\widehat{s}}^2\in (0,s_0^2)\}$, where $\widehat{s}=n\Delta s,n\in {\mathbb{N}}_0$ and $\Delta s={10}^{-2}$. The results of this investigation are illustrated in Figure 1.

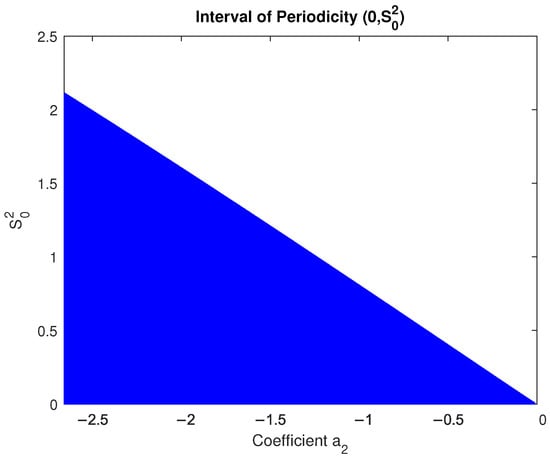
Figure 1. Method’s periodicity interval with respect to the coefficient $a_2$.

It is important to emphasize that the method exhibits a non-zero periodicity interval exclusively when $a_2$ falls within the range of $(-2.67,0)$. Furthermore, the method displays convergence within this identical interval due to its inherent consistency. As depicted in Figure 1, the reduction in the value of $a_2$ corresponds to an expansion of the periodicity interval. In addition, a similar behavior is observed in the case of the local truncation error, evident from Equation (14), and notably from Expression ${\displaystyle \frac{3776-159a_2}{60480}}$. This expression reaches its maximum value as $a_2$ approaches $-{2.67}^{+}$ and its minimum value as $a_2$ tends towards $0^{-}$. Therefore, the objective is to identify the optimal value of $a_2$ that simultaneously minimizes the error and ensures the stability of the method.

4. Numerical Results

4.1. The Problems

The recently introduced method, described above, was applied to three widely recognized oscillatory problems.

• The Schrödinger equation—resonance problem;
• The orbit problem of Stiefel and Bettis;
• The Duffing equation.

The description of these problems is given below.

4.1.1. Schrödinger Equation—Resonance Problem

The one-dimensional or radial Schrödinger equation has the form

$$\begin{array}{c}\hfill y^{″}\left(x\right)+\left(E-{\displaystyle \frac{l(l+1)}{x^2}}-V\left(x\right)\right)y\left(x\right)=0,\end{array}$$

(16)

where

• $x\in {\mathbb{R}}^{\ast }$,
• E is the energy,
• $l(l+1)/x^2$ is the centrifugal potential,
• $V\left(x\right)$ the electric potential

The function $W\left(x\right)=l(l+1)/x^2+V\left(x\right)$ is the effective potential, where ${lim}_{x\to \infty }V\left(x\right)=0$, and so ${lim}_{x\to \infty }W\left(x\right)=0$. Furthermore, there is the boundary condition $y\left(0\right)=0$ and a second boundary condition, which is determined by physical considerations for large values of x.

For our numerical illustration, we will consider the integration domain as $x\in [0,15]$, applying the Woods–Saxon potential:

$$\begin{array}{c}\hfill V\left(x\right)={\displaystyle \frac{u_0}{1+q}}+{\displaystyle \frac{u_{1}q}{{(1+q)}^2}},q=exp\left({\displaystyle \frac{x-x_0}{\alpha }}\right),where\\ \hfill u_0=-50,\alpha =0.6,x_0=7,u_1=-{\displaystyle \frac{u_0}{\alpha }}.\end{array}$$

(17)

For positive energies $(E=k^2)$, the potential $V\left(x\right)$ dies away faster than the centrifugal potential $(l(l+1)/x^2)$; therefore, for large values of x, the Schrödinger equation effectively reduces to

$$y^{″}\left(x\right)+(k^2-{\displaystyle \frac{l(l+1)}{x^2}})y\left(x\right)=0.$$

(18)

Equation $\left(18\right)$ has two linearly independent solutions. These are $kx{j}_l\left(kx\right)$ and $kx{n}_l\left(kx\right)$, where $j_l$ and $n_l$ represent the spherical Bessel and Neumann functions, respectively. As $x\to \infty$, the solution to Equation $\left(16\right)$ takes the following asymptotic form:

$$\begin{array}{c}\hfill y\left(x\right)\simeq Akx{j}_l\left(kx\right)-Bkx{n}_l\left(kx\right)\\ \hfill \simeq D\left[sin\left(kx-{\displaystyle \frac{l\pi }{2}}\right)+tan\left({\delta }_l\right)cos\left(kx-{\displaystyle \frac{l\pi }{2}}\right)\right],\end{array}$$

(19)

where ${\delta }_l$ is the scattering phase shift, which may be approximated by the following expression:

$$tan\left({\delta }_l\right)\simeq {\displaystyle \frac{y\left(x_i\right)S\left(x_{i+1}\right)-y\left(x_{i+1}\right)S\left(x_i\right)}{y\left(x_{i+1}\right)C\left(x_i\right)-y\left(x_i\right)C\left(x_{i+1}\right)}},$$

(20)

where $S\left(x\right)=kx{j}_l\left(kx\right),C\left(x\right)=kx{n}_l\left(kx\right)$ and $x_i<x_{i+1}$ both exist in the asymptotic region.

In the case of positive energies ($E>0$) and for $l=0$, we approximate $\left({\delta }_l\right)$ based on (20) and then compare its value to the exact value $\pi /2$. For this eigenvalue problem, the boundary conditions are $y\left(0\right)=0$ and $y\left(x\right)=cos\left(\sqrt{E}x\right)$ for large x.

We use the eigenenergy $E=989.701916$; for the frequency, we use the suggestion of Ixaru and Rizea [32].

$$\omega =\{\begin{array}{ll}\sqrt{E+50},& x\in [0,6.5]\\ \sqrt{E},\hfill & x\in [6.5,15].\end{array}$$

4.1.2. Orbit Problem of STIEFEL and Bettis

Stiefel and Bettis (1969) [33] studied the orbit problem, which is given below.

$$\begin{array}{c}\hfill {\displaystyle \frac{d^{2}y\left(t\right)}{d{t}^2}}=-y\left(t\right)+ϵexp\left(it\right),y\left(t\right)\in C\\ \hfill y\left(0\right)=1,y^{\prime }\left(0\right)=(1-{\displaystyle \frac{1}{2}}ϵ)i,\end{array}$$

(21)

where $ϵ=0.001$.

The analytical solution of the problem (21) is

$$\begin{array}{c}\hfill y\left(t\right)=cos\left(t\right)+{\displaystyle \frac{1}{2}}ϵtsin\left(t\right)+i[sin\left(t\right)-{\displaystyle \frac{1}{2}}ϵtcos\left(t\right)].\end{array}$$

Equivalently, Problem (21) can be described from the system

$$\begin{array}{ccc}& & {\displaystyle \frac{d^2{y}_1\left(t\right)}{d{t}^2}}=-y_1+0.001\cos \left(t\right),y_1\left(0\right)=1,y_1^{\prime }\left(0\right)=0,\hfill \\ & & {\displaystyle \frac{d^2{y}_2\left(t\right)}{d{t}^2}}=-y_2+0.001sin\left(t\right),y_2\left(0\right)=0,y_2^{\prime }\left(0\right)=0.9995.\hfill \end{array}$$

(22)

The analytical solution of the system (22) is

$$\begin{array}{ccc}& & y_1\left(t\right)=\cos \left(t\right)+0.0005tsin\left(t\right),\hfill \\ & & y_2\left(t\right)=sin\left(t\right)-0.0005t\cos \left(t\right).\hfill \end{array}$$

The estimated frequency for this problem is $\omega =1$.

4.1.3. Duffing Equation

The Duffing equation can be described by

$$\begin{array}{c}\hfill {\displaystyle \frac{d^{2}y\left(t\right)}{d{t}^2}}=-y\left(t\right)-{\left(y\left(t\right)\right)}^3+Bcos\left(\omega t\right),\end{array}$$

(23)

where $B=0.002$

The analytical solution of (23) is

$$y\left(t\right)=A_{1}cos\left(\omega t\right)+A_{3}cos\left(3\omega t\right)+A_{5}cos\left(5\omega t\right)+A_{7}cos\left(7\omega t\right)+A_{9}cos\left(9\omega t\right),$$

where

• $A_1=0.200179477536$,
• $A_3=0.000246946143$,
• $A_5=0.000000304014$,
• $A_7=0.000000000374$ and
• $A_9=0.000000000000$.

The estimated frequency for this problem is $\omega =1.01$.

4.2. The Compared Methods

To evaluate the efficiency of the new method, we compare it with five well-known sixth-algebraic-order phase-fitted explicit methods with variable coefficients. The methods used in the comparison are

• Method A: The new phase-fitted parametric method which was derived in Section 3 (for a wide range of parameter $a_2$).
• Method B: The four-step phase-fitted method, developed by Simos [9].
• Method C: The Numerov-type hybrid method, developed by Konguetsof [14].
• Method D: The Runge–Kutta-type hybrid method, developed by Alolyan and Simos [11].
• Method E: The zero-dissipative hybrid method, developed by Ahmad et al. [10].
• Method F: The high-order method of the Runge–Kutta–Nyström pair, developed by Anastassi and Kosti [1].

4.3. Effectiveness and Optimal Values for the New Parametric Method

In Figure 2, Figure 3 and Figure 4, we visualize the evaluation of the novel parametric approach, which is represented as $-lo{g}_{10}\left(error\right)$, relative to the coefficient $a_2$. The error in this context is determined differently for distinct scenarios: in the case of known accurate solutions, such as the Stiefel–Bettis problem and the Duffing equation, the error corresponds to the maximum absolute error value of the integration interval. In the case of the Schrödinger equation, the error is defined as $|{\delta }_l-\pi /2|$.

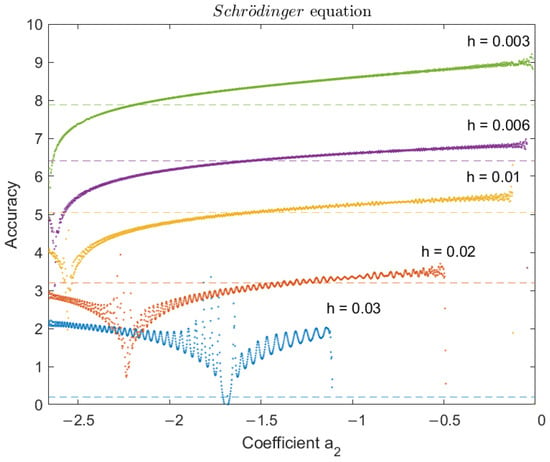
Figure 2. Efficiency of the new method for all values of $a_2$—Schrödinger equation.

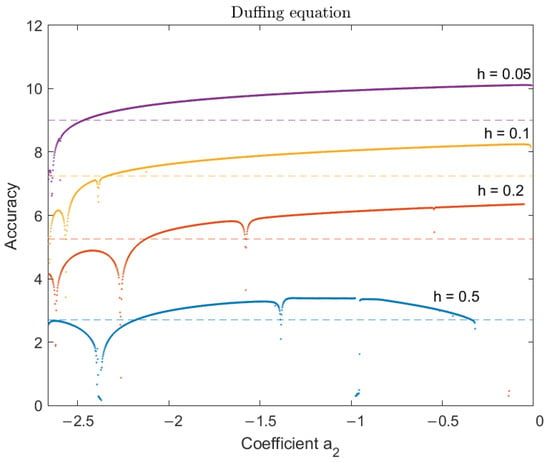
Figure 3. Efficiency of the new method for all values of $a_2$—Duffing equation.

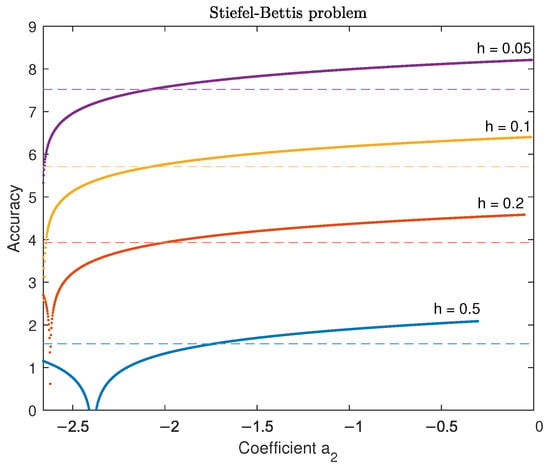
Figure 4. Efficiency of the new method for all values of $a_2$—Stiefel–Bettis problem.

Each of these figures illustrates the accuracy of the new method, represented by small dots (appearing as solid lines) across all values of the parameter $a_2$ and for various integration step sizes h. As expected, smaller integration steps result in higher accuracy. The variety of colors in the graphs corresponds to different integration step lengths, as indicated in the figures’ legends. The dashed line, shown in a specific color, signifies the highest level of accuracy achieved by alternative methods in the comparative analysis (see Section 4.2) while requiring the same computational effort—measured as $lo{g}_{10}$ of the number of function evaluations—as the new parametric method.

For instance, in the case of the Stiefel and Bettis problem (Figure 4), when the new method is employed with a step size of $h=0.05$, its initial accuracy is relatively low (<5.5) for values of $a_2\to -{2.66}^{+}$. However, it progressively improves, surpassing an accuracy level of 8 as $a_2\to 0^{-}$. Among the other methods subjected to the same number of function evaluations required by the new method (for $h=0.05$), the most efficient demonstrates an accuracy of approximately $7.4$, denoted by the same color dashed horizontal line (as accuracy for the other methods does not depend on the coefficient $a_2$). The intersection points reveal that the new parametric method consistently outperforms the other methods under consideration for all values of $a_2$ exceeding approximately $-1.6$. Points where the graph lacks small dots indicate that the parametric method exhibits instability. This typically occurs when employing large step-size values (h) and for high values of the coefficient ($a_2$).

Furthermore, in terms of effectiveness, there exists a substantial range of values for the coefficient $a_2$, where the new method consistently delivers the highest level of accuracy. These specific intervals commence at the point of intersection between the small dots and the dashed line. For the Schrödinger equation, this interval begins at approximately $-1.6$, for the Duffing equation at $-2.2$, and for the Stiefel–Bettis problem at $-2.1$.

Regarding the upper limit of this interval, it varies depending on whether our priority is to obtain a highly accurate solution or a faster, albeit less accurate one. In pursuit of enhanced accuracy, our objective is to choose a value for $a_2$ that closely approaches the upper limit of this interval. When our aim is to achieve a quicker solution with reduced accuracy, for example, an accuracy level of 1 or 2, it becomes necessary to adjust the upper limit of the interval within which $a_2$ operates in order to maintain the method’s stability. Specifically, these adjusted upper limits are as follows: $-1.2$ for the Schrödinger equation and $-0.3$ for the rest of the problems.

The new method’s accuracy exhibits occasional spikes across different combinations of h and $a_2$ values. These spikes are a result of resonances triggered by the presence of spurious roots within the characteristic equation of the method. It is essential to recognize that these resonances vary for different values of $a_2$, and this phenomenon is inherent in all linear multistep methods comprising more than two steps. Quinlan’s extensive investigation of this behavior, with further details available in [34], sheds light on the matter. Fortunately, when considering the recommended optimal $a_2$ values outlined below, the new method consistently outperforms the compared methods.

Considering the examination presented in the preceding paragraphs, the recommended values for the coefficient $a_2$ are presented in Table 1.

Table 1. Optimal values of the parameter $a_2$.

Value of ${\mathit{a}}_2$	Accuracy
$a_2=-{\displaystyle \frac{1}{20}}$	for high accuracy (>8)
$a_2=-1.5$	for fast solution with low accuracy (≈2)
$a_2\in (-1.5,-{\displaystyle \frac{1}{20}})$	for medium accuracy

4.4. Comparison of the New Parametric Method with Other Phase-Fitted Methods Based on Optimal Values and Upper Limits for $a_2$

At this point, we demonstrate the accuracy of the new method against the phase-fitted methods described in Section 4.2 by choosing a value for the coefficient $a_2$ based on the upper limits discussed in Section 4.3. We choose to measure the efficiency of the method by computing the accuracy in the decimal digits, which is $-lo{g}_{10}$ (maximum error through the integration intervals) versus the computational effort measured by the $lo{g}_{10}$ (number of function evaluations required).

Following the analysis preceded in Section 4.3, we choose a value of $-1.2$ for parameter $a_2$, which is the upper limit of the interval for the Schrödinger equation. In Figure 5, Figure 6 and Figure 7, we display the results. According to the results, the proposed method demonstrates superior effectiveness in all three problems, achieving higher accuracy than the other methods in the comparison.

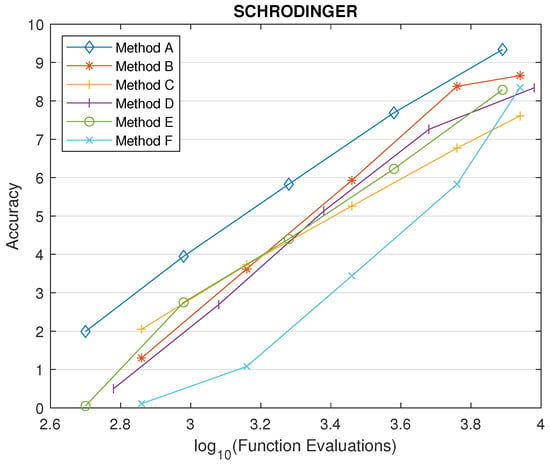
Figure 5. Comparison for the Schrödinger equation.

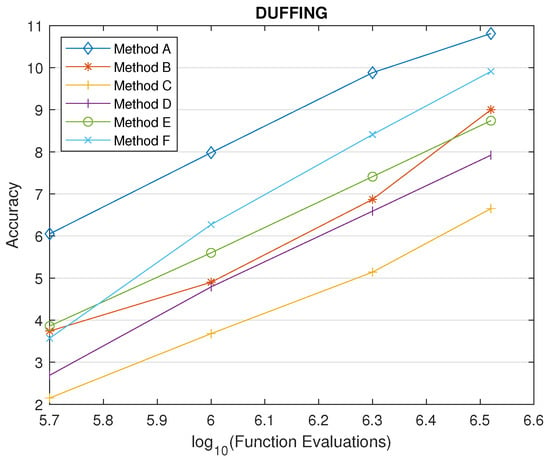
Figure 6. Comparison for the Duffing equation.

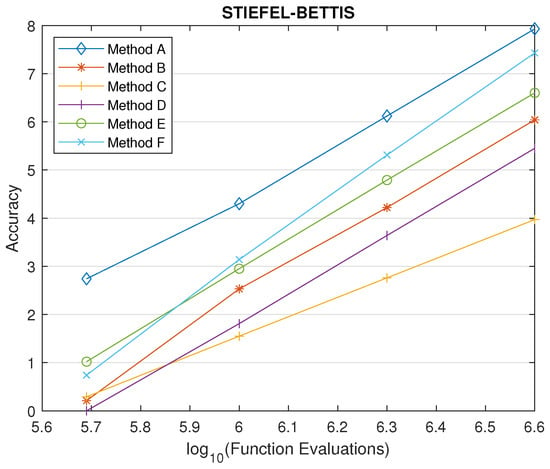
Figure 7. Comparison for the Stiefel–Bettis problem.

5. Conclusions

This study introduces a six-step parametric phase-fitting method with frequency-dependent coefficients for the numerical solution of oscillatory problems. We evaluated the efficiency of our new method across a wide spectrum of parameter values and conducted a comparative assessment against established methods in the existing literature. The numerical results guided us toward identifying optimal values for the parameter, establishing the high efficiency of the new method.

The superiority of the proposed method is demonstrated by its accuracy across all the problems tested in the manuscript. The absence of intermediate stages in the proposed multistep method ensures fast and direct computation of $y_k$, offering an advantage over methods with intermediate stages, such as Runge–Kutta. Furthermore, based on the periodicity interval analysis, researchers can select the optimal parameter value depending on whether their goal is a highly accurate numerical solution or a faster solution with lower accuracy. It is worth noting that, like all linear multistep methods, the proposed method requires a one-step method to compute the initial $y_{k-1}$ values. Additionally, the proposed technique is particularly well suited for the numerical solution of frequency-dependent problems where a good estimate of the frequency is known in advance. In contrast, methods with constant coefficients may be more appropriate for other types of problems.

Determining the periodicity interval computationally presents a significant challenge due to the substantial computational effort required and the rounding errors that may occur during the process. In future research, we aim to tackle these challenges by developing and implementing implicit linear multistep methods and one-step methods based on the proposed technique.