Efficient Estimation and Response Variable Selection in Sparse Partial Envelope Model

Abstract

In this paper, we propose a sparse partial envelope model that performs response variable selection efficiently under the partial envelope model. We discuss its theoretical properties including consistency, an oracle property and the asymptotic distribution of the sparse partial envelope estimator. A large-sample situation and high-dimensional situation are both considered. Numerical experiments demonstrate that the sparse partial envelope estimator has excellent response variable selection performance both in the large-sample situation and the high-dimensional situation. Moreover, simulation studies and real data analysis suggest that the sparse partial envelope estimator has a much more competitive performance than the standard estimator, the oracle partial envelope estimator, the active partial envelope estimator and the sparse envelope estimator, whether it is in the large-sample situation or the high-dimensional situation.

1. Introduction

Consider the multivariate linear regression model, which has the stochastic predictor vector $X\in {\mathbb{R}}^p$ and the multivariate response vector $Y\in {\mathbb{R}}^r$,

$$\begin{array}{c}\hfill Y=\alpha +\beta X+\epsilon ,\end{array}$$

(1)

where $\alpha \in {\mathbb{R}}^r$ is the unknown intercept, $\beta \in {\mathbb{R}}^{r\times p}$ is the unknown regression coefficient matrix, the error vector $\epsilon$ has mean zero and unknown covariance matrix $\mathsf{\Sigma }>0$, which is independent of X. The data comprise n independent realizations $Y_i$ of Y, which are observed at corresponding values $X_i$ of $X(i=1,\dots ,n)$. The multivariate linear regression model (1) is a cornerstone of multivariate statistics, and researching the interrelation between X and Y through the regression coefficient matrix $\beta \in {\mathbb{R}}^{r\times p}$ is the main focus. In this article, we not only center on the correlation between X and Y, but we also pay attention to the response variable selection. Although a response has zero coefficients, it can still improve the estimation efficiency of the nonzero coefficients. In this paper, we suppose that $n>p$ since one of the main focuses of this article is response variable selection.

Cook et al. [1] introduced a response envelope model, and it is based on the idea that a projection of the response vector Y may be immaterial to the purpose of estimating $\beta$, whereas contributing extraneous variation induces the estimator of $\beta$ to be more variable. Envelope estimation explains such extraneous variation, and this operation makes the estimator of $\beta$ potentially much more efficient. On the basis of the research results in Cook et al. [1], many scholars have extended the idea of envelopes to a more general background and have proposed a lot of new models to obtain greater efficiency gains (Su and Cook [2,3,4], Cook et al. [5], Su et al. [6], Cook and Zhang [7,8,9], Khare et al. [10], Li and Zhang [11], Zhang and Li [12], Pan et al. [13], Zhu and Su [14]).

Su et al. [6] proposed the sparse envelope model, which carries out variable selection on the responses and maintains the efficiency gains provided by the envelope model, and discussed response variable selection in both the standard multivariate linear regression and the envelope background. Meanwhile, they established consistency and the oracle property and acquired the asymptotic distribution of the sparse envelope estimator. Zhu and Su [14] proposed the envelope-based sparse partial least squares (SPLS) by employing a connection between envelope models and partial least squares (PLS). They established the consistency, oracle property and asymptotic normality of the envelope-based sparse partial least squares estimator, and considered the large-sample scenario and high-dimensional scenario. Meanwhile, they developed the envelope-based sparse partial least squares estimators under the setting of generalized linear models and discussed its theoretical properties including consistency, oracle property and asymptotic distribution.

In this article, based on the research work of Su et al. [6], we propose a novel sparse partial envelope model that can implement response variable selection and improve parameter estimation efficiency. It has the following major contributions. First, the theoretical properties of the sparse partial envelope estimator can be studied. We build $\sqrt{n}$-consistency, asymptotic normality and the oracle property in the large-sample situation and investigate the rate of convergence and selection consistency in the high-dimensional situation. Second, through the simulation studies, we find that the sparse partial envelope model has excellent response variable selection performances both in small r large n situations and small n large r situations. Furthermore, the sparse partial envelope estimator is much more efficient than the standard estimator, the oracle partial envelope estimator, the active partial envelope estimator and the sparse envelope estimator in small r large n situations. Third, via the real data analysis, we also discover that the sparse partial envelope model has an obvious efficiency gain than the sparse envelope model in small n large r situations. In short, the sparse partial envelope model is more flexible than the sparse envelope model.

The rest of the article is organized as follows. Section 2 reviews the envelope model and the partial envelope model. Section 3 demonstrates how the sparse partial envelope model is proposed. Section 4 shows theoretical properties in the sparse partial envelope model estimators. Simulation studies are carried out in Section 5. A real data analysis is given in Section 6. Some remarks are displayed in Section 7. The proofs of theorems and propositions are provided in the part of Appendix.

2. Review of the Envelope Model and Partial Envelope Model

The envelope model (Cook et al. [1]) is designed to discover the smallest subspace $\mathcal{E}\subseteq {\mathbb{R}}^r$ that satisfies the following two conditions:

$$\begin{array}{cc}\hfill & \left(a\right)Q_{\mathcal{S}}Y|X\sim Q_{\mathcal{S}}Y,\hfill \\ \hfill & \left(b\right)Q_{\mathcal{S}}Y⨿P_{\mathcal{S}}Y|X.\hfill \end{array}$$

(2)

The sign ‘∼’ represents identically distributed, and the sign ‘⨿’ represents statistically independent. The symbol $P_{(·)}$ projects onto the subspace and $Q=I_r-P$. Property (a) implies that the distribution of $Q_{\mathcal{S}}Y$ does not rely on X, so $Q_{\mathcal{S}}Y$ has no information about $\beta$. Property (b) implies that $Q_{\mathcal{S}}Y$ is conditionally independent of $P_{\mathcal{S}}Y$ given X, and thus, $Q_{\mathcal{S}}Y$ cannot transmit information about $\beta$ by virtue of a link with $P_{\mathcal{S}}Y$. The entire immaterial information in Y can be obtained by detecting the smallest subspace $\mathcal{S}$ that satisfies the requirements in (2). Let $\mathcal{B}=\mathrm{span}\left(\beta \right)$. Cook et al. [1] showed that conditions (2) are equal to the following two conditions:

$$\begin{array}{cc}\hfill & \left(2a\right)\mathcal{B}\subseteq \mathcal{S},\hfill \\ \hfill & \left(2b\right)\mathsf{\Sigma }=P_{\mathcal{S}}\mathsf{\Sigma }{P}_{\mathcal{S}}+Q_{\mathcal{S}}\mathsf{\Sigma }{Q}_{\mathcal{S}}.\hfill \end{array}$$

(3)

Condition (2b) holds if and only if $P_{\mathcal{S}}Y$ and $Q_{\mathcal{S}}Y$ are uncorrelated given X, and it is equivalent to claiming that $\mathcal{S}$ is a reducing subspace of $\mathsf{\Sigma }$. Conditions (3) indicate that we can obtain all of the immaterial information by selecting $\mathcal{S}$ to be the intersection of all reducing subspaces of $\mathsf{\Sigma }$ that include $\mathcal{B}$, which is called the $\mathsf{\Sigma }$-envelope of $\mathcal{B}$ and denoted by ${\mathcal{E}}_{\mathsf{\Sigma }}\left(\mathcal{B}\right)$ or shortened to $\mathcal{E}$.

Let $u=\dim \left\{{\mathcal{E}}_{\mathsf{\Sigma }}\left(\mathcal{B}\right)\right\}$, and let $\mathsf{\Gamma }\in {\mathbb{R}}^{r\times u}$ and ${\mathsf{\Gamma }}_0\in {\mathbb{R}}^{r\times (r-u)}$ denote semi-orthogonal basis matrices for ${\mathcal{E}}_{\mathsf{\Sigma }}\left(\mathcal{B}\right)$ and ${\mathcal{E}}_{\mathsf{\Sigma }}^{\perp }\left(\mathcal{B}\right)$ separately. Via imposing conditions (3) on the standard model (1), the coordinate form of the envelope model can be expressed as below:

$$\begin{array}{c}\hfill Y=\alpha +\mathsf{\Gamma }\eta X+\epsilon ,\mathsf{\Sigma }=\mathsf{\Gamma }\mathsf{\Omega }{\mathsf{\Gamma }}^T+{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T,\end{array}$$

(4)

where $\beta =\mathsf{\Gamma }\eta$, $\eta \in {\mathbb{R}}^{u\times p}$ is the coordinates of $\beta$ with respect to $\mathsf{\Gamma }$, and $\mathsf{\Omega }\in {\mathbb{R}}^{u\times u}$ and ${\mathsf{\Omega }}_0\in {\mathbb{R}}^{(r-u)\times (r-u)}$ are both positive definite matrices. Su and Cook [2] extended the envelope model to the partial envelope model. The partial envelopes pay attention to the coefficients consistent with the predictors of interest. They partition X into two sets of predictors $X_1\in {\mathbb{R}}^{p_1}$ and $X_2\in {\mathbb{R}}^{p_2}$, $p_1+p_2=p$, $p_1<r$, and partition correspondingly the columns of $\beta$ into ${\beta }_1$ and ${\beta }_2$. Then, model (1) can be rephrased as $Y=\alpha +{\beta }_1{X}_1+{\beta }_2{X}_2+\epsilon$, where ${\beta }_1$ is corresponding to the coefficients of interest. The $\mathsf{\Sigma }$-envelope for ${\mathcal{B}}_1=\mathrm{span}\left({\beta }_1\right)$ is mainly thought over, leaving ${\beta }_2$ as an unrestricted parameter. This generates the parametric structure ${\mathcal{B}}_1\subseteq {\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)$ and $\mathsf{\Sigma }=P_{{\mathcal{E}}_1}\mathsf{\Sigma }{P}_{{\mathcal{E}}_1}+Q_{{\mathcal{E}}_1}\mathsf{\Sigma }{Q}_{{\mathcal{E}}_1}$, where $P_{{\mathcal{E}}_1}$ denotes the projection onto ${\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)$ called the partial envelope for ${\mathcal{B}}_1$. This is the same as the envelope structure, except the partial envelop is correlated with ${\mathcal{B}}_1$ instead of the larger space $\mathcal{B}$. In order to emphasize the partial envelope, ${\mathcal{E}}_{\mathsf{\Sigma }}\left(\mathcal{B}\right)$ is regarded as the full envelope. Due to ${\mathcal{B}}_1\subseteq \mathcal{B}$, the partial envelope is included in the full envelope, ${\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)\subseteq {\mathcal{E}}_{\mathsf{\Sigma }}\left(\mathcal{B}\right)$. More analogous descriptions of the envelope model and the partial envelope model can be found in Zhang et al. [15], Zhang et al. [16], and Zhang and Huang [17].

Let $u_1=\dim \left\{{\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)\right\}$, and let $\mathsf{\Gamma }\in {\mathbb{R}}^{r\times u_1}$ be a semi-orthogonal matrix with ${\mathsf{\Gamma }}^T\mathsf{\Gamma }=I_{u_1}$, and its columns form a basis for ${\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)$. Let $(\mathsf{\Gamma },{\mathsf{\Gamma }}_0)\in {\mathbb{R}}^{r\times r}$ be an orthogonal matrix and $\eta \in {\mathbb{R}}^{u_1\times p_1}$ be the coordinates of ${\beta }_1$ related to the basis matrix $\mathsf{\Gamma }$. Then, a coordinate version of the partial envelope model can be written as follows:

$$\begin{array}{c}\hfill Y=\alpha +\mathsf{\Gamma }\eta X_1+{\beta }_2{X}_2+\epsilon ,\mathsf{\Sigma }=\mathsf{\Gamma }\mathsf{\Omega }{\mathsf{\Gamma }}^T+{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T,\end{array}$$

(5)

where $\mathsf{\Omega }\in {\mathbb{R}}^{u_1\times u_1}$ and ${\mathsf{\Omega }}_0\in {\mathbb{R}}^{(r-u_1)\times (r-u_1)}$ are both positive definite matrices, and they serve as coordinates of ${\mathsf{\Sigma }}_{{\mathcal{E}}_1}$ and ${\mathsf{\Sigma }}_{{\mathcal{E}}_1^{\perp }}$ separately which are related to the basis matrices $\mathsf{\Gamma }$ for ${\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)$ and ${\mathcal{E}}_{\mathsf{\Sigma }}^{\perp }\left({\mathcal{B}}_1\right)$. For a more in-depth description, $R_{1\mid 2}$ represents the population residuals from the multivariate linear regression of $X_1$ on $X_2$. The predictor X is centered. In this way, the linear model can be re-parameterized as $Y=\alpha +{\beta }_1{R}_{1\mid 2}+{\beta }_2^{\ast }{X}_2+\epsilon$, where ${\beta }_2^{\ast }$ is a linear combination of ${\beta }_1$ and ${\beta }_2$. Next, $R_{Y\mid 2}=Y-\alpha -{\beta }_2^{\ast }{X}_2$ denotes the population residuals from the regression of Y on $X_2$ alone. A linear model which contains ${\beta }_1$ alone is written as $R_{Y\mid 2}={\beta }_1{R}_{1\mid 2}+\epsilon$. The partial envelope ${\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)$ is identical to the full envelope for ${\mathcal{B}}_1$ in the regression of $R_{Y\mid 2}$ on $R_{1\mid 2}$. In other words, the partial envelope can be interpreted in terms of $Q_{\mathcal{S}}Y|X\sim Q_{\mathcal{S}}Y,Q_{\mathcal{S}}Y⨿P_{\mathcal{S}}Y\mid X$, which is applied to the regression of $R_{Y\mid 2}$ on $R_{1\mid 2}$. The predictors are centered, so the maximum likelihood estimator of $\alpha$ is simply $\widehat{\alpha }=\overline{Y}$. The estimators of the remaining parameters require the estimator of ${\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)$. See Zhang et al. [18] for a similar characterization.

The estimator of the partial envelope ${\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)$ is acquired by solving the following optimization problem:

$$\begin{array}{c}\hfill {\widehat{\mathcal{E}}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)=\underset{\mathrm{span}\left(\mathsf{\Gamma }\right)\in \mathcal{G}(r,u_1)}{argmin}\left\{\log |{\mathsf{\Gamma }}^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}\mathsf{\Gamma }|+\log |{\mathsf{\Gamma }}^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}\mathsf{\Gamma }|\right\},\end{array}$$

(6)

where $\mathcal{G}(r,u_1)$ denotes an $r\times u_1$ Grassmann manifold, which is the set of all $u_1$-dimensional subspaces in an r-dimensional space, ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}$ denotes the sample covariance matrix of the residuals from the least squares regression of $R_{Y\mid 2}$ on $R_{1\mid 2}$, and ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}$ denotes the sample covariance matrix of $R_{Y\mid 2}$. The optimization is carried out on $\mathcal{G}(r,u_1)$, (6) is a Grassmann manifold optimization problem. The objective function is non-convex. Because the estimation of ${\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)$ contains manifold optimization, it can be slow in high-dimensional settings. To solve these problems, Cook et al. [19] converted the problems into a non-manifold optimization through a reparameterization of $\mathsf{\Gamma }$. In general, ${\mathsf{\Gamma }}_1$, which is composed of the first $u_1$ rows of $\mathsf{\Gamma }$, is assumed to be nonsingular. Then,

$$\begin{array}{c}\hfill \mathsf{\Gamma }=\left(\begin{array}{c}{\mathsf{\Gamma }}_1\\ {\mathsf{\Gamma }}_2\end{array}\right)=\left(\begin{array}{c}{I}_{u_1}\\ A\end{array}\right){\mathsf{\Gamma }}_1\equiv G_A{\mathsf{\Gamma }}_1,\end{array}$$

where $A={\mathsf{\Gamma }}_2{\mathsf{\Gamma }}_1^{-1}$ and $G_A=\mathsf{\Gamma }{\mathsf{\Gamma }}_1^{-1}$. Note that $A\in {\mathbb{R}}^{(r-u_1)\times u_1}$ characterizes ${\mathcal{E}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)$ since A depends on $\mathsf{\Gamma }$ only through $\mathrm{span}\left(\mathsf{\Gamma }\right)$. Because A is unconstrained, under this parameterization, the optimization problem in (6) is converted to the following unconstrained non-manifold optimization problem:

$$\begin{array}{c}\hfill \widehat{A}=\underset{A\in {\mathbb{R}}^{(r-u_1)\times u_1}}{argmin}\left\{-2\log |G_A^T{G}_A|+\log |G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A|+\log |G_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}{G}_A|\right\}.\end{array}$$

(7)

Once we obtain $\widehat{A}$ from (7), ${\widehat{\mathcal{E}}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)=\mathrm{span}({\widehat{G}}_A)$, and then the partial envelope estimator of ${\beta }_1$ is ${\widehat{\beta }}_{1,\mathrm{penv}}=P_{\widehat{\mathcal{E}},1}{\widehat{\beta }}_{1,\mathrm{ols}}$, where ${\widehat{\beta }}_{1,\mathrm{ols}}$ is the ordinary least squares estimator of ${\beta }_1$. By the results of Su and Cook [2], the partial envelope estimator ${\widehat{\beta }}_{1,\mathrm{penv}}$ is as efficient as or more efficient than ${\widehat{\beta }}_{1,\mathrm{ols}}$.

3. Sparse Partial Envelope Model

We first define active responses and inactive responses. In Su et al. [6], if the corresponding rows of $\mathsf{\Gamma }$ are composed of zeros, such response variables are called inactive; if its corresponding rows in $\mathsf{\Gamma }$ consist of nonzero values, such response variables are called active. Because ${\beta }_1=\mathsf{\Gamma }\eta$, the regression coefficients of the inactive responses are zero. However, an active response may also have zero regression coefficients. Properties of the active responses were researched by Su et al. [6] (Proposition 1) under the background of the sparse response envelope. Analogous results are built for the sparse partial envelope model: if the regression coefficients of an active response are all zero, then the response must have a relation to a response that has nonzero regression coefficients. This proposition demonstrates that if an active response has zero regression coefficients, it still provides information in estimating the nonzero regression coefficients. This is a fresh characteristic of response variable selection.

Without the loss of generality, we can write $Y={\left(Y_{\mathcal{A}}^T,Y_{\mathcal{I}}^T\right)}^T$, and let q denote the dimension of $Y_{\mathcal{A}}(q⩽r)$, where $Y_{\mathcal{A}}\in {\mathbb{R}}^q$ denotes the active responses and $Y_{\mathcal{I}}\in {\mathbb{R}}^{r-q}$ denotes the inactive responses. The subscripts $\mathcal{A}$ and $\mathcal{I}$ are employed to a quantity if it is associated with active and inactive responses. For instance, $r_{\mathcal{A}}$ and $r_{\mathcal{I}}$ denote the number of active and inactive responses, and $r_{\mathcal{A}}+r_{\mathcal{I}}=r$. Then, $\mathsf{\Gamma }$, ${\mathsf{\Gamma }}_0$ and ${\beta }_2$ for the partial envelope model (5) have the following sparse structure:

$$\begin{array}{c}\hfill \mathsf{\Gamma }=\left(\begin{array}{c}{\mathsf{\Gamma }}_{\mathcal{A}}\hfill \\ 0\hfill \end{array}\right),{\mathsf{\Gamma }}_0=\left(\begin{array}{cc}{\mathsf{\Gamma }}_{\mathcal{A},0}\hfill & \hfill 0\\ 0\hfill & \hfill I_{r-q}\end{array}\right)R,{\beta }_2=\left(\begin{array}{c}{\beta }_{2,\mathcal{A}}\hfill \\ 0\hfill \end{array}\right),\end{array}$$

(8)

where ${\mathsf{\Gamma }}_{\mathcal{A}}\in {\mathbb{R}}^{q\times u_1}$ is a semi-orthogonal matrix, ${\mathsf{\Gamma }}_{\mathcal{A},0}\in {\mathbb{R}}^{q\times (q-u_1)}$ is its completion, $R\in$${\mathbb{R}}^{(r-u_1)\times (r-u_1)}$ is an orthogonal matrix, and ${\beta }_{2,\mathcal{A}}\in {\mathbb{R}}^{q\times (p-p_1)}$ denotes the coefficients for the active responses and the zero matrix has the dimension $(r-q)\times (p-p_1)$. Because ${\mathsf{\Gamma }}^{T}Y={\mathsf{\Gamma }}_{\mathcal{A}}^T{Y}_{\mathcal{A}}$, the inactive responses do not occur in the material part.

We call (5) the sparse partial envelope model if $\mathsf{\Gamma }$, ${\mathsf{\Gamma }}_0$ and ${\beta }_2$ have the sparse structure (8). Its estimator of ${\beta }_1$ is the sparse partial envelope estimator. Under the sparse partial envelope model, ${\beta }_1=\mathsf{\Gamma }\eta$ also has a sparse structure, and we denote the coefficients for the active responses as ${\beta }_{1,\mathcal{A}}={\mathsf{\Gamma }}_{\mathcal{A}}\eta \in {\mathbb{R}}^{q\times p_1}$ and the zero matrix has the dimension $(r-q)\times p_1$. The completion of $\mathsf{\Gamma }$ has the general form ${\mathsf{\Gamma }}_0={\tilde{\mathsf{\Gamma }}}_{0}R$, where ${\tilde{\mathsf{\Gamma }}}_0\in {\mathbb{R}}^{r\times (r-u_1)}$ is a completion with a block diagonal structure, and R represents a rotation of the orthogonal basis. The dimension of ${\mathsf{\Gamma }}_{\mathcal{A}}^T{Y}_{\mathcal{A}}$ should be at most the dimension of $Y_{\mathcal{A}}$, so $u_1⩽q$. When $u=q$, there is no immaterial information in the active responses for the sparse envelope model, and ${\mathsf{\Gamma }}_{\mathcal{A}}=I_q$, but as long as $u_1<u$, there is still immaterial information in the active responses for the sparse partial envelope model. When $q=r$, there are no inactive responses and all rows in $\mathsf{\Gamma }$ are nonzero. Then, the sparse partial envelope model is equivalent to the partial envelope model.

The parameterization of A maintains the sparse structure of $\mathsf{\Gamma }$. In other words, $\mathsf{\Gamma }=G_A{\mathsf{\Gamma }}_1$ indicates that a row in $\mathsf{\Gamma }$ is composed of all zeros if and only if the corresponding row in A is composed of all zeros. Hence we can determine the inactive responses from the sparsity structure of A. In order to make the estimator of ${\beta }_1$ a sparse estimator, the row-wise sparsity in A is induced by adding an adaptive group lasso penalty to the objective function in (7):

$$\begin{array}{c}\hfill \widehat{A}=\underset{A\in {\mathbb{R}}^{(r-u_1)\times u_1}}{argmin}\left\{-2log\left|G_A^T{G}_A\right|+log\left|G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A\right|+log\left|G_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}{G}_A\right|\right.\\ \hfill \phantom{=}\left.+\lambda \sum _{i=1}^{r-u_1}{\omega }_i{∥a_i∥}_2\right\},\end{array}$$

(9)

where ${\parallel ·\parallel }_2$ is the norm of a vector, $a_i^T$ denotes the ith row of A, $\lambda$ is the tuning parameter and the ${\omega }_i$s are the adaptive weights. According to Zou [20], we set ${\omega }_i=1/{∥{\widehat{a}}_i∥}_2^{\gamma }$, where $\gamma$ is a tuning parameter and ${\widehat{a}}_i$ is a $\sqrt{n}$-consistent estimator of $a_i$. The tuning parameter $\gamma$ can be selected from a small candidate set such as $\{0.5,1,2,4,8\}$ (Zou [20]).

If r grows to infinity with n, we denote r by $r_n$. When $r_n>n$, ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}$ and ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}$ are both singular, and this is problematic because the objective function in (9) relies on ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}$ and the optimization algorithm that is employed to solve (9) needs ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}^{-1}$. These issues can be solved by employing sparse permutation invariant covariance estimation (Rothman et al. [21], SPICE) to acquire estimators of ${\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}$ and ${\mathsf{\Sigma }}^{-1}$. Since sparse permutation invariant covariance estimation is the only one that does not need a sparsity structure for the target parameter for the sake of establishing the consistency of its estimator. In the sparse partial envelope model, ${\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}$ and ${\mathsf{\Sigma }}^{-1}$ may not involve zero elements. We employ sparse permutation invariant covariance estimators of ${\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}$ and ${\mathsf{\Sigma }}^{-1}$ and denote them as ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}$ and ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}$. Then, we acquire ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}$ and ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}$ by taking the inverses of ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}$ and ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}$ and substitute ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}$ and ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}$ for ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}$ and ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}$ in (9), and the objective function is

$$\begin{array}{c}\hfill \widehat{A}=\underset{A\in {\mathbb{R}}^{\left(r_n-u_1\right)\times u_1}}{argmin}\left\{-2log\left|G_A^T{G}_A\right|+log\left|G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{G}_A\right|+log\left|G_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}{G}_A\right|\right.\\ \hfill \phantom{=}\left.+\lambda \sum _{i=1}^{r_n-u_1}{\omega }_i{∥a_i∥}_2\right\}.\end{array}$$

(10)

The optimizations of (9) and (10) are similar to the optimization problems discussed in Su et al. [6] and Zhu and Su [14]. Once we obtain $\widehat{A}$ from (9) or (10), $\widehat{\mathsf{\Gamma }}$ can be formed by employing an orthogonal basis of $\mathrm{span}\left({\widehat{G}}_A\right)$, and ${\widehat{\mathsf{\Gamma }}}_0$ is taken as a complement of $\widehat{\mathsf{\Gamma }}$. The sparse partial envelope estimators of ${\beta }_1$ and $\mathsf{\Sigma }$ are

$$\begin{array}{c}\hfill \widehat{{\beta }_1}=P_{\widehat{\mathsf{\Gamma }}}{\widehat{\beta }}_{1,\mathrm{ols}},\widehat{\mathsf{\Sigma }}=P_{\widehat{\mathsf{\Gamma }}}{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{P}_{\widehat{\mathsf{\Gamma }}}+Q_{\widehat{\mathsf{\Gamma }}}{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}{Q}_{\widehat{\mathsf{\Gamma }}}.\end{array}$$

(11)

The estimators for the constituent parameters are $\widehat{\eta }={\widehat{\mathsf{\Gamma }}}^T{\widehat{\beta }}_{1,\mathrm{ols}}, \widehat{\mathsf{\Omega }}={\widehat{\mathsf{\Gamma }}}^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}\widehat{\mathsf{\Gamma }}$ and ${\widehat{\mathsf{\Omega }}}_0={\widehat{\mathsf{\Gamma }}}_0^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}{\widehat{\mathsf{\Gamma }}}_0$. Apart from the fact that $\widehat{\mathsf{\Gamma }}$ and ${\widehat{\mathsf{\Gamma }}}_0$ have the special structures in (8), the sparse partial envelope estimators have the identical form to the partial envelope estimators. Because the sparse partial envelope estimator is asymptotically equivalent to the maximum likelihood estimator of the oracle partial envelope model, see Section 4, we can employ likelihood-based procedures such as the Akaike information criterion, the Bayesian information criterion or likelihood ratio testing to select $u_1$. For selecting $\lambda$ and $u_1$, we prefer cross-validation over the Bayesian information criterion and other likelihood-based procedures.

4. Theoretical Properties of the Sparse Partial Envelope Estimator

In this part, we investigate theoretical properties of the sparse partial envelope estimator. Theorems 1–3 provide the consistency and oracle properties of the sparse partial envelope estimator in the large-sample scenario when r is fixed and n tends to infinity. Theorems 4 and 5 give the selection consistency and convergence rate in the scenario when both $r_n$ and n tend to infinity. Set ${\xi }_i=\lambda {\omega }_i$, and let ${\xi }_{\max ,n}=\lambda max\left({\omega }_1,\dots ,{\omega }_{q-u_1}\right)$ and ${\xi }_{\min ,n}=\lambda min\left({\omega }_{q-u_1+1},\dots ,{\omega }_{r-u_1}\right)$.

Theorem 1.

Suppose that the sparse partial envelope models (5) and (8) hold, the errors ε are independent and have finite fourth moment, and we further suppose $n^{1/2}{\xi }_{\max ,n}\to 0$ as n tends to infinity. Then, there exists a local minimizer $\widehat{A}$ of (9), such that $P_{\widehat{\mathsf{\Gamma }}}$ is a $\sqrt{n}$-consistent estimator of $P_{\mathsf{\Gamma }}$, and $\widehat{{\beta }_1}$ is a $\sqrt{n}$-consistent estimator of ${\beta }_1$.

Theorem 1 establishes the $\sqrt{n}$-consistency of the sparse partial envelope estimator of $P_{\mathsf{\Gamma }}$ and ${\beta }_1$. Notice that although the objective function for the sparse partial envelope estimator originates from the normal likelihood, we do not require normality to establish the $\sqrt{n}$-consistency of ${\widehat{\mathcal{E}}}_{\mathsf{\Sigma }}\left({\mathcal{B}}_1\right)$ and $\widehat{{\beta }_1}$.

Proof of Theorem 1.

We denote the objective function in (9) as $f_{\mathrm{obj}}\left(A\right)$. In order to prove Theorem 1, we will demonstrate that for any small $ϵ>0$, there exists a sufficiently large constant C, such that

$$\underset{n\to \infty }{lim}\mathrm{pr}\left\{\underset{\Delta \in {\mathbb{R}}^{(r-u_1)\times u_1},{\parallel \Delta \parallel }_F=C}{inf}{f}_{\mathrm{obj}}(A+n^{-1/2}\Delta )>f_{\mathrm{obj}}\left(A\right)\right\}>1-ϵ.$$

(12)

If (12) holds, then there exists a local minimizer $\widehat{A}$ of $f_{\mathrm{obj}}$ such that $\parallel \widehat{A}{-A\parallel }_F=O_p\left(n^{-1/2}\right)$. Hence, $\widehat{A}$ is a $\sqrt{n}$-consistent estimator of A. Because $P_{\mathsf{\Gamma }}=G_A{(I_{u_1}+A^{T}A)}^{-1}{G}_A^T$ is merely a function of A, $P_{\widehat{\mathsf{\Gamma }}}$ is a $\sqrt{n}$-consistent estimator of $P_{\mathsf{\Gamma }}$. Since ${\widehat{\beta }}_1=P_{\widehat{\mathsf{\Gamma }}}{\widehat{\beta }}_{1,\mathrm{ols}}$, and ${\widehat{\beta }}_{1,\mathrm{ols}}$ is a $\sqrt{n}$-consistent estimator of ${\beta }_1$, then ${\widehat{\beta }}_1$ is a $\sqrt{n}$-consistent estimator of ${\beta }_1$.

Now, we only need to prove (12). We compute $f_{\mathrm{obj}}(A+n^{-1/2}\Delta )-f_{\mathrm{obj}}\left(A\right)$ by employing the Taylor expansion. Because the form of $f_{\mathrm{obj}}$ is a little complex, we write it into four parts

$$\begin{array}{cc}\hfill f_{\mathrm{obj}}\left(A\right)& =-2log|G_A^T{G}_A|+log|G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A|+log|G_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}{G}_A|+\sum _{i=1}^{r-u_1}\lambda {\omega }_i{\parallel a_i\parallel }_2\hfill \\ \hfill & \equiv f_1\left(A\right)+f_2\left(A\right)+f_3\left(A\right)+f_4\left(A\right).\hfill \end{array}$$

We first center on $f_1\left(A\right)=-2log|G_A^T{G}_A|$ and then expand $f_1(A+n^{-1/2}\Delta )$,

$$\begin{array}{c}\hfill f_1(A+n^{-1/2}\Delta )=f_1\left(A\right)+n^{-1/2}\stackrel{\to \Delta }{{df}_1}\left(A\right)+{\displaystyle \frac{1}{2}}{n}^{-1}\stackrel{\to \Delta }{{df}_1^2}\left(A\right)+o_p\left(n^{-1}\right),\end{array}$$

where $\stackrel{\to \Delta }{{df}_1}\left(A\right)$ and $\stackrel{\to \Delta }{{df}_1^2}\left(A\right)$ are the first and second directional derivatives (Dattorro [22]). The first directional derivative is

$$\begin{array}{c}\hfill \stackrel{\to \Delta }{{df}_1}\left(A\right)=tr\left\{{\left[{\displaystyle \frac{d{f}_1\left(A\right)}{dA}}\right]}^T\Delta \right\}=-4tr\left[{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right].\end{array}$$

The second directional derivative is

$$\begin{array}{cc}\hfill \stackrel{\to \Delta }{{df}_1^2}\left(A\right)=& tr\left({\left[{\displaystyle \frac{\stackrel{\to \Delta }{{df}_1}\left(A\right)}{dA}}\right]}^T\Delta \right)\hfill \\ \hfill =& -4tr\left({\left[{\displaystyle \frac{d}{dA}}tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right\}\right]}^T\Delta \right)\hfill \\ \hfill =& -4tr[\left\{-A{(I_{u_1}+A^{T}A)}^{-1}(A^T\Delta +{\Delta }^{T}A){(I_{u_1}+A^{T}A)}^{-1}\right.\hfill \\ \hfill & {\left.+\Delta {(I_{u_1}+A^{T}A)}^{-1}\right\}}^T\Delta ]\hfill \\ \hfill =& 4tr\left\{{(I_{u_1}+A^{T}A)}^{-1}(A^T\Delta +{\Delta }^{T}A){(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right.\hfill \\ \hfill & \left.-{(I_{u_1}+A^{T}A)}^{-1}{\Delta }^T\Delta \right\}.\hfill \end{array}$$

Let

$${\Delta }_{\ast }=\left(\begin{array}{c}0\hfill \\ \Delta \hfill \end{array}\right),$$

then

$$\begin{array}{cc}\hfill & \stackrel{\to \Delta }{{df}_1^2}\left(A\right)\hfill \\ \hfill =& 4tr\left[{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right.\hfill \\ \hfill & \left.+{(I_{u_1}+A^{T}A)}^{-1}{\Delta }^T\left\{A{(I_{u_1}+A^{T}A)}^{-1}{A}^T-I_{r-u_1}\right\}\Delta \right]\hfill \\ \hfill =& 4tr\left[{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right.\hfill \\ & \left.+{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T\left\{G_A{\left(G_A^T{G}_A\right)}^{-1}{G}_A^T-I_r\right\}{\Delta }_{\ast }\right]\hfill \\ \hfill =& 4tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta +{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T(\mathsf{\Gamma }{\mathsf{\Gamma }}^T-I_r){\Delta }_{\ast }\right\}\hfill \\ \hfill =& 4tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta -{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}.\hfill \end{array}$$

Substitute $\stackrel{\to \Delta }{{df}_1}\left(A\right)$ and $\stackrel{\to \Delta }{{df}_1^2}\left(A\right)$ into the expansion for $f_1(A+n^{-1/2}\Delta )$, and we can acquire

$$\begin{array}{cc}\hfill f_1(A+n^{-1/2}\Delta )-f_1\left(A\right)=& -4n^{-1/2}tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right\}\hfill \\ \hfill & +2n^{-1}tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right.\hfill \\ \hfill & \left.-{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}+o_p\left(n^{-1}\right).\hfill \end{array}$$

Now, we expand $f_2\left(A\right)=log|G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A|$. The first directional derivative is

$$\begin{array}{c}\hfill \stackrel{\to \Delta }{{df}_2}\left(A\right)=tr\left\{{\left[{\displaystyle \frac{{df}_2\left(A\right)}{dA}}\right]}^T\Delta \right\}=2tr\left\{{\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A\right)}^{-1}{G}_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\Delta }_{\ast }\right\}.\end{array}$$

Let ${\mathsf{\Sigma }}_{R_{1\mid 2}},{\mathsf{\Sigma }}_{R_{Y\mid 2}}$ and ${\mathsf{\Sigma }}_{R_{Y\mid 2}{R}_{1\mid 2}}$ be the variance matrix of $R_{1\mid 2}$, the variance matrix of $R_{Y\mid 2}$ and the covariance matrix of $R_{Y\mid 2}$ and $R_{1\mid 2}$ in population, and let ${\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}},{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}$ and ${\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}{R}_{Y\mid 2}}$ be the corresponding sample versions. Then, taking advantage of Cook and Setodji [23],

$$\begin{array}{cc}\hfill n^{1/2}({\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}{R}_{1\mid 2}}-{\mathsf{\Sigma }}_{R_{Y\mid 2}{R}_{1\mid 2}})& =n^{-1/2}({\left({\mathbb{R}}_{Y\mid 2}\right)}_c^T{\mathbb{R}}_{1\mid 2}-n{\mathsf{\Sigma }}_{R_{Y\mid 2}{R}_{1\mid 2}})+O_p\left(n^{-1/2}\right),\hfill \\ \hfill n^{1/2}({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}-{\mathsf{\Sigma }}_{R_{1\mid 2}})& =n^{-1/2}({\mathbb{R}}_{1\mid 2}^T{\mathbb{R}}_{1\mid 2}-n{\mathsf{\Sigma }}_{R_{1\mid 2}})+O_p\left(n^{-1/2}\right),\hfill \\ \hfill n^{1/2}({\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}-{\mathsf{\Sigma }}_{R_{Y\mid 2}})& =n^{-1/2}({\left({\mathbb{R}}_{Y\mid 2}\right)}_c^T{\left({\mathbb{R}}_{Y\mid 2}\right)}_c-n{\mathsf{\Sigma }}_{R_{Y\mid 2}})+O_p\left(n^{-1/2}\right),\hfill \end{array}$$

where ${\left({\mathbb{R}}_{Y\mid 2}\right)}_c\in {\mathbb{R}}^{n\times r}$ is the centred data matrix of $R_{Y\mid 2}$, whose ith row is ${({\left(R_{Y\mid 2}\right)}_i-\overline{R_{Y\mid 2}})}^T$. Because ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}={\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}-{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}{R}_{1\mid 2}}{\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}^{-1}{\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}{R}_{Y\mid 2}}$ and ${\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}^{-1}-{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}=-{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}-{\mathsf{\Sigma }}_{R_{1\mid 2}}){\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}+O_p\left(n^{-1}\right)$,

$$\begin{array}{cc}\hfill {\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}=& ({\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}-{\mathsf{\Sigma }}_{R_{Y\mid 2}}+{\mathsf{\Sigma }}_{R_{Y\mid 2}})-({\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}{R}_{1\mid 2}}-{\mathsf{\Sigma }}_{R_{Y\mid 2}{R}_{1\mid 2}}+{\mathsf{\Sigma }}_{R_{Y\mid 2}{R}_{1\mid 2}})\hfill \\ & ({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}^{-1}-{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}+{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1})({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}{R}_{Y\mid 2}}-{\mathsf{\Sigma }}_{R_{1\mid 2}{R}_{Y\mid 2}}+{\mathsf{\Sigma }}_{R_{1\mid 2}{R}_{Y\mid 2}})\hfill \\ \hfill =& \mathsf{\Sigma }+n^{-1/2}\left\{-n^{-1/2}\left({\left({\mathbb{R}}_{Y\mid 2}\right)}_c^T{\mathbb{R}}_{1\mid 2}-n{\mathsf{\Sigma }}_{R_{Y\mid 2}{R}_{1\mid 2}}\right){\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}{\mathsf{\Sigma }}_{R_{1\mid 2}{R}_{Y\mid 2}}\right.\hfill \\ \hfill & +n^{-1/2}{\mathsf{\Sigma }}_{R_{Y\mid 2}{R}_{1\mid 2}}{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}\left({\mathbb{R}}_{1\mid 2}^T{\mathbb{R}}_{1\mid 2}-n{\mathsf{\Sigma }}_{R_{1\mid 2}}\right){\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}{\mathsf{\Sigma }}_{R_{1\mid 2}{R}_{Y\mid 2}}\hfill \\ \hfill & -n^{-1/2}{\mathsf{\Sigma }}_{R_{Y\mid 2}{R}_{1\mid 2}}{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}\left({\mathbb{R}}_{1\mid 2}^T{\left({\mathbb{R}}_{Y\mid 2}\right)}_c-n{\mathsf{\Sigma }}_{R_{1\mid 2}{R}_{Y\mid 2}}\right)\hfill \\ \hfill & \left.+n^{-1/2}\left({\left({\mathbb{R}}_{Y\mid 2}\right)}_c^T{\left({\mathbb{R}}_{Y\mid 2}\right)}_c-n{\mathsf{\Sigma }}_{R_{Y\mid 2}}\right)\right\}+O_p\left(n^{-1}\right)\hfill \\ \hfill \equiv & \mathsf{\Sigma }+n^{-1/2}(T_{1n}+T_{2n}+T_{3n}+T_{4n})+O_p\left(n^{-1}\right),\hfill \end{array}$$

where by means of the central limit theorem, each element in $T_{1n}$, $T_{2n}$, $T_{3n}$ and $T_{4n}$ converges in distribution to a normal random variable with mean 0. As

$$\begin{array}{cc}\hfill {\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A\right)}^{-1}=& {\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}-{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A-G_A^T\mathsf{\Sigma }{G}_A){\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\hfill \\ \hfill & +O_p\left(n^{-1}\right)\hfill \\ \hfill =& {\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\hfill \\ \hfill & -n^{-1/2}{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T(T_{1n}+T_{2n}+T_{3n}+T_{4n})G_A{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\hfill \\ \hfill & +O_p\left(n^{-1}\right),\hfill \end{array}$$

we can expand $\stackrel{\to Z^{\ast }}{{df}_2}\left(\mathsf{\Gamma }\right)$ as

$$\begin{array}{cc}\hfill & 2tr\left\{{\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A\right)}^{-1}{G}_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\Delta }_{\ast }\right\}\hfill \\ \hfill =& 2tr\left\{{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T\mathsf{\Sigma }{\Delta }_{\ast }\right\}+2n^{-1/2}tr\left\{{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T(T_{1n}+T_{2n}+T_{3n}+T_{4n}){\Delta }_{\ast }\right.\hfill \\ \hfill & \left.-{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T(T_{1n}+T_{2n}+T_{3n}+T_{4n})G_A{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T\mathsf{\Sigma }{\Delta }_{\ast }\right\}+O_p\left(n^{-1}\right)\hfill \\ \hfill =& 2tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{G}_A^T{\Delta }_{\ast }\right\}\hfill \\ \hfill & +2n^{-1/2}tr\left[{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T(T_{1n}+T_{2n}+T_{3n}+T_{4n})\left\{I_r-G_A{(I_{u_1}+A^{T}A)}^{-1}{G}_A^T\right\}{\Delta }_{\ast }\right]\hfill \\ \hfill & +O_p\left(n^{-1}\right)\hfill \\ \hfill =& 2tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right\}+2n^{-1/2}tr\left\{{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T(T_{3n}+T_{4n}){\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}\hfill \\ \hfill & +O_p\left(n^{-1}\right)\hfill \\ \hfill =& 2tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right\}+2n^{-1/2}tr\left\{{\mathsf{\Gamma }}_1{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}^T(T_{3n}+T_{4n}){\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}+O_p\left(n^{-1}\right).\hfill \end{array}$$

The second equality is because $\mathsf{\Gamma }=G_A{\mathsf{\Gamma }}_1$, so

$$\begin{array}{cc}\hfill {\mathsf{\Gamma }}_1^T{G}_A^T{G}_A{\mathsf{\Gamma }}_1=I& \Rightarrow {\mathsf{\Gamma }}_1^T(I_{u_1}+A^{T}A){\mathsf{\Gamma }}_1=I\hfill \\ & \Rightarrow I_{u_1}+A^{T}A={\left({\mathsf{\Gamma }}_1^T\right)}^{-1}{\left({\mathsf{\Gamma }}_1\right)}^{-1}\hfill \\ & \Rightarrow {(I_{u_1}+A^{T}A)}^{-1}={\mathsf{\Gamma }}_1{\mathsf{\Gamma }}_1^T,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill {\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T\mathsf{\Sigma }& ={\left\{{\left(\mathsf{\Gamma }{\mathsf{\Gamma }}_1^{-1}\right)}^T\mathsf{\Sigma }\mathsf{\Gamma }{\mathsf{\Gamma }}_1^{-1}\right\}}^{-1}{\left(\mathsf{\Gamma }{\mathsf{\Gamma }}_1^{-1}\right)}^T\mathsf{\Sigma }\hfill \\ & ={\mathsf{\Gamma }}_1{\mathsf{\Omega }}^{-1}\mathsf{\Omega }{\mathsf{\Gamma }}^T={\mathsf{\Gamma }}_1{\mathsf{\Gamma }}_1^T{G}_A^T={(I_{u_1}+A^{T}A)}^{-1}{G}_A^T.\hfill \end{array}$$

By the Cauchy–Schwarz inequality for the matrix trace (Magnus and Neudecker [24]),

$$\begin{array}{cc}\hfill \left|tr\left\{{\mathsf{\Gamma }}_1{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}^T\left(T_{3n}+T_{4n}\right){\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}\right|& \le {∥{\Delta }_{\ast }∥}_F{∥{\mathsf{\Gamma }}_1{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}^T\left(T_{3n}+T_{4n}\right){\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T∥}_F\hfill \\ \hfill & ={\parallel \Delta \parallel }_F{∥{\mathsf{\Gamma }}_1{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}^T\left(T_{3n}+T_{4n}\right){\mathsf{\Gamma }}_0∥}_F.\hfill \end{array}$$

The second directional derivative of $f_2$ is

$$\begin{array}{cc}\hfill \stackrel{\to \Delta }{{df}_2^2}\left(A\right)=& 2tr\left({\left[{\displaystyle \frac{d}{dA}}tr\left\{{\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A\right)}^{-1}{G}_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\Delta }_{\ast }\right\}\right]}^T\Delta \right)\hfill \\ \hfill =& 2tr\left\{{\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A\right)}^{-1}{\Delta }_{\ast }^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\Delta }_{\ast }\right.\hfill \\ \hfill & \left.-{\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A\right)}^{-1}(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\Delta }_{\ast }+{\Delta }_{\ast }^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A){\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{G}_A\right)}^{-1}{G}_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\Delta }_{\ast }\right\}\hfill \\ \hfill =& 2tr\left\{{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{\Delta }_{\ast }^T\mathsf{\Sigma }{\Delta }_{\ast }\right.\hfill \\ \hfill & \left.-{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}(G_A^T\mathsf{\Sigma }{\Delta }_{\ast }+{\Delta }_{\ast }^T\mathsf{\Sigma }{G}_A){\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T\mathsf{\Sigma }{\Delta }_{\ast }\right\}\hfill \\ \hfill & +O_p\left(n^{-1/2}\right)\hfill \\ \hfill =& 2tr\left[-{(I_{u_1}+A^{T}A)}^{-1}{G}_A^T{\Delta }_{\ast }{(I_{u_1}+A^{T}A)}^{-1}{G}_A^T{\Delta }_{\ast }\right.\hfill \\ \hfill & \left.+{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{\Delta }_{\ast }^T\mathsf{\Sigma }\left\{I_r-G_A{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T\mathsf{\Sigma }\right\}{\Delta }_{\ast }\right]+O_p\left(n^{-1/2}\right)\hfill \\ \hfill =& 2tr\left[-{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right.\hfill \\ \hfill & +\left\{{\left({\mathsf{\Gamma }}_1^{-1}\right)}^T\mathsf{\Omega }{\mathsf{\Gamma }}_1^{-1}{\}}^{-1}{\Delta }_{\ast }^T\mathsf{\Sigma }\left\{I_r-G_A{(I_{u_1}+A^{T}A)}^{-1}{G}_A^T\right\}{\Delta }_{\ast }\right]+O_p\left(n^{-1/2}\right)\hfill \\ \hfill =& 2tr\left\{-{\left(I_{u_1}+A^{T}A\right)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta +{\mathsf{\Gamma }}_1{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T\mathsf{\Sigma }{\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}\hfill \\ & +O_p\left(n^{-1/2}\right)\hfill \\ \hfill =& 2tr\left\{-{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta +{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right\}\hfill \\ \hfill & +O_p\left(n^{-1/2}\right).\hfill \end{array}$$

Substitute $\stackrel{\to \Delta }{{df}_2}\left(A\right)$ and $\stackrel{\to \Delta }{{df}_2^2}\left(A\right)$ into the expansion for $f_2(A+n^{-1/2}\Delta )$, and we obtain

$$\begin{array}{cc}\hfill & f_2(A+n^{-1/2}\Delta )-f_2\left(A\right)\hfill \\ \hfill =& 2n^{-1/2}tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right\}+2n^{-1}tr\left\{{\mathsf{\Gamma }}_1{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}^T(T_{3n}+T_{4n}){\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}\hfill \\ \hfill & +n^{-1}tr\left\{-{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta +{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right\}\hfill \\ \hfill & +o_p\left(n^{-1}\right)\hfill \\ \hfill \ge & 2n^{-1/2}tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right\}-2n^{-1}{\parallel \Delta \parallel }_F{∥{\mathsf{\Gamma }}_1{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}^T(T_{3n}+T_{4n}){\mathsf{\Gamma }}_0∥}_F\hfill \\ \hfill & +n^{-1}tr\left\{-{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta +{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right\}\hfill \\ \hfill & +o_p\left(n^{-1}\right).\hfill \end{array}$$

Notice that $f_3$ and $f_2$ have a similar structure, except that ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}$ is replaced by ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}$. Let $T_{5n}=-n^{-1/2}{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}\left({\left({\mathbb{R}}_{Y\mid 2}\right)}_c^T{\left({\mathbb{R}}_{Y\mid 2}\right)}_c-n{\mathsf{\Sigma }}_{R_{Y\mid 2}}\right){\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}$. By means of the central limit theorem, $T_{5n}$ converges in distribution to a normal random variable with mean 0. Then, we implement the same expansion to $f_3$ and obtain

$$\begin{array}{cc}\hfill & f_3(A+n^{-1/2}\Delta )-f_3\left(A\right)\hfill \\ \hfill =& 2n^{-1/2}tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right\}+2n^{-1}tr\left\{{\mathsf{\Gamma }}_1(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}^T{T}_{5n}{\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}\hfill \\ \hfill & +n^{-1}tr\left\{-{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right.\hfill \\ \hfill & \left.+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0^{-1}{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right\}\hfill \\ \hfill & +o_p\left(n^{-1}\right)\hfill \\ \hfill \ge & 2n^{-1/2}tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right\}-2n^{-1}{\parallel \Delta \parallel }_F{∥{\mathsf{\Gamma }}_1(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}^T{T}_{5n}{\mathsf{\Gamma }}_0∥}_F\hfill \\ \hfill & +n^{-1}tr\left\{-{(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta {(I_{u_1}+A^{T}A)}^{-1}{A}^T\Delta \right.\hfill \\ \hfill & \left.+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0^{-1}{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right\}\hfill \\ \hfill & +o_p\left(n^{-1}\right).\hfill \end{array}$$

Now, we expand $f_4\left(A\right)={\sum }_{i=1}^{r-u_1}\lambda {\omega }_i{\parallel a_i\parallel }_2$. Let ${\delta }_i^T$ be the ith row of $\Delta$, then

$$\begin{array}{cc}\hfill f_4(A+n^{-1/2}\Delta )-f_4\left(A\right)& \ge \sum _{i=1}^{q-u_1}\left(\lambda {\omega }_i\parallel a_i+n^{-1/2}{\delta }_i{\parallel }_2-\lambda {\omega }_i{\parallel a_i\parallel }_2\right)\hfill \\ \hfill & \ge -{\displaystyle \frac{1}{2}}(q-u_1)n^{-1/2}{\xi }_{\max ,n}\underset{i}{max}\left(\parallel a_i{\parallel }_2^{-1}{\parallel {\delta }_i\parallel }_2\right)\{1+o_p\left(1\right)\}\hfill \\ \hfill & =-{\displaystyle \frac{1}{2}}{n}^{-1}(q-u_1)n^{1/2}{\xi }_{\max ,n}\underset{i}{max}\left(\parallel a_i{\parallel }_2^{-1}{\parallel {\delta }_i\parallel }_2\right)\{1+o_p\left(1\right)\}.\hfill \end{array}$$

The second inequality is based on the Taylor expansion at $a_i$. When $n^{1/2}{\xi }_{\max ,n}\to 0$ as $n\to \infty$, $n\left\{f_4(A+n^{-1/2}\Delta )-f_4\left(A\right)\right\}=o_p\left(1\right)$. Combine the results for $f_1$, $f_2$, $f_3$ and $f_4$, and we have

$$\begin{array}{cc}\hfill & f_{\mathrm{obj}}(A+n^{-1/2}\Delta )-f_{\mathrm{obj}}\left(A\right)\hfill \\ \hfill \ge & -2n^{-1}{\parallel \Delta \parallel }_F{∥{\mathsf{\Gamma }}_1{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}^T(T_{3n}+T_{4n}){\mathsf{\Gamma }}_0∥}_F-2n^{-1}{\parallel \Delta \parallel }_F{∥{\mathsf{\Gamma }}_1(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}^T{T}_{5n}{\mathsf{\Gamma }}_0∥}_F\hfill \\ \hfill & +n^{-1}tr\left\{{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0^{-1}{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right.\hfill \\ \hfill & \left.-2{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}-{\displaystyle \frac{1}{2}}{n}^{-1}(q-u_1)n^{1/2}{\xi }_{\max ,n}\underset{i}{max}\left(\parallel a_i{\parallel }_2^{-1}{\parallel {\delta }_i\parallel }_2\right)\hfill \\ \hfill & +o_p\left(n^{-1}\right).\hfill \end{array}$$

Let $m_1$ be the smallest eigenvalue of M. The matrix M appears in (5.7) of Cook et al. [1]. By Shapiro [25], M is a positive definite matrix and $m_1>0$. Then, we have

$$\begin{array}{cc}\hfill & tr\left\{{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0^{-1}{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right.\hfill \\ \hfill & \left.-2{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}\hfill \\ \hfill =& tr\left\{{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0^{-1}{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right.\hfill \\ \hfill & \left.-2{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right\}\hfill \\ \hfill =& vec{\left({\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right)}^T\left(\mathsf{\Omega }\otimes {\mathsf{\Omega }}_0^{-1}+{\mathsf{\Omega }}^{-1}\otimes {\mathsf{\Omega }}_0-2I_{u_1}\otimes I_{r-u_1}\right.\hfill \\ \hfill & \left.+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T\otimes {\mathsf{\Omega }}_0^{-1}\right)vec\left({\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right)\hfill \\ \hfill \equiv & vec{\left({\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right)}^{T}Mvec\left({\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right)\hfill \\ \hfill \ge & m_1{∥{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1∥}_F^2\hfill \\ \hfill =& m_{1}tr\left({\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0\right)\hfill \\ \hfill =& m_{1}tr\left\{{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0\right\}\hfill \\ \hfill =& m_{1}tr\left\{{\Delta }_{\ast }{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T(I_r-\mathsf{\Gamma }{\mathsf{\Gamma }}^T)\right\}\hfill \\ \hfill =& m_{1}tr\left[{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T\left\{I_r-G_A{(I_{u_1}+A^{T}A)}^{-1}{G}_A^T\right\}{\Delta }_{\ast }\right]\hfill \\ \hfill =& m_{1}tr\left[{(I_{u_1}+A^{T}A)}^{-1}{\Delta }^T\left\{I_{r-u_1}-A{(I_{u_1}+A^{T}A)}^{-1}{A}^T\right\}\Delta \right]\hfill \\ \hfill =& m_{1}tr\left\{{(I_{u_1}+A^{T}A)}^{-1}{\Delta }^T{(I_{u_1}+A^{T}A)}^{-1}\Delta \right\}\hfill \\ \hfill =& m_{1}vec{(\Delta )}^T\left\{{(I_{u_1}+A^{T}A)}^{-1}\otimes {(I_{u_1}+A^{T}A)}^{-1}\right\}vec(\Delta )\hfill \\ \hfill \ge & m_1{m}_2^2{\parallel \Delta \parallel }_F^2,\hfill \end{array}$$

where $m_2$ is the smallest eigenvalue of ${\left(I_{u_1}+A^{T}A\right)}^{-1}$. When ${\parallel \Delta \parallel }_F>C$ for sufficiently large C, the terms with order ${\parallel \Delta \parallel }_F^2$ dominate the terms with order ${\parallel \Delta \parallel }_F$. When ${\parallel \Delta \parallel }_F=C$ for sufficiently large C, conclusion (12) follows. □

Theorem 2.

Suppose that the conditions in Theorem 1 hold, and further suppose that $n^{1/2}{\xi }_{\min ,n}\to \infty$. Then, $pr\left({\widehat{a}}_i=0\right)\to 1$ for $i=q-u_1+1,\dots ,r-u_1$.

Theorem 2 establishes the selection consistency of the sparse partial envelope estimator and shows that the inactive responses are identified by the sparse partial envelope model with the probability tending to 1.

Proof of Theorem 2.

We prove Theorem 2 by contradiction. Assume that $\parallel {\widehat{a}}_i{\parallel }_2>0$ for $i=q+1-u_1,\dots ,r-u_1$. Let $e_i$ be the ith column of $I_r$. The first derivative of $f_{\mathrm{obj}}$ concerning $a_i$ should be 0 evaluated at the local minimum ${\widehat{a}}_i$. The first derivative of $f_{\mathrm{obj}}$ concerning $a_i^T(i=q+1-u_1,\dots ,r-u_1)$ is

$$\begin{array}{cc}\hfill {\displaystyle \frac{d{f}_{\mathrm{obj}}\left(A\right)}{d{a}_i^T}}{|}_{a_i={\widehat{a}}_i}=& -4e_i^T{\widehat{G}}_A{(I_{u_1}+{\widehat{A}}^T\widehat{A})}^{-1}+2e_i^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\widehat{G}}_A{\left({\widehat{G}}_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\widehat{G}}_A\right)}^{-1}\hfill \\ \hfill & +2e_i^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}{\widehat{G}}_A{\left({\widehat{G}}_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}{\widehat{G}}_A\right)}^{-1}+{\displaystyle \frac{\lambda {\omega }_i{\widehat{a}}_i^T}{{∥{\widehat{a}}_i∥}_2}}=0.\hfill \end{array}$$

(13)

Since ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}$, ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}$ and $\widehat{A}$ are $\sqrt{n}$-consistent estimators of $\mathsf{\Sigma }$, ${\mathsf{\Sigma }}_{R_{Y\mid 2}}$ and A, so $\mathsf{\Sigma }=\mathsf{\Gamma }\mathsf{\Omega }{\mathsf{\Gamma }}^T+{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T$ and ${\mathsf{\Sigma }}_{R_{Y\mid 2}}=\mathsf{\Gamma }(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}^T+{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T$, then

$$\begin{array}{cc}\hfill & -4e_i^T{\widehat{G}}_A{(I_{u_1}+{\widehat{A}}^T\widehat{A})}^{-1}+2e_i^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\widehat{G}}_A{\left({\widehat{G}}_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\widehat{G}}_A\right)}^{-1}+2e_i^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}{\widehat{G}}_A{\left({\widehat{G}}_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}{\widehat{G}}_A\right)}^{-1}\hfill \\ \hfill =& -4e_i^T{G}_A{(I_{u_1}+A^{T}A)}^{-1}+2e_i^T\mathsf{\Sigma }{G}_A{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\hfill \\ \hfill & +2e_i^T{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}{G}_A{\left(G_A^T{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}{G}_A\right)}^{-1}+O_p\left(n^{-1/2}\right)\hfill \\ \hfill =& -4a_i^T{(I_{u_1}+A^{T}A)}^{-1}+2e_i^T{G}_A{(I_{u_1}+A^{T}A)}^{-1}+2e_i^T{G}_A{(I_{u_1}+A^{T}A)}^{-1}+O_p\left(n^{-1/2}\right)\hfill \\ \hfill =& -4a_i^T{(I_{u_1}+A^{T}A)}^{-1}+2a_i^T{(I_{u_1}+A^{T}A)}^{-1}+2a_i^T{(I_{u_1}+A^{T}A)}^{-1}+O_p\left(n^{-1/2}\right)\hfill \\ \hfill =& O_p\left(n^{-1/2}\right).\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill & n^{1/2}\left\{-4e_i^T{\widehat{G}}_A{(I_{u_1}+{\widehat{A}}^T\widehat{A})}^{-1}+2e_i^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\widehat{G}}_A{\left({\widehat{G}}_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}{\widehat{G}}_A\right)}^{-1}\right.\hfill \\ \hfill & \left.+2e_i^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}{\widehat{G}}_A{\left({\widehat{G}}_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}{\widehat{G}}_A\right)}^{-1}\right\}\hfill \\ \hfill =& O_p\left(1\right).\hfill \end{array}$$

(14)

On the other side, let v be the element in $a_i$ that has the largest absolute value, then $|v|/\parallel a_i{\parallel }_2>\sqrt{u_1}$ where $|·|$ denotes the absolute value. Because we have $n^{1/2}{\xi }_{min,n}\to \infty$, there is, at the lowest, one element in $n^{1/2}\lambda {\omega }_i{a}_i^T/{\parallel a_i\parallel }_2$ that tends to infinity. With (13), this is a contradiction of (14). Hence, for $i=q+1-u_1,\dots ,r-u_1$, we have $pr\left({\widehat{a}}_i=0\right)\to 1$. □

Next, we define the oracle partial envelope estimator and study its properties. Under the partial envelope model, the inactive response involves information on ${\beta }_{1,\mathcal{A}}$ through its covariance with the active response. Then, the oracle partial envelope model is defined as

$$\left(\begin{array}{c}{Y}_{\mathcal{A}}\\ Y_{\mathcal{I}}\end{array}\right)=\alpha +\mathsf{\Gamma }\eta X_1+\left(\begin{array}{c}{\beta }_{2,\mathcal{A}}\\ 0\end{array}\right)X_2+\epsilon ,\mathsf{\Sigma }=\mathsf{\Gamma }\mathsf{\Omega }{\mathsf{\Gamma }}^T+{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T,\mathsf{\Gamma }=\left(\begin{array}{c}{\mathsf{\Gamma }}_{\mathcal{A}}\\ 0\end{array}\right).$$

(15)

The oracle partial envelope model (15) is analogous to the sparse partial envelope models (5) and (8), and the difference between them is that, in (15), we know q and which rows in $\mathsf{\Gamma }$ and ${\beta }_2$ are formed from only zeros. A subscript ‘O’ is attached if an estimator is the oracle partial envelope estimator. Let ${\widehat{\mathsf{\Sigma }}}_{{\left(R_{Y\mid 2}\right)}_{\mathcal{A}}\mid R_{1\mid 2}}\in {\mathbb{R}}^{q\times q}$ be the sample covariance matrix of the residuals from the regression of ${\left(R_{Y\mid 2}\right)}_{\mathcal{A}}$ on $R_{1\mid 2}$, and let ${\left({\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}\right)}_{\mathcal{A}}\in {\mathbb{R}}^{q\times q}$ be the $q\times q$ upper left block of ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}$. Let ${\tilde{\mathsf{\Omega }}}_0={\tilde{\mathsf{\Gamma }}}_0^T\mathsf{\Sigma }{\tilde{\mathsf{\Gamma }}}_0$. Under the basis ${\tilde{\mathsf{\Gamma }}}_0$, we denote the coordinates ${\mathsf{\Omega }}_0$ as ${\tilde{\mathsf{\Omega }}}_0$, where

$${\tilde{\mathsf{\Omega }}}_0=\left(\begin{array}{cc}{\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}& {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mathcal{I}}\\ {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mathcal{I}}^T& {\tilde{\mathsf{\Omega }}}_{0,\mathcal{I}}\end{array}\right),{\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}\in {\mathbb{R}}^{(q-u_1)\times (q-u_1)},{\tilde{\mathsf{\Omega }}}_{0,\mathcal{I}}\in {\mathbb{R}}^{(r-q)\times (r-q)}.$$

Proposition 1 provides the maximum likelihood estimator ${\widehat{\beta }}_{1,\mathcal{A},O}$ and its asymptotic distribution. Let ${\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}={\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}-{\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mathcal{I}}{\tilde{\mathsf{\Omega }}}_{0,\mathcal{I}}^{-1}{\tilde{\mathsf{\Omega }}}_{0,\mathcal{I}\mathcal{A}}$. The symbol ‘$\stackrel{d}{⟶}$’ denotes a convergence in the distribution.

Proposition 1.

Suppose that the oracle partial envelope model (15) holds and the errors are normally distributed. Then, the maximum likelihood estimator of ${\beta }_{1,\mathcal{A}}$ under the oracle partial model is ${\widehat{\beta }}_{1,\mathcal{A},O}=P_{{\widehat{\mathsf{\Gamma }}}_{\mathcal{A},O}}{\widehat{\beta }}_{1,\mathcal{A},\mathrm{ols}}$, where

$$\mathrm{span}\left({\widehat{\mathsf{\Gamma }}}_{\mathcal{A},O}\right)=\underset{\mathrm{span}\left(G\right)\in \mathcal{G}(q,u_1)}{argmin}log|G^T{\widehat{\mathsf{\Sigma }}}_{{\left(R_{Y\mid 2}\right)}_{\mathcal{A}}\mid R_{1\mid 2}}G|+log|G^T{\left({\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}\right)}_{\mathcal{A}}G|.$$

Furthermore,

$$\sqrt{n}\left\{\mathrm{vec}\left({\widehat{\beta }}_{1,\mathcal{A},O}\right)-\mathrm{vec}\left({\beta }_{1,\mathcal{A}}\right)\right\}\stackrel{d}{⟶}N(0,V_O),$$

where $V_O={\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}\otimes {\mathsf{\Gamma }}_{\mathcal{A}}\mathsf{\Omega }{\mathsf{\Gamma }}_{\mathcal{A}}^T+({\eta }^T\otimes {\mathsf{\Gamma }}_{\mathcal{A},0})T^{-1}(\eta \otimes {\mathsf{\Gamma }}_{\mathcal{A},0}^T)$, and $T=\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}^{-1}+\mathsf{\Omega }\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}^{-1}+{\mathsf{\Omega }}^{-1}\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}-2I_{u_1}\otimes I_{q-u_1}$.

By means of Proposition 1, we can find that ${\left(R_{Y\mid 2}\right)}_{\mathcal{I}}$ occurs in the objective function for $\mathrm{span}\left({\widehat{\mathsf{\Gamma }}}_{\mathcal{A},O}\right)$ and hence influences ${\widehat{\beta }}_{1,\mathcal{A},O}$. The active partial envelope model that involves only the active partial responses is defined as follows:

$$\begin{array}{c}\hfill Y_{\mathcal{A}}={\alpha }_{\mathcal{A}}+{\mathsf{\Gamma }}_{\mathcal{A}}\eta X_1+{\beta }_{2,\mathcal{A}}{X}_2+{\epsilon }_{\mathcal{A}},{\mathsf{\Sigma }}_{\mathcal{A}}={\mathsf{\Gamma }}_{\mathcal{A}}\mathsf{\Omega }{\mathsf{\Gamma }}_{\mathcal{A}}^T+{\mathsf{\Gamma }}_{\mathcal{A},0}{\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}{\mathsf{\Gamma }}_{\mathcal{A},0}^T.\end{array}$$

(16)

Proposition 2.

Suppose that the conditions in Proposition 1 hold. Then, the maximum likelihood estimator of ${\beta }_{1,\mathcal{A}}$ under the active partial envelope model is ${\widehat{\beta }}_{1,\mathcal{A},2}=P_{{\widehat{\mathsf{\Gamma }}}_{\mathcal{A},2}}{\widehat{\beta }}_{1,\mathcal{A},\mathrm{ols}}$, where

$$\mathrm{span}\left({\widehat{\mathsf{\Gamma }}}_{\mathcal{A},2}\right)=\underset{\mathrm{span}\left(G\right)\in \mathcal{G}(q,u_1)}{argmin}log|G^T{\widehat{\mathsf{\Sigma }}}_{{\left(R_{Y\mid 2}\right)}_{\mathcal{A}}\mid R_{1\mid 2}}G|+log|G^T{\widehat{\mathsf{\Sigma }}}_{{\left(R_{Y\mid 2}\right)}_{\mathcal{A}}}^{-1}G|.$$

Furthermore,

$$\sqrt{n}\left\{\mathrm{vec}\left({\widehat{\beta }}_{1,\mathcal{A},2}\right)-\mathrm{vec}\left({\beta }_{1,\mathcal{A}}\right)\right\}\stackrel{d}{⟶}N(0,V_3),$$

where $V_3={\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}\otimes {\mathsf{\Gamma }}_{\mathcal{A}}\mathsf{\Omega }{\mathsf{\Gamma }}_{\mathcal{A}}^T+({\eta }^T\otimes {\mathsf{\Gamma }}_{\mathcal{A},0})T_2^{-1}(\eta \otimes {\mathsf{\Gamma }}_{\mathcal{A},0}^T)$, and $T_2=\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}^{-1}+\mathsf{\Omega }\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}^{-1}+{\mathsf{\Omega }}^{-1}\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}-2I_{u_1}\otimes I_{q-u_1}$.

From Proposition 2, we see that ${\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}^{-1}⩾{\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}^{-1},T_2^{-1}⩾T^{-1}$, so $V_3\ge V_O$, and the oracle partial envelope model (15) is more efficient than the active partial envelope model (16) in estimating ${\beta }_{1,\mathcal{A}}$. Hence, containing $Y_{\mathcal{I}}$ also improves efficiency in the oracle partial envelope model.

Proof of Proposition 1 and Proposition 2.

We prove Proposition 2 based on the standard theory of the partial envelope model in Su and Cook [2]. Next, we prove Proposition 1. In this proof, we do not employ the normality of the errors but just require that the errors have finite fourth moments. The derivation of the maximum likelihood estimator of ${\beta }_{1,\mathcal{A}}$ is analogous to the derivation of the maximum likelihood estimator of ${\beta }_1$ under the partial envelope model in Su and Cook [2]. We take advantage of Proposition 4.1 in Shapiro [25] to obtain the asymptotic variance. First, we match our notations with Shapiro’s by checking the assumptions in Proposition 4.1 in Shapiro [25]. Similar to those in the proof of Theorem 2 in Su and Cook [3], we can verify that when the errors have finite fourth moments, x is asymptotically normally distributed. We use Shapiro’s $\xi$ to denote our ${\left\{\mathrm{vec}{\left({\beta }_{1,\mathcal{A}}\right)}^T,\mathrm{vech}{\left(\mathsf{\Sigma }\right)}^T\right\}}^T$. Let l be the log-likelihood function in (14) and let $l_{\max }$ be its maximum value. The minimum discrepancy function is defined as $f_{\mathrm{MDF}}=l_{\max }-l$. Since $f_{\mathrm{MDF}}$ is acquired from the normal likelihood function, it satisfies the four conditions in Section 3 of Shapiro [25]. We use Shapiro’s $\theta$ to denote our ${\left\{\mathrm{vec}{\left(\eta \right)}^T,\mathrm{vec}{\left({\mathsf{\Gamma }}_{\mathcal{A}}\right)}^T,\mathrm{vech}{\left(\mathsf{\Omega }\right)}^T,\mathrm{vech}{\left({\mathsf{\Omega }}_0\right)}^T\right\}}^T$. Hence, the function g connects $\xi$ and $\theta$, and $\xi =g\left(\theta \right)$ is twice differentiable. All the conditions in Proposition 1 are satisfied. Let ${\widehat{\mathsf{\Sigma }}}_O$ be the estimator of $\mathsf{\Sigma }$ under the oracle partial envelope model (15), then $n^{1/2}\left[{\left\{\mathrm{vec}{\left({\widehat{\beta }}_{1,\mathcal{A},O}\right)}^T,\mathrm{vech}{\left({\widehat{\mathsf{\Sigma }}}_O\right)}^T\right\}}^T-{\left\{\mathrm{vec}{\left({\beta }_{1,\mathcal{A}}\right)}^T,\mathrm{vech}{\left(\mathsf{\Sigma }\right)}^T\right\}}^T\right]$ is asymptotically normally distributed with zero mean and some covariance matrix.

We employ the normal errors to provide closed-form expressions for the asymptotic variance of $\mathrm{vec}\left({\widehat{\beta }}_{1,\mathcal{A},O}\right)$. Proposition 2 demonstrates that the asymptotic variance has the form $H{\left(H^{T}JH\right)}^{†}{H}^T$, where ‘†’ denotes Moore–Penrose inverse, J is the Fisher information, and H is the Jacobian matrix

$$H=\left(\begin{array}{cccc}{I}_{p_1}\otimes {\mathsf{\Gamma }}_{\mathcal{A}}& {\eta }^T\otimes I_q& 0& 0\\ 0& 2C_r(I_r\otimes \mathsf{\Gamma }\mathsf{\Omega }-{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T\otimes \mathsf{\Gamma })L& C_r(\mathsf{\Gamma }\otimes \mathsf{\Gamma })E_{u_1}& C_r({\mathsf{\Gamma }}_0\otimes {\mathsf{\Gamma }}_0)E_{r-u_1}\end{array}\right),$$

where $L={(K_{q{u}_1}^T,0)}^T\in {\mathbb{R}}^{r{u}_1\times q{u}_1}$, and $K_{q{u}_1}\in {\mathbb{R}}^{q{u}_1\times q{u}_1}$ is a commutation matrix (Magnus and Neudecker [26]). After some algebra, we can obtain the closed form for the asymptotic variance of $\mathrm{vec}\left({\widehat{\beta }}_{1,\mathcal{A},O}\right)$:

$$\begin{array}{c}\hfill n^{1/2}\left\{\mathrm{vec}\left({\widehat{\beta }}_{1,\mathcal{A},O}\right)-\mathrm{vec}\left({\beta }_{1,\mathcal{A}}\right)\right\}\to N(0,V_O)\end{array}$$

in distribution, where $V_O={\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}\otimes {\mathsf{\Gamma }}_{\mathcal{A}}\mathsf{\Omega }{\mathsf{\Gamma }}_{\mathcal{A}}^T+({\eta }^T\otimes {\mathsf{\Gamma }}_{\mathcal{A},0})T(\eta \otimes {\mathsf{\Gamma }}_{\mathcal{A},0}^T)$, and $T=\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}^{-1}+\mathsf{\Omega }\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}^{-1}+{\mathsf{\Omega }}^{-1}\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}-2I_{u_1}\otimes I_{q-u_1}$. Notice that we ignore $\alpha$, ${\mathsf{\Sigma }}_X$ and ${\beta }_2$ in the J and H matrices. This does not influence the results since they are not contained in the parameterization of ${\beta }_1$ and $\mathsf{\Sigma }$, and their maximum likelihood estimates are asymptotically independent of the estimates of ${\beta }_1$ and $\mathsf{\Sigma }$. □

Next, we continue to discuss the theoretical properties of the sparse partial envelope estimator.

Theorem 3.

Suppose that the conditions in Theorem 2 hold. Then, as $n\to \infty$, $\sqrt{n}\left\{\mathrm{vec}\left({\widehat{\beta }}_{1,\mathcal{A}}\right)-\mathrm{vec}\left({\beta }_{1,\mathcal{A}}\right)\right\}$ is asymptotically normally distributed with mean zero and asymptotic variance is equal to that of ${\widehat{\beta }}_{1,\mathcal{A},O}$. Further, assume that the errors are normally distributed, then we have a closed form for the asymptotic variance V: $V={\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}\otimes {\mathsf{\Gamma }}_{\mathcal{A}}\mathsf{\Omega }{\mathsf{\Gamma }}_{\mathcal{A}}^T+({\eta }^T\otimes {\mathsf{\Gamma }}_{\mathcal{A},0})T^{-1}(\eta \otimes {\mathsf{\Gamma }}_{\mathcal{A},0}^T)$, where $T=\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}^{-1}+\mathsf{\Omega }\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}^{-1}+{\mathsf{\Omega }}^{-1}\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}-2I_{u_1}\otimes I_{q-u_1}$.

From Theorem 3, we can see that the sparse partial envelope estimator is asymptotically normal and has an asymptotic distribution. Together with Theorem 2, it shows that the sparse partial envelope estimator enjoys the oracle property: the sparse partial envelope model selects the inactive responses with the probability tending to 1 and estimates the coefficients for the active responses with the same efficiency as does the oracle partial envelope model.

Proof of Theorem 3.

Let ${\widehat{A}}_{\mathcal{A}}$ denote the nonzero rows in the sparse partial envelope estimator $\widehat{A}$, and ${\widehat{A}}_O$ denote the nonzero rows in the oracle partial envelope estimator. Suppose we can prove ${\widehat{A}}_{\mathcal{A}}={\widehat{A}}_O+O_p\left(a_n\right)$ for a sequence $a_n=o\left(n^{-1/2}\right)$, then $P_{\widehat{\mathsf{\Gamma }}}=P_{{\widehat{\mathsf{\Gamma }}}_O}+O_p\left(a_n\right)$ with $P_{\mathsf{\Gamma }}=G_A{\left(G_A^T{G}_A\right)}^{-1}{G}_A^T$. Hence, ${\widehat{\beta }}_1-{\widehat{\beta }}_{1,O}=(P_{\widehat{\mathsf{\Gamma }}}-P_{{\widehat{\mathsf{\Gamma }}}_O}){\widehat{\beta }}_{1,\mathrm{ols}}=(P_{\widehat{\mathsf{\Gamma }}}-P_{{\widehat{\mathsf{\Gamma }}}_O})({\widehat{\beta }}_{1,\mathrm{ols}}-{\beta }_1)+(P_{\widehat{\mathsf{\Gamma }}}-P_{{\widehat{\mathsf{\Gamma }}}_O}){\beta }_1=O_p\left(a_n\right)o_p\left(1\right)+O_p\left(a_n\right)=O_p\left(a_n\right)$. So $n^{1/2}({\widehat{\beta }}_1-{\widehat{\beta }}_{1,O})\to 0$ in probability. By Slutsky’s theorem, $n^{1/2}({\widehat{\beta }}_1-{\beta }_1)$ has the identical asymptotic distribution to $n^{1/2}({\widehat{\beta }}_{1,O}-{\beta }_1)$. If we can prove ${\widehat{A}}_{\mathcal{A}}={\widehat{A}}_O+O_p\left(a_n\right)$ for $a_n=o\left(n^{-1/2}\right)$, therefore, the conclusion of Theorem 3 follows. Since $n^{1/2}{\xi }_{\max ,n}\to 0$, ${\xi }_{\max ,n}=o\left(n^{-1/2}\right)$. Concerning the selection of $a_n$, we can take $a_n={\left(n^{-1/2}{\xi }_{max,n}\right)}^{1/2}$.

We set B to be a $(q-u_1)\times u_1$ matrix, and

$$G_B=\left(\begin{array}{c}{I}_{u_1}\\ B\end{array}\right)\in {\mathbb{R}}^{q\times u_1}.$$

The objective function to estimate B is

$$\begin{array}{cc}\hfill f_{\mathrm{obj},\mathcal{A}}\left(B\right)=& -2log|G_B^T{G}_B|+log|G_B^T{\widehat{\mathsf{\Sigma }}}_{{\left(R_{Y\mid 2}\right)}_{\mathcal{A}}\mid R_{1\mid 2}}{G}_B|\hfill \\ \hfill & +log|G_B^T{\left({\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}^{-1}\right)}_{\mathcal{A}}{G}_B|+\sum _{i=1}^{q-u_1}\lambda {\omega }_i{\parallel b_i\parallel }_2,\hfill \end{array}$$

where $b_i$ is the ith row of B. Since the sparse partial envelope model enjoys the selection consistency, ${\widehat{A}}_{\mathcal{A}}=arg{min}_{B\in {\mathbb{R}}^{(q-u_1)\times u_1}}{f}_{\mathrm{obj},\mathcal{A}}\left(B\right)$. For the sake of proving ${\widehat{A}}_{\mathcal{A}}={\widehat{A}}_O+O_p\left(a_n\right)$, it is sufficient to demonstrate that for any small $\epsilon >0$, there exists a sufficiently large constant C, such that

$$\underset{n\to \infty }{lim}\mathrm{pr}\left\{\underset{\Delta \in {\mathbb{R}}^{(q-u_1)\times u_1},{\parallel \Delta \parallel }_F=C}{inf}{f}_{\mathrm{obj},\mathcal{A}}({\widehat{A}}_O+a_n\Delta )>f_{\mathrm{obj},\mathcal{A}}\left({\widehat{A}}_O\right)\right\}>1-ϵ.$$

(17)

If (17) holds, then we have ${\widehat{A}}_{\mathcal{A}}={\widehat{A}}_O+O_p\left(a_n\right)$ for $a_n=o\left(n^{-1/2}\right)$. Now, we prove (17). Following the proof of Theorem 1, we expand $f_{\mathrm{obj},\mathcal{A}}({\widehat{A}}_O+a_n\Delta )$ and calculate $f_{\mathrm{obj},\mathcal{A}}({\widehat{A}}_O+a_n\Delta )-f_{\mathrm{obj},\mathcal{A}}\left({\widehat{A}}_O\right)$. The objective function $f_{\mathrm{obj},\mathcal{A}}\left(B\right)$ can be partitioned into four parts: $f_{\mathrm{obj},\mathcal{A}}\left(B\right)\equiv f_{1,\mathcal{A}}\left(B\right)+f_{2,\mathcal{A}}\left(B\right)+f_{3,\mathcal{A}}\left(B\right)+f_{4,\mathcal{A}}\left(B\right)$. The first directional derivatives of $f_{1,\mathcal{A}}\left(B\right),f_{2,\mathcal{A}}\left(B\right)$ and $f_{3,\mathcal{A}}\left(B\right)$ at ${\widehat{A}}_O$ are

$$\begin{array}{c}\hfill \stackrel{\to \Delta }{{df}_{1,\mathcal{A}}}\left({\widehat{A}}_O\right)=tr\left\{{\displaystyle \frac{d}{dB}}{f}_{1,\mathcal{A}}{\left(B\right)}^T{|}_{B={\widehat{A}}_O}\Delta \right\},\\ \hfill \stackrel{\to \Delta }{{df}_{2,\mathcal{A}}}\left({\widehat{A}}_O\right)=tr\left\{{\displaystyle \frac{d}{dB}}{f}_{2,\mathcal{A}}{\left(B\right)}^T{|}_{B={\widehat{A}}_O}\Delta \right\},\\ \hfill \stackrel{\to \Delta }{{df}_{3,\mathcal{A}}}\left({\widehat{A}}_O\right)=tr\left\{{\displaystyle \frac{d}{dB}}{f}_{3,\mathcal{A}}{\left(B\right)}^T{|}_{B={\widehat{A}}_O}\Delta \right\}.\end{array}$$

Because ${\widehat{A}}_O$ is a minimizer of $f_{1,\mathcal{A}}\left(B\right)+f_{2,\mathcal{A}}\left(B\right)+f_{3,\mathcal{A}}\left(B\right)$,

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dB}}{f}_{1,\mathcal{A}}{\left(B\right)|}_{B={\widehat{A}}_O}+{\displaystyle \frac{d}{dB}}{f}_{2,\mathcal{A}}\left(B\right){{|}_{B={\widehat{A}}_O}+{\displaystyle \frac{d}{dB}}{f}_{3,\mathcal{A}}\left(B\right)|}_{B={\widehat{A}}_O}=0.\end{array}$$

Then, $\stackrel{\to \Delta }{{df}_{1,\mathcal{A}}}\left({\widehat{A}}_O\right)+\stackrel{\to \Delta }{{df}_{2,\mathcal{A}}}\left({\widehat{A}}_O\right)+\stackrel{\to \Delta }{{df}_{3,\mathcal{A}}}\left({\widehat{A}}_O\right)=0$.

The computation on the second directional derivatives of $f_{1,\mathcal{A}}\left(B\right),f_{2,\mathcal{A}}\left(B\right)$ and $f_{3,\mathcal{A}}\left(B\right)$ at ${\widehat{A}}_O$ and the expansion of $f_{4,\mathcal{A}}\left(B\right)$ are parallel to those in Theorem 1. Combining all those terms together, we have

$$\begin{array}{cc}\hfill & f_{\mathrm{obj},\mathcal{A}}({\widehat{A}}_O+a_n\Delta )-f_{\mathrm{obj},\mathcal{A}}\left({\widehat{A}}_O\right)\hfill \\ \hfill \ge & a_n^{2}tr\left\{{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast \mathcal{A}}^T{\mathsf{\Gamma }}_{\mathcal{A},0}{\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}{\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}{\mathsf{\Gamma }}_1\right.\hfill \\ \hfill & +(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}_1^T{\Delta }_{\ast \mathcal{A}}^T{\mathsf{\Gamma }}_{\mathcal{A},0}{\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}^{-1}{\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}{\mathsf{\Gamma }}_1\hfill \\ \hfill & \left.-2{\left(I_{u_1}+A_{\mathcal{A}}^T{A}_{\mathcal{A}}\right)}^{-1}{\Delta }_{\ast \mathcal{A}}^T{\mathsf{\Gamma }}_{\mathcal{A},0}{\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}\right\}\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{a}_n(q-u_1){\xi }_{\max ,n}\underset{i}{max}\left(\parallel a_i{\parallel }_2^{-1}{\parallel {\delta }_i\parallel }_2\right)+o_p\left(a_n^2\right),\hfill \end{array}$$

where $A_{\mathcal{A}}\in {\mathbb{R}}^{(q-u_1)\times u_1}$ includes the nonzero rows in A and ${\Delta }_{\ast \mathcal{A}}={(0_{u_1\times u_1},{\Delta }^T)}^T\in {\mathbb{R}}^{q\times u_1}$. According to the definition of $a_n$, we have ${\xi }_{\max ,n}=o_p\left(a_n\right)$, so the second term is dominated by the first term. If the trace in the first term is positive, then we can establish (17), and we have

$$\begin{array}{cc}\hfill & tr\left\{{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast \mathcal{A}}^T{\mathsf{\Gamma }}_{\mathcal{A},0}{\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}{\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}{\mathsf{\Gamma }}_1+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}_1^T{\Delta }_{\ast \mathcal{A}}^T{\mathsf{\Gamma }}_{\mathcal{A},0}{\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}^{-1}{\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}{\mathsf{\Gamma }}_1\right.\hfill \\ \hfill & \left.-2{\left(I_{u_1}+A_{\mathcal{A}}^T{A}_{\mathcal{A}}\right)}^{-1}{\Delta }_{\ast \mathcal{A}}^T{\mathsf{\Gamma }}_{\mathcal{A},0}{\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}\right\}\hfill \\ \hfill =& vec{\left({\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}{\mathsf{\Gamma }}_1\right)}^T\left\{{\mathsf{\Omega }}^{-1}\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}\right.\hfill \\ \hfill & \left.+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T)\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}\mid \mathcal{I}}^{-1}-2I_{u_1}\otimes I_{q-u_1}\right\}vec\left({\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}{\mathsf{\Gamma }}_1\right)\hfill \\ \hfill \ge & vec{\left({\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}{\mathsf{\Gamma }}_1\right)}^T\left\{{\mathsf{\Omega }}^{-1}\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}\right.\hfill \\ \hfill & \left.+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T)\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}^{-1}-2I_{u_1}\otimes I_{q-u_1}\right\}vec\left({\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}{\mathsf{\Gamma }}_1\right)\hfill \\ \hfill \ge & m_3{\parallel {\mathsf{\Gamma }}_{\mathcal{A},0}^T{\Delta }_{\ast \mathcal{A}}{\mathsf{\Gamma }}_1^T\parallel }_F\hfill \\ \hfill \ge & m_3{m}_2^2{\parallel \Delta \parallel }_F^2,\hfill \end{array}$$

where $m_2$ is the smallest eigenvalue of ${(I_{u_1}+A_{\mathcal{A}}^T{A}_{\mathcal{A}})}^{-1}$, and $m_3$ is the smallest eigenvalue of ${\mathsf{\Omega }}^{-1}\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T)\otimes {\tilde{\mathsf{\Omega }}}_{0,\mathcal{A}}^{-1}-2I_{u_1}\otimes I_{q-u_1}$. The derivation of the last inequality is identical to the derivation of a similar inequality at the end of the proof of Theorem 1. □

Now, we discuss the convergence rate and selection consistency of the sparse partial envelope estimator when $r_n$ tends to infinity with n. We make the same assumptions as Su et al. [6]:

• (A1) There exist positive constants $\overline{l}$ and $\underline{l}$ such that ${\gamma }_{\max }\left(\mathsf{\Sigma }\right)⩽\overline{l}$ and ${\gamma }_{\min }\left(\mathsf{\Sigma }\right)⩾\underline{l}$, where ${\gamma }_{\max }\left(\mathsf{\Sigma }\right)$ and ${\gamma }_{\min }\left(\mathsf{\Sigma }\right)$ are the largest and smallest eigenvalues of $\mathsf{\Sigma }$.
• (A2) The samples of $\epsilon$ are independent and identically sampled from a sub-Gaussian distribution, for example, $E\left\{exp\left({\tau }_1^T\epsilon \right)\right\}⩽exp\left(c_1{\tau }_1^T\mathsf{\Sigma }{\tau }_1\right)$ for some constant $c_1>0$ and every ${\tau }_1\in {\mathbb{R}}^{r_n}$. Samples of X are independent and identically distributed, and $X-{\mu }_X$ follows a sub-Gaussian distribution, for example, $E\left[exp\left\{{\tau }_2^T\left(X-{\mu }_X\right)\right\}\right]⩽exp\left(c_2{\tau }_2^T{\mathsf{\Sigma }}_X{\tau }_2\right)$ for some constant $c_2>0$ and every ${\tau }_2\in {\mathbb{R}}^p$. Let $s_1$ and $s_2$ denote the number of nonzero off-diagonal elements in the lower triangle of ${\mathsf{\Sigma }}^{-1}$ and ${\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}$, respectively, and let $s=max\{s_1,s_2\}$. We employ ${\parallel ·\parallel }_F$ to denote the Frobenius norm of a matrix.

Theorem 4.

Suppose that the sparse partial envelope models (5) and (8) hold, under (A1) and (A2), if ${\xi }_{\max ,n}=o\left(\sqrt{(r_n+s)log\left(r_n\right)/n}\right)$, then as $n\to \infty$, there exists a local minimizer $\widehat{A}$ of (10) such that $\parallel \widehat{A}{-A\parallel }_F=O_{\mathrm{p}}\left(\sqrt{(r_n+s)log\left(r_n\right)/n}\right)$, and the sparse partial envelope estimator ${\widehat{\beta }}_1$ converges at the same rate: $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F=O_p\left(\sqrt{(r_n+s)log\left(r_n\right)/n}\right)$.

Theorem 4 shows that the convergence rate of the sparse partial envelope estimator is finite by the convergence rate of ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}$ and ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}$. If there is a different inverse covariance matrix estimator, then we can improve the convergence rate of the sparse partial envelope estimator to a faster rate. Meanwhile, we need (A1) and (A2) for the consistency of ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}$ and ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}$.

Proof of Theorem 4.

We first show that

$$\begin{array}{cc}\hfill \parallel {\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}^{-1}{\parallel }_F& =O_p\left[{\left\{(r_n+s_1)log\left(r_n\right)/n\right\}}^{1/2}\right],\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \parallel {\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}{\parallel }_F& =O_p\left[{\left\{(r_n+s_2)log\left(r_n\right)/n\right\}}^{1/2}\right],\hfill \end{array}$$

(19)

where ${\parallel ·\parallel }_{\max }$ denotes the max norm of a matrix, which is the maximum of the absolute values of all elements in the matrix. In order to build (18) and (19), it is sufficient to demonstrate that there exist positive constants $C_{R_{Y\mid 2}}>0$ and $C_{\mathrm{res}}>0$ such that

$$\begin{array}{cc}\hfill \underset{i,j}{max}|{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},ij}-{\mathsf{\Sigma }}_{R_{Y\mid 2},ij}|& \le C_{R_{Y\mid 2}}{\left\{log\left(r_n\right)/n\right\}}^{1/2},\hfill \\ \hfill \underset{i,j}{max}|{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},ij}-{\mathsf{\Sigma }}_{ij}|& \le C_{\mathrm{res}}{\left\{log\left(r_n\right)/n\right\}}^{1/2}.\hfill \end{array}$$

(20)

Let Q be an m-dimensional random vector with mean ${\mu }_Q$ and covariance matrix ${\mathsf{\Sigma }}_Q$, and $Q-{\mu }_Q$ follow a sub-gaussian distribution. Assuming that $Q_1,\dots ,Q_n$ are n independent and identically distributed samples of Q, then $\overline{Q}={\sum }_{i=1}^n{Q}_i$ and

$$\begin{array}{cc}\hfill {\widehat{\mathsf{\Sigma }}}_Q=& {\displaystyle \frac{1}{n}}\sum _{k=1}^n(Q_k-\overline{Q}){(Q_k-\overline{Q})}^T\hfill \\ \hfill =& {\displaystyle \frac{1}{n}}\sum _{k=1}^n(Q_k-{\mu }_Q){(Q_k-{\mu }_Q)}^T-(\overline{Q}-{\mu }_Q){(\overline{Q}-{\mu }_Q)}^T.\hfill \end{array}$$

From Lemma 1 in Ravikumar et al. [27], there exist positive constants $C_i$ such that

$$\begin{array}{cc}\hfill pr\left(|{\widehat{\mathsf{\Sigma }}}_{Q,ij}-{\mathsf{\Sigma }}_{Q,ij}|>\delta \right)\le & pr\left[\left|{\left\{{\displaystyle \frac{1}{n}}\sum _{k=1}^n(Q_k-{\mu }_Q){(Q_k-{\mu }_Q)}^T\right\}}_{ij}-{\mathsf{\Sigma }}_{Q,ij}\right|>{\displaystyle \frac{\delta }{2}}\right]\hfill \\ \hfill & +pr\left[\left|{\left\{(\overline{Q}-{\mu }_Q){(\overline{Q}-{\mu }_Q)}^T\right\}}_{ij}\right|>{\displaystyle \frac{\delta }{2}}\right]\hfill \\ \hfill \le & C_{1}exp(-C_{2}n{\delta }^2)+C_{3}exp(-C_{4}n{\delta }^2),\hfill \end{array}$$

where $\delta \in (0,b_1)$, and $|·|$ denotes the absolute value. Let $\delta =C_5{\{log\left(m\right)/n\}}^{1/2}$ for some $C_5>0$. By the union sum inequality, there exists a positive constant $C_6$ such that

$$\begin{array}{c}\hfill \underset{i,j}{max}|{\widehat{\mathsf{\Sigma }}}_{Q,ij}-{\mathsf{\Sigma }}_{Q,ij}|\le C_6{\{log\left(m\right)/n\}}^{1/2},\end{array}$$

with probability tending to 1 as $n\to \infty$.

Let $Q={(R_{1\mid 2}^T,{\epsilon }^T)}^T\in {\mathbb{R}}^{p_1+r_n}$ with mean ${({\mu }_{R_{1\mid 2}}^T,0^T)}^T$, which has a block diagonal covariance matrix with diagonal blocks being ${\mathsf{\Sigma }}_{R_{1\mid 2}}$ and $\mathsf{\Sigma }$. Then, there exists the constant $C_0$ such that ${max}_{i,j}\mid {\widehat{\mathsf{\Sigma }}}_{Q,ij}-{\mathsf{\Sigma }}_{Q,ij}\mid \le C_0{\left\{log(r_n+p_1)/n\right\}}^{1/2}$. For fixed $p_1$, there exists the constant $C_0^{\ast }$ such that ${max}_{i,j}|{\widehat{\mathsf{\Sigma }}}_{Q,ij}-{\mathsf{\Sigma }}_{Q,ij}|\le C_0^{\ast }{\left\{log\left(r_n\right)/n\right\}}^{1/2}$. So, we have

$$\begin{array}{cc}\hfill \underset{i,j}{max}|{\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2},ij}-{\mathsf{\Sigma }}_{R_{1\mid 2},ij}|& \le C_0^{\ast }{\left\{log\left(r_n\right)/n\right\}}^{1/2},\hfill \\ \hfill \underset{i,j}{max}|{\widehat{\mathsf{\Sigma }}}_{\epsilon ,ij}-{\mathsf{\Sigma }}_{ij}|& \le C_0^{\ast }{\left\{log\left(r_n\right)/n\right\}}^{1/2},\hfill \\ \hfill \underset{i,j}{max}|{\widehat{\mathsf{\Sigma }}}_{\epsilon R_{1\mid 2},ij}|& \le C_0^{\ast }{\left\{log\left(r_n\right)/n\right\}}^{1/2}.\hfill \end{array}$$

Because ${\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2}}={\beta }_1{\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}{\beta }_1^T+{\widehat{\mathsf{\Sigma }}}_{\epsilon }+{\beta }_1{\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}\epsilon }+{\widehat{\mathsf{\Sigma }}}_{\epsilon R_{1\mid 2}}{\beta }_1^T$, for some $C_{R_{Y\mid 2}}>0$, we have

$$\begin{array}{c}\hfill \underset{i,j}{max}|{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},ij}-{\mathsf{\Sigma }}_{R_{Y\mid 2},ij}|\le C_{R_{Y\mid 2}}{\left\{log\left(r_n\right)/n\right\}}^{1/2},\end{array}$$

Since ${\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}={\widehat{\mathsf{\Sigma }}}_{\epsilon }-{\widehat{\mathsf{\Sigma }}}_{\epsilon R_{1\mid 2}}{\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}^{-1}{\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}\epsilon }$, we have

$$\begin{array}{cc}\hfill {\widehat{\mathsf{\Sigma }}}_{\mathrm{res}}-\mathsf{\Sigma }=& ({\widehat{\mathsf{\Sigma }}}_{\epsilon R_{1\mid 2}}-{\mathsf{\Sigma }}_{\epsilon R_{1\mid 2}}){\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}{\mathsf{\Sigma }}_{R_{1\mid 2}\epsilon }+{\mathsf{\Sigma }}_{\epsilon R_{1\mid 2}}({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}^{-1}-{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}){\mathsf{\Sigma }}_{R_{1\mid 2}\epsilon }\hfill \\ \hfill & +{\mathsf{\Sigma }}_{\epsilon R_{1\mid 2}}{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}\epsilon }-{\mathsf{\Sigma }}_{R_{1\mid 2}\epsilon })+({\widehat{\mathsf{\Sigma }}}_{\epsilon R_{1\mid 2}}-{\mathsf{\Sigma }}_{\epsilon R_{1\mid 2}})({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}^{-1}-{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}){\mathsf{\Sigma }}_{R_{1\mid 2}\epsilon }\hfill \\ \hfill & +{\mathsf{\Sigma }}_{\epsilon R_{1\mid 2}}({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}^{-1}-{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1})({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}\epsilon }-{\mathsf{\Sigma }}_{R_{1\mid 2}\epsilon })\hfill \\ \hfill & +({\widehat{\mathsf{\Sigma }}}_{\epsilon R_{1\mid 2}}-{\mathsf{\Sigma }}_{\epsilon R_{1\mid 2}}){\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}\epsilon }-{\mathsf{\Sigma }}_{R_{1\mid 2}\epsilon })\hfill \\ \hfill & +({\widehat{\mathsf{\Sigma }}}_{\epsilon R_{1\mid 2}}-{\mathsf{\Sigma }}_{\epsilon R_{1\mid 2}})({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}^{-1}-{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1})({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}\epsilon }-{\mathsf{\Sigma }}_{R_{1\mid 2}\epsilon })+{\widehat{\mathsf{\Sigma }}}_{\epsilon }-\mathsf{\Sigma }.\hfill \end{array}$$

If $M\in {\mathbb{R}}^{d_1\times d_2},N\in {\mathbb{R}}^{d_2\times d_3}$, then ${\parallel MN\parallel }_{\max }\le d_2{\parallel M\parallel }_{\max }{\parallel N\parallel }_{\max }$, where ${\parallel ·\parallel }_{\max }$ is the matrix max norm. Exploiting this fact, for some $C_{\mathrm{res}}>0$, we have

$$\begin{array}{c}\hfill \underset{i,j}{max}|{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},ij}-{\mathsf{\Sigma }}_{ij}|\le C_{\mathrm{res}}{\left\{log\left(r_n\right)/n\right\}}^{1/2},\end{array}$$

and hence, (18) and (19) hold.

Let $a_n={\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}$. The objective function in (10) can be denoted as $f_{\mathrm{obj},2}$. Theorem 4 holds if for any small $\epsilon >0$, there exists a sufficiently large constant C such that

$$\underset{n\to \infty }{lim}\mathrm{pr}\left\{\underset{\Delta \in {\mathbb{R}}^{(q-u_1)\times u_1},{\parallel \Delta \parallel }_F=C}{inf}{f}_{\mathrm{obj},2}(A+a_n\Delta )>f_{\mathrm{obj},2}\left(A\right)\right\}>1-ϵ.$$

(21)

Let ${\Delta }_{\ast }={\left(0_{u_1\times u_1},{\Delta }^T\right)}^T\in {\mathbb{R}}^{q\times u_1}$. Following the computations as in the proof of Theorem 1, we calculate the Taylor expansion of $f_{\mathrm{obj},2}(A+a_n\Delta )$ at A and obtain

$$\begin{array}{cc}\hfill & f_{\mathrm{obj},2}(A+a_n\Delta )-f_{\mathrm{obj},2}\left(A\right)\hfill \\ \hfill \ge & 2a_{n}tr\left[{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T({\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}-\mathsf{\Sigma }){\Delta }_{\ast }\right.\hfill \\ \hfill & +\left\{{\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{G}_A\right)}^{-1}-{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\right\}{G}_A^T\mathsf{\Sigma }{\Delta }_{\ast }\hfill \\ \hfill & +\left\{{\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{G}_A\right)}^{-1}-{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\right\}{G}_A^T({\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}-\mathsf{\Sigma }){\Delta }_{\ast }\hfill \\ \hfill & +{\left(G_A^T{\mathsf{\Sigma }}_{R_{Y\mid 2},\mathrm{spice}}^{-1}{G}_A\right)}^{-1}{G}_A^T({\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}){\Delta }_{\ast }\hfill \\ \hfill & +\left\{{\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}{G}_A\right)}^{-1}-{\left(G_A^T{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}{G}_A\right)}^{-1}\right\}{G}_A^T{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}{\Delta }_{\ast }\hfill \\ \hfill & +\left.\left\{{\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}{G}_A\right)}^{-1}-{\left(G_A^T{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}{G}_A\right)}^{-1}\right\}{G}_A^T({\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}){\Delta }_{\ast }\right]\hfill \\ \hfill & +a_n^{2}tr\left\{{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0^{-1}{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right.\hfill \\ \hfill & \left.-2{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}-{\displaystyle \frac{1}{2}}{a}_n(q-u_1){\xi }_{\max ,n}\underset{i}{max}\left(\parallel a_i{\parallel }_2^{-1}{\parallel {\delta }_i\parallel }_2\right)+o_p\left(a_n^2\right).\hfill \end{array}$$

Notice that

$$\begin{array}{c}\hfill {\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}-\mathsf{\Sigma }=-\mathsf{\Sigma }({\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}^{-1})\mathsf{\Sigma }+o_p({\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}^{-1}).\end{array}$$

Let $\parallel ·\parallel$ be the spectral norm of a matrix. For two matrices $M\in {\mathbb{R}}^{d_1\times d_2}$ and $N\in {\mathbb{R}}^{d_2\times d_3}$, ${\parallel MN\parallel }_F\le {\parallel M\parallel \parallel N\parallel }_F$. So,

$$\begin{array}{c}\hfill {∥\mathsf{\Sigma }({\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}^{-1})\mathsf{\Sigma }∥}_F\le {\parallel \mathsf{\Sigma }\parallel }^2\parallel {\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}^{-1}{\parallel }_F\le {\overline{k}}^2{\parallel {\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}^{-1}\parallel }_F,\end{array}$$

and $\parallel {\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{-\mathsf{\Sigma }\parallel }_F=O_p\left[{\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}\right]$. Then,

$$\begin{array}{cc}\hfill & tr\left[{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T({\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}-\mathsf{\Sigma }){\Delta }_{\ast }\right]\hfill \\ \hfill \ge & -{\overline{k}}^2{\parallel \Delta \parallel }_F\parallel {\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}^{-1}{\parallel }_F∥{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}∥{\parallel G_A\parallel }_F.\hfill \end{array}$$

Now, we have

$$\begin{array}{cc}\hfill & {\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{G}_A\right)}^{-1}-{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\hfill \\ \hfill =& -{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{G}_A-G_A^T\mathsf{\Sigma }{G}_A){\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\hfill \\ \hfill & +o_p(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{G}_A-G_A^T\mathsf{\Sigma }{G}_A)\hfill \\ \hfill =& -{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T({\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}-\mathsf{\Sigma })G_A{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\hfill \\ \hfill & +o_p\left[{\left\{(r_n+s_1)log\left(r_n\right)/n\right\}}^{1/2}\right]\hfill \\ \hfill =& -{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}{G}_A^T\mathsf{\Sigma }({\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}^{-1})\mathsf{\Sigma }{G}_A{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\hfill \\ \hfill & +o_p\left[{\left\{(r_n+s_1)log\left(r_n\right)/n\right\}}^{1/2}\right].\hfill \end{array}$$

So,

$$\begin{array}{cc}\hfill & tr\left[\left\{{\left(G_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{G}_A\right)}^{-1}-{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}\right\}{G}_A^T\mathsf{\Sigma }{\Delta }_{\ast }\right]\hfill \\ \hfill \ge & -u_1^{1/2}{\overline{k}}^2{\parallel \Delta \parallel }_F\parallel {\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}^{-1}{\parallel }_F∥{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}∥{\parallel G_A\parallel }_F.\hfill \end{array}$$

Collecting all these inequalities and results together, we apply these inequalities to the terms in the first four lines of $f_{\mathrm{obj},2}(A+a_n\Delta )-f_{\mathrm{obj},2}\left(A\right)$, then

$$\begin{array}{cc}\hfill & f_{\mathrm{obj},2}(A+a_n\Delta )-f_{\mathrm{obj},2}\left(A\right)\hfill \\ \hfill \ge & 2M_1{a}_n{\parallel \Delta \parallel }_F\parallel {\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}^{-1}{\parallel }_F+2M_2{a}_n{\parallel \Delta \parallel }_F{\parallel {\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}-{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}\parallel }_F\hfill \\ \hfill & +a_n^{2}tr\left\{{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0^{-1}{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right.\hfill \\ \hfill & \left.-2{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}\hfill \\ \hfill & -{\displaystyle \frac{1}{2}}{a}_n(q-u_1){\xi }_{\max ,n}\underset{i=1,\dots ,q-u_1}{max}\left(\parallel a_i{\parallel }_2^{-1}{\parallel {\delta }_i\parallel }_2\right)+o_p\left(a_n^2\right),\hfill \end{array}$$

where $M_1=-2u_1^{1/2}{\overline{k}}^2∥{\left(G_A^{\mathrm{T}}\mathsf{\Sigma }{G}_A\right)}^{-1}∥{\parallel G_A\parallel }_F$, $M_2=-2∥{\left(G_A^T{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}{G}_A\right)}^{-1}∥{\parallel G_A\parallel }_F$ and ${\xi }_{\max ,n}=o\left[{\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}\right]=o_p\left(a_n\right)$. Based on the proof at the end of Theorem 1, there exists the positive constant $m_1$ by Theorem 1 such that

$$\begin{array}{cc}\hfill & tr\left\{{\mathsf{\Omega }}^{-1}{\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1+(\mathsf{\Omega }+\eta {\mathsf{\Sigma }}_{R_{1\mid 2}}{\eta }^T){\mathsf{\Gamma }}_1^T{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0^{-1}{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }{\mathsf{\Gamma }}_1\right.\hfill \\ \hfill & \left.-2{(I_{u_1}+A^{T}A)}^{-1}{\Delta }_{\ast }^T{\mathsf{\Gamma }}_0{\mathsf{\Gamma }}_0^T{\Delta }_{\ast }\right\}\hfill \\ \hfill \ge & m_1{\parallel \Delta \parallel }_F^2,\hfill \end{array}$$

Then, with sufficiently large C, the second order term of ${\parallel \Delta \parallel }_F$ dominates the first-order term, and $f_{\mathrm{obj},2}(A+a_n\Delta )-f_{\mathrm{obj},2}\left(A\right)>0$ with the probability tending to 1. Therefore, (21) holds, and $\parallel \widehat{A}{-A\parallel }_F=O_p\left[{\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}\right]$. Since $P_{\mathsf{\Gamma }}=G_A{(I_{u_1}+A^{T}A)}^{-1}{G}_A^T$ is a simple and continuous function of A, then $\parallel P_{\widehat{\mathsf{\Gamma }}}-P_{\mathsf{\Gamma }}{\parallel }_F=O_p\left[{\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}\right]$.

Because

$$\begin{array}{cc}\hfill {\widehat{\beta }}_{1,\mathrm{ols}}-{\beta }_1=& {\widehat{\mathsf{\Sigma }}}_{\epsilon R_{1\mid 2}}{\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}^{-1}-{\mathsf{\Sigma }}_{\epsilon R_{1\mid 2}}{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}\hfill \\ \hfill =& ({\widehat{\mathsf{\Sigma }}}_{\epsilon R_{1\mid 2}}-{\mathsf{\Sigma }}_{\epsilon R_{1\mid 2}}){\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1}+{\mathsf{\Sigma }}_{\epsilon R_{1\mid 2}}({\widehat{\mathsf{\Sigma }}}_{R_{1\mid 2}}^{-1}-{\mathsf{\Sigma }}_{R_{1\mid 2}}^{-1})\hfill \\ \hfill & +o_p\left[{\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}\right],\hfill \end{array}$$

there exists the constant $C_{\mathrm{ols}}$ such that

$$\begin{array}{c}\hfill \underset{i,j}{max}|{\widehat{\beta }}_{1,\mathrm{ols},ij}-{\beta }_{1,ij}|\le C_{\mathrm{ols}}{\left\{log\left(r_n\right)/n\right\}}^{1/2}.\end{array}$$

Since $\parallel {\widehat{\beta }}_{1,\mathrm{ols}}-{\beta }_1{\parallel }_F\le {\left(p_1{r}_n\right)}^{1/2}{\parallel {\widehat{\beta }}_{1,\mathrm{ols}}-{\beta }_1\parallel }_{\max }$, then

$$\begin{array}{cc}\hfill \parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F\le & {∥(P_{\widehat{\mathsf{\Gamma }}}-P_{\mathsf{\Gamma }}){\widehat{\beta }}_{1,\mathrm{ols}}∥}_F+{∥P_{\mathsf{\Gamma }}({\widehat{\beta }}_{1,\mathrm{ols}}-{\beta }_1)∥}_F\hfill \\ \hfill \le & {∥(P_{\widehat{\mathsf{\Gamma }}}-P_{\mathsf{\Gamma }}){\widehat{\beta }}_{1,\mathrm{ols}}∥}_F+{∥{\widehat{\beta }}_{1,\mathrm{ols}}-{\beta }_1∥}_F.\hfill \end{array}$$

Hence, the sparse partial envelope estimator ${\widehat{\beta }}_1$ converges to ${\beta }_1$ with rate ${\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}$. □

Theorem 5.

Assume that the conditions in Theorem 4 hold, $\sqrt{(r_n+s)log\left(r_n\right)/n}\to 0$ as $n\to \infty$ and $\sqrt{(r_n+s)log\left(r_n\right)/n}=o\left({\xi }_{\min ,n}\right)$. Then, $\mathrm{pr}({\widehat{a}}_i\ne 0,i=1,\dots ,q-u_1)\to 1$ as $n\to \infty$, and $\mathrm{pr}({\widehat{a}}_i=0,i=q-u_1+1,\dots ,r_n-u_1)\to 1$ as $n\to \infty$.

Theorem 5 establishes the selection consistency of the sparse partial envelope estimator. When $r_n$ grows with n, the sparse partial envelope estimator correctly identifies active and inactive responses with the probability tending to 1.

Proof of Theorem 5.

We make

$$\begin{array}{c}\hfill \rho =\underset{i=1,\dots ,q-u_1}{min}{\parallel a_i\parallel }_2>0,\end{array}$$

then $\rho$ is the smallest norm of the non-sparse rows in A. Because

$$\begin{array}{c}\hfill \parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F=O_p\left[{\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}\right]and{\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}\to 0,\end{array}$$

then $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F<\rho /2$ with the probability tending to 1. This means $\parallel {\widehat{a}}_i-a_i{\parallel }_2<\rho /2$ for $i=1,\dots ,r_n$. For $i=1,\dots ,q$, $\parallel {\widehat{a}}_i{\parallel }_2>{\parallel a_i\parallel }_2-\rho /2>0$. Hence, the sparse partial envelope estimator identifies the nonzero rows with the probability tending to 1.

For $a_i,i=q-u_1+1,\dots ,r_n-u_1$, assuming ${\widehat{a}}_i\ne 0$, we take the derivative of $f_{\mathrm{obj},2}$ concerning $a_i$ and evaluate at ${\widehat{a}}_i$, and we have

$$\begin{array}{cc}\hfill & -4e_i^T{\widehat{G}}_A{(I_{u_1}+{\widehat{A}}^T\widehat{A})}^{-1}+2e_i^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{\widehat{G}}_A{\left({\widehat{G}}_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{\widehat{G}}_A\right)}^{-1}\hfill \\ \hfill & +2e_i^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}{\widehat{G}}_A{\left({\widehat{G}}_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}{\widehat{G}}_A\right)}^{-1}+\lambda {\omega }_i{\displaystyle \frac{{\widehat{a}}_i^T}{\parallel {\widehat{a}}_i{\parallel }_2}}=0.\hfill \end{array}$$

Since $-4e_i^T{G}_A{(I_{u_1}+A^{T}A)}^{-1}+2e_i^T\mathsf{\Sigma }{G}_A{\left(G_A^T\mathsf{\Sigma }{G}_A\right)}^{-1}+2e_i^T{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}{G}_A{\left(G_A^T{\mathsf{\Sigma }}_{R_{Y\mid 2}}^{-1}{G}_A\right)}^{-1}=0$, then we have

$$\begin{array}{cc}\hfill & ∥-4e_i^T{\widehat{G}}_A{(I_{u_1}+{\widehat{A}}^T\widehat{A})}^{-1}+2e_i^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{\widehat{G}}_A{\left({\widehat{G}}_A^T{\widehat{\mathsf{\Sigma }}}_{\mathrm{res},\mathrm{spice}}{\widehat{G}}_A\right)}^{-1}\hfill \\ \hfill & {+2e_i^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}{\widehat{G}}_A{\left({\widehat{G}}_A^T{\widehat{\mathsf{\Sigma }}}_{R_{Y\mid 2},\mathrm{spice}}^{-1}{\widehat{G}}_A\right)}^{-1}∥}_F=O_p\left[{\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}\right].\hfill \end{array}$$

But

$$\begin{array}{c}\hfill {∥\lambda {\omega }_i{\displaystyle \frac{{\widehat{a}}_i^T}{\parallel {\widehat{a}}_i{\parallel }_2}}∥}_F=\lambda {\omega }_i={\xi }_i\ge {\xi }_{\min ,n}.\end{array}$$

Because ${\left\{(r_n+s)log\left(r_n\right)/n\right\}}^{1/2}=o\left({\xi }_{\min ,n}\right)$, this is a contradiction. Hencem we have $pr({\widehat{a}}_i=0)\to 1$ for $i=q-u_1+1,\dots ,r_n-u_1$ as $n\to \infty$. □

5. Simulation Study

Now, in this part, we report results on the numerical performance of the sparse partial envelope estimator on parameter estimation and response variable selection. We discussed it through the large-sample setting and the high-dimensional setting. In the first situation, we set $r=20$, $q=5$, $p=3$, $p_1=2$, $u=3$ and $u_1=2$. The matrix $({\mathsf{\Gamma }}_{\mathcal{A}},{\mathsf{\Gamma }}_{\mathcal{A},0})$ was obtained by orthogonalizing a $q\times q$ matrix of independent uniform $(0,1)$ variates. Then, we employed the structure in (8) to construct $\mathsf{\Gamma }$, ${\mathsf{\Gamma }}_0$ and ${\beta }_2$. The elements in $\eta$ were independent $N(0,4)$ random variables. The errors were simulated independently from $N(0,\mathsf{\Sigma })$ distributions, and the error covariance matrix followed the structure $\mathsf{\Sigma }=\mathsf{\Gamma }\mathsf{\Omega }{\mathsf{\Gamma }}^T+{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T$, where $\mathsf{\Omega }=I_{u_1}$ and ${\mathsf{\Omega }}_0$ was a block diagonal matrix with the upper left block being $25I_{q-u_1}$ and the lower right block being $0.09I_{r-q}$. The coefficient ${\beta }_{2,\mathcal{A}}$ was a matrix of independent normal variates. The predictors $X_1$ were generated from a multivariate normal distribution with mean 0 and covariance matrix $4I_{p_1}$, and the elements in $X_2$ were generated from independent $N(0,1)$ random variables. The sample size were 50, 150, 350, 750, 1350, and 2150, respectively, and we generated 200 replications for each sample size. With each sample size, the standard deviation of each element in ${\widehat{\beta }}_1$ over the replicates was computed, which we called the actual standard deviations of the elements in ${\widehat{\beta }}_1$. The bootstrap standard errors were acquired by calculating the standard deviations for 200 bootstrap samples as a way to estimate the actual estimation standard deviations. Because of the excessively long computation time, the results of the sparse envelope model were based on 20 replications.

For each replication, we fitted the standard model (1), the oracle partial envelope model (15), the active partial envelope model (16), the sparse partial envelope models (5) and (8). Then, we acquired their estimators of ${\widehat{\beta }}_1$ and computed the estimation standard deviation for each element in ${\widehat{\beta }}_1$. The results for a randomly selected element in ${\widehat{\beta }}_1$ are summarized in Figure 1. For better visibility, we only display the asymptotic standard deviation of the standard model. From the left panel of Figure 1, we can see that the actual standard deviations of the three models from large to small are the active partial envelope model, the oracle partial envelope model and the sparse partial envelope model, respectively. From the right panel of Figure 1, we can see that the asymptotic standard deviations of the four models from large to small are the standard model, the active partial envelope model, the oracle partial envelope model and the sparse partial envelope model separately. To sum up, we can observe that the sparse partial envelope estimator is more efficient than the standard estimator, the oracle partial envelope estimator and the active partial envelope estimator. The ratio of the asymptotic standard deviation of the standard estimator to that of the sparse partial envelope estimator is 11.68. The ratio of the asymptotic standard deviation of the oracle partial envelope estimator to that of the sparse partial envelope estimator is 1.27. The ratio of the asymptotic standard deviation of the active partial envelope estimator to that of the sparse partial envelope estimator is 6.22. The difference between the sparse partial envelope estimator and the oracle partial envelope estimator becomes quite small as the sample size n increases, which confirms the oracle property stated in Theorem 3.

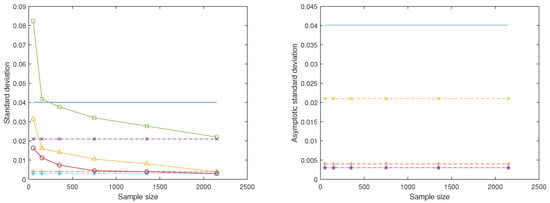
Figure 1. Comparison of the standard deviations for four model estimators. The − line marks the asymptotic standard deviation of the standard model. The lines ‘$-△$’ and $--$ with + mark the actual and asymptotic standard deviations of the oracle partial envelope model. The lines ‘$-\square$’ and $--$ with × mark the actual and asymptotic standard deviations of the active partial envelope model. The lines ‘$-◯$’ and $-·$ with * mark the actual and asymptotic standard deviations of the sparse partial envelope model.

We also studied the variable selection performance of the sparse partial envelope estimator on true positive rate (TPR) and true negative rate (TNR) over 200 repeated samples. The true positive rate is calculated by ${\pi }_1/q$, where ${\pi }_1$ is the number of active responses correctly chosen, and the true negative rate is calculated by ${\pi }_2/(r-q)$, where ${\pi }_2$ is the number of inactive responses correctly chosen. Table 1 reports the variable selection results in the first situation under the large-sample setting. Compared to the sparse envelope estimator, the sparse partial envelope estimator has a better selection performance in this case. The proposed sparse partial envelope estimation procedure can correctly identify all the active sets, and the true negative rate tends to 1 as n increases, which confirms the selection consistency stated in Theorem 2.

Table 1. Comparison of selection performances of the sparse partial envelope estimator and the sparse envelope estimator in the first situation.

	Sparse Partial Envelope		Sparse Envelope
n	TPR	TNR	TPR	TNR
50	100%	100%	100%	6.67%
80	100%	100%	100%	93.33%
100	100%	100%	100%	53.33%
150	100%	100%	100%	73.33%
200	100%	100%	100%	100%
250	100%	100%	100%	93.33%
300	100%	100%	100%	100%
350	100%	100%	100%	100%

In the second situation, except for letting $u=q=5$, the other parameters were the same as those in the first situation. When $u=q$, there is no immaterial information in the active responses for the sparse envelope model, and ${\mathsf{\Gamma }}_{\mathcal{A}}=I_q$, but as long as $u_1<u$, there is still immaterial information in the active responses for the sparse partial envelope model. In this sense, the sparse partial envelope model is more flexible than the sparse envelope model. Figure 2 plots the standard deviations of a chosen element in ${\widehat{\beta }}_1$ and $\widehat{\beta }$ when $u=q$. From the left panel of Figure 2, we can see that the actual standard deviations of the three models from large to small are the active partial envelope model, the oracle partial envelope model and the sparse partial envelope model, respectively. From the right panel of Figure 2, we can see that the asymptotic standard deviations of the four models from large to small are the standard model, the active partial envelope model, the oracle partial envelope model and the sparse partial envelope model separately. So, in summary, we can obtain that the sparse partial envelope estimator is more efficient than the standard estimator, the oracle partial envelope estimator and the active partial envelope estimator. The ratio of the asymptotic standard deviation of the standard estimator to that of the sparse partial envelope estimator is 11.68. The ratio of the asymptotic standard deviation of the oracle partial envelope estimator to that of the sparse partial envelope estimator is 1.27. The ratio of the asymptotic standard deviation of the active partial envelope estimator to that of the sparse partial envelope estimator is 6.22. The ratio of the asymptotic standard deviation of the sparse envelope estimator to that of the sparse partial envelope estimator is 1.35. As the sample size n increases, the difference between the sparse partial envelope estimator and the oracle partial envelope estimator also diminishes step by step.

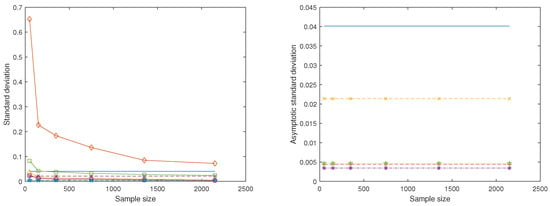
Figure 2. Comparison of the standard deviations for five model estimators. The − line marks the asymptotic standard deviation of the standard model. The lines ‘$-△$’ and $--$ with + mark the actual and asymptotic standard deviations of the oracle partial envelope model. The lines ‘$-\square$’ and $--$ with × mark the actual and asymptotic standard deviations of the active partial envelope model. The lines ‘$-◊$’ and ⋯ with ✩ mark the actual and asymptotic standard deviations of the sparse envelope model. The lines ‘$-◯$’ and $-·$ with * mark the actual and asymptotic standard deviations of the sparse partial envelope model.

Table 2 reports the variable selection results in the second situation. From Table 2, we can see that the variable selection performance of the sparse partial envelope estimator is the same as that of the sparse envelope estimator. Table 3 shows that comparisons of computing time in minutes among the standard model, the oracle partial envelope model, the active partial envelope model, the sparse partial envelope model and the sparse envelope model. It is obvious that the calculation speeds of the sparse partial envelope model and the sparse envelope model are significantly slower than those of the standard model, the oracle partial envelope model and the active partial envelope model, and the computation speed of the sparse envelope model is the slowest of the five models.

Table 2. Comparison of selection performances of the sparse partial envelope estimator and the sparse envelope estimator in the second situation.

	Sparse Partial Envelope		Sparse Envelope
n	TPR	TNR	TPR	TNR
50	100%	100%	100%	100%
80	100%	100%	100%	100%
100	100%	100%	100%	100%
150	100%	100%	100%	100%
200	100%	100%	100%	100%
250	100%	100%	100%	100%
300	100%	100%	100%	100%
350	100%	100%	100%	100%

Table 3. Comparison of computing time in minutes for the five models in the second situation.

Model Type	Computing Time
Standard model	0.53
Oracle partial envelope	1.17
Active partial envelope	0.62
Sparse partial envelope	359.40
Sparse envelope	3673.44

In the third situation, we set $r=100$, $q=26$, $p=50$, $p_1=30$, and $u=22$ and varied $u_1$ from 2 to 20. The matrix $\left({\mathsf{\Gamma }}_{\mathcal{A}},{\mathsf{\Gamma }}_{\mathcal{A},0}\right)$ was obtained by orthogonalizing the $q\times q$ matrix of independent standard normal variates. Accordingly, we used the structure in (8) to build $\mathsf{\Gamma }$, ${\mathsf{\Gamma }}_0$ and ${\beta }_2$. The elements in $\eta$ were independent normal variates with mean 0 and variance 0.16, and the error covariance matrix had the structure $\mathsf{\Sigma }=\mathsf{\Gamma }\mathsf{\Omega }{\mathsf{\Gamma }}^T+{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T$ with $\mathsf{\Omega }=I_{u_1}$ and ${\mathsf{\Omega }}_0=25I_{r-u_1}$. The predictors $X_1$ were generated from a multivariate normal distribution with mean 0 and covariance matrix $I_{p_1}$, and the predictors $X_2$ were generated from a multivariate normal distribution with mean 0 and covariance matrix $I_{p-p_1}$. The standard deviation of a randomly chosen element in ${\widehat{\beta }}_1$ is displayed under different $u_1$ in Figure 3. We see that when $u_1$ is small, there is a bigger immaterial part, and so we anticipate a more substantial efficiency gain by employing the sparse partial envelope estimator. Meanwhile, we see that the standard deviation of the sparse partial envelope model is significantly smaller than that of the standard model, so we can acquire that the sparse partial envelope estimator is much more efficient than the standard estimator.

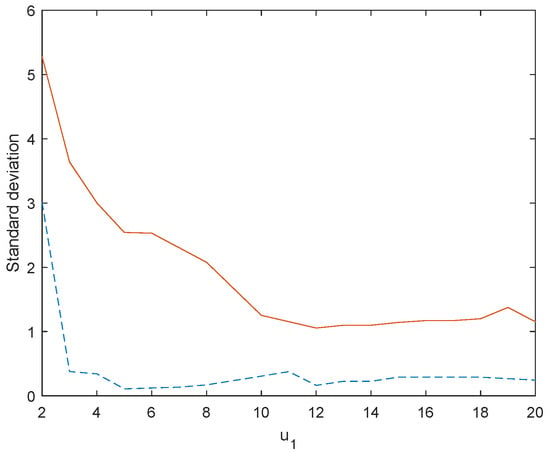
Figure 3. Comparison of the standard deviations for the sparse partial envelope estimator (dashed) and the standard estimator (solid).

In the fourth situation, we had $n<r$ and set $r=1000$, $q=10$, $p=20$, $p_1=15$, $u=3$ and $u_1=2$. The first $q/2$ rows in ${\mathsf{\Gamma }}_{\mathcal{A}}$ were ${\{{(1/q)}^{1/2},0\}}^T$ and the remaining $q/2$ rows in ${\mathsf{\Gamma }}_{\mathcal{A}}$ were ${\{0,{(1/q)}^{1/2}\}}^T$. Then, we employed the structure in (8) to construct $\mathsf{\Gamma }$, ${\mathsf{\Gamma }}_0$ and ${\beta }_2$. The elements in $\eta$ were independent $N(0,36)$ random variables, and the error covariance matrix followed the structure $\mathsf{\Sigma }=\mathsf{\Gamma }\mathsf{\Omega }{\mathsf{\Gamma }}^T+{\mathsf{\Gamma }}_0{\mathsf{\Omega }}_0{\mathsf{\Gamma }}_0^T$, where $\mathsf{\Omega }=0.25I_{u_1}$ and ${\mathsf{\Omega }}_0$ was a block diagonal matrix with the upper left block being $16I_{q-u_1}$ and lower right block being $9I_{r-q}$. The coefficient ${\beta }_{2,\mathcal{A}}$ was a matrix of independent normal variates. The predictors $X_1$ and $X_2$ were generated from independent $N(0,1)$ random variables. The sample sizes were 50, 100, 200, 400, 600, and 800, respectively, and we generated 200 replications for each sample size. Table 4 shows the variable selection performance of the sparse partial envelope estimator in the fourth situation under the high-dimensional setting. Figure 4 plots the average of $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F$ over 200 replications versus sample size n, and Figure 5 describes the convergence of $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F$, which is indicated in Theorem 4. Again, the left panel in Figure 4 provides a comparison of $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F$ among the standard estimator, the sparse partial envelope actual estimator and the sparse partial envelope bootstrap estimator, and the right panel highlights the comparison between sparse partial envelope actual estimator and sparse partial envelope bootstrap estimator. Meanwhile, Figure 5 also provides a comparison of ${\left[n/\left\{(r_n+s)log\left(r_n\right)\right\}\right]}^{1/2}{\parallel {\widehat{\beta }}_1-{\beta }_1\parallel }_F$ among the standard estimator, the sparse partial envelope actual estimator and the sparse partial envelope bootstrap estimator. The bootstrap estimator of $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F$ is computed based on the average of 200 bootstrap samples. With each bootstrap sample, we acquired the sparse partial envelope estimator ${\widehat{\beta }}_{1,\mathrm{boot}}$ and calculated $\parallel {\widehat{\beta }}_{1,\mathrm{boot}}-{\widehat{\beta }}_1{\parallel }_F$. Figure 4 and Figure 5 both demonstrate that $\parallel {\widehat{\beta }}_{1,\mathrm{boot}}-{\widehat{\beta }}_1{\parallel }_F$ is a good approximation to $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F$ and also display that $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F$ is much smaller than $\parallel {\widehat{\beta }}_{1,\mathrm{ols}}-{\beta }_1{\parallel }_F$.

Table 4. The selection performance of the sparse partial envelope estimator in the fourth situation under the high-dimensional setting.

n	TPR	TNR
50	100%	8.38%
100	100%	33.03%
200	100%	91.01%
400	100%	99.19%
600	100%	99.80%
800	100%	100%

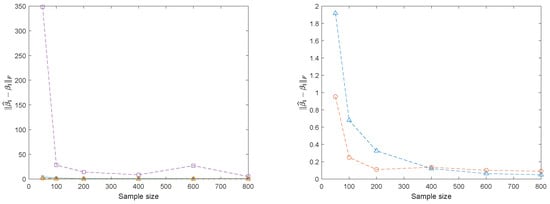
Figure 4. Comparison of the standard estimator (dashed with □), the sparse partial envelope actual estimator (dashed with ◯) and bootstrap estimator (dashed with ▵).

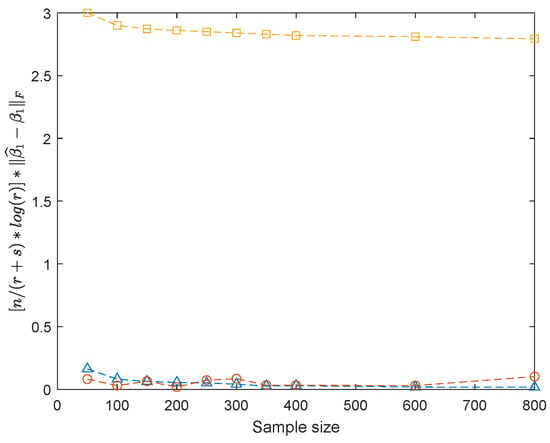
Figure 5. Comparison of the standard estimator (dashed with □), the sparse partial envelope actual estimator (dashed with ◯) and bootstrap estimator (dashed with ▵).

In the fifth situation, we still had $n<r$ and set $r=1000$, $q=10$, $p=5$, $p_1=3$, $u=2$ and $u_1=1$. The first $q/2$ rows in ${\mathsf{\Gamma }}_{\mathcal{A}}$ were ${(1/q)}^{1/2}$ and the remaining $q/2$ rows in ${\mathsf{\Gamma }}_{\mathcal{A}}$ were ${(2/q)}^{1/2}$. The other parameters were the same as those in the fourth situation. The sample sizes were 50, 100, 200, 400, 600, and 800, respectively, and we generated 200 replications for each sample size. Table 5 shows the variable selection performance of the sparse partial envelope estimator in the fifth situation under the high-dimensional setting.

Table 5. The selection performance of the sparse partial envelope estimator in the fifth situation under the high-dimensional setting.

n	TPR	TNR
50	100%	2.22%
100	100%	1.82%
200	100%	10.51%
400	100%	83.94%
600	100%	96.87%
800	100%	99.40%

6. Real Data Analysis

This section is dedicated to a real data example that elaborates aspects of the sparse partial envelope model in the case of $n<r$. This example comes from full-scale experiments at a paper factory in Norway. It is well known that the quality of paper is typically depicted by several variables and is then highly multivariate. Furthermore, the production of paper is a very complex process, relying on a host of variables, where some can be controlled and others cannot. The experiment was carried out at the factory of the paper plant Saugbruksforeningen, Norway. The data consist of 30 observations (rows) and 41 variables (columns), and we can acquire $n=30$ observations. See Aldrin [28] for a much more detailed description.

In this experiment, the goal is to find the influence of 9 predictor variables on the quality of the paper measured by 32 response variables. Response variables correspond to columns 1 to 32, which depict various qualities of the paper, so $r=32$. Predictor variables correspond to columns 33 to 41. The first three predictor variables are $x_1$ in column 33, $x_2$ in column 34 and $x_3$ in column 35, respectively, and are changed methodically by the experiment. The next three predictor variables which are corresponding to columns 36 to 38, are established by $x_1\ast 2$, $x_2\ast 2$ and $x_3\ast 2$. The last three predictor variables, which correspond to columns 39 to 41, are established by $x_1\ast x_2$, $x_1\ast x_3$ and $x_2\ast x_3$. So, we can obtain $p=9$. The predictors $x_1$, $x_2$, $x_3$, $x_1\ast x_2$, $x_1\ast x_3$ and $x_2\ast x_3$ are assigned to the main predictors, so $p_1=6$. The sparse partial envelope model was fitted to the data, and cross-validation suggested $u_1=1$. The model identified all the response variables as active responses. We estimated $\parallel {\widehat{\beta }}_{1,\mathrm{ols}}-{\beta }_1{\parallel }_F$ and $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F$ in the sparse partial envelope model by the average of 200 bootstrap samples and also estimated $\parallel \widehat{\beta }{-\beta \parallel }_F$ in the sparse envelope model by the average of 200 bootstrap samples. The ratio of the estimated $\parallel {\widehat{\beta }}_{1,\mathrm{ols}}-{\beta }_1{\parallel }_F$ to $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F$ is 2.34, and the ratio of the estimated $\parallel \widehat{\beta }{-\beta \parallel }_F$ in the sparse envelope model to $\parallel {\widehat{\beta }}_1-{\beta }_1{\parallel }_F$ in the sparse partial envelope model is 1.73. By and large, they both demonstrate an obvious efficiency gain as a result of the sparse partial envelope model.

For purpose of testing the prediction performance, we randomly split the data into two parts of equal size. Half of the data are used as the training set and the other half are used as the testing set. The prediction error is computed as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \mathrm{Prediction}\mathrm{error}=\sqrt{{\displaystyle \frac{1}{n_{\mathrm{test}\mathrm{set}}}}{\displaystyle \sum _{i\in \mathrm{test}\mathrm{set}}}{\left({\mathbf{Y}}_i-{\widehat{\mathbf{Y}}}_{i,\mathrm{predict}}\right)}^T\left({\mathbf{Y}}_i-{\widehat{\mathbf{Y}}}_{i,\mathrm{predict}}\right)}.\end{array}\end{array}$$

(22)

Then, the prediction error is averaged over 100 random splits, and the average prediction error is reported. The sparse envelope model has a prediction error of 11.8162, and the sparse partial envelope model has a prediction error of 2.8131, which is a 76% reduction.

7. Discussion

In this article, we propose a sparse partial envelope model under the multivariate linear regression model, which can implement response variable selection and improve parameter estimation efficiency. Then, we demonstrate its theoretical properties containing consistency, an oracle property and the asymptotic distribution of the sparse partial envelope estimator. Meanwhile, we both consider the large-sample scenario and high-dimensional scenario. Finally, we provide simulation studies and real data analysis to support the theories. In this paper, the predictor and response variables in the sparse partial envelope model are both vector-valued. Interesting topics for further studies involve researching the case where the predictor and response variables in the sparse partial envelope model are applied to matrix-valued data or tensor-valued data.