A System of Tensor Equations over the Dual Split Quaternion Algebra with an Application

Abstract

In this paper, we propose a definition of block tensors and the real representation of tensors. Equipped with the simplification method, i.e., the real representation along with the M-P inverse, we demonstrate the conditions that are necessary and sufficient for the system of dual split quaternion tensor equations $(\mathcal{A}{\ast }_N\mathcal{X},\mathcal{X}{\ast }_S\mathcal{C})=(\mathcal{B},\mathcal{D})$, when its solution exists. Furthermore, the general expression of the solution is also provided when the solution of the system exists, and we use a numerical example to validate it in the last section. To the best of our knowledge, this is the first time that the aforementioned tensor system has been examined on dual split quaternion algebra. Additionally, we provide its equivalent conditions when its Hermitian solution $\mathcal{X}={\mathcal{X}}^{\ast }$ and $\eta$-Hermitian solutions $\mathcal{X}={\mathcal{X}}^{\eta \ast }$ exist. Subsequently, we discuss two special dual split quaternion tensor equations. Last but not least, we propose an application for encrypting and decrypting two color videos, and we validate this algorithm through a specific example.

1. Introduction

The Irish mathematician W.R. Hamilton pioneered research on the concept of quaternions in 1843 [1]. There has been a rapid development in quaternions during recent years. There exist various kinds of related work about quaternions that achieve valuable results [2,3]. Most recently, researchers have focused on the theories for solving quaternion matrix equations, i.e., general and special solutions of quaternion matrix equations [4]. Quaternions and quaternion matrices have been comprehensively applied to multiple areas including algebra, analysis, topology, and physics. In particular, they are crucial in several fields, such as signal processing [5], image processing [6], and quantum physics [7].

In 1849, building upon Hamilton’s work, James Cockle further introduced “split quaternions” [8]. The set of split quaternions is denoted as follows:

$$\begin{array}{c}\hfill {\mathbb{H}}_S=\{q=q_0+q_{1}i+q_{2}j+q_{3}k:q_0,q_1,q_2,q_3\in \mathbb{R}\},\end{array}$$

where

$$\begin{array}{c}\hfill i^2=-j^2=-k^2=-1,ij=-ji=k,jk=-kj=-i,ki=-ik=j.\end{array}$$

As a derivative version of quaternions, its form is similar to the original definition of quaternions, but they are indeed two different algebras. The definition proposed by James Cockle has a more complex algebraic structure. Split quaternions play a significant role in various fields, e.g., physics, quantum mechanics, signal processing, and deep learning. Split quaternions have been applied to denote Lorentz rotations, and Lorentz transformations can be represented as $2\times 2$ unitary matrices of split quaternions, which reveals the geometric and physical importance of split quaternions [9,10,11,12,13,14,15].

Clifford [16] later proposed dual numbers and dual quaternions in 1873, and they have already become the basis for handling some typical engineering problems [17]. Dual split quaternions, like dual quaternions, expand the idea of dual numbers to include split quaternions. Building on the principles of split quaternions, dual split quaternions have been applied to diverse disciplines including algebra, geometry, and physics [18,19,20,21].

Below is a typical matrix equation system, which we will mainly focus on. There exists some related work providing solutions to it, but we will explore this equation system as defined in the domain of dual split quaternion tensors.

$$\left\{\begin{array}{c}AX=B,\hfill \\ XC=D.\hfill \end{array}\right.$$

(1)

Due to its wide applications in fields such as biology, inverse problems in vibration theory, and linear programming, system (1) has been extensively studied. Rao and Mitra [22] established the criteria for the solvability of system (1) and also presented their general solutions. Khatri and Mitra [23] examined their Hermitian solutions within the complex field. Wang [24] derived conditions for solvability and provided solutions for bi-symmetric cases of system (1) in the quaternion skew field. Li and others [25] examined generalized reflexive solutions for complex system (1). Yuan [26] used spectral decomposition to investigate least squares solutions for system (1). Xie [27] applied the M-P inverse, as well as the rank of quaternion matrices, to determine the equivalent conditions when there existed solutions, and then proposed the general solution. Si and others [15] used real representations to establish various solutions of system (1) and their equivalent conditions over split quaternion field.

Tensors are useful in engineering and science, and there are some papers focusing on the solutions of tensor equations [28,29,30,31,32,33]. With dual split quaternions that can represent rotations and translations commonly used in artificial intelligence [18], tensors over dual split quaternions can be further applied to more scenarios. For instance, using dual split quaternion tensors allows for the simultaneous encryption of two videos, enhancing the efficiency of encryption and decryption. Moreover, due to the complexity of the mathematical structure of dual split quaternions, videos encrypted with dual split quaternion tensors are not easily decrypted. Considering these advantages, tensors over dual split quaternions should be explored both in theory and in reality for better applications.

In this paper, we focus on solving system (1), defined in the space of dual split quaternion tensors. To the best of our knowledge, it is the first exploration of the above system within the dual split quaternion tensor algebra. Specifically, it aims to solve the following system of dual split quaternion tensor equations:

$$\left\{\begin{array}{c}\mathcal{A}{\ast }_N\mathcal{X}=\mathcal{B},\hfill \\ \mathcal{X}{\ast }_S\mathcal{C}=\mathcal{D}.\hfill \end{array}\right.$$

(2)

This paper is designed with the following structure: Section 2 describes essential definitions and corollaries that are essential to our subsequent analysis. Section 3 investigates the conditions that are equivalent for system (2) when there exist solutions. In this section, we further demonstrate its general solution in cases where solutions are attainable. Furthermore, we present the sufficient and necessary criteria when system (2) have $\eta$-Hermitian solutions. Based on these results, we introduce the equivalent condition for the Hermitian solution, along with the general expressions of solutions for two specific dual split quaternion tensor equations. Ultimately, we present a specific numerical example and an encryption and decryption algorithm as an application.

In this paper, the dual number field, quaternion field, split quaternion field, dual quaternion field, and dual split quaternion field are represented by $\mathbb{D}$, $\mathbb{H}$, ${\mathbb{H}}_s$, $\mathbb{DQ}$, and ${\mathbb{DQ}}_s$, respectively. All $I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N$ tensors over ${\mathbb{DQ}}_s$ are represented using ${\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$.

2. Preliminary

In this section, there are three parts that provide fundamental knowledge for the subsequent demonstration of this paper. In the first part, we will give the definition of dual split quaternion tensors. The second part will cover some definitions and propositions about tensors. Lastly, we will present various real representations of split quaternion tensors.

2.1. Dual Split Quaternion Tensors

$\mathcal{A}={\left(a_{j_1\cdots j_M}\right)}_{1\le j_k\le J_k(k=1,\dots ,M)}$ is a multidimensional array tensor with $J_1\times J_2\times \cdots \times J_M$ entries. Let ${\mathbb{R}}^{J_1\times \cdots \times J_M}$, ${\mathbb{H}}^{J_1\times \cdots \times J_M}$, and ${\mathbb{H}}_s^{J_1\times \cdots \times J_M}$, respectively, represent the sets of the order M tensors with $J_1\times \cdots \times J_M$ dimensions over the real field $\mathbb{R}$, real quaternion algebra $\mathbb{H}$, and real split quaternion algebra ${\mathbb{H}}_s$.

For $\mathcal{A}=\left(a_{i_1\cdots i_M{l}_1\cdots l_N}\right)\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$, $\mathcal{B}=\left(b_{l_1\cdots l_N{i}_1\cdots i_M}\right)\in {\mathbb{H}}_s^{L_1\times \cdots \times L_N\times I_1\times \cdots \times I_M}$. When $b_{l_1\cdots l_N{i}_1\cdots i_M}=a_{i_1\cdots i_M{l}_1\cdots l_N}$, $\mathcal{B}$ is referred to as the transpose of $\mathcal{A}$ and is denoted by ${\mathcal{A}}^T$. When $b_{l_1\cdots l_M{i}_1\cdots i_N}={\overline{a}}_{i_1\cdots i_N{l}_1\cdots l_M}$, $\mathcal{B}$ is the conjugate transpose of $\mathcal{A}$, represented as ${\mathcal{A}}^{\ast }$. A diagonal tensor $\mathcal{D}=\left(d_{t_1\cdots t_M{t}_1\cdots t_M}\right)\in {\mathbb{H}}_s^{T_1\times \cdots \times T_M\times T_1\times \cdots \times T_M}$ has all zero entries, except for the elements $d_{t_1\cdots t_M{t}_1\cdots t_M}$. When all diagonal elements of $\mathcal{D}$ are equal to 1, $\mathcal{D}$ is referred to as a unit tensor, expressed as $\mathcal{I}$. Specifically, if $\mathcal{I}\in {\mathbb{H}}_s^{T_1\times \cdots \times T_M\times T_1\times \cdots \times T_M}$, it is expressed as ${\mathcal{I}}_M$. $\mathcal{O}$ denotes the zero tensor whose elements are all zero.

Definition 1

([16,34]). The field of dual numbers is expressed as follows:

$$\mathbb{D}=\{q=q_0+q_1ϵ:q_0,q_1\in \mathbb{R},ϵ\ne 0,{ϵ}^2=0\},$$

where ϵ is the infinitesimal unit.

By extending quaternions and split quaternions to include dual numbers, we derive the definitions of dual quaternions and dual split quaternions as follows:

$$\mathbb{DQ}=\{q=q_0+q_1ϵ:q_0,q_1\in \mathbb{H},ϵ\ne 0,{ϵ}^2=0\},$$

$${\mathbb{DQ}}_s=\{q=q_0+q_1ϵ:q_0,q_1\in {\mathbb{H}}_s,ϵ\ne 0,{ϵ}^2=0\}.$$

The sets of dual quaternion tensors and dual split quaternion tensors [18,34] are represented as follows:

$$\begin{array}{cc}\hfill & {\mathbb{DQ}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}=\{Q=Q_0+Q_1ϵ:Q_0,Q_1\in {\mathbb{H}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N},ϵ\ne 0,{ϵ}^2=0\},\hfill \\ \hfill & {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}=\{Q=Q_0+Q_1ϵ:Q_0,Q_1\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N},ϵ\ne 0,{ϵ}^2=0\}.\hfill \end{array}$$

For $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_1ϵ,\mathcal{Y}={\mathcal{Y}}_0+{\mathcal{Y}}_1ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$, $\mathcal{X}=\mathcal{Y}$ means that ${\mathcal{X}}_0={\mathcal{Y}}_0$ and ${\mathcal{X}}_1={\mathcal{Y}}_1$, and vice versa. ${\mathcal{X}}^{\ast }={\mathcal{X}}_0^{\ast }+{\mathcal{X}}_1^{\ast }ϵ$ is called the conjugate transpose of $\mathcal{X}$. ${\mathcal{X}}^{\eta \ast }={\mathcal{X}}_0^{\eta \ast }+{\mathcal{X}}_1^{\eta \ast }ϵ$ are called the $\eta$-conjugate transposes of $\mathcal{X}$, where $\eta =\{i,j,k\}$.

For $\mathcal{X}\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$, $\mathcal{X}$ is uniquely identified as $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_{1}i+{\mathcal{X}}_{2}j+{\mathcal{X}}_{3}k$, where ${\mathcal{X}}_0,{\mathcal{X}}_1,{\mathcal{X}}_2$, and ${\mathcal{X}}_3\in {\mathbb{R}}^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$. The conjugate transpose of $\mathcal{X}$ satisfies ${\mathcal{X}}^{\ast }={\mathcal{X}}_0^T-{\mathcal{X}}_1^{T}i-{\mathcal{X}}_2^{T}j-{\mathcal{X}}_3^{T}k$. Additionally, for $\eta \in \{i,j,k\}$, the $\eta$-conjugates and $\eta$-conjugate transposes [35] of $\mathcal{X}$ have the following forms:

$$\begin{array}{cc}\hfill {\mathcal{X}}^i& =i^{-1}\mathcal{X}i={\mathcal{X}}_0+{\mathcal{X}}_{1}i-{\mathcal{X}}_{2}j-{\mathcal{X}}_{3}k,\hfill \\ \hfill {\mathcal{X}}^j& =j^{-1}\mathcal{X}j={\mathcal{X}}_0-{\mathcal{X}}_{1}i+{\mathcal{X}}_{2}j-{\mathcal{X}}_{3}k,\hfill \\ \hfill {\mathcal{X}}^k& =k^{-1}\mathcal{X}k={\mathcal{X}}_0-{\mathcal{X}}_{1}i-{\mathcal{X}}_{2}j+{\mathcal{X}}_{3}k,\hfill \end{array}$$

and

$$\begin{array}{c}{\mathcal{X}}^{i\ast }=i^{-1}{\mathcal{X}}^{\ast }i={\mathcal{X}}_0^T-{\mathcal{X}}_1^{T}i+{\mathcal{X}}_2^{T}j+{\mathcal{X}}_3^{T}k,\\ {\mathcal{X}}^{j\ast }=j^{-1}{\mathcal{X}}^{\ast }j={\mathcal{X}}_0^T+{\mathcal{X}}_1^{T}i-{\mathcal{X}}_2^{T}j+{\mathcal{X}}_3^{T}k,\\ {\mathcal{X}}^{k\ast }=k^{-1}{\mathcal{X}}^{\ast }k={\mathcal{X}}_0^T+{\mathcal{X}}_1^{T}i+{\mathcal{X}}_2^{T}j-{\mathcal{X}}_3^{T}k.\end{array}$$

Definition 2.

Let $\mathcal{X}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_N\times I_1\times \cdots \times I_N}$. Provided that $\mathcal{X}$ fulfills the following criteria:

$$\mathcal{X}={\mathcal{X}}^{\eta \ast }:={\eta }^{-1}{\mathcal{X}}^{\ast }\eta ,\eta \in \{i,j,k\},$$

we refer to $\mathcal{X}$ as a η-Hermitian tensor.

For $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_1ϵ,\mathcal{Y}={\mathcal{Y}}_0+{\mathcal{Y}}_1ϵ\in {\mathbb{DQ}}_s^{T_1\times \cdots \times T_M\times J_1\times \cdots \times J_N}$; then, we can derive that ${(\mathcal{X}+\mathcal{Y})}^{\eta \ast }={\mathcal{X}}^{\eta \ast }+{\mathcal{Y}}^{\eta \ast }$ and ${\left({\mathcal{X}}^{\eta \ast }\right)}^{\eta \ast }=\mathcal{X}$. Furthermore, $\mathcal{X}=\mathcal{Y}$ means that ${\mathcal{X}}_0^{\eta \ast }={\mathcal{Y}}_0^{\eta \ast }$ and ${\mathcal{X}}_1^{\eta \ast }={\mathcal{Y}}_1^{\eta \ast }$, and vice versa.

2.2. Basic Theory with Einstein Product

Definition 3

([36]). Let $\mathcal{X}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$ and $\mathcal{Y}\in {\mathbb{DQ}}_s^{L_1\times \cdots \times L_N\times K_1\times \cdots \times K_S}$. Then, we can define the Einstein product of tensors $\mathcal{X}$ and $\mathcal{Y}$ through the operation ${\ast }_N$ as follows:

$$\begin{array}{c}\hfill {\left(\mathcal{X}{\ast }_N\mathcal{Y}\right)}_{i_1\cdots i_M{k}_1\cdots k_S}=\sum _{l_1\cdots l_N}{x}_{i_1\cdots i_M{l}_1\cdots l_N}{y}_{l_1\cdots l_N{k}_1\cdots k_S}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_S}.\end{array}$$

Proposition 1.

Let $\mathcal{X}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_S}$ and $\mathcal{Y}\in {\mathbb{DQ}}_s^{L_1\times \cdots \times L_S\times K_1\times \cdots \times K_T}$. Then, the following are true:

1. 

${\left(\mathcal{X}{\ast }_S\mathcal{Y}\right)}^{\ast }={\mathcal{Y}}^{\ast }{\ast }_S{\mathcal{X}}^{\ast }$;

2. 

${\mathcal{I}}_S{\ast }_S\mathcal{Y}=\mathcal{Y}$ and $\mathcal{Y}{\ast }_T{\mathcal{I}}_T=\mathcal{Y}$.

Definition 4

([33,37]). Let $\mathcal{A}\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_T}$ and $\mathcal{Y}\in {\mathbb{H}}_s^{L_1\times \cdots \times L_T\times I_1\times \cdots \times I_M}$. $\mathcal{Y}$ is referred to as the Moore–Penrose inverse of $\mathcal{A}$, expressed as ${\mathcal{A}}^{†}$, if the following conditions are all fulfilled:

1. 

$\mathcal{A}{\ast }_T\mathcal{Y}{\ast }_M\mathcal{A}=\mathcal{A}$;

2. 

$\mathcal{Y}{\ast }_M\mathcal{A}{\ast }_T\mathcal{Y}=\mathcal{Y}$;

3. 

${\left(\mathcal{A}{\ast }_T\mathcal{Y}\right)}^{\ast }=\mathcal{A}{\ast }_T\mathcal{Y}$;

4. 

${\left(\mathcal{Y}{\ast }_M\mathcal{A}\right)}^{\ast }=\mathcal{Y}{\ast }_M\mathcal{A}$.

Furthermore, projectors ${\mathcal{L}}_{\mathcal{A}}$ and ${\mathcal{R}}_{\mathcal{A}}$ have the following forms:

$${\mathcal{L}}_{\mathcal{A}}={\mathcal{I}}_T-{\mathcal{A}}^{†}{\ast }_M\mathcal{A},{\mathcal{R}}_{\mathcal{A}}={\mathcal{I}}_M-\mathcal{A}{\ast }_T{\mathcal{A}}^{†}.$$

Similar to block matrices, reference [37] provides the definition of block tensors and reference [38] provides the definition of block tensors when their sizes are the same. Next, we extend the definitions from references [37,38] to split quaternion tensors to give the definition of block tensors with the same size.

Definition 5.

Let $\mathcal{X}=\left(x_{l_1\cdots l_T{k}_1\cdots k_N}\right)$ and $\mathcal{Y}=\left(y_{l_1\cdots l_T{k}_1\cdots k_N}\right)\in {\mathbb{H}}_s^{L_1\times \cdots \times L_T\times K_1\times \cdots \times K_N}$. Then, the following are true:

1. 

The ’row block tensor’ formed by $\mathcal{X}$ and $\mathcal{Y}$ is $\left[\mathcal{X}\mathcal{Y}\right]\in {\mathbb{H}}_s^{L_1\times \cdots \times L_T\times K_1\times \cdots \times K_{N-1}\times 2K_N}$, and

$$\begin{array}{cc}\hfill & {\left[\mathcal{X}\mathcal{Y}\right]}_{l_1\cdots l_T{k}_1\cdots k_N}\hfill \\ & =\left\{\begin{array}{cc}{x}_{l_1\cdots l_T{k}_1\cdots k_N},\hfill & l_1\cdots l_T\in \left[L_1\right]\times \cdots \times \left[L_T\right],k_1\cdots k_N\in \left[K_1\right]\times \cdots \times \left[K_N\right];\hfill \\ y_{l_1\cdots l_T{k}_1\cdots (k_N-K_N)},\hfill & l_1\cdots l_T\in \left[L_1\right]\times \cdots \times \left[L_T\right],k_1\cdots k_N\in \left[K_1\right]\times \cdots \times \mathrm{\Gamma },\hfill \end{array}\right.\hfill \end{array}$$

where $\mathrm{\Gamma }=\{K_N+1,K_N+2\dots ,2K_N\}$.

2. 

The ’column block tensor’ formed by $\mathcal{X}$ and $\mathcal{Y}$ is $\left[\begin{array}{c}\mathcal{X}\\ \mathcal{Y}\end{array}\right]\in {\mathbb{H}}_s^{L_1\times \cdots \times L_{T-1}\times 2L_T\times K_1\times \cdots \times K_N}$, and

$$\begin{array}{cc}\hfill & {\left[\begin{array}{c}\mathcal{X}\\ \mathcal{Y}\end{array}\right]}_{l_1\cdots l_T{k}_1\cdots k_N}\hfill \\ & =\left\{\begin{array}{cc}{x}_{l_1\cdots l_T{k}_1\cdots k_N},\hfill & l_1\cdots l_T\in \left[L_1\right]\times \cdots \times \left[L_T\right],k_1\cdots k_N\in \left[K_1\right]\times \cdots \times \left[K_N\right];\hfill \\ y_{l_1\cdots (l_T-L_T)k_1\cdots k_N},\hfill & l_1\cdots l_T\in \left[L_1\right]\times \cdots \times \mathrm{\Gamma },k_1\cdots k_N\in \left[K_1\right]\times \cdots \times \left[K_N\right],\hfill \end{array}\right.\hfill \end{array}$$

where $\mathrm{\Gamma }=\{L_T+1,L_T+2\dots ,2L_T\}$.

In particular, let ${\mathcal{X}}_{11}$, ${\mathcal{X}}_{12}$, ${\mathcal{X}}_{21}$ and ${\mathcal{X}}_{22}\in {\mathbb{H}}_s^{L_1\times \cdots \times L_T\times K_1\times \cdots \times K_N}$. Then, the following is true:

$$\begin{array}{c}\hfill \left[\begin{array}{c}{\mathcal{X}}_{11}{\mathcal{X}}_{12}\\ {\mathcal{X}}_{21}{\mathcal{X}}_{22}\end{array}\right]\in {\mathbb{H}}_s^{L_1\times \cdots \times L_{T-1}\times 2L_T\times K_1\times \cdots \times K_{N-1}\times 2K_N}.\end{array}$$

Remark 1.

${\mathcal{X}}_{ij}$ is the tensor located at row i, column $j(i,j=1,2)$ in the aforementioned block tensor, and it will be used in the following statement.

Lemma 1

([37]). Let ${\mathcal{X}}_i\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N},i=\{1,2,3,4\}$, ${\mathcal{Y}}_j\in {\mathbb{H}}_s^{J_1\times \cdots \times J_N\times T_1\times \cdots \times T_S}$, $j=\{1,2\}$, and ${\mathcal{Z}}_k\in {\mathbb{H}}_s^{S_1\times \cdots \times S_N\times I_1\times \cdots \times I_M}$, $k=\{1,2\}$. Then, the following are true:

1. 

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{\mathcal{X}}_1& {\mathcal{X}}_3\\ {\mathcal{X}}_2& {\mathcal{X}}_4\end{array}\right]{\ast }_N\left[\begin{array}{c}{\mathcal{Y}}_1\\ {\mathcal{Y}}_2\end{array}\right]=\left[\begin{array}{c}{\mathcal{X}}_1{\ast }_N{\mathcal{Y}}_1+{\mathcal{X}}_3{\ast }_N{\mathcal{Y}}_2\\ {\mathcal{X}}_2{\ast }_N{\mathcal{Y}}_1+{\mathcal{X}}_4{\ast }_N{\mathcal{Y}}_2\end{array}\right];\end{array}$$

2. 

$$\begin{array}{c}\hfill \left[\begin{array}{cc}{\mathcal{Z}}_1& {\mathcal{Z}}_2\end{array}\right]{\ast }_M\left[\begin{array}{cc}{\mathcal{X}}_1& {\mathcal{X}}_3\\ {\mathcal{X}}_2& {\mathcal{X}}_4\end{array}\right]=\left[\begin{array}{cc}{\mathcal{Z}}_1{\ast }_M{\mathcal{X}}_1+{\mathcal{Z}}_2{\ast }_M{\mathcal{X}}_2& {\mathcal{Z}}_1{\ast }_M{\mathcal{X}}_3+{\mathcal{Z}}_2{\ast }_M{\mathcal{X}}_4\end{array}\right].\end{array}$$

Next, we will introduce the definition of the transformation t between a tensor and a matrix within split quaternion algebra [33,39]. Under this definition, we can simplify the tensor into a matrix.

Definition 6.

The transformation $t:{\mathbb{T}}_{I_1,I_2,\dots ,I_M,L_1,L_2,\dots ,L_N}\left({\mathbb{H}}_s\right)\to {\mathbb{M}}_{I_1·I_2\cdots I_M,L_1·L_2\cdots L_N}\left({\mathbb{H}}_s\right)$ with $t\left(\mathcal{X}\right)=X$ is defined as follows:

$$\begin{array}{c}\hfill {\left(\mathcal{X}\right)}_{i_1{i}_2\cdots i_M{l}_1{l}_2\cdots l_N}\stackrel{t}{\to }{\left(X\right)}_{[i_1+{\sum }_{k=2}^M(i_k-1){\prod }_{s=1}^{k-1}{I}_s][l_1+{\sum }_{k=2}^N(l_k-1){\prod }_{s=1}^{k-1}{L}_s]},\end{array}$$

where $\mathcal{X}\in {\mathbb{T}}_{I_1,I_2,\dots ,I_M,L_1,L_2,\dots ,L_N}\left({\mathbb{H}}_s\right)$ and $X\in {\mathbb{M}}_{I_1·I_2\cdots I_M,L_1·L_2\cdots L_N}\left({\mathbb{H}}_s\right)$.

Lemma 2

([33]). Let $\mathcal{X}\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times L_1\times \cdots \times L_N}$ and $\mathcal{Y}\in {\mathbb{H}}_s^{L_1\times \cdots \times L_N\times K_1\times \cdots \times K_S}$. Then, t satisfies the following properties:

1. 

The map t is bijective and its inverse map $t^{-1}$ exists as follows:

$$\begin{array}{c}\hfill {\mathbb{M}}_{I_1·I_2\cdots I_{M-1}·I_M,L_1·L_2\cdots L_{N-1}·L_N}\left({\mathbb{H}}_s\right)\stackrel{t^{-1}}{\to }{\mathbb{T}}_{I_1,I_2,\cdots ,I_{M-1},I_M,L_1,L_2,\cdots ,L_{N-1},L_N}\left({\mathbb{H}}_s\right);\end{array}$$

2. 

t satisfies: $t\left(\mathcal{X}{\ast }_N\mathcal{Y}\right)=t\left(\mathcal{X}\right)·t\left(\mathcal{Y}\right)$ and $t\left({\mathcal{X}}^{†}\right)=t{\left(\mathcal{X}\right)}^{†}$.

Example 1.

Let $\mathcal{A}\in {\mathbb{H}}_s^{2\times 2\times 2\times 2}$ be defined by the following:

$$\begin{array}{cc}\hfill & {\left(\mathcal{A}\right)}_{1111}=i+2k,{\left(\mathcal{A}\right)}_{1121}=k,{\left(\mathcal{A}\right)}_{1112}=3i,{\left(\mathcal{A}\right)}_{1122}=2,\hfill \\ \hfill & {\left(\mathcal{A}\right)}_{2111}=0,{\left(\mathcal{A}\right)}_{2121}=i+j,{\left(\mathcal{A}\right)}_{2112}=2k,{\left(\mathcal{A}\right)}_{2122}=i+2j,\hfill \\ \hfill & {\left(\mathcal{A}\right)}_{1211}=-i+2j,{\left(\mathcal{A}\right)}_{1221}=4k,{\left(\mathcal{A}\right)}_{1212}=0,{\left(\mathcal{A}\right)}_{1222}=3j,\hfill \\ \hfill & {\left(\mathcal{A}\right)}_{2211}=4i+2k,{\left(\mathcal{A}\right)}_{2221}=i+3j,{\left(\mathcal{A}\right)}_{2212}=2+3i+j,{\left(\mathcal{A}\right)}_{2222}=1+2j+5k.\hfill \end{array}$$

Then,

$$\begin{array}{cc}\hfill A=t\left(\mathcal{A}\right)& =\left(\begin{array}{cccc}{\left(\mathcal{A}\right)}_{1111}& {\left(\mathcal{A}\right)}_{1121}& {\left(\mathcal{A}\right)}_{1112}& {\left(\mathcal{A}\right)}_{1122}\\ {\left(\mathcal{A}\right)}_{2111}& {\left(\mathcal{A}\right)}_{2121}& {\left(\mathcal{A}\right)}_{2112}& {\left(\mathcal{A}\right)}_{2122}\\ {\left(\mathcal{A}\right)}_{1211}& {\left(\mathcal{A}\right)}_{1221}& {\left(\mathcal{A}\right)}_{1212}& {\left(\mathcal{A}\right)}_{1222}\\ {\left(\mathcal{A}\right)}_{2211}& {\left(\mathcal{A}\right)}_{2221}& {\left(\mathcal{A}\right)}_{2212}& {\left(\mathcal{A}\right)}_{2222}\end{array}\right)\hfill \\ \hfill & =\left(\begin{array}{cccc}i+2k& k& 3i& 2\\ 0& i+j& 2k& i+2j\\ -i+2j& 4k& 0& 3j\\ 4i+2k& i+3j& 2+3i+j& 1+2j+5k\end{array}\right).\hfill \end{array}$$

Consequently, there is a one-to-one correspondence between the elements of the split quaternion matrix and the split quaternion tensor. Thus, we can make use of the above definition to transform the tensor into a matrix for further calculations.

2.3. Real Representations of Split Quaternion Tensors

In this section, we will provide various real representations using the definition of block tensors in the above section.

Let $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_{1}i+{\mathcal{X}}_{2}j+{\mathcal{X}}_{3}k\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, where ${\mathcal{X}}_i\in {\mathbb{R}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, $i=\{0,1,2,3\}$. We will define three kinds of real representations of $\mathcal{X}$ based on the real representation in [11], as follows:

$${\mathcal{X}}^{{\sigma }_i}:=\left[\begin{array}{cccc}{\mathcal{X}}_0& {\mathcal{X}}_1& {\mathcal{X}}_2& {\mathcal{X}}_3\\ -{\mathcal{X}}_1& {\mathcal{X}}_0& -{\mathcal{X}}_3& {\mathcal{X}}_2\\ {\mathcal{X}}_2& -{\mathcal{X}}_3& {\mathcal{X}}_0& -{\mathcal{X}}_1\\ {\mathcal{X}}_3& {\mathcal{X}}_2& {\mathcal{X}}_1& {\mathcal{X}}_0\end{array}\right]\in {\mathbb{R}}^{I_1\times \cdots \times 4I_M\times J_1\times \cdots \times 4J_N}.$$

Definition 7

([15,35]). Let $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_{1}i+{\mathcal{X}}_{2}j+{\mathcal{X}}_{3}k\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, where ${\mathcal{X}}_0$, ${\mathcal{X}}_1$, ${\mathcal{X}}_2$, ${\mathcal{X}}_3\in {\mathbb{R}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, ${\mathcal{I}}_M\in {\mathbb{R}}^{I_1\times \cdots \times I_M\times I_1\times \cdots \times I_M}$. Then, we define the following:

$$\begin{array}{cc}\hfill {\mathcal{X}}^{{\sigma }_j}:={\mathcal{V}}_M{\ast }_M{\mathcal{X}}^{{\sigma }_i}=\left[\begin{array}{cccc}{\mathcal{X}}_0& {\mathcal{X}}_1& {\mathcal{X}}_2& {\mathcal{X}}_3\\ {\mathcal{X}}_1& -{\mathcal{X}}_0& {\mathcal{X}}_3& -{\mathcal{X}}_2\\ -{\mathcal{X}}_2& {\mathcal{X}}_3& -{\mathcal{X}}_0& {\mathcal{X}}_1\\ {\mathcal{X}}_3& {\mathcal{X}}_2& {\mathcal{X}}_1& {\mathcal{X}}_0\end{array}\right],& {\mathcal{V}}_M=\left[\begin{array}{cccc}{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& \mathcal{O}& {\mathcal{I}}_M\end{array}\right];\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{X}}^{{\sigma }_k}:={\mathcal{W}}_M{\ast }_M{\mathcal{X}}^{{\sigma }_i}=\left[\begin{array}{cccc}{\mathcal{X}}_0& {\mathcal{X}}_1& {\mathcal{X}}_2& {\mathcal{X}}_3\\ {\mathcal{X}}_1& -{\mathcal{X}}_0& {\mathcal{X}}_3& -{\mathcal{X}}_2\\ {\mathcal{X}}_2& -{\mathcal{X}}_3& {\mathcal{X}}_0& -{\mathcal{X}}_1\\ -{\mathcal{X}}_3& -{\mathcal{X}}_2& -{\mathcal{X}}_1& -{\mathcal{X}}_0\end{array}\right],& {\mathcal{W}}_M=\left[\begin{array}{cccc}{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M\end{array}\right];\hfill \end{array}$$

$$\begin{array}{cc}\hfill {\mathcal{X}}^{{\sigma }_1}:={\mathcal{P}}_M{\ast }_M{\mathcal{X}}^{{\sigma }_i}=\left[\begin{array}{cccc}{\mathcal{X}}_0& {\mathcal{X}}_1& {\mathcal{X}}_2& {\mathcal{X}}_3\\ -{\mathcal{X}}_1& {\mathcal{X}}_0& -{\mathcal{X}}_3& {\mathcal{X}}_2\\ -{\mathcal{X}}_2& {\mathcal{X}}_3& -{\mathcal{X}}_0& {\mathcal{X}}_1\\ -{\mathcal{X}}_3& -{\mathcal{X}}_2& -{\mathcal{X}}_1& -{\mathcal{X}}_0\end{array}\right],& {\mathcal{P}}_M=\left[\begin{array}{cccc}{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M\end{array}\right],\hfill \end{array}$$

where ${\mathcal{V}}_M,{\mathcal{W}}_M$, and ${\mathcal{P}}_M\in {\mathbb{R}}^{I_1\times \cdots \times 4I_M\times I_1\times \cdots \times 4I_M}$.

As shown in the next proposition, we present the relevant characteristics of real representations discussed previously. These properties will play a crucial role in subsequent sections and can be easily obtained through simple calculations. Let the following be true:

$$\begin{array}{c}\hfill {\mathcal{R}}_M=\left[\begin{array}{cccc}\mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\\ {\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M\\ \mathcal{O}& \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}\end{array}\right],{\mathcal{S}}_M=\left[\begin{array}{cccc}\mathcal{O}& \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}\\ \mathcal{O}& \mathcal{O}& \mathcal{O}& -{\mathcal{I}}_M\\ {\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\\ \mathcal{O}& -{\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\end{array}\right],{\mathcal{T}}_M=\left[\begin{array}{cccc}\mathcal{O}& \mathcal{O}& \mathcal{O}& {\mathcal{I}}_M\\ \mathcal{O}& \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}\\ \mathcal{O}& {\mathcal{I}}_M& \mathcal{O}& \mathcal{O}\\ {\mathcal{I}}_M& \mathcal{O}& \mathcal{O}& \mathcal{O}\end{array}\right].\end{array}$$

Proposition 2.

For $\eta =\{i,j,k\}$, let $\mathcal{X},\mathcal{Y}\in {\mathbb{H}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N},\mathcal{P}\in {\mathbb{H}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_T}$, and $\lambda \in \mathbb{R}$. Then, the following is true:

1. 

$\mathcal{X}=\mathcal{Y}\iff {\mathcal{X}}^{\eta \ast }={\mathcal{Y}}^{\eta \ast }$;

2. 

${(\mathcal{X}+\mathcal{Y})}^{{\sigma }_{\eta }}={\mathcal{X}}^{{\sigma }_{\eta }}+{\mathcal{Y}}^{{\sigma }_{\eta }},{\left(\lambda \mathcal{X}\right)}^{{\sigma }_{\eta }}=\lambda {\mathcal{X}}^{{\sigma }_{\eta }};$

3. 

${\left(\mathcal{X}{\ast }_N\mathcal{P}\right)}^{{\sigma }_i}={\mathcal{X}}^{{\sigma }_i}{\ast }_N{\mathcal{P}}^{{\sigma }_i},{\left(\mathcal{X}{\ast }_N\mathcal{P}\right)}^{{\sigma }_j}={\mathcal{X}}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{P}}^{{\sigma }_j},{\left(\mathcal{X}{\ast }_N\mathcal{P}\right)}^{{\sigma }_k}={\mathcal{X}}^{{\sigma }_k}{\ast }_N{\mathcal{W}}_N{\ast }_N{\mathcal{P}}^{{\sigma }_k},{\left(\mathcal{X}{\ast }_N\mathcal{P}\right)}^{{\sigma }_1}={\mathcal{X}}^{{\sigma }_1}{\ast }_N{\mathcal{P}}_N{\ast }_N{\mathcal{P}}^{{\sigma }_1}$;

4. 

(a)  ${\mathcal{R}}_M^T{\ast }_M{\mathcal{X}}^{{\sigma }_i}{\ast }_N{\mathcal{R}}_N={\mathcal{X}}^{{\sigma }_i},{\mathcal{S}}_M^T{\ast }_M{\mathcal{X}}^{{\sigma }_i}{\ast }_N{\mathcal{S}}_N={\mathcal{X}}^{{\sigma }_i},{\mathcal{T}}_M^T{\ast }_M{\mathcal{X}}^{{\sigma }_i}{\ast }_N{\mathcal{T}}_N={\mathcal{X}}^{{\sigma }_i}$;

(b)  ${\mathcal{R}}_M^T{\ast }_M{\mathcal{X}}^{{\sigma }_j}{\ast }_N{\mathcal{R}}_N=-{\mathcal{X}}^{{\sigma }_j},{\mathcal{S}}_M^T{\ast }_M{\mathcal{X}}^{{\sigma }_j}{\ast }_N{\mathcal{S}}_N=-{\mathcal{X}}^{{\sigma }_j},{\mathcal{T}}_M^T{\ast }_M{\mathcal{X}}^{{\sigma }_j}{\ast }_N{\mathcal{T}}_N={\mathcal{X}}^{{\sigma }_j}$;

(c)  ${\mathcal{R}}_M^T{\ast }_M{\mathcal{X}}^{{\sigma }_k}{\ast }_N{\mathcal{R}}_N=-{\mathcal{X}}^{{\sigma }_k},{\mathcal{S}}_M^T{\ast }_M{\mathcal{X}}^{{\sigma }_k}{\ast }_N{\mathcal{S}}_N={\mathcal{X}}^{{\sigma }_k},{\mathcal{T}}_M^T{\ast }_M{\mathcal{X}}^{{\sigma }_k}{\ast }_N{\mathcal{T}}_N=-{\mathcal{X}}^{{\sigma }_k}$;

5. 

${\left({\mathcal{X}}^{\ast }\right)}^{{\sigma }_1}={\left({\mathcal{X}}^{{\sigma }_1}\right)}^T,{\left({\mathcal{X}}^{\eta \ast }\right)}^{{\sigma }_{\eta }}={\left({\mathcal{X}}^{{\sigma }_{\eta }}\right)}^T$;

6. 

(a)  $\mathcal{X}={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_M& i{\mathcal{I}}_M& j{\mathcal{I}}_M& k{\mathcal{I}}_M\end{array}\right]{\ast }_M{\mathcal{X}}^{{\sigma }_i}{\ast }_N\left[\begin{array}{c}{\mathcal{I}}_N\\ i{\mathcal{I}}_N\\ j{\mathcal{I}}_N\\ k{\mathcal{I}}_N\end{array}\right]$;

(b)  $\mathcal{X}={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_M& -i{\mathcal{I}}_M& -j{\mathcal{I}}_M& k{\mathcal{I}}_M\end{array}\right]{\ast }_M{\mathcal{X}}^{{\sigma }_j}{\ast }_N\left[\begin{array}{c}{\mathcal{I}}_N\\ i{\mathcal{I}}_N\\ j{\mathcal{I}}_N\\ k{\mathcal{I}}_N\end{array}\right]$;

(c)  $\mathcal{X}={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_M& -i{\mathcal{I}}_M& j{\mathcal{I}}_M& -k{\mathcal{I}}_M\end{array}\right]{\ast }_M{\mathcal{X}}^{{\sigma }_k}{\ast }_N\left[\begin{array}{c}{\mathcal{I}}_N\\ i{\mathcal{I}}_N\\ j{\mathcal{I}}_N\\ k{\mathcal{I}}_N\end{array}\right]$;

7. 

${\left({\mathcal{X}}^i\right)}^{{\sigma }_1}={\mathcal{P}}_M{\ast }_M{\mathcal{X}}^{{\sigma }_1}{\ast }_N{\mathcal{P}}_N,{\left({\mathcal{X}}^k\right)}^{{\sigma }_j}={\mathcal{V}}_M{\ast }_M{\mathcal{X}}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N,{\left({\mathcal{X}}^j\right)}^{{\sigma }_k}={\mathcal{W}}_M{\ast }_M{\mathcal{X}}^{{\sigma }_k}{\ast }_N{\mathcal{W}}_N$.

3. The General Solution to System (2)

Using the definitions and lemmas outlined above, this part will examine the solutions to system (2). At the beginning of this section, we present two lemmas. Utilizing Definition 6, we can transform tensors into matrices. Consequently, the subsequent lemmas can be readily proven using matrix proof techniques found in references [27,40], so this paper will not delve into the details. Building on these lemmas, split quaternion tensors’ real representations are used for obtaining the necessary and sufficient criteria when system (2) has solutions, as well as the general solution expression.

Lemma 3

([40]). Let ${\mathcal{A}}_1,{\mathcal{A}}_2\in {\mathbb{H}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, ${\mathcal{B}}_1,{\mathcal{B}}_2\in {\mathbb{H}}^{L_1\times \cdots \times L_S\times K_1\times \cdots \times K_T}$, and ${\mathcal{C}}_1,{\mathcal{C}}_2\in {\mathbb{H}}^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_T}$. Set the following:

$$\begin{array}{cc}\hfill \mathcal{K}& ={\mathcal{A}}_2{\ast }_N{\mathcal{L}}_{{\mathcal{A}}_1},\mathcal{F}={\mathcal{R}}_{{\mathcal{B}}_1}{\ast }_S{\mathcal{B}}_2,\mathcal{G}={\mathcal{C}}_2-{\mathcal{A}}_2{\ast }_N{\mathcal{A}}_1^{†}{\ast }_M{\mathcal{C}}_1{\ast }_T{\mathcal{B}}_1^{†}{\ast }_S{\mathcal{B}}_2,\mathcal{H}={\mathcal{R}}_{\mathcal{K}}{\ast }_M{\mathcal{A}}_2,\hfill \\ \hfill \mathcal{Q}& ={\mathcal{A}}_1^{†}{\ast }_M{\mathcal{C}}_1{\ast }_T{\mathcal{B}}_1^{†}+{\mathcal{L}}_{{\mathcal{A}}_1}{\ast }_N{\mathcal{K}}^{†}{\ast }_M\mathcal{G}{\ast }_T{\mathcal{B}}_2^{†}-{\mathcal{L}}_{{\mathcal{A}}_1}{\ast }_N{\mathcal{K}}^{†}{\ast }_M{\mathcal{A}}_2{\ast }_N{\mathcal{H}}^{†}{\ast }_M{\mathcal{R}}_{\mathcal{K}}{\ast }_M\mathcal{G}{\ast }_T{\mathcal{B}}_2^{†}\hfill \\ \hfill & +{\mathcal{H}}^{†}{\ast }_M{\mathcal{R}}_{\mathcal{K}}{\ast }_M\mathcal{G}{\ast }_T{\mathcal{F}}^{†}{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_1}.\hfill \end{array}$$

Then,

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill {\mathcal{A}}_1{\ast }_N\mathcal{X}{\ast }_S{\mathcal{B}}_1& ={\mathcal{C}}_1,\hfill \\ \hfill {\mathcal{A}}_2{\ast }_N\mathcal{X}{\ast }_S{\mathcal{B}}_2& ={\mathcal{C}}_2\hfill \end{array}\right.\end{array}$$

(3)

is consistent if and only if the following is true:

$$\begin{array}{c}\hfill {\mathcal{R}}_{{\mathcal{A}}_1}{\ast }_M{\mathcal{C}}_1=0,{\mathcal{C}}_1{\ast }_T{\mathcal{L}}_{{\mathcal{B}}_1}=0,{\mathcal{R}}_{{\mathcal{A}}_2}{\ast }_M{\mathcal{C}}_2=0,{\mathcal{C}}_2{\ast }_T{\mathcal{L}}_{{\mathcal{B}}_2}=0,{\mathcal{R}}_{\mathcal{K}}{\ast }_M\mathcal{G}{\ast }_T{\mathcal{L}}_{\mathcal{F}}=0.\end{array}$$

Building on this, the general solution for system (3) is stated in the following form:

$$\begin{array}{c}\hfill \mathcal{X}=\mathcal{Q}+{\mathcal{L}}_{{\mathcal{A}}_1}{\ast }_N{\mathcal{L}}_{\mathcal{K}}{\ast }_N{\mathcal{W}}_1+{\mathcal{W}}_2{\ast }_S{\mathcal{R}}_{\mathcal{F}}{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_1}+{\mathcal{L}}_{{\mathcal{A}}_1}{\ast }_N{\mathcal{W}}_3{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_2}+{\mathcal{L}}_{{\mathcal{A}}_2}{\ast }_N{\mathcal{W}}_4{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_1},\end{array}$$

where ${\mathcal{W}}_i(i=\overline{1,4})$ are arbitrary tensors of appropriate size defined on $\mathbb{H}$.

Lemma 4

([27]). Suppose that $\mathcal{A}={\mathcal{A}}_0+{\mathcal{A}}_1ϵ\in {\mathbb{DQ}}^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, $\mathcal{B}={\mathcal{B}}_0+{\mathcal{B}}_1ϵ\in {\mathbb{DQ}}^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_S}$, $\mathcal{C}={\mathcal{C}}_0+{\mathcal{C}}_1ϵ\in {\mathbb{DQ}}^{K_1\times \cdots \times K_S\times L_1\times \cdots \times L_T}$, and $\mathcal{D}={\mathcal{D}}_0+{\mathcal{D}}_1ϵ\in {\mathbb{DQ}}^{J_1\times \cdots \times J_N\times L_1\times \cdots \times L_T}$. Set the following:

$$\begin{array}{cc}\hfill {\mathcal{A}}_2& ={\mathcal{A}}_1{\ast }_N{\mathcal{L}}_{{\mathcal{A}}_0},{\mathcal{C}}_2={\mathcal{R}}_{{\mathcal{C}}_0}{\ast }_S{\mathcal{C}}_1,{\mathcal{B}}_2={\mathcal{B}}_1-{\mathcal{A}}_1{\ast }_N\left({\mathcal{A}}_0^{†}{\ast }_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{D}}_0{\ast }_T{\mathcal{C}}_0^{†}\right),\hfill \\ \hfill {\mathcal{A}}_3& ={\mathcal{R}}_{{\mathcal{A}}_0}{\ast }_M{\mathcal{A}}_2,{\mathcal{B}}_3={\mathcal{R}}_{{\mathcal{C}}_0},{\mathcal{D}}_2={\mathcal{D}}_1-\left({\mathcal{A}}_0^{†}{\ast }_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{D}}_0{\ast }_T{\mathcal{C}}_0^{†}\right){\ast }_S{\mathcal{C}}_1,\hfill \\ \hfill {\mathcal{C}}_3& ={\mathcal{R}}_{{\mathcal{A}}_0}{\ast }_M{\mathcal{B}}_2,{\mathcal{A}}_4={\mathcal{L}}_{{\mathcal{A}}_0},{\mathcal{B}}_4={\mathcal{C}}_2{\ast }_T{\mathcal{L}}_{{\mathcal{C}}_0},{\mathcal{C}}_4={\mathcal{D}}_2{\ast }_T{\mathcal{L}}_{{\mathcal{C}}_0},{\mathcal{A}}_5={\mathcal{A}}_4{\ast }_N{\mathcal{L}}_{{\mathcal{A}}_3},\hfill \\ \hfill {\mathcal{B}}_5& ={\mathcal{R}}_{{\mathcal{B}}_3}{\ast }_S{\mathcal{B}}_4,{\mathcal{C}}_5={\mathcal{C}}_4-{\mathcal{A}}_4{\ast }_N{\mathcal{A}}_3^{†}{\ast }_M{\mathcal{C}}_3{\ast }_S{\mathcal{B}}_3^{†}{\ast }_S{\mathcal{B}}_4,{\mathcal{D}}_5={\mathcal{R}}_{{\mathcal{A}}_5}{\ast }_N{\mathcal{A}}_4,\hfill \\ \hfill \mathcal{F}& ={\mathcal{A}}_3^{†}{\ast }_M{\mathcal{C}}_3{\ast }_S{\mathcal{B}}_3^{†}+{\mathcal{L}}_{{\mathcal{A}}_3}{\ast }_N{\mathcal{A}}_5^{†}{\ast }_N{\mathcal{C}}_5{\ast }_T{\mathcal{B}}_4^{†}-{\mathcal{L}}_{{\mathcal{A}}_3}{\ast }_N{\mathcal{A}}_5^{†}{\ast }_N{\mathcal{A}}_4{\ast }_N{\mathcal{D}}_5^{†}{\ast }_N{\mathcal{R}}_{{\mathcal{A}}_5}{\ast }_N{\mathcal{C}}_5{\ast }_T{\mathcal{B}}_4^{†}\hfill \\ \hfill & +{\mathcal{D}}_5^{†}{\ast }_N{\mathcal{R}}_{{\mathcal{A}}_5}{\ast }_N{\mathcal{C}}_5{\ast }_T{\mathcal{B}}_5^{†}{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_3}.\hfill \end{array}$$

Then, the following descriptions are equivalent:

1. 

System (2) is solvable.

2. 

$$\begin{array}{cc}\hfill & {\mathcal{R}}_{{\mathcal{A}}_0}{\ast }_M{\mathcal{B}}_0=0,{\mathcal{D}}_0{\ast }_T{\mathcal{L}}_{{\mathcal{C}}_0}=0,{\mathcal{A}}_0{\ast }_N{\mathcal{D}}_0={\mathcal{B}}_0{\ast }_S{\mathcal{C}}_0,\hfill \\ \hfill & {\mathcal{A}}_0{\ast }_N{\mathcal{D}}_1-{\mathcal{B}}_0{\ast }_S{\mathcal{C}}_1={\mathcal{B}}_1{\ast }_S{\mathcal{C}}_0-{\mathcal{A}}_1{\ast }_N{\mathcal{D}}_0,{\mathcal{R}}_{{\mathcal{A}}_3}{\ast }_M{\mathcal{C}}_3=0,\hfill \\ \hfill & {\mathcal{C}}_3{\ast }_S{\mathcal{L}}_{{\mathcal{B}}_3}=0,{\mathcal{R}}_{{\mathcal{A}}_4}{\ast }_N{\mathcal{C}}_4=0,{\mathcal{C}}_4{\ast }_T{\mathcal{L}}_{{\mathcal{B}}_4}=0,{\mathcal{R}}_{{\mathcal{A}}_5}{\ast }_N{\mathcal{C}}_5{\ast }_T{\mathcal{L}}_{{\mathcal{B}}_5}=0.\hfill \end{array}$$

Based on these, the general solution for system (2) is represented as $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_1ϵ$, where the following is true:

$$\begin{array}{cc}\hfill {\mathcal{X}}_0& ={\mathcal{A}}_0^{†}{\ast }_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{D}}_0{\ast }_T{\mathcal{C}}_0^{†}+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N\mathcal{W}{\ast }_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill {\mathcal{X}}_1& ={\mathcal{A}}_0^{†}{\ast }_M({\mathcal{B}}_2-{\mathcal{A}}_2{\ast }_N\mathcal{W}{\ast }_S{\mathcal{R}}_{{\mathcal{C}}_0})+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N({\mathcal{D}}_2-{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N\mathcal{W}{\ast }_S{\mathcal{C}}_2){\ast }_T{\mathcal{C}}_0^{†}\hfill \\ \hfill & +{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{W}}_1{\ast }_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill \mathcal{W}& =\mathcal{F}+{\mathcal{L}}_{{\mathcal{A}}_3}{\ast }_N{\mathcal{L}}_{{\mathcal{A}}_5}{\ast }_N{\mathcal{W}}_2+{\mathcal{W}}_3{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_5}{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_3}+{\mathcal{L}}_{{\mathcal{A}}_3}{\ast }_N{\mathcal{W}}_4{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_4}\hfill \\ & +{\mathcal{L}}_{{\mathcal{A}}_4}{\ast }_N{\mathcal{W}}_5{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_3},\hfill \end{array}$$

and ${\mathcal{W}}_i(i=\overline{1,5})$ are random tensors with suitable dimensions.

Remark 2.

Note that the set of real tensors is included within the set of quaternion tensors, since real numbers are special cases of quaternions with all imaginary parts set to 0. Thus, the conclusions above also hold in the field of real tensors.

Theorem 1.

Suppose that $\mathcal{A}={\mathcal{A}}_{00}+{\mathcal{A}}_{01}ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, $\mathcal{B}={\mathcal{B}}_{00}+{\mathcal{B}}_{01}ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_S}$, $\mathcal{C}={\mathcal{C}}_{00}+{\mathcal{C}}_{01}ϵ\in {\mathbb{DQ}}_s^{K_1\times \cdots \times K_S\times L_1\times \cdots \times L_T}$, and $\mathcal{D}={\mathcal{D}}_{00}+{\mathcal{D}}_{01}ϵ\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times L_1\times \cdots \times L_T}$. Set the following:

$$\begin{array}{cc}\hfill & {\mathcal{A}}_0={\mathcal{A}}_{00}^{{\sigma }_i},{\mathcal{A}}_1={\mathcal{A}}_{01}^{{\sigma }_i},{\mathcal{B}}_0={\mathcal{B}}_{00}^{{\sigma }_i},{\mathcal{B}}_1={\mathcal{B}}_{01}^{{\sigma }_i},{\mathcal{C}}_0={\mathcal{C}}_{00}^{{\sigma }_i},{\mathcal{C}}_1={\mathcal{C}}_{01}^{{\sigma }_i},{\mathcal{D}}_0={\mathcal{D}}_{00}^{{\sigma }_i},{\mathcal{D}}_1={\mathcal{D}}_{01}^{{\sigma }_i},\hfill \\ \hfill & {\mathcal{A}}_{11}={\mathcal{A}}_1{\ast }_N{\mathcal{L}}_{{\mathcal{A}}_0},{\mathcal{C}}_{11}={\mathcal{R}}_{{\mathcal{C}}_0}{\ast }_S{\mathcal{C}}_1,{\mathcal{B}}_{11}={\mathcal{B}}_1-{\mathcal{A}}_1{\ast }_N\left({\mathcal{A}}_0^{†}{\ast }_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{D}}_0{\ast }_T{\mathcal{C}}_0^{†}\right),\hfill \\ \hfill & {\mathcal{D}}_{11}={\mathcal{D}}_1-\left({\mathcal{A}}_0^{†}{\ast }_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{D}}_0{\ast }_T{\mathcal{C}}_0^{†}\right){\ast }_S{\mathcal{C}}_1,{\mathcal{A}}_2={\mathcal{R}}_{{\mathcal{A}}_0}{\ast }_M{\mathcal{A}}_{11},{\mathcal{B}}_2={\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill & {\mathcal{C}}_2={\mathcal{R}}_{{\mathcal{A}}_0}{\ast }_M{\mathcal{B}}_{11},{\mathcal{A}}_3={\mathcal{L}}_{{\mathcal{A}}_0},{\mathcal{B}}_3={\mathcal{C}}_{11}{\ast }_T{\mathcal{L}}_{{\mathcal{C}}_0},{\mathcal{C}}_3={\mathcal{D}}_{11}{\ast }_T{\mathcal{L}}_{{\mathcal{C}}_0},{\mathcal{A}}_4={\mathcal{A}}_3{\ast }_N{\mathcal{L}}_{{\mathcal{A}}_2},\hfill \\ \hfill & {\mathcal{B}}_4={\mathcal{R}}_{{\mathcal{B}}_2}{\ast }_S{\mathcal{B}}_3,{\mathcal{C}}_4={\mathcal{C}}_3-{\mathcal{A}}_3{\ast }_N{\mathcal{A}}_2^{†}{\ast }_M{\mathcal{C}}_2{\ast }_S{\mathcal{B}}_2^{†}{\ast }_S{\mathcal{B}}_3,{\mathcal{D}}_4={\mathcal{R}}_{{\mathcal{A}}_4}{\ast }_N{\mathcal{A}}_3,\hfill \\ \hfill & \mathcal{F}={\mathcal{A}}_2^{†}{\ast }_M{\mathcal{C}}_2{\ast }_S{\mathcal{B}}_2^{†}+{\mathcal{L}}_{{\mathcal{A}}_2}{\ast }_N{\mathcal{A}}_4^{†}{\ast }_N{\mathcal{C}}_4{\ast }_T{\mathcal{B}}_3^{†}-{\mathcal{L}}_{{\mathcal{A}}_2}{\ast }_N{\mathcal{A}}_4^{†}{\ast }_N{\mathcal{A}}_3{\ast }_N{\mathcal{D}}_4^{†}{\ast }_N{\mathcal{R}}_{{\mathcal{A}}_4}{\ast }_N{\mathcal{C}}_4{\ast }_T{\mathcal{B}}_3^{†}\hfill \\ \hfill & +{\mathcal{D}}_4^{†}{\ast }_N{\mathcal{R}}_{{\mathcal{A}}_4}{\ast }_N{\mathcal{C}}_4{\ast }_T{\mathcal{B}}_4^{†}{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_2}.\hfill \end{array}$$

Then, the following descriptions are equivalent:

1. 

The system of dual split quaternion tensor Equation (2) is solvable.

2. 

The system of real tensor equations, namely

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{\ast }_N{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{X}}_0{\ast }_S{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{\ast }_N{\mathcal{X}}_1+{\mathcal{A}}_1{\ast }_N{\mathcal{X}}_0={\mathcal{B}}_1,\hfill \\ {\mathcal{X}}_0{\ast }_S{\mathcal{C}}_1+{\mathcal{X}}_1{\ast }_S{\mathcal{C}}_0={\mathcal{D}}_1\hfill \end{array}\right.\end{array}$$

(4)

is consistent.

3. 

$$\begin{array}{cc}\hfill & {\mathcal{R}}_{{\mathcal{A}}_0}{\ast }_M{\mathcal{B}}_0=0,{\mathcal{D}}_0{\ast }_T{\mathcal{L}}_{{\mathcal{C}}_0}=0,{\mathcal{A}}_0{\ast }_N{\mathcal{D}}_0={\mathcal{B}}_0{\ast }_S{\mathcal{C}}_0,\hfill \\ & {\mathcal{A}}_0{\ast }_N{\mathcal{D}}_1-{\mathcal{B}}_0{\ast }_S{\mathcal{C}}_1={\mathcal{B}}_1{\ast }_S{\mathcal{C}}_0-{\mathcal{A}}_1{\ast }_N{\mathcal{D}}_0,{\mathcal{R}}_{{\mathcal{A}}_2}{\ast }_M{\mathcal{C}}_2=0,\hfill \\ & {\mathcal{C}}_2{\ast }_S{\mathcal{L}}_{{\mathcal{B}}_2}=0,{\mathcal{R}}_{{\mathcal{A}}_3}{\ast }_N{\mathcal{C}}_3=0,{\mathcal{C}}_3{\ast }_T{\mathcal{L}}_{{\mathcal{B}}_3}=0,{\mathcal{R}}_{{\mathcal{A}}_4}{\ast }_N{\mathcal{C}}_4{\ast }_T{\mathcal{L}}_{{\mathcal{B}}_4}=0.\hfill \end{array}$$

Based on these circumstances, the general solution of system (2) can be represented as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$, where

$$\begin{array}{cc}\hfill {\mathcal{X}}_{00}& ={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{\ast }_N({\mathcal{X}}_0+{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{T}}_S^T){\ast }_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \\ \hfill {\mathcal{X}}_{01}& ={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{\ast }_N({\mathcal{X}}_1+{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{T}}_S^T){\ast }_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \\ \hfill {\mathcal{X}}_0& ={\mathcal{A}}_0^{†}{\ast }_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{D}}_0{\ast }_T{\mathcal{C}}_0^{†}+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N\mathcal{W}{\ast }_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill {\mathcal{X}}_1& ={\mathcal{A}}_0^{†}{\ast }_M({\mathcal{B}}_{11}-{\mathcal{A}}_{11}{\ast }_N\mathcal{W}{\ast }_S{\mathcal{R}}_{{\mathcal{C}}_0})+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N({\mathcal{D}}_{11}-{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N\mathcal{W}{\ast }_S{\mathcal{C}}_{11}){\ast }_T{\mathcal{C}}_0^{†}\hfill \\ \hfill & +{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{W}}_1{\ast }_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill \mathcal{W}& =\mathcal{F}+{\mathcal{L}}_{{\mathcal{A}}_2}{\ast }_N{\mathcal{L}}_{{\mathcal{A}}_4}{\ast }_N{\mathcal{W}}_2+{\mathcal{W}}_3{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_4}{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_2}+{\mathcal{L}}_{{\mathcal{A}}_2}{\ast }_N{\mathcal{W}}_4{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_3}+{\mathcal{L}}_{{\mathcal{A}}_3}{\ast }_N{\mathcal{W}}_5{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_2},\hfill \end{array}$$

and ${\mathcal{W}}_i(i=\overline{1,5})$ are random tensors with proper dimensions.

Proof. 

(1) ⇔ (2)

If condition (1) holds, it indicates that system (2) possesses a solution. Thus, we can express the solution for system (2) as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_S}$, where ${\mathcal{X}}_{00},{\mathcal{X}}_{01}\in {\mathbb{H}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_S}$. By substituting $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$ into system (2), we obtain the following split quaternion tensor equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}{\ast }_N{\mathcal{X}}_{00}={\mathcal{B}}_{00},\hfill \\ {\mathcal{X}}_{00}{\ast }_S{\mathcal{C}}_{00}={\mathcal{D}}_{00},\hfill \\ {\mathcal{A}}_{00}{\ast }_N{\mathcal{X}}_{01}+{\mathcal{A}}_{01}{\ast }_N{\mathcal{X}}_{00}={\mathcal{B}}_{01},\hfill \\ {\mathcal{X}}_{00}{\ast }_S{\mathcal{C}}_{01}+{\mathcal{X}}_{01}{\ast }_S{\mathcal{C}}_{00}={\mathcal{D}}_{01}.\hfill \end{array}\right.\end{array}$$

(5)

Let ${\mathcal{X}}_0={\mathcal{X}}_{00}^{{\sigma }_i}$ and ${\mathcal{X}}_1={\mathcal{X}}_{01}^{{\sigma }_i}$. Apply the real representation to the system, and, using (2) and (3) of Proposition 2, we then obtain the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}^{{\sigma }_i}{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_i}={\mathcal{B}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_i}{\ast }_S{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{A}}_{00}^{{\sigma }_i}{\ast }_N{\mathcal{X}}_{01}^{{\sigma }_i}+{\mathcal{A}}_{01}^{{\sigma }_i}{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_i}={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_i}{\ast }_S{\mathcal{C}}_{01}^{{\sigma }_i}+{\mathcal{X}}_{01}^{{\sigma }_i}{\ast }_S{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{01}^{{\sigma }_i}.\hfill \end{array}\right.\end{array}$$

(6)

i.e.,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{\ast }_N{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{X}}_0{\ast }_S{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{\ast }_N{\mathcal{X}}_1+{\mathcal{A}}_1{\ast }_N{\mathcal{X}}_0={\mathcal{B}}_1,\hfill \\ {\mathcal{X}}_0{\ast }_S{\mathcal{C}}_1+{\mathcal{X}}_1{\ast }_S{\mathcal{C}}_0={\mathcal{D}}_1.\hfill \end{array}\right.\end{array}$$

(7)

Thus, $({\mathcal{X}}_0,{\mathcal{X}}_1)$ is a pair of solutions to system (4).

On the other hand, let $({\mathcal{X}}_0,{\mathcal{X}}_1)$ be the solutions for system (4). Using 4a of Proposition 2, we obtain the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{R}}_M^T{\ast }_M{\mathcal{A}}_0{\ast }_N{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0={\mathcal{R}}_M^T{\ast }_M{\mathcal{B}}_0{\ast }_S{\mathcal{R}}_S,\hfill \\ {\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T{\ast }_S{\mathcal{C}}_0{\ast }_T{\mathcal{R}}_T={\mathcal{R}}_N^T{\ast }_N{\mathcal{D}}_0{\ast }_T{\mathcal{R}}_T,\hfill \\ {\mathcal{R}}_M^T{\ast }_M{\mathcal{A}}_0{\ast }_N{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_1+{\mathcal{R}}_M^T{\ast }_M{\mathcal{A}}_1{\ast }_N{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0={\mathcal{R}}_M^T{\ast }_M{\mathcal{B}}_1{\ast }_S{\mathcal{R}}_S,\hfill \\ {\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T{\ast }_S{\mathcal{C}}_1{\ast }_T{\mathcal{R}}_T+{\mathcal{X}}_1{\ast }_S{\mathcal{R}}_S^T{\ast }_S{\mathcal{C}}_0{\ast }_T{\mathcal{R}}_T={\mathcal{R}}_N^T{\ast }_N{\mathcal{D}}_1{\ast }_T{\mathcal{R}}_T.\hfill \end{array}\right.\end{array}$$

(8)

i.e.,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{\ast }_N{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T={\mathcal{B}}_0,\hfill \\ {\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T{\ast }_S{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{\ast }_N{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{R}}_S^T+{\mathcal{A}}_1{\ast }_N{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T={\mathcal{B}}_1,\hfill \\ {\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T{\ast }_S{\mathcal{C}}_1+{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{R}}_S^T{\ast }_S{\mathcal{C}}_0={\mathcal{D}}_1.\hfill \end{array}\right.\end{array}$$

(9)

Thus, $({\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T,{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{R}}_S^T)$ represent solutions to the system of real tensor equations. Likewise, $({\mathcal{S}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{S}}_S^T,{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{S}}_S^T)$ and $({\mathcal{T}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{T}}_S^T,{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{T}}_S^T)$ are also solutions to the system. Then, we define the following:

$${\mathcal{Y}}_0:={\displaystyle \frac{1}{4}}({\mathcal{X}}_0+{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{T}}_S^T),$$

$${\mathcal{Y}}_1:={\displaystyle \frac{1}{4}}({\mathcal{X}}_1+{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{T}}_S^T).$$

Set the following:

$${\mathcal{X}}_0=\left[\begin{array}{cccc}{\mathcal{V}}_{11}& {\mathcal{V}}_{12}& {\mathcal{V}}_{13}& {\mathcal{V}}_{14}\\ {\mathcal{V}}_{21}& {\mathcal{V}}_{22}& {\mathcal{V}}_{23}& {\mathcal{V}}_{24}\\ {\mathcal{V}}_{31}& {\mathcal{V}}_{32}& {\mathcal{V}}_{33}& {\mathcal{V}}_{34}\\ {\mathcal{V}}_{41}& {\mathcal{V}}_{42}& {\mathcal{V}}_{43}& {\mathcal{V}}_{44}\end{array}\right]\in {\mathbb{R}}^{J_1\times \cdots \times 4J_N\times K_1\times \cdots \times 4K_S},$$

$${\mathcal{X}}_1=\left[\begin{array}{cccc}{\mathcal{W}}_{11}& {\mathcal{W}}_{12}& {\mathcal{W}}_{13}& {\mathcal{W}}_{14}\\ {\mathcal{W}}_{21}& {\mathcal{W}}_{22}& {\mathcal{W}}_{23}& {\mathcal{W}}_{24}\\ {\mathcal{W}}_{31}& {\mathcal{W}}_{32}& {\mathcal{W}}_{33}& {\mathcal{W}}_{34}\\ {\mathcal{W}}_{41}& {\mathcal{W}}_{42}& {\mathcal{W}}_{43}& {\mathcal{W}}_{44}\end{array}\right]\in {\mathbb{R}}^{J_1\times \cdots \times 4J_N\times K_1\times \cdots \times 4K_S}.$$

Using direct computation, we obtain the following:

$${\mathcal{Y}}_0=\left[\begin{array}{cccc}{\mathcal{B}}_0& {\mathcal{B}}_1& {\mathcal{B}}_2& {\mathcal{B}}_3\\ -{\mathcal{B}}_1& {\mathcal{B}}_0& -{\mathcal{B}}_3& {\mathcal{B}}_2\\ {\mathcal{B}}_2& -{\mathcal{B}}_3& {\mathcal{B}}_0& -{\mathcal{B}}_1\\ {\mathcal{B}}_3& {\mathcal{B}}_2& {\mathcal{B}}_1& {\mathcal{B}}_0\end{array}\right]$$

and

$${\mathcal{Y}}_1=\left[\begin{array}{cccc}{\mathcal{D}}_0& {\mathcal{D}}_1& {\mathcal{D}}_2& {\mathcal{D}}_3\\ -{\mathcal{D}}_1& {\mathcal{D}}_0& -{\mathcal{D}}_3& {\mathcal{D}}_2\\ {\mathcal{D}}_2& -{\mathcal{D}}_3& {\mathcal{D}}_0& -{\mathcal{D}}_1\\ {\mathcal{D}}_3& {\mathcal{D}}_2& {\mathcal{D}}_1& {\mathcal{D}}_0\end{array}\right],$$

where

$${\mathcal{B}}_0={\displaystyle \frac{1}{4}}({\mathcal{V}}_{11}+{\mathcal{V}}_{22}+{\mathcal{V}}_{33}+{\mathcal{V}}_{44}),{\mathcal{B}}_1={\displaystyle \frac{1}{4}}({\mathcal{V}}_{12}-{\mathcal{V}}_{21}-{\mathcal{V}}_{34}+{\mathcal{V}}_{43}),$$

$${\mathcal{B}}_2={\displaystyle \frac{1}{4}}({\mathcal{V}}_{13}+{\mathcal{V}}_{24}+{\mathcal{V}}_{31}+{\mathcal{V}}_{42}),{\mathcal{B}}_3={\displaystyle \frac{1}{4}}({\mathcal{V}}_{14}-{\mathcal{V}}_{23}-{\mathcal{V}}_{32}+{\mathcal{V}}_{41}),$$

and

$${\mathcal{D}}_0={\displaystyle \frac{1}{4}}({\mathcal{W}}_{11}+{\mathcal{W}}_{22}+{\mathcal{W}}_{33}+{\mathcal{W}}_{44}),{\mathcal{D}}_1={\displaystyle \frac{1}{4}}({\mathcal{W}}_{12}-{\mathcal{W}}_{21}-{\mathcal{W}}_{34}+{\mathcal{W}}_{43}),$$

$${\mathcal{D}}_2={\displaystyle \frac{1}{4}}({\mathcal{W}}_{13}+{\mathcal{W}}_{24}+{\mathcal{W}}_{31}+{\mathcal{W}}_{42}),{\mathcal{D}}_3={\displaystyle \frac{1}{4}}({\mathcal{W}}_{14}-{\mathcal{W}}_{23}-{\mathcal{W}}_{32}+{\mathcal{W}}_{41}).$$

Then, we let the following be true:

$${\mathcal{X}}_{00}={\mathcal{B}}_0+{\mathcal{B}}_{1}i+{\mathcal{B}}_{2}j+{\mathcal{B}}_{3}k={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{\ast }_N{\mathcal{Y}}_0{\ast }_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right]$$

and

$${\mathcal{X}}_{01}={\mathcal{D}}_0+{\mathcal{D}}_{1}i+{\mathcal{D}}_{2}j+{\mathcal{D}}_{3}k={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{\ast }_N{\mathcal{Y}}_1{\ast }_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],$$

where ${\mathcal{X}}_{00}$ and ${\mathcal{X}}_{01}\in {\mathbb{H}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_S}$.

Due to 6a of Proposition 2, ${\mathcal{Y}}_0={\mathcal{X}}_{00}^{{\sigma }_i}$ and ${\mathcal{Y}}_1={\mathcal{X}}_{01}^{{\sigma }_i}$. Thus, the following is true:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}^{{\sigma }_i}{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_i}={\mathcal{B}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_i}{\ast }_S{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{A}}_{00}^{{\sigma }_i}{\ast }_N{\mathcal{X}}_{01}^{{\sigma }_i}+{\mathcal{A}}_{01}^{{\sigma }_i}{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_i}={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_i}{\ast }_S{\mathcal{C}}_{01}^{{\sigma }_i}+{\mathcal{X}}_{01}^{{\sigma }_i}{\ast }_S{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{01}^{{\sigma }_i},\hfill \end{array}\right.\end{array}$$

(10)

Due to the above, we can obtain $({\mathcal{X}}_{00},{\mathcal{X}}_{01})$ as the solution of system (5). Furthermore, it is clear that system (2) and system (5) are equivalent. Therefore, when system (2) has solutions, system (4) also has solutions, and vice versa. In addition, we can deduce the general solution of system of dual split quaternion tensor equations using Lemma 4 as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$, where the following is true:

$$\begin{array}{cc}\hfill & {\mathcal{X}}_{00}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{\ast }_N({\mathcal{X}}_0+{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{T}}_S^T){\ast }_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \\ \hfill & {\mathcal{X}}_{01}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{\ast }_N({\mathcal{X}}_1+{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{T}}_S^T){\ast }_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \\ \hfill & {\mathcal{X}}_0={\mathcal{A}}_0^{†}{\ast }_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{D}}_0{\ast }_T{\mathcal{C}}_0^{†}+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N\mathcal{W}{\ast }_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill & {\mathcal{X}}_1={\mathcal{A}}_0^{†}{\ast }_M({\mathcal{B}}_{11}-{\mathcal{A}}_{11}{\ast }_N\mathcal{W}{\ast }_S{\mathcal{R}}_{{\mathcal{C}}_0})+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N({\mathcal{D}}_{11}-{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N\mathcal{W}{\ast }_S{\mathcal{C}}_{11}){\ast }_T{\mathcal{C}}_0^{†}\hfill \\ \hfill & +{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{W}}_1{\ast }_S{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill & \mathcal{W}=\mathcal{F}+{\mathcal{L}}_{{\mathcal{A}}_2}{\ast }_N{\mathcal{L}}_{{\mathcal{A}}_4}{\ast }_N{\mathcal{W}}_2+{\mathcal{W}}_3{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_4}{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_2}+{\mathcal{L}}_{{\mathcal{A}}_2}{\ast }_N{\mathcal{W}}_4{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_3}+{\mathcal{L}}_{{\mathcal{A}}_3}{\ast }_N{\mathcal{W}}_5{\ast }_S{\mathcal{R}}_{{\mathcal{B}}_2},\hfill \end{array}$$

and ${\mathcal{W}}_i(i=\overline{1,5})$ are random tensors with suitable size.

Additionally, (2) and (3) are equivalent to each other, which can be easily proven using Lemmas 3 and 4. We will not elaborate further on these points here.    □

In the following section, we will propose equivalent conditions required when system (2) has $\eta$-Hermitian solutions.

Theorem 2.

Suppose that $\mathcal{A}={\mathcal{A}}_{00}+{\mathcal{A}}_{01}ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, $\mathcal{B}={\mathcal{B}}_{00}+{\mathcal{B}}_{01}ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$, $\mathcal{C}={\mathcal{C}}_{00}+{\mathcal{C}}_{01}ϵ\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_T}$, and $\mathcal{D}={\mathcal{D}}_{00}+{\mathcal{D}}_{01}ϵ\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times K_1\times \cdots \times K_T}$.

Set the following:

$$\begin{array}{cc}\hfill {\mathcal{A}}_0& =\left\{\begin{array}{cc}{\mathcal{A}}_{00}^{{\sigma }_i},\hfill & \eta =i,\hfill \\ {\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j},\hfill & \eta =j,\hfill \\ {\left({\mathcal{A}}_{00}^j\right)}^{{\sigma }_k},\hfill & \eta =k,\hfill \end{array}\right.{\mathcal{A}}_1=\left\{\begin{array}{cc}{\mathcal{A}}_{01}^{{\sigma }_i},\hfill & \eta =i,\hfill \\ {\left({\mathcal{A}}_{01}^k\right)}^{{\sigma }_j},\hfill & \eta =j,\hfill \\ {\left({\mathcal{A}}_{01}^j\right)}^{{\sigma }_k},\hfill & \eta =k,\hfill \end{array}\right.\hfill \\ \hfill {\mathcal{B}}_0& ={\mathcal{B}}_{00}^{{\sigma }_i},{\mathcal{B}}_1={\mathcal{B}}_{01}^{{\sigma }_i},{\mathcal{C}}_0={\mathcal{C}}_{00}^{{\sigma }_i},{\mathcal{C}}_1={\mathcal{C}}_{01}^{{\sigma }_i},\eta =\{i,j,k\}\hfill \\ \hfill {\mathcal{D}}_0& ={\mathcal{D}}_{00}^{{\sigma }_{\eta }},{\mathcal{D}}_1={\mathcal{D}}_{01}^{{\sigma }_{\eta }},\eta =\{i,j,k\}.\hfill \end{array}$$

Then, system (2) has η-Hermitian solutions $\mathcal{X}={\mathcal{X}}^{\eta \ast }\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times J_1\times \cdots \times J_N},\eta =\{i,j,k\}$, and this means that system (4) possesses a pair of solutions $({\mathcal{X}}_0,{\mathcal{X}}_1)$ that satisfies ${\mathcal{X}}_0={\mathcal{X}}_0^T$ and ${\mathcal{X}}_1={\mathcal{X}}_1^T$, and vice versa.

Proof. 

It is only necessary to demonstrate the situation for $\eta =j$; the other situations are identical to it, so we omit them. Let us assume that $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ\in {\mathbb{DQ}}_s^{J_1\times \cdots \times J_N\times J_1\times \cdots \times J_N}$, which is a j-Hermitian solution of system (2), where $\mathcal{X}={\mathcal{X}}^{j\ast }$. Then, we obtain the following:

$$\begin{array}{c}\hfill {\mathcal{X}}_{00}={\mathcal{X}}_{00}^{j\ast },{\mathcal{X}}_{01}={\mathcal{X}}_{01}^{j\ast }.\end{array}$$

By substituting $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$ into system (2), system (2) then corresponds to the subsequent system as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}{\ast }_N{\mathcal{X}}_{00}=B_{00},\hfill \\ {\mathcal{X}}_{00}{\ast }_N{\mathcal{C}}_{00}={\mathcal{D}}_{00},\hfill \\ {\mathcal{A}}_{00}{\ast }_N{\mathcal{X}}_{01}+{\mathcal{A}}_{01}{\ast }_N{\mathcal{X}}_{00}=B_{01},\hfill \\ {\mathcal{X}}_{00}{\ast }_N{\mathcal{C}}_{01}+{\mathcal{X}}_{01}{\ast }_N{\mathcal{C}}_{00}={\mathcal{D}}_{01}.\hfill \end{array}\right.\end{array}$$

(11)

Let ${\mathcal{X}}_0={\mathcal{X}}_{00}^{{\sigma }_j},{\mathcal{X}}_1={\mathcal{X}}_{01}^{{\sigma }_j}$. Apply the real representation to the system, and, using 2 and 3 of Proposition 2, we then obtain the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{A}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{X}}_{01}^{{\sigma }_j}+{\mathcal{A}}_{01}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{01}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{01}^{{\sigma }_j}+{\mathcal{X}}_{01}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{01}^{{\sigma }_j}.\hfill \end{array}\right.\end{array}$$

(12)

i.e.,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{V}}_M{\ast }_M{\mathcal{A}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{V}}_M{\ast }_M{\mathcal{B}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{V}}_M{\ast }_M{\mathcal{A}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{X}}_{01}^{{\sigma }_j}+{\mathcal{V}}_M{\ast }_M{\mathcal{A}}_{01}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{V}}_M{\ast }_M{\mathcal{B}}_{01}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{01}^{{\sigma }_j}+{\mathcal{X}}_{01}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{01}^{{\sigma }_j}.\hfill \end{array}\right.\end{array}$$

(13)

According to 7 of Proposition 2 and the definition of real representation, we obtain the following:

$$\begin{array}{cc}\hfill & {\mathcal{V}}_M{\ast }_M{\mathcal{A}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N={\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j},{\mathcal{V}}_M{\ast }_M{\mathcal{A}}_{01}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N={\left({\mathcal{A}}_{01}^k\right)}^{{\sigma }_j},\hfill \\ \hfill & {\mathcal{V}}_M{\ast }_M{\mathcal{B}}_{00}^{{\sigma }_j}={\mathcal{B}}_{00}^{{\sigma }_i},{\mathcal{V}}_M{\ast }_M{\mathcal{B}}_{01}^{{\sigma }_j}={\mathcal{B}}_{01}^{{\sigma }_i},{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{C}}_{00}^{{\sigma }_i},{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{C}}_{00}^{{\sigma }_i}.\hfill \end{array}$$

Thus, the above system can be expressed as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{\ast }_N{\mathcal{X}}_{01}^{{\sigma }_j}+{\left({\mathcal{A}}_{01}^k\right)}^{{\sigma }_j}{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{C}}_{01}^{{\sigma }_i}+{\mathcal{X}}_{01}^{{\sigma }_j}{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{01}^{{\sigma }_j},\hfill \end{array}\right.\end{array}$$

(14)

i.e.,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{\ast }_N{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{X}}_0{\ast }_N{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{\ast }_N{\mathcal{X}}_1+{\mathcal{A}}_1{\ast }_N{\mathcal{X}}_0={\mathcal{B}}_1,\hfill \\ {\mathcal{X}}_0{\ast }_N{\mathcal{C}}_1+{\mathcal{X}}_1{\ast }_N{\mathcal{C}}_0={\mathcal{D}}_1.\hfill \end{array}\right.\end{array}$$

(15)

Using 5 in Proposition 2, we obtain the following:

$${\left({\mathcal{X}}_{00}^{j\ast }\right)}^{{\sigma }_j}={\left({\mathcal{X}}_{00}^{{\sigma }_j}\right)}^T,{\left({\mathcal{X}}_{01}^{j\ast }\right)}^{{\sigma }_j}={\left({\mathcal{X}}_{01}^{{\sigma }_j}\right)}^T.$$

Consequently,

$$\begin{array}{c}\hfill {\mathcal{X}}_{00}^{{\sigma }_j}={\left({\mathcal{X}}_{00}^{j\ast }\right)}^{{\sigma }_j}={\left({\mathcal{X}}_{00}^{{\sigma }_j}\right)}^T,{\mathcal{X}}_{01}^{{\sigma }_j}={\left({\mathcal{X}}_{01}^{j\ast }\right)}^{{\sigma }_j}={\left({\mathcal{X}}_{01}^{{\sigma }_j}\right)}^T,\end{array}$$

i.e.,

$${\mathcal{X}}_0={\mathcal{X}}_0^T,{\mathcal{X}}_1={\mathcal{X}}_1^T.$$

On the other hand, if system (4) has a pair of solutions $({\mathcal{X}}_0,{\mathcal{X}}_1)$ that satisfies ${\mathcal{X}}_0={\mathcal{X}}_0^T$ and ${\mathcal{X}}_1={\mathcal{X}}_1^T$, then the system (4) can be denoted as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{\ast }_N{\mathcal{X}}_0={\mathcal{B}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_0{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{\ast }_N{\mathcal{X}}_1+{\left({\mathcal{A}}_{01}^k\right)}^{{\sigma }_j}{\ast }_N{\mathcal{X}}_0={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_0{\ast }_N{\mathcal{C}}_{01}^{{\sigma }_i}+{\mathcal{X}}_1{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{01}^{{\sigma }_j}\hfill \end{array}\right.\end{array}$$

(16)

and

$$\begin{array}{c}\hfill {\mathcal{X}}_0={\mathcal{X}}_0^T,{\mathcal{X}}_1={\mathcal{X}}_1^T.\end{array}$$

As indicated by 4b in Proposition 2,

$$\begin{array}{cc}\hfill & (-{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_N{\mathcal{R}}_N^T,-{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_1{\ast }_N{\mathcal{R}}_N^T),\hfill \\ & (-{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_0{\ast }_N{\mathcal{S}}_N^T,-{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_1{\ast }_N{\mathcal{S}}_N^T),\hfill \\ & ({\mathcal{T}}_N{\ast }_N{\mathcal{X}}_0{\ast }_N{\mathcal{T}}_N^T,{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_1{\ast }_N{\mathcal{T}}_N^T)\hfill \end{array}$$

are also solutions to the system. Next, we define the following:

$$\begin{array}{c}\hfill {\mathcal{Y}}_0:={\displaystyle \frac{1}{4}}({\mathcal{X}}_0-{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_N{\mathcal{R}}_N^T-{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_0{\ast }_N{\mathcal{S}}_N^T+{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_0{\ast }_N{\mathcal{T}}_N^T),\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{Y}}_1:={\displaystyle \frac{1}{4}}({\mathcal{X}}_1-{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_1{\ast }_N{\mathcal{R}}_N^T-{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_1{\ast }_N{\mathcal{S}}_N^T+{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_1{\ast }_N{\mathcal{T}}_N^T).\end{array}$$

Set the following:

$$\begin{array}{c}\hfill {\mathcal{X}}_0=\left[\begin{array}{cccc}{\mathcal{V}}_{11}& {\mathcal{V}}_{12}& {\mathcal{V}}_{13}& {\mathcal{V}}_{14}\\ {\mathcal{V}}_{21}& {\mathcal{V}}_{22}& {\mathcal{V}}_{23}& {\mathcal{V}}_{24}\\ {\mathcal{V}}_{31}& {\mathcal{V}}_{32}& {\mathcal{V}}_{33}& {\mathcal{V}}_{34}\\ {\mathcal{V}}_{41}& {\mathcal{V}}_{42}& {\mathcal{V}}_{43}& {\mathcal{V}}_{44}\end{array}\right]\in {\mathbb{R}}^{J_1\times \cdots \times 4J_N\times J_1\times \cdots \times 4J_N},\end{array}$$

$$\begin{array}{c}\hfill {\mathcal{X}}_1=\left[\begin{array}{cccc}{\mathcal{W}}_{11}& {\mathcal{W}}_{12}& {\mathcal{W}}_{13}& {\mathcal{W}}_{14}\\ {\mathcal{W}}_{21}& {\mathcal{W}}_{22}& {\mathcal{W}}_{23}& {\mathcal{W}}_{24}\\ {\mathcal{W}}_{31}& {\mathcal{W}}_{32}& {\mathcal{W}}_{33}& {\mathcal{W}}_{34}\\ {\mathcal{W}}_{41}& {\mathcal{W}}_{42}& {\mathcal{W}}_{43}& {\mathcal{W}}_{44}\end{array}\right]\in {\mathbb{R}}^{J_1\times \cdots \times 4J_N\times J_1\times \cdots \times 4J_N}.\end{array}$$

Using direct computation, we obtain the following:

$${\mathcal{Y}}_0=\left[\begin{array}{cccc}{\mathcal{B}}_0& {\mathcal{B}}_1& {\mathcal{B}}_2& {\mathcal{B}}_3\\ {\mathcal{B}}_1& -{\mathcal{B}}_0& {\mathcal{B}}_3& -{\mathcal{B}}_2\\ -{\mathcal{B}}_2& {\mathcal{B}}_3& -{\mathcal{B}}_0& {\mathcal{B}}_1\\ {\mathcal{B}}_3& {\mathcal{B}}_2& {\mathcal{B}}_1& {\mathcal{B}}_0\end{array}\right]$$

and

$${\mathcal{Y}}_1=\left[\begin{array}{cccc}{\mathcal{D}}_0& {\mathcal{D}}_1& {\mathcal{D}}_2& {\mathcal{D}}_3\\ {\mathcal{D}}_1& -{\mathcal{D}}_0& {\mathcal{D}}_3& -{\mathcal{D}}_2\\ -{\mathcal{D}}_2& {\mathcal{D}}_3& -{\mathcal{D}}_0& {\mathcal{D}}_1\\ {\mathcal{D}}_3& {\mathcal{D}}_2& {\mathcal{D}}_1& {\mathcal{D}}_0\end{array}\right],$$

where

$${\mathcal{B}}_0={\displaystyle \frac{1}{4}}({\mathcal{V}}_{11}-{\mathcal{V}}_{22}-{\mathcal{V}}_{33}+{\mathcal{V}}_{44}),{\mathcal{B}}_1={\displaystyle \frac{1}{4}}({\mathcal{V}}_{12}+{\mathcal{V}}_{21}+{\mathcal{V}}_{34}+{\mathcal{V}}_{43}),$$

$${\mathcal{B}}_2={\displaystyle \frac{1}{4}}({\mathcal{V}}_{13}-{\mathcal{V}}_{24}-{\mathcal{V}}_{31}+{\mathcal{V}}_{42}),{\mathcal{B}}_3={\displaystyle \frac{1}{4}}({\mathcal{V}}_{14}+{\mathcal{V}}_{23}+{\mathcal{V}}_{32}+{\mathcal{V}}_{41}),$$

and

$${\mathcal{D}}_0={\displaystyle \frac{1}{4}}({\mathcal{W}}_{11}-{\mathcal{W}}_{22}-{\mathcal{W}}_{33}+{\mathcal{W}}_{44}),{\mathcal{D}}_1={\displaystyle \frac{1}{4}}({\mathcal{W}}_{12}+{\mathcal{W}}_{21}+{\mathcal{W}}_{34}+{\mathcal{W}}_{43}),$$

$${\mathcal{D}}_2={\displaystyle \frac{1}{4}}({\mathcal{W}}_{13}-{\mathcal{W}}_{24}-{\mathcal{W}}_{31}+{\mathcal{W}}_{42}),{\mathcal{D}}_3={\displaystyle \frac{1}{4}}({\mathcal{W}}_{14}+{\mathcal{W}}_{23}+{\mathcal{W}}_{32}+{\mathcal{W}}_{41}).$$

Then, we let the following be true:

$$\begin{array}{c}\hfill {\mathcal{X}}_{00}={\mathcal{B}}_0+{\mathcal{B}}_{1}i+{\mathcal{B}}_{2}j+{\mathcal{B}}_{3}k={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_N& -i{\mathcal{I}}_N& -j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{\ast }_N{\mathcal{Y}}_0{\ast }_N\left[\begin{array}{c}{\mathcal{I}}_N\\ i{\mathcal{I}}_N\\ j{\mathcal{I}}_N\\ k{\mathcal{I}}_N\end{array}\right]\end{array}$$

and

$${\mathcal{X}}_{01}={\mathcal{D}}_0+{\mathcal{D}}_{1}i+{\mathcal{D}}_{2}j+{\mathcal{D}}_{3}k={\displaystyle \frac{1}{2}}\left[\begin{array}{cccc}{\mathcal{I}}_N& -i{\mathcal{I}}_N& -j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{\ast }_N{\mathcal{Y}}_1{\ast }_N\left[\begin{array}{c}{\mathcal{I}}_N\\ i{\mathcal{I}}_N\\ j{\mathcal{I}}_N\\ k{\mathcal{I}}_N\end{array}\right],$$

where ${\mathcal{X}}_{00}$ and ${\mathcal{X}}_{01}\in {\mathbb{H}}_s^{J_1\times \cdots \times J_N\times J_1\times \cdots \times J_N}$.

Due to 6b of Proposition 2, ${\mathcal{Y}}_0={\mathcal{X}}_{00}^{{\sigma }_j}$ and ${\mathcal{Y}}_1={\mathcal{X}}_{01}^{{\sigma }_j}$. Thus, the following is true:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{00}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\left({\mathcal{A}}_{00}^k\right)}^{{\sigma }_j}{\ast }_N{\mathcal{X}}_{01}^{{\sigma }_j}+{\left({\mathcal{A}}_{01}^k\right)}^{{\sigma }_j}{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{C}}_{01}^{{\sigma }_i}+{\mathcal{X}}_{01}^{{\sigma }_j}{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_i}={\mathcal{D}}_{01}^{{\sigma }_j}.\hfill \end{array}\right.\end{array}$$

(17)

That is, $({\mathcal{X}}_{00}^{{\sigma }_j},{\mathcal{X}}_{01}^{{\sigma }_j})$ is a pair of solutions of system (4). Then, the following is true:

$$\begin{array}{cc}\hfill {\mathcal{X}}_{00}^{{\sigma }_j}& ={\left({\mathcal{X}}_{00}^{{\sigma }_j}\right)}^T={\left({\mathcal{X}}_{00}^{j\ast }\right)}^{{\sigma }_j},\hfill \\ \hfill {\mathcal{X}}_{01}^{{\sigma }_j}& ={\left({\mathcal{X}}_{01}^{{\sigma }_j}\right)}^T={\left({\mathcal{X}}_{01}^{j\ast }\right)}^{{\sigma }_j}.\hfill \end{array}$$

According to 7 of Proposition 2 and Definition 7, we obtain the following:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{V}}_M{\ast }_M{\mathcal{A}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{V}}_M{\ast }_M{\mathcal{B}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{00}^{{\sigma }_j},\hfill \\ {\mathcal{V}}_M{\ast }_M{\mathcal{A}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{X}}_{01}^{{\sigma }_j}+{\mathcal{V}}_M{\ast }_M{\mathcal{A}}_{01}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{X}}_{00}^{{\sigma }_j}={\mathcal{V}}_M{\ast }_M{\mathcal{B}}_{01}^{{\sigma }_j},\hfill \\ {\mathcal{X}}_{00}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{01}^{{\sigma }_j}+{\mathcal{X}}_{01}^{{\sigma }_j}{\ast }_N{\mathcal{V}}_N{\ast }_N{\mathcal{C}}_{00}^{{\sigma }_j}={\mathcal{D}}_{01}^{{\sigma }_j},\hfill \end{array}\right.\end{array}$$

(18)

i.e.,

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_{00}{\ast }_N{\mathcal{X}}_{00}={\mathcal{B}}_{00},\hfill \\ {\mathcal{X}}_{00}{\ast }_N{\mathcal{C}}_{00}={\mathcal{D}}_{00},\hfill \\ {\mathcal{A}}_{00}{\ast }_N{\mathcal{X}}_{01}+{\mathcal{A}}_{01}{\ast }_N{\mathcal{X}}_{00}={\mathcal{B}}_{01},\hfill \\ {\mathcal{X}}_{00}{\ast }_N{\mathcal{C}}_{01}+{\mathcal{X}}_{01}{\ast }_N{\mathcal{C}}_{00}={\mathcal{D}}_{01}\hfill \end{array}\right.\end{array}$$

(19)

and

$$\begin{array}{c}\hfill {\mathcal{X}}_{00}={\mathcal{X}}_{00}^{j\ast },{\mathcal{X}}_{01}={\mathcal{X}}_{01}^{j\ast }.\end{array}$$

It is obvious that system (19) and system (2) are equivalent. Consequently, $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ={\mathcal{X}}_{00}^{j\ast }+{\mathcal{X}}_{01}^{j\ast }ϵ={\mathcal{X}}^{j\ast }$ is a j-Hermitian solution of system (2).    □

Based on the above theorems and lemmas, we will next present the equivalent condition when system (2) possesses a Hermitian solution. Additionally, we will put forward the equivalent criteria when two specific equations, $\mathcal{A}{\ast }_N\mathcal{X}=\mathcal{B}$ and $\mathcal{X}{\ast }_M\mathcal{C}=\mathcal{D}$, have solutions, along with their general solution expressions.

Corollary 1.

Let $\mathcal{A}={\mathcal{A}}_{00}+{\mathcal{A}}_{01}ϵ$, $\mathcal{B}={\mathcal{B}}_{00}+{\mathcal{B}}_{01}ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_S}$, $\mathcal{C}={\mathcal{C}}_{00}+{\mathcal{C}}_{01}ϵ$, and $\mathcal{D}={\mathcal{D}}_{00}+{\mathcal{D}}_{01}ϵ\in {\mathbb{DQ}}_s^{K_1\times \cdots \times K_S\times S_1\times \cdots \times S_T}$. Set the following:

$$\begin{array}{cc}\hfill {\mathcal{A}}_0& ={\left({\mathcal{A}}_{00}^i\right)}^{{\sigma }_1},{\mathcal{A}}_1={\left({\mathcal{A}}_{01}^i\right)}^{{\sigma }_1},{\mathcal{B}}_0={\mathcal{B}}_{00}^{{\sigma }_i},{\mathcal{B}}_1={\mathcal{B}}_{01}^{{\sigma }_i},\hfill \\ \hfill {\mathcal{C}}_0& ={\mathcal{C}}_{00}^{{\sigma }_i},{\mathcal{C}}_1={\mathcal{C}}_{01}^{{\sigma }_i},{\mathcal{D}}_0={\mathcal{D}}_{00}^{{\sigma }_1},{\mathcal{D}}_1={\mathcal{D}}_{01}^{{\sigma }_1}.\hfill \end{array}$$

Then, system (2) has a Hermitian solution, $\mathcal{X}={\mathcal{X}}^{\ast }\in {\mathbb{DQ}}_s^{K_1\times \cdots \times K_S\times K_1\times \cdots \times K_S}$, and it means that the following system of real tensor equations has a pair of symmetric solutions $({\mathcal{X}}_0,{\mathcal{X}}_1)$, and vice versa:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{\ast }_S{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{X}}_0{\ast }_S{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{\ast }_S{\mathcal{X}}_1+{\mathcal{A}}_1{\ast }_S{\mathcal{X}}_0={\mathcal{B}}_1,\hfill \\ {\mathcal{X}}_0{\ast }_S{\mathcal{C}}_1+{\mathcal{X}}_1{\ast }_S{\mathcal{C}}_0={\mathcal{D}}_1.\hfill \end{array}\right.\end{array}$$

Corollary 2.

Let $\mathcal{A}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times T_1\times \cdots \times T_N}$ and $\mathcal{B}\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times K_1\times \cdots \times K_S}$, where $\mathcal{A}={\mathcal{A}}_{00}+{\mathcal{A}}_{01}ϵ,\mathcal{B}={\mathcal{B}}_{00}+{\mathcal{B}}_{01}ϵ$. Set the following:

$$\begin{array}{cc}\hfill & {\mathcal{A}}_0={\mathcal{A}}_{00}^{{\sigma }_i},{\mathcal{A}}_1={\mathcal{A}}_{01}^{{\sigma }_i},{\mathcal{B}}_0={\mathcal{B}}_{00}^{{\sigma }_i},{\mathcal{B}}_1={\mathcal{B}}_{01}^{{\sigma }_i},{\mathcal{B}}_2={\mathcal{B}}_1-{\mathcal{A}}_1{\ast }_N{\mathcal{A}}_0^{†}{\ast }_M{\mathcal{B}}_0,\hfill \\ \hfill & {\mathcal{A}}_2={\mathcal{A}}_1{\ast }_N{\mathcal{L}}_{{\mathcal{A}}_0},{\mathcal{A}}_3={\mathcal{R}}_{{\mathcal{A}}_0}{\ast }_M{\mathcal{A}}_2,{\mathcal{C}}_3={\mathcal{R}}_{{\mathcal{A}}_0}{\ast }_M{\mathcal{B}}_2.\hfill \end{array}$$

Then, the subsequent descriptions correspond to each other as follows:

1. 

Dual split quaternion tensor equation $\mathcal{A}{\ast }_N\mathcal{X}=\mathcal{B}$ is solvable.

2. 

The following system of real tensor equations is consistent:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{\ast }_N{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{A}}_0{\ast }_N{\mathcal{X}}_1+{\mathcal{A}}_1{\ast }_N{\mathcal{X}}_0={\mathcal{B}}_1.\hfill \end{array}\right.\end{array}$$

(20)

3. 

${\mathcal{R}}_{{\mathcal{A}}_0}{\ast }_M{\mathcal{B}}_0=0,{\mathcal{R}}_{{\mathcal{A}}_3}{\ast }_M{\mathcal{C}}_3=0$.

Based on these circumstances, the general solution of tensor equation $\mathcal{A}{\ast }_N\mathcal{X}=\mathcal{B}$ is represented as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$, where the following is true:

$$\begin{array}{cc}\hfill & {\mathcal{X}}_{00}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{\ast }_N({\mathcal{X}}_0+{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_0{\ast }_S{\mathcal{T}}_S^T){\ast }_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \\ \hfill & {\mathcal{X}}_{01}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_N& i{\mathcal{I}}_N& j{\mathcal{I}}_N& k{\mathcal{I}}_N\end{array}\right]{\ast }_N({\mathcal{X}}_1+{\mathcal{R}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{R}}_S^T+{\mathcal{S}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{S}}_S^T+{\mathcal{T}}_N{\ast }_N{\mathcal{X}}_1{\ast }_S{\mathcal{T}}_S^T){\ast }_S\left[\begin{array}{c}{\mathcal{I}}_S\\ i{\mathcal{I}}_S\\ j{\mathcal{I}}_S\\ k{\mathcal{I}}_S\end{array}\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mathcal{X}}_0& ={\mathcal{A}}_0^{†}{\ast }_M{\mathcal{B}}_0+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N\mathcal{V},\hfill \\ \hfill {\mathcal{X}}_1& ={\mathcal{A}}_0^{†}{\ast }_M({\mathcal{B}}_2-{\mathcal{A}}_2{\ast }_N\mathcal{V})+{\mathcal{L}}_{{\mathcal{A}}_0}{\ast }_N{\mathcal{V}}_1,\hfill \\ \hfill \mathcal{V}& ={\mathcal{A}}_3^{†}{\ast }_M{\mathcal{C}}_3+{\mathcal{L}}_{{\mathcal{A}}_3}{\ast }_N{\mathcal{V}}_2,\hfill \end{array}$$

and ${\mathcal{V}}_1$ and ${\mathcal{V}}_2$ are arbitrary real tensors with appropriate dimensions.

Corollary 3.

Suppose that $\mathcal{C}={\mathcal{C}}_0+{\mathcal{C}}_1ϵ\in {\mathbb{DQ}}_s^{I_1\times \cdots \times I_M\times J_1\times \cdots \times J_N}$ and $\mathcal{D}={\mathcal{D}}_0+{\mathcal{D}}_1ϵ\in {\mathbb{DQ}}_s^{K_1\times \cdots \times K_T\times J_1\times \cdots \times J_N}$. Let the following be true:

$$\begin{array}{cc}\hfill & {\mathcal{C}}_0={\mathcal{C}}_{00}^{{\sigma }_i},{\mathcal{C}}_1={\mathcal{C}}_{01}^{{\sigma }_i},{\mathcal{D}}_0={\mathcal{D}}_{00}^{{\sigma }_i},{\mathcal{D}}_1={\mathcal{D}}_{01}^{{\sigma }_i},{\mathcal{D}}_2={\mathcal{D}}_1-{\mathcal{D}}_0{\ast }_N{\mathcal{C}}_0^{†}{\ast }_M{\mathcal{C}}_1,\hfill \\ & {\mathcal{C}}_2={\mathcal{R}}_{{\mathcal{C}}_0}{\ast }_M{\mathcal{C}}_1,{\mathcal{B}}_3={\mathcal{C}}_2{\ast }_N{\mathcal{L}}_{{\mathcal{C}}_0},{\mathcal{C}}_3={\mathcal{D}}_2{\ast }_N{\mathcal{L}}_{{\mathcal{C}}_0}.\hfill \end{array}$$

Then, the descriptions below correspond to each other:

1. 

The dual split quaternion tensor equation $\mathcal{X}{\ast }_M\mathcal{C}=\mathcal{D}$ is solvable.

2. 

The following system of real tensor equations is consistent:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{X}}_0{\ast }_M{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{X}}_0{\ast }_M{\mathcal{C}}_1+{\mathcal{X}}_1{\ast }_M{\mathcal{C}}_0={\mathcal{D}}_1.\hfill \end{array}\right.\end{array}$$

(21)

3. 

${\mathcal{D}}_0{\ast }_N{\mathcal{L}}_{{\mathcal{C}}_0}=0,{\mathcal{C}}_3{\ast }_N{\mathcal{L}}_{{\mathcal{B}}_3}=0$.

Based on these situations, the general solution of tensor equation $\mathcal{X}{\ast }_M\mathcal{C}=\mathcal{D}$ can be expressed as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$, where the following is true:

$$\begin{array}{cc}\hfill & {\mathcal{X}}_{00}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_T& i{\mathcal{I}}_T& j{\mathcal{I}}_T& k{\mathcal{I}}_T\end{array}\right]{\ast }_T({\mathcal{X}}_0+{\mathcal{R}}_T{\ast }_T{\mathcal{X}}_0{\ast }_M{\mathcal{R}}_M^T+{\mathcal{S}}_T{\ast }_T{\mathcal{X}}_0{\ast }_M{\mathcal{S}}_M^T+{\mathcal{T}}_T{\ast }_T{\mathcal{X}}_0{\ast }_M{\mathcal{T}}_M^T){\ast }_M\left[\begin{array}{c}{\mathcal{I}}_M\\ i{\mathcal{I}}_M\\ j{\mathcal{I}}_M\\ k{\mathcal{I}}_M\end{array}\right],\hfill \\ \hfill & {\mathcal{X}}_{01}={\displaystyle \frac{1}{8}}\left[\begin{array}{cccc}{\mathcal{I}}_T& i{\mathcal{I}}_T& j{\mathcal{I}}_T& k{\mathcal{I}}_T\end{array}\right]{\ast }_T({\mathcal{X}}_1+{\mathcal{R}}_T{\ast }_T{\mathcal{X}}_1{\ast }_M{\mathcal{R}}_M^T+{\mathcal{S}}_T{\ast }_T{\mathcal{X}}_1{\ast }_M{\mathcal{S}}_M^T+{\mathcal{T}}_T{\ast }_T{\mathcal{X}}_1{\ast }_M{\mathcal{T}}_M^T){\ast }_M\left[\begin{array}{c}{\mathcal{I}}_M\\ i{\mathcal{I}}_M\\ j{\mathcal{I}}_M\\ k{\mathcal{I}}_M\end{array}\right],\hfill \end{array}$$

where

$$\begin{array}{cc}\hfill {\mathcal{X}}_0& ={\mathcal{D}}_0{\ast }_N{\mathcal{C}}_0^{†}+\mathcal{W}{\ast }_M{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill {\mathcal{X}}_1& =({\mathcal{D}}_2-\mathcal{W}{\ast }_M{\mathcal{C}}_2){\ast }_N{\mathcal{C}}_0^{†}+{\mathcal{W}}_1{\ast }_M{\mathcal{R}}_{{\mathcal{C}}_0},\hfill \\ \hfill \mathcal{W}& ={\mathcal{C}}_3{\ast }_N{\mathcal{B}}_3^{†}+{\mathcal{W}}_2{\ast }_M{\mathcal{R}}_{{\mathcal{B}}_3},\hfill \end{array}$$

and ${\mathcal{W}}_1$ and ${\mathcal{W}}_2$ denote random tensors over $\mathcal{R}$ with suitable dimensions.

4. Numerical Example

This segment will give an example to substantiate Theorem 1 and an example as an application of Theorem 1.

Example 2.

Let $\mathcal{A}={\mathcal{A}}_{00}+{\mathcal{A}}_{01}ϵ$, $B=B_{00}+B_{01}ϵ$, $\mathcal{C}={\mathcal{C}}_{00}+{\mathcal{C}}_{01}ϵ$, and $\mathcal{D}={\mathcal{D}}_{00}+{\mathcal{D}}_{01}ϵ$, where the following is true:

$$\begin{array}{cc}\hfill & {\left({\mathcal{A}}_{00}\right)}_{1111}=i,{\left({\mathcal{A}}_{00}\right)}_{1121}=j,{\left({\mathcal{A}}_{00}\right)}_{1112}=k,{\left({\mathcal{A}}_{00}\right)}_{1122}=1,\hfill \\ \hfill & {\left({\mathcal{A}}_{00}\right)}_{2111}=0,{\left({\mathcal{A}}_{00}\right)}_{2121}=k,{\left({\mathcal{A}}_{00}\right)}_{2112}=i,{\left({\mathcal{A}}_{00}\right)}_{2122}=i+j,\hfill \\ \hfill & {\left({\mathcal{A}}_{00}\right)}_{1211}=-i,{\left({\mathcal{A}}_{00}\right)}_{1221}=1,{\left({\mathcal{A}}_{00}\right)}_{1212}=0,{\left({\mathcal{A}}_{00}\right)}_{1222}=j,\hfill \\ \hfill & {\left({\mathcal{A}}_{00}\right)}_{2211}=0,{\left({\mathcal{A}}_{00}\right)}_{2221}=i,{\left({\mathcal{A}}_{00}\right)}_{2212}=j,{\left({\mathcal{A}}_{00}\right)}_{2222}=1,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{A}}_{01}\right)}_{1111}=j,{\left({\mathcal{A}}_{01}\right)}_{1121}=k,{\left({\mathcal{A}}_{01}\right)}_{1112}=i,{\left({\mathcal{A}}_{01}\right)}_{1122}=0,\hfill \\ \hfill & {\left({\mathcal{A}}_{01}\right)}_{2111}=1+j,{\left({\mathcal{A}}_{01}\right)}_{2121}=i-k,{\left({\mathcal{A}}_{01}\right)}_{2112}=0,{\left({\mathcal{A}}_{01}\right)}_{2122}=j\hfill \\ \hfill & {\left({\mathcal{A}}_{01}\right)}_{1211}=i,{\left({\mathcal{A}}_{01}\right)}_{1221}=i-2k,{\left({\mathcal{A}}_{01}\right)}_{1212}=1,{\left({\mathcal{A}}_{01}\right)}_{1222}=j,\hfill \\ \hfill & {\left({\mathcal{A}}_{01}\right)}_{2211}=2,{\left({\mathcal{A}}_{01}\right)}_{2221}=i,{\left({\mathcal{A}}_{01}\right)}_{2212}=j,{\left({\mathcal{A}}_{01}\right)}_{2222}=k\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{B}}_{00}\right)}_{1111}=1,{\left({\mathcal{B}}_{00}\right)}_{1121}=-1,{\left({\mathcal{B}}_{00}\right)}_{1112}=j,{\left({\mathcal{B}}_{00}\right)}_{1122}=i,\hfill \\ \hfill & {\left({\mathcal{B}}_{00}\right)}_{2111}=0,{\left({\mathcal{B}}_{00}\right)}_{2121}=1,{\left({\mathcal{B}}_{00}\right)}_{2112}=-1-i-k,{\left({\mathcal{B}}_{00}\right)}_{2122}=0,\hfill \\ \hfill & {\left({\mathcal{B}}_{00}\right)}_{1211}=j-k,{\left({\mathcal{B}}_{00}\right)}_{1221}=1,{\left({\mathcal{B}}_{00}\right)}_{1212}=-i,{\left({\mathcal{B}}_{00}\right)}_{1222}=0,\hfill \\ \hfill & {\left({\mathcal{B}}_{00}\right)}_{2211}=-j+k,{\left({\mathcal{B}}_{00}\right)}_{2221}=-i+j,{\left({\mathcal{B}}_{00}\right)}_{2212}=-2,{\left({\mathcal{B}}_{00}\right)}_{2222}=1+i-j,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{B}}_{01}\right)}_{1111}=1-j,{\left({\mathcal{B}}_{01}\right)}_{1121}=-k,{\left({\mathcal{B}}_{01}\right)}_{1112}=-1+2j-k,{\left({\mathcal{B}}_{01}\right)}_{1122}=1+i-j+k,\hfill \\ \hfill & {\left({\mathcal{B}}_{01}\right)}_{2111}=1-i+j,{\left({\mathcal{B}}_{01}\right)}_{2121}=1,{\left({\mathcal{B}}_{01}\right)}_{2112}=i+2j,{\left({\mathcal{B}}_{01}\right)}_{2122}=-1-j-k,\hfill \\ \hfill & {\left({\mathcal{B}}_{01}\right)}_{1211}=-2-3i+3k,{\left({\mathcal{B}}_{01}\right)}_{1221}=-i+2k,{\left({\mathcal{B}}_{01}\right)}_{1212}=i-j,{\left({\mathcal{B}}_{01}\right)}_{1222}=-3-k,\hfill \\ \hfill & {\left({\mathcal{B}}_{01}\right)}_{2211}=-j+k,{\left({\mathcal{B}}_{01}\right)}_{2221}=-1+2i+j+k,{\left({\mathcal{B}}_{01}\right)}_{2212}=2+i,{\left({\mathcal{B}}_{01}\right)}_{2222}=2-i,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{C}}_{00}\right)}_{1111}=k,{\left({\mathcal{C}}_{00}\right)}_{1121}=0,{\left({\mathcal{C}}_{00}\right)}_{1112}=i,{\left({\mathcal{C}}_{00}\right)}_{1122}=1+j,\hfill \\ \hfill & {\left({\mathcal{C}}_{00}\right)}_{2111}=1,{\left({\mathcal{C}}_{00}\right)}_{2121}=j,{\left({\mathcal{C}}_{00}\right)}_{2112}=i-k,{\left({\mathcal{C}}_{00}\right)}_{2122}=i,\hfill \\ \hfill & {\left({\mathcal{C}}_{00}\right)}_{1211}=j,{\left({\mathcal{C}}_{00}\right)}_{1221}=-k,{\left({\mathcal{C}}_{00}\right)}_{1212}=0,{\left({\mathcal{C}}_{00}\right)}_{1222}=i,\hfill \\ \hfill & {\left({\mathcal{C}}_{00}\right)}_{2211}=1+i,{\left({\mathcal{C}}_{00}\right)}_{2221}=1,{\left({\mathcal{C}}_{00}\right)}_{2212}=-j,{\left({\mathcal{C}}_{00}\right)}_{2222}=k,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{C}}_{01}\right)}_{1111}=0,{\left({\mathcal{C}}_{01}\right)}_{1121}=i,{\left({\mathcal{C}}_{01}\right)}_{1112}=-k,{\left({\mathcal{C}}_{01}\right)}_{1122}=1,\hfill \\ \hfill & {\left({\mathcal{C}}_{01}\right)}_{2111}=j,{\left({\mathcal{C}}_{01}\right)}_{2121}=2,{\left({\mathcal{C}}_{01}\right)}_{2112}=-i,{\left({\mathcal{C}}_{01}\right)}_{2122}=0,\hfill \\ \hfill & {\left({\mathcal{C}}_{01}\right)}_{1211}=k,{\left({\mathcal{C}}_{01}\right)}_{1221}=i,{\left({\mathcal{C}}_{01}\right)}_{1212}=j,{\left({\mathcal{C}}_{01}\right)}_{1222}=-k,\hfill \\ \hfill & {\left({\mathcal{C}}_{01}\right)}_{2211}=1,{\left({\mathcal{C}}_{01}\right)}_{2221}=k,{\left({\mathcal{C}}_{01}\right)}_{2212}=0,{\left({\mathcal{C}}_{01}\right)}_{2222}=j,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{D}}_{00}\right)}_{1111}=j,{\left({\mathcal{D}}_{00}\right)}_{1121}=0,{\left({\mathcal{D}}_{00}\right)}_{1112}=-1+j-k,{\left({\mathcal{D}}_{00}\right)}_{1122}=i+j,\hfill \\ \hfill & {\left({\mathcal{D}}_{00}\right)}_{2111}=-1-i+j+2k,{\left({\mathcal{D}}_{00}\right)}_{2121}=k,{\left({\mathcal{D}}_{00}\right)}_{2112}=-2i,\hfill \\ \hfill & {\left({\mathcal{D}}_{00}\right)}_{2122}=1-i+j,{\left({\mathcal{D}}_{00}\right)}_{1211}=-1+j-k,{\left({\mathcal{D}}_{00}\right)}_{1221}=-i+2j,\hfill \\ \hfill & {\left({\mathcal{D}}_{00}\right)}_{1212}=-1-i,{\left({\mathcal{D}}_{00}\right)}_{1222}=-2-i-j+k,{\left({\mathcal{D}}_{00}\right)}_{2211}=-1+2i+j,\hfill \\ \hfill & {\left({\mathcal{D}}_{00}\right)}_{2221}=i,{\left({\mathcal{D}}_{00}\right)}_{2212}=i-2k,{\left({\mathcal{D}}_{00}\right)}_{2222}=-k,\hfill \end{array}$$

$$\begin{array}{cc}\hfill & {\left({\mathcal{D}}_{01}\right)}_{1111}=4k,{\left({\mathcal{D}}_{01}\right)}_{1121}=3i+j-k,{\left({\mathcal{D}}_{01}\right)}_{1112}=1+2i+j,{\left({\mathcal{D}}_{01}\right)}_{1122}=2j-k,\hfill \\ \hfill & {\left({\mathcal{D}}_{01}\right)}_{2111}=1+k-2j,{\left({\mathcal{D}}_{01}\right)}_{2121}=-3+i,{\left({\mathcal{D}}_{01}\right)}_{2112}=-1+2i+3j+k,\hfill \\ \hfill & {\left({\mathcal{D}}_{01}\right)}_{2122}=-1+2i+2j-k,{\left({\mathcal{D}}_{01}\right)}_{1211}=1+j-k,{\left({\mathcal{D}}_{01}\right)}_{1221}=-2i+2j+k,\hfill \\ \hfill & {\left({\mathcal{D}}_{01}\right)}_{1212}=-2+i+k,{\left({\mathcal{D}}_{01}\right)}_{1222}=-i,{\left({\mathcal{D}}_{01}\right)}_{2211}=2+2i+j+k,\hfill \\ \hfill & {\left({\mathcal{D}}_{01}\right)}_{2221}=i+2j-k,{\left({\mathcal{D}}_{01}\right)}_{2212}=-1+i+j+2k,{\left({\mathcal{D}}_{01}\right)}_{2222}=-2+i+k.\hfill \end{array}$$

Using MATLAB 7.0, it can be proven that part (3) of Theorem (1) in this paper holds, as follows:

$$\begin{array}{cc}\hfill & {\mathcal{R}}_{{\mathcal{A}}_0}{\ast }_M{\mathcal{B}}_0=0,{\mathcal{D}}_0{\ast }_T{\mathcal{L}}_{{\mathcal{C}}_0}=0,{\mathcal{R}}_{{\mathcal{A}}_2}{\ast }_M{\mathcal{C}}_2=0,{\mathcal{C}}_2{\ast }_S{\mathcal{L}}_{{\mathcal{B}}_2}=0,\hfill \\ \hfill & {\mathcal{R}}_{{\mathcal{A}}_3}{\ast }_N{\mathcal{C}}_3=0,{\mathcal{C}}_3{\ast }_T{\mathcal{L}}_{{\mathcal{B}}_3}=0,{\mathcal{R}}_{{\mathcal{A}}_4}{\ast }_N{\mathcal{C}}_4{\ast }_T{\mathcal{L}}_{{\mathcal{B}}_4}=0,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & t\left({\mathcal{A}}_0{\ast }_N{\mathcal{D}}_0\right)=t\left({\mathcal{B}}_0{\ast }_S{\mathcal{C}}_0\right)=\hfill \\ \hfill & \left[\begin{array}{cccccccccccccccc}-1& 0& 0& 1& 1& 2& 0& -1& 0& -1& 0& 0& 1& 0& 0& -1\\ 1& 1& 0& 1& -1& 0& 1& 0& -1& 0& 0& -1& -1& 1& -1& 0\\ 0& 0& 0& 2& -1& 0& 1& 0& 0& 0& -1& 1& -1& 0& -2& -1\\ 1& 2& 2& 0& 2& 1& 1& 0& -2& -1& -1& -2& 1& 1& -1& 1\\ -1& -2& 0& 1& -1& 0& 0& 1& -1& 0& 0& 1& 0& -1& 0& 0\\ 1& 0& -1& 0& 1& 1& 0& 1& 1& -1& 1& 0& -1& 0& 0& -1\\ 1& 0& -1& 0& 0& 0& 0& 2& 1& 0& 2& 1& 0& 0& -1& 1\\ -2& -1& -1& 0& 1& 2& 2& 0& -1& -1& 1& -1& -2& -1& -1& -2\\ 0& -1& 0& 0& -1& 0& 0& 1& -1& 0& 0& 1& -1& -2& 0& 1\\ -1& 0& 0& -1& 1& -1& 1& 0& 1& 1& 0& 1& 1& 0& -1& 0\\ 0& 0& -1& 1& 1& 0& 2& 1& 0& 0& 0& 2& 1& 0& -1& 0\\ -2& -1& -1& -2& -1& -1& 1& -1& 1& 2& 2& 0& -2& -1& -1& 0\\ 1& 0& 0& -1& 0& -1& 0& 0& 1& 2& 0& -1& -1& 0& 0& 1\\ -1& 1& -1& 0& -1& 0& 0& -1& -1& 0& 1& 0& 1& 1& 0& 1\\ -1& 0& -2& -1& 0& 0& -1& 1& -1& 0& 1& 0& 0& 0& 0& 2\\ 1& 1& -1& 1& -2& -1& -1& -2& 2& 1& 1& 0& 1& 2& 2& 0\end{array}\right],\hfill \end{array}$$

$$\begin{array}{cc}\hfill & t({\mathcal{A}}_0{\ast }_N{\mathcal{D}}_1-{\mathcal{B}}_0{\ast }_S{\mathcal{C}}_1)=t({\mathcal{B}}_1{\ast }_S{\mathcal{C}}_0-{\mathcal{A}}_1{\ast }_N{\mathcal{D}}_0)=\hfill \\ \hfill & \left[\begin{array}{cccccccccccccccc}-1& 0& 0& -1& 2& 2& 0& 1& -1& -1& 1& -1& 2& 0& 0& 0\\ 1& 0& 0& -2& 0& 2& 0& -1& 0& 2& -1& 0& 2& 0& 0& -3\\ 2& -1& 1& -1& -1& 2& -1& 1& 2& 0& 2& -1& -1& -1& 0& -3\\ 1& 1& -1& -3& 3& 0& 0& 0& 2& 0& 0& 1& 2& -1& 3& 0\\ -2& -2& 0& -1& -1& 0& 0& -1& -2& 0& 0& 0& -1& -1& 1& -1\\ 0& -2& 0& 1& 1& 0& 0& -2& -2& 0& 0& 3& 0& 2& -1& 0\\ 1& -2& 1& -1& 2& -1& 1& -1& 1& 1& 0& 3& 2& 0& 2& -1\\ -3& 0& 0& 0& 1& 1& -1& -3& -2& 1& -3& 0& 2& 0& 0& 1\\ -1& -1& 1& -1& -2& 0& 0& 0& -1& 0& 0& -1& -2& -2& 0& -1\\ 0& 2& -1& 0& -2& 0& 0& 3& 1& 0& 0& -2& 0& -2& 0& 1\\ 2& 0& 2& -1& 1& 1& 0& 3& 2& -1& 1& -1& 1& -2& 1& -1\\ 2& 0& 0& 1& -2& 1& -3& 0& 1& 1& -1& -3& -3& 0& 0& 0\\ 2& 0& 0& 0& -1& -1& 1& -1& 2& 2& 0& 1& -1& 0& 0& -1\\ 2& 0& 0& -3& 0& 2& -1& 0& 0& 2& 0& -1& 1& 0& 0& -2\\ -1& -1& 0& -3& 2& 0& 2& -1& -1& 2& -1& 1& 2& -1& 1& -1\\ 2& -1& 3& 0& 2& 0& 0& 1& 3& 0& 0& 0& 1& 1& -1& -3\end{array}\right],\hfill \end{array}$$

i.e.,

$${\mathcal{A}}_0{\ast }_N{\mathcal{D}}_0={\mathcal{B}}_0{\ast }_S{\mathcal{C}}_0,{\mathcal{A}}_0{\ast }_N{\mathcal{D}}_1-{\mathcal{B}}_0{\ast }_S{\mathcal{C}}_1={\mathcal{B}}_1{\ast }_S{\mathcal{C}}_0-{\mathcal{A}}_1{\ast }_N{\mathcal{D}}_0.$$

Then, it can be deduced that the system of dual split quaternion tensor Equation (2) is solvable, and a solution for this system can be expressed as $\mathcal{X}={\mathcal{X}}_{00}+{\mathcal{X}}_{01}ϵ$, as follows:

$$\begin{array}{cc}\hfill & {\left({\mathcal{X}}_{00}\right)}_{1111}=j,{\left({\mathcal{X}}_{00}\right)}_{1121}=i,{\left({\mathcal{X}}_{00}\right)}_{1112}=1,{\left({\mathcal{X}}_{00}\right)}_{1122}=0,\hfill \\ \hfill & {\left({\mathcal{X}}_{00}\right)}_{2111}=j,{\left({\mathcal{X}}_{00}\right)}_{2121}=-1,{\left({\mathcal{X}}_{00}\right)}_{2112}=i,{\left({\mathcal{X}}_{00}\right)}_{2122}=k,\hfill \\ \hfill & {\left({\mathcal{X}}_{00}\right)}_{1211}=-1,{\left({\mathcal{X}}_{00}\right)}_{1221}=0,{\left({\mathcal{X}}_{00}\right)}_{1212}=i-j,{\left({\mathcal{X}}_{00}\right)}_{1222}=j,\hfill \\ \hfill & {\left({\mathcal{X}}_{00}\right)}_{2211}=0,{\left({\mathcal{X}}_{00}\right)}_{2221}=j,{\left({\mathcal{X}}_{00}\right)}_{2212}=k,{\left({\mathcal{X}}_{00}\right)}_{2222}=i,\hfill \end{array}$$

and

$$\begin{array}{cc}\hfill & {\left({\mathcal{X}}_{01}\right)}_{1111}=1,{\left({\mathcal{X}}_{01}\right)}_{1121}=0,{\left({\mathcal{X}}_{01}\right)}_{1112}=i,{\left({\mathcal{X}}_{01}\right)}_{1122}=0,\hfill \\ \hfill & {\left({\mathcal{X}}_{01}\right)}_{2111}=k,{\left({\mathcal{X}}_{01}\right)}_{2121}=i,{\left({\mathcal{X}}_{01}\right)}_{2112}=j,{\left({\mathcal{X}}_{01}\right)}_{2122}=-1,\hfill \\ \hfill & {\left({\mathcal{X}}_{01}\right)}_{1211}=0,{\left({\mathcal{X}}_{01}\right)}_{1221}=1,{\left({\mathcal{X}}_{01}\right)}_{1212}=-k,{\left({\mathcal{X}}_{01}\right)}_{1222}=j,\hfill \\ \hfill & {\left({\mathcal{X}}_{01}\right)}_{2211}=-j,{\left({\mathcal{X}}_{01}\right)}_{2221}=k,{\left({\mathcal{X}}_{01}\right)}_{2212}=1,{\left({\mathcal{X}}_{01}\right)}_{2222}=0.\hfill \end{array}$$

Example 3.

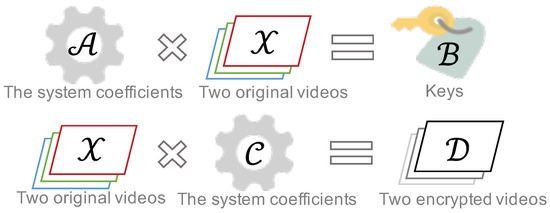
In this section, we propose a method for video encryption and decryption using Theorem 1 and provide a specific example to demonstrate this method.

Similar to quaternions [6], it has been demonstrated that split quaternions can represent color images [41]. Split quaternion tensors can represent color videos, as long as the video is segmented into multiple image slices. Therefore, the dual split quaternion tensor can represent two color videos.

We can encrypt two color videos through system (2), and the following model is the encryption process based on system (2) (Figure 1):

Figure 1. The model for encrypting two videos.

It is clear that system (2) and the following system are equivalent, so we can use system (22) to encrypt and decrypt videos.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{A}}_0{\ast }_S{\mathcal{X}}_0={\mathcal{B}}_0,\hfill \\ {\mathcal{X}}_0{\ast }_S{\mathcal{C}}_0={\mathcal{D}}_0,\hfill \\ {\mathcal{A}}_0{\ast }_S{\mathcal{X}}_1+{\mathcal{A}}_1{\ast }_S{\mathcal{X}}_0={\mathcal{B}}_1,\hfill \\ {\mathcal{X}}_0{\ast }_S{\mathcal{C}}_1+{\mathcal{X}}_1{\ast }_S{\mathcal{C}}_0={\mathcal{D}}_1\hfill \end{array}\right.\end{array}$$

(22)

We use two original videos, ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$, each composed of 51 slices of color images, which are $540\times 540$ pixels in size, denoted by ${\mathbb{H}}_s^{540\times 540\times 51}$ [42]. That is, $\mathcal{X}={\mathcal{X}}_0+{\mathcal{X}}_1ϵ\in {\mathbb{DQ}}_s^{540\times 540\times 51}$. $\mathcal{A}={\mathcal{A}}_0+{\mathcal{A}}_1ϵ$ and $\mathcal{C}={\mathcal{C}}_0+{\mathcal{C}}_1ϵ\in {\mathbb{DQ}}_s^{540\times 540}$ are the system coefficients. For simplicity, we select all ${\mathcal{A}}_0$, ${\mathcal{A}}_1$, ${\mathcal{C}}_0$, and ${\mathcal{C}}_1$ as real matrices, and they are invertible. Furthermore, we use ${\mathcal{B}}_0$ and ${\mathcal{B}}_1\in {\mathbb{H}}_s^{540\times 540\times 51}$ to denote the keys. ${\mathcal{D}}_0$ and ${\mathcal{D}}_1\in {\mathbb{H}}_s^{540\times 540\times 51}$ represent two encrypted videos. The process of encryption is described below (Algorithm 1):

Algorithm 1 Encryption process

1: Input: Two original videos and system coefficients. 2: Let ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$ represent the first original video and the second original video. Then, $X_{0i}$ and $X_{1i}$ represent ith slice of video ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$, where $i=1,\cdots ,51$. The system coefficients are ${\mathcal{A}}_0$, ${\mathcal{A}}_1$, ${\mathcal{C}}_0$, and ${\mathcal{C}}_1$. 3: Encrypt ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$ using system (22). 4: ${\mathcal{B}}_{0i}$ and ${\mathcal{B}}_{1i}$ denote keys. ${\mathcal{D}}_{0i}$ and ${\mathcal{D}}_{1i}$ represent ith slice of the two encrypted videos, where $i=1,\cdots ,51$. So, we have obtained two encrypted videos, ${\mathcal{D}}_0$ and ${\mathcal{D}}_1$. 5: Output: Two encrypted videos and keys.

For the decryption process, we use two encrypted videos, ${\mathcal{D}}_0$ and ${\mathcal{D}}_1$, obtained from the encryption process, along with keys ${\mathcal{B}}_0$ and ${\mathcal{B}}_1$, as well as the system coefficients ${\mathcal{A}}_0$, ${\mathcal{A}}_1$, ${\mathcal{C}}_0$, and ${\mathcal{C}}_1$, to recover the two original color videos. The decryption algorithm is represented as follows (Algorithm 2):

Algorithm 2 Decryption process

1: Input: System coefficients, keys, and two encrypted videos. 2: ${\mathcal{B}}_0$ and ${\mathcal{B}}_1$ represent the keys. ${\mathcal{D}}_0$ and ${\mathcal{D}}_1$ denote the encrypted videos. ${\mathcal{A}}_0$, ${\mathcal{A}}_1$, ${\mathcal{C}}_0$, and ${\mathcal{C}}_1$ are the system coefficients and they are reversible. 3: Using the real representation, we obtain ${\mathcal{A}}_p^{{\sigma }_i}$, ${\mathcal{B}}_p^{{\sigma }_i}$, ${\mathcal{C}}_p^{{\sigma }_i}$, and ${\mathcal{D}}_p^{{\sigma }_i}$, where $p=1,2$. 4: Using Theorem (1), we obtain ${\mathcal{XD}}_0$ and ${\mathcal{XD}}_1$. 5: Convert ${\mathcal{XD}}_0$ and ${\mathcal{XD}}_1$ into ${\mathcal{XD}}_{00}$ and ${\mathcal{XD}}_{01}$ using Theorem (1), respectively. 6: The two decrypted videos are ${\mathcal{XD}}_{00}$ and ${\mathcal{XD}}_{01}$, respectively. 7: Output: Two decrypted videos.

The encryption’s CPU time is 59.2300 s and the decryption’s CPU time is 145.9600 s. The figure below illustrates a portion of slices from the encrypted and decrypted videos’ results (Figure 2).

Figure 2. The original, encrypted, and decrypted images of randomly selected slices from color videos ${\mathcal{X}}_0$ and ${\mathcal{X}}_1$.

To assess the quality of the encryption and decryption algorithm for color videos, we utilize the peak signal-to-noise ratio (PSNR), the structural similarity index measure (SSIM) and the feature similarity index measure (FSIM), the results of which are presented in Table 1 and Table 2. A higher PSNR value usually indicates smaller errors, meaning that the quality of the processed image is higher. The results show that the PSNR values are all greater than 30 and that all SSIM and FSIM values are equal to 1, indicating a high degree of similarity between the decrypted videos and the original videos. This further demonstrates the effectiveness of our encryption and decryption algorithms.

Table 1. PSNR, SSIM, and FSIM of Video 1.

Video 1	PSNR	SSIM	FSIM
1	279.8545	1	1
2	280.0351	1	1
3	279.8906	1	1
4	279.4681	1	1

Table 2. PSNR, SSIM, and FSIM of Video 2.

Video 2	PSNR	SSIM	FSIM
1	248.0390	1	1
2	248.2462	1	1
3	247.9977	1	1
4	246.5033	1	1

5. Conclusions

We use the real representations of split quaternions to simplify the system of dual split quaternion tensor equations $(\mathcal{A}{\ast }_N\mathcal{X},\mathcal{X}{\ast }_S\mathcal{C})=(\mathcal{B},\mathcal{D})$ into real tensor equations. Based on this, we put forward the equivalent conditions for this system’s solvability and the general expression of solutions. Subsequently, this proposed theorem is applied to two specific cases of dual split quaternion tensor equations. Furthermore, the paper presents the equivalent conditions when the Hermitian solution (denoted as $\mathcal{X}={\mathcal{X}}^{\ast }$) and $\eta$-Hermitian solutions (denoted as $\mathcal{X}={\mathcal{X}}^{\eta \ast }$) of system (2) exist, using various real representations. Additionally, we provide a numerical example using MATLAB to validate the correctness of the key theorem presented in this paper. Finally, we use Theorem 1 to present a method for encrypting and decrypting two color videos, along with a specific example. The algorithm’s efficacy is demonstrated by PSNR, SSIM, and FSIM.