Abstract
In this paper, we study a novel static bike-sharing repositioning problem. There is a set of stations spread over a given area, each containing a number of operative bikes, damaged bikes, and free slots. The customers may pick up an operative bike from a station, use it, and return it to another station. Each station should have a target number of operative bikes to make it likely to meet customer demands. Furthermore, the damaged bikes should be removed from the stations. Given a fleet of available vehicles, the repositioning problem consists of designing the vehicles’ routes and calculating the number of operative (usable) and damaged (unusable) bikes that will be moved (loading instructions/loading policy) between stations and/or the depot. The objective is to minimize the weighted sum of the deviation from the target number of bikes for each station, the number of damaged bikes not removed, and the total time used by vehicles. To solve this problem, we propose a matheuristic based on a variable neighborhood search combined with several improving algorithms, including an integer linear programming model to optimize loading instructions. The algorithm was tested in instances based on real-world data and could find good solutions in reasonable computing times.
Keywords:
vehicle routing problem; static bike-sharing repositioning problem; matheuristic based on variable neighborhood search MSC:
90B06
1. Introduction
public bike-sharing systems (PBSs) have become a sustainable mobility model that has attracted significant interest worldwide. These were first introduced in Amsterdam in 1965 [1], and the number of cities with PBSs has grown rapidly since then due to the reduction of the users’ environmental impact and the lower usage costs compared to other means of transportation. According to the consultancy PBSC Urban Solutions [2], as of August 2021, there were nearly 10 million shared bikes and 3000 bike-sharing systems worldwide.
There are two primary categories within PBSs. The first category is the station-based bike-sharing system (SBBS), allowing users to rent bicycles at fixed stations and return them to the same station or any other designated station after usage [1]. SBBSs were first introduced in Denmark in 1991 [3]. The second category is the free-floating bike-sharing systems (FFBSs), where bicycles can be conveniently picked up and returned anywhere according to the users’ preferences [4]. In these systems, there may be no fixed stations. The FFBSs were first introduced in China in 2016 [5]. This study focuses on the station-based bike-sharing system.
In the SBBS category, a user takes a bike from one fixed station, uses it, and returns it to another station from the system. Each station has a number of bike parking slots, some of which may be empty or occupied by operational or damaged bikes. During the day, some stations may not have operative bikes or free slots to park, preventing the correct service use. In order to avoid these situations, a fleet of vehicles is used to move bikes between the stations (and also the depot) to approximate the inventory levels of the stations to their desired (or target) levels. Finding good strategies for this process constitutes the so-called bike-sharing repositioning problem (BRP). An example of such a situation is shown in Figure 1.
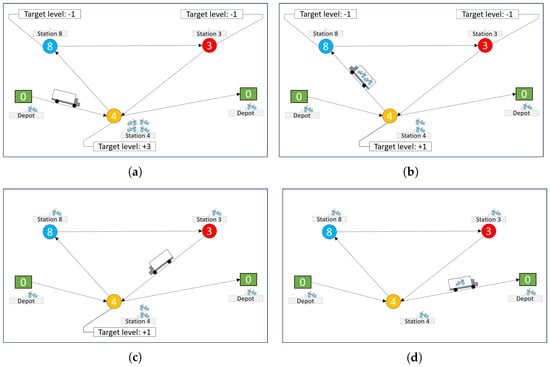
Figure 1.
The example illustrates a BRP where a truck with a maximum capacity of 2 bikes must complete the tour (0, 4, 8, 3, 4, 0). Part (a) shows the target levels for stations 4, 8, and 3, as +3, -1, -1, respectively. Station 4 has a surplus (+) of 3 bikes, leaving no free parking slots and preventing customers from completing their trips. At stations 8 and 3, there is a deficit (-) of 1 bike each, meaning no operational bikes are available for customers. In part (b), the truck picks up 2 bikes from station 4 (partially balancing it) and then moves to stations 8 and 3, delivering 1 bike to each and balancing it. Part (c) shows the truck returning to station 4 to pick up the remaining bike and completely balance it. Finally, in part (d), the truck heads back to the depot to complete the tour and unload the bikes.
According to DeMaio [3], a good system of repositioning (or redistribution) must be present in a successful bike-sharing program. Recently, some SBBSs used incentives that persuade the customers to move bikes in such a way as to reduce the imbalance of the stations (see, for example, Haider et al. [6]), although this strategy may have to be combined with the use of a fleet of trucks to balance the stations completely.
The BRP implies two main decisions: (1) Designing the routes that vehicles must follow to visit the stations from the depot. (2) Deciding the number of bikes to be picked up or delivered at each station. This is called the loading policy (or loading instructions).
Furthermore, there are two types of bike-sharing repositioning problems: The dynamic and static. In the first one, the redistribution is carried out while the users are using the system (e.g., during the day). Therefore, the inventory levels of the stations change continuously. In the dynamic case, the operation is linked to the redistributions conducted during peak system usage throughout the day, causing the stations’ demands to change during the redistribution period. In the second case, the operation is performed when the demand is low or the system is closed (e.g., at night). Hence, the state of the stations changes only as a result of the repositioning process. Both types of repositioning are evident in real-world scenarios. However, the predominant focus in the literature is on the static case, which is already acknowledged as a challenging problem. For instance, Chemla et al. [7] show that a simple variant of the static-BRP is NP-hard.
1.1. Main Contributions of the Paper
As shown in Figure 2. this study focuses on the static bike-sharing repositioning problem (s-BRP) variant in station-based bike-sharing systems (SBBSs).
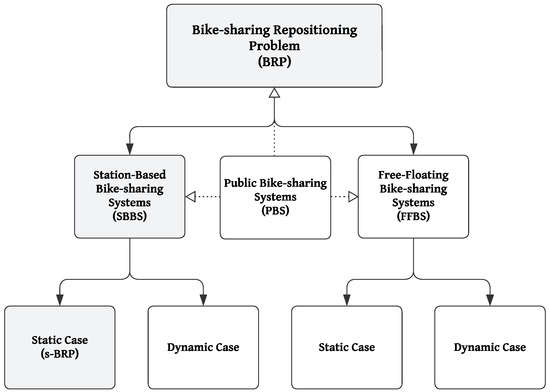
Figure 2.
The concept map highlights in gray the type of problem to which this study belongs.
This paper contributes significantly to the literature in the following ways:
- Introducing a novel s-BRP in SBBSs, this paper considers operational and damaged bikes and multiple visits to the depot and stations. It utilizes a heterogeneous fleet to implement a joint repositioning strategy, enabling the simultaneous movement (pick-up and delivery) of operational (usable) and damaged (unusable) bikes between stations and the depot.
- Designing a new arc flow formulation to model the novel static bike-sharing repositioning problem variant in the station-based bike-sharing systems proposed in this paper.
- Proposing two innovative approaches to optimize the number of bikes to be moved for each visit (loading instructions). The first is a heuristic approach, where we design two heuristic methods to compute the loading policy given the sequence of visits. Additionally, a second mathematical programming-based approach is proposed, in which we formulate the problem of finding the optimal loading instructions as an integer linear programming (ILP) model.
- Presenting an effective matheuristic based on a variable neighborhood search combined with several improving and perturbation algorithms, including an integer linear programming model to optimize loading policy.
The proposed matheuristic approach addresses the pressing operational challenges in public bike-sharing systems (PBSs); for instance, in the Bogotá bike-sharing system (Colombia), which serves a city of over 15 million residents with approximately 300 stations, 3450 bikes, and 40,000 weekly trips. Despite its popularity, the system faces significant logistical issues as up to 47% of bikes can be reported damaged daily, creating bottlenecks for users and operators. This situation is further complicated by the system’s limited repair infrastructure, consisting of only one maintenance shop, making efficient repositioning and timely maintenance crucial. The novel algorithmic solution proposed in this study introduces a targeted and adaptable approach to optimizing the static bike-sharing repositioning problem within station-based bike-sharing systems, demonstrating high practicality and the potential for widespread applicability across similar urban systems in Latin America and globally.
1.2. The Outline of the Paper
The remainder of the paper is organized as follows: Section 2 provides the state of the art literature review. Section 3 describes the research problem and arc flow formulation proposed. Section 4 presents a constructive heuristic approach designed to build the initial solution. Section 5 describes two procedures to optimize loading instructions: one heuristic approach and one mathematical formulation-based approach. Section 6 provides the general scheme of the proposed matheuristic algorithm and several improvement moves and perturbation mechanisms. In Section 7, we introduce the set of instances based on the real-world data used in this study and report the results of our computational evaluation. Finally, the conclusions are presented in Section 8.
2. Literature Review
The rapid growth of PBSs worldwide has attracted scholars’ attention in the past decade. Consequently, a substantial number of studies addressing various variants of the BRP have been published in recent years. This paper mainly reviews the characteristics of the s-BRP, its objectives, and the optimization methods used to resolve it.
2.1. Problem Characteristics
Below, we present the characteristics of the problems studied in the literature regarding vehicle fleet, number of visits to stations, s-BRP subtypes, and types of bikes to reposition.
2.1.1. Fleet of Vehicles
The literature encompasses works that explore either homogeneous or heterogeneous fleets of vehicles. The studies employing a homogeneous fleet include those by Dell’Amico et al. [8,9], Ho and Szeto [10], Kloimüllner and Raidl [11], and others. On the other hand, works addressing a heterogeneous fleet can be found in papers by Alvarez-Valdes et al. [1], Rainer-Harbach et al. [12,13], Raviv et al. [14], Wang and Szeto [15], among others. The majority of these studies opt for a heterogeneous fleet of vehicles. The problem’s complexity is greater when a heterogeneous fleet is incorporated, which leads to a more realistic variant. Our problem considers a heterogeneous fleet.
2.1.2. Multiple Visits to the Stations
This characteristic is present in the works by Alvarez-Valdes et al. [1], Kloimüllner and Raidl [11], Rainer-Harbach et al. [12,13], Raviv et al. [14], Wang and Szeto [15], Casazza [16], Di Gaspero et al. [17,18,19], Espegren et al. [20], Forma et al. [21], Papazek et al. [22,23], Raidl et al. [24], Schuijbroek et al. [25]. Multiple visits to the stations are allowed in two different ways: (1) when a station can be visited by several vehicles but cannot be visited several times by the same vehicle (similarly to the split delivery vehicle routing problem), and (2) when the stations can be visited several times by the same or different vehicles. In this paper, we consider this last possibility. Note that when the deviation between the desired (or target) inventory level and the initial one is larger than the vehicle capacity, multiple visits to stations and the depot are necessary.
2.1.3. Subtypes of the s-BRP
The subtype of the static bike-sharing repositioning problem (s-BRP) could be with repositioning Complete or Partial. In the repositioning Complete, operators are required to precisely achieve the target inventory level at all stations (see Dell’Amico et al. [8,9], Wang and Szeto [15], Sorensen and Vergeylen [26], Lahoorpoor et al. [27], Zhang et al. [28]).
In cases where the available repositioning duration or the number of rebalancing trucks is insufficient, partial target inventory levels are met at some or all stations, leading to what is known as repositioning Partial (see Alvarez-Valdes et al. [1], Ho and Szeto [10], Kloimüllner and Raidl [11], Rainer-Harbach et al. [12,13], Raviv et al. [14], Di Gaspero et al. [17,18,19], Espegren et al. [20], Forma et al. [21], Papazek et al. [22,23], Raidl et al. [24], Schuijbroek et al. [25], Kinable [29], Kloimüllner et al. [30], Li et al. [31], Tang et al. [32], Lv et al. [33].
In many PBSs, it may be unrealistic to require that all the stations receive their target levels because sometimes it is impossible (the number of available bikes is not enough to meet the demand) or simply too expensive (in terms of labor, time, or fuel costs). In this paper, we consider a more general problem where obtaining perfectly balanced stations is an objective rather than a requirement. This feature considerably increases the solution space. This approach can be called a static partial bike-sharing repositioning problem (sp-BRP).
2.1.4. Types of Bikes
Concerning the types of bikes, most of the works deal with only one type of bike. Alvarez-Valdes et al. [1], Wang and Szeto [15] contemplate the possibility that some of the bikes are damaged (unusable), so it is advisable to remove them from the stations. On the other hand, Li et al. [31] considers different types of bikes, but they do not deal with the possibility of having damaged bikes. Finally, we find the work of Du et al. [34], which contemplates the possibility of collecting damaged bicycles, but in free-floating bike-sharing systems (FFBSs).
According to Kaspi et al. [35,36], the most critical component of the operating costs in the PBS, apart from the repositioning, is maintenance, which includes the detection of damaged bikes and their collection to be repaired. These processes are critical because the damaged bikes, undetected and not collected to be repaired, appear in the information systems as available ones. This situation may adversely affect the user’s route choices and service level. Studies like Castro Fernandez [37] on the Barcelona bike-sharing system show that 67% of all its bikes had some defect affecting their normal usage. Furthermore, DeMaio and Meddin [38] indicate that nearly 2000 bikes required daily maintenance in the Hangzhou bike-sharing system. For these reasons, these processes have recently received substantial attention in the literature. For example, Kaspi et al. [35] and Kaspi et al. [36] study the detection and analysis of damaged bikes, respectively, while the work of Alvarez-Valdes et al. [1], Wang and Szeto [15], Du et al. [34], and this paper, consider the collection of damaged (unusable) bikes.
2.2. Objectives
In addition to the previously analyzed characteristics, the objectives considered in the literature of the static bike-sharing repositioning problem vary widely. Usually, the studies aim to minimize one or various performance measures, including the total travel cost (Dell’Amico et al. [8,9], Casazza [16], Kinable [29], Benchimol et al. [39], Erdoğan et al. [40]), the total travel distance (Chemla et al. [7], Cruz et al. [41]), the weighted sum of total absolute deviation from the target number of bikes and total travel time (Di Gaspero et al. [18]), the total travel and handling cost (Erdoğan et al. [42]), the weighted sum of total unmet demand (Sorensen and Vergeylen [26]), the makespan of the rebalancing fleet (Pal and Zhang [4]), the weighted sum of the deviation over all stations, the travel time for each vehicle, and service or loading instructions for each station (Rainer-Harbach et al. [12,13], Papazek et al. [22,23], Raidl et al. [24]), among other things.
In this paper, we minimize the weighted sum of three terms. The first two terms represent the total unbalance of the bikes usable in the stations and the number of damaged (unusable) bikes not picked up. The third term is the total time used by all the vehicles divided by an upper bound. Thus, we consider a hierarchical objective: the first objective is to minimize the dissatisfaction (in terms of unbalanced and damaged bikes not removed), and the second is to minimize the total repositioning time.
2.3. Optimization Methods
Most of the methods of solution for the static bike-sharing repositioning problem (s-BRP) are heuristics. Among them we find: ant colony optimization (Di Gaspero et al. [17]), genetic algorithm (Lahoorpoor et al. [27], Du et al. [34], Kadri et al. [43]), greedy randomized adaptive search procedure (Rainer-Harbach et al. [13], Papazek et al. [22,23]), large neighborhood search (Pal and Zhang [4], Ho and Szeto [10], Di Gaspero et al. [18,19]), iterated local search (Tang et al. [32], Cruz et al. [41]), variable neighborhood descent (Pal and Zhang [4], Rainer-Harbach et al. [12,13], Papazek et al. [22,23], Zhang et al. [28], Cruz et al. [41]), variable neighborhood search (Rainer-Harbach et al. [12,13], Raidl et al. [24], Lv et al. [33]), particle swarm optimization (Zhang et al. [28]), Tabu search (Chemla et al. [7]), among other things.
This paper proposes a matheuristic based on the general variable neighborhood search first proposed by Mladenović and Hansen [44,45]. The algorithm combines the variable neighborhood search metaheuristic with several improving and perturbation algorithms, including two procedures to optimize the number of bikes to move for each visit: one heuristic approach, and one mathematical formulation-based.
2.4. Summary
As is evident from the above review, it can be concluded that numerous studies have been carried out on the bike-sharing repositioning problem (BRP). However, as for the repositioning considering the collection of damaged (unusable) bikes, to the best of our knowledge, there is little research that, in addition to this feature, includes a heterogeneous fleet and multiple visits to stations and the depot in the station-based bike-sharing system (SBBS), carrying out a repositioning Partial (sp-BRP).
This paper introduces a novel static bike-sharing repositioning problem (s-BRP) in SBBSs, considering operational (usable) and damaged (unusable) bikes and multiple visits to the depot and stations. It utilizes a heterogeneous fleet to implement a joint repositioning strategy, enabling the simultaneous movement (pick-up or delivery) of operational and damaged bikes between stations and/or the depot. The objective of our problem is to minimize the weighted sum of the deviation from the target number of bikes usable for each station, the number of damaged bikes not removed, and the total time used by vehicles. To solve this problem, we propose a matheuristic approach based on variable neighborhood search, combined with several improvement and perturbation algorithms, including an integer linear programming model to optimize the number of bikes to move for each visit.
From a practical standpoint, this matheuristic approach adapts seamlessly to dynamic scenarios, positioning it as a versatile tool for operational planning in public bike-sharing systems (PBSs). By encompassing both operational and damaged bikes within its scope, the proposed approach provides a realistic framework that better aligns than existing models with the dynamic needs of urban PBSs. Additionally, our study provides a robust algorithmic foundation for future work in the BRP field, with implications for developing adaptable, real-time solutions in cities where PBSs must contend with rapidly fluctuating conditions and resource constraints. This work, therefore, stands as a significant contribution to the optimization of PBS logistics, with insights applicable across urban contexts.
3. Problem Research
The novel static bike-sharing repositioning problem (s-BRP) that we consider in this paper is described by a set of stations, a depot, and a heterogeneous fleet of vehicles. For each station, the current and desired number of operative bikes and the number of damaged bikes are known. The problem is to design the routes of the vehicles and the number of both operative and damaged bikes to be moved at each station and the depot to minimize the sum of the final imbalance of the stations and the damaged bikes that have not been taken to the depot. As a secondary objective, the total time of the routes is minimized. Routes have to satisfy vehicle capacity and maximum time constraints. Both the stations and the depot can be visited multiple times.
The s-BRP proposed is defined by a complete and directed graph whose node-set, , represents the bike stations and the depot (node 0) and whose arcs are associated with the best feasible paths that can be traveled by the repositioning vehicles between stations and the depot. The time needed to travel along arc is denoted by .
The following sections detail the characteristics of the nodes set, vehicle fleet, routes, proposed function objective, and the notation to represent a feasible solution.
3.1. Characteristics for Stations and the Depot
The stations may contain operative (or usable) bikes and damaged (or unusable) bikes. Throughout the paper, operative bikes and damaged bikes are abbreviated as o-bikes and d-bikes, respectively. It is assumed that the depot has an unlimited capacity to store bikes and that o-bikes are available at the depot initially. For simplicity, the time for loading/unloading operations is not considered. We denote the set of stations as . For each station , we have:
- , the number of lockers available to store bikes (capacity).
- , the desired (or target) number of o-bikes at the station.
- , the initial number of o-bikes at the station.
- , the initial number of d-bikes at the station.
- , the station priority.
We denote the initial imbalance of station v as , that is, , and say that v is a deficit station if , a surplus station if , and a balanced station if . We denote the sets of deficit, surplus, and balanced stations as , , and , respectively. We also denote the set of stations with at least one d-bike as .
We call conflicted station to a deficit station for which . Note that for these stations, it is necessary to pick up some d-bikes before delivering the number of o-bikes that are necessary to balance the station. The set of conflicted stations is denoted as .
3.2. Characteristics for Vehicles and Routes
The repositioning is carried out by set vehicles L with the following characteristics:
- The vehicles can transport both o-bikes and d-bikes.
- The total vehicle capacity is denoted by .
- Each vehicle route must start and end at the depot, and the route’s total time cannot exceed T, which represents the maximum time available to carry out the repositioning.
- It is not necessary to specify at which time the stations are visited by the vehicles.
- In each visit to a station, the vehicle can load/unload o-bikes and load d-bikes.
- The vehicle can also visit the depot several times, and on each visit, it can load/unload o-bikes and unload d-bikes.
- Any station can be visited several times by the same or different vehicles during the repositioning.
- The vehicles can only load o-bikes at a surplus station and unload o-bikes at a deficit station, so the stations cannot be used to store bikes temporarily. Similarly, the d-bikes can only be loaded at the stations and unloaded at the depot.
It is also assumed that a conflicted station is visited by only one vehicle (although it can be visited several times). Without this assumption, we could obtain a solution where, for example, vehicle A picks up some d-bikes from a conflicted station u and vehicle B delivers some o-bikes in it. Therefore, given that we do not specify at which time the stations are visited by the vehicles when such a solution was implemented in reality, it could happen that vehicle B visited u before the d-bikes are picked up, so there would not be enough free slots to unload the o-bikes (recall that ).
3.3. Function Objective Proposed
Let and be the number of o-bikes and d-bikes, respectively, at station after the repositioning process, and let be the time used by vehicle in the repositioning. The objective of our problem is to minimize the following function:
The first two terms of the objective function represent the total imbalance of o-bikes at the stations and the number of d-bikes not removed from them, respectively. The third term is the total time used by all the vehicles divided by , so it is always less than or equal to one. , , and are scaling factors controlling the relative importance of the respective terms. Thus, we consider a hierarchical objective, where the primary objective minimizes the dissatisfaction and the secondary objective minimizes the total repositioning time.
The gamma parameters would yield alternative solutions depending on the relative weighting of these three terms. However, such variations would shift the focus of the study toward determining which factor is more critical, an issue outside the scope of our current research. The intent here is to provide a flexible, adaptable framework that organizations can customize by adjusting the importance of each term according to their unique strategic needs without altering the core objective function, allowing implementing organizations to prioritize terms based on their strategic goals without requiring modifications to the objective function. In other words, this prioritization is inherently contextual and best left to the implementing organization, as different operational environments may value these terms differently.
3.4. Notation for Feasible Solutions
A feasible solution for our s-BRP consists of a set of routes, one for each vehicle, and a set of loading instructions (or loading policy) that specifies the number of bikes to be loaded or unloaded in each visit to the stations and the depot.
Unless otherwise stated, we will denote the route of the vehicle l as , where denotes the number of visits on route l, is the depot or station visited in i-th place, and is the visits to the depot. The loading instructions for the vehicle l are denoted as , where, for each :
- is the number of o-bikes loaded (if ) or unloaded (if ) at , and
- is the number of d-bikes loaded (if ) or unloaded (if ) at
3.5. Arc Flow Formulation
3.5.1. Elements to Configure Graph
To formulate the s-BRP presented in Section 3, we construct a new non-complete directed graph , where are the node sets representing the stations and the depot, and are the arcs representing the shortest paths between each pair of nodes. Each arc has a cost representing the travel time between u and v. To reposition, we have a homogeneous fleet of vehicles with capacity Q and a route time no longer than T. The elements for nodes and arcs are detailed below:
- The nodes set is formed by:
- (i)
- A nodes set containing copies of each , each with demand 1 if or if .
- (ii)
- A nodes set containing copies of each , each with demand 1.
- (iii)
- A nodes set containing N copies of the depot, for potential intermediate visits of all vehicles.
- (iv)
- Two nodes, and , copies of the depot, acting as source and sink, respectively.
- The set of arcs is formed by:
- (i)
- A set of arcs formed by the arcs for all .
- (ii)
- A set of arcs formed by the arcs for all .
- (iii)
- A set of arcs formed by the arcs for all .
- (iv)
- A set of arcs formed by the arcs for all and or for all and .
- (v)
- An arc .
In addition to the usual notation for directed graphs (such as o ), we need the following notation:
- Given , denotes the nodes of which it is a copy.
- Given , denotes the travel time if and 0 otherwise.
3.5.2. Assumptions
- The fleet of vehicles can make at most N intermediate visits to the depot. At each of these visits, o-bikes and/or d-bikes can be dropped off, but only o-bikes can be taken from the initial depot inventory.
- For the moment, that there are no conflicting stations.
3.5.3. Decision Variables
- : 1 if any vehicle uses the arc , 0 otherwise.
- : number of vehicles not used.
- : number of o-bikes in the vehicle that crosses the arc .
- : number of d-bikes in the vehicle that crosses the arc .
- : cumulative time of the route through the arc .
- : number of o-bikes picked up in the intermediate visit to the depot i.
- : number of o-bikes delivered in the intermediate visit to the depot i.
3.5.4. Mathematical Model
Our problem can be modeled as:
s.t.:
The objective function (2) minimizes the total imbalance of o-bikes at the stations, the number of d-bikes not removed from them, and the total time used by all the vehicles divided by . The scaling factors , , and control the relative importance of the respective terms. The flow constraint (3) ensures that the amount of flow entering a node is equal to the amount of flow leaving it, except for the source and destination nodes. The constraint (4) ensures that a node {} can have a maximum of one visit. Constraints (5) and (6) ensure that the number of vehicles leaving node and arriving at node are equal . Constraints (7)–(10) control the amount of o-bikes on the vehicle at each visit to a surplus, deficit, damage station or the depot, respectively. Constraints (11)–(13) control the amount of d-bikes in the vehicle at each visit to a node belonging to the sets , and {}, respectively. Constraints (14)–(17) determine the cumulative time on the route and constrain that the maximum repositioning time T is not exceeded. Constraint (18) ensures the vehicle’s capacity is met. Constraint (19) limits the number of bikes picked up and delivered to the depot. Finally, constraints (20)–(24) define the domain of the variables.
4. Construction of the Initial Solution
4.1. General Schema
To build an initial solution for our s-BRP, we developed a multi-start heuristic called randomized constructive heuristic (RCH). This multi-start procedure is based on the heuristics presented by Rainer-Harbach et al. [13] and Daza-Escorcia and Alvarez-Martinez [46], and it has been adapted to solve the research problem proposed in Section 3.
This heuristic sequentially builds a route for each vehicle. The routes are created by iteratively inserting a new node at the end of the partial route following a greedy strategy. From the last visit u of a partial route (or initially, the depot), we first determine the set of feasible successors, and, for each candidate , we compute a ratio between the maximum number of bikes to be moved at the node v and the time . Among the candidates with the largest ratio value, one is chosen to be inserted as the next visit of the current route. See Algorithm 1.
| Algorithm 1 RCH |
Input: Problem Instance I Input: Parameter Max. number of iterations
Return a feasible solution |
The following sections detail the steps developed in the RCH.
4.2. Updating States
We have built a partial solution at each algorithm stage that includes station visits and loading/unloading operations on them. Let us suppose that the route being constructed is l, and u is the last node inserted in this partial route. As a result of the partial solution so far constructed, the states of the depot and the stations have changed.
4.2.1. States for Stations and the Depot
For each station , let us denote as and , respectively, the imbalance and the number of d-bikes according to the partial solution built, and the remaining number of o-bikes at the depot that can be taken by vehicle l (that is, they have not been left by another vehicle). We denote as
- the set of deficit station,
- the set of surplus station,
- the set of balanced station, and
- the set of stations with at least one d-bike.
4.2.2. States for the Vehicles
We denote as and , respectively, the number of o-bikes and d-bikes on the vehicle l after visiting u and let be the partial traveling time of route l. Additionally, we denote as the minimum number of free lockers in the vehicle in the section of the current route from the last visit to the depot to node u.
4.3. Selection of Successors
The election of the next visit on route l is as follows. Firstly, a set of potential candidates F is built. This set initialized with all the nodes , , such that , that is, those nodes not balanced or with d-bikes that could be inserted after u in the current route without exceeding the time limit T (considering also the time needed to return to the depot). The depot is added to F if and . Finally, the conflicted stations that have been visited by other vehicles in the current partial solution are removed from F. For each potential candidate , , we compute the maximum number of o-bikes and d-bikes we can move if v is inserted after node u in the current route. These quantities are computed as
Note that in the case where with , we could consider to have taken more o-bikes from the depot if . To carry this out, we also have to check if there is enough capacity in the vehicle to carry them from the depot to v, which is represented by . This is the reason to consider in (25). Finally, if , we assume that the d-bikes that are on the vehicle would be unloaded in the depot. The final candidate set of successors of u in the route is obtained by the removal of F from those stations v with . If , we close the route by adding a visit to the depot and unloading all the bikes on the vehicle. Otherwise, for each we compute a ratio as follows:
where , , and are parameters that are used to tune the algorithm. A value is used to prevent selecting stations with a large number of bikes to be moved, but that are far away from u, against stations that are closer to u although the number of bikes to be moved is not so large. Furthermore, if , then the visits to the depot are promoted. Finally, parameters are used to promote the visits to conflicted stations; thus, we set for and , with , for .
In a deterministic scheme, we would choose as the next visit in the route the candidate such that . However, we have embedded the algorithm into an aleatorized multi-start scheme that executes the construction of the solution a number of times equal to and outputs the best solution generated. In this algorithm the next node is randomly selected among the candidates with highest values of ratio . Specifically, let be a random number in , then is randomly selected among the candidates such that .
Once the node has been selected for the next visit, the number of o-bikes and d-bikes to be moved at the station or the depot is given by and , respectively. In the case where and , additional o-bikes are taken in the last visit to the depot, and the values of and are consequently updated.
5. Approaches for Optimizing Loading Instructions
Given a feasible solution provided by the randomized constructive heuristic described above, we apply a variable neighborhood search (VNS) method to improve it. This method is based, among other things, on minor modifications (usually called moves) that slightly change a given solution. The classical moves used in vehicle routing problems involve modifying the sequence of visits in the routes to produce new sequences of visits. In basic routing problems, it is straightforward to evaluate the cost of the move as the increment in distance or time.
In our problem, the most important part of the objective is to minimize the total imbalance of the stations and the number of d-bikes transported to the depot. Therefore, we need to determine the best loading instructions for the new sequence to evaluate the cost of the move. This is not an easy task because a little modification in the sequence (for example, just removing one visit) may change the loading policy of many of the remaining visits. In order to evaluate many moves in a reasonable time, we need a method to compute the loading instructions of the new sequence quickly. To solve this, we propose two approaches. The first is a heuristic approach, where we design two heuristic methods to compute the loading policy given the sequence of visits. Additionally, a second mathematical programming-based approach is proposed, in which we formulate the problem of finding the optimal loading instructions as an integer linear programming model. In the following sections, we detail the two proposed approaches.
5.1. Heuristic Approach
We have designed two heuristics that are based on the same idea; a global heuristic, named g-LH, that computes the loading policy of all the vehicles, and a heuristic that computes the loading instructions of only one vehicle, assuming that the loading instructions of the other vehicles are known. This last heuristic will be called sv-LH.
5.1.1. Single-Vehicle Loading Heuristic: sv-LH
- Notations and General Definitions
Let l be the vehicle for which we want to compute the loading instructions, assuming that it is a known sequence of visits (or route). Additionally, assume that the other vehicles’ routes and loading instructions are known.
In this section, and denote the number of o-bikes and d-bikes, respectively, that would be in station v, assuming that the routes and the loading instructions of all the vehicles different from l are performed, and let be the number of o-bikes in the depot that have not been used by the other vehicles. In other words, the numbers , , and represent the residual state of each station and the depot after the operations (pickup/delivery) for a route (or section of the route). We define the station imbalance as . Furthermore, and denote the number of o-bikes and d-bikes, respectively, that are on the vehicle after the visit i.
We call intermediate visits to those visits to the depot different from the first and last ones. In the case that the route of the vehicle makes intermediate visits to the depot, we split the route into sections in such a way that each section starts and ends at the depot but does not have any intermediate visits to it. Let us assume that the current section contains the visits from to , so , i.e., the depot.
- General Scheme
In the single-vehicle loading heuristic (sv-LH), we first compute the loading policy of all the sections, and then they are merged to obtain the loading instructions for the whole route. Once we compute the loading instructions for the first section, the computation for the second section assumes that the operations designed for the first section have been carried out, and so on. The sv-LH consists of two steps. In Step I, the visits to the stations are considered consecutively, and at each station, the load/unload instruction tries to achieve the greatest possible balance, taking into account the number of bikes on the vehicle before the visit and its capacity. In Step II, the sequence of visits is traversed backward from the last visit, and the number of d-bikes to load at each station is decided so that the vehicle’s capacity is not exceeded. Finally, all the loaded bikes are unloaded into the depot on the last visit of the section. The Algorithm 2 shows a detailed pseudo-code for sv-LH.
| Algorithm 2 sv-LH |
Input: Solution
|
- Detailed Procedural Outline
Step I: Algorithm 2 for the single-vehicle loading heuristic (sv-LH) starts with the definition of variables (line 2) described in section Notations and General Definitions. Then, for each visit on the route sections (lines 3 to 29), we proceed to calculate the load instructions, trying to reach the maximum possible balance in the visited stations. In this step, we do not pick up d-bikes; we only pick up and/or drop off o-bikes at the corresponding stations.
If the next visited is in surplus station (lines (lines 4 to 9), then we proceed to pick up the o-bikes that the available space of the truck allows (line 5), then we update the bikes carried by the truck (line 6), the number of o-bikes at the visited station (line 7) and the minimum residual capacity of the truck (line 8).
If the next visited is in deficit station (lines 10 to 28), then we proceed to deliver o-bikes (line 11) and update the bikes carried by the truck (line 12). Initially, it is assumed that the vehicle leaves the depot empty. However, suppose it visits a deficit station, and the number of o-bikes that are on the vehicle is less than the number of bikes needed to balance that station () (lines 13 to 23). In that case, the possibility of loading a larger number of o-bikes from the depot is considered, provided that the capacity of the vehicle is not exceeded in its path from the depot to (line 14). Then, we update the amount of delivered o-bikes and the bikes carried by the truck (line 15), the minimum residual capacity of the truck (line 16), the number of o-bikes at the station and the depot (lines 17 to 19). Finally, update the bikes carried by the truck for each of the previous visits up to the current one (lines 20 to 22). Finally, in the case of conflicted stations, the algorithm loads the necessary number of d-bikes to unload the decided number of o-bikes (lines 24 to 27).
Step II: This second step aims to collect the d-bikes from the stations as long as the truck has enough space (lines 31 to 44). Initially, we define the minimum residual capacity of the truck (line 31), which we use to visit the stations with d-bikes (line 34). Then, we determine the number of d-bikes to be loaded on the truck (lines 35 and 36), update the number of d-bikes left in the station (line 37) and the minimum residual capacity of the truck (line 38). Then, we update the truck’s number of d-bikes at each visit (lines 39 to 41). Finally, we unload all the bikes carried by the truck at the depot (line 45).
Route loading instructions: Once the Algorithm 2 has been applied to all the sections of the route, we have to define the loading instructions of the whole route. Note that the order in which the sections are traversed by the vehicle can be modified arbitrarily because each section starts and ends at the depot. If, for instance, at the end of one section, some o-bikes are unloaded at the depot, it is advisable that this section be traversed at the beginning of the route, as the o-bikes unloaded at the depot could be useful for balancing deficit stations in subsequent sections.
Therefore, we use the following strategy: Firstly, Step I of Algorithm 2 is applied to each section, assuming, for all of them, that there is an infinite number of available o-bikes at the depot. We estimate in this way the number of o-bikes that each section would load from the depot at the beginning and the number that would unload at the end. Then, the sections are ordered in decreasing order of the net number of o-bikes that would be unloaded at the depot. Secondly, the Algorithm 2 is applied to the sections ordered in this way.
Finally, the loading instructions of the successive sections are joined. An obvious correction is carried out when two consecutive sections are joined. If, for instance, xo-bikes are unloaded into the depot at the end of one section and o-bikes are loaded from the depot at the beginning of the next section, then the number of o-bikes that are unloaded at the end of the first section is .
5.1.2. Global Loading Heuristic: g-LH
This procedure determines heuristically the loading policy for all the vehicles, provided that the routes (sequence of visits) are known for all of them. The procedure works as follows. The loading instructions for the vehicles are computed sequentially in an arbitrary order. This time, the quantities , , and are computed assuming that the loading policy of the vehicles already considered has been performed.
A similar method to sv-LH is applied for each route. Firstly, the route is divided into sections determined by consecutive visits to the depot. Then, Step I of Algorithm 2 is applied twice to each section of the route, as in method sv-LH, the first one to decide the order in which the sections should be traversed, and the second time using this order to compute the load instructions of the sections that are finally joined. Nevertheless, this time, the loading instructions are corrected in such a way that the only o-bikes that are unloaded at the depot are those to be used by successive sections of the route. This is easily performed by traversing the route from the last station visited backward and decreasing, if necessary, the number of o-bikes that are loaded at each surplus station visited and would be unloaded at the depot. The reason for doing this is that the o-bikes that are unloaded at the depot cannot be used by the other vehicles, and, on the other hand, the imbalance of the surplus stations could be balanced by the subsequent vehicles.
Once the loading policy for all the vehicles has been computed, a last correction is made. This correction allows the vehicles to load d-bikes and o-bikes at the stations that will be unloaded on the next visit to the depot. The depot plays a crucial role in this correction, as it is the point of reference for unloading and loading. This correction, similarly to Step II of Algorithm 2, ensures that each section is traversed from the end backward, and at each station, the possibility of loading o-bikes and d-bikes is considered if it would balance the station and if the capacity of the vehicle allows it.
5.2. Mathematical Programming-Based Approach
We have formulated the problem of finding the optimal loading instructions for a given set of vehicle routes as an integer linear programming (ILP) model. The objective function of this formulation does not include the time used by the routes. Given that the time for load operations is not considered and the sequence of visits is assumed to be fixed, the total time does not depend, in principle, on the loading policy. This is not entirely true because if the optimal load instructions include some visits without operation, those visits could be skipped so that the total time would decrease. Given that the importance of the total time in our repositioning problem is small, we have decided not to consider this possibility.
The formulation is based on the variables that define the loading policy that were described in Section 3.4: , are the number of o-bikes and d-bikes, respectively, that are loaded (if positive) or unloaded (if negative) in the vehicle l at visit i, . For convenience, we use another variable, , representing the number of o-bikes loaded by vehicle l from the depot. As in the heuristic above, we denote as the station (or depot) visited in i-th place in the vehicle route l, . Let be the set of vehicles with nonempty routes and, for and , .
s.t.:
The objective function minimizes the total imbalance of the stations and the number of d-bikes that have not been collected from the stations. Constraints (29)–(30) guarantee that the number of o-bikes and the total number of bikes on the vehicle are non-negative and below capacity, respectively, at each visit. Constraint (31) ensures that all o-bikes are unloaded at the end of each route. Constraint (32) guarantees that all d-bikes are unloaded at each visit to the depot. Constraints (33)–(35) limit the number of bikes that can be managed in the stations. Constraint (36) limits the number of o-bikes that can be taken from the depot by all the vehicles, and constraint (37) controls the number of o-bikes that can be taken in each visit to the depot. Constraint (38) prevents the capacity of a conflicted station from being exceeded. Finally, constraints (39)–(46) define the domain of the variables.
This model can be solved quickly with CPLEX 20.0 [47] for the size of the instances we have tried. Compared with the heuristic approach described in Section 5.1, the model provides better solutions, even though in the heuristic approach, it is allowed to slightly change the routes by altering the order in which the successive visits to the depot are traversed. The improvements have been observed with solutions that perform multiple station visits. In fact, we conjecture that our heuristic method is optimal if the stations are visited only once.
6. Framework of the Proposed Matheuristic
To solve our s-BRP described in Section 3, we present a matheuristic approach based on variable neighborhood search that consists of two phases. In the first phase, an initial solution is constructed with the randomized constructive heuristic (RCH) presented in Section 4. The second phase consists of three stages: first, the optimal loading policy for the solution provided by the RCH is computed with the integer linear programming (ILP) model presented in Section 5.2; then, the resulting solution is used as the input for the generalized variable neighborhood search (GVNS) described in Section 6.1, Section 6.2, Section 6.3 and Section 6.4; finally, the loading policy of the solution obtained by the GVNS is optimized with the integer linear programming (ILP) model. The framework of the proposed matheuristic is shown in Figure 3.
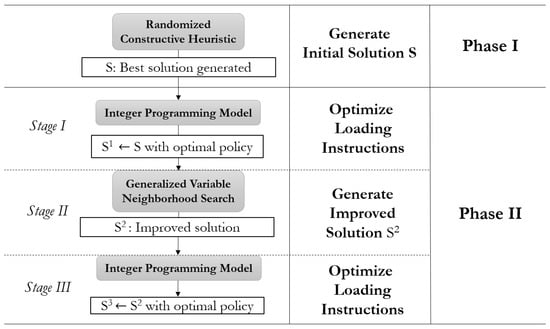
Figure 3.
Matheuristic scheme of solution method proposed.
6.1. Variable Neighborhood Search
The metaheuristic variable neighborhood search (VNS), proposed by Mladenović and Hansen [44,45], tries to avoid being trapped in a local minimum by systematically changing the neighborhood structures where the search is performed. When a deterministic rule controls this change, the VNS is renamed variable neighborhood descent (VND) (Hansen and Mladenović [48]).
The VND procedure is outlined in Algorithm 3. The procedure consists of a sequence of local moves based on different neighborhoods, denoted by . The best solution obtained in the exploration of neighborhood of solution is denoted by . In case the best move of the current neighborhoods succeeds (i.e., the solution is improved), the method restarts with the first neighborhood (line 6). Otherwise, the next neighborhood is used (line 8) with solution . The solution obtained at the end of this method is a local minimum with respect to all neighborhoods.
| Algorithm 3 VND |
Input: Solution Input: Set of neighborhoods
|
6.2. General Variable Neighborhood Search
The general variable neighborhood search (GVNS) is a more elaborate implementation that is based on two complementary methods: a local search method (or improvement) that consists of a VND and a perturbation method (or shaking), where the solution is drastically changed.
The GVNS (Algorithm 4) systematically uses the principles of intensification and diversification to avoid being trapped in a local minimum. The intensification task is performed by the VND (line 6). In contrast, the diversification (line 5) is based on a set of so-called perturbation procedures (). After a perturbation procedure is applied to a solution, the VND is used to improve it. The perturbation procedures are managed similarly to the neighborhood structures in the VND; when it succeeds in improving the incumbent solution, j is reset to 1; otherwise, j is increased by one. The GVNS ends when the stopping criterion is met, in our case, when a prefixed number of iterations has been performed.
| Algorithm 4 GVNS |
Input: Solution Input: Set of neighborhoods Input: Set of perturbation procedures
|
In the following sections, we present in detail the improvement and perturbation procedures that we use in our algorithm.
6.3. Improvement Moves
Six improvement moves have been implemented to be used in the VND (Algorithm 3). The corresponding neighborhoods are denoted by . The moves are described below in terms of the changes in the sequence of visits to the stations and the depot. Recall that to evaluate one particular move, it is necessary to determine the loading instructions in each visit, which is implemented by applying the sv-LH heuristic described in Section 5.1.1. Furthermore, the best improvement strategy is used in all the cases: all the solutions in the neighborhood are evaluated, and the best one is chosen. If a better solution than the incumbent is found, we tried to further improve the solution using the g-LH procedure presented in Section 5.1.2.
- Insert or change unsolved stations—An unsolved station is one that is still imbalanced or has damaged bikes in the current solution. This move tries to improve the current solution by inserting a new visit to an unsolved station (see Figure 4). For each unsolved station and any route, two possibilities are tried: to insert a visit to that station or to replace one visit (to another station) in the route with a visit to the unsolved station. Both situations are shown in Figure 4b and Figure 4c, respectively.
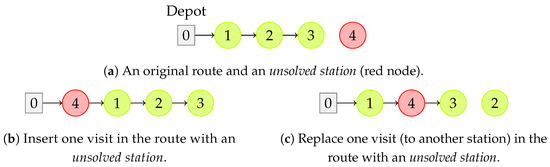 Figure 4. An original route and two of its neighbors, through improvement move .
Figure 4. An original route and two of its neighbors, through improvement move . - Remove or relocate a visit—This move consists of removing the visit to a station or depot, discarding it, or inserting it in another position on the same or different route. Both situations are shown in Figure 5b and Figure 5c, respectively.
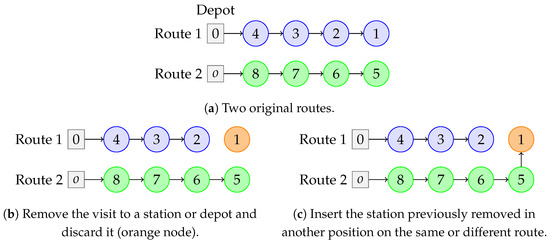 Figure 5. Two original routes and two of its neighbors, through improvement move .
Figure 5. Two original routes and two of its neighbors, through improvement move . - Relocate a segment intra-route—In this move, a segment of l consecutive visits, where , is removed from a route and re-inserted at another position in the same route, with the same or the reverse orientation. The segment may include intermediate visits to the depot. Both situations are shown in Figure 6b and Figure 6c, respectively.
 Figure 6. An original route and two of its neighbors, through improvement move .
Figure 6. An original route and two of its neighbors, through improvement move . - Relocate a segment inter-route—This move is similar to the one defining , but the segment is inserted in another route. Segments that include visits to conflicted stations are not considered. See Figure 7.
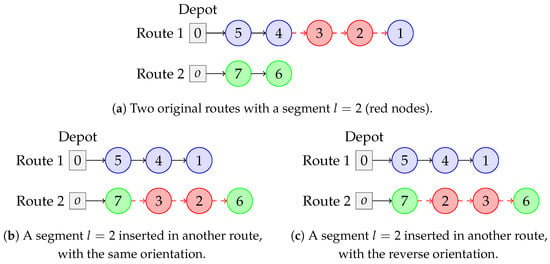 Figure 7. Two original routes and two of its neighbors, through improvement move .
Figure 7. Two original routes and two of its neighbors, through improvement move . - Intra-route segment exchange—Two non-overlapping segments of a route, both with a number of visits between 1 and 4, change their positions in the route, may be with the reverse orientation in both cases. Segments with intermediate visits to the depot are also considered. See Figure 8.
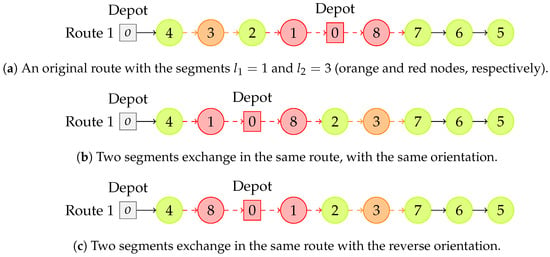 Figure 8. An original route and two of its neighbors, through improvement move .
Figure 8. An original route and two of its neighbors, through improvement move . - Inter-route segment exchange—This move is similar to the one defining , but the segments are taken from different routes. See Figure 9.
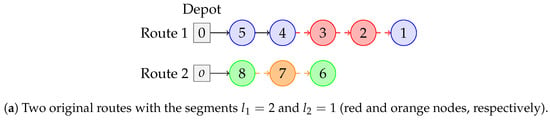
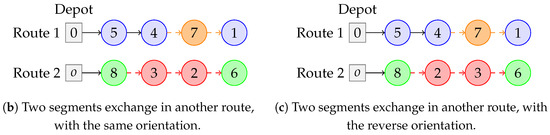 Figure 9. Two original routes and two of its neighbors, through improvement move .
Figure 9. Two original routes and two of its neighbors, through improvement move .
Note that the current solution may include empty routes (i.e., vehicles not used in the solution) that can be filled with visits by some of the preceding moves. Note also that the insertion or replacement of one or several visits in a route may result in a route that contains consecutive visits to the same node, which are substituted by a single visit. Furthermore, as the sv-LH heuristic is used to calculate the loading instructions, it may happen that no loading or unloading had to be made in some visits; then, obviously, those visits are removed from the route. If the final route after the move and all these corrections exceed the maximum time allowed T, the move is discarded.
6.4. Perturbation Mechanisms
Three perturbation mechanisms, , have been implemented in our GVNS (see Algorithm 4). For all perturbation mechanisms, the operations are executed times.
- (-Shift): The following operation is executed times. Randomly select two routes and (one of them may be empty), and then randomly select one visit i in and one visit j in . The visit i is removed from route and inserted just before visit j in route . Positions i and j are different from the first and last ones in the routes. See Figure 10.
 Figure 10. Two routes and its neighbor, through perturbation mechanism .
Figure 10. Two routes and its neighbor, through perturbation mechanism . - (-Swap): The following operation is executed times. Randomly select two routes and (one of them may be empty), and then randomly select one visit i in and one visit j in . The visit i of route is interchanged with the visit j in route . Positions i and j are different from the first and last ones in the routes. See Figure 11.
 Figure 11. Two routes and its neighbor, through perturbation mechanism .
Figure 11. Two routes and its neighbor, through perturbation mechanism . - (-Segment): The following operation is executed times. Chose a random integer L between 2 and 4 visits. Select randomly one route and one visit i in that route. Then, for each , a route , and a position j in it, are randomly chosen, and visit i is removed from and inserted in position j of . See Figure 12.
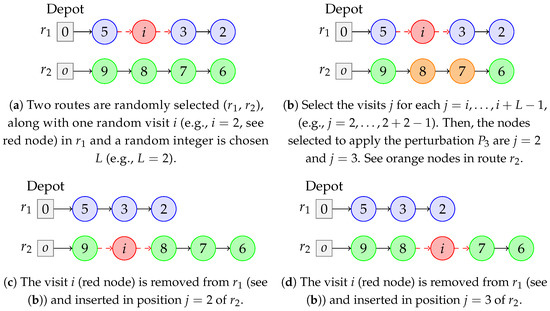 Figure 12. Two routes and its neighbors, through perturbation mechanism .
Figure 12. Two routes and its neighbors, through perturbation mechanism .
The solution obtained after any of these perturbations is simplified in a similar way as was explained for moves: repeated visits to nodes are merged, loading instructions are computed using the g-LH algorithm (see Section 5.1.2), and visits with no loading/unloading operation are removed. Furthermore, in case a route exceeds the maximum time T, starting from the last visit to a station and backwards, some visits are removed until a feasible route is obtained; then new loading policies are computed with the g-LH heuristic.
7. Computational Experiments
The computational analysis to assess the performance of our algorithm is structured as follows:
- Experiment Setup: Section 7.1 describes the instances based on real-world data used for testing and introduces the parameter information used in our solution method.
- First Experiment: Section 7.2 presents an exhaustive performance analysis for the randomized constructive heuristic (RCH) described in Section 4.
- Second Experiment: Section 7.3 provides an in-depth analysis of the general variable neighborhood search (GNVS) detailed in Section 6.2, evaluating its performance across various scenarios.
- Third Experiment: Section 7.4, we compare the results obtained by our method with the recommended parameter setting and the best solutions obtained over all the experiments made with any parameter setting while tuning the algorithm. Given that there are no previous studies on this model, it is difficult to assess the quality of the solutions obtained. Therefore, we analyze the results of the two phases of our matheuristic proposed in Section 6.
7.1. Instances and Parameter Setting
We evaluated the performance of our algorithms using 136 instances, categorized into two groups:
- Palma: This set contains 28 instances, based on the PBS of Palma de Mallorca, Spain, that were proposed in Alvarez-Valdes et al. [1]. Each instance contains 28 stations and one depot with an initial inventory of 10 usable bikes, i.e., . There are seven variants with respect to the imbalance and number of damaged bikes in the stations (corresponding to the seven days of a week). For each day, two fleet sizes (two and three vehicles with capacity ) and two variants of maximum time (2 and 4 h) were considered.
- Wien: These instances were taken from Rainer-Harbach et al. [13] and adapted to our problem by randomly replacing a few operating bikes in the stations with damaged bikes. These instances have 20, 30, 60, and 90 stations and one depot (with no initial inventory, i.e., ). Two values for the maximum time (4 and 8 h) and two fleet sizes were considered. For the instances with 20 or 30 stations, the fleet sizes considered are two and four, while for the instances with 60 or 90 stations, the fleet sizes are three and five vehicles. In all the cases, the capacity of the vehicles is 20. There are five instances in each group, making a total of 80 instances in this set.
All algorithms were implemented in C++ and run on a PC with an Intel(R) Core(TM) i5-4200 CPU at 1.60 GHz and 4.00 GB of RAM. Throughout the experiments, only a single thread was utilized. In the integer linear programming (ILP) model described in Section 5.2, to determine loading instructions, CPLEX 20.0 [47] was used with default settings, except for restricting CPLEX [47] to only use a single thread.
After some preliminary testing, we set the number of iterations in the RCH to 5000 and 100 in the GVNS. For the parameters of route construction presented in Section 4, we set , , and for . Therefore, we set for the perturbation mechanisms described in Section 6.4. Finally, we set for the scaling factors in the objective function described in Section 3. By employing these factors, enhancing the system balance and collecting damaged bikes will consistently have a greater impact on the objective value than reducing the total time of the routes.
7.2. Performance Analysis for RCH
Table 1 shows the average results obtained by the randomized constructive heuristic (RCH) approach on both sets of instances. Below, we evaluate its performance across scenarios for 1000, 2000, 3000, 4000, and 5000 iterations. The first four columns show the characteristics of each group of instances. Then, the results obtained with the RCH for each iteration scenario are displayed. In each case, the average objective value of the solutions obtained with our method (), the () time in seconds, and the number of vehicles used () after the repositioning are shown.

Table 1.
Average results of performance analysis for RCH.
For the Palma instances, our method was able to balance the stations and collect all the damaged bikes in all instances since 3000 iterations. The CPU time in this set was less than 2 s, up to 3000 iterations. Then, it dropped to less than 1 s. In 5000 iterations, we found the best solutions on average in the Palma instances using a single vehicle. For the Wien instances, we observe that the average solutions tend to improve when the maximum repositioning time is higher (240 min); when this time is lower, the vehicle fleet is insufficient to balance the system and pick up all the damaged bikes.
For the Palma instances, we note that, on average, the solutions improve considerably between 1000 and 2000 iterations. After this, the decrease in the objective function values decreases by a smaller proportion. This occurs until after 4000 iterations when the objective function drops considerably. This can be observed in Figure 13a. For the Wien instances, we note that, on average, the solutions improve considerably between 4000 and 5000 iterations. Prior to this, the decrease in the values of the objective function drops in a smaller proportion. The above can be observed in Figure 13b.
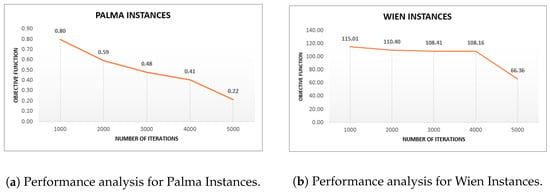
Figure 13.
Performance analysis for RCH.
7.3. Performance Analysis for GVNS
Table 2 shows the average results obtained by general variable neighborhood search (GNVS) on both sets of instances. The initial solution for this experimentation is the best solution obtained in Section 7.2. Below, we present an exhaustive performance analysis of scenarios of 1000, 2000, 3000, 4000, and 5000 iterations. The first four columns show the characteristics of each group of instances. Then, the results obtained with the GNVS for each iteration scenario are displayed. In each case, the average objective value of the solutions obtained with our method () and the () time in seconds are shown.

Table 2.
Average results of performance analysis for GVNS.
For the Palma instances, our method was able to balance the stations and collect all the damaged bikes in all instances since 1000 iterations. The CPU time in this set was less than 1 s, up to 4000 iterations. Then, it dropped to less than 2 s. In 2000 iterations, we found the best solutions on average in the Palma instances using a single vehicle. For the Wien instances, we observe that the average solutions tend to improve when the maximum repositioning time is higher (2 h); when this time is lower, the vehicle fleet is insufficient to balance the system and pick up all the damaged bikes, for instance, in more than 30 stations. The most challenging instances are the 90-station instances, which only improve from iteration 4000.
For the Palma instances, we note that, on average, the solutions improve considerably between 1000 and 2000 iterations. Prior to this, the decrease in the values of the objective function drops in a smaller proportion. The above can be observed in Figure 14a. For the Wien instances, we note that, on average, the solutions improve considerably between 1000 and 2000 iterations. After this, the decrease in the objective function values decreases by a smaller proportion. This occurs until after 4000 iterations when the objective function drops considerably. This can be observed in Figure 14b.
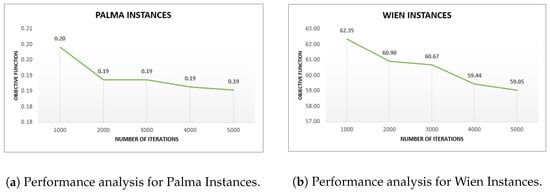
Figure 14.
Performance analysis for GVNS.
7.4. Results Comparison RCH and GVNS
Table 3 shows the average results obtained by our algorithms on both sets of instances. The comparison is carried out between the best solution obtained in Section 7.2 and the best solution obtained in Section 7.3. The first four columns show the characteristics of each group of instances. The fifth column presents the best-known solutions (BKS) obtained over all the experiments made with any parameter setting. Then, the results obtained with the randomized constructive heuristic RCH (Phase I) and the whole matheuristic algorithm (Phase II) are displayed. In each case, the average value of the solutions (), the () time in seconds, and the number of vehicles used () are shown. The next column (dif) presents the overall improvement of the results obtained in Phase II over Phase I. The last three columns show the total imbalance and number of damaged bikes in the stations, before and after the repositioning is implemented according to the solution obtained with our method and the percentage of improvement achieved.

Table 3.
Average results for each instance sets.
For the instances in Palma, our method was able to totally balance the stations and collect all the damaged bikes using a single vehicle. The CPU time in this set was less than 1 s in Phase I and less than 7 s in Phase II. The average improvement obtained in Phase II relative to Phase I was 11.6%. Similar results were obtained for the Wien instances with 20 stations.
Instances with 30–90 stations in Wien are more complex. All the vehicles were used in practically all these instances; furthermore, in many cases, the solution was not able to perform all the tasks, i.e., to balance all the stations and pick up all the damaged bikes. The average of tasks performed in this subset of instances was 88%. Of course, an improvement is observed when the number of vehicles or the maximum time T increases. The CPU time needed in this group was 9.7 s. in the worst case in Phase I and 786.4 s. in Phase II, respectively. The overall improvement of the results obtained by Phase II over Phase I was 20.7% on average.
8. Concluding Remarks
This paper introduces a new static bike-sharing repositioning problem in which a heterogeneous fleet transports operative and damaged bikes between the stations and the depot. Our model includes some features that are not found together in the literature and makes it more realistic: the stations can have damaged bikes that have to be taken to the depot, the depot may contain usable bikes to be distributed to the stations, and both the stations and the depot can be visited several times by the same or different vehicles.
An integer linear programming model and two heuristic approaches are proposed to optimize the loading policy for the vehicles’ given routes. These methods are successfully combined in a metaheuristic based on variable neighborhood search, which considerably improves the solutions obtained by a randomized constructive heuristic.
The studies found in the bike-sharing repositioning problem literature that use local search usually evaluate the moves just by the travel cost. Once the best move is selected, the loading instructions for each visit are computed. In our method, we evaluate each move by computing the loading instructions, which allows us to evaluate it more properly.
Computational results show that the method generates solutions in reasonable computing times, although, given that there are no previous studies on this model, it is difficult to assess the quality of the solutions obtained. We only compare the results obtained by our method with the recommended parameter setting and the best solutions obtained over all the experiments made with any parameter setting while tuning the algorithm. We intend to develop an exact method in the future.
Finally, while this study provides a robust framework for addressing the static repositioning problem in station-based bike-sharing systems, certain limitations offer avenues for future exploration. Applying the studied features to dynamic repositioning scenarios and free-floating bike-sharing systems could yield further insights into adaptable PBS strategies. Additionally, practical challenges such as real-time adaptation to fluctuating demand, limited repair infrastructure, and maintenance constraints highlight areas where enhanced algorithmic solutions could significantly impact operational efficiency.
Author Contributions
Conceptualization, J.M.D.-E. and D.Á.-M.; methodology, J.M.D.-E. and D.Á.-M.; validation, J.M.D.-E.; formal analysis, J.M.D.-E.; investigation, J.M.D.-E.; resources, J.M.D.-E. and D.Á.-M.; writing—original draft preparation, J.M.D.-E.; writing—review and editing, D.Á.-M.; supervision, D.Á.-M.; project administration, D.Á.-M.; funding acquisition, D.Á.-M. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by Universidad de los Andes.
Data Availability Statement
All the problem instances generated for this work and used for the experimental evaluation can be downloaded at https://github.com/juliomariodaza/s-BRP-Instances, accessed on 1 November 2024.
Acknowledgments
We want to acknowledge the anonymous referees for their valuable comments to improve the original version of our paper. The authors would like to thank the Vice Presidency of Research & Creation’s Publication Fund at Universidad de los Andes for its financial support. All authors acknowledge financial support provided by the Vice Presidency for Research & Creation publication fund at the Universidad de los Andes.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Alvarez-Valdes, R.; Belenguer, J.M.; Benavent, E.; Bermudez, J.D.; Muñoz, F.; Vercher, E.; Verdejo, F. Optimizing the level of service quality of a bike-sharing system. Omega 2016, 62, 163–175. [Google Scholar] [CrossRef]
- PBSC Urban Solutions. The Meddin Bike-sharing World Map Report. 2022. Available online: https://www.pbsc.com/ (accessed on 31 December 2023).
- DeMaio, P. Bike-sharing: History, impacts, models of provision, and future. J. Public Transp. 2009, 12, 41–56. [Google Scholar] [CrossRef]
- Pal, A.; Zhang, Y. Free-floating bike sharing: Solving real-life large-scale static rebalancing problems. Transp. Res. Part C Emerg. Technol. 2017, 80, 92–116. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Sun, L.; Liu, Q. Free-Floating Bike Sharing in Jiangsu: Users’ Behaviors and Influencing Factors. Energies 2018, 11, 1664. [Google Scholar] [CrossRef]
- Haider, Z.; Nikolaev, A.; Kang, J.E.; Kwon, C. Inventory rebalancing through pricing in public bike sharing systems. Eur. J. Oper. Res. 2018, 270, 103–117. [Google Scholar] [CrossRef]
- Chemla, D.; Meunier, F.; Wolfler Calvo, R. Bike sharing systems: Solving the static rebalancing problem. Discret. Optim. 2013, 10, 120–146. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Hadjicostantinou, E.; Iori, M.; Novellani, S. The bike sharing rebalancing problem: Mathematical formulations and benchmark instances. Omega 2014, 45, 7–19. [Google Scholar] [CrossRef]
- Dell’Amico, M.; Iori, M.; Novellani, S.; Stützle, T. A destroy and repair algorithm for the bike sharing rebalancing problem. Comput. Oper. Res. 2016, 71, 149–162. [Google Scholar] [CrossRef]
- Ho, S.C.; Szeto, W.Y. A hybrid large neighborhood search for the static multi-vehicle bike-repositioning problem. Transp. Res. Part Methodol. 2017, 95, 340–363. [Google Scholar] [CrossRef]
- Kloimüllner, C.; Raidl, G.R. Full-load route planning for balancing bike sharing systems by logic-based Benders decomposition. Networks 2017, 69, 270–289. [Google Scholar] [CrossRef]
- Rainer-Harbach, M.; Papazek, P.; Hu, B.; Raidl, G.R. Balancing bicycle sharing systems: A variable neighborhood search approach. In Proceedings of the Evolutionary Computation in Combinatorial Optimization, EvoCOP 2013, Vienna, Austria, 3–5 April 2013; Lecture Notes in Computer Science. Middendorf, M., Blum, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7832, pp. 121–132. [Google Scholar] [CrossRef]
- Rainer-Harbach, M.; Papazek, P.; Raidl, G.R.; Hu, B.; Kloimüllner, C. PILOT, GRASP, and VNS approaches for the static balancing of bicycle sharing systems. J. Glob. Optim. 2015, 63, 597–629. [Google Scholar] [CrossRef]
- Raviv, T.; Tzur, M.; Forma, I.A. Static repositioning in a bike-sharing system: Models and solution approaches. EURO J. Transp. Logist. 2013, 2, 187–229. [Google Scholar] [CrossRef]
- Wang, Y.; Szeto, W. Static green repositioning in bike sharing systems with broken bikes. Transp. Res. Part D Transp. Environ. 2018, 65, 438–457. [Google Scholar] [CrossRef]
- Casazza, M. Exactly Solving the Split Pickup and Split Delivery Vehicle Routing Problem on a Bike-Sharing System; Technical Report; [hal-01304433]; Università degli Studi di Milano: Milano, Italy; Université Paris: Paris, France, 2016; Volume 13. [Google Scholar]
- Di Gaspero, L.; Rendl, A.; Urli, T. A hybrid ACO+CP for balancing bicycle sharing systems. In Proceedings of the Hybrid Metaheuristics, HM 2013, Ischia, Italy, 23–25 May 2013; Lecture Notes in Computer Science. Blesa, M.J., Blum, C., Festa, P., Roli, A., Sampels, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7919, pp. 198–212. [Google Scholar] [CrossRef]
- Di Gaspero, L.; Rendl, A.; Urli, T. Constraint-based approaches for balancing bike sharing systems. In Proceedings of the Principles and Practice of Constraint Programming, CP 2013, Uppsala, Sweden, 16–20 September 2013; Lecture Notes in Computer Science. Schulte, C., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8124, pp. 758–773. [Google Scholar] [CrossRef]
- Di Gaspero, L.; Rendl, A.; Urli, T. Balancing bike sharing systems with constraint programming. Constraints 2016, 21, 318–348. [Google Scholar] [CrossRef]
- Espegren, H.M.; Kristianslund, J.; Andersson, H.; Fagerholt, K. The static bicycle repositioning problem-literature survey and new formulation. In Proceedings of the Computational Logistics, ICCL 2016, Lisbon, Portugal, 7–9 September 2013; Lecture Notes in Computer Science. Paias, A., Ruthmair, M., Voß, S., Eds.; Springer: Cham, Switzerland, 2016; Volume 9855, pp. 337–351. [Google Scholar] [CrossRef]
- Forma, I.A.; Raviv, T.; Tzur, M. A 3-step math heuristic for the static repositioning problem in bike-sharing systems. Transp. Res. Part B Methodol. 2015, 71, 230–247. [Google Scholar] [CrossRef]
- Papazek, P.; Raidl, G.R.; Rainer-Harbach, M.; Hu, B. A PILOT/VND/GRASP hybrid for the static balancing of public bicycle sharing systems. In Proceedings of the Computer Aided Systems Theory—EUROCAST 2013, Canaria, Spain, 10–15 February 2013; Lecture Notes in Computer Science. Moreno-Díaz, R., Pichler, F., Quesada-Arencibia, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8111, pp. 372–379. [Google Scholar] [CrossRef]
- Papazek, P.; Kloimüllner, C.; Hu, B.; Raidl, G.R. Balancing bicycle sharing systems: An analysis of path relinking and recombination within a GRASP hybrid. In Proceedings of the Parallel Problem Solving from Nature—PPSN XIII, PPSN 2014, Ljubljana, Slovenia, 13–17 September 2014; Lecture Notes in Computer Science. Bartz-Beielstein, T., Branke, J., Filipič, B., Smith, J., Eds.; Springer: Cham, Switzerland, 2014; Volume 8672, pp. 792–801. [Google Scholar] [CrossRef]
- Raidl, G.R.; Hu, B.; Rainer-Harbach, M.; Papazek, P. Balancing bicycle sharing systems: Improving a VNS by efficiently determining optimal loading operations. In Proceedings of the Hybrid Metaheuristics, HM 2013, Ischia, Italy, 23–25 May 2013; Lecture Notes in Computer Science. Blesa, M.J., Blum, C., Festa, P., Roli, A., Sampels, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 7919, pp. 130–143. [Google Scholar] [CrossRef]
- Schuijbroek, J.; Hampshire, R.C.; van Hoeve, W.J. Inventory rebalancing and vehicle routing in bike sharing systems. Eur. J. Oper. Res. 2017, 257, 992–1004. [Google Scholar] [CrossRef]
- Sorensen, K.; Vergeylen, N. The bike request scheduling problem. In Proceedings of the Computer Aided Systems Theory—EUROCAST 2015, Canaria, Spain, 8–13 February 2015; Lecture Notes in Computer Science. Moreno-Díaz, R., Pichler, F., Quesada-Arencibia, A., Eds.; Springer: Cham, Switzerland, 2015; Volume 9520, pp. 294–301. [Google Scholar] [CrossRef]
- Lahoorpoor, B.; Faroqi, H.; Sadeghi-Niaraki, A.; Choi, S.M. Spatial Cluster-Based Model for Static Rebalancing Bike Sharing Problem. Sustainability 2019, 11, 3205. [Google Scholar] [CrossRef]
- Zhang, S.; Xiang, G.; Huang, Z. Bike-Sharing Static Rebalancing by Considering the Collection of Bicycles in Need of Repair. J. Adv. Transp. 2018, 2018, 1–18. [Google Scholar] [CrossRef]
- Kinable, J. A reservoir balancing constraint with applications to bike-sharing. In Proceedings of the Integration of AI and OR Techniques in Constraint Programming, CPAIOR 2016, Banff, AB, Canada, 29 May–1 June 2016; Lecture Notes in Computer Science. Quimper, C.G., Ed.; Springer: Cham, Switzerland, 2016; Volume 9676, pp. 216–228. [Google Scholar] [CrossRef]
- Kloimüllner, C.; Papazek, P.; Hu, B.; Raidl, G.R. A cluster-first route-second approach for balancing bicycle sharing systems. In Proceedings of the Computer Aided Systems Theory—EUROCAST 2015, Las Palmas de Gran Canaria, Spain, 8–13 February 2015; Lecture Notes in Computer Science. Moreno-Díaz, R., Pichler, F., Quesada-Arencibia, A., Eds.; Springer: Cham, Switzerland, 2015; Volume 9520, pp. 439–446. [Google Scholar] [CrossRef]
- Li, Y.; Szeto, W.Y.; Long, J.; Shui, C.S. A multiple type bike repositioning problem. Transp. Res. Part B Methodol. 2016, 90, 263–278. [Google Scholar] [CrossRef]
- Tang, Q.; Fu, Z.; Zhang, D.; Qiu, M.; Li, M. An Improved Iterated Local Search Algorithm for the Static Partial Repositioning Problem in Bike-Sharing System. J. Adv. Transp. 2020, 2020, 1–15. [Google Scholar] [CrossRef]
- Lv, C.; Zhang, C.; Lian, K.; Ren, Y.; Meng, L. A hybrid algorithm for the static bike-sharing re-positioning problem based on an effective clustering strategy. Transp. Res. Part Methodol. 2020, 140, 1–21. [Google Scholar] [CrossRef]
- Du, M.; Cheng, L.; Li, X.; Tang, F. Static rebalancing optimization with considering the collection of malfunctioning bikes in free-floating bike sharing system. Transp. Res. Part E Logist. Transp. Rev. 2020, 141, 102012. [Google Scholar] [CrossRef]
- Kaspi, M.; Raviv, T.; Tzur, M. Detection of unusable bicycles in bike-sharing systems. Omega 2016, 65, 10–16. [Google Scholar] [CrossRef]
- Kaspi, M.; Raviv, T.; Tzur, M. Bike sharing systems: User dissatisfaction in the presence of unusable bicycles. IIE Trans. 2017, 49, 144–458. [Google Scholar] [CrossRef]
- Castro Fernandez, A. The contribution of bike-sharing to sustainable mobility in Europe. Ph.D. Thesis, Technischen Universität Wien, Vienna, Austria, 2011. [Google Scholar]
- DeMaio, P.; Meddin, R. The Bike-Sharing World—First Week of June 2014. 2014. Available online: http://bike-sharing.blogspot.com.es/2014/06/the-bike-sharing-world-first-week-of.html (accessed on 31 December 2023).
- Benchimol, M.; Benchimol, P.; Chappert, B.; De la Taille, A.; Laroche, F.; Meunier, F.; Robinet, L. Balancing the stations of a self service bike hire system. RAIRO Oper. Res. 2011, 45, 37–61. [Google Scholar] [CrossRef]
- Erdoğan, G.; Battarra, M.; Wolfler Calvo, R. An exact algorithm for the static rebalancing problem arising in bicycle sharing systems. Eur. J. Oper. Res. 2015, 245, 667–679. [Google Scholar] [CrossRef]
- Cruz, F.; Subramanian, A.; Bruck, B.P.; Iori, M. A heuristic algorithm for a single vehicle static bike sharing rebalancing problem. Comput. Oper. Res. 2017, 79, 19–33. [Google Scholar] [CrossRef]
- Erdoğan, G.; Laporte, G.; Wolfler Calvo, R. The static bicycle relocation problem with demand intervals. Eur. J. Oper. Res. 2014, 238, 451–457. [Google Scholar] [CrossRef]
- Kadri, A.A.; Kacem, I.; Labadi, K. A branch-and-bound algorithm for solving the static rebalancing problem in bicycle-sharing systems. Comput. Ind. Eng. 2016, 95, 41–52. [Google Scholar] [CrossRef]
- Mladenović, N.; Hansen, P. A variable neighborhood algorithm: A new metaheuristic for combinatorial optimization. In Proceedings of the Abstract for Papers presented at Optimization Days, Montreal, QC, Canada, 8–10 May 1995; p. 112. [Google Scholar]
- Mladenović, N.; Hansen, P. Variable neighborhood search. Comput. Oper. Res. 1997, 24, 1097–1100. [Google Scholar] [CrossRef]
- Daza-Escorcia, J.M.; Alvarez-Martinez, D. A Matheuristic Multi-Start Algorithm for a Novel Static Repositioning Problem in Public Bike-Sharing Systems. In Proceedings of the Metaheuristics, MIC 2014, Lorient, France, 4–7 June 2024; Lecture Notes in Computer Science. Sevaux, M., Ed.; Springer Nature: Cham, Switzerland, 2014; Volume 14754, pp. 188–203. [Google Scholar] [CrossRef]
- CPLEX. Optimization Studio ILOG IBM CPLEX. 2017. Available online: https://www.ibm.com/us-en/marketplace/ibm-ilog-cplex (accessed on 31 December 2023).
- Hansen, P.; Mladenović, N. Variable neighborhood search. In Handbook of Metaheuristics; Glover, F., Gary, K., Eds.; Kluwer Academic Publishers: Boston, MA, USA, 2003; Chapter 6; pp. 145–184. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).