Linearly Implicit Conservative Schemes for the Nonlocal Schrödinger Equation

Abstract

This paper introduces two high-accuracy linearly implicit conservative schemes for solving the nonlocal Schrödinger equation, employing the extrapolation technique. These schemes are based on the generalized scalar auxiliary variable approach and the symplectic Runge–Kutta method. By integrating these advanced methods, the proposed schemes aim to significantly enhance computational accuracy and efficiency, while maintaining the essential conservative properties necessary for accurate physical modeling. This offers a structured approach to handle auxiliary variables, ensuring stability and conservation, while the symplectic Runge–Kutta method provides a robust framework with high accuracy. Together, these techniques offer a powerful and reliable approach for researchers dealing with complex quantum mechanical systems described by the nonlocal Schrödinger equation, ensuring both accuracy and stability in their numerical simulations.

1. Introduction

The nonlocal nonlinear Schrödinger (NLS) equation is a fundamental equation in quantum mechanics that extends the classical Schrödinger equation by incorporating nonlocal interactions. This modification allows for a more accurate representation of systems where the interactions cannot be adequately described by the local potentials alone. Nonlocal interactions are crucial in various physical contexts, such as in the study of quantum fluids [1], Bose–Einstein condensates [2], and in modeling long-range interactions in condensed matter physics [3]. In this paper, we consider the following nonlocal NLS equation [4]:

$$\begin{array}{c}\hfill \mathrm{i}{\displaystyle \frac{\partial u(\mathit{x},t)}{\partial t}}-{(-\mathcal{L})}^{\gamma }u(\mathit{x},t)+\beta {\left|u(\mathit{x},t)\right|}^{2}u(\mathit{x},t)=0,\mathit{x}\in \mathrm{\Omega }\subset {\mathbb{R}}^2,t\in (0,T],\end{array}$$

(1)

with the initial condition

$$\begin{array}{c}\hfill u(\mathit{x},0)=u_0\left(\mathit{x}\right),\mathit{x}\in \mathrm{\Omega },\end{array}$$

where ${\mathrm{i}}^2=-1$, $0<\gamma \le 1$, and consider the domain $\mathrm{\Omega }:=[-L,L]\times [-L,L]$. The function $u(\mathit{x},t)$ represents a complex-valued wave function with period $2L$, and $u_0\left(\mathit{x}\right)$ is a prescribed smooth function. The constant $\beta$ is a positive real number associated with focusing nonlinearity. Within a finite computational domain, the fractional Laplacian operator can be defined as [5]

$$\begin{array}{c}\hfill {\mathcal{L}}^{\gamma }\phi (\mathit{x},t)=-\sum _{k_1\in \mathbb{Z}}\sum _{k_2\in \mathbb{Z}}{|{\nu }_{k_1}^2+{\nu }_{k_2}^2|}^{{\displaystyle \frac{\gamma }{2}}\widehat{\prime }}{\mathbf{k}}^{e^{\mathrm{i}{\mathit{\nu }}_{\mathbf{k}}·(\mathit{x}+\mathit{L})}},\end{array}$$

where ${\nu }_{k_i}={\displaystyle \frac{k_i\pi }{L}}$ (i = 1, 2), ${\mathit{\nu }}_{\mathbf{k}}·(\mathit{x}+\mathit{L}):={\displaystyle \sum _{i=1}^2}{\nu }_{k_i}(x_i+L)$, ${\widehat{\prime }}_{\mathbf{k}}={\displaystyle \frac{1}{{\left(2L\right)}^2}}{\int }_{\mathrm{\Omega }}\phi (\mathit{x},t)e^{-\mathrm{i}{\mathit{\nu }}_k·(\mathit{x}+\mathit{L})}d\mathit{x}.$

Recently, scholars have developed many methods to obtain analytic solutions for partial differential equations, such as the Adomian decomposition method [6], the Lie symmetry approach [7], and the variational iteration method [8]. However, the analytic solution of nonlocal differential equations is generally difficult or impossible to obtain, due to the non-locality of the nonlocal operators. As a result, many numerical methods have been developed for solving nonlocal NLS equations, such as spectral methods [9], finite element methods [10], and finite difference methods [11]. These numerical approaches are essential for studying the behavior of solutions, especially in cases where traditional analytical techniques fail to provide explicit solutions, thereby enabling researchers to explore the complex dynamics of fractional differential systems.

By setting $u=p+\mathrm{i}q$, System (1) can be transformed into a pair of real-valued equations,

$$\begin{array}{cc}\hfill & p_t={(-\mathcal{L})}^{\gamma }q-\beta (p^2+q^2)q,\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill & q_t=-{(-\mathcal{L})}^{\gamma }p+\beta (p^2+q^2)p.\hfill \end{array}$$

(3)

We can easily demonstrate that the above system possesses a nonlocal energy conservation law under appropriate boundary conditions, which are given by

$$\begin{array}{c}\hfill \mathcal{H}(p,q)={\displaystyle \frac{1}{2}}{\int }_{\mathrm{\Omega }}\left[{\left({(-\mathcal{L})}^{\gamma }p\right)}^2+{\left({(-\mathcal{L})}^{\gamma }q\right)}^2\right]d\mathit{x}-{\displaystyle \frac{\beta }{4}}{\int }_{\mathrm{\Omega }}{(p^2+q^2)}^{2}d\mathit{x},\end{array}$$

(4)

where $\mathcal{H}$ represents the energy function. Utilizing the variational derivative formula with nonlocal operator [12], Systems (2) and (3) can be reformulated as an infinite-dimensional Hamiltonian system,

$$\begin{array}{c}\hfill {\displaystyle \frac{d\mathit{z}}{dt}}=J^{-1}{\displaystyle \frac{\delta \mathcal{H}}{\delta \mathit{z}}},\mathrm{with}\mathit{z}={(p,q)}^T,J=\left(\begin{array}{cc}0& 1\\ -1& 0\end{array}\right),\end{array}$$

and this representation highlights the Hamiltonian structure underlying the nonlocal system.

Structure-preserving algorithms have achieved significant success in the numerical analysis of classical differential equations, inspiring the development of similar approaches for nonlocal differential equations [13,14,15]. Many researchers are focused on designing numerical methods that preserve the energy of nonlocal NLS equations, especially in long-time simulations. For instance, Xiao developed an energy-preserving difference scheme for equations with nonlocal derivatives [11]. Li et al. proposed a fast finite element method that maintains the energy and mass conservation of the problem [10]. There is extensive related research in this field, and readers are encouraged to consult relevant review articles for more information [16,17,18]. However, many energy-preserving schemes for the nonlocal NLS equation are fully implicit, resulting in high computational costs. To address this, some researchers have recently developed linearly implicit energy-preserving schemes to reduce complexity. However, the resulting schemes have only second-accuracy in time, and exhibit poor accuracy, particularly when modeling complex physical phenomena or capturing fine details in the solution.

Over the past decade, various numerical methods have been developed to achieve high-accuracy conservative schemes for conservative systems [19,20]. However, these methods are typically fully implicit, requiring the solution of nonlinear equations at each time step, which substantially increases computational cost, particularly in large-scale simulations. Linearly implicit schemes, on the other hand, provide a computationally efficient alternative to fully implicit methods. They offer a good balance between accuracy and computational efficiency, making them more suitable for large-scale simulations on modern computing platforms. Consequently, there is a growing interest in developing and analyzing high-accuracy linearly implicit conservative numerical schemes specifically tailored for the nonlocal NLS equation. The symplectic Runge–Kutta method is renowned for maintaining the energy and geometric properties of Hamiltonian systems, ensuring both long-term stability and accuracy in numerical simulations [21]. These strengths form a foundation for designing high-accuracy conservation schemes. This paper aims to utilize the generalized scalar auxiliary variable (GSAV) method [22] combined with the Runge–Kutta approach to develop high-accuracy, linearly implicit conservative schemes for the nonlocal NLS equation. The main goals are: (I) to develop linearly implicit high-order schemes capable of efficiently obtaining numerical solutions, and (II) to ensure the schemes conserve the system’s energy, enhancing stability in simulations. Overall, the objective is to design a numerical method that achieves a balance between accuracy and computational efficiency, making it well-suited for large-scale simulations while preserving the intrinsic energy properties of the system. However, the convergence analysis of these proposed schemes has not been covered, and remains a subject for future research.

2. Semi-Discrete Conservative System

First, we derive a semi-discrete conservative system for the nonlocal NLS equation by using the Fourier pseudo-spectral method in the space direction.

2.1. Structure-Preserving Spatial Discretization

Let $N_x$, $N_y$, and N be positive even integers. Define the spatial step sizes $h_x={\displaystyle \frac{2L}{N_x}}$ and $h_y={\displaystyle \frac{2L}{N_y}}$, and set the time step $\tau ={\displaystyle \frac{T}{N}}$. The spatial grid points are

$${\mathrm{\Omega }}_h=\left\{(x_i,y_j)|x_i=-L+i{h}_x,y_j=-L+j{h}_y,0\le i\le N_x-1,0\le j\le N_y-1\right\}.$$

Define the vector space of grid functions on ${\mathrm{\Omega }}_h$ as

$${\mathcal{V}}_h=\left\{\mathit{v}\right|\mathit{v}={(v_{0,0},\cdots ,v_{N_x-1,0},v_{0,1},\cdots ,v_{N_x-1,1},\cdots ,v_{0,N_y-1},\cdots ,v_{N_x-1,N_y-1})}^T\}.$$

For any $\mathit{u},\mathit{v}\in {\mathcal{V}}_h$, the discrete inner product and norms are defined by

$${⟨\mathit{u},\mathit{v}⟩}_h=h_x{h}_y\sum _{i=0}^{N_x-1}\sum _{j=0}^{N_y-1}{u}_{i,j}{\overline{v}}_{i,j},\parallel \mathit{u}\parallel =\sqrt{{⟨\mathit{u},\mathit{u}⟩}_h}{,\parallel \mathit{u}\parallel }_{\infty }=\underset{(x_i,y_j)\in {\mathrm{\Omega }}_h}{max}\left|u_{i,j}\right|,$$

where ${\overline{v}}_{i,j}$ denotes the complex conjugate of $v_{i,j}$.

Let $(x_i,y_j)\in {\mathrm{\Omega }}_h$ be the Fourier collocation points. Using the interpolation polynomial $I_{\mathbf{N}}p(x,y)$ to approximate $p_{\mathbf{N}}(x,y)$ of the function $p(x,y)$, which is defined by

$$I_{\mathbf{N}}p(x,y)=p_{\mathbf{N}}(x,y)=\sum _{k_1=-N_x/2}^{N_x/2}\sum _{k_2=-N_y/2}^{N_y/2}{\tilde{p}}_{k_1,k_2}{e}^{i{k}_1\mu (x+L)}{e}^{i{k}_2\mu (y+L)},$$

where $\mu ={\displaystyle \frac{\pi }{L}}$, the coefficients ${\tilde{p}}_{k_1,k_2}$ are given by

$${\tilde{p}}_{k_1,k_2}={\displaystyle \frac{1}{N_x{c}_{k_1}}}{\displaystyle \frac{1}{N_y{c}_{k_2}}}\sum _{i=0}^{N_x-1}\sum _{j=0}^{N_y-1}p(x_i,y_j)e^{-i{k}_1\mu (x_i+L)}{e}^{-i{k}_2\mu (y_j+L)},$$

with

$$c_{k_1}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}|k_1|<N_x/2,\hfill \\ 2,\hfill & \mathrm{if}{k}_1=\pm N_x/2,\hfill \end{array}\right.c_{k_2}=\left\{\begin{array}{cc}1,\hfill & \mathrm{if}|k_2|<N_y/2,\hfill \\ 2,\hfill & \mathrm{if}{k}_2=\pm N_y/2.\hfill \end{array}\right.$$

Then, the nonlocal Laplacian $-{(-\mathcal{L})}^{\gamma }p(x,y)$ can be approximated by

$$-{(-\mathcal{L})}^{\gamma }{p}_{\mathbf{N}}(x_i,y_j)=-\sum _{\mathbf{k}=-\mathbf{N}/2}^{\mathbf{N}/2}{|{\mu }^2{k}_1^2+{\mu }^2{k}_2^2|}^{\gamma }{\tilde{p}}_{k_1,k_2}{e}^{-i\mu \mathbf{k}·(\mathbf{x}+\mathbf{L})},$$

where ${\sum }_{\mathbf{k}=-\mathbf{N}/2}^{\mathbf{N}/2}={\sum }_{k_1=-N_x/2}^{N_x/2}{\sum }_{k_2=-N_y/2}^{N_y/2}$ and $\mathbf{k}·(\mathbf{x}+\mathbf{L})=k_1(x+L)+k_2(y+L)$.

We denote ${\mu }^2{\mathbf{k}}^2={\mu }^2(k_1^2+k_2^2)$ and substitute ${\tilde{p}}_{k_1,k_2}$ into the equation above. The nonlocal Laplacian $-{(-\mathcal{L})}^{\gamma }$ can be approximated in matrix form [12],

$$-{(-\mathcal{L})}^{\gamma }{p}_{\mathbf{N}}(x_i,y_j)={\left(D^{\gamma }\mathbf{p}\right)}_{i+j{N}_x},$$

where the spectral differentiation matrix $D^{\gamma }$ is symmetric with elements

$${\left(D^{\gamma }\right)}_{i+j{N}_x,l+m{N}_x}=-\sum _{\mathbf{k}=-\mathbf{N}/2}^{\mathbf{N}/2}{\displaystyle \frac{1}{N_x{c}_{k_1}}}{\displaystyle \frac{1}{N_y{c}_{k_2}}}{\left|{\mu }^2{\mathbf{k}}^2\right|}^{\gamma }{e}^{-i\mu \left[k_1(x_i-x_l)+k_2(y_j-y_m)\right]}.$$

2.2. Semi-Discrete System

By applying the Fourier pseudo-spectral method to the real-valued Equations (2) and (3), we obtain the following semi-discrete system:

$$\begin{array}{cc}\hfill & {\mathit{p}}_t=-D^{\gamma }\mathit{q}-\beta ({\mathit{p}}^2+{\mathit{q}}^2)\mathit{q},\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill & {\mathit{q}}_t=D^{\gamma }\mathit{p}+\beta ({\mathit{p}}^2+{\mathit{q}}^2)\mathit{p}.\hfill \end{array}$$

(6)

Theorem 1. 

The proposed Schemes, (5) and (6), can preserve the following semi-discrete energy:

$${\displaystyle \frac{d}{dt}}\mathcal{E}\left(t\right)=0,$$

(7)

where

$$\mathcal{E}\left(t\right)=\left({⟨\mathit{p},D^{\gamma }\mathit{p}⟩}_h+{⟨\mathit{q},D^{\gamma }\mathit{q}⟩}_h\right)+{\displaystyle \frac{\beta }{2}}{⟨{\mathit{p}}^2+{\mathit{q}}^2,{\mathit{p}}^2+{\mathit{q}}^2⟩}_h,$$

(8)

where ${⟨·,·⟩}_h$ denotes the discrete inner product.

Proof. 

Computing ${\displaystyle \frac{d}{dt}}\mathcal{E}\left(t\right)$, we can derive

$${\displaystyle \frac{d}{dt}}\mathcal{E}\left(t\right)=2{⟨{\displaystyle \frac{d}{dt}}\mathit{p},D^{\gamma }\mathit{p}⟩}_h+2{⟨{\displaystyle \frac{d}{dt}}\mathit{q},D^{\gamma }\mathit{q}⟩}_h+\beta {⟨{\mathit{p}}^2+{\mathit{q}}^2,{\displaystyle \frac{d}{dt}}({\mathit{p}}^2+{\mathit{q}}^2)⟩}_h.$$

(9)

Calculating the time derivative for ${\displaystyle \frac{d}{dt}}({\mathit{p}}^2+{\mathit{q}}^2)$, we can obtain

$${\displaystyle \frac{d}{dt}}({\mathit{p}}^2+{\mathit{q}}^2)=2(\mathit{p}{\mathit{p}}_t+\mathit{q}{\mathit{q}}_t).$$

(10)

Substituting this into Equation (9), we can obtain

$${\displaystyle \frac{d}{dt}}\mathcal{E}\left(t\right)=2{⟨{\mathit{p}}_t,D^{\gamma }\mathit{p}⟩}_h+2{⟨{\mathit{q}}_t,D^{\gamma }\mathit{q}⟩}_h+2\beta {⟨{\mathit{p}}^2+{\mathit{q}}^2,\mathit{p}{\mathit{p}}_t+\mathit{q}{\mathit{q}}_t⟩}_h.$$

(11)

From Equations (5) and (6), we have

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}\mathcal{E}\left(t\right)& =2{⟨-D^{\gamma }\mathit{q}-\beta ({\mathit{p}}^2+{\mathit{q}}^2)\mathit{q},D^{\gamma }\mathit{p}⟩}_h+2{⟨D^{\gamma }\mathit{p}+\beta ({\mathit{p}}^2+{\mathit{q}}^2)\mathit{p},D^{\gamma }\mathit{q}⟩}_h\hfill \\ \hfill & +2\beta {⟨{\mathit{p}}^2+{\mathit{q}}^2,\mathit{p}\left(-D^{\gamma }\mathit{q}-\beta ({\mathit{p}}^2+{\mathit{q}}^2)\mathit{q}\right)+\mathit{q}\left(D^{\gamma }\mathit{p}+\beta ({\mathit{p}}^2+{\mathit{q}}^2)\mathit{p}\right)⟩}_h.\hfill \end{array}$$

(12)

Noting that

$$\begin{array}{cc}\hfill & 2{⟨-D^{\gamma }\mathit{q},D^{\gamma }\mathit{p}⟩}_h+2{⟨D^{\gamma }\mathit{p},D^{\gamma }\mathit{q}⟩}_h=-2{⟨D^{\gamma }\mathit{q},D^{\gamma }\mathit{p}⟩}_h+2{⟨D^{\gamma }\mathit{p},D^{\gamma }\mathit{q}⟩}_h=0.\hfill \end{array}$$

(13)

and

$$\begin{array}{cc}\hfill & 2{\beta }^2{⟨{\mathit{p}}^2+{\mathit{q}}^2,-\mathit{p}({\mathit{p}}^2+{\mathit{q}}^2)\mathit{q}+\mathit{q}({\mathit{p}}^2+{\mathit{q}}^2)\mathit{p}⟩}_h\hfill \\ \hfill & =2{\beta }^2{⟨{\mathit{p}}^2+{\mathit{q}}^2,-\mathit{p}({\mathit{p}}^2+{\mathit{q}}^2)\mathit{q}+\mathit{q}({\mathit{p}}^2+{\mathit{q}}^2)\mathit{p}⟩}_h=0.\hfill \end{array}$$

(14)

After simplification, all terms sum to zero, namely

$${\displaystyle \frac{d}{dt}}\mathcal{E}\left(t\right)=0,$$

(15)

which implies that the discrete energy $\mathcal{E}\left(t\right)$ is conserved over time, i.e., $\mathcal{E}\left(t\right)=\mathcal{E}\left(0\right)$ for all $t\ge 0$. Therefore, the semi-discrete Systems (5) and (6) satisfy the energy conservation law. □

3. Equivalent System with ESAV Approach

Following the idea of the GSAV approach, we aim to apply an equivalent transformation to the real-valued Equations (5) and (6). We introduce an auxiliary variable $r\left(t\right)$ as follows:

$$r\left(t\right)=\mathcal{G}(\mathit{p},\mathit{q}):=\mathcal{G}\left({⟨{\mathit{p}}^2+{\mathit{q}}^2,{\mathit{p}}^2+{\mathit{q}}^2⟩}_h\right),$$

(16)

where $\mathcal{G}$ is an invertible function. The discrete energy functional can be rewritten using the auxiliary variable $r\left(t\right)$ as

$$E\left(t\right)={⟨\mathit{p},D^{\gamma }\mathit{p}⟩}_h+{⟨\mathit{q},D^{\gamma }\mathit{q}⟩}_h+{\displaystyle \frac{\beta }{2}}{\mathcal{G}}^{-1}\left(r\right).$$

(17)

We can express the nonlinear terms in the system using $r\left(t\right)$,

$$({\mathit{p}}^2+{\mathit{q}}^2)\mathit{q}={\displaystyle \frac{r}{\mathcal{G}(\mathit{p},\mathit{q})}}({\mathit{p}}^2+{\mathit{q}}^2)\mathit{q},$$

(18)

$$({\mathit{p}}^2+{\mathit{q}}^2)\mathit{p}={\displaystyle \frac{r}{\mathcal{G}(\mathit{p},\mathit{q})}}({\mathit{p}}^2+{\mathit{q}}^2)\mathit{p}.$$

(19)

Differentiating $r\left(t\right)$ with respect to time t, we obtain

$${\displaystyle \frac{dr}{dt}}=4{\mathcal{G}}^{\prime }\left({⟨{\mathit{p}}^2+{\mathit{q}}^2,{\mathit{p}}^2+{\mathit{q}}^2⟩}_h\right){⟨{\mathit{p}}^2+{\mathit{q}}^2,\mathit{p}{\mathit{p}}_t+\mathit{q}{\mathit{q}}_t⟩}_h,$$

(20)

where ${\mathcal{G}}^{\prime }$ denotes the derivative of $\mathcal{G}$ with respect to its argument. From the property of $\mathcal{G}$, we have

$${\left({\mathcal{G}}^{-1}\right)}^{\prime }\left(r\right)={\displaystyle \frac{1}{{\mathcal{G}}^{\prime }\left({⟨{\mathit{p}}^2+{\mathit{q}}^2,{\mathit{p}}^2+{\mathit{q}}^2⟩}_h\right)}}.$$

(21)

We reformulate Systems (5) and (6) as

$$\begin{array}{cc}\hfill & {\mathit{p}}_t=-D^{\gamma }\mathit{q}-\beta A^{\mathit{p},\mathit{q}},\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & {\mathit{q}}_t=\phantom{-}{D}^{\gamma }\mathit{p}+\beta B^{\mathit{p},\mathit{q}},\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}}{\mathcal{G}}^{-1}\left(r\right)=4{⟨A^{\mathit{p},\mathit{q}},{\mathit{q}}_t⟩}_h+4{⟨B^{\mathit{p},\mathit{q}},{\mathit{p}}_t⟩}_h,\hfill \end{array}$$

(24)

where

$$\begin{array}{c}\hfill A^{\mathit{p},\mathit{q}}={\displaystyle \frac{r}{\mathcal{G}(\mathit{p},\mathit{q})}}({\mathit{p}}^2+{\mathit{q}}^2)\mathit{q},\end{array}$$

(25)

$$\begin{array}{c}\hfill B^{\mathit{p},\mathit{q}}={\displaystyle \frac{r}{\mathcal{G}(\mathit{p},\mathit{q})}}({\mathit{p}}^2+{\mathit{q}}^2)\mathit{p}.\end{array}$$

(26)

The initial conditions for the transformed system are

$$\mathit{p}\left(0\right)={\mathit{p}}_0,\mathit{q}\left(0\right)={\mathit{q}}_0,r\left(0\right)=\mathcal{G}({\mathit{p}}_0,{\mathit{q}}_0),$$

(27)

where ${\mathit{p}}_0$ and ${\mathit{q}}_0$ are the initial values of $\mathit{p}$ and $\mathit{q}$, respectively.

Remark 1. 

By choosing different functions for $\mathcal{G}\left(x\right)$, we can derive various Scalar Auxiliary Variable (SAV) approaches, as discussed in [22]. For instance, setting $\mathcal{G}\left(x\right)=tanh\left({\displaystyle \frac{x}{\mathbf{C}}}\right)$ or $\mathcal{G}\left(x\right)=exp\left({\displaystyle \frac{x}{\mathbf{C}}}\right)$ with $\mathbf{C}>0$ allows us to construct new numerical schemes. Notably, if we choose $\mathcal{G}\left(x\right)=\sqrt{x+\mathbf{C}}$, the GSAV approach becomes equivalent to the traditional SAV method presented in [23,24,25].

Theorem 2. 

Under the periodic boundary condition, Systems (22)–(24) possess the following modified energy conservation law:

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}E\left(t\right)=0,\end{array}$$

(28)

where $E\left(t\right)$ is given by (17).

Proof. 

Computing the time derivative of $E\left(t\right)$, we can derive

$${\displaystyle \frac{d}{dt}}E\left(t\right)=2{⟨{\mathit{p}}_t,D^{\gamma }\mathit{p}⟩}_h+2{⟨{\mathit{q}}_t,D^{\gamma }\mathit{q}⟩}_h+{\displaystyle \frac{\beta }{2}}{\displaystyle \frac{d}{dt}}{\mathcal{G}}^{-1}\left(r\right).$$

(29)

Substituting ${\mathit{p}}_t$ and ${\mathit{q}}_t$ from Equations (22) and (23), we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}E\left(t\right)& =2({⟨-D^{\gamma }\mathit{q}-\beta A^{\mathit{p},\mathit{q}},D^{\gamma }\mathit{p}⟩}_h+{⟨D^{\gamma }\mathit{p}+\beta B^{\mathit{p},\mathit{q}},D^{\gamma }\mathit{q}⟩}_h)-{\displaystyle \frac{\beta }{2}}{\displaystyle \frac{d}{dt}}{\mathcal{G}}^{-1}\left(r\right)\hfill \\ \hfill & =2(-{⟨D^{\gamma }\mathit{q},D^{\gamma }\mathit{p}⟩}_h-\beta {⟨A^{\mathit{p},\mathit{q}},D^{\gamma }\mathit{p}⟩}_h)\hfill \\ \hfill & +2({⟨D^{\gamma }\mathit{p},D^{\gamma }\mathit{q}⟩}_h+\beta {⟨B^{\mathit{p},\mathit{q}},D^{\gamma }\mathit{q}⟩}_h)+{\displaystyle \frac{\beta }{2}}{\displaystyle \frac{d}{dt}}{\mathcal{G}}^{-1}\left(r\right).\hfill \end{array}$$

(30)

Noting that

$$-{⟨D^{\gamma }\mathit{q},D^{\gamma }\mathit{p}⟩}_h+{⟨D^{\gamma }\mathit{p},D^{\gamma }\mathit{q}⟩}_h=0.$$

Therefore,

$${\displaystyle \frac{d}{dt}}E\left(t\right)=-2\beta {⟨A^{\mathit{p},\mathit{q}},D^{\gamma }\mathit{p}⟩}_h+2\beta {⟨B^{\mathit{p},\mathit{q}},D^{\gamma }\mathit{q}⟩}_h+{\displaystyle \frac{\beta }{2}}{\displaystyle \frac{d}{dt}}{\mathcal{G}}^{-1}\left(r\right).$$

(31)

From Equation (24), we have

$$4\left({⟨A^{\mathit{p},\mathit{q}},D^{\gamma }\mathit{p}⟩}_h-{⟨D^{\gamma }\mathit{q},B^{\mathit{p},\mathit{q}}⟩}_h\right)={\displaystyle \frac{d}{dt}}{\mathcal{G}}^{-1}\left(r\right).$$

(32)

Substituting (32) into (31), we obtain

$$\begin{array}{cc}\hfill {\displaystyle \frac{d}{dt}}E\left(t\right)& =-2\beta \left({\displaystyle \frac{1}{4}}{\displaystyle \frac{d}{dt}}{\mathcal{G}}^{-1}\left(r\right)\right)+{\displaystyle \frac{\beta }{2}}{\displaystyle \frac{d}{dt}}{\mathcal{G}}^{-1}\left(r\right)\hfill \\ \hfill & =-{\displaystyle \frac{\beta }{2}}{\displaystyle \frac{d}{dt}}{\mathcal{G}}^{-1}\left(r\right)+{\displaystyle \frac{\beta }{2}}{\displaystyle \frac{d}{dt}}{\mathcal{G}}^{-1}\left(r\right)\hfill \\ \hfill & =0.\hfill \end{array}$$

(33)

We complete the proof. □

4. Linearly Implicit Energy-Preserving Schemes

In this section, we introduce a family of high-order fully discrete conservative schemes for approximating Systems (22)–(24) by employing symplectic Runge–Kutta methods combined with extrapolation techniques. To begin, we present essential notations related to symplectic Runge–Kutta methods (Table 1).

Table 1. Coefficients of symplectic RK methods of order 4 (top) and 6 (bottom).

$\frac{1}{2}-\frac{\sqrt{3}}{6}$	$\frac{1}{4}$	$\frac{1}{4}-\frac{\sqrt{3}}{6}$
${\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sqrt{3}}{6}}$	${\displaystyle \frac{1}{4}}+{\displaystyle \frac{\sqrt{3}}{6}}$	${\displaystyle \frac{1}{4}}$
	${\displaystyle \frac{1}{2}}$	${\displaystyle \frac{1}{2}}$
${\displaystyle \frac{1}{2}}-{\displaystyle \frac{\sqrt{15}}{10}}$	${\displaystyle \frac{5}{36}}$	${\displaystyle \frac{2}{9}}-{\displaystyle \frac{\sqrt{15}}{15}}$	${\displaystyle \frac{5}{36}}-{\displaystyle \frac{\sqrt{15}}{30}}$
${\displaystyle \frac{1}{2}}$	${\displaystyle \frac{5}{36}}+{\displaystyle \frac{\sqrt{15}}{24}}$	${\displaystyle \frac{2}{9}}$	${\displaystyle \frac{5}{36}}-{\displaystyle \frac{\sqrt{15}}{24}}$
${\displaystyle \frac{1}{2}}+{\displaystyle \frac{\sqrt{15}}{10}}$	${\displaystyle \frac{5}{36}}+{\displaystyle \frac{\sqrt{15}}{30}}$	${\displaystyle \frac{2}{9}}+{\displaystyle \frac{\sqrt{15}}{15}}$	${\displaystyle \frac{5}{36}}$
	${\displaystyle \frac{5}{18}}$	${\displaystyle \frac{4}{9}}$	${\displaystyle \frac{5}{18}}$

4.1. Symplectic RK Methods

We consider the ordinary differential equation

$$\begin{array}{c}\hfill {\displaystyle \frac{dw\left(t\right)}{dt}}=f\left(t\right),w\left(t_0\right)=w_0.\end{array}$$

(34)

Let $\tau$ be the time step size, and define $t_n=n\tau$ for $n=0,1,\cdots ,N$. Let $a_{ij}$, $b_i$, and $c_i={\displaystyle \sum _{j=1}^s}{a}_{ij}$ be real numbers. Over the interval $[t_n,t_{n+1}]$, the s-stage Runge–Kutta (RK) method for solving Equation (34) is given by [21]

$$\begin{array}{cc}\hfill w_i& =w^n+\tau \sum _{j=1}^s{a}_{ij}{k}_j,k_i=f(t_n+c_i\tau ),i=1,2,\cdots ,s,\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill w^{n+1}& =w^n+\tau \sum _{i=1}^s{b}_i{k}_i.\hfill \end{array}$$

(36)

If the coefficients satisfy, for $i,j=1,2,\cdots ,s$,

$$\begin{array}{c}\hfill a_{ij}{b}_i+a_{ji}{b}_j=b_i{b}_j,\end{array}$$

(37)

then the RK method is symplectic, and preserves the quadratic invariants for conservative systems. We refer to Equation (37) as the condition for RK symplecticity.

Without loss of generality, we choose the $2s$-stage fourth- and sixth-order symplectic RK methods, which are provided by the Butcher tableau [21].

4.2. Construction of the Linearly Implicit Schemes

To reduce the computational complexity associated with fully implicit schemes that require nonlinear iterations during numerical simulations, this subsection uses extrapolation methods to construct linearly implicit conservative schemes, thereby improving computational efficiency. Let $t_{ni}=t_n+c_i\tau$ for $i=1,2,\dots ,s$ and $n=0,1,2,\dots$, where $c_1,c_2,\dots ,c_s$ are distinct real numbers, typically within $[0,1]$. We denote the approximations of $u(x,t)$ at times $t_n$ and $t_{ni}$ by ${\mathit{u}}^n$ and ${\mathit{u}}^{ni}$, respectively. Assuming numerical solutions of u are known for $t\le t_n$, we construct the Lagrange interpolating polynomial $u^{\ast }(x,t)$ based on the points $(t_n,{\mathit{u}}^n)$ and $(t_{ni},{\mathit{u}}^{ni})$. This polynomial $u^{\ast }(x,t)$ is then utilized to approximate the nonlinear terms of Systems (22)–(24) over the interval $(t_n,t_{n+1})$.

We proceed to apply the symplectic Runge–Kutta method to the reformulated Systems (22)–(24). By incorporating extrapolation techniques for discretizing the nonlinear terms, we derive the equations for the internal stages as follows:

$$\left\{\begin{array}{cccc}\hfill {\mathit{p}}_i^n& ={\mathit{p}}^n+\tau \sum _{j=1}^s{a}_{ij}{k}_p^j,\hfill & \hfill & k_p^i=-D^{\gamma }\mathit{q}-\beta A^{{\overline{\mathit{p}}}_i^{n,\ast },{\overline{\mathit{q}}}_i^{n,\ast }},\hfill \\ \hfill {\mathit{q}}_i^n& ={\mathit{q}}^n+\tau \sum _{j=1}^s{a}_{ij}{k}_q^j,\hfill & \hfill & k_q^i=D^{\gamma }\mathit{q}+\beta B^{{\overline{\mathit{p}}}_i^{n,\ast },{\overline{\mathit{q}}}_i^{n,\ast }},\hfill \\ \hfill {\mathit{r}}_i^n& =\mathcal{G}\left({\mathcal{G}}^{-1}\left({\mathit{q}}^n\right)+\tau \sum _{j=1}^s{a}_{ij}{k}_r^j\right),\hfill & \hfill & k_r^i=4{⟨A^{{\overline{\mathit{p}}}_i^{n,\ast },{\overline{\mathit{q}}}_i^{n,\ast }}⟩}_h+4{⟨B^{{\overline{\mathit{p}}}_i^{n,\ast },{\overline{\mathit{p}}}_i^{n,\ast }}⟩}_h.\hfill \end{array}\right.$$

(38)

Then, $({\mathit{p}}^{n+1},{\mathit{q}}^{n+1},{\mathit{r}}^{n+1})$ can be updated by

$$\left\{\begin{array}{cc}\hfill & {\mathit{p}}^{n+1}={\mathit{u}}^n+\tau \sum _{i=1}^s{b}_i{k}_p^i,\hfill \\ \hfill & {\mathit{q}}^{n+1}={\mathit{q}}^n+\tau \sum _{i=1}^s{b}_i{k}_q^i,\hfill \\ \hfill & {\mathit{r}}^{n+1}={\mathit{r}}^n+\tau \sum _{i=1}^s{b}_i{k}_r^i,\hfill \end{array}\right.$$

(39)

For $s=2$, the extrapolation technique for the nonlinear terms is expressed as

$$\begin{array}{cc}\hfill {\overline{\mathit{z}}}_1^{n,\ast }& =(2\sqrt{3}-4){\mathit{z}}^{n-1}+(7\sqrt{3}-11){\mathit{z}}_1^{n-1}+(6-5\sqrt{3}){\mathit{z}}_2^{n-1}+(10-4\sqrt{3}){\mathit{z}}^n,\hfill \\ \\ \hfill {\overline{\mathit{z}}}_2^{n,\ast }& =(-2\sqrt{3}-4){\mathit{z}}^{n-1}+(6+5\sqrt{3}){\mathit{z}}_1^{n-1}-(7\sqrt{3}+11){\mathit{z}}_2^{n-1}+(10+4\sqrt{3}){\mathit{z}}^n.\hfill \end{array}$$

These methods achieve third-order accuracy [21]. For $s=3$, the extrapolation technique is given by

$$\begin{array}{cc}\hfill {\overline{\mathit{z}}}_1^{n,\ast }& =(6\sqrt{15}-26){\mathit{z}}^{n-1}+{\displaystyle \frac{33-5\sqrt{15}}{3}}{\mathit{z}}_1^{n-1}+{\displaystyle \frac{16\sqrt{15}-72}{3}}{\mathit{z}}_2^{n-1}+{\displaystyle \frac{120-29\sqrt{15}}{3}}{\mathit{z}}_3^{n-1},\hfill \\ \\ \hfill {\overline{\mathit{z}}}_2^{n,\ast }& =-17{\mathit{z}}^{n-1}+{\displaystyle \frac{35+5\sqrt{15}}{2}}{\mathit{z}}_1^{n-1}-17{\mathit{z}}_2^{n-1}+{\displaystyle \frac{35-5\sqrt{15}}{2}}{\mathit{z}}_3^{n-1},\hfill \\ \\ \hfill {\overline{\mathit{z}}}_3^{n,\ast }& =(-26-6\sqrt{15}){\mathit{z}}^{n-1}+{\displaystyle \frac{120+29\sqrt{15}}{3}}{\mathit{z}}_1^{n-1}-{\displaystyle \frac{72+16\sqrt{15}}{3}}{\mathit{z}}_2^{n-1}+{\displaystyle \frac{33+5\sqrt{15}}{3}}{\mathit{z}}_3^{n-1}.\hfill \end{array}$$

where $\mathit{z}=\mathit{p},\mathit{q}$. These methods attain fourth-order accuracy [21]. In the subsequent discussions, we denote Schemes (38) and (39), which satisfy the symplectic condition, as the LI3 and LI4 schemes for $s=2$ and $s=3$, respectively.

Theorem 3. 

Systems (38) and (39) can inherit the following energy, i.e.,

$$\begin{array}{c}\hfill E^n=E^0,\end{array}$$

where $E^n$ is the energy function, which has the form

$$\begin{array}{c}\hfill E^n={⟨{\mathcal{D}}^{\gamma }{\mathit{p}}^n,{\mathit{p}}^n⟩}_h+{⟨{\mathcal{D}}^{\gamma }{\mathit{q}}^n,{\mathit{q}}^n⟩}_h+{\displaystyle \frac{\beta }{2}}{⟨{\mathcal{G}}^{-1}({\mathit{p}}^n,{\mathit{q}}^n),1⟩}_h.\end{array}$$

(40)

Proof. 

First, we define

$$\Delta E=E^{n+1}-E^n=\Delta E_p+\Delta E_q+\Delta E_r,$$

(41)

where

$$\begin{array}{cc}\hfill \Delta E_p& ={⟨{\mathcal{D}}^{\gamma }{\mathit{p}}^{n+1},{\mathit{p}}^{n+1}⟩}_h-{⟨{\mathcal{D}}^{\gamma }{\mathit{p}}^n,{\mathit{p}}^n⟩}_h,\hfill \\ \hfill \Delta E_q& ={⟨{\mathcal{D}}^{\gamma }{\mathit{q}}^{n+1},{\mathit{q}}^{n+1}⟩}_h-{⟨{\mathcal{D}}^{\gamma }{\mathit{q}}^n,{\mathit{q}}^n⟩}_h,\hfill \\ \hfill \Delta E_r& ={\displaystyle \frac{\beta }{2}}\left({⟨{\mathcal{G}}^{-1}\left({\mathit{r}}^{n+1}\right),1⟩}_h-{⟨{\mathcal{G}}^{-1}\left({\mathit{r}}^n\right),1⟩}_h\right).\hfill \end{array}$$

Using the updates from (39), we derive

$$\begin{array}{cc}\hfill \Delta E_p& =⟨{\mathcal{D}}^{\gamma }({\mathit{p}}^n+\tau \sum _{i=1}^s{b}_i{k}_p^i),{\mathit{p}}^n+\tau \sum _{i=1}^s{b}_i{k}_p^i{⟩}_h-{⟨{\mathcal{D}}^{\gamma }{\mathit{p}}^n,{\mathit{p}}^n⟩}_h,\hfill \\ \hfill \Delta E_q& =⟨{\mathcal{D}}^{\gamma }({\mathit{q}}^n+\tau \sum _{i=1}^s{b}_i{k}_q^i),{\mathit{q}}^n+\tau \sum _{i=1}^s{b}_i{k}_q^i{⟩}_h-⟨{\mathcal{D}}^{\gamma }{\mathit{q}}^n,{\mathit{q}}^n{⟩}_h.\hfill \end{array}$$

Expanding and simplifying using the symmetry of ${\mathcal{D}}^{\gamma }$ and the symplectic condition, (37), we obtain

$$\begin{array}{cc}\hfill \Delta E_p+\Delta E_q& =\tau \sum _{i=1}^s{b}_i\left({⟨{\mathcal{D}}^{\gamma }{\mathit{p}}^n,k_p^i⟩}_h+{⟨{\mathcal{D}}^{\gamma }{\mathit{q}}^n,k_q^i⟩}_h\right)+{\displaystyle \frac{{\tau }^2}{2}}\sum _{i,j=1}^s{b}_i{b}_j\left({⟨{\mathcal{D}}^{\gamma }{k}_p^i,k_p^j⟩}_h+{⟨{\mathcal{D}}^{\gamma }{k}_q^i,k_q^j⟩}_h\right)\hfill \\ \hfill & =-{\displaystyle \frac{\beta }{2}}\left(\tau \sum _{i=1}^s{b}_i{k}_r^i\right).\hfill \end{array}$$

(42)

From (39), we have

$$\Delta E_r={\displaystyle \frac{\beta }{2}}\left({⟨{\mathcal{G}}^{-1}\left({\mathit{r}}^{n+1}\right),1⟩}_h-{⟨{\mathcal{G}}^{-1}\left({\mathit{r}}^n\right),1⟩}_h\right)={\displaystyle \frac{\beta }{2}}\left(\tau \sum _{i=1}^s{b}_i{k}_r^i\right).$$

(43)

Using the definitions of $k_p^i$, $k_q^i$, and $k_r^i$, along with the properties of the inner product and the symmetry of ${\mathcal{D}}^{\gamma }$, we find that the sum $\Delta E_p+\Delta E_q+\Delta E_r=0$.

Since $\Delta E=0$, we have $E^{n+1}=E^n$. Therefore, the numerical scheme preserves the discrete energy.

The proof is completed. □

Remark 2. 

Currently, we are unable to demonstrate the convergence of the proposed scheme due to the following challenges:

• Obtaining convergence analysis results for high-dimensional problems is a challenging task.
• Incorporating a new variable and extrapolation techniques into the numerical schemes adds complexity to the system, making it harder to establish the convergence of the proposed schemes.

In future work, we aim to address these challenges and provide a rigorous convergence proof for the schemes.

5. Numerical Examples

This section focuses on verifying the energy conservation and effectiveness of the proposed schemes. Furthermore, we present a method for comparison to evaluate their performance.

• CN-SAV: a second-order energy-preserving scheme for the nonlocal wave equation based on the SAV method.
• AVF: a second-order energy-preserving scheme for the nonlocal wave equation based on the averaged vector field (AVF) method.

Example 1. 

In this subsection, we study the 1D nonlocal NLS equation

$$\begin{array}{c}\hfill i{u}_t-{(-\Delta )}^{{\displaystyle \frac{\alpha }{2}}}u+2{\left|u\right|}^{2}u=0,\end{array}$$

(44)

with the initial condition

$$\begin{array}{c}\hfill u(x,0)=exp(-x^2)\exp (-ix),\end{array}$$

(45)

and we take the space interval $\mathrm{\Omega }=[-40,40]$.

In practical computations, we take $\mathcal{G}\left(x\right)=exp\left(x\right)$, and set $\mathcal{N}=256$ to ensure that spatial discretization errors are minimal, allowing us to focus on evaluating the temporal discretization errors of the proposed energy-preserving methods. We compute the numerical errors by using the formula ${\parallel e\parallel }_{\infty }={\parallel z(h,\tau )-z(h,\tau /2)\parallel }_{\infty },$ where $z(h,\tau )$ represent the numerical solution at $(h,\tau )$. Table 2 compares the errors and convergence rates of four numerical schemes: CN-SAV, LI3, LI4, and AVF, evaluated at $t=1$ with different time step sizes $\tau$ and parameters $\gamma$. The CN-SAV and AVF schemes exhibit second-order convergence, as indicated by rates close to 2, confirming their expected accuracy. The LI3 scheme shows third-order convergence with rates near 3, validating its higher accuracy. Similarly, the LI4 scheme demonstrates fourth-order convergence, maintaining high precision with rates consistently close to 4. Overall, the LI3 and LI4 schemes provide superior performance due to their higher convergence orders, making them more suitable for applications requiring greater numerical accuracy compared to the second-order CN-SAV and AVF schemes.

Table 2. Errors and corresponding temporal observation orders of four conservative schemes with different $\gamma$ at $t=1$.

$\mathit{\gamma }$	$\mathit{\tau }$	$\mathbf{CN}\text{-}\mathbf{SAV}\mathbf{Scheme}$		$\mathbf{LI}3\mathbf{Scheme}$		$\mathbf{LI}4\mathbf{Scheme}$		$\mathbf{AVF}\mathbf{Scheme}$
		${\mathsf{\parallel }\mathit{e}\mathsf{\parallel }}_{\mathsf{\infty }}$	Rate	${\mathsf{\parallel }\mathit{e}\mathsf{\parallel }}_{\mathsf{\infty }}$	Rate	${\mathsf{\parallel }\mathit{e}\mathsf{\parallel }}_{\mathsf{\infty }}$	Rate	${\mathsf{\parallel }\mathit{e}\mathsf{\parallel }}_{\mathsf{\infty }}$	Rate
0.6	0.01	4.15 × 10−4	-	4.72 × 10−6	-	6.47 × 10−7	-	5.68 × 10−4	-
	0.005	1.06 × 10−4	1.97	7.33 × 10−7	2.69	4.99 × 10−8	3.69	1.46 × 10−4	1.96
	0.0025	2.68 × 10−5	1.98	1.02 × 10−7	2.85	3.43 × 10−9	3.86	3.68 × 10−5	1.99
0.8	0.01	2.24 × 10−5	-	1.53 × 10−7	-	1.56 × 10−8	-	1.79 × 10−3	-
	0.005	5.95 × 10−6	1.91	2.25 × 10−8	2.76	1.14 × 10−9	3.78	4.61 × 10−4	1.95
	0.0025	1.53 × 10−6	1.96	3.05 × 10−9	2.89	7.68 × 10−11	3.89	1.17 × 10−4	1.97

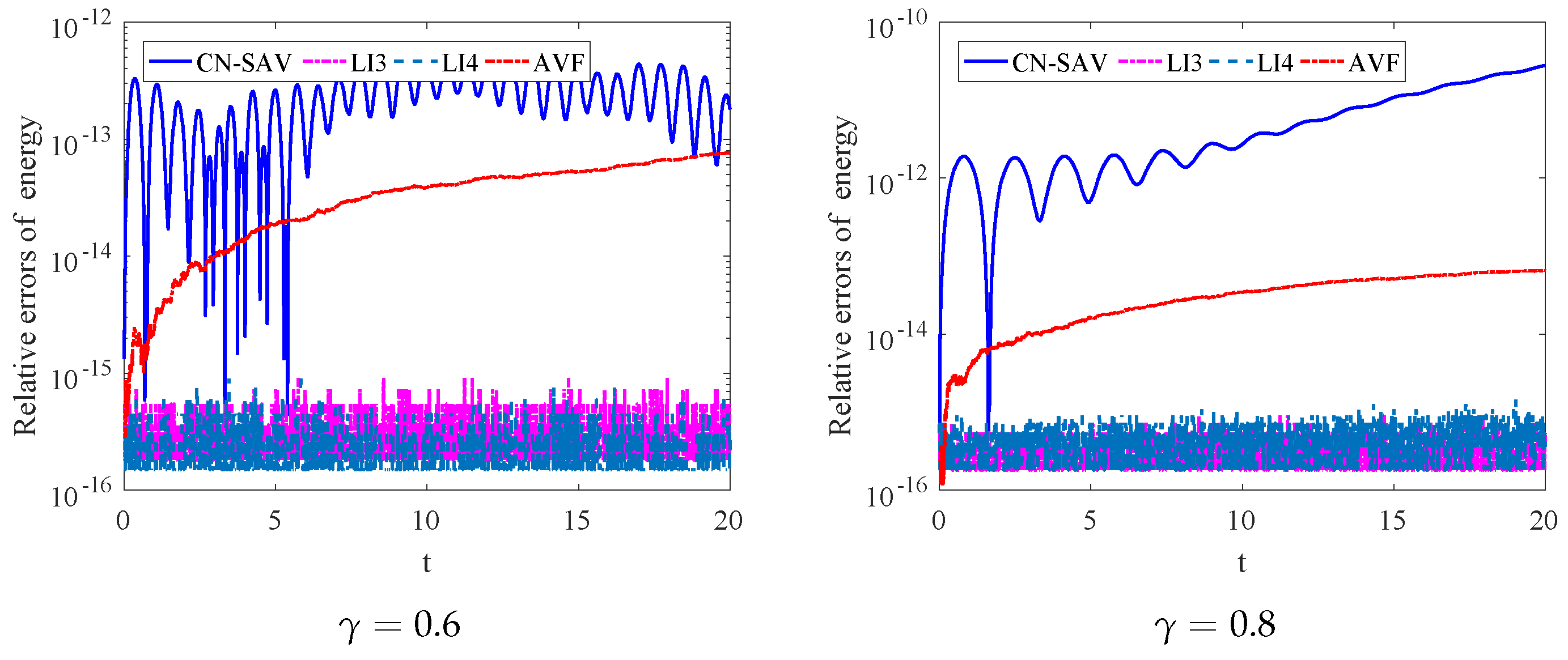
Figure 1 presents a comparison of the relative errors in energy conservation for four different numerical schemes under varying values of the parameter $\gamma$. The two graphs depict the relative error of these schemes for $\gamma =0.6$ and $\gamma =0.8$, plotted over time. For $\gamma =0.4$, the CN-SAV method exhibits oscillations in energy error, with values fluctuating between ${10}^{-12}$ and ${10}^{-13}$, whereas the AVF scheme shows a steady increase in error, starting at around ${10}^{-15}$ and rising to ${10}^{-13}$. In contrast, the L13 and LI4 methods maintain significantly lower and stable errors around ${10}^{-14}$ to ${10}^{-15}$, demonstrating excellent energy conservation properties. As $\gamma$ increases to 0.6, the CN-SAV method experiences even larger oscillations, with errors reaching up to ${10}^{-11}$, while the AVF scheme again shows a gradual increase in error, this time reaching around ${10}^{-11}$. However, the LI3 and L14 methods continue to display superior performance, maintaining low relative errors similar to the case with $\gamma =0.4$. Overall, the comparison highlights that, regardless of the value of $\gamma$, the L13 and L14 schemes consistently provide the best results in terms of energy conservation, while the CN-SAV and AVF schemes exhibit larger errors, with the errors growing more pronounced as $\gamma$ increases.

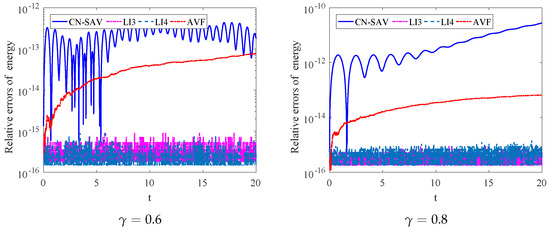
Figure 1. The relative errors of conservative laws for four schemes with $\tau =0.01$, $h=80/256$ for different $\gamma$.

Example 2. 

We analyze the two-dimensional nonlocal NLS equation with $\beta =1$. The initial condition is specified as

$$\begin{array}{c}\hfill u(x,y,0)={\displaystyle \frac{2}{\sqrt{\pi }}}exp(-x^2-y^2).\end{array}$$

(46)

For this study, we consider fractional orders $\alpha =0.65$ and $\alpha =0.95$. The computations are carried out over the spatial domain $\mathrm{\Omega }=[-10,10]\times [-10,10]$.

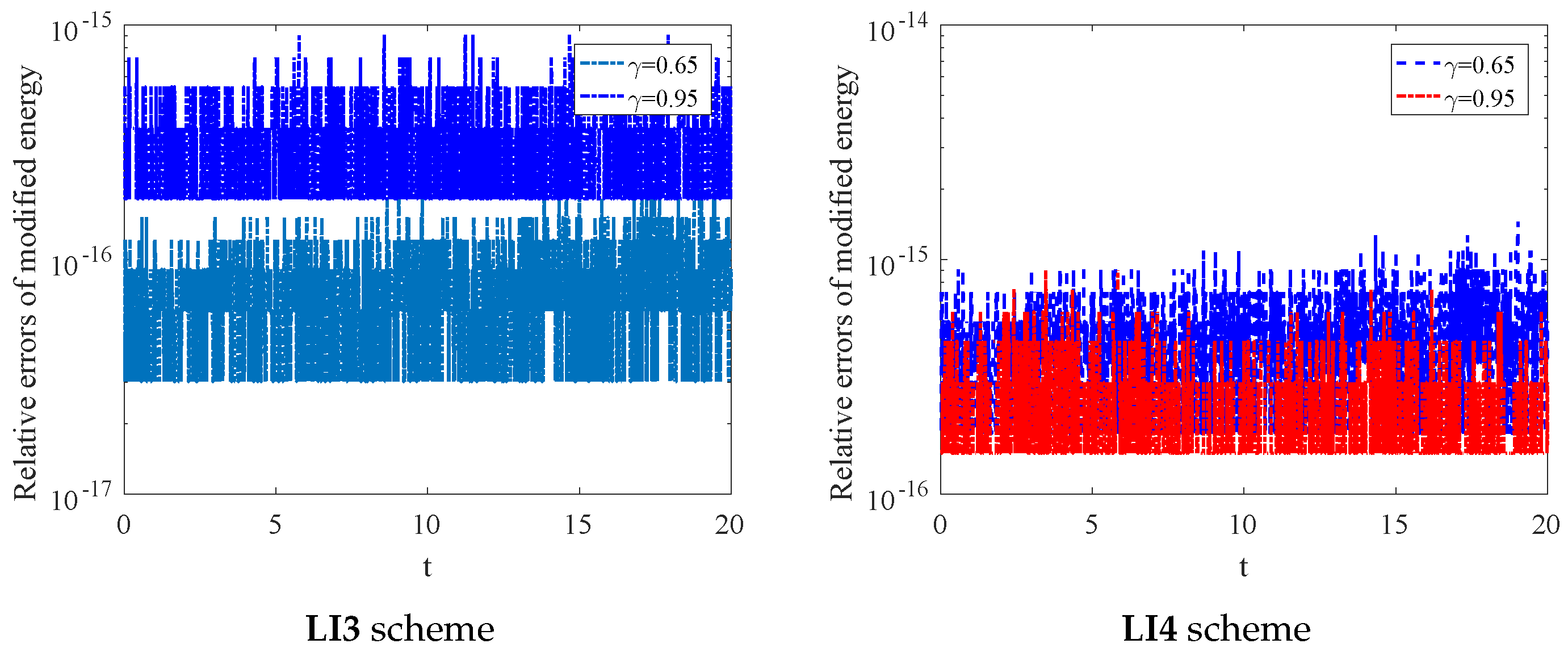
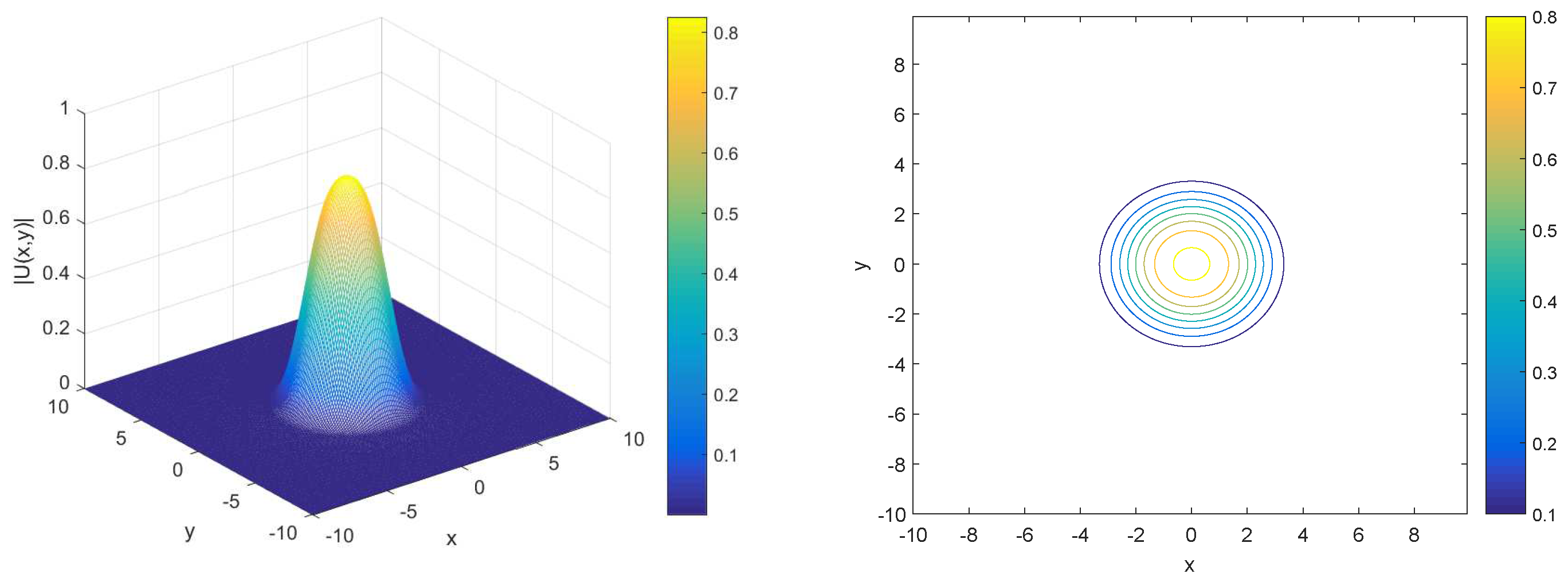
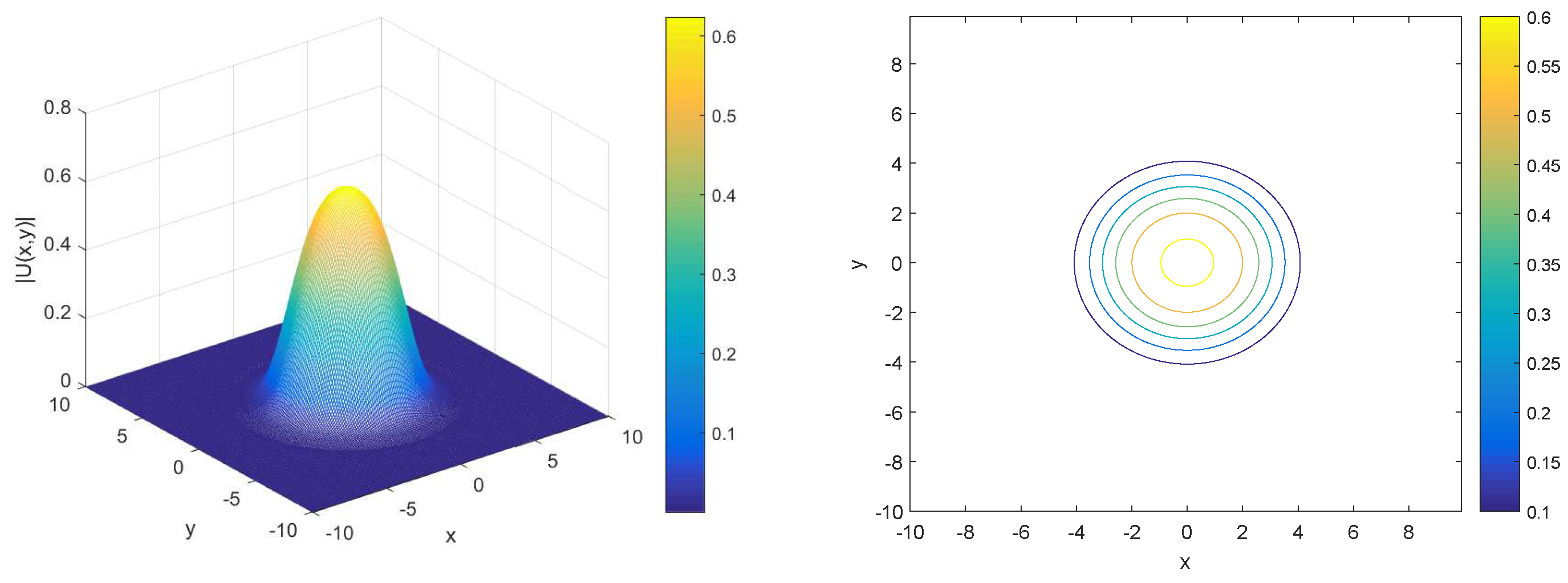
Figure 2 compares the relative errors in modified energy for the LI3 and LI4 schemes under two different values of the parameter $\gamma$, specifically $\gamma =0.65$ and $\gamma =0.95$. The LI3 scheme (left plot) exhibits consistently low relative errors between ${10}^{-16}$ and ${10}^{-15}$, with small fluctuations over time, slightly more noticeable for $\gamma =0.65$. In the LI4 scheme (right plot), the relative error also remains low, but with slightly larger fluctuations, especially for $\gamma =0.65$, where the error reaches up to ${10}^{-14}$. For $\gamma =0.95$, both schemes perform better, with smaller fluctuations and relative errors closer to ${10}^{-15}$. Overall, both schemes demonstrate strong energy conservation. Then, we investigate the relationship between the evolution of the soliton and the $\gamma$ for nonlocal system Figure 3 displays the profile (left) and contour plot (right) of the numerical solutions for two different values of $\gamma$. The top row shows the results for $\gamma =0.65$, where the 3D profile indicates a smooth, symmetric peak centered around $(x,y)=(0,0)$ with values decreasing radially. The contour plot on the right confirms this radial symmetry, with evenly spaced concentric rings representing decreasing values as one moves outward from the center. The bottom row illustrates the same type of plots for $\gamma =0.95$. Figure 3 and Figure 4 depict the evolution of the solution, with the main difference being the height of the peak between $\gamma =0.65$ and $\gamma =0.95$, suggesting a slight change in the intensity of the solution based on the value of $\gamma$.

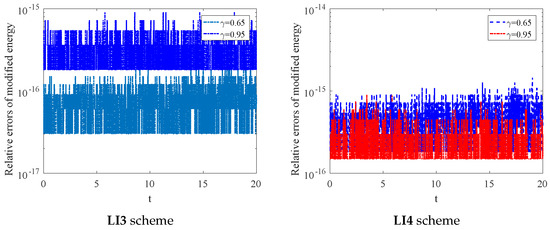
Figure 2. The relative errors of conservative laws for two schemes with $\tau =0.01$, $h=20/128$ for different $\gamma$.

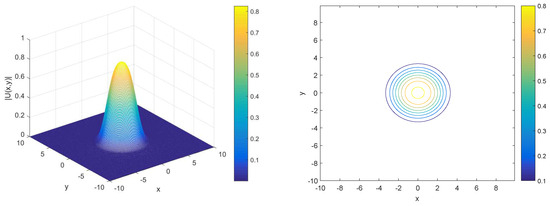
Figure 3. Profile (left) and contour plot (right) of numerical solution for $\gamma =0.65$.

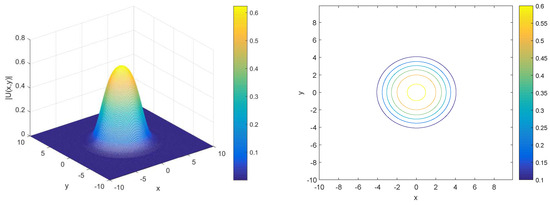
Figure 4. Profile (left) and contour plot (right) of numerical solution for $\gamma =0.95$.

6. Conclusions

In this paper, we construct linearly implicit schemes to solve the nonlocal NLS equation. The proposed schemes offer high accuracy, and ensure preservation of the modified energy. Numerical experiments further confirm their robust stability. Moreover, these methods can be extended to other conservative differential equations. Future work will focus on overcoming the challenges of proving the convergence of these schemes and developing efficient conservative methods that can preserve the system’s original energy.