Topological Interactions Between Homotopy and Dehn Twist Varieties

Abstract

The topological Dehn twists have several applications in mathematical sciences as well as in physical sciences. The interplay between homotopy theory and Dehn twists exposes a rich set of properties. This paper generalizes the Dehn twists by proposing the notion of pre-twisted space, orientations of twists and the formation of pointed based space under a homeomorphic continuous function. It is shown that the Dehn twisted homotopy under non-retraction admits a left lifting property (LLP) through the local homeomorphism. The LLP extends the principles of Hurewicz fibration by avoiding pullback. Moreover, this paper illustrates that the Dehn twisted homotopy up to a base point in a based space can be formed by considering retraction. As a result, two disjoint continuous functions become point-wise continuous at the base point under retracted homotopy twists. Interestingly, the oriented Dehn twists of a pre-twisted space under homotopy retraction mutually commute in a contractible space.

1. Introduction

In general, the mathematical concepts of twisting have applications in physical systems and in mathematics, which have interplays with topology as well as the topological dynamics of the respective systems [1,2,3,4]. Interestingly, algebraic operator-based twisting can be formulated by employing the homotopy theory of Donovan–Karoubi, and it leads to the notion of symmetric spectra of a topological space $(E,X)$ under retraction as well as the twist $M(k)\times M(l)\stackrel{twist}{\to }M(l)\times M(k)$, where $E$ is the total space, $X$ is the retracted topological space and $M(k)\times M(l)$ represents a Cartesian product of monoids [5,6]. A Dehn twist is a special class of twisted structure, which can be formulated by employing the algebraic operators (named after mathematician Max Dehn). Interestingly, if we consider that the topological surface is a Klein bottle, then the Dehn twist and the corresponding $Y-$ homeomorphism are essentially the varieties of automorphisms [1]. Dehn twists have several applications in analyzing physical systems [1,2,3]. It is known that the topologically ordered state of matter is stable if it is in a topologically trivial state preventing degeneracy [2]. However, under degeneracy, Dehn twists can be applied to form braid structures, and corresponding nontrivial operations are obtained. Moreover, from the application point of view, it is shown that Dehn twists encode the topological spins of parity-symmetric anyons (i.e., the exchanges of such anyons) in a physical system [1,2]. In addition to applications in physical systems, a Dehn twist has interplays with homotopy and associated algebraic structures, exposing a rich set of interesting mathematical properties. First, we present the concept of a Dehn twist, in brief (Section 1.1). Next, we present the motivation and contributions made in this paper in Section 1.2 and Section 1.3, respectively. In this paper, the unit interval in real values is denoted by $I$; the index set is denoted by $\mathsf{\Lambda }$; and the sets of real numbers and integers are denoted by $R,Z$, respectively. If $A$ and $B$ are homeomorphic, then it is denoted as $Hom(A,B)$.

1.1. General Dehn Twist

Let us consider an oriented (arbitrary) surface of genus $g$, represented as $(S,g)$, containing a simple closed curve $f:I\to S$. Suppose $N_f$ is a regular neighborhood of the curve $f(.)$ and there exists an orientation-preserving homeomorphism given by $h:S^1\times I\to N_f$. If the function $T_f:S^1\times I\to S^1\times I$ is a directed twist such that $T_f(\theta ,t)=(\theta \pm 2\pi t,t), t\in I$, then we can define a standard Dehn twist as follows [7,8]:

Definition 1.

If the continuous function $T_f:S\to S$ is a homeomorphism on $(S,g)$, then it is a Dehn twist about $f:I\to S$ if it preserves the following properties:

$$\begin{array}{l}[x\in N_f]\Rightarrow [T_f(x)=(h\circ T_f\circ h^{-1})(x)],\\ [x\in S\backslash N_f]\Rightarrow [T_f(x)=x].\end{array}$$

(1)

Remark 1.

Note that a Dehn twist can have directions, such as a right twist or left twist, as indicated by the corresponding signs. Moreover, if we consider two simple closed (disjoint) curves $f:I\to S$ and $v:I\to S$ in an isotopy class, then the Dehn twist admits the commutative algebraic property, which is given as $T_f{T}_v=T_v{T}_f$.

The fundamental property of a Dehn twist is its uniqueness, as presented in the following Lemma [7]:

Lemma 1.

If we consider two Dehn twists $T_f:S\to S$ and $T_v:S\to S$ about the respective disjoint and simple closed curves, then we can conclude that $[T_f=T_v]\Rightarrow [f(I)=v(I)]$ and $[f(I)\ne v(I)]\Rightarrow [T_f\ne T_v]$.

It is interesting to note that a Dehn twist can be formulated considering a fundamental group ${\pi }_1(S,p)$ on a surface $(S,g)$ without requiring any additional modifications of the concept [8].

1.2. Motivation

Homotopy analysis methods have wide arrays of applications. For example, homotopy analysis methods are applied for solving integrodifferential equations by admitting the convergence criteria of the associated series [9]. Note that in such applications, the homotopy is employed as an operator. Interestingly, the metrizable topological space of Grothendieck manifold admits the coarse sheaf cohomology as well as cohomology groups [10]. In this case, the coarse cohomologies are homotopy invariant [10]. There are interplays between the homotopy of algebraic topology, Dehn twists and the lifting with a rich set of properties. For example, suppose $To{r}^2\subset R^2$ is a flat torus and there exists the area-preserving homeomorphism $f:To{r}^2\to To{r}^2$, where $f(.)$ is homotopic to the identity of the respective flat torus. If $f_l:R^2\to R^2$ is a lifting of $f(.)$, then there is a rotation set $\rho (f_l)$, which is a generalization of the rotational number of circle homeomorphisms preserving the orientations [11]. Moreover, let us consider a (area-preserving) homeomorphism $f:T_D(To{r}^2)\to T_D(To{r}^2)$, where $T_D(To{r}^2)$ denotes a set of homotopic Dehn twists of the respective flat torus. If $f_{Tl}:T_D(To{r}^2)\to S^1\times R$ is lifting with a zero vertical rotational number, then all points have uniformly bounded motion under the corresponding lifting [12,13]. This has applications in dynamical systems and in fixed point theory [13]. Note that the aforesaid topological properties are restricted to the flat torus under Dehn twists while preserving the area.

It is known that homotopy and retraction are two inter-related concepts in algebraic topology, where Dehn twists play an interesting role. Thus, the relevant motivating question is as follows: can we further generalize or extend a Dehn twist in relation to its application in homotopy and retraction? More specifically, interesting questions are (1) what are the topological properties of interactions between extended Dehn twists and non-contractible spaces under homotopy; (2) what are the interplays between the homotopic retraction of a topological space and Dehn twists? Furthermore, the question is as follows: is there any lifting of such twisted homotopy and what is its relationship with Hurewicz fibration? This paper addresses these questions in relative detail from the viewpoint of algebraic topology.

1.3. Contributions

First, we note the following fundamental observation presented as Theorem 1 [14]. We present our proof (formulated by the author of this paper) of the corresponding theorem (Theorem 1).

Theorem 1.

If $f:I\to (S,g)$ is a simple closed curve on a compact oriented surface $(S,g)$ of genus $g$, then the generalized Dehn twists about $f:I\to (S,g)$ generate automorphism of fundamental group $\pi (S,f(0))$. Moreover, it forms the corresponding homotopy class $[f]$ on $(S,g)$ under the Dehn twists.

Proof. 

Let $(S,g)$ be a compact oriented surface of genus $g$. Suppose $A\subset S$ is a connected based subspace such that $f:I\to A$ is a simple closed curve with the base point $f(0)=f(1)=b$. Thus, it forms a fundamental group ${\pi }_1(A,b)$ on $(S,g)$. If $T_D:A\to A$ is a base point preserving a Dehn twist about $f:I\to A$, then $T_D(f(I))$ admits the conditions given by (1) $Hom(T_D(f(I)),f(I))$, (2) $Hom(T_D(f(I)),S^1)$ and (3) $T_D^n(\{b\})\cong \left\{b\right\}$, where $1\le n<+\infty$. Thus, it results in the formation of homotopy class $[f]=\{T_D^n(f(I)):n\in [1,k],k<+\infty \}$, where $\forall h\in [f]$ and the fundamental group ${\pi }_1(A,b)$ admits automorphism under a finite number of Dehn twists. □

The important constraint on $T_D(f(I))$ is that it should result in a set of simple closed curves in the homotopy class $[f]$ within the based space.

Theorem 1 and our proof illustrate that a based topological space plays an interesting role in generating fundamental groups under Dehn twists. This paper introduces the notion of pre-twisted space and the formation of an $f-base$ space under homeomorphism, such that the $f-base$ space essentially becomes a based topological space. The formulation of a generalized as well as an extended Dehn twist of a pre-twisted space is presented in this paper, where a Dehn twist has a specific orientation and the Dehn twists with opposite orientations mutually commute. We show that a non-contractible space can be subjected to the extended Dehn twists under homotopy and the resulting twisted homotopy with non-retraction can be lifted (LLP) by employing the local homeomorphism. Thus, the proposed formulation extends the principles of Hurewicz fibration by avoiding pullback. Furthermore, the topological properties of twisted homotopy up to an $f-base$ point with retraction under a Dehn twist are presented in this paper. As a result, two disjoint continuous functions become continuous at the $f-base$ point under the Dehn-twisted homotopy with retraction. We show that the commutative relation between the homotopic retraction and Dehn twists is preserved.

The rest of the paper is organized as follows: Section 2 presents preliminary concepts. The definitions of pre-twisted space, extended Dehn twists and twisted homotopy are presented in Section 3. The topological properties of the varieties of twisted homotopies are presented in Section 4. Finally, Section 5 concludes the paper.

2. Preliminaries

We present the preliminary concepts in two parts. First, we present the results related to Dehn twists in Section 2.1. Next, we present the discussions about the Dehn twists, isotopy and fibration in Section 2.2.

2.1. Curves and Dehn Twists

Suppose we consider an oriented surface of genus $g$ represented as $(S,g)$ and let $f:I\to S$ be a simple closed curve. The curve is called trivial if $A\subset S:f(I)=\partial A$ and it maintains the condition given by $Hom(A^o,D_2)$, where $D_2=D_2^o$ represents an open disk. Note that every trivial curve $f:I\to S$ admits a Dehn twist, which is equivalent to the corresponding diffeomorphism [15]. There is an inter-relationship between the closed curve, the Dehn twist about the curve and the respective automorphic homeomorphism of a closed surface, which is presented as follows [15,16]:

Lemma 2.

Let $(S,g)$ denote a closed surface $S$ of genus $g$ and the two-sided closed curve on $S$ be given as $f:I\to S$. Suppose $T_f$ is a Dehn twist about $f(.)$ and $h:S\to S$ is an automorphic homeomorphism preserving $f:I\to S$. If the Dehn twist $T_f$ reverses the orientations of neighborhoods of $f:I\to S$, then the following properties are preserved:

$$\begin{array}{l}{T}_f=h{(T_f)}^{-1}{h}^{-1},\\ \forall n\in Z:{(T_f)}^{2n}={(T_f)}^n{(T_f)}^n.\end{array}$$

(2)

The corresponding commutator under homeomorphism can be denoted as $[{(T_f)}^n,h]$. Note that in this case, the closed two-sided curve is not bounding any disk. The concept of a compression body and the associated Dehn twist on a manifold with a boundary are defined as follows [17]:

Definition 2.

A compression body is a connected three-manifold $M^3$ generated from a compact surface $S$ with no components such that the $Hom(S,S^2)$ property is preserved, where $S\times \left\{1\right\}$ is the attached one-handle.

It is important to note that a compression body is irreducible.

Definition 3.

Let $M^3$ be a three-manifold with a boundary and the continuous function $h:M^3\to M^3$ be a homeomorphism. The function restricted to boundary $h{|}_{\partial M^3}:M^3\to M^3$ is a Dehn twist if it is isotopic to the identity of the subspace and it is complement to a set of closed as well as simple curves $\{f_i:I\to \partial M^3:i\in \mathsf{\Lambda }\}$, such that $[i\ne k]\Rightarrow [f_i(I)\cap f_k(I)=\phi ]$.

Remark 2.

Note that the Dehn twist on a closed surface about a closed two-sided curve does not bound any disk. However, in the case of manifold with a boundary, the Dehn twist (restricted to the boundary) about a set of disjoint closed and simple curves essentially bounds a set of disks generated by $\{f_i(I)\}$.

This leads to the following theorem involving the Dehn twist of a compression body [17]:

Theorem 2.

Let $S$ be a compression body and $h:S\to S$ be a homeomorphism. The Dehn twist about the function $h:S\to S$ is a composition of a set of Dehn twists about the simple, closed and disjoint curves $\{f_i:I\to \partial S:i\in \mathsf{\Lambda }\}$, which are isotopic, and each of $f_i(I)$ bounds a disk such that the $Hom(f_i(I),S^1)$ condition is maintained.

There are interplays between the Dehn twists and the intersection numbers of multiple simple closed curves generated by $f:I\to S$ and $g:I\to S$ on the surface $(S,g)$ with genus $g$. Let us denote the intersection number as $\lambda =|f(I)\cap g(I)|$. This results in the commutative invariance theorem of Dehn twists of $T_f,T_g$ if the $\lambda =0$ condition is maintained on the surface [18].

Theorem 3.

If $f:I\to S$ and $g:I\to S$ are two-sided curves on the surface $(S,g)$ such that $Hom(f(I),S^1)$ and $Hom(g(I),S^1)$ conditions are maintained, then $\exists j,k\in Z^{+}$ such that the following implication is admitted: $[{(T_f)}^j{(T_g)}^k={(T_g)}^k{(T_f)}^j]\Rightarrow [\lambda =0]$.

The proof of the commutative invariance under multiple Dehn twists about the non-intersecting curves is detailed in [18]. A similar result can be extended to Lagrangian n-sphere $S_L^n$ embedded within the symplectic m-manifold $M^m$ for $m=n=2$ admitting Milnor fibration, where the twist is a standard Dehn twist [19]. Moreover, in such a case, the standard Dehn twist commutes considering two disjoint Lagrangian $S_L^n$ for $n=2$. Interestingly, there may not be any inter-relationship between two Dehn twists, even if the intersection number is non-zero, which is presented in the Ishida theorem as follows [19]:

Theorem 4.

Let a surface of genus $g$ and the puncture $p$ be given as $(S,g,p)$. Suppose two simple closed curves are $f:I\to (S,g,p)$ and $g:I\to (S,g,p)$ such that $\lambda \ge 2$. In this case, there is no inter-relationship between the Dehn twists $T_f,T_g$.

Note that the value of $\lambda$ is considered to be minimum in this case. A detailed discussion is given in [19,20].

2.2. Dehn Twists, Isotopy and Fibration

The topological properties of Dehn twists vary depending on the dimensions of the spaces. The Dehn twist around a non-trivial loop on a surface $(S,g>1)$ with a non-zero genus generates a one-dimensional Teichmüller disk [21]. A Teichmüller disk is completely geodesic with respect to the Teichmüller metric. If we consider a two-manifold $M^2$ representing a surface, then there is an isotopy $\lambda :M^2\times [0,1]\to M^2$ without fixing $\partial M^2$ such that it is homotopic up to a periodic and irreducible variety [22]. If $h:M^2\to M^2$ is a homeomorphism fixing $\partial M^2$, then the fractional Dehn twist coefficient of $h(.)$ represents the winding number of the arc $\left\{b\right\}\times [0,1]$, where $b\in \partial M^2$ is a base point [22].

Interestingly, there is an inter-relationship between the fundamental group and Hurewicz arc system on a two-disk (represented as $D_2$). Let us consider a Lefschetz fibration $f:X\to D_2$, where $X$ is a compact four-manifold. Let us choose a base point $b\in \partial D_2$ and a finite set of points $\left\{p_i\right\}\subset {(D_2)}^o$. If we consider a set of arcs $\left\{A_i\right\}\subset D_2$ such that $A_i\cap A_k=\left\{b\right\}$, then $⟨\left\{p_i\right\},\left\{A_i\right\}⟩$ is a Hurewicz arc system admitting a right-handed Dehn twist generating ${\pi }_1(D_2\backslash \{p_i\},b)$, which is called the Hurewicz generator system [23].

It is known that the Dehn twists of various four-manifolds may not always preserve the smooth isotopy with respect to the identity function along the twist. For example, Kronheimer and Mrowka have shown that if we consider a manifold $K3\#K3$, then the Dehn twist along the submanifold $S^3$ within the respective manifold does not admit smooth isotopy with respect to the identity function [24,25]. In order to avoid non-smooth isotopy, the sequences of stabilizations are often necessary. Interestingly, the Dehn twist along $S^3$ within $K3\#K3$ cannot be made smooth after a single stabilization [24].

3. Homotopy Under Dehn Twists: Definitions

Let a topological space be given as $(X,{\tau }_X)$ such that $\dim (X)=n$ and $n\in (1,+\infty )$. We denote a real plane of dimension $m\le n$ as $R{P}^m$, and a planar convex open m-disk is denoted as $D_m=\{x\in R{P}^m:|x|<1\}$. If we consider a topological subspace $F\subset X$, then the corresponding homotopy can be formulated through $H_n:F\times I\to Y$ by following the conventions of algebraic topology. Let us denote a homotopic subspace of $A=F\times \{a\in I\}$ as $A_{(F,a)}\subset F\times I$. Moreover, if $f:I\to F\times I$ is a continuous function such that $f(\{b\}\subset I)\cap A_{(F,a)}=\left\{x_{ab}\right\}$, then we represent the position of the point $x_{ab}$ as $p({\theta }_b,a)$, where ${\theta }_b$ is a clock-wise angular displacement with respect to a fixed reference point on $A_{(F,a)}$. Let us consider the low-dimensional topological space such that $n\le 3$, for simplicity. First, we present the definition of pre-twist ${\theta }_{Dp}$ of a Dehn variety as follows:

Definition 4.

Let $X\subset R^2$ be a topological space and $F\subset X$ such that the $Hom(F,\overline{D_2})$ condition is preserved. If $f:I\to \partial F\times I$ and $g:I\to \partial F\times I$ are two disjoint continuous functions, where $g(.)$ maintains the $Hom(g(I),P_g\subset R{P}^1)$ property, then ${\theta }_{Dp}\ge 0$ is the pre-twist of a Dehn variety if the following conditions are maintained:

$$\begin{array}{l}\left\{x_{ac}\right\}=g(I)\cap A_{(F,a)},\\ \left\{x_{ab}\right\}=f(I)\cap A_{(F,a)},\\ {\theta }_{Dp}=|p({\theta }_c,a)-p({\theta }_b,a)|.\end{array}$$

(3)

It is important to note that ${\theta }_{Dp}\ge 0$ is considered as extremely small, such that $\inf {\theta }_{Dp}=\underset{k\to M}{\lim }(2\pi /k)$ in general, where $M\in (1,+\infty ]$ and $M>>1$. It is important to note that in the remaining sections of this paper, we are algebraically denoting the position $p({\theta }_b,a)$ and the corresponding point $x_{ab}$ together as $p({\theta }_b,a)$ to avoid representational complexities (i.e., $x_{ab}\equiv p({\theta }_b,a)$ for simplicity).

Definition 5.

Let $U$ be a simply connected topological space such that $U=\overline{U}$ and let $f:U\to Y$ be a continuous function. The ordered pair ${(U,f)}_Y$ is defined as an $f-base$ forming a fixed based space ${(Y,y_{\ast })}_f$ if $f(U)=\left\{y_{\ast }\right\}$. The point $y_{\ast }$ is called an $f-base$ point in $Y$.

Note that the $f-base$ ${(U,f)}_Y$ admits homeomorphism such that if $h:Y\to V$ is a homeomorphism, then $(h\circ f)(U)=h(y_{\ast })$.

Remark 3.

There exists an $H_{2\ast }:F\times I\to Y$, which is a null-homotopy up to an $f-base$ point $y_{\ast }\in Y$ in a fixed-based space ${(Y,y_{\ast })}_f$ such that $H_{2\ast }(A_{(F,1)})=\left\{y_{\ast }\right\}$. Note that in this case, $F$ is also a simply connected space. Moreover, if $r:F\to F$ is a retraction and $h:F\to Y$ is continuous, then $\exists c\in F$ such that $(h\circ r)(F)=h(c)=\left\{y_{\ast }\right\}$. Furthermore, it can be observed that $H_{2\ast }(A_{(F,1)})=(h\circ r)(F)$, indicating that in this case, $H_{2\ast }:F\times I\to Y$ is a null-homotopic retraction up to the $f-base$ point $y_{\ast }$.

Definition 6.

Let a continuous function be given as ${\Delta }_{D(\pm m\epsilon )}:F\times I\to F\times I$, where $\epsilon \in R^{+}$ and $m\in Z^{+}$. The function ${\Delta }_{D(\pm m\epsilon )}$ is an extended Dehn twist if $\forall p({\theta }_{Dp},t)\in F\times \left\{t\right\}$; the function induces twist as ${\Delta }_{D(\pm m\epsilon )}(p({\theta }_{Dp},t))=p(({\theta }_{Dp}\pm 2\pi m\epsilon t),t)$, such that $\epsilon \in (0,1]$ and $t\in I$.

The extended Dehn twist generalizes the standard Dehn twist by admitting a variable factor or weight $\epsilon$ of the twist, while covering a finite order $m\in [1,+\infty )$ of the twist. Note that the extended Dehn twist introduces the notion of the direction of a twist within a homotopy space.

Remark 4.

If we consider that $\epsilon =1$, then the extended twist ${\Delta }_{D(\pm m\epsilon )}$ is transformed into a standard Dehn twist of order $m$. If we consider a positively (clock-wise) oriented twist ${\Delta }_{D(+m\epsilon )}$, then the corresponding inverse is given by ${\Delta }_{D(-m\epsilon )}$. It is important to note that, in general, the directed as well as extended Dehn twists are mutually commutative such that they admit the condition given as $({\Delta }_{D(+m\epsilon )}\circ {\Delta }_{D(-m\epsilon )})=({\Delta }_{D(-m\epsilon )}\circ {\Delta }_{D(+m\epsilon )})=i{d}_{F\times I}$, where $i{d}_{F\times I}:F\times I\to F\times I$ is an identity function.

4. Topological Properties

In this section, we present the topological properties of extended Dehn twists on two varieties of homotopy spaces. First, we present the topological analysis of the application of an extended Dehn twist on a homotopy space, which is not contractible and not null-homotopic. Next, we consider a null-homotopic topological space and we apply the extended Dehn twist on the respective homotopy space.

4.1. Extended Dehn Twist in Non-Contractible Space

Let us consider a continuous function $g:I\to S^1\times I$ such that the $Hom(g(I),P_g\subset R{P}^1)$ property is maintained. Suppose we consider that $p({\theta }_{Dp},0)=g(0)$ and $p({\theta }_{Dp},1)=g(1)$. Suppose a homotopy is given by $H:S^1\times I\to E$ and a covering map is given by $q:E\to X$. We define a homotopy under the extended Dehn twist, which is given by $H_{\Delta }:S^1\times I\to X$, such that the following algebraic properties are preserved:

$$\begin{array}{l}t\in [0,1]:H_{\Delta }(S^1\times \{t\})\cong (H\circ {\Delta }_{D(\pm m\epsilon )})(S^1\times \{t\}),\\ t\in [0,1]:Hom(H_{\Delta }(S^1\times \left\{t\right\}),S^1\times \{t\}).\end{array}$$

(4)

Note that, in this particular case, we can consider that ${\theta }_{Dp}=0$ with respect to $P_g\subset R{P}^1$ and the corresponding twisted homotopy can be formulated as $H_{\Delta }(S^1\times \{t\})=q_{\ast }(H\circ {\Delta }_{D(\pm m\epsilon )})(S^1\times \{t\})$. As a result, we obtain ${\Delta }_{D(\pm 11)}(p(0,t)\in S^1\times \{t\})=p(\pm 2\pi t,t)$, where $t\in [0,1]$. It results in the following commutative diagram as illustrated in Figure 1, where $(H\circ {\Delta }_{D(\pm m\epsilon )}):S^1\times I\to E$ is a homotopy lifting under the extended Dehn twist and $h:E\to S^1\times \left\{0\right\}$ is a local homeomorphism in $E$:

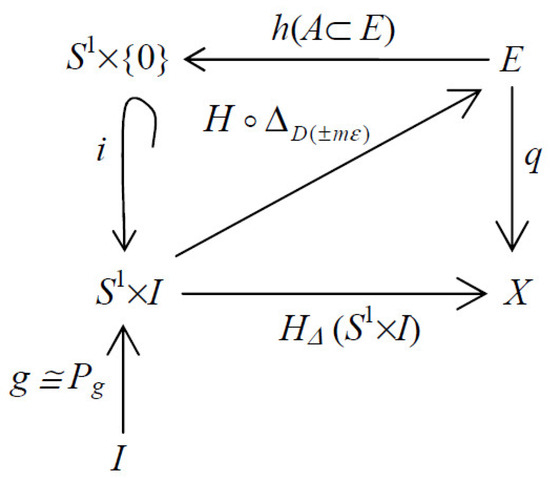
Figure 1. Twisted homotopy lifting and fibration with no retraction.

Interestingly, the homotopy lifting under the extended Dehn twist with no retraction have resemblances to the Hurewicz fibration with necessary modifications.

Remark 5.

It is important to note that the covering map of a homotopic extended Dehn twist $q:E\to X$ has a left lifting property (LLP) because it admits the condition given by $(q\circ (H\circ {\Delta }_{D(\pm m\epsilon )})\circ i\circ h)=(H_{\Delta }\circ i)$. Furthermore, the lifting $(H\circ {\Delta }_{D(\pm m\epsilon )}):S^1\times I\to E$ is a twisted homotopy lifting because it preserves the $q_{\ast }H\circ {\Delta }_{D(\pm m\epsilon )}=H_{\Delta }$ property.

Theorem 5.

If $H_{\Delta }:S^1\times I\to X$ is a twisted homotopy with $m\epsilon =1$, then it admits the following two properties: (a) $H_{\Delta }(S^1,0)\cong H(S^1,0)$ and (b) $H_{\Delta }(S^1,1)\cong H(S^1,1)$.

Proof. 

Let us consider a twisted homotopy $H_{\Delta }:S^1\times I\to X$. Note that in this case, ${\Delta }_{D(\pm 11)}(p(0,t)\in S^1\times \{t\})=p(\pm 2\pi t,t)$ for all $t\in [0,1]$. Let us consider an identity function given as $id:S^1\times I\to S^1\times I$. As a result, the extended Dehn twist results in the following properties:

$$\begin{array}{l}{\Delta }_{D(\pm 11)}(S^1\times \{0\})=id(S^1\times \{0\}),\\ and,\\ {\Delta }_{D(\pm 11)}(S^1\times \{1\})=id(S^1\times \{1\}).\end{array}$$

(5)

Hence, we can conclude that $H_{\Delta }(S^1,0)\cong H(S^1,0)$ and $H_{\Delta }(S^1,1)\cong H(S^1,1)$ because $H_{\Delta }(S^1,0)=q_{\ast }H\circ id(S^1,0)$ and $H_{\Delta }(S^1,1)=q_{\ast }H\circ id(S^1,1)$. □

4.2. Homotopic Retraction Under Extended Dehn Twist

In this section, we consider that the three-space $A_{(F,a)}\subset F\times I$ can be topologically retracted and it is null-homotopic. If we first apply the extended Dehn twist to $A_{(F,a)}$ as ${\Delta }_{D(\pm m\epsilon )}(A_{(F,a)})$, and next, we apply retraction under $r:A_{(F,a)}\to (B_{(F,a)}\subset A_{(F,a)})$, then we obtain the following equations:

$$\begin{array}{l}{\Delta }_{D(\pm m\epsilon )}(p({\theta }_{Dp},a)\in \partial A_{(F,a)})=p({\theta }_{Dp}\pm 2\pi m\epsilon a,a),\\ (r\circ {\Delta }_{D(\pm m\epsilon )})(p({\theta }_{Dp},a))=p{({\theta }_{Dp}\pm 2\pi m\epsilon a,a)}_B\in \partial B_{(F,a)}.\end{array}$$

(6)

If we apply the extended Dehn twist and retraction in the reverse order, then it results in the following equations:

$$\begin{array}{l}p({\theta }_{Dp},a)\in \partial A_{(F,a)},\\ r(A_{(F,a)})=B_{(F,a)},\\ p{({\theta }_{Dp},a)}_B\in \partial B_{(F,a)},\\ {\Delta }_{D(\pm m\epsilon )}(p{({\theta }_{Dp},a)}_B)=p{({\theta }_{Dp}\pm 2\pi m\epsilon a,a)}_B.\end{array}$$

(7)

It leads to the following commutative diagram illustrated in Figure 2.

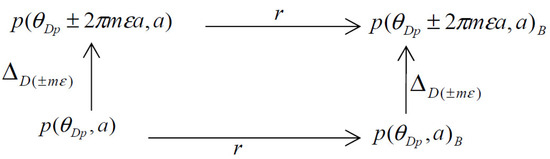
Figure 2. Commutative diagram for retraction and extended Dehn twist.

It is relatively easy to observe that the aforesaid commutative property is admitted for all points in the null-homotopic space. This results in the following theorem:

Theorem 6.

Let $H_{2\ast }:F\times I\to Y$ be a null-homotopic retraction up to $y_{\ast }\in Y$ in ${(Y,y_{\ast })}_f$, where it preserves the $Hom(F,\overline{D_2})$ property. If $h:I\to \partial F\times I$ and $g:I\to \partial F\times I$ are two disjoint continuous functions, then it results in $H_{2\ast }(F\times \{g(1)\})\cap H_{2\ast }(F\times \{h(1)\})=\left\{y_{\ast }\right\}$ in ${(Y,y_{\ast })}_f$.

Proof. 

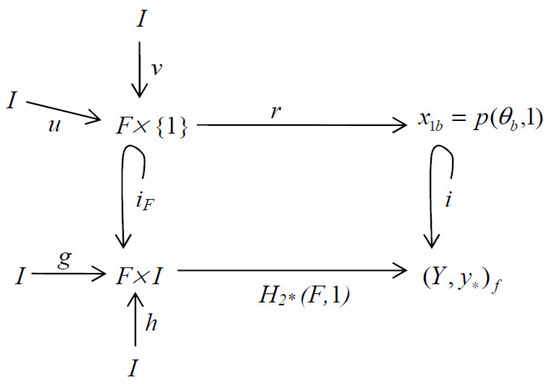
Let $F\subset X\subset R^2$ be a topological space such that the $Hom(F,\overline{D_2})$ property is maintained and $H_{2\ast }:F\times I\to Y$ is the corresponding homotopy. Let us consider that $H_{2\ast }:F\times I\to Y$ is a null-homotopy up to an $f-base$ point $y_{\ast }$ in ${(Y,y_{\ast })}_f$ such that $H_{2\ast }(A_{(F,1)})=\left\{y_{\ast }\right\}$. This implies that there is a retraction with embedding $(i\circ r):A_{(F,1)}\to {(Y,y_{\ast })}_f$ such that $(i\circ r)(A_{(F,1)})=H_{2\ast }(A_{(F,1)})$, where $r:A_{(F,1)}\to A_{(F,1)}$ is a retraction with $r(A_{(F,1)})=\left\{x_{1b}\right\}\subset A_{(F,1)}$ and $i:A_{(F,1)}\to {(Y,y_{\ast })}_f$ is the respective (injective) embedding with $i(x_{1b})=y_{\ast }$. Thus, the homotopy $H_{2\ast }:F\times I\to Y$ is a null-homotopic retraction variety. Let us consider that $h:I\to \partial F\times I$ and $g:I\to \partial F\times I$ are two disjoint continuous functions such that $h(1)\in \partial A_{(F,1)}$ and $g(1)\in \partial A_{(F,1)}$. As $H_{2\ast }:F\times I\to Y$ is a null-homotopic retraction, we can infer that $H_{2\ast }(F\times \{g(1)\})=H_{2\ast }(F\times \{h(1)\})$. Hence, we conclude that $H_{2\ast }(F\times \{g(1)\})\cap H_{2\ast }(F\times \{h(1)\})=(i\circ r)(A_{(F,1)})$ in ${(Y,y_{\ast })}_f$. It results in the following commutative diagram as illustrated in Figure 3, where $u:I\to F\times \left\{1\right\}$ and $v:I\to F\times \left\{1\right\}$ are two constant (continuous) functions such that $u(I)=\left\{x_{1k}\right\}$ and $v(I)=\left\{x_{1c}\right\}$ within the topological space. □

Figure 3. Commutative diagram representing Theorem 6.

This immediately leads to the following corollary:

Corollary 1.

There exist two injective embeddings under homotopy $H_{2\ast }$ and the restrictions in $F\times I$, which are given as $i_{emH2*}:(F\times I){|}_g\to {(Y,y_{\ast })}_f$ and $i_{emH2*}:(F\times I){|}_h\to {(Y,y_{\ast })}_f$ such that $i_{emH2*}((F\times I){|}_g)\cap i_{emH2*}((F\times I){|}_h)=\left\{y_{\ast }\right\}$.

We can view this as the admission of the base-point preservation principle within a based topological space.

Remark 6.

Finally, this is to note that the proposed concepts and formulations (excluding our proof of Theorem 1) in this paper are employing the elements of algebraic topology without resorting to the algebraic operator theory of twisted structures. Moreover, the proposed formulations generalize the Dehn twist under retraction in terms of algebraic topology. It would be interesting to investigate the relationships between the proposed concepts and the twisted (algebraic) K-theoretical structures in future.

5. Conclusions

The general form of Dehn twists can be extended involving the pre-twisted topological based spaces and the orientations of twists, where the based space is formed through the continuous function retaining homeomorphism. Extended Dehn twists can be applied to homotopy under two conditions: (1) the non-retraction of a space and (2) under the retraction of the topological space. The resulting twisted homotopies behave differently. The Dehn twisted homotopy with non-retraction can admit a left lifting property (LLP) by following the modified form of Hurewicz fibration, avoiding pullback. However, the Dehn twisted homotopy under retraction up to the base point within a based space admits the point-wise continuity of two disjoint continuous functions at the base point. In a contractible space, the extended Dehn twists and retractions mutually commute.