Abstract
Finding the highest possible cardinality, , of the set of k-dimensional subspaces in , also known as codewords, is a fundamental problem in constant dimension codes (CDCs). CDCs find applications in a number of domains, including distributed storage, cryptography, and random linear network coding. The goal of recent research papers has been to establish We further improved the echelon-Ferrers construction with an algorithm, and enhanced the inserting construction by swapping specified columns of the generator matrix to obtain new lower bounds.
Keywords:
constant dimension codes; linkage construction; greedy algorithm; echelon-Ferrers construction MSC:
94B05
1. Introduction
Assume that is a finite field with q elements. The set of all k-dimensional subspaces of a -vector space V is denoted by . In vector space , the projective space over the finite field of order n, represented as , often includes all of the subspaces. These subspaces constitute a metric space when combined. Together, and the defining metric is the subspace distance. It is described as
CDCs are a special class of subspace codes with important applications in network coding, especially in random network coding. In recent years, network coding has garnered significant attention as an innovative method for transmitting data over networks. It is extensively used in distributed storage systems, peer-to-peer networks, social networks, wireless communication networks, and other types of networks. In random network coding, conventional error-correcting code techniques may not be adequate due to the unpredictability of network topologies. The ability of CDCs to preserve vector space properties makes them an effective tool for addressing this issue.
Since Köetter and Kschischang [] first introduced subspace codes, there has been extensive research on them [,,,,,,]. Heinlein et al. [] provide more details regarding their theoretical foundation. Additionally, the most recent bounds on constant dimension codes and subspace codes can be found there.
To create CDCs, rank metric codes (RMCs), specifically maximum rank distance (MRD) codes, are employed. One technique for creating CDCs using rank metric codes is the lifting construction [], which forms a subspace by concatenating an identity matrix with a matrix of RMCs. In the context of random linear network coding, lifted MRD codes can produce asymptotically optimal CDCs and can be decoded effectively. Etzion and Silberstein [] introduced a new family of Ferrers diagram RMCs to generalize the lifted MRD code architecture, which they called the multilevel construction.
Today, there are primarily two approaches used to build CDCs in conjunction with parallel linkage construction. The first technique is called parallel multilevel construction []. Another approach is the block inserting construction, initially introduced in []. CDCs built using matrix blocks are inserted into the parallel linkage construction through the block inserting construction.
In [], MinYao Niu proposed a new method for constructing constant dimension codes. The parallel linkage construction can incorporate the constant dimension codes derived from this method.
In [], Xianmang He presented a construction for subspace codes of constant dimension that involves the insertion of a composite structure made up of an MRD code and its sub-codes, providing some improved lower bounds over previous results.
Building CDCs is a useful application of lifting Ferrers diagram codes. Furthermore, the discovery of linkage construction enables the creation of a large number of CDCs. In [], Fagang Li derived some new CDC lower bounds for small parameters by combining the two construction techniques.
In [], Troha introduced a construction called the linkage construction from Corollary 39 in []. This construction involves joining two CDCs of shorter length and results in the establishment of a lower bound for the following CDCs.
where
In this paper, we are inspired by [,]. The linkage construction and insertion construction have been effectively improved. The paper is structured as follows: In Section 1, we review some fundamental concepts of CDC. In Section 2, we introduce effective methods for constructing CDCs, including parallel linkage construction, Ferrers diagram construction, and sub-code construction. The main part of this article is in Section 3, where we first propose an improved algorithm based on the greedy algorithm that yields a better set of identification vectors. We then describe an insertion construction method by swapping specific columns of the generator matrix. Using our approach, we derive several new lower bounds.
2. Preliminaries
2.1. Rank-Metric Codes
Over the field , let be a matrices space. The rank-metric is defined as follows for any two distinct matrices :
A rank-metric code is a subset of with the rank-metric. We can refer to a rank-metric code as linear rank-metric code if it is a linear subspace of . Clearly, the rank-distance of a rank-metric code is defined as
We know that the upper bound of its cardinality is . A rank-metric code attaining this bound is called an MRD code (see [,]). A linear MRD code with distanced d is denoted by , and its cardinality is denoted by . Additionally, if the rank of each codewords is at most r, we use the notation to represent it, and we refer to it as a rank-restricted RMC (RRMC). Its cardinality is usually denoted by .
Lemma 1
([]). Let is a linear MRD code with rank distance . Its rank distribution is given by
where representing the cardinality of codewords in with rank r.
2.2. Ferrers Diagram Maximum Rank Distance Codes
Let X be a k-dimensional subspace within a space . Its structure can be described by a generating matrix whose rows span the bases of X. This generator matrix can be transformed into a unique row-reduced echelon matrix using Gaussian elimination. Moreover, we define an identifying vector , which is labeled with 1 at each pivot position in , and is located in the space . The space can be classified into distinct classes based on these identifying vectors, with each class having the same identifying vector.
To transform the subspace X into the Ferrers diagram form , a series of operations is applied to . First, any leading zeros in the rows to the left of the pivots are removed. Second, the pivot column is removed, and the remaining entries are shifted to the right. The Ferrers diagram of X, denoted , is the resulting processed matrix. and are closely related, and can be obtained by replacing the entries of with dots.
For example, if the generator matrix of a 4-dimensional subspace X in the space is reduced to a row-reduced echelon form, the corresponding Ferrers diagram of X can be easily constructed by applying the aforementioned procedures.
Subsequently, the identifying vector representing X is designated as = Furthermore, is recorded as the Ferrers table form of X, which is
And is recorded as the Ferrers diagrams form of X, which is
Definition 1
([]). Assume that and are two vectors of length n, represents the j-th component in the vector , , The Hamming distance
for , when
Lemma 2
([]). Let , is identifying vector of , then
Definition 2
([]). Let be a Ferrers diagram, where the rightmost column contains m points and the topmost row contains ℓ points. A linear rank-metric code associated with a Ferrers diagram is called a Ferrers diagram rank metric code (FDRM) if it satisfies the following condition: For any code word M in , if M is not in some term of , then the value of that term must be zero. Moreover, for any nonzero code word A, if its rank is no less than δ, the dimension of is Based on these conditions, we represent the FDRM code as the FDRM code.
Lemma 3
([]). Let be a Ferrers diagram, it has ℓ points in the first row, and m points in the last column, and is an FDRM code, and it meets the following conditions: rank. Then , where represents the number of points in the that are neither in the first i row nor in the rightmost column, where i ranges from 0 to
Lemma 4
([]). Let be an FDRM code, then the lifted FDRM code is an CDC.
In order to construct an CDC on we first screen out a subset which has two key properties. Firstly, the weight is equal to k for any vector; secondly is that these vectors have a minimum Hamming distance of Then we treat these vectors in as identifying vectors, and for each identifying vector, we construct a corresponding FDRM code. According to Lemmas 2 and 3, these lifted FDRM codes are combined to form an CDC. The structural design on which this construction method is based, which is commonly called multilevel construction (see [,]).
2.3. Linkage Construction
Given some matrices , the row space of M over are expressed as the rs
Definition 3
([]). Let be a set of matrices, if rank, and for any two different matrices we denoted it as an SC-representing set. Then the set is CDC, and we denoted it by
Lemma 5
([]). Let and is an MRD code, is a RRMC code. Then is an CDC, where
Lemma 6
([]). Let be an SC-representation set of CDC with cardinality , and be a linear rank metric code with cardinality . Assume that the identifying vectors with length n and weight k satisfy the following conditions.
(a) For each , the number of in the last positions is more than or equal to
(b) The Hamming distance of two different identifying vectors is more than or equal to d.
Let be an FDRM code, with the corresponding identifying vector , are lifted FDRM code of . Define as the subspace code of length n, where
Then is an CDC with .
2.4. Sub-Codes Construction
Lemma 7
([]). The sub-codes construction can be described as follows: Let , , , , , be positive integers such that , and . For , assume is a MRD code, where , . For any and (where , and , we know that when , rank, and when , rank Then is an CDC, where consists of subspaces of the form:
, . is the identity matrix of size , and , are zero matrices of size and .
Lemma 8
([]). Suppose are positive integers such that and , for and be as defined above. Let be an MRD code. Then is an CDC with
where for and are zero matrices with
3. Main Results
In this section, we first propose Algorithm 1, which incorporates the construction method from Lemma 6. With the help of this algorithm, we obtain improved new lower bounds for linkage construction and echelon-Ferrers constructions. Then, inspired by [], we refine the insertion construction by swapping specific columns of the generator matrix, and as a result, we derive several new lower bounds.
| Algorithm 1: Modified greedy algorithm |
 |
3.1. Algorithm
Regarding recent improvements in the echelon-Ferrers construction, we refer to []. As for improvements in linkage construction, determining the optimal parameters for a new set of identifying vectors is a challenging problem. In this part, we use an improved algorithm based on a greedy approach to obtain a better set of identifying vectors, denoted by .
We made a minor enhancement to the greedy algorithm, focusing on selecting the identifying vectors with the maximum and second maximum dimensions as the best candidates. That is, we randomly added the identifying vectors from and to the set until the set was empty. Finally, after repeated experiments, we selected the final result.
Corollary 1.
and for
Proof.
Let , and be lifted FDRM code corresponding to the identifying vector in Table A1, by Lemma 6, so we have , it is known that andfor. The result is obviously valid. □
The best known lower bound is given in [], i.e., for Our result is above it.
Corollary 2.
and for
Proof.
Let , and be lifted FDRM code corresponding to identifying vector in Table A2, by Lemma 6 and . The result is obviously valid. □
The best known lower bound is given in [], i.e., for Our result is above it.
3.2. Construction
Niu et al. presented an improved inserting construction by exchanging some specified columns of the generator matrix of the CDC in []. Based on this, we have enhanced the column-swapping procedure.
Proposition 1.
Let be a vector with length and weight , where , and the number of ones in the last positions of is at least , the Hamming distance between distinct vectors in is at least d. Then, the set contains at least distinct vectors.
Next, we explain Proposition 1 using Algorithm 2.
| Algorithm 2: |
Input: d Output: target vector set
|
We present a portion of the results here. When and 8, as shown in Table 1.

Table 1.
Identifying vector set .
Theorem 1.
Using the notation from Lemma 6, , is an RRMC code. Let be obtained by swapping columns and of , and . Then is an CDC with .
Proof.
From , it is easy to see that the codewords of form a k-dimensional subspace of The minimum subspace distance of is at least d, as proven from two aspects:
Let the sets and be the distinct codewords of and and .
- where
I. If , that is, the positions of the swapped columns are the same, this is equivalent to proving that are CDCs for
There are the following three cases.
(1) if then rank.
(2) if , that is or , then .
(3) if , . then
II. If , that is the positions of the swapped columns are different, this is equivalent to proving that the subspace distance between and is at least d for
It easy to see that By Lemma 2,
Hence, is an CDC with □
Example 1. 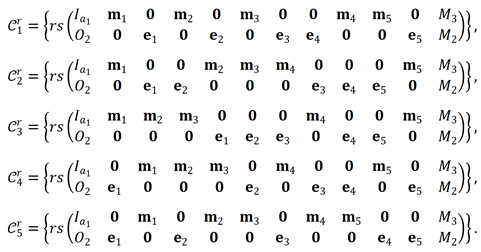
Let , , , , , . By Theorem 1, we take and , where is an MRD code, is an MRD code, , , and is a RRMC code. The following are the generator matrices of for . Then is an CDC.
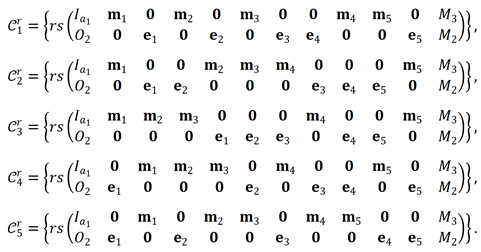
Theorem 2.
With the same notations as Theorem 1. Let and be as in Lemma 5, and as in Theorem 1. Then is an CDC with .
Proof.
where rank because there is at most non-zero columns in S. Then, . Let , we have
Let , and
- where and
The proof is composed of two parts:
I. The subspace distance between CDCs and is at least d.
It is easy to see that the identifying vector corresponding to is by and , it follows that has at least ones in the last k position, and at most ones in the first k position. Then Therefore, by Lemma 2, we have .
II. The subspace distance between CDCs and is at least d.
Hence, we can obtain
Combining all the aforementioned discussions, we arrive at the conclusion that is an CDC with . □
Corollary 3.
By Theorem 2, we have
Corollary 4.
For and , , we have
Example 2.
By Corollary 4, we have
,
,
,
- which improve the lower bounds in [].
4. Conclusions
This paper presents two improved construction methods for CDCs. First, we propose an enhanced algorithm that combines linkage structures and echelon-Ferrers designs, improving the lower bounds of and . Secondly, we enhance the inserting construction through column transformations of the generator matrix and obtain new lower bounds for , , and . We hope that these construction methods and the algorithms for computing identifying vectors will provide inspiration for the construction of other CDCs.
Author Contributions
Funding acquisition, Y.N.; methodology, Y.N.; supervision, Y.N.; writing—original draft, X.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (No. 12301665), the Basic Science (Natural Science) Research Projects of Universities in Jiangsu Province under Grant Agreement (No. 22KJB110009), and Applied Basic Research Support Project of Changzhou Science and Technology (No. CJ20235031).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank the referees and editors for their very useful suggestions, which significantly improved this paper.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CDC | Constant dimension code |
| RMC | Rank metric code |
| MRD | Maximum rank distance |
| RRMC | Rank-restricted RMC |
Appendix A

Table A1.
Construction for .
Table A1.
Construction for .
| Identifying Vector | Dimension | Identifying Vector | Dimension | ||
|---|---|---|---|---|---|
| 1 | 11000000110000 | 18 | 31 | 00000110011000 | 11 |
| 2 | 00110000110000 | 16 | 32 | 00010100100001 | 10 |
| 3 | 10100000101000 | 16 | 33 | 00001001100100 | 10 |
| 4 | 00001100110000 | 14 | 34 | 00101000001001 | 9 |
| 5 | 01100000011000 | 15 | 35 | 10000010100001 | 9 |
| 6 | 01100000100100 | 15 | 36 | 00100010001010 | 8 |
| 7 | 01010000101000 | 15 | 37 | 00011000000110 | 9 |
| 8 | 10010000100100 | 14 | 38 | 10001000000101 | 8 |
| 9 | 10100000010100 | 14 | 39 | 01000100010001 | 9 |
| 10 | 10010000011000 | 14 | 40 | 00110000000011 | 8 |
| 11 | 11000000001100 | 14 | 41 | 10000100001001 | 8 |
| 12 | 00110000001100 | 12 | 42 | 01010000000101 | 9 |
| 13 | 10001000100010 | 12 | 43 | 00010001100010 | 9 |
| 14 | 00000011110000 | 12 | 44 | 00010100001010 | 9 |
| 15 | 01010000010010 | 12 | 45 | 00100010010001 | 8 |
| 16 | 00001010101000 | 12 | 46 | 00000011001100 | 8 |
| 17 | 01001000010100 | 12 | 47 | 00100001100001 | 8 |
| 18 | 00010100010100 | 11 | 48 | 01000100000110 | 8 |
| 19 | 00100100100010 | 11 | 49 | 10000010000110 | 7 |
| 20 | 00011000010001 | 10 | 50 | 01000010001001 | 7 |
| 21 | 01001000100001 | 11 | 51 | 00010001001001 | 6 |
| 22 | 00000101101000 | 11 | 52 | 00100001000110 | 6 |
| 23 | 01000010100010 | 10 | 53 | 00001100000011 | 6 |
| 24 | 00001100001100 | 10 | 54 | 00100100000101 | 7 |
| 25 | 00001001011000 | 10 | 55 | 10000001010001 | 7 |
| 26 | 00101000010010 | 11 | 56 | 10000001001010 | 7 |
| 27 | 00000110100100 | 11 | 57 | 00000000111001 | 3 |
| 28 | 01001000001010 | 10 | 58 | 00000011000011 | 4 |
| 29 | 11000000000011 | 10 | 59 | 00000000110110 | 2 |
| 30 | 10000100010010 | 10 | 60 | 00000000001111 | 0 |

Table A2.
Construction for .
Table A2.
Construction for .
| Identifying Vector | Dimension | Identifying Vector | Dimension | ||
|---|---|---|---|---|---|
| 1 | 110000000000110000 | 22 | 43 | 010000010000100001 | 12 |
| 2 | 101000000000101000 | 20 | 44 | 010000100000001010 | 12 |
| 3 | 001100000000110000 | 20 | 45 | 010100000000000101 | 13 |
| 4 | 010100000000101000 | 19 | 46 | 001001000000010001 | 13 |
| 5 | 100100000000100100 | 18 | 47 | 000000110000001100 | 12 |
| 6 | 110000000000001100 | 18 | 48 | 001010000000001001 | 13 |
| 7 | 100100000000011000 | 18 | 49 | 000100100000010001 | 12 |
| 8 | 101000000000010100 | 18 | 50 | 001001000000001010 | 13 |
| 9 | 011000000000011000 | 19 | 51 | 000000001010101000 | 12 |
| 10 | 011000000000100100 | 19 | 52 | 000000000011110000 | 12 |
| 11 | 000011000000110000 | 18 | 53 | 100000010000000110 | 10 |
| 12 | 100010000000100010 | 16 | 54 | 001000000100100010 | 11 |
| 13 | 000110000000010100 | 16 | 55 | 000011000000000011 | 10 |
| 14 | 001100000000001100 | 16 | 56 | 000000000110011000 | 11 |
| 15 | 000010100000101000 | 16 | 57 | 001000100000000110 | 11 |
| 16 | 010100000000010010 | 16 | 58 | 100000001000001010 | 10 |
| 17 | 000000110000110000 | 16 | 59 | 100000010000010001 | 11 |
| 18 | 000110000000100001 | 15 | 60 | 000000101000010010 | 11 |
| 19 | 000001100000011000 | 15 | 61 | 000000000101101000 | 11 |
| 20 | 100001000000010010 | 14 | 62 | 000000001001011000 | 10 |
| 21 | 110000000000000011 | 14 | 63 | 000000001100001100 | 10 |
| 22 | 000110000000001010 | 14 | 64 | 000100010000001001 | 10 |
| 23 | 010001000000010100 | 15 | 65 | 100000100000001001 | 11 |
| 24 | 010001000000100010 | 15 | 66 | 000000100100010100 | 11 |
| 25 | 100001000000100001 | 14 | 67 | 000000010100010010 | 10 |
| 26 | 000001010000101000 | 15 | 68 | 000000000110100100 | 11 |
| 27 | 010010000000010001 | 14 | 69 | 000000001001100100 | 10 |
| 28 | 000010010000011000 | 14 | 70 | 001000010000000101 | 9 |
| 29 | 000100100000100010 | 14 | 71 | 000000001010010001 | 8 |
| 30 | 000011000000001100 | 14 | 72 | 000001001000000101 | 8 |
| 31 | 001010000000010010 | 15 | 73 | 000000010010001010 | 8 |
| 32 | 000010010000100100 | 14 | 74 | 000000110000000011 | 8 |
| 33 | 000001100000100100 | 15 | 75 | 000000000011001100 | 8 |
| 34 | 000000001100110000 | 14 | 76 | 000000001010000110 | 7 |
| 35 | 000101000000000110 | 12 | 77 | 000000001100000011 | 6 |
| 36 | 001000100000100001 | 13 | 78 | 000000100010000101 | 6 |
| 37 | 000000011000100010 | 12 | 79 | 000000000101010001 | 7 |
| 38 | 010001000000001001 | 12 | 80 | 000000000101000110 | 6 |
| 39 | 100010000000000101 | 12 | 81 | 000000000000111100 | 4 |
| 40 | 001100000000000011 | 12 | 82 | 000000000011000011 | 4 |
| 41 | 010010000000000110 | 13 | 83 | 000000000000110011 | 2 |
| 42 | 000000011000010100 | 12 | 84 | 000000000000001111 | 0 |
References
- Koetter, R.; Kschischang, F.R. Coding for errors and erasures in random network coding. IEEE Trans. Inf. Theory 2008, 54, 3579–3591. [Google Scholar] [CrossRef]
- Etzion, T.; Silberstein, N. Codes and designs related to lifted MRD codes. IEEE Trans. Inf. Theory 2013, 59, 1004–1017. [Google Scholar] [CrossRef]
- Tao, F.; Kurz, S.; Liu, S. Bounds for the multilevel construction. arXiv 2020, arXiv:2011.06937. [Google Scholar]
- Heinlein, D.; Kurz, S. Coset construction for subspace codes. IEEE Trans. Inf. Theory 2017, 63, 7651–7660. [Google Scholar] [CrossRef]
- Kurz, S. The interplay of different metrics for the construction of constant dimension codes. Adv. Math. Commun. 2023, 17, 152–171. [Google Scholar] [CrossRef]
- Niu, Y.; Yue, Q.; Huang, D. New constant dimension subspace codes from generalized inserting construction. IEEE Commun. Lett. 2021, 25, 1066–1069. [Google Scholar] [CrossRef]
- Niu, Y.; Yue, Q.; Huang, D. New constant dimension subspace codes from parallel linkage construction and multilevel construction. Cryptogr. Commun. 2022, 14, 201–214. [Google Scholar] [CrossRef]
- Zhu, C.; Wang, Q.; Xie, Y.; Xu, S. Multiview latent space learning with progressively fine-tuned deep features for unsupervised domain adaptation. Inf. Sci. 2024, 662, 120223. [Google Scholar] [CrossRef]
- Heinlein, D.; Kiermaier, M.; Kurz, S.; Wassermann, A. Tables of subspace codes. arXiv 2016, arXiv:1601.02864. [Google Scholar]
- Etzion, T.; Silberstein, N. Error-correcting codes in projective spaces via rank-metric codes and Ferrers diagrams. IEEE Trans. Inf. Theory 2009, 55, 2909–2919. [Google Scholar] [CrossRef]
- Lao, H.; Chen, H. New constant dimension subspace codes from multilevel linkage construction. Adv. Math. Commun. 2022, 18, 956–966. [Google Scholar] [CrossRef]
- Lao, H.; Chen, H.; Tan, X. New constant dimension subspace codes from block inserting constructions. Cryptogr. Commun. 2022, 14, 87–99. [Google Scholar] [CrossRef]
- Niu, M.; Xiao, J.; Gao, Y. New constructions of constant dimension codes by improved inserting construction. Appl. Math. Comput. 2023, 446, 127885. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.; Zhang, Z.; Zhou, K. New Construction for Constant Dimension Subspace Codes via a Composite Structure. IEEE Commun. Lett. 2021, 25, 1422–1426. [Google Scholar] [CrossRef]
- Li, F. Construction of constant dimension subspace codes by modifying linkage construction. IEEE Trans. Inf. Theory 2020, 66, 2760–2764. [Google Scholar] [CrossRef]
- Gluesing-Luerssen, H.; Troha, C. Construction of subspace codes through linkage. Adv. Math. Commun. 2016, 10, 525–540. [Google Scholar] [CrossRef]
- Silberstein, N.; Trautmann, A.L. Subspace codes based on graph matchings, Ferrers diagrams, and pending blocks. IEEE Trans. Inf. Theory 2015, 61, 3937–3953. [Google Scholar] [CrossRef]
- He, X.; Chen, Y.; Zhang, Z. Improving the linkage construction with echelon-Ferrers for constant-dimension codes. IEEE Commun. Lett. 2020, 24, 1875–1879. [Google Scholar] [CrossRef]
- Delsarte, P. Bilinear forms over a finite field, with applications to coding theory. J. Comb. Theory A 1978, 25, 226–241. [Google Scholar] [CrossRef]
- Gabidulin, E.M. Theory of codes with maximum rank distance. Problemy Peredachi Informatsii. Probl. Peredachi Informatsii 1985, 21, 3–16. [Google Scholar]
- Berlekamp, E.R. Introduction to Coding Theory; Springer: Vienna, Austria, 1970; pp. 5–11. [Google Scholar]
- Xu, L.; Chen, H. New constant-dimension subspace codes from maximum rank distance codes. IEEE Trans. Inf. Theory 2018, 64, 6315–6319. [Google Scholar] [CrossRef]
- Cossidente, A.; Kurz, S.; Marino, G.; Pavese, F. Combining subspace codes. Adv. Math. Commun. 2023, 17, 536–550. [Google Scholar] [CrossRef]
- Kurz, S. Lifted codes and the multilevel construction for constant dimension codes. arXiv 2020, arXiv:2004.14241. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).