On the Containment of the Unit Disc Image by Analytical Functions in the Lemniscate and Nephroid Domains

Abstract

Suppose that ${\mathcal{A}}_1$ is a class of analytic functions $f:\mathfrak{D}=\{z\in \mathbb{C}:|z|<1\}\to \mathbb{C}$ with normalization $f(0)=1$. Consider two functions ${\mathcal{P}}_l(z)=\sqrt{1+z}$ and ${\mathsf{\Phi }}_{N_e}(z)=1+z-z^3/3$, which map the boundary of $\mathfrak{D}$ to a cusp of lemniscate and to a twi-cusped kidney-shaped nephroid curve in the right half plane, respectively. In this article, we aim to construct functions $f\in {\mathcal{A}}_0$ for which (i) $f(\mathfrak{D})\subset {\mathcal{P}}_l(\mathfrak{D})\cap {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$ (ii) $f(\mathfrak{D})\subset {\mathcal{P}}_l(\mathfrak{D})$, but $f(\mathfrak{D})\not\subset {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$ (iii) $f(\mathfrak{D})\subset {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$, but $f(\mathfrak{D})\not\subset {\mathcal{P}}_l(\mathfrak{D})$. We validate the results graphically and analytically. To prove the results analytically, we use the concept of subordination. In this process, we establish the connection lemniscate (and nephroid) domain and functions, including ${\mathtt{g}}_{\alpha }(z):=\sqrt{1+\alpha z^2}$, $|\alpha |\le 1$, the polynomial ${\mathtt{g}}_{\alpha ,\beta }(z):=1+\alpha z+\beta z^3$, $\alpha ,\beta \in \mathbb{R}$, as well as Lerch’s transcendent function, Incomplete gamma function, Bessel and Modified Bessel functions, and confluent and generalized hypergeometric functions.

1. Introduction

Recently, research into the theory of geometric functions related to nephroid and leminscate domains has gained prominence [1,2,3,4,5,6]. Here, the leminscate domain refers to the image of $\mathfrak{D}=\{z:|z|<1\}$ through the function ${\mathcal{P}}_l(z)=\sqrt{1+z}$, while the image of $\mathfrak{D}$ through the function ${\mathsf{\Phi }}_{N_e}(z)=1+z-z^3/3$ is known as the nephroid domain. The mapping of boundary of unit disc $\mathfrak{D}$ by ${\mathcal{P}}_l$ and ${\mathsf{\Phi }}_{N_e}$ is given in Figure 1.

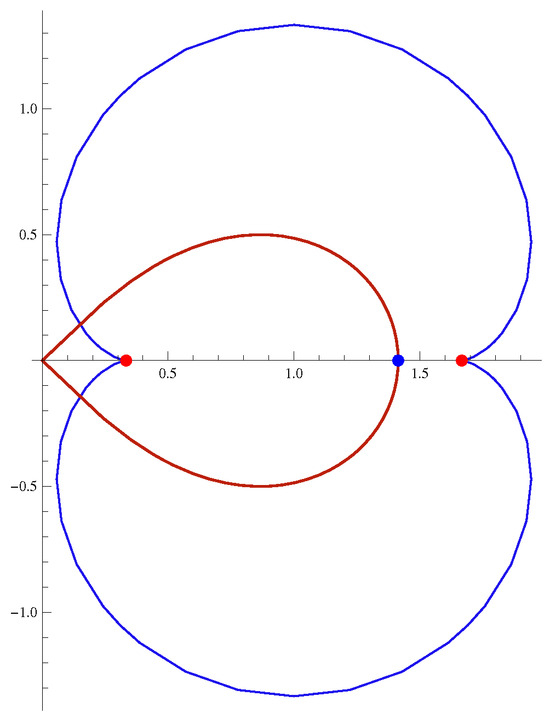
Figure 1. Mapping of the boundary of the unit disc using the lemniscate and nephroid curve.

Now, we recall a few basic concepts of the geometric function theory. The class of functions f defined on the open unit disk $\mathfrak{D}=\{z:|z|<1\}$, and normalized by the conditions $f(0)=0=f^{\prime }(0)-1$, is denoted by $\mathcal{A}$. We say $f\in {\mathcal{A}}_1$ if $f(0)=1$ is the normalized condition. Generally, $f\in \mathcal{A}$ possess power series

$$\begin{array}{c}\hfill f(z)=z+\sum _{n=2}^{\infty }{a}_n{z}^n,\end{array}$$

while $f\in {\mathcal{A}}_1$ has the power series

$$\begin{array}{c}\hfill f(z)=1+\sum _{n=1}^{\infty }{b}_n{z}^n.\end{array}$$

Definition 1 

(Subordination). For two functions f and g, which are analytic in $\mathfrak{D}$, we say that f is subordinate to g, and write $f\prec g$ in $\mathfrak{D}$, if there exists a Schwartz function $w(z)$, which is analytic in $\mathfrak{D}$ with $w(0)=0$ and $|w(z)|<1$$(z\in \mathfrak{D})$, such that $f(z)=g(w(z))$.

Subordination [7] is one of the important concepts of geometric function theory that is useful in studying the geometric properties of analytic functions. There are several important sub-classes of $\mathcal{A}$, namely the class of starlike and convex functions denoted by ${\mathcal{S}}^{*}$ and $\mathcal{C}$, respectively. The Cárath}eodory class $\mathcal{P}$ includes analytic functions p that satisfy $p(0)=1$ and $Rep(z)>0$ in $\mathfrak{D}$. These sub-classes are related to each other. In analytical terms, $f\in {\mathcal{S}}^{*}$ if $z{f}^{\prime }(z)/f(z)\in \mathcal{P}$, and $f\in \mathcal{C}$ if $1+z{f}^{″}(z)/f^{\prime }(z)\in \mathcal{P}$.

If $1+(z{f}^{″}(z)/f^{\prime }(z))$ is within the region bounded by the right half of the lemniscate of Bernoulli, denoted by $\{w:|w^2-1|=1\}$, then the function $f\in \mathcal{A}$ is known as the lemniscate convex. This is equivalent to subordination $1+(z{f}^{″}(z)/f^{\prime }(z))\prec \sqrt{1+z}$. In an analogous way, if $z{f}^{\prime }(z)/f(z)\prec \sqrt{1+z}$, then the function f is lemniscate starlike. Moreover, if $f^{\prime }(z)\prec \sqrt{1+z}$, then the function $f\in \mathcal{A}$ is lemniscate Carathéodory. It is evident that the lemniscate Carathéodory function is univalent as it is a Carathéodory function. More details about the geometric properties associated with lemniscate can be seen in [5,8,9].

In this article, we are going to study the following functions or a combination of them. Details about the nature of the functions are provided in the associated section or subsection. The listed functions are as follows:

• Section 2: The function ${\mathtt{g}}_{\alpha }(z):=\sqrt{1+\alpha z^2}$, $|\alpha |\le 1$,
• Section 3: The polynomial ${\mathtt{g}}_{\alpha ,\beta }(z):=1+\alpha z+\beta z^3$, $\alpha ,\beta \in \mathbb{R}$,
• Section 5: Lerch’s transcendent function,
• Section 6: Incomplete gamma function,
• Section 7: Bessel and Modified Bessel functions.

Our aim is to derive the condition for which an analytic function or a polynomial, let us denote it as f, maps the unit disc to a domain such that following implication holds: (i) $f(\mathfrak{D})\subset {\mathcal{P}}_l(\mathfrak{D})\cap {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$ (ii) $f(\mathfrak{D})\subset {\mathcal{P}}_l(\mathfrak{D})$, but $f(\mathfrak{D})\not\subset {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$ (iii) $f(\mathfrak{D})\subset {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$, but $f(\mathfrak{D})\not\subset {\mathcal{P}}_l(\mathfrak{D})$.

2. Results Involving ${\mathtt{g}}_{\mathit{\alpha }}(\mathit{z}):=\sqrt{\mathbf{1}+\mathit{\alpha }{\mathit{z}}^{\mathbf{2}}}$

In this section, we consider the function ${\mathtt{g}}_{\alpha }(z):=\sqrt{1+\alpha z^2}$, $|\alpha |\le 1$. Using the definition of subordination, we derived conditions on the parameter $\alpha$ for which ${\mathtt{g}}_{\alpha }(z)\prec \sqrt{1+z}$ and ${\mathtt{g}}_{\alpha }(z)\prec {\mathsf{\Phi }}_{N_e}(z)$. We also validate the result through graphical representation. Using ${\mathtt{g}}_{\alpha }$, we also construct a function that is lemniscate and nephroid starlike under the same condition as $\alpha$.

Theorem 1. 

The containment ${\mathtt{g}}_{\alpha }(\mathfrak{D})\subset {\mathcal{P}}_l(\mathfrak{D})$ holds for $|\alpha |\le 1$, while the containment ${\mathtt{g}}_{\alpha }(\mathfrak{D})\subset {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$ is true for $|\alpha |\le 8/9$.

Proof. 

Consider the function $\omega (z)=\alpha z^2$. Then, $\omega (0)=0$ and $|\omega (z)|<|\alpha |\le 1$. Thus, by the definition of subordination,

$$\begin{array}{c}\hfill \sqrt{1+\alpha z^2}=\sqrt{1+w(z)}\Rightarrow \sqrt{1+\alpha z^2}\prec \sqrt{1+z}.\end{array}$$

(1)

Hence, ${\mathtt{g}}_{\alpha }(\mathfrak{D})\subset {\mathcal{P}}_l(\mathfrak{D})$ holds for $|\alpha |\le 1$.

For the second part, first we note that ${\mathsf{\Phi }}_{N_e}$ intercepts the x-axis, at ${\mathsf{\Phi }}_{N_e}(-1)=1/3$ and ${\mathsf{\Phi }}_{N_e}(1)=5/3$. Furthermore, $g_{\alpha }$ intercepts the x-axis, at ${\mathtt{g}}_{\alpha }(\pm i)=\sqrt{1-\alpha }$ and at ${\mathtt{g}}_{\alpha }(\pm 1)=\sqrt{1+\alpha }$. From Figure 1, it is evident that ${\mathtt{g}}_{\alpha }(\mathfrak{D})\subset {\mathcal{P}}_l(\mathfrak{D})$ implies ${\mathtt{g}}_{\alpha }(\mathfrak{D})\subset {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$, provided the left side intercept of ${\mathtt{g}}_{\alpha }$ with the x-axis is above $1/3$.

In this aspect, ${\mathtt{g}}_{\alpha }(z)\prec {\mathsf{\Phi }}_{N_e}(z)$ implies the validity of the following inequalities:

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{3}}& <{\mathtt{g}}_1(\pm i)<1<{\mathtt{g}}_1(\pm 1)<{\displaystyle \frac{5}{3}},\mathrm{when}0\le \alpha \le 1.\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{3}}& <{\mathtt{g}}_1(\pm 1)<1<{\mathtt{g}}_1(\pm i)<{\displaystyle \frac{5}{3}},\mathrm{when}-1\le \alpha <0.\hfill \end{array}$$

(3)

In (2), the left side inequality holds if $\sqrt{1-\alpha }>1/3$, which is equivalent to $0<\alpha <8/9$. On the other hand, the right hand side inequality holds if $\sqrt{1+\alpha }<5/3$ is equivalent to $0<\alpha <16/9$. Thus, both inequalities hold when $0<\alpha <8/9$. Similarly, in (3), the left side inequality holds if $\sqrt{1+\alpha }>1/3$, which is equivalent to $\alpha >-8/9$, and the right hand side inequality holds if $\sqrt{1-\alpha }<5/3$ is equivalent to $\alpha >-16/9$. Thus, both inequalities hold when $0>\alpha >-8/9$. Finally, we conclude that $\sqrt{1+\alpha z^2}\prec {\mathsf{\Phi }}_{N_e}(z)$, equivalently ${\mathtt{g}}_{\alpha }(\mathfrak{D})\subset {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$ holds only when $|\alpha |<8/9$. □

We can interpret the result in Theorem 1 from the following visualization (Figure 2) by considering different $\alpha$, namely $\alpha =-35/36,-1/2,1/2,8/9,35/36$.

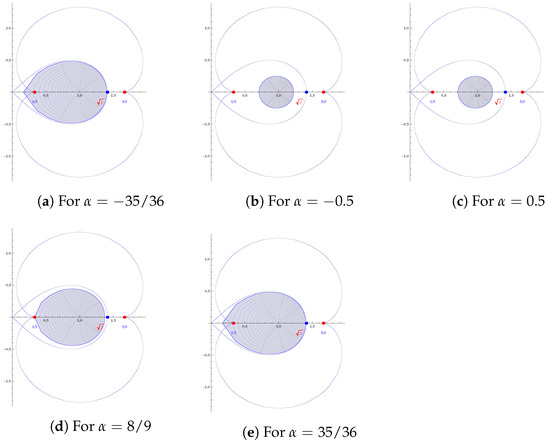
Figure 2. Graphical interpretation of Theorem 1 for different $\alpha$.

Theorem 2. 

For $\alpha ,\beta \in \mathbb{R}$ and $z\in \mathfrak{D}$, the function

$$\begin{array}{c}\hfill {\mathtt{F}}_{\alpha }(z):={\displaystyle \frac{2}{e}}{\displaystyle \frac{zexp\left(\sqrt{1+\alpha z^2}\right)}{1+\sqrt{1+\alpha z^2}}},\end{array}$$

(4)

is lemniscate starlike for $|\alpha |\le 1$ and nephriod starlike when $|\alpha |<8/9$.

Proof. 

To show lemniscate or nephroid starlikeness, our aim is to prove, respectively,

$$\begin{array}{c}\hfill {\displaystyle \frac{z{\mathtt{F}}_{\alpha }^{\prime }(z)}{{\mathtt{F}}_{\alpha }(z)}}\prec \sqrt{1+z}\mathrm{and}{\displaystyle \frac{z{\mathtt{F}}_{\alpha }^{\prime }(z)}{{\mathtt{F}}_{\alpha }(z)}}\prec 1+z-\frac{z^3}{3}.\end{array}$$

It is clear that ${\mathtt{F}}_{\alpha }(0)=0$, and a logarithmic differentiation of both sides in (4) yields

$$\begin{array}{ll}{\displaystyle \frac{{\mathtt{F}}_{\alpha }^{\prime }(z)}{{\mathtt{F}}_{\alpha }(z)}}& ={\displaystyle \frac{\alpha z}{\sqrt{\alpha z^2+1}}}-{\displaystyle \frac{\alpha z}{\sqrt{\alpha z^2+1}\left(\sqrt{\alpha z^2+1}+1\right)}}+{\displaystyle \frac{1}{z}}\\ & ={\displaystyle \frac{\alpha z}{\sqrt{\alpha z^2+1}+1}}+{\displaystyle \frac{1}{z}}\\ & ={\displaystyle \frac{\alpha z^2+\sqrt{\alpha z^2+1}+1}{z\left(\sqrt{\alpha z^2+1}+1\right)}}\\ & ={\displaystyle \frac{\sqrt{\alpha z^2+1}}{z}}.\end{array}$$

(5)

Further simplification of (5) leads

$$\begin{array}{c}\hfill {\mathtt{F}}_{\alpha }^{\prime }(z)={\displaystyle \frac{\sqrt{\alpha z^2+1}}{z}}{\mathtt{F}}_{\alpha }(z)={\displaystyle \frac{2}{e}}{\displaystyle \frac{exp\left(\sqrt{1+\alpha z^2}\right)\sqrt{\alpha z^2+1}}{1+\sqrt{1+\alpha z^2}}}.\end{array}$$

(6)

Thus, ${\mathtt{F}}_{\alpha }^{\prime }(0)=1$. It is also follows from (5) that

$$\begin{array}{c}\hfill {\displaystyle \frac{z{\mathtt{F}}_{\alpha }^{\prime }(z)}{{\mathtt{F}}_{\alpha }(z)}}=\sqrt{1+\alpha z^2}={\mathtt{g}}_{\alpha }(z).\end{array}$$

(7)

As Theorem 1 provides us ${\mathtt{g}}_{\alpha }(z)\prec {\mathcal{P}}_l(z)$ for $|\alpha |\le 1$ and ${\mathtt{g}}_{\alpha }(z)\prec {\mathsf{\Phi }}_{N_e}(z)$ for $|\alpha |\le 8/9$, we have the conclusion from (7). □

3. Result Related to ${\mathit{g}}_{\mathit{\alpha },\mathit{\beta }}(\mathit{z})=\mathbf{1}+\mathit{\alpha }\mathit{z}+\mathbf{3}\mathit{\beta }{\mathit{z}}^{\mathbf{3}}$

For $\alpha ,\beta \in \mathbb{R}$, define the function

$$\begin{array}{c}\hfill {\mathtt{G}}_{\alpha ,\beta }(z)=z{e}^{\alpha z+\beta z^3}.\end{array}$$

(8)

Clearly, ${\mathtt{G}}_{\alpha ,\beta }(0)=0$ and ${\mathtt{G}}_{\alpha ,\beta }^{\prime }(0)=1$. In our next result, we will find conditions for $\alpha$ and $\beta$ for which the function ${\mathtt{G}}_{\alpha ,\beta }(z)$ is lemniscate and nephroid starlike. First, we need the following result.

Theorem 3. 

For $\alpha ,\beta \in \mathbb{R}$, the function $g_{\alpha ,\beta }(z)=1+\alpha z+3\beta z^3\prec \sqrt{1+z}$ for $|\alpha |+3|\beta |\le \sqrt{2}-1$ and $g_{\alpha ,\beta }(z)\prec 1+z-z^3/3$ when $|\alpha |\le 1$ and $\beta =-{\alpha }^3/9$.

Proof. 

Consider the function $w_1(z)=2(\alpha z+3\beta z^3)+{(\alpha z+3\beta z^3)}^2$. Clearly, $w_1(0)=0$ and

$$\begin{array}{c}\hfill \sqrt{1+w_1(z)}=\sqrt{1+2(\alpha z+3\beta z^3)+{(\alpha z+3\beta z^3)}^2}=1+\alpha z+3\beta z^3.\end{array}$$

Now, for $|z|<1$ and $|\alpha |+3|\beta |\le \sqrt{2}-1$, it follows

$$\begin{array}{c}\hfill |w_1(z)|<2(|\alpha |+3|\beta |)+(|\alpha |+{3|\beta |)}^2={(1+|\alpha |+3|\beta |)}^2-1\le 1.\end{array}$$

From the definition of subordination, we can conclude that $1+\alpha z+3\beta z^3\prec \sqrt{1+z}$.

In similar way, the second part of the result follows if we consider $w_2(z)=\alpha z$. Clearly, $w_2(0)=0$ and $|w_2(z)|<|\alpha |\le 1$. Now, by taking $\beta =-{\alpha }^3/9$, we have

$$\begin{array}{c}\hfill 1+w_2(z)-{\displaystyle \frac{w_2^3(z)}{3}}=1+\alpha z-{\displaystyle \frac{{\alpha }^3}{3}}{z}^3=1+\alpha z+\beta z^3.\end{array}$$

This provides the required subordination. □

A logarithmic differentiation of (8) yields

$$\begin{array}{c}\hfill {\displaystyle \frac{z{\mathtt{G}}_{\alpha ,\beta }^{\prime }(z)}{{\mathtt{G}}_{\alpha ,\beta }(z)}}=g_{\alpha ,\beta }(z).\end{array}$$

Therefore, Theorem 3 immediately leads to the following conclusion.

Theorem 4. 

For $\alpha ,\beta \in \mathbb{R}$, and $z\in \mathfrak{D}$, the function ${\mathtt{G}}_{\alpha ,\beta }(z)$ is lemniscate starlike for $|\alpha |+3|\beta |\le \sqrt{2}-1$ and nephroid starlike when $|\alpha |\le 1$ and $\beta =-{\alpha }^3/9$.

4. Results Related to Taylor Series of an Analytic Functions and It’s Partial Sum

Consider a function $\mathfrak{A}:\mathbb{N}\times [1/2,\infty )$, such that

$$\sum _{k=1}^{\infty }(k\beta +1)|\mathfrak{A}(k,\beta )|$$

is convergent for $\beta \ge 1/2$, and also the function

$$\begin{array}{c}\hfill f_{\beta }(z)=1+\sum _{k=1}^{\infty }\mathfrak{A}(k,\beta )z^k\in {\mathcal{A}}_1.\end{array}$$

(9)

We denote the n-th partial sum of the series $f_{\beta }$ as $S_n(f_{\beta },z)$.

For our next result, we need following

Lemma 1

([6], Theorem 3.2). Suppose that the function $p(z)\in {\mathcal{A}}_1$ satisfies the subordination $p(z)+\beta z{p}^{\prime }(z)\prec 1+z$ for $\beta >0$. Then, $p(z)\prec {\mathsf{\Phi }}_{N_e}(z)$ whenever $\beta \ge 1/2$, and this estimate on β is sharp.

Theorem 5. 

For $\beta \ge 1/2$ and $z\in \mathfrak{D}$, the partial sum $S_n(f_{\beta },z)\prec 1+z-z^3/3$ provided

$$\begin{array}{c}\hfill \sum _{k=1}^n(k\beta +1)|\mathfrak{A}(k,\beta )|\le 1.\end{array}$$

(10)

In general, the function ${\displaystyle f_{\beta }(z)=\underset{n\to \infty }{lim}{S}_n(f_{\beta },z)\prec 1+z-z^3/3}$ provided

$$\begin{array}{c}\hfill \sum _{k=1}^{\infty }(k\beta +1)|\mathfrak{A}(k,\beta )|\le 1.\end{array}$$

(11)

Proof. 

Denote $p_1(z)=S_n(f_{\beta },z)$. Then, a calculation yields

$$\begin{array}{c}\hfill p_1(z)+\beta z{p}_1^{\prime }(z)=1+\sum _{k=1}^n(k\beta +1)\mathfrak{A}(k,\beta )z^k.\end{array}$$

Now, consider the Schwarz function

$$w(z)=\sum _{k=1}^n(k\beta +1)\mathfrak{A}(k,\beta )z^k.$$

Clearly, $w(0)=0$. As $|z|<1$, the hypothesis (10) implies

$$|w(z)|\le \sum _{k=1}^n{(k\beta +1)|\mathfrak{A}(k,\beta )||z|}^k<\sum _{k=1}^n(k\beta +1)|\mathfrak{A}(k,\beta )|\le 1.$$

Finally, $p_1(z)+\beta z{p}_1^{\prime }(z)=1+w(z)$ yields $p_1(z)+\beta z{p}_1^{\prime }(z)\prec 1+z$. The final conclusion follows from Lemma 1.

Similarly, the general part holds by considering the Schwarz function as

$$w(z)=\sum _{k=1}^{\infty }(k\beta +1)\mathfrak{A}(k,\beta )z^k.$$

We omit the details proof for this part. □

Remark 1. 

Instead of the partial sum $S_n(f_{\beta },z)$, the result is still holds if we consider the n th degree polynomial defined by $P_n(z):=1+{\sum }_{k=1}^n\mathfrak{A}(k,\beta )z^k$.

Now, judicious choice of $\mathfrak{A}(k,\beta )$ in Theorem 5 leads to several interesting examples. Because of the independent significance of each example, we present them as a theorem.

Theorem 6. 

For $\beta \ge 1/2$ and $z\in \mathfrak{D}$, the polynomials ${\mathfrak{F}}_{\beta }(z)=1\pm z/(1+\beta )\prec {\mathsf{\Phi }}_{N_e}(z)$.

Proof. 

In virtue of Theorem 5 and Remark 1, we have $\mathfrak{A}(k,\beta )=\pm {\displaystyle \frac{1}{k\beta +1}}$, $n=1$ and, hence, $k=1$. Thus, $P_1(z)={\mathfrak{F}}_{\beta }(z)$. Clearly, $(k\beta +1)|\mathfrak{A}(k,\beta )|=1$. Thus, the result follows from Theorem 5. □

Remark 2. 

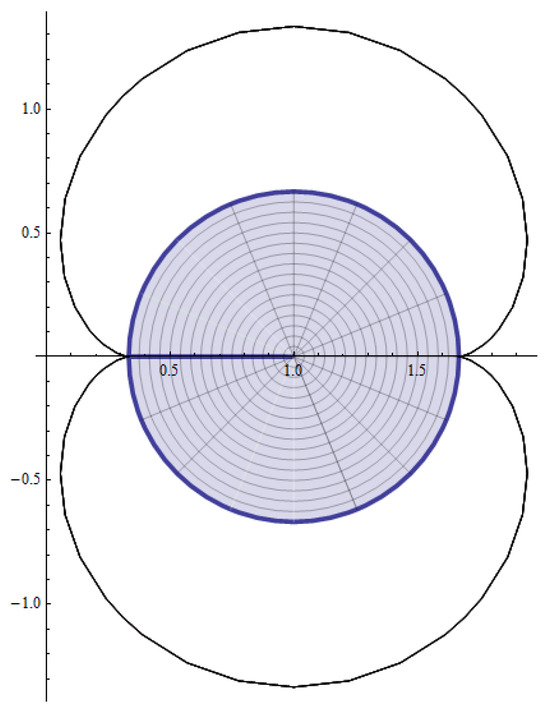
The function ${\mathfrak{F}}_{1/2}(z)$ is one of the best fitting subordinated functions of ${\mathsf{\Phi }}_{N_e}(z)$, as is evident from the Figure 3.

Figure 3. Image of $\mathfrak{D}$ by the polynomial ${\mathfrak{F}}_{1/2}(z)$.

5. Results Related to Lerch’s Transcendent Functions

Next, we consider the function

$$\begin{array}{c}\hfill {\varpi }_n(z,r,a):=\sum _{k=0}^n{\displaystyle \frac{a^r{z}^k}{{(k+a)}^r}},n\in \mathbb{N}\mathrm{and}r\in \mathbb{R}.\end{array}$$

(12)

Here, $a\ne 0,-1,-2,-3,\dots ,-n$ when $r>0$ and a is any real number when $r\le 0$.

For $n\to \infty$, the function ${\displaystyle \underset{n\to \infty }{lim}{\varpi }_n(z,r,a)=a^r\mathsf{\Phi }(z,r,a)}$ which is well known Lerch’s transcendent. The Lerch’s transcendent $\mathsf{\Phi }(z,r,a)$ is given by its power series as

$$\begin{array}{c}\hfill \mathsf{\Phi }(z,r,a)=\sum _{k=0}^{\infty }{\displaystyle \frac{z^k}{{(k+a)}^r}},\end{array}$$

(13)

which is convergent for $a\notin -\mathbb{N}$ when $z\in \mathfrak{D}$. For this study, we consider $r>-1$ and $a>-1$. Our aim is to find the answer to the following problem.

Problem 1. 

Find the triplet $(r,a,n)$, such that ${\varpi }_n(z,r,a)$ and $\mathsf{\Phi }(z,r,a)$ are subordinate by ${\mathcal{P}}_l(z)$ and ${\mathsf{\Phi }}_{N_e}(z)$.

To answer Problem 1, we need to further discuss $\mathsf{\Phi }(z,r,a)$. The Lerch’s transcendent generalized various special functions, namely

• The Hurwitz Zeta function: The function is defined when $z=1$ and is represented as

  $$\begin{array}{c}\hfill \zeta (r,a)=\mathsf{\Phi }(1,r,a)=\sum _{k=0}^{\infty }{\displaystyle \frac{1}{{(k+a)}^s}}.\end{array}$$

  (14)
• Poly-logarithm function: The function is defined as

  $$\begin{array}{c}\hfill L{i}_r(z)=z\mathsf{\Phi }(z,r,1)=\sum _{k=1}^{\infty }{\displaystyle \frac{z^k}{k^s}}.\end{array}$$

  (15)

For more details about this function, see [10].

Theorem 7. 

For $r>-1$, $a>-1$, and $z\in \mathfrak{D}$, the function ${\varpi }_n(z,r,a)\prec \sqrt{1+z}$ provides

$$\begin{array}{c}\hfill a^r\left(\zeta (r,1+a)-\zeta (r,1+a+n)\right)<\sqrt{2}-1.\end{array}$$

(16)

Proof. 

Define

$$\begin{array}{c}\hfill W_n(z):=2\sum _{k=1}^n{\displaystyle \frac{a^r{z}^k}{{(k+a)}^r}}+{\left(\sum _{k=1}^n{\displaystyle \frac{a^r{z}^k}{{(k+a)}^r}}\right)}^2.\end{array}$$

(17)

Clearly, $W_n(0)=0$. Now, to find the condition for which $|W_n(z)|<1$, we rearrange the terms $\zeta (r,a)$, and it follows from (14) that

$$\begin{array}{cc}\hfill \sum _{k=1}^n{\displaystyle \frac{a^r}{{(k+a)}^r}}& =\sum _{k=0}^{\infty }{\displaystyle \frac{a^r}{{(k+1+a)}^r}}-\sum _{k=n+1}^{\infty }{\displaystyle \frac{a^r}{{(k+a)}^r}}\hfill \\ \hfill & =a^r\zeta (r,1+a)-a^r\sum _{k=0}^{\infty }{\displaystyle \frac{1}{{(k+n+1+a)}^r}}\hfill \\ \hfill & =a^r\left(\zeta (r,1+a)-\zeta (r,1+a+n)\right).\hfill \end{array}$$

Now, for $|z|<1$, the hypothesis in (16) yields

$$\begin{array}{cc}\hfill |W_n(z)|& <2\sum _{k=1}^n{\displaystyle \frac{a^r}{{(k+a)}^r}}+{\left(\sum _{k=1}^n{\displaystyle \frac{a^r}{{(k+a)}^r}}\right)}^2,\hfill \\ \hfill & =2a^r\left(\zeta (r,1+a)-\zeta (r,1+a+n)\right)+a^{2r}{\left(\zeta (r,1+a)-\zeta (r,1+a+n)\right)}^2\hfill \\ \hfill & ={\left(1+a^r\zeta (r,1+a)-a^r\zeta (r,1+a+n)\right)}^2-1<1.\hfill \end{array}$$

The result follows from the definition of subordination. □

A natural question arises about the existence of triplet $(r,a,n)$, for which the hypothesis (16) of Theorem 7 is true. We investigate numerically two possible cases to explain that such triplets exist.

• Fixed r and n: In the following table, we present $a_0$, such that the inequality (16) holds for fixed n, r. Here, $a_0$ is the solution to the equation

  $$a^r(\zeta (r,1+a)-\zeta (r,1+a+n))=\sqrt{2}-1.$$
  Denote, $\mathrm{H}(a):=a^r(\zeta (r,1+a)-\zeta (r,1+a+n))-\sqrt{2}+1$. Then,

  $$\begin{array}{cc}\hfill H^{\prime }(a)& =-r{a}^r\zeta (r+1,1+a)+r{a}^r\zeta (r+1,1+a+n)\hfill \\ \hfill & =-r{a}^r\sum _{k=0}^{\infty }{\displaystyle \frac{1}{{(k+1+a)}^{r+1}}}+r{a}^r\sum _{k=0}^{\infty }{\displaystyle \frac{1}{{(k+1+a+n)}^{r+1}}}\hfill \\ \hfill & =r{a}^r\sum _{k=0}^{\infty }{\displaystyle \frac{{(k+1+a)}^{r+1}-{(k+1+a+n)}^{r+1}}{{(k+1+a+n)}^{r+1}{(k+1+a)}^{r+1}}}<0.\hfill \end{array}$$
  Thus, $\mathrm{H}(a)$ is a decreasing function of a, and hence the inequality (16) holds for $a\ge a_0$.
  Table 1 lists a few values for $a_0$ with fixed r and n.

  Table 1. The values for $a_0$ with fixed r and n.

  	1/2	3/2	2	5/2	3
  1	0.207107	1.25057	1.80579	2.3658	2.92823
  2	0.0617472	0.733443	1.13638	1.55064	1.97081
  3	0.033622	0.607962	0.980932	1.36935	1.76586
  4	0.0224263	0.549594	0.911624	1.29195	1.68176
  5	0.0165764	0.515237	0.872399	1.24991	1.63784
  6	0.0130345	0.492324	0.847168	1.2239	1.61168
  7	0.0106812	0.475811	0.82958	1.20642	1.5947
  8	0.00901404	0.463262	0.816619	1.19397	1.58302
  9	0.00777637	0.453352	0.806673	1.18471	1.5746
  10	0.00682406	0.445295	0.798799	1.1776	1.56834

  Table 1. The values for $a_0$ with fixed r and n.

  	1/2	3/2	2	5/2	3
  1	0.207107	1.25057	1.80579	2.3658	2.92823
  2	0.0617472	0.733443	1.13638	1.55064	1.97081
  3	0.033622	0.607962	0.980932	1.36935	1.76586
  4	0.0224263	0.549594	0.911624	1.29195	1.68176
  5	0.0165764	0.515237	0.872399	1.24991	1.63784
  6	0.0130345	0.492324	0.847168	1.2239	1.61168
  7	0.0106812	0.475811	0.82958	1.20642	1.5947
  8	0.00901404	0.463262	0.816619	1.19397	1.58302
  9	0.00777637	0.453352	0.806673	1.18471	1.5746
  10	0.00682406	0.445295	0.798799	1.1776	1.56834

• Fixed r and a: In this part, we fix r and a and test the validity of inequality (16) by finding the numerical values of $a^r(\zeta (r,1+a)-\zeta (r,1+a+n))$ for $n=1,2,3,4,5$. If the values is less than $\sqrt{2}-1=0.414214$, we have the triplet $(r,a,n)$.
  The standout values are bigger than $\sqrt{2}-1=0.414214$ and the combination of $(r,a,n)$ is not of interest to us. The trend for higher n and a can be easily observed from the data in Table 2.

From Table 2, one can observe that the number of standout values reduces when r increases. Now, we test the inequality (16) when $r=3$, $a=1,2,3,4,5$, and n is large, for example, $n=100,500,1000,2000,5000,10000,100000$, and the outcome is presented in Table 3. It is clear from Table 3 that, for a large n, the value of $a^r(\zeta (r,1+a)-\zeta (r,1+a+n))$ may converge to a specific real number. This observation is conducted for each row individually. This raises questions regarding how the exact values should be formulated when $n\to \infty$. The answer can be found in the following result.

Table 3. Validation of inequality (16) for fixed $r=3$ and higher values of n.

a/n	100	500	1000	10,000	15,000	20,000
0.1	0.000930679	0.000930727	0.000930728	0.00093073	0.00093073	0.00093073
0.2	0.00591175	0.00591213	0.00591214	0.0059121	0.0059121	0.0059121
0.33	0.0202925	0.0202942	0.0202943	0.0202943	0.0202943	0.0202943
0.5	0.0517937	0.0517995	0.0517997	0.0517998	0.0517998	0.0517998
0.75	0.118504	0.118523	0.118524	0.118524	0.118524	0.118524
1	0.202008	0.202055	0.202056	0.202057	0.202057	0.202057
1.5	0.398432	0.398588	0.398593	0.398594	0.398594	0.398594
1.52	0.406829	0.40699	0.406996	0.406997	0.406997	0.406997
1.53	0.411039	0.411204	0.411209	0.411211	0.411211	0.411211

Table 2. Validation of inequality (16) for fixed $r=0.5,2,2.5,3$.

a/n	1	2	3	4	5
r = 0.5
$0.1$	0.301511	$\cancel{0.519729}$	$\cancel{0.699335}$	$\cancel{0.855508}$	$\cancel{0.995536}$
$0.2$	0.408248	$\cancel{0.70976}$	$\cancel{0.95976}$	$\cancel{1.17798}$	$\cancel{1.37409}$
$0.33$	$\cancel{0.5}$	$\cancel{0.877964}$	$\cancel{1.19419}$	$\cancel{1.47154}$	$\cancel{1.72154}$
r = 2
0.1	0.00826446	0.010532	0.0115726	0.0121675	0.012552
0.2	0.0277778	0.0360422	0.0399485	0.0422161	0.0436954
0.33	0.0615637	0.081623	0.0914436	0.097252	0.101085
0.5	0.111111	0.151111	0.171519	0.183865	0.192129
0.75	0.183673	0.258054	0.298054	0.322984	0.339998
1	0.25	0.361111	$\cancel{0.423611}$	$\cancel{0.463611}$	$\cancel{0.491389}$
r = 2.5
0.1	0.00249183	0.00298665	0.00317355	0.00326645	0.00332029
0.2	0.0113402	0.0138321	0.0148086	0.0153034	0.0155936
0.33	0.0306659	0.038215	0.0413065	0.04291	0.0438638
0.5	0.06415	0.0820386	0.0897521	0.0938674	0.0963592
0.75	0.120243	0.159086	0.176975	0.186881	0.193026
1	0.176777	0.240927	0.272177	0.290065	0.301405
1.25	0.230048	0.32179	0.368704	0.396365	$\cancel{0.414254}$
1.5	0.278855	0.399097	$\cancel{0.463247}$	$\cancel{0.502091}$	$\cancel{0.527674}$
1.75	0.323045	$\cancel{0.471816}$	$\cancel{0.554203}$	$\cancel{0.605304}$	$\cancel{0.639528}$
r = 3
0.1	0.000751315	0.000859295	0.000892862	0.000907371	0.00091491
0.2	0.00462963	0.00538094	0.00562509	0.00573306	0.00578996
0.33	0.0152752	0.0181162	0.0190894	0.0195321	0.0197694
0.5	0.037037	0.045037	0.0479525	0.0493242	0.0500755
0.75	0.0787172	0.0990027	0.107003	0.110939	0.113158
1	0.125	0.162037	0.177662	0.185662	0.190292
1.25	0.171468	0.228364	0.253806	0.267304	0.275304
1.5	0.216	0.294717	0.331754	0.35204	0.364329
1.75	0.257701	0.359331	0.409338	$\cancel{0.437529}$	$\cancel{0.454955}$
2	0.296296	$\cancel{0.421296}$	$\cancel{0.485296}$	$\cancel{0.522333}$	$\cancel{0.545657}$

Table 2. Validation of inequality (16) for fixed $r=0.5,2,2.5,3$.

a/n	1	2	3	4	5
r = 0.5
$0.1$	0.301511	$\cancel{0.519729}$	$\cancel{0.699335}$	$\cancel{0.855508}$	$\cancel{0.995536}$
$0.2$	0.408248	$\cancel{0.70976}$	$\cancel{0.95976}$	$\cancel{1.17798}$	$\cancel{1.37409}$
$0.33$	$\cancel{0.5}$	$\cancel{0.877964}$	$\cancel{1.19419}$	$\cancel{1.47154}$	$\cancel{1.72154}$
r = 2
0.1	0.00826446	0.010532	0.0115726	0.0121675	0.012552
0.2	0.0277778	0.0360422	0.0399485	0.0422161	0.0436954
0.33	0.0615637	0.081623	0.0914436	0.097252	0.101085
0.5	0.111111	0.151111	0.171519	0.183865	0.192129
0.75	0.183673	0.258054	0.298054	0.322984	0.339998
1	0.25	0.361111	$\cancel{0.423611}$	$\cancel{0.463611}$	$\cancel{0.491389}$
r = 2.5
0.1	0.00249183	0.00298665	0.00317355	0.00326645	0.00332029
0.2	0.0113402	0.0138321	0.0148086	0.0153034	0.0155936
0.33	0.0306659	0.038215	0.0413065	0.04291	0.0438638
0.5	0.06415	0.0820386	0.0897521	0.0938674	0.0963592
0.75	0.120243	0.159086	0.176975	0.186881	0.193026
1	0.176777	0.240927	0.272177	0.290065	0.301405
1.25	0.230048	0.32179	0.368704	0.396365	$\cancel{0.414254}$
1.5	0.278855	0.399097	$\cancel{0.463247}$	$\cancel{0.502091}$	$\cancel{0.527674}$
1.75	0.323045	$\cancel{0.471816}$	$\cancel{0.554203}$	$\cancel{0.605304}$	$\cancel{0.639528}$
r = 3
0.1	0.000751315	0.000859295	0.000892862	0.000907371	0.00091491
0.2	0.00462963	0.00538094	0.00562509	0.00573306	0.00578996
0.33	0.0152752	0.0181162	0.0190894	0.0195321	0.0197694
0.5	0.037037	0.045037	0.0479525	0.0493242	0.0500755
0.75	0.0787172	0.0990027	0.107003	0.110939	0.113158
1	0.125	0.162037	0.177662	0.185662	0.190292
1.25	0.171468	0.228364	0.253806	0.267304	0.275304
1.5	0.216	0.294717	0.331754	0.35204	0.364329
1.75	0.257701	0.359331	0.409338	$\cancel{0.437529}$	$\cancel{0.454955}$
2	0.296296	$\cancel{0.421296}$	$\cancel{0.485296}$	$\cancel{0.522333}$	$\cancel{0.545657}$

Theorem 8. 

The Lerch’s transcendent $a^r\mathsf{\Phi }(z,r,a)\prec \sqrt{1+z}$ when $a^r\zeta (r,1+a)<\sqrt{2}-1.$

Theorem 8 can be obtained by considering

$$W(z)=2\sum _{k=1}^{\infty }{\displaystyle \frac{a^r{z}^k}{{(k+a)}^r}}+{\left(\sum _{k=1}^{\infty }{\displaystyle \frac{a^r{z}^k}{{(k+a)}^r}}\right)}^2.$$

Next, we will find the pair $(r,a)$, such that the inequality $a^r\zeta (r,1+a)<\sqrt{2}-1$ holds well. We discuss this part numerically with a fixed a and find a range of r. It is to be noted here that $\zeta (r,1+a)$ is not defined for $r=1$. So, we will consider the case for $r\in (1,\infty )$.

• For $r>1$, the inequality holds for $r>r_{0.5}$, where $r_{0.5}=1.7085$ is the root of ${(0.5)}^r\zeta (r,1.5)=\sqrt{2}-1$ in $(1,\infty )$. The range of r with fixed $a=0.5$ is presented in Figure 4.
• Finally, for any $a>0$, there exists $r_a$, the root of $a^r\zeta (r,1+a)=\sqrt{2}-1$ in $(1,\infty )$ such that $a^r\zeta (r,1+a)<\sqrt{2}-1$ for $r>r_a$. We consider a few arbitrary values of a and determine $r_a$. The outcome is presented in Table 4. It can be observed that $r_a$ is increasing along with a.

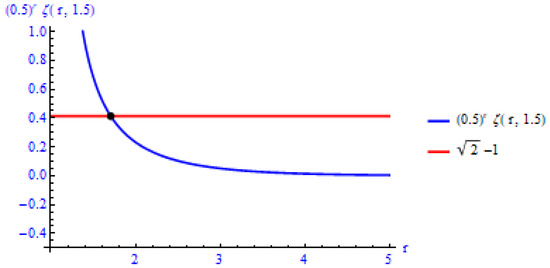
Figure 4. Range of r with fixed $a=0.5$.

Table 4. Range of r for arbitrary a.

a	${\mathit{r}}_{\mathit{a}}$	a	${\mathit{r}}_{\mathit{a}}$
0.001	1.00024	0.01	1.02208
$0.05$	$1.09511$	$0.09$	$1.15867$
$0.1$	$1.17379$	$0.2$	$1.31624$
$0.33$	$1.48966$	$0.5$	$1.7085$
$0.75$	$2.0236$	1	$2.33521$
$1.25$	$2.64515$	$1.5$	$2.95417$
1.75	$3.26265$	2	$3.57076$
5	$7.25935$	15	$19.5408$
20	$25.6808$	30	$37.9605$
40	$50.2401$	50	$62.5197$
100	123.917	500	615.096

Table 4. Range of r for arbitrary a.

a	${\mathit{r}}_{\mathit{a}}$	a	${\mathit{r}}_{\mathit{a}}$
0.001	1.00024	0.01	1.02208
$0.05$	$1.09511$	$0.09$	$1.15867$
$0.1$	$1.17379$	$0.2$	$1.31624$
$0.33$	$1.48966$	$0.5$	$1.7085$
$0.75$	$2.0236$	1	$2.33521$
$1.25$	$2.64515$	$1.5$	$2.95417$
1.75	$3.26265$	2	$3.57076$
5	$7.25935$	15	$19.5408$
20	$25.6808$	30	$37.9605$
40	$50.2401$	50	$62.5197$
100	123.917	500	615.096

Theorem 9. 

Suppose that $\beta \ge 1/2$. Then, the polynomial ${\beta }^r{\varpi }_n(z,r,\beta )\prec {\mathsf{\Phi }}_{N_e}(z)$ provided

$$\begin{array}{c}\hfill {\beta }^{1-r}\left(\zeta \left(r-1,{\displaystyle \frac{\beta +1}{\beta }}\right)-\zeta \left(r-1,n+{\displaystyle \frac{\beta +1}{\beta }}\right)\right)<1.\end{array}$$

(18)

In general, ${\beta }^r\mathsf{\Phi }(z,r,\beta )\prec {\mathsf{\Phi }}_{N_e}(z)$ when

$$\begin{array}{c}\hfill {\beta }^{1-r}\zeta \left(r-1,{\displaystyle \frac{\beta +1}{\beta }}\right)<1.\end{array}$$

(19)

Next, we need to find out the existence of $(\beta ,r,n)$ and $(\beta ,r)$ for which the inequalities (18) and (19) hold well. We answer this problem numerically.

• Case I: $(1/2,2,n)$: Taking $\beta =1/2$ and $r=2$, we will try to find the range of n for which the inequality (18) holds. The numerical values for different n are tabulated in Table 5.
  Table 5. Validity of inequality (18) for $\beta =1/2=a$ and $r=2$.

  1	0.166667	2	0.246667	3	0.297687	4	0.334724
  5	0.36365	6	0.387318	10	0.45346	20	0.542364
  40	0.630341	100	0.745748	761	0.999961	762	1.00013

  It is clear that for $n\ge 762$, the inequality (18) failed.
• Case II: $(1/2,3)$: In this case, we consider $\beta =1/2$ and $r=3$ to validate the inequality (18). The numerical values for different n are tabulated in Table 6.
  Table 6. Validity of inequality (19) for $\beta =1/2=a$ and $r=3$.

  1	0.0555556	2	0.0715556	3	0.0788442	4	0.0829594
  5	0.085589	6	0.0874097	7	0.088743	8	0.0897607
  9	0.0905626	10	0.0912105	11	0.0912105	12	0.0921927
  13	0.0925737	14	0.0929018	15	0.0931871	16	0.0934375
  17	0.0936591	18	0.0938565	19	0.0940335	20	0.0941931

  It is clear from Table 6 that the value is increasing with n, but if we take $n\to \infty$, we have

  $$\begin{array}{c}\hfill \sum _{k=1}^{\infty }{\displaystyle \frac{a^r(k\beta +1)}{{(k+a)}^r}}={\displaystyle \frac{1}{8}}\sum _{k=1}^{\infty }{\displaystyle \frac{(k\frac{1}{2}+1)}{{(k+\frac{1}{2})}^3}}={\displaystyle \frac{1}{32}}\left(21\zeta (3)+{\pi }^2-32\right)=0.097275.\end{array}$$

  (20)
  Thus, in this case, inequality (18) holds for all n and inequality (19) is also true. This case implies

  $${\displaystyle \frac{1}{8}}\mathsf{\Phi }\left(z,3,\frac{1}{2}\right)\prec {\mathsf{\Phi }}_{N_e}(z).$$

6. Results Involving Incomplete Gamma Function

Our next example involves incomplete gamma function. The Euler’s integral form of gamma function is defined as

$$\begin{array}{c}\hfill \mathsf{\Gamma }(a)={\int }_0^{\infty }{e}^{-t}{t}^{a-1}dt.\end{array}$$

(21)

The incomplete gamma function arises by decomposing the integration (21) into two parts as

$$\begin{array}{c}\hfill \gamma (a,z)={\int }_0^z{e}^{-t}{t}^{a-1}dt\end{array}$$

(22)

$$\begin{array}{c}\hfill \mathsf{\Gamma }(a,z)={\int }_z^{\infty }{e}^{-t}{t}^{a-1}dt.\end{array}$$

(23)

The function $\gamma (a,z)$ is well-known as a lower incomplete gamma function and $\mathsf{\Gamma }(a,z)$ is an upper incomplete function. Next, define the function $\mathsf{\Gamma }(a,z_1,z_2)=\mathsf{\Gamma }(a,z_1)-\mathsf{\Gamma }(a,z_2)$. Then,

$$\begin{array}{c}\hfill \mathsf{\Gamma }(a,z_1,z_2)={\int }_{z_1}^{z_2}{e}^{-t}{t}^{a-1}dt.\end{array}$$

(24)

Theorem 10. 

For $\beta \ge 1/2$, the function

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}+{\displaystyle \frac{z^{-1/\beta }}{2\beta }}\mathsf{\Gamma }\left({\displaystyle \frac{1}{\beta }},0,z\right)\prec {\mathsf{\Phi }}_{N_e}(z).\end{array}$$

(25)

Proof. 

From (24), it follows

$$\begin{array}{ll}{\displaystyle \frac{z^{-1/\beta }}{2\beta }}\mathsf{\Gamma }\left({\displaystyle \frac{1}{\beta }},0,z\right)& ={\displaystyle \frac{z^{-1/\beta }}{2\beta }}{\int }_0^z{e}^{-t}{t}^{{\displaystyle \frac{1}{\beta }}-1}dt\\ & ={\displaystyle \frac{z^{-1/\beta }}{2\beta }}\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k}{k!}}{\int }_0^z{t}^{k+{\displaystyle \frac{1}{\beta }}-1}dt\\ & ={\displaystyle \frac{z^{-1/\beta }}{2\beta }}\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k}{k!}}{\displaystyle \frac{z^{k+\frac{1}{\beta }}}{k+\frac{1}{\beta }}}\\ & ={\displaystyle \frac{1}{2}}\sum _{k=0}^{\infty }{\displaystyle \frac{{(-1)}^k}{k!}}{\displaystyle \frac{z^k}{k\beta +1}}.\end{array}$$

Thus,

$$\begin{array}{cc}\hfill {\displaystyle \frac{1}{2}}+{\displaystyle \frac{z^{-1/\beta }}{2\beta }}\mathsf{\Gamma }\left({\displaystyle \frac{1}{\beta }},0,z\right)& =1+{\displaystyle \frac{1}{2}}\sum _{k=1}^{\infty }{\displaystyle \frac{{(-1)}^k}{k!}}{\displaystyle \frac{z^k}{k\beta +1}}.\hfill \end{array}$$

Now,

$$\begin{array}{c}\hfill {\displaystyle \frac{1}{2}}+\sum _{k=1}^{\infty }{\displaystyle \frac{k\beta +1}{k!}}{\displaystyle \frac{1}{k\beta +1}}={\displaystyle \frac{1}{2}}\sum _{k=1}^{\infty }{\displaystyle \frac{1}{k!}}={\displaystyle \frac{e-1}{2}}=0.859141<1.\end{array}$$

Finally, the result follows from Theorem 5. □

The result stated in Theorem 10 is visible in Figure 5 for $\beta =1/2$ and $\beta =1$.

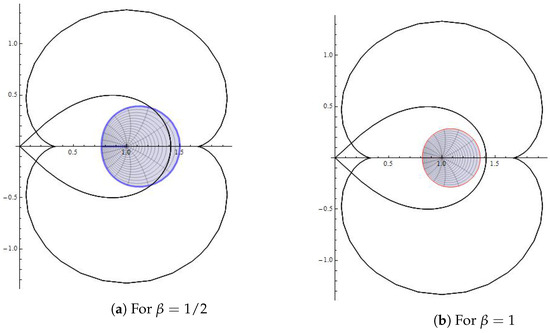
Figure 5. Graphical interpretation of Theorem 10 for different $\beta =1/2$ and $\beta =1$.

7. Results Involving Bessel and Modified-Bessel Function

Next, we consider a function involving well-known Bessel and modified-Bessel functions, which have series form

$$\begin{array}{cc}\hfill J_v(z)& ={\displaystyle \frac{z^v}{2^v}}\sum _{n=0}^{\infty }{\displaystyle \frac{{(-1)}^n{z}^{2n}}{4^{n}n!\mathsf{\Gamma }(n+v+1)}}\hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill I_v(z)& ={\displaystyle \frac{z^v}{2^v}}\sum _{n=0}^{\infty }{\displaystyle \frac{z^{2n}}{4^{n}n!\mathsf{\Gamma }(n+v+1)}}.\hfill \end{array}$$

(27)

For further use, we recall here the notation ${(x)}_n$, the well known Pochhammer symbol, defined as

$$\begin{array}{c}\hfill {(x)}_n=x(x+1)\dots (x+n-1)={\displaystyle \frac{\mathsf{\Gamma }(x+n)}{\mathsf{\Gamma }(x)}}.\end{array}$$

Theorem 11. 

Suppose that $\beta \ge 1/2$ and $\alpha >0$. Then, the functions

$$\begin{array}{c}\hfill {\mathcal{I}}_{\alpha ,\beta }(z)={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\mathsf{\Gamma }(\alpha +\beta )z^{\frac{1-\alpha -\beta }{2}}{I}_{\alpha +\beta -1}(2\sqrt{z})\prec {\mathsf{\Phi }}_{N_e}(z),\end{array}$$

(28)

$$\begin{array}{c}\hfill {\mathcal{J}}_{\alpha ,\beta }(z)={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\mathsf{\Gamma }(\alpha +\beta )z^{\frac{1-\alpha -\beta }{2}}{J}_{\alpha +\beta -1}(2\sqrt{z})\prec {\mathsf{\Phi }}_{N_e}(z),\end{array}$$

(29)

when

$$\begin{array}{c}\hfill \beta \mathsf{\Gamma }(\alpha +\beta )I_{\alpha +\beta }(2)+{}_{0}F_1(\alpha +\beta ;1)<3.\end{array}$$

(30)

In particular, for $\beta =1/2$, the result holds for $\alpha >{\alpha }_0(1/2)$. Here, ${\alpha }_0(1/2)=0.532446$ is the solution of

$$\begin{array}{c}\hfill \mathsf{\Gamma }(\alpha +\frac{1}{2})I_{\alpha +\frac{1}{2}}(2)+2_0{F}_1\left(\alpha +\frac{1}{2},1\right)=6.\end{array}$$

(31)

Proof. 

From the series (27), it follows that

$$\begin{array}{ll}{\mathcal{I}}_{\alpha ,\beta }(z)& ={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\mathsf{\Gamma }(\alpha +\beta )z^{\frac{1-\alpha -\beta }{2}}{I}_{\alpha +\beta -1}(2\sqrt{z})\\ & ={\displaystyle \frac{1}{2}}+{\displaystyle \frac{1}{2}}\mathsf{\Gamma }(\alpha +\beta )\sum _{n=0}^{\infty }{\displaystyle \frac{z^n}{n!\mathsf{\Gamma }(n+\alpha +\beta )}}\\ & =1+\sum _{n=1}^{\infty }{\displaystyle \frac{z^n}{2n!{(\alpha +\beta )}_n}}.\end{array}$$

Similarly, from the series (26), we have

$$\begin{array}{cc}\hfill {\mathcal{J}}_{\alpha ,\beta }(z)& =1+{\displaystyle \frac{1}{2}}\sum _{n=1}^{\infty }{\displaystyle \frac{{(-1)}^n{z}^n}{n!{(\alpha +\beta )}_n}}.\hfill \end{array}$$

Now, define

$$\begin{array}{c}\hfill \mathfrak{h}(\alpha ,\beta ):={\displaystyle \frac{1}{2}}\sum _{n=1}^{\infty }{\displaystyle \frac{\beta n+1}{n!{(\alpha +\beta )}_n}}.\end{array}$$

It is easy to verify that for any fixed $\beta \ge 1/2$, the function $\mathfrak{h}(\alpha ,\beta )$ is a decreasing function of $\alpha$. Our aim is to find the range of $\alpha$ for which $\mathfrak{h}(\alpha ,\beta )<1$ for all $\beta \ge 1/2$.

A careful re-arrangement of terms of $\mathfrak{h}(\alpha ,\beta )$ along with (27) leads to

$$\begin{array}{ll}\mathfrak{h}(\alpha ,\beta )& ={\displaystyle \frac{\beta }{2}}\sum _{n=1}^{\infty }{\displaystyle \frac{n}{n!{(\alpha +\beta )}_n}}+{\displaystyle \frac{1}{2}}\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n!{(\alpha +\beta )}_n}}\\ & ={\displaystyle \frac{\beta }{2}}\sum _{n=1}^{\infty }{\displaystyle \frac{\mathsf{\Gamma }(\alpha +\beta )}{(n-1)!\mathsf{\Gamma }(n+\alpha +\beta )}}+{\displaystyle \frac{1}{2}}\sum _{n=1}^{\infty }{\displaystyle \frac{1}{n!{(\alpha +\beta )}_n}}\\ & ={\displaystyle \frac{\beta \mathsf{\Gamma }(\alpha +\beta )}{2}}\sum _{n=0}^{\infty }{\displaystyle \frac{1}{n!\mathsf{\Gamma }(n+1+\alpha +\beta )}}+{\displaystyle \frac{1}{2}}\left({}_{0}F_1(\alpha +\beta ;1)-1\right)\\ & ={\displaystyle \frac{1}{2}}\left(\beta \mathsf{\Gamma }(\alpha +\beta )I_{\alpha +\beta }(2)+{}_{0}F_1(\alpha +\beta ;1)-1\right).\end{array}$$

Thus, $\mathfrak{h}(\alpha ,\beta )<1$ is equivalent to

$$\begin{array}{c}\hfill \beta \mathsf{\Gamma }(\alpha +\beta )I_{\alpha +\beta }(2)+{}_{0}F_1(\alpha +\beta ;1)<3.\end{array}$$

(32)

For a fixed $\beta$, the inequality (32) holds for $\alpha \ge {\alpha }_0(\beta )$, where ${\alpha }_0(\beta )$ is the root of the equation

$$\begin{array}{c}\hfill \beta \mathsf{\Gamma }(\alpha +\beta )I_{\alpha +\beta }(2)+{}_{0}F_1(\alpha +\beta ;1)=3.\end{array}$$

The root ${\alpha }_0(\beta )$ depends on $\beta$ and decreases for increasing $\beta$. Thus, the result holds for all $\beta \ge 1/2$ and $\alpha \ge {\alpha }_0(1/2)$. This is equivalent to $\alpha \ge {\alpha }_0(1/2)=0.532446$, where ${\alpha }_0(1/2)$ is the root of

$$\begin{array}{c}\hfill \mathsf{\Gamma }(\alpha +\frac{1}{2})I_{\alpha +\frac{1}{2}}(2)+2{}_{0}F_1(\alpha +\frac{1}{2};1)=6.\end{array}$$

The inequality (32) reduces to

$$\begin{array}{c}\hfill \mathsf{\Gamma }(\alpha +\frac{1}{2})I_{\alpha +\frac{1}{2}}(2)+2{}_{0}F_1(\alpha +\frac{1}{2};1)<6.\end{array}$$

(33)

This completes the proof. □

One of the most important functions in the literature is the generalized and normalized Bessel functions of the form

$$\begin{array}{c}\hfill {\mathtt{U}}_{p,b,c}(z)=\sum _{n=0}^{\infty }{\displaystyle \frac{{(-1)}^n{c}^n}{4^n{(p+\frac{b+1}{2})}_n}}{\displaystyle \frac{z^n}{n!}},\end{array}$$

(34)

where $b\in \mathbb{R}$, such that $p+(b+1)/2\ne 0,-2,-4,-6,\dots$.

The function ${\mathtt{U}}_{p,b,c}$ yields the Spherical Bessel function for $b=2$, $c=1$ and reduces to the normalized classical Bessel (modified Bessel) functions of order p when $b=c=1$ ($b=-c=1$). There is a large amount research related to the inclusion of ${\mathtt{U}}_p$ in different subclasses of univalent functions theory [11,12,13,14,15,16] and some references therein. In [11], the lemniscate convexity and additional properties of ${\mathtt{U}}_p$ are examined in detail. The lemniscate starlikeness of $z{\mathtt{U}}_p$ is discussed in [1].

For this study, we introduce the function ${\mathfrak{V}}_{p,b,c,\beta }$ defined as

$$\begin{array}{c}\hfill {\mathfrak{V}}_{p,b,c,\beta }(z):=\sum _{n=0}^{\infty }{\displaystyle \frac{{(-1)}^n{c}^n}{4^n{(p+\frac{b}{2}+\beta )}_n}}{\displaystyle \frac{z^n}{n!}}.\end{array}$$

(35)

We note here that ${\mathfrak{V}}_{p,b,c,1/2}(z)={\mathtt{U}}_{p,b,c}(z)$. Now, we state and prove the following result involving ${\mathfrak{V}}_{p,b,c,\beta }$.

Theorem 12. 

For $\beta \ge 1/2$, the function ${\mathfrak{V}}_{p,b,c,\beta }(z)\prec {\mathsf{\Phi }}_{N_e}(z)$ if

$$\begin{array}{c}\hfill \beta |c|{\mathfrak{V}}_{p+1,b,|c|,\beta }(-1)+4\left(p+\frac{b}{2}+\beta \right){\mathfrak{V}}_{p,b,|c|,\beta }(-1)<16\left(p+\frac{b}{2}+\beta \right).\end{array}$$

(36)

In particular, ${\mathtt{U}}_{p,b,c}(z)\prec {\mathsf{\Phi }}_{N_e}(z)$ if

$$\begin{array}{c}\hfill |c|{\mathtt{U}}_{p+1,b,|c|}(-1)+8\left(p+\frac{b+1}{2}\right){\mathtt{U}}_{p,b,|c|}(-1)<16\left(p+\frac{b+1}{2}\right).\end{array}$$

(37)

Proof. 

The proof is based on Theorem 5. Let us denote

$$\mathfrak{U}(n,\beta )={\displaystyle \frac{{(-1)}^n{c}^n}{4^n{(p+\frac{b}{2}+\beta )}_{n}n!}}.$$

Then,

$$\begin{array}{ll}\sum _{n=1}^{\infty }(n\beta +1)|\mathfrak{U}(n,\beta )|& =\sum _{n=1}^{\infty }{\displaystyle \frac{{(n\beta +1)|c|}^n}{4^n{(p+\frac{b}{2}+\beta )}_n}}{\displaystyle \frac{1}{n!}}\\ & =\beta \sum _{n=1}^{\infty }{\displaystyle \frac{{|c|}^n}{4^n{(p+\frac{b}{2}+\beta )}_n(n-1)!}}+\sum _{n=1}^{\infty }{\displaystyle \frac{{|c|}^n}{4^n{(p+\frac{b}{2}+\beta )}_{n}n!}}\\ & =\frac{\beta |c|}{4\left(p+\frac{b}{2}+\beta \right)}\sum _{n=1}^{\infty }\frac{{|c|}^{n-1}}{4^{n-1}{(p+1+\frac{b}{2}+\beta )}_{n-1}(n-1)!}+\sum _{n=1}^{\infty }\frac{{|c|}^n}{4^n{(p+\frac{b}{2}+\beta )}_{n}n!}\\ & ={\displaystyle \frac{\beta |c|}{4\left(p+\frac{b}{2}+\beta \right)}}{\mathfrak{V}}_{p+1,b,|c|,\beta }(-1)+{\mathfrak{V}}_{p,b,|c|,\beta }(-1)-1\end{array}$$

Now, inequality (11) holds if

$$\begin{array}{c}\hfill {\displaystyle \frac{\beta |c|}{4\left(p+\frac{b}{2}+\beta \right)}}{\mathfrak{V}}_{p+1,b,|c|,\beta }(-1)+{\mathfrak{V}}_{p,b,|c|,\beta }(-1)-1<1\end{array}$$

After a routine simplification, we have

$$\begin{array}{c}\hfill \beta |c|{\mathfrak{V}}_{p+1,b,|c|,\beta }(-1)+4\left(p+\frac{b}{2}+\beta \right){\mathfrak{V}}_{p,b,|c|,\beta }(-1)<8\left(p+\frac{b}{2}+\beta \right).\end{array}$$

(38)

As stated before, if $\beta =1/2$, then ${\mathfrak{V}}_{p+1,b,c,1/2}(z)={\mathtt{U}}_{p,b,c}(z)$. Thus, taking $\beta =1/2$ in (38), we have ${\mathtt{U}}_{p,b,c}(z)\prec {\mathsf{\Phi }}_{N_e}(z)$ if

$$\begin{array}{c}\hfill |c|{\mathtt{U}}_{p+1,b,|c|}(-1)+8\left(p+\frac{b+1}{2}\right){\mathtt{U}}_{p,b,|c|}(-1)<16\left(p+\frac{b+1}{2}\right).\end{array}$$

(39)

This completes the proof. □

The normalized form of the classical Bessel and Modified Bessel functions as defined in (26) and (27) are given as

$$\begin{array}{cc}\hfill {\mathtt{J}}_v(z)& ={\displaystyle \frac{z^{-v}}{2^{-v}}}\mathsf{\Gamma }(v+1)J_v(\sqrt{z})=\sum _{n=0}^{\infty }{\displaystyle \frac{{(-1)}^n{z}^n}{4^{n}n!{(v+1)}_n}}\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\mathtt{I}}_v(z)& ={\displaystyle \frac{z^{-v}}{2^{-v}}}\mathsf{\Gamma }(v+1)I_v(\sqrt{z})=\sum _{n=0}^{\infty }{\displaystyle \frac{z^n}{4^{n}n!{(v+1)}_n}}\hfill \end{array}$$

(41)

Notice that ${\mathtt{J}}_v(-1)={\mathtt{I}}_v(1)$. Now, by taking $b=c=1$ and $b=-c=1$ in (39), we have the following result from Theorem 12.

Corollary 1. 

For $\nu \ge {\nu }_0$, the subordination ${\mathtt{J}}_{\nu }(z)\prec {\mathsf{\Phi }}_{N_e}(z)$ and ${\mathtt{I}}_{\nu }(z)\prec {\mathsf{\Phi }}_{N_e}(z)$. Here, ${\nu }_0\approx -0.5791$ is the root of the equation

$$\begin{array}{c}\hfill \delta (\mu ):{\mathtt{I}}_{\nu +1}(1)+8\left(\nu +1\right){\mathtt{I}}_{\nu }(1)-16\left(\nu +1\right)=0.\end{array}$$

(42)

We calculate the value of ${\nu }_0$ using Mathematica Software and the validity of inequality can be observed from Figure 6.

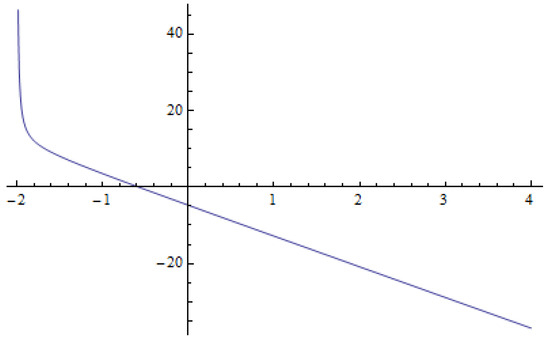
Figure 6. The graph of $\delta (\mu )$.

We visualize the subordination ${\mathtt{J}}_{\nu }(z)\prec {\mathsf{\Phi }}_{N_e}(z)$ and ${\mathtt{I}}_{\nu }(z)\prec {\mathsf{\Phi }}_{N_e}(z)$ for $\nu ={\nu }_0,-0.5,0.5$, and present it in Figure 7 and Figure 8, respectively. We further note that

$$\begin{array}{cc}\hfill {\mathtt{J}}_{-0.5}(z)=cos(\sqrt{z})& {\mathtt{J}}_{0.5}(z)={\displaystyle \frac{sin(\sqrt{z})}{\sqrt{z}}}\hfill \\ \hfill {\mathtt{I}}_{-0.5}(z)=cosh(\sqrt{z})& {\mathtt{I}}_{0.5}(z)={\displaystyle \frac{sinh(\sqrt{z})}{\sqrt{z}}}.\hfill \end{array}$$

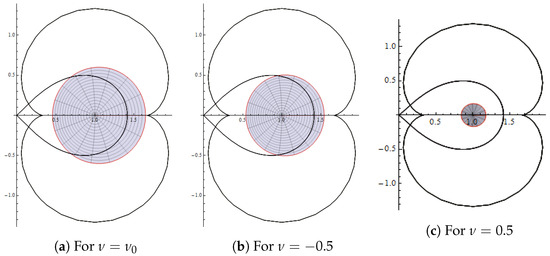
Figure 7. Image of ${\mathtt{J}}_{\nu }(\mathbb{D})$ for $\nu ={\nu }_0,-0.5,0.5$.

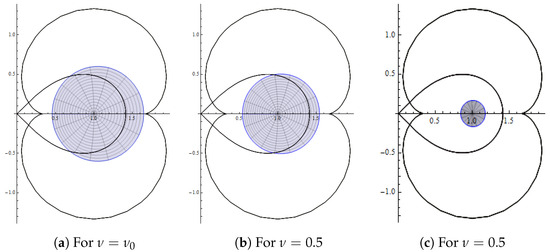
Figure 8. Image of ${\mathtt{I}}_{\nu }(\mathbb{D})$ for $\nu ={\nu }_0,-0.5,0.5$.

8. Results Involving Confluent and Generalized Hypergeometric Function

The well-known confluent hypergeometric function ${}_{1}F_1(\alpha ,\beta ,z)$ is represented by series

$$\begin{array}{c}\hfill {}_{1}F_1({\alpha }_1,{\alpha }_2,z)=\sum _{n=0}^{\infty }{\displaystyle \frac{{({\alpha }_1)}_n{z}^n}{{({\alpha }_2)}_{n}n!}}.\end{array}$$

(43)

Here, ${\alpha }_2\ne -1,-2,\dots$ In the context of geometric functions theory, the confluent hypergeometric functions has a high significance. Miller and Mocanu [17] proved that $Re{}_{1}F_1({\alpha }_1,{\alpha }_2,z)>0$ in $\mathfrak{D}$ for real ${\alpha }_1$ and ${\alpha }_2$, satisfying either ${\alpha }_1>0$ and ${\alpha }_2\ge {\alpha }_1$, or ${\alpha }_1\le 0$ and ${\alpha }_2\ge 1+\sqrt{1+{\alpha }_1^2}$. Conditions for which $Re{}_{1}F_1({\alpha }_1,{\alpha }_2,z)>\delta$, $0\le \delta \le 1/2$ are obtained by Ponnusamy and Vuorinen ([18] Theorem 1.9, p. 77). In addition, they established that $({\alpha }_2/{\alpha }_1)\left({}_{1}F_1({\alpha }_1,{\alpha }_2,z)-1\right)$ is close-to-convex of the positive order with respect to the identity function. A connection between the confluent and lemniscate is established in [19,20] and the references therein.

Now, we state and prove a result involving ${}_{1}F_1$.

Theorem 13. 

For $\beta \ge 1/2$, the confluent hypergeometric function ${}_{1}F_1(1/2;\beta +1;z)\prec {\mathsf{\Phi }}_{N_e}(z)$, provided

$$\begin{array}{c}\hfill \beta {}_{1}F_1\left({\displaystyle \frac{3}{2}};\beta +2;1\right)+2(\beta +1){}_{1}F_1\left({\displaystyle \frac{1}{2}};\beta +1;1\right)\le 4(\beta +1).\end{array}$$

(44)

Proof. 

By following the notion of Theorem 5 and series (43), we have

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{\displaystyle \frac{(\beta n+1){\left(\frac{1}{2}\right)}_n}{{\left(1+\beta \right)}_{n}n!}}={\displaystyle \frac{\beta {}_{1}F_1\left(\frac{3}{2};\beta +2;1\right)}{2(\beta +1)}}+{}_{1}F_1\left({\displaystyle \frac{1}{2}};\beta +1;1\right)-1<1\end{array}$$

(45)

when the hypothesis (44) holds. The conclusion follows from Theorem 5. □

Remark 3. 

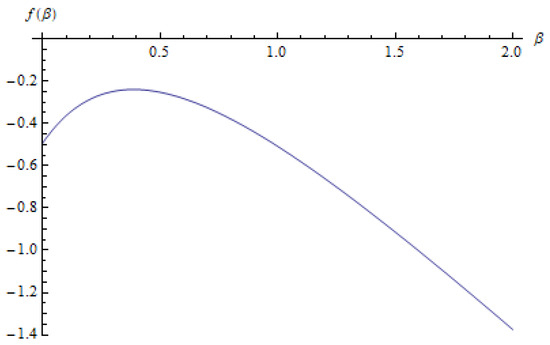
Let us denote

$$\begin{array}{c}\hfill \mathfrak{P}(\beta )=\beta {}_{1}F_1\left({\displaystyle \frac{3}{2}};\beta +2;1\right)+2(\beta +1){}_{1}F_1\left({\displaystyle \frac{1}{2}};\beta +1;1\right)-4(\beta +1).\end{array}$$

Numerical calculation provides $\mathfrak{P}(1/2)=-0.252904$ and from Figure 9, it is clear that $\mathfrak{P}(\beta )$ is a decreasing function of β when $\beta \ge 1/2$.

Figure 9. Graph of $\mathfrak{P}(\beta )$.

Thus, the inequality (44) holds for all $\beta \ge 1/2$, and hence the condition (44) can be relaxed from Theorem 13. However, as we are not able to prove this inequality analytically, we keep the condition (44).

Our last example is on generalized hypergeometric functions.

Consider

$$\mathfrak{A}(n,\beta )={\displaystyle \frac{{(\beta -1)}_n}{n!{(\beta )}_n{(\beta +1)}_n}};$$

substituting in (11), we have

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }(n\beta +1)|\mathfrak{A}(n,\beta )|={\displaystyle \frac{(\beta -1){}_{1}F_2(\beta ;\beta +1,\beta +2;1)}{\beta +1}}+{}_{1}F_2(\beta -1;\beta ,\beta +1;1).\end{array}$$

(46)

Here, ${}_{1}F_2$ is known as generalized hypergeometric functions. The generalized hypergeometric functions denoted by

$${}_{m}F_n(a_1,a_2,\cdots ,a_m;b_1,b_2,\cdots ,b_n;z)$$

with series representation

$$\begin{array}{c}\hfill {}_{m}F_n(a_1,a_2,\cdots ,a_m;b_1,b_2,\cdots ,b_n;z)=\sum _{r=0}^{\infty }{\displaystyle \frac{{(a_1)}_r{(a_2)}_r\cdots {(a_m)}_r}{{(b_1)}_r{(b_2)}_r\cdots {(b_n)}_r}}{\displaystyle \frac{z^n}{n!}}\end{array}$$

(47)

where $b_i,1\le i\le n$ are positive. The series (47) converges if

(i)

Any of $a_j,1\le j\le m$ are non-positive.

(ii)

$m<n+1$, the series converges for any finite value of z and, hence, is entire.

Now, for $\beta \ge 1/2$, the graphical representation of the right side of (46) is given in Figure 10. As the graph is asymptotic about the parallel line $y=1$, we have that

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }(n\beta +1)|\mathfrak{A}(n,\beta )|={\displaystyle \frac{(\beta -1){}_{1}F_2(\beta ;\beta +1,\beta +2;1)}{\beta +1}}+{}_{1}F_2(\beta -1;\beta ,\beta +1;1)<1.\end{array}$$

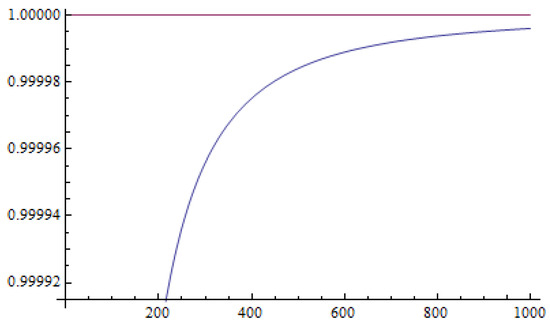
Figure 10. Graph of the right hand side of (46).

Based on this observation, we have the following result:

Theorem 14. 

For $\beta \ge 1/2$, the generalized hypergeometric function ${}_{1}F_2(\beta -1;\beta ,\beta +1;1)\prec {\mathsf{\Phi }}_{N_e}(z)$.

9. Conclusions

The article presents several analytic functions that map the unit disk to domain that are subordinated by lemniscate and nephroid curves. Analogous problems involving subordination implications have been examined previously [2,3,5,6,11,20,21,22,23]. The current article adopts the concept of subordination as its primary approach. In the context of subordination by ${\mathsf{\Phi }}_{N_e}$, we have established an extremal function. As far as the author is aware, there is no known result in geometric functions theory involving incomplete gamma functions. Likewise, there is no evidence linking Lerch transcendent to the lemniscate and nephrooid domains. Both relations are established in this work. The relation of the Bessel function and modified Bessel function with nephroid domains is also presented.

The results also establish following:

• $f(\mathfrak{D})\subset {\mathcal{P}}_l(\mathfrak{D})\cap {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$: This is the easiest example because of the large intersecting parts between ${\mathcal{P}}_l(\mathfrak{D})$ and ${\mathsf{\Phi }}_{N_e}(\mathfrak{D})$ and the existence of such a function is evident in Figure 2b–d and Figure 5b (Involving incomplete gamma function), Figure 7c ($cos(\sqrt{z})$), and Figure 8c ($cosh(\sqrt{z})$).
• $f(\mathfrak{D})\subset {\mathcal{P}}_l(\mathfrak{D})$, but $f(\mathfrak{D})\not\subset {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$: This is the toughest part to establish as an example, as a very small section of ${\mathcal{P}}_l(\mathfrak{D})$ is out of ${\mathsf{\Phi }}_{N_e}(\mathfrak{D})$, but we have been able to construct an example in Figure 2a,e.
• $f(\mathfrak{D})\subset {\mathsf{\Phi }}_{N_e}(\mathfrak{D})$, but $f(\mathfrak{D})\not\subset {\mathcal{P}}_l(\mathfrak{D})$: Figure 5a ((Involving incomplete gamma function), Figure 7b ($cos(\sqrt{z})$), Figure 8b ($cosh(\sqrt{z})$), Figure 7a and Figure 8a.

Finally, we remark that we were restricted by using only a few examples. Using Theorem 5 and series representation of functions, we can include many other functions such as Struve functions, Gaussian hypergeometric functions, and Bessel–Struve functions.