Euler Method for a Class of Linear Impulsive Neutral Differential Equations
Abstract
1. Introduction
2. Convergence of Euler’s Method for INDDEs
3. Asymptotical Stability of INDDEs
3.1. Asymptotical Stability of the Exact Solutions of INDDEs
- (i)
- The solution is stable if , or, equivalently, if the following conditions are satisfied:
- (ii)
- The solution is asymptotically stable if ;
- (iii)
- The solution is unstable if .
- (i)
- The solution is stable if , or, equivalently, if the following conditions are satisfied:
- (ii)
- The solution is asymptotically stable if ;
- (iii)
- The solution is unstable if .
3.2. Asymptotical Stability of Euler’s Method for IDDEs
- (i)
- The solution is stable if , or, equivalently, if the following conditions are satisfied:
- (ii)
- The solution is asymptotically stable if ;
- (iii)
- The solution is unstable if .
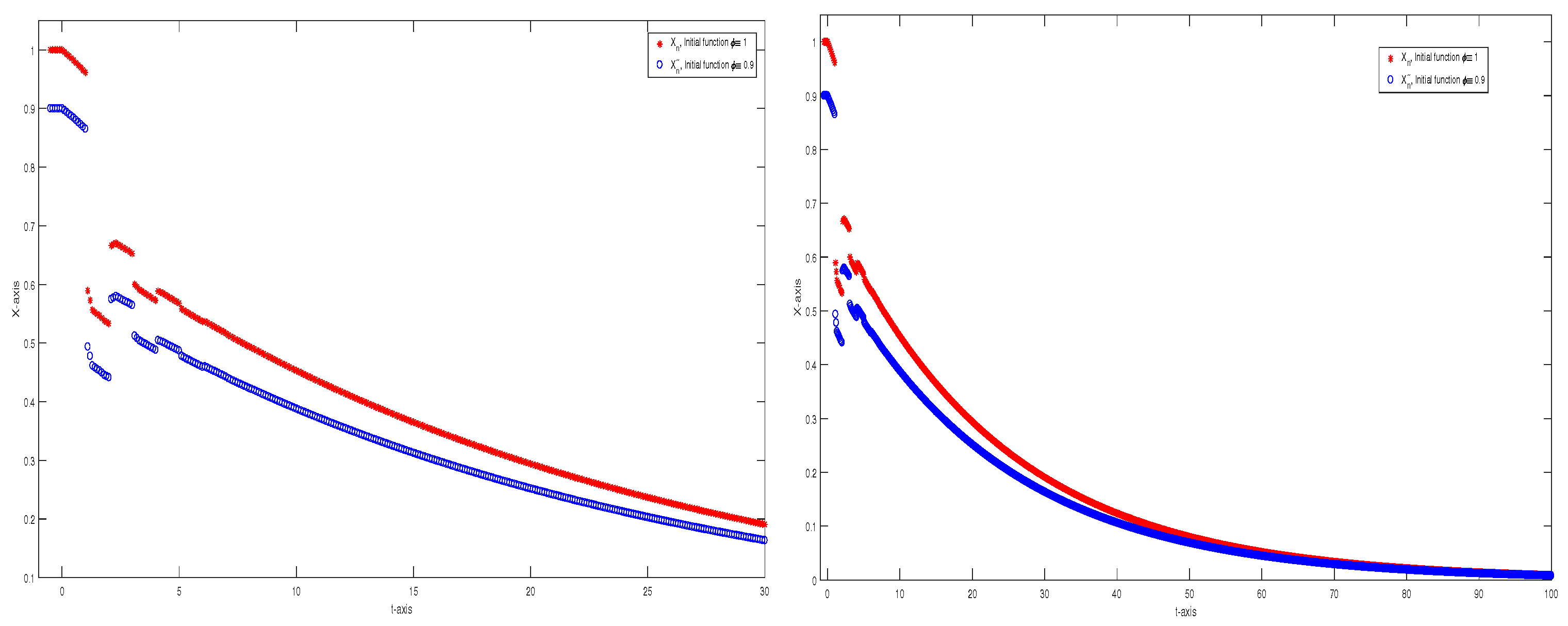
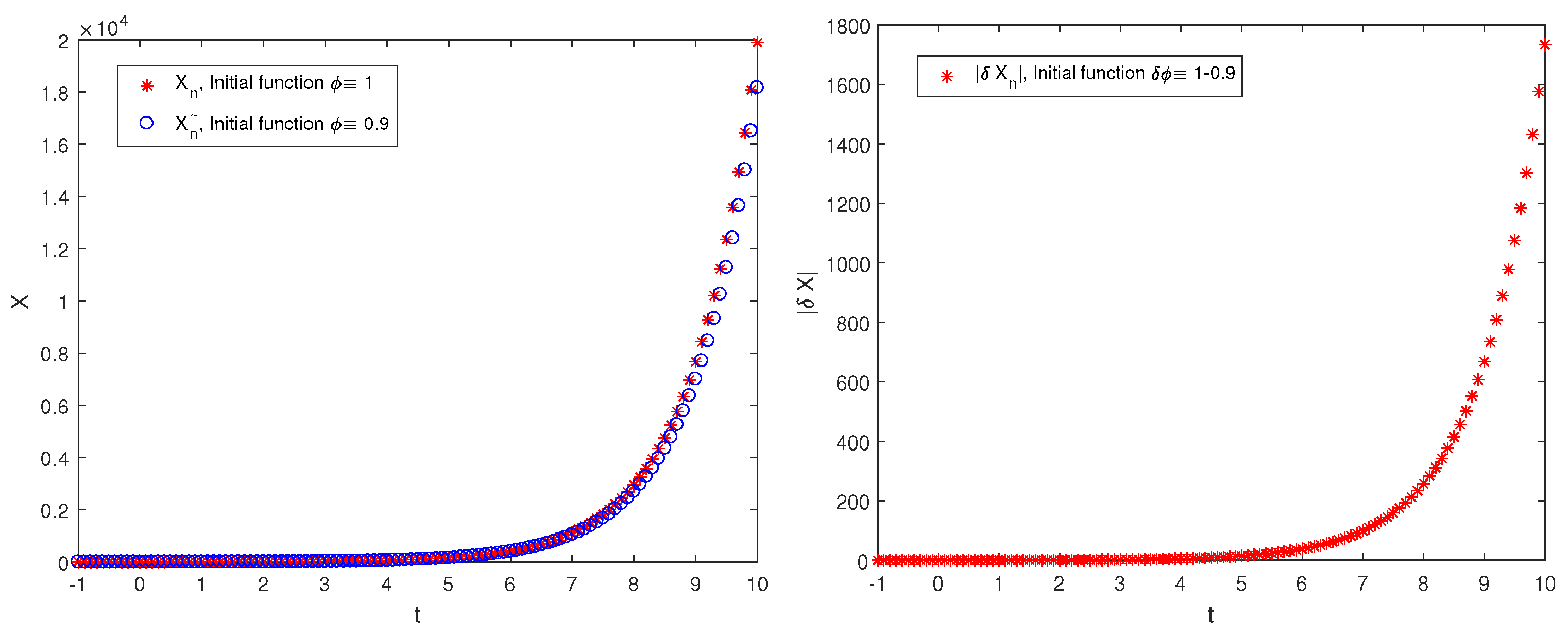
4. Numerical Examples
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Faria, T.; Oliveira, J.J. General criteria for asymptotic and exponential stabilities of neural network models with unbounded delays. Appl. Math. Comput. 2011, 217, 9646–9658. [Google Scholar] [CrossRef]
- Song, X.; Xin, X.; Huang, W. Exponential stability of delayed and impulsive cellular neural networks with partially Lipschitz continuous activation functions. Neural Netw. 2012, 29–30, 80–90. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Xu, D. Stability analysis of delay neural networks with impulsive effects. IEEE Trans. Circuits Syst.-II Express Briefs 2005, 52, 517–521. [Google Scholar] [CrossRef]
- Li, W.; Huo, H. Global attractivity of positive periodic solutions for an impulsive delay periodic model of respiratory dynamics. J. Comput. Appl. Math. 2005, 174, 227–238. [Google Scholar] [CrossRef][Green Version]
- Lee, H.J.; Park, J.B.; Joo, Y.H. Robust control for uncertain Takagi-Sugeno fuzzy with time-varying input delay. ASME J. Dyn. Syst. Meas. Control 2005, 127, 302–306. [Google Scholar] [CrossRef]
- Li, C.; Sun, J. Stability analysis of nonlinear stochastic differential delay systems under impulsive control. Phys. Lett. A 2010, 374, 1154–1158. [Google Scholar] [CrossRef]
- Wu, K.; Ding, X. Stability and stabilization of impulsive stochastic delay differential equations. Math. Probl. Eng. 2012, 176375. [Google Scholar] [CrossRef]
- Hernández, E. Global solutions for abstract impulsive neutral differential equations. Math. Comput. Model. 2011, 53, 196–204. [Google Scholar] [CrossRef]
- Lakrib, M. Existence of solutions for impulsive neutral functional differential equations with multiple delays. Electron. J. Differ. Equ. 2008, 2008, 1–7. [Google Scholar]
- Li, M. Existence results for nondensely defined impulsive neutral functional differential equations with infinite delay. Nonlinear Anal. Hybrid Syst. 2011, 5, 502–512. [Google Scholar] [CrossRef]
- Ye, R. Existence of solutions for impulsive partial neutral functional differential equation with infinite delay. Nonlinear Anal. Theory Methods Appl. 2010, 73, 155–162. [Google Scholar] [CrossRef]
- Sun, X.; Huo, H.; Ma, C. Periodic solutions of a class of impulsive neutral delay differential equation. Appl. Math. Comput. 2012, 219, 3947–3955. [Google Scholar] [CrossRef]
- Duan, Y.; Tian, P.; Zhang, S. Oscillation and stability of nonlinear neutral impulsive delay differential equations. J. Comput. Appl. Math. 2003, 11, 243–253. [Google Scholar] [CrossRef]
- Graef, J.R.; Shen, J.H.; Stavroulakis, I.P. Oscillation of impulsive neutral delay differential equations. J. Math. Anal. Appl. 2002, 268, 310–333. [Google Scholar] [CrossRef]
- Luo, Z.; Shen, J. Oscillation for solutions of nonlinear neutral differential equations with impulses. Comput. Math. Appl. 2001, 42, 1285–1292. [Google Scholar] [CrossRef]
- Li, X.; Deng, F. Razumikhin method for impulsive functional differential equations of neutral type. Chaos Solitons Fractals 2017, 101, 41–49. [Google Scholar] [CrossRef]
- Bainov, D.D.; Stamova, I.M. Uniform asymptotic stability of impulsive differential-difference equations of neutral type by Lyapunov’s direct method. J. Comput. Appl. Math. 1995, 62, 359–369. [Google Scholar] [CrossRef][Green Version]
- Xu, D.; Yang, Z.; Yang, Z. Exponential stability of nonlinear impulsive neutral differential equations with delays. Nonlinear Anal. Theory Methods Appl. 2007, 67, 1426–1439. [Google Scholar] [CrossRef]
- Xu, L.; Xu, D. Exponential stability of nonlinear impulsive neutral integro-differential equations. Nonlinear Anal. 2008, 69, 2910–2923. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, Z.; Sun, Y.; Liu, T. Asymptotical stability criteria for exact solutions and numerical solutions of nonlinear impulsive neutral delay differential equations. Axioms 2023, 12, 988. [Google Scholar] [CrossRef]
- Zhang, G.; Sun, Y.; Wang, Z. Asymptotical stability of the exact solutions and the numerical solutions for impulsive neutral differential equations. Comput. Appl. Math. 2024, 43, 8. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, G.; Wang, Z.; Liu, T. Convergence of the Euler method for impulsive neutral delay differential equations. Mathematics 2023, 11, 4684. [Google Scholar] [CrossRef]
- Yeniçerioğlu, A.F. Stability of linear impulsive neutral differential equations with constant coefficients. J. Math. Anal. Appl. 2019, 479, 2196–2213. [Google Scholar] [CrossRef]
- Philos, C.G.; Purnaras, I.K. Purnaras, Periodic first order linear neutral delay differential equations. Appl. Math. Comput. 2001, 117, 203–222. [Google Scholar]
- Philos, C.G.; Purnaras, I.K. On the behavior of the solutions for certain first order linear autonomous functional differential equations. Rocky Mountain J. Math. 2006, 36, 1999–2019. [Google Scholar] [CrossRef]
- Kordonis, I.G.; Philos, C.G. On the behavior of the solutions for linear autonomous neutral delay difference equations. J. Differ. Equ. Appl. 1999, 5, 219–233. [Google Scholar] [CrossRef]

| Stepsize | Ratio | Ratio | ||
|---|---|---|---|---|
| 1/20 | 0.0066590383 | 6.0532924880 | ||
| 1/40 | 0.0033576411 | 0.5042231270 | 3.3600485518 | 0.5550778454 |
| 1/80 | 0.0016859400 | 0.5021203734 | 1.7654071490 | 0.52541120220 |
| 1/160 | 8.4476115143 | 0.5010624028 | 9.0430888108 | 0.5122381438 |
| 1/320 | 4.2282978351 | 0.5005317572 | 4.5758856992 | 0.5060091519 |
| Stepsize | Ratio | Ratio | ||
|---|---|---|---|---|
| 1/100 | 0.0134679990 | 0.0730382471 | ||
| 1/200 | 0.0067647055 | 0.5022799238 | 0.0367309910 | 0.5029007739 |
| 1/400 | 0.0033900841 | 0.5011428898 | 0.0184189152 | 0.5014543502 |
| 1/800 | 0.0016969818 | 0.5005721798 | 0.0092228697 | 0.5007281696 |
| 1/1600 | 8.4897669001 | 0.5002862740 | 0.0046147951 | 0.5003643339 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.-L.; Sun, Y.; Zhang, Y.-X.; Liu, C. Euler Method for a Class of Linear Impulsive Neutral Differential Equations. Mathematics 2024, 12, 2833. https://doi.org/10.3390/math12182833
Zhang G-L, Sun Y, Zhang Y-X, Liu C. Euler Method for a Class of Linear Impulsive Neutral Differential Equations. Mathematics. 2024; 12(18):2833. https://doi.org/10.3390/math12182833
Chicago/Turabian StyleZhang, Gui-Lai, Yang Sun, Ya-Xin Zhang, and Chao Liu. 2024. "Euler Method for a Class of Linear Impulsive Neutral Differential Equations" Mathematics 12, no. 18: 2833. https://doi.org/10.3390/math12182833
APA StyleZhang, G.-L., Sun, Y., Zhang, Y.-X., & Liu, C. (2024). Euler Method for a Class of Linear Impulsive Neutral Differential Equations. Mathematics, 12(18), 2833. https://doi.org/10.3390/math12182833