Knowledge Graph Embedding Using a Multi-Channel Interactive Convolutional Neural Network with Triple Attention

Abstract

Knowledge graph embedding (KGE) has been identified as an effective method for link prediction, which involves predicting missing relations or entities based on existing entities or relations. KGE is an important method for implementing knowledge representation and, as such, has been widely used in driving intelligent applications w.r.t. question-answering systems, recommendation systems, and relationship extraction. Models based on convolutional neural networks (CNNs) have achieved good results in link prediction. However, as the coverage areas of knowledge graphs expand, the increasing volume of information significantly limits the performance of these models. This article introduces a triple-attention-based multi-channel CNN model, named ConvAMC, for the KGE task. In the embedding representation module, entities and relations are embedded into a complex space and the embeddings are performed in an alternating pattern. This approach helps in capturing richer semantic information and enhances the expressive power of the model. In the encoding module, a multi-channel approach is employed to extract more comprehensive interaction features. A triple attention mechanism and max pooling layers are used to ensure that interactions between spatial dimensions and output tensors are captured during the subsequent tensor concatenation and reshaping process, which allows preserving local and detailed information. Finally, feature vectors are transformed into prediction targets for embedding through the Hadamard product of feature mapping and reshaping matrices. Extensive experiments were conducted to evaluate the performance of ConvAMC on three benchmark datasets compared with state-of-the-art (SOTA) models, demonstrating that the proposed model outperforms all compared models across all evaluation metrics on two of the datasets, and achieves advanced link prediction results on most evaluation metrics on the third dataset.

1. Introduction

Knowledge graphs consist of effective triplets in the form of head entity, relation, and tail entity, and are represented as directed graphs that depict the knowledge of entities and their relationships in the objective world. In these graphs, nodes and edges, respectively, represent the entities and relations between entities in the real world. As an effective knowledge resource, knowledge graphs are widely applied in artificial intelligence tasks, including recommendation systems [1], question-answering systems [2], and information retrieval systems. Large-scale knowledge graphs, such as YAGO [3], Freebase [4], DBpedia [5], and WordNet [6], store vast amounts of structured data. However, many effective triplets are lost during the construction of a knowledge graph, resulting in poor performance in downstream tasks.

The primary task in a knowledge graph is to predict missing entities or relations within the graph. An effective method currently used for link prediction is called knowledge graph embedding (KGE). It aims to embed entities and relations into a vector space, where numerous additions or multiplications are performed. Finally, a scoring function evaluates whether the predicted entities or relations conform to objective facts. Existing KGE models could broadly be categorized into translation-based models, semantic matching models, and neural-network-based models. Typical examples of translation-based models include TransE [7], TransH [8], and TransR [9]. These models use distance as a criterion to measure the semantic similarity between entities and relations and are characterized by their use of additive operations. The main representatives of semantic matching models are DistMult [10] and ComplEx [11], which capture the semantics of relationships through matrix multiplication, and are typical examples of multiplicative operation models. Based on these approaches, powerful models such as RotatE [12] and TuckER [13] have been further developed.

With the success of neural networks in the field of knowledge graphs, convolutional neural networks (CNNs) enter the researchers’ horizons. For instance, ConvE [14] utilizes a two-dimensional (2D) convolution to extract features from a matrix, where the elements of the matrix represent entity or relationship information. However, only one convolutional channel is used as an input channel, which limits the interaction between entities and relations. Additionally, the interpretability of the reshaping and concatenation process is not strong. HypER [15] enhances the interaction between entities and relations by using entities as the input for convolution and relations as filters. In M-DCN [16], multi-scale filters are dynamically generated in the convolutional layer, with the weights of the filters dynamically related to each relationship to learning different features between input embeddings. Although these models have optimized CNNs and achieved commendable results, the process of feature interaction is still not perfect, and the extraction of detailed information is insufficient, thus limiting their performance.

The scale of knowledge graphs in the real world is increasing, which requires higher performance from models, especially in terms of their computational efficiency and scalability. The data volume of knowledge graphs is rapidly increasing, and how to handle larger entities and relations has become a major challenge. The time and space complexities of many proposed models may grow exponentially on large-scale datasets, requiring a search for more efficient models. One can also build a distributed computing framework to process large-scale knowledge-graph data.

Therefore, in this article, a highly expressive KGE model, named ConvAMC, is elaborated on. In this model, initially, entities and relations are embedded as a whole to preserve their original semantic information as much as possible. Entities and relations are then reshaped and concatenated in an alternating manner to extract additional feature interactions. Secondly, a multi-channel convolution is utilized in the convolutional process to learn different features between input embeddings and output feature mappings. To capture local features and detailed information during the interaction between entities and relations, a max pooling layer is inserted in each convolutional channel. This approach preserves key feature information while reducing the number of model’s parameters and computational load to prevent overfitting. To enhance the capture of interactions between spatial dimensions and input tensor channels during the multi-channel convolutional process, an attention module is introduced. This module applies a triple attention mechanism in each convolutional channel, focusing specifically on the entities and relations of triplets to extract their interaction features more comprehensively. The computational cost added by the cross-channel convolutional process remains within an acceptable range. Finally, the feature mapping tensors obtained from the multi-channel convolution are concatenated and reshaped again, then mapped to a complex space after a 2D convolution. The vectors of entities and relations are computed using the Hadamard product, returning scores for the predicted triplets.

The main contributions of this article can be summarized as follows:

• A multi-channel CNN is proposed to ensure interaction between entities and relations across multiple channels, along with a max pooling layer added to each convolutional channel to capture more local features.
• The CNN structure is optimized by introducing a triple attention mechanism during the multi-channel convolutional process, enhancing the extraction of global information for entities and relations across the convolutional channels.
• The feature mapping tensors obtained from the multi-channel convolution are concatenated in the form of a Hadamard product, and traditional inner product operations are abandoned in the complex space. Instead, a more comprehensive Hadamard product is employed to achieve better predictions.

In conducted extensive experiments, the ConvAMC model is compared with state-of-the-art (SOTA) models. By comparing link prediction results, it was found that ConvAMC achieves better embedding effects and leads on most metrics.

The rest of this article is organized as follows. In Section 2, the related work about KGE is briefly reviewed and analyzed. The research problem is formally defined and the details of the ConvAMC are introduced in Section 3. Experimental results achieved by the proposed model on three public databases are presented in Section 4. Finally, the conclusions and future work directions are presented in Section 5.

2. Related Work

The use of KGE models to predict missing entities and relations in knowledge graphs has received widespread attention, leading to a range of classic KGE models. As mentioned in the Introduction, KGE models can be divided into three main categories: translation-based models, semantic matching models, and neural-network-based models.

A typical representative of the translation-based models is TransE [7], which views the relationship between entities in a fact triplet as a translation distance in a low-dimensional vector space. For a given fact triplet $(h, r, t)$, TransE learns to generate vectors $(h, r, t)$ and aims to maintain that $h+r \approx t$ for valid triplets. The loss function is optimized as follows:

$$\mathcal{L}={\sum }_{\left(h,r,t\right)\cup \left(h\mathrm{’},\mathrm{r},\mathrm{t}\mathrm{’}\right)}max\left(0,\parallel {h+r-t\parallel }_{\mathcal{P}}-\parallel {h\prime +r-t\prime \parallel }_{\mathcal{P}}+\gamma \right)$$

(1)

where $\mathcal{P}$ denotes the L1 or L2 norm,$\parallel h\prime +r+t\prime \parallel$ denotes an invalid triplet, γ denotes the hyperparameter margin, and $max(0, y)$ is used to extract the larger score between 0 and $y$. TransE is a fast and efficient model for link prediction, but it is only suitable for one-to-one relationships and does not perform well in handling complex relationships. Consequently, many embedding models have extended it, such as TransH [8], which introduces a hyperplane. This simple approach overcomes the shortcomings of TransE in handling complex relationships while maintaining almost the same model complexity as TransE. TransR [9] builds on the foundation of TransH by assuming that entities and relations exist on different semantic hyperplanes. TransD [17] represents entities using two vectors and constructs a triplet-specific mapping matrix to facilitate subsequent projections, thus significantly improving the performance. These extended models have variously enhanced the performance of TransE.

KGE methods, based on semantic matching models, utilize tensors to represent entities and relations. These models employ tensor decomposition for modeling the relationships and propose a scoring function composed of a bilinear product of entity vectors and object vectors, and a full-rank relationship matrix. RESCAL [18] is one of the earliest models based on semantic matching. It employs an optimized scoring function to address the problem of KGE. However, RESCAL tends to overfit due to the substantial number of parameters required during its training. Inspired by this, DistMult [10] a special case of RESCAL- replaces the full-rank relationship matrix with a diagonal matrix, effectively reducing the number of parameters and establishing a method for training symmetric relationships. While DistMult reduces the likelihood of overfitting, it also imposes certain limitations on entity embeddings, making it unable to model asymmetric relationships. ComplEx extends the embedding space of DistMult into the complex space, utilizing complex conjugate relationships to represent the subject and object embeddings of triplets. This introduces asymmetry into tensor decomposition, addressing the limitation of DistMult, which can only handle symmetric relationships. This enhancement improves the capability to manage various relationship patterns. Inspired by Euler’s formula, RotatE [12] projects entities and relations into a complex vector space and interprets relations as rotations between entities. The scores of triplets are computed using the Hadamard product. RotatE is not only scalable but also excels in inferring and simulating various relationship patterns, particularly in modeling symmetric relationships, making it a powerful model. However, the performance of RotatE in handling commutative and non-commutative combination modes still needs improvement. Therefore, based on RotatE, Rotate3D was proposed in [19], which maps entities into a 3D space and represents relations as rotations. By using the composition property of rotations in the 3D space, Rotate3D can naturally preserve the order of relations and outperforms RotatE in modeling both commutative and non-commutative composition patterns.

The current research, focused on KGE models, has gradually shifted toward neural-network-based models. For instance, ConvE [14] represents a significant breakthrough in the application of CNNs to the KGE field, whereby the characteristics of 2D CNNs are analyzed, and input features are processed using 2D convolutional filters to produce corresponding output vectors. Then, scores for predicted triplets are obtained by computing the inner product of these output vectors with the embeddings of the tail entities. ConvKB [20] considers that one-dimensional (1D) convolution operations are beneficial for capturing global relationships; hence, it uses 1D convolutional filters to convolve embeddings to calculate scores for triplets. HypER [15] utilizes a set of 1D convolutional filters specific to relationships, generated by a hypernetwork, to fully convolve the embeddings of head entities. ConvR [21] improves upon the interaction flaws introduced by ConvE by using adaptive relationship-specific filters instead of global filters. AcrE [22] employs a novel CNN structure, using various types of filters to extract interaction features between entities and relations. In M-DCN [16], filters of different weights are generated in the convolutional layer, with each dynamically related to a relation to the model’s diverse types of relationships. CTKGC [23] proposes combining a 2D CNN with a translation-based model, suggesting that the multiplicative approximation of entities and relations is equivalent to the factual representation of the object. ConvEICF [24] enhances and optimizes four critical aspects of CNNs in link prediction tasks. ConvHLE [25] introduces a network model, designed for convolution of high- and low-level feature interactions, which effectively captures entity and relation information, generating more information-rich vector representations. In addition, in order to overcome the huge storage challenge caused by excessive embedding parameters in the knowledge graphs for practical applications, researchers have proposed KGE distillation models, such as DualDE [26], which compresses KGEs into a low-dimensional space, considers the interaction between students and teachers, effectively transfers the teacher’s knowledge to students, greatly reduces the number of parameters, and improves its efficiency and performance.

Models, based on CNNs, are recognized as having better feature extraction and expressive capabilities compared to the other two categories of models. However, the parameters of these models do not scale with the expansion of datasets. Consequently, when facing increasingly large knowledge graph datasets, these models can only extract features at a single level, and there remains room for improvement in extracting deeper local information.

Table 1 summarizes the scoring functions, embedding spaces, and relationship parameters of several classic and advanced KGE models, where $d_e$ and $d_r$ denote the embedding dimensions of entities and relations, respectively, $\mathbb{R}$ and $\mathbb{C}$ denote the Euclidean space and the complex space, respectively, ∗ denotes a convolution operation, $\left[e_h;e_r;e_t\right]$ denote the reshaping and concatenation of the head entity, relation, and tail entity within a triplet, $e_t$ denotes the conjugate form of the tail entity in the complex space, Re() denotes the real part, $f\left(·\right)$ denotes the nonlinear function operation, and $⟨·⟩$ denotes the dot product operation.

Table 1. Comparison of scoring functions, embedding spaces, and relationship parameters of different KGE models.

Model	Scoring Function	Embedding Space	Relationship Parameters
TransE [7]	${\parallel e_h+e_r{-e}_t\parallel }_p$	$e_h,e_r{,e}_t\in \mathbb{R}$	$e^r\in {\mathbb{R}}^{d_r}$
DistMult [10]	$⟨e_h,e_r{,e}_t⟩$	$e_h,e_r{,e}_t\in \mathbb{R}$	$e^r\in {\mathbb{R}}^{d_r^2}$
ComplEx [11]	$\mathrm{R}\mathrm{e}\left(⟨ e_h,e_r{,e}_t ⟩\right)$	$e_h,e_r{,e}_t\in \mathbb{C}$	$e^r\in {\mathbb{C}}^{d_e}$
ConvE [14]	$f\left(vec\left(f\left(\left[e_h;e_r\right]\ast w\right)\right)W\right)e_t$	$e_h,e_r{,e}_t\in \mathbb{R}$	$e^r\in {\mathbb{R}}^{d_r}$
ConvKB [20]	$f\left(vec\left(f\left(\left[e_h;e_r;e_t\right]\ast w\right)\right)W\right)$	$e_h,e_r{,e}_t\in \mathbb{R}$	$e^r\in {\mathbb{R}}^{d_r}$
TuckER [13]	$W\times {}_{1}e_h\times {}_{2}e_r\times {}_{3}e_t$	$e_h,e_r{,e}_t\in \mathbb{R}$	$e^r\in {\mathbb{R}}^{d_r}$
RotatE [12]	$-\parallel e_h\circ e_r{-e}_t\parallel$	$e_h,e_r{,e}_t\in \mathbb{C}$	$e^r\in {\mathbb{C}}^{d_e}$
SimplE [27]	$1/2\left(⟨h_{e_h},e_r,t_{e_t}⟩+h_{e_h},e_r,t_{e_t}\right)$	$e_h,e_r{,e}_t\in \mathbb{R}$	$e^r\in {\mathbb{R}}^{d_e}$
ConvAMC (proposed)	Re$\left(⟨e_h;e_r⟩,e_h,e_r,e_t\right)$	$e_h,e_r{,e}_t\in \mathbb{C}$	$e^r\in {\mathbb{C}}^{d_{2e}}$

Starting with the mathematical meaning of the convolution, presented as follows:

$$f\left(t\right)\ast g\left(t\right)={\int }_{-\infty }^{+\infty }f\left(r\right)g\left(x-r\right)dr$$

(2)

the essence of convolution is the process of flipping, multiplying, and adding. In CNNs, the loss function gradually decreases as the number of iterations increases during training, so that the model’s parameters converge to a stable value. The output of the convolutional layer can be represented as follows:

$$y=\left(W\ast x\right)+b$$

(3)

where $x$ denotes the input feature map, $W$ denotes the convolution kernel weight, $b$ denotes the bias, and $\ast$ denotes the convolution operation.

During the training of the proposed model, we use gradient descent to optimize the model’s parameters, as follows:

$$\begin{gathered} W\leftarrow W-\eta {\displaystyle \frac{\partial L}{\partial W}} \\ b\leftarrow b-\eta {\displaystyle \frac{\partial L}{\partial b}} \end{gathered}$$

(4)

where $\eta$ denotes the learning rate and $L$ denotes the loss function.

In the convolutional channels of the proposed ConvAMC model, the loss function is bounded and continuous with respect to the model’s parameters. The gradient descent algorithm is also bounded, ensuring the convergence of the CNN layers.

The triple attention mechanism used to enhance information flow and feature expression ability of the proposed model involves three different attentions, namely, self-attention, context-attention, and inter-attention, with the following weighted attention computations:

$$\begin{gathered} A_{self}=SoftMax\left({\displaystyle \frac{Q.K^T}{\sqrt{d_k}}}\right) \\ {A}_{context}=SoftMax\left({\displaystyle \frac{Q\prime .{K\prime }^T}{\sqrt{d_k}}}\right) \\ {A}_{inter}=SoftMax\left({\displaystyle \frac{Q″.{K″}^T}{\sqrt{d_k}}}\right) \end{gathered}$$

(5)

where $Q, Q^{\prime }$ and $Q^{″}$ denote the matrices of the queries, $K, K^{\prime }$ and $K^{″}$ denote the matrices of the keys, respectively, for each attention type, and $d_k$ denotes the dimension of the keys.

The stability of the triple attention mechanism lies in the normalization operation, where the SoftMax function converts the input into a probability distribution, ensuring that the sum of all weights is equal to 1, as per the following formula:

$$SoftMax\left(z_i\right)={\displaystyle \frac{e^{z_i}}{\sum _j{e}^{z_i}}}$$

(6)

If the input $z_i$ is bounded, then the output $SoftMax\left(z_i\right)$ is also bounded.

During the model training process, stability also relates to changes in the gradient of the loss function with respect to attention weights:

$${\displaystyle \frac{\partial L}{\partial A}}={\displaystyle \frac{\partial L}{\partial y}}·{\displaystyle \frac{\partial y}{\partial A}}$$

(7)

where $y$ denotes the final output. As the derivative of the SoftMax function is a bounded function, small changes in the input will not cause drastic fluctuations in the output, thus ensuring the stability of the gradient, which implies stability in the triple attention mechanism utilized by the proposed model.

3. Proposed Model

In this section, a detailed description is provided of the novel CNN-based KGE model proposed in this article, named ConvAMC. The structure of ConvAMC, shown in Figure 1, comprises three main modules: an embedding representation module, an encoding module, and a prediction and scoring module.

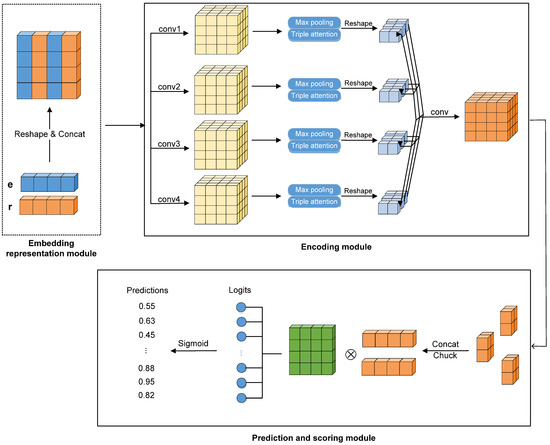
Figure 1. The end-to-end structure of the proposed ConvAMC model (e denotes entity embedding; r denotes relation embedding; Reshape and Concat denote reshaping and splicing operations, respectively; conv denotes convolution operation; Chuck denotes segmentation operation; denotes the Hadamard product operation).

The embedding representation module initializes all entities and relations to form a K-dimensional embedding matrix of entities and relations, facilitating subsequent processing and computation of entities and relations. The encoding module processes the embedding matrix of entities and relations through a multi-channel convolution and a triple attention mechanism to obtain the feature mapping matrix of entities and relations, which serves as an input matrix for the rating prediction and scoring module, where this matrix is projected into the complex space and is split into real and imaginary parts, based on the embedding dimensions of entities and relations. The scores of each candidate entity are obtained by using a scoring function, whereby the scores are arranged from high to low.

3.1. Embedding Representation Module

In knowledge graphs, triplets exist in forms such as text, numerical values, and symbols, which cannot be directly computed. Therefore, $n$-dimensional embeddings are initialized for all entities $e\in \{e_1,e_2,e_3,\cdot \cdot \cdot ,e_n\}$ and relations $r\in \{r_1,r_2,r_3,\cdot \cdot \cdot ,r_n\}$, generating vector representations for entities $e^e=\{e_1^e,e_2^e,e_3^e,···,e_n^e\}\in {\mathbb{R}}^n$ and relations $r^r=\{r_1^r,r_2^r,r_3^r,···,r_n^r\}\in {\mathbb{R}}^n$. In order to more accurately establish the connections between entities and relations, the entity embeddings and relation embeddings are treated as a whole to capture more semantic information. During the vector reshaping process, the traditional stacking method is abandoned in favor of the alternating reshaping method, aimed at enhancing the interaction between entities and relations to capture more latent information. As shown in Figure 2, the alternating reshaping method is used to connect an entity and a relation, resulting in the following matrix $\mathit{M}$ [16]:

$$\mathit{M}=\left[e\oplus r\right]\in {\mathbb{R}}^{2\times n}$$

(8)

where $\oplus$ denotes the concatenation operation of entities and relations as a whole, resulting in the following matrix $\overline{\mathit{M}}$ after the alternating reshaping process:

$$\overline{\mathit{M}}=\left[e\oplus r\right]\in {\mathbb{R}}^{n_h\times n_w}$$

(9)

where [∙] denotes the reshaping operation and $2\times n=n_w\times n_h$. 2D convolution operations are employed to generate more interaction features between the combined entity and relation, thus more clearly articulating the connections between the entity and the relation.

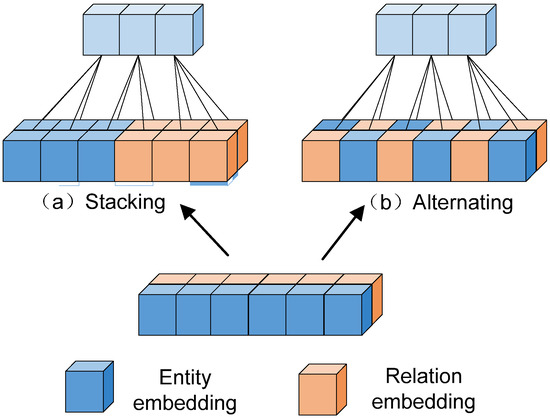
Figure 2. Two reshaping methods: (a) stacking; (b) alternating.

3.2. Encoding Module

In the encoding module, to best match the mapping relationships between head entities, relations, and tail entities, a linear transformation is chosen during the interaction between entities and relations. Initially, entity features and relation features are concatenated to form a long feature vector. This concatenated feature vector is then input into a linear layer, where a linear transformation is applied to derive new embedding representations for entities and relations. The concatenated feature representation is mapped to the complex space to better capture the complex relationships between entities and relations. The entity-relation interaction method is shown below:

$$L_{e\_r}=\left[e\oplus r\right]W_{L_{e\_r}}+b_{L_{e\_r}}$$

(10)

where $L_{e\_r}\in {\mathbb{R}}^{2\times n}$ and $W_{L_{e\_r}}\in {\mathbb{R}}^{2n\times 2n}$, and after the interaction between entities and relations, the reshaped result is dimensioned as $1\times H\times W$, where $H$ and $W$ denote the dimensions of the input 2D matrix such that $2n=H\times W$. Consequently, convolution is used to extract additional feature information for modeling the entities and relations.

During the convolutional process, the features extracted by a single convolutional channel contain less detail but more comprehensive semantic information. To capture multi-level feature information and further improve the quality of entity-relation interactions, four 2D convolutional channels, each having a max pooling layer, are employed. New feature matrices generated during the interaction between entities and relations serve as input matrices for the convolutional channels, allowing for better extraction of detailed features between channels. Subsequently, the most prominent features of the feature matrices are extracted through the max pooling layers, significantly reducing the size of the feature tensor and alleviating the computational pressure, compensating for the lack of detail in features extracted by the convolutional process.

A max pooling operation is performed on each convolutional channel to compute the channel attention. Using the multi-layer perceptron (MLP) to extract channel features, the interaction features of entities and relations after max pooling operation are represented as follows:

$$M_p=\sigma \left(MLP\left(MaxPool\left(L_{e\_r}\right)\right)\right)$$

(11)

where $\sigma$ denotes the tanh function.

During the convolutional process, the use of max pooling operations results in some information loss, which is not conducive to prediction tasks. To address this issue, a triple attention mechanism is employed between each convolutional channel. Compared to the channel attention method used in CBAM, which shows significant performance improvements, these improvements do not stem from enhanced interaction between channels but rather from prioritizing the dimension reduction during the channel attention computation, which is superfluous for capturing local dependencies between channels. In contrast, the triple attention mechanism, utilized by the proposed model, emphasizes capturing interactions between spatial dimensions and input tensor channels rather than reducing the dimensions. This eliminates the indirect correspondence between channels and weights, and the additional computational cost is negligible. Therefore, the effectiveness of feature extraction is further enhanced. The feature extraction results of the four convolutional channels are shown below:

$$\begin{gathered} T_1\left(e,r\right)=f_1^{3\times 3}\left(TA\left(MP\left(L_{e\_r}\right)\right)\right) \\ {T}_2\left(e,r\right)=f_2^{3\times 3}\left(TA\left(MP\left(L_{e_r}\right)\right)\right) \\ {T}_3\left(e,r\right)=f_3^{3\times 3}\left(TA\left(MP\left(L_{e_r}\right)\right)\right) \\ {T}_4\left(e,r\right)=f_4^{3\times 3}\left(TA\left(MP\left(L_{e\_r}\right)\right)\right) \end{gathered}$$

(12)

where $f_i^{3\times 3}$ denotes the $i$-th $3\times 3$ convolutional channel, $T_i\left(e,r\right)\in {\mathbb{R}}^{C\times H\times W}$ denotes the interaction features extracted by the $i$-th convolutional channel, $TA$ denotes the utilized triple attention mechanism, and $MP$ denotes the utilized max pooling operation. For ease of computation during convolution operations, padding is applied in the convolutional channels to ensure the accuracy of feature extraction.

Subsequently, the processed feature maps of the convolutional channels are concatenated, reshaped, and fused through a fully connected layer, as follows:

$$F_{concat}=\left[re\left(T_1\right),re\left(T_2\right),re\left(T_3\right),re\left(T_4\right)\right]=concat\left(re\left(T_1\right),re\left(T_2\right),re\left(T_3\right),re\left(T_4\right)\right)$$

(13)

where re (⋅) denotes a reshape operation and concat(⋅) denotes a concatenation operation.

Regularization is applied through dropout on the maximum pooling operation and triple attention mechanism in each channel, including feature maps after convolution and hidden layers after fully connected layer projection. The commonly used $1-N$ scoring technique in KGE can be significantly improved through the addition of dropout operation. Batch normalization (BN) is used after each layer to stabilize, regularize, and improve convergence speed. The Adam optimizer, as a fast and computationally efficient gradient-based optimization tool, is used to minimize the loss function, helping to reduce the computational overhead through this series of operations. The processed feature mapping matrix is obtained as follows:

$$\mathrm{C}\mathrm{M}\mathrm{T}\left(e\_r\right)=Drop\left(BN\left(F_{concat}\right)\right)$$

(14)

where C represents the multi-channel convolutional processing, M represents the max pooling operation processing, and T represents the triple attention mechanism.

Finally, the feature interactions obtained through multiple convolutional channels, max pooling operations, and the triple attention mechanism are connected and reshaped through fully connected layers. The output matrix, obtained through the 2D convolution operation, is used as an input to the prediction and scoring module.

The overall mathematical model of ConvAMC can be summarized as follows:

$$\mathrm{C}\mathrm{M}\mathrm{T}\left(e\_r\right)=Drop\left(BN\left(concat\left(\sum _{i=1}^{4}TA\left(MP\left(\left[e⨁r\right]W_{L_{e\_r}}+b_{L_{e\_r}}\right)\right)\right)\right)\right)$$

3.3. Prediction and Scoring Module

In the prediction and scoring module, a $1-N$ scoring pattern is employed to obtain scores for all candidate objects. The semantic similarity of all candidates is computed by extracting the interaction features between the head entity and the relation and considering the calculated scores. The candidate with the highest score, indicating the highest match, is selected as the final prediction result.

During the encoding process, the feature extraction result $\mathrm{C}\mathrm{M}\mathrm{T}(e\_r)$ undergoes a linear transformation to ensure consistency with the dimensions of the predicted entity. Subsequently, the tensor $\mathbf{C}\mathbf{M}\mathbf{T}(\mathbf{e}\_\mathbf{r})$ is reshaped into a vector $\mathrm{v}\mathrm{e}\mathrm{c}\mathrm{C}\mathrm{M}\mathrm{T}(\mathrm{e}\_\mathrm{r})\in {\mathbb{R}}^{C\times H\times W}$. The reshaped feature vector is then concatenated according to the Hadamard product formula to produce the output of the convolutional channel. This output is split into two parts, based on the dimensions of the entity embeddings and relation embeddings, corresponding to the real part ($Rel$) and the imaginary part ($Im$) of the feature vectors in the complex space. A matrix $\mathrm{W}\in {\mathbb{R}}^{CHW\times n}$ is then used to project the parameterized linear transformation into the complex space. The prediction results are obtained by the Hadamard product on the real and imaginary parts of the entity and the relation, and each prediction score is calculated using the Sigmoid function. The highest-scoring candidate object is selected as the prediction result by using the following scoring function:

$$\begin{gathered} ConvAMC\left(e_h,r,e_t\right)=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(e_h,r)e_t \\ =\left(Rel\left(CMT\left({e_h}_{e_t}\right)\right),Rel\left(CMT\left(r\right)\right)\right)+\left(Rel\left(CMT\left({e_h}_{e_t}\right)\right),Im\left(CMT\left(r\right)\right)\right) \\ +\left(Im\left(CMT\left(e_h\_e_t\right)\right),Rel\left(CMT\left(r\right)\right)\right)-\left(Im\left(CMT\left(e_h\_e_t\right)\right),Im\left(CMT\left(r\right)\right)\right) \end{gathered}$$

(15)

The design of our scoring function is mainly inspired by the Hadamard product, whereby the feature interaction matrix of entities and relations processed through multi-channel convolution, max pooling operation, and triple attention mechanism is divided into two parts—a real and an imaginary part in the complex space. Due to the special method of computing the Hadamard product, we can transform the method of obtaining the real and imaginary parts of entities and relations in the complex space, thus increasing the efficiency of the model in processing symmetric and antisymmetric relationships in knowledge graphs.

3.4. Loss Function

It is expected that when training the proposed model, the scores for valid triplets will be equal to 1, whereas for invalid triplets, they will be equal to 0. The model parameters are trained using the cross-entropy loss function, and label smoothing techniques are utilized for optimization to achieve better results. The loss function is defined as follows:

$$\mathcal{L}=-{\displaystyle \frac{1}{N_e}}{\sum }_{i=1}^N\left[ylog\left(\mathsf{\phi }\left(e_h,r,e_t\right)\right)+\left(1-y\right)log\left(1-\mathsf{\phi }\left(e_h,r,e_t\right)\right)\right]$$

(16)

$$y=\left\{\begin{array}{c}1 \mathsf{\phi }\left(e_h,r,e_t\right)\in \mathcal{T}\\ 0 \mathsf{\phi }\left(e_h,r,e_t\right)\in \mathcal{T}\prime \end{array}\right.$$

(17)

where $\mathcal{T}$ and $\mathcal{T}\prime$ denote, respectively, the set of valid and invalid triplets in the test set.

4. Experiments and Results

4.1. Datasets

Extensive experiments on the link prediction task were conducted using the proposed ConvAMC model on three knowledge-graph benchmark datasets: FB15k-237 [28], WN18RR [14], and YAGO3-10 [29]. Detailed information about these datasets is shown in Table 2. As indicated in [14,28], the WN18 and FB15k datasets contain too many reversible relationships, making the prediction of most triplets overly simplistic. Consequently, the subsets WN18RR and FB15k-237 were created to eliminate reversible relationships.

Table 2. Detailed information of the datasets, considered for use in the experiments.

Dataset	Entities	Relations	Triplets
			Train	Valid	Test
FB15k	14,951	1345	483,142	50,000	59,071
WN18	40,943	18	141,442	5000	5000
FB15k-237	14,541	237	272,115	17,535	20,446
WN18RR	40,943	11	86,835	3034	3134
YAGO3-10	123,182	37	1,079,040	5000	5000

FB15k [7] is extracted from Freebase and includes 14,591 entities and 1345 types of relations, encompassing real-world information about movies, celebrities, sports teams, awards, and other aspects. WN18 [7] is extracted from WordNet and includes 40,943 entities and 18 types of relations. The entities primarily reflect word meanings, while the relations represent lexical relationships between words, such as hypernymy and superlative relationships. FB15k-237 is a subset of FB15k, from which reversible relationships have been removed. It includes 14,541 entities and 237 types of relations. WN18RR is a subset of WN18, from which reversible relationships have been removed, including 40,943 entities and 11 types of relations. YAGO3-10 is a subset of YAGO, containing 123,182 entities and 37 types of relations, primarily describing attributes of people, professions, names, and identity information. Each entity participates in multiple relationships.

4.2. Evaluation Metrics

In order to comprehensively and objectively evaluate the performance of the proposed ConvAMC model from different perspectives on embedding effects, four main metrics were used, namely the mean reciprocal rank (MRR), Hits@10, Hits@3, and Hits@1, defined as follows:

$$\mathrm{M}\mathrm{R}\mathrm{R}:{\displaystyle \frac{1}{\left|{\mathcal{T}}_{test}\right|}}{\sum }_{i=1}^{\left|{\mathcal{T}}_{test}\right|}\left({\displaystyle \frac{1}{{rank}_i}}\right)$$

(18)

$$\mathrm{H}\mathrm{i}\mathrm{t}@\mathrm{k}:{\displaystyle \frac{1}{\left|{\mathcal{T}}_{test}\right|}}{\sum }_{i=1}^{\left|{\mathcal{T}}_{test}\right|}f\left({rank}_i\right),f\left(x\right)=\left\{\begin{array}{c}0 x>k\\ 1 x\le k\end{array}\right.$$

(19)

where ${\mathcal{T}}_{test}$ denotes the number of triplets in the test set, while ${rank}_i$ denotes the rank of the correctly predicted tail entity among all candidate entities. MRR is defined as the arithmetic mean of the reciprocal ranks of all triplets in the test set, exhibiting smoothness and less susceptibility to outliers. Higher values of MRR and Hits@k indicate better link prediction performance of a model and more effective KGE. The values of all these metrics range from 0 to 1.

4.3. SOTA Models for Comparison

ConvAMC was compared with various SOTA models categorized into three groups: (1) translation-based models, such as TransE [7] and RotatE [12]; (2) semantic matching models, like DistMult [10], ComplEx [11], and TuckER [13], with the latter improving upon the former and offering stronger competitiveness in KGE; and (3) neural-network-based models, including ConvE [14], InteractE [30], CTKGC [23], LTE-ConvE [31], ConvHLE [25], and ConvEICF [24].

4.4. Experimental Setting

During the operation of ConvAMC, hyperparameters were selected via grid search on the validation set. The selection ranges for the hyperparameters were as follows: batch size$\mathrm{b}\mathrm{s}:\{256,512,1024\}$, default embedding dimension for entities and relations $\mathrm{d}\mathrm{r}=200$, learning rate $\mathrm{l}\mathrm{r}:\{0.01,0.005,0.001,0.0005\}$, decay weight ratio $\mathrm{d}\mathrm{r}:\{0.99,1.0\}$, label smoothing ratio $\mathrm{l}\mathrm{s}:\{0.1,0.2,0.3\}$, input layer dropout rate $\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}:\{0.1,0.2,0.3\}$, embedding layer dropout rate, and feature mapping dropout rate $\mathrm{h}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{n}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}1$ and $\mathrm{h}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{n}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}2:\{0.1,0.2,0.3,0.4,0.5\}$, with a convolution kernel size of 3 × 3.

For optimal performance across different datasets, the hyperparameter selections were as follows. For the FB15k-237 dataset, $\mathrm{b}\mathrm{s}=256$, $\mathrm{l}\mathrm{r}=0.0005$, $\mathrm{d}\mathrm{r}=0.99$, $\mathrm{l}\mathrm{s}=0.1$, $\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}=0.2$, $\mathrm{h}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{n}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}1=0.5$, $\mathrm{h}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{n}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}2=0.5$. For the WN18RR dataset, $\mathrm{b}\mathrm{s}=1024$, $\mathrm{l}\mathrm{r}=0.005$, $\mathrm{d}\mathrm{r}=1.0$, $\mathrm{l}\mathrm{s}=0.2$, $\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}=0.3$, $\mathrm{h}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{n}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}1=0.3$, $\mathrm{h}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{n}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}2=0.3$. For the YAGO3-10 dataset, $\mathrm{b}\mathrm{s}=512$, $\mathrm{l}\mathrm{r}=0.01$, $\mathrm{d}\mathrm{r}=1.0$, $\mathrm{l}\mathrm{s}=0.1$, $\mathrm{i}\mathrm{n}\mathrm{p}\mathrm{u}\mathrm{t}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}=0.3$, $\mathrm{h}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{n}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}1=0.2$, and $\mathrm{h}\mathrm{i}\mathrm{d}\mathrm{d}\mathrm{e}\mathrm{n}\_\mathrm{d}\mathrm{r}\mathrm{o}\mathrm{p}\mathrm{o}\mathrm{u}\mathrm{t}2=0.3$.

Additionally, batch normalization was performed after each operation to prevent model overfitting and accelerate the model convergence. The Adam optimizer was used to minimize the model’s loss, and label smoothing was utilized to reduce overfitting problems caused by nonlinear output saturation on the labels.

4.5. Results and Analysis

4.5.1. Link Prediction

To validate the practicality of the ConvAMC model proposed in this article, comparisons were made with recent SOTA models for link prediction on three commonly used datasets, namely WN18RR, FB15k-237, and YAGO3-10. Analysis of the obtained results, shown in Table 3, Table 4 and Table 5, is conducted below. Most of results were taken from the original papers, cited in the tables, although a small portion of data is missing because it was not mentioned in the original publications. The best results in the tables are displayed in bold.

Table 3. Link prediction results on the WN18RR dataset.

Model	MRR	Hit@1	Hit@3	Hit@10
TransE &	0.230	-	-	0.501
DistMult &	0.430	0.390	0.440	0.490
ComplEx †	0.440	0.410	0.460	0.510
ConvE [14]	0.430	0.400	0.440	0.520
InteractE [30]	0.463	0.430	-	0.528
TuckER [13]	0.470	0.443	0.482	0.526
RotatE [12]	0.476	0.428	0.492	0.571
ConvHLE [25]	0.469	0.437	0.482	0.532
ConEx [32]	0.481	0.448	0.493	0.550
ConvEICF [24]	0.486	0.446	0.501	0.560
RAGAT [33]	0.489	0.452	0.503	0.562
TransERR [34]	0.501	0.450	0.520	0.605
ConvAMC (proposed)	0.438	0.470	0.514	0.559

‘^&’ indicates results taken from [35]; ‘^†’ indicates results taken from [15].

Table 4. Link prediction results on the FB15k-237 dataset.

Model	MRR	Hit@1	Hit@3	Hit@10
TransE &	0.294	-	-	0.465
DistMult &	0.241	0.155	0.263	0.419
ComplEx †	0.247	0.158	0.275	0.428
ConvE [14]	0.325	0.237	0.356	0.501
InteractE [30]	0.354	0.263	-	0.535
TuckER [13]	0.358	0.246	0.380	0.544
RotatE [12]	0.338	0.241	0.375	0.533
ConvHLE [25]	0.360	0.268	0.395	0.544
ConEx [32]	0.366	0.271	0.403	0.555
ConvEICF [24]	0.365	0.271	0.401	0.554
RAGAT [33]	0.365	0.273	0.401	0.547
ConvRot [36]	0.386	0.290	0.423	0.575
TransERR [34]	0.360	0.264	0.396	0.555
ConvAMC (proposed)	0.414	0.320	0.459	0.602

‘^&’ indicates results taken from [35]; ‘^†’ indicates results taken from [15].

Table 5. Link prediction results on the YAGO3-10 dataset.

Model	MRR	Hit@1	Hit@3	Hit@10
TransE &	0.501	0.406	-	0.632
ComplEx &	0.360	0.260	0.400	0.550
ComplEx-N3 ‡	0.569	0.498	0.609	0.701
DistMult [10]	0.501	0.413	-	0.690
ConvE [14]	0.440	0.350	0.490	0.620
InteractE [30]	0.541	0.462	-	0.687
RotatE [12]	0.495	0.402	0.550	0.670
RotatHS [37]	0.551	0.468	0.603	0.699
ConEx [32]	0.553	0.474	0.601	0.696
M-DCN [16]	0.505	0.423	0.587	0.682
HypER [15]	0.533	0.455	0.580	0.678
ConvRot [36]	0.538	0.448	0.593	0.700
ConvAMC (proposed)	0.610	0.540	0.677	0.766

‘^&’ indicates results taken from [35]; ‘^‡’ indicates results taken from [38].

The experimental results show that ConvAMC surpasses SOTA models according to all metrics, on two of the datasets—FB15k-237 and YAGO3-10. On the FB15k-237 dataset, ConvAMC outperforms the best SOTA model by 7.3% in MRR, 10.3% on Hit@1, 8.5% in Hit@3, and 4.7% in Hit@10. Similarly, on the YAGO3-10 dataset, ConvAMC holds a definitive lead in all metrics, with increases of 7.2% in MRR, 8.4% in Hit@1, 11.2% for Hit@3, and 9.3% in Hit@10 compared to the best performing SOTA model. On the WN18RR dataset, ConvAMC is ranked first, based on Hits@1, with a growth value of 4.0%. However, its ranking for Hits@3 and Hits@10 has dropped to second and fifth place, respectively, and for MRR it has fallen to tenth place.

Overall, the proposed ConvAMC model holds the lead when predicting objects ranked in the top three positions, indicating its advantage in link prediction accuracy. It is also undeniable that the proposed model holds the leading position on Hit@1. Compared to semantic matching models, which are easy to train and can quickly build knowledge graphs, the proposed model achieves comprehensive leadership in all metrics, except for a slight underperformance in MRR and Hit@10 on the WN18RR dataset compared to RotatE and partly to TuckER and ComplEx. Across the other metrics and on the other two datasets, ConvAMC established an all-around lead. When compared to other CNN-based models, ConvAMC leads in all metrics to varying degrees, which is particularly evident in Hit@1 and Hit@3. This thoroughly demonstrates the proposed model’s significant advantage in link prediction accuracy.

Overall, the demonstrated effectiveness and versatility of ConvAMC in link prediction tasks is primarily due to the use of a joint embedding approach for entities and relations during the embedding process, which maximally preserves the original semantic connections between entities and relations as they are fused into a 2D matrix. In the process of generating a 2D matrix for CNNs, the embeddings of entities and relations are reshaped and concatenated, which can alter semantic information. To address this issue, four convolutional channels are used to reshape and concatenate the embeddings of entities and relations, extracting interaction information between the channels, thus endowing a reshaped 2D matrix with more interaction features. At the same time, multi-channel convolution may lead to the loss of certain information details. The use of max pooling layers and a triple attention mechanism highlights feature information within the 2D matrix, making the interaction features between channels more complete and prominent, thereby providing more reference information for subsequent prediction tasks. Additionally, adjustments have been made in the choice of embedding space. A complex space has been chosen, which more fully expresses semantic information. Vectors in the complex space, consisting of real and imaginary parts, can reflect different attributes of entities and relations from various perspectives, offering richer semantic information.

4.5.2. Symmetric Relationship Modeling

The WN18RR and FB15k-237 datasets contain a large number of entities with various relationships; hence, the practicality of the proposed model for symmetric relationships can be validated on these datasets. Symmetric relationships should exhibit the property $r·\mathit{r}=1$. In the Hadamard product, the approach involves extracting the imaginary part of the embedding vectors by using the real parts of the entity and relation embeddings and extracting the real part of the embedding vectors by using the imaginary parts of the entity and relation embeddings. From a mathematical perspective, this involves swapping the real and imaginary parts of the embedding vectors for entities and relations, and observing whether the experimental results are within an acceptable error range compared to the normal model’s prediction scores. From the perspective of mathematical formulas, this assesses whether the commutative property of the Hadamard product is satisfied. The ConvAMC’s ability to model complex relationships was evaluated using MRR, Hit@1, Hit@3, and Hit@10 as metrics. The obtained experimental results are presented in Table 6.

Table 6. ConvAMC’s link prediction results after swapping real and imaginary parts of the embedding vectors for entities and relations.

Dataset	MRR	Hit@1	Hit@3	Hit@10
WN18RR	0.435 ± 0.003	0.470 ± 0.003	0.512 ± 0.003	0.555 ± 0.003
FB15k-237	0.412 ± 0.003	0.320 ± 0.003	0.457 ± 0.003	0.600 ± 0.003
YAGO3-10	0.609 ± 0.003	0.538 ± 0.003	0.673 ± 0.003	0.765 ± 0.003

As evident from Table 6, ConvAMC can successfully model symmetric relationships within an acceptable error margin (0.3%) across all four evaluation metrics used. By swapping the real and imaginary parts of the embedding vectors for entities and relations in the complex space, the following formulae have been satisfied:

$$\begin{gathered} {\left(h\_r\right)}_1=\left(e_1\_rel+e_1\_im\right)\times \left(r_1\_rel+r_1\_im\right)= \\ \left(e_1\_rel:r_1\_rel\right)+\left(e_1\_rel:r_1\_im\right)+\left(e_1\_im:r_1\_rel\right)+\left(e_1\_im:r_1\_im\right) \end{gathered}$$

(20)

$$\begin{gathered} {\left(h\_r\right)}_2=\left(e_2\_im+e_2\_rel\right)\times \left(r_2\_im+r_2\_rel\right)= \\ \left(e_2\_im:r_2\_im\right)+\left(e_2\_im:r_2\_rel\right)+\left(e_2\_rel:r_2\_im\right)+\left(e_2\_rel:r_2\_rel\right) \end{gathered}$$

(21)

Based on the above formulae, one can infer the following:

$${ \left(h\_r\right)}_1={\left(h\_r\right)}_2$$

(22)

According to the obtained experimental results in Table 6 and the presented mathematical reasoning, the proposed model is capable of effectively handling symmetric relationships between entities.

4.5.3. Ablation Study

A set of ablation study experiments was conducted to investigate the effectiveness of each main module within the proposed ConvAMC model, with experiments conducted on the FB15k-237 and WN18RR datasets, as shown in Table 7. First, to study the role of the triple attention mechanism, it was removed during the multi-channel convolutional process (referred to as ’without TA’). Next, to explore the advantages of the multi-channel convolution in extracting multi-level information, a single-channel convolution was used instead (referred to as ’without MC’). Finally, to examine the role of the max pooling in the feature extraction process of the multi-channel convolution, the max pooling layer was removed (referred to as ’without MP’).

Table 7. Ablation study results.

ConvAMC	FB15k-237				WN18RR
	MRR	Hit@1	Hit@3	Hit@10	MRR	Hit@1	Hit@3	Hit@10
Without TA	0.388	0.294	0.423	0.573	0.423	0.459	0.496	0.534
Without MP	0.391	0.299	0.426	0.579	0.426	0.460	0.499	0.541
Without MC	0.386	0.296	0.422	0.576	0.436	0.464	0.498	0.538
Full model (with all modules)	0.414	0.320	0.459	0.602	0.438	0.470	0.514	0.559

Bold font represents the results of the full ConvAMC model.

In order to fully demonstrate the work conducted in the ablation study experiments and present the specific contributions of each module more clearly, we have modified the scoring function applicable to individual ablation study experiments, based on the original scoring function after removing (i) the triple attention mechanism, as shown in (23); (ii) the max pooling operation, as shown in (24); and (iii) the multi-channel convolution, as shown in (25):

$$\begin{gathered} without TA\left(e_h,r,e_t\right)=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(e_h,r)e_t \\ =\left(Rel\left(CM\left({e_h}_{e_t}\right)\right),Rel\left(CM\left(r\right)\right)\right)+\left(Rel\left(CM\left({e_h}_{e_t}\right)\right),Im\left(CM\left(r\right)\right)\right) \\ +\left(Im\left(CM\left(e_h\_e_t\right)\right),Rel\left(CM\left(r\right)\right)\right)-\left(Im\left(CM\left(e_h\_e_t\right)\right),Im\left(CM\left(r\right)\right)\right) \end{gathered}$$

(23)

$$\begin{gathered} without MP\left(e_h,r,e_t\right)=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(e_h,r)e_t \\ =\left(Rel\left(CT\left({e_h}_{e_t}\right)\right),Rel\left(CT\left(r\right)\right)\right)+\left(Rel\left(CT\left({e_h}_{e_t}\right)\right),Im\left(CT\left(r\right)\right)\right) \\ +\left(Im\left(CT\left(e_h\_e_t\right)\right),Rel\left(CT\left(r\right)\right)\right)-\left(Im\left(CT\left(e_h\_e_t\right)\right),Im\left(CT\left(r\right)\right)\right) \end{gathered}$$

(24)

$$\begin{gathered} without MC\left(e_h,r,e_t\right)=\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{v}(e_h,r)e_t \\ =\left(Rel\left(MT\left({e_h}_{e_t}\right)\right),Rel\left(MT\left(r\right)\right)\right)+\left(Rel\left(MT\left({e_h}_{e_t}\right)\right),Im\left(MT\left(r\right)\right)\right) \\ +\left(Im\left(MT\left(e_h\_e_t\right)\right),Rel\left(MT\left(r\right)\right)\right)-\left(Im\left(MT\left(e_h\_e_t\right)\right),Im\left(MT\left(r\right)\right)\right) \end{gathered}$$

(25)

Our ablation study experimental model is inspired by TeAST [39], which uses empirical and analytical methods to demonstrate the effectiveness of each model component. First, we removed the triple attention mechanism from the encoding module, as per (23). According to the obtained experimental results, shown in Table 7, on both datasets, the values of all four metrics decreased, indicating that our idea of using a triple attention mechanism in multi-channel convolution is correct, as it can help the model capture the interaction between spatial dimensions and input tensor channels, providing more interaction information for the feature mapping matrix of entities and relations. Next, we removed the max pooling operation from the encoding module, as per (24), whereby the values of all four metrics decreased on both datasets, which indicates that using a max pooling operation to compute the channel attention in the feature extraction process on each convolutional channel is effective, as it can significantly reduce the size of the feature tensor and extract more significant feature information from the entity- and relation exchange matrices. Finally, we removed the multi-channel convolution from the encoding module and used an ordinary single-channel convolution instead. According to the obtained experimental results, shown in Table 7, on both datasets, the values of all metrics decreased, which indicates that using a multi-channel convolution in the encoding module is effective, as it can extract interactive features of entities and relations at different levels from multiple input channels in a multi-channel manner, and then concatenate and reshape them to form a brand new mapping matrix, which has more complete semantic information, which helps the model improve its accuracy in subsequent prediction tasks.

According to the experimental results shown in Table 7, the predictive performance comparison between ’without TA’ and the full ConvAMC model demonstrates that on the WN18RR dataset, the MRR, Hit@1, Hit@3, and Hit@10 values decreased by 3.5%, 2.4%, 3.6%, and 4.7%, respectively. On the FB15k-237 dataset, the values of these metrics decreased by 6.7%, 8.8%, 8.5%, and 5.1%, respectively, indicating that introducing the triple attention mechanism in multi-channel CNNs effectively enhances link prediction performance. The comparison between ’without MP’ and the full ConvAMC model shows that on the WN18RR dataset, the MRR, Hit@1, Hit@3, and Hit@10 values decreased by 2.8%, 2.2%, 3.0%, and 3.3% respectively, whereas, on the FB15k-237 dataset, they decreased by 5.9%, 7.0%, 7.7%, and 4.0%, respectively, demonstrating that the max pooling layer added to the multi-channel convolution process enhances the extraction of local information. By comparing ’without MC’ and the full ConvAMC model, it is observed that on the WN18RR dataset, the MRR, Hit@1, Hit@3, and Hit@10 values decreased by 0.5%, 1.3%, 3.2%, and 3.9%, respectively, and on the FB15k-237 dataset, they decreased by 7.3%, 8.1%, 8.8%, and 4.5%, respectively, proving the advantages of multi-channel CNNs in extracting multi-level information.

Overall, according to the results of the ablation study experiments, it can be observed that the impact on link prediction of ConvAMC is relatively minor on the WN18RR dataset, while it is more significant on the FB15k-237 dataset. As noted in Table 2, FB15k-237 contains a greater variety and complexity of relationships with fewer entities. Therefore, it is believed that ConvAMC is better suited to handle knowledge graphs with a larger number and more complex relationships, as it can extract additional feature interactions between channels during the extraction of entity- and relation information. Moreover, compared to the single-channel convolution, the increased computational cost of the multi-channel convolution is within an acceptable range.

4.5.4. Influence of Convolutional Kernel Size

To investigate the role of the convolution kernel size in the link prediction performance of the proposed model, corresponding experiments were conducted on the FB15k-237 and WN18RR datasets, with the following kernel sizes: {2 × 2, 3 × 3, 4 × 4, 5 × 5, to 7 × 7}. The obtained MRR and Hit@10 results are depicted in Figure 3.

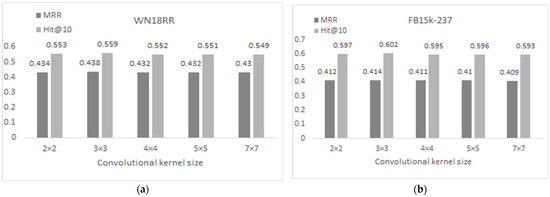
Figure 3. The influence of the convolutional kernel size on ConvAMC’s link prediction performance. (a) WN18RR results; (b) FB15k-237 results.

Overall, the size of the convolution kernel has a minimal impact on the FB15k-237 dataset, with MRR and Hit@10 varying only within a range of 1.2% and 1.5%, respectively. From Figure 3, it is evident that the 3 × 3 convolution kernel performs the best, both in terms of MRR and Hit@10. The slightly smaller 2 × 2 kernel performs better than the 4 × 4 and 5 × 5 kernels. When the kernel size increases to 7 × 7, there is a noticeable decline in both MRR and Hit@10. On the WN18RR dataset, the impact of the kernel size is slightly greater than that on FB15k-237, with both MRR and Hit@10 within a range of 1.8%. Similarly, the 3 × 3 kernel exhibits the best performance here, with the 2 × 2 kernel slightly outperforming the 4 × 4 and 5 × 5 kernels again. When the kernel size is increased to 7 × 7, there is a significant drop in both MRR and Hit@10.

When the convolution kernel is smaller than 3 × 3, the feature interaction during the multi-channel convolutional process does not extract comprehensive information. However, when the kernel size exceeds 3 × 3, the amount of information overlooked during the convolutional process increases, particularly when the kernel size reaches 7 × 7, resulting in more information loss and the greatest impact on the model performance. Accurately assessing the size of the convolution kernel ensures better capture of local interactions between embeddings, while reducing the dimensions helps avoid overfitting.

5. Conclusions and Future Work

Single-level feature interaction between entities and relations is a common approach used in most KGE models but with certain limitations. To address this issue, an attention-based multi-channel CNN model, named ConvAMC, has been introduced in this article to facilitate multi-level feature interactions between entities and relations. During the feature interaction process, the model focuses on capturing local and detailed information, thereby enriching its expressive capabilities. Notably, ConvAMC excels in performing on knowledge graph datasets containing a variety of complex relationships and also offers advantages in link prediction accuracy. The performance of the proposed model has been comprehensively evaluated on three benchmark datasets, showing that it surpasses the SOTA models across all evaluation metrics on two of these datasets. Experiments on symmetric relationship modeling have demonstrated that the proposed model is also effective in handling symmetric relationships. Additionally, the impact of convolution kernel size on the link prediction performance of the model has also been studied. In the future, we will extend and optimize the model, using large-scale knowledge graphs for inference and querying in social networks, recommendation systems, and search engines. In addition, we will construct and analyze a multimodal knowledge graph by combining other data types.

However, the proposed ConvAMC model has its own limitations. Although max pooling layers and a triple attention mechanism have been utilized to reduce the computational overhead, the multi-channel CNN design inevitably occupies considerable time and space. Therefore, the proposed model does not have an advantage in terms of training time. Additionally, while focusing more on the interaction process and acquisition of local information during the multi-channel convolutional process for entities and relations, the semantic information carried by the names of entities and relations also merits study. In future work, plans are in place to further reduce the time and space dimensions of the proposed model through other means. As the sampling of useful negative triplet training samples in link prediction tasks is equally important, the exploration of the use of the latest generative adversarial networks (GANs) to generate negative triplets will be fostered. At the same time, we are also considering expanding the functionality of the model, with the main goal of handling temporal knowledge graphs or integrating it with federated learning frameworks to increase its practicality and generalization.