Existence of Solutions for a Viscoelastic Plate Equation with Variable Exponents and a General Source Term

Abstract

The subject of this study is a nonlinear viscoelastic plate equation with variable exponents and a general source term. Through the application of the Faedo–Galerkin approximation method and a fixed point theorem under appropriate assumptions, we proved the existence of weak solutions.

1. Introduction

In this study, we consider the following nonlinear viscoelastic plate problem

$$\left\{\begin{array}{cc}{\mathcal{Y}}_{\tau \tau }+{\Delta }^2\mathcal{Y}-{\int }_0^{\tau }k\left(\tau -a\right){\Delta }^2\mathcal{Y}\left(a\right)da+{\left|{\mathcal{Y}}_{\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{\tau }=g(x,\mathcal{Y}),\hfill & \mathrm{in}\mathcal{D}\times \left(0,S\right),\hfill \\ \mathcal{Y}\left(x,\tau \right)={\displaystyle \frac{\partial }{\partial x}}\mathcal{Y}\left(x,\tau \right)=0,\hfill & \mathrm{on}\partial \mathcal{D}\times \left(0,S\right),\hfill \\ \mathcal{Y}\left(x,0\right)={\mathcal{Y}}_0\left(x\right),{\mathcal{Y}}_{\tau }\left(x,0\right)={\mathcal{Y}}_1\left(x\right)\hfill & \mathrm{in}x\in \mathcal{D},\hfill \end{array}\right.$$

(1)

where $\mathcal{D}$ is a bounded domain in ${\mathbb{R}}^d$ with $d\ge 2$, and $\partial \mathcal{D}$ is a smooth boundary.

$S>0$ is small enough and will be determined later.

Firstly, we make some assumptions about the functions $g:\mathcal{D}\times \mathbb{R}\to \mathbb{R}$ and p:

$$g(x,\mathcal{Y})\le {\left|\mathcal{Y}\right|}^{q-2}\mathcal{Y},\forall (x,\mathcal{Y})\in \mathcal{D}\times \mathbb{R},$$

(2)

and

$$2\le p_1=ess\underset{x\in \mathcal{D}}{inf}p\left(x\right)\le q\le ess\underset{x\in \mathcal{D}}{sup}p\left(x\right)=p_2\le {\displaystyle \frac{2d}{d-4}},d\ge 5.$$

(3)

Also, we insert the Log-Hölder continuity condition

$$\left|p\left(\alpha \right)-p\left(\beta \right)\right|\le -{\displaystyle \frac{A}{ln\left|\alpha -\beta \right|}},$$

(4)

for all $\alpha ,\beta \in \Omega$, where $A>0$ and $0<\eta <1$ with $\left|\alpha -\beta \right|<\eta .$

Variable exponent PDEs are present in different fields of science such as elasticity theory, nonlinear electrorheological fluids, image processing, and filtration processes in porous media [1,2,3,4,5,6,7].

Hamadouche [8] studied the local existence and blow-up of solutions to the Petrovsky problem

$${\mathcal{Y}}_{\tau \tau }+{\Delta }^2\mathcal{Y}+{\left|{\mathcal{Y}}_{\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{\tau }={\left|\mathcal{Y}\right|}^{q-2}\mathcal{Y},$$

with no viscoelastic term, i.e., ($k\equiv 0$).

A variable exponent nonlinear viscoelastic problem was invesitigated by Al-Mahdi et al. In [9]

$${\mathcal{Y}}_{\tau \tau }+{\Delta }^2\mathcal{Y}-{\int }_0^{\tau }k\left(\tau -a\right)\Delta \mathcal{Y}\left(a\right)da+{\left|{\mathcal{Y}}_{\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{\tau }-\Delta {\mathcal{Y}}_{\tau }=0,$$

they also provided some stability results.

Park and Kang in [10] and Piskin in [11] considered a similar problem involving a variable exponent in the second term, using the following equation

$${\mathcal{Y}}_{\tau \tau }-\Delta \mathcal{Y}+{\int }_0^{\tau }k\left(\tau -a\right)\Delta \mathcal{Y}\left(a\right)da+a{\left|{\mathcal{Y}}_{\tau }\right|}^{m\left(x\right)-2}{\mathcal{Y}}_{\tau }=b{\left|\mathcal{Y}\right|}^{p\left(x\right)-2}\mathcal{Y},$$

and proved results on the existence and blow up of solutions.

The aim of this paper is to prove the local existence of weak solutions for problem (1), which can be seen as a generalization of many previously cited nonlinear viscoelastic problems. To achieve this, we used the Faedo–Galerkin approximation method and a fixed point theorem.

Before stating our main result, let us recall some necessary preliminaries.

2. Preliminaries

In this section, we present fundamental concepts related to variable exponent Lebesgue and Sobolev spaces ([5,12,13,14]). Moreover, we will provide crucial assumptions and lemmas.

Let $\mathcal{D}$ be a domain in ${\mathbb{R}}^d$, let and $p:\mathcal{D}\to \left[1,\infty \right]$ be a measurable function. The variable exponent Lebesgue space is defined by

$$L^{p\left(x\right)}\left(\mathcal{D}\right)=\left\{\mathcal{Y}:\mathcal{D}⟶\mathbb{R};\mathcal{Y}\mathit{measurable}\mathit{in}\mathcal{D}:{\rho }_{p\left(·\right)}\left(\nu \mathcal{Y}\right)<\infty ,\mathit{for}\mathit{some}\nu >0\right\},$$

where

$${\rho }_{p\left(·\right)}\left(\mathcal{Y}\right)={\int }_{\mathcal{D}}{\left|\mathcal{Y}\left(x\right)\right|}^{p\left(x\right)}dx.$$

This is a Banach space equipped with the Luxembourg-type norm

$${∥\mathcal{Y}∥}_{p\left(·\right)}=inf\left\{\nu >0:{\int }_{\mathcal{D}}{\left|{\displaystyle \frac{\mathcal{Y}\left(x\right)}{\nu }}\right|}^{p\left(x\right)}dx\le 1\right\}.$$

We also consider the following variable exponent Sobolev space

$$W^{2,p\left(x\right)}\left(\mathcal{D}\right)=\left\{\mathcal{Y}\in L^{p\left(x\right)}\left(\mathcal{D}\right)\mathrm{such}\mathrm{that}\Delta \mathcal{Y}\mathrm{exist}\mathrm{and}\left|\Delta \mathcal{Y}\right|\in L^{p\left(x\right)}\left(\mathcal{D}\right)\right\}.$$

In the following lemmas, we assume that p is a measurable function on $\mathcal{D}$ satisfying (3).

Lemma 1

([5]). A positive constant B exists, veifying

$${∥\mathcal{Y}∥}_{p\left(·\right)}\le B{∥\Delta \mathcal{Y}∥}_2,\forall \mathcal{Y}\in H_0^2\left(\mathcal{D}\right).$$

i.e., the embedding $H_0^2\left(\mathcal{D}\right)\hookrightarrow L^p\left(\mathcal{D}\right)$ is compact and continuous.

In paticular, the embedding $H_0^2\left(\mathcal{D}\right)\hookrightarrow L^q\left(\mathcal{D}\right)$ is also compact and continuous.

Lemma 2

([5]). For almost every $x\in$$\mathcal{D}$, we have

$${∥\mathcal{Y}∥}_{p\left(·\right)}\le 1\iff {\rho }_{p\left(·\right)}\left(\mathcal{Y}\right)\le 1$$

$$min\left\{{∥\mathcal{Y}∥}_{p\left(·\right)}^{p_1},{∥\mathcal{Y}∥}_{p\left(·\right)}^{p_2}\right\}\le {\rho }_{p\left(·\right)}\left(\mathcal{Y}\right)\le max\left\{{∥\mathcal{Y}∥}_{p\left(·\right)}^{p_1},{∥\mathcal{Y}∥}_{p\left(·\right)}^{p_2}\right\},$$

for all $\mathcal{Y}\in L^{p\left(·\right)}\left(\mathcal{D}\right).$

Now, we suggest these assumptions about k:

(H1)

$k:\left[0,\infty \right)\to \left(0,\infty \right)$ is a non-increasing function of class $C^1\left({\mathbb{R}}^{+}\right)$ satisfying

$$k\left(0\right)>0,1-{\int }_0^{\infty }k\left(a\right)da=l>0,$$

(5)

(H2)

$${\int }_0^{\infty }k\left(a\right)da<{\displaystyle \frac{\frac{p_1}{2}-1}{\frac{p_1}{2}-1+\frac{1}{2p_1}}}.$$

(6)

Some calculations lead to

$$\begin{array}{ccc}\hfill {\int }_0^{\tau }k\left(\tau -a\right)\left(\Delta \mathcal{Y}\left(a\right),\Delta {\mathcal{Y}}_{\tau }\left(\tau \right)\right)da& =& -{\displaystyle \frac{1}{2}}k\left(\tau \right){∥\Delta \mathcal{Y}\left(\tau \right)∥}^2+{\displaystyle \frac{1}{2}}\left(k^{\prime }\circ \Delta \mathcal{Y}\right)\left(\tau \right)\hfill \\ & & -{\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{d\tau }}\left[\left(k\circ \Delta \mathcal{Y}\right)\left(\tau \right)-\left({\int }_0^{\tau }k\left(a\right)da\right){∥\Delta \mathcal{Y}\left(\tau \right)∥}^2\right],\hfill \end{array}$$

where

$$\left(k\circ \Delta \mathcal{Y}\right)\left(\tau \right)={\int }_0^{\tau }k\left(\tau -a\right){∥\Delta \mathcal{Y}\left(\tau \right)-\Delta \mathcal{Y}\left(a\right)∥}^{2}da.$$

Lemma 3

([15]). Assuming that $\Psi \in C^2\left(\left[0,S\right]\right)$ with

$$\begin{array}{ccc}\hfill \Psi {\Psi }_{\tau \tau }-\omega {\Psi }_{\tau }^2+\delta \Psi {\Psi }_{\tau }+\gamma \Psi & \ge & 0,\omega >1,\gamma \ge 0,\delta \ge 0,\hfill \\ \hfill \Psi \left(\tau \right)& \ge & 0,\Psi \left(0\right)>0,\hfill \end{array}$$

(7)

and

$${\Psi }_{\tau }\left(0\right)>{\displaystyle \frac{\delta }{\omega -1}}\Psi \left(0\right),{\left({\Psi }_{\tau }\left(0\right)-{\displaystyle \frac{\delta }{\omega -1}}\Psi \left(0\right)\right)}^2>{\displaystyle \frac{2\gamma }{2\omega -1}}\Psi \left(0\right).$$

Then,

$$\underset{\tau \to S}{lim}sup\Psi \left(\tau \right)=+\infty ,$$

where

$$S\le {\displaystyle \frac{{\Psi }^{1-\omega }\left(0\right)}{A_1}},A_1^2={\left(\omega -1\right)}^2{\Psi }^{-2\omega }\left(0\right)\left[{\left({\Psi }_{\tau }\left(0\right)-{\displaystyle \frac{\delta }{\omega -1}}\Psi \left(0\right)\right)}^2-{\displaystyle \frac{2\gamma }{2\omega -1}}\Psi \left(0\right)\right].$$

Furthermore, $\Psi \left(\tau \right)$ satisfies

$$\Psi \left(\tau \right)\ge {\displaystyle \frac{e_1^{\frac{\delta \tau }{\omega -1}}}{{\left[{\Psi }^{1-\omega }\left(0\right)-A_1\tau \right]}^{\frac{1}{\omega -1}}}}.$$

3. Existence of Local Solution

In this section, we examine the local existence result for problem (1), which can be acquired throught the Faedo–Galerkin approximation technique. Presently, we investigate the fourth-order initial-boundary value problem as follows:

$$\left\{\begin{array}{cc}{\mathcal{Y}}_{\tau \tau }+{\Delta }^2\mathcal{Y}-{\int }_0^{\tau }k\left(\tau -a\right){\Delta }^2\mathcal{Y}\left(a\right)da+{\left|{\mathcal{Y}}_{\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{\tau }=\dot{h}\left(x,\tau \right),\hfill & \mathrm{in}\mathcal{D}\times \left(0,S\right),\hfill \\ \mathcal{Y}\left(x,\tau \right)={\displaystyle \frac{\partial }{\partial \mathcal{V}}}\mathcal{Y}\left(x,\tau \right)=0,\hfill & \mathrm{on}\partial \mathcal{D}\times \left(0,S\right),\hfill \\ \mathcal{Y}\left(x,0\right)={\mathcal{Y}}_0\left(x\right),{\mathcal{Y}}_{\tau }\left(x,0\right)={\mathcal{Y}}_1\left(x\right),\hfill & \mathrm{with}x\in \mathcal{D}.\hfill \end{array}\right.$$

(8)

Theorem 1.

Let $\dot{h}$$\in L^2\left(\mathcal{D}\times \left(0,S\right)\right)$. Suppose that the exponent $p\left(x\right)$ and the function k from the above problem (8) satisfy assumptions (3), (4), and (5). Then, for any inatial data $\left({\mathcal{Y}}_0,{\mathcal{Y}}_1\right)\in H_0^2\left(\mathcal{D}\right)\times$$L^2\left(\mathcal{D}\right)$, problem, (8) admits a unique local solution for some $S>0$,

$$\mathcal{Y}\in L^{\infty }\left(\left(0,S\right);H_0^2\left(\mathcal{D}\right)\right),{\mathcal{Y}}_{\tau }\in L^{\infty }\left(\left(0,S\right);L^2\left(\mathcal{D}\right)\right)\cap L^{p\left(·\right)}\left(\mathcal{D}\times \left(0,S\right)\right).$$

Proof. 

Existence: We begin this proof by introducing the finite-dimensional subspace ${\mathcal{V}}_{\dot{m}}=span\left\{{\mathcal{V}}_1,\dots ,{\mathcal{V}}_{\dot{m}}\right\}$, where ${\left\{{\mathcal{V}}_i\right\}}_{i=1}^{\infty }$ is an orthonormal basis of $H_0^2\left(\mathcal{D}\right)$, i.e.,

$$\left\{\begin{array}{c}{\Delta }^2{\mathcal{V}}_i={\nu }_i{\mathcal{V}}_i\mathrm{in}\mathcal{D},\hfill \\ {\mathcal{V}}_i=0\mathrm{on}\partial \mathcal{D}.\hfill \end{array}\right.$$

Through normalization, we obtain $∥{\mathcal{V}}_i∥=1,$ and for any given integer $\dot{m},$ we investigate the approximate problem

$${\mathcal{Y}}^{\dot{m}}\left(x,\tau \right)=\sum _{i=1}^{\dot{m}}{c}_i\left(\tau \right){\mathcal{V}}_i.$$

$$\left\{\begin{array}{c}{\int }_{\mathcal{D}}{\mathcal{Y}}_{\tau \tau }^{\dot{m}}\left(x,\tau \right){\mathcal{V}}_i\left(x\right)dx+{\int }_{\mathcal{D}}\Delta {\mathcal{Y}}^{\dot{m}}\left(x,\tau \right)\Delta {\mathcal{V}}_i\left(x\right)dx\hfill \\ -{\int }_{\mathcal{D}}{\int }_0^{\tau }k\left(\tau -\sigma \right)\Delta {\mathcal{Y}}^{\dot{m}}\left(x,\sigma \right)\Delta {\mathcal{V}}_i^{\dot{m}}\left(x\right)d\sigma dx\hfill \\ +{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }^{\dot{m}}\left(x,\tau \right)\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{\tau }^{\dot{m}}\left(x,\tau \right){\mathcal{V}}_i\left(x\right)dx={\int }_{\mathcal{D}}\dot{h}\left(x,\tau \right){\mathcal{V}}_i\left(x\right)dx,\hfill \\ \begin{array}{ccc}{\mathcal{Y}}^{\dot{m}}\left(x,0\right)={\mathcal{Y}}_0^{\dot{m}},& {\mathcal{Y}}_{\tau }^{\dot{m}}\left(x,0\right)={\mathcal{Y}}_1^{\dot{m}}& \forall i=1,...,\dot{m},\end{array}\hfill \end{array}\right.$$

(9)

where ${\mathcal{Y}}_0^{\dot{m}}={\sum }_{i=0}^{\dot{m}}\left({\mathcal{Y}}_0,{\mathcal{V}}_i\right){\mathcal{V}}_i$ and ${\mathcal{Y}}_1^{\dot{m}}={\sum }_{i=0}^{\dot{m}}\left({\mathcal{Y}}_1,{\mathcal{V}}_i\right){\mathcal{V}}_i$ are both sequences in $H_0^2\left(\mathcal{D}\right)$ and $L^2\left(\mathcal{D}\right),$ respectively,

$${\mathcal{Y}}_0^{\dot{m}}\to {\mathcal{Y}}_0\mathrm{in}{H}_0^2\left(\mathcal{D}\right)\mathrm{and}{\mathcal{Y}}_1^{\dot{m}}\to {\mathcal{Y}}_1\mathrm{in}{L}^2\left(\mathcal{D}\right).$$

As we obtained a system of ordinary differential equations, we can justify the local existence of solutions to the problem (9) uisnfg the Picard–Lindelof theorem. This solution exists localy in interval $\left[0,{\tau }_{\dot{m}}\right)$ with $0<{\tau }_{\dot{m}}<S$ for all $S>0$. Then, we show that it can be extended to $\left[0,S\right]$ for any given $S>0$.

Multiplying (9) by $c_i^{\prime }\left(\tau \right)$ and sum over i, we obtain

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{d\tau }}\left[{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }^{\dot{m}}\left(\tau \right)\right|}^{2}dx+\left(1-{\int }_0^{\tau }k\left(a\right)da\right){\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}^{\dot{m}}\left(\tau \right)\right|}^{2}dx+\left(ko\Delta {\mathcal{Y}}^{\dot{m}}\right)\left(\tau \right)\right]\hfill \\ & & +{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }^{\dot{m}}\left(x,\tau \right)\right|}^{p\left(x\right)}dx\hfill \\ & =& {\displaystyle \frac{1}{2}}\left(k^{\prime }o\Delta {\mathcal{Y}}^{\dot{m}}\right)\left(\tau \right)-{\displaystyle \frac{1}{2}}k\left(\tau \right){\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}^{\dot{m}}\left(\tau \right)\right|}^{2}dx+{\int }_{\mathcal{D}}\dot{h}\left(x,\tau \right){\mathcal{Y}}_{\tau }^{\dot{m}}\left(x,\tau \right)dx,\hfill \end{array}$$

an integration over $\left(0,\tau \right)$ leads to

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{2}}\left[{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }^{\dot{m}}\left(\tau \right)\right|}^{2}dx+\left(1-{\int }_0^{\tau }k\left(a\right)da\right){\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}^{\dot{m}}\left(\tau \right)\right|}^{2}dx+\left(ko\Delta {\mathcal{Y}}^{\dot{m}}\right)\left(\tau \right)\right]\hfill \\ & & +{\int }_0^{\tau }{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }^{\dot{m}}\left(x,a\right)\right|}^{p\left(x\right)}dxda\hfill \\ & \le & {\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_1^{\dot{m}}\right|}^{2}dx+{\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}_1^{\dot{m}}\right|}^{2}dx+{\int }_0^{\tau }{\int }_{\mathcal{D}}\dot{h}\left(x,a\right){\mathcal{Y}}_{\tau }^{\dot{m}}\left(x,a\right)dxda\hfill \\ & \le & {\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_1^{\dot{m}}\right|}^{2}dx+{\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}_1^{\dot{m}}\right|}^{2}dx+{\displaystyle \frac{1}{4}}{\int }_0^{\tau }{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }^{\dot{m}}\left(x,a\right)\right|}^{2}dxd\sigma +{\int }_0^S{\int }_{\mathcal{D}}{\left|\dot{h}\left(x,a\right)\right|}^{2}dxda\hfill \\ & \le & C_1+{\displaystyle \frac{1}{4}}\underset{\left(0,{\tau }_{\dot{m}}\right)}{sup}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }^{\dot{m}}\left(x,\tau \right)\right|}^{2}dx,\forall \tau \in \left[0,{\tau }_{\dot{m}}\right).\hfill \end{array}$$

So, we obtain

$$\underset{\left(0,{\tau }_{\dot{m}}\right)}{sup}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }^{\dot{m}}\left(\tau \right)\right|}^{2}dx+\underset{\left(0,{\tau }_{\dot{m}}\right)}{sup}l{\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}^{\dot{m}}\left(\tau \right)\right|}^{2}dx+{\int }_0^{\tau }{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }^{\dot{m}}\left(x,a\right)\right|}^{p\left(x\right)}dxda\le C_1.$$

Therefore, the solution can be extended to $\left[0,S\right)$, indeed

$$\left\{\begin{array}{c}\left({\mathcal{Y}}^{\dot{m}}\right)\mathrm{is}\mathrm{a}\mathrm{bounded}\mathrm{sequence}\mathrm{in}{L}^{\infty }\left(\left(0,S\right);H_0^2\left(\mathcal{D}\right)\right),\hfill \\ \left({\mathcal{Y}}_{\tau }^{\dot{m}}\right)\mathrm{is}\mathrm{a}\mathrm{bounded}\mathrm{sequence}\mathrm{in}{L}^{\infty }\left(\left(0,S\right);L^2\left(\mathcal{D}\right)\right)\cap L^{p\left(·\right)}\left(\mathcal{D}\times \left(0,S\right)\right).\hfill \end{array}\right.$$

So, we can extract $\left({\mathcal{Y}}^{\dot{k}}\right)$ from $\left({\mathcal{Y}}^{\dot{m}}\right)$ such that

$$\left\{\begin{array}{c}{\mathcal{Y}}^{\dot{k}}\to \mathcal{Y}\mathrm{weak}\mathrm{star}\mathrm{in}{L}^{\infty }\left(\left(0,S\right);H_0^2\left(\mathcal{D}\right)\right),\hfill \\ {\mathcal{Y}}_{\tau }^{\dot{k}}\to \mathcal{Y}\mathrm{weak}\mathrm{star}\mathrm{in}{L}^{\infty }\left(\left(0,S\right);N^2\left(\mathcal{D}\right)\right)\mathrm{and}\mathrm{weakly}\mathrm{in}{L}^{p\left(·\right)}\left(\mathcal{D}\times \left(0,S\right)\right).\hfill \end{array}\right.$$

As stated by Lions lemma (see [16]), we obtain that $\mathcal{Y}\in C\left(\right[0,S]$; $L^2\left(\mathcal{D}\right))$. As $\left({\mathcal{Y}}_{\tau }^{\dot{k}}\right)$ is bounded in $L^{p\left(·\right)}\left(\mathcal{D}\times \left(0,S\right)\right)$, then

$${\left|{\mathcal{Y}}_{\tau }^{\dot{k}}\right|}^{p\left(·\right)-2}{\mathcal{Y}}_{\tau }^{\dot{k}}\mathrm{is}\mathrm{bounded}\mathrm{in}{L}^{{\displaystyle \frac{p\left(·\right)}{p\left(·\right)-1}}}\left(\mathcal{D}\times \left(0,S\right)\right).$$

Then, just like in Messaoudi et al. [17], we conclude

$${\left|{\mathcal{Y}}_{\tau }^{\dot{k}}\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{\tau }^{\dot{k}}\to {\left|{\mathcal{Y}}_{\tau }\right|}^{p\left(·\right)-2}{\mathcal{Y}}_{\tau }\mathrm{weakly}\mathrm{in}{L}^{{\displaystyle \frac{p\left(·\right)}{p\left(·\right)-1}}}\left(\mathcal{D}\times \left(0,S\right)\right).$$

Hence, $\forall \mathcal{V}\in L^{p\left(·\right)}\left(\left(0,S\right)\times H_0^2\left(\mathcal{D}\right)\right),$

$${\int }_{\mathcal{D}}\left[{\mathcal{Y}}_{\tau \tau }\mathcal{V}+\Delta \mathcal{Y}\Delta \mathcal{V}-{\int }_0^{\tau }k\left(\tau -\sigma \right)\Delta \mathcal{Y}\left(a\right)\Delta \mathcal{V}da+{\left|{\mathcal{Y}}_{\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{\tau }\mathcal{V}\right]dx={\int }_{\mathcal{D}}\dot{h}\left(x,\tau \right)\mathcal{V}dx$$

which provides

$${\mathcal{Y}}_{\tau \tau }+{\Delta }^2\mathcal{Y}-{\int }_0^{\tau }k\left(\tau -a\right){\Delta }^2\mathcal{Y}\left(a\right)da+{\left|{\mathcal{Y}}_{\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{\tau }=\dot{h}\left(x,\tau \right).$$

Uniqueness: Suppose that (8) admits two solutions $\mathcal{Y}$ and $\dot{z}.$ Then, $\dot{w}=\mathcal{Y}-\dot{z}$ satisfies

$$\left\{\begin{array}{cc}{\dot{w}}_{\tau \tau }+{\Delta }^2\dot{w}-{\int }_0^{\tau }k\left(\tau -a\right){\Delta }^2\dot{w}\left(a\right)da+{\left|{\dot{w}}_{\tau }\right|}^{p\left(x\right)-2}{\dot{w}}_{\tau }=0\hfill & \mathrm{in}\mathcal{D}\times \left(0,S\right),\hfill \\ \dot{w}\left(x,\tau \right)={\displaystyle \frac{\partial }{\partial \mathcal{V}}}\dot{w}\left(x,\tau \right)=0\hfill & \mathrm{on}\partial \mathcal{D}\times \left(0,S\right),\hfill \\ \dot{w}\left(x,0\right)=0,{\dot{w}}_{\tau }\left(x,0\right)=0\hfill & x\in \mathcal{D},\hfill \end{array}\right.$$

After multiplication by ${\dot{w}}_{\tau }$ and integration over $\mathcal{D},$ we obtain

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{2}}{\displaystyle \frac{d}{d\tau }}\left[{\int }_{\mathcal{D}}{\left|{\dot{w}}_{\tau }\left(\tau \right)\right|}^{2}dx+\left(1-{\int }_0^{\tau }k\left(a\right)da\right){\int }_{\mathcal{D}}{\left|\Delta \dot{w}\left(\tau \right)\right|}^{2}dx+\left(ko\Delta \dot{w}\right)\left(\tau \right)\right]\hfill \\ & & +{\displaystyle \frac{1}{2}}k\left(\tau \right){\int }_{\mathcal{D}}{\left|\Delta \dot{w}\left(\tau \right)\right|}^{2}dx\hfill \\ & =& -{\int }_{\mathcal{D}}\left({\left|{\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{p\left(x\right)}-{\left|{\dot{z}}_{\tau }\left(\tau \right)\right|}^{p\left(x\right)}\right)\left({\mathcal{Y}}_{\tau }\left(\tau \right)-{\dot{z}}_{\tau }\left(\tau \right)\right)dx+{\displaystyle \frac{1}{2}}\left(k^{\prime }\circ \Delta \mathcal{Y}\right)\left(\tau \right).\hfill \end{array}$$

Then, from inequality

$$\left({\left|a\right|}^{p\left(x\right)-2}a-{\left|b\right|}^{p\left(x\right)-2}b\right)\left(a-b\right)\ge 0,$$

(10)

∀$a,b$$\in {\mathbb{R}}^d$ and almost every x $\in \mathcal{D}$, we get

$${\int }_{\mathcal{D}}{\left|{\dot{w}}_{\tau }\left(\tau \right)\right|}^{2}dx+l{\int }_{\mathcal{D}}{\left|\Delta {\dot{w}}_{\tau }\left(\tau \right)\right|}^{2}dx=0,$$

Therefore $\dot{w}=0$, since $\dot{w}=0$ on $\partial \mathcal{D}.$ □

Theorem 2.

Consider any initial data $\left({\mathcal{Y}}_0,{\mathcal{Y}}_1\right)\in H_0^2$$\left(\mathcal{D}\right)\times L^2\left(\mathcal{D}\right)$ and assume that condition (5) is satisfied, with $p\left(x\right),q$ verify (3), (4), where

$$2<q<{\displaystyle \frac{2\left(d-2\right)}{d-4}},d\ge 5.$$

(11)

There exists $S>0$, such that problem (1) on the interval $\left(0,S\right)$ admits a local solution

$$\mathcal{Y}\in C\left(\left[0,S\right];H_0^2\left(\mathcal{D}\right)\right),{\mathcal{Y}}_{\tau }\in C\left(\left[0,S\right];L^2\left(\mathcal{D}\right)\right)\cap L^{p\left(x\right)}\left(\mathcal{D}\times \left(0,S\right)\right).$$

Proof. 

Let $\mathcal{V}\in L^{\infty }\left(\left(0,S\right);H_0^2\left(\mathcal{D}\right)\right)$ and $2\left(q-1\right)\le {\displaystyle \frac{2d}{d-4}},$ then from (2)

$${∥g\left(x,\mathcal{V}\right)∥}^2\le {\int }_{\mathcal{D}}{\left|\mathcal{V}\right|}^{2\left(q-1\right)}dx<\infty ,$$

so,

$$g\left(x,\mathcal{V}\right)\in L^2\left(\mathcal{D}\times \left(0,S\right)\right).$$

Using Theorem 5, for evey $\mathcal{V}\in L^{\infty }\left(\left(0,S\right);H_0^2\left(\mathcal{D}\right)\right)$, there exists a unique

$$\mathcal{Y}\in L^{\infty }\left(\left(0,S\right);H_0^2\left(\mathcal{D}\right)\right),{\mathcal{Y}}_{\tau }\in L^{\infty }\left(\left(0,S\right);L^2\left(\mathcal{D}\right)\right)\cap L^{p\left(x\right)}\left(\mathcal{D}\times \left(0,S\right)\right),$$

that veifies

$$\left\{\begin{array}{cc}{\mathcal{Y}}_{\tau \tau }+{\Delta }^2\mathcal{Y}-{\int }_0^{\tau }k\left(\tau -a\right){\Delta }^2\mathcal{Y}\left(a\right)da+{\left|{\mathcal{Y}}_{\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{\tau }=g\left(x,\mathcal{V}\right),\hfill & \mathrm{in}\mathcal{D}\times \left(0,S\right),\hfill \\ \mathcal{Y}\left(x,\tau \right)={\displaystyle \frac{\partial }{\partial \mathcal{V}}}\mathcal{Y}\left(x,\tau \right)=0,\hfill & \mathrm{on}\partial \mathcal{D}\times \left(0,S\right),\hfill \\ \mathcal{Y}\left(x,0\right)={\mathcal{Y}}_0\left(x\right),{\mathcal{Y}}_{\tau }\left(x,0\right)={\mathcal{Y}}_1\left(x\right),\hfill & \mathrm{in}x\in \mathcal{D}.\hfill \end{array}\right.$$

(12)

Let us define the following map $\mathcal{F}:{\mathcal{A}}_S\to {\mathcal{A}}_S$ by $\mathcal{F}\left(\mathcal{V}\right)=\mathcal{Y},$ where

$${\mathcal{A}}_S=C\left(\left[0,S\right];H_0^2\left(\mathcal{D}\right)\right)\cap C^2\left(\left[0,S\right];L^2\left(\mathcal{D}\right)\right),$$

we associate to this space the following norm

$${∥\dot{w}∥}_{{\mathcal{A}}_S}^2=\underset{0\le \tau \le S}{max}\left\{{\int }_{\mathcal{D}}{\left|{\dot{w}}_{\tau }\left(\tau \right)\right|}^{2}dx+{\int }_{\mathcal{D}}l{\left|\Delta {\dot{w}}_{\tau }\left(\tau \right)\right|}^{2}dx\right\}.$$

a multiplication by ${\mathcal{Y}}_{\tau }$ in (12), then, an integration over the domain $\mathcal{D}\times \left(0,\tau \right),$ leads to

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{2}dx+{\displaystyle \frac{1}{2}}\left(1-{\int }_0^{\tau }k\left(a\right)da\right){\int }_{\mathcal{D}}{\left|\Delta \mathcal{Y}\left(\tau \right)\right|}^{2}dx\hfill \\ & & +{\displaystyle \frac{1}{2}}\left(k\circ \Delta \mathcal{Y}\right)\left(\tau \right)-{\displaystyle \frac{1}{2}}{\int }_0^{\tau }\left(k^{\prime }\circ \Delta \mathcal{Y}\right)\left(a\right)da\hfill \\ & & +{\displaystyle \frac{1}{2}}{\int }_0^{\tau }k\left(a\right){\int }_{\mathcal{D}}{\left|\Delta \mathcal{Y}\left(a\right)\right|}^{2}dxda+{\int }_0^{\tau }{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(a\right)\right|}^{p\left(x\right)}dxda\hfill \\ & =& {\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\mathcal{Y}}_1^{2}dx+{\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}_0\right|}^{2}dx+{\int }_0^{\tau }{\int }_{\mathcal{D}}g\left(x,\mathcal{V}\right){\mathcal{Y}}_{\tau }\left(a\right)dxda.\hfill \end{array}$$

(13)

From the Sobolev embedding $H_0^2\left(\mathcal{D}\right)\hookrightarrow L^{{\displaystyle \frac{2d}{d-4}}}\left(\mathcal{D}\right)$ and a Young’s inequality, we obtain

$$\begin{array}{ccc}\hfill \left|{\int }_{\mathcal{D}}g\left(x,\mathcal{V}\right){\mathcal{Y}}_{\tau }\left(a\right)dx\right|& \le & {\displaystyle \frac{\xi }{4}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(a\right)\right|}^{2}dx+{\displaystyle \frac{1}{\xi }}{\int }_{\mathcal{D}}{\left|\mathcal{V}\right|}^{2\left(q-1\right)}dx\hfill \\ & \le & {\displaystyle \frac{\xi }{4}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(a\right)\right|}^{2}dx+{\displaystyle \frac{c_{\xi }}{\xi }}\left[{∥\Delta \mathcal{V}∥}^{2\left(q-1\right)}\right],\hfill \end{array}$$

(14)

where $c_{\xi }$ is the embedding constant. From (5), we obtain

$${\displaystyle \frac{1}{2}}\left(k\circ \Delta \mathcal{Y}\right)\left(a\right)-{\displaystyle \frac{1}{2}}{\int }_0^{\tau }\left(k^{\prime }\circ \Delta \mathcal{Y}\right)\left(a\right)da+{\displaystyle \frac{1}{2}}{\int }_0^{\tau }k\left(a\right){\int }_{\mathcal{D}}{\left|\Delta \mathcal{Y}\left(a\right)\right|}^{2}dxda\ge 0.$$

(15)

Combining (13)–(15), we obtain

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{2}dx+{\displaystyle \frac{l}{2}}{\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{2}dx+{\int }_0^{\tau }{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(a\right)\right|}^{p\left(x\right)}dxda\hfill \\ & \le & {\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\mathcal{Y}}_1^{2}dx+{\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}_0\right|}^{2}dx\hfill \\ & & +{\displaystyle \frac{\xi S}{4}}\underset{\left(0,S\right)}{sup}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{2}dx+{\displaystyle \frac{c_{\xi }}{\xi }}\left[{\int }_0^S{∥\Delta \mathcal{V}∥}^{2\left(q-1\right)}da\right],\hfill \end{array}$$

which yields

$$\begin{array}{ccc}& & {\displaystyle \frac{1}{2}}\underset{\left(0,S\right)}{sup}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{2}dx+{\displaystyle \frac{l}{2}}{\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{2}dx+{\int }_0^{\tau }{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(a\right)\right|}^{p\left(x\right)}dxda\hfill \\ & \le & {\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\mathcal{Y}}_1^{2}dx+{\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}_0\right|}^{2}dx+{\displaystyle \frac{\xi S}{4}}\underset{\left(0,S\right)}{sup}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{2}dx\hfill \\ & & +{\displaystyle \frac{c_{\xi }S}{\xi l}}\left[{∥\Delta \mathcal{V}∥}_{{\mathcal{A}}_S}^{2\left(q-1\right)}\right].\hfill \end{array}$$

Taking $\xi$, such that $\xi S=1$, we obtain

$$\begin{array}{ccc}\hfill {∥\mathcal{Y}∥}_{{\mathcal{A}}_S}^2& \le & 2{\int }_{\mathcal{D}}{\mathcal{Y}}_1^{2}dx+2{\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}_0\right|}^{2}dx+{\displaystyle \frac{1}{4}}\underset{\left(0,S\right)}{sup}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{2}dx\hfill \\ & & +c_{0}S\left[{∥\Delta \mathcal{V}∥}_{{\mathcal{A}}_S}^{2\left(q-1\right)}\right],\hfill \end{array}$$

where $c_0={\displaystyle \frac{4c_{\xi }}{\xi }}.$ We assume that ${∥\Delta \mathcal{V}∥}_{{\mathcal{A}}_S}\le T$ for $T>0$ and $S>0.$ By ensuring T is large enough to verify

$$2{\int }_{\mathcal{D}}{\mathcal{Y}}_1^{2}dx+2{\int }_{\mathcal{D}}{\left|\Delta {\mathcal{Y}}_0\right|}^{2}dx\le {\displaystyle \frac{T^2}{4}},$$

and S is small enough so that

$$S\le {\displaystyle \frac{1}{2c_0{T}^{2q-4}}},$$

we have

$${∥\mathcal{Y}∥}_{{\mathcal{A}}_S}^2\le T^2.$$

Now, consider $\mathcal{F}:\mathcal{G}\left(Q,S\right)\to \mathcal{G}\left(Q,S\right)$, where $\mathcal{G}\left(Q,S\right)=$$\left\{\begin{array}{c}\dot{w}\in C\left(\left[0,S\right];H_0^2\left(\mathcal{D}\right)\right),{\dot{w}}_{\tau }\in C\left(\left[0,S\right];L^2\left(\mathcal{D}\right)\right)\\ \mathrm{such}\mathrm{that}{∥\dot{w}∥}_{{\mathcal{A}}_S}\le T\end{array}\right\}$.

Let us prove that it is a contraction.

So, for $\mathcal{F}\left({\mathcal{V}}_1\right)={\mathcal{Y}}_1$ and $\mathcal{F}\left({\mathcal{V}}_2\right)={\mathcal{Y}}_2$ with $\mathcal{Y}={\mathcal{Y}}_1-{\mathcal{Y}}_2$, then $\mathcal{Y}$ satisfies

$$\left\{\begin{array}{cc}\begin{array}{c}{\mathcal{Y}}_{\tau \tau }+{\Delta }^2\mathcal{Y}-{\int }_0^{\tau }k\left(\tau -a\right){\Delta }^2\mathcal{Y}\left(a\right)da+{\left|{\mathcal{Y}}_{1\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{1\tau }\\ -{\left|{\mathcal{Y}}_{2\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{2\tau }=g(x,{\mathcal{V}}_1)-g(x,{\mathcal{V}}_2)\end{array}\hfill & \mathrm{in}\mathcal{D}\times \left(0,S\right),\hfill \\ \mathcal{Y}\left(x,\tau \right)={\displaystyle \frac{\partial }{\partial \mathcal{V}}}\mathcal{Y}\left(x,\tau \right)=0,\hfill & \mathrm{on}\partial \mathcal{D}\times \left(0,S\right),\hfill \\ \mathcal{Y}\left(x,0\right)={\mathcal{Y}}_0\left(x\right),{\mathcal{Y}}_{\tau }\left(x,0\right)={\mathcal{Y}}_1\left(x\right),\hfill & \mathrm{in}x\in \mathcal{D}.\hfill \end{array}\right.$$

(16)

Multiplying (16) by ${\mathcal{Y}}_{\tau }$ and integrating it over $\mathcal{D}\times \left(0,S\right)$, we obtain

$$\begin{array}{c}{\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{2}dx+{\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|\Delta \mathcal{Y}\right|}^{2}dx+{\displaystyle \frac{1}{2}}\left(1-{\int }_0^{\tau }k\left(a\right)da\right){\int }_{\mathcal{D}}{\left|\Delta \mathcal{Y}\left(\tau \right)\right|}^{2}dx\hfill \\ +{\displaystyle \frac{1}{2}}\left(k\circ \Delta \mathcal{Y}\right)\left(\tau \right)+{\displaystyle \frac{1}{2}}{\int }_0^{\tau }k\left(a\right)d\sigma {\int }_{\mathcal{D}}{\left|\Delta \mathcal{Y}\left(\tau \right)\right|}^{2}dxda\hfill \\ -{\displaystyle \frac{1}{2}}{\int }_0^{\tau }\left(k^{\prime }\circ \Delta \mathcal{Y}\right)\left(a\right)da+{\int }_0^{\tau }{\int }_{\mathcal{D}}\left({\left|{\mathcal{Y}}_{1\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{1\tau }-{\left|{\mathcal{Y}}_{2\tau }\right|}^{p\left(x\right)-2}{\mathcal{Y}}_{2\tau }\right)dxda\hfill \\ ={\int }_0^{\tau }{\int }_{\mathcal{D}}\left(g(x,{\mathcal{V}}_1)-g(x,{\mathcal{V}}_2)\right){\mathcal{Y}}_{\tau }\left(a\right)dxda.\hfill \end{array},$$

From (5) and (10), we have

$${\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(\tau \right)\right|}^{2}dx+{\displaystyle \frac{1}{2}}{\int }_{\mathcal{D}}{\left|\Delta \mathcal{Y}\right|}^{2}dx+{\displaystyle \frac{l}{2}}{\int }_{\mathcal{D}}{\left|\Delta \mathcal{Y}\left(\tau \right)\right|}^{2}dx\le {\int }_0^{\tau }{\int }_{\mathcal{D}}\left(g(x,{\mathcal{V}}_1)-g(x,{\mathcal{V}}_2)\right){\mathcal{Y}}_{\tau }\left(a\right)dxda.$$

(17)

Again, using Sobolev embedding and Young’s inequality with (11), we obtain

$$\begin{array}{ccc}& & {\int }_0^{\tau }{\int }_{\mathcal{D}}\left(g(x,{\mathcal{V}}_1)-g(x,{\mathcal{V}}_2)\right){\mathcal{Y}}_{\tau }\left(a\right)dxda\hfill \\ & =& {\int }_{\mathcal{D}}\left|r^{\prime }\left(\chi \right)\right|\left|\mathcal{V}\right|{\mathcal{Y}}_{\tau }\left(a\right)dx\hfill \\ & \le & {\displaystyle \frac{\eta }{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(a\right)\right|}^{2}dx+{\displaystyle \frac{1}{2\eta }}{\int }_{\mathcal{D}}{\left|r^{\prime }\left(\chi \right)\right|}^2{\left|\mathcal{V}\right|}^{2}dx\hfill \\ & \le & {\displaystyle \frac{\eta }{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(a\right)\right|}^{2}dx+{\displaystyle \frac{\left(q-1\right)}{2\eta }}{\int }_{\mathcal{D}}{\left|\chi \right|}^{2\left(q-2\right)}{\left|\mathcal{V}\right|}^{2}dx\hfill \\ & \le & {\displaystyle \frac{\eta }{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(a\right)\right|}^{2}dx+{\displaystyle \frac{\left(q-1\right)}{2\eta }}{\left({\int }_{\mathcal{D}}{\left|\mathcal{V}\right|}^{{\displaystyle \frac{2d}{d-4}}}dx\right)}^{{\displaystyle \frac{d-4}{d}}}\hfill \\ & & \times {\left({\int }_{\mathcal{D}}{\left|\chi \right|}^{d\left(q-2\right)}dx\right)}^{{\displaystyle \frac{2}{d}}}\hfill \\ & \le & {\displaystyle \frac{\eta }{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(a\right)\right|}^{2}dx+{\displaystyle \frac{\left(q-1\right)c_{\xi }}{2\eta }}{∥\mathcal{V}∥}^2{∥\Delta \chi ∥}^{2\left(q-2\right)}\hfill \\ & \le & {\displaystyle \frac{\eta }{2}}{\int }_{\mathcal{D}}{\left|{\mathcal{Y}}_{\tau }\left(a\right)\right|}^{2}dx+{\displaystyle \frac{\left(q-1\right)c_{\xi }}{\eta \setminus \left(q-1\right)}}{T}^{2\left(q-2\right)}{∥\Delta \mathcal{V}∥}^2,\hfill \end{array}$$

(18)

where $\mathcal{V}={\mathcal{V}}_1-{\mathcal{V}}_2$ and $\chi =\Psi {\mathcal{V}}_1+\left(1-\Psi \right){\mathcal{V}}_2$, $0\le \Psi \le 1$. Combining (18) with (17) and taking a small value for $\eta$, we obtain

$${∥\mathcal{Y}∥}_{X_S}^2\le {\displaystyle \frac{4\left(q-1\right)c_{\xi }S}{\eta \setminus (q-1)}}{T}^{2\left(q-2\right)}{∥\mathcal{V}∥}^2.$$

(19)

Selecting S small enough so that ${\displaystyle \frac{4c_{\xi }S}{\eta }}{T}^{2\left(q-2\right)}<1,$ (19) proves that $\mathcal{F}$ is a contraction. Using the Banach fixed-point theorem, we conclude the existence of a unique solution $\mathcal{Y}$∈$\mathcal{G}\left(Q,S\right)$ verifying $\mathcal{F}\left(\mathcal{Y}\right)=\mathcal{Y}.$ Thus, $\mathcal{Y}$ is a solution of (1). □

4. Numerical Study

Here, we present a numerical exemple by providing initial data and numerically illustrating the behavior of the solution for problem (1). For this, we utilize a numerical scheme relying on the finite element method for dimension $d=2$.

For the sake of simplicity, let $g(x,\mathcal{Y})=\mathcal{Y}$ and $p\left(x\right)=2$.

Multiplying the equation in problem (1) by $\varphi \in H_0^2\left(\mathcal{D}\right)$, integrating it over $\mathcal{D}$ and using the Green formula, we obtain

$$\begin{array}{ccc}& & {\int }_{\mathcal{D}}{\mathcal{Y}}_{\tau \tau }\left(x,\tau \right)\varphi \left(x\right)dx+{\int }_{\mathcal{D}}\Delta \mathcal{Y}\left(x,\tau \right)\Delta \varphi \left(x\right)dx-{\int }_{\mathcal{D}}{\int }_0^{\tau }k\left(\tau -\sigma \right)\Delta \mathcal{Y}\left(x,\sigma \right)\Delta \varphi \left(x\right)d\sigma dx\hfill \\ & & +{\int }_{\mathcal{D}}{\mathcal{Y}}_{\tau }\left(x,\tau \right)\varphi \left(x\right)dx={\int }_{\mathcal{D}}\mathcal{Y}\left(x,\tau \right)\varphi \left(x\right)dx,\forall \varphi \in H_0^2\left(\mathcal{D}\right),\tau \in \left(0,S\right)\hfill \end{array}$$

(20)

with $\mathcal{Y}\left(0\right)={\mathcal{Y}}_0$ and ${\mathcal{Y}}_{\tau }\left(0\right)={\mathcal{Y}}_1$.

To approximate the solution, we utilize a Galerkin finite element method for discretization. Let

$$\mathcal{D}=\bigcup _{i=1}^{M_j}{D}_i$$

(21)

Each $D_i=A_{D_i}\left(E\right)$ is a component of the triangulation, where E is the reference simplex and $A_{D_i}$ is an invertible affine transformation.

We introduce the related finite element space by

$${\Omega }_j=\{K_j\in C^0\left(\mathcal{D}\right):K_j{D}_i\circ A_{D_i}\in {\mathbb{P}}_1\left(E\right)\}$$

(22)

${\mathbb{P}}_1\left(E\right)$ represents the set of polynomials with a maximum degree of one on E.

Substituting $H_0^2\left(\mathcal{D}\right)$ with the finite-dimensional subspace ${\Omega }_j$, we obtain the subsequent semi-discrete form of (20),

$$\begin{array}{ccc}& & {\int }_{\mathcal{D}}{\stackrel{j}{\mathcal{Y}}}_{\tau \tau }\left(x,\tau \right)\varphi \left(x\right)dx+{\int }_{\mathcal{D}}\Delta \stackrel{j}{\mathcal{Y}}\left(x,\tau \right)\Delta \varphi \left(x\right)dx-{\int }_{\mathcal{D}}{\int }_0^{\tau }k\left(\tau -\sigma \right)\Delta \stackrel{j}{\mathcal{Y}}\left(x,\sigma \right)\Delta \varphi \left(x\right)d\sigma dx\hfill \\ & & +{\int }_{\mathcal{D}}{\stackrel{j}{\mathcal{Y}}}_{\tau }\left(x,\tau \right)\varphi \left(x\right)dx={\int }_{\mathcal{D}}\stackrel{j}{\mathcal{Y}}\left(x,\tau \right)\varphi \left(x\right)dx,\forall \varphi \in {\Omega }_j,\tau \in \left(0,S\right).\hfill \end{array}$$

(23)

with $\stackrel{j}{\mathcal{Y}}\left(0\right)={\Pi }_j{\mathcal{Y}}_0$ and $\stackrel{j}{{\mathcal{Y}}_{\tau }}\left(0\right)={\Pi }_j{\mathcal{Y}}_1$, where ${\Pi }_j$ is the $L^2$ projection from $L^2(0,1)$ onto ${\Omega }_j$.

Now, consider the nodal basis of ${\Omega }_j$ denoted by ${\left\{{\varphi }_i\right\}}_{i=1,\dots ,M_j}$, then we can provide the approximate solution $\stackrel{j}{\mathcal{Y}}\left(\tau \right)$ by

$$\stackrel{j}{\mathcal{Y}}\left(\tau \right)=\sum _{i=1}^{M_j}{\zeta }_i\left(\tau \right){\varphi }_i\left(x\right)$$

(24)

with ${\zeta }_i\left(\tau \right)\in \mathbb{R}$ being coefficients that vary over time.

For ${\tau }_n=n\Delta \tau$, which is a patition of $(0,S)$, where $n=0,\dots ,M_{\tau }$, and $\Delta \tau =S/M_{\tau }$. Using (24) and taking $\varphi ={\varphi }_i$, $i=1,\dots ,M_j$ in $\left(23\right)$, we realize that the approximate solution

$${\mathcal{Y}}^n={\left({\zeta }_1\left({\tau }_n\right),\dots ,{\zeta }_{M_j}\left({\tau }_n\right)\right)}^T$$

(25)

veifies the following matricial problem

$$\left\{\begin{array}{c}A{\mathcal{Y}}_{\tau \tau }^n+R{\mathcal{Y}}^n-R\underset{0}{\overset{{\tau }_n}{\int }}k\left({\tau }_n-\sigma \right){\mathcal{Y}}^n\left(\sigma \right)d\sigma +A{\mathcal{Y}}_{\tau }^n=A{\mathcal{Y}}^{n-1}\hfill \\ \\ A\mathcal{Y}\left(0\right)={\Pi }_j{\mathcal{Y}}_0,A{\mathcal{Y}}_{\tau }\left(0\right)={\Pi }_j{\mathcal{Y}}_1\hfill \end{array}\right.$$

(26)

here, M and R represent the mass and stiffness matrices, respectively, associated with the shape operators.

Now, we employ a Newmark method to solve the problem (26). So, in this two-dimensional scenario ($d=2$), we consider the following choices:

$$\mathcal{D}=\{(x,y)/x^2+y^2\le 1\},k\left(\tau \right)={\mathrm{e}}^{-2\tau }$$

(27)

and initial conditions:

$${\mathcal{Y}}_0(x,y)=4096(1-x^2-y^2),{\mathcal{Y}}_1=40{\mathcal{Y}}_0.$$

(28)

There are 281 triangles in the triangulation $D_j$. Using MATLAB, we created a mech geneator, as shown in Figure 1. The time step is small enough $\Delta \tau =0.01$.

Figure 1. Uniform mesh grid of $\mathcal{D}$.

Depending on various time iterations $n=1$ ($\tau =0$), $n=2$ ($\tau =0.01$), $n=6$ ($\tau =0.05$), and $n=9$ ($\tau =0.08$), we provide the aproximate solutions ${\mathcal{Y}}^n$ In Figure 2. The solutions are displayed in 3D and their 2D projections are shown in the right column for better visualization. Notice that the colors indicate the values.

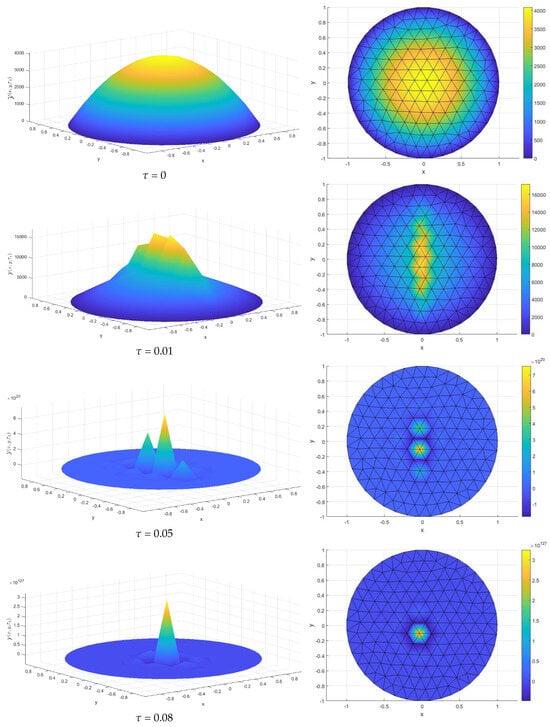
Figure 2. Numerical values of ${\mathcal{Y}}^n$ at different times.

Also, the numerical values of $\parallel {\mathcal{Y}}^n{\parallel }_2$ are displayed over time in Figure 3, indicating an interesting blow-up for this solution at $\tau =0.08$, which has been observed for many other numerical examples tested using these problems. A theoretical study of blow-up in time for the solutions to our problem is needed to confirm these obsevations.

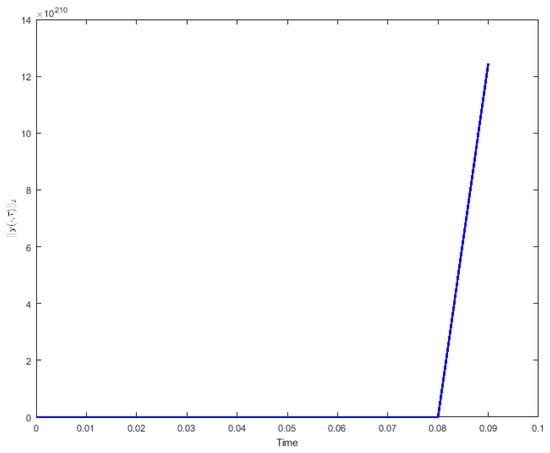
Figure 3. ${\displaystyle \parallel }{\mathcal{Y}}^n{\left(\tau \right)\parallel }_2$.

5. Conclusions

In this work, the existence of a weak solution to problem (1) has been obtained via the Faedo–Galerkin approximation method and a fixed point theorem. The result can be seen as a generalization of many similar existence results in the literature, with only a few conditions on the general source term $g(x,\mathcal{Y})$. Regarding future research, using energy methods, it may be possible to apply Lemma 3 and impose additional conditions on the second term to study the asymptotic behavior of these solutions.