Preview Control for Cyber–Physical Systems under Periodic Denial-of-Service Attacks

Abstract

In this paper, the preview control problem for cyber–physical systems (CPSs) under denial-of-service (DOS) attacks is studied. First, we employ an attack-tolerant strategy to design an augmented error system (AES) for scenarios where both state and reference signal channels are subject to periodic attacks. We then discuss the stochastic stability conditions for the AES and derive the corresponding controller. Subsequently, the preview controller for the original system is developed. Finally, the effectiveness of the obtained results is demonstrated through a numerical simulation using an unmanned ground vehicle (UGV) model, indicating the practical applicability of the proposed control strategy.

1. Introduction

Preview control is a concept that enhances tracking effectiveness and suppresses disturbance by utilizing information about reference signals or disturbances ahead of time [1,2,3]. In a preview control model, measuring these signals in advance and incorporating this “future” information into the controller can save total energy consumption during tracking, thereby improving overall efficiency. Additionally, by applying “future” disturbance information to design a reverse buffer in advance, the impact caused by disturbances can be mitigated. Research on preview control has garnered significant attention, with the augmented error system (AES) being a key technology in the optimal preview control theory [1,2,3]. When designing a preview controller, the AES is first established, which includes the state equation, the error equation, and some equalities regarding previewable signals. Using the maximum principle and solving an equation with previewable signals backwards, an optimal preview controller can be derived. Building upon a fractionation tower model, a series of preview control problems for multi-rate setting systems have been solved [4,5,6]. The core method to address this involves introducing the discrete lifting technique to convert the multi-rate setting system into a single-setting one.

In [7,8], the authors address the preview repetitive control problem. They develop optimal and robust preview repetitive controllers, which are applied in research on permanent magnet synchronous motor drive systems. Similarly, in [9,10,11], preview control technology is applied to carrier-based unmanned aerial vehicles. For the problem of safe auto-landing, deck motion and air-wake disturbances are treated as preview signals. The authors derive optimal and robust control algorithms for both linear and nonlinear models.

Cyber–physical systems (CPSs) are complex dynamic systems that require the transmission and reception of various signals. They are sorts of intelligence systems that can realize the combination and cooperation of multi-dimensional resources [12,13]. By utilizing environmental perception, CPSs can monitor and control physical entities through the integration of embedded computing, network communication, and control engineering. CPSs have been applied to various fields, including autonomous driving [14,15], power systems [16], healthcare [17], etc. Compared to traditional network control systems (NCSs), CPSs offer more efficient and versatile communication modes [18]. CPSs are vital in an interconnected world, bridging the gap between the physical and digital realms. They enable advanced real-time monitoring, automation, and control across a wide range of critical applications to enhance efficiency, safety, and innovation, making them indispensable for the advancement of technology and the functioning of modern society.

However, as CPSs become increasingly essential, they also face significant security threats, such as eavesdropping, denial-of-service (DoS) attacks, man-in-the-middle attacks, spoofing, and falsified messages [19]. These attacks can disrupt communication channels, delay critical signals, and compromise system functionality, leading to potential failures or even catastrophic consequences in vital applications. Among these, DoS attacks are particularly common and easy to implement. By overwhelming network resources or disrupting communication channels, DoS attacks can render essential services unavailable, leading to severe disruptions in operations, financial losses, and even endangering lives in sectors like healthcare, transportation, and energy. Therefore, ensuring the security and resilience of CPSs against such threats is of paramount importance.

Some studies investigate effective defense control strategies from the perspective of attacked systems [20,21,22,23]. In [20], the issue of attack-resilient distributed formation control through online adaptation is explored. A novel distributed control algorithm is proposed, enabling operators to adjust their strategies in real time by utilizing the most recent information gathered on adversaries. The authors of ref. [21] study the problem of designing elastic control strategies for NCSs under DoS attacks. The study proposes analog and digital predictor-based controllers with state resetting, which successfully achieved the targeted control objective across a broad range of DoS signals. In ref. [22], utilizing a simplified model of CPSs and accounting for DoS attacks on the wireless channel of the system’s state signal, a set of attack-tolerance strategies is employed to derive sufficient conditions for ensuring system stochastic stability. Based on these conditions, a controller is subsequently designed. In [23], the problem of output feedback stabilization is examined for a class of discrete-time NCSs with an uncertain transition probability matrix and random packet dropouts. The study establishes sufficient conditions for the existence of an output feedback controller that ensures the stochastic stability of the NCS, utilizing a stochastic Lyapunov function and a linear matrix inequality approach.

When addressing the tracking problems of CPSs, both state and reference sensors can be targeted by attackers. The loss of the reference signals can degrade tracking performance or even cause serious accidents, similar to the blinding effect experienced when driving at night due to oncoming high beams. Motivated by [22,23], this paper examines the preview tracking problem for CPSs under periodic DoS attacks and extends the attack-tolerant strategy to the reference signal channel. Based on this strategy, we discuss the stochastic stability conditions for the constructed AES and design the corresponding preview controller.

Our primary goals are to address the challenges of tracking with DoS attacks in both state and reference signal channels by proposing an attack-tolerant strategy and preview controller. The key contributions of our work include the following:

(a)

We propose an attack-tolerant strategy for reference signal channels when the reference signal can be previewed;

(b)

Based on the proposed attack-tolerant strategy, we design a corresponding AES and preview controller;

(c)

We discuss the stochastic stability of the closed-loop system of the AES under the designed controller.

The paper is organized as follows. In Section 2, we explain the fundamentals, including the system model, DoS attack model, attack-tolerant strategy, and construction of the AES. In Section 3, we present the necessary conditions for the stochastic stability of the AES and propose a preview controller under DoS attacks. In Section 4, the effectiveness of the preview controller from Section 3 is demonstrated through an example involving an unmanned ground vehicle (UGV).

Notations: The notations in this paper are standard. $A\in {ℝ}^n$ and $A\in {ℝ}^{m\times n}$ denote an $n$-dimensional matrix and an $m\times n$ matrix, respectively. ${ℝ}^{+}$ denotes the set of positive real numbers. $\mathcal{E}(\cdot )$ stands for the expected value of a random variable. For any matrix $A$, $A>0(\ge 0)$ indicates that $A$ is positive definite (semi-definite), and $A^T$ denotes the transpositions of $A$. $I$ is the identity matrix, and the symbol $*$ in a matrix indicates symmetric entries.

2. Problem Statement

Let us consider a class of CPSs with two communication channels subject to DoS attacks, as shown in Figure 1.

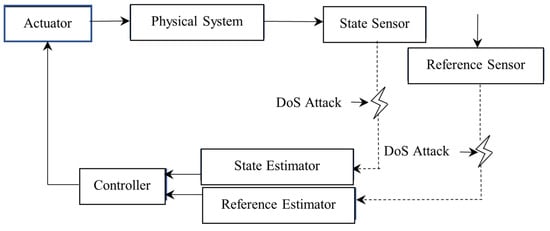
Figure 1. Structure of CPSs under DoS attacks.

Figure 1 illustrates the structure of CPSs when both the state and reference signal channels are under DoS attacks. Data in Figure 1 are transmitted wirelessly from the state and reference sensors to the controller and through wired channels among other system components. The estimators contain buffers that store the last successfully updated data packets.

Remark 1.

The reference channel described in Figure 1 is justifiable. In [24,25], data on car-following performance, such as the acceleration, speed, and position of tracked vehicles, are collected in a database. All this information can be considered as reference signals and can assist in achieving automatic driving through detectors. However, since the transmission process is wireless, it is susceptible to attacks.

2.1. System Model

First, consider the system defined by

$$\left\{\begin{array}{l}x(k+1)=Ax(k)+Bu(k)+Dd(k)\\ y(k)=Cx(k)\end{array}\right.,x(0)=x_0.$$

(1)

where $x(k)\in {ℝ}^m$ is the state vector; $u(k)\in {ℝ}^n$, $y(k)\in {ℝ}^p$, and $d(k)\in {ℝ}^q(‖d(k)‖\le d^{*})$ are the control input, the output vector of the plant, and the disturbance, respectively. $A\in {ℝ}^{m\times m}$, $B\in {ℝ}^{m\times n}$, $C\in {ℝ}^{p\times m}$, and $D\in {ℝ}^{q\times m}$ are constant matrices.

We denote the reference signal as $r(k)\in {ℝ}^p$. Since future reference signals over a period are available in the preview control problem model, the following assumption is introduced.

Assumption 1 ([26]).

At time instant $k_0$, the future reference signals $r(k_0+i)(i=1,2,\cdots ,M_r)$ are acquirable, where $M_r$ represents the preview length. For $r(k)$ after time instant  $k_0+M_r$, we have

$$r(k_0+M_r+i)=0,(i=1,2,3,\cdots ).$$

(2)

Remark 2.

Assumption 1 is a common assumption in the preview control problem. In (2), it is reasonable to set $r(k_0+M_r+i)=0,(i=1,2,3,\cdots )$ beyond the previewable range. From a practical application perspective, when designing a preview controller, more focus should be given to preview information that will imminently impact the system, while the importance of information that is further away should gradually decrease. Information outside the previewable range should be considered invalid. To effec-tively utilize relevant previewable information and exclude invalid data from the controller design, (2) is established.

The measurement of the reference signals, as described above, is shown in Figure 2.

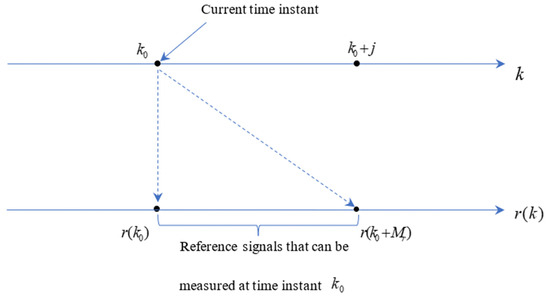
Figure 2. Reference signals known at time instant $k_0$ in the preview control model.

The tracking error is defined as

$$\begin{array}{l}e(k)=y(k)-r(k)\\ \hspace{1em}=Cx(k)-r(k).\end{array}$$

(3)

Letting

$$q(k)={\displaystyle \sum _{i=0}^{k}e(i)}$$

(4)

be the sum of $e(k)$, we have

$$\begin{array}{l}q(k+1)=q(k)+e(k+1)\\ \hspace{1em}\hspace{1em}\hspace{0.17em}=q(k)+C[Ax(k)+Bu(k)+Dd(k)]-r(k+1).\end{array}$$

(5)

The objective of this paper is to design a preview controller that enables the system output $y(k)$ to track the reference signal $r(k)$ under periodic DOS attacks. This means that under the designed controller, if $\underset{k\to \infty }{\lim }q(k)=c$, where $c$ is a constant, then the system error $e(k)$ satisfies $\underset{k\to \infty }{\lim }e(k)=0$.

2.2. DoS Attack Model

In this paper, we consider a type of energy-constrained periodic DoS attack model as described in [22]. Each attack cycle consists of a dormancy stage and an attack stage. During the dormancy stage, $(n-1)T\le k\le (n-1)T+T_{off}$, the attackers conserve energy for the upcoming attack. In the attack stage, $(n-1)T+T_{off}<k<nT$, they continuously target the estimators, where $T_{off}\in {ℝ}^{+}$ is the duration of dormancy.

Let $\theta (k)$ and $\phi (k)$ denote the data reception status of the state and reference signals under periodic DoS attacks at time instant $k$, respectively, as follows:

$$\theta (k)=\left\{\begin{array}{l}1,\mathrm{if}\mathrm{the}\mathrm{state}\mathrm{signal}\mathrm{received};\\ 0,\mathrm{if}\mathrm{the}\mathrm{state}\mathrm{signal}\mathrm{not}\mathrm{received}.\end{array}\right.$$

(6)

$$\phi (k)=\left\{\begin{array}{l}1,\mathrm{if}\mathrm{the}\mathrm{reference}\mathrm{signal}\mathrm{received};\\ 0,\mathrm{if}\mathrm{the}\mathrm{reference}\mathrm{signal}\mathrm{not}\mathrm{received}.\end{array}\right.$$

(7)

We define $p_{attack}$ and $q_{attack}$ as the probabilities that $\theta (k)=1$ and $\phi (k)=1$ during the attack stage and $p_{dorm}$ and $q_{dorm}$ as the probabilities that $\theta (k)=1$ and $\phi (k)=1$ during the dormancy stage, respectively.

Remark 3.

Even during the dormancy stage, packet loss can occur in wireless channels. This is because wireless transmission is subject to multi-path fading and signal degradation, which can in-termittently cause packet loss. These factors are crucial and should be considered when de-signing controllers. As a result, in practice, the values of $p_{dorm}$ and $q_{dorm}$ are typically less than 1.

2.3. Attack-Tolerant Strategy

To simplify the complexity, this paper adopts a common attack-tolerant strategy from [22] for state signals, extending it to reference signals.

Given the unknown attack strategy of the DoS attackers targeting state signal channel, let $\overline{x}(k)$ represent the state vector used for calculation. If the controller successfully receives the data packets from the sensor, then $\overline{x}(k)=x(k)$. Otherwise, $\overline{x}(k)=\overline{x}(k-1)$. That means that in the state estimator, if the new state information is lost, the previously recorded $\overline{x}(k-1)$ in the buffer will be used instead. Thus, we have

$$\overline{x}(k)=\theta (k)x(k)+(1-\theta (k))\overline{x}(k-1).$$

(8)

For the reference signals, the attack-tolerant strategy differs. Let $\overline{r}(k)$ be the reference signal used to calculate $u(k)$. According to Assumption 1, if $\phi (k)=0$, then $\overline{r}(k+j)(j=0,1,2,\cdots ,M_r-1)$ are known, having been used for calculating $u(k-1)$, and only $\overline{r}(k+M_r)$ is unknown. In this case, we set $\overline{r}(k+M_r)=\overline{r}(k+M_r-1)$. If $\phi (k)=1$, then $\overline{r}(k+j)(j=0,1,2,\cdots ,M_r)$ are updated by $r(k+j)(j=0,1,2,\cdots ,M_r)$. Consequently, $\overline{r}(k+j)(j=0,1,2,\cdots ,M_r)$ can be expressed as

$$\overline{r}(k+j)=\left\{\begin{array}{l}\phi (k)r(k+j)+(1-\phi (k))\overline{r}(k+j)\hspace{1em}\hspace{1em}(0\le j<M_r)\\ \phi (k)r(k+j)+(1-\phi (k))\overline{r}(k+j-1)\hspace{1em}(j=M_r)\end{array}\right..$$

(9)

Further, we define

$$\begin{array}{l}\overline{q}(k)=\overline{q}(k-1)+C\overline{x}(k)-\overline{r}(k)\\ \hspace{1em}\hspace{1em}=\overline{q}(k-1)+C[\theta (k)x(k)+(1-\theta (k))\overline{x}(k-1)]\\ \hspace{1em}\hspace{1em}-[\phi (k)r(k)+(1-\phi (k))\overline{r}(k)]\end{array}$$

(10)

as the sum of $e(k)$ used in $u(k)$ after introducing the attack-tolerant strategy.

In the following, an AES based on attack-tolerant strategies (8)–(10) is constructed.

2.4. The Construction of the AES

Firstly, we establish some equalities on $r(k+j)(j=0,1,\cdots ,M_r)$ and $\overline{r}(k+j)(j=0,1,\cdots ,M_r)$.

Denote

$$X_r(k)=\left[\begin{array}{c}r(k)\\ r(k+1)\\ ⋮\\ r(k+M_r)\end{array}\right]\mathrm{and}{A}_r=\left[\begin{array}{ccccc}0& I& 0& \cdots & 0\\ ⋮& \ddots & \ddots & \ddots & ⋮\\ ⋮& & \ddots & \ddots & 0\\ ⋮& & & \ddots & I\\ 0& \cdots & \cdots & \cdots & 0\end{array}\right],$$

Then, we can obtain the following identity

$$X_r(k+1)=A_r{X}_r(k).$$

(11)

Let

$${\overline{X}}_r(k)=\left[\begin{array}{c}\overline{r}(k)\\ \overline{r}(k+1)\\ ⋮\\ \overline{r}(k+M_r)\end{array}\right],{\overline{A}}_{r0}(k)=\left[\begin{array}{cccc}\phi (k)I& & & \\ & \phi (k)I& & \\ & & \ddots & \\ & & & \phi (k)I\end{array}\right],$$

$${\overline{A}}_r(k)=\left[\begin{array}{cccccc}0& (1-\phi (k))I& 0& \cdots & \cdots & 0\\ 0& 0& \ddots & \ddots & & 0\\ ⋮& ⋮& \ddots & \ddots & \ddots & ⋮\\ ⋮& ⋮& & \ddots & \ddots & 0\\ 0& 0& \cdots & \cdots & 0& (1-\phi (k))I\\ 0& 0& \cdots & \cdots & 0& (1-\phi (k))I\end{array}\right],$$

Then, we have

$${\overline{X}}_r(k)={\overline{A}}_{r0}(k)X_r(k)+{\overline{A}}_r(k){\overline{X}}_r(k-1).$$

(12)

Define

$$X_0(k)=\left[\begin{array}{c}q(k)\\ x(k)\end{array}\right],{\overline{X}}_0(k)=\left[\begin{array}{c}\overline{q}(k)\\ \overline{x}(k)\end{array}\right],$$

$${\tilde{A}}_x=\left[\begin{array}{cc}I& CA\\ 0& A\end{array}\right],{\tilde{B}}_x=\left[\begin{array}{c}CB\\ B\end{array}\right],{\tilde{D}}_x=\left[\begin{array}{c}CD\\ D\end{array}\right],G_r=\left[\begin{array}{ccccc}0& -I& 0& \cdots & 0\\ 0& 0& 0& \cdots & 0\end{array}\right],$$

$${\overline{A}}_{x0}(k)=\left[\begin{array}{cc}0& \theta (k)C\\ 0& \theta (k)I\end{array}\right],{\overline{A}}_x(k)=\left[\begin{array}{cc}I& (1-\theta (k))C\\ 0& (1-\theta (k))I\end{array}\right],$$

$${\overline{G}}_{r0}(k)=\left[\begin{array}{ccccc}-\phi (k)I& 0& 0& \cdots & 0\\ 0& 0& 0& \cdots & 0\end{array}\right],{\overline{G}}_r(k)=\left[\begin{array}{ccccc}0& -(1-\phi (k))I& 0& \cdots & 0\\ 0& 0& 0& \cdots & 0\end{array}\right].$$

Combining Equations (1), (5), (8), and (10)–(12), we obtain

$$X(k+1)=\tilde{A}(k)X(k)+\tilde{B}u(k)+\tilde{D}d(k),$$

(13)

where

$$\begin{array}{c}X(k)=\left[\begin{array}{c}{X}_0(k)\\ X_r(k)\\ {\overline{X}}_0(k-1)\\ {\overline{X}}_r(k-1)\end{array}\right],\tilde{A}(k)=\left[\begin{array}{cccc}{\tilde{A}}_x& G_r& 0& 0\\ 0& A_r& 0& 0\\ {\overline{A}}_{x0}(k)& {\overline{G}}_{r0}(k)& {\overline{A}}_x(k)& {\overline{G}}_r(k)\\ 0& {\overline{A}}_{r0}(k)& 0& {\overline{A}}_r(k)\end{array}\right],\\ \tilde{B}=\left[\begin{array}{c}{\tilde{B}}_x\\ 0\\ 0\\ 0\end{array}\right],\tilde{D}=\left[\begin{array}{c}{\tilde{D}}_x\\ 0\\ 0\\ 0\end{array}\right]\end{array}$$

(14)

.

As a result, the output $y(k)$ in (1) can be expressed as

$$y(k)=Cx(k)=\tilde{C}X(k),$$

(15)

where $\tilde{C}=\left[\begin{array}{cccc}0& C& 0& 0\end{array}\right]$. Combining (13) and (15) yields

$$\left\{\begin{array}{l}X(k+1)=\tilde{A}(k)X(k)+\tilde{B}u(k)+\tilde{D}d(k)\\ y(k)=\tilde{C}X(k)\end{array}\right..$$

(16)

Thus, (16) represents the AES for calculating the preview controller.

Remark 4.

Unlike the AES construction method in [26], the difference method for the state equation is not used here in (13). The reason for this is that, under the aforementioned attack-tolerant strategies, the AES constructed using the method in [26] must account for the signal reception status at both time instants $k$ and $k-1$. This makes the AES a non-Markov jump system, complicating stability analysis.

3. Preview Controller Design and Stability Analysis

First, consider the preview controller with the following form

$$u(k)=K{\overline{X}}_0(k)+F{\overline{X}}_r(k),$$

(17)

where the feedback gain matrices $K=\left[\begin{array}{cc}{K}_1& K_2\end{array}\right]$ and $F=\left[\begin{array}{cccc}{F}_0& F_1& \cdots & F_{M_r}\end{array}\right]$ are block matrices of appropriate dimensions.

Substituting the control input (17) into (16), the closed-loop system becomes

$$\begin{array}{l}X(k+1)=\tilde{A}(k)X(k)+\tilde{B}(K{\overline{X}}_0(k)+F{\overline{X}}_r(k))+\tilde{D}d(k)\\ \hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}=\tilde{A}(k)X(k)+\tilde{B}\left[K_1\overline{q}(k)+K_2\overline{x}(x)+{\displaystyle \sum _{i=0}^{M_r}{F}_i}\overline{r}(k+i))\right]+\tilde{D}d(k)\end{array}$$

(18)

Substituting (8)–(10) into (18) and defining

$$H_1(k)=\left[\begin{array}{cc}0& \theta (k)C\\ 0& \theta (k)I\end{array}\right],H_2(k)=\left[\begin{array}{cc}I& (1-\theta (k))C\\ 0& (1-\theta (k))I\end{array}\right],$$

$$G_1(k)=\left[\begin{array}{cccc}-\phi (k)I& 0& \cdots & 0\\ 0& 0& \cdots & 0\end{array}\right],G_2(k)=\left[\begin{array}{cccc}0& -(1-\phi (k))I& \cdots & 0\\ 0& 0& \cdots & 0\end{array}\right],$$

$$G_3(k)=\left[\begin{array}{cccc}\phi (k)I& & & \\ & \phi (k)I& & \\ & & \ddots & \\ & & & \phi (k)I\end{array}\right],G_4(k)=\left[\begin{array}{cccc}0& (1-\phi (k))I& & \\ & \ddots & \ddots & \\ & & 0& (1-\phi (k))I\\ & & & (1-\phi (k))I\end{array}\right].$$

(18) can be briefly rewritten as

$$X(k+1)={\mathsf{\Phi }}_{\gamma (k+1)}X(k)+\tilde{D}d(k),$$

(19)

where

$${\mathsf{\Phi }}_{\gamma (k+1)}=\tilde{A}(k)+\tilde{B}\left(K\tilde{H}(k)+F\tilde{G}(k)\right).$$

(20)

and

$$\tilde{H}(k)=\left[\begin{array}{cccc}{H}_1(k)& G_1(k)& H_2(k)& G_2(k)\end{array}\right],\tilde{G}(k)=\left[\begin{array}{cccc}0& G_3(k)& 0& G_4(k)\end{array}\right].$$

Since $\theta (k)$ and $\phi (k)$ can only take values of 0 or 1, (19) represents four different systems. We use $\gamma (k)=1,2,3,4$ to distinguish between these systems, and they can be summarized in Table 1.

Table 1. Values of $\gamma (k)$ corresponding to different combinations of $\theta (k)$ and $\phi (k)$.

$\mathit{\gamma }(\mathit{k})$	$\mathit{\theta }(\mathit{k})$	$\mathit{\phi }(\mathit{k})$
1	1	1
2	0	1
3	1	0
4	0	0

Let the state transition probability of $\gamma (k)$ from time instant $k$ to $k+1$ be denoted by

$$\mathrm{Pr}\{\gamma (k+1)=j\}={\pi }_j\ge 0.$$

(21)

According to (20) and Table 1, the transition probability ${\pi }_j$ depends only on the probabilities of $\theta (k)$ and $\phi (k)$. Therefore, System (19) is a Markovian jump system.

Next, the stochastic stability of (19) is analyzed.

To ensure that the closed-loop system (19) is stochastically stable, the following definition and lemma are needed.

Definition 1 ([22]).

For the Markov jump system (19) without disturbance, if there exists $\mathsf{\Omega }>0$ such that

$${\displaystyle \sum _{k=0}^{\infty }\mathcal{E}\left\{{‖X(k)‖}^2\right|X(0)\}}\le X^T(0)\mathsf{\Omega }X(0)$$

(22)

holds, then (19) is stochastically stable, where$X(0)$is the initial state of (19).

Lemma 1 (Schur’s complement [27]).

The following three inequalities are equivalent.

(1) 

$\left[\begin{array}{cc}{S}_{11}& S_{12}\\ S_{12}^T& S_{22}\end{array}\right]<0$;

(2) 

$S_{11}<0,S_{22}-S_{12}^T{S}_{11}^{-1}{S}_{12}<0$;

(3) 

$S_{22}<0,S_{11}-S_{12}{S}_{22}^{-1}{S}_{12}^T<0$.

Then, we can derive the following theorem.

Theorem 1.

For $i=1,2,3,4$ and a given positive scalar $\beta$, if there exist matrices $P_i>0$, such that the following inequalities

$$\left[\begin{array}{ccccc}-P_1^{-1}& 0& 0& 0& \sqrt{{\pi }_1}{\mathsf{\Xi }}_1\\ *& -P_2^{-1}& 0& 0& \sqrt{{\pi }_2}{\mathsf{\Xi }}_2\\ *& *& -P_3^{-1}& 0& \sqrt{{\pi }_3}{\mathsf{\Xi }}_3\\ *& *& *& -P_4^{-1}& \sqrt{{\pi }_4}{\mathsf{\Xi }}_4\\ *& *& *& *& -Q_i\end{array}\right]<0$$

(23)

hold, where ${\mathsf{\Xi }}_i=\left[\begin{array}{cc}{\mathsf{\Phi }}_j& D\end{array}\right]$ and $Q_i=\left[\begin{array}{cc}{P}_i& \\ & \beta I\end{array}\right]$, then the closed-loop system (19) is stochastically stable.

Proof of Theorem 1. 

Consider the Lyapunov function of the form

$$V(k)=X^T(k)P_{\gamma (k)}X(k).$$

By analyzing the forward difference in $V(k)$ along with System (19), we have

$$\begin{array}{l}\mathcal{E}(\mathsf{\Delta }V(k))-\beta d^T(k)d(k)=\mathcal{E}(V(k+1))-V(k)-\beta d^T(k)d(k)\\ \hspace{1em}\hspace{1em}=\mathcal{E}(X^T(k+1)P_{\gamma (k+1)}X(k+1))-X^T(k)P_{\gamma (k)}X(k)-\beta d^T(k)d(k)\\ \hspace{1em}\hspace{1em}=\mathcal{E}((X^T(k){\mathsf{\Phi }}_{\gamma (k+1)}^T+d^T(k)D^T)P_{\gamma (k+1)}({\mathsf{\Phi }}_{\gamma (k+1)}X(k)+Dd(k)))\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}-X^T(k)P_{\gamma (k)}X(k)-\beta d^T(k)d(k)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}={\tilde{X}}^T(k)\left[{\displaystyle \sum _{j=1}^4{\pi }_j{\mathsf{\Xi }}_j^T{P}_j}{\mathsf{\Xi }}_j-Q_i\right]\tilde{X}(k),\end{array}$$

(24)

where $\tilde{X}(k)={\left[\begin{array}{cc}{X}^T(k)& d^T(k)\end{array}\right]}^T$, ${\mathsf{\Xi }}_j={\left[\begin{array}{cc}{\mathsf{\Phi }}_j^T& D^T\end{array}\right]}^T$, and $Q_i=\left[\begin{array}{cc}{P}_i& \\ & \beta I\end{array}\right]$.

If ${\mathsf{\Psi }}_i={\displaystyle \sum _{j=1}^4{\pi }_j{\mathsf{\Xi }}_j^T{P}_j}{\mathsf{\Xi }}_j-Q_i<0$, then we can obtain

$$\mathcal{E}(\mathsf{\Delta }V(k))\le {\lambda }_{\max }({\mathsf{\Psi }}_i){‖\tilde{X}(k)‖}^2+\beta {‖d(k)‖}^2.$$

(25)

where ${\lambda }_{\max }({\mathsf{\Psi }}_i)<0$ is the maximal eigenvalue of matrix ${\mathsf{\Psi }}_i$. Summing both sides of inequality (25) from 0 to $T$, then we have

$$\mathcal{E}(V(X(T+1)))-\mathcal{E}(V(X(0)))\le {\lambda }_{\max }({\mathsf{\Psi }}_i)\mathcal{E}({\displaystyle \sum _{k=0}^T{‖\tilde{X}(k)‖}^2})+\beta {\displaystyle \sum _{k=0}^T{‖d(k)‖}^2}.$$

(26)

Letting $T\to \infty$, (26) is equal to

$$\mathcal{E}({\displaystyle \sum _{k=0}^T{‖X(k)‖}^2})\le \mathcal{E}({\displaystyle \sum _{k=0}^T{‖\tilde{X}(k)‖}^2})\le -{\displaystyle \frac{1}{{\lambda }_{\max }({\mathsf{\Psi }}_i)}}(\mathcal{E}(V(X(0)))+\beta {\displaystyle \sum _{k=0}^T{‖d(k)‖}^2})<\infty .$$

(27)

We set $d(k)=0$, and according to Definition 1, (27) implies stochastic stability.

By Lemma 1, the inequalities ${}_i{\displaystyle \sum _{j=1}^4{\pi }_j{\mathsf{\Xi }}_j^T{P}_j}{\mathsf{\Xi }}_j-Q_i<0(i=1,2,3,4)$ are equivalent to (23), which completes the proof. □

Due to the simultaneous inclusion of $P_i^{-1}$ and $P_i$ in (23), (23) does not represent linear matrix inequalities (LMIs). To solve for $K$, $F$ in $\mathsf{\Phi }$, and $P_i$, we follow the approach in [22] by introducing $X_i$ to replace $P_i^{-1}$ in (23). Then, using the Cone Complementarity Linearization (CCL) method from [28], the problem of solving (23) is transformed into the following minimization problem constrained by LMIs

$$\underset{X_i,P_i}{\min }Trace\left({\displaystyle \sum _{i=1}^4{P}_i{X}_i}\right);$$

(28)

$$\mathrm{s}.\mathrm{t}.\left[\begin{array}{cc}{\mathsf{\Omega }}_1& {\mathsf{\Omega }}_2\\ *& {\mathsf{\Omega }}_3\end{array}\right]<0,\left[\begin{array}{cc}{P}_i& I\\ I& X_i\end{array}\right]>0,$$

(29)

where

$${\mathsf{\Omega }}_1=-diag\{X_1,X_2,X_3,X_4\},$$

$${\mathsf{\Omega }}_2={\left[\begin{array}{cccc}\sqrt{{\pi }_1}{\mathsf{\Xi }}_1^T& \sqrt{{\pi }_2}{\mathsf{\Xi }}_2^T& \sqrt{{\pi }_3}{\mathsf{\Xi }}_3^T& \sqrt{{\pi }_4}{\mathsf{\Xi }}_4^T\end{array}\right]}^T,$$

$${\mathsf{\Omega }}_3=\left[\begin{array}{cc}-P_i& \\ & \beta I\end{array}\right].$$

This minimization problem still cannot be solved directly by the ‘mincx’ solver in the LMI toolbox of Matlab because it contains the quadratic terms $P_i{X}_i$. However, we can obtain $P_i$ and the feedback gain matrices $K$ and $F$ using the following algorithm.

• Step 1: Initialize $k=0$. Find a feasible solution group $P_i^k$, $X_i^k$, $K^k$, and $F^k$ for LMIs in (29).
• Step 2: Minimize the following problem

  $$\underset{X_i,P_i}{\min }Trace\left({\displaystyle \sum _{i=1}^4(P_i^k{X}_i+P_i{X}_i^k)}\right);$$

  (30)

  subject to the LMIs in (29). Denote the feasible solutions for this problem as $P_i^{k+1}$, $X_i^{k+1}$, $K^{k+1}$, and $F^{k+1}$.
• Step 3: If

  $${‖P_i^{k+1}{X}_i^{k+1}-I‖}_{Fro}<l,$$

  where ${‖\cdot ‖}_{Fro}$ represents the Frobenius norm of a matrix and $l$ is a given stopping criterion, then exit. Otherwise, set $k=k+1$ and return to step 2.

Additionally, we derive the following corollary for the preview controller of System (1) when both the state and the reference signal channels are subject to DoS attacks.

Corollary 1.

According to Assumption 1, for $i=1,2,3,4$, and a given positive scalar $\beta$, if there exist matrices $P_i>0$ $(i=1,2,3,4)$ such that the LMIs (23) hold, then the controller (17) functions as the preview controller for System (1) under periodic DoS attacks.

4. Numerical Simulation

Consider an example of an unmanned ground vehicle (UGV) taken from [29]. It is assumed that the UGV travels in a straight line and comes to a complete stop before rotating. The dynamic model is described as follows:

$$\left\{\begin{array}{l}\left[\begin{array}{c}\dot{s}(t)\\ \dot{v}(t)\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& {\displaystyle \frac{-b}{M}}\end{array}\right]\left[\begin{array}{c}s(t)\\ v(t)\end{array}\right]+\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{M}}\end{array}\right]F(t)\\ \left[\begin{array}{c}\dot{\rho }(t)\\ \dot{\omega }(t)\end{array}\right]=\left[\begin{array}{cc}0& 1\\ 0& {\displaystyle \frac{-b_r}{J}}\end{array}\right]\left[\begin{array}{c}\rho (t)\\ \omega (t)\end{array}\right]+\left[\begin{array}{c}0\\ {\displaystyle \frac{1}{J}}\end{array}\right](L(t)+d_0(t))\\ y_i(t)=C_i\left[\begin{array}{c}s(t)\\ v(t)\\ \rho (t)\\ \omega (t)\end{array}\right]\end{array}\right.,$$

(31)

where the variables $s$, $v$, $\rho$, and $\omega$ represent the position, linear velocity, angular position, and angular velocity, respectively. $M$ and $J$ denote the mass and moment of inertia. $b$ and $b_r$ are the translational and rotational friction coefficients. The inputs $F$ and $L$ are the force and torque applied of the UGV, and $d_0$ is the output disturbance. We set $M=1$, $J=2$, $b=1$, and $b_r=1$. Additionally, $C_1=\left[\begin{array}{cccc}1& 0& 0& 0\end{array}\right]$ and $C_2=\left[\begin{array}{cccc}0& 0& 1& 0\end{array}\right]$ represent the transmission channels.

By applying the forward Euler method to discretize the system with a step size of $T=0.1$, we obtain the following discrete-time system:

$$\left\{\begin{array}{l}\left[\begin{array}{c}s(k+1)\\ v(k+1)\end{array}\right]=\left[\begin{array}{cc}1& 0.1\\ 0& 0.9\end{array}\right]\left[\begin{array}{c}s(k)\\ v(k)\end{array}\right]+\left[\begin{array}{c}0\\ 0.1\end{array}\right]F(k)\\ y_1(k)=s(k)\end{array}\right.,$$

(32)

$$\left\{\begin{array}{l}\left[\begin{array}{c}\rho (k+1)\\ \omega (k+1)\end{array}\right]=\left[\begin{array}{cc}1& 0.1\\ 0& 0.95\end{array}\right]\left[\begin{array}{c}\rho (k)\\ \omega (k)\end{array}\right]+\left[\begin{array}{c}0\\ 0.05\end{array}\right](L(k)+d_0(k))\\ y_2(k)=\rho (k)\end{array}\right..$$

(33)

We set the initial state to ${\left[\begin{array}{cc}s(0)& v(0)\end{array}\right]}^T={\left[\begin{array}{cc}0.1& 0.1\end{array}\right]}^T$ and define the reference signal

$$r_s(k)=\left\{\begin{array}{cc}0& 0\le k<80\\ \sin (0.02\pi (k-80))& 80\le k<280\\ 0& 280\le k\le 400\end{array}\right..$$

for straight path movement. For the rotating part, we choose the initial angular position ${\left[\begin{array}{cc}\rho (0)& w(0)\end{array}\right]}^T={\left[\begin{array}{cc}0.15& 0.05\end{array}\right]}^T$ and define the reference signal

$$r_{\rho }(k)=\left\{\begin{array}{c}\begin{array}{cc}0& 0\le k<100\\ 0.01(k-100)& 100\le k<200\\ 1& 200\le k\le 400\end{array}\end{array}\right.,$$

and the disturbance

$$d_0(k)=\left\{\begin{array}{cc}0& 0\le k<300\\ 1& 300\le k\le 400\end{array}\right..$$

Under the condition of data packet reception, we have Figure 3.

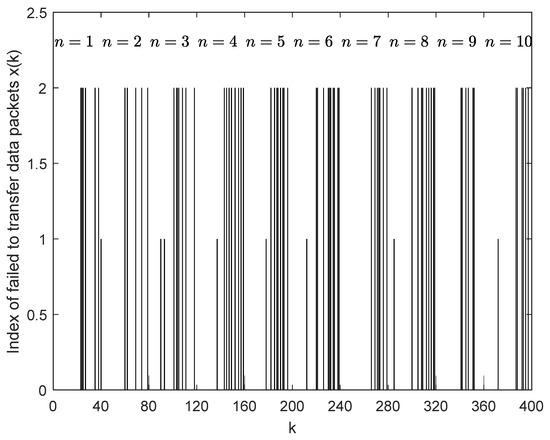
Figure 3. Packet reception affected by periodic DoS attacks, with $T=20$ and $T_{off}=10$.

Figure 3 illustrates an example of packet reception. In this figure, the long segments represent the packet loss during the attack stages, while the short segments represent the packet loss during the dormancy stages. This is consistent with the packet reception conditions described in Section 2.2, where $p_{attack}=0.7$, and $p_{dorm}=0.95$.

The tracking results for System (32) are presented below.

Figure 4 illustrates the output responses using the method from [22] in scenarios with packet loss in both the state signal and reference signal channels. The minimum $p_{attack}$ and $q_{attack}$ values that ensure system stochastic stability are 0.26 and 0.27, respectively. In Figure 4a, the parameters are set to $q_{attack}=q_{dorm}=1$, $p_{dorm}=0.95$, and $p_{attack}=0.9,0.7,0.5$. This subfigure reveals that tracking effectiveness diminishes as $p_{attack}$ decreases, indicating that packet loss in the state signal channel results in degraded tracking performance. In Figure 4b, the parameters are set to $p_{attack}=p_{dorm}=1$, $q_{dorm}=0.95$, and $q_{attack}=0.9,0.7,0.5$. Similarly, this subfigure shows that the tracking effectiveness declines with decreasing $q_{attack}$, demonstrating that packet loss in the reference signal channel also causes poorer tracking quality. However, the impact on tracking effectiveness is less severe than the loss in the state signal channel.

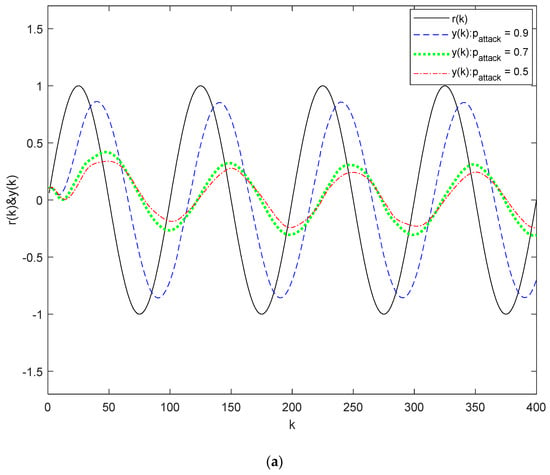
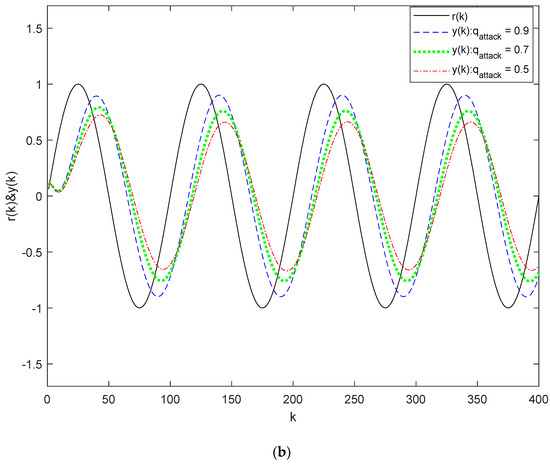
Figure 4. Output responses for System (32) using the method from [22]: (a) Output responses with different $p_{attack}$; (b) Output responses with different $q_{attack}$.

When using the preview controller, the tracking results are as follows.

Figure 5 compares the output responses under different preview conditions and the method from [22], when there is packet loss in both the state signal and reference signal channels. When $M_r=1$, the minimum $p_{attack}$ value that ensures system stochastic stability is 0.26, and the system is stable for any $q_{attack}$. In Figure 5a, we set $q_{attack}=q_{dorm}=1$, $p_{attack}=0.7$, $p_{dorm}=0.95$, and apply varying preview conditions: the method described in [22] (without preview), $M_r=1$ and $M_r=3$. Similarly, in Figure 5b, we use $p_{attack}=p_{dorm}=1$, $q_{attack}=0.7$, $q_{dorm}=0.95$, and the same preview conditions. From these subfigures, it is evident that as the preview length $M_r$ increases, the system output can track the reference signal better.

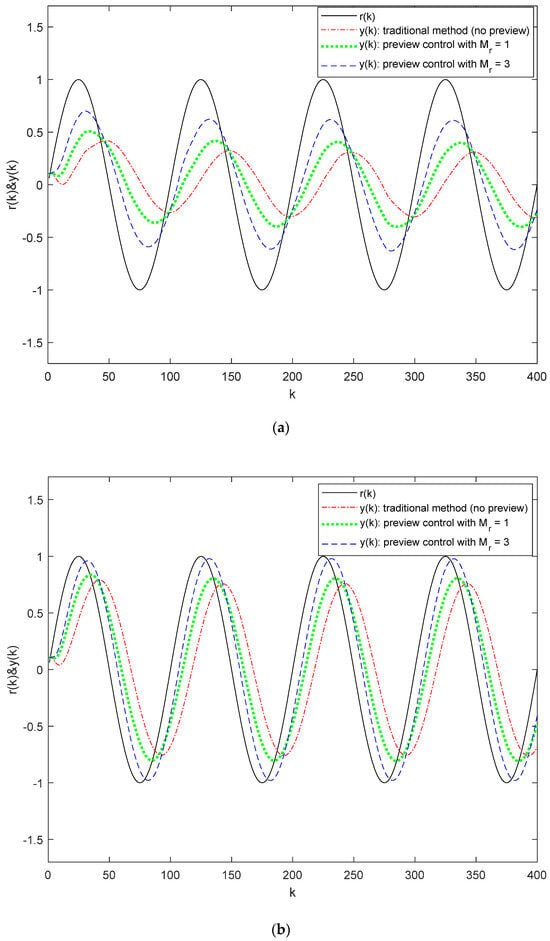
Figure 5. Output responses for System (32) using the preview controller proposed in this paper and method from [22]: (a) Output responses with packet loss in state signal channel; (b) Output responses with packet loss in reference signal channel.

Next, we consider the case with disturbance, i.e., System (33), and provide an evaluation of the system’s performance. We set $\beta =1$ in Theorem 1; then, we have the following figures.

Figure 6 illustrates the output responses and error under different preview conditions when there is packet loss in both the state signal and reference signal channels. Figure 6a,c show the system output, and Figure 6b,d show the error. In Figure 6a,b, we set $q_{attack}=q_{dorm}=1$, $p_{attack}=0.7$, $p_{dorm}=0.95$, and apply varying preview conditions: the method described in [22] (without preview), $M_r=1$ and $M_r=3$. In Figure 6c,d, we use $p_{attack}=p_{dorm}=1$, $q_{attack}=0.7$, $q_{dorm}=0.95$, and the same preview conditions. From these subfigures, it is evident that the system remains stable under the disturbance $d_0(k)$, and as the preview length $M_r$ increases, the system output can track the reference signal more effectively.

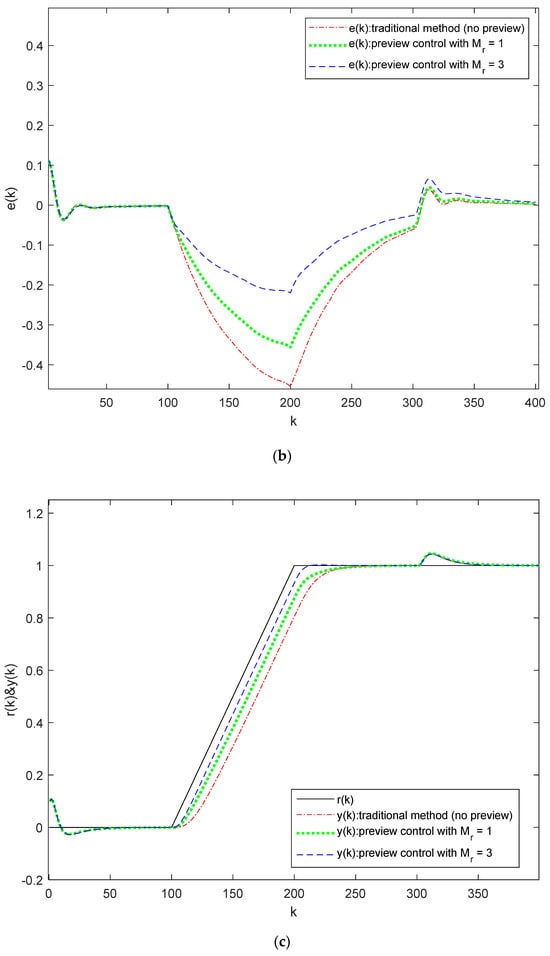
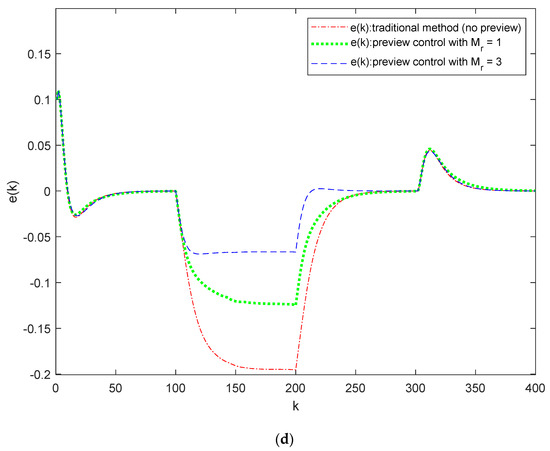
Figure 6. Output responses and error for System (33) using the preview controller proposed in this paper and the method from [22] (without preview): (a) Output responses with packet loss in state signal channel; (b) Error with packet loss in state signal channel; (c) Output responses with packet loss in reference signal channel; (d) Error with packet loss in reference signal channel.

We use the following index to evaluate the system’s performance

$$J={\displaystyle \sum _{i=1}^{\infty }{e}^2(i)}.$$

(34)

We set $M_r=3$, $q_{attack}=q_{dorm}=1$, and $p_{dorm}=0.95$. Based on different $p_{attack}$, we obtain the following table of system performance.

We set $M_r=3$, $p_{attack}=p_{dorm}=1$, and $q_{dorm}=0.95$. Based on different $q_{attack}$, we obtain the following table of system performance.

It can be seen from Table 2 and Table 3 that as the level of DoS attacks intensifies, indicated by the decrease in $p_{attack}$ and $q_{attack}$, the tracking performance of the system gradually deteriorates. Under the same level of DoS attacks, the degradation in tracking performance is more pronounced when packet loss occurs in the state signal channel compared to the reference signal channel. The presence of preview control leads to improvement in the system’s tracking performance.

Table 2. System performance under different $p_{attack}$.

${\mathit{p}}_{\mathit{a}\mathit{t}\mathit{t}\mathit{a}\mathit{c}\mathit{k}}$	$\mathbf{System}\mathbf{Performance}({\mathit{M}}_{\mathit{r}}=3$)	System Performance (without Preview) Method from [22]
0.9	0.6448	2.1533
0.7	2.2887	5.1785
0.5	51.3451	52.3229

Table 3. System performance under different $q_{attack}$.

${\mathit{q}}_{\mathit{a}\mathit{t}\mathit{t}\mathit{a}\mathit{c}\mathit{k}}$	$\mathbf{System}\mathbf{Performance}({\mathit{M}}_{\mathit{r}}=3$)	System Performance (without Preview) Method from [22]
0.9	0.2604	1.0309
0.7	0.5131	1.3200
0.5	0.8119	1.5142

Finally, we analyze the advantages of the reference signal attack-tolerant strategy designed in this paper.

We set $d_0(k)=0$; for different reference signal packet loss scenarios and varying preview conditions, we obtain the following system outputs.

Figure 7 and Figure 8 display the output responses under different packet loss conditions in the reference signal channels, with varying preview conditions. Figure 7a and Figure 8a represent the case without preview, while Figure 7b and Figure 8b correspond to the case with a preview length of $M_r=7$. The other parameters used are $p_{attack}=p_{dorm}=0.95$, $q_{dorm}=0.95$, and $q_{attack}=0.9,0.5$. By comparing Figure 7a,b, as well as Figure 8a,b, we observe that the tracking error significantly decreases between $q_{attack}=0.9$ and $q_{attack}=0.5$, indicating that the preview controller based on the reference signal channel attack-tolerant strategy can mitigate the tracking error between different packet losses in the reference signal channel.

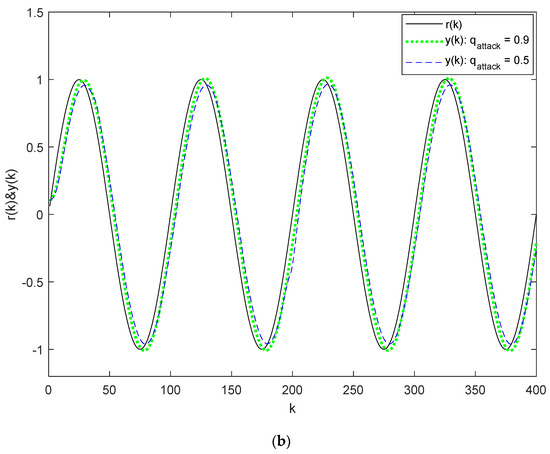
Figure 7. Output responses for System (32) under different packet loss conditions in the reference signal channel and varying preview conditions: (a) Output responses without preview; (b) Output responses with preview length $M_r=7$.

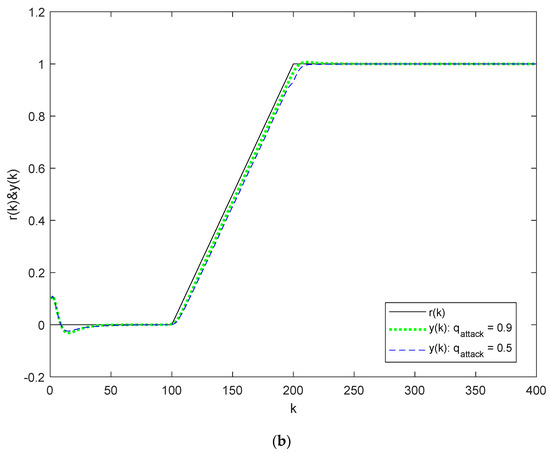
Figure 8. Output responses for System (33) under different packet loss conditions in the reference signal channel and varying preview conditions: (a) Output responses without preview; (b) Output responses with preview length $M_r=7$.

5. Conclusions

This paper presents the design of a preview controller for CPSs subject to periodic DoS attacks. Using an attack-tolerant strategy, a Markovian jump AES is constructed to address these challenges. This study investigates the stochastic stability of the AES and successfully develops a corresponding preview controller. This controller effectively tracks reference signals ahead of time, even under periodic DoS attacks affecting both the state and reference signal channels, and mitigates the tracking error between different packet loss in the reference signal channel. The validity of the proposed approach is demonstrated through a numerical simulation with a UGV model, confirming its practical applicability.

Future research could consider the design of preview controllers for CPSs under actuator saturation and state-constrained conditions and explore the extension of this approach to other types of attacks and evaluate their performance in real-world scenarios.