Research on Model Selection-Based Weighted Averaged One-Dependence Estimators

Abstract

The Averaged One-Dependence Estimators (AODE) is a popular and effective method of Bayesian classification. In AODE, selecting the optimal sub-model based on a cross-validated risk minimization strategy can further enhance classification performance. However, existing cross-validation risk minimization strategies do not consider the differences in attributes in classification decisions. Consequently, this paper introduces an algorithm for Model Selection-based Weighted AODE (SWAODE). To express the differences in attributes in classification decisions, the ODE corresponding to attributes are weighted, with mutual information commonly used in the field of machine learning adopted as weights. Then, these weighted sub-models are evaluated and selected using leave-one-out cross-validation (LOOCV) to determine the best model. The new method can improve the accuracy and robustness of the model and better adapt to different data features, thereby enhancing the performance of the classification algorithm. Experimental results indicate that the algorithm merges the benefits of weighting with model selection, markedly enhancing the classification efficiency of the AODE algorithm.

1. Introduction

Naive Bayes, within the realm of Bayesian network classifiers, has garnered significant interest and ranks among the top ten traditional algorithms in data mining [1,2,3,4]. Naive Bayes assumes that the attributes of a given category are independent of each other. This assumption simplifies the computation of the likelihood function and makes it easy to predict the sample category by maximizing the posterior probability. Given a test sample x with vector $⟨x_1,\dots ,x_d⟩$, Naive Bayes predicts the class of the given test sample as follows:

$$\begin{array}{c}y\left(\mathbf{x}\right)=arg\underset{yϵY}{max}P\left(y\right)\prod _{j=1}^{d}P\left(x_j\right|y)\hfill \end{array}$$

(1)

where d is the number of attributes, $x_j(j=1,2,\dots ,d)$ is the attribute value of the jth attribute, y is a specific value in random variable Y, and $y\left(\mathbf{x}\right)$ is the class label of x predicted by the Bayesian network classifier.

Despite its popularity, the Naive Bayes algorithm often fails to consider the correlation between features, resulting in inaccurate classification. In response to the limitations of the Naive Bayes algorithm, the AODE (Averaged One-Dependence Estimators) algorithm emerged [5]. The AODE algorithm is built upon the Bayesian network, which considers the relationship between features when constructing the model. Unlike the Naive independence assumption, AODE does not assume independence between features. In order to consider dependencies between attributes in a limited scope while keeping the network structure simple, AODE allows dependencies between attributes and assumes that they all depend on a common parent attribute, forming a One-Dependence Estimator (ODE) [6]. Then, by rotating all attributes as parent attributes, the average of the posterior probabilities is used to predict the class of the sample, thus it achieves good results in classification tasks.

In AODE, to enhance both the performance and robustness of classification algorithms, some researchers have proposed cross-validation risk minimization strategies, among which the leave-one-out cross-validation (LOOCV) technique [7] is a commonly used method for cross-validation risk minimization. For example, Chen et al. [8] pointed out that the performance of classification algorithms can be evaluated more accurately by a cross-risk minimization strategy to avoid overfitting of training data. The cross-validation risk minimization strategy is a technique used for evaluating and selecting models by estimating the generalization error of the model using cross-validation during model training to select the optimal model. By introducing the cross-validation risk minimization strategy, the AODE algorithm can better adapt to the characteristics of different datasets and improve the generalization ability of the classifier. However, existing cross-validation risk minimization strategies do not consider the differences in attributes in classification decisions, so this paper proposes a Model Selection-based Weighted AODE (SWAODE) algorithm. The SWAODE algorithm adopts the mutual information as the weights for each ODE and evaluates and selects these weighted sub-models using a leave-one-out cross-validation (LOOCV) technique to determine the best model. The AODE algorithm’s classification efficiency is greatly enhanced by this technique, which also boasts strong robustness and broad applicability.

The main contributions of this paper are as follows:

1. The variability between ODEs and between sub-models is fully taken into account by weighting each ODE and selecting the sub-models in this paper. In this way, the quality of each ODE can be evaluated more finely, and the optimal set of models can be selected, which provides a new perspective for the optimization of the AODE algorithm.

2. We propose a new Model Selection-based Weighted AODE (SWAODE) algorithm, which effectively combines the advantages of weighting and model selection. The goal of the SWAODE algorithm is to enhance the performance and robustness of the AODE classification algorithm. The SWAODE algorithm is able to classify data more accurately and improve the model’s ability to generalize by integrating weighting and model selection strategies.

3. This paper compares the SWAODE algorithm with other advanced algorithms using 70 datasets from the UCI repository [9], along with conducting ablation experiments. Experimental results indicate the superiority of the SWAODE algorithm over other advanced algorithms.

The sections of this paper are structured as follows: In Section 1, we introduce relevant research focused on improving AODE. Section 2 discusses AODE and the process of model selection. The SWAODE algorithm is outlined in Section 3. In Section 4, we provide a detailed description of the experimental setup and its results. Finally, our conclusions are presented in Section 5.

2. Related Work

In recent years, various strategies have been suggested to alleviate the effects of assumptions about attribute independence. Current research can be generally divided into three types: attribute weighting, attribute selection, and structure extension.

2.1. Attribute Weighting

Jiang and Zhang [10] first proposed the idea of assigning different weights to each attribute in AODE. Jiang et al. [11] then argued that it is not reasonable to have the same weight for every One-Dependence Estimator (ODE) in AODE, so in their paper, they proposed the classification model WAODE that assigned different weights to different ODEs. Wu et al. [12] introduced an adaptive SPODE named SODE, which leveraged the principles of immunity from the artificial immune system to autonomously and flexibly determine the weights of each SPODE.

2.2. Attribute Selection

Zheng et al. [13] introduced attribute selection methods for AODE, including Backward Sequential Elimination (BSE) and Forward Sequential Selection (FSS), but these techniques are not very practical for large datasets. Meanwhile, Yang et al. [14,15] conducted a comparison of attribute selection and weighting techniques in AODE. Chen et al. [16] introduced an innovative method for selecting attributes, suitable for extensive model space searches with just a single extra training dataset. The experimental results indicated that the novel technique markedly diminished the bias of AODE, but the training time was slightly increased. This low bias and efficient computation made it suitable for big data learning, but the article did not mention the effect of model selection.

2.3. Structure Extension to NB

Friedman et al. [17] introduced the Tree-Augmented Naive Bayes (TAN) method as an enhancement to Naive Bayes (NB), incorporating a tree structure to mitigate the independence assumptions of NB. TAN mandates that the class variables lack parent nodes, with each attribute containing the class variable and at most one other attribute as parent nodes. This one-traversal algorithm acquires the necessary probability distributions from the training samples during one-traversal learning to construct the network structure and conditional probability tables.

The K-dependent Bayesian classifier (KDB) [18] is a method to improve Naive Bayes (NB). It relaxes the independence assumption of Naive Bayes by allowing each attribute to possess a maximum of k parent attributes. As a result, NB can be viewed as a zero-dependent Bayesian classifier, whereas KDB can include a higher degree of attribute dependence by increasing the value of k. KDB can construct classifiers at any value of k, retaining most of the computational properties of NB and selecting for each attribute a network structure with up to k parent attributes for each attribute.

Another notable enhancement to NB is AODE [5], which relaxes the independence assumption of Naive Bayes by allowing some degree of dependence between features. AODE constructs multiple One-Dependence Estimators by considering the relationship between each feature and category, and then averages them to obtain the final classification result. This approach can more effectively utilize the correlation between features and ultimately improve classification accuracy.

3. AODE and Model Selection Analysis

We discuss the Averaged One-Dependence Estimators (AODE) algorithm and its model selection process in this section.

In order to make the paper more readable, we summarize all the symbols that are defined in the paper in Table 1 for quick reference and understanding by the reader.

Table 1. Tables of symbols.

Symbols	Definition
$\mathcal{D}$	Set of training data
n	Number of training samples
$X,X_i$	Variable representing the attribute
$x,x_i$	Value of attribute variable X or $X_i$
$v_i,v_j$	Number of values of attribute $X_i$ or $X_j$
$\mathbf{x}=⟨x_1,\dots ,x_d⟩$	Vector representing a sample
${\mathbf{x}}_{\mathbf{i}}$	ith sample
$x_{i,j}$	jth value of the ith attribute
Y	Variable representing the category
y	A specific value in random variable Y
$y_i$	True category of the ith sample
c	Number of categories
d	Number of attributes
m	Smoothing parameter
r	Number of attributes as parent attributes
s	Number of attributes as child attributes
$w_j$	Weight of the jth $(j=1,2,\dots ,d)$ ODE
$m^{\prime }$	Threshold

3.1. Constructing the AODE Model

AODE only allows one dependence between attributes; attribute $X_i$ can only depend on some attribute $X_j$ and category Y, where $X_j$ is called the parent attribute of $X_i$. At the same time, in order to keep the computation simple, it is assumed that all attributes depend on a common parent attribute $X_j$ which constitutes a Bayesian network called One-Dependence Estimator (ODE) [6]. Based on this ODE, the joint probability $p(y,\mathbf{x})$ can be estimated as:

$$\begin{array}{c}{P}_{ODE}(y,\mathbf{x})=P(y,x_j)\prod _{i=1}^{d}P\left(x_i\right|y,x_j)\hfill \end{array}$$

(2)

To eliminate the bias introduced by the selection of the parent attribute, it is allowed that all the attributes can be used as the parent attribute in turn, thus obtaining d ODEs, and finally, the posteriori probabilities estimated from these d ODE are averaged to obtain the posterior probability estimate of the sample. Thus, the AODE algorithm calculates the joint probability as:

$$\begin{array}{c}{P}_{AODE}(y,\mathbf{x})={\displaystyle \frac{{\sum }_{j=1}^{d}P(y,x_j){\prod }_{i=1}^{d}P\left(x_i\right|y,x_j)}{d}}\hfill \end{array}$$

(3)

where $P\left(x_i\right|y,x_j)$ can be obtained from the ratio of $P(x_i,y,x_j)$ and $P(y,x_j)$, so only the basic probabilities $P(y,x_j)$ and $P(x_i,y,x_j)$ need to be estimated, which can be obtained by an M-estimation:

$$\begin{array}{c}\widehat{P}(y,x_j)={\displaystyle \frac{F(y,x_j)+{\displaystyle \frac{m}{c\ast v_i}}}{n+m}}\hfill \end{array}$$

(4)

$$\begin{array}{c}\widehat{P}(x_i,y,x_j)={\displaystyle \frac{F(x_i,x_j,y)+{\displaystyle \frac{m}{c\ast v_i\ast v_j}}}{n+m}}\hfill \end{array}$$

(5)

where $F(•)$ is the frequency of occurrence of the parameter item in the training dataset. $v_i$ is the number of values of attribute $X_i$, c is the number of categories, and m is the smoothing parameter in the M-estimation, which is a commonly used parameter estimation method. By introducing the smoothing parameter m, the M-estimation can prevent the probability estimates from being zero and improves the robustness of the estimates.

The frequency F containing class labels and attribute values can be realized in a three-dimensional table in practical implementation, where the first and second dimensions represent the values taken for the first and second attributes. The third dimension represents the values taken for the category, and the values in the table record the frequency values on the values of that dimension. Assuming that there are two attributes $X_1,X_2$ and two categories $class1,class2$ where $X_1$ has two attribute values, $X_2$ has three attribute values, the frequency table is shown in Table 2.

Table 2. Frequency table with two attributes and two class variables.

				$\mathbf{Class}1$	$\mathbf{Class}2$
$X_2$	$x_{2,1}$	$X_1$	$x_{1,1}$
		$X_1$	$x_{1,2}$
$X_2$	$x_{2,2}$	$X_1$	$x_{1,1}$
		$X_1$	$x_{1,2}$
$X_2$	$x_{2,3}$	$X_1$	$x_{1,1}$
		$X_1$	$x_{1,2}$

The training process of AODE is described by Algorithm 1.

Algorithm 1 AODE training process

Require:  Set of training data $\mathcal{D}$ Ensure:  Frequency table F containing a combination of category labels and two attributes 1: All frequencies in the frequency table F are initialized to zero 2: for each training sample $\mathbf{x}$ from $\mathcal{D}$ do 3:     Obtain the class label y for sample $\mathbf{x}$ and set i and j to zero 4:     while $i<d$ do 5:         Read the value $x_i$ of attribute $X_i$ in sample $\mathbf{x}$ 6:         while $j<i$ do 7:            Read the value $x_j$ of attribute $X_j$ in sample $\mathbf{x}$ 8:            Find the frequency at positions $x_i$, $x_j$, y in the frequency table F and increase by one 9:            $j=j+1$ 10:        end while 11:        $i=i+1$ 12:     end while 13: end for 14: return the finally calculated frequency table F

Algorithm 1 reveals that the AODE training process’s time complexity is influenced by the quantity of samples and attributes, where there are d parent and child attributes, so the total time complexity of the AODE training process is $O\left(n{d}^2\right)$, where d denotes the number of attributes, and n denotes the number of samples for each attribute. AODE typically exhibits a marginally greater time complexity compared to NB, as AODE represents a singular attribute dependency, aligning more closely with the real data. Therefore, the classification performance is significantly improved compared with NB.

3.2. Model Selection-Based AODE

To fully present the Model Selection-based AODE(SAODE) algorithm in this section, the model space is first constructed here. Then, the attributes are ranked based on mutual information. Finally, the best model is selected using the leave-one-out cross-validation error.

3.2.1. Building the Model Space

When constructing the AODE model space, we introduce the threshold $m^{\prime }$. When a particular value $x_j$ of the parent attribute in the training data occurs more often than or as often as a threshold $m^{\prime }$, the ODE model corresponding to that value is included in the computation of the AODE model. If we choose the former r attributes as parent attributes and the former s attributes as child attributes, where $1\le r,s\le d$, the AODE model is approximated by:

$$\begin{array}{c}{P}_{AODE}{(y,\mathbf{x})}_{r,s}={\displaystyle \frac{{\sum }_{j:1\le j\le r\wedge \mathrm{F}\left(x_j\right)\ge m^{\prime }}\mathrm{P}(y,x_j){\prod }_{i=1}^s\mathrm{P}(x_i\mid y,x_j)}{\left|\{j:1\le j\le r\wedge \mathrm{F}\left(x_j\right)\ge m^{\prime }\}\right|}}\hfill \end{array}$$

(6)

where $F\left(x_j\right)$ is the frequency of $x_j$, and $m^{\prime }$ is the minimum frequency that takes the value $x_j$. The AODE algorithm with the inclusion of a threshold $m^{\prime }$ improves the overall performance and prediction accuracy of the model by ensuring that the number of samples for the parent attribute is sufficient, avoiding the problems of high variance and unreliable conditional probability estimation caused by data sparsity. This mechanism enables AODE to maintain high predictive stability and reliability in the face of uneven data distribution. When both r and s are equal to d, it can be seen from the formula that when calculating $P_{AODE}{(y,\mathbf{x})}_{d,d}$, at most $d^2$ subsets of attributes are created as sub-models.

All these approximate AODE models are just a small extension of the previous model. For example, $P_{AODE}{(y,\mathbf{x})}_{1,2}$ is obtained by adding the child attribute $x_2$ to $P_{AODE}{(y,\mathbf{x})}_{1,1}$. All of these models can be applied to test instances in a single nested computation. Thus, all models can be evaluated efficiently.

3.2.2. Attribute Sorting

Constructing a model of the later attributes depends on the model of the earlier attributes when constructing the AODE model space. Therefore, this method of nesting models depends on the order of the attributes. Thus, here, the mutual information is used to sort the attributes. The mutual information is calculated as:

$$\begin{array}{cc}MI(X,Y)\hfill & =H\left(X\right)-H\left(X\right|Y)\hfill \\ \hfill & =\sum _{y\in Y}\sum _{x\in X}P(x,y){log}_2{\displaystyle \frac{P(x,y)}{P\left(x\right)P\left(y\right)}}\hfill \end{array}$$

(7)

where $H\left(X\right)$ is the entropy of X, $H\left(X\right|Y)$ is the conditional entropy, $p(x,y)$ is the joint probability of x and y, and $p\left(x\right)$ and $p\left(y\right)$ are the probabilities of x and y, respectively. Therefore, the MI is used as an indicator of the correlation between attribute X and category Y. The larger the value of the MI, the stronger the correlation between attribute X and category Y is indicated.

An advantage of employing the MI is its ability to efficiently compute the MI between attributes and classes within a single training session. While the MI can identify the discriminative power of individual attributes, it cannot directly assess the discriminative power of combinations of attributes. However, this shortcoming is compensated for the fact that the ranking based on MI can be searched in a wide model space.

3.2.3. Model Selection

For evaluating the distinctiveness of different models and preventing overfitting, leave-one-out cross-validation errors are employed. Through gradual cross-validation, the impact of the absent sample in each fold is deducted from the frequency table to create a model excluding that sample. The technique offers a lower bias estimate of the generalization error and assesses the model using a single training dataset.

In addition, as shown in Equation (6), these models are nested together, with each model being a straightforward extension of another, providing an effective means of evaluating them. That is, these models can be evaluated simultaneously during their construction for the training samples missed in each fold.

Among the more common methods used to evaluate the model selection are the 0–1 loss, Root-Mean-Square Error (RMSE), LogLoss, and AUC value. For example, Chen [19] proposed the RMSE as a criterion for model evaluation, where a lower RMSE indicated a better model. Therefore, we also use the RMSE as a criterion for model evaluation as a way to select the optimal model in Section 3.

4. Model Selection-Based Weighted AODE

In this section, our focus is on the weighting strategy for AODE and the methodology for model selection on the weighted AODE model, given that we have already described the construction methodology of the AODE model in detail in Section 2.

4.1. Weighting the AODE Model

The contribution of each ODE to the final classification result may be different in the AODE algorithm, and certain sub-models may discriminate more accurately for specific categories while others may perform weakly. Therefore, weighting each sub-model can more accurately reflect its importance in the overall classification process, thus improving the overall model performance [11].

The classification ability of ODEs composed of different parent attributes $X_j$ is different, so different weights can be applied to different ODEs [11]. Thus, the formula transforms into:

$$\begin{array}{c}{P}_{WAODE}(y,\mathbf{x})={\displaystyle \frac{{\sum }_{j=1}^d{w}_{j}P(y,x_j){\prod }_{i=1}^{d}P\left(x_i\right|y,x_j)}{d}}\hfill \end{array}$$

(8)

where $w_j$ is the weight of the jth ($j=1,2,\dots ,d$) ODE, where the weights are obtained by calculating the MI through Equation (8). When attribute X and category Y are completely independent, the MI is 0, indicating that there is no information sharing or dependency between them.

Weighting each ODE can better improve the performance and robustness of the overall model, thus enhancing the reliability and validity of the model in practical applications.

4.2. Model Selection for WAODE

We first construct the model space of WAODE in this subsection. Then, the attributes are ranked according to the MI. Finally, we use the RMSE as the cross-validation error and select the optimal sub-model by minimizing the RMSE.

4.2.1. Building the Model Space

As shown in Equation (6), for the WAODE algorithm, where we also introduce the threshold $m^{\prime }$, the joint probability is given by:

$$\begin{array}{c}{P}_{WAODE}{(y,\mathbf{x})}_{r,s}={\displaystyle \frac{{\sum }_{j:1\le j\le r\wedge \mathrm{F}\left(x_j\right)\ge m^{\prime }}{\mathrm{w}}_{j}P(y,x_j){\prod }_{i=1}^s\mathrm{P}(x_i\mid y,x_j)}{\left|\{j:1\le j\le r\wedge \mathrm{F}\left(x_j\right)\ge m^{\prime }\}\right|}}\hfill \end{array}$$

(9)

Similar to the AODE model’s construction in Section 2, all of these approximate WAODE models constitute the model space depicted in Table 3, since each model is simply a small extension of the previous one. Thus, every model is capable of being assessed with efficiency.

Table 3. Space of approximate models of WAODE with d attributes.

Parent	Children
	${\mathit{x}}_{\mathbf{1}}$	⋯	${\mathit{x}}_{\mathit{s}}$	⋯	${\mathit{x}}_{\mathit{d}}$
$x_1$	${\mathrm{P}}_{\mathrm{WAODE}}{(y,\mathbf{x})}_{1,1}$	⋯	${\mathrm{P}}_{\mathrm{WAODE}}{(y,\mathbf{x})}_{1,s}$	⋯	${\mathrm{P}}_{\mathrm{WAODE}}{(y,\mathbf{x})}_{1,d}$
…	…	…	…	…	…
$x_r$	${\mathrm{P}}_{\mathrm{WAODE}}{(y,\mathbf{x})}_{r,1}$	⋯	${\mathrm{P}}_{\mathrm{WAODE}}{(y,\mathbf{x})}_{r,s}$	⋯	${\mathrm{P}}_{\mathrm{WAODE}}{(y,\mathbf{x})}_{r,d}$
…	…	…	…	…	…
$x_d$	${\mathrm{P}}_{\mathrm{WAODE}}{(y,\mathbf{x})}_{d,1}$	⋯	${\mathrm{P}}_{\mathrm{WAODE}}{(y,\mathbf{x})}_{d,s}$	⋯	${\mathrm{P}}_{\mathrm{WAODE}}{(y,\mathbf{x})}_{d,d}$

4.2.2. Attribute Sorting

In constructing the WAODE model space, the model for later attributes is dependent on the model for earlier attributes, as shown in Table 3. This approach of nested models is influenced by the order in which the attributes are considered. To address this, we utilize the MI to rank the attributes. Additionally, we observe that the sorting process also involves selecting attributes, and by sorting first, we can more easily identify the attributes that have a significant impact on categorization. To calculate the MI, we use Equation (8).

4.2.3. Model Selection

We used a 10-fold CV in our experiments to make the results more objective, and we used the LOOCV error as a criterion for model selection. Figure 1 describes the relationship between LOOCV and 10-fold CV. The test set in the 10-fold CV loops through the 10 folds of samples. At the same time, the test instance in LOOCV loops through all the LOOCV instances.

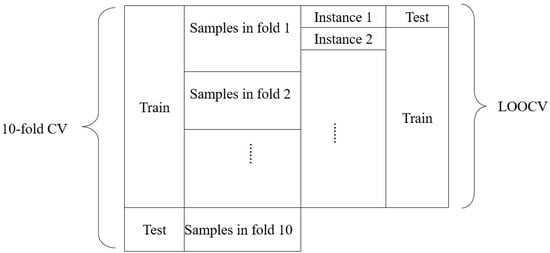
Figure 1. The relationship between LOOCV and 10-fold CV.

LOOCV errors were used to evaluate model distinctiveness and prevent overfitting by excluding one sample at a time from the training data and assessing the model without it. This method provides a lower bias estimate of the generalization error and evaluates the model using nearly all available data for training.

The 0–1 loss (ZOL) and the Root-Mean-Square Error (RMSE) are the most common evaluation criteria used as model selection. The 0–1 loss simply assigns “0” to correct classifications and “1” to misclassifications, considering all misclassifications as equally undesirable. However, the RMSE is more sensitive to the severity of misclassification, so it is able to make more fine-grained probabilistic predictions. The RMSE can be expressed as:

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{\left(1-P(y\left({\mathbf{x}}_i\right)=y_i\mid {\mathbf{x}}_i)\right)}^2}$$

(10)

where $y_i$ is the true class of sample ${\mathbf{x}}_i$. The smaller the RMSE, the smaller the discrepancy between the model’s predictions and the true labels. Compared to the 0–1 loss, the RMSE is able to assess model uncertainty on a continuous basis rather than simply telling us whether the model is classified correctly or not. Meanwhile, the RMSE penalizes model uncertainty more strictly, so it provides a more fine-grained calibration metric for probability estimation. Consequently, the RMSE was employed to assess potential models in our study.

Therefore, the process of choosing the best model can be framed as the following optimization problem:

$${⟨r,s⟩}^{*}=\underset{⟨r,s⟩}{argmin}\sqrt{{\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n}{\left(1-{\displaystyle P_{\mathrm{WAODE}}^{\mathrm{LOO}}}{(y\left({\mathbf{x}}_i\right)=y_i\mid {\mathbf{x}}_i)}_{r,s}\right)}^2}$$

(11)

where ${\displaystyle P_{WAODE}^{LOO}}{(y\mid {\mathbf{x}}_i)}_{r,s}$ can be computed by first estimating ${\displaystyle P_{WAODE}^{LOO}}{(y,{\mathbf{x}}_i)}_{r,s}$ from training set $(\mathcal{D}-\left\{⟨y_i,x_i⟩\right\})$ as in Equation (9), and then normalizing across all possible y’s.

4.3. Algorithm Description

Utilizing the aforementioned method, we formulated a training algorithm for the Selection-based Weighted AODE (SWAODE) model, as shown in Algorithm 2.

Algorithm 2 Training algorithm for Model Selection-based Weighted AODE (SWAODE)

1: First pass: Form the table of joint frequencies of all combinations of x attribute values and the class label as in Algorithm 1 2: Compute the mutual information 3: Weighting each ODE and rank the attributes 4: Second pass: Perform LOOCV on the sample set 5: for sample $\mathbf{x}\in \mathcal{D}$ do 6:     Remove sample x from the frequency table 7:     Obtain category for sample x and set i and j to zero 8:     Build $d^2$ models for AODE 9:     for $j<d$ do 10:         for $i<d$ do 11:            Predict sample x using all models in Equation (9) 12:            Accumulate the squared error for each model 13:            $i=i+1$ 14:         end for 15:         $j=j+1$ 16:     end for 17:     Add sample x back to the frequency table 18: end for 19: Compute the root-mean-square error for each model 20: Select the model with the lowest RMSE

The SWAODE algorithm for weighting and model selection needs to consider the time complexity involved in computing the MI and LOOCV, respectively, where the total time complexity of calculating the MI in the WAODE-MI algorithm is $O\left(c{d}^2\right)$, and the time complexity of model selection with LOOCV is $O\left(cn{d}^2\right)$, so the total time complexity of the SWAODE algorithm is $O\left(cn{d}^2\right)+O\left(c{d}^2\right)$, which is almost similar to the time complexity of the SAODE algorithm, where d is the number of attributes, n is the number of samples, and c is the number of categories.

5. Experiments and Discussion

We ran the above algorithm on 70 datasets from the UCI repository [9]. The comprehensive features of the datasets are presented in Table 4, arranged in an increasing sequence based on the count of instances. The experiments were carried out based on the high-performance computing platform of Nanjing Audit University, the computing node CPU was an Intel E5, the amount of memory was 188 G, and the operating system was CentOS7.9-x64. The algorithms were based on the Petal Machine Learning Platform [19] implemented in C++. Compared to the well-known machine learning experimental platform Weka [20], the Petal platform has one significant difference: missing values are viewed as a single value in Petal, whereas the Weka system employs means (numerical attributes) or modes (discrete attributes) instead.

Table 4. Datasets.

No.	Name	Inst	Att	Class
1	contact-lenses	24	4	3
2	lung-cancer	32	56	3
3	labor-negotiations	57	16	2
4	post-operative	90	8	3
5	zoo	101	16	7
6	promoters	106	57	2
7	echocardiogram	131	6	2
8	lymphography	148	18	4
9	iris	150	4	3
10	teaching-ae	151	5	3
11	hepatitis	155	19	2
12	wine	178	13	3
13	autos	205	25	7
14	sonar	208	60	2
15	glass-id	214	9	3
16	new-thyroid	215	5	3
17	audio	226	69	24
18	hungarian	294	13	2
19	heart-disease-c	303	13	2
20	haberman	306	3	2
21	primary-tumor	339	17	22
22	ionosphere	351	34	2
23	dermatology	366	34	6
24	horse-colic	368	21	2
25	house-votes-84	435	16	2
26	cylinder-bands	540	39	2
27	chess	551	39	2
28	syncon	600	60	6
29	balance-scale	625	4	3
30	soybean	683	35	19
31	credit-a	690	15	2
32	breast-cancer-w	699	9	2
33	pima-ind-diabetes	768	8	2
34	vehicle	846	18	4
35	anneal	898	38	6
36	tic-tac-toe	958	9	2
37	vowel	990	13	11
38	german	1000	20	2
39	led	1000	7	10
40	contraceptive-mc	1473	9	3
41	yeast	1484	8	10
42	volcanoes	1520	3	4
43	car	1728	6	4
44	segment	2310	19	7
45	hypothyroid	3163	25	2
46	splice-c4.5	3177	60	3
47	kr-vs-kp	3196	36	2
48	abalone	4177	8	3
49	spambase	4601	57	2
50	phoneme	5438	7	50
51	wall-following	5456	24	4
52	page-blocks	5473	10	5
53	optdigits	5620	64	10
54	satellite	6435	36	6
55	musk2	6598	166	2
56	mushrooms	8124	22	2
57	thyroid	9169	29	20
58	pendigits	10,992	16	10
59	sign	12,546	8	3
60	nursery	12,960	8	5
61	magic	19,020	10	2
62	letter-recog	20,000	16	26
63	adult	48,842	14	2
64	shuttle	58,000	9	7
65	connect-4	67,557	42	3
66	waveform	100,000	21	3
67	localization	164,860	5	11
68	census-income	299,285	41	2
69	poker-hand	1,025,010	10	10
70	donation	5,749,132	11	2

5.1. Comparison on ZOL

In this experiment, in order to verify the performance of the SWAODE algorithm, we compared it with classical algorithms such as NB [1], KDB (k = 1) [18], AODE [5], WAODE-MI [11], WAODE-KL [21], and so on. We adopted ZOL as the evaluation index, where the loss was one when the sample was misclassified and zero when it was correctly classified, and then we calculated the percentage of total loss in the total number of test samples in order to comprehensively assess the performance of different algorithms in the classification task. The W/D/L metrics tracked the number of wins, draws, and losses for each algorithm across multiple datasets, allowing for a comparison of their performance on the same dataset. For instance, SWAODE demonstrated strong performance with 52 wins, 5 draws, and 13 losses when compared to NB, providing an objective assessment of the algorithms’ respective strengths and weaknesses. Through this professional evaluation method, we can more comprehensively and objectively assess the advantages of the SWAODE algorithm over other algorithms and provide a scientific basis for its performance evaluation, as shown in Table 5. Meanwhile, in order to facilitate the observation of SWAODE’s experimental data, we bolded the row where SWAODE is located in all subsequent tables and presents the experimental data for each dataset in Appendix Table A1.

Table 5. Win/draw/loss of ZOL for SWAODE.

	NB	KDB	AODE	WAODE-MI	WAODE-KL	SAODE
SWAODE	52/5/13	52/2/16	39/8/23	34/12/24	32/14/24	27/22/21
NB		24/2/44	15/4/51	14/3/53	15/3/52	14/3/53
KDB			21/3/46	21/1/48	20/2/48	15/3/52
AODE				20/15/35	20/13/37	21/8/41
WAODE-MI					9/51/10	25/8/37
WAODE-KL						26/7/37

The analysis in Table 5 reveals that the SWAODE algorithm outperformed other advanced algorithms. Compared to the AODE algorithm, the SWAODE algorithm achieved 39 wins, 8 draws, and 23 losses, representing a significant improvement. Additionally, the weighted AODE classification algorithm also showed improvement when different weights were assigned. The WAODE-KL algorithm, which uses KL divergence as weights, achieved 37 wins, 13 draws, and 20 losses compared to the AODE algorithm, demonstrating a clear advantage. However, even the excellent WAODE-KL algorithm did not surpass our new algorithm, the SWAODE algorithm. In comparison, the SWAODE algorithm achieved 32 wins, 13 draws, and 24 losses, showing a clear advantage. Overall, our SWAODE algorithm demonstrated strong performance and brought significant improvement to the classification task.

We also represented the scatter plot of SWAODE with respect to WAODE-MI in terms of ZOL in Figure 2. Points above the diagonal represent datasets whose ZOL values are lower than those of WAODE-MI. It can be found that SWAODE consistently provided better predictions than the regular WAODE-MI in a statistically significant way.

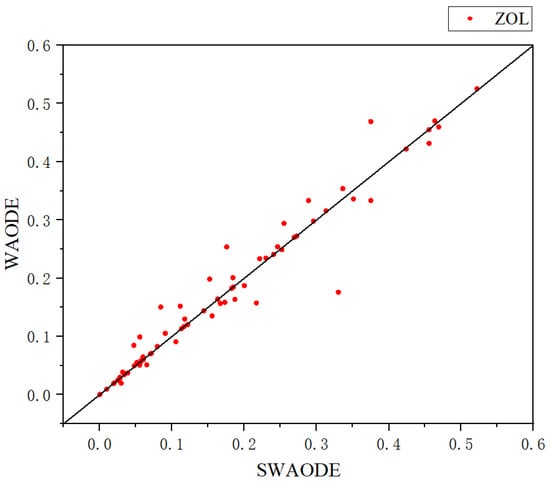
Figure 2. Scatter plot of ZOL.

5.2. Comparison on LogLoss

When assessing the effectiveness of the SWAODE algorithm, it is common to use LogLoss as an evaluation metric. LogLoss is a widely used metric for evaluating the predictive accuracy of a classification model. It measures the deviation between the model’s predicted probability for each sample and the actual label. To compare the SWAODE algorithm with other advanced algorithms, their LogLoss values on a test dataset can be calculated and visualized. Additionally, the W/D/L (win/draw/loss) metric can be used to analyze the strengths and weaknesses of different algorithms in the experimental results. By comparing the LogLoss values of the SWAODE algorithm with those of other algorithms, the strengths and weaknesses on different datasets can be determined, as shown in Table 6. Meanwhile, we also show the experimental data in detail in Appendix Table A2.

Table 6. Win/draw/loss of LogLoss for SWAODE.

	NB	KDB	AODE	WAODE-MI	WAODE-KL	SAODE
SWAODE	60/0/10	56/0/14	48/1/21	42/7/21	42/6/22	40/4/26
NB		28/0/42	11/0/59	11/0/59	11/0/59	10/0/60
KDB			18/0/52	18/0/52	18/0/52	12/0/58
AODE				25/1/44	22/1/47	17/2/51
WAODE-MI					19/28/23	24/0/46
WAODE-KL						26/0/44

According to the data analysis in Table 6, the SWAODE algorithm presented excellent performance on LogLoss. In the comparison with AODE, it achieved 48 wins/1 draw/21 losses. In addition, the SWAODE algorithm also performed outstandingly compared to the weighted AODE algorithm. The SWAODE algorithm beat the WAODE-MI algorithm and the WAODE-KL algorithm on 42 of the 70 datasets, respectively. These results show that the SWAODE algorithm is adaptable to various datasets and outperforms other algorithms in most cases. Therefore, the SWAODE algorithm is a very efficient algorithm for AODE improvement.

Meanwhile, we also represented the scatter plot of SWAODE with respect to WAODE-MI in terms of LogLoss in Figure 3. It can be found that SWAODE consistently provided better predictions than the regular WAODE-MI algorithm in a statistically significant way.

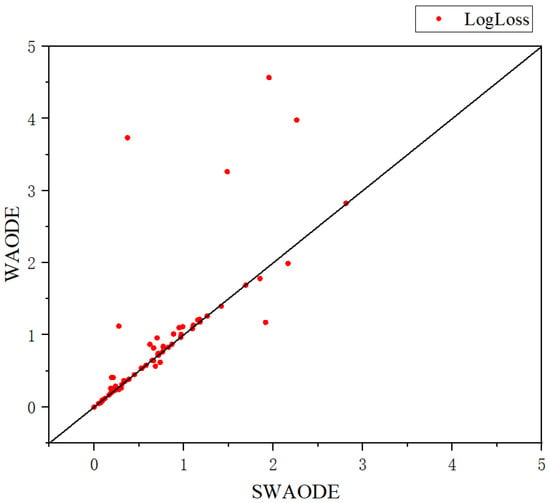
Figure 3. Scatter plot of LogLoss.

5.3. Ablation Studies

To delve deeper into the necessity of weighting and model selection for the AODE classification algorithm, we conducted two ablation study experiments to validate its impact in this section, again using W/D/L (win/draw/loss) as the measure. These experiments aimed to dissect the performance of the SWAODE algorithm in the absence of weighting and model selection, thus highlighting the crucial role of weighting and model selection in improving the classification performance of SWAODE. In our experiments, we implemented the WAODE-MI algorithm, which uses MI as a weight, and the SAODE algorithm, which performs model selection on AODE. The SWAODE algorithm was compared with these two algorithms in terms of ZOL and LogLoss metrics.

According to Table 7, the SWAODE algorithm achieved 34 wins/12 draws/24 losses and 42 wins/7 draws/21 losses in the two comparisons with the WAODE-MI algorithm. It also performed well in the comparison with SAODE, achieving 27 wins/22 draws/21 losses and 40 wins/4 draws/26 losses, respectively. Therefore, we can conclude that both weighting and model selection are necessary and indispensable in the SWAODE algorithm, and the algorithm is able to fully draw on the advantages of weighting and model selection to greatly improve the classification performance of the AODE algorithm.

Table 7. Ablation Studies.

		WAODE-MI	SAODE
ZOL	SWAODE	34/12/24	27/22/21
	WAODE-MI		25/8/37
LogLoss	SWAODE	42/7/21	40/4/26
	WAODE-MI		24/0/46

6. Conclusions

This study proposed a new AODE classification algorithm, the SWAODE algorithm, which aimed to solve the problem of existing cross-validation risk minimization strategies not considering the difference in attributes in classification decisions. The core idea of the algorithm lay in first weighting each ODE in the AODE which used the MI values as the weights. Subsequently, a leave-one-out cross-validation (LOOCV) method was used to perform model selection on these weighted sub-models in order to select the optimal model. Experimental results indicated the SWAODE algorithm markedly surpassed other well-known popular classification algorithms on multiple datasets, exhibiting higher classification efficiency and generalization ability.

However, we recognize that this is only one aspect of model selection and that many potential extensions deserve further exploration. The next step of our work will focus on exploring the extension of attribute-weighted AODE classification models. Overall, further exploration of attribute-weighted AODE classification models is a challenging but promising research direction. By delving into this area, we hope to bring innovative ideas and tools to research related to machine learning and data mining.