Abstract
Recently, studies on early-exit mechanisms have emerged to reduce the computational cost during the inference process of deep learning models. However, most existing early-exit architectures simply determine early exiting based only on a target confidence level in the prediction, without any consideration of the computational cost. Such an early-exit criterion fails to balance accuracy and cost, making it difficult to use in various environments. To address this problem, we propose a novel, cost-effective early-exit architecture in which an early-exit criterion is designed based on the Markov decision process (MDP). Since the early-exit decisions within an early-exit model are sequential, we model them as an MDP problem to maximize accuracy as much as possible while minimizing the computational cost. Then, we develop a cost-effective early-exit algorithm using reinforcement learning that solves the MDP problem. For each input sample, the algorithm dynamically makes early-exit decisions considering the relative importance of accuracy and computational cost in a given environment, thereby balancing the trade-off between accuracy and cost regardless of the environment. Consequently, it can be used in various environments, even in a resource-constrained environment. Through extensive experiments, we demonstrate that our proposed architecture can effectively balance the trade-off in different environments, while the existing architectures fail to do so since they focus only on reducing their cost while preventing the degradation of accuracy.
MSC:
68T01
1. Introduction
With the advancement of machine learning through extensive research, deep learning models have emerged that achieve remarkable performance in various applications [1]. Although these models have excellent performance across a wide range of applications [2,3,4], they often require significant computational burdens for execution due to their complex structures. As a result, using deep learning models often poses a problem in terms of time-consuming processing and a high computational cost [5]. In particular, this problem is severe in computational resource-constrained environments such as mobile devices and edge computing environments [6,7]. To address this issue, several recent studies have focused on improving the efficiency of the inference process in deep learning models [8]. One such study of an early-exit mechanism [9] leverages the fact that an inference using the intermediate features that can be obtained in the middle of the inference process via a deep learning model can be accurate enough as well [10]. Specifically, the mechanism uses an early-exit deep learning model architecture that includes one or more additional intermediate exit points, each of which can produce a model prediction using the intermediate features at the exit point. As input data propagate through the model and arrive at each exit point, the model prediction is returned, and the mechanism determines whether to exit early with the prediction using an early-exit criterion.
This early-exit mechanism can reduce the computational costs of the inference process by avoiding the execution of the entire model and thus has been widely studied [11,12,13,14,15,16,17,18]. However, at the same time, it can deteriorate the model’s accuracy because the features at deeper layers are not used [19]. Therefore, when using the early-exit mechanism, it is important to carefully consider the trade-off between accuracy and cost, which can be controlled by the early-exit criterion. Nevertheless, most existing works on early-exit architectures design the criterion focusing on the accuracy [11,12,15]; they compute the credibility of the prediction at each early-exit point and then compare it with a predefined fixed threshold. This criterion simply reduces the computational cost while preventing the accuracy from degrading beyond a certain target level, and it has no capability to balance the trade-off between accuracy and costs according to different environments. Therefore, it is especially difficult to use in resource-constrained environments, where cost reduction is more significant than accuracy. Furthermore, the criterion cannot dynamically adapt to the input sample of each inference, which implies that early-exit decisions do not consider the characteristics of each sample.
To address such dynamic decision-making as in the early-exit deep learning model, Markov decision-making (MDP) can be used. MDP provides a mathematical framework for modeling sequential decision-making to achieve a specific goal, where the environment has different states and actions [20]. It has been widely used to address decision-making problems in various applications, from recommendation systems [21,22] to communication networks [23,24]. The early-exit decision-making in early-exit models is sequential because of the nature of deep learning models. Specifically, in the inference process of a model, the input features propagate in a forward direction, passing through each layer of the model sequentially [25]. Therefore, MDP can be used for dynamic decision-making in early-exit models to balance the trade-off between accuracy and costs.
1.1. Preliminaries on Early-Exit Architecture
A typical early-exit model consists of two main components: a backbone neural network and early-exit points. The backbone neural network indicates neural network models for feature representation, such as ResNet [5] and VGG-Net [26], which are composed of multiple layers that transform the input sample. The backbone neural network serves as a base deep learning model for constructing the early-exit model. As an input sample propagates through the backbone neural network, the features from the input sample are extracted at each layer by progressively transforming the input sample into higher-level features. Early-exit points are strategically placed between two consecutive layers within the backbone neural network to enable intermediate predictions based on the intermediate features. Each early-exit point includes a predictor that returns an intermediate model prediction using the intermediate features at the early-exit point, which are computed from the first layer of the network to that point. To train the early-exit model, the loss function is defined by jointly considering the classification loss at the predictors, including those at the early-exit points [11]. Then, as in typical deep learning, the early-exit model is trained on a given dataset by using the loss function.
In an inference process of the early-exit model after training, an early-exit decision at each early-exit point should be determined differently for each input sample, since the prediction at each early-exit point depends on the input sample. Once an input sample arrives, it sequentially passes through the backbone layers until reaching the first early-exit point, extracting features along the way. Upon reaching the first early-exit point, the predictor at that early-exit point computes the intermediate model prediction using the intermediate features. Then, the decision of whether to exit at that point is determined by using an early-exit criterion. There may be a variety of approaches to the early-exit criterion, but for the sake of generalized description, we do not specify the criterion here. If the early-exit criterion is met, the model stops its computation for the inference process and uses the intermediate model prediction from the predictor at the early-exit point as a model output; otherwise, the model continues with the computations on the backbone layers until it reaches the next early-exit point. This procedure is repeated until the model stops its inference process at any early-exit point or the final layer of the backbone neural network. The early-exit model can reduce computational costs by exiting the inference process earlier. However, this may lead to a degradation in accuracy due to the omission of feature extraction by the later layers.
To prevent a decrease in accuracy, existing early-exit models use the credibility of predictions as an early-exit criterion [11,12,13,14,15,16,17,18]. For example, in classification problems, they use the entropy or maximum predicted class probability of a classification result as a measure of confidence in the prediction. Then, the early-exit decision is made by simply comparing it with a predefined fixed threshold, as illustrated in Figure 1. In the figure, denotes the estimated credibility of predictions at exit point t with a given , where is the predicted probabilities over classes at exit point t and is the target credibility (i.e., the threshold for early exit). If the credibility at each exit point exceeds the target credibility (i.e., ), the early-exit model decides to exit at that point and uses the predicted class probabilities at that point for prediction. This simple threshold-based early-exit decision allows the model to reduce its computational cost while preventing the accuracy from falling below a certain target level. However, it severely restricts the flexibility of early-exit models in the trade-off between accuracy and costs so as to effectively address diverse environments. In particular, there is no explicit way to find the best threshold for each early-exit point to balance the trade-off in a given environment. For instance, a threshold suitable for an input sample may not be appropriate for another input sample, which leads to a decrease in performance. Therefore, to overcome this limitation, a novel early-exit criterion is necessary that makes early-exit decisions adaptively to the given environment and input sample, rather than using such a fixed threshold.
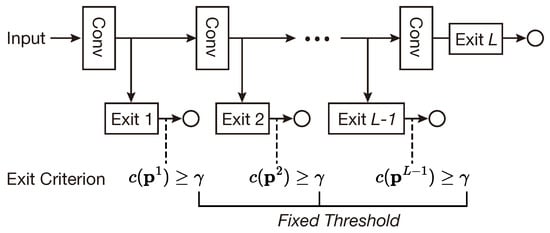
Figure 1.
The illustration of the conventional early-exit architecture. The circles represent a prediction of the model. In the exit criterion, denotes the estimated credibility of prediction at exit point t, and is a predefined fixed threshold that represents the target credibility in the early-exit architecture.
1.2. Our Contributions
In this paper, we propose a novel cost-effective early-exit architecture based on MDP that makes early-exit decisions dynamically instead of simply using a fixed early-exit criterion. To this end, we first formulate a cost-effective early-exit problem for sequential early-exit decision-making in the form of MDP. The problem maximizes accuracy as much as possible while minimizing computational costs, considering the relative importance between them. We then develop a cost-effective early-exit algorithm to solve the problem by using reinforcement learning. For a given early-exit model, the algorithm learns the optimal cost-effective early-exit policy that can address the sequential decision-making of the model. By using the policy as an early-exit criterion for the given early-exit model, the proposed architecture can make the early-exit decisions dynamically, considering both computational cost and accuracy. The cost-effective early-exit architecture is illustrated in Figure 2. The main contributions of the paper are summarized as follows:
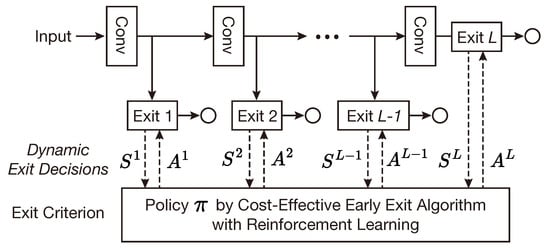
Figure 2.
The illustration of the cost-effective early-exit architecture with reinforcement learning. The circles represent a prediction of the model.
- We model the procedure in a typical early-exit model as an MDP formulation that makes sequential early-exit decisions at each exit point. This formulation allows us to design an early-exit criterion of the model that dynamically decides whether to exit or not to exit at each exit point in order to systematically achieve a goal specified as a cumulative reward in MDP.
- We propose a cost-effective early-exit architecture that can be applied to any type of early-exit model. The cost-effective early-exit algorithm in the architecture enables the early-exit model to balance the trade-off between accuracy and cost regardless of the environment, using reinforcement learning. Furthermore, it adaptively makes early-exit decisions to each input sample for prediction, considering the characteristics of the input sample.
- Through experimental results using a synthetic early-exit model, we verify that our proposed architecture addresses the trade-off according to the relative importance of computational cost compared with accuracy. Furthermore, we demonstrate via experiments using real datasets that it can do so effectively even in various practical environments, while the state-of-the-art baselines cannot.
1.3. Paper Structure
This paper is organized as follows. Section 2 provides the MDP formulation for cost-effective early exiting considered in this paper. In Section 3, we develop a cost-effective early-exit architecture based on reinforcement learning. We provide experimental results in Section 4 and finally conclude in Section 5.
2. MDP Formulation for Cost-Effective Early Exiting
2.1. Deep Learning Model with Early-Exit Architecture
We consider a typical early-exit model trained on dataset for classification with total K classes. (It is worth noting that the classification model is considered for clear presentation in the context of most related works [11,12,13,14,15,16,17,18,19]. The architecture proposed in this paper can also be used for a wide range of applications for which the existing early-exit architectures are used.) We denote the index of early-exit points as . At each early-exit point, the model determines whether to exit early based on the early-exit criterion, based on the computations performed in the backbone neural network before the early-exit point. To make the early-exit decision, the model requires intermediate information such as the index of exit points and the predicted class probabilities. We first define the location vector at exit point t, as a one-hot vector with L dimensions, where the t-th element is 1 and all other elements are 0. It represents the location of the exit point within the model. At each exit point, the classifier outputs the predicted class probabilities. We denote the predicted class probability of class k at exit point t by . Then, we define the vector of predicted class probabilities at exit point t as , where ⊤ denotes a transpose operator to ensure is a column vector. The model can make the early-exit decision using the intermediate information at early-exit point t. For example, in the conventional early-exit architecture, the entropy or maximum predicted class probability based on is compared to a predefined fixed threshold as a measure of confidence in the prediction to determine whether to exit early. If it decides to exit, the inference is made, i.e., making a class prediction , using the predicted class probabilities at exit point t without any further computations from the exit point to the final layer. Typically, the class prediction at exit point t is determined by using the class probabilities at the exit point as
where is the set of classes. On the other hand, if it does not exit, the model executes the subsequent layers, which can extract more advanced features until the next exit point. Such an additional computation typically results in higher prediction accuracy but, at the same time, incurs additional computational costs. Thus, there exists a trade-off between accuracy and cost in early-exit decisions.
2.2. Design of Early-Exit Criterion Based on MDP
For cost-effective early exiting, early-exit decisions should be carefully determined considering the trade-off between accuracy and costs. However, the existing early-exit architectures decide early exiting using a confidence level to the prediction only, without any consideration of computational costs [11,12,15]. Hence, they do not carefully consider the trade-off in early-exit decisions.
To address this issue, we first formulate an early-exit problem that determines early-exit decisions in the form of MDP. For each data sample that arrives at the model, early-exit decisions (i.e., whether to exit or not to exit) should be determined at the early-exit points until the inference for the data sample is complete. Furthermore, from the perspective of the trade-off between accuracy and cost, each decision at the exit point incurs a corresponding reward such as computational cost (i.e., negative reward) and prediction result (i.e., positive reward). In the context of MDP, such a sequential inference process of each data sample can be represented as a single episode with a finite horizon. Specifically, each episode consists of a trajectory of exit points, and its termination corresponds to the completion of inference. Therefore, the length of the horizon is limited by the number of early-exit points within the early-exit model. This sequential decision-making in the early-exit model can be described well by MDP, as illustrated in Figure 3. Using this MDP formulation, we can design an early-exit criterion of early-exit models that can systematically achieve a goal specified as a cumulative reward. Such a criterion dynamically determines whether to exit or not to exit at each exit point with the given state information in the exit point to maximize the expected cumulative reward. Therefore, using the MDP formulation for sequential early-exit decisions, we can design a variety of early-exit criteria, each of which pursues a different goal specified by an appropriate reward structure.
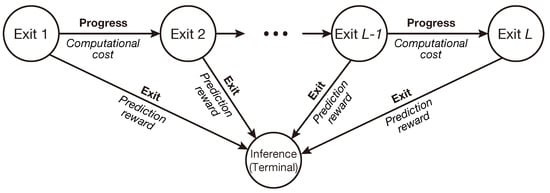
Figure 3.
The illustration of sequential early-exit decisions in MDP. The text on each edge in bold denotes an action and that in italics denotes a reward.
2.3. MDP-Based Cost-Effective Early-Exit Problem
Here, we will define the MDP problem for the cost-effective early-exit architecture by appropriately defining the state information at each exit point and the corresponding reward for the early-exit decision. Then, a cost-effective early-exit criterion that solves the problem can balance the trade-off between computational cost and accuracy. For the cost-effective early-exit MDP problem, we define the inference state information at exit point t as , which can implicitly represent the credibility of the inference. For example, the vector of predicted class probabilities at exit point t, , or the measures of the confidence in the prediction, such as the entropy or the maximum predicted class probability, can be used for . This inference state information depends on each input sample, thereby allowing the cost-effective early exit problem to consider the sample-wise characteristics such as how easy it is to predict. Then, the state at exit point t is
where is the state space. We also define the action at exit point t, which represents whether the model exits or not at exit point t as
where is the action space, denotes an early exit action, and denotes a progression action to exit point . Note that when is chosen, the episode will be terminated, and at the final layer, is forcibly chosen (i.e., ).
After the model decides the action at exit point t, the corresponding reward is observed. For , the reward is determined based on the class prediction in (1), with a value of 1 assigned if it is correct (i.e., if , where y is a true label) and with a value of 0 assigned otherwise; for , the reward is given as a penalty for the computational cost until the next exit point, denoted by . Note that the penalty can be considered as a negative reward. Then, the reward at exit point t is summarized as
where is an indicator function that takes a value of 1 if the argument is true and 0 otherwise. The size of the penalty for the computational cost at each exit point allows the MDP problem to control how much the cost is emphasized compared with the prediction reward. The expected cumulative reward is given as
where denotes the exit point at which the model exits. From the cumulative reward in (5), in typical cases, we can see that the sum of the penalties should satisfy the following condition:
Since in (4), the reward for a correct prediction is given as 1, the optimal policy for early-exit decisions never decides on actions whose total penalty due to computational costs exceeds the value of 1. Therefore, this condition ensures that the early-exit model can use the entire layers for prediction.
Based on the above ingredients, we can formulate the MDP problem of finding the optimal policy that maximizes the expected cumulative rewards over episodes as
where is the reward in (4) with the action followed by policy . At the end of each episode (i.e., when the model exits the inference process), the cumulative reward consists of not only the reward from the class prediction but also the cumulative penalties from the first layer to the exit point (i.e., the computational cost for the prediction). Thus, the optimal policy determines whether to exit or not to exit at each exit point while balancing the trade-off between accuracy and costs. Specifically, it tries to maximize the accuracy as much as possible (to earn the prediction reward) while minimizing the computational costs (to minimize the penalty). Furthermore, the penalty can be tailored according to the goal of utilizing a model but considering the condition (6). For instance, if the primary goal of the model is to save computational costs, it can be achieved by increasing the penalty. With such a large penalty, the model will exit earlier even if it sacrifices accuracy. Conversely, if the primary goal of the model is to achieve higher accuracy, it can be accomplished by decreasing the penalty. If the penalty is smaller, the model will not exit early to improve accuracy, even if it incurs more penalty. In an extreme case, if the penalty is zero, then the architecture always uses the entire model.
Remark 1.
This MDP formulation can address the case with a large number of exit points. Suppose there is an early-exit model with infinite early-exit points (i.e., ). Then, there is a particular exit point where the accumulated computational cost exceeds the reward of correctly predicting the class. There is no cause for a progression beyond the particular exit point since the progression will always result in a negative cumulative reward. As a result, the optimal policy in that case is expected to always not progress beyond the particular exit point while behaving similarly to the policy in the case with finite early-exit points near the input layer.
3. Cost-Effective Early Exit with Reinforcement Learning
3.1. Cost-Effective Early-Exit Architecture with Deep Reinforcement Learning
To design a cost-effective early-exit architecture, we propose a cost-effective early-exit algorithm to solve the cost-effective early-exit problem in (7). The policy obtained by solving the problem makes dynamic early-exit decisions while balancing the trade-off between accuracy and costs. Then, to implement the cost-effective early-exit architecture, it can be used as an early-exit criterion, as illustrated in Figure 2. The MDP problems can be solved by using dynamic programming algorithms if the transition probabilities are perfectly known and stationary. In other words, the optimal policy for the MDP problem can be identified by solving the MDP problem using dynamic programming algorithms. The optimal policy allows us to determine the optimal action for any given state. However, in problem (7), it is impractical that the transition of the inference state information is perfectly known in advance. In addition, it is difficult to directly use dynamic programming algorithms for the cost-effective early exit problem due to the continuous nature of the state space. Therefore, we use reinforcement learning to solve the cost-effective early exit problem, which is one of the representative approaches to solving MDP problems.
Here, we consider a typical deep Q-network (DQN) method with experience replay and a target Q-network rather than traditional reinforcement learning methods such as Q-learning and SARSA, due to their computational issues with complex systems [27]. It is worth noting that we use the DQN, a well-known deep reinforcement learning method, but any other deep reinforcement learning methods can also be used. The DQN method can find the optimal policy by approximating the optimal state-action value function , even without any prior information on the transition probabilities. It stably and efficiently trains a neural network to approximate across the continuous state space thanks to the representational capability of the neural network. Although the DQN method does not theoretically guarantee learning the optimal policy , it has been widely shown that the DQN method typically converges to the near-optimal performance [28]. We refer the readers to [29] for details about DQN. First, the algorithm trains a cost-effective early-exit policy, and then, the trained policy is used for early-exit decision-making to implement a cost-effective early-exit architecture as in Figure 2.
3.2. Description of Cost-Effective Early-Exit Algorithm
To describe the cost-effective early-exit algorithm, we consider a target early-exit model trained on the dataset and computational costs . The target model is a model to which the algorithm will be applied so as to implement the cost-effective early-exit architecture. The algorithm comprises a training stage and an exploitation stage. In the training stage, a cost-effective early exit policy is trained for target early-exit model with given computational costs to which the policy will be applied. It is worth noting that the dataset used to train the early-exit model can also be used to train the cost-effective early exit policy, so no additional dataset is required. Specifically, the data for training the cost-effective early exit policy (i.e., the experience in reinforcement learning) can be generated using dataset during the training stage. The details will be described in the following. In the exploitation stage, the trained policy is used to make early-exit decisions for the model. The cost-effective early-exit algorithm is summarized in Algorithm 1.
| Algorithm 1: Cost-Effective Early-Exit Algorithm |
|
In the training stage, first, a replay buffer and Q-networks and are initialized, where and are the weights of the main and target Q-networks, respectively (line 2). Then, a training process in lines 3–13 of Algorithm 1 is repeated for the samples in dataset , where each sample represents a single episode. For each sample, exit point t is initialized as 1, and state s at exit point 1 is observed from early-exit model (line 4). In exit point t, action a is chosen using -greedy with to ensure exploration if , and otherwise, action a is chosen as since it is at the final layer (line 6). The -greedy strategy for sampling action is given as
This strategy ensures the exploration across the actions by choosing a random action with probability . Such an exploration strategy can help the algorithm identify the best one. It is worth noting that another action sampling strategy to balance exploration and exploitation [30]. The early-exit model performs action a and then observes the state at exit point , , and reward, as in (4) (line 7). Specifically, if action a is , the model executes the subsequent layers until the exit point, resulting in the next state and the corresponding penalty ; otherwise, the model completes the inference of the current sample, resulting in the corresponding reward according to the class prediction. After observing the next state and reward according to state s and action a, the experience for training the Q-networks can be constructed. Then, the experience is stored in the replay buffer (line 8). The stored experiences are sampled later to construct a minibatch for training the Q-networks instead of being used immediately. This mitigates the correlation problem of the consecutive experiences. Once the operation at exit point t is complete, then state s is updated to the next state , and the index of exit point t is incremented by 1 (line 9). These operations are repeated until action a is given by . After a sufficient number of experiences are stored in the replay buffer, a minibatch is randomly sampled from the replay buffer. This experience sampling from the replay buffer avoids overfitting the Q-network with recent experiences by ensuring that the experiences used for training are not too closely correlated. The target state-action value for experience is calculated by using the target Q-networks as
Using each sampled experience in the minibatch, the loss function is established using the target state-action value in (9) as follows:
The main Q-network is trained using a gradient descent method, minimizing the loss function L with respect to (line 11). In addition, the target Q-network is periodically updated as the weights of the main Q-network for every target update interval (line 12). This target Q-network, separate from the main one, ensures that the target state-action value will be stable from changing with each update of the weights of the main Q-network.
In the exploitation stage, the cost-effective early-exit policy for early-exit model can be implemented by using the trained Q-network , which approximates the optimal state–action value function . Since the trained Q-network provides the approximated optimal state–action value (i.e., the expected cumulative reward) for each state–action pair, the model can deterministically choose the action that has the maximum state–action value for any given state. In summary, for any given state from model , we can obtain the approximated optimal action using . To this end, first, the Q-network of the trained policy is loaded using the weights of the trained Q-network (line 16). Then, for each arrival sample at early-exit model , the trained policy is applied (lines 17–25). As in the training stage, at each exit point, action a is chosen by using the Q-network with given state s. However, in the exploitation stage, exploration is no longer required. Therefore, the action is chosen greedily (line 20), not with the -greedy strategy, as follows:
Then, the early-exit model performs the chosen action a, and the next state is observed (lines 21). As in the training stage, once the operation at exit point t is complete, state s is updated to the next state and the index of exit point t is incremented by 1 (lines 22). This procedure is repeated until the model exits, as illustrated in Figure 2. After exiting, the model terminates the inference process for the arrival sample to output the class prediction at the exit point (line 24).
4. Experimental Result
In this section, we present experimental results in three environments to demonstrate the effectiveness of our proposed cost-effective early-exit architecture (CE3A). In a toy example environment, we validate that CE3A works as expected by using synthetic early-exit scenarios with Gaussian noise. On the other hand, in a real dataset environment, we apply CE3A to the CIFAR-10 and CIFAR-100 datasets to evaluate CE3A with the existing early-exit architectures using thresholds. For each environment, we run 10 experiment instances with 10,000 data samples and average their results. In the figures, the minimum and maximum values are provided.
4.1. Toy Example Environment
In the toy example environment, instead of constructing an actual early-exit model for real datasets, we simply emulate the inference process of an early-exit classification model with five early-exit points. Specifically, in the emulation, whether each (virtual) data sample will be correctly classified at exit point t is probabilistically determined, where the probability is denoted by . To generate the probability, we define the base probabilities for exit points as , reflecting the increasing classification accuracy as exit points move farther from the first layer. Then, for each data sample, the probability at exit point t is set by adding Gaussian noise with a standard deviation of 0.1 to its base probability. Finally, we use such an emulated early-exit model for CE3A, where is used as (i.e., the state at exit point t is given by ). Using the emulated model, we train the cost-effective early-exit algorithm with reinforcement learning and run CE3A for testing. It is worth emphasizing that through experiments in this toy example environment, we can verify the behavior of CE3A without any bias or imprecision that might be caused by using real datasets.
In Table 1, we provide the experimental results of CE3A, including the accuracy, cost, and cumulative reward. The results are provided by varying the penalty as , each of which represents the environment with different resource limitations. To evaluate CE3A, we provide the results of a model without early exiting, whose cost is therefore always given by four times the penalty. From the table, we can see that CE3A achieves cumulative rewards larger than or equal to those of the non-early-exit model regardless of the penalty, which implies a better capability to address the trade-off between accuracy and cost. When the penalty is excessively large compared with the reward that can be earned via correct predictions (e.g., 0.3), CE3A reduces the costs while sacrificing accuracy. On the other hand, when the penalty is negligible (e.g., 0.01), it achieves the accuracy and cost significantly close to those of the no early-exit model.

Table 1.
The experimental results varying the penalty in the toy example environment.
For further investigation of the behavior of CE3A, we provide the ratio of the number of data samples that have exited at each exit point by CE3A according to the penalty in Figure 4. From the figure, when the penalty is excessively large, we can see that CE3A exits most data samples at the first exit point to avoid the penalty. As the penalty decreases, it becomes more forgiving of the computations up to the next exit point. This trend clearly shows that CE3A can address the trade-off between accuracy and computational costs in the early-exit model.
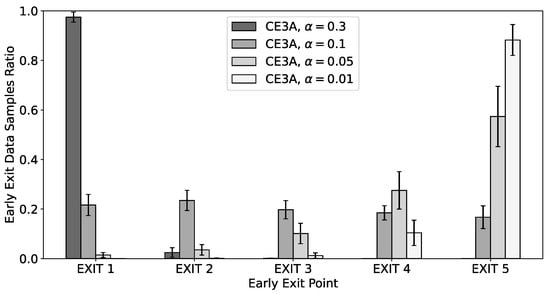
Figure 4.
The ratio of the number of data samples that have exited at each exit point in the toy-example environment.
4.2. Real Dataset Environment with CIFAR-10
In the real dataset environment, first, we construct and train an actual early exit classification model with five early-exit points based on ResNet [5] using the CIFAR-10 dataset. The trained model achieves accuracies of at each exit point for the validation data samples. For the state at exit point t used in CE3A the vector of the predicted class probabilities at exit point t, , is used as (i.e., the state at exit point t is given by ). We then perform the cost-effective early-exit algorithm with reinforcement learning using the training dataset. Through experiments in this real dataset environment, we can validate the practicality of CE3A in the real world and evaluate its performance by comparing it with existing state-of-the-art early-exit decision approaches.
In particular, we compare CE3A with the following two major early-exit decision approaches: an approach with an entropy-based threshold (Entropy) [11,12,13,14] and an approach with a maximum class probability-based threshold (MaxProb) [15,16,17,18]. In Entropy, the entropy of the predicted class probabilities at each exit point is calculated. Since the lower entropy implies a more confident prediction, if the entropy is lower than its threshold, it makes a decision to exit early. In MaxProb, the maximum probability across the predicted class probabilities at each exit point is compared with its threshold. If the maximum probability is larger than the threshold, MaxProb decides to exit early. In the simulation, we set the thresholds of Entropy and MaxProb to be 0.2 and 0.85, respectively, considering the threshold values optimized in the related works using ResNet for evaluation [11,17,19]. We summarize the existing early-exit decision approaches in Table 2.

Table 2.
The comparison of the existing early-exit decision approaches.
In Table 3, we provide the experimental results of CE3A with penalties , similar to the results in the toy example environment. In addition, the results of the existing approaches (i.e., Entropy and MaxProb) are presented. It is worth noting that the penalty (i.e., the computational cost in the model) does not affect the early-exit decisions by Entropy and MaxProb, so their accuracy is identical regardless of the penalty. From the table, we can see that CE3A achieves larger cumulative rewards compared with the existing approaches regardless of the penalty. As shown in the results in the toy example environments, CE3A balances the trade-off between accuracy and cost to maximize the cumulative reward, while the existing approaches fail to do so. In particular, as the penalty becomes larger, the gap in the cumulative rewards between CE3A and the other approaches becomes larger as well. This is because they decide to exit early only if the confidence in the predictions is high regardless of the penalty, causing a significant increment in computation costs.

Table 3.
The evaluation results varying the penalty in the CIFAR-10 dataset environment.
We provide the ratio of the number of data samples that have exited at each exit point in Figure 5 to further investigate the results. The ratio of Entropy and MaxProb is not provided for the different penalties since their early-exit decisions are not affected by the penalty . First, Entropy and MaxProb decide to similarly exit most data samples at exit points 4 or 5 due to their thresholds, which ensure high confidence in predictions. On the other hand, the behavior of CE3A highly depends on the penalty. The overall trend of CE3A in the real dataset environment is similar to that in the toy example environment; when the penalty is large, CE3A favors the exit points near the input layer; otherwise, it favors those near the final layer. However, when we examine it in more detail, we can see that a significant proportion of data samples exit at the exit points near the input layer (e.g., exit points 1 and 2), even if the penalty is sufficiently small (e.g., 0.01). Furthermore, the accuracy of CE3A does not deteriorate, as presented in Table 3, despite such early-exit decisions being near the input layer and the quite low average accuracies at the exit points. This happens because each sample in the real dataset has different characteristics (e.g., how easy to predict it is). Indeed, in image classification, some samples can be easily classified only using feature extraction with a low effort, while some samples cannot [31]. Hence, this result demonstrates that CE3A makes its early-exit decisions adaptively considering the characteristics of each sample. From those results using the real dataset, we can see that CE3A can effectively address the trade-off between accuracy and cost in practice by determining early exit adaptively to each sample.
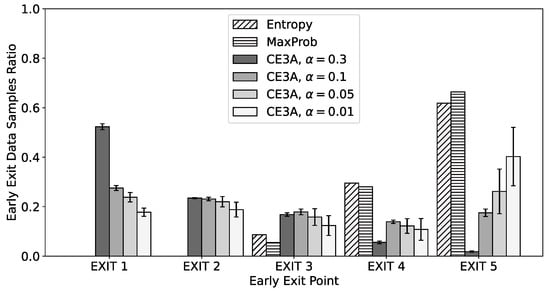
Figure 5.
The ratio of the number of data samples that have exited at each exit point in the CIFAR-10 dataset environment.
4.3. Real Dataset Environment with CIFAR-100
We now use the CIFAR-100 dataset to consider a more realistic environment compared with CIFAR-10. As in the environment with CIFAR-10, we construct an early exit classification model with five early-exit points based on ResNet and train it using the CIFAR-100 dataset. The trained model achieves accuracies of at each exit point for the validation data samples. The state at exit point t is defined as , identical to that in the environment with CIFAR-10. We then use the CIFAR-100 training dataset to perform the cost-effective early-exit algorithm. It is worth emphasizing that in the environment with CIFAR-100, the dimension of is very large due to its large number of classes, i.e., , which leads to a large state space. Therefore, this further experiment with CIFAR-100 clearly validates the practicality of CE3A in realistic environments where the size of the state space is large. We compare CE3A with the existing early-exit decision approaches presented in Table 2.
Table 4 provides the experimental results of Entropy, MaxProb, and CE3A with penalties . In the table, CE3A achieves the larger or close cumulative rewards compared to Entropy and MaxProb, regardless of the penalty. This result shows that CE3A maximizes the cumulative reward by balancing accuracy and cost, as also shown in the results above, even in the larger state space with the CIFAR-100 dataset of 100 classes. In addition, the existing approaches fail to balance accuracy and cost, as shown in the experimental results with CIFAR-10. The similar trend of this result to the result with CIFAR-10 clearly shows the practicalness of CE3A even with a dataset with a larger number of classes.

Table 4.
The evaluation results varying the penalty in the CIFAR-100 dataset environment.
For further investigation of the results, we provide the ratio of the number of data samples that have exited at each exit point in Figure 6. From the figure, we can see that the overall trend in the ratio of the number of data samples is similar to that in the environment with CIFAR-10: CE3A favors exit points near the input layer when the penalty is large and otherwise favors exit points near the final layer; Entropy and MaxProb favors exit points near the final layer. In particular, contrary to the existing approaches, CE3A does not decide to exit at exit point 4 in most cases since the difference in accuracy between exit points 3 and 4 is not large enough to tolerate the additional cost penalty. These results clearly show the capability of CE3A to address the trade-off between accuracy and cost by dynamically making the early-exit decision.
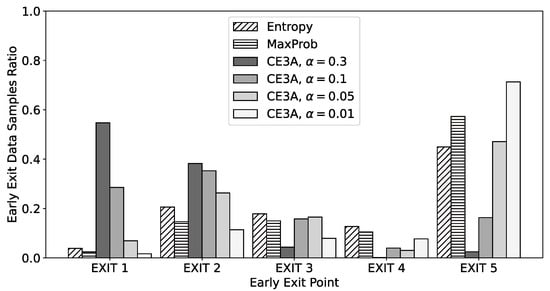
Figure 6.
The ratio of the number of data samples that have exited at each exit point in the CIFAR-100 dataset environment.
5. Conclusions and Future Work
In this paper, we proposed a novel cost-efficient early-exit architecture based on MDP to allow early-exit models to dynamically make early-exit decisions while considering the trade-off between accuracy and cost. To this end, we first modeled the early-exit decision-making in typical early-exit deep learning models in the form of MDP. This enables the architecture to determine the decisions dynamically considering a goal specified by a reward structure. Based on the MDP formulation, we defined the cost-effective early-exit MDP problem that maximizes accuracy while minimizing computational costs, considering the relative importance between them. Then, we developed a cost-effective early-exit algorithm using reinforcement learning to find a policy that solves the problem. The proposed architecture can be applied to any type of early-exit model to appropriately address the trade-off between accuracy and cost in the early-exit model. Through experiments using synthetic and two real datasets, we demonstrated that the proposed architecture can achieve cost-efficiency by effectively balancing the trade-off, while the existing architectures fail to do so. In particular, it is shown that the proposed architecture can address different environments in which the relative importance of computational cost compared with accuracy varies by simply adjusting the penalty. Consequently, it outperforms the existing early-exit criterion based on the prediction credibility evaluation.
As a future work, a non-stationary environment in which the resource constraints dynamically change can be considered in the proposed framework. In such an environment, the characteristics of the cost-effective early-exit MDP problem change. Therefore, the cost-effective early exit policy should adaptively change its strategy according to the environment. In addition, the proposed framework can be improved by focusing on various applications such as semantic segmentation and natural language processing and is not limited to the classification tasks considered in this paper.
Author Contributions
Conceptualization, H.-S.L. and K.-S.K.; methodology, K.-S.K.; software, K.-S.K.; validation, K.-S.K.; formal analysis, H.-S.L. and K.-S.K.; investigation, K.-S.K.; resources, H.-S.L.; data curation, K.-S.K.; writing—original draft preparation, K.-S.K.; writing—review and editing, H.-S.L.; visualization, H.-S.L.; supervision, H.-S.L.; project administration, H.-S.L.; funding acquisition, H.-S.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Technology Innovation Program (RS-2022-00154678, Development of Intelligent Sensor Platform Technology for Connected Sensor) funded by the Ministry of Trade, Industry & Energy (MOTIE, Korea).
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Pouyanfar, S.; Sadiq, S.; Yan, Y.; Tian, H.; Tao, Y.; Reyes, M.P.; Shyu, M.L.; Chen, S.C.; Iyengar, S.S. A survey on deep learning: Algorithms, techniques, and applications. ACM Comput. Surv. (CSUR) 2018, 51, 1–36. [Google Scholar] [CrossRef]
- Santana, L.M.Q.d.; Santos, R.M.; Matos, L.N.; Macedo, H.T. Deep Neural Networks for Acoustic Modeling in the Presence of Noise. IEEE Lat. Am. Trans. 2018, 16, 918–925. [Google Scholar] [CrossRef]
- Falcini, F.; Lami, G.; Costanza, A.M. Deep Learning in Automotive Software. IEEE Softw. 2017, 34, 56–63. [Google Scholar] [CrossRef]
- Dai, Y.; Wang, G. A deep inference learning framework for healthcare. Pattern Recognit. Lett. 2020, 139, 17–25. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Kim, Y.D.; Park, E.; Yoo, S.; Choi, T.; Yang, L.; Shin, D. Compression of Deep Convolutional Neural Networks for Fast and Low Power Mobile Applications. In Proceedings of the International Conference on Learning Representations (ICLR), Juan, Puerto Rico, 2–4 May 2016. [Google Scholar]
- Le, K.H.; Le-Minh, K.H.; Thai, H.T. BrainyEdge: An AI-enabled framework for IoT edge computing. ICT Express 2023, 9, 211–221. [Google Scholar] [CrossRef]
- Chen, J.; Ran, X. Deep learning with edge computing: A review. Proc. IEEE 2019, 107, 1655–1674. [Google Scholar] [CrossRef]
- Scardapane, S.; Scarpiniti, M.; Baccarelli, E.; Uncini, A. Why should we add early exits to neural networks? Cogn. Comput. 2020, 12, 954–966. [Google Scholar] [CrossRef]
- Laskaridis, S.; Kouris, A.; Lane, N.D. Adaptive Inference through Early-Exit Networks: Design, CHALLENGES and directions. In Proceedings of the International Workshop on Embedded and Mobile Deep Learning (EMDL), Virtual, 24 June 2021. [Google Scholar]
- Teerapittayanon, S.; McDanel, B.; Kung, H.T. BranchyNet: Fast Inference via Early Exiting from Deep Neural Networks. In Proceedings of the IEEE International Conference on Pattern Recognition (ICPR), Cancun, Mexico, 4–8 December 2016; pp. 2464–2469. [Google Scholar]
- Wang, M.; Mo, J.; Lin, J.; Wang, Z.; Du, L. DynExit: A Dynamic Early-Exit Strategy for Deep Residual Networks. In Proceedings of the IEEE International Workshop on Signal Processing Systems (SiPS), Nanjing, China, 20–23 October 2019; pp. 178–183. [Google Scholar]
- Liu, W.; Zhou, P.; Zhao, Z.; Wang, Z.; Deng, H.; Ju, Q. Fastbert: A self-distilling bert with adaptive inference time. arXiv 2020, arXiv:2004.02178. [Google Scholar]
- Xin, J.; Tang, R.; Lee, J.; Yu, Y.; Lin, J. DeeBERT: Dynamic early exiting for accelerating BERT inference. arXiv 2020, arXiv:2004.12993. [Google Scholar]
- Bonato, V.; Bouganis, C.S. Class-specific early exit design methodology for convolutional neural networks. Appl. Soft Comput. 2021, 107, 107316. [Google Scholar] [CrossRef]
- Savchenko, A. Fast inference in convolutional neural networks based on sequential three-way decisions. Inf. Sci. 2021, 560, 370–385. [Google Scholar] [CrossRef]
- Dong, R.; Mao, Y.; Zhang, J. Resource-Constrained Edge AI with Early Exit Prediction. J. Commun. Inf. Netw. 2022, 7, 122–134. [Google Scholar] [CrossRef]
- Bajpai, D.J.; Trivedi, V.K.; Yadav, S.L.; Hanawal, M.K. SplitEE: Early Exit in Deep Neural Networks with Split Computing. arXiv 2023, arXiv:2309.09195. [Google Scholar]
- Lee, C.; Hong, S.; Hong, S.; Kim, T. Performance analysis of local exit for distributed deep neural networks over cloud and edge computing. ETRI J. 2020, 42, 658–668. [Google Scholar] [CrossRef]
- Van Otterlo, M.; Wiering, M. Reinforcement Learning and Markov Decision Processes. In Reinforcement Learning: State-of-the-Art; Springer: Berlin/Heidelberg, Germany, 2012; pp. 3–42. [Google Scholar]
- Shani, G.; Heckerman, D.; Brafman, R.I.; Boutilier, C. An MDP-based recommender system. J. Mach. Learn. Res. 2005, 6, 1265–1295. [Google Scholar]
- Lu, Z.; Yang, Q. Partially observable markov decision process for recommender systems. arXiv 2016, arXiv:1608.07793. [Google Scholar]
- Ferrá, H.L.; Lau, K.; Leckie, C.; Tang, A. Applying Reinforcement Learning to Packet Scheduling in Routers. In Proceedings of the Innovative Applications Conference on Artificial Intelligence (IAAI), Acapulco, Mexico, 12–14 August 2003; pp. 79–84. [Google Scholar]
- Wei, Y.; Yu, F.R.; Song, M.; Han, Z. User Scheduling and Resource Allocation in HetNets With Hybrid Energy Supply: An Actor-Critic Reinforcement Learning Approach. IEEE Trans. Wirel. Commun. 2018, 17, 680–692. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An introduction to deep reinforcement learning. Found. Trends Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef]
- Achiam, J.; Knight, E.; Abbeel, P. Towards characterizing divergence in deep Q-learning. arXiv 2019, arXiv:1903.08894. [Google Scholar]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Ladosz, P.; Weng, L.; Kim, M.; Oh, H. Exploration in deep reinforcement learning: A survey. Inf. Fusion 2022, 85, 1–22. [Google Scholar] [CrossRef]
- Wu, T.; Ding, X.; Zhang, H.; Gao, J.; Tang, M.; Du, L.; Qin, B.; Liu, T. Discrimloss: A universal loss for hard samples and incorrect samples discrimination. IEEE Trans. Multimed. 2024, 26, 1957–1968. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).