A Method with Double Inertial Type and Golden Rule Line Search for Solving Variational Inequalities

Abstract

In this work, we study a new line-search rule for solving the pseudomonotone variational inequality problem with non-Lipschitz mapping in real Hilbert spaces as well as provide a strong convergence analysis of the sequence generated by our suggested algorithm with double inertial extrapolation steps. In order to speed up the convergence of projection and contraction methods with inertial steps for solving variational inequalities, we propose a new approach that combines double inertial extrapolation steps, the modified Mann-type projection and contraction method, and the line-search rule, which is based on the golden ratio $(\sqrt{5}+1)/2$. We demonstrate the efficiency, robustness, and stability of the suggested algorithm with numerical examples.

1. Introduction

Let H be a real Hilbert space, C be a nonempty closed convex subset of H, and $⟨·,·⟩$ denote the inner product with the induced norm $\left|\right|·\left|\right|$. The variational inequality problem (VIP) with respect to G is a problem of finding $x\in C$ such that

$$⟨Gx,y-x⟩\ge 0,\forall y\in C,$$

(1)

where G is an operator from C into H. We denote by VI(C,G) the set of solutions of (1). In equilibrium situations where no party may unilaterally enhance their position, this inequality (1) frequently occurs. Applications of VIPs can be found in many domains, including engineering, economics, and optimization. They are strongly associated with equilibrium analysis, game theory, and convex optimization. It offers a more comprehensive foundation for gradient-based algorithms than only gradient descent. These algorithms play a key role in solving large-scale, high-dimensional machine learning challenges. Additionally, decisions made by patients and providers can be informed by machine learning techniques applied to actual healthcare data. According to Hess et al. [1], VIPs can aid in the optimization of treatment plans, resource allocation, as well as customized treatments. Decision making in multi-agent systems requires participant interactions and equilibria. VIPs assist in simulating these interactions and identifying solutions that meet equilibrium requirements. VIPs serve as a strong lens through which we may improve decision making across a variety of areas, generally bridging the gap between optimization, equilibrium, and decision making. Understanding VIPs is crucial for effectively addressing real-world difficulties as machine learning advances (see [1,2] for more information). Moreover, in the context of the equilibrium interpretation, VIPs look for solutions in situations in which none of the participants can strengthen their position. This is similar to the idea of fixed points, which are points that do not change when they undergo a transformation. The computational methods and mathematical underpinnings of fixed-point problems and VIPs are similar. Our capacity to tackle challenging issues in a variety of fields is improved by a better understanding of their relationships. In fact, the set of solutions of the VIP can be expressed in terms of fixed points:

$$\begin{array}{c}\hfill \mathrm{find}{x}^{*}\in C\mathrm{such}\mathrm{that}{x}^{*}=P_C(I-\tau G)x^{*},\end{array}$$

where $\tau$ is a positive real number, I is the identity mapping, and $P_C$ is a metric projection onto C. Recently, many methods have been applied for solving $VI(C,G);$ (see [3,4,5,6,7,8,9,10,11]). In finite-dimensional Euclidean spaces, Korpelvich [12] and Antipin [13] proposed the extragradient method (EM), which is one of the most simple approaches to solving VIP for a monotone and L-Lipschitz continuous mapping G in the following way:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_0\in C,\tau >0,\hfill \\ y_n=P_C(x_n-\tau G{x}_n),\hfill \\ x_{n+1}=P_C(x_n-\tau G{y}_n),\forall n\ge 1,\hfill \end{array}\right.\end{array}$$

(2)

where $L>0,\tau \in (0,\frac{1}{L})$. If $VI(C,G)$ is not empty, the sequence $\left\{x_n\right\}$ generated by EM (2) converges to an element of $VI(C,G)$. However, it should be noted that in EM, one needs to calculate two projections onto the feasible set C in each iteration. If the set C is not simple, the EM becomes very difficult and expensive to implement. In addition, the convergence of the method (2) requires a prior estimate of the Lipschitz constant, which is often difficult to estimate, and we emphasize that the step size defined by the process is too small and reduces the convergence rate of the method.

One of the methods to overcome these drawbacks is known as Projection and Contraction Method (PCM) proposed by He [14] for solving VIP. The PCM can be summarized as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_0\in H,\hfill \\ y_n=P_C(x_n-\tau G{x}_n),\hfill \\ d(x_n,y_n):=(x_n-y_n)-\tau (G{x}_n-G{y}_n),\hfill \\ x_{n+1}=x_n-ϵ{\eta }_{n}d(x_n,y_n),\forall n\ge 0,\hfill \end{array}\right.\end{array}$$

(3)

where $ϵ\in (0,2),\tau \in (0,1/L)$ and

$$\begin{array}{c}\hfill {\eta }_n:=\frac{\varphi (x_n,y_n)}{\parallel d(x_n,y_n){\parallel }^2},\varphi (x_n,y_n):=⟨x_n-y_n,d(x_n,y_n)⟩,\forall n\ge 0.\end{array}$$

where G is a monotone and L-Lipschitz continuous mapping on H. By the assumption of monotonicity on G, they proved that the sequence $\left\{x_n\right\}$ generated by (3) converges weakly to an element of VI(C,G). Many improvements have been made to the projection and contraction approach, which has drawn a lot of attention (see [15,16,17]). To specifically tackle the problem (VIP), Dong et al. [17] combined the projection and contraction approach with the inertial method to create an inertial PCM algorithm.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_0,x_1\in H,\hfill \\ w_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ y_n=P_C(w_n-\tau G{w}_n),\hfill \\ d(w_n,y_n)=(w_n-y_n)-\tau (G{w}_n-G{y}_n),\hfill \\ x_{n+1}=w_n-ϵ{\eta }_{n}d(w_n,y_n),\forall n\ge 1,\hfill \end{array}\right.\end{array}$$

(4)

where $ϵ\in (0,2),\tau \in (0,1/L)$ and

$$\begin{array}{c}\hfill {\eta }_n:=\left\{\begin{array}{c}\frac{\varphi (w_n,y_n)}{\parallel d(w_n,y_n{\parallel }^2},\mathrm{if}d(w_n,y_n)\ne 0,\hfill \\ 0,\mathrm{if}d(w_n,y_n)=0,\hfill \end{array}\right.\end{array}$$

(5)

where $\varphi (w_n,y_n):=⟨w_n-y_n,d(w_n,y_n)⟩$ and $\left\{{\theta }_n\right\}$ is a sequence in $(0,1)$ that controls the inertial term. They proved that under some conditions on the control parameters, the sequence $\left\{x_n\right\}$ generated by (4) converges weakly to an element of $VI(C,G)$. As the step size depends on the Lipschitz constant L, note that the iterative techniques (2) to (4) may not work when the mapping G is not L-Lipschitz continuous or if its Lipschitz constant is unknown. But the behavior of iterative algorithms toward convergence is known to be strongly influenced by the step size selection. The step size is often determined by researchers using the operator’s Lipschitz constant (see [13,14,15,16,17] and references therein). Yet, this method can be limited, particularly when working with mappings that are not Lipschitz. Instead of relying exclusively on the Lipschitz constant, researchers have put forth an alternate step size rule. In 2021, Tian and Xu [18] proposed the following inertial projection and contraction method in a way to avoid this obstacle.

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_0,x_1\in H,\hfill \\ w_n=x_n+{\theta }_n(x_n-x_{n-1}),\hfill \\ y_n=P_C(w_n-{\tau }_{n}G{w}_n),\hfill \\ d(w_n,y_n)=(w_n-y_n)-{\tau }_n(G{w}_n-G{y}_n),\hfill \\ z_n=w_n-ϵ{\eta }_{n}d(w_n,y_n),\hfill \\ x_{n+1}=(1-{\alpha }_n-{\beta }_n)w_n+{\beta }_n{z}_n,\forall n\ge 1,\hfill \end{array}\right.\end{array}$$

(6)

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\}$ are control sequences in $(0,1)$, $ϵ\in (0,2)$ and ${\eta }_n$ is defined in (5). The step size ${\tau }_n$ is chosen to be the largest $\tau \in \{\gamma ,\gamma l,\gamma l^2,\cdots \}$ such that

$$\tau \left|\right|G{w}_n-G{y}_n\left|\right|\le \kappa \left|\right|w_n-y_n\left|\right|,\gamma >0,l\in (0,1),\kappa \in (0,1).$$

They prove that the sequence $\left\{x_n\right\}$ generated by (6) converges strongly to a point in VI(C,G).

It is assumed by this Equation (6) that G is uniformly continuous on C and pseudomonotone. For the purpose of resolving variational inequalities and associated optimization problems, numerous numerical techniques with inertial exponentiation steps have been developed; refer to [3,4,6,17,19,20,21,22,23,24] as well as the citations included. Furthermore, in 2022, Yao et al. [25] introduced double inertial extrapolation steps into extragradient subgradient methods to improve the effectiveness and speed up the rate of convergence of techniques for solving variational inequality problems. The algorithm stability and performance of the approach are enhanced by these steps, which add more momentum. They proposed the following double inertial steps subgradient extragradient method:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{x}_0,x_1\in H,\hfill \\ w_n=x_n+\theta (x_n-x_{n-1}),\hfill \\ u_n=x_n+\delta (x_n-x_{n-1}),\hfill \\ y_n=P_C(u_n-{\tau }_{n}G{u}_n),\hfill \\ x_{n+1}=(1-\alpha )w_n+\alpha P_C(u_n-{\tau }_{n}G{y}_n),\forall n\ge 1,\hfill \end{array}\right.\end{array}$$

(7)

where $G:H\to H$ is L-Lipschitz continuous and pseudomontone. They demonstrated how given the right circumstances, $\left\{x_n\right\}$ produced by (7) converges weakly to an element in VI(C,G). Since then, the study of double inertial-type algorithms for variational inequality problems has attracted more attention (see [26,27,28,29,30]).

With this in mind, we would like to develop a modified double inertial projection and contraction approach that converges at a lesser condition. Specifically, we take the operator to be a uniformly continuous pseudomonotone. We propose a new method that combines the modified Mann-type projection and contraction method, the line-search rule, which is based on the golden ratio $(\sqrt{5}+1)/2$, and double inertial extrapolation steps to speed up the convergence of projection and contraction methods with inertial terms for solving variational inequalities. We provide numerical examples to illustrate the behavior of the proposed method.

2. Preliminaries

We state some known and useful results which will be needed in the proof of our main theorem. In the sequel, we denote strong and weak convergence by “→” and “⇀”, respectively.

Let C be a closed convex subset of a real Hilbert space H. Then, for each $x\in H$, there exists a unique point $z=P_C\left(x\right)$ such that

$$\left|\right|x-z\left|\right|=\underset{y\in C}{inf}\left|\right|x-y\left|\right|.$$

Theoperator $P_C:H\to C$ is called the metric projection from H onto C. The following lemma highlights some important characteristics of the projection operator.

Lemma 1

([20]). Let $x\in H$, and $z\in C$ be any point. Then, we have that $z=P_C\left(x\right)$ if and only if the following relation holds

$$\begin{array}{c}\hfill ⟨x-z,y-z⟩\le 0,\forall y\in C.\end{array}$$

(8)

Definition 1.

An operator $G:H\to H$ is said to be

(a) 

L-Lipschitz continuous with $L>0$ if

$$\left|\right|Gx-Gy\left|\right|\le L\left|\right|x-y\left|\right|,\forall x,y\in H;$$

(b) 

monotone if

$$⟨Gx-Gy,x-y⟩\ge 0,\forall x,y\in H;$$

(c) 

pseudomonotone if

$$\begin{array}{c}\hfill ⟨Gx,y-x⟩\ge 0\Rightarrow ⟨Gy,y-x⟩\ge 0,\forall x,y\in H.\end{array}$$

(9)

Lemma 2

([20,31]). Let H be a real Hilbert space. Then, for all $x,y\in H$ and $\alpha \in \mathbb{R}$, the following hold

(i) 

$\left|\right|x-{y\left|\right|}^2={\left|\right|x\left|\right|}^2+{\left|\right|y\left|\right|}^2-2⟨x,y⟩$,

(ii) 

$\left|\right|x+{y\left|\right|}^2\le {\left|\right|x\left|\right|}^2+2⟨y,x+y⟩,$

(iii) 

$\left|\right|\alpha x+{(1-\alpha )y\left|\right|}^2={\alpha \left|\right|x\left|\right|}^2+{(1-\alpha )\left|\right|y\left|\right|}^2-\alpha (1-\alpha )\left|\right|x-{y\left|\right|}^2.$

Proof. 

For (iii), let $x,y\in H$ and $\alpha \in \mathbb{R}$, then using Lemma 2(i), we obtain

$$\begin{array}{ccc}\hfill \left|\right|\alpha x+{(1-\alpha )y\left|\right|}^2& =& {\alpha }^2{\left|\right|x\left|\right|}^2+2\alpha (1-\alpha )⟨x,y⟩+{(1-\alpha )}^2{\left|\right|y\left|\right|}^2\hfill \\ & =& {\alpha }^2{\left|\right|x\left|\right|}^2+{\alpha (1-\alpha )[|\left|x\right||}^2+{\left|\right|y\left|\right|}^2-\left|\right|x-{y\left|\right|}^2]\hfill \\ & & +{(1-\alpha )}^2{\left|\right|y\left|\right|}^2\hfill \\ & =& [{\alpha }^2+\alpha (1-\alpha )]{\left|\right|x\left|\right|}^2+{(1-\alpha )[\alpha +1-\alpha ]\left|\right|y\left|\right|}^2\hfill \\ & & -\alpha (1-\alpha )\left|\right|x-{y\left|\right|}^2\hfill \\ & =& {\alpha \left|\right|x\left|\right|}^2+{(1-\alpha )\left|\right|y\left|\right|}^2-\alpha (1-\alpha )\left|\right|x-{y\left|\right|}^2.\hfill \end{array}$$

   □

Lemma 3

([32]). Let $\left\{p_n\right\}$ be a sequence of nonnegative real numbers and $\left\{{\alpha }_n\right\}$ be a sequence of real numbers in $(0,1)$ with the following condition:

$$\sum _{n=1}^{\infty }{\alpha }_n=\infty$$

and $\left\{b_n\right\}$ be a sequence of real numbers. Assume that

$$p_{n+1}\le (1-{\alpha }_n)p_n+{\alpha }_n{b}_n,\forall n\ge 1.$$

If $\underset{k\to \infty }{limsup}{b}_{n_k}\le 0$ for every subsequence $\left\{p_{n_k}\right\}$ of $\left\{p_n\right\}$ satisfying the condition

$$\underset{k\to \infty }{liminf}(p_{n_k+1}-p_{n_k})\ge 0,$$

then ${\displaystyle \underset{n\to \infty }{lim}}{p}_n=0.$

3. Main Result

In order to solve pseudomonotone (VIP) in real Hilbert spaces, we present novel iterative techniques in the following section that are based on the double inertial PCM. With the help of the new line-search method and Mann-type method, these algorithms ensure robust convergence. Our methods have the benefit of not requiring us to know the mapping’s Lipschitz constant beforehand. It is actually not necessary for the variational inequality mapping to satisfy the Lipschitz continuity; rather, it simply has to satisfy the uniform continuity criterion. The following presumptions must be met by the mapping and parameters used in our methods in order to examine the convergence of the algorithms.

Assumption 1.

(L1) 

H is a Hilbert space and C is a nonempty, closed and convex subset of H.

(L2) 

$G:H\to H$ is pseudomonotone and uniformly continuous on H.

(L3) 

G is weakly sequentially continuous, that is for any $\left\{x_n\right\}\subset H$, we have $x_n\rightharpoonup x^{*}$ implies $G{x}_n\rightharpoonup G{x}^{*}$.

We assume that $\left\{{\beta }_n\right\}$ is a sequence such that ${\beta }_n\in [a,b]\subset (0,1)$, and $\left\{{\alpha }_n\right\}\subset (0,1)$ satisfies the conditions

$$\underset{n\to \infty }{lim}{\alpha }_n=0\mathrm{and}\sum _{n=1}^{\infty }{\alpha }_n=\infty .$$

We present in (Algorithm 1) a double inertial extrapolation with the Mann-type projection and contraction methods using golden rule line search for an approximate solution to the pseudomonotone variational inequality problem.

Algorithm 1: Double inertial PCM-type method for solving pseudomonotone VIP

Initialization: Given ${\lambda }_1>0,\gamma >0,v,{\theta }_n,ϵ\in (0,2)$, ${\delta }_n\in (0,1)$, $\phi =\frac{1+\sqrt{5}}{2}$, $\mu \in (0,\frac{2}{\phi }),$$\theta =\phi -1$, $\alpha >0$. Let $x_0,x_1\in H$ be given starting points. Set $n=1$. Iterative Steps:  Calculate $x_{n+1}$ as follows: 1:  Compute $$\begin{array}{c}\hfill \left\{\begin{array}{c}{u}_n=x_n+{\delta }_n(x_n-x_{n-1}),\hfill \\ w_n=(1-{\alpha }_n)[x_n+{\theta }_n(x_n-x_{n-1})],\hfill \\ v_n=P_C(w_n-{\lambda }_{n}G{w}_n).\hfill \end{array}\right.\end{array}$$ (10) If $x_n=w_n=v_n$ or $G{w}_n=0$, STOP, then $v_n$ is a solution of $VI(C,G)$. Otherwise go to 2:  Compute $$\begin{array}{c}\hfill \left\{\begin{array}{c}{y}_n=w_n-ϵ{\tau }_n{d}_n(w_n,v_n),\hfill \\ d_n(w_n,v_n):=w_n-v_n-{\lambda }_n(G{w}_n-G{v}_n),\hfill \end{array}\right.\end{array}$$ where $${\tau }_n=(1-\frac{\mu }{2\phi })\frac{\left|\right|w_n-v_n{\left|\right|}^2}{\left|\right|d_n(w_n,v_n){\left|\right|}^2}$$ and ${\lambda }_n=\gamma {\nu }^{m_n}$, $m_n$ is the smallest nonnegative integer m satisfying $$\begin{array}{c}\hfill \gamma {\nu }^m\left|\right|G\left(w_n\right)-G\left(v_n\right)\left|\right|\le \frac{\mu }{2\phi }\left|\right|w_n-v_n\left|\right|.\end{array}$$ (11) 3:  Compute $$\begin{array}{c}\hfill \left\{\begin{array}{c}{t}_n=(1-\theta )u_n+\theta x_n,\hfill \\ x_{n+1}=(1-{\beta }_n)t_n+{\beta }_n{y}_n,n\ge 1.\hfill \end{array}\right.\end{array}$$ (12) Set $n:=n+1$ and return to Step 1.

Remark 1.

(a) 

The new line-search rule (11) is not the same as the one that was taken into consideration in earlier studies [18,33]. Notably, more efficient numerical solutions are obtained when the step size is selected using the golden ratio.

(b) 

An alternate strategy for solving variational inequalities is provided by the modified projection and contraction method with the new line-search rule (11). This algorithm uses the golden ratio $(\sqrt{5}+1)/2$ to efficiently estimate the step size, in contrast to earlier methods (see [34,35,36]), which employed a different line-search method. Its efficacy is shown by numerical experiments, which makes it a promising substitute for solving variational inequalities with non-Lipschitz mappings in real Hilbert spaces.

(c) 

Our initial computational findings demonstrate that in comparison to the inertial PCM approaches in [17,18], our suggested double inertial extrapolation method is more effective and converges with greater speed (both in CPU time and number of iterations).

The following lemmas are very helpful in analyzing the convergence of Algorithm 1.

Lemma 4

([37]). Assume that (C1)–(C3) holds, then the line-search rule (11) is well defined. In addition, we have ${\lambda }_n\le \gamma$.

Lemma 5

([37]). Suppose that Assumption (C1)–(C3) holds. Let $\left\{w_n\right\}$ and $\left\{v_n\right\}$ be two sequences generated by Algorithm 1. If there exists a subsequence $\left\{w_{n_k}\right\}$ of $\left\{w_n\right\}$ such that $\left\{w_{n_k}\right\}$ converges weakly to $z\in H$ and ${\displaystyle \underset{k\to \infty }{lim}}\left|\right|w_{n_k}-v_{n_k}\left|\right|=0$, then $z\in VI(C,G)$.

We can obtain the conclusions of Lemmas 4 and 5 by a simple modification of Lemma 3.1 and 3.2 in [37], respectively. To avoid repetitive expression, we omit their proofs here.

Lemma 6.

Suppose that Assumption 1 (C1)–(C3) holds. Let $\left\{w_n\right\}$, $\left\{v_n\right\}$ and $\left\{y_n\right\}$ be three sequences generated by Algorithm 1. Then, for all $z^{*}\in VI(C,G)$

$$\begin{array}{c}\hfill \left|\right|y_n-z^{*}{\left|\right|}^2\le \left|\right|w_n-z^{*}{\left|\right|}^2-\frac{2-ϵ}{ϵ}\left|\right|y_n-w_n{\left|\right|}^2.\end{array}$$

(13)

Proof. 

For $z^{*}\in VI(C,G)$, we obtain

$$\begin{array}{ccc}\hfill ⟨w_n-z^{*},d_n(w_n,v_n)⟩& =& ⟨w_n-v_n,d_n(w_n,v_n)⟩+⟨v_n-z^{*},d_n(w_n,v_n)⟩\hfill \\ & =& ⟨w_n-v_n,d_n(w_n,v_n)⟩\hfill \\ & & +⟨v_n-z^{*},w_n-v_n-{\lambda }_n(G{w}_n-G{v}_n)⟩.\hfill \end{array}$$

(14)

From (8), and the definition of $\left(v_n\right)$ in (10), it follows that

$$\begin{array}{c}\hfill ⟨w_n-v_n-{\lambda }_{n}G{w}_n,v_n-z^{*}⟩\ge 0,\end{array}$$

(15)

since $v_n\in C$ and $z^{*}\in VI(C,G)$, it follows that $⟨G{z}^{*},v_n-z^{*}⟩\ge 0$ and according to the pseudomonotonicity of G, we obtain $⟨G{v}_n,v_n-z^{*}⟩\ge 0$ which together with (15), implies that

$$\begin{array}{c}\hfill ⟨w_n-v_n-{\lambda }_n(G\left(w_n\right)-G\left(v_n\right)),v_n-z^{*}⟩\ge 0.\end{array}$$

(16)

Combining (14) and (16), we obtain

$$\begin{array}{ccc}\hfill ⟨w_n-z^{*},d_n(w,v_n)⟩& =& ⟨w_n-v_n,d_n(w,v_n)⟩+⟨v_n-z^{*},d_n(w,v_n)⟩\hfill \\ & =& ⟨w_n-v_n,d(w_n,v_n)⟩+⟨v_n-z^{*},w_n-v_n-{\lambda }_n(G{w}_n-G{v}_n)⟩\hfill \\ & \ge & ⟨w_n-v_n,d(w_n,v_n)⟩\hfill \\ & =& ⟨w_n-v_n,w_n-v_n-{\lambda }_n(G{w}_n-G{v}_n)⟩\hfill \\ & =& ⟨w_n-v_n,w_n-v_n⟩-{\lambda }_n⟨w_n-v_n,G{w}_n-G{v}_n⟩\hfill \\ & \ge & \left|\right|w_n-v_n{\left|\right|}^2-{\lambda }_n\left|\right|w_n-v_n\left|\right|\left|\right|G{w}_n-G{v}_n\left|\right|\hfill \\ & \ge & \left|\right|w_n-v_n{\left|\right|}^2-\frac{\mu }{2\phi }\left|\right|w_n-v_n{\left|\right|}^2\hfill \\ & =& \left(1-\frac{\mu }{2\phi }\right)\left|\right|w_n-v_n{\left|\right|}^2\hfill \end{array}$$

(17)

On the other hand, from (17) and the definition of $\left(y_n\right)$, we have

$$\begin{array}{ccc}\hfill \left|\right|y_n-z^{*}{\left|\right|}^2& =& \left|\right|w_n-z^{*}-ϵ{\tau }_{n}d(w_n,v_n){\left|\right|}^2\hfill \\ & =& \left|\right|w_n-z^{*}{\left|\right|}^2-2ϵ{\tau }_n⟨d_n(w_n,v_n),w_n-z^{*}⟩+{ϵ}^2{\tau }_n^2\left|\right|d_n(w_n,v_n){\left|\right|}^2\hfill \\ & \le & \left|\right|w_n-z^{*}{\left|\right|}^2-2ϵ{\tau }_n\left(1-\frac{\mu }{2\phi }\right)\left|\right|w_n-v_n{\left|\right|}^2+{ϵ}^2{\tau }_n^2\left|\right|d_n(w_n,v_n){\left|\right|}^2\hfill \\ & =& \left|\right|w_n-z^{*}{\left|\right|}^2-2ϵ{\tau }_n^2\left|\right|d_n(w_n,v_n){\left|\right|}^2+{ϵ}^2{\tau }_n^2\left|\right|d_n(w_n,v_n){\left|\right|}^2\hfill \\ & =& \left|\right|w_n-z^{*}{\left|\right|}^2-\frac{2-ϵ}{ϵ}{\left(ϵ{\tau }_n\right)}^2\left|\right|d_n(w_n,v_n){\left|\right|}^2\hfill \\ & =& \left|\right|w_n-z^{*}{\left|\right|}^2-\frac{2-ϵ}{ϵ}\left|\right|y_n-w_n{\left|\right|}^2\hfill \end{array}$$

□

Theorem 1.

Suppose that Assumption (C1)–(C3) holds and ${\theta }_n,{\delta }_n\in (0,1)$ are chosen such that

$$\underset{n\to \infty }{lim}\frac{{\theta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|=0and\underset{n\to \infty }{lim}\frac{{\delta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|=0,$$

where ${\theta }_n=\circ \left({\alpha }_n\right)$, ${\delta }_n=\circ \left({\alpha }_n\right)$. Then, the sequence $\left\{x_n\right\}$ generated by Algorithm 1 converges strongly to $z^{*}\in VI(C,G)$, where $\left|\right|z^{*}\left|\right|=min\left\{\right|\left|z\right||:z\in VI(C,G)\}$.

Proof. 

Let $z^{*}\in VI(C,G)$. The proof is divided into the following four stages.

Stage 1. We prove that the sequence $\left\{x_n\right\}$ is bounded. Indeed, from Lemma 4, it follows that

$$\begin{array}{c}\hfill \left|\right|y_n-z^{*}\left|\right|\le \left|\right|w_n-z^{*}\left|\right|.\end{array}$$

(18)

Moreover, from the definition of $\left(u_n\right)$ and $\left(w_n\right)$, we obtain

$$\begin{array}{ccc}\hfill \left|\right|u_n-z^{*}\left|\right|& =& \left|\right|x_n+{\delta }_n(x_n-x_{n-1})-z^{*}\left|\right|\hfill \\ & \le & \left|\right|x_n-z^{*}\left|\right|+{\delta }_n\left|\right|x_n-x_{n-1}\left|\right|\hfill \\ & =& \left|\right|x_n-z^{*}\left|\right|+{\alpha }_n\times \frac{{\delta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|.\hfill \end{array}$$

(19)

and letting $h_n=x_n+{\theta }_n(x_n-x_{n-1})$, then $w_n=(1-{\alpha }_n)h_n$. Therefore, following the same argument of (19), we have

$$\begin{array}{c}\hfill \left|\right|h_n-z^{*}\left|\right|\le \left|\right|x_n-z^{*}\left|\right|+\frac{{\theta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|.\end{array}$$

(20)

Thus,

$$\begin{array}{ccc}\hfill \left|\right|w_n-z^{*}\left|\right|& =& \left|\right|(1-{\alpha }_n)h_n-z^{*}\left|\right|\hfill \\ & \le & (1-{\alpha }_n)\left|\right|h_n-z^{*}\left|\right|+{\alpha }_n\left|\right|z^{*}\left|\right|.\hfill \end{array}$$

(21)

Combining (20) and (21), we obtain

$$\begin{array}{ccc}\hfill \left|\right|w_n-z^{*}\left|\right|& \le & (1-{\alpha }_n)\left[\right||x_n-z^{*}\left|\right|+{\alpha }_n\times \frac{{\theta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|]+{\alpha }_n\left|\right|z^{*}\left|\right|\hfill \\ & \le & (1-{\alpha }_n)\left|\right|x_n-z^{*}\left|\right|+{\alpha }_n\left[\frac{{\theta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|+\left|\right|z^{*}\left|\right|\right].\hfill \end{array}$$

(22)

With the condition that $\left\{\frac{{\theta }_n}{{\alpha }_n}\right||x_n-x_{n-1}|\left|\right\}$ and $\left\{\frac{{\delta }_n}{{\alpha }_n}\right||x_n-x_{n-1}|\left|\right\}$ converges to 0 as $n\to \infty$, then there exist positive numbers $M_1,M_2$ such that

$$\frac{{\theta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|\le M_1\mathrm{and}\frac{{\delta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|\le M_2$$

for all $n\ge 1$. Therefore, letting $M^{*}=max\{M_1+\left|\right|z^{*}\left|\right|,M_2\}$, we respectively obtain from (20) and (21) that

$$\begin{array}{c}\hfill \left|\right|u_n-z^{*}\left|\right|\le \left|\right|x_n-z^{*}\left|\right|+{\alpha }_n{M}^{*}\end{array}$$

(23)

and

$$\begin{array}{c}\hfill \left|\right|w_n-z^{*}\left|\right|\le (1-{\alpha }_n)\left|\right|x_n-z^{*}\left|\right|+{\alpha }_n{M}^{*}\end{array}$$

(24)

On the other hand, from the definition of $\left\{t_n\right\}$ and (23)

$$\begin{array}{ccc}\hfill \left|\right|t_n-z^{*}\left|\right|& =& \left|\right|(1-\theta )u_n+\theta x_n-z^{*}\left|\right|\hfill \\ & \le & (1-\theta )\left|\right|u_n-z^{*}\left|\right|+\theta \left|\right|x_n-z^{*}\left|\right|\hfill \\ & \le & (1-\theta )\left[\right||x_n-z^{*}\left|\right|+{\alpha }_n{M}^{*}]+\theta ||x_n-z^{*}\left|\right|\hfill \\ & =& \left|\right|x_n-z^{*}\left|\right|+{\alpha }_n(1-\theta )M^{*}\hfill \end{array}$$

and using the fact that for all $n\ge 1$, $\beta \in [a,b]\subset (0,1)$, we obtain

$$\begin{array}{ccc}\hfill \left|\right|x_{n+1}-z^{*}\left|\right|& =& \left|\right|(1-{\beta }_n)t_n+{\beta }_n{y}_n-z^{*}\left|\right|\hfill \\ & \le & (1-{\beta }_n)\left|\right|t_n-z^{*}\left|\right|+{\beta }_n\left|\right|y_n-z^{*}\left|\right|\hfill \\ & \le & (1-{\beta }_n)\left|\right|t_n-z^{*}\left|\right|+{\beta }_n\left|\right|w_n-z^{*}\left|\right|\hfill \\ & \le & (1-{\beta }_n)\left[\right||x_n-z^{*}\left|\right|+{\alpha }_n{M}^{*}]\hfill \\ & & +{\beta }_n[(1-{\alpha }_n)\left|\right|x_n-z^{*}\left|\right|+{\alpha }_n{M}^{*}]\hfill \\ & =& (1-{\alpha }_n{\beta }_n)\left|\right|x_n-z^{*}\left|\right|+{\alpha }_n{M}^{*}\hfill \\ & \le & (1-{\alpha }_{n}a)\left|\right|x_n-z^{*}\left|\right|+{\alpha }_{n}a(M^{*}/a)\hfill \\ & \le & max\left\{\right||x_n-z^{*}||,M^{*}/a\}\hfill \\ & & ⋮\hfill \\ & \le & max\left\{\right||x_1-z^{*}||,M^{*}/a\}.\hfill \end{array}$$

Therefore, $\left\{x_n\right\}$ is bounded and so $\left\{t_n\right\}$, $\left\{y_n\right\}$, $\left\{w_n\right\}$ and $\left\{u_n\right\}$ are also bounded.

Stage 2. We show, for some $K>0$, that

$$\begin{array}{c}\hfill \frac{2-ϵ}{ϵ}a\left|\right|v_n-w_n{\left|\right|}^2+a(1-b)\left|\right|t_n-y_n{\left|\right|}^2\le \left|\right|x_n-z^{*}{\left|\right|}^2-\left|\right|x_{n+1}-z^{*}{\left|\right|}^2+{\alpha }_{n}K.\end{array}$$

(25)

Indeed, from the definition of $\left(x_{n+1}\right)$ and Lemma 2, we obtain

$$\begin{array}{ccc}\hfill \left|\right|x_{n+1}-z^{*}{\left|\right|}^2=& & \left|\right|(1-{\beta }_n)t_n+{\beta }_n{y}_n-z^{*}{\left|\right|}^2\hfill \\ & =& \left|\right|(1-{\beta }_n)(t_n-z^{*})+{\beta }_n(y_n-z^{*}){\left|\right|}^2\hfill \\ & =& (1-{\beta }_n)\left|\right|t_n-z^{*}{\left|\right|}^2+{\beta }_n\left|\right|y_n-z^{*}{\left|\right|}^2-{\beta }_n(1-{\beta }_n)\left|\right|t_n-y_n{\left|\right|}^2\hfill \\ & \le & (1-{\beta }_n)[(1-\theta )\left|\right|u_n-z^{*}{\left|\right|}^2+\theta \left|\right|x_n-z^{*}{\left|\right|}^2]+{\beta }_n\left|\right|y_n-z^{*}{\left|\right|}^2\hfill \\ & & -{\beta }_n(1-{\beta }_n)\left|\right|t_n-y_n{\left|\right|}^2\hfill \\ & \le & (1-{\beta }_n)\left|\right|u_n-z^{*}{\left|\right|}^2+(1-{\beta }_n)\left|\right|x_n-z^{*}{\left|\right|}^2+{\beta }_n\left|\right|y_n-z^{*}{\left|\right|}^2\hfill \\ & & -{\beta }_n(1-{\beta }_n)\left|\right|t_n-y_n{\left|\right|}^2.\hfill \end{array}$$

(26)

It follows from (13) and (26) that

$$\begin{array}{ccc}\hfill \left|\right|x_{n+1}-z^{*}{\left|\right|}^2& \le & (1-{\beta }_n)\left|\right|u_n-z^{*}{\left|\right|}^2+(1-{\beta }_n)\left|\right|x_n-z^{*}{\left|\right|}^2+{\beta }_n\left|\right|w_n-z^{*}{\left|\right|}^2\hfill \\ & & -{\beta }_n\frac{2-ϵ}{ϵ}\left|\right|v_n-w_n{\left|\right|}^2-{\beta }_n(1-{\beta }_n)\left|\right|t_n-y_n{\left|\right|}^2\hfill \end{array}$$

(27)

and

$$\begin{array}{ccc}\hfill \left|\right|u_n-z^{*}{\left|\right|}^2& =& \left|\right|x_n+{\delta }_n(x_n-x_{n-1})-z^{*}\left|\right|\hfill \\ & \le & \left|\right|x_n-z^{*}{\left|\right|}^2+2{\delta }_n⟨x_n-x_{n-1},u_n-z^{*}⟩\hfill \\ & \le & \left|\right|x_n-z^{*}{\left|\right|}^2+2{\delta }_n\left|\right|x_n-x_{n-1}\left|\right|\left|\right|u_n-z^{*}\left|\right|\hfill \end{array}$$

(28)

Since $\left\{u_n\right\}$ is bounded and $\left\{\frac{{\delta }_n}{{\alpha }_n}\right||x_n-x_{n-1}|\left|\right\}$ converges, then there exists $M_3>0$ such that for all $n\ge 1$

$$\left|\right|x_n-x_{n-1}\left|\right|\left|\right|u_n-z^{*}\left|\right|\le M_3$$

thus

$$\begin{array}{c}\hfill \left|\right|u_n-z^{*}{\left|\right|}^2\le \left|\right|x_n-z^{*}{\left|\right|}^2+2{\alpha }_n{M}_3.\end{array}$$

(29)

It follows from (24), (27) and (29) that

$$\begin{array}{l}{\displaystyle \left|\right|x_{n+1}-z^{*}{\left|\right|}^2\le (1-{\beta }_n)\left[\right||x_n-z^{*}{\left|\right|}^2+2{\alpha }_n{M}_3]+{\beta }_n[(1-{\alpha }_n)\left|\right|x_n-z^{*}\left|\right|+{\alpha }_n{M}^{*}{]}^2}\\ \begin{array}{l}\hspace{1em}\hspace{1em}-{\beta }_n\frac{2-ϵ}{ϵ}\left|\right|v_n-w_n{\left|\right|}^2-{\beta }_n(1-{\beta }_n)\left|\right|t_n-y_n{\left|\right|}^2\\ \hspace{1em}\le (1-{\beta }_n)\left|\right|x_n-z^{*}{\left|\right|}^2+2{\alpha }_n(1-{\beta }_n)M_3+{\beta }_n(1-{\alpha }_n)\left|\right|x_n-z^{*}{\left|\right|}^2\\ \hspace{1em}\hspace{1em}+2{\alpha }_n{\beta }_n(1-{\beta }_n)M^{*}+{\left({\alpha }_n{M}^{*}\right)}^2-{\beta }_n\frac{2-ϵ}{ϵ}\left|\right|v_n-w_n{\left|\right|}^2-{\beta }_n(1-{\beta }_n)\left|\right|t_n-y_n{\left|\right|}^2\\ \hspace{1em}\le (1-{\alpha }_n{\beta }_n)\left|\right|x_n-z^{*}{\left|\right|}^2+{\alpha }_n[2M_3+2M^{*}+{\alpha }_n{M}^{*2}]\\ \hspace{1em}\hspace{1em}-{\beta }_n\frac{2-ϵ}{ϵ}\left|\right|v_n-w_n{\left|\right|}^2-{\beta }_n(1-{\beta }_n)\left|\right|t_n-y_n{\left|\right|}^2.\end{array}\end{array}$$

Thus, for some $K>0$, we obtain

$$\begin{array}{ccc}\hfill \frac{2-ϵ}{ϵ}a\left|\right|v_n-w_n{\left|\right|}^2+a(1-b)\left|\right|t_n-y_n{\left|\right|}^2& \le & \frac{2-ϵ}{ϵ}{\beta }_n\left|\right|v_n-w_n{\left|\right|}^2+{\beta }_n(1-{\beta }_n)\left|\right|t_n-y_n{\left|\right|}^2\hfill \\ & \le & \left|\right|x_n-z^{*}{\left|\right|}^2-\left|\right|x_{n+1}-z^{*}{\left|\right|}^2\hfill \\ & & +{\alpha }_n[2M_3+2M^{*}+{\alpha }_n{M}^{*2}-{\beta }_n\left|\right|x_n-z^{*}{\left|\right|}^2]\hfill \\ & \le & \left|\right|x_n-z^{*}{\left|\right|}^2-\left|\right|x_{n+1}-z^{*}{\left|\right|}^2+{\alpha }_{n}K.\hfill \end{array}$$

Stage 3. Next, we estimate that

$$\begin{array}{c}\hfill \left|\right|x_{n+1}-z^{*}{\left|\right|}^2\le (1-{\alpha }_n{\beta }_n)\left|\right|x_n-z^{*}{\left|\right|}^2+{\alpha }_n{\beta }_n{\Psi }_n,\end{array}$$

(30)

where

$$\begin{array}{ccc}\hfill {\Psi }_n& =& {\alpha }_n\left|\right|z^{*}{\left|\right|}^2+2(1-{\alpha }_n)⟨h_n-z^{*},-z^{*}⟩\hfill \\ & & +\frac{2{\delta }_n\left|\right|x_n-x_{n-1}\left|\right|\left|\right|u_n-z^{*}\left|\right|+2{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|\left|\right|h_n-z^{*}\left|\right|}{{\alpha }_n}\hfill \end{array}$$

From the definition of $\left\{x_{n+1}\right\}$ and (28), we obtain

$$\begin{array}{c}{\displaystyle \left|\right|x_{n+1}-z^{*}{\left|\right|}^2=\left|\right|(1-{\beta }_n)t_n+{\beta }_n{y}_n-z^{*}{\left|\right|}^2}\hfill \\ \le (1-{\beta }_n)\left|\right|t_n-z^{*}{\left|\right|}^2+{\beta }_n\left|\right|y_n-z^2{\left|\right|}^2\hfill \\ =(1-{\beta }_n)\left|\right|(1-\theta )(u_n-z^{*})+\theta (x_n-z^{*}){\left|\right|}^2+{\beta }_n\left|\right|y_n-z^{*}{\left|\right|}^2\hfill \\ \le (1-{\beta }_n)[(1-\theta )\left|\right|u_n-z^{*}{\left|\right|}^2+\theta \left|\right|x_n-z^{*}{\left|\right|}^2]+{\beta }_n\left|\right|w_n-z^{*}{\left|\right|}^2\hfill \\ \le (1-{\beta }_n)[(1-\theta )\left[\right||x_n-z^{*}{\left|\right|}^2+{\delta }_n\left|\right|x_n-x_{n-1}\left|\right|u_n-z^{*}\left|\right|]+\theta \left|\right|x_n-z^{*}{\left|\right|}^2]\hfill \\ +{\beta }_n\left|\right|(1-{\alpha }_n)h_n-z^{*}{\left|\right|}^2\hfill \\ \le (1-{\beta }_n)\left|\right|x_n-z^{*}{\left|\right|}^2+2{\delta }_n\left|\right|x_n-x_{n-1}\left|\right|\left|\right|u_n-z^{*}\left|\right|+{\beta }_n\left|\right|(1-{\alpha }_n)(h_n-z^{*})-{\alpha }_n{z}^{*}{\left|\right|}^2\hfill \\ \le (1-{\beta }_n)\left|\right|x_n-z^{*}{\left|\right|}^2+2{\delta }_n\left|\right|x_n-x_{n-1}\left|\right|\left|\right|x_n-z^{*}\left|\right|+{\beta }_n[(1-{\alpha }_n)\left|\right|h_n-z^{*}{\left|\right|}^2+{\alpha }_n^2\left|\right|z^{*}{\left|\right|}^2\hfill \\ +2{\alpha }_n(1-{\alpha }_n)⟨h_n-z^{*},-z^{*}⟩]\hfill \\ \le (1-{\beta }_n)\left|\right|x_n-z^{*}{\left|\right|}^2+2{\delta }_n\left|\right|x_n-x_{n-1}\left|\right|\left|\right|u_n-z^{*}\left|\right|+{\beta }_n(1-{\alpha }_n)\left|\right|x_n-z^{*}{\left|\right|}^2\hfill \\ +2{\beta }_n{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|\left|\right|h_n-z^{*}\left|\right|+{\beta }_n{\alpha }_n^2\left|\right|z^{*}{\left|\right|}^2+2{\beta }_n{\alpha }_n(1-{\alpha }_n)⟨h_n-z^{*},-z^{*}⟩\hfill \\ \le (1-{\alpha }_n{\beta }_n)\left|\right|x_n-z^{*}{\left|\right|}^2+{\alpha }_n{\beta }_n({\alpha }_n\left|\right|z^{*}{\left|\right|}^2+2(1-{\alpha }_n)⟨h_n-z^{*},-z^{*}⟩\hfill \\ +2\frac{{\delta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|\left|\right|u_n-z^{*}\left|\right|+2\frac{{\theta }_n}{{\alpha }_n}\left|\right|x_n-x_{n-1}\left|\right|\left|\right|h_n-z^{*}\left|\right|]\hfill \\ =(1-{\alpha }_n{\beta }_n)\left|\right|x_n-z^{*}{\left|\right|}^2+{\alpha }_n{\beta }_n{\Psi }_n.\hfill \end{array}$$

where

$$\begin{array}{ccc}\hfill {\Psi }_n& =& {\alpha }_n\left|\right|z^{*}{\left|\right|}^2+2(1-{\alpha }_n)⟨h_n-z^{*},-z^{*}⟩\hfill \\ & & +\frac{2{\delta }_n\left|\right|x_n-x_{n-1}\left|\right|\left|\right|u_n-z^{*}\left|\right|+2{\theta }_n\left|\right|x_n-x_{n-1}\left|\right|\left|\right|h_n-z^{*}\left|\right|}{{\alpha }_n}\hfill \end{array}$$

Stage 4. Finally, we prove that the sequence $\left\{\right||x_n-z^{*}|\left|\right\}$ converges to zero.

Let $\left\{\right||x_{n_k}-z^{*}|\left|\right\}$ be a subsequence of $\left\{\right||x_n-z^{*}|\left|\right\}$ such that

$$\underset{k\to \infty }{liminf}\left(\right||x_{n_k+1}-z^{*}\left|\right|-\left|\right|x_{n_k}-z^{*}\left|\right|)\ge 0.$$

Then

$$\begin{array}{ccc}& & \underset{k\to \infty }{liminf}\left(\left|\right|x_{n_k+1}-z^{*}{\left|\right|}^2-\left|\right|x_{n_k}-z^{*}{\left|\right|}^2\right)\hfill \\ & & =\underset{k\to \infty }{liminf}\left[\left(\right||x_{n_k+1}-z^{*}\left|\right|-\left|\right|x_{n_k}-z^{*}\left|\right|\left)\right(\left|\right|x_{n_k+1}-z^{*}\left|\right|+\left|\right|x_{n_k}-z^{*}\left|\right|)\right]\hfill \\ & & \ge 0.\hfill \end{array}$$

From (25) and using ${\alpha }_n\to 0$ as $n\to \infty$, we obtain

$$\begin{array}{ccc}& & \underset{k\to \infty }{limsup}\left[\frac{2-ϵ}{ϵ}a\left|\right|v_{n_k}-w_{n_k}{\left|\right|}^2+a(1-b)\left|\right|t_{n_k}-y_{n_k}{\left|\right|}^2\right]\hfill \\ & \le & \underset{k\to \infty }{limsup}\left[\right||x_{n_k}-z^{*}{\left|\right|}^2-\left|\right|x_{n_k+1}-z^{*}{\left|\right|}^2]+\underset{k\to \infty }{limsup}{\alpha }_{n_k}K\hfill \\ & & \le -\underset{k\to \infty }{liminf}\left[\right||x_{n_k+1}-z^{*}{\left|\right|}^2-\left|\right|x_{n_k}-z^{*}{\left|\right|}^2]\hfill \\ & & \le 0,\hfill \end{array}$$

This implies that

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\left|\right|v_{n_k}-w_{n_k}\left|\right|=0\mathrm{and}\underset{k\to \infty }{lim}\left|\right|t_{n_k}-y_{n_k}\left|\right|=0\end{array}$$

(31)

From (11), the definition of $\left(d_n\right)$ and $\left({\tau }_n\right)$, we obtain

$$\begin{array}{c}\hfill \left|\right|d_n(w_n,v_n)\ge \left|\right|w_n-v_n\left|\right|-\frac{\mu }{2\phi }\left|\right|w_n-v_n\left|\right|=\left(1-\frac{\mu }{2\phi }\right)\left|\right|w_n-v_n\left|\right|\end{array}$$

and then

$$\begin{array}{c}\hfill {\tau }_n\left|\right|d_n(w_n,v_n)\left|\right|=\left(1-\frac{\mu }{2\phi }\right)\frac{\left|\right|w_n-v_n{\left|\right|}^2}{\left|\right|d_n(w_n,v_n)\left|\right|}\le \left|\right|w_n-v_v\left|\right|.\end{array}$$

It follows from the definition of $\left(y_n\right)$ that

$$\begin{array}{c}\hfill \left|\right|y_n-w_n\left|\right|=ϵ{\tau }_n\left|\right|d_n(w_n,v_n)\left|\right|\le ϵ\left|\right|w_n-v_n\left|\right|\end{array}$$

(32)

Using (31) in (32), we obtain

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\left|\right|y_{n_k}-w_{n_k}\left|\right|=0.\end{array}$$

(33)

Combining (31) and (33), we obtain

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\left|\right|t_{n_k}-w_{n_k}\left|\right|=0.\end{array}$$

(34)

Also, from $w_n=(1-{\alpha }_n)h_n$, where $h_n=x_n+{\theta }_n(x_n-x_{n_1})$, we obtain

$$\begin{array}{c}\hfill \left|\right|h_{n_k}-x_{n_k}\left|\right|\le {\alpha }_{n_k}\times \frac{{\theta }_{n_k}}{{\alpha }_{n_k}}\left|\right|x_{n_k}-x_{n_k-1}\left|\right|\to 0\end{array}$$

(35)

as $k\to \infty$, and since ${\alpha }_n\to 0$ as $n\to \infty$, then

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\left|\right|w_{n_k}-h_{n_k}\left|\right|=0.\end{array}$$

(36)

Combining (35) and (36), we obtain

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\left|\right|w_{n_k}-x_{n_k}\left|\right|=0,\end{array}$$

(37)

from (34) and (37), we obtain

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\left|\right|t_{n_k}-x_{n_k}\left|\right|=0.\end{array}$$

(38)

Andsince $\left|\right|x_{n+1}-t_n\left|\right|\le {\beta }_n\left|\right|t_n-y_n\left|\right|$, then from (31), we obtain

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\left|\right|x_{n_k+1}-t_{n_k}\left|\right|=0\end{array}$$

(39)

which follows from (38) that

$$\begin{array}{c}\hfill \underset{k\to \infty }{lim}\left|\right|x_{n_k+1}-x_{n_k}\left|\right|=0.\end{array}$$

(40)

Since $\left\{x_{n_k}\right\}$ is bounded, there exists a subsequence $\left\{x_{n_{k_j}}\right\}$ of $\left\{x_{n_k}\right\}$ such that $x_{n_{k_j}}\rightharpoonup p\in H$. From (37), we obtain $w_{n_{k_j}}\rightharpoonup p$, and it follows from (29) and Lemma 5 that $p\in VI(C,G)$. Furthermore, since $p\in VI(C,G)$ and $\left|\right|z^{*}\left|\right|=min\left\{\right|\left|z\right||:z\in VI(C,G)\}$, from Lemma 1, we obtain

$$\begin{array}{c}\hfill \underset{k\to \infty }{limsup}⟨x_{n_k}-z^{*},-z^{*}⟩=\underset{j\to \infty }{lim}⟨x_{n_{k_j}}-z^{*},-z^{*}⟩=⟨p-z^{*},-z^{*}⟩\le 0\end{array}$$

it follows from (35) that

$$\begin{array}{ccc}\hfill \underset{k\to \infty }{limsup}⟨h_{n_k}-z^{*},-z^{*}⟩& =& \underset{k\to \infty }{limsup}⟨h_{n_{k_j}}-x_{n_k},-z^{*}⟩+\underset{k\to \infty }{limsup}⟨h_{n_k}-z^{*},-z^{*}⟩\hfill \\ & =& ⟨p-z^{*},-z^{*}⟩\le 0\hfill \end{array}$$

which implies that $\underset{k\to \infty }{limsup}{\Psi }_{n_k}\le 0$. Therefore, it follows from (33) and Lemma 3 that $x_n\to z^{*}$ as $n\to \infty$. □

4. Numerical Example

In order to demonstrate how the stability and convergence rate of Mann-type inertial projection and contraction methods for solving variational inequality problems can be improved through the additional momentum of inertial terms, known as double inertial extrapolation terms, we first present Example 1 as a comparison in this section. Second, we compare the inertial projection and contraction techniques presented in [18] [Equation (4)] and [17] [Equation (6)] with Algorithm 1 using a computational experiment.

Example 1.

Let $H=L_2[0,1]$ and $C=\{x\in L_2[0,1]:⟨a,x⟩\le b\}$, where $a=t^2+1$ and $b=1$, with norm $\left|\right|x\left|\right|=\sqrt{{\int }_0^1{\left|x\left(t\right)\right|}^{2}dt}$ and inner product $⟨x,y⟩={\int }_0^{t}x\left(t\right)y\left(t\right)dt$, for all $x,y\in L_2\left([0,1]\right)$, $t\in [0,1]$. Define metric projection $P_C$ as follows:

$$P_C\left(x\right)=\left\{\begin{array}{c}x,\mathit{if}x\in C\hfill \\ \hfill \\ \frac{b-⟨a,x⟩}{{\left|\right|a\left|\right|}_{L_2}}a+x,\mathit{otherwise}.\hfill \end{array}\right.$$

(41)

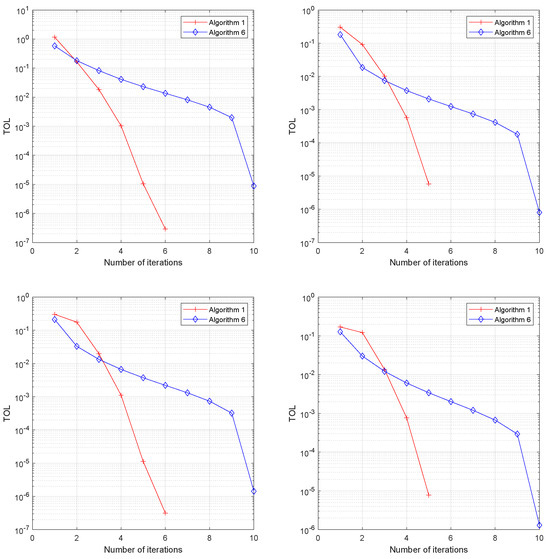
Let $G:L_2[0,1]\to L_2[0,1]$ be defined by $G\left(x\left(t\right)\right)=e^{-\left|\right|x\left|\right|}{\int }_0^{t}x\left(s\right)ds$, for all $x\in L_2[0,1]$, $t,s\in [0,1]$; then, G is pseudomonotone and uniformly continuous mapping (see [38]). We choose the following parameters for the algorithms: ${\alpha }_n=\frac{1}{\sqrt{1+n}}$, ${\beta }_n=\frac{n}{2(n+1)}(1-{\alpha }_n)$, ${\delta }_n=\theta =\frac{1}{{(1+n)}^{0.1}}$, $\mu =1.1$, $\nu =0.5$, $\gamma =0.5$, $\kappa =0.5$ and $ϵ=1.9$. We define the sequence ${TOL}_n:=\left|\right|x_{n+1}-x_n{\left|\right|}^2$ and apply the stopping criterion ${TOL}_n<\epsilon$ for the iterative processes because the solution to the problem is unknown. ε is the predetermined error. Here, the terminating condition is set to $\epsilon ={10}^{-5}$. For the numerical experiments illustrated in Figure 1 and Table 1 below, we take into consideration the resulting cases.

Figure 1. (Top Left): Case 1; (Top Right): Case 2; (Bottom Left): Case 3; (Bottom Right): Case 4, the error plotting of comparison of Algorithm 1, and Equation (6) for Example 1.

Table 1. Comparison of Algorithm 1 and Equation (6).

Cases		Algorithm 1	Equation (6)
1	Iter. CPU (time)	6 0.6209	10 0.6549
2	Iter. CPU (time)	5 0.5492	10 0.5824
3	Iter. CPU (time)	6 0.6075	10 0.6115
4	Iter. CPU (time)	6 0.5463	10 0.6069

Case 1: 

$x_0=t^3$ and $x_1=t^2+t$.

Case 2: 

$x_0=2t^3+t$ and $x_1=\frac{t^2}{2}$.

Case 3: 

$x_0=6t^3+t^2+t$ and $x_1=\frac{t^5}{2}$.

Case 4: 

$x_0=t^7+4t$ and $x_1=\frac{t^3}{6}$.

From the numerical results, it is clear that our Algorithm 1 solves the problem with a smaller number of iterations and CPU−time (second). This shows the advantage of using a double inertial terms and golden ratio in Algorithm 1.

Example 2.

Let $H={\mathbb{R}}^N$. Define $G:{\mathbb{R}}^N\to {\mathbb{R}}^N$ by $A\left(x\right)=Mx+q$, where the matrix M is formed as $M=V\sum V^{\prime }$, where $V=I-\frac{2v{v}^{\prime }}{{\parallel v\parallel }^2}$ and $\sum =diag({\sigma }_{11},{\sigma }_{12},\cdots ,{\sigma }_{1N})$ are the householder and the diagonal matrix, and

$$\begin{array}{c}\hfill {\sigma }_{1j}=cos\frac{j\pi }{N+1}+1+\frac{cos\frac{\pi }{N+1}+1-\widehat{C}(cos\frac{N\pi }{N+1}+1)}{\widehat{C}-1},j=1,2,\cdots ,N,\end{array}$$

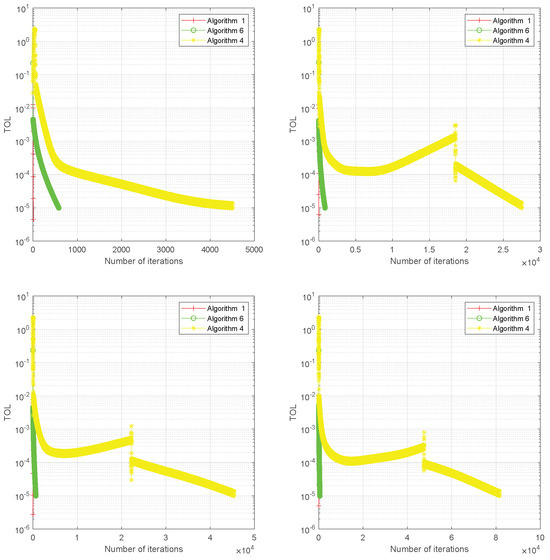
with $\widehat{C}$ being the present condition number of M ([39], Example 5.2). In the numerical computation, we choose $\widehat{C}={10}^4$, $q=0$ and uniformly take the vector $v\in {\mathbb{R}}^N$ in $(-1,1)$. Thus, G is pseudomonotone and Lipschitz continuous with $K=\left|\right|M\left|\right|$ (see [39]). By setting $C=\{x\in {\mathbb{R}}^N:|\left|x\right||\le 1\}$, Matlab is used to efficiently compute the projection onto C. Moreover, we examine various instances of the problem’s dimension. That is, $N=20,40,60,80$, with starting points $x_1={(1,1,\cdots ,1)}^{\prime }$ and $x_0={(0,0,\cdots ,0)}^{\prime }$. We choose the following parameters for Algorithm 1: $\gamma =0.5$, $\nu =0.5$, $\mu =1.2$, $ϵ=1.9$, ${\alpha }_n=1/(100n+1)$, ${\theta }_n={\delta }_n=\frac{{\alpha }_n}{n^{0.01}}$, ${\beta }_n=0.5-{\alpha }_n$. We take $l=0.11$, $\kappa =0.5$, $ϵ=0.5$, ${\theta }_n=\frac{{\alpha }_n}{n^{0.01}}$, and ${\beta }_n=0.5-{\alpha }_n$ for Equations (4) and (6). In this example, we take the stopping criterion to be $\epsilon ={10}^{-5}$ and obtain the numerical results shown in Table 2 and Figure 2.

Table 2. Numerical results for Example 2 with $\epsilon ={10}^{-5}$.

N		Algorithm 1	Equation (6)	Equation (4)
20	Iter. CPU	7 0.0161	585 0.0223	4512 0.0331
40	Iter. CPU	7 0.0267	855 0.0278	27,541 0.4378
60	Iter. CPU	7 0.0200	647 0.0303	45,469 1.0728
80	Iter. CPU	7 0.0216	479 0.0238	81,719 2.8491

Figure 2. The behavior of ${TOL}_n$ with $\epsilon ={10}^{-5}$ for Example 2: (Top Left): $N=20$; (Top Right): $N=40$; (Bottom Left): $N=60$; (Bottom Right): $N=80$.

The numerical results show that Algorithm 1 performs better than both Equations (4) and (6) in terms of the number of iterations and CPU time needed for computation. These results are shown in Table 2 and Figure 2. This increase in performance highlights the advantages of using double inertial extrapolation steps, which boost the methods’ effectiveness and accelerate their rate of convergence. These steps also give more momentum to the algorithm, improving its overall performance and stability significantly.

5. Conclusions

The pseudomonotone variational inequality problem in the context of real Hilbert spaces is addressed in this paper using a Mann-type projection and contraction technique. Our approach uses a double inertial extrapolation method, as specified, together with a novel line search step size based on the golden rule to accelerate the rate of convergence. To demonstrate how well our suggested approach works, we provided a numerical example.