On the Problems of $\mathcal{CF}$-Connected Graphs for K_l,m,n

Abstract

A connected graph, G, is Crossing Free-connected ($\mathcal{CF}$-connected) if there is a path between every pair of vertices with no crossing on its edges for each optimal drawing of G. We conjecture that a complete tripartite graph, $K_{l,m,n}$, is $\mathcal{CF}$-connected if and only if it does not contain any of the following as a subgraph: $K_{1,2,7}$, $K_{1,3,5}$, $K_{1,4,4}$, $K_{2,2,5}$, $K_{3,3,3}$. We examine the idea that $K_{1,2,7}$, $K_{1,3,5}$, $K_{1,4,4}$, and $K_{2,2,5}$ are the first non-$\mathcal{CF}$-connected complete tripartite graphs. The $\mathcal{CF}$-connectedness of $K_{l,m,n}$ with $l,m,n\ge 3$ is dependent on the knowledge of crossing numbers of $K_{3,3,n}$. In this paper, we prove various results that support this conjecture.

1. Introduction

Various types of connectedness have already been examined on graphs, either from the point of view of vertices or edges of the entire graph or of one of its subgraphs. One such problem is the describability of the subclass of graphs for which we get a connected subgraph after removing crossed edges throughout all of their optimal drawings. This is also why in such research we only deal with classes of finite simple graphs, and of course the most appropriate choice is some classes of symmetric graphs. The issue dealing with this connectedness for complete bipartite graphs, $K_{m,n}$, and the complete graphs, $K_n$, has already been estimated by Staš and Valiska, [1] and [2], respectively. The goal of our paper is to extend this knowledge for a relatively large class of the complete tripartite graphs, $K_{l,m,n}$. When examining this class of graphs, the importance of using knowledge on the class of complete bipartite graphs gradually became apparent.

The main result of this article is the determination that $K_{1,2,7}$, $K_{1,3,5}$, $K_{1,4,4}$, and $K_{2,2,5}$ are the first of the complete tripartite graphs for which there exists a disconnected subgraph, $C{F}_{D\left(G\right)}$, induced on uncrossed edges in some of its optimal drawing, D. This list can be supplemented with the graph $K_{3,3,3}$ if a minimum possible number of edge crossings over all drawings of $K_{3,3,3}$ in the plane is equal to fifteen. The idea of a concept of a crossing sequence will be strongly used in the proofs of all statements. For the needs of our research on tripartite graphs, we will distinguish three possible forms of such a sequence on individual partitions. We emphasize that the crossing sequence is defined only over optimal drawings. The problem of reducing the number of crossings on edges in the drawings of graphs has been investigated in many areas because graphs are widely used to represent complex networks. Graphs are used to represent geographic features [3], and reducing the number of edge crossings is helpful in visualizing and understanding complex data [4]. Probably the most important area is VLSI technology. This is also why this new property of the $\mathcal{CF}$-connectedness of graphs is studied only for the drawings of graphs with the smallest number of crossings, i.e., on their optimal drawings.

2. Definitions and Preliminary Results

The crossing number, $\mathrm{cr}\left(G\right)$, of a simple graph, G, with the vertex set $V\left(G\right)$ and the edge set $E\left(G\right)$ is the minimum possible number of edge crossings over all drawings of G in the plane (for the definition of a drawing, see Klešč [5]). It is easy to see that a drawing with a minimum number of crossings (an optimal drawing) is always a good drawing, meaning that no edge crosses itself, no two edges cross more than once, and two edges incident with the same vertex do not cross.

Let D be an optimal drawing of a simple graph, $G=(V,E)$, with $V\left(G\right)=\{v_1,\dots ,v_n\}$. Let ${\mathrm{cr}}_D\left(v_p\right)$, $1\le p\le n$ denote the number of crossings on all edges, $v_p{v}_q$, for some $q\in \{1,\dots ,n\}$. Each crossing in D is counted on two edges with four vertices at their ends and based on the fact that we obtain

$$\sum _{p=1}^n{\mathrm{cr}}_D\left(v_p\right)=4{\mathrm{cr}}_D\left(G\right),$$

(1)

where ${\mathrm{cr}}_D\left(G\right)$ denotes the number of crossings in D. In the case of a complete bipartite graph, $K_{m,n}$, the sums of vertex crossings on both partitions are the same and therefore equal to twice the crossing number of $K_{m,n}$. The crossing sequence,$d_{D\left(G\right)}$, of the graph, G, in the drawing, D, is the non-increasing sequence of its vertex crossings, ${\mathrm{cr}}_D\left(v_p\right)$. The crossing sequence is a drawing of the graph invariant, and so two isomorphic drawings of one graph have the same crossing sequence. However, the crossing sequence does not, in general, uniquely identify a drawing of a considered graph. Two non-isomorphic optimal drawings of the same graph sometimes have the same crossing sequence. For example, we also show in Section 3 that each of four non-isomorphic optimal drawings of $K_{1,3,3}$ can have one of two possible crossing sequences.

Since we deal with a special class of tripartite graphs, it will be useful to introduce crossing subsequences as well. Let $K_{l,m,n}$ be the complete tripartite graph with partitions of size $|V_1|=l$, $|V_2|=m$ and $|V_3|=n$. In the rest of this paper, the vertices of $V_1$, $V_2$, and $V_3$ will be denoted by $u_i$, $v_j$, and $w_k$ for $i\in \{1,\dots ,l\}$, $j\in \{1,\dots ,m\}$, and $k\in \{1,\dots ,n\}$, respectively. The first crossing subsequence,$d_{D\left(K_l\right)}$, of the graph $K_{l,m,n}$ in the drawing, D, is the non-increasing sequence of its vertex crossings, ${\mathrm{cr}}_D\left(u_i\right)$, for $u_i\in V_1$. The second crossing subsequence,$d_{D\left(K_m\right)}$, and the third crossing subsequence,$d_{D\left(K_n\right)}$, of $K_{l,m,n}$ is defined by the vertex crossings ${\mathrm{cr}}_D\left(v_j\right)$ and ${\mathrm{cr}}_D\left(w_k\right)$, respectively. Due to isomorphism, it is clear that $\mathrm{cr}\left(K_{l,m,n}\right)=\mathrm{cr}\left(K_{l,n,m}\right)$ and so, in what follows, we will assume that $l\le m\le n$.

For any optimal drawing D of $G=(V,E)$, let us denote by $C{F}_{D\left(G\right)}$ the subgraph of G with the vertex set $V\left(G\right)$ and the edge set $\{e\in E\left(G\right):{\mathrm{cr}}_D\left(G\right)={\mathrm{cr}}_D(G\setminus e)\}$. A connected graph, G, is said to be $\mathcal{CF}$-connected if its subgraph, $C{F}_{D\left(G\right)}$, is connected for each optimal drawing D of G. Equivalently, we can also say that a connected graph, G, is $\mathcal{CF}$-connected if there is a path induced on uncrossed edges between every pair of different vertices of G in each optimal drawing D of G. In order to make it easier to check, we will illustrate uncrossed edges in red and individual crossings on edges with small red circles in all considered drawings.

Throughout the proofs of this paper, some parts will be based on Kleitman’s result [6] on the crossing numbers for some $K_{m,n}$. He showed that

$$\mathrm{cr}\left(K_{m,n}\right)=⌊\frac{m}{2}⌋⌊\frac{m-1}{2}⌋⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋,\mathrm{with}min\{m,n\}\le 6.$$

(2)

3. The Complete Tripartite Graphs ${\mathit{K}}_{\mathbf{1},\mathit{m},\mathit{n}}$ for $\mathit{m}\ge \mathbf{1}$, $\mathit{n}\ge \mathbf{2}$

The complete tripartite graphs $K_{1,1,n}$ are $\mathcal{CF}$-connected because they have planar drawings for each $n\ge 1$; see Figure 1. By planar drawings we mean drawings without any crossing of edges.

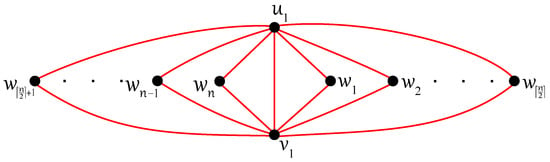
Figure 1. Planar drawing of the complete tripartite graph $K_{1,1,n}$.

The crossing number $\mathrm{cr}\left(K_{1,2,n}\right)=⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ was established by Ho [7].

Theorem 1.

The graphs $K_{1,2,n}$ are $\mathcal{CF}$-connected for all $2\le n\le 6$.

Proof. 

Let D be any optimal drawing of the graph $K_{1,2,n}$ for some $n\in \{2,\dots ,6\}$. As $\mathrm{cr}\left(K_{1,2,n}\right)=\mathrm{cr}\left(K_{3,n}\right)=⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$, the pair of edges, $u{v}_1$ and $u{v}_2$, cannot be crossed in D. The third crossing subsequence, $d_{D\left(K_n\right)}$, consists of values of two at most according to ${\mathrm{cr}}_D\left(K_{1,2,n}\right)-\mathrm{cr}\left(K_{1,2,n-1}\right)=⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋-⌊\frac{n-1}{2}⌋⌊\frac{n-2}{2}⌋\le 2$. For each $k=1,\dots ,n$, the vertex $w_k$ is adjacent in $C{F}_{D\left(K_{1,2,n}\right)}$ with at least one of the vertices u, $v_1$, or $v_2$ because its crossing number is less than three. Since the corresponding subgraph $C{F}_{D\left(K_{1,2,n}\right)}$ is connected, the proof is complete. □

For $n\ge 7$, the optimal drawing D of $K_{1,2,n}$ shown in Figure 2 offers a disconnected subgraph, $C{F}_{D\left(K_{1,2,n}\right)}$, with the isolated vertex $w_2$ and so the next result is obvious.

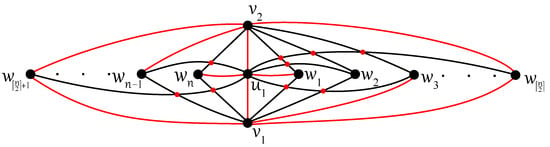
Figure 2. Optimal drawing of $K_{1,2,n}$ with $⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ crossings for $n\ge 7$.

Theorem 2.

The graphs $K_{1,2,n}$ are not $\mathcal{CF}$-connected for all $n\ge 7$.

In the following, $\mathcal{CF}$-connectedness for the graph $K_{1,3,n}$ will be solved thanks to the well-known result $\mathrm{cr}\left(K_{1,3,n}\right)=2⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋$ by Asano [8]. The nonplanarity of the complete bipartite graph $K_{3,3}$ is one of its most important properties. Further, there is the unique drawing of $K_{3,3}$ up to homeomorphisms given in Figure 3 by Bokal and Leaños [9].

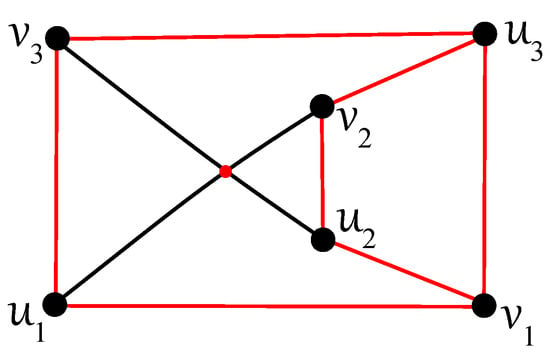
Figure 3. One optimal drawing of the complete bipartite graph $K_{3,3}$.

Lemma 1.

Let D be any optimal drawing of $K_{1,3,3}$ with ${\mathrm{cr}}_D\left(u\right)\ne 0$. Then, ${\mathrm{cr}}_D\left(u\right)=2$ and $D(K_{1,3,3}\setminus u)$ obtained by removing u from $K_{1,3,3}$ induced by D is also an optimal drawing of $K_{3,3}$.

Proof. 

In the rest of the proof, let $J=K=\{1,2,3\}$. Let D be an optimal drawing of the graph $K_{1,3,3}$ with ${\mathrm{cr}}_D\left(u\right)\ge 1$, that is, ${\mathrm{cr}}_D\left(K_{1,3,3}\right)=3$. As $\mathrm{cr}\left(K_{3,3}\right)=1$ and $\mathrm{cr}\left(K_{1,2,3}\right)=1$, the crossing sequence $d_{D\left(K_{1,3,3}\right)}$ consists of values of two at most, otherwise, by deleting the vertex u or $v_j$ for $j\in J$ (or $w_k$ for $k\in K$) of the considered partition with ${\mathrm{cr}}_D\left(u\right)>2$ or ${\mathrm{cr}}_D\left(v_j\right)>2$ (or ${\mathrm{cr}}_D\left(w_k\right)>2$), a planar drawing of the graph homeomorphic to $K_{3,3}$ or $K_{1,2,3}$ is obtained, respectively. Using (1) in the form

$${\mathrm{cr}}_D\left(u\right)+\sum _{j\in J}{\mathrm{cr}}_D\left(v_j\right)+\sum _{k\in K}{\mathrm{cr}}_D\left(w_k\right)=4{\mathrm{cr}}_D\left(K_{1,3,3}\right)=12.$$

If any value is null, then $d_{D\left(K_{1,3,3}\right)}=(2,2,2,2,2,2,0)$ with ${\mathrm{cr}}_D\left(u\right)=2$. In the following, let none of the values be less than one, i.e., $d_{D\left(K_{1,3,3}\right)}=(2,2,2,2,2,1,1)$. For a contradiction, suppose that ${\mathrm{cr}}_D\left(u\right)=1$. Without loss of generality, let an edge $u{v}_j$ be crossed in D for some $j\in J$ and let $D^{\prime }$ be the subdrawing of $K_{1,3,3}\setminus \{u{v}_j:j\in J\}$ induced by D. In the rest of the proof, we will write $K_{3,4}$ instead of $K_{1,3,3}\setminus \{u{v}_j:j\in J\}$ due to their isomorphism. As ${\mathrm{cr}}_{D^{\prime }}\left(K_{3,4}\right)=2$ and $\mathrm{cr}\left(K_{3,3}\right)=1$, the crossing subsequence $d_{D^{\prime }\left(K_4\right)}$ consists of values of one at most, and four vertices from the second partition of $K_{3,4}$ produce

$${\mathrm{cr}}_{D^{\prime }}\left(u\right)+\sum _{j\in J}{\mathrm{cr}}_{D^{\prime }}\left(v_j\right)=2{\mathrm{cr}}_{D^{\prime }}\left(K_{3,4}\right)=4.$$

Therefore, $d_{D^{\prime }\left(K_4\right)}=(1,1,1,1)$, which yields that ${\mathrm{cr}}_{D^{\prime }}\left(u\right)=1$ and ${\mathrm{cr}}_D\left(u\right)=2$. The obtained contradiction confirms that ${\mathrm{cr}}_D\left(u\right)=2$. Since ${\mathrm{cr}}_D(K_{1,3,3}\setminus u)=1$, the drawing $D\left(K_{3,3}\right)$ induced by D must be optimal. □

Corollary 1.

There are four non-isomorphic optimal drawings of $K_{1,3,3}$.

Proof. 

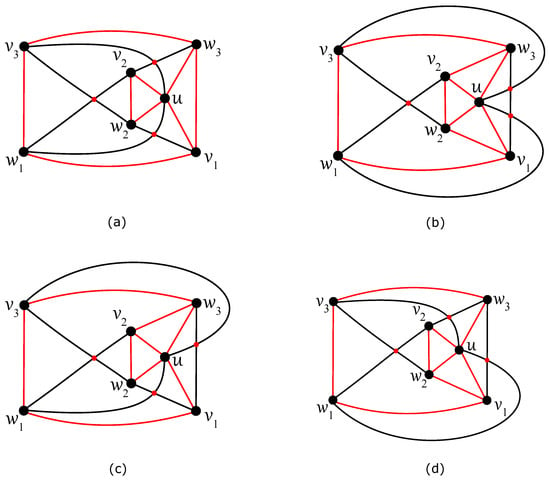
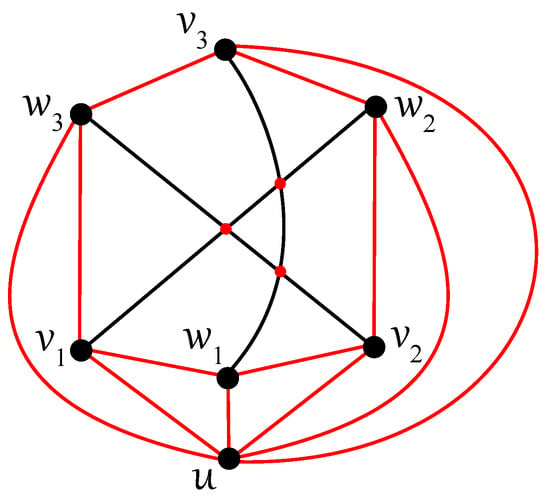
All optimal drawings D of $K_{1,3,3}$ with ${\mathrm{cr}}_D\left(u\right)\ge 1$ can be achieved by adding a new vertex u with six corresponding edges into some region of an optimal drawing of $K_{3,3}$ according to Lemma 1. Let $D^{\prime }$ be the subdrawing of $K_{3,3}$ induced by D without the vertex u, i.e., it is isomorphic to the drawing given in Figure 3. Without loss of generality, let the drawing $D^{\prime }$ be illustrated with a change in the labeling of the vertices $u_i$ to $w_k$ compared to the original drawing in Figure 3. As $\mathrm{cr}\left(K_{1,3,3}\right)=3$, there are only two regions in which it is possible to insert the vertex u with subsequent six edges and exactly two new crossings. Due to their symmetry, let the new vertex be inserted into the inner quadrangular region with four vertices, $v_1$, $w_3$, $v_2$, and $w_2$, on its boundary. In this way, we get four optimal drawings of $K_{1,3,3}$, three of which, given in Figure 4a–c, are non-isomorphic. An isomorphism of two drawings in Figure 4c,d is not preserved with respect to the considered labeling of vertices. The crossings sequences of all four drawings are equal to $(2,2,2,2,2,1,1)$, as follows from the proof of Lemma 1.

Figure 4. Four optimal drawings of $K_{1,3,3}$ with $d_{D\left(K_{1,3,3}\right)}=(2,2,2,2,2,1,1)$: (a) the subgraph $C{F}_{D\left(K_{1,3,3}\right)}$ on nine edges and with the cut vertex u; (b) the subgraph $C{F}_{D\left(K_{1,3,3}\right)}$ on ten edges; (c) the subgraph $C{F}_{D\left(K_{1,3,3}\right)}$ on nine edges, with no cut vertex and two vertices, $v_2$, $w_3$, of degree three; (d) the subgraph $C{F}_{D\left(K_{1,3,3}\right)}$ on nine edges, with no cut vertex and two vertices, $v_1$, $w_2$, of degree three.

Finally, let us suppose an optimal drawing D of $K_{1,3,3}$ with ${\mathrm{cr}}_D\left(u\right)=0$. There is the unique drawing of $K_{3,3}$ (up to homeomorphisms) with three crossings on edges and a location of all six vertices of $K_{3,3}$ on a boundary of one region. Since ${\mathrm{cr}}_D(K_{1,3,3}\setminus v_j)=1$ and ${\mathrm{cr}}_D(K_{1,3,3}\setminus w_k)=1$ for each $j,k=1,2,3$, thanks to $d_{D(K_{1,3,3)}}=(2,2,2,2,2,2,0)$ and also by the proof of Lemma 1, the mentioned drawing of $K_{3,3}$ can be obtained from the drawing of $K_{2,3}$ with one crossing and a location of all five vertices on a boundary of one region; see [10]. In the following, the vertex u is adjacent to all six vertices of $K_{3,3}$ without any additional crossing, and we obtain the last optimal drawing of $K_{1,3,3}$ shown in Figure 5. □

Figure 5. One optimal drawing of $K_{1,3,3}$ with $d_{D\left(K_{1,3,3}\right)}=(2,2,2,2,2,2,0)$.

It is easy to see that the corresponding subgraphs $C{F}_{D\left(K_{1,3,3}\right)}$ are connected for all four possible non-isomorphic optimal drawings of $K_{1,3,3}$ presented in Figure 4 and Figure 5, and therefore the complete tripartite graph $K_{1,3,3}$ is also $\mathcal{CF}$-connected.

Theorem 3.

The graph $K_{1,3,3}$ is $\mathcal{CF}$-connected.

Theorem 4.

The graph $K_{1,3,4}$ is $\mathcal{CF}$-connected.

Proof. 

In the rest of the proof, let $J=\{1,2,3\}$ and $K=\{1,2,3,4\}$. Let D be an optimal drawing of the graph $K_{1,3,4}$ for which the subgraph $C{F}_{D\left(K_{1,3,4}\right)}$ is disconnected. We can also assume that the third crossing subsequence $d_{D\left(K_4\right)}$ consists of values of three at most, provided by ${\mathrm{cr}}_D\left(K_{1,3,4}\right)-\mathrm{cr}\left(K_{1,3,3}\right)=6-3=3$. For $k\in K$, if there is at least one vertex $w_k$ from the third partition with ${\mathrm{cr}}_D\left(w_k\right)=3$, then the subdrawing $D(K_{1,3,4}\setminus w_k)$ obtained by removing $w_k$ from $K_{1,3,4}$ induced by D is also an optimal drawing of $K_{1,3,3}$. We already know that there exist only four non-isomorphic optimal drawings of $K_{1,3,3}$, as given in Figure 4 and Figure 5.

Let $D^{\prime }$ be a subdrawing of $K_{1,3,3}$ induced by D without the considered vertex $w_k$ and thus with a decrease of three crossings. For $k=4$, let us first consider the drawing $D^{\prime }$ of $K_{1,3,3}$, as given in Figure 4a. It is not difficult to verify that at most two edges of $C{F}_{D^{\prime }\left(K_{1,3,3}\right)}$ can be crossed by inserting the vertex $w_4$ with ${\mathrm{cr}}_D\left(w_4\right)=3$ into arbitrary region, such that the subgraph $C{F}_{D^{\prime }\left(K_{1,3,3}\right)}$ preserves its connectedness, that is, $C{F}_{D\left(K_{1,3,4}\right)}$ must be connected. The same reason gives a connectedness of $C{F}_{D\left(K_{1,3,4}\right)}$ for three other possible drawings of $K_{1,3,3}$, as shown in Figure 4. For $D^{\prime }\left(K_{1,3,3}\right)$ presented in Figure 4b, three edges of $C{F}_{D^{\prime }\left(K_{1,3,3}\right)}$ can only be crossed by inserting $w_4$ into the region incident with both vertices u and $v_2$, but a connectedness remains intact. It is important to deal with both drawings in Figure 4c,d (despite their isomorphism), because their isomorphism is not preserved with respect to the considered labeling of vertices and for a subsequent insertion of a new vertex from the third partition. Finally, suppose $D^{\prime }$ of $K_{1,3,3}$ given in Figure 5. The vertex $w_4$ can only be placed in a region of $D^{\prime }\left(K_{1,3,3}\right)$ with the vertex u of $K_{1,3,3}$ on its boundary, and exactly three of the six edges incident with u become crossed. We receive a connectedness of $C{F}_{D\left(K_{1,3,4}\right)}$ in all considered cases. In the following, let us suppose that none of the values in $d_{D\left(K_4\right)}$ can be greater than two.

Since ${\mathrm{cr}}_D\left(K_{1,3,4}\right)-\mathrm{cr}\left(K_{3,4}\right)=6-2=4$ and ${\mathrm{cr}}_D\left(K_{1,3,4}\right)-\mathrm{cr}\left(K_{1,2,4}\right)=6-2=4$, both crossing subsequences $d_{D\left(K_1\right)}$ and $d_{D\left(K_3\right)}$ consist of values of four at most. Using (1) in the form

$${\mathrm{cr}}_D\left(u\right)+\sum _{j\in J}{\mathrm{cr}}_D\left(v_j\right)+\sum _{k\in K}{\mathrm{cr}}_D\left(w_k\right)=4{\mathrm{cr}}_D\left(K_{1,3,4}\right)=24,$$

the crossings numbers of all vertices are uniquely determined. Therefore, $d_{D\left(K_{1,3,4}\right)}=(4,4,4,4,2,2,2,2)$, where $d_{D\left(K_1\right)}=\left(4\right)$, $d_{D\left(K_3\right)}=(4,4,4)$, and $d_{D\left(K_4\right)}=(2,2,2,2)$. An isolated vertex cannot be a connected component of the disconnected subgraph $C{F}_{D\left(K_{1,3,4}\right)}$ because the degree of each vertex of $K_{1,3,4}$ is greater than its crossing number. As $K_{1,3,4}\setminus \{u{w}_k:k\in K\}\cong K_{3,5}$ and $K_{1,3,4}\setminus \{u{v}_j:j\in J\}\cong K_{4,4}$, the well-known results $\mathrm{cr}\left(K_{3,5}\right)=4$ and $\mathrm{cr}\left(K_{4,4}\right)=4$, thanks to (2), enforce exactly two crossings on four edges $\{u{w}_k:k\in K\}$ and three edges $\{u{v}_j:j\in J\}$ in D, respectively.

Any edge $u{w}_k$ can be crossed once at most in D, otherwise two crossings on the edge $u{w}_k$ result in no crossing on six edges $\{v_j{w}_k,u{w}_l:j\in J,l\in K,l\ne k\}$; a connectedness of $K_{1,3,4}$ within the subgraph $C{F}_{D\left(K_{1,3,4}\right)}$ is obtained thanks to at least one uncrossed edge $u{v}_j$ for some $j\in J$. Without loss of generality, let u be adjacent in $C{F}_{D\left(K_{1,3,4}\right)}$ with both vertices, $w_1$, $w_2$, and let each edge, $u{w}_3$ and $u{w}_4$, be crossed just once in D. In the rest of the proof (using ${\mathrm{cr}}_D\left(w_1\right)=2$), also let the edge $v_3{w}_1$ be uncrossed in D. Then, at least one of the vertices, $v_1$, $v_2$ and $w_3$, $w_4$, say $v_1$ and $w_3$, must be included in other connected components of $C{F}_{D\left(K_{1,3,4}\right)}$ as the vertices u, $w_1$, $w_2$ and $v_3$. Both edges $u{w}_3$ and $v_3{w}_3$ are crossed in D according to their incorporation into different connected components. Thus, the edge $v_2{w}_3$ must be contained in $C{F}_{D\left(K_{1,3,4}\right)}$ without any crossing provided by ${\mathrm{cr}}_D\left(w_3\right)=2$. Next, each of the edges $v_1{w}_4$ and $v_2{w}_4$ cannot be crossed in D because the edge $u{w}_4$ offers one crossing and ${\mathrm{cr}}_D\left(w_4\right)=2$. Therefore, the second connected component of $C{F}_{D\left(K_{1,3,4}\right)}$ must be isomorphic to the complete bipartite graph $K_{2,2}$, with the vertex set consisting of $v_1$, $v_2$, $w_3$ and $w_4$. The edges $u{v}_1$ and $u{v}_2$ must be crossed only once in D, and therefore both vertices $v_1$ and $v_2$ offer two crossings on an incident edge with $w_1$ or $w_2$. The obtained contradiction with $d_{D\left(K_4\right)}=(2,2,2,2)$ completes the proof of Theorem 4. □

Non $\mathcal{CF}$-connectedness of the remaining complete tripartite graphs $K_{1,m,n}$ is summarized in Theorems 5 and 6 thanks to the optimal drawings of $K_{1,3,n}$ with the isolated vertex $w_2$ and $K_{1,4,n}$, with the connected component on the five vertices $u_1$, $v_1$, $v_2$, $w_1$, and $w_n$ given in Figure 6 and Figure 7, respectively. The exact value for the crossing number $\mathrm{cr}\left(K_{1,4,n}\right)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋$, again by Ho [7], is well-known.

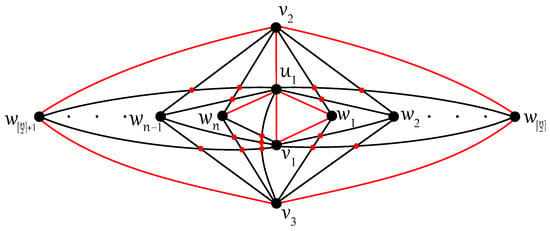
Figure 6. Optimal drawing of $K_{1,3,n}$ with $2⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+⌊\frac{n}{2}⌋$ crossings for $n\ge 5$.

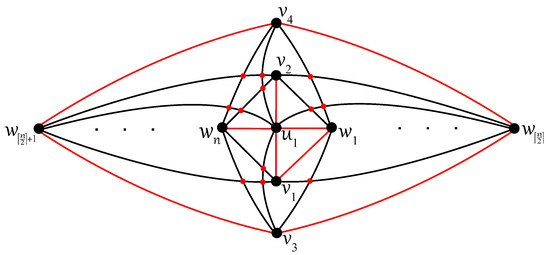
Figure 7. Optimal drawing of $K_{1,4,n}$ with $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2⌊\frac{n}{2}⌋$ crossings for $n\ge 4$.

Theorem 5.

The graphs $K_{1,3,n}$ are not $\mathcal{CF}$-connected for all $n\ge 5$.

Theorem 6.

The graphs $K_{1,4,n}$ are not $\mathcal{CF}$-connected for all $n\ge 4$.

4. The Complete Tripartite Graphs ${\mathit{K}}_{\mathbf{2},\mathit{m},\mathit{n}}$ for $\mathit{m},\mathit{n}\ge \mathbf{2}$

The issue of $\mathcal{CF}$-connectedness of the complete bipartite graphs $K_{m,n}$ has been introduced by Staš and Valiska [1]. One of the important results is the existence of only two possible non-isomorphic optimal drawings of the complete bipartite graph $K_{3,4}$, as presented in Figure 8 with corresponding crossing sequences.

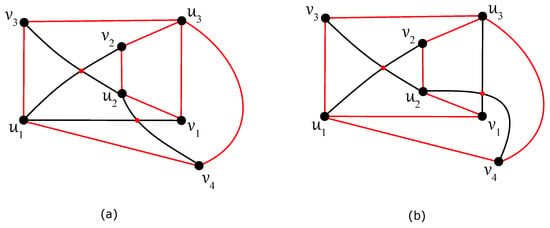
Figure 8. Two non-isomorphic optimal drawings of the complete bipartite graph $K_{3,4}$: (a) the drawing with $d_{D\left(K_{3,4}\right)}=(2,2,1,1,1,1,0)$; (b) the drawing with $d_{D\left(K_{3,4}\right)}=(2,1,1,1,1,1,1)$.

Lemma 2

([1], Corollary 3.3). There are two non-isomorphic optimal drawings of $K_{3,4}$.

Klešč and Schrötter [11] determined $\mathrm{cr}\left(K_{2,2,n}\right)=2⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ for all $n\ge 1$.

Corollary 2.

There is only one optimal drawing of $K_{2,2,3}$.

Proof. 

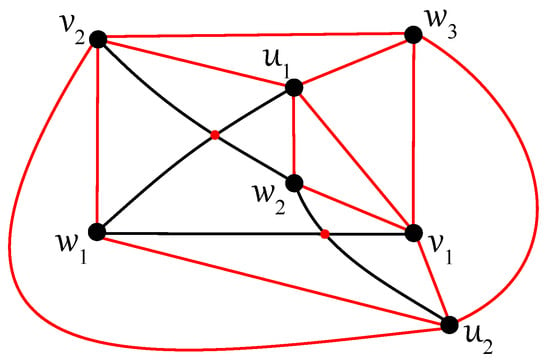
Let D be any optimal drawing of $K_{2,2,3}$. Since the crossings numbers of both graphs $K_{2,2,3}$ and $K_{4,3}$ are the same and equal to two, none of the four edges between the first two partitions can be crossed in D. By Lemma 2, its induced subdrawing $D\left(K_{4,3}\right)$ must be isomorphic to one optimal drawing of $K_{3,4}$, as given in Figure 8. For the drawing presented in Figure 8a, there is only one possibility to connect four vertices into one cycle $C_4$ without increasing the number of crossings.

Such a way is shown in Figure 9, with a corresponding change in vertex labeling due to three partitions instead of the original two. The optimal drawing D cannot be obtained from the drawing of $K_{3,4}$ given in Figure 8b because the vertex $v_1$ can only be connected to the vertex $v_4$ without additional crossing. □

Figure 9. One optimal drawing of the complete tripartite graph $K_{2,2,3}$.

Since $\mathrm{cr}\left(K_{2,2,2}\right)=0$ and the corresponding subgraph $C{F}_{D\left(K_{2,2,3}\right)}$ given in Figure 9 is connected, both graphs $K_{2,2,2}$ and $K_{2,2,3}$ are $\mathcal{CF}$-connected.

Lemma 3.

Let D be any optimal drawing of the complete tripartite graph $K_{2,2,4}$. For any vertex $w_k$ with $k=1,\dots ,4$, the subdrawing $D(K_{2,2,4}\setminus w_k)$ obtained by removing $w_k$ from $K_{2,2,4}$ induced by D is also an optimal drawing of $K_{2,2,3}$.

Proof. 

Let D be any optimal drawing of the graph $K_{2,2,4}$, that is, ${\mathrm{cr}}_D\left(K_{2,2,4}\right)=4$. None of the four edges between the first two partitions can be crossed in D because the crossing number of its subgraph $K_{4,4}$ is also four. As $\mathrm{cr}\left(K_{2,2,3}\right)=2$, the third crossing subsequence $d_{D\left(K_4\right)}$ consists of values of two at most. Each crossing in D is counted on two edges with two vertices from the third partition at their ends, and therefore property (1) can be easily adjusted to

$$2\sum _{k=1}^4{\mathrm{cr}}_D\left(w_k\right)=4{\mathrm{cr}}_D\left(K_{2,2,4}\right)=16.$$

So, $d_{D\left(K_4\right)}=(2,2,2,2)$. Since ${\mathrm{cr}}_D(K_{2,2,4}\setminus w_k)=2$ for each $k=1,\dots ,4$, the drawing $D\left(K_{2,2,3}\right)$ induced by D must be optimal. □

Theorem 7.

The graph $K_{2,2,4}$ is $\mathcal{CF}$-connected.

Proof. 

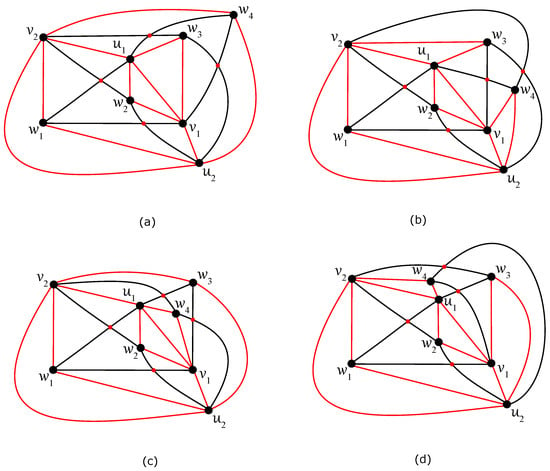
By Lemma 3, all optimal drawings of $K_{2,2,4}$ can only be achieved by adding a new vertex $w_4$ with four corresponding edges into a region of the optimal drawing of $K_{2,2,3}$ in such a way as shown in Figure 9. As $\mathrm{cr}\left(K_{2,2,4}\right)=4$, there are only four regions in which it is possible to insert the vertex $w_4$ with subsequent four edges and exactly two new crossings. For all four such cases given in Figure 10, their corresponding subgraphs $C{F}_{D\left(K_{2,2,4}\right)}$ are connected, and this completes the proof of Theorem 7. □

Figure 10. Four optimal drawings of $K_{2,2,4}$ with $d_{D\left(K_{2,2,4}\right)}=(2,2,2,2,2,2,2,2)$: (a) the subgraph $C{F}_{D\left(K_{2,2,4}\right)}$ does not contain any cycle on eight vertices as a subgraph; (b) the subgraph $C{F}_{D\left(K_{2,2,4}\right)}$ contains a cycle on eight vertices as a subgraph; (c) the subgraph $C{F}_{D\left(K_{2,2,4}\right)}$ does not contain any cycle on eight vertices as a subgraph; (d) the subgraph $C{F}_{D\left(K_{2,2,4}\right)}$ contains a cycle on eight vertices as a subgraph.

Figure 11 shows an optimal drawing D of the complete tripartite graph $K_{2,2,n}$ for n at least five with a disconnected subgraph $C{F}_{D\left(K_{2,2,n}\right)}$ with the isolated vertex $w_2$, which makes the next result obvious.

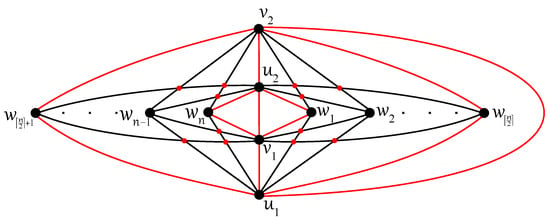
Figure 11. Optimal drawing of $K_{2,2,n}$ with $2⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋$ crossings for $n\ge 5$.

Theorem 8.

The graphs $K_{2,2,n}$ are not $\mathcal{CF}$-connected for all $n\ge 5$.

The exact value for the crossing number $\mathrm{cr}\left(K_{2,3,n}\right)=4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n$ was also established by Asano [8]. Let $D_n$ denote the discrete graph (sometimes called the empty graph) on n vertices. As $K_{2,3,n}\cong K_{2,3}+D_n$, the four following statements will be based on the properties of the join product of two graphs, $K_{2,3}$ and $D_n$ (for the definition of a join product, see Klešč [5]). For each $k=1,\dots ,n$, the vertex $w_k$ is adjacent to every vertex of the graph $K_{2,3}$, and let $T^{w_k}$ denote the subgraph induced by five edges incident with the vertex $w_k$. The graph $T^{w_1}\cup \dots \cup T^{w_n}$ is isomorphic to the complete bipartite graph $K_{5,n}$ and

$${\mathrm{cr}}_D(K_{2,3}+D_n)={\mathrm{cr}}_D\left(\bigcup _{k=1}^n{T}^{w_k}\right)+{\mathrm{cr}}_D\left(K_{2,3},\bigcup _{k=1}^n{T}^{w_k}\right)+{\mathrm{cr}}_D\left(K_{2,3}\right)$$

(3)

for all good drawings D of $K_{2,3}+D_n$. Two different vertices, $w_{k_1}$ and $w_{k_2}$, of $D_n$ are antipodal in an optimal drawing D of $K_{2,3}+D_n$ if the subdrawing $D(T^{w_{k_1}}\cup T^{w_{k_2}})$ induced by D is planar. In the drawing D, the rotation${\mathrm{rot}}_D\left(w_k\right)$ of a vertex $w_k$ is the cyclic permutation of adjacent vertices of $K_{2,3}$ that records the (cyclic) counter-clockwise order in which the edges leave $w_k$; see Woodall [12]. Notice that two different vertices, $w_{k_1}$ and $w_{k_2}$, of $D_n$ are antipodal in D if and only if ${\mathrm{rot}}_D\left(w_{k_1}\right)$ is inverse to ${\mathrm{rot}}_D\left(w_{k_2}\right)$.

Theorem 9.

The graph $K_{2,3,3}$ is $\mathcal{CF}$-connected.

Proof. 

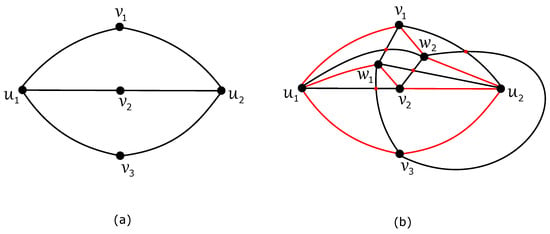
In the rest of the proof, let $I=\{1,2\}$ and $J=K=\{1,2,3\}$. Let D be an optimal drawing of the graph $K_{2,3,3}$ for which the subgraph $C{F}_{D\left(K_{2,3,3}\right)}$ is disconnected. Since $K_{2,3,3}\setminus \{u_i{v}_j:i\in I,j\in J\}\cong {\bigcup }_{k\in K}{T}^{w_k}\cong K_{3,5}$ and ${\mathrm{cr}}_D\left(K_{3,5}\right)\ge 4$ thanks to (2), the edges of $K_{2,3}$ can be crossed three times at most in D. For the subgraph $K_{2,3}$ induced on the first two partitions of $K_{2,3,3}$, we will discuss possibilities for the number of crossings among edges of $K_{2,3}$, and we show that there is a contradiction with the assumption that optimality of the drawing D or a disconnectedness of the subgraph $C{F}_{D\left(K_{2,3,3}\right)}$ can be obtained in all cases.

Case 1: The subdrawing of $K_{2,3}$ induced by D is nonplanar, that is, ${\mathrm{cr}}_D\left(K_{2,3}\right)\ge 1$. If no region of $D\left(K_{2,3}\right)$ is incident with all five vertices of $K_{2,3}$, then each subgraph $T^{w_k}$ crosses some edge of $K_{2,3}$ and we obtain at least four crossings on the edges of $K_{2,3}$. At least four more crossings among the edges of ${\bigcup }_{k\in K}{T}^{w_k}$ confirms a contradiction with an optimality of the drawing D. There are only two possible nonplanar drawings of the graph $K_{2,3}$ with all five vertices located on a boundary of one region; see also [10].

For the subdrawing $D\left(K_{2,3}\right)$ given in Figure 12a, all three subgraphs $T^{w_k}$ cannot cross any edge of $K_{2,3}$ due to ${\mathrm{cr}}_D\left(K_{2,3}\right)=3$. All three vertices, $w_k$, can only be placed in the outer region of $D\left(K_{2,3}\right)$ with the same rotation $\left(u_1{v}_3{v}_2{v}_1{u}_2\right)$, but any two different subgraphs $T^{w_{k_1}}$ and $T^{w_{k_2}}$ with the same rotation cross each other at least $\lfloor \frac{5}{2}\rfloor \lfloor \frac{4}{2}\rfloor =4$ times, according to Woodall [12]. In this way, $4\left(\genfrac{}{}{0pt}{}{3}{2}\right)+3=15$ justified crossings contradict an optimality of D. If we consider $D\left(K_{2,3}\right)$, as shown in Figure 12b, with ${\mathrm{cr}}_D\left(K_{2,3}\right)=1$, then at least one subgraph $T^{w_k}$, say $T^{w_1}$, cannot cross any edge of $K_{2,3}$. Each of the two remaining subgraphs, $T^{w_2}$ and $T^{w_3}$, cannot cross the edges of the graph $K_{2,3}\cup T^{w_1}$ at least four times because we obtain a contradiction with an optimality of D. There is only one way to get less than four crossings on the edges of $K_{2,3}\cup T^{w_1}$, and so, at least one vertex $w_k$, say $w_2$, must be placed in the region of $D\left(K_{2,3}\right)$ with three vertices, $u_1$, $u_2$, and $v_3$, of $K_{2,3}$ on its boundary, such that both edges $w_2{v}_1$ and $w_2{v}_2$ cross some edge of $K_{2,3}$. The last subgraph $T^{w_3}$ cannot cross any edge of $K_{2,3}$ due to ${\mathrm{cr}}_D(K_{2,3}\cup T^{w_2})=3$. Both subgraphs $T^{w_1}$ and $T^{w_3}$ have the same rotation $\left(u_1{v}_3{v}_2{v}_1{u}_2\right)$, and therefore, due to an optimality of D, the edges $w_2{v}_1$ and $w_2{v}_2$ cross the edges $u_2{v}_2$ and $u_1{v}_1$, respectively. Finally, it is not difficult to verify a contradiction with a supposed disconnectedness of the subgraph $C{F}_{D\left(K_{2,3,3}\right)}$.

Figure 12. Two possible nonplanar drawings of the graph $K_{2,3}$, where all five vertices of $K_{2,3}$ are located on a boundary of one region: (a) the drawing of $K_{2,3}$ with ${\mathrm{cr}}_D\left(K_{2,3}\right)=3$; (b) the drawing of $K_{2,3}$ with ${\mathrm{cr}}_D\left(K_{2,3}\right)=1$.

Case 2: The subdrawing $D\left(K_{2,3}\right)$ is planar, that is, it is isomorphic to one possible planar drawing of $K_{2,3}$, as given in Figure 13a. The drawing $D\left(K_{2,3}\right)$ does not contain any region incident with all five vertices of $K_{2,3}$, which yields that all three subgraphs $T^{w_k}$ must cross the edges of $K_{2,3}$ exactly once, and also ${\mathrm{cr}}_D\left({\bigcup }_{k\in K}{T}^{w_k}\right)=4$. We can also assume that the third crossing subsequence, $d_{D\left(K_3\right)}$, consists of values of five at most, provided by ${\mathrm{cr}}_D\left(K_{2,3,3}\right)-\mathrm{cr}\left(K_{2,2,3}\right)=7-2=5$. Note that the drawing D has a pair of antipodal vertices if and only if there is a vertex $w_k$ with ${\mathrm{cr}}_D\left(w_k\right)=5$ for some $k\in K$, because ${\mathrm{cr}}_D(T^{w_{k_1}},T^{w_{k_2}})=0$ applies if and only if ${\mathrm{cr}}_D(K_{2,3}\cup T^{w_{k_1}}\cup T^{w_{k_2}},T^{w_{k_3}})=1+4=5$ for any three different $k_1,k_2,k_3\in K$. In the following, two possible subcases may occur:

Figure 13. (a) One planar drawing of $K_{2,3}$; (b) the drawing of $K_{2,3}\cup T^{w_1}\cup T^{w_2}$ with ${\mathrm{cr}}_D(T^{w_1},T^{w_2})=2$.

• The drawing D has no pair of antipodal vertices. The planar subdrawing $D\left(K_{2,3}\right)$ consists of three regions (mutually isomorphic), and let the vertices of $K_{2,3}$ be denoted in such a way as shown in Figure 13a. Without the loss of generality, let the vertex $w_1$ be placed in the region of $D\left(K_{2,3}\right)$ with four vertices, $u_1$, $v_2$, $u_2$, and $v_1$, of $K_{2,3}$ on its boundary, and also let only the edge $u_1{v}_2$ be crossed by $T^{w_1}$. Let us first consider that there is at least one other vertex $w_k$, say $w_2$, located in the same region of $D\left(K_{2,3}\right)$ as the vertex $w_1$. The edges of the subgraphs $T^{w_1}$ and $T^{w_2}$ cannot cross each other more than twice in D due to ${\mathrm{cr}}_D\left({\bigcup }_{k\in K}{T}^{w_k}\right)=4$ and no antipodal pair of vertices. Assuming ${\mathrm{cr}}_D(T^{w_1},T^{w_2})\le 2$, we obtain an unique subdrawing of $K_{2,3}\cup T^{w_1}\cup T^{w_2}$ with two crossings, as given in Figure 13b. As ${\mathrm{cr}}_D(T^{w_1},T^{w_3})=1$ and ${\mathrm{cr}}_D(T^{w_2},T^{w_3})=1$, the vertex $w_3$ cannot be located in the same region of $D\left(K_{2,3}\right)$ as $w_1$ or $w_2$. If $w_3$ is placed in the region of $D\left(K_{2,3}\right)$ with the vertices $u_1$, $v_2$, $u_2$, $v_3$ of $K_{2,3}$ on its boundary, then $w_3{u}_1$ and $w_3{v}_1$ must cross $w_1{v}_3$ and $u_2{v}_3$, $w_2{v}_3$, respectively. Similarly, for the region of $D\left(K_{2,3}\right)$ with the vertices $u_1$, $v_3$, $u_2$, $v_1$ of $K_{2,3}$ on its boundary, $w_3{u}_2$ and $w_3{v}_2$ must cross $w_2{v}_3$ and $u_1{v}_3$, $w_1{v}_3$, respectively. Both subcases force a connected subgraph $C{F}_{D\left(K_{2,3,3}\right)}$.
  Now, suppose there is no pair of vertices of the third partition located in the same region of $D\left(K_{2,3}\right)$. In the rest of the paper, let ${\mathrm{cr}}_D(T^{w_1},T^{w_2})=2$, ${\mathrm{cr}}_D(T^{w_1},T^{w_3})=1$, and ${\mathrm{cr}}_D(T^{w_2},T^{w_3})=1$. If the vertex $w_3$ is placed in the region of $D\left(K_{2,3}\right)$ with the vertices $u_1$, $v_2$, $u_2$, $v_3$ of $K_{2,3}$ on its boundary, then $w_3{u}_1$ and $w_3{v}_1$ must cross $w_1{v}_3$ and $u_2{v}_3$, respectively. Consequently, the vertex $w_2$ is placed in the region of $D\left(K_{2,3}\right)$ with the vertices $u_1$, $v_3$, $u_2$, $v_1$ of $K_{2,3}$ on its boundary, such that $w_2{u}_2$ and $w_2{v}_2$ cross $w_3{v}_1$ and $u_1{v}_1$, respectively. Moreover, the edge $w_2{v}_2$ must also cross two edges incident with the vertex $w_1$. Similarly, if $w_3$ is placed in the region with $u_1$, $v_3$, $u_2$, $v_1$ of $K_{2,3}$ on its boundary, then $w_3{v}_2$ crosses either $u_1{v}_3$, $w_1{v}_3$ or $u_2{v}_1$, $u_2{w}_1$. In the first subcase, $w_2{u}_1$ and $w_2{v}_1$ must cross $w_3{v}_2$, $w_1{v}_3$ and $u_2{v}_2$, $u_2{w}_1$, respectively. In the second one, the edge $w_2{u}_1$ crosses $w_1{v}_3$, and the edge $w_2{v}_1$ crosses either $w_1{v}_3$, $u_1{v}_3$, $u_1{w}_3$ or $u_2{v}_2$, $u_2{w}_1$, $v_2{w}_3$. A connected subgraph $C{F}_{D\left(K_{2,3,3}\right)}$ is obtained in all considered subcases.
• There exists a pair of antipodal vertices in D. Without loss of generality, let $w_1$ and $w_3$ be antipodal vertices, that is, the edges of $K_{2,3}\cup T^{w_1}\cup T^{w_3}$ are crossed by the subgraph $T^{w_2}$ just five times. For $k\in K$, the vertex $w_k$ is adjacent in $C{F}_{D\left(K_{2,3,3}\right)}$, with at least one vertex of $K_{2,3}$. For ${\mathrm{cr}}_D\left(w_k\right)<5$, the degree of $w_k$ is greater than its crossing number. If ${\mathrm{cr}}_D\left(w_k\right)=5$, then each region of $D(K_{2,3,3}\setminus w_k)$ contains at least one vertex $u_i$ or $v_j$ of $K_{2,3}$ on its boundary, and the corresponding edge $u_i{w}_k$ or $v_j{w}_k$ must be uncrossed in D according to its optimality. In the following, we will justify a connectedness of $K_{2,3}$ within the subgraph $C{F}_{D\left(K_{2,3,3}\right)}$. Let $D^{\prime }$ be the subdrawing of $K_{2,3}+D_2$ induced by D with the considered pair of antipodal vertices and thus with a decrease of five crossings. The obtained drawing $D^{\prime }$ of $K_{2,2,3}$ with just two crossings must be optimal, which yields that it is isomorphic to the drawing given in Figure 9. Without loss of generality, let the drawing $D^{\prime }$ be illustrated in such a way as shown in Figure 14 with a change in the labeling of the vertices compared to the original drawing in Figure 9.
  

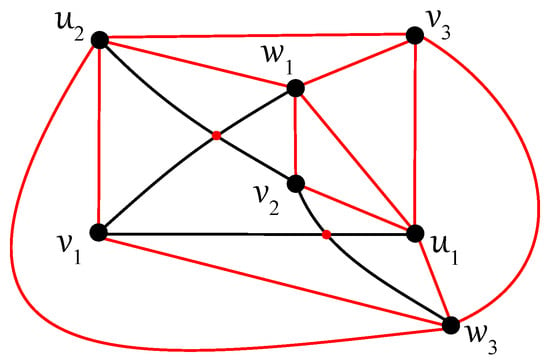  Figure 14. The optimal subdrawing of $K_{2,3}+D_2$ with the pair of antipodal vertices $w_1$ and $w_3$.
  First, let us turn to some restrictions for possible intersections of edges of the graph $K_{2,3}$ by the subgraph $T^{w_2}$. If $T^{w_2}$ crosses some already crossed edge of $K_{2,3}$ (by $T^{w_1}$ or $T^{w_3}$), then a connectedness of $K_{2,3}$ is preserved. By inserting the vertex $w_2$ into some region $\omega$ of $D^{\prime }\left(K_{2,2,3}\right)$, if an edge of $K_{2,3}$ located on a boundary of the region $\omega$ is crossed by $T^{w_2}$, then the broken connectedness of $K_{2,3}$ is repaired using $w_2$. Now, we can analyze the options for inserting the vertex $w_2$ into any of the three regions of $D^{\prime }\left(K_{2,3}\right)$. Let $w_2$ be inserted in the region of $D^{\prime }\left(K_{2,3}\right)$ where $w_1$ and $w_3$ are not contained. The vertex $w_2$ must be included in the region of $D^{\prime }(K_{2,3}\cup T^{w_1}\cup T^{w_3})$ with the vertices $v_1$ and $v_2$ on its boundary, and a connectedness of $K_{2,3}$ is achieved thanks to the path $v_1{w}_2{v}_2$. If $w_1$ and $w_2$ are in the same region of $D^{\prime }\left(K_{2,3}\right)$, then the path $u_2{w}_1{v}_2$ maintains a connectedness of $K_{2,3}$ in the case of the region of $D^{\prime }(K_{2,3}\cup T^{w_1}\cup T^{w_3})$ with $u_1$, $v_3$, and $w_1$ on its boundary. Finally, due to the previously mentioned symmetries of $K_{2,3}$, we again obtain a connectedness of $K_{2,3}$ using the path $v_1{w}_3{u}_1$ for the region of $D^{\prime }(K_{2,3}\cup T^{w_1}\cup T^{w_3})$ with $u_2$, $v_3$, and $w_3$ on its boundary.

All subcases force a connected subgraph $C{F}_{D\left(K_{2,3,3}\right)}$, and this completes the proof of Theorem 9. □

Lemma 4.

The subdrawing $D\left(K_{2,3}\right)$ induced by any optimal drawing D of $K_{2,3,4}$ is planar.

Proof. 

Let D be an optimal drawing of $K_{2,3,4}$, i.e., ${\mathrm{cr}}_D(K_{2,3}+D_4)=12$, using the results of Asano [8]. Since the graph ${\bigcup }_{k=1}^4{T}^{w_k}$ is isomorphic to the complete bipartite graph $K_{5,4}$ with $\mathrm{cr}\left(K_{5,4}\right)=8$ and

$${\mathrm{cr}}_D(K_{2,3}+D_4)={\mathrm{cr}}_D\left(K_{2,3}\right)+{\mathrm{cr}}_D\left(\bigcup _{k=1}^4{T}^{w_k}\right)+{\mathrm{cr}}_D\left(K_{2,3},\bigcup _{k=1}^4{T}^{w_k}\right),$$

there are four crossings at most on the six edges of $K_{2,3}$ in D. If there is no region of $D\left(K_{2,3}\right)$ with all five vertices of $K_{2,3}$ on its boundary, then each subgraph, $T^{w_k}$, must cross the edges of $K_{2,3}$ just once, and the subdrawing $D\left(K_{2,3}\right)$ should be planar. In the following, let there be a region of $D\left(K_{2,3}\right)$ with five vertices of $K_{2,3}$ on its boundary, that is, the subdrawing $D\left(K_{2,3}\right)$ is not planar. As ${\mathrm{cr}}_D\left(K_{2,3}\right)\ge 1$, there is at least one subgraph $T^{w_k}$ by which the edges of $K_{2,3}$ are not crossed. In the rest of the proof, let $T^{w_4}$ be such a subgraph.

Let us first consider the subdrawing $D\left(K_{2,3}\right)$ given in Figure 12a. The subdrawing of $K_{2,3}\cup T^{w_4}$ induced by D is uniquely determined (up to homeomorphism), and we can easily verify over all its possible regions that the edges of $K_{2,3}\cup T^{w_4}$ are crossed at least three times by each other subgraph $T^{w_k}$ for $k=1,2,3$. Thus, we obtain at least

$${\mathrm{cr}}_D\left(\bigcup _{k=1}^3{T}^{w_k}\right)+{\mathrm{cr}}_D\left(K_{2,3}\cup T^{w_4},\bigcup _{k=1}^3{T}^{w_k}\right)+{\mathrm{cr}}_D\left(K_{2,3}\right)\ge 4+3\times 3+3=16$$

crossings in D using (2) and (3), where ${\bigcup }_{k=1}^3{T}^{w_k}\cong K_{3,5}$. Finally, suppose $D\left(K_{2,3}\right)$, as presented in Figure 12b. Let $\alpha$ be the number of subgraphs $T^{w_k}$, $k\in \{1,2,3\}$, by which the edges of $K_{2,3}\cup T^{w_4}$ are crossed just twice in D. For each such considered subgraph $T^{w_k}$, the vertex $w_k$ must be placed in the region of $D\left(K_{2,3}\right)$ with three vertices, $u_1$, $u_2$, and $v_3$, of $K_{2,3}$ on its boundary, and also the edges $w_k{v}_1$ and $w_k{v}_2$ cross the edges $u_2{v}_2$ and $u_1{v}_1$, respectively. Assuming no more than four crossings on the edges of $K_{2,3}$, the number $\alpha$ cannot be greater than one. For $\alpha \le 1$, again by fixing $K_{2,3}\cup T^{w_4}$, we receive

$${\mathrm{cr}}_D\left(\bigcup _{k=1}^3{T}^{w_k}\right)+{\mathrm{cr}}_D\left(K_{2,3}\cup T^{w_4},\bigcup _{k=1}^3{T}^{w_k}\right)+{\mathrm{cr}}_D\left(K_{2,3}\right)\ge 4+2\alpha +3(3-\alpha )+1\ge 13$$

crossings in D. Both discussed subcases contradict the assumption of an optimality of the drawing D, and so the subdrawing $D\left(K_{2,3}\right)$ must be planar. □

Note that there exists an optimal drawing D of $K_{2,3,3}$ with the nonplanar subdrawing $D\left(K_{2,3}\right)$. Also for this reason, the same idea of planarity of $D\left(K_{2,3}\right)$ cannot be used in the proof of Theorem 9 over all optimal drawings D of $K_{2,3,3}$.

Corollary 3.

In any optimal drawing D of $K_{2,3,4}$, all four subgraphs $T^{w_k}$ cross the edges of $K_{2,3}$ exactly once and $d_{D\left(K_4\right)}=(5,5,5,5)$.

Proof. 

As ${\mathrm{cr}}_D\left(K_{2,3,4}\right)-\mathrm{cr}\left(K_{2,3,3}\right)=12-7=5$, the third crossing subsequence $d_{D\left(K_4\right)}$ consists of values of five at most. By Lemma 4, the subdrawing $D\left(K_{2,3}\right)$ is planar, and therefore each subgraph $T^{w_k}$ crosses the edges of $K_{2,3}$ at least once. Therefore,

$$20\ge \sum _{k=1}^4{\mathrm{cr}}_D\left(w_k\right)=2{\mathrm{cr}}_D\left(K_{5,4}\right)+{\mathrm{cr}}_D\left(K_{2,3},\bigcup _{k=1}^4{T}^{w_k}\right)\ge 16+4=20,$$

forcing $d_{D\left(K_4\right)}=(5,5,5,5)$ and ${\mathrm{cr}}_D(K_{2,3},T^{w_k})=1$ for each $k=1,\dots ,4$. □

Theorem 10.

The graph $K_{2,3,4}$ is $\mathcal{CF}$-connected.

Proof. 

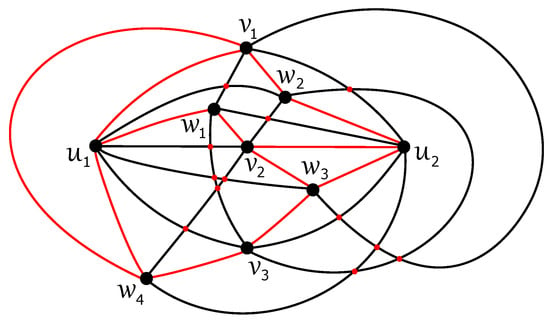
In the rest of the proof, let $K=\{1,2,3,4\}$. Let D be an optimal drawing of the graph $K_{2,3,4}$ with a disconnected subgraph $C{F}_{D\left(K_{2,3,4}\right)}$. The subdrawing of $K_{2,3}$ induced by D must be planar, and there are exactly five crossings on the edges of each subgraph $T^{w_k}$, $k\in K$, including one on the edges $K_{2,3}$ due to Lemma 4 and Corollary 3, respectively. Since the subdrawing $D\left(K_{2,3}\right)$ consists of three regions (mutually isomorphic), there are at least two different vertices, $w_{k_1}$ and $w_{k_2}$, located in the same region of $D\left(K_{2,3}\right)$. Without loss of generality, let $w_1$ and $w_2$ be two such vertices. Next, we will discuss the following two cases:

Case 1: The drawing D of $K_{2,3}+D_4$ has no pair of antipodal vertices. It is not difficult to verify that ${\mathrm{cr}}_D(T^{w_{k_1}},T^{w_{k_2}})\ge 2$ holds for any pair of different vertices $w_{k_1}$ and $w_{k_2}$ located in the same region of $D\left(K_{2,3}\right)$. As ${\mathrm{cr}}_D\left({\bigcup }_{k\in K}{T}^{w_k}\right)=8$ and $d_{D\left(K_4\right)}=(5,5,5,5)$, we obtain ${\mathrm{cr}}_D(T^{w_1},T^{w_2})=2$, which yields that ${\mathrm{cr}}_D(T^{w_1},T^{w_3})=1$, ${\mathrm{cr}}_D(T^{w_1},T^{w_4})=1$, ${\mathrm{cr}}_D(T^{w_2},T^{w_3})=1$, ${\mathrm{cr}}_D(T^{w_2},T^{w_4})=1$, and ${\mathrm{cr}}_D(T^{w_3},T^{w_4})=2$. Without loss of generality, using the planar drawing of $K_{2,3}$ shown in Figure 13a, let the vertex $w_1$ be placed in the region of $D\left(K_{2,3}\right)$ with four vertices, $u_1$, $v_2$, $u_2$ and $v_1$, of $K_{2,3}$ on its boundary, and also let only the edge $u_1{v}_2$ be crossed by $T^{w_1}$. Assuming ${\mathrm{cr}}_D(T^{w_1},T^{w_2})=2$, we obtain a unique subdrawing of $K_{2,3}\cup T^{w_1}\cup T^{w_2}$, as given in Figure 13b. Neither of the vertices $w_3$ and $w_4$ can be located in the same region of $D\left(K_{2,3}\right)$ as $w_1$ or $w_2$. For $k\in \{3,4\}$, if the vertex $w_k$ is placed in the region of $D\left(K_{2,3}\right)$ with the vertices $u_1$, $v_2$, $u_2$, $v_3$ of $K_{2,3}$ on its boundary, then $w_k{u}_1$ and $w_k{v}_1$ must cross $w_1{v}_3$ and $u_2{v}_3$, $w_2{v}_3$, respectively. Similarly, for the region of $D\left(K_{2,3}\right)$ with the vertices $u_1$, $v_3$, $u_2$, $v_1$ of $K_{2,3}$ on its boundary, $w_k{u}_2$ and $w_k{v}_2$ must cross $w_2{v}_3$ and $u_1{v}_3$, $w_1{v}_3$, respectively. Both vertices $w_3$ and $w_4$ cannot be placed in the same region due to ${\mathrm{cr}}_D(T^{w_3},T^{w_4})=2$. Therefore, we get a forced optimal drawing of $K_{2,3,4}$, as shown in Figure 15, where the connected subgraph $C{F}_{D\left(K_{2,3,4}\right)}$ contradicts the assumptions of D.

Figure 15. Optimal drawing of $K_{2,3,4}$ with no pair of antipodal vertices.

Case 2: There exists a pair of antipodal vertices in D. Let $D^{\prime }$ be the subdrawing of $K_{2,3}+D_2$ induced by D without the considered pair of antipodal vertices and thus with a decrease of ten crossings. The obtained drawing $D^{\prime }$ of $K_{2,2,3}$ with just two crossings must be optimal, which yields that it is isomorphic to the drawing given in Figure 9. Without loss of generality, let the drawing $D^{\prime }$ be illustrated in such a way as shown in Figure 14, with a change in the labeling of the vertices compared to the original drawing in Figure 9.

The planarity of the subdrawing $D^{\prime }(T^{w_1}\cup T^{w_3})$ in Figure 14 enforces the antipodality of the pair of vertices $w_1$ and $w_3$ in D. For $k\in K$, the vertex $w_k$ is adjacent in $C{F}_{D\left(K_{2,3,4}\right)}$ to at least one vertex of $K_{2,3}$, because otherwise removing its antipodal partner results an optimal drawing of $K_{2,3,3}$, and the contradiction with Theorem 9 is obtained. In the following, we will justify a connectedness of $K_{2,3}$ within the subgraph $C{F}_{D\left(K_{2,3,4}\right)}$. For $i\in \{1,2\}$, we can also use the knowledge that there are at most two crossings on the triple of edges $u_i{v}_1$, $u_i{v}_2$, $u_i{v}_3$ in D according to the well-known result of $\mathrm{cr}((K_{1,3}\cup K_1)+D_4)=10$ by Klešč and Staš [13]. Since both vertices $w_1$ and $w_2$ are located in the same region of $D\left(K_{2,3}\right)$, four alternatives may occur with regard to the possible intersections of any of the edges of 4-cycle $v_2{u}_1{v}_3{u}_2{v}_2$ by the subgraph $T^{w_2}$.

• The subgraph $T^{w_2}$ crosses the edge $v_2{u}_1$, and both edges $u_1{v}_3$ and $v_3{u}_2$ are not crossed in D. As ${\mathrm{cr}}_D\left(w_2\right)=5$, the vertex $w_2$ can be located in two regions of $D^{\prime }\left(K_{2,2,3}\right)$ with the rotation $\left(u_1{v}_3{u}_2{v}_2{v}_1\right)$. If $w_2$ is placed in the region with the vertices $u_1$, $v_3$, $w_1$ of $K_{2,2,3}$ on its boundary, then $v_2{w}_1{u}_2{v}_3{u}_1$ forms the path in $C{F}_{D\left(K_{2,3,4}\right)}$; see Figure 16.
  

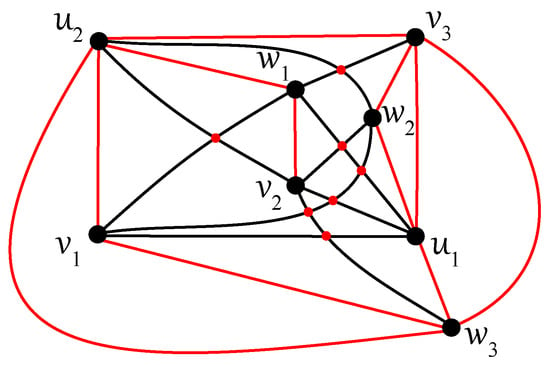  Figure 16. One subdrawing of $K_{2,3}+D_3$ induced by D.
  If the vertex $w_2$ is placed in the region with the vertices $u_1$, $w_1$, $v_2$ of $K_{2,2,3}$ on its boundary, then we obtain the path $v_2{w}_2{u}_1{v}_3{u}_2$, as presented in Figure 17. Two options for drawing the edge $w_2{u}_2$ are shown by dashed lines.
  

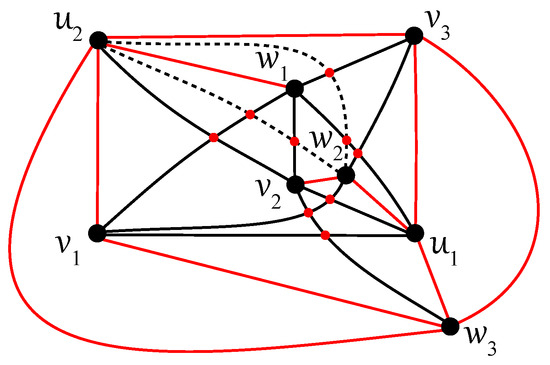  Figure 17. Two possible subdrawings of $K_{2,3}+D_3$ induced by D.
  Due to the antipodality of the vertices $w_2$ and $w_4$, the edge $w_4{v}_2$ of $T^{w_4}$ crosses the edge $v_1{u}_2$ of $K_{2,3}$. Finally, if the vertex $w_4$ is located in the region with the vertices $w_3$, $v_1$, $u_2$ or $w_3$, $u_2$, $v_3$ of $K_{2,2,3}$ on its boundary, then $v_1{w}_4$, $w_4{u}_2$ or $v_1{w}_3$, $w_3{u}_1$ are included in $C{F}_{D\left(K_{2,3,4}\right)}$, respectively.
• The subgraph $T^{w_2}$ crosses the edge $u_1{v}_3$, and both edges $v_2{u}_1$ and $v_3{u}_2$ are not crossed in D. The vertex $w_2$ can only be placed in the region with the vertices $u_1$, $v_3$, $w_1$ of $D^{\prime }\left(K_{2,2,3}\right)$ on its boundary with the rotation $\left(u_1{v}_1{v}_3{u}_2{v}_2\right)$, and so $v_2{u}_1{w}_2{v}_3{u}_2$ forms the path in $C{F}_{D\left(K_{2,3,4}\right)}$. Due to the antipodality of the vertices $w_2$ and $w_4$, the edge $w_4{v}_3$ of $T^{w_4}$ crosses the edge $v_1{u}_2$ of $K_{2,3}$. If the vertex $w_4$ is located in the region with the vertices $v_1$, $u_2$ or $v_1$, $v_2$ of $K_{2,2,3}$ on its boundary, then $v_1{w}_4$, $w_4{u}_2$ or $v_1{w}_4$, $w_4{v}_2$ are not crossed in D, respectively.
• The subgraph $T^{w_2}$ crosses the edge $v_3{u}_2$, and both edges $v_2{u}_1$ and $u_1{v}_3$ are not crossed in D. In this case, the edge $u_2{v}_1$ also cannot be crossed in D because there are already two crossings on the pair of edges $u_2{v}_2$ and $u_2{v}_3$. If the vertex $w_2$ is located in the region with the vertices $w_1$, $v_3$, $u_2$ or $w_1$, $u_1$, $v_3$ of $K_{2,2,3}$ on its boundary, then $v_1{u}_2{w}_2{v}_3{u}_1{v}_2$ or $v_1{u}_2{w}_1{v}_2{u}_1{v}_3$ forms the path in $C{F}_{D\left(K_{2,3,4}\right)}$, respectively.
• If the subgraph $T^{w_2}$ crosses the edge $u_2{v}_2$, then there exists the path $v_2{u}_1{v}_3{u}_2{v}_1$ in $C{F}_{D\left(K_{2,3,4}\right)}$ using the knowledge of already two crossings on the edge $u_2{v}_2$ in D.

All discussed subcases contradict the assumption of a disconnectedness of the subgraph $C{F}_{D\left(K_{2,3,4}\right)}$, and the proof is done. □

Note that Theorem 11 is obvious due to an obtained disconnected subgraph $C{F}_{D\left(K_{2,3,n}\right)}$ with the isolated vertex $w_2$ shown in Figure 18.

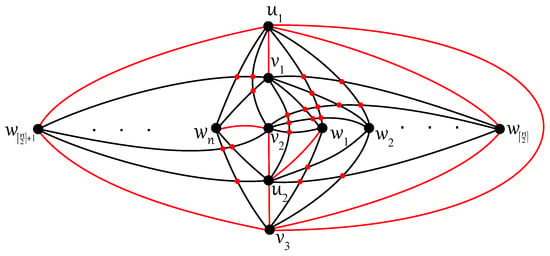
Figure 18. Optimal drawing of $K_{2,3,n}$ with $4⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+n$ crossings for $n\ge 5$.

Theorem 11.

The graphs $K_{2,3,n}$ are not $\mathcal{CF}$-connected for all $n\ge 5$.

The exact value for the crossing numbers of the complete tripartite graphs $K_{2,4,n}$ were established by Ho [14]. For $n\ge 4$, the optimal drawing D of $K_{2,4,n}$ shown in Figure 19 offers a disconnected subgraph $C{F}_{D\left(K_{2,4,n}\right)}$, with the connected component on the five vertices $w_1$, $v_3$, $u_2$, $v_4$, $w_{\lceil \frac{n}{2}\rceil }$, and so the next result is also obvious.

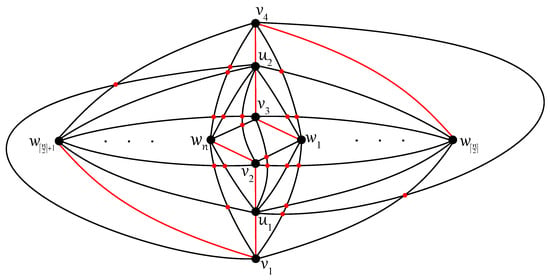
Figure 19. Optimal drawing of $K_{2,4,n}$ with $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n$ crossings for $n\ge 4$.

Theorem 12.

The graphs $K_{2,4,n}$ are not $\mathcal{CF}$-connected for all $n\ge 4$.

5. The Complete Tripartite Graphs ${\mathit{K}}_{\mathit{l},\mathit{m},\mathit{n}}$ for $\mathit{l},\mathit{m},\mathit{n}\ge \mathbf{3}$

Ho [15] also showed that $\mathrm{cr}\left(K_{3,3,n}\right)$ can be determined if the Zarankiewicz’s conjecture holds for $m=7$ and $n\le 20$ (for more, see also [16,17]).

Using the good drawing of $K_{3,3,n}$ with the isolated vertex $w_1$ in Figure 20, we can offer a partial answer contained in Theorem 13 for this problem.

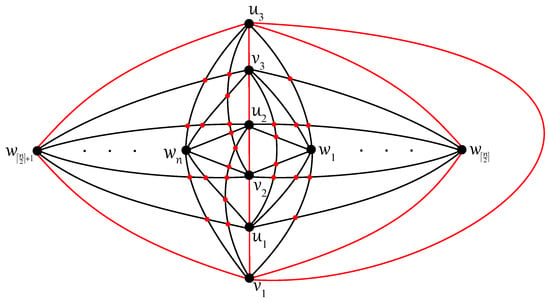
Figure 20. Good drawing of $K_{3,3,n}$ with $6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+2⌊\frac{n}{2}⌋+1$ crossings for $n\ge 3$.

Theorem 13.

If $\mathrm{cr}\left(K_{3,3,n}\right)=6⌊\frac{n}{2}⌋⌊\frac{n-1}{2}⌋+2n+2⌊\frac{n}{2}⌋+1$, then the graphs $K_{3,3,n}$ are not $\mathcal{CF}$-connected for all $n\ge 3$.

Note that the crossing numbers of complete tripartite graphs $K_{l,m,n}$ have already been established for all cases where $l+m\le 6$, except for $K_{3,3,n}$. Recently achieved result for $\mathrm{cr}(K_{3,3}\setminus e+D_n)$ by Staš [18] could be helpful for confirming Ho’s conjecture. Without confirming the Zarankiewicz’s conjecture, it will be very difficult to find $\mathrm{cr}\left(K_{l,m,n}\right)$ with $l+m\ge 7$ and $n\ge m\ge l\ge 3$. Consequently, it is all the more difficult to determine an answer for $\mathcal{CF}$-connectedness without knowing the exact value of the crossing number of such an investigated graph.

6. Conclusions

All complete tripartite graphs, $K_{l,m,n}$, that are $\mathcal{CF}$-connected and not $\mathcal{CF}$-connected are collected in Table 1. The graphs $K_{l,m,n}$ with $l,m,n\ge 3$ cannot be added to this table without confirming the exact value of $\mathrm{cr}\left(K_{3,3,n}\right)$.

Table 1. Table with overview of complete tripartite graphs that are $\mathcal{CF}$-connected and also those ones that are not $\mathcal{CF}$-connected.

Tripartite Graph	$\mathcal{CF}$-Connected	Not $\mathcal{CF}$-Connected
$K_{1,1,n}$	$1\le n$	-
$K_{1,2,n}$	$2\le n\le 6$	$n\ge 7$
$K_{1,3,n}$	$3\le n\le 4$	$n\ge 5$
$K_{1,4,n}$	-	$n\ge 4$
$K_{2,2,n}$	$2\le n\le 4$	$n\ge 5$
$K_{2,3,n}$	$3\le n\le 4$	$n\ge 5$
$K_{2,4,n}$	-	$n\ge 4$

Another very important class of symmetric graphs is the class of regular graphs, namely the class of circulant graphs, $C{i}_n\left(L\right)$, defined on n vertices with the list L and the class of generalized Petersen graphs, $GP(n,k)$, constructed by taking the union of the cycle graph, $C_n$, with the circulant graph, $C{i}_n\left(k\right)$. We expect that a similar discussion with respect to a modified crossing sequence (subsequence) can be used to examine $\mathcal{CF}$-connectedness on such graphs.