Abstract
In this paper, we introduce the concept of Rota–Baxter skew braces, and provide classifications of Rota–Baxter operators on various skew braces, such as and . We also present a necessary and sufficient condition for a skew brace to be a co-inverse skew brace. Additionally, we describe some constructions of Rota–Baxter quasiskew braces, and demonstrate that every Rota–Baxter skew brace can induce a quasigroup and a Rota–Baxter quasiskew brace.
MSC:
14L35; 14L99
1. Introduction
In 2007, braces were introduced by Rump in [1] to study the non-degenerate involutive set-theoretic solutions of the Yang–Baxter equation. Braces generalize Jacobson radical rings and can effectively imitate ring theory to discuss braided groups and sets. Moreover, braces possess an inherent left quasigroup structure. The development of brace theory is currently progressing rapidly and with great momentum, as evidenced by [2,3,4,5,6,7].
In 2017, Guarnieri and Vendramin introduced the concept of skew left braces [8] and proved that every skew left brace provides a non-involutive solution to the Yang–Baxter equation. Skew left braces have been widely applied in various branches of mathematics, including connections to regular subgroups [9], Hopf–Galois extensions [10], triply factorized groups [11], Garside theory [12,13], ring theory [14,15], flat manifolds [16], and pre-Lie algebras [17].
In 2021, Guo, Lang, and Sheng introduced Rota–Baxter groups in [18]. Smooth Rota–Baxter operators on Lie groups were proved to be differentiable, which, in turn, led to the derivation of the factorization theorem of Semenov–Tian–Shansky for Lie groups via the factorization theorem for Rota–Baxter Lie groups.
A Rota–Baxter group is a group G equipped with a map satisfying the identity
where . This notion emerged as a group version of Rota–Baxter operators that was defined on an algebra. In the 1960s, Rota–Baxter algebras first appeared in the work of Baxter [19] in the realm of probability theory. In the context of Lie algebras, physicists rediscovered the Rota–Baxter operator of weight zero in the 1980s as the operator form of the classical Yang–Baxter equation [20]. In 2000, Aguiar demonstrated that a Rota–Baxter algebra of weight zero possesses the structure of a dendriform algebra, thereby establishing a connection between Rota–Baxter algebras and dendriform algebras [21]. In 2019, Li Guo and Zongzhu Lin studied the representation and module theory of Rota–Baxter algebras [22]. Subsequently, Zheng, Guo, and Zhang presented a natural generalization of Rota–Baxter modules, namely the concept of Rota–Baxter paired modules [23]. Later research on Rota–Baxter algebra has connections with mathematical physics (classical and quantum Yang–Baxter equations) [24], mixable shuffle product constructions [25], Hopf algebras [26,27,28], and renormalization of perturbative quantum field theory [29]. For further details, see [30].
After the seminal work [18], investigations into Rota–Baxter groups progressed through subsequent research [31,32,33,34]. In 2022, Bardakov and Gubarev studied Rota–Baxter operators on abstract groups, and established a connection between Rota–Baxter groups and skew left braces [35]. They proved that every Rota–Baxter group can obtain a skew left brace by defining a new binary operation , where . Additionally, they showed that each skew left brace could be embedded into a Rota–Baxter group.
In light of the aforementioned facts, it is natural to ask: can Rota–Baxter operators be directly defined on skew braces, and how does one provide such a definition?
The purpose of this paper is to introduce the concept of Rota–Baxter operators on skew braces and study the structures of Rota–Baxter skew braces.
The research background and content of this paper are summarized in the diagram—the black arrows represent the background of the research, while the red arrows denote the main research content.
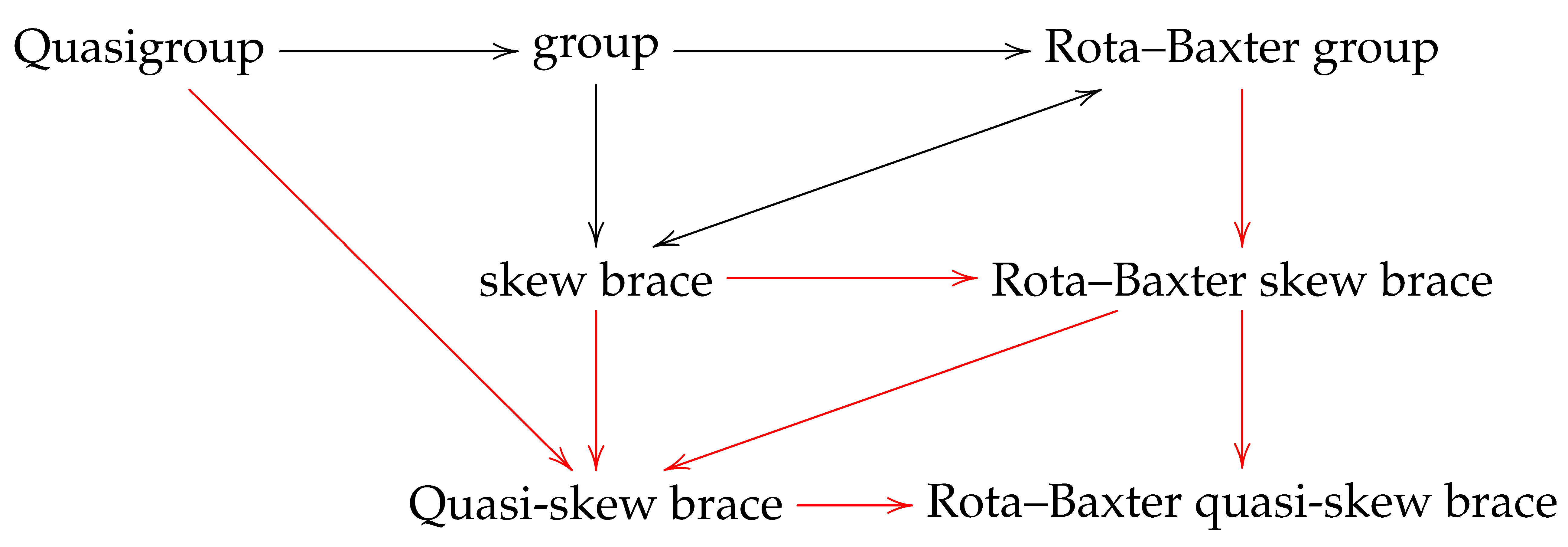
This paper is arranged and organized as follows: In Section 2, we introduce the concept of co-inverse skew braces and provide a necessary and sufficient condition for every skew brace to be a co-inverse skew brace. In Section 3, we introduce the concept of Rota–Baxter skew braces and classify Rota–Baxter operators on specific skew braces, namely, and . We also study the structures of Rota–Baxter skew braces. In Section 4, we present constructions of Rota–Baxter quasiskew braces and demonstrate that every Rota–Baxter skew brace can define a quasigroup and a Rota–Baxter quasiskew brace.
2. Skew Brace and Co-Inverse Skew Braces
In this section, we introduce the notion of co-inverse skew braces for the first time and provide the necessary and sufficient conditions for a skew brace to be a co-inverse skew brace. We also study the relationships between co-inverse skew braces and two-sided skew braces.
Definition 1
([8,36]). (1) A skew left brace is a set equipped with two group operations “∘” and “·” such that the following equation:
holds for all , where is the inverse of an element a in .
(2) A skew left brace is called trivial if for all .
(3) A skew left brace is called a two-sided skew brace if
for all .
For a skew left brace , we easily see that the two groups and have the same identity element denoted by e.
Without further comment, we call a skew left brace simply a skew brace, and denote by for , and denote the inverse of an element a in by .
Example 1
([35,37]). (1) Let be an integer additive group. Then, is a skew brace, where
for all .
(2) The additive group is a skew brace with circ operation “∘”:
for any .
Example 2.
Let be a skew brace with an Abelian group . Then, it is also a two-sided skew brace.
Proof.
It suffices to show that , for any . Since is a skew brace and is an Abelian group, we can obtain that
□
Definition 2.
A skew brace is called a co-inverse skew brace if the inverses and of every element a in two groups and are identical.
Remark 1.
(1) It is obvious that every trivial skew brace is a co-inverse skew brace.
(2) Let be an almost trivial skew brace, that is, is a skew brace satisfying the condition “" for any . Then, it is easy to see that is a co-inverse skew brace.
(3) It is easy to see that the skew brace in Example 1 is not a two-sided skew brace. This is since
Moreover, the skew brace is not a co-inverse skew brace since
Proposition 1.
Let be a co-inverse skew brace. Then, it is a two-sided skew brace.
Proof.
Since is a skew brace, we have
for all . Hence,
that is, we have
Thus, is a two-sided skew brace. □
Remark 2.
It is easy to check that the skew brace in Example 1 is a two-sided brace by Example 2. But it is not a co-inverse skew brace since
Lemma 1.
Let be a two-sided skew brace. Then, for any ,
- (1)
- (2)
Proof.
Firstly, since
we obtain that
Secondly, since
we can obtain that
□
Lemma 2
([8]). Let be a skew brace and
Then, λ is a group homomorphism, and it follows that
Proposition 2.
Let be a skew brace. Then, is a co-inverse skew brace if, and only if, for all .
Proof.
Assume that is a co-inverse skew brace. Then, by Lemma 2, we have
for any so .
Conversely, if for all , we have
So, we have , that is, . □
Remark 3.
The skew brace in Example 1 is not a non-trivial co-inverse subskew brace.
In fact, it is easy to see that every subskew brace of is the form . If is a co-inverse skew brace, then, by Proposition 2, we have
for all , that is, .
However, it is easy to see that is a trivial skew brace.
3. Rota–Baxter Skew Braces
In this section, we first introduce the notion of Rota–Baxter skew braces and give the classification of Rota–Baxter operators on some skew braces and , respectively. Furthermore, we study the structures of Rota–Baxter skew braces.
Definition 3.
Let be a skew brace.
- (1)
- A map is called a Rota–Baxter operator of weight 1 if for any ,
- (2)
- A map is called a Rota–Baxter operator of weight if
In what follows, we call the quadruple a Rota–Baxter skew brace if R is a Rota–Baxter operator of weight 1 on a skew brace .
Proposition 3.
Let be a co-inverse Rota–Baxter skew brace of weight 1 . Define for all . Then, is a co-inverse Rota–Baxter skew brace of weight .
Proof.
In fact, for any , we have
So, is a co-inverse Rota–Baxter skew brace of weight .
In a similar way, we can prove the other situation. □
Example 3.
All Rota–Baxter operators on the skew brace in Example 1 are given as follows:
- (1)
- Let
- (i)
- if , we know that for any ; so, in this case, ;
- (ii)
- if , where a is an odd number, we have
- (2)
- Let where b is an odd number.
- (iii)
- if , we have
- (iv)
- if , where c is an odd number, we have
Proof.
Assume that R is a Rota–Baxter operator on the skew brace . Then, it must satisfy the following equation:
for any .
Firstly, we show that . If taking , we have
so .
Secondly, we find that or some odd number for an odd number α. Taking in the Equation (3), we have
So, by , we know that
Next, we discuss , which can be divided into two cases.
- (1)
- If . Taking in the Equation (3), then, we havefor all .
- (i)
- If . Let in the Equation (3). Then, we havefor all so R is a map with period 2 by Equations (4) and (5).Since , we know that for all
- (ii)
- If , which is an odd number. Let in the Equation (3). Then, we havefor all ; so, R is a map with period 4 by Equations (4) and (6).Combining with , we easily obtain that
- (2)
- (iii)
- If . Let in the Equation (3). Then, we havefor all ; so, R is a map with period 4 by Equations (7) and (8).Combining with , we easily obtain that
- (iv)
- If , which is an odd number. Let in the Equation (3). Then, we havefor all , so by Equations (7) and (9).Combining and with , by the induction method, we easily obtain that
□
Example 4.
All Rota–Baxter operators on the skew brace in Example 1 are given as follows:
where and in
Proof.
Assume that R is a Rota–Baxter operator on the skew brace . Then, it must satisfy the following equation:
for any /(4).
Firstly, we show that . If taking , then we have . So,
Secondly, taking in the Equation (10), we have
for all .
Next, we discuss , which can be divided into four cases.
- (1)
- If , then we have . So, if , then . Thus,
- (2)
- If , then we have . So, if , then . Thus,
- (3)
- If , then we have So, if , then . Thus,
- (4)
- If , then we have So, if , then . Thus,
□
Lemma 3.
Let R be a Rota–Baxter operator on the skew brace . Then, for any
- (1)
- ;
- (2)
- ;
- (3)
- ;
- (4)
- If a group is an Abelian group, then R is a homomorphism of a group , and .
Proof.
(1) It follows from the equality (1) considered with .
(2) It follows from the equality (1) considered with
(3) It follows from the equality
(4) The conclusion is obvious when a group is Abelian. □
Proposition 4.
Let be a Rota–Baxter skew brace. Then, a group is Abelian if R is an automorphism of a group .
In particular, the converse holds if R is a bijection.
Proof.
Since
for any , . That is, ; so, a group is Abelian.
The converse is satisfied by the Equation (1). □
Corollary 1.
Let be a skew brace. Define a map as follows:
for some . Then, R is a Rota–Baxter operator and , if, and only if, a group is Abelian, and R is a homomorphism of a group .
Proof.
It is easy to prove that R is a bijection. Suppose that a group is Abelian, and R is a homomorphism of a group , then it is easy to see that the Equation (1) holds, So, R is a Rota–Baxter operator on the skew brace A. Since , then .
Conversely, if R is a Rota–Baxter operator on the skew brace A and , then for any , we have
That is, R is an automorphism of a group . Again, by Proposition 4, a group is Abelian. □
Lemma 4.
Let R be a Rota–Baxter operator on the skew brace . Then, Ker and Im are subgroups of a group . Moreover, if R is a homomorphism of a group , then Ker and Im are subskew braces.
Proof.
Firstly, we show that Ker is a subgroup of a group .
As a matter of fact, for all Ker, since
that is, Ker. Moreover, for all Ker, we have
that is, Ker; so, Ker is a subgroup of a group .
Secondly, we show that Im is a subgroup of a group .
Indeed, if Im, we have Im by Lemma 3. And Im by the Equation (1), for any Im; thus, Im is a subgroup of a group .
Moreover, if R is a homomorphism of a group , it is easy to see that Ker and Im are subgroups of a group ; thus, Ker and Im are subskew braces of . □
Lemma 5
([8]). Let be a skew brace. A subset I of the skew brace is called an ideal if it is both a normal subgroup of a group and a normal subgroup of a group and for all .
Let I be an ideal of the skew brace . Then, the following conclusions hold:
- (1)
- for all ;
- (2)
- I and are skew braces.
In what follows, we give a differentiated condition for a given subgroup (Ker in Lemma 4 to be a Rota–Baxter skew brace.
Lemma 6.
Let R be a Rota–Baxter operator on the skew brace . Then, we have the following conclusions:
- (1)
- Assume that R is a Rota–Baxter operator of weight 1. Then, if , for all .Furthermore, if is the decomposition of a group in the disjoint union of right cosets, then if x and y lie in the same right coset.
- (2)
- Assume that R is a Rota–Baxter operator of weight . Then, if , for all .Furthermore, if is the decomposition of a group in the disjoint union of left cosets, then if x and y lie in the same left coset.
Proof.
(1) Since , we obtain that
for all .
Furthermore, if , we know that for some , so
The converse is obvious.
(2) It can be similarly proved. □
By the above lemmas, we can obtain the following:
Proposition 5.
Let be a Rota–Baxter skew brace of weight (resp.1). If a group is an Abelian group and R is a group homomorphism of a group , then is also a Rota–Baxter skew brace of weight (resp.1)
Proof.
It is easy to see that is both a normal subgroup of a group and a normal subgroup of a group .
Firstly, we prove that is an ideal of A. As a matter of fact, we have
for any . According to Lemma 2, ; so, is an ideal of A.
Secondly, we check that R is also a Rota–Baxter operator on the skew brace .
In fact, for any , we have
So, R is a Rota–Baxter operator of weight on the skew brace . □
4. Constructions of Rota–Baxter Quasiskew Braces
In this section, we discuss the conditions under which a Rota–Baxter operator on a group is also a Rota–Baxter operator on a skew brace induced by a Rota–Baxter group. We also introduce the concept of quasigroups and Rota–Baxter quasiskew braces, and prove that every Rota–Baxter skew brace can be associated with a Rota–Baxter quasiskew brace. Moreover, we provide some constructions of Rota–Baxter quasiskew braces.
Lemma 7
([18]). Let be a Rota–Baxter group. Then, we have the following conclusions.
- (1)
- The pair , with the multiplication:is also a group, called the descendent group of a Rota–Baxter group .
- (2)
- R is also a Rota–Baxter operator on a group , and is a skew brace.
- (3)
- The map is a homomorphism of Rota–Baxter groups.
In the following, we discuss the conditions under which a Rota–Baxter operator on a group is also a Rota–Baxter operator on a skew brace induced by a Rota–Baxter group.
Proposition 6.
Let be a Rota–Baxter group. Define
for all . Then, is a Rota–Baxter skew brace if R is a group homomorphism for a group .
Proof.
By Lemma 7, we know that is a skew brace. In what follows, it suffices to show that R is a Rota–Baxter operator on the skew brace .
In fact, for any , we have
So, is a Rota–Baxter skew brace. □
In [31], it has been established that for any is always a Rota–Baxter operator on a group . However, we know that this result does not hold true for a Rota–Baxter skew brace.
In the following example, we can see that neither nor is a Rota–Baxter operator on a given skew brace .
Example 5.
Let be a skew brace introduced in Example 1. Then, neither nor is a Rota–Baxter operator on the skew brace .
Proof.
(1) is not a Rota–Baxter operator.
It is easy to see that . If taking and , we have
so,
(2) is not a Rota–Baxter operator. Since , if taking , we have
so, □
Let be a skew brace. Define the two adjoint actions: for any ,
Proposition 7.
Let be a skew brace, and for any . Then, R is a Rota–Baxter operator on the skew brace if, and only if, R is a Rota–Baxter operator on a group .
In particular, if is a co-inverse skew brace and for any , then is a Rota–Baxter operator on the skew brace .
Proof.
Let R be a Rota–Baxter operator on the skew brace . Then, for any ,
that is, R is a Rota–Baxter operator on a group .
We can similarly prove the converse.
It is obvious that is a Rota–Baxter operator on a group . Thus, by the above result, we know that is a Rota–Baxter operator on the co-inverse skew brace . □
Definition 4
([38]). A left quasigroup is a set equipped with a binary operation “*” such that for all a and b in A, there is a unique element c such that
In what follows, a left quasigroup is simply called a quasigroup.
Definition 5.
(1) A left quasiskew brace is a set equipped with two binary operations “∘” and “·” such that is a quasigroup, is a group and satisfies the following equation:
for all .
(2) A map is called a Rota–Baxter operator on the left quasiskew brace if for any ,
(3) Let and be two quasiskew braces. A map is called a Rota–Baxter quasiskew brace homomorphism if f is both a quasigroup homomorphism from the to , and a group homomorphism from the to such that
Without further comment, we call a left quasiskew brace simply a quasiskew brace.
Example 6.
(1) It is obvious that every Rota–Baxter skew brace is a quasiskew brace.
(2) Let be a set of integers. Then, is a quasiskew brace with two operations subtraction “−” and addition “+”.
Moreover, all Rota–Baxter operators on the quasiskew brace are all group homomorphisms of the additive group .
Proof.
(1) It is straightforward. (2) It is easy to see that is a quasigroup and is a group.
Moreover, for all , we have
So, is a quasiskew brace.
Assume that R is a Rota–Baxter operator on a quasiskew brace . Then, by the equality (11), R satisfies the following equation:
for any . This means that all group homomorphisms of the additive group are Rota–Baxter operators on the quasiskew brace . □
In the following, we give a construction of Rota–Baxter quasiskew braces via Rota–Baxter skew braces.
Lemma 8.
Let be a Rota–Baxter skew brace. Define
for any . Then, is a quasigroup.
Proof.
It is easy to see that
for any . So, there is a unique element such that . □
Proposition 8.
Let be a Rota–Baxter skew brace. Then, we have the following conclusions:
The triple with the multiplication
is a quasiskew brace, called the descendent quasiskew brace of the Rota–Baxter skew brace .
In particular, if R is a homomorphism on a group , then is a Rota–Baxter quasiskew brace, and is a homomorphism of Rota–Baxter quasiskew braces.
Proof.
(1) It follows that is a quasigroup by Lemma 8. Moreover, for any , we have
So, is a quasiskew brace.
(2) Suppose that R is an endomorphism of a group . Then, for all , we have
So, R is a Rota–Baxter operator on the quasiskew brace .
It is easy to see that is a Rota–Baxter quasiskew brace. In what follows, we need to show that R is a quasigroup homomorphism from to .
In fact, for any , we have
□
Concluding remarks: The concept of Rota–Baxter skew braces is first introduced, which is a generalization of Rota–Baxter groups. The structures of Rota–Baxter skew braces are studied and investigated. However, we demonstrate that every Rota–Baxter skew brace can only induce a quasiskew brace instead of a skew brace.
Author Contributions
X.W. writes the first draft, while L.Z. and C.Z. examine and revise this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Rump, W. Braces, radical rings, and the quantum Yang–Baxter equation. J. Algebra 2007, 307, 153–170. [Google Scholar] [CrossRef]
- Bachiller, D. Classification of braces of order p3. J. Pure Appl. Algebra 2015, 219, 3568–3603. [Google Scholar] [CrossRef]
- Bachiller, D. Extensions, matched products, and simple braces. J. Pure Appl. Algebra 2018, 222, 1670–1691. [Google Scholar] [CrossRef]
- Brzeziński, T. Trusses: Between braces and rings. Trans. Am. Math. Soc. 2019, 372, 4149–4176. [Google Scholar] [CrossRef]
- Cedó, F.; Jespers, E.; Okniński, J. Braces and the Yang-Baxter equation. Commun. Math. Phys. 2014, 327, 101–116. [Google Scholar] [CrossRef]
- Rump, W. Modules over braces. J. Algebra Discret. Math. 2006, 2, 127–137. [Google Scholar]
- Smoktunowicz, A.; Vendramin, L. On skew braces (with an appendix by N. byott and L. vendramin). J. Comb. Algebra 2018, 2, 47–86. [Google Scholar] [CrossRef]
- Guarnieri, L.; Vendramin, L. Skew braces and the Yang–Baxter equation. Math. Comput. 2017, 86, 2519–2534. [Google Scholar] [CrossRef]
- Caranti, A. Bi-skew braces and regular subgroups of the holomorph. J. Algebra 2020, 562, 647–665. [Google Scholar] [CrossRef]
- Childs, L.N. Skew braces and the Galois correspondence for Hopf Galois structures. J. Algebra 2018, 511, 270–291. [Google Scholar] [CrossRef]
- Ballester-Bolinches, A.; Esteban-Romero, R. Triply factorised groups and the structure of skew left braces. Commun. Math. Stat. 2022, 10, 353–370. [Google Scholar] [CrossRef]
- Chouraqui, F. Garside groups and Yang-Baxter equation. Commun. Algebra 2010, 38, 4441–4460. [Google Scholar] [CrossRef]
- Dehornoy, P. Set-theoretic solutions of the Yang–Baxter equation, rc-calculus, and garside germs. Adv. Math. 2015, 282, 93–127. [Google Scholar] [CrossRef]
- Cedó, F. Left braces: Solutions of the Yang-Baxter equation. Adv. Group Theory Appl. 2018, 5, 33–90. [Google Scholar]
- Colazzo, I.; Jespers, E.; Kubat, Ł.; Van Antwerpen, A. Structure algebras of finite set-theoretic solutions of the Yang-Baxter equation. arXiv 2023, arXiv:2305.06023. [Google Scholar]
- Rump, W. The brace of a classical group. Note Di Mat. 2014, 34, 115–145. [Google Scholar]
- Bai, C.M.; Guo, L.; Sheng, Y.H.; Tang, R. Post-groups, (Lie-)Butcher groups and the Yang–Baxter equation. Math. Ann. 2023, 388, 3127–3167. [Google Scholar] [CrossRef]
- Guo, L.; Lang, H.L.; Sheng, Y.H. Integration and geometrization of Rota-Baxter lie algebras. Adv. Math. 2021, 387, 107834. [Google Scholar] [CrossRef]
- Baxter, G. An analytic problem whose solution follows from a simple algebraic identity. Pac. J. Math. 1960, 10, 731–742. [Google Scholar] [CrossRef]
- Kupershmidt, B.A. What a classical r-matrix really is. J. Nonlinear Math. Phys. 1999, 6, 448–488. [Google Scholar] [CrossRef]
- Aguiar, M. Pre-poisson algebras. Lett. Math. Phys. 2000, 54, 263–277. [Google Scholar] [CrossRef]
- Guo, L.; Lin, Z.Z. Representations and modules of Rota-Baxter algebras. arXiv 2019, arXiv:1905.01531. [Google Scholar] [CrossRef]
- Zheng, H.H.; Guo, L.; Zhang, L.Y. Rota-Baxter paired modules and their constructions from Hopf algebras. J. Algebra 2020, 559, 601–624. [Google Scholar] [CrossRef]
- Aguiar, M. Infinitesimal Hopf algebras. Contemp. Math. 2000, 267, 1–30. [Google Scholar]
- Guo, L.; Keigher, W. Baxter algebras and shuffle products. arXiv 2004, arXiv:math/0407155. [Google Scholar] [CrossRef]
- Goncharov, M. Rota-Baxter operators on cocommutative Hopf algebras. J. Algebra 2021, 582, 39–56. [Google Scholar] [CrossRef]
- Zheng, H.H.; Li, F.S.; Ma, T.S.; Zhang, L.Y. Hopf brace, braid equation and bicrossed coproduct. Math. Rep. 2023, 25, 481–493. [Google Scholar] [CrossRef]
- Zheng, H.H.; Ma, T.S.; Zhang, L.Y. Rota-Baxter operators on cocommutative Hopf algebras and Hopf braces. arXiv 2023, arXiv:2304.07684. [Google Scholar]
- Connes, A.; Kreimer, D. Renormalization in quantum field theory and the Riemann–Hilbert problem i: The Hopf algebra structure of graphs and the main theorem. Commun. Math. Phys. 2000, 210, 249–273. [Google Scholar] [CrossRef]
- Guo, L. An Introduction to Rota-Baxter Algebra; International Press Somerville: Somerville, MA, USA, 2012; Volume 2. [Google Scholar]
- Bardakov, V.G.; Gubarev, V. Rota–Baxter operators on groups. Proc.-Math. Sci. 2023, 133, 4. [Google Scholar] [CrossRef]
- Bardakov, V.G.; Nikonov, I.M. Relative Rota–Baxter operators on groups and Hopf algebras. arXiv 2023, arXiv:2311.09311. [Google Scholar]
- Caranti, A.; Stefanello, L. Skew braces from Rota-Baxter operators: A cohomological characterisation and some examples. Ann. Di Mat. Pura Ed Appl. 2023, 202, 1–13. [Google Scholar] [CrossRef]
- Jiang, J.; Sheng, Y.H.; Zhu, C.C. Lie theory and cohomology of relative Rota–Baxter operators. J. Lond. Math. Soc. 2024, 109, e12863. [Google Scholar] [CrossRef]
- Bardakov, V.G.; Gubarev, V. Rota—Baxter groups, skew left braces, and the Yang—Baxter equation. J. Algebra 2022, 596, 328–351. [Google Scholar] [CrossRef]
- Trappeniers, S. On two-sided skew braces. J. Algebra 2023, 631, 267–286. [Google Scholar] [CrossRef]
- Vendramin, L. Skew braces: A brief survey. arXiv 2023, arXiv:2311.07112. [Google Scholar]
- Stanovskỳ, D. Left Distributive Left Quasigroups. Ph.D. Thesis, Charles University in Prague, Prague, Czech Republic, 2004. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).