A Class of Bi-Univalent Functions in a Leaf-Like Domain Defined through Subordination via $\mathrm{q}̧$-Calculus

Abstract

Bi-univalent functions associated with the leaf-like domain within open unit disks are investigated, and a new subclass is introduced and studied in the research presented here. This is achieved by applying the subordination principle for analytic functions in conjunction with $\mathit{q}$-calculus. The class is proved to not be empty. By proving its existence, generalizations can be given to other sets of functions. In addition, coefficient bounds are examined with a particular focus on $|{\alpha }_2|$ and $|{\alpha }_3|$ coefficients, and Fekete–Szegö inequalities are estimated for the functions in this new class. To support the conclusions, previous works are cited for confirmation.

1. Introduction, Definitions, and Motivation

Let $\psi \left(\mathsf{\zeta }\right)$ be an analytic function defined in the open unit disk $\mathrm{U}̧=\{\mathsf{\zeta }\in \mathbb{C}:|\mathsf{\zeta }|<1\}$. We can classify this function as a member of a specific class $\mathcal{A}$ if it can be represented as:

$$\psi \left(\mathsf{\zeta }\right)=\mathsf{\zeta }+\sum _{n=2}^{\infty }{\alpha }_n{\mathsf{\zeta }}^n.$$

(1)

satisfying the normalization conditions:

$${\psi }^{\prime }\left(0\right)=1\mathrm{and}\psi \left(0\right)=0.$$

(2)

Denote $\mathcal{S}$ as the subclass of all functions of $\mathcal{A}$ that are univalent in $\mathrm{U}̧$. The study of the characteristics of normalized univalent functions that fall under this class and are defined in the open unit disk $\mathrm{U}̧$ is the main focus of the geometry theory of functions.

An analytic function $\eta$ that satisfies $\left|\eta \right(\mathsf{\zeta }\left)\right|<1$ and $\eta \left(0\right)=0$ within the domain $\mathrm{U}̧$ is called a Schwarz function. When considering two functions ${\psi }_1$ and ${\psi }_2$ from $\mathcal{A}$, ${\psi }_1$ is referred to as subordinate to ${\psi }_2$, denoted by ${\psi }_1\prec {\psi }_2$, if a Schwarz function $\eta$ exists such that ${\psi }_1\left(\mathsf{\zeta }\right)={\psi }_2\left(\eta \left(\mathsf{\zeta }\right)\right)$ for all $\mathsf{\zeta }\in \mathrm{U}̧$.

The class $\mathrm{P}$ is associated with Carathéodory functions, as defined by Miller [1]. These functions are analytic and satisfy the following conditions:

$$\phi \left(0\right)=1\mathrm{and}\Re e\left\{\phi \right(\mathsf{\zeta }\left)\right\}>0,\forall \mathsf{\zeta }\in \mathrm{U}̧.$$

Let $\phi \in \mathrm{P}$; then, the power series expansion is

$$\phi \left(\mathsf{\zeta }\right)=1+{\mathit{\ell }}_1\mathsf{\zeta }+{\mathit{\ell }}_2{\mathsf{\zeta }}^2+{\mathit{\ell }}_3{\mathsf{\zeta }}^3+\cdots =1+\sum _{n=1}^{\infty }{\mathit{\ell }}_n{\mathsf{\zeta }}^n,(\mathsf{\zeta }\in \mathrm{U}̧).$$

(3)

where

$$|{\mathit{\ell }}_n|\le 2,\mathrm{for}\mathrm{all}n\ge 1.$$

(4)

This is in accordance with the renowned Carathéodory’s Lemma (see [2]). In essence, $\phi \in \mathrm{P}$ if and only if

$$\phi \left(\mathsf{\zeta }\right)\prec \frac{1+\mathsf{\zeta }}{1-\mathsf{\zeta }},(\mathsf{\zeta }\in \mathrm{U}̧).$$

As the foundation upon which many important subclasses of analytic functions are built, the class $\mathrm{P}$ is crucial to the study of analytic functions. For any function $\mathsf{\psi }$ in the subfamily $\mathcal{S}$ of $\mathcal{A}$, there exists an inverse function denoted as ${\mathsf{\psi }}^{-1}$ and defined by

$$\mathsf{\zeta }={\mathsf{\psi }}^{-1}\left(\mathsf{\psi }\left(\mathsf{\zeta }\right)\right),\mathsf{\xi }=\mathsf{\psi }\left({\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)\right)\left(r_0\left(\mathsf{\psi }\right)\ge \frac{1}{4};\left|\mathsf{\xi }\right|<r_0\left(\mathsf{\psi }\right);\mathsf{\zeta }\in \mathrm{U}̧\right),$$

where

$${\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)=\mathsf{\xi }\left(1-{\alpha }_2\mathsf{\xi }+{\mathsf{\xi }}^2(-{\alpha }_3+2{\alpha }_2^2)-{\mathsf{\xi }}^3({\alpha }_4+5{\alpha }_2^3-5{\alpha }_3{\alpha }_2)+\cdots \right).$$

(5)

A function $\mathsf{\psi }\in \mathcal{S}$ is said to be bi-univalent if its inverse function ${\mathsf{\psi }}^{-1}\in \mathcal{S}$. The subclass of $\mathcal{S}$ denoted by $\Sigma$ contains all bi-univalent functions in $\mathrm{U}̧$. A table illustrating certain functions within the class $\Sigma$ and their inverse functions is provided below as Table 1.

Table 1. Some functions in class $\Sigma$ along with their inverses.

The Function	The Corresponding Inverse
${\mathsf{\psi }}_1\left(\mathsf{\zeta }\right)=\frac{\mathsf{\zeta }}{1-\mathsf{\zeta }}$	${\mathsf{\psi }}_1^{-1}\left(\mathsf{\xi }\right)=\frac{\mathsf{\xi }}{1+\mathsf{\xi }}$
${\mathsf{\psi }}_2\left(\mathsf{\zeta }\right)=-log\left(1-\mathsf{\zeta }\right)$	${\mathsf{\psi }}_2^{-1}\left(\mathsf{\xi }\right)=\frac{e^{2\mathsf{\xi }}-1}{e^{2\mathsf{\xi }}+1}$
${\mathsf{\psi }}_3\left(\mathsf{\zeta }\right)=\frac{1}{2}log\left(\frac{1+\mathsf{\zeta }}{1-\mathsf{\zeta }}\right)$	${\mathsf{\psi }}_3^{-1}\left(\mathsf{\xi }\right)=e^{-\mathsf{\xi }}\left(e^{\mathsf{\xi }}-1\right)$

Analytic functions and their subclasses have been the subject of extensive research in the field of complex analysis, especially from the geometric function theory point of view. The class ${\mathcal{S}}^{*}$, is one of these subclasses that has attracted a lot of interest. Here is how the class of starlike functions is defined:

$${\mathcal{S}}^{*}=\left\{\psi \in \mathcal{S}\mathrm{and}Re\left\{\frac{\mathsf{\zeta }{\psi }^{\prime }\left(\mathsf{\zeta }\right)}{\psi \left(\mathsf{\zeta }\right)}\right\}>0,(\mathsf{\zeta }\in \mathrm{U}̧)\right\}.$$

The study of ${\mathcal{S}}^{*}$ and its properties is fundamental. Scholars aim to comprehend the geometric and analytic characteristics of functions in this class, investigating mappings, singularities, and other properties. Through exploring the challenges of ${\mathcal{S}}^{*}$, researchers hope to gain a better understanding of the structure and behavior of analytic functions, which will enhance their knowledge of complex analysis and its uses.

In 1992, Ma and Minda [3] introduced the set $S^{*}(\Omega )$ by employing the concept of subordination, outlined as follows:

$$S^{*}(\Omega )=\left\{\mathsf{\psi }\in \mathcal{A}:\frac{\mathsf{\zeta }{\mathsf{\psi }}^{\prime }\left(\mathsf{\zeta }\right)}{\mathsf{\psi }\left(\mathsf{\zeta }\right)}\prec \Omega \left(\mathsf{\zeta }\right)\right\}.$$

Here, $\Omega$ represents an analytic function in $\mathcal{A}$ with $\Re e\left\{\Omega \left(\mathsf{\zeta }\right)\right\}>0$$(\mathsf{\zeta }\in \mathrm{U}̧)$. Table 2 below shows how different authors approached the problem of defining additional subclasses of starlike functions by choosing particular expressions for $\Omega$.

Table 2. Some subclasses of starlike functions defined by subordination.

Author/s	$\mathbf{\Omega }\left(\mathsf{\zeta }\right)$	Year	Reference
Sokól and Stankiewicz	$\sqrt{1+\mathsf{\zeta }}$	1996	[4]
Raina and Sokól	$\mathsf{\zeta }+\sqrt{1+{\mathsf{\zeta }}^2}$	2015	[5]
Priya and Sharma	$\mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^2}$	2018	[6]
Rath et al.	$1/(1-\mathsf{\zeta })$	2022	[7]
Mahmoud et al.	$e^{\mathsf{\zeta }}$	2019	[8]
Ullah et al.	$1+tanh\mathsf{\zeta }$	2021	[9]
Shi et al.	$1+sin\mathsf{\zeta }$	2022	[10]

In 2015, Raina and Sokól [5] explored a new set of starlike functions linked to the function $\Omega \left(\mathsf{\zeta }\right)=\mathsf{\zeta }+\sqrt{1+{\mathsf{\zeta }}^2}$, characterized by their association with a shell-shaped region. They derived coefficient inequalities for this family of functions. Following their research, Priya and Sharma introduced two distinct classes of functions. The first class is subordinate to $\Omega \left(\mathsf{\zeta }\right)=\zeta +\sqrt[3]{1+{\mathsf{\zeta }}^2}$, corresponding to a leaf-like domain. The second class is subordinate to $\Omega \left(\mathsf{\zeta }\right)=\mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^3}$, also associated with the leaf-like domain, as depicted in Figure 1.

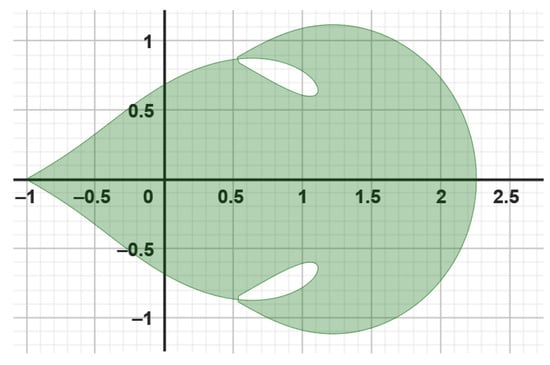
Figure 1. Leaf-shaped region, displays the image of $\Omega \left(\mathrm{U}̧\right)$ (in green color) where $\Omega \left(\mathsf{\zeta }\right)=\mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^3}$.

Quantum calculus, or $\mathrm{q}̧$-calculus, does not use the idea of a derivative as the limit of a ratio as the increment tends to zero. Instead, it relies on the $\mathrm{q}̧$-operator, which is crucial for our discussion. This calculus expands the traditional concepts of mathematical analysis by introducing the parameter $\mathrm{q}̧\in (0,1)$. For a detailed exploration of this topic, readers are advised to check the comprehensive treatise by Gasper and Rahman [11], which offers in-depth explanations and practical applications of $\mathrm{q}̧$-difference calculus in a variety of disciplines, including number theory, physics, and combinatorics.

Definition  1

([12]). The $q̧$-bracket represented by ${\left[\mathbb{k}\right]}_{q̧}$ is defined explicitly for $0<q̧<1$ as follows:

$${\left[\mathbb{k}\right]}_{q̧}=\left\{\begin{array}{cc}\frac{1-{q̧}^{\mathbb{k}}}{1-q̧}\hfill & ,\mathrm{if}\mathbb{k}\in \mathbb{C}\setminus \left\{0\right\}\hfill \\ q{̧}^{\mathbb{k}-1}+q{̧}^{\mathbb{k}-2}+\cdots +q̧+1={\displaystyle \sum _{\mathit{j}=0}^{\mathbb{k}-1}}q{̧}^{\mathit{j}}\hfill & ,\mathrm{if}\mathbb{k}\in \mathbb{N}\hfill \\ 1\hfill & ,\mathrm{if}q̧\to 0^{+},\mathbb{k}\in \mathbb{C}\setminus \left\{0\right\}\hfill \\ \mathbb{k}\hfill & ,\mathrm{if}q̧\to 1^{-},\mathbb{k}\in \mathbb{C}\setminus \left\{0\right\}\hfill \end{array}\right.,$$

With the useful identity ${[\mathbb{k}+1]}_{\mathrm{q}̧}-{\left[\mathbb{k}\right]}_{\mathrm{q}̧}={\mathrm{q}̧}^{\mathbb{k}}$.

Definition 2

([12]). The $q̧$-difference operator, or $q̧$-derivative, of a function $\mathsf{\psi }$ is defined for $0<q̧<1$ by:

$${\partial }_{q̧}\mathsf{\psi }\left(\mathsf{\zeta }\right)=\left\{\begin{array}{cc}\frac{\mathsf{\psi }\left(\mathsf{\zeta }\right)-\mathsf{\psi }\left(q̧\mathsf{\zeta }\right)}{\mathsf{\zeta }-q̧\mathsf{\zeta }},\hfill & \mathrm{if}\mathsf{\zeta }\ne 0,\hfill \\ & \\ {\mathsf{\psi }}^{\prime }\left(0\right),\hfill & \mathrm{if}\mathsf{\zeta }=0,\hfill \\ & \\ {\mathsf{\psi }}^{\prime }\left(\mathsf{\zeta }\right),\hfill & \mathrm{if}q̧\to 1^{-},\mathsf{\zeta }\ne 0.\hfill \end{array}\right..$$

Remark 1.

For $\mathsf{\psi }\in \mathcal{A}$ of the form (1), it can easily be seen that

$${\partial }_{q̧}\mathsf{\psi }\left(\mathsf{\zeta }\right)={\partial }_{q̧}\left\{\mathsf{\zeta }+\sum _{n=2}^{\infty }{\alpha }_n{\mathsf{\zeta }}^n\right\}=1+\sum _{n=2}^{\infty }{\left[n\right]}_q{\alpha }_n{\eta }^{n-1},(\mathsf{\zeta }\in \mathrm{U}̧),$$

and for ${\mathsf{\psi }}^{-1}$ of the form (5), we have

$${\partial }_{q̧}\left({\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)\right)=1-{\left[2\right]}_q{\alpha }_2\mathsf{\xi }+{\left[3\right]}_q(2{\alpha }_2^3-{\alpha }_3){\mathsf{\xi }}^2+\cdots ,(\mathsf{\xi }\in \mathrm{U}̧).$$

Because of its numerous applications in physics, quantum mechanics and mathema tics—particularly in the field of geometric function theory—researchers are still drawn to the study of $\mathrm{q}̧$-calculus. A significant aspect of $\mathrm{q}̧$-calculus is the operator ${\partial }_{q̧}$, which is important for the analysis of different classes of analytic functions. In 1990, Ismail et al. [13] made a significant breakthrough by introducing the concept of $\mathrm{q}̧$-extension for starlike functions in the unit disk. This breakthrough opened the door for further investigations in geometric function theory. For example, in [14], Srivastava and his colleagues explored $\mathrm{q}̧$-starlike functions in conic domains and conducted studies on the upper bounds of the Fekete–Szegö functional. Recently, Srivastava provided a comprehensive survey that explains the mathematical foundations and practical applications of $\mathrm{q}̧$-derivative operators, within the context of geometric function theory [15]. For those interested in delving deeper into $\mathrm{q}̧$-calculus and its implications in this field, an abundance of research is at one’s disposal, starting with classical publications [16,17], continuing with studies like [18,19,20] and considering very recent research outcome on the topic like [21,22,23,24,25,26,27,28].

Definition 3

([13]). A function $\mathsf{\psi }\in \mathcal{A}$ of the form (1) is said to belong to the class ${\mathrm{S}}_{q̧}^{*}$ if it satisfies the condition given by

$$\left|\frac{\mathsf{\zeta }\left({\partial }_{q̧}\mathsf{\psi }\left(\mathsf{\zeta }\right)\right)}{\mathsf{\psi }\left(\mathsf{\zeta }\right)}-\frac{1}{1-q̧}\right|\le \frac{1}{1-q̧},(\mathsf{\zeta }\in \mathrm{U}̧),$$

(6)

t5

In a notable observation made by Khan et al. [29], it becomes apparent that as $\mathrm{q}̧$ approaches $1^{-}$, the inequality lies in:

$$\left|\mathsf{w}-\frac{1}{1-q̧}\right|\le \frac{1}{1-q̧},\mathrm{q}̧\in (0,1).$$

Furthermore, it is noteworthy that the closed disk mentioned above pertains solely to the right-half plane. Consequently, the class ${\mathcal{S}}_{q̧}^{*}$ of $\mathrm{q}̧$-starlike functions undergoes a transformation into the well-known class ${\mathcal{S}}^{*}$. Similarly, the relationship in Equation (6) can be expressed as follows (see [18]) using the idea of subordination:

$$\frac{\mathsf{\zeta }{\partial }_{\mathrm{q}̧}\mathsf{\psi }\left(\mathsf{\zeta }\right)}{\mathsf{\psi }\left(\mathsf{\zeta }\right)}\prec \frac{1+\mathsf{\zeta }}{1-\mathrm{q}̧\mathsf{\zeta }},(0<\mathrm{q}̧<1).$$

(7)

In 2020, Khan et al. [29] used $\mathrm{q}̧$-calculus to establish a new subclass of analytic functions related to a specific leaf-like domain. By applying the principles mentioned earlier and the concept of subordination, they were able to identify unique characteristics of this subclass.

Definition 4

([29]). A function $\mathsf{\psi }\in \mathcal{S}$ is said to belong to the class ${\mathrm{R}}_{q̧}(\Omega )$ if its satisfies the condition given by

$$\mathsf{\zeta }{\partial }_{q̧}\mathsf{\psi }\left(\mathsf{\zeta }\right)\prec \Omega \left(\mathsf{\zeta }\right),(\mathsf{\zeta }\in \mathrm{U}̧),$$

(8)

where

$$\Omega \left(\mathsf{\zeta }\right)=\frac{(1+q̧)\mathsf{\zeta }}{2+(1-q̧)\mathsf{\zeta }}+\sqrt[3]{1+{\left(\frac{(1+q̧)\mathsf{\zeta }}{2+(1-q̧)\mathsf{\zeta }}\right)}^3}$$

Remark 2.

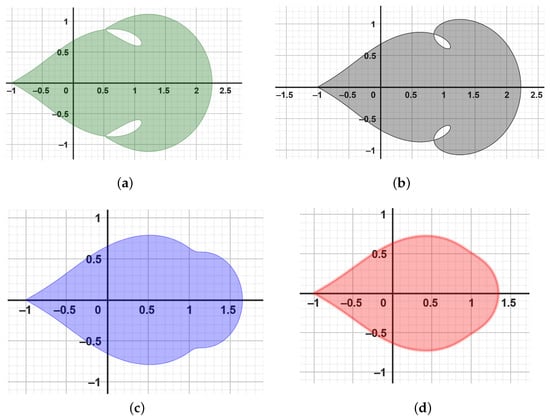
The unit disk is mapped onto a leaf-shaped region via the analytic and univalent function $\Omega \left(\mathsf{\zeta }\right)$. With regard to the real axis, it is symmetric. The function $\Omega \left(\mathsf{\zeta }\right)$ satisfies $\Omega \left(0\right)={\partial }_{q̧}\Omega \left(0\right)=1$ and has a positive real part. Figure 2 was generated using Geogebra computer software.

Figure 2. The figure illustrates the leaf-shaped region $\Omega \left(\mathrm{U}̧\right)$, which is bounded and symmetric with respect to the real axis. (a) depicts the image of $\Omega \left(\mathrm{U}̧\right)$ in green color, with $\mathrm{q}̧$ approaches $1^{-}$; (b) displays the image of $\Omega \left(\mathrm{U}̧\right)$ in gray color, with $\mathrm{q}̧=0.98$; (c) shows the image of $\Omega \left(\mathrm{U}̧\right)$ in blue color, with $\mathrm{q}̧=0.5$; (d) illustrates the image of $\Omega \left(\mathrm{U}̧\right)$ in red color as $\mathrm{q}̧$ approaches $0^{+}$.

The primary objective of this research is to investigate new categories of bi-univalent functions located within the leaf-like domain of the open unit disk $\mathrm{U}̧$. The next section will define the class under examination and provide illustrative examples to facilitate the achievement of this goal. Following that, Section 3 will derive coefficient estimates for the newly defined class, while Section 4 will delve into the evaluation of the Fekete–Szegö functional. Section 5 will then present corollaries that correspond to the given examples, which are generated by the theorems established in the preceding sections.

2. Definition and Examples

We will use the $\mathrm{q}̧$-calculus theory and the previously mentioned subordination principle among analytic functions to give an exact mathematical description of the newly defined class ${\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$ of bi-univalent functions related to a leaf-like domain. The definition of this class is provided below:

Definition 5

A bi-univalent function $\mathsf{\psi }$ of the type (1) belongs to the class ${\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$ if it fulfills the following subordinations:

$$\Phi \left(\mathsf{\zeta }\right)=(1-\chi )\frac{\mathsf{\psi }\left(\mathsf{\zeta }\right)}{\mathsf{\zeta }}+\chi \left({\partial }_{q̧}\mathsf{\psi }\left(\mathsf{\zeta }\right)\right)\prec \Omega \left(\mathsf{\zeta }\right),(\mathsf{\zeta }\in U̧),$$

(9)

and

$$\Psi \left(\mathsf{\xi }\right)=(1-\chi )\frac{{\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)}{\mathsf{\xi }}+\chi \left({\partial }_{q̧}{\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)\right)\prec \Omega \left(\mathsf{\xi }\right)(\mathsf{\xi }\in U̧),$$

(10)

where

$$\Omega \left(\mathsf{\zeta }\right)=\frac{(1+q̧)\mathsf{\zeta }}{2+(1-q̧)\mathsf{\zeta }}+\sqrt[3]{1+{\left(\frac{(1+q̧)\mathsf{\zeta }}{2+(1-q̧)\mathsf{\zeta }}\right)}^3},$$

(11)

with $\Omega \left(0\right)=1$ and $\chi \ge 1$.

Remark 3.

The class ${\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$ is nonempty. There exist two approaches in validating this claim: the analytical approach and the graphical approach.

• Analytically (see [30]): The function ${\psi }_1$ defined by

  $$\begin{array}{cc}\hfill {\psi }_1\left(\mathsf{\zeta }\right)& =\mathsf{\zeta }+\frac{q̧+1}{2(1+q̧\chi )}{\mathsf{\zeta }}^2-\frac{1-q{̧}^2}{4(1+q̧{\left[2\right]}_{q̧}\chi )}{\mathsf{\zeta }}^3+\frac{q^3+1}{6(1+q̧{\left[3\right]}_{q̧}\chi )}{\mathsf{\zeta }}^4-\frac{1-q^4}{8(1+q̧{\left[4\right]}_{q̧}\chi )}{\mathsf{\zeta }}^5+\cdots .\hfill \end{array}$$

  (12)

  is univalent due to being the extremal functions of the class of univalent functions. To show ${\psi }_1\in {\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$, we proceed as follows.
  By putting ${\psi }_1$ in (9), we have:

  $$\begin{array}{cc}\hfill {\Phi }_1\left(\mathsf{\zeta }\right)& =(1-\chi )\frac{{\mathsf{\psi }}_1\left(\mathsf{\zeta }\right)}{\mathsf{\zeta }}+\chi \left({\partial }_{q̧}{\mathsf{\psi }}_1\left(\mathsf{\zeta }\right)\right)\hfill \\ & =(1-\chi )\left(\mathsf{\zeta }+\frac{q̧+1}{2(1+q̧\chi )}{\mathsf{\zeta }}^2-\frac{1-q{̧}^2}{4(1+q̧{\left[2\right]}_{q̧}\chi )}{\mathsf{\zeta }}^3+\cdots \right)\hfill \\ & +\chi \left(1+\frac{{\left[2\right]}_{q̧}(q̧+1)}{2(1+q̧\chi )}\mathsf{\zeta }-\frac{{\left[3\right]}_{q̧}(1-q{̧}^2)}{4(1+q̧{\left[2\right]}_{q̧}\chi )}{\mathsf{\zeta }}^3+\cdots \right)\hfill \\ & =1+\frac{1}{2}(q+1)\mathsf{\zeta }-\frac{1}{4}(1-q{̧}^2){\mathsf{\zeta }}^2+\frac{1}{6}\left(q^3+1\right){\mathsf{\zeta }}^3-\frac{1}{8}(1-q{̧}^4){\mathsf{\zeta }}^4+\cdots .\hfill \end{array}$$

  (13)

  On the other hand, the Maclaurin series expansion of $\Omega \left(\mathsf{\zeta }\right)$ on the LHS of (11) is as follows:

  $$\begin{array}{c}\hfill \Omega \left(\mathsf{\zeta }\right)=1+\frac{1}{2}(q̧+1)\mathsf{\zeta }-\frac{1}{4}(1-q{̧}^2){\mathsf{\zeta }}^2+\frac{1}{6}\left(q{̧}^3+1\right){\mathsf{\zeta }}^3-\frac{1}{8}(1-q{̧}^4){\mathsf{\zeta }}^4+\cdots .\end{array}$$

  (14)

  This means that ${\psi }_1\in {\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$ and $\Phi \left(U̧\right)\subset \Omega \left(U̧\right).$
  Now, we check if ${\psi }_1\left(\mathsf{\zeta }\right)\in \mathcal{S}$ satisfies the second part of the definition.

  $$\mathsf{\xi }=(1-\chi )\frac{\mathsf{\psi }\left(\mathsf{\zeta }\right)}{\mathsf{\zeta }}+\chi \left({\partial }_{q̧}\mathsf{\psi }\left(\mathsf{\zeta }\right)\right),$$

  (15)

  which implies

  $$\mathsf{\zeta }=(1-\chi )\frac{{\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)}{\mathsf{\xi }}+\chi \left({\partial }_{q̧}{\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)\right)=\mathsf{\xi }+A_2{\mathsf{\xi }}^2+A_3{\mathsf{\xi }}^3+\cdots .$$

  (16)

  Now, substitute (16) into (15), which gives

  $$\begin{array}{cc}\hfill \mathsf{\xi }& =1+\frac{1}{2}(q̧+1)\left(\mathsf{\xi }+A_2{\mathsf{\xi }}^2+A_3{\mathsf{\xi }}^3+\cdots \right)-\frac{1}{4}(1-q{̧}^2){\left(\mathsf{\xi }+A_2{\mathsf{\xi }}^2+A_3{\mathsf{\xi }}^3+\cdots \right)}^2\hfill \\ & +\frac{1}{6}\left(q{̧}^3+1\right){\left(\mathsf{\xi }+A_2{\mathsf{\xi }}^2+A_3{\mathsf{\xi }}^3+\cdots \right)}^3-\frac{1}{8}(1-q{̧}^4){\left(\mathsf{\xi }+A_2{\mathsf{\xi }}^2+A_3{\mathsf{\xi }}^3+\cdots \right)}^4+\cdots .\hfill \end{array}$$

  (17)

  Substituting $A_2$ and $A_3$ into (16), we have

  $$\mathsf{\zeta }=(1-\chi )\frac{{\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)}{\mathsf{\xi }}+\chi \left({\partial }_{q̧}{\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)\right)=\mathsf{\xi }+(1-q){\mathsf{\xi }}^2-\frac{1}{3}(1+q^2-q){\mathsf{\xi }}^3+\cdots ,$$

  (18)

  for the left-hand side of (10). The inverse of ${\Omega }^{-1}\left(\mathsf{\zeta }\right)$ follows the same solving process as the L.H.S of (10), since (13) and (14) are equal. That is,

  $$\begin{array}{cc}\hfill \mathsf{\zeta }=& {\Omega }^{-1}\left(\mathsf{\xi }\right)={\left(\frac{(1+q̧)\mathsf{\zeta }}{2+(1-q̧)\mathsf{\zeta }}+\sqrt[3]{1+{\left(\frac{(1+q̧)\mathsf{\zeta }}{2+(1-q̧)\mathsf{\zeta }}\right)}^3}\right)}^{-1}\hfill \\ & =\mathsf{\xi }+(1-q){\mathsf{\xi }}^2-\frac{1}{3}(1+q^2-q){\mathsf{\xi }}^3+\cdots ,\hfill \end{array}$$

  (19)

  Comparing (18) and (19), we deduce that both sides are equal. We conclude that they also satisfy both equations in Definition 5.
  Now, we can conclude that the extremal function given in (12) shows that our defined class of analytic and bi-univalent function is not empty.
• Geometrically: (see [31]) Let ${\mathsf{\psi }}_{*}$ denote the functions given by:

  $${\mathsf{\psi }}_{*}\left(\mathsf{\zeta }\right)=\frac{\mathsf{\zeta }}{1-\vartheta \mathsf{\zeta }},\left|\vartheta \right|<0.21,$$

  (20)

  To establish the univalence of the function ${\mathsf{\psi }}_{*}\left(\mathsf{\zeta }\right)$, we commence by assuming that ${\mathsf{\psi }}_{*}\left({\mathsf{\zeta }}_1\right)={\mathsf{\psi }}_{*}\left({\mathsf{\zeta }}_2\right)$. Our objective is to demonstrate that this assumption implies ${\mathsf{\zeta }}_1={\mathsf{\zeta }}_2$. We initiate the proof by considering the given condition:

  $$\frac{{\zeta }_1}{1-\vartheta {\mathsf{\zeta }}_1}=\frac{{\zeta }_2}{1-\vartheta {\mathsf{\zeta }}_2}\mathit{where}\left|\vartheta \right|<0.21.$$

  Now, let us correct the second equation:

  $${\zeta }_1-\vartheta {\mathsf{\zeta }}_1{\mathsf{\zeta }}_2={\mathsf{\zeta }}_2-\vartheta {\mathsf{\zeta }}_1{\mathsf{\zeta }}_2\mathit{where}\left|\vartheta \right|<0.21$$

  This simplifies to:

  $${\mathsf{\zeta }}_1-{\mathsf{\zeta }}_2=0.$$

  So, indeed, we have shown that ${\mathsf{\zeta }}_1={\mathsf{\zeta }}_2$, thus proving that ${\psi }_{*}\left(\zeta \right)$ is univalent; moreover, ${\mathsf{\psi }}_{*}\in \Sigma$ with its inverse:

  $${\mathsf{\psi }}_{*}^{-1}\left(\mathsf{\xi }\right)=\frac{\mathsf{\xi }}{1+\vartheta \mathsf{\xi }}.\left|\vartheta \right|<0.21.$$

  (21)

  By utilizing the notations provided in Equations (9) and (10), we can easily demonstrate through a straightforward calculation that

  $$\begin{array}{cc}\hfill \Phi \left(\mathsf{\zeta }\right)& =\frac{1+(\chi -1)q̧\vartheta \mathsf{\zeta }}{(1-\vartheta \mathsf{\zeta })(1-q̧\vartheta \mathsf{\zeta })},\left|\vartheta \right|<0.21\hfill \\ \hfill \Psi \left(\mathsf{\xi }\right)& =\frac{1-(\chi -1)q̧\vartheta \mathsf{\xi }}{(1+\vartheta \mathsf{\xi })(1+q̧\vartheta \mathsf{\xi })},\left|\vartheta \right|<0.21.\hfill \end{array}$$

  (22)

  Furthermore, for every $\mathsf{\zeta }\in U̧$, it follows that $\Phi (-\vartheta \mathsf{\zeta })=\Psi \left(\vartheta \mathsf{\zeta }\right)$, thereby implying that $\Phi \left(U̧\right)=\Psi \left(U̧\right)$. Hence, we can conclude that $\mathsf{\psi }\left(\mathsf{\zeta }\right)\in {\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$, and there exist certain values for the parameters χ and for the identity function $\Phi \left({\mathsf{\psi }}_{*}\left(\mathsf{\zeta }\right)\right)$ such that

  $${\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))\setminus \{\Phi \left({\mathsf{\psi }}_{*}\right)\}\ne \varphi .$$

We employ the Geogebra computer software (we omit the Geogebra codes for the figures we used throughout the article) to generate the visual representations of the boundary $\partial \mathrm{U}̧$ using the functions $\Omega$, $\Phi$, and $\Omega$, as illustrated in Figure 3. This is applicable to various scenarios where the conditions $\left|\vartheta \right|<0.21$, $\chi \ge 0$, and $\mathrm{q}̧\in (0,1)$ are satisfied. It is worth noting that $\Omega$ is a univalent function within $\mathrm{U}̧$. As a consequence, the relationships $\Phi \left(\mathsf{\zeta }\right)\prec \Omega \left(\mathsf{\zeta }\right)$ and $\Psi \left(\mathsf{\xi }\right)\prec \Omega \left(\mathsf{\xi }\right)$ are valid. These relationships can be justified by the facts that $\Phi \left(0\right)=\Psi \left(0\right)=\Omega \left(0\right)=1$, $\Phi \left(\mathrm{U}̧\right)\subset \Omega \left(\mathrm{U}̧\right)$, and $\Psi \left(\mathrm{U}̧\right)\subset \Omega \left(\mathrm{U}̧\right)$. Please refer to Figure 3, Figure 4 and Figure 5 for further clarification.

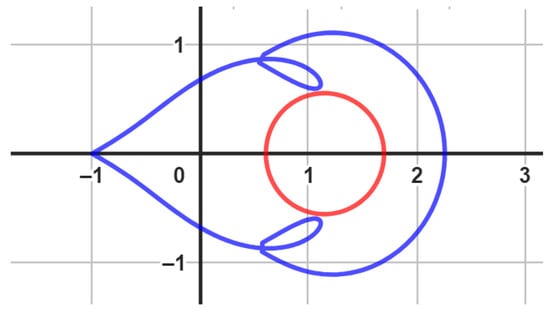
Figure 3. An image of $\Phi \left(e^{i\theta }\right)$, $\Psi \left(e^{i\theta }\right)$ (red color) and $\Omega \left(e^{i\theta }\right)$ (blue color) with $\mathrm{q}̧=1$, $\chi =2$, $\vartheta =0.17$ and $\theta \in [0,2\pi )$.

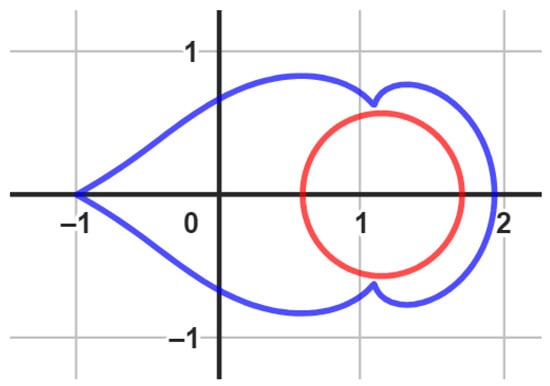
Figure 4. An image of $\Phi \left(e^{i\theta }\right)$, $\Psi \left(e^{i\theta }\right)$ (red color) and $\Omega \left(e^{i\theta }\right)$ (blue color) with $\mathrm{q}̧=0.77$, $\chi =2.5$, $\vartheta =0.18$ and $\theta \in [0,2\pi )$.

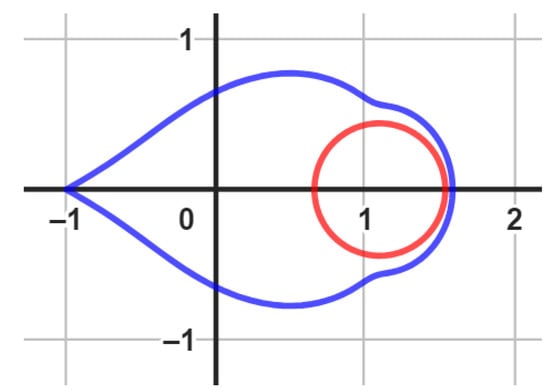
Figure 5. An image of $\Phi \left(e^{i\theta }\right)$, $\Psi \left(e^{i\theta }\right)$ (red color) and $\Omega \left(e^{i\theta }\right)$ (blue color) with $\mathrm{q}\mathrm{̧}=0.4$, $\chi =3$, $\vartheta =0.19$ and $\theta \in [0,2\pi )$.

Remark 4.

Special cases:

• Letting $\chi =1$, the expression $\Sigma q̧(1,\Omega (\mathsf{\zeta }\left)\right)$ is reduced to $\Sigma q̧(\Omega (\mathsf{\zeta }\left)\right)$, representing the bi-univalent class of functions $\mathsf{\psi }\left(\mathsf{\zeta }\right)$, provided the following subordination conditions hold:

  $$\begin{array}{cc}\hfill {\partial }_{q̧}\mathsf{\psi }\left(\mathsf{\zeta }\right)& \prec \frac{(1+q̧)\mathsf{\zeta }}{2+(1-q̧)\mathsf{\zeta }}+\sqrt[3]{1+{\left(\frac{(1+q̧)\mathsf{\zeta }}{2+(1-q̧)\mathsf{\zeta }}\right)}^3},(\mathsf{\zeta }\in U̧),\hfill \\ & \\ \hfill {\partial }_{q̧}{\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)& \prec \frac{(1+q̧)\mathsf{\xi }}{2+(1-q̧)\mathsf{\xi }}+\sqrt[3]{1+{\left(\frac{(1+q̧)\mathsf{\xi }}{2+(1-q̧)\mathsf{\xi }}\right)}^3},(\mathsf{\xi }\in U̧).\hfill \end{array}$$
• If $q\to 1^{-}$, then the class ${\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$ is reduced to $\Sigma (\chi ,\mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^3})$, representing the bi-univalent class of functions $\mathsf{\psi }\left(\mathsf{\zeta }\right)$, provided the following subordination conditions hold:

  $$\begin{array}{cc}\hfill (1-\chi )\frac{\mathsf{\psi }\left(\mathsf{\zeta }\right)}{\mathsf{\zeta }}+\chi {\mathsf{\psi }}^{\prime }\left(\mathsf{\zeta }\right)& \prec \mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^3},(\mathsf{\zeta }\in U̧),\hfill \\ & \\ \hfill (1-\chi )\frac{{\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)}{\mathsf{\xi }}+\chi {\left({\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)\right)}^{\prime }& \prec \mathsf{\xi }+\sqrt[3]{1+{\mathsf{\xi }}^3},(\mathsf{\xi }\in U̧).\hfill \end{array}$$
• Let $\chi =1$ and $q̧\to 1^{-}$. Then, the class ${\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$ is reduced to $\Sigma \left(\mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^3}\right)$, representing the bi-univalent class of functions $\mathsf{\psi }\left(\mathsf{\zeta }\right)$, provided the following subordination conditions hold:

  $$\begin{array}{cc}\hfill {\mathsf{\psi }}^{\prime }\left(\mathsf{\zeta }\right)& \prec \mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^3},(\mathsf{\zeta }\in U̧),\hfill \\ & \\ \hfill {\left({\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)\right)}^{\prime }& \prec \mathsf{\xi }+\sqrt[3]{1+{\mathsf{\xi }}^3},(\mathsf{\xi }\in U̧).\hfill \end{array}$$

Up to this moment, there has been a scarcity of academic research on the numerous parameters that influence the functional classification of a leaf-like domain. The fundamental purpose of this work is to examine the initial Taylor–Maclaurin coefficients of functions $\mathsf{\psi }$, as given by Equation (1), which are significant for the class ${\Sigma }_{\mathrm{q}̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$ related to a leaf-like domain. Furthermore, we seek to study the estimated value of the Fekete–Szegö functional.

3. The Bounds of the Coefficients within the ${\mathbf{\Sigma }}_{\mathbf{q}̧}\mathbf{(}\mathbf{\chi }\mathbf{,}\mathbf{\Omega }\mathbf{\left(}\mathsf{\zeta }\mathbf{\right)}\mathbf{)}$ Class

Initially, the estimates for the coefficients of the class ${\Sigma }_{\mathrm{q}̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$, as defined in Definition 5, are provided.

Theorem 1.

Let $\mathsf{\psi }\in \Sigma$ of the type (1) belong to the class ${\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$. Then,

$$\left|{\alpha }_2\right|\le \frac{1+q̧}{\sqrt{2\begin{array}{c}|\left(1+q̧{\left[2\right]}_{q̧}\chi \right){\left[2\right]}_{q̧}-{(1+q̧\chi )}^2(3-q̧)|\end{array}}},$$

and

$$|{\alpha }_3|\le \frac{1+q̧}{2}\left(\frac{{\left[2\right]}_{q̧}}{2{(1+q̧\chi )}^2}+\frac{1}{1+q̧{\left[2\right]}_{q̧}\chi }\right).$$

Proof. 

If $\mathsf{\psi }\in {\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$. As per Definition 5, the presence of certain analytic functions ${\eta }_1$ and ${\eta }_2$ can be established, satisfying the conditions ${\eta }_1\left(0\right)={\eta }_2\left(0\right)=0$, and $|{\eta }_1\left(\mathsf{\zeta }\right)|<1$, $|{\eta }_2\left(\mathsf{\xi }\right)|<1$ for all $\mathsf{\zeta },\mathsf{\xi }\in \mathrm{U}̧$. Setting

$${\phi }_1\left(\mathsf{\zeta }\right)=\frac{1+{\eta }_1\left(\mathsf{\zeta }\right)}{1-{\eta }_1\left(\mathsf{\zeta }\right)}=1+{\mathit{\ell }}_1\mathsf{\zeta }+{\mathit{\ell }}_2{\mathsf{\zeta }}^2+\cdots ,(\mathsf{\zeta }\in \mathrm{U}̧),$$

and

$${\phi }_2\left(\mathsf{\xi }\right)=\frac{1+{\eta }_2\left(\mathsf{\xi }\right)}{1-{\eta }_2\left(\mathsf{\xi }\right)}=1+{\mathit{j}}_1\mathsf{\xi }+{\mathit{j}}_2{\mathsf{\xi }}^2+\cdots ,(\mathsf{\xi }\in \mathrm{U}̧),$$

then ${\phi }_1,{\phi }_2\in P̧$. From the above relations, we have

$${\eta }_1\left(\mathsf{\zeta }\right)=\frac{{\phi }_1\left(\mathsf{\zeta }\right)-1}{{\phi }_1\left(\mathsf{\zeta }\right)+1}(\mathsf{\zeta }\in \mathrm{U}̧),$$

and

$${\eta }_2\left(\mathsf{\xi }\right)=\frac{{\phi }_2\left(\mathsf{\xi }\right)-1}{{\phi }_2\left(\mathsf{\xi }\right)+1}(\mathsf{\xi }\in \mathrm{U}̧).$$

From (9) and (10), it follows that

$$\begin{array}{cc}\hfill \Omega \left({\eta }_1\left(\mathsf{\zeta }\right)\right)& =\frac{(1+\mathrm{q}̧)\left({\phi }_1\left(\mathsf{\zeta }\right)-1\right)}{1+3{\phi }_1\left(\mathsf{\zeta }\right)+\mathrm{q}̧\left(1-{\phi }_1\left(\mathsf{\zeta }\right)\right)}+\sqrt[3]{1+{\left(\frac{(1+\mathrm{q}̧)\left({\phi }_1\left(\mathsf{\zeta }\right)-1\right)}{1+3{\phi }_1\left(\mathsf{\zeta }\right)+\mathrm{q}̧\left(1-{\phi }_1\left(\mathsf{\zeta }\right)\right)}\right)}^3}\hfill \\ & =1+\frac{1+\mathrm{q}̧}{4}{\mathit{\ell }}_1\mathsf{\zeta }+\frac{1+\mathrm{q}̧}{4}\left({\mathit{\ell }}_2-\frac{(3-\mathrm{q}̧)}{4}{\mathit{\ell }}_1^2\right){\mathsf{\zeta }}^2+\cdots ,\left(\mathsf{\zeta }\in \mathrm{U}̧\right),\hfill \end{array}$$

(23)

and

$$\begin{array}{cc}\hfill \Omega \left({\eta }_2\left(\mathsf{\xi }\right)\right)& =\frac{(1+\mathrm{q}̧)\left({\phi }_2\left(\mathsf{\xi }\right)-1\right)}{1+3{\phi }_2\left(\mathsf{\xi }\right)+\mathrm{q}̧\left(1-{\phi }_2\left(\mathsf{\xi }\right)\right)}+\sqrt[3]{1+{\left(\frac{(1+\mathrm{q}̧)\left({\phi }_2\left(\mathsf{\xi }\right)-1\right)}{1+3{\phi }_2\left(\mathsf{\xi }\right)+\mathrm{q}̧\left(1-{\phi }_2\left(\mathsf{\xi }\right)\right)}\right)}^3}\hfill \\ & =1+\frac{1+\mathrm{q}̧}{4}{\mathit{j}}_1\mathsf{\xi }+\frac{1+\mathrm{q}̧}{4}\left({\mathit{j}}_2-\frac{(3-\mathrm{q}̧)}{4}{\mathit{j}}_1^2\right){\mathsf{\xi }}^2+\cdots ,\left(\mathsf{\zeta }\in \mathrm{U}̧\right),\hfill \end{array}$$

(24)

Also,

$$\begin{array}{cc}& (1-\chi )\frac{\mathsf{\psi }\left(\mathsf{\zeta }\right)}{\mathsf{\zeta }}+\chi \left({\partial }_{\mathrm{q}̧}\mathsf{\psi }\left(\mathsf{\zeta }\right)\right)=1+(1+\mathrm{q}̧\chi ){\alpha }_2\mathsf{\zeta }+\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right){\alpha }_3{\mathsf{\zeta }}^2+\cdots ,\hfill \end{array}$$

(25)

and

$$\begin{array}{cc}& (1-\chi )\frac{{\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)}{\mathsf{\xi }}+\chi \left({\partial }_{\mathrm{q}̧}{\mathsf{\psi }}^{-1}\left(\mathsf{\xi }\right)\right)=1-(1+\mathrm{q}̧\chi ){\alpha }_2\mathsf{\xi }+\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)\left(2{\alpha }_2^2-{\alpha }_3\right){\mathsf{\xi }}^2+\cdots ,\hfill \end{array}$$

(26)

Comparing (23) and (25) yields

$$\begin{array}{cc}& 1+\frac{1+\mathrm{q}̧}{4}{\mathit{\ell }}_1\mathsf{\zeta }+\frac{1+\mathrm{q}̧}{4}\left({\mathit{\ell }}_2-\frac{(3-\mathrm{q}̧)}{4}{\mathit{\ell }}_1^2\right){\mathsf{\zeta }}^2+\cdots =1+(1+\mathrm{q}̧\chi ){\alpha }_2\mathsf{\zeta }+\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right){\alpha }_3{\mathsf{\zeta }}^2+\cdots .\hfill \end{array}$$

(27)

Furthermore, comparing (24) and (26) yields

$$\begin{array}{cc}& 1+\frac{1+\mathrm{q}̧}{4}{\mathit{j}}_1\mathsf{\xi }+\frac{1+\mathrm{q}̧}{4}\left({\mathit{j}}_2-\frac{(3-\mathrm{q}̧)}{4}{\mathit{j}}_1^2\right){\mathsf{\xi }}^2+\cdots =1-(1+\mathrm{q}̧\chi ){\alpha }_2\mathsf{\xi }+\hfill \\ & \left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)\left(2{\alpha }_2^2-{\alpha }_3\right){\mathsf{\xi }}^2+\cdots ,\hfill \end{array}$$

(28)

By comparing the pertinent coefficients in (27) and (28), we arrive at the following:

$$\begin{array}{cc}\hfill (1+\mathrm{q}̧\chi ){\alpha }_2& =\frac{1+\mathrm{q}̧}{4}{\mathit{\ell }}_1,\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill -(1+\mathrm{q}̧\chi ){\alpha }_2& =\frac{1+\mathrm{q}̧}{4}{\mathit{j}}_1,\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill \left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right){\alpha }_3& =\frac{1+\mathrm{q}̧}{4}\left({\mathit{\ell }}_2-\frac{(3-\mathrm{q}̧)}{4}{\mathit{\ell }}_1^2\right),\hfill \end{array}$$

(31)

and

$$\begin{array}{cc}\hfill \left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)\left(2{\alpha }_2^2-{\alpha }_3\right)& =\frac{1+\mathrm{q}̧}{4}\left({\mathit{j}}_2-\frac{(3-\mathrm{q}̧)}{4}{\mathit{j}}_1^2\right).\hfill \end{array}$$

(32)

It follows from (29) and (30) that

$${\mathit{\ell }}_1=-{\mathit{j}}_1\mathrm{and}{\mathit{\ell }}_1^2={\mathit{j}}_1^2,$$

(33)

and

$$\begin{array}{cc}\hfill 2{(1+\mathrm{q}̧\chi )}^2{\alpha }_2^2& =\frac{{(1+\mathrm{q}̧)}^2}{16}\left({\mathit{\ell }}_1^2+{\mathit{j}}_1^2\right)\hfill \\ \hfill {\alpha }_2^2& =\frac{{(1+\mathrm{q}̧)}^2}{32{(1+\mathrm{q}̧\chi )}^2}\left({\mathit{\ell }}_1^2+{\mathit{j}}_1^2\right)⟺{\mathit{\ell }}_1^2+{\mathit{j}}_1^2=\frac{32{(1+\mathrm{q}̧\chi )}^2}{{(1+\mathrm{q}̧)}^2}{\alpha }_2^2.\hfill \end{array}$$

(34)

Adding (31) and (32) and performing calculations, we obtain

$$\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right){\alpha }_2^2=\frac{1+\mathrm{q}̧}{8}\left(({\mathit{\ell }}_2+{\mathit{j}}_2)+\frac{(3-\mathrm{q}̧)}{4}\left({\mathit{\ell }}_1^2+{\mathit{j}}_1^2\right)\right).$$

Substituting the value of $\left({\mathit{\ell }}_1^2+{\mathit{j}}_1^2\right)$ from (34), we obtain

$$\left[\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)-\frac{{(1+\mathrm{q}̧\chi )}^2(3-\mathrm{q}̧)}{1+\mathrm{q}̧}\right]{\alpha }_2^2=\frac{1+\mathrm{q}̧}{8}({\mathit{\ell }}_2+{\mathit{j}}_2).$$

Moreover,

$${\alpha }_2^2=\frac{{\left[2\right]}_{\mathrm{q}̧}^2}{8\left[{\left[2\right]}_{\mathrm{q}̧}\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)-{(1+\mathrm{q}̧\chi )}^2(3-\mathrm{q}̧)\right]}({\mathit{\ell }}_2+{\mathit{j}}_2).$$

(35)

Applying (4) for the coefficients ${\mathit{\ell }}_2$ and ${\mathit{j}}_2$, we obtain

$$\left|a_2\right|\le \frac{{\left[2\right]}_{\mathrm{q}̧}}{\sqrt{2\begin{array}{c}|{\left[2\right]}_{\mathrm{q}̧}\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)-{(1+\mathrm{q}̧\chi )}^2(3-\mathrm{q}̧)|\end{array}}},$$

By subtracting (32) from (31) and using ${\mathit{\ell }}_1^2={\mathit{j}}_1^2$, we have

$${\alpha }_3-{\alpha }_2^2=\frac{{\left[2\right]}_{\mathrm{q}̧}}{8\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)}\left({\mathit{\ell }}_2-{\mathit{j}}_2\right).$$

(36)

Then, in view of (34), (36) becomes

$${\alpha }_3=\frac{{\left[2\right]}_{\mathrm{q}̧}^2}{32{(1+\mathrm{q}̧\chi )}^2}\left({\mathit{\ell }}_1^2+{\mathit{j}}_1^2\right)+\frac{{\left[2\right]}_{\mathrm{q}̧}}{8\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)}\left({\mathit{\ell }}_2-{\mathit{j}}_2\right).$$

Thus, applying (4), we conclude that

$$|{\alpha }_3|\le \frac{{\left[2\right]}_{\mathrm{q}̧}^2}{4{(1+\mathrm{q}̧\chi )}^2}+\frac{{\left[2\right]}_{\mathrm{q}̧}}{2\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)}.$$

The proof of the theorem has been successfully concluded. □

4. The Fekete–Szegö Functional

Both Fekete and Szegö published their work in 1933, establishing a precise limit for the functional $\mu a_2^2-a_3$ [32]. This limit, known as the classical Fekete–Szegö inequality, was derived using real values of $\mu (0\le \mu \le 1)$. It is a challenging task to establish precise boundaries for a given function within a compact family of functions $\mathsf{\psi }\in \mathcal{A}$, for a real parameter $\mu$. In this context, the Fekete–Szegö inequality for functions belonging to the class ${\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$ is examined, considering the findings of Zaprawa [33].

Theorem 2.

Let $\mathsf{\psi }$ be an element of Σ defined by (1) and belonging to the class ${\Sigma }_{q̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$ and $\mu \in \mathbb{R}$. Then, we have

$$|a_3-\mu a_2^2|\le \left\{\begin{array}{cc}\frac{{\left[2\right]}_{q̧}}{8\left(1+q̧{\left[2\right]}_{q̧}\chi \right)},\hfill & |1-\mu |\le \left|1-\frac{(3-q̧){(1+q̧\chi )}^2}{{\left[2\right]}_{q̧}\left(1+q̧{\left[2\right]}_{q̧}\chi \right)}\right|,\hfill \\ & \\ \frac{{\left[2\right]}_{q̧}}{4}\left|\mathcal{Y}\left(\mu \right)\right|,\hfill & |1-\mu |\ge \left|1-\frac{(3-q̧){(1+q̧\chi )}^2}{{\left[2\right]}_{q̧}\left(1+q̧{\left[2\right]}_{q̧}\chi \right)}\right|.\hfill \end{array}\right.$$

where

$$\mathcal{Y}\left(\mu \right)=\frac{(1-\mu ){\left[2\right]}_{q̧}}{{\left[2\right]}_{q̧}\left(1+q̧{\left[2\right]}_{q̧}\chi \right)-{(1+q̧\chi )}^2(3-q̧)}.$$

Proof. 

If $\mathsf{\psi }\in {\Sigma }_{\mathrm{q}̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$ is given by (1), from (35) and (36), we have

$$\begin{array}{cc}\hfill a_3-\mu a_2^2=& \frac{(1-\mu ){\left[2\right]}_{\mathrm{q}̧}^2({\mathit{\ell }}_2+{\mathit{j}}_2)}{8\left[{\left[2\right]}_{\mathrm{q}̧}\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)-{(1+\mathrm{q}̧\chi )}^2(3-\mathrm{q}̧)\right]}+\frac{{\left[2\right]}_{\mathrm{q}̧}}{8\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)}\left({\mathit{\ell }}_2-{\mathit{j}}_2\right)\hfill \\ \hfill =& \frac{{\left[2\right]}_{\mathrm{q}̧}}{8}\left[\left(\mathcal{Y}\left(\mu \right)+\frac{1}{\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)}\right){\mathit{\ell }}_2+\left(\mathcal{Y}\left(\mu \right)-\frac{1}{\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)}\right){\mathit{j}}_2\right]\hfill \end{array}$$

where

$$\mathcal{Y}\left(\mu \right)=\frac{(1-\mu ){\left[2\right]}_{\mathrm{q}̧}}{{\left[2\right]}_{\mathrm{q}̧}\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)-{(1+\mathrm{q}̧\chi )}^2(3-\mathrm{q}̧)}$$

Then, we conclude that

$$|a_3-\mu a_2^2|\le \left\{\begin{array}{cc}\frac{{\left[2\right]}_{\mathrm{q}̧}}{8\left(1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi \right)},\hfill & \left|\mathcal{Y}\left(\mu \right)\right|\le \frac{1}{1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi },\hfill \\ & \\ \frac{{\left[2\right]}_{\mathrm{q}̧}}{4}\left|\mathcal{Y}\left(\mu \right)\right|,\hfill & \left|\mathcal{Y}\left(\mu \right)\right|\ge \frac{1}{1+\mathrm{q}̧{\left[2\right]}_{\mathrm{q}̧}\chi }.\hfill \end{array}\right.$$

This completes the proof of Theorem 2. □

5. Corollaries

Theorems 1 and 2 generate the corollaries below, which generally correspond to Examples 1–3.

Corollary 1.

If $\mathsf{\psi }$ is an element of Σ defined by (1) and belongs to the class ${\Sigma }_{q̧}(\Omega \left(\mathsf{\zeta }\right))$, then we can state the following:

$$\begin{array}{cc}\hfill \left|a_2\right|& \le \frac{{\left[2\right]}_{q̧}}{\sqrt{2|{\left[2\right]}_{q̧}\left(1+q̧{\left[2\right]}_{q̧}\right)-{(1+q̧)}^2(3-q̧)|}}\hfill \\ \hfill |{\alpha }_3|& \le \frac{{\left[2\right]}_{q̧}^2}{4{(1+q̧)}^2}+\frac{{\left[2\right]}_{q̧}}{2\left(1+q̧{\left[2\right]}_{q̧}\right)},\hfill \end{array}$$

and

$$|a_3-\mu a_2^2|\le \left\{\begin{array}{cc}\frac{{\left[2\right]}_{q̧}}{8\left(1+q̧{\left[2\right]}_{q̧}\right)},\hfill & |1-\mu |\le \left|1-\frac{(3-q̧){(1+q̧)}^2}{{\left[2\right]}_{q̧}\left(1+q̧{\left[2\right]}_{q̧}\right)}\right|,\hfill \\ & \\ \frac{{|1-\mu |\left[2\right]}_{q̧}^2}{4|{\left[2\right]}_{q̧}\left(1+q̧{\left[2\right]}_{q̧}\right)-{(1+q̧)}^2(3-q̧)|},\hfill & |1-\mu |\ge \left|1-\frac{(3-q̧){(1+q̧)}^2}{{\left[2\right]}_{q̧}\left(1+q̧{\left[2\right]}_{q̧}\right)}\right|.\hfill \end{array}\right.$$

Corollary 2.

If $\mathsf{\psi }$ is an element of Σ defined by (1) and belongs to the class $\Sigma (\chi ,\mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^3})$ and $\mu \in \mathbb{R}$, then we can state the following:

$$\left|a_2\right|\le \frac{1}{\sqrt{\begin{array}{c}|\left(1+2\chi \right)-{(1+\chi )}^2|\end{array}}},\left|{\alpha }_3\right|\le \frac{1}{{(1+\chi )}^2}+\frac{1}{\left(1+2\chi \right)},$$

and

$$|a_3-\mu a_2^2|\le \left\{\begin{array}{cc}\frac{1}{4\left(1+2\chi \right)},\hfill & |1-\mu |\le \left|1-\frac{{(1+\chi )}^2}{\left(1+2\chi \right)}\right|,\hfill \\ & \\ \frac{|1-\mu |}{2|(1+2\chi )-{(1+\chi )}^2|},\hfill & |1-\mu |\ge \left|1-\frac{{(1+\chi )}^2}{\left(1+2\chi \right)}\right|.\hfill \end{array}\right.$$

Corollary 3.

If $\mathsf{\psi }\in \Sigma$ is defined by (1) and belongs to the class $\Sigma (\mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^3})$, then we can state the following:

$$\begin{array}{cc}\hfill \left|a_2\right|& \le 1,|{\alpha }_3|\le \frac{7}{12}\mathrm{and}|a_3-\mu a_2^2|\le \left\{\begin{array}{cc}\frac{1}{12},\hfill & |1-\mu |\le \frac{1}{3},\hfill \\ \hfill & \\ \frac{|1-\mu |}{2},\hfill & |1-\mu |\ge \frac{1}{3}.\hfill \end{array}\right.\hfill \end{array}$$

6. Conclusions

In this study, we have conducted an investigation on coefficient problems related to recently defined subclasses of bi-univalent functions in $\mathrm{U}̧$ given in Definition 5. The investigated subclasses are ${\Sigma }_{\mathrm{q}̧}(\chi ,\Omega \left(\mathsf{\zeta }\right))$, ${\Sigma }_{\mathrm{q}̧}(\Omega \left(\mathsf{\zeta }\right))$, $\Sigma (\chi ,\mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^3})$, and $\Sigma (\mathsf{\zeta }+\sqrt[3]{1+{\mathsf{\zeta }}^3})$. We have computed the Taylor–Maclaurin coefficients $|{\alpha }_2|$ and $|{\alpha }_3|$, along with estimates for the Fekete–Szegö functional problem, for functions belonging to each of these bi-univalent function classes.

In future research, the exploration of upper bounds for the Zaclman conjecture and the investigation of Hankel determinants of orders two and three within the aforementioned subclasses show potential for new avenues of research and exploration.