Abstract
Starting with the most fundamental differential-geometric principles we derive here new explicit parameterizations of the Delaunay surfaces of revolution which depend on two real parameters with fixed ranges. Besides, we have proved that these parameters have very clear geometrical meanings. The first one is responsible for the size of the surface under consideration and the second one specifies its shape. Depending on the concrete ranges of these parameters any of the Delaunay surfaces which is neither a cylinder nor the plane is classified unambiguously either as a first or a second kind Delaunay surface. According to this classification spheres are Delaunay surfaces of first kind while the catenoids are Delaunay surfaces of second kind. Geometry of both classes is established meaning that the coefficients of their fundamental forms are found in explicit form.
Keywords:
Delaunay surfaces; surfaces of revolution; constant mean curvature surfaces; elliptic functions and integrals; roulettes MSC:
53A04; 53A05; 53A10; 33E05
1. Introduction
By its very definition (cf. any book on differential geometry), the mean curvature H at some point of a given surface in the three-dimensional Euclidean space is the arithmetic mean of the two principal curvatures (maximal and minimal ones) at that point.
In the most intuitive representation (the so-called Monge parameterization) of , which relies on the Cartesian coordinates in the space , the surface is given as a graph defined over some domain U of the plane, i.e.,
Then, according to the formula available in the classical differential geometry (see [1,2,3,4]), the mean curvature is expressed in the form
in which
Unfortunately, solving the equation
turns out to be a formidably complicated task!
In this situation the French astronomer and mathematician Charles-Eugène Delaunay immediately abandoned the general problem stated above and has restricted his considerations to axially-symmetric surfaces. In doing this he undertakes a genuinely geometric approach by showing that all profile curves (meridional sections) of the CMC surfaces of revolution (except for the plane) can be obtained as roulettes of the conic sections [5] (named after him Delaunay roulettes).
In fact, these Delaunay roulettes are nothing else, but traces of the foci of the non-degenerate conic sections when they roll (without slipping) along the axis of revolution (Figure 1).
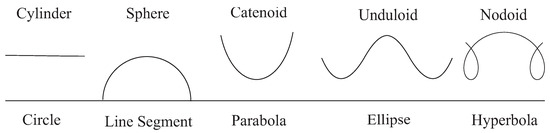
Figure 1.
Delaunay roulettes (the profile curves of the Delaunay surfaces, excluding the plane) are generated as traces of the foci of the non-degenerated conic sections by rolling them along the axis of revolution (the horizontal line).
In parallel, in a note to the same Delaunay’s paper, Sturm [6] had proposed another approach of variational nature in which these surfaces are characterized as surfaces of revolution having a minimal lateral surface area for a given (fixed in advance) volume.
More recent accounts on the subject can found in the paper by Eells [7] and in the handbook by Krivoshapko-Ivanov [8] (pp. 155–157).
Let us recall that in the case of a rotational CMC surface the principle curvatures are known as a parallel and a meridional curvatures and therefore one should solve the equation
where is an arbitrary constant.
This has been done already by Delaunay in 1841, who has found also the first analytical (integral) representation of the constant mean curvatures (CMC) surfaces of revolution [5]. The complete list of such surfaces consists of planes, cylinders, sequences of spheres, catenoids, unduloids, and nodoids (see Figure 2), known nowadays just as Delaunay surfaces.
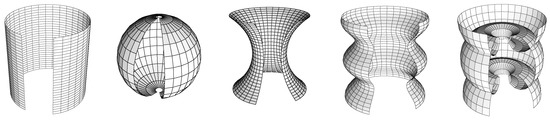
Figure 2.
The open parts of the cylinder, sphere, catenoid, unduloid and nodoid shown here are obtained by revolving the profile curves in Figure 1 about symmetry axis taken this time in vertical position.
In his paper Delaunay has introduced the constant mean curvature of the surfaces in question in the form
where by definition and are the parallel and meridional curvature radii respectively and at the beginning the parameter a was just an arbitrary constant. Latter on this parameter has been recognized as the major semi-axis of the rolling conic.
In the variational approach respectively, a initially has played the role of the Lagrangian multiplier, but at the end it was also identified as a length of the semi-axis. In both considerations, during the processes of integrations another integration constant appears which was recognized readily as the length of the minor semi-axis of the rolling conic.
Viewed in this way, the situation is a little bit strange: the profile curve depends on two parameters, but the mean curvature of the generated rotational surface depends only on one of them!
In what follows the problem will be considered from a different viewpoint and the first step in this direction will be to rewrite the expression for the mean curvature H in another form.
This possibility is based on the obvious observation that any profile curve has a point which is situated at a maximal distance, say R from the symmetry axis. It is clear also that at such point the tangent to the curve is parallel to the symmetry axis of the surface and that its normal is parallel to the axis. From here, one can conclude that the radius of the parallel curvature is just R and that along the circle (which will be further referred as equator) with this radius the meridional curvature is also constant (due to the basic assumption (4) about the surface). The ratio of these radii, will be denoted further on by , i.e.,
So, we have in place of (5) the equation
The bottom line of all above is that the problem of describing the Delaunay surfaces with mean curvature specified by (4) transforms into that of finding the axially-symmetric surfaces which mean curvature is fixed by Formula (7).
Remark 1.
The above reasoning is valid mutatis mutandis for the minimal distance r as well!
The actual organization of the paper is as follows. The main results are presented in the next Section 2 in which by relying on the first differential-geometric principles the fundamental equations behind the Delaunay surfaces are derived. Their solutions are formulated as two Propositions associated with the two different kinds of Delaunay surfaces and later on they are unified as Theorem 1 describing in explicit form all Delaunay surfaces. The above results are illustrated by various graphics which aims are to make them more clear.
As it is well known the intrinsic geometry of the surfaces in the Euclidean space is encoded into their fundamental forms which have been found explicitly in Section 3.
The Section 4 points out the importance of these surfaces for other branches of the sciences outside the mathematics. Finally, we have added an Appendix A in which we have collected all known (to the authors) explicit parameterizations of the Delaunay surfaces that can be useful for theoretical and applied purposes in the future.
2. The New Parameterizations
The starting point of our considerations will be some basic facts in the classical differential geometry which can be easily located in any of the above cited books [1,2,3,4].
Namely, let the axially-symmetric surface is generated by revolving about the “vertical” axis a curve lying in the -plane of the Cartesian coordinate system (Figure 3). If the generating curve is parameterized as
then the principal curvatures of can be calculated by the well-known formulas
where , etc.
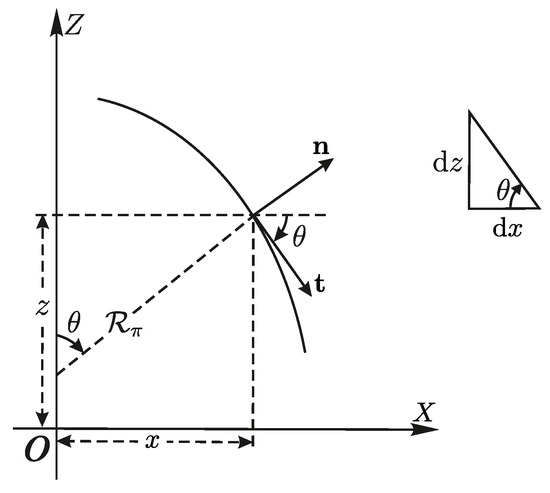
Figure 3.
Geometry of the generating profile curve .
Besides, by making use of the explicit formulas in (9) it is straightforward to check directly that the above expressions satisfy the fundamental identity
Combined with the defining Equation (4), the last equality produces (after integration) the solution
where is some integration constant. Inserting this back in (10) gives directly
In this setting it remains only to fix the new integration constant m and for this purpose let us consider the last equality at . As it is well-known at such point of we have (cf. (7))
and it is easy to conclude from (12) that
Having all this, we can write the final results for both curvatures as
The natural question that arises: for what these formulas are useful, can be answered immediately.
First, we can solve the first equation in (9) with respect to and by doing this we obtain the differential equation
Second, by inserting there the expression for from (15) we end up with the explicit equation
Let us replace x with another independent variable, say , via the formula
Performing this change in (17) one can see that z is defined by the integral
One thing that this formula make clear is that the parameters R and which appear in the expression (7) of the mean curvature are separated multiplicatively and that the problem of finding the CMC surfaces reduces to the evaluation of the integral in (19).
Technically, this depends on the location of the roots of the quartic polynomial under the radical sign. Two of them are known, namely, these are coming from the first factor in the quartic. It is easy to see that the other two roots can be easily found to be , where
Still on technical level one needs to know also if these roots are inside or outside of the interval on the real line. Some elementary analysis tells us that for , while for ,
This situation is depicted by the graphics in Figure 4.
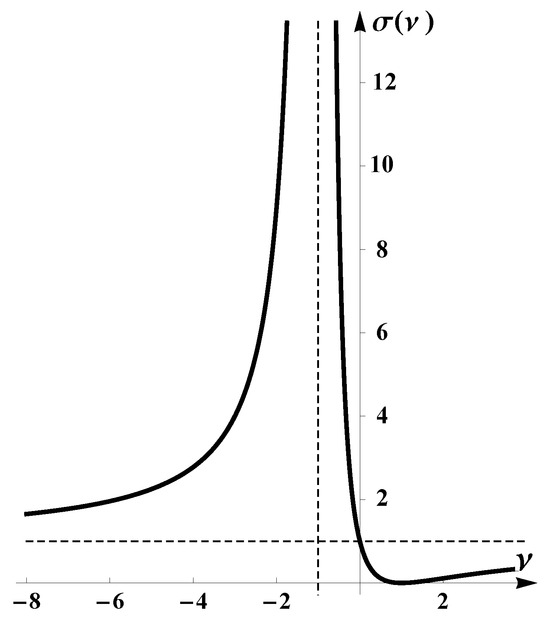
Figure 4.
Graphics of versus . The dashed lines indicate the asymptotic values of the function.
We will consider first the case when , which implies that the integral in (19) can be cast in the form
Taking into account that the uniformization of the integral
meaning its reduction to some trivial integrals, is ensured by the Jacobian elliptic function dn(), where u is the uniformization variable and is the so-called elliptical modulus, the result of the integration can be written in the form
Here is the Jacobian amplitude function and denotes the set of all positive real numbers. More details about Jacobian elliptic function, elliptic integrals and related subjects can be found in any of the books [9,10] and the well-known Tables of elliptic integrals [11,12,13,14].
We should add also that all of the above mentioned differential geometry books [1,2,3,4] offer an implementation of the computer algebra systems for visualization of the analytical results and in this way provide a great help in increasing the reader’s understanding.
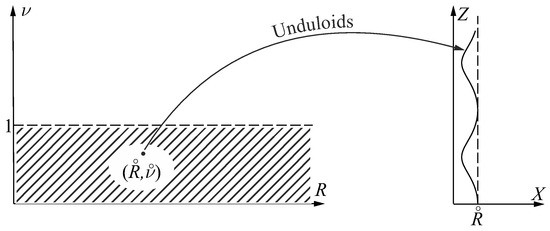
Figure 5.
Any point within the striped area where on the left produces (via Equation (23)) an unduloid shown on the right.
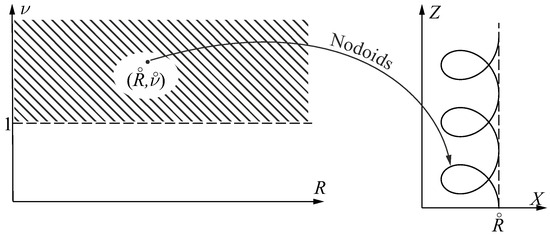
Figure 6.
With any point in the striped region in the left part is associated a nodoid (via Equation (23)) shown on the right side of the figure.
Remark 2.
Our next task will be the case when , i.e., the parameter is assumed to be negative. Then, the relevant integral for z is of the form
It will be convenient to replace the negative number in the above integral with the positive number via the formula
Performing the same change in (25) we end up with the problem of evaluation of the integral
In this case the integral that has to be uniformized is
and this can be achieved introducing as uniformization variable u via the function
In these circumstances the evaluation of the integral in (27) produces at the very end the result
An unduloid and a nodoid generated this time via the above formula are shown below in Figure 7 and Figure 8.
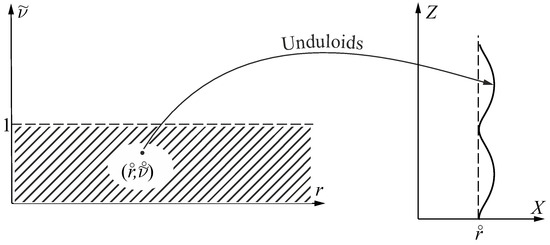
Figure 7.
With any point in the striped region in the left part is associated an unduloid (via Equation (30)) shown on the right hand side of the figure.
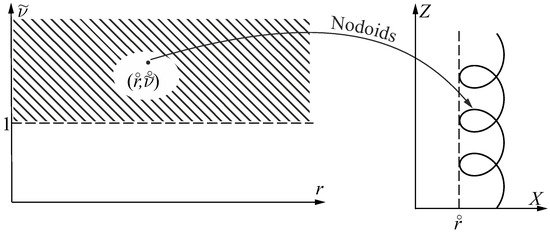
Figure 8.
Any point in the striped region on the left hand side generates a nodoid (via Equation (30)) shown on the right hand side of the figure.
Remark 3.
Actually, the results obtained above can be unified as the following propositions.
Proposition 1.
With any point within the first quadrant in the plane is associated a unique Delaunay surface which profile curve in plane lies inside the strip . The profile curves of the line are semi-circles which radii coincide with the respective .
Their explicit parameterizations through the parameters in the specified range are given by the formulas
or
respectively.
Proposition 2.
With any point within the first quadrant in the plane is associated a unique Delaunay surface which profile curve in plane lies outside the strip . The profile curves of the line are catenaries which focal distances coincide with the respective .
Parameterizations of these surfaces associated with the positive numbers are provided by the formulas
or
Definition 1.
Surfaces described in Proposition 1 will be referred further on as Delaunay surfaces of first kind and those introduced in Proposition 2 as Delaunay surfaces of second kind.
Now we are ready to formulate our results as
Theorem 1.
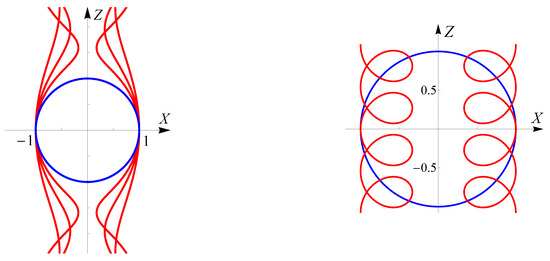
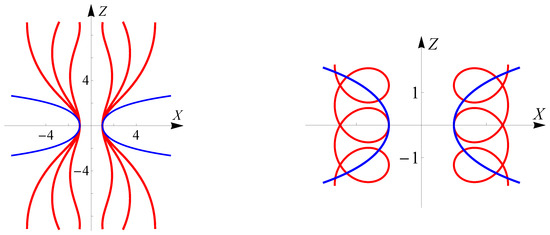
The analytical descriptions of all non-trivial Delaunay surfaces of the first, respectively the second kind, are given by Formulas (34) and (35) which are illustrated in Figure 9 and Figure 10.

Figure 9.
An ensemble of undularies (left) and a circle along with an ensemble of nodaries and with a different scaling the same circle (in blue) on the right.

Figure 10.
Portions of a few undularies (left), along a nodary (right) in the presence of a catenary in both cases.
All results presented up to now can be illustrated schematically as shown in Figure 11.
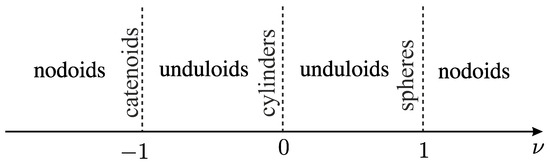
Figure 11.
Distribution of the Delaunay surfaces specified by the chosen range of . The normal direction to the horizontal line is reserved for the first parameter R from the suggested classification of the Delaunay surfaces.
3. Geometry of Delaunay Surfaces
One of the most fundamental theorem in the classical differential geometry [1,2,3,4] states that any surface
in the Euclidean space is defined up to a motion there (i.e., translation and rotation) by the coefficients of its first and second fundamental forms
These coefficients are given by the formulas
where is the unit normal vector to
In our settings and after some tedious computations we end up with the following results.
For the first kind Delaunay surfaces these coefficients turns out to be
Respectively, for the second kind Delaunay surfaces we have
In the above cited books on differential geometry [1,2,3,4] the reader will find also some classical formulas which describe the two principal types of curvatures at every point of the surface. These are the so-called Gaussian curvature K, and the mean (meaning average) curvature H, the latter being of immediate interest here, i.e.,
It can be checked that the second formula above produces for the first kind of Delaunay surfaces the result
while for the second kind of Delaunay surfaces one obtains
However, despite that they seem different, one should keep in mind that according to its very definition (26), the parameter has just the opposite value of , so that the above formulas produce obviously absolutely identical results (as should be).
Remark 4.
Having such complete and explicit description of the Delaunay surfaces opens the possibility to consider more subtle features of these surfaces like geodesics on them. Some preliminary results about geodesics on the unduloids can be found in [15].
4. Conclusions
Up to now we have been interested in purely mathematical questions like how to describe Delaunay surfaces starting with the first principles in differential geometry?
Actually, using the obtained results we have been able to characterize them globally by some intrinsic entities like the coefficients of their fundamental forms or (as we shall see in the Appendix A) via the intrinsic equation of their profile curves.
However, the historical development does not follow exactly the same route. The fundamental fact established by Sturm [6] about minimal property of the lateral area for a fixed volume was quite essential in the treatment of soap bubbles and liquid drops [16,17,18,19] as become evident by Plateau’s [20] experiments. In fact, Plateau is also the originator who coined the names Undulary and Nodary. More recently, these surfaces have been recognized to play the main role in the explanation of the myelin shapes [21], the “pearling” states [22], the capillarity models [23] and that of cells under compression in biology [24,25].
In view of their importance in science and technology we have collected the available parameterizations in the Appendix A below and we will be much obliged to the tempted readers for informing us about any other parameterization which they know but is not listed inside it.
Another our hope is that some of the talented readers of the Mathematics will succeed in finding the relationships between different parameters entering in these parameterizations.
Author Contributions
Conceptualization, C.D.M. and I.M.M.; methodology, C.D.M. and I.M.M.; formal analysis, C.D.M. and I.M.M.; investigation, C.D.M. and I.M.M.; writing—original draft preparation, C.D.M. and I.M.M.; writing—review and editing, C.D.M. and I.M.M.; visualization, C.D.M. and I.M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors would like to thank Vladimir I. Pulov (Varna Technical University) for the useful and constructive discussions on the subject, and to Venelin Chernogorov for his help with some of the figures presented in the paper. The authors are thankful also to all three reviewers for their valuable remarks and suggestions which definitely led to improvement of the presentation.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A
Here we collect the available parameterizations of the Delaunay surfaces starting with the seminal work of Delaunay on the subject. In all cases the original notation have been preserved.
- 1841 Ch. Delaunay [5] (p. 313)Here and —are three arbitrary real constants. The symmetry axis of the generated surfaces is and their mean curvatures are
- 1886 A. Lane [26] (p. 133)Introducingin which a and b are semi-axes of the ellipse rolling on the line, he presents the respective roulette in the formDelaunay or Sturm are not mentioned in the paper at all.
- 1911 G. Loria [27] (p. 127)The symmetry axis of the surfaces is , a and e are real parameters and s is the natural parameter along the curve. Thenis the equation of the profile curve in which e is the eccentricity of the rolling curve.Loria gives credit about this result to the relatively obscure paper published in 1868 by Spitzer [28], in which he does not mention either Delaunay or Sturm.However on the same page Loria presents also the natural equation of Delaunay curves in the formThe natural equation is listed here for later comparison.
- 1969 M. Hady [29] (pp. 380–381)The profile curve with symmetry axis is parameterized by the formulasin which and C are arbitrary real constants.Neither Delaunay, Sturm or some of the above mentioned people were cited in the paper.
- 1980 K. Kenmotsu [30] (p. 150)The profile curve of CMC surfaces with symmetry axis is presented in the formin which s is the arc-length parameter, H denotes the fixed mean curvature and B is another real constant.An updated version of this work along nice pictures can be found in the book [31].
- 2002 I. Mladenov [32] (pp. 22–24)The derived parameterization of the Delaunay surfaces is of the formin which have the meaning used up to now, , and ± signs refer to unduloids/nodoids.
- 2002 I. Mladenov [33] (p. 329)The symmetry axis in this case is , and denote the complete elliptic integrals of the first, respectively second kind [11,12,13,14]. The parameterization is provided by the formulasThe coefficients of the first and the second fundamental forms for this parameterization are found to beand applying the formula from (42) one immediately obtains that
- 2003 I. Mladenov and J. Oprea [15] (p. 220)The parameterization derived in this paper has the formwhile the coefficients of the first and the second fundamental forms were found to be
- 2004 I. Mladenov [34] (pp. 164–166)This paper presents the derivation of the conformal parameterizations for unduloidsand respectively, nodoidsAn alternative approach for finding such parameterizations can be seen in [35].
- 2008 I. Mladenov, M. Hadzhilazova, P. Djondjorov and V. Vassilev [36] (p. 278)The profile curve which symmetry axis is taken to be , is parameterized via the natural parameter s in the form . Relying on the intrinsic equation of the Delaunay curveswhere is the curvature of the profile curve which explicit form is found to beand this leads toHere and are real parameters with specific ranges and the other ingredients are given by the expressions
- 2014 E. Bendito, M. Bowick and A. Medina [37] (pp. 33–35)If the symmetry axis is , roulettes of the ellipses were found to be described by the formulaswhile that ones of hyperbolas are given by
- 2014 B. Athukorallage, T. Paragoda and M. Toda [38] (pp. 6–10)The parameterization of undulary with symmetry axis is cast into the formand that one corresponding to undulary is given by the formulas
- 2014 V. Pulov, M. Hadzhilazova and I. Mladenov [39] (p. 222)In this paper the reader will find the parameterization of the most interesting cases of Delaunay surfaces, namely—unduloids and nodoids, in terms of the complete set of the Weierstrassian elliptic functions, i.e., Weierstrass p-function , and . Assuming that the -axis coincides with the axis of revolution and the generating curves of the surfaces lie in the -plane, the parameterization of the undularies (upper signs) and nodaries (lower signs) have the formwhereThe above functions are built with the so-called invariants of the Weierstrassian functions given by the expressionsin which and are arbitrary real constants. Here u denotes the argument of which produces the value for , , , and , etc. The mean curvature of the generated unduloids, respectively nodoids, is
- 2017 M. Koiso and B. Palmer [40] (p. 14)Relying on variational arguments the authors have concluded that the surface of revolution with symmetry axis will have CMC if its coordinates are given by the formulasin which H denotes the mean curvature and F is the so-called flux parameter of the surface under consideration.
References
- Klimek, G.; Klimek, M. Discovering Curves and Surfaces with MAPLE; Springer: New York, NY, USA, 1997. [Google Scholar]
- Gray, A. Modern Differential Geometry of Curves and Surfaces with Mathematica®, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1998. [Google Scholar]
- Rovenski, V. Geometry of Curves and Surfaces with Maple; Birkhäuser: New York, NY, USA, 2000. [Google Scholar]
- Oprea, J. Differential Geometry and Its Applications, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Delaunay, C. Sur la surface de révolution dont la courbure moyenne est constante. J. Math. Pures Appl. 1841, 6, 309–314. [Google Scholar]
- Sturm, M. Note, à l’occasion de l’article précédent. J. Math. Pures Appl. 1841, 6, 315–320. [Google Scholar]
- Eells, J. The surfaces of Delaunay. Math. Intell. 1987, 9, 53–57. [Google Scholar] [CrossRef]
- Krivoshapko, S.; Ivanov, V. Encyclopedia of Analytical Surfaces; Springer: New York, NY, USA, 2015. [Google Scholar]
- Whittaker, E.; Watson, G. A Course of Modern Analysis, 4th ed.; Cambridge University Press: Cambridge, UK, 1927. [Google Scholar]
- Mladenov, I.; Hadzhilazova, M. The Many Faces of Elastica; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Byrd, P.; Friedman, M. Handbook of Elliptic Integrals for Engineers and Scientists, 2nd ed.; Springer: New York, NY, USA, 1971. [Google Scholar]
- Janhke, E.; Emde, F.; Lösch, F. Tafeln Höherer Funktionen; Teubner Verlag: Stuttgart, Germany, 1960. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. (Eds.) Handbook of Mathematical Functions; Dover: New York, NY, USA, 1972. [Google Scholar]
- Olver, F.; Lozier, D.; Boisvert, R.; Clark, C. The NIST Handbook of Mathematical Functions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Mladenov, I.; Oprea, J. Unduloids and their closed geodesics. Geom. Integr. Quant. 2003, 4, 206–234. [Google Scholar]
- Pulov, V.; Mladenov, I.M. Rotating liquid drops and Delaunay surfaces. J. Geom. Symmetry Phys. 2019, 54, 55–78. [Google Scholar] [CrossRef]
- Thompson, D.W. On Growth and Form; University Press: Cambridge, UK, 1917; Available online: https://www.gutenberg.org/files/55264/55264-h/55264-h.htm#fig63 (accessed on 5 March 2024).
- Isenberg, C. The Science of Soap Films and Soap Bubbles; Dover: New York, NY, USA, 1992. [Google Scholar]
- Oprea, J. The Mathematics of Soap Films: Explorations with Maple®; AMS: Providence, RI, USA, 2000. [Google Scholar]
- Plateau, J. Statique Expérimetal et Théorique des Liquides Soumis Aux Seules Forces Moléculares, 2 Volumes; Gauthier-Villars: Paris, France, 1873. [Google Scholar]
- Deuling, H.; Helfrich, W. A theoretical explanation for the myelin shapes of red blood cells. Blood Cells 1977, 73, 713–720. [Google Scholar]
- Bar-Ziv, R.; Moses, E. Instability and “pearling” states produced in tubular membranes by competition of curvature and tension. Phys. Rev. Lett. 1994, 73, 1392–1395. [Google Scholar] [CrossRef]
- Perera, B.; Paragoda, T.; Dharmasena, D. A survey of Delaunay surfaces with applications in capillary surfaces. J. Geom. Symmetry Phys. 2022, 64, 51–65. [Google Scholar] [CrossRef]
- Yoneda, M. Tension at the surface of sea-urchin egg: A critical examination of Cole’s Eexpariment. J. Exp. Biol. 1964, 41, 893–906. [Google Scholar] [CrossRef]
- Hadzhilazova, M.; Mladenov, I. Membrane approach to balloons and some related surfaces. Geom. Integr. Quant. 2006, 7, 176–186. [Google Scholar]
- Lane, A. Note on a Roulette. Am. J. Math. 1886, VIII, 132–137. [Google Scholar] [CrossRef]
- Loria, G. Spezielle Algebraische Transzendent Ebene Kurven: Theorie und Geschichte; Teubner Verlag: Leipzig, Germany, 1911. [Google Scholar]
- Spitzer, S. Merkwürdige Eigenschaft derjenigen Curve, welche von Brennpunkte einer Ellipse beschrieben wird, wenn diese auf einer Geraden rollt. Arch. Math. Phys. 1868, VIII, 235–238. [Google Scholar]
- Hady, M. Eine chrakterstische Eigenschaft der Sphäre as rotationsfläche. Math. Nachrichten 1969, 42, 379–385. [Google Scholar] [CrossRef]
- Kenmotsu, K. Surfaces of revolution with prescribed mean curvature. Tôhoku Math. J. 1980, 32, 147–153. [Google Scholar] [CrossRef]
- Kenmotsu, K. Surfaces with Constant Mean Curvature (Translated by Katsuhiro Molriya); AMS: Providence, RI, USA, 2003. [Google Scholar]
- Mladenov, I.M. Delaunay surfaces revisited. C. R. Acad. Sci. 2002, 55, 19–24. [Google Scholar]
- Mladenov, I.M. New solutions of the shape equation. Eur. Phys. J. B 2002, 29, 327–330. [Google Scholar] [CrossRef]
- Mladenov, I.M. Conformal immersions of Delaunay surfaces and their duals. Geom. Integr. Quant. 2004, 5, 158–168. [Google Scholar]
- Bracken, P. Delaunay surfaces expressed in terms of a Cartan moving frame. J. Appl. Anal. 2020, 26, 153–160. [Google Scholar] [CrossRef]
- Mladenov, I.; Hadzhilazova, M.; Djondjorov, P.; Vassilev, V. On the intrinsic equation behind the Delaunay surfaces. AIP Conf. Proc. 2008, 1079, 274–280. [Google Scholar]
- Bendito, E.; Bowick, M.; Medina, A. A natural parameterization of the roulettes of the conics generating the Delaunay surfaces. J. Geom. Symmetry Phys. 2014, 33, 27–45. [Google Scholar]
- Athukorallage, B.; Paragoda, T.; Toda, M. Roulettes of conics, Delaunay surfaces and applications. Surv. Math. Math. Sci. 2014, 4, 1–23. [Google Scholar]
- Pulov, V.; Hadzhilazova, M.; Mladenov, I.M. Delaunay surfaces in terms of Weierstrassian functions. In Proceedings of the International Conference on Integrability, Recursion Operators and Soliton Interactions, Sofia, Bulgaria, 29–31 August 2012; Aneva, B., Grahovski, G., Ivanov, R., Mladenov, D., Eds.; Avangard Prima: Sofia, Bulgaria, 2014; pp. 218–224. [Google Scholar]
- Koiso, M.; Palmer, B. Higher order variations of constant mean curvature surfaces. Calc. Var. 2017, 56, 159. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).