Robustness of Real-World Networks after Weight Thresholding with Strong Link Removal
Abstract
1. Introduction
2. Methods
2.1. Real-World Networks
2.2. Attack Strategies
- Strength (Str): A node’s strength is the total weight of the links connected to that node [33], also called a weighted degree.
- Weighted Betweenness (WBet): Weighted betweenness of a node is defined as the number of weighted shortest paths passing through that node [34].
2.3. Weight Thresholding
2.4. Network Robustness Indicator
- One way was to normalize the LCC after node removal using the initial LCC value (before node attack) of the network after WT. In this case, we considered each thresholded network an independent network, and we did not account for the LCC decrease directly caused by the WT procedure.
- A second way was to normalize the LCC after node removal using the initial LCC at WT = 0, i.e., we normalized using the LCC of the original network. In this second case, we also considered the LCC decrease triggered by the link removal of the WT procedure. This normalization was intended to analyze the joint effect of the weight thresholding and node attack to decrease the LCC (total LCC decrease).
3. Results and Discussion
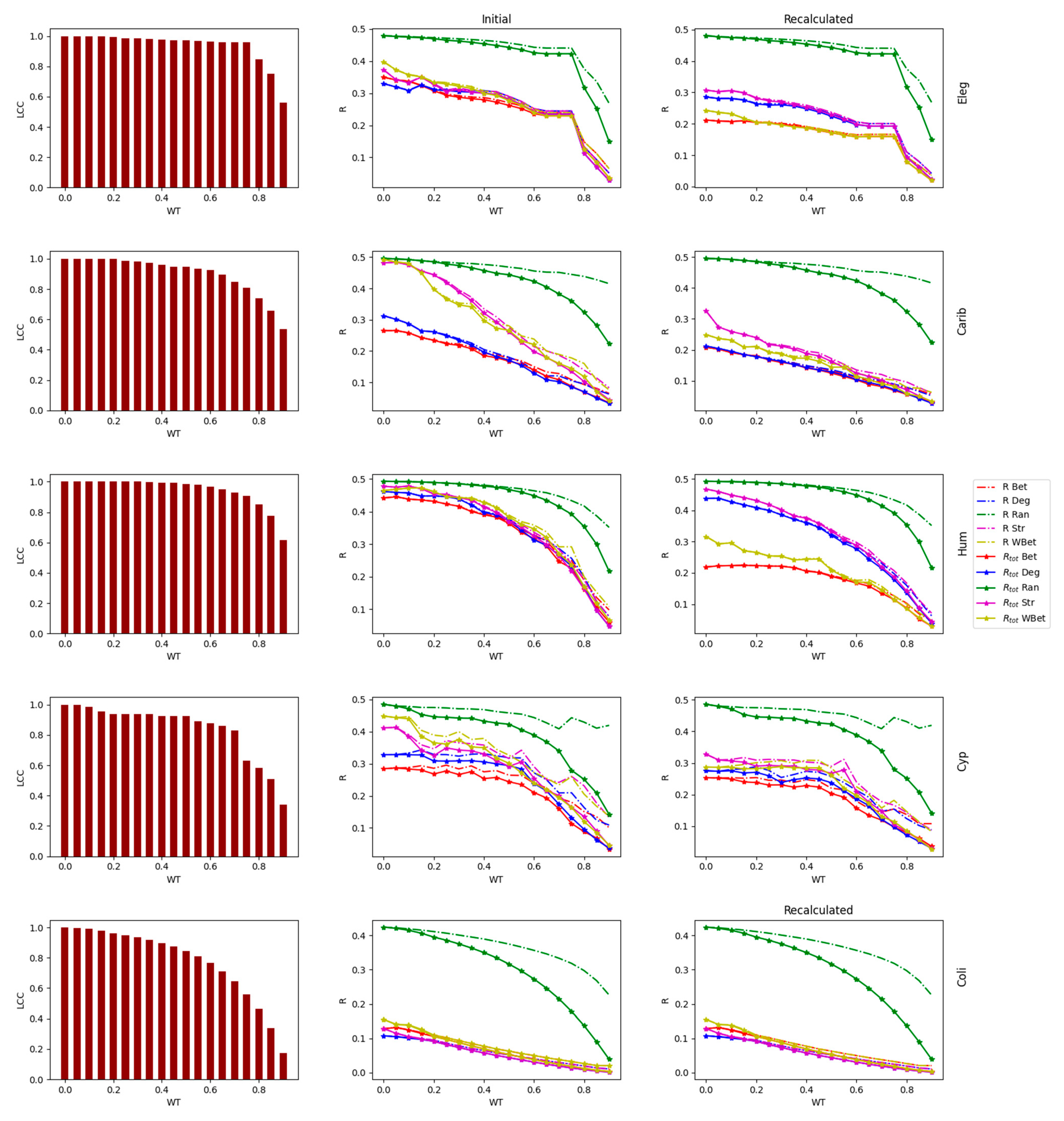
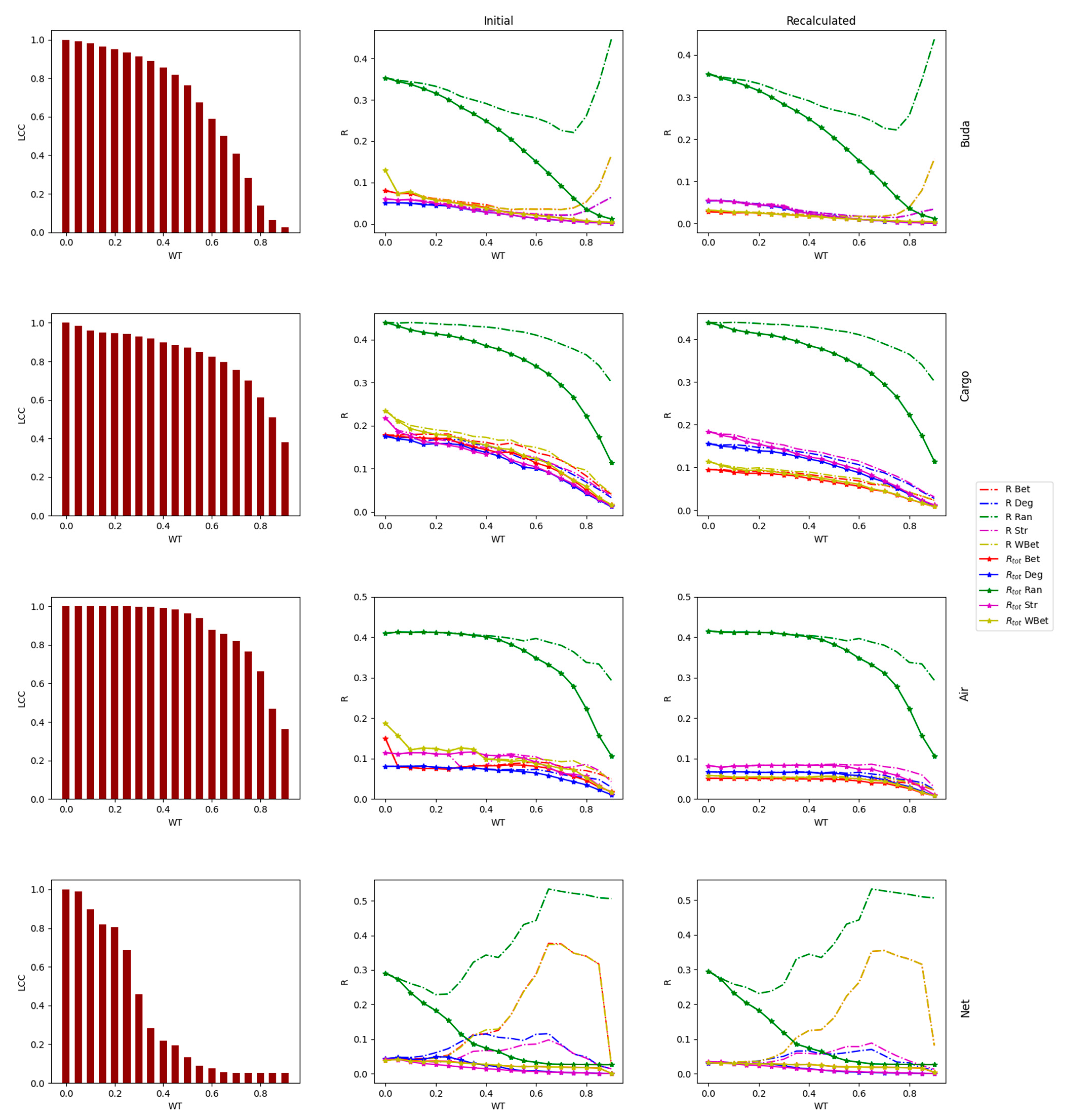
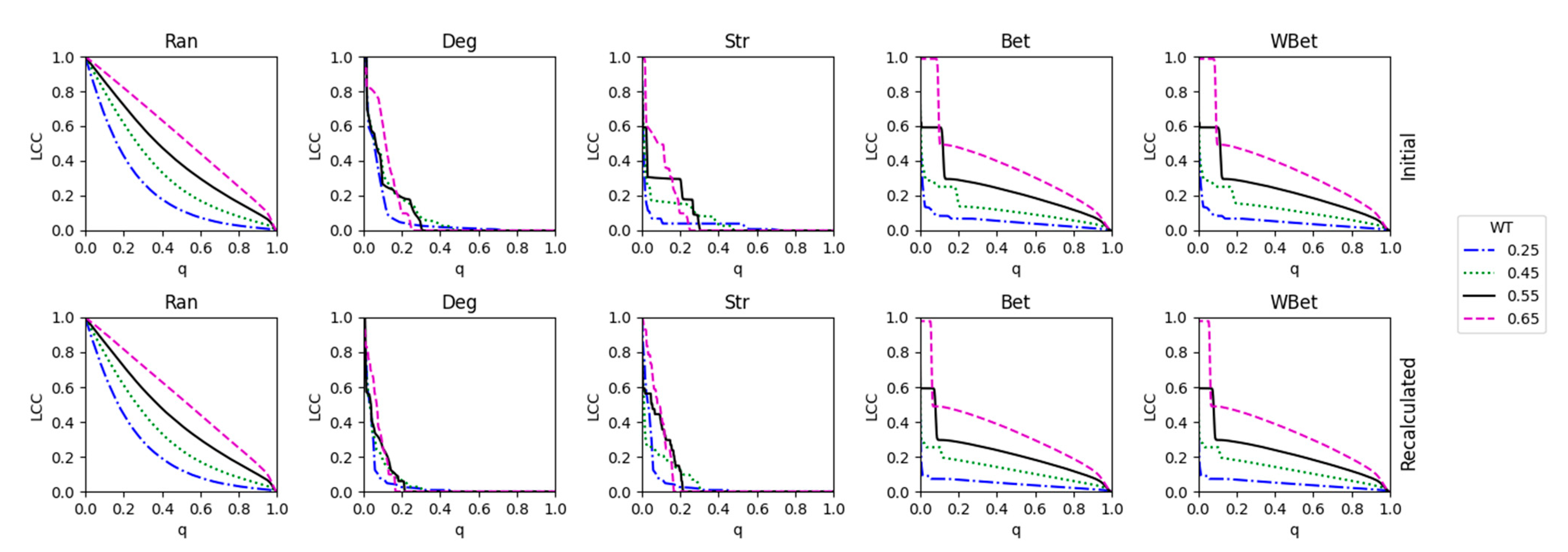
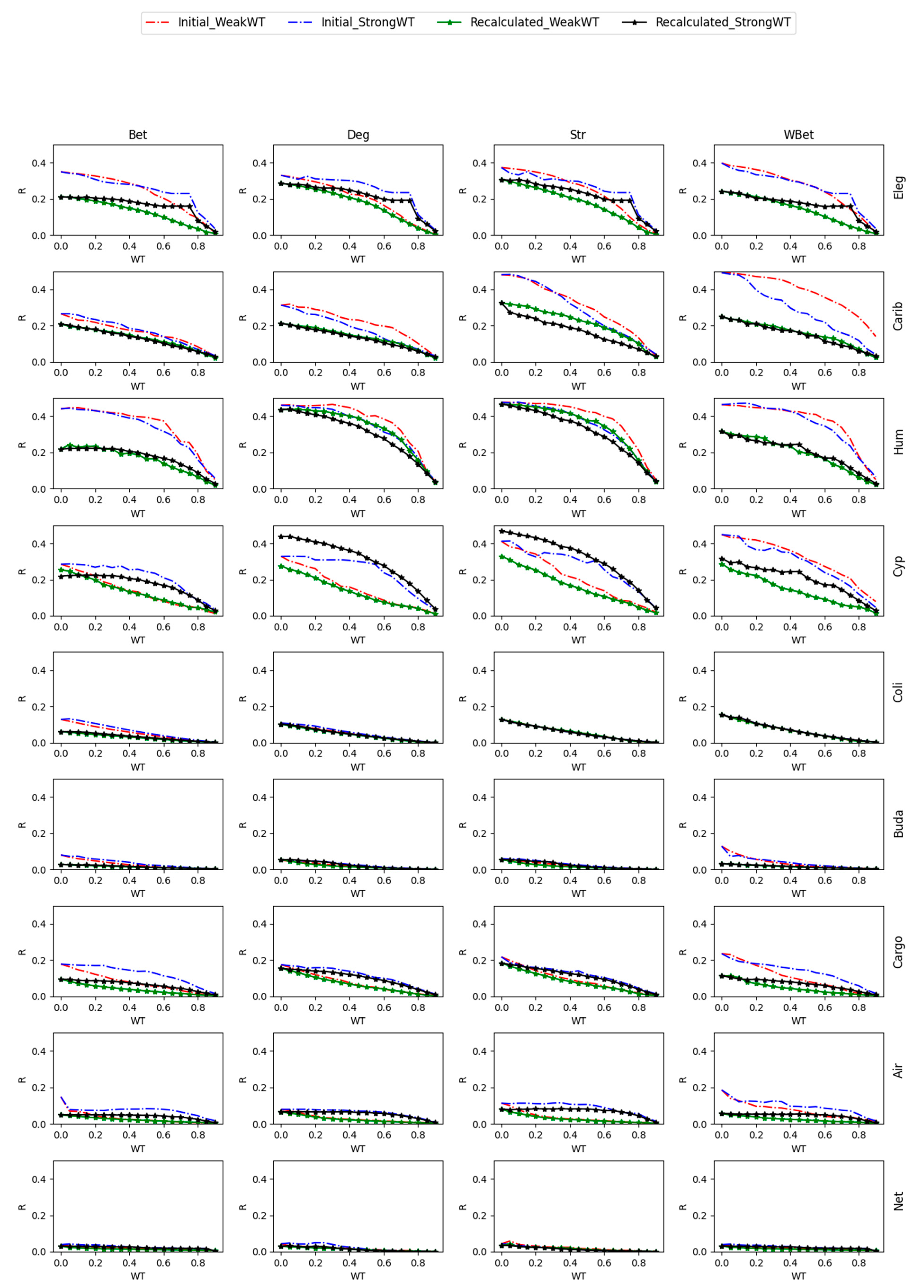
3.1. Robustness against WT
3.2. Robustness to WT and Node Attack
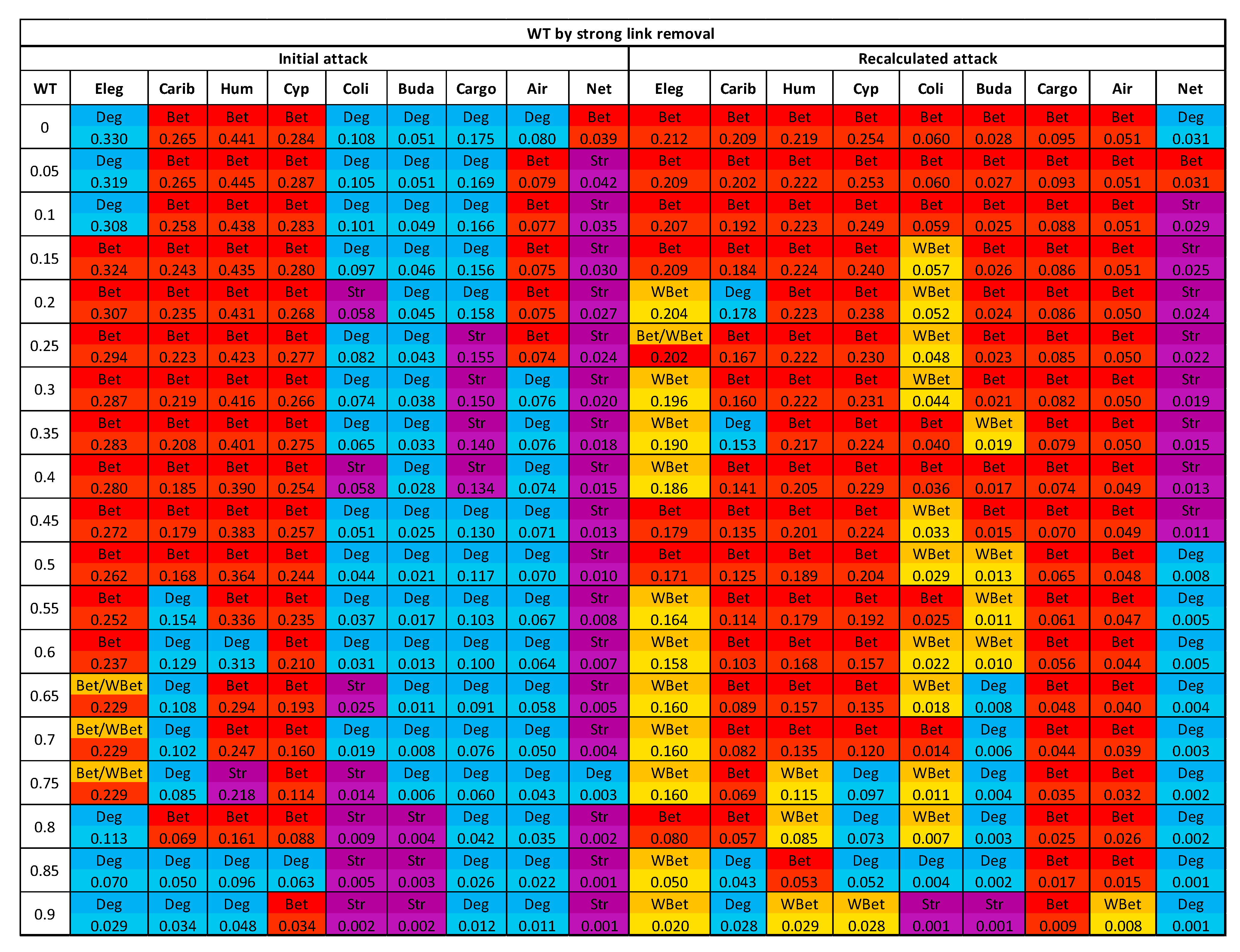
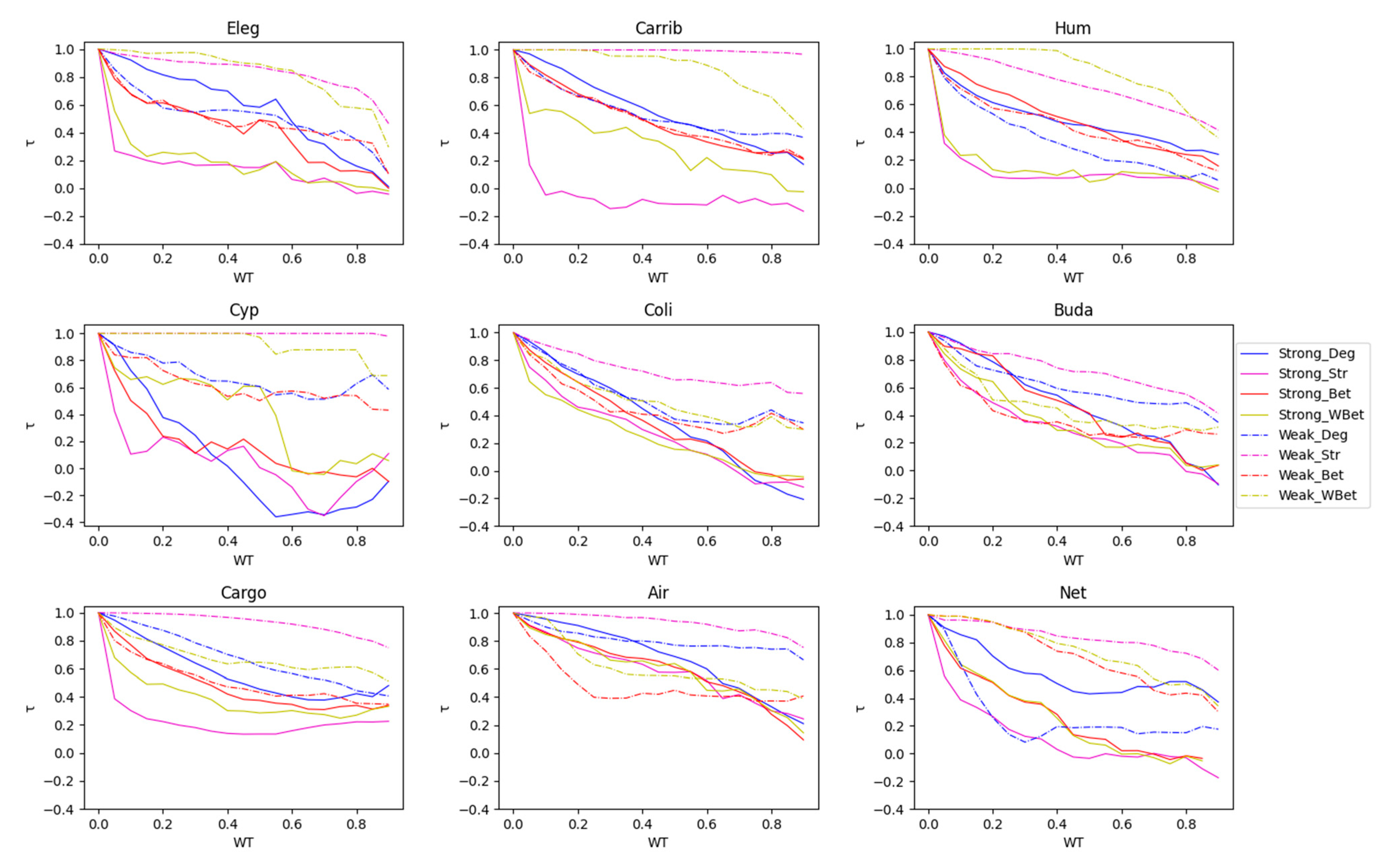
3.3. The Efficacy of the Node Attack Strategies
3.4. Comparing Strong and Weak WT Procedures
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Yan, X.; Jeub, L.G.S.; Flammini, A.; Radicchi, F.; Fortunato, S. Weight thresholding on complex networks. Phys. Rev. E 2018, 98, 042304. [Google Scholar] [CrossRef]
- John, J.M.; Bellingeri, M.; Lekha, D.S.; Cassi, D.; Alfieri, R. Effect of Weight Thresholding on the Robustness of Real-World Complex Networks to Central Node Attacks. Mathematics 2023, 11, 3482. [Google Scholar] [CrossRef]
- Namaki, A.; Shirazi, A.H.; Raei, R.; Jafari, G. Network analysis of a financial market based on genuine correlation and threshold method. Phys. A Stat. Mech. Its Appl. 2011, 390, 3835–3841. [Google Scholar] [CrossRef]
- Lynall, M.-E.; Bassett, D.S.; Kerwin, R.; McKenna, P.J.; Kitzbichler, M.; Muller, U.; Bullmore, E. Functional connectivity and brain networks in schizophrenia. J. Neurosci. 2010, 30, 9477–9487. [Google Scholar] [CrossRef] [PubMed]
- Allesina, S.; Bodini, A.; Bondavalli, C. Secondary extinctions in ecological networks: Bottlenecks unveiled. Ecol. Model. 2006, 194, 150–161. [Google Scholar] [CrossRef]
- Garrison, K.A.; Scheinost, D.; Finn, E.S.; Shen, X.; Constable, R.T. The (in) stability of functional brain network measures across thresholds. Neuroimage 2015, 118, 651–661. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Mather, P.M. Assessing artificial neural network pruning algorithms. In Proceedings of the 24th Annual Conference and Exhibition of the Remote Sensing Society, Greenwich, UK, 9–11 September 1998. [Google Scholar]
- Hongwu, P.; Deniz, G.; Shaoyi, H.; Tong, G.; Weiwen, J.; Orner, K.; Caiwen, D. Towards Sparsification of Graph Neural Networks. In Proceedings of the IEEE 40th International Conference on Computer Design (ICCD), Olympic Valley, CA, USA, 23–26 October 2022. [Google Scholar]
- Albert, R.; Barabasi, A.-L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47–97. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabasi, A.-L. Error and attack tolerance of complex networks. Nat. Vol. 2000, 406, 378–382. [Google Scholar] [CrossRef] [PubMed]
- Garas, A.; Argyrakis, P.; Havlin, S. The structural role of weak and strong links in a financial market network. Eur. Phys. J. B 2008, 63, 265–271. [Google Scholar] [CrossRef]
- Onnela, J.-P.; Saramäki, J.; Hyvönen, J.; Szabó, G.; De Menezes, M.A.; Kaski, K.; Barabási, A.-L.; Kertész, J. Analysis of a large-scale weighted network of one-to-one human communication. New J. Phys. 2007, 9, 179. [Google Scholar] [CrossRef]
- Onnela, J.-P.; Saramäki, J.; Hyvönen, J.; Szabó, G.; Lazer, D.; Kaski, K.; Kertész, J.; Barabási, A.-L. Structure and tie strengths in mobile communication networks. Proc. Natl. Acad. Sci. USA 2007, 104, 7332–7336. [Google Scholar] [CrossRef] [PubMed]
- Pan, R.K.; Saramaki, J. The strength of strong ties in scientific collaboration networks. Europhys. Lett. 2012, 97, 18007. [Google Scholar] [CrossRef]
- Pajevic, S.; Plenz, D. The organization of strong links in complex networks. Nat. Phys. 2012, 8, 429–436. [Google Scholar] [CrossRef] [PubMed]
- Bellingeri, M.; Vincenzi, S. Robustness of empirical food webs with varying consumer’s sensitivities to loss of resources. J. Theor. Biol. 2013, 333, 18–26. [Google Scholar] [CrossRef] [PubMed]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’ networks. Nature 1998, 393, 440–442. [Google Scholar] [CrossRef]
- Latora, V.; Nicosia, V.; Russo, G. Complex Networks: Principles, Methods and Applications; Cambridge University Press: Cambridge, UK, 2017. [Google Scholar]
- Allard, A.; Serrano, M.A.; Garcia-Perez, G.; Boguna, M. The geometric nature of weights in real complex networks. Nat. Commun. 2017, 8, 14103. [Google Scholar] [CrossRef]
- Colizza, V.; Pastor-Satorras, R.; Vespignani, A. Reaction-diffusion processes and metapopulation models in heterogeneous. Nat. Phys. 2007, 3, 276–282. [Google Scholar] [CrossRef]
- Serrano, A.M.; Boguna, M.; Sagues, F. Uncovering the hidden geometry behind metabolic networks. Mol. BioSystems 2012, 8, 843–850. [Google Scholar] [CrossRef] [PubMed]
- Newman, M.E.J. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. 2006, 74, 036104. [Google Scholar] [CrossRef]
- Avena-Koenigsberger, A.; Goni, J.; Betzel, R.F.; Heuvel, M.P.V.D.; Griffa, A.; Hagmann, P.; Thiran, J.-P.; Sporns, O. Using Pareto optimality to explore the topology and dynamics of the human connectome. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2014, 369, 20130530. [Google Scholar] [CrossRef]
- Hagmann, P.; Cammoun, L.; Gigandet, X.; Meuli, R.; Honey, C.J.; Wedeen, V.J.; Sporns, O. Mapping the structural core of human cerebral cortex. PLoS Biol. 2008, 6, 1479–1493. [Google Scholar] [CrossRef] [PubMed]
- Bellingeri, M.; Bodini, A. Food web’s backbones and energy delivery in ecosystems. Oikos 2016, 125, 586–594. [Google Scholar] [CrossRef]
- Opitz, S. Trophic Interactions in Caribbean Coral Reefs; ICLARM: Penang, Malaysia, 1996. [Google Scholar]
- Heymans, J.J.; Ulanowicz, R.E.; Bondavalli, C. Network analysis of the South Florida Everglades graminoid marshes and comparison with nearby cypress ecosystems. Ecol. Model. 2002, 149, 5–23. [Google Scholar] [CrossRef]
- Szalkai, B.; Kerepesi, C.; Varga, B.; Grolmusz, V. The Budapest Reference Connectome Server v2.0. Neurosci. Lett. 2015, 595, 60–62. [Google Scholar] [CrossRef] [PubMed]
- Holme, P.; Kim, B.J.; Yoon, C.N.; Han, S.K. Attack vulnerability of complex networks. Phys. Rev. E 2002, 65, 056109. [Google Scholar] [CrossRef] [PubMed]
- Bellingeri, M.; Cassi, D.; Vincenzi, S. Efficiency of attack strategies on complex model and real-world networks. Phys. A Stat. Mech. Its Appl. 2014, 414, 174–180. [Google Scholar] [CrossRef]
- Iyer, S.; Killingback, T.; Sundaram, B.; Wang, Z. Attack robustness and centrality of complex networks. PLoS ONE 2013, 8, e59613. [Google Scholar] [CrossRef]
- Cohen, R.; Erez, K.; Ben-Avraham, D.; Havlin, S. Breakdown of the internet under intentional attack. Phys. Rev. Lett. 2001, 86, 3682–3685. [Google Scholar] [CrossRef] [PubMed]
- Bellingeri, M.; Cassi, D. Robustness of weighted networks. Phys. A Stat. Mech. Its Appl. 2018, 489, 47–55. [Google Scholar] [CrossRef]
- Nguyen, Q.; Nguyen, N.K.K.; Cassi, D.; Bellingeri, M. New betweenness centrality node attack strategies for real-world complex weighted networks. Complexity 2021, 2021, 1677445. [Google Scholar] [CrossRef]
- Bellingeri, M.; Bevacqua, D.; Sartori, F.; Turchetto, M.; Scotognella, F.; Alfieri, R.; Nguyen, N.K.K.; Le, T.T.; Nguyen, Q.; Cassi, D. Considering weights in real social networks: A review. Front. Phys. 2023, 11, 1152243. [Google Scholar] [CrossRef]
- Bellingeri, M.; Bevacqua, D.; Scotognella, F.A.; Alfieri, R.; Cassi, D. A comparative analysis of link removal strategies in real complex weighted networks. Sci. Rep. 2020, 10, 3911. [Google Scholar] [CrossRef] [PubMed]
- Jordán, F. Keystone Species and Food Webs. Philos. Trans. R. Soc. Lond. Ser. B Biol. Sci. 2009, 364, 1733–1741. [Google Scholar] [CrossRef] [PubMed]
- Nie, T.; Guo, Z.; Zhao, K.; Lu, Z.-M. New attack strategies for complex networks. Phys. A Stat. Mech. Its Appl. 2015, 424, 248–253. [Google Scholar] [CrossRef]
- Kendall, M.G. The treatment of ties in ranking problems. Biometrika 1945, 33, 239–251. [Google Scholar] [CrossRef] [PubMed]
- Lü, L.; Chen, D.; Ren, X.-L.; Zhang, Q.-M.; Zhang, Y.-C.; Zhou, T. Vital nodes identification in complex networks. Phys. Rep. 2016, 650, 1–63. [Google Scholar] [CrossRef]
- Dunne, J.A.; Williams, R.J.M.D. Network structure and biodiversity loss in food webs: Robustness increases with connectance. Ecol. Lett. 2002, 5, 558–567. [Google Scholar] [CrossRef]
- Shang, K.-K.; Small, M.; Yin, D.; Li, T.-C.; Yan, W. The key to the weak-ties phenomenon. Europhys. Lett. 2019, 127, 48002. [Google Scholar] [CrossRef]

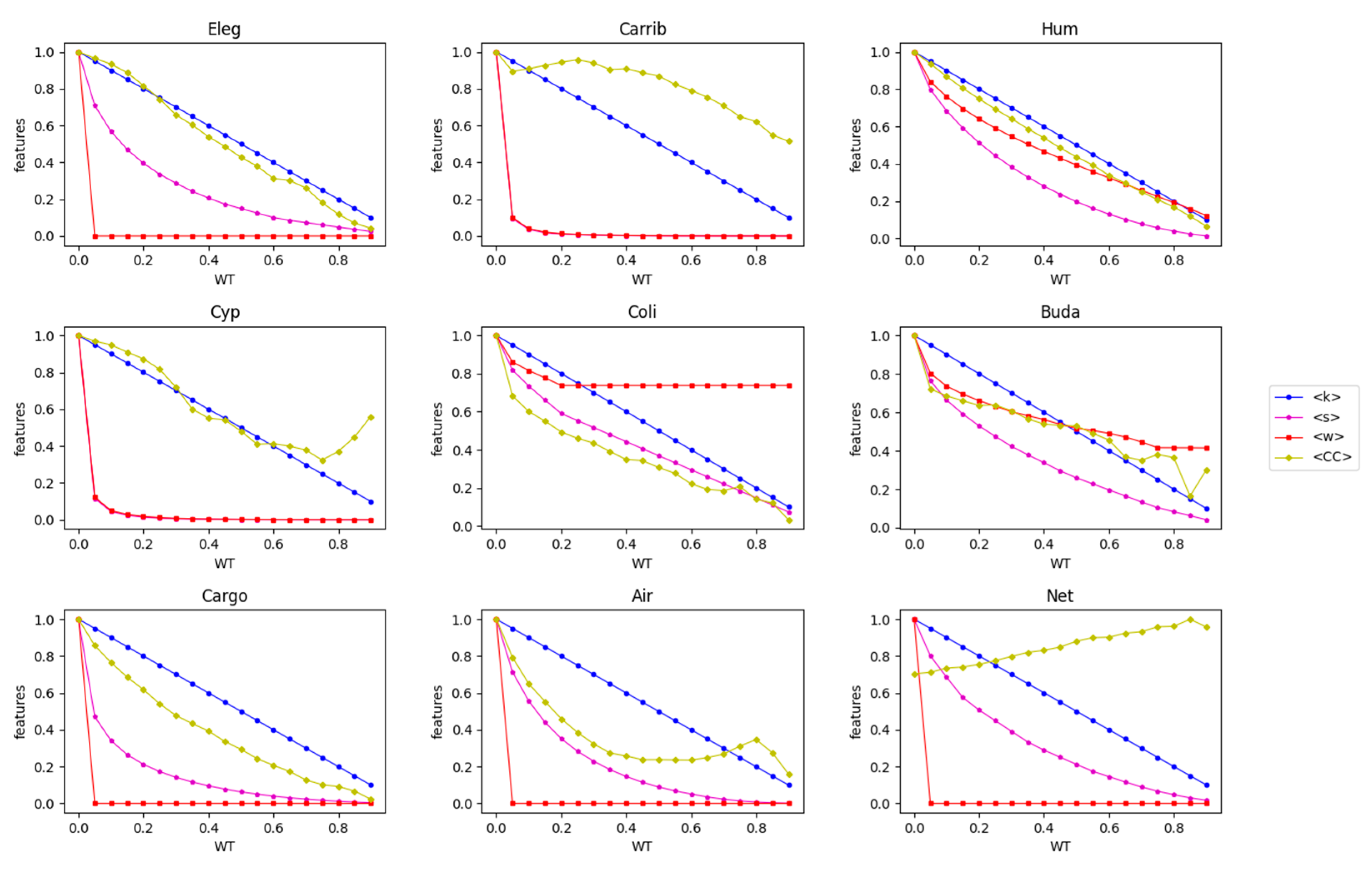

| Networks | Key | Ref. | Type | Node | Link | Weight | N | L | <k> | <w> | <CC> | LCC |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| C. Elegans | Eleg | [17,18] | Biological | Neurons | Neurons connection | Number of Connections | 297 | 2344 | 15.8 | 3.761 | 0.181 | 297 |
| Cargoship | Cargo | [19] | Transport | Ports | Route | Shipping journeys | 834 | 4348 | 10.4 | 97.709 | 0.222 | 821 |
| US airport | Air | [20] | Transport | Airports | Route | Passengers | 500 | 2979 | 11.9 | 152320.2 | 0.351 | 500 |
| E. Coli | Coli | [19,21] | Biological | Metabolites | Common reaction | Number of Common reactions | 1100 | 3636 | 6.61 | 1.364 | 0.139 | 1100 |
| Netscience | Net | [22] | Social | Authors | Coauthorship | Number of Common papers | 1461 | 2741 | 3.75 | 0.434 | 0.693 | 379 |
| Human 12a | Hum | [23,24] | Biological | Brain regions | Connection between regions | Connection density | 501 | 6038 | 24.1 | 0.01 | 0.457 | 501 |
| Caribbean | Carib | [25,26] | Ecological Food web | Species | Trophic relation | Amount of biomass | 249 | 3503 | 28.13 | 0.067 | 0.172 | 249 |
| CypDry | Cyp | [16,27] | Ecological Food web | Species | Trophic relation | Amount of biomass | 66 | 503 | 15.24 | 0.358 | 0.421 | 65 |
| Budapest | Buda | [28] | Biological | Brain regions | Neural connection | Amount of track flow | 480 | 1000 | 4.167 | 5.024 | 0.120 | 467 |
| Abbreviation | Full Name |
|---|---|
| WT | Weight thresholding |
| LCC | Size of largest connected component |
| N | Number of nodes |
| L | Number of links |
| <w> | Average link weight |
| <k> | Average node degree |
| <CC> | Global clustering coefficient |
| Ran | Random node attack |
| Deg | Degree node attack |
| Str | Strength node attack |
| Bet | Betweenness node attack |
| WBet | Weighted Betweenness node attack |
| G | Weighted network |
| G’ | Thresholded network |
| L’ | Number of links in G’ |
| q | Fraction of nodes removed |
| R | Robustness |
| Rtot | Total Robustness |
| <s> | Average node strength |
| Initial_Weak WT | WT by weak link removal with initial node attack strategy |
| Initial_Strong WT | WT by strong link removal with initial node attack strategy |
| Recalculated_Weak WT | WT by weak link removal with recalculated node attack strategy |
| Recalculated_Strong WT | WT by strong link removal with recalculated node attack strategy |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
John, J.M.; Bellingeri, M.; Lekha, D.S.; Cassi, D.; Alfieri, R. Robustness of Real-World Networks after Weight Thresholding with Strong Link Removal. Mathematics 2024, 12, 1568. https://doi.org/10.3390/math12101568
John JM, Bellingeri M, Lekha DS, Cassi D, Alfieri R. Robustness of Real-World Networks after Weight Thresholding with Strong Link Removal. Mathematics. 2024; 12(10):1568. https://doi.org/10.3390/math12101568
Chicago/Turabian StyleJohn, Jisha Mariyam, Michele Bellingeri, Divya Sindhu Lekha, Davide Cassi, and Roberto Alfieri. 2024. "Robustness of Real-World Networks after Weight Thresholding with Strong Link Removal" Mathematics 12, no. 10: 1568. https://doi.org/10.3390/math12101568
APA StyleJohn, J. M., Bellingeri, M., Lekha, D. S., Cassi, D., & Alfieri, R. (2024). Robustness of Real-World Networks after Weight Thresholding with Strong Link Removal. Mathematics, 12(10), 1568. https://doi.org/10.3390/math12101568







