Abstract
In this paper, we investigate the impact of latency aging on exchangeable (invariant under permutation of indices) inter-arrival times arising from mixed renewal point processes (statistical mixtures of point processes with renewal inter-arrival times) and explore the implications for reliability and survival analysis. We prove that aging preserves the exchangeability of inter-arrival times. Our data analysis, which includes both surrogate data and a Bayesian approach to high-frequency currency exchange-rate data, shows how aging impacts key survival analysis metrics such as failure survival, renewal, and hazard rate functions.
Keywords:
renewal processes; exchangeability; statistical aging; survival analysis; high frequency exchange rates MSC:
60G55; 60G09; 60K10
1. Introduction
In this paper, we numerically and analytically investigate the impact of aging on exchangeable inter-arrival times in renewal point processes. Renewal theory focuses on stochastic systems whose temporal evolution is punctuated by events called renewals. It has been extensively examined in seminal works [1,2,3] and is widely applied to reliability and survival analysis [4,5]. The theory does not need to specify the meaning or effect of single events, which is why renewal processes are at the core of many stochastic problems found in applied mathematics throughout many fields of science, engineering, and economics [6,7,8].
This article explores two important notions in the theory of renewal stochastic point processes, the exchangeability of inter-event times and a type of aging that we call “latency aging”, since we consider a delay in the event detection process. Its main purpose is to combine these two notions to describe the effect of latency aging on renewal point processes with exchangeable inter-event times.
The first idea, exchangeability, was introduced by Bruno de Finetti [9,10]—a sequence is defined to be exchangeable if its joint probability distribution is a symmetric function of its arguments. Its significance is largely connected with "de Finetti’s representation theorem" and its generalized formulations, elucidating conditions connecting frequencies with subjective probabilities [10,11,12]. In the context of a generalized renewal theory for stochastic processes, see [13,14], exchangeability replaces the conventional assumption of observations being “independent and identically distributed with an unknown distribution,” considering exchangeable observations as a sequence of conditionally independent and identically distributed (i.i.d.) random variables. Building upon the concept of exchangeability, a recent development in point processes has led to the introduction of mixed renewal point processes, as in [15,16,17], where inter-event time intervals are exchangeable rather than i.i.d.
The second concept, latency aging, is a specific form of aging rooted in the traditional definition found in the physics literature, particularly within the realm of complex systems such as glasses and spin glasses [18,19,20,21], as well as in discussions on stochastic processes [22,23] and dynamical systems [24,25]. The phenomenon of aging, in general, entails a reliance of properties—such as relaxation times or correlation functions—on the time at which those properties are measured. In the context of latency aging, observation of events is always followed by a delay in event detection, see [26,27]: when an event takes place, the detection process pauses for a time, , known as the age. This “freezing” generates waiting times with altered statistical properties [28,29,30]. If such a situation occurs, the correspondent point process is said to be affected by renewal aging defined by exchangeable lifetime intervals. However, we prove that if the original sequence of inter-event time intervals is exchangeable, observational latency preserves exchangeability of the new waiting-times. In the field of quantitative finance, reliability and renewal theory are used in the study of market micro-structure models for the estimation of arrival times of trades or orders in financial markets [31,32,33,34]. At the same time, understanding the aging behavior of time series is fundamental to studies of the stability of financial markets [34,35,36].
Finally, as a case study, we examine high-frequency data of exchange rates among currency pairs. Employing a Bayesian approach to survival analysis, we note that latency in event recording introduces a significant change in the assessment of volatility risk. Specifically, the practical implication is that delays in event detection create a false perception of improved system performance compared to its true behavior. In essence, the system shows a decreased likelihood of events happening immediately after activation (during the latency period).
The paper is organized as follows: in Section 2, we remind the reader of some of the central concepts in reliability theory and survival analysis of the renewal process under the exchangeability assumption of inter-event time intervals. Later, in Section 3, we analytically assess the implications of aging on exchangeable lifetimes. We formulate aged versions of some key metrics in the survival analysis of exchangeable renewal processes, such as the marginal distribution of waiting times (i.e., failure survival function), the average number of events (i.e., renewal function), and the rate of failure at any instant (hazard rate function). After the theoretical results, in Section 4 we discuss some archetypal examples of mixed renewal processes with intrinsic fluctuations of the underlying parameters due the fact that inter-arrival times between events may exhibit variability. We compare analytical and numerical results for some exchangeable mixture models where the effect of aging on the renewal process has some interesting implications for survival analysis. At the end of the section, we present some empirical findings. As a case study, we investigate high-frequency financial time series and, in particular, we use currency pairs with tick-by-tick historical exchange rates, treated as conditional observations on which we apply the survival analysis for exchangeable sequences. Finally, Section 5 will summarize the results obtained and highlight the novel contribution to the literature of renewal theory and reliability analysis from a subjective perspective.
2. Preliminaries
In this section, we report some fundamental definitions and propositions on exchangeability of sequences of time-interval variables in renewal processes. Later, we will frame such property in the field of renewal theory for point processes with inter-event times that are exchangeable rather than independent and identically distributed (i.i.d.).
A sequence of inter-event time intervals is said to be exchangeable if the order of observations does not carry relevant information [11,37]. More precisely:
Definition 1.
Let be a sequence of random variables defined over the probability space , where the sample space , the event space is a measurable subset of positive reals (namely a Borel set in ), and the probability is defined in terms of the cumulative distribution function.
A finite sequence of random variables is called exchangeable if ,
where is the group of permutations of . If the sequence is infinite, it is said to be exchangeable if the finite collections are exchangeable for every finite or every permutation .
Let us note that the equivalence in distribution, , simply means that the two probability distribution functions are the same. So the sequence takes values in a standard Borel space , where is the positive reals and is all of the Borel subsets of the positive reals. Exchangeability generalizes the notion of a sequence of random variables being independent and identically distributed (i.i.d.) and, in the frequentist approach to statistics, observed data is assumed to be generated by a series of i.i.d. random variables with distribution parameterized by some unknown parameter that, contrary to the Bayesian perspective, has some prior distribution, so the random variables that provide the data are no longer independent. The representation theorem states that any infinite exchangeable sequence of random variables is a mixture of independent and identically distributed (i.i.d.) sequences, in the sense of the following proposition, which covers the general case for real-valued exchangeable random quantities as in [12,38,39], known as generalized de Finetti’s theorem:
Proposition 1
(representation theorem). Consider an infinitely exchangeable sequence , where there exists a probability of de Finetti’s measure μ over the space of all distribution functions on , such that the joint distribution function of the sequence has the form:
where μ is the probability distribution of the empirical random distribution defined by .
The previous proposition implies that we should proceed as if the observations are independent conditional on F, an unknown cumulative distribution (an infinite-dimensional parameter), with a belief distribution for F, having the operational interpretation in Equation (2) of what we believe the empirical distribution function would look like for a large sample. This means that infinite sequences of exchangeable random variables can be regarded equivalently as sequences of conditionally i.i.d. random variables, based on some underlying distributional form described by the de Finetti probability measure . Note that this equivalence does not quite hold for finite exchangeability, in the sense that there are finite exchangeable sequences that cannot be represented as a mixture of i.i.d. processes. However, they can be modeled as approximately being conditionally i.i.d., as shown in [40,41,42], under the condition that the sample size , where k represents the first outcomes of the sample of size n in a sampling scheme of drawing without replacement. In the trivial case, when the sequence is generated by a de Finetti mixture with a degenerate mixing distribution, i.e., when , with denoting a unit point mass at a, then the sequence is (unconditionally) i.i.d. So, it is evident how the condition of exchangeability is weaker than independence, but it is stronger than the identically distributed property. The close relationship between exchangeable sequences of random variables and the i.i.d. allows the application of the law of large numbers to the empirical distribution function, as follows [43,44,45]:
Proposition 2.
For any distribution given , the empirical distribution can be written as:
where is the empirical distribution function defined by the first n random variables . Then, it holds that the limiting empirical distribution function is:
which exists almost surely, so the empirical distribution is a sufficient statistic for the unknown ‘parameter’ F.
This is particularly interesting when combined with de Finetti’s Theorem 1 where, by the law of large numbers (which we apply after conditioning on the draw ), the unknown (random) distribution F can be recovered from the observed sequence by taking the limit of its empirical distribution. In conclusion, the empirical distribution functions are sufficient statistics for the sequence , in the sense that probabilities conditional on the cumulative counting depend only on and are independent of the choice of exchangeable P, which assigns the same probability to any two exchangeable patterns. Furthermore, the probability distribution represents the beliefs about the outcomes about i.e., through the empirical distribution .
In what follows, we recall the class of exchangeable mixed renewal processes, as studied in [15,16,17]. Let us consider a counting process that counts the number of some type of events occurring during a time interval and let us suppose are random times at which a certain event occurs. The time elapsed between consecutive events are random variables and represent the inter-occurrence times . The are called renewal times, are the inter-event time intervals, and is the number of renewal events in .
Definition 2.
Let the inter-renewal times be a sequence of non negative exchangeable random variables with de Finetti’s measure μ, and empirical distribution F, such that . Labeling to be the epoch of the nth occurrence given by the sum , then the arrival process , defined as:
This is an exchangeable (or mixed) renewal counting process.
In other words, counts the number of renewal events in , and since then , where . According to the above assumptions and definitions for renewal processes under exchangeability, the latency assessment in renewal sequences is studied in the following Section 3. Another important function of interest in survival analysis is the so called renewal function , which represents the expected numbers of renewals in an interval for a renewal process with underlying distribution F. The renewal function can be recovered from [15] to be:
where is the conditional renewal function and denotes the n-fold convolution of F. The previous relation shows that the renewal function, in the exchangeable case, is a weighted average of independent renewal functions, where the weight is given through the de Finetti’s measure .
Bayesian analysis frequently employs a mixture modeling paradigm [12,46,47] where, in many practical cases, the attention is often focused on representing data in terms of a finite-dimensional parameter rather than an infinite-dimensional label F. Therefore, it is useful to write the generalized de Finetti representation theorem in its parametric version as:
Proposition 3.
Under the conditions as in Proposition 1, if the distribution function F is indexed by parameter , with probability distribution , then the joint distribution function of can be written as:
where denotes the a priori probability density on θ, when defined, and is the parametric model labeled by the parameter θ.
In other words, when data are considered exchangeable, it implies that the data constitutes a random sample from a probability model, and there exists a prior distribution over the parameters of that model. Consequently, de Finetti’s representation theorem is frequently regarded as the fundamental motivation for Bayesian analysis.
At this point, we have shown all the necessary notions to discuss the statistical aging effect on point processes with exchangeable inter-event time intervals (i.e., renewal failures).
3. Statistical Aging in Mixed Renewal Processes
The concept of latency aging, as previously discussed, involves the introduction of a delay time denoted as in event detection. This time, , signifies the period during which a detection system temporarily fails to detect new events. Essentially, it remains "blind" for a duration of after the observation of the last event. Consequently, to assess the waiting time until the next event, one must position the observation time at a distance of from each previously recorded event. This form of aging, termed latency aging in this article, is informed by studies on aging experiments, as exemplified by research such as [48,49,50]. The experiment begins by considering the sequence of event occurrence times: . Given an aging time , for each time we record the first time of the sequence at a distance from equal to or larger than : . Then, we record the time distance , which we call waiting times, and they coincides with inter-event times when . Then, the procedure continues for all the times of the sequence . At this point, as a last step, we reshuffle (permutation sampling) the aged sequenced so we have a new sequence , which is a permutation of the original aged sequence . Figure 1 illustrates how to conduct the aging experiment with a given latency period for a sequence of events. We move a window of size along the time series, locating the left size of the window on the time of occurrence of an event. The window size prevents us from assessing whether or not there are events before the end of the window. We record the time distance between the end of the window and the occurrence time of the first event that we can perceive.
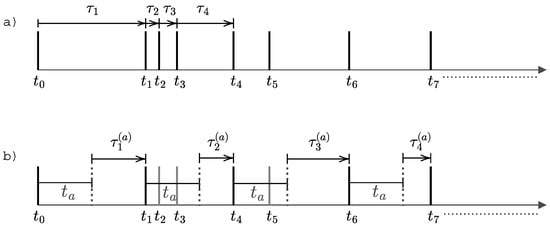
Figure 1.
Illustration of an aging experiment for the latency assessment in order to establish the exchangeable renewal nature of the process. In (a), we show a sequence of events with inter-event interval times . In (b), we age the sequence of events using the observation time , from which the observer is ready to detect the next coming event. So, the observer cannot detect any other events before another time is passed, thus registering new aged time intervals that are the waiting times for that given latency period of . As a consequence, we collect the new (aged) intervals , i.e., the waiting times. Let us note that the observation rate in the process could have an impact to the statistical properties of the inter-arrival intervals.
It is evident that the times we record are portions of the original waiting times. In this case, the aging experiment illustrated by Figure 1, generating only fractions of the original inter-event time interval, has the effect of favoring the long-time periods, and the short-time periods are affected much more from the delayed observation. Consequently we introduce a mathematical formalization of the latency assessment through the aging experiment as follows:
Definition 3
(aging). The operator , where is the aging operator defined by taking a sequence to , with , where and is the least number such that . If no such exists, then aging results in the empty sequence. Similarly, assuming have been found, , where and is the smallest integer such that . If no such integer exists, then
The intuition behind this definition is that one has a sequence of events, say, times at which there is a decay in a sample of radioactive material. Suppose one is using a detector with a “dead time” (time during which no decays can be detected) of duration . Then, given that the true sequence of times between decays is , the detected sequence of times (after subtracting ) is The sequence of detected decays often ends before the true sequence, when the last decay is lost to the final dead time of the detector. Note that there are different possible conventions as to the distance between the event pertaining to the end of one aged inter-event time and the the beginning of the window from which the next is counted. We have chosen one that makes the proof of exchangeability more succinct.
We now present a crucial invariance property of exchangeability: we take an exchangeable sequence, then we apply the aging operator as in Definition 3 so we obtain an aged sequence, which we will prove is still exchangeable:
Theorem 1
(aging preserves exchangeability). Let be the latency period in the aging experiment and be a sequence of positive real numbers. Applying the aging operator, one has For every , if τ is exchangeable, then so is
Proof.
Let be an arbitrary permutation and be the corresponding permutation that preserves the blocks of indices in the aging construction. In particular, if one has for all , where the are as in Definition 3 and By Definition 1, it suffices to prove that Then, by using the definition of the aging operator, one has that
where the middle equality holds since the exchangeability of implies that for every one has which implies the equivalence of the above distributions since the blocks of random variables do not overlap. Since was arbitrary in the above equations, they hold for all . Thus, is exchangeable. □
So, in other words, the property of exchangeability of waiting times between consecutive events is preserved under the latency assessment, and the arrival process in Definition 2 can be re-written as , with and where the epoch of the nth waiting time is . We denote with the aged cumulative distribution function of waiting times of a point process. It represents the probability that, given a latency period , the time until the next event is less than or equal to , or, equivalently, the probability that the next event occurs within the time interval . Consequently, for an aged -renewal process, similarly to Proposition 2, the aged probability measure is the limiting distribution of the aged empirical cumulative function . Despite that, the aged sequence according to the representation theorem is equivalent to conditionally i.i.d. random variables that, however, could be affected in some of their statistical properties in respect to the non-aged case.
Let us now focus on the effect of aging on the empirical distribution function of the aged exchangeable sequences, so as to find a relation between the aged distribution function and the non aged one . The following theorem will provide an implicit analytical derivation of such aged CDF.
Theorem 2.
Let τ be an exchangeable random variable with an absolutely continuous cumulative distribution function F. Let be a double Laplace transform of the CDF in respect to the variable u (conjugate of τ) and the variable (conjugate of ). The aged unconditional CDF of the aged process at a latency period can be written, in a double Laplace space, as the marginal distribution of mixed type:
Proof.
Let be the CDF of an aged process; one can decompose the possible scenarios for the occurrence of events in the aging window into the cases in which no events occur and those in which at least one event occurs, along the lines of [51,52]. In the first case, the probability of observing at most a time t before the first event after is . By integrating over the nuisance variable x, the second case has a probability given by an integral of the renewal function with the complement of the CDF as , where the sum of convolutions takes into account all the possible sequences of intervals of time with no event before a new event eventually occurs, i.e., , where . So, since F is absolutely continuous, its derivative indicates the probability that the last of n events occurs at the given time, and is the rate of events as defined from Equation (6). The final result gives as the distribution for a first observed event at time t. The equation for can be written in terms of the Laplace–Stieltjes transformations, which are used to transform functions that possess both discrete and continuous parts, and in the case of probability distribution functions the double Lapalce transform is defined as whenever that integral exist [53,54]. The integral reduces to the standard Laplace transform in the fully continuous case. Moreover, since , the convolution can be written as ; consequently the joint distribution factorizes in Laplace space, and we can finally write:
□
From the previous theorems we can directly derive many propositions that are of practical use in reliability theory and the survival analysis of renewal processes. Let us write the aged-probability density function in the parametric version as:
Corollary 1.
If the de Finetti measure μ is induced by a parametric construction, we can write the aged distribution functions:
Under absolutely continuous assumption of the CDF, the probability density function of the aged process at a latency period can be written in Laplace space as:
Let us note that, in the degenerate case of i.i.d. sequences, Equation (1) recovers the known expression for ordinary renewal process [23,55], i.e., .
The renewal function for aged processes represents the expected numbers of renewals for a renewal process with underlying lifetime distribution F. In particular, after aging, the following statement holds:
Proposition 4.
The aged mixed renewal function at a latency period can be written as the mean rate of events , which is the expected number of renewals between time .
Proof.
The result is derived directly from the de Finetti’s representation theorem and from the definition of the renewal function ; as in Equation (6), we can write in the parametric version of the de Finetti measure as:
which, in the case of the aged process, can be written in one variable Laplace space:
□
In the case of no aging, i.e., latency , Equation (6) for the renewal function can be written as:
Let us observe that in the degenerate case of the de Finetti measure, , one recovers the usual renewal function with i.i.d. inter-renewal times so that the renewal function is .
At this point, let us describe the effect of latency assessment on a mixed renewal process by comparing the brand-new distribution (where there is no latency) and the aged distribution with a given latency period :
Definition 4.
Let be the sequence of inter-event time intervals of a renewal counting process and let be the sequence of waiting times after the aging experiment of a latency period .
Then, the mixed renewal process is said to be characterized by renewalneutralaging if:
and the mixed renewal process is said to be characterized by renewaleffectualaging if
that is, the unconditional empirical distribution function at given latency period is not the same as the unconditional empirical distribution of inter-event time intervals of the original (brand-new) renewal process.
So, the aged empirical distribution function is still a sufficient statistic for exchangeability of the correspondent aged -renewal point process, but it does not necessarily converge to the same limiting distribution function as for the original non-aged process F. However, if a process is renewal it is renewal for the all ages. If, on the contrary, the process is not renewal but Equation (16) is still verified, then the process is characterized by a non-renewal effectual aging. Let us note that in the case of a null latency, , we recover the ordinary result of .
The concept of aging describes how a system or a process improves or deteriorates in relation to the latency period, and it can be restated in terms of stochastic ordering between waiting-times sequence respect and the brand-new inter-event time intervals (i.e., waiting times where ) in a subjective aging framework [56,57]. Let us observe that the case of no aging (”neutral aging”) in renewal processes implies that the distribution of the waiting times for an occurrence (the time until the next event from the observation time) is not affected by the latency period. Consequently, all stochastic orders based on CDF used in reliability theory will result in being neutral.
For the sake of completeness, we will now write the expression of the hazard function (or failure rate) for aged mixed renewal processes under statistical aging. The hazard function is an important notion often used as the criteria of aging in renewal processes, and it represents a conditional density, given that the event in question has not yet occurred prior to time t. Usually, the failure rate of a system depends on time, with the rate varying over the life cycle of the system. Let us call S the survival function (also known as reliability function) which is simply the complementary of the cumulative density function (i.e., life distribution) . In the particular case of aged exchangeable inter-failure times [56,58], the hazard function for aged mixed renewal processes has the following property:
Proposition 5.
In the absolutely continuous case, the (unconditional) hazard rate function for the aged mixed renewal process, with exchangeable inter-failure intervals under statistical aging, can be written as:
Moreover, the mean residual lifetime can be written as:
where
The function can be interpreted by the Bayes formula to be the conditional density of θ given the observation of the survival .
Proof.
Let us remember that is the conditional cumulative hazard rate, and the conditional (instantaneous) hazard rate is . Consequently, the survival distribution and its probability density can be expressed in terms of those functions as:
and
Finally, considering the definition , the proposition follows. Regarding the mean residual lifetime for aged mixed renewal process, we have:
□
Let us note that both the failure rate function and the mean residual lifetime are conditional concepts, since they are conditioned on survival to time t. Note that also for the aged hazard rate we found that it is a mixture of the conditional hazard rate functions . But, differently from what happens for probability distribution F and renewal function , the prior distribution this time is , which varies with t. This fact has important consequences in the study of the aging properties of exchangeable failure time intervals as a mixture of conditional i.i.d. variables.
4. Analysis of Exchangeable Event Sequences: Simulations and Empirical Results
In this section, we will validate our analysis against synthetic samples of events generated by some archetypal mixed renewal processes. There are different methods to generate exchangeable random variables [59,60]. We will use the procedure where one chooses randomly the parameter of a family of distributions and then select a random sequence from the distribution with the chosen parameter. In fact, exchangeability has been shown [12] to be mathematically equivalent to assuming a hierarchical structure in the models; so, such hierarchical models, also called multi-level or a mixed models, give us the statistical framework to combine multiple sources of information in a single ensemble.
4.1. Exchangeable Mixture Models
In more conventional terminology, if a sequence of observations is judged to be exchangeable, then any finite subset of them is a random sample of some model , and there exists a prior distribution , which describes the initially available information about the parameter that labels the model. As stated in Proposition 1, the generalized representation de Finetti’s theorem can be summarized in the hierarchical form as:
where the symbol ∼ denotes “has the probability distribution of”. We thus have that, in any infinite sequence of exchangeable random variables, the random variables are a mixture of conditional i.i.d. sequences. In terms of random variables and sequences, the way to generate an infinite exchangeable sequence is to first randomly chose a distribution for , and then keep drawing all later , independently from that same distribution. Since the sequences are exchangeable, the random variables are identically distributed according their marginal mixed-type distribution as . The simulation method to generate mixed point processes follows the hierarchical prescription in Equation (23). Algorithm 1 gives the pseudo-code to simulate an exchangeable sequence conditioned upon the value of the parameter vector and its prior distribution . Generating multiple sequences with different values of , we obtain a mixed renewal point process with exchangeable inter-event time intervals.
| Algorithm 1 Generation of a Single Exchangeable Sequence Conditional to a Prior |
|
In the context discussed, it is important that the sequences be virtually infinite. A finite-dimensional exchangeable distribution is not necessarily a mixture of finite-dimensional i.i.d. distributions, though in a sense it must be close to such a mixture, as discussed in the validation of Proposition 1. Note that a mixture of i.i.d. distributions is not generally i.i.d.
4.1.1. Mixture of Exponentials
In this section, we generate a sequence of inter-event times with an exponential distribution, where the rate is derived from a (compound) distribution. In the first instance, the rate follows a uniform (compound) distribution, while in the second case it follows a gamma (compound) distribution. The exponential distribution serves as a mathematical framework for events characterized by a consistent failure rate, making it a staple in reliability analysis. It derives from a Poisson point process where events occur with a constant intensity. Practitioners often rely on this distribution under the assumption that the failure rate remains constant or undergoes negligible change, simplifying the computation of reliability metrics. In superstatistics literature, it is about obtaining Pareto probability distribution (fat-tail) by mixing exponential distributions using uniform and gamma distributions as weights. We will show that despite the fact that conditional processes exhibit neutral aging, the marginal process, under proper weights, does show effectual aging.
- At this point, we will switch our analysis to an exchangeable sequence delineated by inter-event intervals, denoted as . These intervals are represented as random variables drawn from an exponential distribution with a rate parameter , such that , where the rate parameter itself is taken from a uniform distribution, denoted as . The marginal density function of the waiting times is given by the unconditional mixed-type pdf, as from Equation (12):The equation above is valid since the the Laplace transform of conditional aged probability density function can be written as , so that:Essentially, in this example case the renewal process is affected by neutral aging. Moreover, the mixed renewal function can be written in terms of the Laplace transform as from Proposition 4:so the mean rate of events is:so that the average number of renewals increases linearly with time, even in the presence of aging, since it is independent from the latency period .Moreover, regarding the hazard rate, we have:so that the hazard rate is a decreasing function, which is different from its conditional hazard counterpart, which is constant. Finally, the asymptotic mean residual lifetime is . In Figure 2, we compare the analytical results against simulations in the case where . From Figure 2a, it is clear that, as expected, the marginal distribution of both before and after the aging experiment follows the same fat-tail distribution function with an asymptotic behavior of , in agreement with Equation (24). Moreover, in Figure 2b we show the agreement regarding the simulated and the analytical estimate of the hazard rate, which does not depend on latency aging as predicted by Equation (26). Finally, in Figure 2c,d we show the numerical and analytical estimate of the renewal function before and after latency aging, as predicted by Equation (25), and the renewal function maintain the same trend event after aging. In all cases, the numerical simulations and analytical results are in perfect agreement.
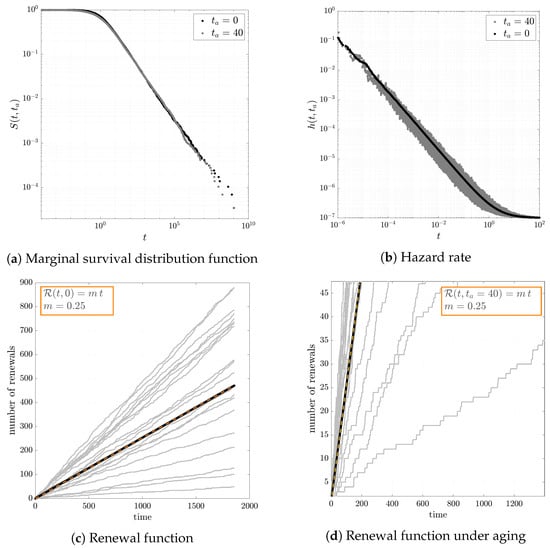 Figure 2. An example of an exchangeable renewal point process, where the inter-event time intervals are exponentially distributed conditional to a rate that is a uniform random variable, i.e., with where . In (a), we see how the marginal survival distribution has a power law tail behavior so that the probability density function is , which does not change after aging so that . In (b), the hazard rate is a decreasing function in t, both before and after aging, with . In (c,d), finally, we plot the number of renewal events of some conditional i.i.d. sequences (in gray); the black bold line represent the renewal function as the average number of events and the orange dashed line the theoretical expected renewal function; the orange dashed line represent the expected trend fitted as in the legend box.
Figure 2. An example of an exchangeable renewal point process, where the inter-event time intervals are exponentially distributed conditional to a rate that is a uniform random variable, i.e., with where . In (a), we see how the marginal survival distribution has a power law tail behavior so that the probability density function is , which does not change after aging so that . In (b), the hazard rate is a decreasing function in t, both before and after aging, with . In (c,d), finally, we plot the number of renewal events of some conditional i.i.d. sequences (in gray); the black bold line represent the renewal function as the average number of events and the orange dashed line the theoretical expected renewal function; the orange dashed line represent the expected trend fitted as in the legend box. - As a more general example, let us assume again , but now the exponential rate follows a gamma distribution, i.e., , where is the shape factor and is the scale factor. So, in this case, the marginal density function of the waiting times is given by the unconditional mixed-type pdf:which is is a Pareto Lomax density function. So, even in this case the process shows a neutral aging since there is no dependence on the latency period . In addition, it is easy to see that the unconditional hazard function is:Consequently, the cumulative hazard rate is . Similarly, one can find that the mean residual lifetime asymptotic behavior is . Finally, the mixed renewal function can be written as:so the average number of renewals is:which increases linearly with time even in presence of aging, as in the previous example.Essentially, all the survival analysis is quite similar to the one in previous example.
4.1.2. Mixture of Generalized Exponentials
We now introduce an example of an exchangeable renewal process that can be expressed as a mixture of gamma-distributed time-intervals so as to obtain an exponential marginal distribution, which manifests effective aging rather than neutral aging. Let us consider a with constant shape parameter and a random scale parameter . The gamma distribution can be frequently found in reliability studies in characterizing phenomena where consecutive events or perturbations contribute to eventual system failure, as well as in modeling renewal processes. The shape parameter may be interpreted as the number of events till failure; meanwhile, the scale parameter represents the rate or frequency of events.
In this case, the generic marginal density function of the waiting times is given by the unconditional mixed-type probability density:
In particular, a gamma-distributed random variable with and uniformly distributed marginally yields an exponential distribution that is affected by aging, and the probability density, as derived in Appendix A.1, has the following asymptotic function:
which clearly shows the presence of effective aging on the mixed renewal process since the aged marginal pdf is . In conclusion, in this example, despite the unconditional pdf being of the exponential type, the renewal process exhibits effective aging. Subsequently, the cumulative hazard function is:
which is asymptotically linear in respect to t for large times.
Finally, the mixed renewal function has the following asymptotic behavior:
as derived in Appendix A.2. Let us note that, in the asymptotic behavior of the brand new renewal function, the average number of renewals increases linearly with a constant of .
We highlight that the numerical simulations as in Figure 3 fully confirm the analytical prediction for renewal aging in the survival analysis: the marginal distribution function from Equation (27), the cumulative hazard rate in Equation (28), and the renewal function Equation (29) have the behavior without and with aging, as predicted by the analytical calculations, showing a shift in trend when the latency aging is applied. Also in this case, the numerical simulations align perfectly with the analytical outcomes.
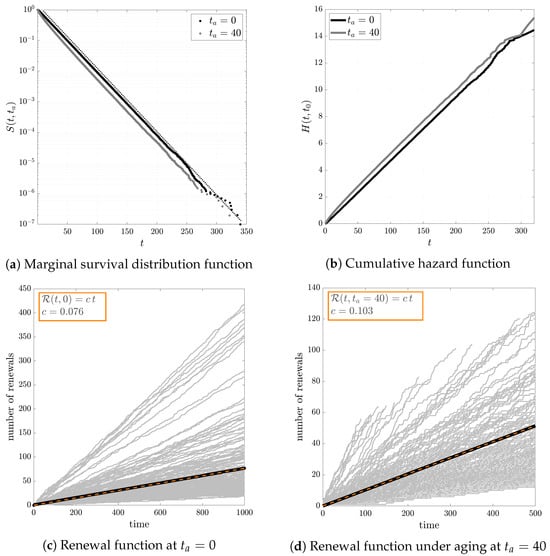
Figure 3.
An example of an exchangeable renewal process where the inter-event time intervals are gamma distributed conditional to a rate that is a uniform random variable, i.e., , with where and . In (a), we see how the marginal survival distribution is exponential with estimation , as expected from Equation (27). The marginal distribution undergoes effective aging since , as represented by the dotted line. In (b), the cumulative hazard function is linear over t, both before and after aging , as predicted by Equation (28), where the shift in the aged rate is also explained. In (c,d), finally, we graphically
represent the count of renewal events for certain conditionally independent and identically distributed
sequences (depicted in gray). The bold black line symbolizes the renewal function, which is the
average number of events, while the dashed orange line illustrates the theoretical renewal function,
the orange dashed line represent the expected trend fitted as in the legend box.
4.1.3. Mixture of Heavy-Tail Distributions
As a final example, we discuss mixed renewal processes with Mittag–Leffler (ML) inter-arrival time distribution conditional to a prior distribution of the ML scale parameter. As a consequence, we obtain a fat-tail marginal distribution of inter-event time intervals, which exhibits effective aging. The Mittag–Leffler waiting time distribution has been studied by many authors and has considerable applications [61,62] since it can characterize both heavy and fat tails, meaning that there is a higher probability of observing extreme values compared to some other distributions, like the exponential. In mathematics, the Mittag–Leffler functions play an important role in fractional calculus and stochastic models [63,64,65]. Let us assume that , where the Mittag–Leffler probability distribution is defined in terms of its survival function for and as:
showing two types of heavy-tail behaviors, i.e., the stretched exponential (subexponential-type) and the inverse power-law (Pareto-type) distributions. The ML distribution can be easily written in the Laplace space as so that the pdf is . Consequently, in double Laplace space the conditional Mittag–Leffler probability density function under aging with latency can be written as:
where we have indicated the original (brand new) conditional pdf at as:
Consequently, the unconditional pdf is given in general by:
where .
In particular, let us make constant, and the scale parameter a uniform random variable with . Consequently, the aged marginal probability density, as derived in Appendix A.3, is the following asymptotic expression:
where if and .
Subsequently, the cumulative hazard rate is:
which for times much larger than the latency period reads as .
Finally, as derived in Appendix A.4, the mixed renewal function reads:
where is a function of . Thus, for the renewal function is super-linear for small t and sub-linear for large t. In Figure 4, we show and discuss the results of the numerical simulations against the analytical predictions.
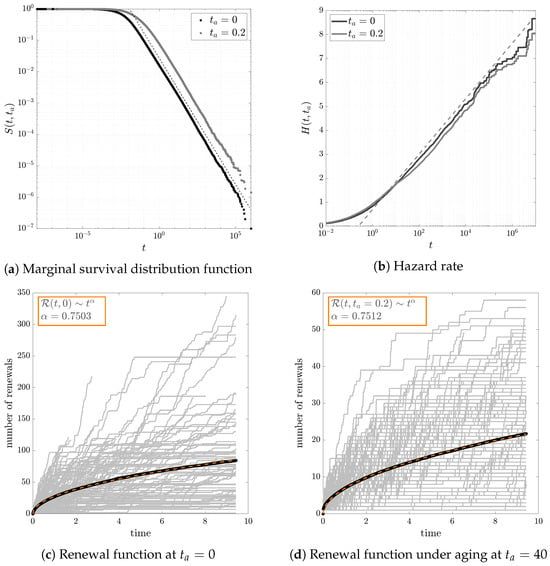
Figure 4.
An example of an exchangeable renewal process where the inter-event time intervals are generated conditional to a Mittag–Leffler distribution, where is a uniform random variable with . In (a), we see that the marginal survival distribution has a power law tail with coefficient , as expected from Equation (30). The marginal distribution undergoes effective aging since . In (b), the cumulative hazard function is linear over t, both before and after aging , as predicted by Equation (31), where the shift in the aged rate is also explained. In (c,d), finally, through numerical simulations we plot the renewal function and see
that it changes after aging. Both cases show, in gray, some of the trajectories for single sequences
of events, in bold black we show the estimated renewal function as the average number of events,
and the orange dashed line shows the expected renewal function as predicted in Equation (32), with
α = 0.75.
4.2. Case Study: High-Frequency Exchange Rates
Here, we analyze the times between successive events of the exchange-rate transactions. In particular, financial time series exhibit a pronounced non-uniform temporal pattern, particularly concerning aspects like volatility and activity, defined as the number of transactions per unit of time [66,67,68]. When examining the return variance within a given time frame, one can discern periods of relatively constant and predictable behavior interspersed with intervals characterized by significant variations in price (or exchange rate). Similarly, fluctuations exist in the frequency of transactions, with some days witnessing sparse trading and others marked by a considerably higher volume of trades. This substantial variability in both volatility and activity is commonly denoted as volatility clustering or intermittency in volatility and activity, which have a proportional relationship, as discussed in the literature on financial volatility modeling [69,70,71,72]. As an example of real-world financial sequences, we will make use of currency pairs with tick-by-tick historical rates retrieved from [73]. In particular, we use top-of-book tick-by-tick market data, with fractional pip spreads in millisecond detail, so they represent ultra high-frequency data for exchange-rate markets. We have used exchange rates for nine different currency pairs in Table 1 whose transactions occurred in the month of November 2023 at the level of tick-by-tick data for a total of approximately ticks with time resolutions of milliseconds.

Table 1.
Exchange rate currency pair names.
Moreover, each tick represents a trade (transaction), and we call it a marker of the time series. Time intervals between two consecutive markers are not independent because of the presence of peaks (or clusters) in the mean activity followed by periods of relative calm. In order to detect meaningful insights, we define as events the peaks of activity (i.e., the event of volatility clustering) that are separated by periods with a low number of transactions. We use a peak detection algorithm in order to define the events of intense activity out of the tick markers (threshold has been used as minimum height difference between a peak and its neighbors, so as to detect abrupt changes). In Figure 5a, we see a schematic representation where the intensity, for example, x3 of the third peak, corresponds to the total number of transactions attributed to this peak. In Figure 5b, the arrivals of events are plotted for all the nine exchange-rate time series. Finally, in Figure 5c we show their conditional distributions.
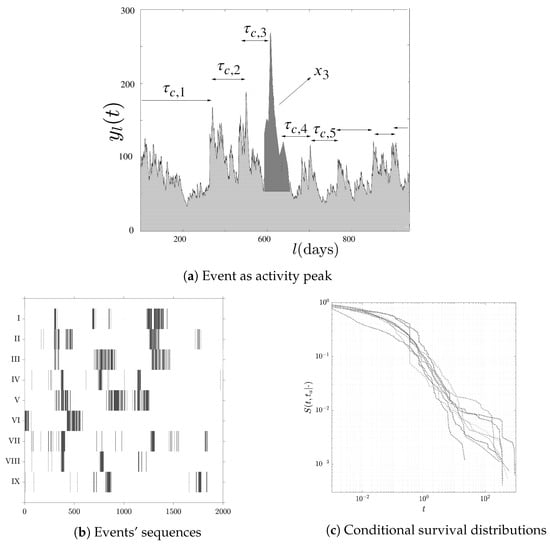
Figure 5.
Survival analysis of EURUSD exchange rates. In (a), there is a schematic example of the definition of inter-event times between two consecutive peaks, seen as activity bursts of large volumes of trades, ; figure inspired by [68]. In (b), we plot the arrival sequences of the times between successive peaks for all the nine exchange-rate pairs. Finally, in (c), we show the conditional survival distributions of each of the nine event sequences.
Despite discussions regarding financial modeling is out of the scope of this study, the analysis presented herein can offer valuable perspectives for empirical interpretations in the examination of financial market dynamics of price fluctuations in high-frequency trading [35,74,75]. The survival analysis in Figure 6 illustrates that the empirical process responsible for generating exchange-rate events is compatible with a Mittag–Leffler function as a prior distribution. As possible implications, we observe, in Figure 6a, that the time intervals between peaks, denoted as , follow a probability density function that asymptotically behaves as , with . Furthermore, we identify the occurrence of unconditional negative aging, given that , implying that the aged variable is greater than the original in stochastic ordering. The event-time distribution is thus characterized as “new worse than observed”, signifying that a latency in the event detection process creates an illusion of the system performing better than its actual behavior. In other words, the system exhibits a reduced probability of events occurring immediately after activation (latency period). Similarly, in Figure 6b we compare the brand new and the aged cumulative hazard rate functions. We can note that, since the aged cumulative hazard rate function is stochastically smaller than the brand new one, the aged process has a lower cumulative risk of volatility events. Finally, the analysis of the renewal function in Figure 6c indicates that the expected number of arrivals (i.e., renewal function) is nonlinear, a behavior maintained even after latency aging, as shown and commented in Figure 6d.
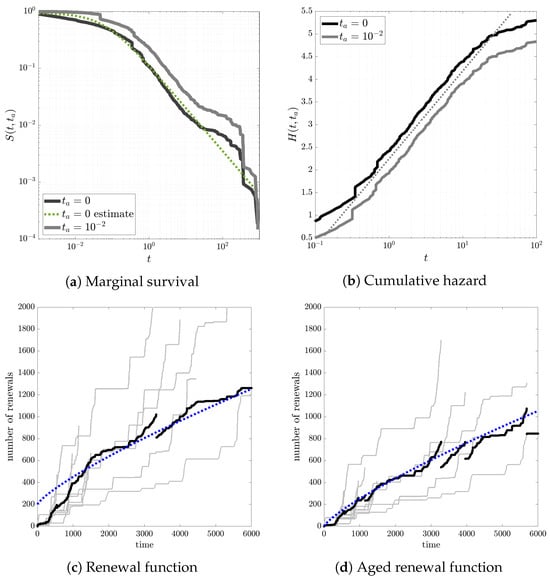
Figure 6.
Survival analysis of EURUSD exchange rates. In (a), we plot the complementary cumulative distribution function and the estimate of the power law coefficient, showing an asymptotic Pareto distribution with exponent . In (b), we plot the cumulative hazard behavior for both. The blue dotted line indicate the expected renewal function in cases of no latency and of a latency of . The plot shows that there is only a shift between the two functions, and in the central part of the time axis there is a linear trend so that with . In (c,d), we plot the number of renewal events for all the nine exchange-rate sequences (in light gray) and the average number of renewals up to time t (solid black line). Finally, we superimpose (in dotted blue) the expected renewal function under exchangeability assumption for Mittag–Leffler priors so that the asymptotic trend is , as in ML case Equation (32).
5. Concluding Remarks
In our research within the domain of reliability theory, we have introduced the idea of statistical aging as latency, specifically in the framework of mixed renewal processes where the intervals between events are considered exchangeable. This approach provides a more accurate representation of the interdependence among failure events that occur at unpredictable intervals, while preserving manageability. Simultaneously, it acknowledges some level of dependence among events. Furthermore, it is important to note that the event rate of a system can display fluctuations due to a variety of aging and latency factors. These can include environmental conditions, operational stresses, or delays in detection. The findings of this paper consist of a set of new propositions that asses how latency aging affects the survival analysis of mixed renewal processes. Survival and aging analysis involves analyzing data regarding time until an event of interest occurs and is particularly relevant in finance due to the importance of modeling risk and uncertainty [76,77]. From that perspective, we have provided evidence that exchange rates can be affected by a “new worse than observed” event distribution, which implies that detection latency can make the system appear more efficient than it truly is, with a decreased likelihood of immediate post-activation events. Concurrently, an aged process exhibits a diminished cumulative risk of volatility events.
We have focused our study on an analysis of events, in general. In practical applications, as in the case of Section 4.2, these events are generated by latent processes that describe the nature of the system under investigation. For example, the phenomenon of aging in physics has been known for a long time as a property of spin glasses and polymers. The manifestation of aging behavior often signifies that the system has not achieved equilibrium and continues to evolve over time. A prevalent observation in aging phenomena concerns two-time correlation functions that depend on two distinct moments, and , rather than solely on their time difference, . The rate of decay relative to diminishes as increases. Aging is believed to stem from systems being out of equilibrium, with their return to equilibrium taking longer than the observation period [78,79,80,81].
In a subjective probability perspective of complex systems, the notion of mixed renewal processes is related to the concept of superstatistics, which indicates a superposition of several statistics on different scales [82,83]. A superstatistical interpretation of renewal processes has been applied in various fields, including financial markets, traffic delays, air pollution dynamics, and hydrodynamic turbulence [84,85,86,87]. In future work, we would like to establish a connection between the concept of superstatisics and the phenomenon of persistence within the realm of non-equilibrium statistical mechanics. Persistence refers to the long-time decay of the survival probability of stochastic processes [88,89], and mixed renewal processes could be crucial for a deeper understanding of persistence phenomena. Furthermore, we plan to explore the effect of aging on the persistence at different timescales in diffusive processes, such as those used in the context of stock markets [90,91].
A related future research direction will be the development of an event-sequence technique that may detect the presence of memory between the events through the effect of renewal aging. This problem is of great interest in reliability assessment research [92,93] under the assumption that events are exchangeable rather than i.i.d., which is a common hypothesis that may not always be valid, especially in cases where repairs fail to fully restore the system. Renewal aging can be exploited as a crucial property to determine whether a pattern of events is compatible with a renewal process in the classical sense of being i.i.d. rather than in the exchangeability sense. In terms of policy implications, financial institutions and investors can make informed decisions by considering the changing dynamics of market behavior influenced by fixed latency periods and their associated aging patterns.
Author Contributions
Conceptualization, F.V. and D.L.; methodology, F.V. and D.L.; software, F.V.; validation, F.V. and D.L.; formal analysis, F.V. and D.L.; investigation, F.V. and D.L.; resources, F.V. and D.L.; data curation, F.V.; writing—original draft preparation, F.V. and D.L.; writing—review and editing, F.V. and D.L.; visualization, F.V.; supervision, F.V. and D.L.; project administration, F.V. and D.L. All authors have read and agreed to the published version of the manuscript.
Funding
D.L. has received financial support through NIH sub-award GMO:240910 PO: 0000003121.
Data Availability Statement
The data presented in this study are available in truefx website at https://www.truefx.com/truefx-historical-downloads (accessed on 20 March 2024).
Acknowledgments
F.V. wants to acknowledge to be a member of GNAMPA-INdAM.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| CDF | Cumulative Distribution Function |
| eCDF | empirical Cumulative Distribution Function |
| probability density function | |
| i.i.d. | independent identically distributed |
| EXP | Exponential |
| GA | Gamma |
| ML | Mittag–Leffler |
Appendix A. Mixture Models Derivations
Appendix A.1. Derivation of Equation (27)
We can write the double Laplace transform of the aged conditional pdf as:
where
is the original, brand new, conditional pdf without any latency effect on the mixed renewal process. Then, the single space Laplace transform of the conditional pdf is:
Consequently, moving back to the time variable, the asymptotic expression of the aged unconditional probability density is:
Appendix A.2. Derivation of Equation (29)
The mixed renewal function can be written in terms of the Laplace transform as, from Proposition 4:
which, for large times, can be directly expressed as:
Appendix A.3. Derivation of Equation (30)
At the slowest order, ; so, one can write the asymptotic behavior of the unconditional aged pdf in the time variable in the regime of large times () as:
where if and .
Appendix A.4. Derivation of Equation (32)
Let us now focus on the mixed renewal function . It can be written in terms of the laplace transform as from Proposition 4 as:
where:
So, the renewal function can be written for large times as:
where is the hypergeometric function . Consequently, the renewal function, in temporal coordinates, is:
and, for , the asymptotic aged renewal function is .
References
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 1968; Volume 1. [Google Scholar]
- Feller, W. An Introduction to Probability Theory and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 1991; Volume 2. [Google Scholar]
- Cox, D.R. Renewal Theory; Methuen: London, UK, 1967; Volume 1. [Google Scholar]
- Barlow, R.E.; Proschan, F. Statistical Theory of Reliability and Life Testing: Probability Models; Holt, Rinehart and Winston: New York, NY, USA, 1975; Volume 1. [Google Scholar]
- Lio, Y.; Chen, D.G.; Ng, H.T.; Tsai, T.R. Bayesian Inference and Computation in Reliability and Survival Analysis; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- Pergamenshchikov, S.; Pchelintsev, E. Renewal Theory and Its Applications. Hal-Ope Sci. 2020. Available online: https://hal.science/hal-02485643 (accessed on 20 March 2024).
- Cha, J.H.; Finkelstein, M. Point Processes for Reliability Analysis; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Schulz, J.H.; Barkai, E.; Metzler, R. Aging renewal theory and application to random walks. Phys. Rev. X 2014, 4, 011028. [Google Scholar] [CrossRef]
- De Finetti, B. Funzione caratteristica di un fenomeno aleatorio. In Proceedings of the Atti del Congresso Internazionale dei Matematici, Bologna, Italy, 3–10 September 1928; pp. 179–190. [Google Scholar]
- De Finetti, B. La prévision: Ses lois logiques, ses sources subjectives. Ann. L’institut Henri Poincaré 1937, 7, 1–68. [Google Scholar]
- Aldous, D.J. Exchangeability and related topics. In École d’Été de Probabilités de Saint-Flour XIII—1983; Springer: Berlin/Heidelberg, Germany, 1985; pp. 1–198. [Google Scholar]
- Bernardo, J.M.; Smith, A.F. Bayesian Theory; John Wiley & Sons: Berlin/Heidelberg, Germany, 2009; Volume 405. [Google Scholar]
- Mitov, K. Renewal Processes; Springer: Cham, Switzerland, 2014. [Google Scholar]
- Akimoto, T. Statistics of the number of renewals, occupation times, and correlation in ordinary, equilibrium, and aging alternating renewal processes. Phys. Rev. E 2023, 108, 054113. [Google Scholar] [CrossRef]
- Coen, A.; Gutiérrez, L.; Mena, R.H. Modelling failures times with dependent renewal type models via exchangeability. Statistics 2019, 53, 1112–1130. [Google Scholar] [CrossRef]
- Huang, W.J. On the characterization of point processes with the exchangeable and Markov properties. Sankhyā Indian J. Stat. Ser. A 1990, 52, 16–27. [Google Scholar]
- Lyberopoulos, D.P.; Macheras, N.D. Some characterizations of mixed renewal processes. Math. Slovaca 2022, 72, 197–216. [Google Scholar] [CrossRef]
- Monthus, C.; Bouchaud, J.P. Models of traps and glass phenomenology. J. Phys. A Math. Gen. 1996, 29, 3847. [Google Scholar] [CrossRef]
- Parisi, G. Short-time aging in binary glasses. J. Phys. A Math. Gen. 1997, 30, L765. [Google Scholar] [CrossRef]
- Baity-Jesi, M.; Calore, E.; Cruz, A.; Fernandez, L.; Gil-Narvion, J.; Gonzalez-Adalid Pemartin, I.; Gordillo-Guerrero, A.; Iñiguez, D.; Maiorano, A.; Marinari, E.; et al. Memory and rejuvenation effects in spin glasses are governed by more than one length scale. Nat. Phys. 2023, 19, 978–985. [Google Scholar] [CrossRef]
- Böhmer, T.; Gabriel, J.P.; Costigliola, L.; Kociok, J.N.; Hecksher, T.; Dyre, J.C.; Blochowicz, T. Time reversibility during the ageing of materials. Nat. Phys. 2024, 20, 637–645. [Google Scholar] [CrossRef]
- Laloux, L.; Le Doussal, P. Aging and diffusion in low dimensional environments. Phys. Rev. E 1998, 57, 6296. [Google Scholar] [CrossRef]
- Godreche, C.; Luck, J. Statistics of the occupation time of renewal processes. J. Stat. Phys. 2001, 104, 489–524. [Google Scholar] [CrossRef]
- Barkai, E. Aging in subdiffusion generated by a deterministic dynamical system. Phys. Rev. Lett. 2003, 90, 104101. [Google Scholar] [CrossRef]
- Akimoto, T.; Barkai, E. Aging generates regular motions in weakly chaotic systems. Phys. Rev. E 2013, 87, 032915. [Google Scholar] [CrossRef]
- Allegrini, P.; Aquino, G.; Grigolini, P.; Palatella, L.; Rosa, A. Generalized master equation via aging continuous-time random walks. Phys. Rev. E 2003, 68, 056123. [Google Scholar] [CrossRef]
- Cox, D.R.; Isham, V. Point Processes; CRC Press: Boca Raton, FL, USA, 1980; Volume 12. [Google Scholar]
- Metzler, R.; Jeon, J.H.; Cherstvy, A.G.; Barkai, E. Anomalous diffusion models and their properties: Non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys. Chem. Chem. Phys. 2014, 16, 24128–24164. [Google Scholar] [CrossRef]
- Bianco, S.; Grigolini, P.; Paradisi, P. Fluorescence intermittency in blinking quantum dots: Renewal or slow modulation? J. Chem. Phys. 2005, 123, 174704. [Google Scholar] [CrossRef] [PubMed]
- Brokmann, X.; Hermier, J.P.; Messin, G.; Desbiolles, P.; Bouchaud, J.P.; Dahan, M. Statistical aging and nonergodicity in the fluorescence of single nanocrystals. Phys. Rev. Lett. 2003, 90, 120601. [Google Scholar] [CrossRef] [PubMed]
- Gupta, A.K.; Zeng, W.B.; Wu, Y. Probability and Statistical Models: Foundations for Problems in Reliability and Financial Mathematics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Hens, T.; Schenk-Hoppé, K.R. Handbook of Financial Markets: Dynamics and Evolution; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Barbiero, A.; Hitaj, A. Discrete half-logistic distributions with applications in reliability and risk analysis. Ann. Oper. Res. 2024, 1–31. [Google Scholar] [CrossRef]
- Bianco, S.; Grigolini, P. Aging in financial market. Chaos Solitons Fractals 2007, 34, 41–50. [Google Scholar] [CrossRef]
- Fama, E.F. The behavior of stock-market prices. J. Bus. 1965, 38, 34–105. [Google Scholar] [CrossRef]
- Cherstvy, A.G.; Vinod, D.; Aghion, E.; Chechkin, A.V.; Metzler, R. Time averaging, ageing and delay analysis of financial time series. New J. Phys. 2017, 19, 063045. [Google Scholar] [CrossRef]
- Niepert, M.; Domingos, P. Exchangeable variable models. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 271–279. [Google Scholar]
- Poirier, D.J. 40 Exchangeability, Representation Theorems, and Subjectivity. In The Oxford Handbook of Bayesian Econometrics; Oxford University Press: Oxford, UK, 2011. [Google Scholar] [CrossRef]
- Hewitt, E.; Savage, L.J. Symmetric measures on Cartesian products. Trans. Am. Math. Soc. 1955, 80, 470–501. [Google Scholar] [CrossRef]
- Diaconis, P.; Freedman, D. Finite exchangeable sequences. Ann. Probab. 1980, 8, 745–764. [Google Scholar] [CrossRef]
- Kerns, G.J.; Székely, G.J. Definetti’s theorem for abstract finite exchangeable sequences. J. Theor. Probab. 2006, 19, 589–608. [Google Scholar] [CrossRef]
- Kallenberg, O. Probabilistic Symmetries and Invariance Principles; Springer: New York, NY, USA, 2005. [Google Scholar]
- O’Neill, B. Exchangeability, correlation, and Bayes’ effect. Int. Stat. Rev. 2009, 77, 241–250. [Google Scholar] [CrossRef]
- Barber, R.F.; Candes, E.J.; Ramdas, A.; Tibshirani, R.J. De Finetti’s Theorem and Related Results for Infinite Weighted Exchangeable Sequences. arXiv 2023, arXiv:2304.03927. [Google Scholar]
- Zabell, S.L. Predicting the unpredictable. Synthese 1992, 90, 205–232. [Google Scholar] [CrossRef]
- Bernardo, J.M. Bayesian statistics. Probab. Stat. R. Viertl Ed 1994, 2, 345–407. [Google Scholar]
- Bernardo, J.M. The concept of exchangeability and its applications. Far East J. Math. Sci. 1996, 4, 111–122. [Google Scholar]
- Allegrini, P.; Barbi, F.; Grigolini, P.; Paradisi, P. Aging and renewal events in sporadically modulated systems. Chaos Solitons Fractals 2007, 34, 11–18. [Google Scholar] [CrossRef]
- Paradisi, P.; Grigolini, P.; Bianco, S.; Akin, O.C. Renewal aging in non-homogeneous poisson processes with periodic rate modulation. Int. J. Bifurc. Chaos 2008, 18, 2681–2691. [Google Scholar] [CrossRef]
- Turalska, M.; Lukovic, M.; West, B.J.; Grigolini, P. Complexity and synchronization. Phys. Rev. E 2009, 80, 021110. [Google Scholar] [CrossRef]
- Aquino, G.; Bologna, M.; Grigolini, P.; West, B.J. Aging and rejuvenation with fractional derivatives. Phys. Rev. E 2004, 70, 036105. [Google Scholar] [CrossRef]
- Allegrini, P.; Aquino, G.; Grigolini, P.; Palatella, L.; Rosa, A.; West, B.J. Correlation function and generalized master equation of arbitrary age. Phys. Rev. E 2005, 71, 066109. [Google Scholar] [CrossRef]
- Bernstein, D.L. The double Laplace integral. Duke Math. J. 1941, 8, 460–496. [Google Scholar] [CrossRef]
- Debnath, L.; Bhatta, D. Integral Transforms and Their Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2016; Chapter 4. [Google Scholar]
- Aquino, G.; Palatella, L.; Grigolini, P. Absorption and emission in the non-poisson case: The theoretical challenge posed by renewal aging. Braz. J. Phys. 2005, 35, 418–424. [Google Scholar] [CrossRef]
- Spizzichino, F. Subjective Probability Models for Lifetimes; CRC Press: Boca Raton, FL, USA, 2001. [Google Scholar]
- Lai, C.D.; Xie, M. Stochastic Ageing and Dependence for Reliability; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Nappo, G.; Spizzichino, F. Relations between ageing and dependence for exchangeable lifetimes with an extension for the IFRA/DFRA property. Depend. Model. 2020, 8, 1–33. [Google Scholar] [CrossRef]
- McCall, J.J. An Introduction to Exchangeability and Its Economic Applications; Hoover Institution, Stanford University: Stanford, CA, USA, 1988. [Google Scholar]
- Faragó, A. Decomposition of Random Sequences into Mixtures of Simpler Ones and Its Application in Network Analysis. Algorithms 2021, 14, 336. [Google Scholar] [CrossRef]
- Mainardi, F.; Gorenflo, R.; Vivoli, A. Renewal Processes of Mittag-Leffler and Wright Type. Fract. Calc. Appl. Anal. 2005, 8, 7–38. [Google Scholar]
- Mainardi, F.; Raberto, M.; Gorenflo, R.; Scalas, E. Fractional calculus and continuous-time finance II: The waiting-time distribution. Phys. A Stat. Mech. Its Appl. 2000, 287, 468–481. [Google Scholar] [CrossRef]
- Pramukkul, P.; Svenkeson, A.; Grigolini, P.; Bologna, M.; West, B. Complexity and the fractional calculus. Adv. Math. Phys. 2013, 2013, 498789. [Google Scholar] [CrossRef]
- Apelblat, A. Differentiation of the Mittag-Leffler functions with respect to parameters in the Laplace transform approach. Mathematics 2020, 8, 657. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Scalas, E.; Gorenflo, R.; Mainardi, F. Fractional calculus and continuous-time finance. Phys. A Stat. Mech. Its Appl. 2000, 284, 376–384. [Google Scholar] [CrossRef]
- Gençay, R.; Dacorogna, M.; Muller, U.A.; Pictet, O.; Olsen, R. An Introduction to High-Frequency Finance; Elsevier: Amsterdam, The Netherlands, 2001. [Google Scholar]
- Palatella, L.; Perelló, J.; Montero, M.; Masoliver, J. Activity autocorrelation in financial markets: A comparative study between several models. Eur. Phys. J. Condens. Matter Complex Syst. 2004, 38, 671–677. [Google Scholar] [CrossRef]
- Taylor, S.J. Modeling stochastic volatility: A review and comparative study. Math. Financ. 1994, 4, 183–204. [Google Scholar] [CrossRef]
- Pederzoli, C. Stochastic volatility and GARCH: A comparison based on UK stock data. Eur. J. Financ. 2006, 12, 41–59. [Google Scholar] [CrossRef]
- Fouque, J.P.; Papanicolaou, G.; Sircar, K.R. Derivatives in Financial Markets with Stochastic Volatility; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Cont, R. Statistical modeling of high-frequency financial data. IEEE Signal Process. Mag. 2011, 28, 16–25. [Google Scholar] [CrossRef]
- Corp., I.D. TrueFX Market Exchange Rate Data, 2014. EURUSD Exchange Rates Data. Available online: https://www.truefx.com/truefx-historical-downloads/#93-106-november (accessed on 20 March 2024).
- Scalas 7, E.; Gorenflo, R.; Luckock, H.; Mainardi, F.; Mantelli, M.; Raberto, M. Anomalous waiting times in high-frequency financial data. Quant. Financ. 2004, 4, 695–702. [Google Scholar] [CrossRef]
- Aldrich, E.M.; Heckenbach, I.; Laughlin, G. The random walk of high frequency trading. arXiv 2014, arXiv:1408.3650. [Google Scholar]
- Gao, F.; He, X. Survival Analysis: Theory and Application in Finance. In Handbook of Financial Econometrics, Mathematics, Statistics, and Machine Learning; World Scientific: Singapore, 2021; pp. 4087–4118. [Google Scholar]
- Gepp, A.; Kumar, K. The role of survival analysis in financial distress prediction. Int. Res. J. Financ. Econ. 2008, 16, 13–34. [Google Scholar]
- Calabrese, P.; Gambassi, A. Ageing properties of critical systems. J. Phys. A Math. Gen. 2005, 38, R133. [Google Scholar] [CrossRef]
- Henkel, M.; Pleimling, M. Non-Equilibrium Phase Transitions: Volume 2: Ageing and Dynamical Scaling Far from Equilibrium; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Hase, M.O.; Tomé, T.; de Oliveira, M.J. Aging and fluctuation-dissipation ratio in a nonequilibrium q-state lattice model. Phys. Rev. E 2010, 82, 011133. [Google Scholar] [CrossRef] [PubMed]
- Geisel, T.; Nierwetberg, J.; Zacherl, A. Accelerated diffusion in Josephson junctions and related chaotic systems. Phys. Rev. Lett. 1985, 54, 616. [Google Scholar] [CrossRef] [PubMed]
- Beck, C. Superstatistics: Theory and applications. Contin. Mech. Thermodyn. 2004, 16, 293–304. [Google Scholar] [CrossRef]
- Allegrini, P.; Barbi, F.; Grigolini, P.; Paradisi, P. Renewal, modulation, and superstatistics in times series. Phys. Rev. E 2006, 73, 046136. [Google Scholar] [CrossRef] [PubMed]
- Uchiyama, Y.; Kadoya, T. Superstatistics with cut-off tails for financial time series. Phys. A Stat. Mech. Its Appl. 2019, 526, 120930. [Google Scholar] [CrossRef]
- Schäfer, B.; Heppell, C.M.; Rhys, H.; Beck, C. Fluctuations of water quality time series in rivers follow superstatistics. iScience 2021, 24, 102881. [Google Scholar] [CrossRef] [PubMed]
- Katz, Y.A.; Tian, L. Superstatistical fluctuations in time series of leverage returns. Phys. A Stat. Mech. Its Appl. 2014, 405, 326–331. [Google Scholar] [CrossRef]
- Beck, C. Recent developments in superstatistics. Braz. J. Phys. 2009, 39, 357–363. [Google Scholar] [CrossRef]
- Bray, A.J.; Majumdar, S.N.; Schehr, G. Persistence and first-passage properties in nonequilibrium systems. Adv. Phys. 2013, 62, 225–361. [Google Scholar] [CrossRef]
- Bénichou, O. Anomalous persistence exponents for normal yet aging diffusion. Phys. Rev. E 2020, 102, 062115. [Google Scholar]
- Constantin, M.; Sarma, S.D. Volatility, persistence, and survival in financial markets. Phys. Rev. E 2005, 72, 051106. [Google Scholar] [CrossRef]
- Salcedo-Sanz, S.; Casillas-Pérez, D.; Del Ser, J.; Casanova-Mateo, C.; Cuadra, L.; Piles, M.; Camps-Valls, G. Persistence in complex systems. Phys. Rep. 2022, 957, 1–73. [Google Scholar] [CrossRef]
- Tobias, P.A.; Trindade, D. Applied Reliability; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Wang, P.; Coit, D.W. Repairable systems reliability trend tests and evaluation. In Proceedings of the Annual Reliability and Maintainability Symposium, Citeseer, Alexandria, VA, USA, 24–27 January 2005; pp. 416–421. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).