Abstract
The paper’s primary objective is to examine the dynamic behavior of an integer and noninteger predator–prey system with a Holling type IV functional response in the Caputo sense. Our focus is on understanding how harvesting influences the stability, equilibria, bifurcations, and limit cycles within this system. We employ qualitative and quantitative analysis methods rooted in bifurcation theory, dynamical theory, and numerical simulation. We also delve into studying the boundedness of solutions and investigating the stability and existence of equilibrium points within the system. Leveraging Sotomayor’s theorem, we establish the presence of both the saddle-node and transcritical bifurcations. The analysis of the Hopf bifurcation is carried out using the normal form theorem. The model under consideration is extended to the fractional reaction–diffusion model which captures non-local and long-range effects more accurately than integer-order derivatives. This makes fractional reaction–diffusion systems suitable for modeling phenomena with anomalous diffusion or memory effects, improving the fidelity of simulations in turn. An adaptable numerical technique for solving this class of differential equations is also suggested. Through simulation results, we observe that one of the Lyapunov exponents has a negative value, indicating the potential for the emergence of a stable-limit cycle via bifurcation as well as chaotic and complex spatiotemporal distributions. We supplement our analytical investigations with numerical simulations to provide a comprehensive understanding of the system’s behavior. It was discovered that both the prey and predator populations will continue to coexist and be permanent, regardless of the choice of fractional parameter.
Keywords:
fractional reaction–diffusion; Holling type IV response; Hopf bifurcation; local stability analysis; numerical methods and experiments MSC:
26A33; 35K57; 65M06
1. Introduction
Population dynamics is a prominent field within biomathematics, encompassing the study of how populations change over time. It starts with analyzing single-species dynamics and progresses to more complex models that reflect interactions between different species sharing the same habitat. These models delve into various aspects of ecology, including predator–prey relationships, symbiosis, commensalism, and competition. Numerous publications exist in this field, often exploring multidimensional systems involving prey and predators or scenarios with multiple predators and a prey species. Predator–prey models, in particular, have consistently been a focal point in biomathematics due to their significance in understanding ecological dynamics. For scholars interested in modeling biological and ecological challenges, this area of research offers valuable insights into ongoing work and developments in the field.
Sustainable development is a prominent subject of interest in various fields, and there is a rising concern regarding excessive and unsustainable exploitation. Fisheries, forestry, wildlife, and other biological resources often experience collapses and overexploitation. It is vital to comprehend the dynamics of populations concerning harvesting practices, as this understanding is essential for the effective care of renewable resources (Deacon [1], Idels and Wang [2]).
The three forms of functional responses to prey density proposed by Holling [3] concern the variation in prey caught by predator species per unit time as prey population density becomes unstable or fluctuates. In population dynamical systems, the predator–prey model of the Holling type has always been significant. In the late eighties, Freedman and Wolkowicz [4] first established a broader case, which serves as several research primary models (Huang and Xiao [5], Srinivasu, et al. [6]).
where stands for the predator functional response, which expresses how well a predator can catch prey. The rate at which prey is converted is .
It is clear that in the positive quadrant the Holling type I, II, and III functional responses are monotone. When nutrient concentrations become elevated, they can potentially exert an inhibitory influence on the growth rate. This is indicated by various tests and observations (Huang and Xiao [5], Liu and Huang [7]). In 1968, Andrew [8] proposed a function to demonstrate this circumstance:
which is peculiar to the Monod–Haldane and Holling (type IV) functional responses. The relationship between prey and predator species, when the prey displays collective defense is described by the predator–prey dynamics with Holling type IV (H-IV) functional response. The defense capability will also improve or the capacity to hide will also be improved as the prey population is increasing, which can also hinder the growth of predators in turn.
Over the years, there has been a great number of scientific interests in fractional differentiation and applications. Fractional calculus is a robust and versatile mathematical tool used to address real-world mathematical challenges. It finds widespread application in mathematics, physics, and medical science, often involving noninteger order derivatives in diverse contexts. This field is experiencing steady growth in research, marked by a methodical and sensible approach (Agrawal [9], Liu and Huang [7]). Currently, fractional differential equations represent a particularly dynamic and promising area of study, receiving acclaim from researchers and authors who aim to model real-world issues in applied sciences and engineering.
The concept of fractional differentiation is widely applied in engineering and science, recognized for its versatility. Solving complex problems in these fields, often characterized by significant non-linearity, proves challenging due to their intricate nature. As a result, researchers frequently resort to numerical solutions to address these challenges. Within the literature, various fractional operators with diverse kernels have been introduced. Among the commonly employed fractional operators are the Caputo, Riesz, Riemann–Liouville, Caputo–Fabrizio (CF), and Atangana–Baleanu types (see Jain [10]). These operators play a vital role in addressing complex problems where analytical solutions are impractical.
These various types of operators are valuable for addressing highly intricate processes that cannot be adequately described by a single operator. Additionally, it is feasible to transform more complex fractional-order differential systems into simpler ones by utilizing the characteristics of the Caputo derivative. The versatility of fractional calculus has prompted researchers in diverse fields to develop mathematical models. Particularly notable are applications that closely align with real-world scenarios such as epidemic diseases and various data-driven problems across engineering and scientific domains. Our investigation into biological models revealed that memory effects are integral to biological processes. An essential component of evaluating biological models involves the utilization of fractional-order derivatives. For this reason, we are employing the concept of the Caputo fractional derivative to model the dynamic complexity involving prey and predator species with the Holling type IV functional response.
2. Main Model and Its Mathematical Analysis
This study investigates a predator–prey system characterized by collective defense mechanisms and consistent harvesting practices in both species. Initially, the research focuses on analyzing a predator–prey system with the H-IV functional response, which is described as follows:
where and stand for the prey densities and predator densities, respectively. The growth-like structure of the prey is modeled by adopting a logistic equation without the presence of a predator and harvesting, of which the parameter and stand for the intrinsic growth rate and carrying capacity of the prey population. The predator death rate is given by , while denotes the maximum predation rate, with half-saturation constant . The parameter is given as the denominator of the functional response by setting to guarantee that is non-negative (Huang and Xiao [5]). Hence, the dynamic model (3) is studied for in the first quadrant of the plane.
When the prey–predator is harvested, the dynamics of a predator–prey system with an H-IV functional response are difficult. Some studies only took into account fisheries that were allowed to harvest one species (see for example Chakraborty and Das [11], Zuo and Jiang [12]). Finding a realistic model of interspecies interaction is challenging. This paper considers a situation where all species are subjected to harvesting so that we can present the model above as:
It should be noted that when r = 1 + γ1, ρ = 1, in Equation (4) our model corresponds to system (3.5) in Upadhyay et al. [13], to which we refer our readers for detailed analysis and results in one and two dimensions.
When the integer-order time derivatives in (4) are modeled with the fractional-order operator, the resulting equations become:
where , and and are the prey and predator harvesting efforts, respectively. In actual fact, it is desirable to take these terms as and , where and represent the capturing rates for the prey and predator, respectively (Srinivasu, et al. [6]).
2.1. Boundness
We show that the system (4) is limited in in this section. The system with the starting conditions of and for the local existence, positivity, and boundedness of the solutions is first taken into consideration. As the functions of are smooth and the parameters involved make up the right-hand sides of equations in (4), the local existence and uniqueness properties hold true within the positive quadrant (Bandyopadhyay, et al. [14]). We now establish the boundedness of the dynamic system solutions.
Theorem 1.
The solutions of a dynamic system (4) with the set of initial data are uniformly bounded.
Proof.
Define:
Then, we differentiate w.r.t. , we use (4) and (5) to obtain:
Therefore,
where .
By adopting the theory of differential inequality, one obtains:
As it is not difficult to see that the limit on the right side of the inequality above is so that the function is bounded. Hence, we require to show that all the solutions of (4) are bounded in the interior of . This completes the proof. □
2.2. Existence and Stability of Equilibria
We will examine the local stability of system (4) for equilibrium points in the closed first quadrant in this section. The point at which the prey isocline intersects, where , and the predator isocline, where , define the system’s equilibria. Obviously, the dynamic model has a trivial steady state, an axial steadiness, and at least two interior (nontrivial) steady points, denoted here by , and , where:
It is evident that the steady state, denoted by , exists constantly, and the axial steady point, designated by , is possible if the condition below is satisfied. That is,
Next, we pay attention to the study of the interior state and ; the form can be defined in the following equation:
If it exists, we have the form:
and:
We begin by listing the criteria necessary for the interior steady states in the following result to be conceivably present. For the sake of simplicity, we define , and as follows:
where .
Theorem 2.
(i) If then:
- (a)
- in the case of the system of predation (4) has two nontrivial points;
- (b)
- in the case the dynamic model has a unique interior state;
- (c)
- for condition the predator–prey model has no interior steady state;
(ii) If the system consists of no interior state;
(iii) Specifically, if the model has a unique interior point provided , where the special interior state is defined by .
From a biological perspective, we know that both species and coexist and probably enjoy permanence when the catching efforts can be found in either the first or second quadrants; the predator population could be on the verge of extinction (that is, washout stage) when the harvesting efforts are found in the third and fourth quadrants. We see that both species would become extinct if the prey were over-harvested (Barman and Upadhyay [15], Guo et al. [16], Hasibuan et al. [17]). One can secure the survival of the prey by managing the amount of harvesting, but when the degree of harvesting is in the third quadrant, one cannot guarantee the life of the predator.
Next, we study system (4) for the local asymptotic stability of trivial point that corresponds to the washout state of both species, axial equilibrium point where either of the species is absent, and two biologically meaningful interior equilibrium points and in their existence interval, respectively.
The Jacobian or community matrix for the dynamic model (4) is given in the form:
Theorem 3.
The extinction state is globally asymptotically stable (GAS) if , and is a saddle point if .
Proof.
The community matrix about point is defined by:
It is not difficult to see that at point , the Jacobian has two eigenvalues denoted by and . Hence, if , is a saddle point and if , is asymptotically stable, therefore, we say it is globally asymptotically stable. Let us define the Lyapunov function , to have:
Obviously, if . Therefore, we mean to imply that all solutions approach the point .
From the analysis given above, the point is stable whenever , and this is equivalent to . Biologically, it is an indication that the effort level surpasses the biotechnical productivity, that is the ratio of the biotic potential to the catchability coefficient of the species (see Lv, et al. [18]). It is obvious that the prey species increases with while the predator species decreases with , which is naturally consistent as decreases the number of predators to enhance the existence of the prey population; capturing the prey can lead to the lack of enough resources (in terms of food) for the predator population, which can result in a decrease in the rate at which the predators survive. Assume , and represent the harvesting carrying capacity by . The harvesting process, as indicated in model (4) and , functions as an additional source of mortality for both the prey and predator. This results in a reduction in the prey population’s intrinsic growth rate and carrying capacity. Consequently, this decrease in prey resources leads to an increase in the mortality rate among the predator population (see Lv et al. [18] for details). In reality, when conditions do not change, the carrying capacity of the species swings above and below the average or stays the same. If , it is an indication that the system is not utilized, and the point is always unstable. Biologically, over-exploitation of could cause the extinction of prey and predator species. Therefore, it is reasonable to consider the predator–prey dynamics with harvesting for condition in the present work. □
Theorem 4.
The axial (interior) equilibrium point is a stable point if , and is a saddle point if , where:
Proof.
At the point , the community matrix is given by:
The two eigenvalues are given by:
With the help of the analysis, we say that is stable if and is a saddle point if .
In a biological context, we are aware that predator species would become extinct if their prey were over-exploited. Even if the level of prey harvesting is lower than the level , as long as the level of prey harvesting surpasses the rate of intrinsic growth , the biomass of the predator would eventually decrease to zero since there would no longer be enough prey to support the predator species.
Finally, in what follows we examine the stability of interior equilibrium states. □
Theorem 5.
is locally (asymptotically) stable (LAS) if , and is unstable if , and is a saddle state whenever it exists.
Proof.
The community matrix at is given by:
where:
The trace and the determinant of the Jacobian matrix at interior points are defined by:
and the characteristic polynomial equation is given by:
and:
It should be noted that is always non-positive in its existence range. In other words, we obtain to be a saddle point whenever it exists. Meanwhile, the determinant is always positive, and if , all the roots of Equation (19) above are negative, hence point is LAS, and if , all the roots of the characteristic equation are positive, then we conclude that is an unstable equilibrium point. Here and .
It can be been that , that is,
which is a contradiction to Theorem 2. Therefore, if , then . □
Theorem 6.
Let the point of the dynamical system (4) in Int be locally asymptotically stable. Then, it is globally asymptotically stable if both conditions and are satisfied.
Proof.
To demonstrate that the interior point is globally asymptotically stable, we require to show that it has no periodic orbit in Int. To start, we require to use the transformation , so that the dynamic system (4) can be written as:
Let . One can see that if the maximum-value of . It is obvious that for and
Then, for every , and by following the criteria of Bendixson–Dulac as applied in Jiang and Wang [19], it was shown that there was no close orbit. In addition, we consider conditions for the stability and existence of the interior point , to show that is globally asymptotically stable if its parameters satisfy the conditions:
where:
The interior equilibrium with more prey has no possibility of stability at all, whereas the equilibrium with fewer prey can be stable and, under some circumstances, even globally asymptotically stable. Furthermore, the fact that the world is stable means that exploitation will not entirely devastate the system. As long as the predator is not driven to extinction by overharvesting its prey, the system can recover. The system will asymptotically approach equilibrium after the capturing is terminated. □
2.3. Local Bifurcation Analysis
We will talk about the local bifurcations of the dynamic model (4) in this section. We only take into account the bifurcations in co-dimension one, such as the transcritical, saddle-node, and Hopf bifurcations. Here, we check the transversality criterion for saddle-node and transcritical bifurcation by using the theorem proposed by Sotomayor as reported in Perko [20].
2.3.1. Transcritical Bifurcation
It should be mentioned that the transcritical bifurcation can cause a non-hyperbolic steady state of a dynamic model; here consideration is given to the point . It should be noted that when:
then the point may coincide with .
Theorem 7.
If , the model (4) undergoes a transcritical bifurcation when the system parameters hold for:
Proof.
The community matrix at point is given as:
Since all three requirements for Sotomayor’s theorem are met, transcritical bifurcation may take place at the axial equilibrium point , and a tiny change in the bifurcation parameter will alter this equilibrium point’s stability. □
2.3.2. Saddle-Node Bifurcation
So far, the existence interval of the two interior points and has been discussed. We know that saddle-node bifurcation may arise by varying the control parameter, and when the equilibrium points move toward one another, collide, and destroy one another. It can be verified that if the points and are distinct, or coincide when , and wipe out if . for this reason, a saddle-node bifurcation may occur, that is:
In this case, we give the components of a nontrivial state as:
In a manner similar to that of the transcritical bifurcation analysis, we have:
Theorem 8.
The dynamic model (4) undergoes a saddle-node bifurcation when the conditions and as given in Theorem 2 are satisfied. According to the bifurcation parameter , the saddle-node bifurcation threshold is given by:
Proof.
The Jacobian corresponding to the community matrix at this equilibrium state is given as:
In addition, we have:
Thus, we obtain:
□
2.3.3. Hopf Bifurcation
The equilibrium point may experience Hopf bifurcation under specific parameter constraints, but the equilibrium point is always a saddle point, in accordance with the analysis that came before. If is the bifurcation parameter, then and are the results of the Hopf bifurcation definition.
From:
and:
we conclude that the bifurcation threshold is a non-negative root of trace with given bifurcation parameter which satisfies . Then, we obtain the following result.
Theorem 9.
Let the system parameters satisfy the conditions for the existence of point as defined in Theorem 2. Then, the point changes its equilibrium state through the Hopf bifurcation threshold such that
Proof.
Clearly, at , we let stands for , and the point has eigenvalues . We adopt normal form theorem to analyze Hopf bifurcation. At first, one requires to examine if the transversality criteria for the Hopf bifurcation is achieved (Lv, et al. [18]). We have that:
where:
By fixing at its critical value , one computes the first Lyapunov coefficient (Kuznetsov [21]). The interior point at has the coordinates . At the equilibrium point, we use a change of variable to translate the coordinates:
and expand in the Taylor series, to obtain:
where ‘ represent the elements of the community matrix evaluated at points and . Then, we obtain:
We determine the coefficients of and by:
and:
and:
where and denote the power series in with terms satisfying .
Denote the Lyapunov first number by [20] which has been used to obtain the stability of the limit cycle at the neighborhood of Hopf bifurcation defined by:
The first Lyapunov number for model (4) is given by:
where:
If , the equilibrium point will lose its stability via a supercritical Hopf bifurcation for . □
3. Fractional Predator–Prey Model of Reaction–Diffusion Type and Its Method of Approximation
In multi-component models of predator–prey dynamics, diffusion plays a vital role in understanding how species interact and disperse spatially. Numerous research studies have delved into the influence of diffusion on species interactions within specific habitats. This phenomenon can be likened to the dispersion of individuals within a population over both time and space, particularly from densely populated regions to less populated ones. The process of diffusion elucidates the movement of individuals across various compartments, influenced by factors like interpersonal contact or geographical shifts. In our model, the incorporation of diffusion is pivotal as it enables us to capture the fundamental dynamics underlying the spatial spread of predator and prey species.
Recent progress has extended to the examination of diffusion systems, particularly focusing on fractional-order equations (Alikhanov and Huang [22], Liao, Tang and Zhou [23], Liao, Li and Zhang [24], Owolabi and Jain [25], Owolabi, et al. [26]). Nonetheless, in our literature review, we have incorporated diffusion into our model fractional system (5). In the following section, we will explore how reaction–diffusion influences our dynamic predator–prey model:
with the homogeneous (zero-flux) boundary conditions:
where is the domain/habitat expected to be open and bounded in with boundary . The initial condition:
is also assumed to be positive and uniformly bounded on ; and are either the concentrations of two chemical substances or densities of prey and predator population at time and position . are the diffusion coefficients of the species. The reaction kinetics is given as:
In what follows, we shall discuss the derivation of the numerical scheme for the approximation of the reaction–diffusion problem.
Numerical Approximation Method
To derive an approximation scheme, we are required to consider the compact form of the time-fractional reaction–diffusion system (37) as:
subject to the boundary and initial conditions:
where:
is known as a fractional-order derivative defined in the sense of the Caputo operator, and
denotes diffusion coefficient, and function accounts for the local kinetic reaction. In most cases, the numerical solution of the time-fractional reaction–diffusion Equation (40) cannot be obtained analytically due to its nonlinear and nonlocal properties; hence, it is desirable to solve such problems numerically. Different numerical methods have been proposed for approximating fractional differential equations; the most commonly applied among the existing methods are the finite difference (FD) methods (based on L1 and L2 approximation schemes) (Alikhanov [27], Alikhanov and Huang [22], Wang and Ren [28]), finite element methods, exponential time-differencing schemes such as Garrappa and Popolizio [29], Owolabi [30], and the Fourier spectral techniques of Bueno-Orovio, Kay and Burrage [31], Li and Xu [32], Owolabi [30], among many others which are well-classified in Hilfer [33], Kilbas, Srivastava and Trujillo [34], Oldham and Spanier [35], Podlubny [36], and references therein. For instance, the most commonly applied L1 scheme for the approximation of the Caputo operator as defined in (42) is given as:
where the term represents the truncation error, and . Details of stability and convergence properties for the L1 scheme above can be found in Oldham and Spanier [35] and Podlubny [36]. A three-point L1 approximation for the Caputo fractional derivative of order 3-α is obtained per Dimitrov [37].
Here, we let be a uniform grid. We validate the following qualities for the Caputo fractional operator of order of at point for , that is,
Next, we apply the three points quadratic interpolation of with , and on interval for , to obtain:
so also its derivative:
and:
where , , , ,
In an attempt to approximate function , we use in (44) on for , so that:
where:
It is obvious from Equations (44) and (45) above that the difference approximation for the Caputo operator at points is:
which implies that:
where:
Different cases emerge here for . For instance:
When ,
When ,
And when ,
Theorem 10.
For any and
Proof.
Let ,
where:
and:
In what follows, we estimate the errors and
For we have:
For we have:
Thus,
To derive a numerical approximation method for the right-hand side of (40), we consider here the Fourier spectral method adopted from Trefethen [38], Trefethen and Embere [39].
For a given function that is periodic on the spatial grid with at , we define the discrete Fourier transform (DFT) as:
and the inverse discrete Fourier transform (iDFT):
where denotes the Fourier wave numbers. With the above information, the derivative of can be approximated with the following steps:
- given , compute with the aid of definition (55);
- define to be ;
- compute (that is, the derivative of function ) on the grid by applying (56).
Applying this technique to the reaction–diffusion Equation (40) and leaving the time-stepping in the Fourier space results in a system of ordinary differential equations of the form:
At this stage, the linear term in (40) is diagonal, which is one of the merits of using the Fourier spectral method over other conventional methods such as finite difference or finite element methods.
The suitability and applicability of the numerical techniques derived above are justified by considering the Caputo time diffusion equation:
With , the exact solution is given as Agrawal (2003) [9]:
where is the known one-parameter Mittag-Leffler function expressed in terms of the series:
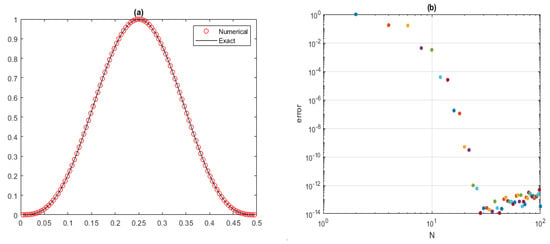
The comparison between the numerical and exact solutions, as well as the convergence of the Fourier spectral method, is shown in Figure 1 for with step size and . □

Figure 1.
Computational results displaying the (a) numerical and exact solutions, and (b) convergence of the Fourier spectral method.
4. Numerical Experiment and Results
To comprehend the dynamic characteristics of the fractional model (5) and its fractional reaction–diffusion case (37), we present the simulation results of numerical experiments using the MATLAB R2021a software running on an Alienware super-fast computer with Intel Core-i7. Showing the experimental results that depict the true nature of the dynamics under consideration would help to foster an understanding the theoretical studies in this work. The parameter values utilized for the numerical simulation are taken as:
We allow and as well as the fractional parameter to vary in the experiments. The existence of prey and predator species for a period of time , is shown in Figure 2 with and . It should be noted that both species oscillate in phase. We perturbed the pair of parameters in the simulation experiment to obtain the fact that the interaction between the prey and predator species under certain parameter perturbation could result to some chaotic behavior. This assertion is evident in Figure 3 with the parameter choice and for final time ; see plots . It is obvious that regardless of time and the method of attack adopted by the predators on the prey population, the ecosystem will be maintained. Both the prey and predators will continue to coexist and be permanent. The Lyapunov exponents results showing spatiotemporal oscillations are given in panel .
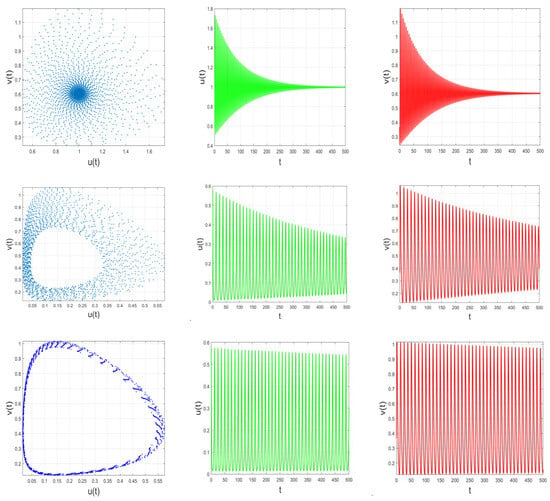
Figure 2.
Time-series and portraits evolution showing the relationship between the dynamic behavior of system (5) and the level of harvesting efforts applied to the prey population with and at time . Rows 1–3 correspond to Ʌ = (0.85, 0.90, 1.00), respectively.
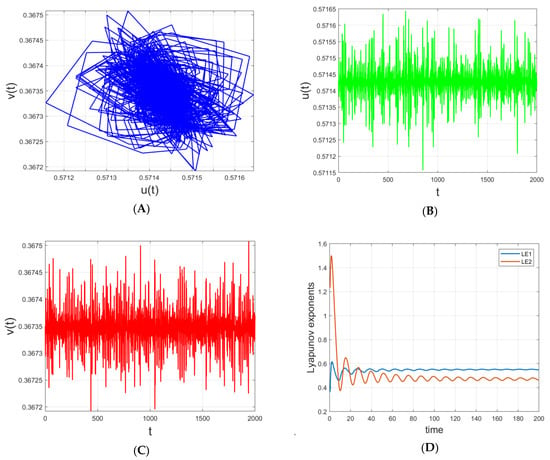
Figure 3.
Plots (A–C) depict complex or chaotic-like interaction between the prey and predator populations at final simulation time . Plot (D) gives the Lyapunov exponents of both species at and .
It is a known fact that reaction–diffusion models are versatile mathematical tools that provide insights into a wide range of natural and engineered systems. They contribute to our understanding of complex spatial phenomena and are indispensable in fields ranging from biology and ecology to chemistry and materials science. Fractional reaction–diffusion systems are an extension of traditional reaction–diffusion models, where the derivatives of fractional order are used in place of integer-order derivatives. These models have gained significance in recent years due to their unique properties and applications. In other words, fractional reaction–diffusion systems offer improved modeling accuracy for a wide range of complex phenomena, making them essential in disciplines where traditional reaction–diffusion models fall short. They have practical applications in understanding and optimizing processes in biology, environmental science, materials science, and engineering.
Due to some known facts about the importance of fractional reaction–diffusion models, we extend our simulation experiment to a one-dimensional fractional reaction–diffusion system (37), where the dynamic interaction between the prey and predator populations will be explored. To achieve this, we utilize the homogeneous Neumann (or zero-flux) boundary conditions which best describe the situation whereby the entire species is confined within a given habitat without any external force, subject to the choice of initial condition carefully chosen to mimic some spatiotemporal evolution. For the simulation experiment results as reported in Figure 4, Figure 5 and Figure 6, we set the diffusion coefficients , , the time-step , and we denote a small perturbation of the equilibrium point , while we allow parameters and fractional-order to be varied as mentioned in the figure captions. Just as observed in the case of model (5), we confirm the spatiotemporal and complex evolution of the species regardless the choice of fractional parameter and the pair of key parameters . In general, this research highlights the significance of utilizing harvesting effort as a control parameter, as it has the potential to alter the system’s dynamics, offering valuable insights for biological management strategies.
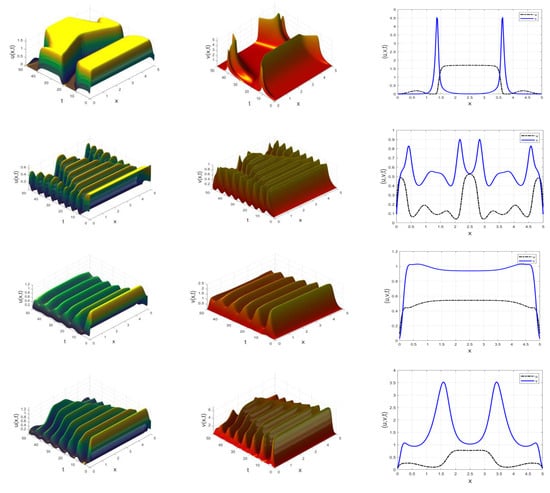

Figure 4.
Dynamic distribution of fractional reaction–diffusion system (37) showing chaotic-like and complex spatiotemporal behavior of the prey and predator populations for different instances of at with . Rows 1 to 5 correspond to , respectively.
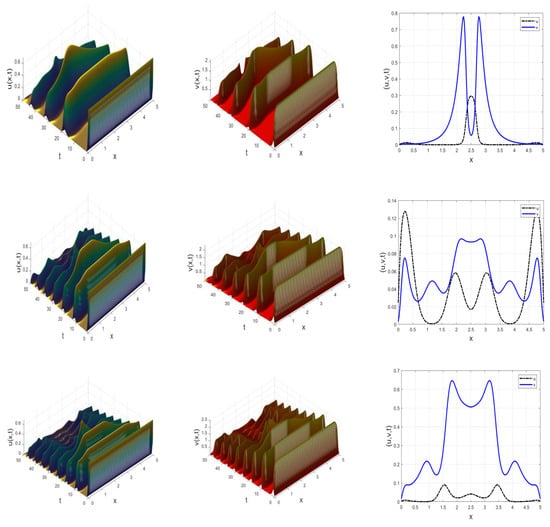
Figure 5.
Snapshot of dynamic system (37) showing chaotic-like and complex spatiotemporal behavior of the prey and predator populations for different instances of and at . Rows 1 to 3 correspond to , respectively.
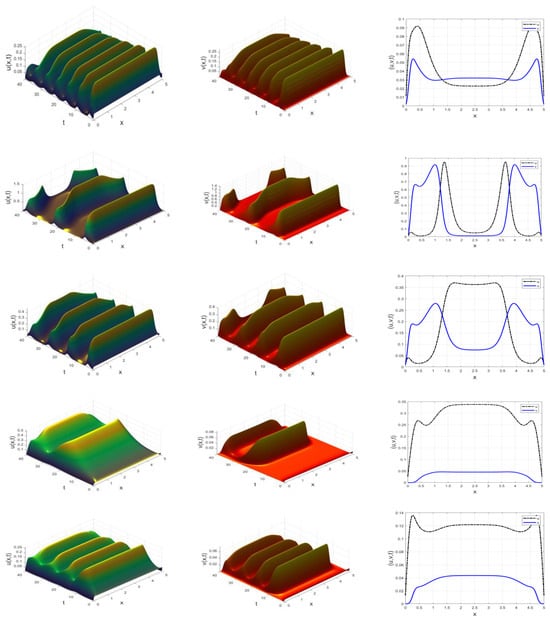
Figure 6.
The dynamic evolution of prey and predator populations in (37) with for various at . For rows 1 to 5, , respectively.
5. Conclusions
This paper explores a scenario involving a predator–prey system featuring a Holling type IV functional response, where both species are subject to capture. The study establishes criteria for ensuring the system remains consistently confined and enduring. Additionally, it delves into assessing the stability of the model’s equilibria. Furthermore, the paper addresses the factors influencing the codimension of a specific bifurcation within the model. It should be mentioned that fractional reaction–diffusion systems offer improved modeling accuracy for a wide range of complex phenomena, making them essential in disciplines where traditional reaction–diffusion models fall short. They have practical applications in understanding and optimizing processes in biology, environmental science, materials science, and engineering. Hence, we give an extension to the integer order derivative to capture non-local and long-range effects more accurately than integer-order derivatives. This makes fractional reaction–diffusion systems suitable for modeling phenomena with anomalous diffusion or memory effects, improving the fidelity of simulations. We developed a viable and robust numerical method to investigate the behavior of the fractional reaction–diffusion model consisting of the prey and predator species numerically. It was observed that both the prey and predator populations will continue to undergo a kind of complex spatiotemporal oscillation in phase, regardless of the choice of key parameters. In future research, the parameters γ1 and γ2 can be studied as a function of time.
Author Contributions
Conceptualization, K.M.O.; Methodology, E.P.; Formal analysis, S.J.; Writing—original draft, K.M.O. and S.J.; Writing—review & editing, S.J.; Supervision, K.M.O. and E.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors have no competing interests.
References
- Deacon, R. Fishery management by harvester cooperatives. Rev. Environ. Econ. Policy 2012, 6, 258–277. [Google Scholar] [CrossRef]
- Idels, L.; Wang, M. Harvesting fisheries management strategies with modified effort function. Int. J. Model. Identif. Control 2008, 3, 83–87. [Google Scholar] [CrossRef]
- Holling, C. The functional response of predators to prey density and its role in mimicry and population regulation. Mem. Entomol. Soc. Can. 1965, 97, 5–60. [Google Scholar] [CrossRef]
- Freedman, H.; Wolkowicz, G. Predator-prey systems with group defence: The paradox of enrichment revisited. Bull. Math. Biol. 1968, 48, 493–508. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; Xiao, D. Analyses of bifurcations and stability in a predator-prey system with Holling type-IV functional response. Acta Math. Appl. Sin. 2004, 20, 167–178. [Google Scholar] [CrossRef]
- Srinivasu, P.; Ismail, S.; Naidu, A.R. Global dynamics and controllability of a harvested prey-predator system. J. Biol. Syst. 2001, 9, 67–69. [Google Scholar] [CrossRef]
- Liu, X.; Huang, Q. The dynamics of a harvested predator-prey system with Holling type IV functional response. BioSystems 2018, 169–170, 26–39. [Google Scholar] [CrossRef] [PubMed]
- Andrews, J. A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates. Biotechnol. Bioeng. 1968, 10, 707–723. [Google Scholar] [CrossRef]
- Agrawal, O.P. Response of a diffusion-wave system subjected to deterministic and stochastic fields. J. Appl. Math. Mech. 2003, 83, 265–274. [Google Scholar] [CrossRef]
- Jain, S. Numerical analysis for the fractional diffusion and fractional Buckmaster equation by the two-step Laplace Adam-Bashforth method. Eur. Phys. J. Plus 2018, 133, 19. [Google Scholar] [CrossRef]
- Chakraborty, K.; Das, S. Biological conservation of a prey-predator system incorporating constant prey refuge through provision of alternative food to predators: A theoretical study. Acta Biotheor. 2014, 62, 183–205. [Google Scholar] [CrossRef] [PubMed]
- Zuo, W.; Jiang, D. Stationary distribution and periodic solution for stochastic predator-prey systems with nonlinear predator harvesting. Commun. Nonlinear Sci. Numer. Simul. 2016, 36, 65–80. [Google Scholar] [CrossRef]
- Upadhyaya, R.K.; Kumaria, N.; Raib, V. Wave of Chaos and Pattern Formation in Spatial Predator-Prey Systems with Holling Type IV Predator Response. Math. Model. Nat. Phenom. 2008, 3, 71–95. [Google Scholar] [CrossRef]
- Bandyopadhyay, M.; Bhattacharya, R.; Chakrabarti, C. A nonlinear two-species oscillatory system: Bifurcation and stability analysis. Int. J. Math. Math. Sci. 2003, 2003, 617217. [Google Scholar] [CrossRef]
- Barman, D.; Upadhyay, R.K. Modelling predator-prey interactions: A trade-off between seasonality and wind speed. Mathematics 2023, 11, 4863. [Google Scholar] [CrossRef]
- Guo, H.; Han, J.; Zhang, G. Hopf Bifurcation and Control for the Bioeconomic Predator-Prey Model with Square Root Functional Response and Nonlinear Prey Harvesting. Mathematics 2023, 11, 4958. [Google Scholar] [CrossRef]
- Hasibuan, A.; Supriatna, A.K.; Rusyaman, E.; Biswas, M.H.A. Predator–Prey Model Considering Implicit Marine Reserved Area and Linear Function of Critical Biomass Level. Mathematics 2023, 11, 4015. [Google Scholar] [CrossRef]
- Lv, Y.; Zhang, Z.; Yuan, R.; Pei, Y. Effect of harvesting and prey refuge in a prey-predator system. J. Biol. Syst. 2014, 22, 133–150. [Google Scholar] [CrossRef]
- Jiang, Q.; Wang, J. Qualitative analysis of a harvested predator-prey system with Holling-type III functional response. Adv. Differ. Equ. 2013, 2013, 249. [Google Scholar] [CrossRef][Green Version]
- Perko, L. Differential Equations and Dynamical Systems; Springer: New York, NY, USA, 1996. [Google Scholar]
- Kuznetsov, Y.A. Elements of Applied Bifurcation Theory; Springer: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Alikhanov, A.A.; Huang, C. A high-order L2 type difference scheme for the time-fractional diffusion equation. Appl. Math. Comput. 2021, 411, 126545. [Google Scholar] [CrossRef]
- Liao, H.-L.; Tang, T.; Zhou, T. A second-order and nonuniform time-stepping maximum-principle preserving scheme for time-fractional Allen-Cahn equations. J. Comput. Phys. 2020, 414, 109473. [Google Scholar] [CrossRef]
- Liao, H.-L.; Li, D.; Zhang, J. Sharp error estimate of nonuniform L1 formula for time-fractional reaction-subdiffusion equations. SIAM J. Numer. Anal. 2018, 56, 1112–1133. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Jain, S. Spatial patterns through diffusion-driven instability in modified predator-prey models with chaotic behaviors. Chaos Solitons Fractals 2023, 174, 113839. [Google Scholar] [CrossRef]
- Owolabi, K.M.; Agarwal, R.P.; Pindza, E.; Bernstein, S.; Osman, M.S. Complex Turing patterns in chaotic dynamics of autocatalytic reactions with the Caputo fractional derivative. Neural Comput. Appl. 2023, 35, 11309–11335. [Google Scholar] [CrossRef]
- Alikhanov, A.A. A new difference scheme for the time fractional diffusion equation. J. Comput. Phys. 2015, 280, 424–438. [Google Scholar] [CrossRef]
- Wang, Y.-M.; Ren, L. A high-order l2-compact difference method for Caputo-type time-fractional sub-diffusion equations with variable coefficients. Appl. Math. Comput. 2019, 342, 71–93. [Google Scholar] [CrossRef]
- Garrappa, R.; Popolizio, M. Generalized exponential time differencing methods for fractional order problems. Comput. Math. Appl. 2011, 62, 876–890. [Google Scholar] [CrossRef]
- Owolabi, K.M. Robust and adaptive techniques for numerical simulation of nonlinear partial differential equations of fractional order. Commun. Nonlinear Sci. Numer. Simul. 2017, 44, 304–317. [Google Scholar] [CrossRef]
- Bueno-Orovio, A.; Kay, D.; Burrage, K. Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numer. Math. 2014, 54, 937–954. [Google Scholar] [CrossRef]
- Li, X.; Xu, C. A space-time spectral method for the time fractional diffusion equation. SIAM J. Numer. Anal. 2009, 47, 2108–2131. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equation; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Oldham, K.B.; Spanier, J. The Fractional Calculus; Academic Press: New York, NY, USA, 1974. [Google Scholar]
- Podlubny. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Dimitrov, Y. Three-point approximation for Caputo fractional derivative. Commun. Appl. Math. Comput. 2017, 31, 413–442. Available online: https://www.researchgate.net/publication/282606336 (accessed on 1 November 2023).
- Trefethen, L.N. Spectral Methods in MATLAB; SIAM: Philadelphia, PA, USA, 2000. [Google Scholar]
- Trefethen, L.N.; Embere, M. Spectral and Pseudospectra: The Behavior of Nonnormal Matrices and Operators; Princeton University Press: Princeton, NJ, USA, 2005. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).