Abstract
As the usage of electric vehicles (EVs) expands, various energy management technologies, including battery energy storage systems, are being developed to efficiently charge EVs using various energy sources. In recent years, many blockchain-based energy trading schemes have been proposed for secure energy trading. However, existing schemes cannot fully solve privacy issues and security problems during energy trading. In this paper, we propose a reliable and privacy-preserving vehicular energy trading scheme utilizing decentralized identifier technology. In the proposed scheme, identity information and trading result information are not revealed publicly; this is due to the use of decentralized identifiers and verifiable credential technologies. Additionally, only parties who have successfully conducted energy trading can manage complete transaction information. We also demonstrate our method’s security and ensure privacy preservation by performing informal and formal security analyses. Furthermore, we analyze the performance and security features of the proposed scheme and related works and show that the proposed scheme has competitive performance.
Keywords:
vehicular energy trading; decentralized identifier; blockchain; verifiable credential; authentication MSC:
68M12
1. Introduction
As the urgency to transition to eco-friendly transportation systems grows in the near future to significantly reduce fossil fuel consumption and CO2 emissions, electric vehicles (EVs) have become critical as a primary mode of transportation by offering emission-free operation. However, the widespread distribution of EVs is creating problems for EV users, who are limited in time and space to charge their EVs. To address these issues and ensure smooth travel for EV users, it is necessary to expand the EV charging infrastructure, which may involve converting existing fossil fuel gas stations into electric-only charging stations and/or constructing new charging stations [1,2].
Specifically, the progress of smart grid (SG), energy management, and internet of vehicle (IoV) technologies enables EVs to charge everywhere from various energy resources, such as a grid stations, homes, and other vehicles [3,4,5,6,7]. However, despite the expansion of the EV market with the technologies mentioned above, the charging infrastructure remains at a preliminary stage in terms of commercialization. According to a report published by the (IEA) in 2020, the number of electric vehicles was estimated to reach 7.2 in 2019. In contrast, the number of charging stations was estimated to be approximately 0.8 million [8]. Furthermore, a market research report indicated that many countries face a shortage of charging stations compared to the growing demand for EVs [9]. Given that EVs are characterized by high mobility and unpredictability, energy demand can become concentrated based on the time and location of operation. Integrating the energy flow for EVs into existing power grids can lead to issues like peak load increases, power loss, and voltage drops during charging and discharging processes. Consequently, high demand for EV charging, combined with inadequate infrastructure, can have severe negative impacts on existing smart grids [10,11]. Recently, to address these challenges, energy trading approaches that utilize smart grid technology such as battery energy storage systems have been researched in order to enable energy to be sourced from external sources rather than relying solely on existing power grids [12,13].
Several energy trading schemes for vehicular energy trading systems [14,15] have been proposed to provide reliable energy management. These schemes, on the one hand, offer an energy trading service based on a centralized infrastructure. However, because their scheme does not account for charging station overload, it is difficult to provide reliable service. Additionally, significant privacy concerns arise as the central authority node, which manages users’ personal data and arranges energy transactions, is exposed to potential adversary attacks. In addition, communications regarding vehicular energy trading are performed on wireless channels, which can be exposed to various threats by attackers, such as impersonation attacks, replay attacks, and man-in-the-middle attacks. If the personal information is leaked to a malicious attacker, the attacker can conjecture the home, workplace, and hobbies of the driver [16,17,18]. Therefore, a secure authentication protocol is necessary.
Recently, research for decentralized energy trading systems [19,20,21,22] has been presented to resolve the security issues of a centralized system. A blockchain is regarded as a trusted distributed ledger that ensures data integrity and decentralization. In previous works, trading records were stored on the blockchain to ensure data privacy [23,24]. However, even if personal data are encrypted before being uploaded to the blockchain, security issues may arise later because the data recorded in the blockchain cannot be deleted or modified. Recently, due to privacy issues with blockchains, it is recommended not to store personal data on blockchains [25,26].
Decentralized identifiers (DIDs) are a new type of identifier that enable verifiable decentralized digital identities. DIDs provide a unique, decentralized way for entities to assert and control their identities without relying on centralized authorities. Each DID is generated by the entity it represents and is accompanied by a DID document containing cryptographic keys and verification methods. DIDs ensure interoperability across various decentralized systems and platforms while offering enhanced privacy and security. Users retain full control over their personal data, mitigating the risks associated with centralized identity management systems. In essence, DIDs empower individuals and organizations to manage their digital identities securely and autonomously in decentralized environments.
In this paper, we propose a reliable and privacy-preserving vehicular energy trading scheme using decentralized Identifiers to resolve the above-mentioned security challenges. In the proposed approach, the blockchain only records the information necessary for user verification, while personal information and transaction details are not stored. Moreover, completed transaction information is recorded using verifiable credentials, which can prove the validity of VCs later without any interaction using the blockchain.
This paper proposes a vehicular energy trading scheme using decentralized identifiers to address the security issues mentioned above while ensuring reliability and privacy protection. The proposed scheme does not store users’ personal data and trading data on the blockchain; instead, the blockchain only operates to verify users’ authenticity. Furthermore, digital signatures and verifiable credential technology are employed to ensure the reliability of transactions, and records of transaction outcomes are stored. Transaction participants can independently prove the validity of future verifiable credentials using the blockchain without the need for third-party assistance.
1.1. Motivation
The main motivation of this work is, first, to propose a solution that protects the privacy of energy traders. In existing decentralized energy trading schemes, most information, including transaction results, is recorded on the blockchain. However, while this method ensures data integrity and transparency, it also carries the risk of potential leakage to other participants. Additionally, storing a lot of data on a blockchain is costly and does not guarantee scalability.
Secondly, we aim to provide a reliable trading solution. Existing vehicle-to-vehicle energy trading methods require vehicles to arrive at the same time and place for energy trading. While advancements in battery energy storage systems (BESSs) have helped overcome the temporal constraints of vehicle-to-vehicle energy trading, the system’s reliability could be compromised if malicious energy sellers pursue financial gain without delivering energy. Therefore, finding a solution that ensures the reliability of energy trading in such cases is essential. To address these issues, we are motivated to use a public blockchain, DID, VC, and commitment approaches to consider security, privacy, and reliability for the vehicular energy trading system.
1.2. Contributions
The main contributions of this paper are below.
- •
- We propose a reliable and privacy-preserving vehicular energy trading scheme using decentralized identifiers (DIDs) and verifiable credential (VC) technologies. The energy purchaser’s DID is not revealed during the authentication process at the reservation phase. Additionally, completed transaction information is not recorded in a public ledger but in VCs.
- •
- In order to ensure reliability in energy trading, the initial VC shared during the reservation phase is incomplete. When the transaction parties successfully perform the energy trade, the signature of the CS is added to the VC, and it becomes valid.
- •
- We analyze the proposed scheme using an ROR model and AVISPA simulation for demonstrating it resists malicious attacks and attains security features.
- •
- We compare the performance and security features of the proposed scheme and related works to showcase the security and efficiency of our approach.
This paper is organized as follows. In Section 2 and Section 3, we review the related works and relevant preliminaries, respectively. In Section 4, we propose a vehicular energy trading system model. Section 5 describes the details of the proposed energy trading scheme. In Section 6, we analyze the security of the proposed scheme. In Section 7, we analyze the performance of the proposed scheme compared to related schemes. Finally, we conclude this paper in Section 8.
2. Related Work
2.1. Decentralized Energy Trading System for Electric Vehicles
Energy trading systems for electric vehicles (EVs) have gained significant attention as a means to promote sustainable energy distribution. The traditional centralized approach to managing these energy transactions has security risks, such as single points of failure and data integrity issues. As a result, there is a growing interest in transitioning to a blockchain-based decentralized structure to enhance security [27,28,29,30]. The transition to a decentralized energy trading system using blockchain offers several security benefits:
- •
- Elimination of single points of failure: In a centralized system, all information is processed through a central authority, creating a vulnerability. Blockchain decentralizes transaction processing, reducing the risk of system-wide failure due to a single compromised node.
- •
- Data integrity and immutability: Blockchain records transactions in a manner that ensures data cannot be tampered with. This immutability is crucial for maintaining accurate and trustworthy records in EV energy trading systems, which allows for robust auditing and accountability.
- •
- Enhanced security through decentralization: By distributing transactions across a network of nodes, blockchain-based systems are inherently more secure against cyber-attacks. Encrypted data and consensus-based verification methods provide additional layers of protection.
- •
- Increased trust and transparency: In a blockchain-based system, all participants can view the transaction history, which enhances transparency. This transparency builds trust among users, as they can independently verify the accuracy and legitimacy of transactions.
2.2. Privacy Protection and Reliability Research for Decentralized Energy Trading Systems
In recent years, research on vehicular energy trading schemes has been proposed to protect user privacy and ensure the reliability of transactions. Gai et al. [31] proposed a privacy-preserving approach for energy trading users in a blockchain-based energy trading system. They proposed a noise-based privacy protection scheme to resist linking attacks that violate energy purchasers’ privacy by linking public information recorded in the blockchain with other datasets. However, their scheme does not consider privacy issues during data transmission and has the problem that energy traders rely on tokens issued by energy brokers to verify the legitimacy of the counterparties. Guan et al. [32] proposed privacy-preserving energy trading based on blockchain and attribute-based encryption (ABE). They focused on the problem of privacy leakage in blockchain-based energy trading systems, which exposes the raw information of users recorded in the blockchain. Their scheme proposed a ciphertext policy ABE-based access control method so that authorized users can access user information recorded in the blockchain. Xia et al. [33] proposed a V2V electricity trading scheme for the Internet of Vehicles by leveraging blockchain technology. Their scheme utilized a Bayesian game framework to model the strategic interactions among vehicles engaged in energy trading. By incorporating Bayesian inference techniques, vehicles can make informed decisions based on their private information and the observed behavior of other vehicles. The authors promote trust among participants by leveraging blockchain technology, which ensures transparency, security, and immutability of transactions, along with smart contracts, which are programmable codes that are reliable. Baza et al. [34] proposed blockchain-enabled secure energy trading schemes for both charging-stations-to-vehicle (CS2V) and vehicle-to-vehicle (V2V) scenarios. This scheme addresses privacy concerns by leveraging blockchain technology and smart contracts to facilitate transparent and tamper-proof transactions while ensuring fairness. The authors proposed a common prefix linkable anonymous authentication scheme to mitigate Sybil attacks and ensure system availability. Additionally, an anonymous and efficient blockchain-based payment system is proposed to prevent double-spending attacks. Li et al. [35] proposed a decentralized energy trading system named FeneChain that ensures privacy protection, verifiable fairness, and access control. They addressed security and privacy concerns in centralized energy trading systems and introduced mechanisms for anonymous authentication, timed commitments, and fine-grained access control. FeneChain addresses fairness issues in peer-to-peer (P2P) energy trading and aims to protect the rights of energy purchasers. Yahaya et al. [36] proposed a two-stage secure P2P energy trading model using a permissioned blockchain and cloud-based aggregator for secure and transparent P2P energy trading. Their scheme ensures mutual authentication, user privacy protection, and fair pricing and incentivizes energy contribution. A permissioned blockchain, off-chain authentication, and a reputation-based scoring system are employed to prevent impersonation and collusion. The model also features a privacy-preserving dynamic pricing mechanism based on the supply–demand ratio (SDR) and contract theory.
However, Baza et al. [34] use smart contracts to authenticate among EVs and take reservations for energy trading. To execute smart contract, EVs must produce transactions containing details regarding energy exchanges, revealing the identities of energy traders. Despite attempts to obscure or encode the data, they remain permanently recorded in the blockchain as transaction. Additionally, the above-mentioned schemes [33,34,35,36] store information regarding energy trading and/or users in the blockchain, which does not solve the privacy issues. Certain blockchain nodes responsible for upkeep of the decentralized ledger possess the capability to decode these transactions. In our scheme, we utilize DIDs and VCs to provide confidentiality and to ensure privacy preservation by avoiding the recording of sensitive information in the blockchain for the vehicular energy trading system. Therefore, we propose a reliable and privacy-preserving vehicular energy trading scheme using decentralized identifiers to overcome the above-mentioned problems.
3. Preliminaries
The proposed scheme utilizes an elliptic curve cryptosystem (ECC), an elliptic curve Pedersen commitment, decentralized identifiers (DIDs), and verifiable credentials (VCs). The definitions and properties are introduced in this section.
3.1. Elliptic Curve Cryptosystem (ECC)
ECC is a public-key cryptosystem based on the mathematical principles of elliptic curves [37]. Let p be a large prime number and : be an elliptic curve over a prime finite field , where , (mod p). G is a generator point on . The features of elliptic curve cryptosystems are defined as follows.
- Elliptic curve discrete logarithm problem (ECDLP): given a base point G and point , it is difficult to find the in probability polynomial time.
- Elliptic curve decisional Diffie–Hellman problem (ECDDHP): given a base points G and two points and , it is difficult to compute in probability polynomial time.
3.2. Elliptic Curve Pedersen Commitment
The elliptic curve Pedersen commitment is an efficient implementation of the Pedersen commitment scheme (PCS) [38,39] that uses the intractability of the ECDLP. In this scheme, a committer commits to secrets such that it is hard for a verifier to open the commitment. The description of the elliptic curve Pedersen commitment is presented in the following steps:
- Setup: Let G be a random generator point on and be a chosen generator point, where . The trusted authority publishes .
- Commit: The committer creates a commitment C; are random numbers, and , where represents a dedicated value created by the committer.
- Open: To confirm the authenticity of C, the committer reveals x and r, and the verifier checks if .
3.3. Decentralized Identifiers (DIDs)
Decentralized identifiers (DIDs) [40] are a new type of identifier that enables users to control their own identities and sovereignty without relying on trusted authorities. The DID ecosystem leverages blockchain technology for the storage of identities in a tamper-proof and interoperable way. A DID address consists of three fields. The first field, denoted as the DID scheme, is the URI schema of the identity. The second field, denoted as the DID method, defines how the DID scheme can be implemented on a particular distributed ledger. The last field, denoted as the DID method-specific identifier, is the unique identification string. DIDs are resolvable to DID documents, which contain public key parameters and additional information associated with a particular DID. The resolved DID document can be used for signature verification and authentication purposes for the DID subject. Figure 1 shows an example of a DID and Figure 2 shows an example of a DID document.

Figure 1.
An example of a DID.

Figure 2.
An example of a DID document.
3.4. Verifiable Credentials (VCs)
A verifiable credential [41] is a tamper-resistant credential containing one or multiple statements about a specific identity. The primary qualification of the VC is to be programmable, privacy-preserving, and secure cryptographically. The issuer signs the VC by using its private key. The public key is stored in the public blockchain. The agent of the user’s DID submits the VC, which includes the required official attestation statements from the issuer. Consequently, it is securely verified that the user can prove specific claims through the presentation of VCs with DID. Only users have the authority to manage and control their DIDs and VCs, and this is done while exposing as little of their claims and personal information as possible. VCs also provide consistent usability across different contexts.
In the W3C VC model [41], the subject should create a decentralized identifier through a verifiable data registry, which is a distributed ledger. The holder requests the issuer to generate a VC representing the specified properties of the identifier. Commonly, the holder is the subject of the VC he/she is maintaining (e.g., a parent maintains VCs for his/her child). The issuer confirms that the identifiers and the properties of the holder are valid, and it has authority to hold the subjects of VCs. Then, the issuer issues the VC. The holder can manage the VC after receiving it from the issuer. As a result, the holder creates a verifiable presentation based on VCs and presents it to the verifier. The identities of the verifiers are unknown to the issuers in this model. Figure 3 shows the workflow for W3C verifiable credentials.
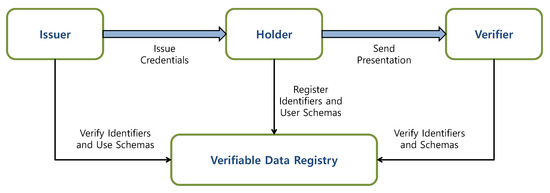
Figure 3.
The workflow for W3C verifiable credentials.
4. Proposed Model
Our proposed blockchain-based V2V energy trading scheme is composed three entities: EVs, RSUs, and the blockchain. We describe each entity below. The proposed system model is also depicted in Figure 4.
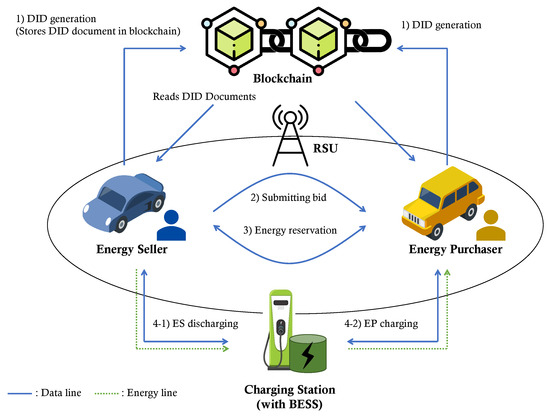
Figure 4.
The proposed system model.
- Electric vehicles (EVs): EVs embedded with OBU devices can communicate with external entities through dedicated short range communication (DSRC) or wireless access in vehicular environment (WAVE) and store data securely. Bidirectional EVs can purchase energy (charge) from electric vehicle supply equipment (EVSE) and sell energy to external loads (discharge). In this paper, we refer to the first vehicle as the energy purchaser and the second vehicle as the energy seller.Energy seller (ES): To sell surplus energy, the ES generates a bid containing the selling price, transaction time, energy volume, and other relevant information; then, it sends it to other EVs via the RSU. When the ES receives a message from an EP seeking to reserve an energy transaction, it verifies the message and shares the incomplete credentials and session key with the EP. Subsequently, the ES transfers energy and commitment to the promised CS according to the credential information and then completes the credentials by adding the signature received from the CS.Energy purchaser (EP): After selecting the optimal bid price, the EP sends a reservation message to the ES to plan energy trading. In the reservation phase, the EP shares incomplete credentials and a session key with the ES. When the EP arrives at the promised CS, the EP proves its commitment to the ES using the session key. If the proof is correct, the ES gets the energy stored in the CS.In this paper, RSU only provides a wide range of wireless communication services to EVs.
- Smart charging stations (CSs): CSs are equipped with battery energy storage and a communication module for EV charging services. The CS receives the commitment and energy from the ES and stores it. The stored energy is passed on to the EP, who proves the same commitment. CSs are a type of semi-trusted authority. Even if the charging station is attacked by a malicious attacker, there is no advantage to the attacker because the charging station does not have specific information about the energy trading.
- Blockchain: The proposed energy trading system utilizes a public blockchain. Public blockchains are fully decentralized infrastructures, allowing all nodes on the network to easily participate without the intervention of a trusted authority and preventing single points of failure. To ensure that all participants in the system agree on a single source of truth, consensus algorithms are employed. In our system, this source comprises DID documents rather than energy trading information between EVs.
5. Proposed Scheme
We present the details of the proposed scheme in a vehicular energy trading environment. It is composed of five phases; initialization phase, DID generation phase, submitting bids phase, reservation phase, and charging phase.
5.1. Initialization Phase
Trusted authorities (TA)s first initiate the system’s public parameters. The TA sets an elliptic curve : over a prime finite field , generators G and H, and a hash function , where . And the TA publishes system parameters .
5.2. DID Generation Phase
In this phase, All system participant generate their own decentralized identifiers. Each EV selects aN identity , password , and random numbers , where is its private key . Then, the EV generates a public key and stores the as a DID document on the blockchain. After the DID document is stored on the blockchain, the EV obtains the decentralized identifier corresponding to the DID document. After that, the EV calculates , , and stores securely in its storage. RSUs and CSs also create their own DIDs in a process similar to the DID generation steps of the EV.
5.3. Submitting Bids Phase
If the user wants to sell surplus energy, discloses the bids to potential buyers. , which endures a lack of energy, reviews bids and selects the best one. The detailed process of the submitting bids phase is as follows and is also shown in Figure 5.

Figure 5.
Submitting bids phase.
- Step 1: user enters identity and password and computes , , , . Then, verifies whether . If it matches, generates a random number and a current timestamp and computes , , signature , and a bid to sell surplus energy, where denote an amount of energy to sell, a selling price, an expiration time for the transaction, respectively. propagates .
- Step 2: checks the freshness of timestamp and uses to retrieve the corresponding DID document. Then, computes and checks whether . It is essential for to select the best bid and, at the same time, check the validity of the bid.
5.4. Reservation Phase
selects the that presented the optimal bid among multiple bids and sends a message to schedule an energy transaction with . When confirms the message and the transaction reservation between and is completed, and share a session key and incompletely verifiable credentials. The credentials contain information related to the energy transaction, including energy volume, price, and energy storage location. The detailed process is as follow and is also shown in Figure 6.

Figure 6.
Reservation phase.
- Step 1: inputs and and then computes , , , . checks . If it is valid, generates a random number and a timestamp and computes , , , , , . Then, sends to .
- Step 2: checks the timestamp and computes , . Then, retrieves ’s document using to obtain and computes , . verifies the signature through .
- Step 3: When and select the optimal charging station for energy trading, generates a temporary credential recording a signature and information about the negotiated transaction and sends encrypted with to .
- Step 4: decrypts the using and verifies the signature of recorded in . After that, adds payment information and a signature to . Then, sends encrypted with to and stores .
- Step 5: decrypts using and verifies the signature of recorded in . Then, stores .
5.5. Charging Phase
In this phase, and trade energy through the promised charging station equipped with BESS according to the initial credentials.
5.5.1. Discharging
According to the negotiation in , stores the surplus energy in and then receives a signature from to make its valid. receives a commitment and energy from and sends its signature to . A complete credential proves that stored the energy in as negotiated. Figure 7 depicts the discharging phase.

Figure 7.
Charging phase— discharging.
- Step 1: generates an and a timestamp . Next, computes , , , , , and sends to
- Step 2: checks the freshness of the and calculates , . If matches, generates and sends to .
- Step 3: calculates and verifies using ’s public key. If the signature is valid, records in and transmits vehicular energy and to .
- Step 4: stores in a database and energy in battery storage.
5.5.2. Charging
When arrives at the entrusted charging station , creates a commitment and submits it to . verifies the integrity of the message and validates the legitimacy of the commitment through a handshake with . If the commitment is valid, transfers the entrusted energy and signature to . adds the received signature to the to complete it. Figure 8 depicts the charging phase.

Figure 8.
Charging phase— charging.
- Step 1: generates random numbers , and timestamps and computes , , , , , , , . Then, sends to .
- Step 2: After receiving the message from , verifies the freshness of the message. calculates , , and checks whether is correct. If it is correct, retrieves and sends a random number to .
- Step 3: computes , and submits to
- Step 4: If is correct, generates , and transfers to .
- Step 5: calculates and verifies using ’s public key. If the signature is valid, records in .
6. Security Analysis
We carry out informal and formal analyses to verify the security of the proposed scheme. We utilize the real-or-random (ROR) oracle model to ensure the security of session keys and employ Automated Validation of Internet Security Protocols and Applications (AVISPA) simulation [42] to assess resilience against several security attacks.
6.1. Informal Analysis
In this section, we carry out an informal analysis to verify that the proposed scheme resists various attacks and achieves security features such as confidentiality, reliability, and mutual authentication.
- Impersonation attack: Malicious attackers can attempt to impersonate a legitimate vehicle. However, as mentioned in Section 3.1, due to ECDLP and ECDDHP, attackers find it challenging to compute the vehicle’s private key and session key , making it difficult to impersonate a legitimate vehicle. Therefore, the proposed scheme is secure against an impersonation attack.
- Replay attack: Attackers can intercept messages transmitted over a public channel and resend or delay them to obtain sensitive information or to execute other security attacks. However, since messages transmitted over the public channel include timestamps and random numbers, recipients can verify the freshness of the message. Therefore, the proposed scheme is secure against replay attacks.
- Man-in-the-middle (MITM) attack: Attackers can participate in communication between two legitimate vehicles during the reservation phase to collect valuable information about the users and to later attempt to forge messages using this information. However, due to the use of one-way hash functions, random numbers, and timestamps, the integrity and freshness of the message is ensured. Additionally, since signatures are generated using private keys , attackers cannot create valid authentication messages. Therefore, the proposed scheme is secure against a man-in-the-middle attack.
- Confidentiality: In the proposed scheme, the DID of the energy purchaser is not exposed in order to conceal transactions between the energy seller and purchaser. However, the DID of the energy seller is exposed to publicly verify the legitimacy of the seller and invoices. Additionally, the charging station, which manages the energy received from the energy seller, provides energy only to vehicles that present the correct commitment , thus not requiring information about the energy purchaser. Moreover, only the parties involved in the energy transaction possess verifiable credentials to prove their participation.
- Reliability: To ensure the reliability of energy transactions between two vehicles in the proposed scheme, both vehicles share verifiable credentials during the reservation phase. These credentials are not valid until they obtain the signature from the charging station. As both vehicles successfully delegate and accept energy through the charging station, they can complete their credentials by obtaining the signature value from the charging station. Therefore, the proposed scheme provides reliability to energy traders so that they can proceed with the normal energy trading process.
- Mutual authentication: and authenticate each other. authenticates by checking whether is correct during the reservation phase. authenticates by verifying whether is correct during the submitting bids phase. Therefore, the proposed scheme ensures mutual authentication.
6.2. Formal Analysis
We conduct a formal security proof by using the AVISPA simulation and the ROR oracle model.
6.2.1. ROR model
The ROR model, which is based on probabilistic game theory, is utilized for analyzing the semantic security of an authenticated key agreement. We utilize the ROR oracle model to evaluate the session key security for the proposed scheme. We briefly introduce the ROR oracle model.
In the ROR model, there are three parties: the energy seller and the energy purchaser , where and are the instances of and . In Table 1, we define queries for the ROR oracle model, such as , , , and . In addition, we use a collision-resistant one-way hash function as a random oracle. We use Zipf’s law to evaluate session key security.

Table 1.
Various queries and descriptions.
Theorem 1.
is assumed that the advantage function of adversary in order to break the session key security of the proposed scheme. Then, we derive the following:
where is the number of , is the range space of the hash function, and is the ’s advantage for breaching ECDDHP.
Proof.
We indicate the four games with , and the probability of for winning game is denoted as .
- Game 0: is considered to be ’s real attacks in our proposed scheme. picks a random bit c at the beginning of . Then, we obtain the following equation:
- Game 1: indicates that executes an eavesdropping attack, in which the transmitted messages are intercepted between and . For this game, executes a query to obtain the communicated messages. After the end of this game, carries out , and queries to compromise session key . To derive , needs the short-term secret values and and private keys and . Hence, ’s probability of winning by eavesdropping on the messages does not increase. Therefore, we obtain the result as follows:
- Game 2: is considered to be active/passive attacks by executing and queries to find hash collision. can intercept the transmitted messages from the submitting bids phase to the reservation phase. The intercepted messages are safeguarded by the collision-resistant one-way hash function . Furthermore, tries to derive by using intercepted messages. However, needs to break the ECDDHP (defined in Section 3.1) in polynomial time t, which is a computationally infeasible problem for to derive . By applying the ECDDHP and the birthday paradox result, we obtain the inequality
After executing all the games, tries to guess the exact bit c to win the game using the query. Thus, we obtain the following:
Equations (2) and (3) help to derive
Furthermore, using Equations (4)–(6), we obtain the following inequality:
Finally, by multiplying both sides of Equation (7), we obtain the stipulated result :
□
6.2.2. AVISPA Simulation
This simulation proves the formal security robustness of the cryptographic protocol against MITM and replay attacks. We implement the security simulation and demonstrate the security result. The AVISPA simulation tool is implemented using “High-Level Protocol Specification Language (HLPSL) to generate input format (IF)” and is linked to four backends, including the on-the-fly mode checker (OFMC), the Tree Automata based on Automatic Approximations for the Analysis of Security Protocols (TA4SP), the SAT-based model checker (SATMC), and the Constraint-Logic-based Attack Searcher (CL-AtSe). Only the CL-AtSe and OFMC provide the operation of bitwise exclusive-or (XOR) in these backends. AVISPA supports the DY model and can verify MITM and replay attacks.
The roles of the energy seller and energy purchaser nodes are described in Figure 9 and Figure 10, respectively. The goals and the roles of the session and environment of the proposed scheme are indicated in Figure 11. The simulation results for the OFMC and CL-ATse backends are presented in Figure 12, which show that the proposed scheme is secure against MITM and replay attacks.

Figure 9.
Role of the energy seller.

Figure 10.
Role of the energy purchaser.

Figure 11.
Environment and goals.

Figure 12.
The result of AVISPA simulation via OFMC and CL-AtSe backends.
7. Performance Analysis
We compare the proposed scheme with related schemes suggested for vehicular energy trading environments. We show that the proposed scheme has comparable or better performances compared to the existing schemes in this section. We perform testbed experiments on cryptographic computation by leveraging MIRACL on PC. The detailed specifications of the PC are as follows: 8 GB memory, Intel Core i7-4790 at 3.60 GHz frequency, and Linux Ubuntu 18.04.4 LTS with 64 bits.
7.1. Security Features
We present the security properties of the proposed scheme and existing schemes [33,34,35,36]. As shown in Table 2, the related schemes [33,34,35,36] are subject to temporal constraints, as transactions can only occur at the same time. Furthermore, our scheme only utilizes the blockchain to retrieve information for authentication (except for the DID generation phase, which is recorded on the blockchain). However, other papers record transactions on the blockchain during the energy trading process, leading to increased costs over time. This can create scalability issues. Therefore, our scheme provides more security features compared to related schemes.

Table 2.
Security and function properties comparison.
7.2. Computation Cost Analysis
We compare the computation costs of the energy trading process (from the authentication phase among EVs to the charging phase) between the proposed scheme and related works [33,34,35,36]. Table 3 shows the notation of each operation and the average cost calculated 100 times for each operator in the set environment.

Table 3.
The notation of each operation and computation costs.
Furthermore, the computation costs of “generating authentication proof” in [34] is similar to . The computational costs comparison of the proposed scheme and the existing schemes are summarized in Table 4. The computational cost of our system is lower than that of [35] but higher than that of [33,34,36]. However, [33] has the drawback of relying on intermediaries to authenticate vehicles, and [34,36] incurs additional gas costs as it requires running Ethereum smart contracts. Therefore, our scheme is more efficient than other schemes in a decentralized energy trading system for vehicles.

Table 4.
Computation costs comparison.
7.3. Communication Cost Analysis
We evaluate the communication costs of the proposed scheme compared to related schemes [33,34,35,36] during the authentication phase, during which the messages are exchanged by the registered vehicles. We first define that the bit lengths of the timestamp, random number, identity, hash output, symmetric encryption, elliptic curve point, and asymmetric encryption to be 32 bits, 160 bits, 160 bits, 160 bits, 256 bits, 320 bits, and 320 bits, respectively. Moreover, the bit length of request information is defined to be 160 bits. The bit length of authentication proof is defined to be 729 bytes [34]. Table 5 shows an analysis of the communication costs of the proposed scheme compared to related protocols. As a result of the comparison, our scheme has similar or slightly higher costs compared to others in terms of performance, but it can be suitable for achieving a reliable and privacy-preserving energy trading environment because it provides more security and functions.

Table 5.
Communication costs comparison.
8. Conclusions
Despite the rapid growth of the electric vehicle market, the problem of insufficient charging infrastructure persists. To address this issue, various technologies are being researched to enable EV charging from diverse energy sources, such as battery energy storage systems. However, vehicles in these systems are vulnerable to various security attacks because they exchange information over public channels. This paper proposes a vehicle energy trading mechanism that addresses the limitations of recent distributed energy trading schemes while ensuring reliability and privacy preservation. In the proposed scheme, only the authentication materials required for the energy transaction are stored in the blockchain, and the transaction results are recorded in verifiable credentials, thereby reducing the storage burden on the blockchain. User privacy is also protected by not storing users’ personal data on the blockchain. We conducted an informal analysis and a formal analysis to include using the AVISPA and ROR oracle models to evaluate the security of the proposed method and ensure that it ensures confidentiality, reliability, and mutual authentication. Finally, we compared the performance and security features of the proposed scheme with related schemes to demonstrate that our proposed scheme provides more security functions without a loss of performance compared to related schemes in a vehicular energy trading environment.
Author Contributions
Conceptualization, M.K.; Methodology, Y.P.; Validation, K.P. and Y.P.; Formal analysis, M.K.; Writing—original draft, M.K.; Writing—review & editing, K.P. and Y.P.; Supervision, Y.P.; Funding acquisition, Y.P. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education under Grant 2020R1I1A3058605.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Global EV Outlook: Understanding the Electric Vehicle Landscapeto. 2020. Available online: https://www.ourenergypolicy.org/wp-content/uploads/2013/09/GlobalEVOutlook_2013.pdf (accessed on 8 April 2024).
- Electric Car Demand Growing, Global Market Hits 740,000 Units. Available online: https://cleantechnica.com/2015/03/28/ev-demand-growing-global-market-hits-740000-units/ (accessed on 8 April 2024).
- Mouli, G.R.C.; Kefayati, M.; Baldick, R.; Bauer, P. Integrated PV charging of EV fleet based on energy prices, V2G and offer of reserves. IEEE Trans. Smart Grid 2019, 10, 1313–1325. [Google Scholar] [CrossRef]
- Zhong, W.; Xie, K.; Liu, Y.; Yang, C.; Xie, S. Topology-aware vehicle-to-grid energy trading for active distribution systems. IEEE Trans. Smart Grid 2019, 10, 2137–2147. [Google Scholar] [CrossRef]
- Alvaro-Hermana, R.; Fraile-Ardanuy, J.; Zufiria, P.J.; Knapen, L.; Janssens, D. Peer to peer energy trading with electric vehicles. IEEE Intell. Transp. Syst. Mag. 2016, 8, 33–44. [Google Scholar] [CrossRef]
- Shurrab, M.; Singh, S.; Otrok, H.; Mizouni, R.; Khadkikar, V.; Zeineldin, H. An efficient vehicle-to-vehicle (V2V) energy sharing framework. IEEE Internet Things J. 2021, 9, 5315–5328. [Google Scholar] [CrossRef]
- Umesh, B.S.; Khadkikar, V.M.; Zeineldin, H.; Singh, S.; Otrok, H.; Mizouni, R. Direct electric vehicle to vehicle (V2V) power transfer using on-board drivetrain and motor windings. IEEE Trans. Ind. Electron. 2021, 69, 10765–10775. [Google Scholar]
- Global EV Outlook. 2020. Available online: https://www.iea.org/reports/global-ev-outlook-2020 (accessed on 8 April 2024).
- Electric Vehicle Market by Component, Vehicle (Passenger Cars, CV), Propulsion (BEV, PHEV, FCEV), Vehicle Drive Type (FWD, RWD, AWD), Vehicle Top Speed (<125 mph, >125 mph), Charging Point, Vehicle Class, V2G, Region-Global Forecast 2030. Available online: https://www.marketsandmarkets.com/Market-Reports/electric-vehicle-market-209371461.html (accessed on 8 April 2024).
- Chekired, D.A.; Khoukhi, L.; Mouftah, H.T. Fog-computing-based energy storage in smart grid: A cut-off priority queuing model for plug-in electrified vehicle charging. IEEE Trans. Ind. Inform. 2020, 16, 3470–3482. [Google Scholar] [CrossRef]
- Zhang, P.; Qian, K.; Zhou, C.; Stewart, B.G.; Hepburn, D.M. A methodology for optimization of power systems demand due to electric vehicle charging load. IEEE Trans. Power Syst. 2012, 27, 1628–1636. [Google Scholar] [CrossRef]
- Chen, J.; Zhang, Y.; Su, W. An anonymous authentication scheme for plug-in electric vehicles joining to charging/discharging station in vehicle-to-Grid (V2G) networks. China Commun. 2015, 12, 9–19. [Google Scholar] [CrossRef]
- Yan, Q.; Zhang, B.; Kezunovic, M. Optimized operational cost reduction for an EV charging station integrated with battery energy storage and PV generation. IEEE Trans. Smart Grid 2019, 10, 2096–2106. [Google Scholar] [CrossRef]
- Li, Z.; Kang, J.; Yu, R.; Ye, D.; Deng, Q.; Zhang, Y. Consortium blockchain for secure energy trading in industrial Internet of Things. IEEE Trans. Ind. Informat. 2018, 14, 3690–3700. [Google Scholar] [CrossRef]
- Aggarwal, S.; Kumar, N.; Gope, P. An efficient blockchain-based authentication scheme for energy-trading in V2G networks. IEEE Trans. Ind. Informat. 2020, 17, 6971–6980. [Google Scholar] [CrossRef]
- Li, D.; Yang, Q.; An, D.; Yu, W.; Yang, X.; Fu, X. On location privacy-preserving online double auction for electric vehicles in microgrids. IEEE Internet Things J. 2019, 6, 5902–5915. [Google Scholar] [CrossRef]
- Yucel, F.; Akkaya, K.; Bulut, E. Efficient and privacy preserving supplier matching for electric vehicle charging. Ad Hoc Netw. 2019, 90, 101730. [Google Scholar] [CrossRef]
- Tandon, R.; Gupta, P.K. SV2VCS: A secure vehicle-to-vehicle communication scheme based on lightweight authentication and concurrent data collection trees. J. Ambient Intell. Human. Comput. 2021, 12, 9791–9807. [Google Scholar] [CrossRef]
- He, Y.; Zhang, C.; Wu, B.; Geng, Z.; Xiao, K.; Li, H. A trusted architecture for EV shared charging based on blockchain technology. High-Confid. Comput. 2021, 1, 100001. [Google Scholar] [CrossRef]
- Huang, X.; Xu, C.; Wang, P.; Liu, H. LNSC: A security model for electric vehicle and charging pile management based on blockchain ecosystem. IEEE Access 2018, 6, 13565–13574. [Google Scholar] [CrossRef]
- Kang, J.; Yu, R.; Huang, X.; Maharjan, S.; Zhang, Y.; Hossain, E. Enabling localized peer-to-peer electricity trading among plug-in hybrid electric vehicles using consortium blockchains. IEEE Trans. Ind. Informat. 2017, 13, 3154–3164. [Google Scholar] [CrossRef]
- Kim, M.; Lee, J.; Oh, J.; Park, K.; Park, Y.; Park, K. Blockchain based energy trading scheme for vehicle-to-vehicle using decentralized identifiers. Appl. Energy 2022, 322, 119445. [Google Scholar] [CrossRef]
- Sun, G.; Dai, M.; Zhang, F.; Yu, H.; Du, X.; Guizani, M. Blockchain-enhanced high-confidence energy sharing in internet of electric vehicles. IEEE Internet Things J. 2020, 7, 7868–7882. [Google Scholar] [CrossRef]
- Son, S.; Lee, J.; Kim, M.; Yu, S.; Das, A.K.; Park, Y. Design of blockchain-based lightweight V2I handover authentication protocol for VANET. IEEE Trans. Netw. Sci. Eng. 2022, 9, 1346–1358. [Google Scholar] [CrossRef]
- Blockchain GDPR Privacy by Design. Available online: https://blockchain.ieee.org/images/files/pdf/blockchain-gdpr-privacy-by-design.pdf (accessed on 8 April 2024).
- Bernabe, J.B.; Canovas, J.L.; Hernandez-Ramos, J.L.; Moreno, R.T.; Skarmeta, A. Privacy-preserving solutions for blockchain: Review and challenges. IEEE Access 2019, 7, 164908–164940. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, J.; Ding, Y. Blockchain-based decentralized and secure keyless signature scheme for smart grid. Eenrgy 2019, 180, 955–967. [Google Scholar] [CrossRef]
- Guan, Z.; Si, G.; Zhang, X.; Wu, L.; Guizani, N.; Du, X.; Ma, Y. Privacy-preserving and efficient aggregation based on blockchain for power grid communications in smart communities. IEEE Commun. Mag. 2018, 56, 82–88. [Google Scholar] [CrossRef]
- Aitzhan, N.Z.; Svetinovic, D. Security and privacy in decentralized energy trading through multi-signatures, blockchain and anonymous messaging streams. IEEE Trans. Dependable Secur. Comput. 2018, 15, 840–852. [Google Scholar] [CrossRef]
- Kumari, A.; Gupta, R.; Tanwar, S.; Tyagi, S.; Kumar, N. When blockchain meets smart grid: Secure energy trading in demand response management. IEEE Netw. 2020, 34, 299–305. [Google Scholar] [CrossRef]
- Gai, K.; Wu, Y.; Zhu, L.; Qiu, M.; Shen, M. Privacy-preserving energy trading using consortium blockchain in smart grid. IEEE Trans. Ind. Inform. 2019, 15, 3548–3558. [Google Scholar] [CrossRef]
- Guan, Z.; Lu, X.; Yang, W.; Wu, L.; Wang, N.; Zhang, Z. Achieving efficient and Privacy-preserving energy trading based on blockchain and ABE in smart grid. J. Parallel Distrib. Comput. 2021, 147, 34–45. [Google Scholar] [CrossRef]
- Xia, S.; Lin, F.; Chen, Z.; Tang, C.; Ma, Y.; Yu, X. A bayesian game based vehicle-to-vehicle electricity trading scheme for blockchain-enabled internet of vehicles. IEEE Trans. Veh. Technol. 2020, 69, 6856–6868. [Google Scholar] [CrossRef]
- Baza, M.; Sherif, A.; Mahmoud, M.M.E.A.; Bakiras, S.; Alasmary, W.; Abdallah, M.; Lin, X. Privacy-preserving blockchain-based energy trading schemes for electric vehicles. IEEE Trans. Veh. Technol. 2021, 70, 9369–9384. [Google Scholar] [CrossRef]
- Li, M.; Hu, D.; Lal, C.; Conti, M.; Zhang, Z. Blockchain-enabled secure energy trading with verifiable fairness in industrial internet of things. IEEE Trans. Ind. Informat. 2020, 16, 6564–6574. [Google Scholar] [CrossRef]
- Yahaya, A.S.; Javaid, N.; Almogren, A.; Ahmed, A.; Gulfam, S.M.; Radwan, A. A two-stage privacy preservation and secure peer-to-peer energy trading model using blockchain and cloud-based aggregator. IEEE Access 2021, 9, 143121–143137. [Google Scholar] [CrossRef]
- Cui, J.; Wu, D.; Zhang, J.; Xu, Y.; Zhong, H. An efficient authentication scheme based on semi-trusted authority in VANETs. IEEE Trans. Veh. Technol. 2019, 68, 2972–2986. [Google Scholar] [CrossRef]
- Chai, H.; Leng, S.; He, J.; Zhang, K.; Cheng, B. Cyberchain: Cybertwin empowered blockchain for lightweight and privacy-preserving authentication in internet of vehicles. IEEE Trans. Veh. Technol. 2022, 71, 4620–4631. [Google Scholar] [CrossRef]
- Cani, A.S.; Bertino, E.; Yuan, D.; Meng, K.; Dong, Z.Y. SPrivAD: A secure and privacy-preserving mutually dependent authentication and data access scheme for smart communities. Comput. Secur. 2022, 115, 102610. [Google Scholar]
- Decentralized Identifiers (DIDs) v1.0 Core Architecture, Data Model, and Representations. Available online: https://www.w3.org/TR/2021/PR-did-core-20210803/ (accessed on 8 April 2024).
- Verifiable Credentials Data Model 1.0 Expressing Verifiable Information on the Web. Available online: https://www.w3.org/TR/2021/REC-vc-data-model-20211109/ (accessed on 8 April 2024).
- Automated Validation of Internet Security Protocols and Applications. Available online: http://www.avispa-project.org/ (accessed on 8 April 2024).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).