A Matrix Coding-Oriented Reversible Data Hiding Scheme Using Dual Digital Images

Abstract

With the development of Internet technology, information security and data protection have become particularly important. Reversible data hiding is an effective technique for data integrity and privacy protection, and secret image sharing is a distinct research field within reversible data hiding. Due to the ability of sharing secret information between two receivers and the larger embedding capacity compared to the traditional reversible data hiding scheme, dual digital images have also attracted extensive research in the past decade. In this paper, we propose a reversible data hiding scheme based on matrix coding using dual digital images. By modifying the bits in the pixels, we can conceal three bits of the secret message in two pixels. In other words, the embedding rate reaches 1.5 bits per pixel (bpp). The experimental results demonstrate that our method has a significantly larger embedding capacity of 786,432 bits compared to previous similar methods while still maintaining acceptable image quality defined by a peak signal-to-noise ratio (PSNR) greater than 30 dB. The proposed scheme is suitable for applications required to pass a large amount of data but with minor security of image quality to be visually acceptable.

1. Introduction

Since the Internet age started, the Internet has dominated our daily lives, with a tremendous amount of data and information transmitted through the Internet and world wide web every single minute. Some of the data can contain sensitive or secretive information, which requires higher levels of protection to prevent illegal hacking or misusage.

Securing of personal information or industrial knowhow has become essential; hence, scholars are encouraged to find solutions to resolve these serious problems in order to safeguard the communication channels and give users peace of mind. Data hiding (DH) [1,2] is one of the essential research areas, which provides methodologies to protect data effectively. Depending on the applications, content owners and data hiders can choose assorted schemes suitable for their requirements. Some receivers may only need to extract secret messages; yet, others may want to fully recover the original media. Therefore, the data hiding is branched out into irreversible [3,4] and reversible [5,6] depending on whether the original media can be retrieved completely or not after data recovery. Because the full reversibility of the original media offers wider applicability, studies of reversible data hiding (RDH) [7,8,9,10,11,12] have become more popular in the recent decades.

Digital images are commonly used media for scientists to exercise and verify their concepts and approaches. Secret image sharing (SIS) technology was proved to be a proficient way to protect private images by generating multiple shares called image shadows. The idea of secret image sharing derived from secret sharing was proposed by Shamir back in 1979 [13]. The secret was shared and recovered by employing Lagrange interpolation. Yan et al. realized an SIS scheme based on the Chinese remainder theorem (CRT) [14] later on. With a twist of the SIS technique, a special edition of RDH using dual images was proposed by Chang et al. in 2007 [15]. Dual-image methods generate two stego images, which increase the safety of the secret data, visual image quality, and embedding capacity. Unless both stego images can be obtained simultaneously, the extraction of the secret data cannot be completed. Because dual image schemes can offer stronger safekeeping and recovery abilities, there is higher demand to discover innovative or improved solutions [16,17,18,19,20] to achieve either better visual quality of stego images or higher embedding capacity. Our novel scheme emphasizes enhancing the embedding capacity but with satisfactory image quality. The experimental results assured us that the embedding rates reached 1.5 bits per pixel (bpp). The contributions of this particular study are:

• The embedding capacity is significantly larger, which can be up to 786,432 bits.
• It is a suitable solution for applications requiring high embedding capacity but that can scarify the image quality to be visually acceptable.
• Both the process of embedding and the process of extraction are simple and have a satisfiable execution time. The shadow construction phase took 0.5242 s, while the secret message extraction and the image reconstruction phase took 0.9158 s.

In Section 2, we describe the fundamental concept of a matrix coding method to be utilized in the scheme. The details of data embedding and extraction are explained in Section 3, and the related experiments and analysis are presented in Section 4. At the end of the study, we summarize the findings and the potential future improvement in Section 5.

2. Related Work

In this section, we would like to refresh the principle of a matrix coding method [21], which was initially proposed by Chang et al. in 2008.

The matrix coding method adopts a parity check matrix $H$ as shown in Equation (1). Suppose we have a 7-dimensional cover vector $v=\left[1010100\right]$ and a secret message $m=\left[110\right]$. According to Equation (2), we can calculate the $Syndrome=\left[110\right]\oplus \left[111\right]=\left[001\right]$. Then, we match the calculated syndrome in Table 1 to obtain the corresponding coset leader $\left[1000000\right]$. Finally, we can calculate the stego vector $v^{\prime }=v\oplus Coset leader=\left[1010100\right]\oplus \left[1000000\right]=\left[0010100\right]$ through Equation (3). To summarize the above process, simply put, the stego vector $v\prime$ changes one bit in $v$ according to the coset leader associated with the syndrome. In this way, the data embedding process is completed. The extraction process is simpler. According to Equation (4), the secret message $m^{\prime }=H{v}^{\prime }=\left[110\right]$ can be easily extracted.

$$H=\left[\begin{array}{c}0\\ 0\\ 1\end{array} \begin{array}{c}0\\ 1\\ 0\end{array} \begin{array}{c}0\\ 1\\ 1\end{array} \begin{array}{c}1\\ 0\\ 0\end{array} \begin{array}{c}1\\ 0\\ 1\end{array} \begin{array}{c}1\\ 1\\ 0\end{array} \begin{array}{c}1\\ 1\\ 1\end{array}\right].$$

(1)

$$Syndrome=m\oplus Hv.$$

(2)

$$v^{\prime }=v\oplus Coset leader.$$

(3)

$$m\prime =Hv\prime .$$

(4)

Table 1. The cosets of the matrix coding with the parity check matrix $H$.

Syndrome	000	001	010	011	100	101	110	111
Coset leader	0000000	1000000	0100000	0010000	0001000	0000100	0000010	0000001

Through the matrix coding method, we can modify only one bit in the vector to effectively embed three secret bits. This remarkable efficiency not only ensures minimal impact on the original data but also provides a high level of security in concealing sensitive information.

3. Proposed Scheme

The dual image technique is employed for the novel scheme. The shadow construction phase is described in Section 3.1, and the secret message extraction and original image reconstruction phase are detailed in Section 3.2. Two covered images ${CI}_1$ and ${CI}_2$ are duplicates from the original image $OI$ with size $m\times n.$ A secret message $S$ is embedded to covered images ${CI}_1$, ${CI}_2$ to create shadow images ${SI}_1$ and ${SI}_2$. The shadow images are sent to designated receivers. When both shadow images appear at the same time, both the recovered secret message $RS$ and the recovered image $RI$ can be extracted. The scheme process is illustrated in Figure 1.

Figure 1. Process of the proposed scheme.

To better understand the process, we show two examples in Figure 2 exercising the whole flow. In Figure 2a, the pixel values of the current pixel pair are converted to their binary format (10100010)₂ from 162 first, four LSBs (0010)₂ are extracted from the cover pixel of the cover image ${CI}_1$ and three LSBs (010)₂ are extracted from the cover pixel of the cover image ${CI}_2$ to form a 7-dimensional cover vector (0010010). There are three secret bits that can be embedded into the cover vector to create a 7-dimentional shadow vector (0000010) using the matrix coding technique. We split the shadow vector into four bits (0000) and three bits (010) and replace the corresponding pixels: four LSBs in the shadow pixel of the shadow image ${CI}_1$ and three LSBs in the shadow pixel of the shadow image ${CI}_2$. A recovery bit is the fourth LSB in the shadow pixel of the shadow image ${CI}_2$, which records the original bit value of the bit altered during data embedding. By bitwise comparison of two shadow pixels, we can recover the original pixel value with the help of the recovery bit. The pixel value (10100000)₂ in the shadow image ${CI}_1$ is 160, and the pixel value (10101010)₂ in the shadow image ${CI}_2$ is 170 after the decimal format conversion.

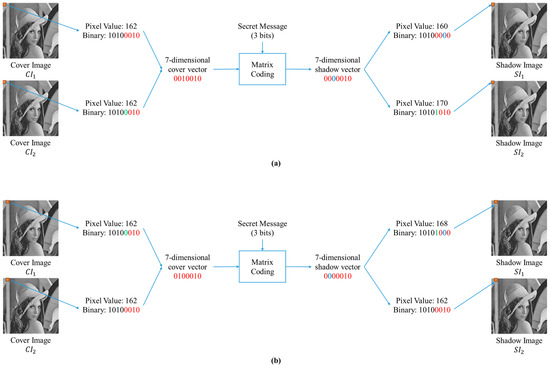
Figure 2. Examples of the proposed flow: (a) the odd pixel count, (b) the even pixel count.

Figure 2b shows an example similar to Figure 2a, except it is a case when the current pixel count is even. The 7-dimensional cover vertex is composed of three LSBs from the cover pixel of the cover image ${CI}_1$ and four LSBs from the cover pixel of the cover image ${CI}_2$. After the shadow vertex is generated, the split is three bits for the shadow pixel of the shadow image ${CI}_1$ and four bits for the shadow pixel of the image ${CI}_2$. The recovery bit becomes the fourth LSB in the shadow pixel of the shadow image ${CI}_1$. The exchanging of the bit-split patterns based on odd or even pixel count is to minimize the visual distortion of the shadow images and to keep a balanced visual quality of the two shadows.

3.1. Shadow Construction Phase

To embed a secret message, we move through a shadow construction phase to generate two shadow images using the matrix code method described in Section 2.

In order to meet the requirement of being reversible, we use a pixel pair, one from cover image ${CI}_1=\left\{p_{\mathrm{1,0}}, p_{\mathrm{1,1}}, \cdots , p_{1,(n\times m)-1}\right\}$ and the corresponding pixel from ${CI}_2=\left\{p_{\mathrm{2,0}}, p_{\mathrm{2,1}}, \cdots , p_{2,(n\times m)-1}\right\}$, where $n$ is the total number of pixels in images. $S=\left\{s_0, s_1, \cdots , s_{k,}\cdots , s_{r-1}\right\}$, where $s_k$∈{0, 1}, and $r$ is the length of secret bits. When a cover pixel pair ${pp}_i$ = $(p_{1i}, p_{2i}),$ the two pixel values for the pair are converted into binary format and represented as $p_{1,i}={\left({b_{\mathrm{1,7}},b}_{\mathrm{1,6}}, b_{\mathrm{1,5}}, \cdots , b_{\mathrm{1,0}}\right)}_2$ and $p_{2,i}={\left({b_{\mathrm{2,7}},b}_{\mathrm{2,6}}, b_{\mathrm{2,5}}, \cdots , b_{\mathrm{2,0}}\right)}_2$. A 7-dimensional cover vector $v_i$ is then constructed by using the least significant bits (LSBs) in these two cover pixels according to Equation (5).

$$v_i=\left\{\begin{array}{c}{(b}_{\mathrm{1,3}}, b_{\mathrm{1,2}},b_{\mathrm{1,1}}, b_{\mathrm{1,0}}, b_{\mathrm{2,2}}, b_{\mathrm{2,1}},b_{\mathrm{2,0}}), if i is odd\\ {(b}_{\mathrm{1,2}}, b_{\mathrm{1,1}},b_{\mathrm{1,0}}, b_{\mathrm{2,3}}, b_{\mathrm{2,2}}, b_{\mathrm{2,1}},b_{\mathrm{2,0}}), if i is even\end{array}\right.,$$

(5)

where $i$ is the index of the current pixel, and $0 \le i \le \left(n\times m\right)-1.$ The $i$ can also be treated as the current pixel count $pc$. Therefore, $pc$ is the same as $i$. Algorithm 1 describes the construction of shadow images ${SI}_1$ and ${SI}_2$ step by step.

Algorithm 1. Shadow Construction
Input	An original image $OI$ and a secret message $S$.
Output	Shadow images ${SI}_1$, ${SI}_2$.
Step 1	Duplicate the original image and create two cover images ${CI}_1$, ${CI}_{2.}$
Step 2	Set the initial secret bit count $bc=0$
Step 3	FOR each $pc, 0\le pc \le \left(n\times m\right)-1$
Step 3a	Obtain three secret bits $s_{bc}+s_{bc+1}+s_{bc+2}$
Step 3b	Select current cover pixel pair ${pp}_i$= $(p_{1,i}, { p}_{2,i}),$ where $i=pc,$ pixel $p_{1,i}$ from the cover image ${CI}_1$ and pixel $p_{2,i}$ from the cover image ${CI}_2.$
Step 3c	Convert pixel values $p_{1,i}$ and $p_{2,i}$ to binary.
Step 3d	Construct the 7-dimensional cover vector $v_i$ using Equation (5).
Step 3e	Calculate the $Syndrome$ and obtain the shadow vector ${sv}_i$ using Equations (2) and (3).
Step 3f	Let $v_i=\left({vb}_{i,6}, {vb}_{i,5 }, {vb}_{i,4 }, {vb}_{i,3 }, {vb}_{i,2 }, {vb}_{i,1 }, {vb}_{i,0}\right)$ and ${sv}_i=\left({sb}_{i,6 }, {sb}_{i,5 }, {sb}_{i,4 }, {sb}_{i,3 }, {sb}_{i,2 }, {sb}_{i,1 }, s{b}_{i,0}\right)$
Step 3g	Set the recovery bit $b_0$ to store the original bit value for recovery as below, $is Same={\left(\right(sb}_{i,5 }, {sb}_{i,4 }, {sb}_{i,3})=={(sb}_{i,2 }, {sb}_{i,1 }, {sb}_{i,0}))$ IF $is Same$ $b_0={vb}_{i,6}$   ELSE $j=0$ WHILE $j<3$ IF ${sb}_{i,j+3}\ne {sb}_{i,j}$ $b_0={vb}_{i,j}$ BREAK END $j=j+1$ END END
Step 3h	Set shadow pixel pair ${spp}_i$ = $\left({sp}_{1,i }{,sp}_{2,i}\right),$ where ${sp}_{1,i, }$ is the current pixel in shadow images ${SI}_1$ and ${sp}_{2,i, }$ is the current pixel in shadow images ${SI}_2$ according to IF $pc$ is odd ${sp}_{1,i }=$ ($b_{\mathrm{1,7}}, b_{\mathrm{1,6}}, b_{\mathrm{1,5}},b_{\mathrm{1,4}}, {sb}_{i,6}, {sb}_{i,5}, {sb}_{i,4}, {sb}_{i,3})$ ${sp}_{2,i }=$ (${b_{\mathrm{2,7}},b}_{\mathrm{2,6}}, b_{\mathrm{2,5}},b_{\mathrm{2,4}},b_0, {sb}_{i,2}, {sb}_{i,1}, {sb}_{i,0})$ ELSE ${sp}_{1,i }$ = ($b_{\mathrm{1,7}}, b_{\mathrm{1,6}}, b_{\mathrm{1,5}},b_{\mathrm{1,4}}, b_0, {sb}_{i,6}, {sb}_{i,5 }, {sb}_{i,4})$ ${sp}_{2,i }$ = ($b_{\mathrm{2,7}},b_{\mathrm{2,6}},b_{\mathrm{2,5}},b_{\mathrm{2,4}}, {sb}_{i,3}, {sb}_{i,2}, {sb}_{i,1},{sb}_{i,0})$ END
	END
Step 4	Export shadow images ${SI}_1$, ${SI}_2$.

3.2. Secret Message Extraction and Original Image Reconstruction Phase

The secret extraction and recovery of the original image is simple and straight forward, which can save computation time. After having both of the shadow images, a shadow vector can be constructed using Equation (5). Secret bits can be extracted from the shadow vector by looking up Table 1 directly. The shadow vector is the coset value in the matrix coding table to obtain the corresponding syndrome, which is the desired three secret bits to be extracted. By using the value of the recovery bit, the shadow vector is converted back to the original vector (or it can be called a recovered vector). The original vector (or recovered vector) is split into two sets of bits and restores the LSBs of the pixel back to the original image (or the recovered image). To clarify the process of extraction and recovery, Algorithm 2 explains the steps in detail.

Algorithm 2. Secret Message Extraction and Original Image Reconstruction
Input	Dual shadow images ${SI}_1$, ${SI}_2$.
Output	Recovered image $RI$, and recovered secret message $RS$.
Step 1	Duplicate ${SI}_1$ to $RI$.
Step 2	Set the initial secret bit count $bc=0$.
Step 3	FOR each $pc, 0 \le pc\le \left(n\times m\right)-1$
	Set $i=pc$
Step 3a	Set the current shadow pixel pair ${spp}_i$ = $\left({sp}_{1,i }{, sp}_{2,i}\right),$ where ${sp}_{1,i, }$ is the current pixel in the shadow image ${SI}_1$ and ${sp}_{2,i, }$ is the current pixel in the shadow images ${SI}_2$.
Step 3b	Convert pixel values ${sp}_{1,i}$ and ${sp}_{2,i}$ to binary and let ${sp}_{1, i}$ = $\left({{sb}_{\mathrm{1,7}}, sb}_{\mathrm{1,6}}, {sb}_{\mathrm{1,5}},{sb}_{\mathrm{1,4}}, {sb}_{\mathrm{1,3}},{sb}_{\mathrm{1,2}},{sb}_{\mathrm{1,1}},{sb}_{\mathrm{1,0}}\right)$ and ${sp}_{2, i}$ = $\left({{sb}_{\mathrm{2,7}}, sb}_{\mathrm{2,6}}, {sb}_{\mathrm{2,5}},{sb}_{\mathrm{2,4}}, {sb}_{\mathrm{2,3}},{sb}_{\mathrm{2,2}},{sb}_{\mathrm{2,1}},{sb}_{\mathrm{2,0}}\right)$.
Step 3c	Construct the shadow vector ${sv}_i$ = $\left({sb}_{i,6 }, {sb}_{i,5 }, {sb}_{i,4 }, {sb}_{i,3 }, {sb}_{i,2 }, {sb}_{i,1 }, {sb}_{i,0}\right)$ using Equation (5) and use it as the coset leader.
Step 3d	Extract three secret bits $s_{bc}+s_{bc+1}+s_{bc+2}$ based on the coset leader in Table 1 and append them to recovered secret message $RS$.
Step 3e	$bc=bc+3$
Step 3f	Obtain the original bit value $b_0,$ IF $pc$ is odd $b_0={sb}_{\mathrm{2,3}}$ ELSE $b_0={sb}_{\mathrm{1,3}}$ END
Step 3g	Let ${rp}_i$= (${rb}_{i,7}, {rb}_{i,6}, {rb}_{i,5}, {rb}_{i,4}, {rb}_{i,3}, {rb}_{i,2}, {rb}_{i,1}, {rb}_{i,0})$
Step 3h	Set the altered bit value back to its original value by the following: $is Same=true$ $j=0$ WHILE $j<3$ IF ${sb}_{i,j+3}\ne {sb}_{i,j}$ ${rb}_{i,j}=b_0$ $is Same=false$ BREAK END $j=j+1$ END IF $is Same=true$ ${rb}_{i,3}=b_0$ END
	END
Step 4	Export recovered images $RI$ and recovered secret message $RS$.

3.3. Processing Flow Examples

Figure 3 shows the embedding, extraction, and recovery procedures using two examples. The flow examples (a) and (b) first illustrate how bits are extracted from two cover images, how an original vector is formed, and how shadow images are set based on intermediate-created shadow vector after secret embedding using matrix coding. Then, they show how a shadow vector is formed from shadow images to recover hidden secrets and show the recovered vector and the recovered image by replacing the altered bit value with the recovery bit value as well.

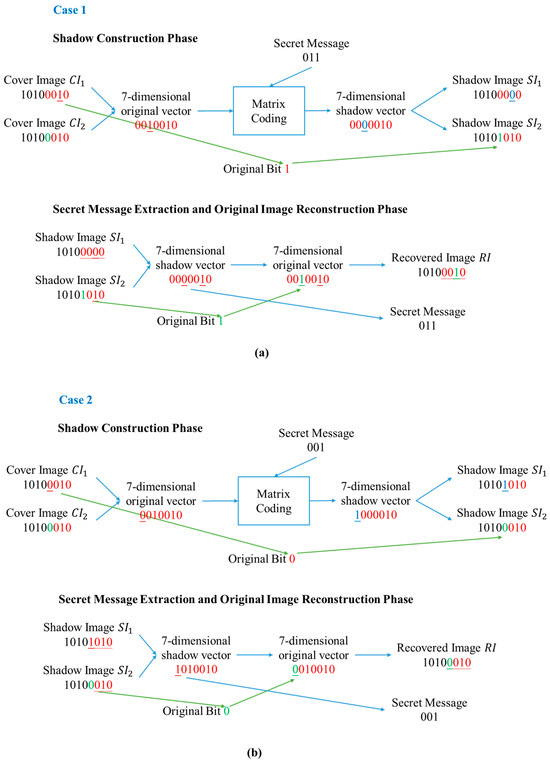
Figure 3. Examples for embedding, extraction, and recovery: (a) the odd pixel count, (b) the even pixel count.

Let us take the example (a), which is the case of dealing with an odd number of pixels. During the shadow construction phase, the two cover pixels are (10100010)₂. A 7-dimensional cover vector (0010010)₂ is formed by four LSBs of a pixel from the cover image 1 and three LSBs of a pixel from the cover image 2. Assume the secret bits are (011)₂, and through lookup Table 1, the syndrome (0010000)₂ is the coset leader corresponding to the secret bits (011)₂ according to Equation (2). Perform XOR calculation with the original vector, and a 7-dimensional shadow vector (0000010)₂ is generated and split to update the four LSBs in the shadow pixel 1 and the three LSBs in the shadow pixel 2. The fourth bit from the left of the shadow pixel 2 is the recovery bit, which records the original bit value (1) for the second bit from the left of the cover pixel 1. In the secret message extraction and the image reconstruction phase, a shadow vector is formed by the two pixels of two shadow images the same way we formed the cover vector from two pixels of two cover images. We can then extract the secret bits (011)₂ by using Table 1 directly. As for recovery of the original image, we can convert the shadow vector back to the original vector using the saved recovery bit value and update the four LSBs with any one of the shadow pixels to recover the original pixel, which can also be called a recovered pixel. Figure 3b moves through the same process with an example dealing with an even number of pixels.

4. Experimental Results

In this section, we evaluate the performance of our proposed matrix coding using a dual digital images scheme. As depicted in Figure 4, we selected eight standard gray images for our experiments. Our experiments were conducted on a laptop running the Windows 10 operating system with MATLAB R2023b. The laptop is equipped with a 3.20 GHz AMD Ryzen 7 CPU and 16 GB of RAM. We also compared the experimental results with other advanced reversible data hiding schemes based on dual images and our scheme demonstrated a significant advantage in embedding capacity (EC).

Figure 4. Eight 512 × 512 test images: (a) airplane, (b) baboon, (c) Barbara, (d) boat, (e) Goldhill, (f) lake, (g) Lena, (h) peppers.

The Peak Signal-to-Noise Ratio (PSNR) and the Structural Similarity Index (SSIM) are widely used as visual quality indicators for evaluating the performance of data hiding. The PSNR is employed to assess the difference in visual quality between two images and is calculated using Equations (6) and (7). In Equation (7), $m$ and $n$ represent the size of the image, while $i$ and $j$ represent individual pixels. In this context, $I$ represents the original image, and $K$ represents the shadow image. A smaller Mean Square Error (MSE) corresponds to less distortion in the image, indicating higher quality in the constructed image. Conversely, because the PSNR and MSE are inversely proportional, a higher PSNR value reflects the same conclusion.

$$PSNR=10\times {log}_{10}\frac{{255}^2}{MSE}$$

(6)

$$MSE=\frac{1}{m\times n}{\sum }_{i=1}^m{\sum }_{j=1}^n{\left[I\left(i,j\right)-K\left(i,j\right)\right]}^2$$

(7)

The SSIM is an indicator that quantifies the similarity between two images. It is primarily used to assess the similarity and dissimilarity between two images, denoted as $x$ and $y$. As shown in Equation (8), the SSIM algorithm separately compares the luminance, contrast, and structure of two images and then combines them using weighted products. In this equation, ${\mu }_x$ and ${\mu }_y$ represent the mean luminance, ${\sigma }_x$ and ${\sigma }_y$ denote the standard deviation of the luminance, ${\sigma }_{xy}$ represents the covariance of $x$ and $y$, and $C$ is a constant used to maintain stability. The closer the SSIM is to 1, the higher the similarity between the two images.

$$SSIM\left(x,y\right)=\frac{\left(2{\mu }_x{\mu }_y+C_1\right)\left(2{\sigma }_{xy}+C_2\right)}{\left({\mu }_x^2+{\mu }_y^2+C_1\right)\left({\sigma }_x^2+{\sigma }_y^2+C_2\right)}.$$

(8)

Figure 5 illustrates the shadow image constructed by our innovative matrix coding scheme. Clearly, the disparity between the constructed shadow image and the original image is minimal. It is challenging for us to discern any perceptible distortion with the naked eye, underscoring the superior visual quality achieved by our scheme. Table 2 illustrates the results obtained using our proposed matrix coding scheme to construct shadow 1 and shadow 2 from test images. It calculates the PSNR and SSIM values between these shadow images and the original image, as well as their average values. The average PSNR is approximately 36.34 dB, which is generally considered challenging to distinguish with the naked eye when it exceeds 30; these data support our conclusion. Furthermore, the average SSIM value is remarkably high at 0.9227, approaching 1. This indicates that the shadows constructed by our proposed scheme closely resemble the original images, confirming their excellent visual quality. These outstanding results substantiate the effectiveness of our solution and demonstrate its superiority in preserving image fidelity.

Figure 5. Shadow images of eight test images, with shadow 1 on the left and shadow 2 on the right: (a,b) airplane, (c,d) baboon, (e,f) Barbara, (g,h) boat, (i,j) Goldhill, (k,l) lake, (m,n) Lena, (o,p) peppers.

Table 2. Proposed scheme for PSNR and SSIM on different images.

Images	PSNR (dB)			SSIM
	Shadow 1	Shadow 2	Average	Shadow 1	Shadow 2	Average
Airplane	36.36	36.35	36.35	0.8990	0.8984	0.8987
Baboon	36.33	36.34	36.33	0.9645	0.9644	0.9645
Barbara	36.36	36.36	36.36	0.9313	0.9313	0.9313
Boat	36.30	36.27	36.28	0.9259	0.9255	0.9257
Goldhill	36.32	36.33	36.32	0.9274	0.9279	0.9277
Lena	36.41	36.37	36.39	0.9030	0.9026	0.9028
Lake	36.34	36.36	36.35	0.9253	0.9256	0.9255
Peppers	36.36	36.36	36.36	0.9053	0.9053	0.9053
Average	36.35	36.34	36.34	0.9227	0.9226	0.9227

Table 3 presents a comparison of the performance indicators between our scheme and other schemes based on reversible data hiding using dual images. Our primary focus is on the EC and PSNR. The embedding rate is expressed in bits per pixel (bpp), calculated as shown in Equation (9), where $M$ and $N$ represent the image dimensions. The embedding capacity is divided by all pixels to signify how many bits can be embedded in each pixel. The experimental results demonstrate that the embedding capacity of our proposed scheme reaches 786,432 bits, which is equivalent to 1.5 bpp calculated as $\frac{\mathrm{786,432}}{512\times 512}$ using Equation (9). The EC of the novel scheme significantly exceeds that of other schemes. When compared to a scheme with the largest embedding capacity, ours is nearly 50% higher than the one with 557,339 bits. Even with our PSNR above 36 dB, it can be still lower than that of other solutions. However, this is consistent with the laws of nature. A larger embedding capacity inherently entails more modifications, resulting in greater distortion. However, our PSNR remains above 30, meeting the criteria for high visual quality. It is challenging for the naked eye to discern any distortion, making this trade-off acceptable in light of the significantly increased embedding capacity.

$$bpp=\frac{EC}{M\times N}$$

(9)

Table 3. Comparison of the maximum EC, bpp, and PSNR values with other reversible data hiding scheme based on dual images.

Scheme	Indicator	Barbara	Goldhill	Lena	Peppers
proposed scheme	EC	786,432	786,432	786,432	786,432
	bpp	1.50	1.50	1.50	1.50
	PSNR1	36.36	36.32	36.41	36.36
	PSNR2	36.36	36.33	36.37	36.36
	PSNRAVG	36.36	36.32	36.39	36.36
Qin et al. [16]	EC	557,339	557,194	557,052	557,245
	bpp	1.06	1.06	1.06	1.06
	PSNR1	52.12	52.12	52.11	51.25
	PSNR2	41.58	41.58	41.58	41.52
	PSNRAVG	46.85	46.85	46.85	46.39
Lu et al. [17]	EC	524,288	524,288	524,288	524,192
	bpp	1.00	1.00	1.00	1.00
	PSNR1	49.14	49.17	49.13	49.11
	PSNR2	49.11	49.09	49.12	49.08
	PSNRAVG	49.13	49.13	49.13	49.10
Jana et al. [19]	EC	74,752	74,752	75,752	73,728
	bpp	0.14	0.14	0.14	0.14
	PSNR1	51.86	51.86	51.85	51.84
	PSNR2	51.96	51.97	51.56	51.94
	PSNRAVG	51.91	51.92	51.71	51.89
Kim et al. [20]	EC	524,288	524,288	524,288	524,288
	bpp	1.00	1.00	1.00	1.00
	PSNR1	54.12	54.16	54.14	54.15
	PSNR2	48.14	48.11	48.13	48.12
	PSNRAVG	51.13	51.14	51.14	51.14

Table 4 shows the execution time of our proposed scheme in the secret message extraction and original image reconstruction phase. It is evident that the execution time is consistently within 1 s at every stage demonstrating the great performance of our scheme.

Table 4. The execution time of our proposed scheme.

Phase	Execution Time (s)
Shadow Construction Phase	0.5242
Secret Message Extraction and Original Image Reconstruction Phase	0.9158

5. Conclusions

In this paper, we propose a reversible data hiding scheme with a high embedding capacity using matrix coding based on dual images. Our solution only requires modifying or not modifying one bit, enabling us to conceal three bits of a secret message in two pixels. The experimental results demonstrate that this solution significantly increases the embedding capacity when compared to other similar methods, allowing for up to 786,432 bits, which is equivalent to 1.5 bpp, all while maintaining a high level of visual quality. This illustrates the superiority and applicability of our scheme.

Applications that require dual sharing of information between two and only two receivers, such as a couple who share secret arrangements, to recover the original media can consider utilizing our scheme. In the future, we will investigate different types of matrix coding to improve the embedding capacity or to improve the visual quality.