Abstract
This paper considers the observer-based leader–follower consensus problem of multi-agent systems with one-sided Lipschitz conditions and quadratic inner-boundedness nonlinearity. Based on the relative outputs of neighboring agents, an adaptive protocol over a directed graph is designed via assigning a time-varying coupling weight to each node. Compared with the existing protocols, the proposed protocol can not only be utilized in the unidirectional flow of information, but it does not require any global graph information for its design. It has been shown that the established criteria can not only make the observer error tendency zero, but one can also achieve the leader–follower consensus of such nonlinear multi-agent systems. Furthermore, the gains of observer and protocol parameters can be constructed by solving the linear matrix inequalities (LMIs), which are conveniently checked. The results are illustrated by numerical simulations.
MSC:
93A16
1. Introduction
In recent years, the consensus problem has attracted a great deal of attention from multidisciplinary research communities. This is owing to the fact that multiple agents’ collective behaviors are greatly widespread in the natural world, the technology field and human society, and also have potential applications in many areas such as UAV formation flying, wireless sensor networks and smart grids. The essence of consensus is to design appropriate protocols such that all the agents reach an agreement about a certain variable of interest [1]. Due to the spatial dispersion of agents and the constrained sensing ranges of sensors, the consensus controller of multi-agent systems should be shifted from central to distributed paradigms. Particularly, a fully distributed controller is fascinating. It removes the dependence of global information and depends only on the local information, such as the states or outputs of each agent and its neighbors [2].
To this day, an abundance of protocols have been put forward to solve the consensus issue for first-order/second-order agents and even high-order multi-agent systems [3,4,5,6]. Recent research interests have been focused on nonlinear multi-agent systems due to motivation by practical applications, such as assembling a group of mobile robots to collaborate with each other to fulfill certain complex tasks [7]. Consensus problems were studied in [8,9] for multi-agent systems consisting of a general linear part and a Lipchitz nonlinear part. However, some examples were presented in [10] to show that certain dynamical systems are not Lipschitz in the classical sense, but are one-sided Lipschitz. Moreover, one-sided Lipschitz systems have important applications in the real world, for instance in numerical analysis [11], the birth–death issue of a population [12] and stiff issues [13,14]. In fact, compared with traditional Lipschitz systems, one-sided Lipschitz systems are more general, and also have more merits in the control and observation field, and particularly in addressing controller design based on an observer [15,16,17,18]. However, the existing results about one-sided Lipschitz systems are mainly limited in the framework of a single system. Until now, the problem of consensus tracking of multi-agent systems with a one-sided Lipschitz design has not been extensively studied, and this motivates our present research.
In most of the existing literature, when designing consensus protocols, it is indispensable to possess some global information, e.g., the spectrum of the Laplacian matrix of topology graphs [19,20,21,22,23]. One can use direct [19,20,21] and indirect methods [22,23] to calculate the eigenvalues of the Laplacian matrix. The direct method is to use the whole topology graphs to compute the spectrums; the indirect method is an exhaustive search method aiming to find all possible graphs for a given number of agents and then calculate their eigenvalues of the Laplacian matrix of each graph. However, in practice, the entire topology graph or the network size is not always available to each agent. Even though it is possible, the calculation task of these eigenvalues may be too large to implement, especially for large-scale networks. Therefore, protocols designed in this manner cannot be implemented in a fully distributed way, i.e., without utilizing global information on topological graphs. Such an issue was discussed in [24,25,26,27,28]. The main idea to solve this issue is to configurate time-varying coupling weights for each node or edge, and these coupling weights adaptively adjust with the consensus evolution. Specifically, during the consensus progress, the coupling weights continue to increase or decrease and eventually achieve some finite values. This idea was applied to cope with the adaptive consensus of a network of lur’e systems in [24,25] and Lipschitz nonlinear systems in [26]. Unfortunately, most of the existing works focus on state feedback protocols and undirected topology graphs. The pinning synchronization of complex one-sided Lipschitz networks with general directed topologies was investigated in [29], where two synchronization criteria with full-state and partial-state coupling were proposed, respectively. However, these criteria depend on some global graph spectrum information, i.e., they are not fully distributed. On the other hand, in general, output feedback based on a dynamic compensator or an observer is superior in function to static output feedback. Therefore, it is considerably urgent to construct fully distributed tracking protocols, especially observer-based protocols, under directed topologies for reaching consensus tracking for multi-agent systems with one-sided Lipschitz nonlinearity, as pointed out in [30].
Motivated by the above analysis, this paper is devoted to designing consensus protocols based on an observer for multi-agent systems subject to one-sided Lipschitz conditions. The key contributions of the present paper are twofold:
- (1)
- The one-sided Lipschitz condition in [10,15,16,17,18] is introduced into multi-agent systems, and the traditional observer design for an individual agent is extended to the output feedback protocol design for multi-agent systems subject to one-sided Lipschitz conditions.
- (2)
- Since the agents’ states are not available in many scenarios, we propose a novel observer-based protocol, and this protocol has two distinctive features. One is that it is independent of any global network information and relies only on the dynamics of agents and their relative outputs, leading it to be fully distributed. Different from the case in [31,32], the interplay of adaptive coupling weights and one-sided Lipschitz dynamics makes convergence analysis very intractable; the other is that it is based on unidirectional information exchange rather than bidirectional exchange [33]. This extension from the undirected graph to the directed case is nontrivial, and the main challenge is that the Laplacian matrices of directed graphs are asymmetric, making the design of adaptive protocols and the construction of the Lyapunov function very tough. Thanks to these two advantages, our protocol seems to be more general and more convenient to apply in engineering. Finally, inspired by the Lyapunov techniques in [2,23], a Lyapunov function with an integral fashion is artfully constructed for achieving the stability of tracking error systems.
The remainder of the paper is given as follows. Section 2 involves preliminaries and problem statements. In Section 3, we design the observer-based adaptive protocol, under which the leader–follower consensus of multi-agent systems subject to one-sided Lipschitz conditions is reached. Simulation examples are presented in Section 4, followed by the Conclusion.
2. Some Preliminaries and Problem Statement
2.1. Preliminaries
is the -dimensional Euclidean space over real numbers. denotes the inner product in , i.e., for any , then , in which indicates the transpose of . and are, respectively, the minimum and maximum eigenvalues of the symmetric matrix . An asterisk ‘’ represents a symmetric term of symmetric block matrices.
This paper involves a group of agents that consist of followers and one leader. The information interaction between followers is depicted by a weighed digraph , in which and are, respectively, the node and edge set, and is the adjacency matrix, with if there exists an edge from to , and otherwise. The Laplacian matrix of is denoted by , in which , and . followers and a leader constitute the augmented graph . The accesses of the followers to the leader are represented by , where if the follower has access to the information of leader, and otherwise.
Unlike the existing adaptive protocols in [20,21,22,24,25,33] that can only be applicable to cases in which the whole graphs are undirected or the subgraphs among the followers are undirected, we relax this assumption to the following case.
Assumption 1.
The augmented graph
is directed, containing a spanning tree whose root node is the leader.
Under the above assumption, define . In the following lemma, we give its property.
Lemma 1
([34]). Under Assumption 1, is invertible. Denote and ; then, and are positive definite matrices.
Lemma 2
(Young’s Inequality [35]). For non-negative real numbers and and positive real numbers and , satisfying , we have .
2.2. Problem Formulation
In this paper, the control purpose is to address the leader–follower consensus issue for multi-agent systems subject to one-sided Lipschitz conditions. By virtue of the relative outputs between a couple of neighboring agents, we first construct a state observer, and then, using the observed states, design an adaptive protocol over the directed graph.
Consider a group of nonlinear agents. The system of the -th agent is given by
where the state , input , and output . are constant matrices. Assume that is controllable and observable. The function is a continuous function characterizing the intrinsic nonlinearity, satisfying the following assumption.
Assumption 2.
1. The function is said to be a one-sided Lipschitz if there exists a such that .
where is a one-side Lipschitz constant. If (2) is valid everywhere in , then this function is called a globally one-side Lipschitz.
2. The function is called quadratic inner-bounded if there exist such that .
Unlike the well-known Lipschitz constant being positive, the parameters and can be positive, negative or zero. Additionally, compared with traditional Lipschitz systems, one-sided Lipschitz systems and quadratically inner-bounded functions are general, including traditional Lipschitz systems as a special case [16].
In practical engineering, the followers are required to synchronize to the virtue leader, whose dynamics are autonomous, given by
Our control objective is to design an observer-based adaptive protocol such that each agent in system (1) can be synced up with trajectory (4) by virtue of a directed communication network.
3. Main Results
In this section, we will first give the theoretical results of current work, and then prove them analytically.
For nonlinear systems (1) and (4), the state observer is proposed:
where is the estimate of , and is the observed output. is the observer gain matrix to be determined later. Based on the roughly estimated values of a couple of neighboring agents, we designed the adaptive controller with time-varying coupling weights as follows:
where , and is a time-varying coupling weight with initial value . The positive definite matrix and the feedback gain matrices , were designed later. The smooth function is monotonically nondecreasing in , satisfying that for any . Let and . From (1) and (5), one can see that
where and . Let , and . Then, . Note that is nonsingular, satisfying Assumption 1. It is not difficult to see that the observer-based consensus tracking issue is solvable if and only if both and converge to zero.
By virtue of (1) and (6), it is easy to obtain that and are governed by the following dynamics:
where , , and .
Next, we present an algorithm (Algorithm 1) which we used to construct the parameters of the adaptive protocol.
Algorithm 1.
Under Assumptions 1 and 2, the controller parameters in (5) and (6) can be constructed as follows:
- The constants of Assumption 2 need to satisfy
- Solve LMI,to obtain and two positive scalars . Take the observer gain matrix .
- For an appropriately small positive scalar, , solve LMI,to obtain and a positive scalar . Choose the feedback gain matrices and and the auxiliary function , where is any given constant.
Next, the main results are given below.
Theorem 1.
Let Assumptions 1 and 2 hold. If there exist feasible solutions to (9)–(11), the leader–follower consensus of systems (1) and (4) can be realized under observer (5) and adaptive law (6), whose parameters are designed in Algorithm 1. Moreover, as , the adaptive function and the coupling weight approach a steady-state constant value.
Proof.
We construct a Lyapunov function candidate as follows:
where , and ; one can get that and by using Lemma 1. A scalar will be determined later, and the matrices and are solutions to (10) and (11). is any given constant. Due to , , referring to (6), we have that holds for . Additionally, note that for . Summing up, the function is positive definite.
By using fact that , along the trajectories of (7), we take the derivative of as follows:
From (2) and (3), we get
where and are positive scalars. Then, adding the terms on the left-hand sides of (14) and (13) yields
where . Together with (10), means .
Along the trajectories of (8), we can take the derivative of as follows:
Subsequently, we abbreviate to without causing ambiguity. By using (8), it can be obtained that
On the other hand, due to , and together with Lemma A1 in Appendix A, we have
By using (17) and (18), and together with , we have
Because with is monotonically increasing and satisfies , for s > 0, it follows that
where in the first and second inequality, we, respectively, use the mean value theorem of integrals and Lemma 2. Substituting (16) and (19) into (20) yields
Due to and , for s > 0, we have
Select
that is,
where will be determined later.
Due to
substituting (22)–(24) into (21) yields
Choose to be sufficiently large such that , and then (25) is turned into
where . From (11), one can get that . By (12), (15) and (26), one can obtain that
Note that and . We can choose the appropriate positive constant such that holds, which is equivalent to . Therefore, one concludes that and both converge to zero. That is, adaptive protocol (6) solves the observer-based consensus tracking problem for systems (1) and (4). Since , we can get that is bounded, implying that is also bounded. It follows from that is monotonically increasing. Therefore, is bound to converge to a certain finite constant value. This completes the proof. □
Remark 1.
Different from the protocols in [19,20,21,22,23], which rely on some global information, adaptive protocol (6) relies only on agent dynamics and estimate states, and therefore it can be implemented by each agent in a fully distributed fashion. On the other hand, adaptive protocol (6) was designed based on the directed graph, which is different from the protocols over undirected graphs in [29,33]. On the other hand, although the distributed adaptive protocols in [2,27] can be applicable to the directed graph, those protocols adopted a state feedback strategy. Since the complete state information is not always available due to economical and/or technological reasons, we inserted observer (5) in the control loop to recover the unavailable states. In short, a distinctive merit of our protocols is the integration of a fully distributed communication fashion, unidirectional communication and dynamic output feedback in a unified framework.
Remark 2.
When Lemma A1 in Appendix A is used to prove Theorem 1, a sufficiently small positive scalar
automatically guarantees that the following constraint conditions hold:
and with .
Since a positive scalar
is appropriately small, the existence of the solutions for LMI (11) can be guaranteed as long as a positive scalar
is appropriately large, such that
holds.
4. Simulation Example
In this section, a simulation example on supercritical Hopf bifurcation is provided to verify the effectiveness of the proposed protocol.
Consider a group of four followers and a leader, governed by (1) and (4) with the parameters
and the one-sided Lipschitz function , The leader’s system is
Using the polar coordinate transformation, and , (27) is rewritten as
System (28) can represent a moving object’s motion. Additionally, some famous examples, such as a supercritical Hopf bifurcation, can be expressed by (28), whose concrete dynamic behaviors are explained in detail in [36]. From the definition of [16], we can get that is a one-sided Lipschitz system in , with . Letting , some calculations in [16] yield , and thus have . We take . For convenience, the directed topology is illustrated in Figure 1, where there are one leader, labeled 0 and four followers, and follower and can acquire the information of the leader, and all the weights on the edges are ones. Taking and solving LMIs (10)–(11), we obtain
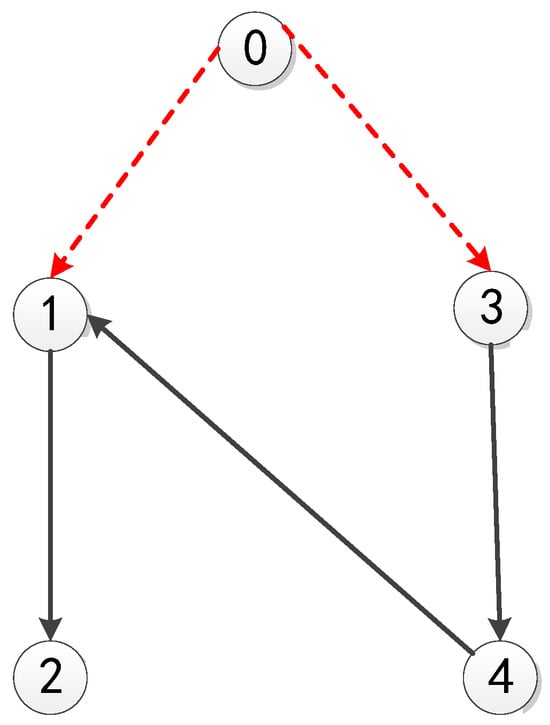
Figure 1.
Directed graph .
Then, the observer and controller gain matrices are given by, respectively,
From the square , we choose the initial conditions of and randomly, and . Set .
As show in Figure 2 and Figure 3, both the estimate errors and the tracking errors all converge to zero. Thereby, the leader–follower consensus is realized when adaptive protocol (6) is imposed onto the four followers. Furthermore, Figure 4 indicates that the adaptive coupling weights converge to constants; Figure 5 shows that the auxiliary functions approach one.
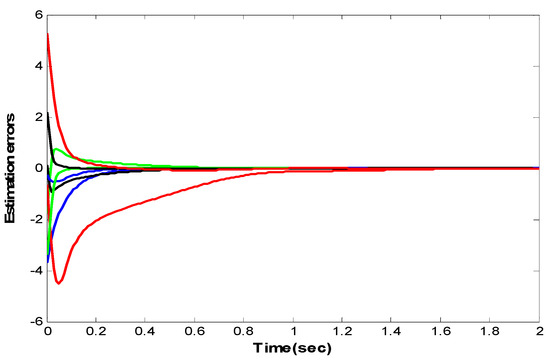
Figure 2.
Evolution of the estimation errors for .
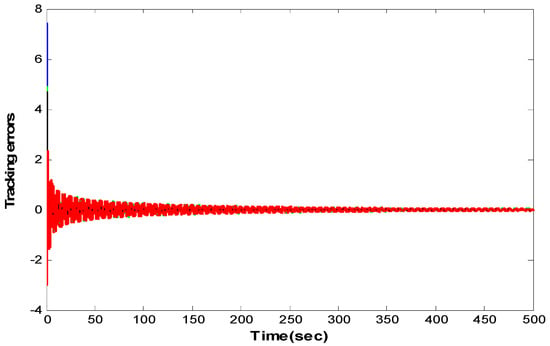
Figure 3.
Evolution of the tracking errors for .
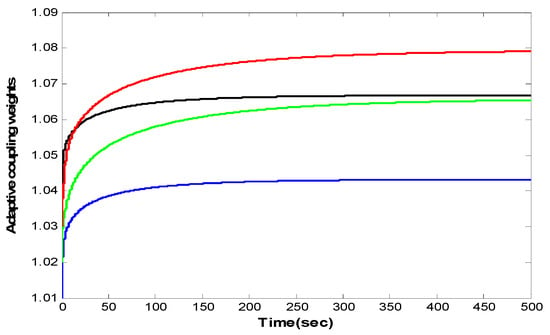
Figure 4.
Evolution of the adaptive coupling weights for .
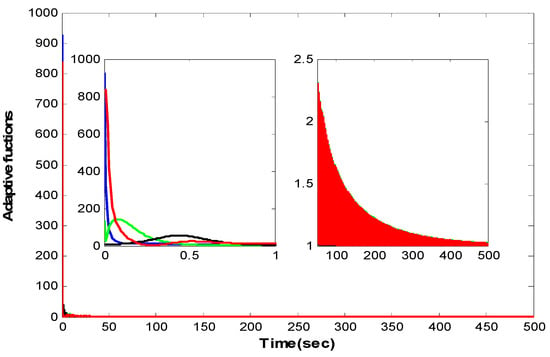
Figure 5.
Evolution of the adaptive functions for .
5. Conclusions
This paper solved the consensus tracking issue for multi-agent systems split into general linear dynamics and one-sided Lipschitz nonlinearity. A novel observer-based adaptive protocol was proposed, and, further, it was shown that both the estimate errors and the tracking errors converge to zero as the time tends to infinity. Different from the existing protocols, the distinctive merit of our protocol is the combination of the directed network, fully distributed communication fashion and observer-based feedback in a uniform framework. Furthermore, the observer gains and protocol parameters can be obtained by solving LMIs, which is easily and numerically tractable via the standard software (Matlab software 9.13, MathWorks, Natick, MA, USA). Investigating the cooperative control issues for other types of nonlinear multi-agent systems is our future work.
Author Contributions
Conceptualization, H.C.; methodology, W.Z.; writing—original draft, X.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work is supported in part by the National Key R&D Program of China under Grant 2022ZD0119903, in part by the National Natural Science Foundation of China under Grants and 62173188 and U2141234, in part by the Shanghai Science and Technology program under Grant 22015810300 and Grant 19510745200, in part by the Hainan Province Science and Technology Special Fund under Grant ZDYF2021GXJS041.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to limited space.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A
Now, we give a technical lemma, which is modified from Theorem 1 in [4] and is instrumental to derive the main results in Section 3.
Lemma A1.
Suppose that
is a positive definition matrix and let
,
. Under Assumption 2, the following inequality holds:
if
and there exists an appropriately small positive scalar
, such that
and
hold.
Proof.
Due to , one can get
From (3), we have . Thus,
Substituting (A3) into (A2) leads to
Knowing that and using the one-sided Lipschitz inequality (2) in (A4), we obtain
We can conclude that (A1) obviously holds. □
References
- Cao, Y.; Yu, W.; Ren, W.; Chen, G. An overview of recent progress in the study of distributed multi-agent coordination. IEEE Trans. Ind. Electron. 2013, 9, 427–438. [Google Scholar] [CrossRef]
- Li, Z.; Wen, G.; Duan, Z.; Ren, W. Designing fully distributed consensus protocols for linear multi-agent systems with directed graphs. IEEE Trans. Autom. Control 2014, 64, 1152–1157. [Google Scholar] [CrossRef]
- Olfati-Saber, R.; Murray, R. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans. Autom. Control 2004, 49, 1520–1533. [Google Scholar] [CrossRef]
- Yu, W.; Zhou, L.; Yu, X.; Lu, J.; Lu, R. Consensus in multi-agent systems with second-order dynamics and sampled data. IEEE Trans. Ind. Inform. 2013, 9, 2137–2146. [Google Scholar] [CrossRef]
- Ni, W.; Cheng, D. Leader-following consensus of multi-agent systems under fixed and switching topologies. Syst. Control Lett. 2010, 59, 209–217. [Google Scholar] [CrossRef]
- Garcia, E.; Cao, Y.; David, W. Decentralized event-triggered consensus with general linear dynamics. Automatica 2014, 50, 2633–4050. [Google Scholar] [CrossRef]
- Li, C.; Qu, Z.; Weitnauer, M.A. Distributed extremum seeking and formation control for nonholonomic mobile network. Syst. Control Lett. 2015, 75, 27–34. [Google Scholar] [CrossRef]
- Wen, G.; Duan, Z.; Chen, G. Consensus tracking of multi-agent systems with Lipschitzt type node dynamics and switching topologies. IEEE Trans. Circuits 2014, 61, 499–511. [Google Scholar]
- Li, Z.; Liu, X.; Fu, M.; Xie, L. Global H∞ consensus of multi-agent systems with Lipschitzt non-linear dynamics. IET Control Theory Appl. 2012, 6, 2041–2048. [Google Scholar] [CrossRef]
- Abbaszadeh, M.; Marquez, H. Nonlinear observer design for one-sided Lipschitz systems. In Proceedings of the IEEE American Control Conference, Baltimore, MD, USA, 29 July 2010. [Google Scholar]
- Stuart, M.; Humphries, A.R. Dynamical Systems and Numerical Analysis; Cambridge University Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Moisan, M.; Bernard, O.; Gouz, J. Near optimal interval observers bundle for uncertain bioreactors. Automatica 2009, 45, 291–301. [Google Scholar] [CrossRef]
- Dekker, K.; Verwer, J. Stability of Runge-Kutta methods for stiff nonlinear differential equations. SIAM J. Numerical Anal. 1984, 31, 1147–1168. [Google Scholar]
- Hairer, E.; Norsett, S.P.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and DAE Problems; Springer: Berlin/Heidelberg, Germany, 1993. [Google Scholar]
- Benallouch, M.; Boutayeb, M.; Zasadzinski, M. Observer design for one-sided Lipschitz discrete-time systems. Syst. Control Lett. 2012, 61, 879–886. [Google Scholar] [CrossRef]
- Zhang, W.; Su, H.; Han, Z. Non-linear observer design for one-sided Lipschitz systems: A linear matrix inequality approach. IET Control Theory Appl. 2012, 6, 1297–1303. [Google Scholar] [CrossRef]
- Zhang, W.; Su, H.; Zhu, F. A Note on observers for discrete-time Lipschitz nonlinear systems. IEEE Trans. Circuits 2012, 59, 123–127. [Google Scholar] [CrossRef]
- Zhang, W.; Su, H.; Wang, H.; Han, Z. Full-order and reduced-order observers for one-sided Lipschitz nonlinear systems using Riccati equations. Commun. Nonlinear Sci. Numer. Simulat. 2012, 17, 4968–4977. [Google Scholar] [CrossRef]
- Li, Z.; Duan, Z. Consensus of multi-agent systems and synchronization of complex networks: A unified viewpoint. IEEE Trans. Circuits 2010, 57, 113–127. [Google Scholar]
- Trentelman, H.L.; Takaba, K.; Monshizadeh, N. Robust synchronization of uncertain linear multi-agent systems. IEEE Trans. Autom. Control 2013, 58, 1511–1523. [Google Scholar] [CrossRef]
- Saboori, I.; Khorasani, K. H∞ Consensus achievement of multi-agent systems with directed and switching topology networks. IEEE Trans. Autom. Control 2014, 59, 3104–3109. [Google Scholar] [CrossRef]
- Su, H.; Chen, M.Q.; Lam, J.; Lin, Z. Semi-global leader-following consensus of linear multi-agent systems with input saturation via low gain feedback. IEEE Trans. Circuits Syst. 2013, 60, 1881–1889. [Google Scholar] [CrossRef]
- Su, H.; Chen, M.Q.; Wang, X.; Lam, J. Semiglobal observer-based leader-following consensus with input saturation. IEEE Ind. Electron. 2014, 61, 2842–2850. [Google Scholar] [CrossRef]
- Zhang, F.; Trentelman, H.L.; Jacquelien, M.A. Fully distributed robust synchronization of networked Lur’e systems with incremental nonlinearities. Automatica 2014, 50, 2515–2526. [Google Scholar] [CrossRef]
- DeLellis, P.; Bernardo, M.D.; Garofalo, F. Adaptive pinning control of networks of circuits and systems in Lur’e form. IEEE Trans. Circuits Syst. 2013, 60, 3033–3042. [Google Scholar] [CrossRef]
- Li, Z.; Ren, W.; Liu, X.; Fu, M. Consensus of multi-agent systems with general linear and lipschitz nonlinear dynamics using distributed adaptive protocols. IEEE Trans. Autom. Control 2013, 58, 1786–1791. [Google Scholar] [CrossRef]
- Wang, C.; Ji, H. Leader-following consensus of multi-agent systems under directed communication topology via distributed adaptive nonlinear protocol. Syst. Control Lett. 2014, 70, 23–29. [Google Scholar] [CrossRef]
- Li, Z.; Ren, W.; Liu, X.; Xie, L. Distributed consensus of linear multi-agent systems with adaptive dynamic protocols. Automatica 2013, 49, 1986–1995. [Google Scholar] [CrossRef]
- Chu, H.; Liu, X.; Zhang, W.; Cai, Y. Observer-based consensus tracking of multi-agent systems with one-sided Lipschitz nonlinearity. J. Franklin Inst. 2016, 353, 1594–1614. [Google Scholar] [CrossRef]
- Yu, W.; Ren, W.; Zheng, W.; Chen, G.; Lu, J. Distributed control gains design for consensus in multi-agent systems with second-order nonlinear dynamics. Automatica 2013, 49, 2107–2115. [Google Scholar] [CrossRef]
- Rehan, M.; Jameel, A.; Ahn, C.K. Distributed consensus control of one-sided Lipschitz nonlinear multiagent systems. IEEE Trans. Syst. Man Cybern. Syst. 2018, 48, 1297–1308. [Google Scholar] [CrossRef]
- Chen, B.; Wang, Z.; Chen, H.; Bai, H. Distributed adaptive consensus control of one-sided Lipschitz nonlinear multi-agent systems with directed graphs. In Proceedings of the 2022 34th Chinese Control and Decision Conference, Hefei, China, 15–17 August 2022. [Google Scholar] [CrossRef]
- Rehan, M.; Jameel, A.; Ah, C.K. Adaptive distributed consensus control of one sided Lipschitz nonlinear multiagents. IEEE Trans. Syst. Man Cybern. Syst. 2019, 49, 568–578. [Google Scholar] [CrossRef]
- Zhang, H.; Lewis, F. Adaptive cooperative tracking control of high-order nonlinear systems with unknown dynamics. Automatica 2012, 48, 1432–3149. [Google Scholar] [CrossRef]
- Bernstein, D. Matrix Mathematics: Theory, Facts, and Formulas; Princeton University: Princeton, NJ, USA, 2009. [Google Scholar]
- Hassan, K. Nonlinear Systems, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).