Physical-Unclonable-Function-Based Lightweight Three-Factor Authentication for Multiserver Architectures

Abstract

To support more complex and robust online services, enterprise-class applications prefer to interconnect multiple servers as the pedestal to enhance the system’s interoperability. However, the multiserver architecture always struggles to reconcile the trade-off between convenience and security, leaving users exposed to a variety of network attack threats. Existing security authentication schemes based on the Chebyshev Chaotic Map for multiserver architectures cannot provide three-factor (including password, biometric feature, and smart card) security. Therefore, we propose a novel Physical-Unclonable-Function-based Lightweight Three-Factor Authentication (PUF-LTA) scheme, which can achieve three-factor security. The PUF-LTA scheme mainly includes two components: (1) PUF-assisted registration and (2) lightweight mutual authentication with one-time interaction. During the PUF-assisted registration process, to defend against side-channel attacks on smart cards, the login credentials of users are XORed with the unique identifier generated by the PUF so that the adversary cannot obtain these secret login credentials. During the lightweight mutual authentication process, we combine the Chebyshev polynomial map and symmetric encryption/decryption to negotiate the session key between users and servers, which only needs one interaction. The security performance of PUF-LTA is theoretically proved by leveraging the random oracle model. In contrast with relevant multiserver authentication schemes, PUF-LTA is more efficient and suitable for resource-constrained multiserver environments because it can ensure secure three-factor authentication and support flexible biometrics and password updates with less computation cost.

1. Introduction

With significant developments in cloud/edge computing and Internet of Things (IoT), intelligent terminals have become an integral part of human society [1,2,3]. Intelligent terminals often serve as a basic interaction tool among users, experts, and institutions, constantly supporting various remote-access services (e.g., online payment, e-health, and e-commerce) and scanning data (e.g., transactional data, medical diagnosis data, and military data).

As the number of intelligent terminals increases rapidly, it is difficult for conventional single server architecture to respond to high concurrent requests from large-scale terminals in real time due to limited computation, communication, and storage resources. This is because these participants communicate mostly over a public channel, such as wireless communication, and information transmitted over public channels is vulnerable to many cyberattacks (e.g., eavesdropping, replay, interception, modification, and impersonation attacks) [4,5,6].

The single-server authentication scheme is not feasible and burdensome when applied in a multiserver scenario. On one hand, it is very inconvenient for users to register on each server because remembering all usernames and passwords on different servers is very hard. On the other hand, users will suffer from password leakage if they register the same password on different servers. Moreover, existing schemes for the multiserver architecture often adopt modular exponentiation operations or elliptic curve scalar multiplication, which leads to high computation overhead [7,8,9,10].

Hence, designing a robust and lightweight multiserver mutual authentication scheme is crucial for high-level security requirements. Chebyshev’s chaotic map is considered a promising approach to tackle the aforementioned issues because of its efficient computation. To improve authentication efficiency, Chatterjee et al. [11] designed an authentication scheme that integrates Chebyshev’s chaotic map, symmetric encryption/decryption, and a one-way hash function to provide a three-factor authentication protocol for multiserver environments. However, according to the analysis by Yu et al. [12], their integrated scheme still could not resist user impersonation attacks, and it also could not provide enough guarantee for user untraceability. Above all, their scheme did not achieve three-factor security as they claimed. Based on this, an extended authentication scheme was designated by Yu et al., and this scheme was claimed to have the ability to defend against all known security attacks and achieve three-factor security in multiserver environments. Unfortunately, because of design flaws, server impersonation attacks, user impersonation attacks, and man-in-the-middle attacks still can be committed successfully in their scheme. Meanwhile, during the authentication process, user untraceability was not achieved for the scheme-linked personally identifiable information in the user authentication request. It is noteworthy that their scheme still did not achieve three-factor security because biometric information could be obtained by any other legitimate user.

Generally, there are three components in a multiserver authentication architecture, including a registration center (RC), users, and servers. In the authentication process, RC publishes system parameters and offers registration services. Subsequently, users and servers conduct mutual authentication, which means the client verifies the authenticity of the server’s identity, and the server also needs to verify the authenticity of the client’s identity. Ultimately, users can securely access services from the server upon successful mutual authentication. To reduce the computation complexity and improve the security of multiserver authentication, a novel Physical-Unclonable-Function-empowered Lightweight Three-factor Authentication (PUF-LTA) scheme is designed in this paper that requires only one registration for users to access all servers. It ensures true three-factor security, simplifying the user experience and reducing the overall administrative burden.

The main contributions of this paper are listed as follows:

(1)

We analyze the three-factor multiserver authentication scheme proposed by Yu et al. [12], and the result shows that their scheme cannot resist man-in-the-middle attacks or user/server impersonation attacks. Furthermore, their scheme also cannot guarantee untraceability or three-factor security.

(2)

A novel Physical-Unclonable-Function-based Lightweight Three-factor Authentication (PUF-LTA) scheme is proposed for multiserver environments. In our scheme, the login credentials of users and servers are protected by the PUF, supporting three-factor security. Additionally, during the mutual authentication phase of PUF-LTA, only a one-time interaction is required between users and servers to negotiate their session key. This is because Chebyshev’s chaotic map and symmetric encryption/decryption are skillfully integrated during the negotiation process.

(3)

Leveraging random oracle models, the security of the proposed PUF-LTA is theoretically proven. To validate the practicality and efficiency of the proposed PUF-LTA for multiserver architectures, comparisons of security performance, and computation complexity are provided.

The structure of this paper is organized as follows. The related work of multiserver authentication and the preliminaries of this paper are presented in Section 2 and Section 3, respectively. We briefly review Yu et al.’s scheme in Section 4. Section 5 clarifies the vulnerabilities of their scheme. The workflow of the proposed PUF-LTA is presented in Section 6, while the formal and informal security analysis of the PUF-LTA are comprehensively provided in Section 7. Section 8 demonstrates the performance comparison and results discussion against existing methods. We conclude our work in Section 9.

2. Related Work

In the single-server environment, it is general to utilize a password-based authentication mechanism to provide secure authentication over a public channel. Unfortunately, such authentication schemes [13,14,15,16] are impractical and insecure when they are applied to multiserver environments. On one hand, it is troublesome for users to register with each server and remember their different login credentials (e.g., usernames and passwords). On the other hand, strong binding between server access rights and user passwords leads to serious vulnerability if the passwords are leaked or smart cards are lost. For example, the scheme of Li et al. [17] is a password-based authentication framework combined with a neural network for multiserver environments. In the password-based authentication scheme, each user is required to register in the registration center, and then the registered users have unrestricted access to all different servers with the same password. Therefore, their scheme will be unsafe as long as a user’s password is leaked. To resist online dictionary guessing attacks and password testing attacks, Zhang et al. [18] designated a single-sign-on authentication scheme that utilized a password-based threshold to thwart adversaries from compromising the identity servers. Specifically, their scheme introduces multiple identity servers and issues authentication tokens in a thresholded way.

The n-factor authentication protocol enhances the security of the system by adding some static information (e.g., smart card, biological information) as verification proofs. Hence, it is also introduced extensively into multiserver environments to provide stronger identity authentication. In 2014, a robust three-factor authentication scheme was proposed in [19], which integrates biometrics and Elliptic Curve Cryptography (ECC) into a multiserver environment. Although this is the first three-factor authentication scheme that can truly be applied in a multiserver environment, the computation cost and communication cost are substantial, and their scheme also fails to resist server/user impersonation attacks. To address the above drawbacks, Odelu et al. [20] proposed a new three-factor multiserver authentication protocol. However, according to the analysis of Zhang et al., their scheme cannot resist Denial of Service (DoS) attacks or insider attacks, and it lacks robustness, which may lead to system collapse. Then, Zhang et al. [21] proposed an improved three-factor multiserver authentication protocol, which integrates Chebyshev’s chaotic map and a secure sketch algorithm to further reduce computation costs. Unfortunately, the leakage of long-lived master keys could lead to the leakage of past session keys in their scheme, which means their scheme was still vulnerable to Perfect Forward Secrecy. Sudhakar et al. [22] designed a two-factor multiserver authentication protocol, but Cho et al. [23] clarified that their protocol could not guarantee the user’s privacy and would suffer from many cyberspace attacks (e.g., session key disclosure attacks, internal corruption attacks, replay attacks, and man-in-the-middle attacks). Therefore, Cho et al. proposed a more powerful multiserver three-factor protocol for e-governance systems, which aims to integrate a fuzzy extractor to utilize both Elliptic Curve Cryptography (ECC) and biometric features to accomplish two-way authentication. Unfortunately, none of these solutions have achieved three-factor secrecy, that is, when an adversary can obtain two of three factors (password, smart card, or biological information), he/she can launch some attacks. The importance of three-factor secrecy lies in the fact that as long as users ensure that one of the three factors is not obtained by attackers, the security of the solution can be guaranteed.

Recently, a Physical Unclonable Function (PUF), acting as a nonvolatile hardware security technique, has been utilized in loT systems to accomplish mutual authentication among devices [24,25,26,27,28]. Subsequently, the PUF could also be applied in multiserver authentication schemes to improve security. In 2021, Zhang et al. [29] integrated the PUF and cancelable biometrics to accomplish a user authentication scheme in a multiserver environment. Their scheme generates cancelable biometrics through biometrics fusion processing and then provides a multiserver authentication scheme based on secret sharing and Biometrics-as-a-Service. Based on this, their scheme not only ensures the privacy of the user but also enhances the credibility of the biometrics. According to the properties of the PUF, once a physical device deployed with a PUF is attacked, the output value of the PUF will change, which can effectively protect the security of the data stored on the physical device.

Furthermore, Self-Certified Public Key Cryptography (SCPKC) has also been utilized in authentication protocols for multiserver environments. Based on SCPKC, He et al. [30] designed a mobile user authentication protocol, which also provides user anonymity. Compared with two other anonymous mobile user authentication protocols, the computational and communicational costs of their scheme are less than 74.93% and 37.43%. However, Ying et al. [31] stated that their protocol still incurs a significant computational complexity due to the integration of bilinear pairing and scalar multiplication computation. Therefore, Ying et al. further proposed a lightweight protocol, which utilizes SCPKC and ECC. Their scheme utilizes ECC instead of any pairing operation to reduce computational overhead. Besides, their scheme ensures user anonymity and untraceability based on dynamic identities. Unfortunately, Ul Haq et al. [32] found that some specific attacks (e.g., user impersonation attacks, identity guessing attacks, and password guessing attacks) can be carried out against Ying et al.’s scheme, and both strong user anonymity and two-factor security are not truly accomplished. Therefore, Ul Haq et al. designed a new two-factor authentication scheme based on SCPKC to refine Ying et al.’s scheme. Their scheme improves the efficiency of computation and communication compared with Ying et al.’s scheme. Furthermore, Xiong et al. [33] proposed a new multiserver authentication scheme for mobile cloud computing (MCC) environments, which integrates hierarchical access control into the authentication protocol. In 2023, Soni et al. [34] proposed a novel multiserver authentication framework for intelligent healthcare systems, which consists of signature-based static authentication and machine-learning-based continuous monitoring.

3. Preliminaries

3.1. Chebyshev’s Chaotic Map

Chebyshev’s chaotic map can defined as $T_n\left(x\right)=2x{T}_{n-1}\left(x\right)-T_{n-2}\left(x\right)$, where $n\ge 2$, $n\in Z$, $x \in [-1, 1]$, $T_0\left(x\right)=1$, $T_1\left(x\right)=x$. When $x \in \left[-1, 1\right]$. The semigroup property of Chebyshev’s chaotic map can be represented as $T_r\left(T_s\left(x\right)\right)=T_{sr}\left(x\right)=T_s\left(T_r\left(x\right)\right)$ [35].

Zhang et al. [36] stated that the semigroup property of Chebyshev’s chaotic map holds for Chebyshev polynomials defined on the interval $[-\infty ,+\infty ]$. That is to say, $T_r\left(T_s\left(x\right)\right)=T_{sr}\left(x\right)=T_s\left(T_r\left(x\right)\right)$, where $T_n\left(x\right)=\cos \left(n\times \mathit{arccos}\left(x\right)\right) mod p$, $n\ge 2$, $n\in Z$, $x \in [-\infty ,+\infty ]$, and $p$ is a large prime number.

The chaotic map discrete logarithm problem $\left(CMDLP\right)$: If there is a Chebyshev chaotic map $y=T_r\left(x\right) mod p$, where $p$ is a large prime number, and $x$ and $y$ are known, it is computationally infeasible in polynomial-time to calculate the value of $r$.

The Computation of Chaotic Maps Diffie–Hellman Problem $\left(CMCDHP\right)$: If there is an extended Chebyshev polynomial $T_s\left(x\right) mod p$ and $T_r\left(x\right) mod p$, where $x \in [-\infty ,+\infty ]$, and $p$ is a large prime number, $CMCDHP$ means that it is computationally infeasible in polynomial-time to calculate the value of $T_{sr}\left(x\right) mod p$.

3.2. Fuzzy Extractor

Biometric information is not completely consistent for the same user (e.g., the different contact surfaces during fingerprint collection). Moreover, considering the threat of information leakage, users hesitate to upload their original biometric information to servers. Therefore, the fuzzy extraction technique is important for biometric application. Dodis et al. [37] proposed the fuzzy extractor algorithm to extract and recover the biometric information. The fuzzy extractor algorithm consists of the generation algorithm $Gen \left(·\right)$ and the reproduction algorithm $Rep(·)$. In contrast to conventional cryptographic keys, their algorithm is neither precisely reproducible nor distributed uniformly. That is, the fuzzy extractor algorithm extracts a uniformly distributed key from repeated noisy readings of a high-entropy secret.

(1)

The generation of the biological key:

$$\left(\sigma , \tau \right)=Gen \left(Bio\right)$$

$Bio$ is the biological information and $Gen \left(·\right)$ is the generation function, $\sigma$ is the biological key, and $\tau$ is the recovery parameter which should be saved.

(2)

The recovery of the biological key:

$$\sigma =Rep\left({Bio}^{\prime }, \tau \right)$$

$Rep \left(·\right)$ is the recovery function, $\sigma$ is the recovery biometric key, $Bio$ is a new biometric information input by user, and $\tau$ is the recovery parameter that is saved in the user’s device.

3.3. Physical Unclonable Function

The Physical Unclonable Function could generate a unique ‘fingerprint’ or trust anchor for a physical entity [38]. Actually, every integrated circuit (IC) has some subtle differences because normal manufacturing cannot avoid slight deviations. For a physical entity with an integrated circuit (IC), the PUF exploits this deviations to generate a unique challenge–response pair.

The PUF has the properties as follows:

• The output of a PUF is dependent on the physical characteristics of the IC.
• The output of a PUF must be unpredictable.
• The PUF circuit is unclonable.
• The output of the PUF will change as long as any alteration happens to the physical characteristics of the system.

Ideally, physically cloning a PUF is infeasible, and PUFs do not store any secrets but generate the response upon a challenge. More importantly, when a PUF circuit is attacked by any active manipulation (e.g., side-channel attacks), its CRP mapping mechanism will be destructed and the challenge-response pair will also change.

3.4. System Model

Figure 1 is a multiserver model. Any service provider may have one or more servers, and users can use multiserver authentication to obtain services from these servers. A multiserver system includes users, servers, and a registration center (RC). RC will publish the system initialization parameters first; then users and servers should register to the RC through a secure channel, respectively; finally, over a public channel, a user and a server will conduct mutual authentication, negotiate the session key, and securely communicate.

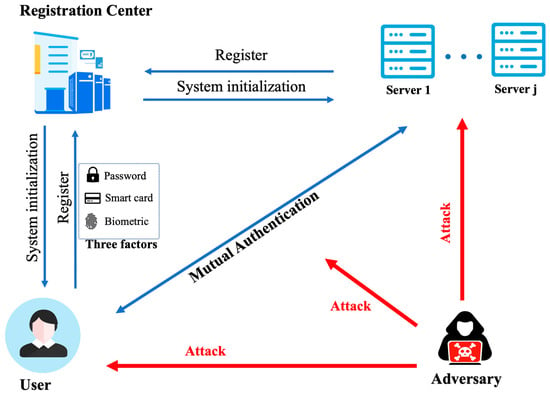
Figure 1. Network model of a multiserver environment.

3.5. Adversarial Model

According to the Dolev–Yao model [39] and the security requirements of multiserver authentication, we define the adversary model as follows:

(1)

An adversary could register as a legitimate user or server, but the registration center is completely trustworthy.

(2)

Users and servers can conspire to impersonate another entity. For example, they can impersonate a user to access another server or impersonate a server to provide false resources to other users.

(3)

An adversary has the ability to intercept, eavesdrop, modify, and replay all messages transmitted by public channels.

(4)

An adversary can obtain any two of the three factors to launch attacks but cannot simultaneously obtain all three factors.

4. Review of a Multi-Server Authentication Scheme

Yu et al. [12] proposed an extended chaotic-map-based authentication and key agreement scheme for a multiserver environment. Their scheme mainly consists of five phases: the system setup phase, server registration phase, user registration phase, login and authentication phase, and user password and biometric update phase. Here, we omit the last phase. Table 1 lists the notations used in this paper.

Table 1. Notations used in this paper.

Symbols	Descriptions
$h(·)$	One-way hash function
$BH(·)$	Biometric hash function
$T_x(·)$	Chebyshev’s chaotic map polynomial
$Gen\left(·\right),Rep\left(·\right)$	The generation and reproduction function of a fuzzy extractor
$PUF(·)$	Physical Unclonable Function
$x,y$	Private key of $RC$
$A_{sj}$	Public key of $S_j$
$K_j$, $a_{sj}$	Private key of $S_j$
${ID}_i$	Identification of $U_i$
${SID}_j$	Identification of $S_j$
${PW}_i$	Password of $U_i$
${Bio}_i$	Biometric information of $U_i$
$E(·)/D(·)$	Symmetric encryption/decryption
${SC}_i$	Smart card of $U_i$
${SK}_{ij}$	Session key between $U_i$ and $S_j$
$\oplus$	Bitwise XOR operation
$\parallel$	String concatenation operation
$mod$	Modulus operation

4.1. System Setup Phase

The $RC$ chooses two random numbers $x$ and $y$ in $[-\infty ,+\infty ]$ and sets them as the system master keys. Then, $RC$ chooses a secure one-way hash function $h(·)$.

4.2. Server Registration Phase

Step 1: $S_j$ chooses identity ${SID}_j$ and transmits it to $RC$ over a secure channel.

Step 2: Once ${SID}_j$ is received, $RC$ computes $K_j=h({SID}_j\parallel y)$ and publishes $\{{SID}_j, z\}$. Afterward, $RC$ transmits $K_j$ back to $S_j$ through a secure channel.

Step 3: $S_j$ receives $K_j$ and stores it safely.

4.3. User Registration Phase

Step 1: $U_i$ inputs ${ID}_i$ and ${PW}_i$, and enters ${Bio}_i$. Then, $U_i$ utilizes the biometric hash function $BH(·)$ to obtain $b_i$ and computes ${PID}_i=h({ID}_i\parallel b_i)$, ${PWB}_i=h({PW}_i\parallel b_i)$. Finally, $U_i$ sends $\left\{{ID}_i,{PID}_i,{PWB}_i\right\}$ to $RC$ to register over a secure channel.

Step 2: Upon $U_i’s$ registration request, $RC$ calculates $A_i=h\left({ID}_i\parallel {PWB}_i\right)mod n$, $B_i=h({PID}_i\parallel x)$, $C_i=B_i\oplus {PWB}_i$, where $2^4\le n\le 2^8$. Then, $RC$ computes $D_{ij}=h(B_i\parallel K_j)$, $E_{ij}=B_i\oplus K_j$, $F_{ij}=D_{ij}\oplus h\left(B_i\right)$, where $1\le j\le m$, and m denotes the maximum number of servers. Next, $\{A_i,C_i,E_{ij},F_{ij},n,h\left(·\right),h\left(x\parallel y\right),z\}$ are stored into the ${SC}_i$, and ${SC}_i$ is distributed to each $U_i$ safely.

Step 3: $U_i$ keeps the ${SC}_i$ card safely.

4.4. Login and Authentication Phase

Step 1: $U_i$ inserts ${SC}_i$ and inputs ${ID}_i$, ${PW}_i$, and enters ${Bio}_i$. ${SC}_i$ calculates $b_i=BH\left({Bio}_i\right)$, ${PID}_i=h({ID}_i\parallel b_j)$, and ${PWB}_i=h({PW}_i\parallel b_i)$ and then verifies whether $A_i=h\left({ID}_i\parallel {PWB}_i\right)mod n$; if not, ${SC}_i$ rejects the session; else, ${SC}_i$ randomly selects a number $n_i$, chooses the server’s identity ${SID}_j$, and computes $N_i=T_{n_i}\left(z\right)$, $P_{ij}=E_{ij}\oplus h({SID}_j\parallel h(x\parallel y)\parallel N_i)$, $N_k=h(B_i\parallel N_i)$, $D_{ij}=F_{ij}\oplus h\left(B_i\right)$, ${CID}_{ij}={PID}_i\oplus h(P_{ij}\parallel B_i)$, and $M_1=h(B_i\parallel D_{ij}\parallel {CID}_{ij}\parallel N_k)$. Finally, $U_i$ sends $\{P_{ij},{CID}_{ij},N_i,M_1\}$ to server $S_j$.

Step 2: Upon the login request from $U_i$, $S_j$ calculates $E_{ij}=P_{ij}\oplus h({SID}_j\parallel h(x\parallel y)\parallel N_i)$, $B_i=E_{ij}\oplus K_j$, $D_{ij}=h(B_i\parallel K_j)$, $N_k=h(B_i\parallel N_i)$, and $M_1^{\ast }=h(B_i\parallel D_{ij}\parallel {CID}_i\parallel N_k)$ and verifies whether $M_1$ equals $M_1^{\ast }$. If not, $S_j$ rejects the session. Else, $S_j$ selects a random number $n_j$ and calculates $N_j=T_{n_j}\left(z\right)$, ${PID}_i={CID}_{ij}\oplus h(P_{ij}\parallel B_i)$, $M_2=h({PID}_i\parallel P_{ij}\parallel D_{ij}\parallel B_i\parallel {SID}_j\parallel N_j)$, and $M_3=N_k\oplus N_j$. Afterward, $S_j$ sends $\{M_2,M_3\}$ to $U_i$.

Step 3: Upon receiving $\{M_2, M_3\}$, $U_i$ calculates $N_j=M_3\oplus N_k$. $U_i$ verifies whether $M_2=h({PID}_i\parallel P_{ij}\parallel D_{ij}\parallel B_i\parallel {SID}_j\parallel N_j)$, if not, $U_i$ rejects the session; otherwise, $U_i$ computes $M_4=$ h($B_i\parallel D_{ij}\parallel N_j\parallel {SID}_j$) and $T_{ij}=T_{n_i}\left(N_j\right)$ and obtains the session key ${SK}_{ij}=h({PID}_i\parallel P_{ij}\parallel T_{ij})$. Finally, $U_i$ sends $\left\{M_4\right\}$ to $S_j$.

Step 4: $S_j$ receives $\left\{M_4\right\}$ and verifies whether $M_4=$ h($B_i\parallel D_{ij}\parallel N_j\parallel {SID}_j$) holds, if not, $S_j$ discards the session; otherwise, $S_j$ calculates $T_{ji}=T_{n_j}\left(N_i\right)$ and negotiates the same session key with $U_i$: ${SK}_{ji}=h\left({PID}_i\parallel P_{ij}\parallel T_{ji}\right)=h\left({PID}_i\parallel P_{ij}\parallel T_{ij}\right)={SK}_{ji}$.

5. Cryptanalysis of a Multi-Server Authentication Scheme

5.1. User Traceability

Assuming that an adversary is a legitimate user $U_a^{\prime }$, he/she can register a legal $U_a^{\prime }$ and obtain ${SID}_j$, $h(x\parallel y)$.

During the login and authentication phase, $P_{ij}=E_{ij}\oplus h({SID}_j\parallel h(x\parallel y)\parallel N_i)$, where $N_i$ was transmitted in public channel, ${SID}_j$ is public, and $h(x\parallel y)$ is written into the adversary’s ${SC}_i$. Then, the adversary can extract $E_{ij}$ from $P_{ij}$, where $E_{ij}=B_i\oplus K_j=h({PID}_i\parallel x)\oplus h({SID}_j\parallel y)$. It is obvious that $E_{ij}$ is bound with ${PID}_i$.

In this case, if an adversary is a legal user, they can distinguish whether two sessions are initiated by one user through $E_{ij}$.

5.2. User Impersonation Attack

Firstly, we assume that an adversary is a legal user $U_a^{\prime }$ and they can register as a legal $U_a^{\prime }$. The adversary computes his/her ${PWB}_i=h({PW}_i\parallel b_i)$ and obtains $C_i=B_i\oplus {PWB}_i$, $E_{ij}=B_i\oplus K_j$ from $RC$. Then, the adversary obtains $B_i=C_i\oplus {PWB}_i$ and finally obtains the server’s $K_j=E_{ij}\oplus B_i$.

Then, the messages sent in the public channel can be eavesdropped on by the adversary. The adversary sends $\left\{P_{ij}^{\ast },{CID}_{ij}^{\ast }, N_i^{\ast }, M_1^{\ast }\right\}$ to the server to impersonate the legal user. As long as the server sends $\left\{M_2^{\ast },M_3^{\ast }\right\}$, the adversary computes $E_{ij}^{\ast }=P_{ij}^{\ast } \oplus h({SID}_j\parallel h(x\parallel y)\parallel N_i^{\ast })$, $B_i^{\ast }$ = $E_{ij}^{\ast }\oplus K_j$, $N_j^{\ast }=M_3^{\ast }\oplus h(B_i^{\ast }\parallel N_i^{\ast })$ obtains ${PID}_i^{\ast }={CID}_{ij}^{\ast }\oplus h(P_{ij}^{\ast }\parallel B_i^{\ast })$, $D_{ij}^{\ast }=h(B_i^{\ast }\parallel K_j^{\prime })$, and computes $M_4^{\ast }=h(B_i^{\ast }\parallel D_{ij}^{\ast }\parallel N_j^{\ast }\parallel {SID}_j)$.

Finally, $S_j$ certifies that the adversary is legal after receiving $M_4^{\ast }$.

5.3. Server Impersonation Attack

At first, an adversary can register a legal $U_a^{\prime }$, therefore, the adversary knows ${PWB}_i=h({PW}_i\parallel b_i)$ and obtain $C_i=B_i\oplus {PWB}_i$, $E_{ij}=B_i\oplus K_j$ from $RC$. Then, the adversary obtains $B_i^{\prime }=C_i\oplus {PWB}_i$, and finally gets server’s $K_j^{\prime }=E_{ij}\oplus B_i$.

Then, the adversary can eavesdrop on the messages in the public channel and obtain $\left\{P_{ij}, {CID}_{ij}, N_i, M_1\right\}$ from $U_i$. The adversary tries to impersonate the legal server. The adversary computes $E_{ij}^{\ast }=P_{ij} \oplus h\left({SID}_j\parallel h\left(x\parallel y\right)\parallel N_i\right)$, $B_i^{\ast }$ = $E_{ij}^{\ast }\oplus K_j^{\prime }$, $D_{ij}^{\ast }=h\left(B_i^{\ast }\parallel K_j^{\prime }\right), N_k^{\ast }=h\left(B_i^{\ast }\parallel K_j^{\prime }\right), M_1^{\ast }=h\left(B_i^{\ast }\parallel D_{ij}^{\ast }\parallel {CID}_{ij}\parallel N_k^{\ast }\right)$ and verifies whether $M_1^{\ast }$ equals $M_1$. Next, the adversary chooses a random number ${\mathrm{n}}_j^{\prime }$ and calculates $N_j^{\prime }=T_{{\mathrm{n}}_j^{\prime }}(z)$, ${PID}_i^{\ast }={CID}_{ij}\oplus h(P_{ij}\parallel B_i^{\ast })$, $M_2^{\prime }=h({PID}_i^{\ast }\parallel P_{ij}\parallel D_{ij}^{\ast }\parallel B_i^{\ast }\parallel {SID}_j\parallel N_j^{\prime })$, ${\mathrm{M}}_3^{\prime }=N_k^{\ast }\oplus N_j^{\prime }$. Afterward, the adversary sends $\{M_2^{\prime },{\mathrm{M}}_3^{\prime }\}$ to $U_i$.

Next, $U_i$ computes $N_j^{\prime }={\mathrm{M}}_3^{\prime }\oplus N_k$, verifies whether $M_2^{\prime }=h({PID}_i\parallel P_{ij}\parallel D_{ij}\parallel B_i\parallel {SID}_j\parallel N_j^{\prime })$ holds, computes $M_4=$ h($B_i\parallel D_{ij}\parallel N_j^{\prime }\parallel {SID}_j$), $T_{ij}=T_{n_i}\left(N_j^{\prime }\right)$, and obtains the session key ${SK}_{ij}=h({PID}_i\parallel P_{ij}\parallel T_{ij})$. Finally, $U_i$ sends $\left\{M_4\right\}$ to the adversary.

In the end, the adversary computes ${SK}_{ji}=h({PID}_i^{\ast }\parallel P_{ij}\parallel T_{ij})$ and impersonates the server successfully.

5.4. Man-in-the-Middle Attack

At first, an adversary can register a legal $U_a^{\prime }$; therefore, the adversary knows ${PWB}_i=h({PW}_i\parallel b_i)$ and obtains $C_i=B_i\oplus {PWB}_i$, $E_{ij}=B_i\oplus K_j$ from $RC$. Then, the adversary obtains $B_i^{\prime }=C_i\oplus {PWB}_i$ and finally obtains the server’s $K_j^{\prime }=E_{ij}\oplus B_i$.

Next, the adversary selects a random number $n_a$ and calculates ${\mathrm{N}}_a=T_{n_a}\left(z\right)$.

After receiving $\left\{P_{ij},{CID}_{ij},N_i,M_1\right\}$ from $U_i$, the adversary computes $E_{ij}^{\ast }=P_{ij}\oplus h\left({SID}_j\parallel h\left(x\parallel y\right)\parallel N_i\right)$, $B_i^{\ast }$ = $E_{ij}^{\ast }\oplus K_j^{\prime }$, $D_{ij}^{\ast }=h\left(B_i^{\ast }\parallel K_j^{\prime }\right),N_k^{\ast }=h\left(B_i^{\ast }\parallel K_j^{\prime }\right),M_1^{\ast }=h\left(B_i^{\ast }\parallel D_{ij}^{\ast }\parallel {CID}_{ij}\parallel N_k^{\ast }\right)$ and verifies whether $M_1^{\ast }$ equals $M_1$. Next, the adversary computes ${PID}_i^{\ast }={CID}_{ij}\oplus h(P_{ij}\parallel B_i^{\ast })$, $M_2^{\prime }=h({PID}_i^{\ast }\parallel P_{ij}\parallel D_{ij}^{\ast }\parallel B_i^{\ast }\parallel {SID}_j\parallel {\mathrm{N}}_a)$, and ${\mathrm{M}}_3^{\prime }=N_k^{\ast }\oplus {\mathrm{N}}_a$. Afterward, the adversary sends $\{M_2^{\prime },{\mathrm{M}}_3^{\prime }\}$ to $U_i$.

After receiving $\{M_2^{\prime },{\mathrm{M}}_3^{\prime }\}$ from the adversary, $U_i$ computes ${\mathrm{N}}_a={\mathrm{M}}_3^{\prime }\oplus N_k$, verifies whether $M_2^{\prime }=h({PID}_i\parallel P_{ij}\parallel D_{ij}\parallel B_i\parallel {SID}_j\parallel N_j^{\prime })$ holds, computes $M_4=$ h($B_i\parallel D_{ij}\parallel N_j^{\prime }\parallel {SID}_j$), $T_{ia}=T_{n_i}\left({\mathrm{N}}_a\right)$, and obtains the session key ${SK}_{ia}=h({PID}_i\parallel P_{ij}\parallel T_{ia})$. Finally, $U_i$ sends $\left\{M_4\right\}$ to the adversary. In the end, the adversary computes ${SK}_{ai}=h({PID}_i^{\ast }\parallel P_{ij}\parallel T_{ia})$ and impersonates the server successfully.

Meanwhile, the adversary computes $P_{ij}^{\prime }=E_{ij}^{\ast }\oplus h\left({SID}_j\parallel h\left(x\parallel y\right)\parallel {\mathrm{N}}_a\right)$, ${CID}_{ij}^{\prime }={PID}_i^{\prime }\oplus h(P_{ij}^{\prime }\parallel B_i^{\ast })$, and $M_1^{\prime }=h\left(B_i^{\ast }\parallel D_{ij}^{\ast }\parallel {CID}_{ij}^{\prime }\parallel {\mathrm{N}}_a\right)$ and sends $\{P_{ij}^{\prime },{CID}_{ij}^{\prime },M_1^{\prime },{\mathrm{N}}_a\}$ to server $S_j$.

After receiving $\{P_{ij}^{\prime }, {CID}_{ij}^{\prime },M_1^{\prime }, {\mathrm{N}}_a\}$ from the adversary, server $S_j$ computes $E_{ij}=P_{ij}^{\prime }\oplus h({SID}_j\parallel h(x\parallel y)\parallel {\mathrm{N}}_a)$, $B_i=E_{ij}\oplus K_j$, $D_{ij}=h(B_i\parallel K_j)$, $N_k=h(B_i\parallel {\mathrm{N}}_a)$, and $M_1^{\ast }=h(B_i\parallel D_{ij}\parallel {CID}_i\parallel N_k)$ and verifies whether $M_1$ equals $M_1^{\ast }$. Then, $S_j$ chooses a random number $n_l$ and calculates $N_j=T_{n_j}\left(z\right)$, ${PID}_i={CID}_{ij}\oplus h(P_{ij}^{\prime }\parallel B_i)$, $M_2=h({PID}_i\parallel P_{ij}\parallel D_{ij}\parallel B_i\parallel {SID}_j\parallel N_j)$, and $M_3=N_k\oplus N_j$. Afterward, $S_j$ sends $\{M_2,M_3\}$ to $U_i$, but the message is hijacked by the adversary. After the adversary receives $\{M_2, M_3\}$ and computes $N_j=M_3\oplus N_K$, $M_4=$ h($B_i^{\ast }\parallel D_{ij}^{\ast }\parallel N_j\parallel {SID}_j$, $T_{aj}=T_{n_i}\left(N_j\right)$, they obtains the session key ${SK}_{aj}=h({PID}_i\parallel P_{ij}\parallel T_{aj})$. Finally, the adversary sends $\left\{M_4\right\}$ to $S_j$.

Step 4: $S_j$ receives $\left\{M_4\right\}$ and verifies whether $M_4$ equals h($B_i\parallel D_{ij}\parallel N_j\parallel {SID}_j$), if not, $S_j$ rejects the session; otherwise, $S_j$ verifies that $U_a^{\prime }$ is the legitimate user. Then, $S_j$ calculates $T_{ja}=T_{{\mathrm{n}}_j^{\prime }}\left(N_a\right)$ and negotiates the session key with the adversary: ${SK}_{ja}=h\left({PID}_i\parallel P_{ij}\parallel T_{ja}\right)=h\left({PID}_i\parallel P_{ij}\parallel T_{aj}\right)={SK}_{ja}$.

Finally, the adversary commits a man-in-the-middle attack successfully.

5.5. Three-Factor Security

According to the definition of three-factor security, if an adversary can obtain the user’s biometric ${Bio}_i$ and the information $\{A_i, C_i, E_{ij}, F_{ij}, n, h\left(·\right), h\left(x\parallel y\right), z\}$ stored in smart card ${SC}_i$, then the adversary can guess the $U_i$’s password ${PW}_{U_i}^{\ast }$ and compute $b_i=BH\left({Bio}_i\right)$, ${PWB}_i^{\ast }=h({PW}_{U_i}^{\ast }\parallel b_i)$, $B_i\prime =C_i\oplus {PWB}_i^{\ast }$, $K_j^{\prime }=E_{ij}⨁B_i\prime$, and $D_{ij}\prime =F_{ij}\oplus h(B_i\prime )$ and check whether $D_{ij}\prime =h(B_i\prime \parallel K_j\prime )$ or not. If yes, the guessed password ${PW}_{U_i}^{\ast }$ is correct. Otherwise, they reguess it again till the correct password is found.

Once the adversary obtains the correct password, he/she can know the correct $B_i, K_j$, $D_{ij}$. And the adversary can also obtain $\{P_{ij}, {CID}_{ij}, N_i, M_1\}$ from the public channel and obtains ${PID}_i$ $={CID}_{ij} \oplus h(P_{ij}\parallel B_i)$. Because ${PID}_i=h({ID}_i\parallel b_i)$, the adversary can guess the correct ${ID}_i$, and the adversary can also launch user impersonation attacks.

Therefore, Yu et al.’s scheme cannot achieve three-factor security.

6. The Proposed Scheme

The proposed scheme consists of five phases: (1) System initialization. (2) Sever registration. (3) User registration. (4) Mutual authentication and key agreement. (5) User password and biometric update phase.

6.1. System Initialization

The $RC$ selects two random numbers $x$ and $y$ in $\left[-\infty ,+\infty \right]$ as master keys of the system. Then, $RC$ chooses a secure one-way hash function $h(·)$.

6.2. Sever Registration

$RC$ selects ${SID}_j$ as an identity of server $S_j$, computes $K_j=h({SID}_j\parallel x)$, and generates a random number $a_{sj}$, computes $A_{sj}=T_{a_{sj}}(z)$, then sends $\left\{K_j, a_{sj}\right\}$ to $S_j$ through a secure channel, and then publishes $\{{SID}_j,A_{sj}\}$.

After receiving $\left\{K_j,a_{sj}\right\}$ from $RC$, $S_j$ generates a challenge $C_j$ and computes $R_j=PUF\left(C_j\right),{PK}_j=K_j\oplus h\left(R_j\parallel 1\right),{PA}_{sj}=a_{sj}\oplus h\left(R_j\parallel 2\right),$ and then $S_j$ stores $\left\{{SID}_j,z,{PK}_j,{PA}_{sj},C_j,PUF(·)\right\}$ secretly.

Figure 2 depicts this phase. It is worth mentioning that using 1 and 2 in calculating the hash functions of ${PK}_j$ and ${PA}_{sj}$ can reduce the problem of selecting and storing random numbers.

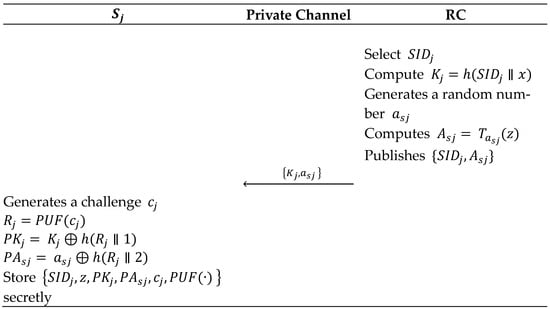
Figure 2. Sever registration phase.

6.3. User Registration

Step 1: The user $U_i$ generates an identity number ${ID}_i$ and password ${PW}_i$ and inputs their biometrics ${Bio}_i$. Then, the fuzzy function $Gen(·)$ is utilized to obtain $\left({\sigma }_i, {\tau }_i \right)$. Then, $U_i$ makes a request $\left\{{ID}_i\right\}$ to the registration center $RC$ to register over a secure channel.

Step 2: Upon the request of $U_i\prime$, $RC$ calculates ${PID}_i=E_x\left({ID}_i\parallel t_i\right)$, where $t_i$ is registration time, $C_{ij}=h({PID}_i\parallel K_j)$. And then, $RC$ sends $\{{PID}_i,C_{ij}\}$ to $U_i$ over a secure channel.

Step 3: Upon sending the message $\{{PID}_i,C_{ij}\}$ from $RC$, $U_i$ calculates $A_i=h\left({ID}_i\parallel {PW}_i\parallel {\sigma }_i\right)mod n$, $n\in (2^4,2^8)$ and generates a challenge $c_i$ and computes $R_i=PUF\left(c_i\right)$, ${PC}_{ij}=C_{ij}\oplus h({\sigma }_i\parallel {ID}_i\parallel {PW}_i\parallel R_i\parallel j)$, ${PPID}_i={PID}_i\oplus h(R_i\parallel {PW}_i\parallel {ID}_i\parallel {\sigma }_i\parallel j)$. Finally, $U_i$ stores {PPID_i, A_i, PC_i, c_i, PUF (·), n, h(·),${\tau }_i,Rep(·)\}$ into ${SC}_i$ and $U_i$ keeps card ${SC}_i$ safely.

Figure 3 depicts this phase. It is worth mentioning that using $mod n$ when calculating $A_i$ can effectively resist password and identity guessing attacks.

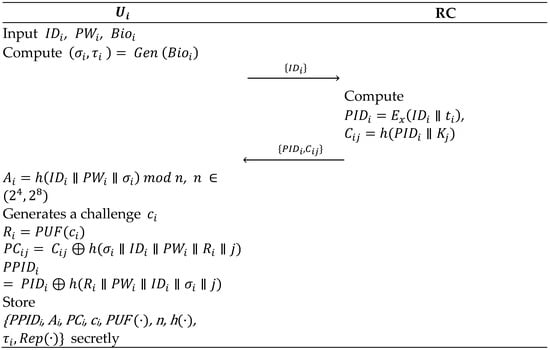
Figure 3. User registration phase.

6.4. Mutual Authentication and Key Agreement

Figure 4 depicts mutual authentication and key agreement phase.

Figure 4. Mutual authentication and key agreement.

Step 1: $U_i$ inserts smart card ${SC}_i$ and inputs the identity number ${ID}_i$, password ${PW}_i$, and biometrics ${Bio}_i^{\prime }$. Then, ${SC}_i$ computes ${\sigma }_i=Rep\left({Bio}_i^{\prime },{\tau }_i\right)$ and verifies whether $A_i=h\left({ID}_i\parallel {PW}_i\parallel {\sigma }_i\right)mod n$ holds, if not, ${SC}_i$ rejects the session; otherwise, ${SC}_i$ computes $R_i=PUF\left(c_i\right)$, $C_{ij}=P{C}_{ij}\oplus h({\sigma }_i\parallel {ID}_i\parallel {PW}_i\parallel R_i\parallel j)$, ${PID}_i={PPID}_i\oplus h(R_i\parallel {PW}_i\parallel {ID}_i\parallel {\sigma }_i\parallel j)$. Then, ${SC}_i$ generates two random numbers, $n_{i1},n_{i2}$, and selects the identity of the server ${SID}_j$ and computes ${\theta }_1=T_{n_{i1}}\left(z\right)$, ${\theta }_2=E_{T_{n_{i1}}\left(A_{sj}\right)}({PID}_i,n_{i2},T_1)$, ${\theta }_3=h(C_{ij}\parallel n_{i2}\parallel T_1\parallel {SID}_j\parallel {PID}_i)$. $U_i$ sends $\{{\theta }_1,{\theta }_2,{\theta }_3\}$ to ${SID}_j$ via a public channel.

Step 2: Upon the login request from $U_i$, $S_j$ decrypts ${\theta }_2$ and obtains $\left({PID}_i,n_{i2},T_1\right)=D_{T_{a_{sj}}\left({\theta }_1\right)}\left({\theta }_2\right)$. Then, $S_j$ verifies the freshness of $T_1$ and computes $C_{ij}=h({PID}_i\parallel K_j)$. If ${\theta }_3\ne h(C_{ij}\parallel n_{i2}\parallel T_1\parallel {SID}_j\parallel {PID}_i)$, $S_j$ rejects the session; otherwise, $S_j$ generates a random number $n_j$ and calculates ${\theta }_4=$ $T_{n_j}\left(z\right)$, ${SK}_{ji}=h\left(T_{n_j}\right({\theta }_1)\parallel {PID}_i\parallel {SID}_j\parallel T_1\parallel T_2)$, ${\theta }_5=E_{n_{i2}}(n_{i2},{\theta }_4,T_2,{SK}_{ij})$. Finally, $S_j$ sends $\left\{{\theta }_5\right\}$ to $U_i$ through a public channel.

Step 3: $U_i$ receives $\left\{{\theta }_5\right\}$ from $S_j$ and decrypts it via Decrypt $\left(n_{i2},{\theta }_4,T_2,{SK}_{ji}\right)=D_{n_{i2}}\left({\theta }_5\right)$. $U_i$ checks the freshness of $T_2$ and the validity of $n_{i2}$. Then, $U_i$ computes ${SK}^{\prime }=h\left(T_{n_{i1}}\right({\theta }_4)\parallel {PID}_i\parallel {SID}_j\parallel T_1\parallel T_2)$. If ${SK}_{ji}\ne {SK}^{\prime }$, $U_i$ terminates the session; othewiser $U_i$ sets the session key ${SK}_{ij}={SK}^{\prime }=h\left(T_{n_{i1}}\right({\theta }_4)\parallel P{ID}_i\parallel {SID}_j\parallel T_1\parallel T_2)$ = ${SK}_{ji}$. The mutual authentication between $U_i$ and $S_j$ is established successfully.

6.5. User Password and Biometric Update Phase

Step 1: $U_i$ inserts card ${SC}_i$, inputs ${ID}_{U_i}$ and ${PW}_i$, and their biometrics ${Bio}_i$. Then, ${SC}_i$ computes ${\sigma }_i=Rep\left({Bio}_i^{\prime },{\tau }_i\right)$ and verifies whether $A_i$ equals $h\left({ID}_i\parallel {PW}_i{\parallel \sigma }_i\right)mod n$, if not, ${SC}_i$ discards the login request; otherwise, ${SC}_i$ asks $U_i$ to enter a new password and new biological information.

Step 2: Upon receiving the new password ${PW}_i^{new}$ and new biometric feature ${Bio}_i^{new}$ of $U_i$, ${SC}_i$ uses the fuzzy extractor to calculate $\left({\sigma }_i^{new},{\tau }_i^{new}\right)=Gen\left({Bio}_i^{new}\right)$, $A_i^{new}=h\left({ID}_i\parallel {PW}_i^{new}\parallel {\sigma }_i^{new}\right)mod n$, ${PC}_{ij}^{new}=P{C}_{ij}\oplus h({\sigma }_i\parallel {ID}_i\parallel {PW}_i\parallel R_i\parallel j)\oplus h({\sigma }_i^{new}\parallel {ID}_i\parallel {PW}_i^{new}\parallel R_i\parallel j)$, ${PPID}_i^{new}={PPID}_i\oplus h(R_i\parallel {PW}_i\parallel {ID}_i\parallel {\sigma }_i\parallel j)\oplus h(R_i\parallel {PW}_i^{new}\parallel {ID}_i\parallel {\sigma }_i^{new}\parallel j)$.

Step 3: ${SC}_i$ replaces ${PPID}_i^{new}$, $A_i^{new}$, ${PC}_{ij}^{new}$, ${\tau }_i^{new}$ with ${PPID}_i$, $A_i$, $P{C}_{ij}$, and ${\tau }_i$.

7. Security Analysis

7.1. Provable Security

Based on the random oracle model, we formally prove the semantic security of our scheme below:

Our scheme is denoted as Scheme II and involves three entities:

(a)

A user $U_i$ with identity ${ID}_i$, password ${PWD}_i$, and biometrics ${Bio}_i$;

(b)

A registration center $RC$ with a private key $x$;

(c)

An application server $S_j$ with identity ${SID}_j$.

They all are treated as an oracle with three possible states:

(a)

$Accepted$;

(b)

$Rejected$;

(c)

$No output$.

In this model, there is a probabilistic polynomial-time ($PPT$) adversary $\mathcal{A}$ and a challenger $\mathcal{C}$. The security of our scheme is proved by a challenge–response game between the $PPT$ adversary $\mathcal{A}$ and the challenger $\mathcal{C}$. In this game, $\mathcal{A}$ simulates varieties of attacks by inquiring to $\mathcal{C}$ in polynomial-time. The queries are listed as follows:

(1)

Hash $h_i\left(x_i\right)$: An initially empty list $L_h^i$ is maintained by challenger $\mathcal{C}$ in this query. When $\mathcal{A}$ executes this query with input $x_i$, $\mathcal{C}$ returns an output $y_i$ if the tuples ($x_i,y_i$) exists. Otherwise, challenger $\mathcal{C}$ selects a random number $y_i\in {\mathbb{Z}}_q^{\ast }$ and sends $y_i$ to $\mathcal{A}$. Meanwhile, $\mathcal{C}$ inserts ($x_i,y_i$) in $L_h^i$ to maintain consistency.

(2)

Execute ($U_i^t,S_j^t$): In this query, the adversary $\mathcal{A}$ can eavesdrop on the entire authentication process of Scheme II. If $\mathcal{A}$ asks $\mathcal{C}$ to execute this query, $\mathcal{C}$ calculates the messages according to the steps in II and returns the results to $\mathcal{A}$.

(3)

Send ($U_i^t/S_j^t$, ${ M}_{sg}$): In this query, $\mathcal{A}$ can attack Scheme II actively. When $\mathcal{A}$ executes this query with a message $M_{sg}$, $\mathcal{C}$ checks if $M_{sg}$ is valid. If it is valid, $\mathcal{C}$ calculates some results as the steps of Scheme II; otherwise, $\mathcal{C}$ ignores this query.

(4)

Reveal ($U_i^t$): In this query, $\mathcal{C}$ returns the current session key between $U_i^t$ and ${AS}_j^t$ to $\mathcal{A}$.

(5)

Corrupt ($U_i^t,c$): $\mathcal{A}$ can obtain any two of three factors: password and smart card, smart card and biometric, or biometric and password. It is impossible to obtain three factors simultaneously. In this query, $\mathcal{C}$ outputs different results as follows:

If c = 0, $\mathcal{C}$ outputs the secret data stored in ${SC}_i$ of $U_i$ to $\mathcal{A}$.

If c = 1, $\mathcal{C}$ outputs the password ${PW}_i$ of $U_i$ to $\mathcal{A}$.

If c = 2, $\mathcal{C}$ outputs the biometric information ${Bio}_i$ of $U_i$ to $\mathcal{A}$.

(6)

Test ($U_i^t$): In this query, $\mathcal{C}$ generates a random secret coin $b\in \left\{\mathrm{0,1}\right\}$. If b = 1, $\mathcal{C}$ returns $\mathcal{A}$ with the correct session key. If b = 0, $\mathcal{C}$ randomly generates a number with the same length of the session and returns it to $\mathcal{A}$.

Definition 1

(AKA-Secure). Pr[S] is denoted as the success probability of $\mathcal{A}$ to breach Scheme II. If $\mathcal{A}$ executes the test query and guesses a correct bit $b^{\prime }\in \{0, 1\}$, we say that $\mathcal{A}$ breaches the semantic security of Scheme II. Then, the advantage of $\mathcal{A}$ to breach the semantic security of Scheme II is denoted as ${Exp}_{II}^{AKA}\left(\mathcal{A}\right)$ = $|Pr\left[S\right]-\frac{1}{2}|$, where AKA represents the authenticated key agreement. Our Scheme II achieves semantic $AKA-secure$ if ${Exp}_{II}^{AKA}$ is negligible for any $PPT$ adversary $\mathcal{A}$.

Theorem 1.

We assume that $\mathcal{D}$ is the password space, $\left|\mathcal{D}\right|\le {10}^6$, $k$ represents the size of the biometric information, and $\mathcal{l}$ represents the length of $h(·)$. Suppose $q_s, q_e$, and $q_h$ denote the number of queries that $\mathcal{A}$ executes send, execute, and hash $h_i$. Then, we have

$$\begin{gathered} {Exp}_{II,\mathcal{A}}^{AKE}\left(t\right) \le \frac{q_h^2}{2^{\mathcal{l}}}+\frac{{\left(q_s+q_e\right)}^2}{2^{\mathcal{l}}}+ \\ 2q_s·\underset{}{\max }\left\{\left(\frac{1}{\left|\mathcal{D}\right|},\frac{1}{2^k},f_p\right)\right\}+\frac{q_s}{2^{\mathcal{l}-1}}+2q_h·{\left(q_s+q_e\right)}^2{Exp}_{\mathcal{A}}^{CDH}\left(t^{\prime }\right), \end{gathered}$$

In polynomial-time $t^{\prime }$, the probability of $\mathcal{A}$ to successfully solve the CDH problem is denoted as ${Exp}_{\mathcal{A}}^{CDH}\left(t^{\prime }\right)$, where $t^{\prime }=t+(q_s+q_e)·T_{ep}$.

Proof. 

We prove the security of the session key in Scheme II by executing the following games $G_i$, $(i=0,1,2,3,4)$. Let $S_i$ refer to the event that $\mathcal{A}$ tries to breach the secrecy of the session key negotiated in each $G_i$. Additionally, we assume that an event E may happen when $\mathcal{A}$ executes Scheme II such that the event E is independent of $S_i$ and can be detected by $\mathcal{C}$. It is noteworthy that $S_i$ and $S_{i+1}$ are indistinguishable, except when E occurs.

Therefore,

$$\left|Pr\left[S_{i+1}\right]-Pr\left[S_i\right]\right| \le \mathrm{Pr}\left[E\right].$$

(1)

(1)

$G_0$: In this game, the simulation of breaching the semantic security of Scheme II is executed in the random oracle model (ROM), and we have

$${Exp}_{II}^{AKE}\left(t\right)=|\mathrm{Pr}\left[S_0\right]-\frac{1}{2}|$$

(2)

(2)

$G_1:$ In this game, $\mathcal{A}$ simulates the ROM by executing queries, including execute, send, and hash queries. In the hash query, $\mathcal{A}$ tries to find the collisions for $\left\{{\theta }_3\right\}$. From the conclusion of a birthday attack, the success probability of a hash collision is $\frac{q_h^2}{2^{\mathcal{l}+1}}$. Executing a send query or an execute query can generates the message. Therefore, the success probability of $\mathcal{A}$ to find a collision is controlled by at most $\frac{{\left(q^s+q^e\right)}^2}{2^{\mathcal{l}+1}}$, where $h_i\left(·\right):{\{0, 1\}}^{\ast }\stackrel{}{\to } {\{0, 1\}}^{\mathcal{l}}$. Then, we have:

$$\left|\mathrm{Pr}\left[S_1\right]-\mathrm{Pr}\left[S_0\right]\right| \le \frac{q_h^2}{2^{\mathcal{l}+1}}+\frac{{\left(q^s+q^e\right)}^2}{2^{\mathcal{l}+1}}.$$

(3)

(3)

$G_2$: Here, $\mathcal{A}$ can execute Corrupt ($U_i^t, c$) to obtain the secret information stored in ${SC}_i$ on the condition that the device is lost or stolen. $\mathcal{A}$ simulates as follows:

(a)

$\mathcal{A}$ executes a Corrupt ($U_i^t, 2$) query to guess the password of $U_i$ from password space $\mathcal{D}$ within a $q_s$ number of send queries. Hence, the probability of a successful guess is $\frac{q_s}{\left|\mathcal{D}\right|}$.

(b)

$\mathcal{A}$ executes a Corrupt ($U_i^t, 1$) query and speculates the biometric key ${\sigma }_i$ of $U_i$.

(i)

The probability of successful guessing ${\sigma }_i$ ($k$-bit) is $\frac{q_s}{2^k}$.

(ii)

$\mathcal{A}$ can take advantage of the false positive $f_p$ to guess ${\sigma }_i$, which is chosen randomly from a uniform distribution ${\{0, 1\}}^k$.

Because $\mathcal{A}$ can guess either the password or biometric key but not both, $\mathcal{A}$ can execute either the $<\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}\left(U_i^t, 0\right),\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}(U_i^t, 1)>$ or $<\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}\left(U_i^t, 0\right),\mathrm{C}\mathrm{o}\mathrm{r}\mathrm{r}\mathrm{u}\mathrm{p}\mathrm{t}(U_i^t, 2)>$ queries. The total probability of success is $\underset{}{\max }\{q_s·(\frac{1}{\left|\mathcal{D}\right|},\frac{1}{2^k},f_p\left)\right\}.$

$$\left|\mathrm{Pr}\right[S_2]-\mathrm{Pr}[S_1\left]\right| \le \underset{}{\max }\{q_s·(\frac{1}{\left|\mathcal{D}\right|},\frac{1}{2^k},f_p\left)\right\}.$$

(4)

(4)

$G_3:$ In this game, to breach the security of mutual authentication, $\mathcal{A}$ executes the queries of send ($Start, U_i$), send ($\left\{{\theta }_1,{\theta }_2, {\theta }_3\right\}, S_j$), and send ($\left\{{\theta }_5\right\}, U_i$) to $\mathcal{C}$.

(a)

Send ($Start, U_i$) query: $\mathcal{A}$ selects two random numbers, $n_{i1}, n_{i2} \in {\mathbb{Z}}_q^{\ast }$, and calculates ${\theta }_1=T_{n_{i1}}\left(z\right)$, ${\theta }_2=E_{T_{n_{i1}}\left(A_{sj}\right)}({PID}_i, n_{i2}, T_1)$, ${\theta }_3=h(C_{ij}\parallel n_{i2}\parallel T_1\parallel {SID}_j\parallel {PID}_i)$. Then, the query answers $\left\{{\theta }_1,{\theta }_2, {\theta }_3\right\}$.

(b)

Send ($\left\{{\theta }_1,{\theta }_2, {\theta }_3\right\}, S_j$) query: Compute $\left({PID}_i, n_{i2}, T_1\right)=D_{T_{a_{sj}}\left({\theta }_1\right)}\left({\theta }_2\right)$, $C_{ij}=h({PID}_i\parallel K_j)$. If ${\theta }_3 \ne h(C_{ij}\parallel n_{i2}\parallel T_1\parallel {SID}_j\parallel {PID}_i)$, $S_j$ rejects the session; otherwise, $S_j$ generates a random number $n_j$ and calculates ${\theta }_4=$ $T_{n_j}\left(z\right)$, ${\theta }_5=E_{n_{i2}}(n_{i2}, {\theta }_4, T_2, {SK}_{ij})$ ${SK}_{ji}=h\left(T_{n_j}\right({\theta }_1)\parallel {PID}_i\parallel {SID}_j\parallel T_1\parallel T_2)$. Afterwards, the query responds with $\left\{{\theta }_5\right\}$.

(c)

Send ($\left\{{\theta }_5\right\}, U_i$) query: Compute $\left(n_{i2}, {\theta }_4, T_2, {SK}_{ji}\right)=D_{n_{i2}}\left({\theta }_5\right)$. $U_i$ checks the freshness of $T_2$ and the validity of $n_{i2}$. Then, $U_i$ computes ${SK}^{\prime }=h\left(T_{n_{i1}}\right({\theta }_4)\parallel {PID}_i\parallel {SID}_j\parallel T_1\parallel T_2)$. If ${SK}_{ji} \ne {SK}^{\prime }$, $U_i$ terminates the session; otherwise $U_i$ ${SK}_{ij}={SK}^{\prime }=h\left(T_{n_{i1}}\right({\theta }_4)\parallel P{ID}_i\parallel {SID}_j\parallel T_1\parallel T_2)$ = ${SK}_{ji}$.

Assume that the adversary $\mathcal{A}$ tries to generate the false value ${\theta }_1=T_{n_{i1}}\left(z\right), {\theta }_2=E_{T_{n_{i1}}\left(A_{sj}\right)}\left({PID}_i, n_{i2}, T_1\right), {\theta }_3=\mathrm{h}(C_{ij}\parallel n_{i2}\parallel T_1\parallel {SID}_j\parallel {PID}_i)$. This game $G_3$ is indistinguishable from the previous game $G_2$, except when $S_j$ refuses a valid $\left\{{\theta }_1,{\theta }_2, {\theta }_3\right\}$ or $U_i$ refuses a valid $\left\{{\theta }_5\right\}$. Therefore, we have

$$\left|\mathrm{Pr}\left[S_3\right]-\mathrm{Pr}\left[S_2\right]\right|\le \frac{q_s}{2^l}.$$

(5)

(5)

$G_4:$ In this game, $\mathcal{A}$ tries to guess the ${SK}_{ij}$. If $\mathcal{A}$ tries to compute the session key ${SK}_{ij}=h\left(T_{n_{i1}}\right(T_{n_j}\left(z\right))\parallel P{ID}_i\parallel {SID}_j\parallel T_1\parallel T_2)$, the CDH problem must be solved for the instance $\left\{{\theta }_1,{\theta }_2, {\theta }_3\right\}$ within the polynomial-time bound $t^{\prime }=t+(q_s+q_e)·T_{ep}$, where $T_2=\mathrm{C}\mathrm{D}\mathrm{H}\left(T_{n_{i1}}\left(z\right), T_{n_j}\left(z\right)\right)=T_{n_{i1}}\left(T_{n_j}\right(z\left)\right)$, since $\{n_{i1}, n_j\}$ are randomly chosen from ${\mathbb{Z}}_q^{\ast }$ uniformly, and $\mathcal{A}$ either implements the execute query or send query.

Therefore, we obtain

$$|\mathrm{Pr}[S_4] -\mathrm{Pr} [S_3]| \le q_h{\left(q_s+q_e\right)}^2{Exp}_{\mathcal{A}}^{CDH}(t^{\prime }).$$

(6)

If $\mathcal{A}$ employs a private oracle $h(·)$, then $\mathcal{C}$ seeks the valid value in $L_h^i$ and conveys it to $\mathcal{A}$. Otherwise, $\mathcal{C}$ sends a random bit string $st \in {\{0, 1\}}^{\mathcal{l}}$. $\mathcal{A}$ tries to guess a bit $b^{\prime } \in \{0, 1\}$, and the probability of successfully guessing $b^{\prime }$ is not more than $\frac{1}{2}$. Therefore, we obtain

$$\mathrm{Pr}[S_4]=\frac{1}{2}.$$

(7)

Finally, we add (1)–(7) and have

$${Exp}_{II}^{AKA}\left(t\right) \le \frac{q_h^2}{2^{\mathcal{l}}}+\frac{{\left(q_s+q_e\right)}^2}{2^{\mathcal{l}}}+2q_s·\underset{}{\max }\left\{\left(\frac{1}{\left|\mathcal{D}\right|},\frac{1}{2^k},f_p\right)\right\}+\frac{q_s}{2^{\mathcal{l}-1}}+2q_h·{\left(q_s+q_e\right)}^2{Exp}_{\mathcal{A}}^{CDH}(t^{\prime }).$$

□

7.2. Informal Security Analysis

(1)

Perfect Forward Secrecy

This feature means that even if the password and biometrics of user are exposed to an adversary, all prior session keys still remain secure. We make the assumption that all private keys $\left\{K_j,{\mathrm{a}}_{\mathrm{s}\mathrm{j}}\right\}$ of the server and $\{{ID}_i$, ${PW}_i$, ${Bio}_i\}$ of the user are compromised, and the adversary obtains $\{{PPID}_i, A_i, {PC}_{ij},c_i,PUF\left(·\right), n_0, h\left(·\right),{\tau }_i, Rep(·\left)\right\}$, which is stored in the smart card. Then, the adversary still cannot acquire the ${PID}_i$ due to the property of the PUF. Moreover, because the session key is ${SK}_{ij}=h\left(T_{n_j}\right({\theta }_1)\parallel {PID}_i\parallel {SID}_j\parallel T_1\parallel T_2)$, even if an adversary can know all the long-term keys used in this protocol, it is computationally infeasible for the adversary to calculate $T_{n_j}\left(T_{n_{i1}}\right(z\left)\right)$ because of the intractability of the Computational Diffie–Hellman Problem (CDHP).

(2)

Known-Key Security

This property means that the adversary cannot compute the next session key, even if he/she has obtained some previous session keys. To be specific, the session key is variable in our scheme due to the random number {$n_{i1},n_{i2}, n_j\}$. Therefore, the adversary cannot know any useful information and cannot compute the next session key, even if they can acquire the session key.

(3)

Session Key Secrecy

Based on our protocol, the user and the server can negotiate a session key for later communication when they finish the mutual authentication and key agreement phase. The session key will be ${SK}_{ij}=h\left(T_{n_{i1}}\right(T_{n_j}\left(z\right))\parallel \mathrm{P}{ID}_i\parallel {SID}_j\parallel T_1\parallel T_2)$ = $h\left(T_{n_j}\right(T_{n_{i1}}\left(z\right))\parallel {PID}_i\parallel {SID}_j\parallel T_1\parallel T_2)$= ${SK}_{ji}$.

(4)

User Anonymity and Untraceability

In our scheme, although the authentication request message {${\theta }_1,{\theta }_2,{\theta }_3$} includes the user’s pseudoidentity ${PID}_i$, the adversary cannot obtain the ${PID}_i$ because of the unknown encryption key $T_{n_{i1}}\left(A_{sj}\right)$. Specifically, the user computes ${\theta }_1=T_{n_{i1}}\left(z\right)$, ${\theta }_2=E_{T_{n_{i1}}\left(A_{sj}\right)}\left({PID}_i,n_{i2},T_1\right)$, ${\theta }_3=\mathrm{h}\left(C_{ij}\parallel n_{i2}\parallel T_1\parallel {SID}_j\parallel {PID}_i\right)$. It is clear that the user’s identity ${PID}_i$ is encrypted by a key negotiate between the user and the server. Moreover, the $RC$ computes ${PID}_i=E_x\left({ID}_i\parallel t_i\right)$, where $t_i$ is the registration time. As a result, the user is anonymous to the server and adversary.

In addition, the random numbers $n_{i1}$, $n_{i2}$ are different in each session, so the authentication request message {${\theta }_1, {\theta }_2, {\theta }_3$} is also different in each session. So, our scheme achieves untraceability.

(5)

Replay Attack

In our scheme, three random numbers ${\{n}_{i1, } n_{i2}, n_j\}$ are utilized to resist the replay attack. Therefore, even if an adversary replays the message {${\theta }_1, {\theta }_2, {\theta }_3$}, they cannot calculate the session key without knowing the random numbers ${\{n}_{i1, } n_{i2}, n_j\}$.

(6)

Offline Identity/Password Guessing Attacks

Because the user’s identity and password is included in $A_i=h\left({ID}_i\parallel {PW}_i\parallel {\sigma }_i\right) mod n$, $n \in (2^4, 2^8)$, if an adversary obtains all the information stored in the device, obtains the user’s biometric information, and guesses ($I{D}_i, P{W}_i$) to satisfy $A_i=h\left({ID}_i\parallel {PW}_i\parallel {\sigma }_i\right) mod n$, $n \in (2^4, 2^8)$, there are $\left|D_{pw}\right|\times \left|D_{id}\right|/n \approx 2^{32}$ candidates for the ($I{D}_i, P{W}_i$) pair when n = 256. Moreover, the adversary cannot know which pair is right due to the property of the PUF.

(7)

Three-Factor Secrecy

If an adversary can know the user’s biometric information ${Bio}_i$ and all the information stored on the device, he/she cannot guess the correct ($I{D}_i, P{W}_i$) pair. If an adversary can know the user’s biometric information ${Bio}_i$ and password, he/she cannot know the {${PID}_i, C_{ij}$} from the authentication messages. If an adversary can know the password and all the information stored in the device, he/she cannot know the user’s biometric information ${Bio}_i$.

(8)

Device Lost Attack

${MD}_i$ of $U_i$ stores $\{{PPID}_i,A_i,{PC}_{ij},c_i,PUF\left(·\right),n_0,h\left(·\right),{\tau }_i,Rep(·\left)\right\}$, where $A_i=h\left({ID}_i\parallel {PW}_i\parallel {\sigma }_i\right)mod n$, $R_i=PUF\left(c_i\right)$, ${PC}_{ij}=C_{ij}\oplus h({\sigma }_i\parallel {ID}_i\parallel {PW}_i\parallel R_i\parallel j)$, ${PPID}_i={PID}_i\oplus h(R_i\parallel {PW}_i\parallel {ID}_i\parallel {\sigma }_i\parallel j)$. So, an adversary cannot obtain {${PID}_i,C_{ij},{PC}_{ij}$} due to the property of the PUF. Therefore, according to above analysis, we can know that an adversary can’t obtain any valuable information to launch attacks even if he/she gets the information stored in device.

(9)

User/Server Impersonation Attacks

Suppose an adversary wants to impersonate the user to access the server; however, they cannot forge the valid message {${\theta }_1, {\theta }_2, {\theta }_3$}, because they cannot know {${PID}_i,C_{ij},{PC}_{ij}$}, which are protected by the PUF.

Suppose an adversary wants to impersonate the server to pass the authentication by the user, however, they cannot forge the valid message $\left\{{\theta }_5\right\}$. Moreover, the adversary does not know the secret key $a_{sj}$ of the server, so the secret message ${\theta }_2$ cannot be decrypted. So the adversary cannot obtain $\{{PID}_i, n_{i2}, T_1\}$ and cannot forge a session key.

(10)

Man-in-the-Middle Attack

Our scheme achieves trustworthy mutual authentication between $U_i$ and $S_j$, and any adversary can neither impersonate users nor servers. So, our scheme can resist man-in-the-middle attacks.

(11)

Stolen-Verifier Attack/Physical Capturing Attacks

Because the important information is stored in the user’s device and the servers, and they are all protected by the PUF, our scheme can resist stolen-verifier attacks and physical capturing attacks.

8. Performance Analysis

In Table 2, we present a comparison of the security features between our scheme and some related multiserver schemes [11,12,23,31,33,34].

Table 2. Security features comparison.

Attributes/Attacks	[11]	[12]	[23]	[31]	[33]	[34]	Ours
Perfect forward secrecy	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$
User anonymity	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$
Untraceability	x	x	$\surd$	$\surd$	$\surd$	x	$\surd$
Known key security	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$
Replay attack	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$
Device lost attack	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$	$\surd$
User impersonation attack	x	x	$\surd$	x	x	x	$\surd$
Server impersonation attack	$\surd$	x	x	$\surd$	$\surd$	x	$\surd$
Offline identity/password guessing attack	$\surd$	$\surd$	$\surd$	x	$\surd$	$\surd$	$\surd$
Man-in-the-middle attack	$\surd$	x	$\surd$	$\surd$	$\surd$	x	$\surd$
Stolen-verifier attack	$\surd$	$\surd$	$\surd$	x	x	$\surd$	$\surd$
N-factor secrecy	x	x	x	x	x	x	$\surd$

$\surd$: can resist the attack or achieve the attribute; x: cannot resist the attack or achieve the attribute.

We also simulated the computation cost in the environment of Intel Pentium4 2600 MHz processor with 1024 MB RAM. Table 3 displays the execution time for different operations. Table 4 shows the comparison of computation costs between ours and related protocols. The computation cost of bitwise operation like XOR is negligible.

Table 3. Execution time of cryptographic operations.

Term	Operation	Time (in Microseconds)
$T_H$	One-way hash function	0.5
$T_{E/D}$	Symmetric encryption/ decryption	8.7
$T_{ECC}$	Point multiplication on elliptic curve	63.075
$T_{CH}$	$T_n\left(x\right)(mod p)$ in a Chebyshev polynomial	21.01
$T_{BH}$	A bio-hashing operation	21.02
$T_{BP}$	A bilinear paring operation	327.12
$T_{EXP}$	An exponentiation operation	22.49

Table 4. Comparison of Computation Costs.

Protocol	User	Server
[11]	$10T_H$ + 3$T_{CH}$ + 2$T_{e/d}$ $\approx$85.43	$6T_H$ + 3$T_{CH}$ + 2$T_{e/d}$ $\approx$ 83.43
[12]	$10T_H$ + 2$T_{CH}$ + $T_{BH}\approx$ 68.04	$8T_H$ + 2$T_{CH}$ $\approx$ 46.02
[23]	8$T_H$ + 4$T_{ECC}$ $\approx$ 256.3	4$T_H$ + 4$T_{ECC}$ $\approx$ 254.3
[31]	7$T_H$ + 5$T_{ECC}$ $\approx$ 318.875	$4T_H$ + 5$T_{ECC}$ $\approx$ 317.375
[33]	8$T_H$ + 2$T_{ECC}$ + 2TEXP + TBP $\approx$ 502.25	8$T_H$ + 2$T_{ECC}$ + 2TEXP + TBP $\approx$ 502.25
[34]	11$T_H$ + 6$T_{ECC}$ $\approx$ 383.95	6$T_H$ + 6$T_{ECC}$ $\approx$ 381.45
Ours	$5T_H$ + 2$T_{CH}$ + 2$T_{e/d}$ $\approx$ 86.56	$3T_H$ + 2$T_{CH}$ + 2$T_{e/d}$ $\approx$ 85.56

We focus on the mutual authentication and key agreement phase because the server and user registration phase executes only once. In terms of the mutual authentication and key agreement phase, our scheme’s computation cost for a user is 86.56 ms, and it is 85.56 ms for a server. According to Table 4, it is obvious that our authentication scheme costs less than [23,31,33,34]. Our scheme’s computation costs are more than [11,12], but this is acceptable because our scheme has stronger security.

It is assumed that the output of hash function $H(·)$ is 160 bits (SHA-1 hash function), the block size of symmetric encryption/decryption (AES) is 128 bits, the elliptic curve point is 320 bits, and the identity, random number, timestamp, and other parameters is 128 bits. We focus on the mutual authentication and key agreement phase because the server and user registration phase executes only once. During the mutual authentication and key agreement phase, only two messages, $\{{\theta }_1, {\theta }_2, {\theta }_3\}$ and $\left\{{\theta }_5\right\}$, are transmitted in our scheme. To be specific, ${\theta }_1=T_{n_{i1}}\left(z\right), {\theta }_2=E_{T_{n_{i1}}\left(A_{sj}\right)}({PID}_i, n_{i2}, T_1)$, ${\theta }_3=\mathrm{h}(C_{ij}\parallel n_{i2}\parallel T_1\parallel {SID}_j\parallel {PID}_i)$, and ${\theta }_5=E_{n_{i2}}(n_{i2}, {\theta }_4, T_2, {SK}_{ji})$. The length of two interactive messages is (128 + 3 × 128 + 160) + 128 × ((128 + 128 + 128 + 160)/128) = 1312.

9. Conclusions

We have shown that Yu et al.’s three-factor multiserver authentication scheme has several security flaws, and we designed a new three-factor lightweight authentication based on Chebyshev’s chaotic map and the PUF. We analyzed our authentication scheme through the random oracle model and proved our scheme is secure. Furthermore, our scheme eliminates the requirement for RC during mutual authentication and only requires a one-time mutual interaction. Therefore, our scheme is more efficient and practical in multiserver environments, especially for resource-restrained mobile devices.