Mean Estimation for Time-Based Surveys Using Memory-Type Logarithmic Estimators

Abstract

This article examines the issue of population mean estimation utilizing past and present data in the form of an exponentially weighted moving average (EWMA) statistic under simple random sampling (SRS). We suggest memory-type logarithmic estimators and derive their properties, such as mean-square error (MSE) and bias up to a first-order approximation. Using the EWMA statistic, the conventional and novel memory-type estimators are compared. Real and artificial populations are used as examples to illustrate the theoretical findings. According to the empirical findings, memory-type logarithmic estimators are superior to the conventional mean estimator, ratio estimator, product estimator, logarithmic-type estimator, and memory-type ratio and product estimators.

1. Introduction

It is a well-developed fact that the variance or mean-squared error in the estimators of population parameters such as population mean, population total, variance, median, regression coefficient, and population correlation coefficient is significantly reduced when auxiliary information is used properly in random sampling. Additional information that is accessible, in addition to the data being examined, is known as auxiliary information. Several situations, such as survey sampling, experimental design, and statistical modeling, can benefit from it. In general, auxiliary information can be a useful tool for enhancing the efficiency, cost effectiveness, and decision making of statistical estimations. It is possible to gather auxiliary information in a variety of ways from various data sources, including census findings, population-based survey reports, expert judgments, and assumptions about population parameters. There are numerous ways to present and use the information from these sources. When there is a positive correlation between the data on the auxiliary variable x and the study variable y, the ratio-type estimators produce accurate findings. Ref. [1] provided a traditional ratio estimator of the population mean under an SRS approach, defined as

$$\begin{array}{c}\hfill {\Im }_r=\overline{y}\frac{\overline{X}}{\overline{x}},\end{array}$$

(1)

where $\overline{X}$ is the population mean of the auxiliary variable and $\overline{y}$ and $\overline{x}$ are the sample means of the study and auxiliary variables, respectively. The MSE and bias expressions of the estimator ${\Im }_r$ are, respectively,

$$\begin{array}{cc}\hfill MSE\left({\Im }_r\right)& =\theta {\overline{Y}}^2(C_x^2+C_y^2-2{\rho }_{xy}{C}_x{C}_y),\hfill \end{array}$$

(2)

$$\begin{array}{cc}\hfill Bias\left({\Im }_r\right)& =\theta \overline{Y}(C_x^2-{\rho }_{xy}{C}_x{C}_y),\hfill \end{array}$$

(3)

where $\overline{Y}$ denotes the population mean of the study variable y; the population coefficients of variation for the auxiliary and study variables are denoted by $C_x=S_x/\overline{X}$ and $C_y=S_y/\overline{Y}$, respectively, where $S_x$ and $S_y$ are the population standard deviations of the auxiliary and study variables, respectively. Furthermore, the population coefficient of correlation between the auxiliary and study variables is denoted by ${\rho }_{xy}$; $\theta =1/n$, where n is the sample size.

When there is a strong negative correlation between the auxiliary and study variables, the product estimators produce accurate results. Ref. [2] provided the traditional product estimator of the population mean under SRS as:

$$\begin{array}{c}\hfill {\Im }_p=\overline{y}\frac{\overline{x}}{\overline{X}}.\end{array}$$

(4)

The MSE and bias expressions of the estimator ${\Im }_p$ are, respectively,

$$\begin{array}{cc}\hfill MSE\left({\Im }_p\right)& =\theta {\overline{Y}}^2(C_x^2+C_y^2+2{\rho }_{xy}{C}_x{C}_y),\hfill \end{array}$$

(5)

$$\begin{array}{cc}\hfill Bias\left({\Im }_p\right)& =\theta \overline{Y}{\rho }_{xy}{C}_x{C}_y.\hfill \end{array}$$

(6)

Ref. [3] proposed a logarithmic estimator under SRS given by:

$$\begin{array}{cc}\hfill {\Im }_a& =\overline{y}{\left[1+log\left(\frac{\overline{x}}{\overline{X}}\right)\right]}^{\lambda },\hfill \end{array}$$

(7)

where $\lambda$ is a properly chosen scalar. The minimum MSE at ${\lambda }_{\left(opt\right)}=-{\rho }_{xy}(C_y/C_x)$ and the bias expressions for the estimator ${\Im }_a$ are, respectively,

$$\begin{array}{cc}\hfill minMSE\left({\Im }_a\right)& =\theta {\overline{Y}}^2{C}_y^2(1-{\rho }_{xy}^2),\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill Bias\left({\Im }_a\right)& =\theta \overline{Y}\left\{\left(\frac{{\lambda }^2}{2}-\lambda \right)C_x^2+\lambda {\rho }_{xy}{C}_x{C}_y\right\}.\hfill \end{array}$$

(9)

Numerous well-known authors developed several enhanced and modified classes of ratio, exponential, product, regression, and logarithmic types of estimators for the estimation of parameters using the available auxiliary information. For example, ref. [4] investigated the population mean estimation utilizing the ratio estimator under SRS and median ranked set sampling. Ref. [5] used double quartile ranked set sampling for computing the population ratio by employing the auxiliary information. Ref. [6] investigated entropy estimation based on ranked set samples, with an application to the test of fit. In the case of tie information, the proportion estimate using ranked set sampling (RSS) was studied by [7]. Ref. [8] suggested an improved modified ratio estimator using robust regression methods. Ref. [9] created a method for evaluating the population mean by iteratively applying an auxiliary variable under the median RSS. Ref. [10] carried out a simulation study using robust regression-ratio-type estimators for the estimation of population mean, employing two auxiliary variables. Ref. [11] suggested a new improved logarithmic ratio-product-type estimator of the mean in stratified random sampling. Ref. [12] measured the effectiveness of the ratio-exponential-log type general class of estimators by utilizing two auxiliary variables. Logarithmic-type predictive estimators for population mean based on an RSS scheme were studied by [13].

A time series can be modeled or described using the EWMA, which is a quantitative or statistical measure. Technical analysis and volatility modeling are the two most common applications of the EWMA in finance. Past data are given lesser weights because of the way the moving average is constructed. The term “exponentially weighted” refers to the fact that weights decrease exponentially with an increasing number of data points. The parameter selection is the sole choice for an EWMA user. In the EWMA calculation, the parameter determines the significance of the current observation. The higher the value of the parameter, the greater the accuracy with which the EWMA monitors the original time series.

It has been established that effective utilization of auxiliary data reduces the variance of the estimators. The study and auxiliary variables are often obtained by considering only the current sample $y_t$ at time t. Nevertheless, incorporating data from more recent and earlier samples, such as ${\overline{y}}_{t-1}$ from time $t-1$, ${\overline{y}}_{t-2}$ from time $t-2$, and so on, may also increase the performance of the estimators. This is usually essential when surveys are conducted over a certain time period, such as quarterly, monthly, or annual periods. Memory-type ratio and product methods of estimation for the population mean utilizing EWMA were developed by [14] for time-scaled surveys, however, [15] utilized the hybrid exponentially weighted moving average (HEWMA) statistic in SRS to build the memory-type ratio and product estimators of population mean. The memory-based estimators of population mean in ranked-based sampling were examined by [16]. The population-mean-based memory-type ratio and product estimators were suggested by [17] in stratified sampling. A memory-based shrinkage estimator of the population mean was presented by [18] for statistical quality control. Memory-type population variance estimators employing the EWMA statistic were proposed by [19] for time-scaled surveys. Recently, ref. [20] suggested memory-type logarithmic estimators by employing the HEWMA statistic.

The traditional estimators in survey sampling theory are established using functional forms, such as exponential, linear combination, and chain functions. However, the development of estimators employing the logarithmic function is new. Advances in data analysis software have increased the computational boundaries of these functions. Mathematical functions based on logarithms are used to reduce a large range in a set of values to a more comprehensible scale. In addition to other disciplines, they are extensively employed in finance, science, engineering, and mathematics. They can be used in measuring relative changes, simplifying some calculations, and in statistical analysis of real data. Additionally, logarithms are useful for measuring exponential growth and decay in a variety of situations, including interest rates, bacterial contamination, and others. Furthermore, in Section 4.2, an example from real life is also provided, and a numerical analysis is performed to illustrate the performance of the suggested estimators. As a result, it is worth investigating the estimators consisting of logarithmic functions for estimating the population parameters, which is what led to the development of the class of suggested estimators. This work seeks to provide a memory type of logarithmic estimators consisting of information on the past and present sample data in the form of the EWMA statistic.

The layout of the remaining text is as follows: The traditional memory-type estimators utilizing SRS are studied in Section 2. In Section 3, the suggested memory-type estimator is discussed with its properties and compared with the properties of some other conventional and memory-type estimators. An empirical comparison consisting of real and artificial populations is presented in Section 4, to examine the superiority of the suggested memory-type estimators as compared to some existing estimators. Section 5 provides the conclusions.

2. Conventional Memory-Type Estimators

The concept of the EWMA statistic was first introduced by [21] to efficiently distinguish the modifications in the elementary process mean in statistical quality control charts. To increase the effectiveness of the estimators, the EWMA statistic combined past data with present data. The EWMA statistics for the study and auxiliary variables are stated below as

$$\begin{array}{cc}\hfill Z_t& =\eta {\overline{y}}_t+(1-\eta )Z_{t-1},t>1,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill Q_t& =\eta {\overline{x}}_t+(1-\eta )Q_{t-1},t>1,\hfill \end{array}$$

(11)

where the weight assigned to the data is indicated by the smoothing constant $\eta$.

A greater value of $\eta$ implies that the current observation is given a larger weight and the past observation a smaller weight, whereas a lower value of $\eta$ suggests that the past observation is given a larger weight and the current observation a smaller weight. The value of $\eta$ ranges from 0 to 1. If $\eta$ is equal to 1, the current data will have received their full weight, and the EWMA statistic will be the same as the usual sample mean.

It is of interest to note here that the expectation and variance of $Z_t$ are, respectively, reported below as

$$E\left(Z_t\right)=\overline{Y}\mathrm{and}V\left(Z_t\right)=\frac{{\sigma }_Y^2}{n}\left[\frac{\eta }{2-\eta }\left(1-{\left(1-\eta \right)}^{2t}\right)\right].$$

The term $Z_{t-1}$ refers to the past data, and the subscript t indicates the number of samples in this EWMA statistic. In addition, the starting values of $Q_t$ and $Z_t$ are considered as the expectation of the mean that can be determined through a pilot sampling survey, which is assumed to be 0 in this instance. The statistics $Z_t$ and $Q_t$ are, respectively, found to be unbiased for the population means $\overline{Y}$ and $\overline{X}$.

To determine the characteristics of the memory-type estimators, let $Z_t=\overline{Y}(1+{\delta }_0)$ and $Q_t=\overline{X}(1+{\delta }_1)$, where ${\delta }_0$ and ${\delta }_1$ are the error terms, such that $E\left({\delta }_0\right)=E\left({\delta }_1\right)=0$, $E\left({\delta }_0^2\right)=\theta \varsigma C_y^2$, $E\left({\delta }_1^2\right)=\theta \varsigma C_x^2$, $E\left({\delta }_0{\delta }_1\right)=\theta \varsigma \rho C_x{C}_y$, $\varsigma =\eta /(2-\eta )$, and $\theta =1/n$.

Ref. [14] adopted the idea of the EWMA statistic and presented the memory types of ratio and product estimators under SRS, with the aim of increasing the effectiveness of the traditional estimators, as

$$\begin{array}{cc}\hfill {\Im }_r^m& =Z_t\frac{\overline{X}}{Q_t},\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\Im }_p^m& =Z_t\frac{Q_t}{\overline{X}},\hfill \end{array}$$

(13)

where “memory” is represented by the superscript m in the above and other estimators.

The MSE and bias of the aforementioned estimators ${\Im }_r^m$ and ${\Im }_p^m$ are given below up to a first-order approximation as

$$\begin{array}{cc}\hfill MSE\left({\Im }_r^m\right)& =\theta {\overline{Y}}^2\varsigma (C_x^2+C_y^2-2{\rho }_{xy}{C}_x{C}_y),\hfill \end{array}$$

(14)

$$\begin{array}{cc}\hfill MSE\left({\Im }_p^m\right)& =\theta {\overline{Y}}^2\varsigma (C_x^2+C_y^2+2{\rho }_{xy}{C}_x{C}_y),\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill Bias\left({\Im }_r^m\right)& =\theta \overline{Y}\varsigma (C_x^2-{\rho }_{xy}{C}_x{C}_y),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill Bias\left({\Im }_p^m\right)& =\theta \overline{Y}\varsigma {\rho }_{xy}{C}_x{C}_y.\hfill \end{array}$$

(17)

For more details, see [14].

3. Proposed Memory-Type Estimators

There are a few significant traits of the logarithmic function, and it plays a crucial part in many scientific and non-scientific professions. The studies of [14,15] served as an inspiration for our proposal to use the EWMA statistic as a memory-type logarithmic estimator (MTLE).

$$\begin{array}{cc}\hfill {\Im }_a^m& =Z_t{\left[1+log\left(\frac{Q_t}{\overline{X}}\right)\right]}^{\alpha },\hfill \end{array}$$

(18)

where $\alpha$ is a properly chosen scalar. Utilizing the notation presented in terms of $\delta$s in the previous section, the estimator ${\Im }_a^m$ will be

$$\begin{array}{c}\hfill {\Im }_a^m-\overline{Y}=\overline{Y}\left({\delta }_0+\alpha {\delta }_1-\alpha {\delta }_1^2+\frac{{\alpha }^2}{2}{\delta }_1^2+\alpha {\delta }_0{\delta }_1\right).\end{array}$$

(19)

Considering the expectations on both sides of (19), we obtain the bias of the suggested estimator as

$$\begin{array}{c}\hfill Bias\left({\Im }_a^m\right)=\theta \overline{Y}\varsigma \left\{\left(\frac{{\alpha }^2}{2}-\alpha \right)C_x^2+\alpha {\rho }_{xy}{C}_x{C}_y\right\}.\end{array}$$

(20)

Squaring and taking into account the expectation on both sides of (19) provides the $MSE$ of the estimator ${\Im }_a^m$ to the first order of approximation as follows:

$$\begin{array}{c}\hfill MSE\left({\Im }_a^m\right)=\theta {\overline{Y}}^2\varsigma (C_y^2+{\alpha }^2{C}_x^2-2\alpha {\rho }_{xy}{C}_x{C}_y).\end{array}$$

(21)

The optimum value of $\alpha$ that minimizes the $MSE\left({\Im }_a^m\right)$ is reported below, as

$$\begin{array}{c}\hfill {\alpha }_{\left(opt\right)}=-{\rho }_{xy}\frac{C_y}{C_x}\end{array}$$

(22)

Using the optimum value of $\alpha$ in $MSE\left({\Im }_a^m\right)$ provides the minimum MSE as follows:

$$\begin{array}{c}\hfill MSE{\left({\Im }_a^m\right)}_{min}=\theta {\overline{Y}}^2\varsigma C_y^2(1-{\rho }_{xy}^2)\end{array}$$

(23)

In addition, we assess how well the suggested MTLE performs relative to the existing traditional and memory type of estimators by comparing the MSE expressions of each, as given below.

(i).

From (2) and (23), we obtain

$$\begin{array}{c}\hfill \mathrm{If}MSE\left({\Im }_r\right)>MSE\left({\Im }_a^m\right)\Rightarrow {\rho }_{xy}^2>\frac{2{\rho }_{xy}{C}_x{C}_y-C_y^2(1-\varsigma )-C_x^2}{\varsigma C_y^2}.\end{array}$$

(24)

(ii).

From (5) and (23), we obtain

$$\begin{array}{c}\hfill \mathrm{If}MSE\left({\Im }_p\right)>MSE\left({\Im }_a^m\right)\Rightarrow {\rho }_{xy}^2>-\frac{(C_y^2(1-\varsigma )+C_x^2+2{\rho }_{xy}{C}_x{C}_y)}{\varsigma C_y^2}.\end{array}$$

(25)

(iii).

From (8) and (23), we obtain

$$\begin{array}{c}\hfill \mathrm{If}MSE\left({\Im }_a\right)>MSE\left({\Im }_a^m\right)\Rightarrow \varsigma <1.\end{array}$$

(26)

(iv).

From (14) and (23), we obtain

$$\begin{array}{c}\hfill \mathrm{If}MSE\left({\Im }_r^m\right)>MSE\left({\Im }_a^m\right)\Rightarrow {\rho }_{xy}^2>\frac{2{\rho }_{xy}{C}_x{C}_y-C_x^2}{C_y^2}.\end{array}$$

(27)

(v).

From (15) and (23), we obtain

$$\begin{array}{c}\hfill \mathrm{If}MSE\left({\Im }_p^m\right)>MSE\left({\Im }_a^m\right)\Rightarrow {\rho }_{xy}^2>-\frac{(2{\rho }_{xy}{C}_x{C}_y+C_x^2)}{C_y^2}.\end{array}$$

(28)

Under these conditions, the suggested MTLE performs better than the reviewed estimators. Furthermore, these conditions are numerically verified using real data in Section 4.2.

4. Empirical Study

This section empirically examines the proposed estimator under the conditions established in the previous section. The performance of the suggested MTLE is demonstrated in the following subsections using a simulation study based on artificially generated data and a numerical study based on real data.

4.1. Simulation Study

The suggested MTLE is compared to the existing traditional and memory-type estimators using a simulation study. The algorithm of the simulation study is described as follows.

(i).

Use R programming language to generate a population of size N = 1000 from a bivariate normal distribution with parameters: $\overline{Y}=11$, $\overline{X}=16$, ${\sigma }_y=14$, ${\sigma }_x=23$, and various values of ${\rho }_{xy}$ = $\pm 0.1$, $\pm 0.3$, $\pm 0.5$, $\pm 0.7$, and $\pm 0.9$. Further, take various values of parameter $\eta$ = 0.15, 0.35, 0.55, 0.75, and 0.95.

(ii).

A total of 30,000 samples have been drawn, with sizes n = 10, 20, 50, 100, 200, and 400.

(iii).

For each estimator considered in this study, the 30,000 values are calculated based on the samples that are drawn in the previous step.

(iv).

Based on the simulation with 30,000 replications, the MSE of each estimator is calculated using $MSE(\Im )=\frac{1}{30,000}{\sum }_{i=1}^{30,000}{(\Im -\overline{Y})}^2,\Im ={\Im }_a^m,{\Im }_r^m,{\Im }_p^m,{\Im }_a,{\Im }_r,{\Im }_p$, and the outcomes are presented in Table 1 and Table 2. The relative efficiency (RE) is calculated using $RE(\Im )=\frac{MSE\left(\overline{y}\right)}{MSE(\Im )}$ and the findings are listed in Table 3 and Table 4. The absolute relative bias (ARB) is calculated using $ARB(\Im )=\left|\frac{{\sum }_{i=1}^{30,000}(\overline{y}-\overline{Y})}{{\sum }_{i=1}^{30,000}(\Im -\overline{Y})}\right|$, and the results are shown in Table 5 and Table 6.

Table 1. $MSE$ of traditional and memory-type estimators for selected positive values of ${\rho }_{xy}$, n, and $\eta$.

					$\mathit{\eta }=0.15$		$\mathit{\eta }=0.35$		$\mathit{\eta }=0.55$		$\mathit{\eta }=0.75$		$\mathit{\eta }=0.95$
${\mathit{\rho }}_{\mathit{xy}}$	$\mathit{n}$	${\Im }_{\mathit{m}}$	${\Im }_{\mathit{r}}$	${\Im }_{\mathit{a}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$
0.1	10	9.642	93.436	9.086	7.576	0.737	19.820	1.927	35.441	3.446	56.062	5.451	84.537	8.220
	20	8.010	25.060	7.624	2.032	0.618	5.316	1.617	9.506	2.892	15.036	4.574	22.674	6.898
	50	3.938	9.022	3.844	0.732	0.312	1.914	0.815	3.422	1.458	5.413	2.307	8.163	3.478
	100	1.968	4.292	1.942	0.348	0.157	0.910	0.412	1.628	0.737	2.575	1.165	3.883	1.757
	200	0.984	2.100	0.977	0.170	0.079	0.445	0.207	0.797	0.370	1.260	0.586	1.900	0.884
	400	0.492	1.040	0.489	0.084	0.040	0.221	0.104	0.394	0.186	0.624	0.294	0.941	0.443
0.3	10	9.427	36.378	8.286	2.950	0.672	7.716	1.758	13.798	3.143	21.827	4.972	32.913	7.497
	20	7.829	20.312	6.953	1.647	0.564	4.309	1.475	7.704	2.637	12.187	4.172	18.377	6.291
	50	3.852	7.146	3.507	0.579	0.284	1.516	0.744	2.710	1.330	4.287	2.104	6.465	3.173
	100	1.924	3.404	1.772	0.276	0.144	0.722	0.376	1.291	0.672	2.042	1.063	3.080	1.603
	200	0.963	1.667	0.891	0.135	0.072	0.354	0.189	0.632	0.338	1.000	0.535	1.508	0.806
	400	0.481	0.826	0.447	0.067	0.036	0.175	0.095	0.313	0.169	0.495	0.268	0.747	0.404
0.5	10	9.303	106.805	6.806	8.660	0.552	22.656	1.444	40.512	2.582	64.083	4.084	96.633	6.158
	20	7.724	25.386	5.711	2.058	0.463	5.385	1.211	9.629	2.166	15.232	3.427	22.968	5.167
	50	3.802	5.142	2.881	0.417	0.234	1.091	0.611	1.951	1.093	3.085	1.729	4.653	2.607
	100	1.898	2.457	1.455	0.199	0.118	0.521	0.309	0.932	0.550	1.474	0.873	2.223	1.317
	200	0.950	1.205	0.732	0.098	0.059	0.256	0.155	0.457	0.278	0.723	0.439	1.090	0.662
	400	0.475	0.597	0.367	0.048	0.030	0.127	0.078	0.226	0.139	0.358	0.220	0.540	0.332
0.7	10	9.273	26.100	4.632	2.116	0.376	5.536	0.982	9.900	1.757	15.660	2.779	23.614	4.191
	20	7.696	10.344	3.886	0.839	0.315	2.194	0.824	3.924	1.474	6.207	2.332	9.359	3.516
	50	3.790	3.101	1.961	0.251	0.159	0.658	0.416	1.176	0.744	1.860	1.176	2.805	1.774
	100	1.892	1.487	0.990	0.121	0.080	0.315	0.210	0.564	0.376	0.892	0.594	1.345	0.896
	200	0.947	0.730	0.498	0.059	0.040	0.155	0.106	0.277	0.189	0.438	0.299	0.661	0.451
	400	0.474	0.362	0.250	0.029	0.020	0.077	0.053	0.137	0.095	0.217	0.150	0.328	0.226
0.9	10	9.350	4.495	1.735	0.364	0.141	0.953	0.368	1.705	0.658	2.697	1.041	4.066	1.570
	20	7.759	2.641	1.456	0.214	0.118	0.560	0.309	1.002	0.552	1.585	0.873	2.389	1.317
	50	3.842	0.575	0.378	0.047	0.031	0.122	0.080	0.218	0.143	0.345	0.227	0.973	0.664
	100	1.908	0.517	0.371	0.042	0.030	0.110	0.079	0.196	0.141	0.310	0.223	0.468	0.336
	200	0.955	0.254	0.187	0.021	0.015	0.054	0.040	0.097	0.071	0.153	0.112	0.230	0.169
	400	0.478	0.126	0.093	0.010	0.008	0.027	0.020	0.048	0.035	0.076	0.056	0.114	0.085

Table 2. $MSE$ of traditional and memory-type estimators for selected negative values of ${\rho }_{xy}$, n, and $\eta$.

					$\mathit{\eta }=0.15$		$\mathit{\eta }=0.35$		$\mathit{\eta }=0.55$		$\mathit{\eta }=0.75$		$\mathit{\eta }=0.95$
${\mathit{\rho }}_{\mathit{xy}}$	$\mathit{n}$	${\Im }_{\mathit{m}}$	${\Im }_{\mathit{p}}$	${\Im }_{\mathit{a}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$
−0.1	10	8.197	35.270	7.683	2.860	0.623	7.481	1.630	13.378	2.914	21.162	4.610	31.911	6.951
	20	6.995	32.187	6.603	2.610	0.535	6.828	1.401	12.209	2.504	19.312	3.962	29.122	5.974
	50	4.033	8.234	3.881	0.668	0.315	1.747	0.823	3.123	1.472	4.940	2.328	7.449	3.511
	100	2.016	3.886	1.960	0.315	0.159	0.824	0.416	1.474	0.744	2.331	1.176	3.516	1.774
	200	1.008	1.899	0.986	0.154	0.08	0.403	0.209	0.720	0.374	1.140	0.591	1.718	0.892
	400	0.504	0.939	0.494	0.076	0.040	0.199	0.105	0.356	0.187	0.564	0.296	0.85 0	0.447
−0.3	10	8.321	18.680	7.115	1.515	0.577	3.962	1.509	7.085	2.699	11.208	4.269	16.901	6.438
	20	7.100	14.279	6.114	1.158	0.496	3.029	1.297	5.416	2.319	8.568	3.669	12.920	5.532
	50	4.092	6.503	3.592	0.527	0.291	1.379	0.762	2.467	1.363	3.902	2.155	5.884	3.250
	100	2.047	3.017	1.815	0.245	0.147	0.640	0.385	1.144	0.688	1.810	1.089	2.729	1.642
	200	1.023	1.463	0.912	0.119	0.074	0.310	0.193	0.555	0.346	0.878	0.547	1.324	0.825
	400	0.512	0.721	0.457	0.058	0.037	0.153	0.097	0.274	0.173	0.433	0.274	0.652	0.414
−0.5	10	8.346	16.030	5.883	1.300	0.477	3.400	1.248	6.080	2.231	9.618	3.530	14.503	5.322
	20	7.122	11.313	5.055	0.917	0.410	2.400	1.072	4.291	1.917	6.788	3.033	10.235	4.574
	50	4.104	4.834	2.969	0.392	0.241	1.025	0.630	1.834	1.126	2.901	1.781	4.374	2.686
	100	2.053	2.180	1.500	0.177	0.122	0.462	0.318	0.827	0.569	1.308	0.900	1.973	1.357
	200	1.027	1.045	0.754	0.085	0.061	0.222	0.160	0.396	0.286	0.627	0.452	0.945	0.682
	400	0.513	0.512	0.378	0.041	0.031	0.109	0.080	0.194	0.143	0.307	0.227	0.463	0.342
−0.7	10	8.291	13.637	3.997	1.106	0.324	2.893	0.848	5.173	1.516	8.182	2.398	12.338	3.617
	20	7.076	9.032	3.435	0.732	0.279	1.916	0.729	3.426	1.303	5.419	2.061	8.172	3.108
	50	4.078	3.193	2.018	0.259	0.164	0.677	0.428	1.211	0.765	1.916	1.211	2.889	1.826
	100	2.039	1.360	1.019	0.110	0.083	0.288	0.216	0.516	0.387	0.816	0.612	1.230	0.922
	200	1.020	0.634	0.512	0.051	0.042	0.135	0.109	0.241	0.194	0.381	0.307	0.574	0.464
	400	0.510	0.307	0.257	0.025	0.021	0.065	0.054	0.116	0.097	0.184	0.154	0.278	0.232
−0.9	10	8.148	13.819	1.482	1.120	0.120	2.931	0.314	5.242	0.562	8.291	0.889	12.503	1.341
	20	6.956	11.598	1.273	0.940	0.103	2.460	0.270	4.399	0.483	6.959	0.764	10.493	1.152
	50	4.010	1.568	0.748	0.127	0.061	0.333	0.159	0.595	0.284	0.941	0.449	1.418	0.677
	100	2.005	0.5490	0.378	0.044	0.031	0.116	0.080	0.208	0.143	0.329	0.227	0.496	0.342
	200	1.003	0.230	0.190	0.019	0.015	0.049	0.040	0.087	0.072	0.138	0.114	0.208	0.172
	400	0.502	0.105	0.095	0.009	0.008	0.022	0.020	0.040	0.036	0.063	0.057	0.095	0.086

Table 3. $RE$ of traditional and memory-type estimators for selected positive values of ${\rho }_{xy}$, n, and $\eta$.

				$\mathit{\eta }=0.15$		$\mathit{\eta }=0.35$		$\mathit{\eta }=0.55$		$\mathit{\eta }=0.75$		$\mathit{\eta }=0.95$
${\mathit{\rho }}_{\mathit{xy}}$	$\mathit{n}$	${\Im }_{\mathit{r}}$	${\Im }_{\mathit{a}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$
0.1	10	0.103	1.061	1.273	13.088	0.486	5.003	0.272	2.798	0.172	1.769	0.114	1.173
	20	0.320	1.051	3.942	12.957	1.507	4.953	0.843	2.77	0.533	1.751	0.353	1.161
	50	0.437	1.024	5.384	12.635	2.058	4.830	1.151	2.701	0.728	1.707	0.482	1.132
	100	0.458	1.013	5.655	12.496	2.161	4.776	1.209	2.671	0.764	1.689	0.507	1.120
	200	0.469	1.008	5.782	12.431	2.210	4.752	1.236	2.657	0.781	1.680	0.518	1.114
	400	0.473	1.005	5.836	12.397	2.231	4.739	1.248	2.650	0.789	1.675	0.523	1.111
0.3	10	0.259	1.138	3.196	14.032	1.222	5.364	0.683	3.000	0.432	1.896	0.286	1.258
	20	0.385	1.126	4.754	13.888	1.817	5.309	1.016	2.969	0.642	1.877	0.426	1.245
	50	0.539	1.098	6.649	13.546	2.542	5.178	1.421	2.896	0.899	1.831	0.596	1.214
	100	0.565	1.086	6.970	13.391	2.664	5.118	1.490	2.862	0.942	1.81	0.625	1.200
	200	0.578	1.080	7.124	13.323	2.723	5.093	1.523	2.848	0.963	1.800	0.638	1.194
	400	0.583	1.077	7.189	13.287	2.748	5.079	1.537	2.840	0.971	1.796	0.644	1.191
0.5	10	0.087	1.367	1.074	16.859	0.411	6.444	0.230	3.604	0.145	2.278	0.096	1.511
	20	0.304	1.352	3.753	16.681	1.434	6.376	0.802	3.566	0.507	2.254	0.336	1.495
	50	0.739	1.320	9.119	16.275	3.486	6.221	1.949	3.479	1.232	2.199	0.817	1.459
	100	0.773	1.304	9.530	16.085	3.643	6.148	2.037	3.438	1.288	2.174	0.854	1.441
	200	0.789	1.298	9.730	16.006	3.719	6.118	2.080	3.421	1.315	2.163	0.872	1.434
	400	0.796	1.294	9.816	15.965	3.752	6.102	2.098	3.413	1.326	2.157	0.880	1.431
0.7	10	0.355	2.002	4.382	24.691	1.675	9.438	0.937	5.278	0.592	3.337	0.393	2.213
	20	0.744	1.980	9.176	24.424	3.507	9.336	1.961	5.221	1.240	3.300	0.822	2.189
	50	1.222	1.933	15.075	23.838	5.762	9.112	3.222	5.096	2.037	3.221	1.351	2.136
	100	1.272	1.910	15.693	23.560	5.999	9.005	3.355	5.036	2.121	3.184	1.406	2.111
	200	1.297	1.901	15.998	23.447	6.115	8.962	3.420	5.012	2.162	3.168	1.434	2.101
	400	1.308	1.896	16.131	23.390	6.166	8.941	3.448	5.000	2.180	3.161	1.446	2.096
0.9	10	2.080	5.390	25.657	66.472	9.807	25.408	5.484	14.209	3.467	8.983	2.299	5.957
	20	2.938	5.330	36.235	65.736	13.850	25.127	7.746	14.052	4.897	8.883	3.247	5.891
	50	3.553	5.204	43.826	64.178	16.752	24.532	9.368	13.719	5.922	8.673	3.928	5.751
	100	3.687	5.144	45.477	63.443	17.383	24.251	9.721	13.562	6.146	8.573	4.075	5.686
	200	3.753	5.120	46.293	63.142	17.695	24.136	9.895	13.497	6.256	8.533	4.149	5.659
	400	3.783	5.108	46.657	63.001	17.834	24.082	9.973	13.467	6.305	8.514	4.181	5.646

Table 4. $RE$ of traditional and memory-type estimators for selected negative values of ${\rho }_{xy}$, n, and $\eta$.

				$\mathit{\eta }=0.15$		$\mathit{\eta }=0.35$		$\mathit{\eta }=0.55$		$\mathit{\eta }=0.75$		$\mathit{\eta }=0.95$
${\mathit{\rho }}_{\mathit{xy}}$	$\mathit{n}$	${\Im }_{\mathit{p}}$	${\Im }_{\mathit{a}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$
−0.1	10	0.232	1.067	2.866	13.158	1.096	5.029	0.613	2.813	0.387	1.778	0.257	1.179
	20	0.217	1.059	2.680	13.066	1.024	4.994	0.573	2.793	0.362	1.766	0.240	1.171
	50	0.490	1.039	6.041	12.817	2.309	4.899	1.291	2.740	0.816	1.732	0.541	1.149
	100	0.519	1.028	6.399	12.683	2.446	4.848	1.368	2.711	0.865	1.714	0.573	1.137
	200	0.531	1.023	6.548	12.617	2.503	4.823	1.400	2.697	0.885	1.705	0.587	1.131
	400	0.537	1.020	6.619	12.584	2.530	4.810	1.415	2.690	0.894	1.701	0.593	1.128
−0.3	10	0.445	1.169	5.494	14.424	2.100	5.513	1.174	3.083	0.742	1.949	0.492	1.293
	20	0.497	1.161	6.133	14.322	2.344	5.474	1.311	3.061	0.829	1.935	0.550	1.283
	50	0.629	1.139	7.761	14.050	2.966	5.370	1.659	3.003	1.049	1.899	0.695	1.259
	100	0.678	1.128	8.367	13.910	3.198	5.317	1.788	2.973	1.131	1.880	0.750	1.247
	200	0.699	1.122	8.625	13.837	3.297	5.289	1.844	2.958	1.166	1.870	0.773	1.240
	400	0.709	1.119	8.750	13.804	3.345	5.276	1.870	2.951	1.182	1.865	0.784	1.237
−0.5	10	0.521	1.419	6.422	17.499	2.455	6.689	1.373	3.741	0.868	2.365	0.575	1.568
	20	0.630	1.409	7.765	17.376	2.968	6.642	1.660	3.714	1.049	2.348	0.696	1.557
	50	0.849	1.382	10.470	17.047	4.002	6.516	2.238	3.644	1.415	2.304	0.930	1.528
	100	0.941	1.369	11.612	16.880	4.438	6.452	2.482	3.608	1.569	2.281	1.041	1.513
	200	0.983	1.362	12.121	16.794	4.633	6.419	2.591	3.590	1.638	2.269	1.086	1.505
	400	1.003	1.359	12.372	16.756	4.729	6.405	2.645	3.582	1.672	2.264	1.109	1.502
−0.7	10	0.608	2.074	7.498	25.580	2.866	9.778	1.603	5.468	1.013	3.457	0.672	2.292
	20	0.783	2.060	9.662	25.405	3.693	9.711	2.065	5.431	1.306	3.433	0.866	2.277
	50	1.277	2.021	15.750	24.925	6.020	9.527	3.367	5.328	2.128	3.368	1.411	2.234
	100	1.500	2.001	18.499	24.678	7.071	9.433	3.954	5.275	2.500	3.335	1.658	2.212
	200	1.608	1.991	19.829	24.555	7.579	9.386	4.239	5.249	2.680	3.318	1.777	2.201
	400	1.662	1.987	20.499	24.503	7.835	9.366	4.382	5.238	2.770	3.311	1.837	2.196
−0.9	10	0.590	5.499	7.272	67.818	2.780	25.923	1.555	14.497	0.983	9.165	0.652	6.078
	20	0.600	5.463	7.397	67.375	2.828	25.754	1.581	14.402	1.000	9.105	0.663	6.038
	50	2.558	5.360	31.548	66.101	12.059	25.266	6.744	14.130	4.263	8.933	2.827	5.924
	100	3.654	5.305	45.063	65.422	17.225	25.007	9.633	13.985	6.090	8.841	4.038	5.863
	200	4.360	5.279	53.768	65.104	20.552	24.885	11.493	13.917	7.266	8.798	4.818	5.834
	400	4.768	5.268	58.809	64.971	22.479	24.835	12.571	13.888	7.947	8.780	5.270	5.822

Table 5. ARB of traditional and memory-type estimators for selected positive values of ${\rho }_{xy}$, n, and $\eta$.

				$\mathit{\eta }=0.15$		$\mathit{\eta }=0.35$		$\mathit{\eta }=0.55$		$\mathit{\eta }=0.75$		$\mathit{\eta }=0.95$
${\mathit{\rho }}_{\mathit{xy}}$	$\mathit{n}$	${\Im }_{\mathit{r}}$	${\Im }_{\mathit{a}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{r}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$
0.1	10	0.385	0.002	0.031	0.005	0.082	0.002	0.146	0.001	0.231	0.001	0.348	0.002
	20	0.123	0.002	0.010	0.001	0.026	0.001	0.047	0.001	0.074	0.001	0.111	0.002
	50	0.040	0.002	0.003	0.000	0.008	0.000	0.015	0.001	0.024	0.001	0.036	0.002
	100	0.017	0.001	0.001	0.000	0.004	0.000	0.007	0.000	0.010	0.001	0.016	0.001
	200	0.009	0.000	0.001	0.000	0.002	0.000	0.004	0.000	0.006	0.000	0.008	0.000
	400	0.005	0.000	0.000	0.000	0.001	0.000	0.002	0.000	0.003	0.000	0.004	0.000
0.3	10	1.613	0.017	0.131	0.001	0.342	0.004	0.612	0.007	0.968	0.01	1.459	0.016
	20	0.098	0.015	0.008	0.001	0.021	0.003	0.037	0.006	0.059	0.009	0.089	0.013
	50	0.033	0.008	0.003	0.001	0.007	0.002	0.012	0.003	0.020	0.005	0.030	0.007
	100	0.015	0.004	0.001	0.000	0.003	0.001	0.006	0.001	0.009	0.002	0.013	0.003
	200	0.007	0.002	0.001	0.000	0.002	0.000	0.003	0.001	0.004	0.001	0.007	0.002
	400	0.004	0.001	0.000	0.000	0.001	0.000	0.002	0.000	0.002	0.001	0.004	0.001
0.5	10	3.267	0.027	0.265	0.002	0.693	0.006	1.239	0.010	1.960	0.016	2.956	0.024
	20	0.488	0.024	0.040	0.002	0.103	0.005	0.185	0.009	0.293	0.015	0.441	0.022
	50	0.025	0.012	0.002	0.001	0.005	0.003	0.010	0.005	0.015	0.007	0.023	0.011
	100	0.012	0.006	0.001	0.000	0.002	0.001	0.004	0.002	0.007	0.004	0.011	0.006
	200	0.005	0.003	0.000	0.000	0.001	0.001	0.002	0.001	0.003	0.002	0.005	0.003
	400	0.003	0.002	0.000	0.000	0.001	0.000	0.001	0.001	0.002	0.001	0.003	0.002
0.7	10	1.112	0.035	0.090	0.003	0.236	0.007	0.422	0.013	0.667	0.021	1.006	0.032
	20	0.062	0.033	0.005	0.003	0.013	0.007	0.023	0.013	0.037	0.020	0.056	0.030
	50	0.017	0.016	0.001	0.001	0.004	0.003	0.007	0.006	0.010	0.010	0.016	0.014
	100	0.008	0.008	0.001	0.001	0.002	0.002	0.003	0.003	0.005	0.005	0.007	0.007
	200	0.004	0.004	0.000	0.000	0.001	0.001	0.001	0.001	0.002	0.002	0.003	0.003
	400	0.002	0.002	0.000	0.000	0.000	0.000	0.001	0.001	0.001	0.001	0.002	0.002
0.9	10	0.075	0.039	0.006	0.003	0.016	0.008	0.028	0.015	0.045	0.024	0.068	0.036
	20	0.028	0.039	0.002	0.003	0.006	0.008	0.010	0.015	0.017	0.023	0.025	0.035
	50	0.009	0.018	0.001	0.001	0.002	0.004	0.004	0.007	0.006	0.011	0.008	0.016
	100	0.005	0.009	0.000	0.001	0.001	0.002	0.002	0.004	0.003	0.006	0.004	0.008
	200	0.002	0.004	0.000	0.000	0.000	0.001	0.001	0.001	0.001	0.002	0.002	0.004
	400	0.001	0.002	0.000	0.000	0.000	0.001	0.000	0.001	0.001	0.001	0.001	0.002

Table 6. ARB of traditional and memory-type estimators for selected negative values of ${\rho }_{xy}$, n, and $\eta$.

				$\mathit{\eta }=0.15$		$\mathit{\eta }=0.35$		$\mathit{\eta }=0.55$		$\mathit{\eta }=0.75$		$\mathit{\eta }=0.95$
${\mathit{\rho }}_{\mathit{xy}}$	$\mathit{n}$	${\Im }_{\mathit{p}}$	${\Im }_{\mathit{a}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$	${\Im }_{\mathit{p}}^{\mathit{m}}$	${\Im }_{\mathit{a}}^{\mathit{m}}$
−0.1	10	0.014	0.017	0.001	0.001	0.003	0.004	0.005	0.006	0.008	0.01	0.012	0.015
	20	0.010	0.012	0.001	0.001	0.002	0.003	0.004	0.005	0.006	0.007	0.009	0.011
	50	0.005	0.005	0.000	0.000	0.001	0.001	0.002	0.003	0.003	0.002	0.004	0.005
	100	0.002	0.002	0.000	0.000	0.000	0.001	0.001	0.001	0.001	0.001	0.002	0.002
	200	0.001	0.001	0.000	0.000	0.000	0.000	0.000	0.001	0.001	0.001	0.001	0.001
	400	0.001	0.001	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.001	0.001
−0.3	10	0.036	0.044	0.003	0.004	0.008	0.009	0.014	0.017	0.022	0.027	0.033	0.040
	20	0.024	0.030	0.002	0.002	0.005	0.006	0.009	0.011	0.015	0.018	0.022	0.027
	50	0.012	0.014	0.001	0.001	0.003	0.003	0.004	0.005	0.007	0.008	0.011	0.005
	100	0.005	0.006	0.000	0.000	0.001	0.001	0.002	0.002	0.003	0.004	0.005	0.006
	200	0.003	0.004	0.000	0.000	0.001	0.001	0.001	0.001	0.002	0.002	0.003	0.003
	400	0.001	0.002	0.000	0.000	0.000	0.000	0.001	0.001	0.001	0.001	0.001	0.002
−0.5	10	0.058	0.076	0.005	0.006	0.012	0.016	0.022	0.029	0.035	0.046	0.053	0.069
	20	0.039	0.051	0.003	0.004	0.008	0.011	0.015	0.019	0.024	0.03	0.036	0.046
	50	0.019	0.024	0.002	0.002	0.004	0.005	0.007	0.009	0.011	0.014	0.017	0.022
	100	0.008	0.010	0.001	0.001	0.002	0.002	0.003	0.004	0.005	0.006	0.008	0.009
	200	0.005	0.007	0.000	0.001	0.001	0.001	0.002	0.003	0.003	0.004	0.005	0.006
	400	0.002	0.003	0.000	0.000	0.000	0.001	0.001	0.001	0.001	0.002	0.002	0.003
−0.7	10	0.097	0.132	0.008	0.011	0.021	0.028	0.037	0.050	0.058	0.079	0.088	0.120
	20	0.055	0.076	0.004	0.006	0.012	0.016	0.021	0.029	0.033	0.045	0.050	0.068
	50	0.027	0.036	0.002	0.003	0.006	0.008	0.010	0.014	0.016	0.022	0.024	0.033
	100	0.012	0.016	0.001	0.001	0.002	0.003	0.004	0.006	0.007	0.009	0.010	0.014
	200	0.008	0.010	0.001	0.001	0.002	0.002	0.003	0.004	0.005	0.006	0.007	0.009
	400	0.003	0.004	0.000	0.000	0.001	0.001	0.001	0.002	0.002	0.002	0.003	0.004
−0.9	10	0.131	0.191	0.011	0.015	0.028	0.041	0.050	0.072	0.079	0.115	0.119	0.173
	20	0.072	0.106	0.006	0.009	0.015	0.022	0.027	0.040	0.043	0.063	0.065	0.096
	50	0.034	0.050	0.003	0.004	0.007	0.011	0.013	0.019	0.021	0.030	0.031	0.045
	100	0.015	0.022	0.001	0.002	0.003	0.005	0.006	0.008	0.009	0.013	0.014	0.020
	200	0.010	0.015	0.001	0.001	0.002	0.003	0.004	0.006	0.006	0.009	0.006	0.009
	400	0.004	0.006	0.000	0.000	0.001	0.001	0.001	0.002	0.002	0.003	0.003	0.005

The main findings of the simulation study are listed below:

(i).

The MSE and RE of the suggested MTLE ${\Im }_a^m$ are, respectively, minimum and maximum regarding the traditional mean estimator $\overline{y}$, traditional ratio estimator ${\Im }_r$, traditional product estimator ${\Im }_p$, logarithmic estimator ${\Im }_a$, and memory-type ratio estimator ${\Im }_r^m$, that are respectively presented in Table 1, Table 2, Table 3 and Table 4. For example, with ${\rho }_{xy}=0.1$, the MSEs of ${\Im }_a^m$ and ${\Im }_a$ are, respectively, 8.220 and 9.086 when $n=10$ and $\eta =0.95$.

(ii).

As the values of the correlation coefficient ${\rho }_{xy}$ range from $\pm 0.1$ to $\pm 0.9$, it has been noticed that the MSE of the suggested MTLE reduces while its RE grows, as shown in Table 1, Table 2, Table 3 and Table 4. As a result, the suggested estimators become more efficient when auxiliary information is used. As an example, for $\eta$ = 0.75, $n=400$, the MSE values of ${\Im }_a^m$ are 0.294 and 0.056 for ${\rho }_{xy}=0.1$, 0.9, respectively.

(iii).

With an increase in sample size n from 10 to 400, for any fixed value of the correlation coefficient ${\rho }_{xy}$, the MSE of the proposed estimators decreases. This demonstrates that the suggested estimators are superior to the existing traditional and memory-type estimators, even when using varied sample sizes.

(iv).

The results of the memory-type estimators, as reported in Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6, are found to be improved by the parameter $\eta$, which is utilized to provide weight to the present and past observations.

(v).

Additionally, when $\eta$ increases, more weight is given to the information that is currently being used rather than the information that is already known, increasing the MSE and decreasing the RE of the memory-type estimators.

4.2. Numerical Study

The performance of the suggested MTLE is demonstrated by using density and stiffness data of size 30 presented in [22]. The same data was considered by [15]. In the data set, the density and the stiffness of a material under production are considered as the study variable (y) and the auxiliary variable (x), respectively.

Plotting the total time on test transform, commonly referred to as the TTT-Transform, can be used in a number of contexts to evaluate the shape of the hazard function for a specific data set. This helps to choose which model is most appropriate to use with that collection of data. Readers can find further details on the TTT-Transform methodology in [23]. According to [24], if the curve is concave (convex), the hazard function is increasing (decreasing). When it starts convex and then becomes concave (or concave and then convex), the hazard function has a bathtub (unimodal) shape. Figure 1 and Figure 2 include the densities and TTT-Transforms of the auxiliary and study variables, respectively.

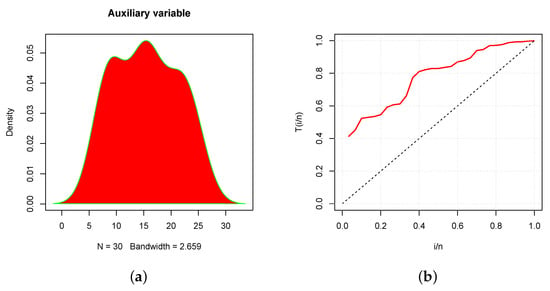
Figure 1. The density (a) and TTT (b) plots for the auxiliary variable of the real data.

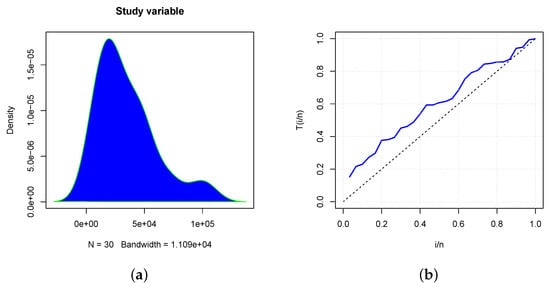
Figure 2. The density (a) and TTT (b) plots for the study variable of the real data.

The population parameters are given by $\overline{Y}$ = 15.47, $\overline{X}$ = 34666.83, ${\sigma }_y^2=34.023$, ${\sigma }_x^2=643,900,000$, and ${\rho }_{xy}=0.89$. By employing simple random sampling without replacement, 25 samples of size 5 are drawn from the population at regular intervals, and the results are compiled in Table 7. Each sample provides the usual mean estimators as $\overline{y}$ and $\overline{x}$, while the classical ratio estimator ${\Im }_r$, logarithmic estimator ${\Im }_a$, memory-type ratio estimator ${\Im }_r^m$, and MTLE ${\Im }_a^m$ are computed using (1), (7), (12), and (18). Each sample is used to construct the EWMA statistic with $\eta =0.25$. The estimates for the variables y and x, as well as the estimates for the memory-based ratio estimator and proposed MTLE, are also presented in Table 7.

Table 7. Computation of memory-type estimators using real data for the value of $\eta =0.25$.

Sample of y					${\overline{\mathit{y}}}_{\mathit{t}}$	Sample of x					${\overline{\mathit{x}}}_{\mathit{t}}$	${\mathit{Q}}_{\mathit{t}}$	${\mathit{Z}}_{\mathit{t}}$	${\mathit{\Im }}_{\mathit{r}}$	${\mathit{\Im }}_{\mathit{a}}$	${\mathit{\Im }}_{\mathit{r}}^{\mathit{m}}$	${\mathit{\Im }}_{\mathit{a}}^{\mathit{m}}$
19.5	13.6	16.7	21.7	6.4	15.58	32,207	18,036	49,499	47,661	8076	31,095.8	33,774.073	15.492	17.369	16.44	15.902	15.680
7	15	15.4	13.6	23.4	14.88	5304	26,222	25,312	18,036	104,170	35,808.8	34,282.754	15.370	14.406	14.64	15.542	15.449
21.2	22.8	9.9	13.6	8.3	15.16	48,218	70,453	14,191	18,036	7573	31,694.2	33,635.616	15.328	16.582	15.85	15.798	15.544
15.2	8.2	14.5	19.8	8.3	13.2	28,028	10,728	22,148	38,138	7573	21,323	30,557.462	14.902	21.460	16.75	16.906	15.852
9.9	8.4	7	21.3	23.3	13.98	14,191	17,502	5304	53,045	49,512	27,910.8	29,895.796	14.718	17.364	15.57	17.066	15.839
23.4	11	16.7	8.2	15	14.86	104,170	19,443	49,499	10,728	25,319	41,831.8	32,879.797	14.746	12.315	13.53	15.548	15.118
23.3	14.8	17.4	8.4	9.8	14.74	49,512	26,751	43,243	17,502	14,007	30,203	32,210.598	14.745	16.919	15.79	15.869	15.270
21.2	15.4	9.9	19.5	19.8	17.16	48,218	25,312	14,191	32,207	38,138	31,613.2	32,061.248	15.228	18.818	17.96	16.466	15.806
11	19.5	25.6	14.5	15.4	17.2	19,443	32,207	96,305	22,148	25,312	39,083	33,816.686	15.622	15.256	16.20	16.015	15.803
23.3	25.6	9.8	14.5	21.3	18.9	49,512	96,305	14,007	22,148	53,045	47,003.4	37,113.365	16.278	13.939	16.25	15.205	15.793
13.6	21.3	15.4	15	19.8	17.02	18,036	53,045	25,312	26,222	38,138	32,150.6	35,872.674	16.426	18.352	14.10	15.874	16.174
23.4	6.4	11	15.2	21.2	15.44	104,170	8076	19,443	28,028	48,218	41,587	37,301.255	16.229	12.871	15.99	15.083	15.711
15	21.7	17.4	9.8	9.5	14.68	26,222	47,661	43,243	14,007	14,814	29,189.4	35,273.291	15.919	17.435	15.51	15.646	15.794
17.4	14.5	11	24.4	9.9	15.44	43,243	22,148	19,443	72,594	14,191	34,323.8	35,035.919	15.823	15.594	15.33	15.657	15.746
14.5	9.9	19.5	9.8	9.5	12.64	22,148	14,191	32,207	14,007	14,814	19,473.4	31,145.289	15.187	22.502	16.73	16.904	15.996
21.2	8.3	25.6	8.4	23.4	17.38	48,218	7573	96,305	17,502	104,170	54,753.6	37,047.367	15.625	11.004	13.88	14.621	15.171
22.8	19.5	15	11	9.8	15.62	70,453	32,207	26,222	19,443	14,007	32,466.4	35,902.125	15.624	16.679	16.14	15.087	15.379
8.2	15.4	16.7	14.5	8.4	12.64	10,728	25,312	49,499	22,148	17,502	25,037.8	33,186.044	15.027	17.501	14.85	15.698	15.337
8.6	6.4	24.4	16.4	7	12.56	9714	8076	72,594	41,792	5304	27,496	31,763.533	14.534	15.836	14.09	15.862	15.156
8.4	9.5	16.7	6.4	15	11.2	17,502	14,814	49,499	8076	25,319	23,042	29,583.15	13.867	16.850	13.69	16.25	15.009
9.5	19.5	23.3	8.6	25.6	17.3	14,814	32,207	49,512	9714	96,305	40,510.4	32,314.962	14.554	14.805	16.00	15.613	15.048
23.4	15.4	9.9	9.8	13.6	14.42	104,170	25,312	14,191	14,007	18,036	35,143.2	33,022.022	14.527	14.225	14.32	15.251	14.862
8.6	15.4	8.2	11	21.2	12.88	9714	25,312	10,728	19,443	48,218	22,683	30,437.266	14.198	19.685	15.87	16.17	15.134
21.2	8.4	17.4	7	19.5	14.7	48,218	17,502	43,243	5304	32,207	29,294.8	30,151.65	14.298	17.396	15.98	16.439	15.317
21.3	15	21.2	9.8	25.6	18.58	53,045	26,222	48,218	14,007	96,305	47,559.4	34,503.587	15.154	13.543	15.88	15.226	15.186

With reference to the aforementioned data, we have $MSE\left({\Im }_r\right)=1.7871$, $MSE\left({\Im }_a\right)=0.2917$, $MSE\left({\Im }_r^m\right)=0.2553$, and $MSE\left({\Im }_a^m\right)=0.0416$, which shows that the suggested MTLE ${\Im }_a^m$ is more efficient than the traditional estimators ${\Im }_r$, ${\Im }_a$, and ${\Im }_r^m$.

Further, we have numerically obtained the conditions derived in Section 3, using the above data set, under which the suggested MTLE dominates the existing traditional and memory-type estimators.

Condition (24).

$$\begin{array}{c}\hfill {\rho }_{xy}^2>\frac{2{\rho }_{xy}{C}_x{C}_y-C_y^2(1-\varsigma )-C_x^2}{\varsigma C_y^2}\Rightarrow 0.7921>-4.2527\end{array}$$

(29)

Condition (25).

$$\begin{array}{c}\hfill {\rho }_{xy}^2>-\frac{(C_y^2(1-\varsigma )+C_x^2+2{\rho }_{xy}{C}_x{C}_y)}{\varsigma C_y^2}\Rightarrow 0.7921>-31.8972\end{array}$$

(30)

Condition (26).

$$\begin{array}{c}\hfill \varsigma <1\Rightarrow 0.25<1\end{array}$$

(31)

Condition (27).

$$\begin{array}{c}\hfill {\rho }_{xy}^2>\frac{2{\rho }_{xy}{C}_x{C}_y-C_x^2}{C_y^2}\Rightarrow 0.7921>-0.3131\end{array}$$

(32)

Condition (28).

$$\begin{array}{c}\hfill {\rho }_{xy}^2>-\frac{(2{\rho }_{xy}{C}_x{C}_y+C_x^2)}{C_y^2}\Rightarrow 0.7921>-7.2243\end{array}$$

(33)

From (29) to (33), it can easily be seen that the real data satisfies the efficiency conditions established in Section 3.

5. Conclusions

In time-scale-based surveys, the past and present data from the sample must be considered simultaneously to improve the performance of the estimators. To overcome this problem, we employed the EWMA statistic and proposed the MTLE of the population mean under SRS and calculated their characteristics, including MSE and bias. The effectiveness of the proposed memory-type estimators has been compared to the existing traditional and memory-type estimators. The superiority of the suggested MTLE is further investigated using an empirical investigation based on simulated and real data. The empirical findings demonstrate that the suggested MTLE is superior to the traditional and the existing memory-based estimators. The suggested MTLE can be examined in more detail when data are available for a number of auxiliary variables.