Estimating the Gerber–Shiu Function in the Two-Sided Jumps Risk Model by Laguerre Series Expansion

Abstract

In this paper, we consider an insurance risk model with two-sided jumps, where downward and upward jumps typically represent claim amounts and random gains, respectively. We use the Laguerre series to expand the Gerber–Shiu function and estimate it based on observed information. Moreover, we show that the estimator is easily computed and has a fast convergence rate. Numerical examples are also provided to show the efficiency of our method when the sample size is finite.

1. Introduction

In this paper, the surplus process of an insurance company is described by the classical risk model

$$\begin{array}{c}\hfill U\left(t\right)=u+ct-S\left(t\right)=u+ct-\sum _{i=1}^{N\left(t\right)}{Z}_i,\end{array}$$

(1)

where $U\left(0\right)=u\ge 0$ is the initial surplus and $c>0$ is the constant premium rate per unit time. The claim number process ${\left\{N\left(t\right)\right\}}_{t\ge 0}$ is a homogeneous Poisson process with intensity $\lambda >0$, and the claim sizes ${\left\{Z_i\right\}}_{i=1}^{\infty }$ form an independent and identically distributed sequence that may be positive or negative. For later use, the density of $Z_i$ is denoted by $f(·)$. We also assume that ${\left\{N\left(t\right)\right\}}_{t\ge 0}$ and ${\left\{Z_i\right\}}_{i=1}^{\infty }$ are independent. Furthermore, since the size of each jump $Z_i$ can be positive or negative, we can think of it as jumping up or down, and the upward and downward jumps can be interpreted as company random gains and random losses, respectively. The size of each upward jump is defined as $X_i$ and its density function is defined as $f_{+}(·)$, the mean value is ${\mu }_{+}$. Similarly, the size of each downward jump is defined as $Y_i$ and the corresponding density function is $f_{-}(·)$, the mean value is ${\mu }_{-}$. Hence, we have

$$f\left(x\right)=p{f}_{+}\left(x\right)I_{\{x>0\}}+q{f}_{-}(-x)I_{\{x<0\}},$$

(2)

where $p,q>0,p+q=1$, $I_{\left\{A\right\}}$ is an indicator function of the event A. To this end, we define $N^{+}\left(t\right)={\displaystyle \sum _{i=1}^{N\left(t\right)}}{I}_{\{Z_i>0\}}$ to be the number of upward jumps until time t. Similarly, let $N^{-}\left(t\right)={\displaystyle \sum _{i=1}^{N\left(t\right)}}{I}_{\{Z_i<0\}}$ be the number of downward jumps until time t. Therefore, the surplus process (1) can be viewed as a risk model with stochastic premium income

$$\begin{array}{c}\hfill U\left(t\right)=u+c-S\left(t\right)=u+c+\sum _{i=1}^{N^{-}\left(t\right)}{Y}_i-\sum _{i=1}^{N^{+}\left(t\right)}{X}_i,t\ge 0.\end{array}$$

(3)

For a more detailed introduction of Equations (1) and (3), please refer to Cheung et al. [1]. Related works can be found in [2,3,4,5], among others.

Define the ruin time by $\tau =inf\{t\ge 0:U(t)<0\}$, and set $\tau =\infty$ if $U\left(t\right)\ge 0$ for all $t\ge 0$. In this paper, we are interested in the Gerber–Shiu expected discounted penalty function that is defined as

$$\begin{array}{c}\hfill m\left(u\right):=E[e^{-\delta \tau }\omega (U(\tau -),|U\left(\tau \right)\left|\right)I_{\{\tau <\infty \}}],u\ge 0.\end{array}$$

where $\delta \ge 0$ is the Laplace transform argument, and $\omega :[0,\infty )\times [0,\infty )\to [0,\infty )$ is a measurable penalty function of the $U(\tau -)$ and $\left|U\right(\tau \left)\right|$. This function was first introduced by Gerber and Shiu [6]. It has become an important and standard risk measure in ruin theory since various quantities of interests in ruin theory can be obtained for different values of the discount factor $\delta$ and different penalty functions $\omega$. Interested readers are referred to [7,8,9,10,11,12,13], among others.

The above-mentioned papers assume that some probability characteristics of the surplus process are known, for example, the probability characteristics of the claim sizes and claim number process; however, these are usually unknown for an insurance company. In fact, we can only obtain some discrete data information about the surplus flow levels, claim numbers, and individual claim sizes (income numbers and individual income sizes). According to these data, more and more actuarial researchers use different methods to calculate statistical estimations of ruin probability and Gerber–Shiu function. Shimizu [14,15] used a regularized version of the inverse Laplace transform to estimate the Gerber–Shiu function in the Lévy risk model and the perturbed compound Poisson risk model, respectively; You and Cai [16] used a regularized version of the inverse Laplace transform to consider the nonparametric estimation of the survival probability for a spectrally negative Lévy risk model based on high-frequency data; Zhang and Yang [17,18] estimated the ruin probability based on high-frequency data and low-frequency data, respectively; Shimizu and Zhang [19] estimated the Gerber–Shiu function in a Lévy risk model based on high-frequency data by Fourier inversion transform. In addition, there are some effective estimation methods. Chau et al. [20,21] used the Fourier-cosine series expansion to estimate ruin probability and Gerber–Shiu function in the Lévy risk models; Yang et al. [22] applied two-dimensional Fourier cosine series expansion to estimate the discounted density function of the deficit at ruin; Xie and Zhang [23] applied the Fourier cosine series expansion to estimate the compound Poisson risk model under a constant barrier dividend strategy; Zhang [24] proposed a new estimator of the Gerber–Shiu function by Fourier sinc series expansion in the perturbed compound Poisson risk model; Chan [25,26] proposed a method based on the complex Fourier series expansion and used it in the actuarial field; Wang et al. [27] considered the pricing problem of variable annuities with guaranteed minimum death benefit by a complex Fourier series method under regime-switching jump diffusion models. For more detail on the statistical estimation of risk models, we refer the interested readers to [28,29,30,31,32,33,34,35,36,37,38,39,40].

The main goal of this paper is to use the Laguerre series expansion method to estimate the Gerber–Shiu function. The Laguerre series expansion method has been used by some authors for solving some statistical problems. For example, Comte and Genon-Catalot [41] used the appropriate Laguerre basis to take into account the estimation of the random strength of the mixed Poisson model; Zhang and Su [42,43] applied Laguerre series to approximate the Gerber–Shiu function in the class compound Poisson risk model and the Lévy risk model, respectively; Zhang and Yong [44] studied the valuation of equity-linked annuity contracts with guaranteed minimum death benefits by Laguerre series expansion; Cheung and Zhang [45] proposed to use Laguerre series expansion as a function of the initial earnings level to approximate the ruin probability of the updated risk model; Albrecher et al. [46] considered the bivariate Laguerre expansions approach for joint ruin probabilities in a two-dimensional insurance risk process; Xie and Zhang [47] considered the finite-time dividend and ruin problems in a class of risk models under the constant dividend barrier strategy by Laguerre series expansion; Su et al. [48] considered the random deviation of premium income (or claim loss), so they studied the statistical estimation of Gerber–Shiu function in the compound Poisson risk model perturbed by diffusion. In the actual insurance business, the premium income of insurance companies, especially small companies, is sometimes random. Therefore, this paper considers the two-sided jumps risk model. For more on the Laguerre series expansion method, we refer the interested readers to [49,50,51,52,53].

The remainder of this paper is organized as follows: In Section 2, we first briefly introduce the Laguerre series expansion method, and then derive Laguerre series expansions of $m\left(u\right)$. In Section 3, we present how to construct estimators for the aforementioned quantities based on observed sample of the surplus process, and in Section 4, we study the consistency rate of our estimator. Finally, numerical examples are given in Section 5 to illustrate that the performance of the estimator behaves well when the sample size is finite.

2. Preliminaries

2.1. The Laguerre Series Expansion

In this subsection, we present some known results on the Laguerre series expansion method. Throughout, let ${\mathbb{L}}^1\left({\mathbb{R}}_{+}\right)$ and ${\mathbb{L}}^2\left({\mathbb{R}}_{+}\right)$ denote the classes of absolutely integrable functions and square integrable functions on the positive axis, respectively, and denote by ${\mathbb{C}}_{+}$ (respectively, ${\mathbb{C}}_{++}$) those complex numbers that have a non-negative (respectively positive) real part, that is

$$\begin{array}{c}\hfill {\mathbb{C}}_{+}:=\{s\in \mathbb{C}:\mathrm{Re}\left(s\right)\ge 0\}\mathrm{and}{\mathbb{C}}_{++}:=\{s\in \mathbb{C}:\mathrm{Re}\left(s\right)>0\}.\end{array}$$

For any complex number s, we denote its real part and imaginary part by $\mathrm{Re}\left(s\right)$ and $\mathrm{Im}\left(s\right)$, respectively. For two positive functions $f_1,f_2$ with a common domain $\mathcal{X}\in \mathbb{R}$, we use $f_1\lesssim f_2$ to mean $f_1\left(x\right)\le C{f}_2\left(x\right)$ uniformly in $x\in \mathcal{X}$. Similarly, we use $f_1\left(x\right)\gtrsim f_2\left(x\right)$ to mean $f_1\left(x\right)\ge C{f}_2\left(x\right)$ uniformly in $x\in \mathcal{X}$. For two sequences of functions $\left\{f_k\right\}$ and $\left\{g_k\right\}$, we use $f_k\lesssim (\mathrm{or}\gtrsim )g_k$ to mean $f_k\left(x\right)\le (\mathrm{or}\ge )C{g}_k\left(x\right)$ uniformly in k and x. Denote the scalar product and ${\mathbb{L}}^2$-norm on ${\mathbb{L}}^2\left({\mathbb{R}}_{+}\right)$ by

$$\begin{array}{c}\hfill ⟨f,g⟩={\int }_0^{\infty }f\left(x\right)g\left(x\right)dx,\parallel f\parallel =\sqrt{{\int }_0^{\infty }f{\left(x\right)}^{2}dx},\forall f,g\in {\mathbb{L}}^2\left({\mathbb{R}}_{+}\right).\end{array}$$

For convenience, let C be a generic positive constant that can take different values from line to line. For any $g\in {\mathbb{L}}^1$, we define its Laplace transform and Fourier transform by $\mathcal{L}g\left(s\right)={\int }_0^{\infty }{e}^{-su}g\left(u\right)du,\mathrm{Re}\left(s\right)\ge 0$ and $\mathcal{F}g\left(s\right)={\int }_0^{\infty }{e}^{isu}g\left(u\right)dus\in \mathbb{R}$. Furthermore, let $T_s$ be the Dickson–Hipp operator, such that

$$\begin{array}{c}\hfill T_{s}f\left(y\right)={\int }_y^{\infty }{e}^{-s(x-y)}f\left(x\right)dx={\int }_0^{\infty }{e}^{-sx}f(x+y)dx,y\ge 0,\end{array}$$

for any integrable real function f. The operator $T_s$ was first introduced in Dickson and Hipp [54] and has many nice properties, which can be found in Li and Garrido [55]. The Laguerre functions are given by

$$\begin{array}{c}\hfill {\psi }_k\left(x\right)=\sqrt{2}{L}_k\left(2x\right)e^{-x},x\ge 0,k=0,1,2,\dots ,\end{array}$$

(4)

where $\left\{L_k\right\}$ is a Laguerre polynomial defined as

$$L_k\left(x\right)=\sum _{j=0}^k{(-1)}^j\left(\genfrac{}{}{0pt}{}{k}{j}\right)\frac{x^j}{j!},x\ge 0.$$

(5)

It is follows that the Laguerre functions are uniformly bounded, i.e.,

$$\begin{array}{c}\hfill |{\psi }_k|\le \sqrt{2},\forall k\ge 0\mathrm{and}\forall x\in {\mathbb{R}}_{+}.\end{array}$$

(6)

We also note that, for the Laguerre functions ${\psi }_k$ and ${\psi }_j$, the following convolution formula holds:

$${\int }_0^x{\psi }_k(x-y){\psi }_j\left(y\right)dy=\frac{1}{\sqrt{2}}[{\psi }_{k+j}\left(x\right)-{\psi }_{k+j+1}\left(x\right)].$$

(7)

For more details on the above results, refer to Abramowitz and Stegun [56].

Remark 1.

Suppose that the collection ${\left\{{\psi }_k\right\}}_{k\ge 0}$ is a complete orthonormal basis of ${\mathbb{L}}^2\left({\mathbb{R}}_{+}\right)$ satisfying

(1) 

$\parallel {\psi }_k\parallel =1$;

(2) 

$⟨{\psi }_k,{\psi }_j⟩=0\mathrm{for}k\ne j$.

Using the orthonormal property of the Laguerre basis ${\left\{{\psi }_k\right\}}_{k\ge 0}$, for any $f\in {\mathbb{L}}^2\left({\mathbb{R}}_{+}\right)$, we can develop it on the Laguerre basis

$$\begin{array}{c}\hfill f\left(x\right)=\sum _{k=0}^{\infty }⟨f,{\psi }_k⟩{\psi }_k\left(x\right).\end{array}$$

In practical applications, we need to truncate the above infinite sum. Hence, for all $K\ge 0$, we have

$$\begin{array}{c}\hfill f\left(x\right)\approx f_K\left(x\right)=\sum _{k=0}^K⟨f,{\psi }_k⟩{\psi }_k\left(x\right).\end{array}$$

To evaluate the convergence rate of the bias $\parallel f_K-f\parallel$, we introduce the Sobolev–Laguerre space (see Bongioanni and Torrea [57]) that is defined by

$$\begin{array}{c}\hfill W({\mathbb{R}}_{+},r,B)=\left\{f:{\mathbb{R}}_{+}\to \mathbb{R},f\in {\mathbb{L}}^2\left({\mathbb{R}}_{+}\right),\sum _{k=0}^{\infty }{k}^r{⟨f,{\psi }_k⟩}^2\le B<\infty \right\},\end{array}$$

where $0<r,B<\infty$. Suppose that r is a positive integer. If $f\in {\mathbb{L}}^2\left({\mathbb{R}}_{+}\right)$, then the following properties are equivalent:

(1)

${\displaystyle \sum _{k=0}^{\infty }}{k}^r{⟨f,{\psi }_k⟩}^2<\infty$.

(2)

For function f admits derivatives up to order $r-1$, with $f^{(r-1)}$ absolutely continuous and for $m=0,1,\dots ,r-1$, the functions

$$\begin{array}{c}\hfill x^{\frac{(m+1)}{2}}{\left(f{e}^x\right)}^{(m+1)}{e}^{-x}=x^{\frac{(m+1)}{2}}\sum _{j=0}^{m+1}\left(\genfrac{}{}{0pt}{}{m+1}{j}\right)f^{\left(j\right)}\end{array}$$

(8)

belong to ${\mathbb{L}}^2\left({\mathbb{R}}_{+}\right)$ (see Comte and Genon-Catalot [41]). If $f\in W({\mathbb{R}}_{+},r,B)$, using the orthonormal property of the Laguerre basis ${\left\{{\psi }_k\right\}}_{k\ge 0}$ (see Zhang and Su [43] and Zhang and Yong [44]), we have

$$\begin{array}{c}\hfill \parallel f_K-f\parallel =\sum _{k=K+1}^{\infty }{⟨f,{\psi }_k⟩}^2\le {(K+1)}^{-r}\sum _{k=K+1}^{\infty }{k}^r{⟨f,{\psi }_k⟩}^2\le B{K}^{-r}.\end{array}$$

2.2. The Laguerre Expansion of Gerber–Shiu Function

In this subsection, we show that the Gerber–Shiu function can be expressed by Laguerre functions. We focus on the $Erlang[n,\beta ]$ distribution, for some $\beta >0$ and a positive integer n, to model the premium sizes (see Labbé et al. [58]). No specific assumption is made on the claim’s distribution. For $u>0$, conditioning on the time of the first event (premium or claim), we obtain

$$\begin{array}{cc}\hfill m\left(u\right)=& {\int }_0^{\infty }\lambda p{e}^{-(\delta +\lambda )t}{\int }_0^{u+ct}m(u+ct-y)f_{+}\left(y\right)dydt+{\int }_0^{\infty }\lambda p{e}^{-(\delta +\lambda )t}\hfill \\ \hfill & \times {\int }_{u+ct}^{\infty }\omega (u+ct,y-u-ct)f_{+}\left(y\right)dydt+{\int }_0^{\infty }\lambda q{e}^{-(\delta +\lambda )t}{\int }_0^{\infty }m(u+ct+y)f_{-}\left(y\right)dydt,\hfill \end{array}$$

hence

$$\begin{array}{c}\hfill m\left(u\right)={\int }_0^{u}m(u-y)f_{\delta }\left(y\right)dy+H_{\delta ,w}\left(u\right),\end{array}$$

(9)

where

$$\begin{array}{cc}\hfill & f_{\delta }\left(y\right)=\frac{p\lambda }{c}\left[{(-1)}^n\sum _{i=1}^{n+1}\frac{{(\beta -{\rho }_i)}^n}{{\displaystyle \prod _{j=1,j\ne i}^{n+1}}({\rho }_i-{\rho }_j)}{T}_{{\rho }_i}{f}_{+}\left(y\right)\right],y\ge 0,\hfill \\ \hfill & H_{\delta ,w}\left(u\right)=\frac{p\lambda }{c}\left[{(-1)}^n\sum _{i=1}^{n+1}\frac{{(\beta -{\rho }_i)}^n}{{\displaystyle \prod _{j=1,j\ne i}^{n+1}}({\rho }_i-{\rho }_j)}{T}_{{\rho }_i}\eta \left(u\right)\right],u\ge 0,\hfill \\ \hfill & \eta \left(u\right)={\int }_u^{\infty }\omega (u,y-u)f_{+}\left(y\right)dy.\hfill \end{array}$$

For any $\delta \ge 0$, in the following Lundberg’s fundamental equation (in s)

$$\begin{array}{c}\hfill \chi \left(s\right):=[\lambda +\delta -cs-p\lambda \mathcal{L}f\left(s\right)]{(\beta -s)}^n-q\lambda {\beta }^n=0,s\in {\mathbb{C}}_{+},\end{array}$$

(10)

${\rho }_i$ and ${\rho }_j$ are the $n+1$ roots of the above equation.

Remark 2.

Assume, in addition, that $n=1$ (i.e., the annuity income amounts follow the exponential distribution).

$$\begin{array}{c}\hfill \chi \left(s\right):=[\lambda +\delta -cs-p\lambda \mathcal{L}{f}_{+}\left(s\right)](\beta -s)-q\lambda \beta =0,s\in {\mathbb{C}}_{+}.\end{array}$$

(11)

The above equation has two positives roots, ${\rho }_1\in (0,\beta )$ and ${\rho }_2\in (\beta ,\infty )$. It is clear from Equation (11) that the continuous function $\chi \left(s\right)$ is such that $\chi \left(0\right)=\delta \beta >0$, $\chi \left(\beta \right)=-q\lambda \beta <0$ and $\underset{s\to \infty }{lim}\chi \left(s\right)=\infty$. Thus, the existence of two distinct roots satisfying $0\le {\rho }_1<\beta <{\rho }_2<\infty$ is established.

$$\begin{array}{cc}\hfill & f_{\delta }\left(y\right)=\frac{p\lambda }{c}\left[\sum _{i=1}^2\frac{({\rho }_i-\beta )}{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{T}_{{\rho }_i}{f}_{+}\left(y\right)\right],y\ge 0,\hfill \\ \hfill & H_{\delta ,w}\left(u\right)=\frac{p\lambda }{c}\left[\sum _{i=1}^2\frac{({\rho }_i-\beta )}{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{T}_{{\rho }_i}\eta \left(u\right)\right],u\ge 0,\hfill \\ \hfill & \eta \left(u\right)={\int }_u^{\infty }\omega (u,y-u)f_{+}\left(y\right)dy.\hfill \end{array}$$

In the following, we suppose that some conditions hold true in this paper, which has also been considered in Shimizu and Zhang [19].

Condition 1.

(Net profit condition.)

$$\begin{array}{c}\hfill ct-E\left[S\left(t\right)\right]=ct+q\lambda t{\mu }_{-}-p\lambda t{\mu }_{+}>0,t>0.\end{array}$$

The above condition guarantees that the expectation of the surplus process will always be positive at any time $t>0$. From a practical point of view, we only consider the case of $c>p\lambda$ in this paper.

Condition 2.

For the penalty function w, it satisfies

$${\int }_0^{\infty }{\int }_0^{\infty }(1+x)\omega (x,y)f_{+}(x+y)dydx<\infty .$$

Condition 3.

For the penalty function w, there exist some integers ${\alpha }_1,{\alpha }_2$ such that

$$w(x,y)\lesssim {(1+x)}^{{\alpha }_1}{(1+y)}^{{\alpha }_2}.$$

In order to use the Laguerre series expansion method to calculate Equation (9), we need to ensure that $m\in {\mathbb{L}}^2\left({\mathbb{R}}^{+}\right)$. Using inequality ${(x+y)}^2\le 2x^2+2y^2$, we obtain

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{m}^2\left(u\right)du& ={\int }_0^{\infty }{\left({\int }_0^{u}m(u-y)f_{\delta }\left(y\right)dy+H_{\delta ,w}\left(u\right)\right)}^{2}du\hfill \\ \hfill & \le 2{\int }_0^{\infty }{\left({\int }_0^{u}m(u-y)f_{\delta }\left(y\right)dy\right)}^{2}du+2{\int }_0^{\infty }{\left(H_{\delta ,w}\left(u\right)\right)}^{2}du.\hfill \end{array}$$

(12)

As can be seen from Equation (12), in order to determine $m\in {\mathbb{L}}^2\left({\mathbb{R}}^{+}\right)$, we need some Lemmas.

Lemma 1.

For function $f_{\delta }$, by $\delta >0$, ${\mu }_{-}=\frac{1}{\beta }$ and Condition 1, we have $f_{\delta }\in {\mathbb{L}}^2\left({\mathbb{R}}^{+}\right)$.

Proof. 

Because

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{f}_{\delta }\left(x\right)dx& =\frac{p\lambda }{c}\sum _{i=1}^2\frac{({\rho }_i-\beta )}{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_0^{\infty }{\int }_x^{\infty }{e}^{-{\rho }_i(y-x)}{f}_{+}\left(y\right)dydx\hfill \\ \hfill & =\frac{p\lambda }{c}\sum _{i=1}^2\frac{({\rho }_i-\beta )}{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_0^{\infty }{\int }_0^y{e}^{-{\rho }_i(y-x)}{f}_{+}\left(y\right)dxdy\hfill \\ \hfill & \le \frac{p\lambda }{c}\sum _{i=1}^2\frac{({\rho }_i-\beta )}{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_0^{\infty }y{f}_{+}\left(y\right)dy\hfill \\ \hfill & =\frac{p\lambda }{c}·{\mu }_{+}<\frac{\lambda }{c}\frac{q}{\beta }+1<\frac{\lambda +c\beta }{c\beta }.\hfill \end{array}$$

Note that

$$\begin{array}{c}\hfill f_{\delta }\left(x\right)\le \frac{p\lambda }{c}\sum _{i=1}^2\frac{({\rho }_i-\beta )}{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_0^{\infty }{f}_{+}\left(y\right)dy<\frac{\lambda }{c}.\end{array}$$

Hence,

$$\begin{array}{c}\hfill {\int }_0^{\infty }{\left(f_{\delta }\left(x\right)\right)}^{2}dx\le \frac{\lambda }{c}{\int }_0^{\infty }{f}_{\delta }\left(x\right)dx\le \frac{{\lambda }^2+c\lambda \beta }{c^2\beta }<\infty .\end{array}$$

(13)

This completes the proof. □

Lemma 2.

Under Condition 2, we have $H_{\delta ,w}\in {\mathbb{L}}^2\left({\mathbb{R}}^{+}\right)$.

Proof. 

$$\underset{u\ge 0}{sup}{H}_{\delta ,w}\left(u\right)\le \frac{p\lambda }{c}{\int }_0^{\infty }\eta \left(u\right)du=\frac{p\lambda }{c}{\int }_0^{\infty }{\int }_0^{\infty }\omega (x,y)f(x+y)dydx<\infty$$

and

$$\begin{array}{cc}\hfill {\int }_0^{\infty }{H}_{\delta ,w}\left(u\right)du=& \frac{p\lambda }{c}\sum _{i=1}^2\frac{({\rho }_i-\beta )}{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_0^{\infty }{\int }_u^{\infty }{\int }_x^{\infty }{e}^{-{\rho }_i(y-x)}\omega (x,y-x)f\left(y\right)dydxdu\hfill \\ \hfill \le & \frac{p\lambda }{c}{\int }_0^{\infty }{\int }_u^{\infty }{\int }_x^{\infty }\omega (x,y-x)f\left(y\right)dydxdu\hfill \\ \hfill =& \frac{p\lambda }{c}{\int }_0^{\infty }{\int }_0^{\infty }x\omega (x,y)f(x+y)dydx<\infty ,\hfill \end{array}$$

which yield

$${\int }_0^{\infty }{\left(H_{\delta ,w}\left(u\right)\right)}^{2}du\le \underset{u\ge 0}{sup}{H}_{\delta ,w}\left(u\right)\times \left({\int }_0^{\infty }{H}_{\delta ,w}\left(u\right)du\right)<\infty .$$

(14)

This completes the proof. □

Lemma 3.

As for m, by Conditions 1 and 2, we obtain $m\in {\mathbb{L}}^2\left({\mathbb{R}}^{+}\right)$.

Proof. 

By Equation (9), we have

$${\int }_0^{\infty }m\left(u\right)du=\frac{{\int }_0^{\infty }{H}_{\delta ,w}\left(u\right)du}{1-{\int }_0^{\infty }{f}_{\delta }\left(y\right)dy}<\infty ,$$

i.e., $m\in {\mathbb{L}}^1\left({\mathbb{R}}^{+}\right)$. According to Theorem 1.4.5 in Stenger [59], we can obtain ${\int }_0^{u}m(u-x)f_{\delta }\left(x\right)dx\in {\mathbb{L}}^2\left({\mathbb{R}}^{+}\right)$ due to $f_{\delta }\in {\mathbb{L}}^2\left({\mathbb{R}}^{+}\right)$. Furthermore, according to Equations (12) and (14), we can obtain $m\in {\mathbb{L}}^2\left({\mathbb{R}}^{+}\right)$. □

In the remainder of this paper, suppose that $m,f_{\delta },H_{\delta ,w}\in {\mathbb{L}}^2\left({\mathbb{R}}^{+}\right)$. Then we can develop them on the Laguerre basis, i.e.,

$$\begin{array}{c}\hfill m\left(u\right)=\sum _{k=0}^{\infty }{P}_k{\psi }_k\left(u\right),u\ge 0,\end{array}$$

(15)

$$\begin{array}{c}\hfill f_{\delta }\left(x\right)=\sum _{k=0}^{\infty }{Q}_k{\psi }_k\left(x\right),x\ge 0,\end{array}$$

(16)

$$\begin{array}{c}\hfill H_{\delta ,w}\left(x\right)=\sum _{k=0}^{\infty }{R}_k{\psi }_k\left(x\right),x\ge 0,\end{array}$$

(17)

where for $k=0,1,2,\dots$

$$P_k=⟨m,{\psi }_k⟩,Q_k=⟨f_{\delta },{\psi }_k⟩,R_k=⟨H_{\delta ,w},{\psi }_k⟩.$$

Plugging the Laguerre series expansion Equations (15)–(17) into the defective renewal Equation (9) and using the convolution Formula (7), we obtain

$$\begin{array}{cc}\hfill \sum _{k=0}^{\infty }{P}_k{\psi }_k\left(u\right)& ={\int }_0^u\sum _{k=0}^{\infty }{P}_k{\psi }_k(u-x)·\sum _{j=0}^{\infty }{Q}_j{\psi }_j\left(x\right)+\sum _{k=0}^{\infty }{R}_k{\psi }_k\left(u\right)\hfill \\ \hfill & =\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }{P}_k{Q}_j{\int }_0^u{\psi }_k(u-x){\psi }_j\left(x\right)+\sum _{k=0}^{\infty }{R}_k{\psi }_k\left(u\right)\hfill \\ \hfill & =\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\frac{1}{\sqrt{2}}{P}_k{Q}_j[{\psi }_{k+j}\left(u\right)-{\psi }_{k+j+1}\left(u\right)]+\sum _{k=0}^{\infty }{R}_k{\psi }_k\left(u\right).\hfill \end{array}$$

(18)

Furthermore, by changing the order of summation we obtain

$$\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\frac{1}{\sqrt{2}}{P}_k{Q}_j{\psi }_{k+j}\left(u\right)=\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\frac{1}{\sqrt{2}}{P}_j{Q}_{k-j}{\psi }_k\left(u\right)$$

and

$$\begin{array}{c}\hfill \sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\frac{1}{\sqrt{2}}{P}_k{Q}_j{\psi }_{k+j+1}\left(u\right)=\sum _{k=0}^{\infty }\sum _{j=0}^{\infty }\frac{1}{\sqrt{2}}{P}_j{Q}_{k-j-1}{\psi }_k\left(u\right).\end{array}$$

As a result, Equation (18) gives

$$\begin{array}{cc}\hfill \sum _{k=0}^{\infty }{P}_k{\psi }_k\left(u\right)=& \left[\frac{1}{\sqrt{2}}{P}_0{Q}_0+R_0\right]{\psi }_0\left(u\right)\hfill \\ \hfill & +\sum _{k=1}^{\infty }\left(\sum _{j=0}^{k-1}\frac{1}{\sqrt{2}}{P}_j(Q_{k-1}-Q_{k-j-1})+\frac{1}{\sqrt{2}}{P}_k{Q}_0+R_k\right){\psi }_k\left(u\right).\hfill \end{array}$$

(19)

After comparing the coefficients for each basis function ${\psi }_k\left(u\right)$ on both sides of Equation (19), we obtain an infinite triangular system of linear equations,

$$\left\{\begin{array}{c}{P}_0=\frac{1}{\sqrt{2}}{P}_0{Q}_0+R_0,\hfill \\ P_k=\sum _{j=0}^{k-1}\frac{1}{\sqrt{2}}{P}_j(Q_{k-1}-Q_{k-j-1})+\frac{1}{\sqrt{2}}{P}_k{Q}_0+R_k,k\ge 1.\hfill \end{array}\right.$$

(20)

Furthermore, let $\overrightarrow{\mathbf{p}}={(P_0,P_1,P_2,\dots )}^{\mathrm{T}}$, $\overrightarrow{\mathbf{r}}={(R_0,R_1,R_2,\dots )}^{\mathrm{T}}$ and

$$\mathbf{A}=\left(\begin{array}{cccc}1-\frac{1}{\sqrt{2}}{Q}_0& 0& 0& \dots \\ \frac{1}{\sqrt{2}}(Q_0-Q_1)& 1-\frac{1}{\sqrt{2}}{Q}_0& 0& \dots \\ \frac{1}{\sqrt{2}}(Q_1-Q_2)& \frac{1}{\sqrt{2}}(Q_0-Q_1)& 1-\frac{1}{\sqrt{2}}{Q}_0& \dots \\ ⋮& ⋮& ⋮& \ddots \end{array}\right):={\left(a_{ij}\right)}_{i,j\ge 1}.$$

Then we can write Equation (20) in the following matrix form

$$\begin{array}{c}\hfill \mathbf{A}\overrightarrow{\mathbf{p}}=\overrightarrow{\mathbf{r}}.\end{array}$$

(21)

Note that $\mathbf{A}$ is a lower triangular Toeplitz matrix, and for the non-zero elements in $\mathbf{A}$, we have

$$\begin{array}{cc}\hfill \left|\frac{1}{\sqrt{2}}(Q_k-Q_{k-1})\right|& \le \frac{1}{\sqrt{2}}{\int }_0^{\infty }{f}_{\delta }\left(x\right)|{\psi }_k\left(x\right)|dx+\frac{1}{\sqrt{2}}{\int }_0^{\infty }{f}_{\delta }\left(x\right)\left|{\psi }_{k-1}\left(x\right)\right|dx\hfill \\ \hfill & \le 2{\int }_0^{\infty }{f}_{\delta }\left(x\right)dx\le 2\left(1+\frac{q\lambda }{c\beta }\right),k\ge 1.\hfill \end{array}$$

Furthermore, we have

$$\begin{array}{cc}\hfill 1-\frac{1}{\sqrt{2}}{Q}_0& =1-\frac{1}{\sqrt{2}}⟨f_{\delta },{\psi }_0⟩=1-\frac{1}{\sqrt{2}}{\int }_0^{\infty }{f}_{\delta }\left(x\right){\psi }_0\left(x\right)dx\hfill \\ & =1-{\int }_0^{\infty }{f}_{\delta }\left(x\right)e^{-x}dx>1-\frac{p\lambda }{c}>0,\hfill \end{array}$$

by Condition 1, then $\mathbf{A}$ is nonsingular and explicitly invertible.

Hence, for all $K\ge 0$, truncating the infinite dimension vectors and matrix in Equation (21) leads to

$$\begin{array}{c}\hfill {\mathbf{A}}_K{\overrightarrow{\mathbf{p}}}_K={\overrightarrow{\mathbf{r}}}_K,\end{array}$$

(22)

where ${\overrightarrow{\mathbf{p}}}_K={(P_0,P_1,P_2,\dots ,P_K)}^{\mathrm{T}}$, ${\overrightarrow{\mathbf{r}}}_K={(R_0,R_1,R_2,\dots ,R_K)}^{\mathrm{T}}$, and ${\mathbf{A}}_K={\left(a_{ij}\right)}_{i,j=1}^{K+1}$. As a result, the matrix ${\mathbf{A}}_K$ is nonsingular and explicitly invertible. Then we have

$$\begin{array}{c}\hfill {\overrightarrow{\mathbf{p}}}_K={\mathbf{A}}_K^{-1}{\overrightarrow{\mathbf{r}}}_K.\end{array}$$

(23)

After solving Equation (23), we can obtain ${\overrightarrow{\mathbf{p}}}_K$, and for a larger K we can approximate the Gerber–Shiu function as follows:

$$\begin{array}{c}\hfill m\left(u\right)\approx m_K\left(u\right):=\sum _{k=0}^K{P}_k{\psi }_k\left(u\right),u\ge 0.\end{array}$$

(24)

3. Estimation Procedure

In this section, we assume that both Poisson intensity and claim size density are unknown, but we can obtain discrete information about the surplus process and the aggregate claims. Assume that we can observe the surplus process over a long time interval $[0,T]$. Let $△>0$ be a fixed inter-observation interval (or sampling interval). Without loss of generality, assume that $T/△$ is an integer, and let $n=T/△$.

(1)

Data-set of surplus levels:

$$\{U_{j△}:j=0,1,2,\dots ,n\},$$

where $U_{j△}$ is the observed surplus level at time $t=j△$.

(2)

Data-set of total claim numbers and claim sizes:

$$\{N_{j△},Z_1,Z_2,\dots ,Z_{N_{j△}}\},j=1,\dots ,n.$$

(3)

Data-set of downward jump numbers and random loss sizes:

$$\{N_{j△}^{+},X_1,X_2,\dots ,X_{N_{j△}^{+}}\},j=1,\dots ,n.$$

(4)

Data-set of upward jump numbers and random income sizes:

$$\{N_{j△}^{-},Y_1,Y_2,\dots ,Y_{N_{j△}^{-}}\},j=1,\dots ,n.$$

where $N_{j△}$ is the total claim number up to time $t=j△$ and $N_{j△}=N_{j△}^{+}+N_{j△}^{-}$.

Next, we shall propose our estimator of the Gerber–Shiu function by Laguerre expansion based on Equation (24). To this end, we need to estimate the vector ${\overrightarrow{\mathbf{p}}}_K$, or equivalently, ${\mathbf{A}}_K$ and ${\overrightarrow{\mathbf{r}}}_K$. By the definitions of ${\mathbf{A}}_K$ and ${\overrightarrow{\mathbf{r}}}_K$, we only need to estimate the following quantities:

$$Q_k,R_k,k=0,1,2,\dots ,K.$$

By the definitions of $Q_k$ and $R_k$ and changing the order of integrals, we can write $Q_k$ and $R_k$ as follows:

$$\begin{array}{cc}\hfill Q_k& =⟨f_{\delta },{\psi }_k⟩={\int }_0^{\infty }{f}_{\delta }\left(x\right){\psi }_k\left(x\right)dx=\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_0^{\infty }{\int }_x^{\infty }{e}^{-{\rho }_i(y-x)}{f}_{+}\left(y\right)dy{\psi }_k\left(x\right)dx\hfill \\ \hfill & =\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_0^{\infty }{\int }_0^y{e}^{-{\rho }_i(y-x)}{\psi }_k\left(x\right)dx{f}_{+}\left(y\right)dy\hfill \\ \hfill & =\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}E\left[{\int }_0^X{e}^{-{\rho }_i(X-x)}{\psi }_k\left(x\right)dx\right]\hfill \end{array}$$

(25)

and

$$\begin{array}{cc}\hfill R_k& =⟨H_{\delta ,w},{\psi }_k⟩={\int }_0^{\infty }{H}_{\delta ,w}\left(u\right){\psi }_k\left(x\right)dx=\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_0^{\infty }{\int }_u^{\infty }{e}^{-{\rho }_i(y-u)}\eta \left(y\right)dy{\psi }_k\left(u\right)du\hfill \\ \hfill & =\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_0^{\infty }{\int }_u^{\infty }{\int }_y^{\infty }{e}^{-{\rho }_i(y-u)}\omega (y,x-y)f_{+}\left(x\right)dxdy{\psi }_k\left(u\right)du\hfill \\ \hfill & =\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_0^{\infty }{\int }_0^x{\int }_u^x{e}^{-{\rho }_i(y-u)}\omega (y,x-y)f_{+}\left(x\right)dy{\psi }_k\left(u\right)dudx\hfill \\ \hfill & =\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}E\left[{\int }_0^X{\int }_u^X{e}^{-{\rho }_i(y-u)}\omega (y,X-y)dy{\psi }_k\left(u\right)du\right].\hfill \end{array}$$

(26)

The above two formulae imply that we have to estimate the Poisson intensity $\lambda ,p,q,\beta$, the root ${\rho }_1,{\rho }_2$, and the expectations appearing in Equations (25) and (26).

According to the property of Poisson distribution, we can estimate p and $\lambda$ by

$$\begin{array}{c}\hfill \widehat{p}=\frac{N_T^{+}}{N_T},\widehat{q}=1-\widehat{p},\widehat{\lambda }=\frac{N_T}{T}.\end{array}$$

Since the premium size Y follows the $Erlang(1,\beta )$ distribution, we have $E\left[Y\right]=1/\beta$, then we can estimate $\beta$ by

$$\begin{array}{c}\hfill \widehat{\beta }=\frac{1}{\frac{1}{N_T^{-}}{\displaystyle \sum _{j=1}^{N_T^{-}}}{Y}_i},\end{array}$$

which are all unbiased estimates. We estimate the root ${\rho }_1,{\rho }_2$ by ${\widehat{\rho }}_1,{\widehat{\rho }}_2$, which is a positive root of the following estimating equation:

$$\begin{array}{c}\hfill \left[\widehat{\lambda }+\delta -cs-\widehat{p}\widehat{\lambda }{\widehat{\mathcal{L}f}}_{+}\left(s\right)\right](\widehat{\beta }-s)-\widehat{q}\widehat{\lambda }\widehat{\beta }=0,s\in {\mathbb{C}}_{+}\end{array}$$

(27)

where ${\widehat{\mathcal{L}f}}_{+}\left(s\right)=\frac{1}{N_T^{+}}{\displaystyle \sum _{j=1}^{N_T^{+}}}{e}^{-s{X}_j}$ is an estimate of the Laplace transform $\mathcal{L}{f}_{+}\left(s\right)$. It follows from Equation (25) that we have

$$\begin{array}{cc}\hfill {\widehat{Q}}_k& =\frac{1}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\widehat{\rho }}_i(X_j-x)}{\psi }_k\left(x\right)dx\hfill \\ \hfill & =\frac{\sqrt{2}}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\widehat{\rho }}_i(X_j-x)-x}{L}_k\left(2x\right)dx\hfill \\ \hfill & =\frac{\sqrt{2}}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)e^{-{\widehat{\rho }}_i{X}_j}{\int }_0^{X_j}{e}^{-(1-{\widehat{\rho }}_i)x}·\frac{x^m}{m!}dx\hfill \\ \hfill & =\frac{\sqrt{2}}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k\frac{{(-2)}^m}{{(1-{\widehat{\rho }}_i)}^{m+1}}\left(\genfrac{}{}{0pt}{}{k}{m}\right)e^{-{\widehat{\rho }}_i{X}_j}\left(1-\sum _{l=0}^m{e}^{-(1-\widehat{{\rho }_i})X_j}\frac{{\left[(1-{\rho }_i)X_j\right]}^l}{l!}\right).\hfill \end{array}$$

(28)

Similarly, we can estimate $R_k$ by

$$\begin{array}{c}\hfill {\widehat{R}}_k=\frac{1}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\widehat{\rho }}_i(x-u)}\omega (x,X_j-x)dx{\psi }_k\left(u\right)du.\end{array}$$

(29)

Now, we define the estimates of ${\mathbf{A}}_K$ and ${\overrightarrow{\mathbf{r}}}_K$ by replacing $Q_k$ and $R_k$ with ${\widehat{Q}}_k$ and ${\widehat{R}}_k$ in their definitions, and denote them by ${\widehat{\mathbf{A}}}_K$ and ${\overrightarrow{\widehat{\mathbf{r}}}}_K$, respectively. Accordingly, the estimate of ${\overrightarrow{\mathbf{p}}}_K$, denoted by ${\overrightarrow{\widehat{\mathbf{p}}}}_K:={({\widehat{P}}_0,{\widehat{P}}_1,\dots ,{\widehat{P}}_K)}^{\mathrm{T}}$, is defined to be the solution of the following linear system:

$$\begin{array}{c}\hfill {\widehat{\mathbf{A}}}_K{\overrightarrow{\widehat{\mathbf{p}}}}_K={\overrightarrow{\widehat{\mathbf{r}}}}_K.\end{array}$$

(30)

Finally, replacing $P_K$ by ${\widehat{P}}_K$ in Equation (23), we obtain the following estimate of the Gerber–Shiu function:

$$\begin{array}{c}\hfill {\widehat{m}}_K\left(u\right)=\sum _{k=0}^K{\widehat{P}}_k{\psi }_k\left(u\right),u\ge 0.\end{array}$$

(31)

Remark 3.

The estimator ${\widehat{R}}_k$ given in Equation (29) is expressed in a two-fold integral, which can be explicitly computed for most of the widely used penalty functions. Here are some examples.

(1)

$\delta =0$ and $\omega =1$. In this case, the Gerber–Shiu function becomes the ruin probability and we have ${\widehat{\rho }}_1=0$ and ${\widehat{\rho }}_2\in (\widehat{\beta },\infty )$. Then

$$\begin{array}{cc}\hfill {\widehat{R}}_k& =\frac{\sqrt{2}}{cT}\frac{\widehat{\beta }}{{\widehat{\rho }}_2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)\left[X_j\left(1-\sum _{l=0}^m{e}^{-X_j}\frac{X_j^l}{l!}\right)-(m+1)\left(1-\sum _{l=0}^{m+1}{e}^{-X_j}\frac{X_j^l}{l!}\right)\right]\hfill \\ \hfill & +\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_2-\widehat{\beta }}{{\widehat{\rho }}_2^2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)\left(1-\sum _{l=0}^m{e}^{-X_j}\frac{X_j^l}{l!}\right)\hfill \end{array}$$

$$\begin{array}{cc}\hfill & -\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_2-\widehat{\beta }}{{\widehat{\rho }}_2^2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k\frac{{(-2)}^m}{{(1-{\widehat{\rho }}_2)}^{m+1}}\left(\genfrac{}{}{0pt}{}{k}{m}\right)e^{-{\widehat{\rho }}_2{X}_j}\left(1-\sum _{l=0}^m{e}^{-(1-{\widehat{\rho }}_2)X_j}\frac{{\left((1-{\widehat{\rho }}_2)X_j\right)}^l}{l!}\right).\hfill \end{array}$$

(2)

$\delta >0$ and $\omega =1$. In this case, the Gerber–Shiu function becomes the Laplace transform of ruin time and we have ${\widehat{\rho }}_1\in (0,\widehat{\beta })$ and ${\widehat{\rho }}_2\in (\widehat{\beta },\infty )$. Then

$$\begin{array}{cc}\hfill {\widehat{R}}_k& =\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_1-\widehat{\beta }}{({\widehat{\rho }}_1-{\widehat{\rho }}_2){\widehat{\rho }}_1}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)\left(1-\sum _{l=0}^m{e}^{-X_j}\frac{X_j^l}{l!}\right)\hfill \\ \hfill & -\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_1-\widehat{\beta }}{({\widehat{\rho }}_1-{\widehat{\rho }}_2){\widehat{\rho }}_1}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k\frac{{(-2)}^m}{{(1-{\widehat{\rho }}_1)}^{m+1}}\left(\genfrac{}{}{0pt}{}{k}{m}\right)e^{-{\widehat{\rho }}_1{X}_j}\left(1-\sum _{l=0}^m{e}^{-(1-{\widehat{\rho }}_1)X_j}\frac{{\left((1-{\widehat{\rho }}_1)X_j\right)}^l}{l!}\right)\hfill \\ \hfill & +\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_2-\widehat{\beta }}{({\widehat{\rho }}_2-{\widehat{\rho }}_1){\widehat{\rho }}_2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)\left(1-\sum _{l=0}^m{e}^{-X_j}\frac{X_j^l}{l!}\right)\hfill \\ \hfill & -\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_2-\widehat{\beta }}{({\widehat{\rho }}_2-{\widehat{\rho }}_1){\widehat{\rho }}_2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k\frac{{(-2)}^m}{{(1-{\widehat{\rho }}_2)}^{m+1}}\left(\genfrac{}{}{0pt}{}{k}{m}\right)e^{-{\widehat{\rho }}_2{X}_j}\left(1-\sum _{l=0}^m{e}^{-(1-{\widehat{\rho }}_2)X_j}\frac{{\left((1-{\widehat{\rho }}_2)X_j\right)}^l}{l!}\right).\hfill \end{array}$$

(3)

$\delta =0$ and $\omega (x,y)=x+y$. In this case, the Gerber–Shiu function becomes the expected claim size causing ruin. Then

$$\begin{array}{cc}\hfill {\widehat{R}}_k& =\frac{\sqrt{2}}{cT}\frac{\widehat{\beta }}{{\widehat{\rho }}_2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)\left[X_j^2\left(1-\sum _{l=0}^m{e}^{-X_j}\frac{X_j^l}{l!}\right)-X_j(m+1)\left(1-\sum _{l=0}^{m+1}{e}^{-X_j}\frac{X_j^l}{l!}\right)\right]\hfill \\ \hfill & +\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_2-\widehat{\beta }}{{\widehat{\rho }}_2^2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{X}_j{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)\left(1-\sum _{l=0}^m{e}^{-X_j}\frac{X_j^l}{l!}\right)\hfill \\ \hfill & -\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_2-\widehat{\beta }}{{\widehat{\rho }}_2^2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k\frac{X_j{(-2)}^m}{{(1-{\widehat{\rho }}_2)}^{m+1}}\left(\genfrac{}{}{0pt}{}{k}{m}\right)e^{-{\widehat{\rho }}_2{X}_j}\left(1-\sum _{l=0}^m{e}^{-(1-{\widehat{\rho }}_2)X_j}\frac{{\left((1-{\widehat{\rho }}_2)X_j\right)}^l}{l!}\right).\hfill \end{array}$$

(4)

$\delta =0$ and $\omega (x,y)=y$. In this case, the Gerber–Shiu function reduces to the expected deficit at ruin. Then

$$\begin{array}{cc}\hfill {\widehat{R}}_k& =\frac{\sqrt{2}}{2cT}\frac{\widehat{\beta }}{{\widehat{\rho }}_2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)\left[X_j^2\left(1-\sum _{l=0}^m{e}^{-X_j}\frac{X_j^l}{l!}\right)-2X_j(m+1)\left(1-\sum _{l=0}^{m+1}{e}^{-X_j}\frac{X_j^l}{l!}\right)\right]\hfill \\ \hfill & +\frac{\sqrt{2}}{2cT}\frac{\widehat{\beta }}{{\widehat{\rho }}_2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)(m+1)(m+2)\left(1-\sum _{l=0}^{m+2}{e}^{-X_j}\frac{X_j^l}{l!}\right)\hfill \\ \hfill & +\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_2-\widehat{\beta }}{{\widehat{\rho }}_2^2}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)\left[X_j\left(1-\sum _{l=0}^m{e}^{-X_j}\frac{X_j^l}{l!}\right)-(m+1)\left(1-\sum _{l=0}^{m+1}{e}^{-X_j}\frac{X_j^l}{l!}\right)\right]\hfill \\ \hfill & -\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_2-\widehat{\beta }}{{\widehat{\rho }}_2^3}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k{(-2)}^m\left(\genfrac{}{}{0pt}{}{k}{m}\right)\left(1-\sum _{l=0}^m{e}^{-X_j}\frac{X_j^l}{l!}\right)\hfill \\ \hfill & +\frac{\sqrt{2}}{cT}\frac{{\widehat{\rho }}_2-\widehat{\beta }}{{\widehat{\rho }}_2^3}\sum _{j=1}^{N_T^{+}}\sum _{m=0}^k\frac{{(-2)}^m}{{(1-{\widehat{\rho }}_2)}^{m+1}}\left(\genfrac{}{}{0pt}{}{k}{m}\right)e^{-{\widehat{\rho }}_2{X}_j}\left(1-\sum _{l=0}^m{e}^{-(1-{\widehat{\rho }}_2)X_j}\frac{{\left((1-{\widehat{\rho }}_2)X_j\right)}^l}{l!}\right).\hfill \end{array}$$

4. Consistency Properties

In this section, we study the asymptotic properties of our estimator. We measure the performance of the estimator ${\widehat{m}}_K$ by the ${\mathbb{L}}^2$-norm distance $\parallel {\widehat{m}}_K-m\parallel$. By ${\mathbb{L}}^2$-norm inequality, we have

$$\begin{array}{c}\hfill \parallel {\widehat{m}}_K{-m\parallel }^2=\parallel {\widehat{m}}_K-m_K+m_K{-m\parallel }^2\le 2\parallel {\widehat{m}}_K-m_K{\parallel }^2+2{\parallel m_K-m\parallel }^2,\end{array}$$

(32)

where $\parallel m_K-m\parallel$ is the series truncation error and $\parallel {\widehat{m}}_K-m_K\parallel$ is the error due to statistical estimation. Now, if $m\in W({\mathbb{R}}_{+},r,B)$, we have

$$\begin{array}{cc}\hfill \parallel m_K{-m\parallel }^2& ={∥\sum _{k=K+1}^{\infty }{P}_k·{\psi }_k∥}^2=\sum _{k=K+1}^{\infty }{P}_k^2=\sum _{k=K+1}^{\infty }{⟨m,{\psi }_k⟩}^2\le \frac{B}{{(K+1)}^r}=O\left(K^{-r}\right)\hfill \end{array}$$

(33)

due to Remark 1. The polynomial convergence rate in Equation (33) can be improved when m has an exponential decay rate.

Next, it remains to study the convergence rate for $\parallel {\widehat{m}}_K-m_K\parallel$, and we obtain the result as follows:

Theorem 1.

Suppose $E{X}^2<\infty$ and Conditions 1–3 hold. If $K=o\left(T^{\frac{1}{2}}\right)$, then

$$\begin{array}{c}\hfill \parallel {\widehat{m}}_K{-m\parallel }^2\le 2{\parallel m_K-m\parallel }^2+O_p\left(K^2{T}^{-1}\right).\end{array}$$

(34)

Further, if $m\in W({\mathbb{R}}_{+},r,B)$, then

$$\begin{array}{c}\hfill \parallel {\widehat{m}}_K{-m\parallel }^2=O\left(K^{-r}\right)+O_p\left(K^2{T}^{-1}\right).\end{array}$$

(35)

In the following, we present some notations on matrix (and vector) norms. For a vector $\overrightarrow{\mathbf{b}}={(b_1,b_2,\dots ,b_n)}^{\mathrm{T}}$, its 2-norm is defined by $\parallel \overrightarrow{\mathbf{b}}{\parallel }_2=\sqrt{{\sum }_{i=1}^n{\left|b_i\right|}^2}$. For a matrix $\mathbf{B}={\left(b_{ij}\right)}_{i,j=1}^n$, its spectral norm is defined by ${\parallel \mathbf{B}\parallel }_2=\sqrt{{\lambda }_{max}\left({\mathbf{B}}^{\mathrm{T}}\mathbf{B}\right)}$, where ${\lambda }_{max}\left({\mathbf{B}}^{\mathrm{T}}\mathbf{B}\right)$ is the largest eigenvalue of ${\mathbf{B}}^{\mathrm{T}}\mathbf{B}$. The Frobenius norm of $\mathbf{B}$ is defined by

$$\begin{array}{c}\hfill {\parallel \mathbf{B}\parallel }_F=\sqrt{\mathrm{tr}\left({\mathbf{B}}^{\mathrm{T}}\mathbf{B}\right)}=\sqrt{\sum _{i=1}^n\sum _{j=1}^n{\left|b_{i,j}\right|}^2}.\end{array}$$

It is known that

$$\begin{array}{c}\hfill \parallel \mathbf{B}\overrightarrow{\mathbf{b}}{\parallel }_2\le {\parallel \mathbf{B}\parallel }_2·\parallel \overrightarrow{\mathbf{b}}{\parallel }_2{,\parallel \mathbf{B}\parallel }_2\le {\parallel \mathbf{B}\parallel }_F.\end{array}$$

(36)

For two square matrices ${\mathbf{B}}_1$ and ${\mathbf{B}}_2$ with the same dimension, we have $\parallel {\mathbf{B}}_1{\mathbf{B}}_2{\parallel }_2\le \parallel {\mathbf{B}}_1{\parallel }_2·{\parallel {\mathbf{B}}_2\parallel }_2$.

By the inequality ${(x+y)}^2\le 2x^2+2y^2$ and the first inequality in Equation (36), we obtain

$$\begin{array}{cc}\hfill & \parallel {\widehat{m}}_K-m_K{\parallel }^2\hfill \\ \hfill & =\parallel \sum _{k=0}^K({\widehat{P}}_k-P_k){\psi }_k{\parallel }^2=\sum _{k=0}^K{({\widehat{P}}_k-P_k)}^2={\parallel {\overrightarrow{\widehat{\mathbf{P}}}}_K-{\overrightarrow{\mathbf{P}}}_K\parallel }_2^2\hfill \\ \hfill & =\parallel {\widehat{\mathbf{A}}}_K^{-1}{\overrightarrow{\widehat{\mathbf{r}}}}_K-{\mathbf{A}}_K^{-1}{\overrightarrow{\mathbf{r}}}_K{\parallel }_2^2={\parallel ({\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1}){\overrightarrow{\widehat{\mathbf{r}}}}_K+{\mathbf{A}}_K^{-1}({\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K)\parallel }_2^2\hfill \\ \hfill & \le 2\parallel ({\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1}){\overrightarrow{\widehat{\mathbf{r}}}}_K{\parallel }_2^2+2\parallel ({\mathbf{A}}_K^{-1}({\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K){\parallel }_2^2\hfill \\ \hfill & \le 4\parallel ({\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1})({\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K){)\parallel }_2^2+4\parallel ({\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1}){\overrightarrow{\widehat{\mathbf{r}}}}_K{\parallel }_2^2+2\parallel ({\mathbf{A}}_K^{-1}({\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K){\parallel }_2^2\hfill \\ \hfill & \le 4\parallel ({\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1}){\parallel }_2^2·\parallel {\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K{)\parallel }_2^2+4\parallel ({\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1}){\parallel }_2^2·\parallel {\overrightarrow{\widehat{\mathbf{r}}}}_K{\parallel }_2^2+2\parallel {\mathbf{A}}_K^{-1}{\parallel }_2^2·{\parallel {\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K\parallel }_2^2.\hfill \end{array}$$

(37)

In order to prove Theorem 1, we can study the convergence rates for the three terms on the right-hand side of Equation (37). To obtain the convergence rates $\parallel {\overrightarrow{\mathbf{r}}}_K{\parallel }_2^2$ and $\parallel {\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K{\parallel }_2^2$, we need the following Lemma:

Lemma 4.

Suppose that Condition 2 holds. Then

$$\begin{array}{c}\hfill \parallel {\overrightarrow{\mathbf{r}}}_K{\parallel }_2^2<{\parallel h\parallel }^2<\infty .\end{array}$$

Moreover, if Conditions 1 and 3 hold and $E{X}^2<\infty$, we have

$$\begin{array}{c}\hfill \parallel {\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K{\parallel }_2^2<{\parallel h\parallel }^2<=O_p\left(K{T}^{-1}\right).\end{array}$$

(38)

Proof. 

First, under Condition 2 we have

$$\begin{array}{c}\hfill \parallel {\overrightarrow{\mathbf{r}}}_K{\parallel }_2^2=\sum _{k=0}^K{R}_k^2<\sum _{k=0}^{\infty }{R}_k^2={\parallel h\parallel }_2^2<\infty .\end{array}$$

Next, we prove Equation (38). We only consider the case $\delta >0$. Under Condition 1 and $E{X}^2<\infty$,

$$\widehat{{\rho }_1}-{\rho }_1=O_p\left(T^{-\frac{1}{2}}\right),\widehat{{\rho }_2}-{\rho }_2=O_p\left(T^{-\frac{1}{2}}\right).$$

Because $N_T$ is Poisson-distributed with intensity $\lambda T$ and is independent from $X_j$, we have

$$\begin{array}{cc}\hfill R_k& =\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}E\left[{\int }_0^X{\int }_u^X{e}^{-{\rho }_i(y-u)}w(y,X-y)dy{\psi }_k\left(u\right)du\right].\hfill \\ \hfill & =\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}E\left[\frac{N_T}{N_T^{+}}·\frac{T}{N_T}·\frac{1}{T}·\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\rho }_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\right]\hfill \\ \hfill & =\frac{1}{cT}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}E\left[\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\rho }_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\right].\hfill \end{array}$$

(39)

Hence,

$$\begin{array}{cc}\hfill {\widehat{R}}_k-R_k=& \frac{1}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\widehat{\rho }}_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\hfill \\ \hfill & -\frac{1}{cT}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}E\left[\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\rho }_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\right]\hfill \\ \hfill =& \frac{1}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}(e^{-{\rho }_i(x-u)}-e^{-{\rho }_i(x-u)})w(x,X_j-x)dx{\psi }_k\left(u\right)du\hfill \\ \hfill & +\left(\frac{1}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{1}{cT}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)\hfill \\ \hfill & \times \sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\rho }_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\hfill \\ \hfill & +\frac{1}{cT}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\{\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\rho }_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\hfill \\ \hfill & -E\left[\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\rho }_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\right]\}\hfill \\ \hfill :=& I_{k,1}+I_{k,2}+I_{k,3}.\hfill \end{array}$$

(40)

Then, using inequality ${(x+y)}^2\le 2x^2+2y^2$, we have

$$\begin{array}{c}\hfill \parallel {\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K{\parallel }_2^2=\sum _{k=0}^K{({\widehat{R}}_K-R_K)}^2\le 2\sum _{k=0}^K{I}_{k,1}^2+4\sum _{k=0}^K{I}_{k,2}^2+4\sum _{k=0}^K{I}_{k,3}^2.\end{array}$$

(41)

By the mean value theorem, it is easy to see that

$$\begin{array}{cc}\hfill \left|e^{-{\widehat{\rho }}_i(x-u)}-e^{-{\rho }_i(x-u)}\right|& =\left|(\widehat{{\rho }_i}-{\rho }_i)(x-u)e^{-{\rho }_i^{*}(x-u)}\right|\hfill \\ & \le |{\widehat{\rho }}_i-{\rho }_i|(x-u),i=1,2,\hfill \end{array}$$

(42)

where ${\rho }_1^{*},{\rho }_2^{*}$ is a random number between $\widehat{{\rho }_i}$ and ${\rho }_i,i=1,2$. First, to estimate ${\displaystyle \sum _{k=0}^K}{I}_{k,1}^2$,

$$\begin{array}{cc}\hfill & \sum _{k=0}^K{I}_{k,1}^2\hfill \\ \hfill =& \frac{2}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\right)}^2\sum _{k=0}^K{\left[\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}(e^{-{\widehat{\rho }}_i(x-u)}-e^{-{\rho }_i(x-u)})w(x,X_j-x)dx{\psi }_k\left(u\right)du\right]}^2\hfill \\ \hfill =& \frac{2}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\right)}^2\sum _{k=0}^K{\left({\int }_0^{\infty }\left[\sum _{j=1}^{N_T^{+}}{\mathbf{I}}_{(u\le X_j)}{\int }_u^{X_j}(e^{-{\widehat{\rho }}_i(x-u)}-e^{-{\rho }_i(x-u)})w(x,X_j-x)dx\right]{\psi }_k\left(u\right)du\right)}^2\hfill \\ \hfill \le & \frac{2K}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\right)}^2{\int }_0^{\infty }{\left[\sum _{j=1}^{N_T^{+}}{\mathbf{I}}_{(u\le X_j)}{\int }_u^{X_j}(e^{-{\widehat{\rho }}_i(x-u)}-e^{-{\rho }_i(x-u)})w(x,X_j-x)dx\right]}^{2}du\hfill \\ \hfill \le & \frac{2K}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\right)}^2{({\widehat{\rho }}_i-{\rho }_i)}^2{N}_T^{+}{\int }_0^{\infty }\sum _{j=1}^{N_T^{+}}{\left[{\mathbf{I}}_{(u\le X_j)}{\int }_u^{X_j}(x-u)w(x,X_j-x)dx\right]}^{2}du\hfill \\ \hfill =& \frac{2K\widehat{\lambda }\widehat{p}}{c^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\right)}^2{({\widehat{\rho }}_i-{\rho }_i)}^2\frac{1}{T}\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\left[{\int }_u^{X_j}(x-u)w(x,X_j-x)dx\right]}^{2}du.\hfill \end{array}$$

(43)

It follows from Condition 3 and Markov’s inequality that

$$\begin{array}{c}\hfill \frac{1}{T}\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\left[{\int }_u^{X_j}(x-u)w(x,X_j-x)dx\right]}^{2}du=O_p\left(1\right),\end{array}$$

hence

$$\begin{array}{c}\hfill \sum _{k=0}^K{I}_{k,1}^2=O_p\left(K{T}^{-1}\right).\end{array}$$

(44)

As for ${\displaystyle \sum _{k=0}^K}{I}_{k,2}^2$, we can obtain

$$\begin{array}{cc}\hfill & \sum _{k=0}^K{I}_{k,2}^2\hfill \\ \hfill & =\sum _{k=0}^K{\left[\left(\frac{1}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{1}{cT}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\rho }_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\right]}^2\hfill \\ \hfill & \le 2\sum _{k=0}^K\sum _{i=1}^2{\left(\frac{1}{cT}\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{1}{cT}\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^2{\left(\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\rho }_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\right)}^2\hfill \\ \hfill & \le \frac{2}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^2\sum _{k=0}^K{\left[{\int }_0^{\infty }\left(\sum _{j=1}^{N_T^{+}}{\mathbf{I}}_{(u\le X_j)}{\int }_u^{X_j}w(x,X-x)dx\right){\psi }_k\left(u\right)du\right]}^2\hfill \\ \hfill & \le \frac{2K}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^2{\int }_0^{\infty }{\left[\sum _{j=1}^{N_T^{+}}{\mathbf{I}}_{(u\le X_j)}{\int }_u^{X_j}w(x,X-x)dx\right]}^{2}du\hfill \\ \hfill & \le \frac{2K\widehat{\lambda }\widehat{p}}{c^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^2\frac{1}{T}\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\left({\int }_u^{X_j}w(x,X-x)dx\right)}^{2}du.\hfill \end{array}$$

(45)

According to $\widehat{\beta }-\beta =O_p\left(T^{-\frac{1}{2}}\right)$, $\widehat{{\rho }_1}-{\rho }_1=O_p\left(T^{-\frac{1}{2}}\right)$ and $\widehat{{\rho }_2}-{\rho }_2=O_p\left(T^{-\frac{1}{2}}\right)$. Then

$$\begin{array}{c}\hfill {\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^2=O_p\left(T^{-1}\right).\end{array}$$

(46)

Hence,

$$\begin{array}{c}\hfill \sum _{k=0}^K{I}_{k,2}^2=O_p\left(K{T}^{-1}\right).\end{array}$$

(47)

For the summation ${\displaystyle \sum _{k=0}^K}{I}_{k,3}^2$, we have

$$\begin{array}{cc}\hfill & E\left[\sum _{k=0}^K{I}_{k,3}^2\right]=\sum _{k=0}^{K}E\left[I_{k,3}^2\right]\hfill \\ \hfill & =\sum _{k=0}^K\frac{2}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^{2}Var\left\{\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{\int }_u^{X_j}{e}^{-{\rho }_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\right\}\hfill \\ \hfill & \le \frac{2p\lambda }{c^{2}T}\sum _{i=1}^2{\left(\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^2\sum _{k=0}^{K}E{\left[{\int }_0^X{\int }_u^X{e}^{-{\rho }_i(x-u)}w(x,X_j-x)dx{\psi }_k\left(u\right)du\right]}^2\hfill \\ \hfill & =\frac{2p\lambda }{c^{2}T}\sum _{i=1}^2{\left(\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^{2}E\left\{\sum _{k=0}^K{\left[{\int }_0^{\infty }\left({\mathbf{I}}_{(u\le X)}{\int }_u^X{e}^{-{\rho }_i(x-u)}w(x,X-x)dx\right){\psi }_k\left(u\right)du\right]}^2\right\}\hfill \\ \hfill & \le \frac{2Kp\lambda }{c^{2}T}\sum _{i=1}^2{\left(\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^{2}E\left[{\int }_0^{\infty }{\left({\mathbf{I}}_{(u\le X)}{\int }_u^X{e}^{-{\rho }_i(x-u)}w(x,X-x)dx\right)}^{2}du\right]\hfill \\ \hfill & =\frac{2Kp\lambda }{c^{2}T}\sum _{i=1}^2{\left(\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^{2}E\left[{\int }_0^X{\left({\int }_u^X{e}^{-{\rho }_i(x-u)}w(x,X-x)dx\right)}^{2}du\right]\hfill \\ \hfill & \le \frac{2Kp\lambda }{c^{2}T}\sum _{i=1}^2{\left(\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^{2}E\left[{\int }_0^X{\left({\int }_u^{X}w(x,X-x)dx\right)}^{2}du\right],\hfill \end{array}$$

(48)

which, together with Condition 3 and Markov’s inequality, yields

$$\begin{array}{c}\hfill \sum _{k=0}^K{I}_{k,3}^2=O_p\left(K{T}^{-1}\right).\end{array}$$

(49)

Finally, we complete the proof. □

In order to obtain the convergence rates of $\parallel {\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K{\parallel }_F^2$, $\parallel {\mathbf{A}}_K^{-1}{\parallel }_2$ and $\parallel {\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1}{\parallel }_2$, we have the following propositions:

Proposition 1.

Let Condition 1 hold and $E{X}^2<\infty$. Then

$$\begin{array}{c}\hfill \parallel {\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K{\parallel }_F^2=O_p\left(K^2{T}^{-1}\right).\end{array}$$

(50)

Proposition 2.

Suppose that Condition 1 holds. Then for all $K\ge 1$,

$$\begin{array}{c}\hfill \parallel {\mathbf{A}}_K^{-1}{\parallel }_2\le \frac{2c}{c-\lambda (p{\mu }_{+}-q{\mu }_{-})}.\end{array}$$

(51)

Proposition 3.

Let Condition 1 hold and $E{X}^2<\infty$. If $K=o\left(T^{\frac{1}{2}}\right)$, then

$$\begin{array}{c}\hfill \parallel {\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1}{\parallel }_2=O_p\left(K{T}^{-\frac{1}{2}}\right).\end{array}$$

(52)

In the rest of the section, we give the proof of Propositions 1, 2 and 3 and Theorem 1.

Proof of Proposition 1.

Using the definitions of ${\widehat{\mathbf{A}}}_K$ and ${\mathbf{A}}_K$, then

$$\begin{array}{cc}\hfill \parallel {\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K{\parallel }_F^2& =\sum _{k=0}^K\sum _{j=0}^k{\left\{\frac{1}{\sqrt{2}}(Q_{k-j}-{\widehat{Q}}_{k-j})-\frac{1}{\sqrt{2}}(Q_{k-j-1}-{\widehat{Q}}_{k-j-1})\right\}}^2\hfill \\ \hfill & =\frac{1}{2}\sum _{k=0}^K\sum _{j=0}^k{\left\{(Q_{k-j}-{\widehat{Q}}_{k-j})-(Q_{k-j-1}-{\widehat{Q}}_{k-j-1})\right\}}^2\hfill \\ \hfill & \le \sum _{k=0}^K\sum _{j=0}^k\left\{{(Q_{k-j}-{\widehat{Q}}_{k-j})}^2-{(Q_{k-j-1}-{\widehat{Q}}_{k-j-1})}^2\right\},\hfill \end{array}$$

(53)

where we have put $Q_{-1}={\widehat{Q}}_{-1}=0$ for convenience.

Because $N_T$ is Poisson-distributed with intensity $\lambda T$ and is independent from $X_j$, we have

$$\begin{array}{cc}\hfill Q_k& =\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}E\left[{\int }_0^X{e}^{-{\rho }_i(X-x)}{\psi }_k\left(x\right)dx\right]\hfill \\ \hfill & =\frac{p\lambda }{c}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}E\left\{\frac{N_T}{N_T^{+}}·\frac{T}{N_T}·\frac{1}{T}·\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\rho }_i(X_j-x)}{\psi }_k\left(x\right)dx\right\}\hfill \\ \hfill & =\frac{1}{cT}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}E\left\{\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\rho }_i(X_j-x)}{\psi }_k\left(x\right)dx\right\}.\hfill \end{array}$$

Then

$$\begin{array}{cc}\hfill {\widehat{Q}}_k-Q_k=& \frac{1}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\left(\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\widehat{\rho }}_i(X_j-x)}{\psi }_k\left(x\right)dx\right)\hfill \\ \hfill & -\frac{1}{cT}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}E\left\{\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\rho }_i(X_j-x)}{\psi }_k\left(x\right)dx\right\}\hfill \\ \hfill =& \frac{1}{cT}\sum _{i=1}^2\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\left[\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}\left(e^{-{\widehat{\rho }}_i(X_j-x)}-e^{-{\rho }_i(X_j-x)}{\psi }_k\left(x\right)dx\right)\right]\hfill \\ \hfill & +\frac{1}{cT}\sum _{i=1}^2\left[\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right]\left(\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\widehat{\rho }}_i(X_j-x)}{\psi }_k\left(x\right)dx\right)\hfill \\ \hfill & +\frac{1}{cT}\sum _{i=1}^2\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\left\{\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\widehat{\rho }}_i(X_j-x)}{\psi }_k\left(x\right)dx-E\left[\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\rho }_i(X_j-x)}{\psi }_k\left(x\right)dx\right]\right\}\hfill \\ \hfill :=& I{I}_{k,1}+I{I}_{k,2}+I{I}_{k,3}.\hfill \end{array}$$

(54)

Plugging the above result into Equation (48), we obtain

$$\begin{array}{cc}\hfill \parallel {\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K{\parallel }_F^2& \le \sum _{k=0}^K\sum _{j=0}^k\left\{{(I{I}_{k-j,1}+I{I}_{k-j,2}+I{I}_{k-j,3})}^2+{(I{I}_{k-j-1,1}+I{I}_{k-j-1,2}+I{I}_{k-j-1,3})}^2\right\}\hfill \\ \hfill & \le 4\sum _{k=0}^K\sum _{j=0}^k\left[I{I}_{k-j,1}+I{I}_{k-j,2}+I{I}_{k-j,3}+I{I}_{k-j-1,1}+I{I}_{k-j-1,2}+I{I}_{k-j-1,3}\right]\hfill \\ \hfill & \le 8K\sum _{k=0}^K\left[I{I}_{k,1}^2+I{I}_{k,2}^2+I{I}_{k,3}^2\right].\hfill \end{array}$$

(55)

First, for $K{\displaystyle \sum _{k=0}^K}I{I}_{k,1}^2$, we can obtain

$$\begin{array}{cc}\hfill K\sum _{k=0}^{K}I{I}_{k,1}^2& =\sum _{k=0}^K\frac{2K}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\right)}^2{\left[\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}\left(e^{-{\widehat{\rho }}_i(X_j-x)}-e^{-{\rho }_i(X_j-x)}\right){\psi }_k\left(x\right)dx\right]}^2\hfill \\ \hfill & \le \frac{2K^2}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\right)}^2{\int }_0^{\infty }{\left[\sum _{j=1}^{N_T^{+}}{\mathbf{I}}_{(x\le X_j)}\left(e^{-{\widehat{\rho }}_i(X_j-x)}-e^{-{\rho }_i(X_j-x)}\right)\right]}^2\hfill \\ \hfill & \le \frac{2K^2}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\right)}^2{({\widehat{\rho }}_i-{\rho }_i)}^2{N}_T^{+}{\int }_0^{\infty }\sum _{j=1}^{N_T^{+}}{\mathbf{I}}_{(x\le X_j)}{\left|(X_j-x)e^{-{\rho }_i^{*}(X_j-x)}\right|}^{2}dx\hfill \\ \hfill & \le \frac{2K^2\widehat{\lambda }\widehat{p}}{c^2}\sum _{i=1}^2{\left(\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}\right)}^2\frac{{({\widehat{\rho }}_i-{\rho }_i)}^2}{{[min\{{\rho }_i,{\widehat{\rho }}_i\}]}^2}·\frac{1}{T}\sum _{j=1}^{N_T^{+}}{X}_j.\hfill \end{array}$$

(56)

It follows from $E\left[\frac{1}{T}{\displaystyle \sum _{j=1}^{N_T^{+}}}{X}_j\right]=p\lambda {\mu }_x<\infty$ and Markov’s inequality that $\frac{1}{T}{\displaystyle \sum _{j=1}^{N_T^{+}}}{X}_j=O_p\left(1\right)$. Then

$$\begin{array}{c}\hfill K\sum _{k=0}^{K}I{I}_{k,1}^2=O_p\left(K^2{T}^{-1}\right).\end{array}$$

(57)

Next, to compute $I{I}_{k,2}$, we can obtain

$$\begin{array}{cc}\hfill K\sum _{k=0}^{K}I{I}_{k,2}^2& =2K\sum _{k=0}^K\sum _{i=1}^2{\left[\frac{1}{cT}\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{1}{cT}\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right]}^2{\left(\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\rho }_i(X_j-x)}{\psi }_k\left(x\right)dx\right)}^2\hfill \\ \hfill & =\frac{2K}{c^2{T}^2}\sum _{k=0}^K\sum _{i=1}^2{\left[\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right]}^2{\left[{\int }_0^{\infty }\sum _{j=1}^{N_T^{+}}{\mathbf{I}}_{(x\le X_j)}{e}^{-{\rho }_i(X_j-x)}{\psi }_k\left(x\right)dx\right]}^2\hfill \\ \hfill & \le \frac{2K^2}{c^2{T}^2}\sum _{i=1}^2{\left[\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right]}^2{\int }_0^{\infty }{\left(\sum _{j=1}^{N_T^{+}}{\mathbf{I}}_{(x\le X_j)}\right)}^{2}dx\hfill \\ \hfill & \le \frac{2K^2\widehat{\lambda }\widehat{p}}{c^2}\sum _{i=1}^2{\left[\frac{{\widehat{\rho }}_i-\widehat{\beta }}{{\displaystyle \prod _{j=1,j\ne i}^2}({\widehat{\rho }}_i-{\widehat{\rho }}_j)}-\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right]}^2\frac{1}{T}\sum _{j=1}^{N_T^{+}}{X}_j.\hfill \end{array}$$

(58)

Then,

$$\begin{array}{c}\hfill K\sum _{k=0}^{K}I{I}_{k,2}^2=O_p\left(K^2{T}^{-1}\right),\end{array}$$

(59)

due to $\widehat{\beta }-\beta =O_p\left(T^{-\frac{1}{2}}\right)$, ${\widehat{\rho }}_1-{\rho }_1=O_p\left(T^{-\frac{1}{2}}\right)$ and ${\widehat{\rho }}_2-{\rho }_2=O_p\left(T^{-\frac{1}{2}}\right)$.

As for $I{I}_{k,3}$, taking expectation, we have

$$\begin{array}{cc}\hfill E\left[K\sum _{k=0}^{K}I{I}_{k,3}^2\right]& =K\sum _{k=0}^{K}E\left[I{I}_{k,3}^2\right]=\sum _{k=0}^K\frac{2K}{c^2{T}^2}\sum _{i=1}^2{\left(\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^2\hfill \\ \hfill & \times Var\left\{\sum _{j=1}^{N_T^{+}}{\int }_0^{X_j}{e}^{-{\rho }_i(X_j-x)}{\psi }_k\left(x\right)dx\right\}\hfill \\ \hfill & =\frac{2\lambda pK}{c^{2}T}\sum _{k=0}^K\sum _{i=1}^2{\left(\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^{2}E\left[{\left({\int }_0^X{e}^{-{\rho }_i(X-x)}{\psi }_k\left(x\right)dx\right)}^2\right]\hfill \\ \hfill & \le \frac{2\lambda p{K}^2}{c^{2}T}\sum _{i=1}^2{\left(\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^{2}E\left[{\int }_0^X{e}^{-2{\rho }_i(X-x)}dx\right]\hfill \\ \hfill & \le \frac{2\lambda p{K}^2}{c^{2}T}\sum _{i=1}^2{\left(\frac{{\rho }_i-\beta }{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}\right)}^{2}E\left(X\right).\hfill \end{array}$$

(60)

Due to ${\mu }_X<\infty$ and Markov’s inequality, hence

$$\begin{array}{c}\hfill K\sum _{k=0}^{K}I{I}_{k,3}^2=O_p\left(K^2{T}^{-1}\right).\end{array}$$

(61)

Finally, substituting Equations (57), (59) and (61) into Equation (55) yields the convergence rate. □

Proof of Proposition 2.

First, let $h=\frac{\lambda }{c}{\displaystyle \sum _{i=1}^2}\frac{({\rho }_i-\beta )}{{\displaystyle \prod _{j=1,j\ne i}^2}({\rho }_i-{\rho }_j)}{\int }_x^{\infty }{e}^{-{\rho }_i(y-x)}(p{f}_{+}\left(y\right)-q{f}_{-}\left(y\right))dy$ and define a sequence ${\left\{c_k\right\}}_{k=0}^{\infty }$ by

$$c_0=1-\frac{1}{\sqrt{2}}{C}_0,c_k=\frac{1}{\sqrt{2}}(C_{k-1}-C_k),k=1,2,\cdots$$

where

$$C_k=⟨h,{\psi }_k⟩\mathrm{for}k=0,1,2\cdots$$

such that $\mathbf{C}$ is an infinite lower triangular Toeplitz matrix generated by $\left\{c_k\right\}$ similar to $\mathbf{A}$

$$\mathbf{C}=\left(\begin{array}{cccc}1-\frac{1}{\sqrt{2}}{C}_0& 0& 0& \dots \\ \frac{1}{\sqrt{2}}(C_0-C_1)& 1-\frac{1}{\sqrt{2}}{C}_0& 0& \dots \\ \frac{1}{\sqrt{2}}(C_1-C_2)& \frac{1}{\sqrt{2}}(C_0-C_1)& 1-\frac{1}{\sqrt{2}}{C}_0& \dots \\ ⋮& ⋮& ⋮& \ddots \end{array}\right).$$

It is easy to see that

$$\parallel {\mathbf{A}}_K^{-1}{\parallel }_2\le {\parallel {\mathbf{C}}_K^{-1}\parallel }_2,$$

where ${\mathbf{C}}_K={\left(c_{ij}\right)}_{i,j=1}^{K+1}$.

By Lemma 4.3 in Zhang and Su [42], we know that $c_k,k\ge 0$ are Fourier coefficients of the function

$$c\left(e^{i\theta }\right)=\sum _{k=0}^{\infty }{c}_k{e}^{i\theta k}=1-\mathcal{L}h\left(\frac{1+i\theta }{1-i\theta }\right),\theta \in \mathbb{R}.$$

Let $\zeta =\{z\in \mathbb{C}:|z|=1\}$ denote the complex unite circle. We have

$$\begin{array}{cc}\hfill \underset{z\in \zeta }{inf}\left|c\left(z\right)\right|& =\underset{z\in \zeta }{inf}|1-\mathcal{L}h\left(\frac{1+i\theta }{1-i\theta }\right)|\ge 1-\underset{z\in \zeta }{sup}\left|\mathcal{L}h\left(\frac{1+i\theta }{1-i\theta }\right)\right|\hfill \\ \hfill & \ge 1-{\int }_0^{\infty }h\left(x\right)dx=1-\frac{\lambda }{c}\sum _{i=1}^2\frac{({\rho }_i-\beta )}{{\prod }_{j=1,j\ne i}^2({\rho }_i-{\rho }_j)}{\int }_0^{\infty }{\int }_x^{\infty }{e}^{-{\rho }_i(y-x)}(p{f}_{+}\left(y\right)-q{f}_{-}\left(y\right))dydx\hfill \\ \hfill & \ge 1-\frac{\lambda }{c}{\int }_0^{\infty }{\int }_x^{\infty }p{f}_{+}\left(y\right)-q{f}_{-}\left(y\right)dydx=1-\frac{\lambda p{\mu }_{+}}{c}+\frac{\lambda q{\mu }_{-}}{c}>0,\hfill \end{array}$$

by Condition 1. Then, by Lemma 3.8 in the work of Böttcher and Grudsky [60], we obtain

$$\parallel {\mathbf{A}}_K^{-1}{\parallel }_2\le {\parallel {\mathbf{C}}_K^{-1}\parallel }_2\le \frac{2}{1-\frac{\lambda p{\mu }_{+}}{c}+\frac{\lambda q{\mu }_{-}}{c}}=\frac{2c}{c-\lambda (p{\mu }_{+}-q{\mu }_{-})}.$$

The proof is completed. □

Proof of Proposition 3.

Note that ${\widehat{\mathbf{A}}}_K={\mathbf{A}}_K+{\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K$ and ${\mathbf{A}}_K$ is invertible. By Propositions 1 and 2,

$$\begin{array}{cc}\hfill \parallel {\mathbf{A}}_K^{-1}·({\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K){\parallel }_2& \le \parallel {\mathbf{A}}_K^{-1}{\parallel }_2·\parallel {\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K{\parallel }_2\le \frac{2c}{c-\lambda (p{\mu }_{+}-q{\mu }_{-})}·{\parallel {\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K\parallel }_2\hfill \\ \hfill & \le \frac{2c}{c-\lambda (p{\mu }_{+}-q{\mu }_{-})}·{\parallel {\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K\parallel }_F=O_p\left(K{T}^{-\frac{1}{2}}\right)=o_p\left(1\right).\hfill \end{array}$$

Then, by the result of Theorem 2.5 of Stewart and Sun [61], we have

$$\begin{array}{cc}\hfill \parallel {\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1}{\parallel }_2& \le \frac{\parallel {\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K{\parallel }_2·{\parallel {\mathbf{A}}_K^{-1}\parallel }_2^2}{1-\parallel {\mathbf{A}}_K^{-1}·({\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K){\parallel }_2}\hfill \\ \hfill & \le {\left(\frac{2c}{c-\lambda (p{\mu }_{+}-q{\mu }_{-})}\right)}^2\frac{\parallel {\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K{\parallel }_F}{1-\parallel {\mathbf{A}}_K^{-1}·({\widehat{\mathbf{A}}}_K-{\mathbf{A}}_K){\parallel }_2}\hfill \\ \hfill & =O_p\left(K{T}^{-\frac{1}{2}}\right).\hfill \end{array}$$

(62)

This completes the proof. □

Finally, by the three terms of (37), Lemma 4, and Propositions 1–3, the proof of Theorem 1 is as follows:

Proof of Theorem 1.

By Lemma 4 and Propositions 1–3, we have

$$\begin{array}{c}\hfill \parallel {\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1}{\parallel }_2^2·{\parallel {\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K\parallel }_2^2=O_p\left(K^3{T}^{-2}\right),\end{array}$$

$$\begin{array}{c}\hfill \parallel {\widehat{\mathbf{A}}}_K^{-1}-{\mathbf{A}}_K^{-1}{\parallel }_2^2·{\parallel {\overrightarrow{\mathbf{r}}}_K\parallel }_2^2=O_p\left(K^2{T}^{-1}\right),\end{array}$$

$$\begin{array}{c}\hfill \parallel {\mathbf{A}}_K^{-1}{\parallel }_2^2·{\parallel {\overrightarrow{\widehat{\mathbf{r}}}}_K-{\overrightarrow{\mathbf{r}}}_K\parallel }_2^2=O_p\left(K{T}^{-1}\right).\end{array}$$

Then,

$$\begin{array}{c}\hfill \parallel {\widehat{m}}_K-m_K{\parallel }^2=O_p\left(K^3{T}^{-2}\right)+O_p\left(K^2{T}^{-1}\right)+O_p\left(K{T}^{-1}\right)=O_p\left(K^2{T}^{-1}\right)\end{array}$$

(63)

under condition $K=o\left(T^{\frac{1}{2}}\right)$. Furthermore, if $m\in W({\mathbb{R}}_{+},r,B)$, Equation (35) follows from Equation (34). □

Remark 4.

Suppose the conditions in Theorem 1. Then, by Equations (33) and (63), we have

$$\begin{array}{c}\hfill \parallel {\widehat{m}}_K{-m\parallel }^2=O\left(K^{-r}\right)+O_p\left(K^2{T}^{-1}\right).\end{array}$$

We can minimize the error bound $O\left(K^{-r}\right)+O_p\left(K^2{T}^{-1}\right)$ to find the optimal truncation parameter, say $m_{op}$, has $O_p\left(T^{-\frac{1}{2}}\right)$. (See Zhang and Su [43] and Su et al. [49].)

5. Numerical Illustration

In this section, we provide some numerical examples to show the performance of our estimator when the observed sample size is finite. Throughout this section, we set $c=1.5,\lambda =2,\beta =1,p=0.5$, and $q=0.5$, and we consider the following three claim density functions at the same time:

(1)

Exponential density function: $f_{+}\left(x\right)=e^{-x},x>0$.

(2)

Erlang (2) density function: $f_{+}\left(x\right)=4x{e}^{-2x},x>0$.

(3)

Combination-of-exponentials density function: $f_{+}\left(x\right)=3e^{-1.5x}-3e^{-3x},x>0$.

As in Zhang [24], we estimate the following four classes of Gerber–Shiu functions:

(1)

Ruin probability (RP): $w(x,y)\equiv 1,\delta =0$.

(2)

Laplace transform of ruin time (LT): $w(x,y)\equiv 1,\delta =0.1$.

(3)

Expected claim size causing ruin (ECS): $w(x,y)\equiv x+y,\delta =0$.

(4)

Expected deficit at ruin (ED): $w(x,y)\equiv y,\delta =0$.

Note that the assumptions of the above three claim density functions all satisfy ${\mu }_1=1$, and through Equations (9) and (11), we can easily obtain the explicit formulae for the above Gerber–Shiu functions by Laplace inversion. For exponential claim density function, the explicit formulae for these Gerber–Shiu functions are given by

(1)

$m\left(u\right)=0.46482{\mathrm{e}}^{-0.53518u},u\ge 0$.

(2)

$m\left(u\right)=0.43217{\mathrm{e}}^{-0.56783u},u\ge 0$.

(3)

$m\left(u\right)=1.8593{\mathrm{e}}^{-0.53518u}-{\mathrm{e}}^{-u},u\ge 0$.

(4)

$m\left(u\right)=0.46482{\mathrm{e}}^{-0.53518u},u\ge 0$.

For Erlang (2) claim size, the explicit formulae for these Gerber–Shiu functions are given by

(1)

$m\left(u\right)=0.53387{\mathrm{e}}^{-0.747u}-0.06037{\mathrm{e}}^{-2.819u},u\ge 0$.

(2)

$m\left(u\right)=0.50866{\mathrm{e}}^{-0.764u}-0.06266{\mathrm{e}}^{-2.816u},u\ge 0$.

(3)

$m\left(u\right)=1.2575{\mathrm{e}}^{-0.747u}+0.41249{\mathrm{e}}^{-2.819u}-{\mathrm{e}}^{-2u},u\ge 0$.

(4)

$m\left(u\right)=0.02046{\mathrm{e}}^{-2.819u}+0.34454{\mathrm{e}}^{-0.747u},u\ge 0$.

For combination-of-exponential claim size, the explicit formulae for these Gerber- Shiu functions are given by

(1)

$m\left(u\right)=0.49493{\mathrm{e}}^{-0.707u}-0.04003{\mathrm{e}}^{-30357u},u\ge 0$.

(2)

$m\left(u\right)=0.48606{\mathrm{e}}^{-0.746u}-0.04136{\mathrm{e}}^{-3.352u},u\ge 0$.

(3)

$m\left(u\right)=1.3522{\mathrm{e}}^{-0.707u}-0.6667{\mathrm{e}}^{-1.5u}-0.3333{\mathrm{e}}^{-3u}+0.33879{\mathrm{e}}^{-3.357u},u\ge 0$.

(4)

$m\left(u\right)=0.35945{\mathrm{e}}^{-0.707u}+0.01625{\mathrm{e}}^{-0.3.357u},u\ge 0$.

Here, we consider $T=120,180,360$. For the cut-off parameter K, we use the result of Remark 4.1 in Su et al. [49] with $K=\lfloor 5T^{\frac{1}{10}}\rfloor$, where $\lfloor ·\rfloor$ means the integer part. Through simulation, we find that even if the truncation parameter K is very small, the satisfactory effect can be obtained. In the case of finite sample size, to test the performance of the estimator, we consider mean value, mean relative error, and integrated mean square error (IMSE) based on 300 experiments, which are computed by

$$\begin{array}{c}\hfill \frac{1}{300}\sum _{j=1}^{300}{\widehat{m}}_{K,j}\left(u\right),\frac{1}{300}\sum _{j=1}^{300}\frac{{\widehat{m}}_{K,j}\left(u\right)}{m\left(u\right)}-1,\frac{1}{300}\sum _{j=1}^{300}{\int }_0^{30}{|{\widehat{m}}_{K,j}\left(u\right)-m\left(u\right)|}^{2}du,\end{array}$$

where ${\widehat{m}}_{K,j}\left(u\right)$ is the estimate of Gerber–Shiu function in the j-th experiment. For IMSE, we computed the integral on the finite domain $[0,30]$ instead of $[0,\infty ]$, since when u is large, both the true value and the estimates are very close to zero.

For Figure 1, we consider the comparison between the 30 estimated curves and the value curves when $T=180$ and the exponential claim size density. It is easily observed that the estimated curves are close to each other and close to the true value curve, which indicates that our estimation method has good stability. Next, in Figure 2 and Figure 3, based on 300 experiments, we respectively show the mean value curves and true value curves of the exponential claim size density and the combination-of-exponentials claim size density at different observed intervals T. It is easy to see from the figure above that it is difficult to distinguish the true value curves from the mean value curves when T is larger.

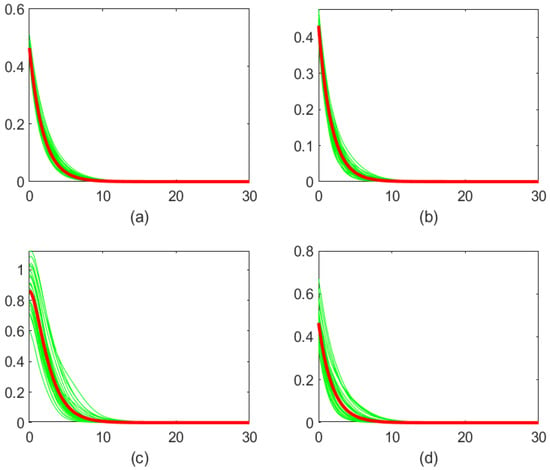
Figure 1. Estimation of the Gerber–Shiu function for exponential density function: red line (true values) and green lines (30 estimated curves) when T = 180. (a) Ruin probability; (b) Laplace transform of ruin time; (c) expected claim size causing ruin; (d) expected deficit at ruin.

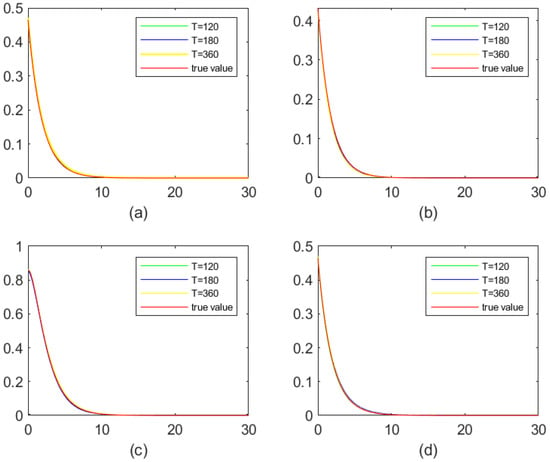
Figure 2. Estimation of the Gerber–Shiu function for exponential density function: mean curves. (a) Ruin probability; (b) Laplace transform of ruin time; (c) expected claim size causing ruin; (d) expected deficit at ruin.

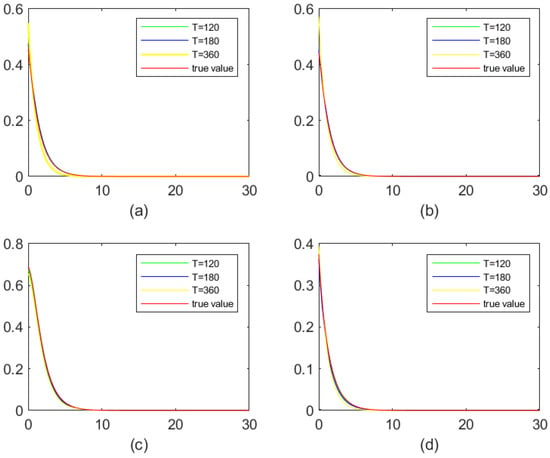
Figure 3. Estimation of the Gerber–Shiu function for combination-of-exponentials density function: mean curves. (a) Ruin probability; (b) Laplace transform of ruin time; (c) expected claim size causing ruin; (d) expected deficit at ruin.

We also provide the situation of the mean relative error curves at the Erlang (2) claim size density in Figure 4. It can be noted that (1) the mean relative error curves first increase and then decrease with the increase in u; (2) when T is larger, the average relative error curve is smaller. This fact can be explained as follows: (1) when the initial surplus u is small, the true value $m\left(u\right)$ as the denominator is large, which leads to a small mean relative error; (2) with the increase in u, the true value $m\left(u\right)$ decreases, so the mean relative error increases; (3) as u continues to increase, the estimated value ${\widehat{m}}_K\left(u\right)$ as the numerator decreases faster than the true value $m\left(u\right)$ as the denominator, which makes the subsequent mean relative error curve drop below zero level.

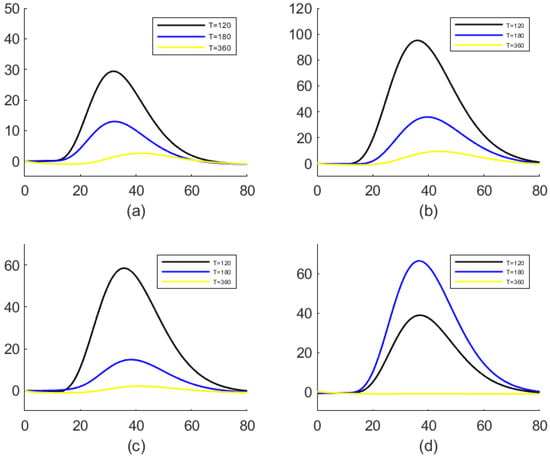
Figure 4. Estimation of the Gerber–Shiu function for Erlang (2) density function: mean relative error curves. (a) Ruin probability; (b) Laplace transform of ruin time; (c) expected claim size causing ruin; (d) expected deficit at ruin.

In addition, based on the above 300 repeated experiments, we give a series of IMSE values of Gerber–Shiu function estimation under three kinds of claim distribution assumptions in Table 1. All the numerical experiments in this paper were completed in MATLAB. Taking exponential density as an example, when $T=120$, we completed 300 independent repeated experiments in 176.06 s. For each claim density function, the IMSE of the Gerber–Shiu function decreases as T increases. This conclusion also shows the stability of the estimation method in this paper. Finally, we compare the Laguerre series expansion method with FFT method used in Shimizu and Zhang [19]. The parameter setting of FFT is the same as in Shimizu and Zhang [19]. First, we present the IMSE values for both methods in Table 2, and we find that the Laguerre series expansion method can lead to smaller IMSEs compared with the FFT method. Moreover, we set $T=120$ and display the mean relative error curves in Figure 5, and we find that the Laguerre series expansion method can yield smaller mean relative errors.

Table 1. IMSEs for the estimated Gerber–Shiu functions.

Claim Size	T	RP	LT	ECS	ED
	120	0.02167	0.00555	0.44172	0.01433
Exponential	180	0.01811	0.00304	0.42494	0.00682
	360	0.01649	0.00181	0.39796	0.00468
	120	0.00196	0.00707	0.22613	0.32025
Erlang (2)	180	0.00099	0.00153	0.16997	0.24374
	360	0.00097	0.00023	0.13564	0.16738
	120	0.00394	0.00192	0.02533	0.00501
Combination-of-exponentials	180	0.00271	0.00082	0.02261	0.00108
	360	0.00205	0.00055	0.00163	0.00053

Table 2. IMSEs for the estimated Gerber–Shiu functions.

Claim Size	T	RP	LT	ECS	ED
Exponential	Laguerre	0.02167	0.00555	0.44172	0.01433
	FFT	0.02379	0.00613	0.47373	0.02041
Erlang (2)	Laguerre	0.00196	0.00707	0.22613	0.32025
	FFT	0.00214	0.00813	0.24715	0.41079
Combination-of-exponentials	Laguerre	0.00394	0.00192	0.02533	0.00501
	FFT	0.00424	0.00231	0.03141	0.00673

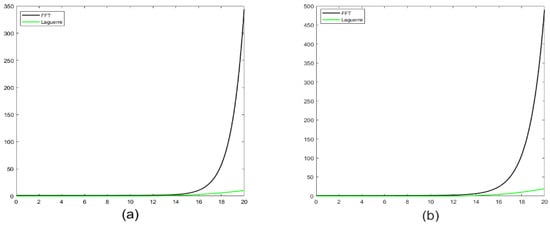
Figure 5. Comparing with FFT method for Erlang (2) density function: mean relative error curves. (a) Ruin probability; (b) Laplace transform of ruin time.

6. Conclusions

This paper introduces how to use the Laguerre series expansion method to estimate the Gerber–Shiu function of the two-sided jumps risk model and gives the nonparametric estimation of the corresponding ruin characteristic quantity. First, we prove that the Gerber–Shiu function of the two-sided jumps risk model can be expanded by Laguerre series, then Laguerre coefficient can be obtained by solving system of linear equations, and then the unknown coefficients can be estimated based on sample information on claim numbers and individual claim sizes. We derive the consistency property of this estimator when the sample size is large. Finally, when the sample size is limited, we demonstrate the high accuracy of the estimation method through numerical experiments. More importantly, it should be noted that our methods are not limited to be applied to the two-sided jumps risk model, but can be widely applied to other risk models in insurance. In addition, the following studies could be extended to other mathematical methods and models.