Global Existence and Uniform Blow-Up to a Nonlocal Parabolic System with Nonlinear Boundary Conditions Arising in a Thermal Explosion Theory

Abstract

This paper deals with a nonlinear nonlocal parabolic system with nonlinear heat-loss boundary conditions, which arise in the thermal explosion model. Firstly, we prove a comparison principle for some kinds of parabolic systems under nonlinear boundary conditions. Using this, we improve a new theorem of the sub-and-super solution. Secondly, based on the new sub-and-super solution theorem, the sufficient conditions that the solution exists and blows up uniformly in finite time are presented. Then, we generalize some of the lemmas related to uniform blow-up solutions, which are used to introduce the uniform blow-up profiles of solutions. Finally, we give several numerical simulations to illustrate the existence and uniform blow-up of solutions.

1. Introduction

In this paper, we discuss the following semi-linear parabolic system with nonlinear nonlocal sources and nonlinear boundary conditions:

$$\left\{\begin{array}{cc}{\displaystyle u_t=\mathsf{\Delta }u+k_1{\int }_{\mathsf{\Omega }}{u}^m(x,t)v^n(x,t)dx,}\hfill & (x,t)\in Q_T,\hfill \\ {\displaystyle v_t=\mathsf{\Delta }v+k_2{\int }_{\mathsf{\Omega }}{u}^p(x,t)v^q(x,t)dx,}\hfill & (x,t)\in Q_T,\hfill \\ \mathit{n}·\nabla u+g_1\left(u\right)u=\mathit{n}·\nabla v+g_2\left(v\right)v=0,\hfill & (x,t)\in S_T,\hfill \\ u(x,0)=u_0\left(x\right),v(x,0)=v_0\left(x\right),\hfill & x\in \mathsf{\Omega },\hfill \end{array}\right.$$

(1)

where $k_1,k_2,m,n,p,q$ are positive constants, $Q_T=\mathsf{\Omega }\times (0,T]$, $S_T=\partial \mathsf{\Omega }\times (0,T]$, $T>0$ and $\mathsf{\Omega }$ is a bounded region in $R^N$ ($N>1$ is an integer) with a smooth boundary $\partial \mathsf{\Omega }$, $\mathit{n}$ is an outward unit normal vector of $\partial \mathsf{\Omega }$, $g_1,g_2,u_0,v_0$ are nonnegative continuous functions satisfying some assumptions, and $\left|\mathsf{\Omega }\right|$ denotes the Lebesgue measure of $\mathsf{\Omega }$.

Our study is motivated by [1,2], in which the existence and blow-up of partial differential equations under nonlinear boundary conditions were researched. As stated in [1], in certain thermal explosion problems that require long induction times (times prior to ignition), such as the safe storage of energetic materials or nuclear waste, the Dirichlet boundary condition $u=v=0$ is no longer applicable because during this time the boundary of the reaction material will be preheated to a temperature significantly higher than the surrounding temperature. As a result, we need the heat-loss boundary conditions in (1) to describe the temperature distribution of the boundary. In recent years, many authors have investigated the reaction-diffusion system with Dirichlet boundary conditions as follows:

$$\left\{\begin{array}{cc}{u}_t-d_1(x,t)\mathsf{\Delta }u=f(u,v),\hfill & (x,t)\in \mathsf{\Omega }\times (0,T),\hfill \\ v_t-d_2(x,t)\mathsf{\Delta }v=g(u,v),\hfill & (x,t)\in \mathsf{\Omega }\times (0,T),\hfill \\ u(x,t)=v(x,t)=0,\hfill & (x,t)\in \partial \mathsf{\Omega }\times (0,T),\hfill \\ u(x,0)=u_0\left(x\right),v(x,0)=v_0\left(x\right),\hfill & x\in \mathsf{\Omega },\hfill \end{array}\right.$$

(2)

For details, see [3,4,5,6,7] and their references. In [3], the blow-up and global existence criteria of the nonlocal parabolic system

$$\begin{array}{cc}\hfill {\displaystyle u_t=f\left(u\right)\left(\mathsf{\Delta }u+a{\int }_{\mathsf{\Omega }}vdx\right),}& {\displaystyle v_t=g\left(v\right)\left(\mathsf{\Delta }v+b{\int }_{\mathsf{\Omega }}udx\right)}\end{array}$$

(3)

were obtained. In [4,7], the authors studied nonlocal nonlinear parabolic systems of the form

$$\begin{array}{cc}\hfill {\displaystyle u_t-u^{s_1}\mathsf{\Delta }u=a{u}^m{\int }_{\mathsf{\Omega }}{v}^{n}dx,}& {\displaystyle v_t-v^{s_2}\mathsf{\Delta }v=b{v}^p{\int }_{\mathsf{\Omega }}{u}^{q}dx}\end{array}$$

(4)

where $m,n,p,q,s_1,s_2>0$ are constants. They all gave some results on the existence of solutions, the blow-up solutions, and the blow-up rate or profile. In [5], Li et al. suggested that if one of $\alpha >1,\beta >1$ or $pq>(1-\alpha )(1-\beta )$ holds, the solution of (2) blows up in finite time for sufficiently large initial data, when

$$\begin{array}{cc}\hfill {\displaystyle f(u,v)={\int }_{\mathsf{\Omega }}{u}^{\alpha }{v}^{p}dx,}& {\displaystyle g(u,v)={\int }_{\mathsf{\Omega }}{u}^q{v}^{\beta }dx}\end{array}$$

(5)

and $d_i=1,i=1,2$. Furthermore, they also obtained the blow-up profile of the solution

$$\begin{array}{c}{\displaystyle \underset{t\to T^{*}}{lim}u(x,t){(T^{*}-t)}^{\frac{p-\beta +1}{pq-(1-\alpha )(1-\beta )}}={\left(\frac{q-\alpha +1}{p-\beta +1}\right)}^{\frac{p}{pq-(1-\alpha )(1-\beta )}}}\\ {\displaystyle \times {\left(\frac{p-\beta +1}{\left|\mathsf{\Omega }\right|(pq-(1-\alpha \left)\right(1-\beta \left)\right)}\right)}^{\frac{p-\beta +1}{pq-(1-\alpha )(1-\beta )}},}\\ {\displaystyle \underset{t\to T^{*}}{lim}v(x,t){(T^{*}-t)}^{\frac{q-\alpha +1}{pq-(1-\alpha )(1-\beta )}}={\left(\frac{p-\beta +1}{q-\alpha +1}\right)}^{\frac{q}{pq-(1-\alpha )(1-\beta )}}}\\ {\displaystyle \times {\left(\frac{q-\alpha +1}{\left|\mathsf{\Omega }\right|(pq-(1-\alpha \left)\right(1-\beta \left)\right)}\right)}^{\frac{q-\alpha +1}{pq-(1-\alpha )(1-\beta )}},}\end{array}$$

uniformly on any compact subset of $\mathsf{\Omega }$, if $q>\alpha -1$, $p>\beta -1$, and $pq>(1-\alpha )(1-\beta )$. Thereafter, in [8], Kong and Wang extended these results to parabolic systems with nonlocal boundaries

$$\begin{array}{cc}\hfill {\displaystyle u={\int }_{\mathsf{\Omega }}\phi (x,y)u(y,t)dy,}& {\displaystyle v={\int }_{\mathsf{\Omega }}\psi (x,y)v(y,t)dy}\end{array}$$

(6)

by improving the methods used in [9,10].

In addition, there are some interesting results on the global well-posed theory related to our work that can be found in [11,12,13,14].

In this paper, we present the global existence, the uniform blow-up criteria, and the uniform blow-up profiles of system (1) with nonlinear heat-loss boundary conditions. To this end, we first give the following assumptions.

(H1)

$u_0$, $v_0\in C^{2+\alpha }\left(\mathsf{\Omega }\right)\cap C^1\left(\overline{\mathsf{\Omega }}\right)(0<\alpha <1)$ are nonnegative, bounded, and $\frac{\partial u_0}{\partial \mathit{n}}$, $\frac{\partial v_0}{\partial \mathit{n}}<0$;

(H2)

$g_i>0,i=1,2$ satisfy the local Lipschitz condition;

(H3)

$g_i,i=1,2$ are increasing functions.

This paper is divided into five sections. In Section 2, we prove some new comparison principles for a modification of our system and using the obtained principles, we can obtain the local existence of (1) if our system has sub- and super-solutions as we define. In Section 3, we give some new definitions of uniform blow-up solutions and global solutions and present the global existence and uniform blow-up criteria of solutions to system (1), respectively, with the help of the methods used in [8,15]. In Section 4, we generalize several relevant lemmas from [9,10] and based on them give the blow-up profile of (1), which describes the asymptotic behavior of the solution near the blow-up time. In Section 5, we simulate numerically the global existence and uniform blow-up of solutions.

2. Local Existence

In this section, we intend to prove the local existence of solutions to (1) using the monotone iterative technique (see [16,17,18]) and the fixed-point theorem. To do this, we need to define the sub- and super-solutions, as well as to generalize the comparison principle from [2,8,15]. Here we define the sub- and super-solutions as follows.

Definition 1.

A pair of nonnegative functions $(\overline{u}(x,t),\overline{v}(x,t))$ is called a super-solution of (1) if $(\overline{u},\overline{v})\in (C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right))\times (C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right))$, $0<T\le +\infty$ and satisfies

$$\left\{\begin{array}{cc}{\displaystyle {\overline{u}}_t\ge \mathsf{\Delta }\overline{u}+k_1{\int }_{\mathsf{\Omega }}{\overline{u}}^m(x,t){\overline{v}}^n(x,t)dx,}\hfill & (x,t)\in Q_T,\hfill \\ {\displaystyle {\overline{v}}_t\ge \mathsf{\Delta }\overline{v}+k_2{\int }_{\mathsf{\Omega }}{\overline{u}}^p(x,t){\overline{v}}^q(x,t)dx,}\hfill & (x,t)\in Q_T,\hfill \\ \mathit{n}·\nabla \overline{u}+g_1\left(\overline{u}\right)\overline{u}\ge 0,\mathit{n}·\nabla \overline{v}+g_1\left(\overline{v}\right)\overline{v}\ge 0,\hfill & (x,t)\in S_T,\hfill \\ \overline{u}(x,0)\ge u_0\left(x\right),\overline{v}(x,0)\ge v_0\left(x\right),\hfill & x\in \mathsf{\Omega }.\hfill \end{array}\right.$$

(7)

Similarly, a sub-solution can be defined with reversed inequalities in (7).

Then, we prove the following comparison principle.

Lemma 1.

Suppose that $a_i$ and $b_i$ are the continuous and bounded functions on ${\overline{Q}}_T$, respectively; $c_i$ and $d_i$ are the nonnegative and bounded functions in $Q_T$; and $f_i$ and $h_i$ are the nonnegative functions and the positive increasing functions on $\overline{\mathsf{\Omega }}$, respectively. If $u,v\in C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right)$ satisfy

$$\left\{\begin{array}{cc}{\displaystyle u_t-a_1\mathsf{\Delta }u\ge b_{1}u+f_1\left(x\right){\int }_{\mathsf{\Omega }}(c_{1}u+d_{1}v)dx,}\hfill & (x,t)\in Q_T,\hfill \\ {\displaystyle v_t-a_2\mathsf{\Delta }v\ge b_{2}v+f_2\left(x\right){\int }_{\mathsf{\Omega }}(c_{2}u+d_{2}v)dx,}\hfill & (x,t)\in Q_T,\hfill \\ \mathit{n}·\nabla u+h_1\left(u\right)u\ge 0,\mathit{n}·\nabla v+h_2\left(v\right)v\ge 0,\hfill & (x,t)\in S_T,\hfill \\ u(x,0)=u_0\left(x\right)\ge 0,v(x,0)=v_0\left(x\right)\ge 0,\hfill & x\in \mathsf{\Omega }\hfill \end{array}\right.$$

(8)

then $u,v\ge 0$ in $Q_T$.

Proof. 

Firstly, we prove that if $u,v$ satisfy

$$\left\{\begin{array}{cc}\mathit{n}·\nabla u+h_1\left(u\right)u>0,\mathit{n}·\nabla v+h_2\left(v\right)v>0,\hfill & (x,t)\in S_T,\hfill \\ u(x,0)=u_0\left(x\right)>0,v(x,0)=v_0\left(x\right)>0,\hfill & x\in \mathsf{\Omega }\hfill \end{array}\right.$$

(9)

then $u,v>0$ in $Q_T$.

Let ${\overline{b}}_i={\displaystyle \underset{{\overline{Q}}_T}{max}}{b}_i$, $i=1,2$ and ${\gamma }_1>max\{{\overline{b}}_1,{\overline{b}}_2\}$. Set $w=e^{-{\gamma }_{1}t}u$, $z=e^{-{\gamma }_{1}t}v$, then we have

$$\left\{\begin{array}{cc}{\displaystyle w_t-a_1\mathsf{\Delta }w+({\gamma }_1-b_1)w\ge f_1\left(x\right){\int }_{\mathsf{\Omega }}(c_{1}w+d_{1}z)dx,}\hfill & (x,t)\in Q_T,\hfill \\ {\displaystyle z_t-a_2\mathsf{\Delta }z+({\gamma }_1-b_2)z\ge f_2\left(x\right){\int }_{\mathsf{\Omega }}(c_{2}w+d_{2}z)dx,}\hfill & (x,t)\in Q_T,\hfill \\ \mathit{n}·\nabla w+h_1\left(u\right)w>0,\mathit{n}·\nabla z+h_2\left(v\right)z>0,\hfill & (x,t)\in S_T,\hfill \\ w(x,0)=u_0\left(x\right)>0,z(x,0)=v_0\left(x\right)>0,\hfill & x\in \mathsf{\Omega }.\hfill \end{array}\right.$$

(10)

By boundary conditions and Assumption (H1), $w,z>0$ on $S_T$ can be obtained. Considering initial conditions $w(x,0)>0$, $z(x,0)>0$, by continuity, there exists a $t>0$ such that $w(x,t)>0$, $z(x,t)>0$ for all $(x,t)\in \mathsf{\Omega }\times [0,t]$. Let $A=\{t<T:w,z>0\mathrm{in}\mathsf{\Omega }\times [0,t\left]\right\}$ and take $\overline{t}=supA$, then we have $0<\overline{t}\le T$. If $\overline{t}=T$, the conclusion is proven, and if $\overline{t}<T$, with no loss of generality we can suppose that there are some $\overline{x}\in \overline{\mathsf{\Omega }}$ such that $w(\overline{x},\overline{t})=0$. Therefore, w takes the minimum on $\overline{\mathsf{\Omega }}\times (0,\overline{t}]$. According to the first inequality of (10), we obtain

$$\begin{array}{cc}\hfill w_t-a_1\mathsf{\Delta }w\ge (b_1-{\gamma }_1)w,& (x,t)\in \mathsf{\Omega }\times (0,\overline{t}].\end{array}$$

(11)

By the strong maximum principle (Theorem 1 in [19] Chap. 2), $w\equiv 0$ can be obtained, which is a contradiction. Hence, $w,z>0$; that is $u,v>0$.

Then, we prove that if $u,v$ satisfy

$$\left\{\begin{array}{cc}\mathit{n}·\nabla u+h_1\left(u\right)u\ge 0,\mathit{n}·\nabla v+h_2\left(v\right)v\ge 0,\hfill & (x,t)\in S_T,\hfill \\ u(x,0)=u_0\left(x\right)\ge 0,v(x,0)=v_0\left(x\right)\ge 0,\hfill & x\in \mathsf{\Omega }\hfill \end{array}\right.$$

(12)

then $u,v\ge 0$.

Let ${\overline{b}}_i={\displaystyle \underset{Q_T}{max}}\left|b_i\right|$, ${\overline{c}}_i={\displaystyle \underset{Q_T}{max}}(c_i+d_i)$, ${\overline{f}}_i={\displaystyle \underset{\mathsf{\Omega }}{max}}{f}_i$, $i=1,2$ and

$$\begin{array}{cc}\hfill w(x,t)=u(x,t)+\eta e^{{\gamma }_{2}t},& z(x,t)=v(x,t)+\eta e^{{\gamma }_{2}t},\end{array}$$

(13)

where ${\gamma }_2\ge {\displaystyle \underset{i=1,2}{max}}({\overline{b}}_i+{\overline{f}}_i{\overline{c}}_i\left|\mathsf{\Omega }\right|)$, $\eta$ is an arbitrary positive real number. Then, we know $w(x,0)=u_0\left(x\right)+\eta >0$, $z(x,0)=v_0\left(x\right)+\eta >0$. Due to the boundary conditions, we have

$$\left\{\begin{array}{c}\mathit{n}·\nabla w+h_1\left(w\right)w\ge \mathit{n}·\nabla u+h_1\left(u\right)u+\eta h_1\left(w\right)e^{{\gamma }_{2}t}\ge \eta h_1\left(w\right)e^{{\gamma }_{2}t}>0,\hfill \\ \mathit{n}·\nabla z+h_2\left(z\right)z\ge \mathit{n}·\nabla v+h_2\left(v\right)v+\eta h_2\left(z\right)e^{{\gamma }_{2}t}\ge \eta h_2\left(z\right)e^{{\gamma }_{2}t}>0,\hfill \end{array}\right.$$

(14)

which holds in $S_T$. Further, in $Q_T$, we have

$$\left\{\begin{array}{c}{\displaystyle w_t-a_1\mathsf{\Delta }w-b_{1}w-f_1{\int }_{\mathsf{\Omega }}(c_{1}w+d_{1}z)dx\ge ({\gamma }_2-b_1-f_1(c_1+d_1)\left|\mathsf{\Omega }\right|)\eta e^{{\gamma }_{2}t}\ge 0,}\hfill \\ {\displaystyle z_t-a_2\mathsf{\Delta }z-b_{2}z-f_2{\int }_{\mathsf{\Omega }}(c_{2}w+d_{2}z)dx\ge ({\gamma }_2-b_2-f_2(c_2+d_2)\left|\mathsf{\Omega }\right|)\eta e^{{\gamma }_{2}t}\ge 0.}\hfill \end{array}\right.$$

(15)

Therefore, we know that $w,z>0$, then, letting $\eta \to 0^{+}$, $u,v\ge 0$ is obtained. The proof of Lemma 1 is completed. □

We give the following conclusion about the properties of the sub-solutions and super-solutions.

Lemma 2.

Suppose Assumptions (H1)–(H3) hold, $g_1$, $g_2$ are derivable, and the nonnegative $(\underline{u},\underline{v})$, $(\overline{u},\overline{v})\in (C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right))\times (C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right))$, $0<T\le +\infty$ are the sub- and super-solutions to system (1), respectively. $(u,v)\in (C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right))\times (C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right))$ is a solution to problem (1). If Case (i)

$$\left\{\begin{array}{cc}\mathit{n}·\nabla \overline{u}+g_1\left(\overline{u}\right)\overline{u}>0,\mathit{n}·\nabla \overline{v}+g_1\left(\overline{v}\right)\overline{v}>0,\hfill & (x,t)\in S_T,\hfill \\ \overline{u}(x,0)>u_0\left(x\right),\overline{v}(x,0)>v_0\left(x\right)\hfill & x\in \mathsf{\Omega }\hfill \end{array}\right.$$

(16)

is satisfied, we have $\overline{u}>u$, $\overline{v}>v$; otherwise, if Case (ii)

$$\left\{\begin{array}{cc}\mathit{n}·\nabla \underline{u}+g_1\left(\underline{u}\right)\underline{u}<0,\mathit{n}·\nabla \underline{v}+g_1\left(\underline{v}\right)\underline{v}<0,\hfill & (x,t)\in S_T,\hfill \\ \underline{u}(x,0)<u_0\left(x\right),\underline{v}(x,0)<v_0\left(x\right)\hfill & x\in \mathsf{\Omega }\hfill \end{array}\right.$$

(17)

is satisfied, we have $u>\underline{u}$, $v>\underline{v}$.

Proof. 

Case (i). We assume that (16) holds. Let $w=\overline{u}-u$, $z=\overline{v}-v$, and ${\psi }_1\left(s\right)=g_1^{\prime }\left(s\right)s+g_1\left(s\right)$, ${\psi }_2\left(s\right)=g_2^{\prime }\left(s\right)s+g_2\left(s\right)$; obviously, ${\psi }_1$, ${\psi }_2>0$. According to (1), and using the mean value theorem, we have

$$\left\{\begin{array}{c}{\displaystyle w_t-\mathsf{\Delta }w\ge k_1{\int }_{\mathsf{\Omega }}({\overline{u}}^m{\overline{v}}^n-u^m{v}^n)dx}\hfill \\ {\displaystyle =k_1{\int }_{\mathsf{\Omega }}(m{\xi }_1^{m-1}{\xi }_2^{n}w+n{\xi }_1^m{\xi }_2^{n-1}z)dx,}& (x,t)\in Q_T,\hfill \\ {\displaystyle z_t-\mathsf{\Delta }z\ge k_2{\int }_{\mathsf{\Omega }}({\overline{u}}^p{\overline{v}}^q-u^p{v}^q)dx}\hfill \\ {\displaystyle =k_2{\int }_{\mathsf{\Omega }}(p{\xi }_1^{p-1}{\xi }_2^{q}w+q{\xi }_1^p{\xi }_2^{q-1}z)dx,}& (x,t)\in Q_T,\hfill \\ \mathit{n}·\nabla w+{\psi }_1\left({\zeta }_1\right)w>0,\mathit{n}·\nabla z+{\psi }_2\left({\zeta }_2\right)z>0,\hfill & (x,t)\in S_T,\hfill \\ w(x,0)>0,z(x,0)>0,\hfill & x\in \mathsf{\Omega }.\hfill \end{array}\right.$$

(18)

where ${\xi }_1$, ${\zeta }_1$ are between u and $\overline{u}$; ${\xi }_2$, ${\zeta }_2$ are between v and $\overline{v}$. Similar to the proof of Lemma 1, let $\tilde{w}=e^{-t}w$, $\tilde{z}=e^{-t}z$, then, (18) can be transformed into

$$\left\{\begin{array}{cc}{\displaystyle {\tilde{w}}_t-\mathsf{\Delta }\tilde{w}+\tilde{w}\ge k_1{\int }_{\mathsf{\Omega }}(m{\xi }_1^{m-1}{\xi }_2^{n}w+n{\xi }_1^m{\xi }_2^{n-1}z)dx,}\hfill & (x,t)\in Q_T,\hfill \\ {\displaystyle {\tilde{z}}_t-\mathsf{\Delta }\tilde{z}+\tilde{z}\ge k_2{\int }_{\mathsf{\Omega }}(p{\xi }_1^{p-1}{\xi }_2^{q}w+q{\xi }_1^p{\xi }_2^{q-1}z)dx,}\hfill & (x,t)\in Q_T,\hfill \\ \mathit{n}·\nabla \tilde{w}+{\psi }_1\left({\zeta }_1\right)\tilde{w}>0,\mathit{n}·\nabla \tilde{z}+{\psi }_2\left({\zeta }_2\right)\tilde{z}>0,\hfill & (x,t)\in S_T,\hfill \\ \tilde{w}(x,0)>0,\tilde{z}(x,0)>0,\hfill & x\in \mathsf{\Omega }.\hfill \end{array}\right.$$

(19)

By boundary conditions and ${\psi }_1$, ${\psi }_2>0$, we have $\tilde{w}$, $\tilde{z}>0$ on $S_T$. Since $\tilde{w}(x,0)$, $\tilde{z}(x,0)>0$, by continuity, there exists a $t>0$ such that $\tilde{w}$, $\tilde{z}>0$ for all $(x,t)\in \mathsf{\Omega }\times [0,t]$. Let $A=\{t<T:\tilde{w},\tilde{z}>0\mathrm{in}\mathsf{\Omega }\times [0,t]\}$ and $\overline{t}=supA$, then we have $0<t\le T$. When $\overline{t}=T$, the conclusion is obvious and we discuss the case $\overline{t}<T$. Supposing that there are some $\overline{x}\in \overline{\mathsf{\Omega }}$ such that $\tilde{w}(\overline{x},\overline{t})=0$, $\tilde{w}$ takes the minimum on $\overline{\mathsf{\Omega }}\times (0,\overline{t}]$. According to the first inequality of (19), we obtain

$$\begin{array}{cc}\hfill {\tilde{w}}_t-\mathsf{\Delta }\tilde{w}\ge -\tilde{w},& (x,t)\in \mathsf{\Omega }\times (0,\overline{t}].\end{array}$$

By the strong maximum principle (Theorem 1 in [19] Chap. 2), $\tilde{w}\equiv 0$ can be obtained, which is a contradiction. We have $\tilde{w}$, $\tilde{z}>0$; that is, w, $z>0$. $\overline{u}>u$ and $\overline{v}>v$ are proved.

Case (ii). The proof of Case (ii) is similar to that of Case (i), and we omit it. □

Based on Definition 1 and Lemma 1, we give the theorem describing the local existence of (1).

Theorem 1.

Suppose Assumptions (H1)–(H3) hold, the nonnegative $(\underline{u},\underline{v})$, $(\overline{u},\overline{v})\in (C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right))\times (C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right))$, $0<T\le +\infty$ are the sub- and super-solutions to system (1), respectively, and $\underline{u}\le \overline{u}$, $\underline{v}\le \overline{v}$, then there exists a pair of functions $(u,v)$ satisfying $\underline{u}\le u\le \overline{u}$, $\underline{v}\le v\le \overline{v}$, which is a solution to system (1).

Proof. 

According to Assumptions (H1)(H2), we know that for any $u_1\ge u_2$ given, since the function $-g_1\left(u\right)u$ is Lipschitz continuous, there exists a fixed real number $L_1$ such that

$$|-g_1\left(u_1\right)u_1-(-g_1\left(u_2\right)u_2)|\le L_1|u_1-u_2|,$$

(20)

thus

$$-g_1\left(u_1\right)u_1-(-g_1\left(u_2\right)u_2)\ge -L_1(u_1-u_2).$$

(21)

Let $G_{l_1}=-g_1\left(u\right)u+L_{1}u$ and similarly $G_{l_2}\left(v\right)=-g_2\left(v\right)v+L_{2}v$, which are increasing. Then, we consider the following auxiliary problem

$$\left\{\begin{array}{cc}{\displaystyle w_t-\mathsf{\Delta }w+w=u+k_1{\int }_{\mathsf{\Omega }}{u}^m{v}^{n}dx,}\hfill & (x,t)\in Q_T,\hfill \\ {\displaystyle z_t-\mathsf{\Delta }z+z=v+k_2{\int }_{\mathsf{\Omega }}{u}^p{v}^{q}dx,}\hfill & (x,t)\in Q_T,\hfill \\ \mathit{n}·\nabla w+L_{1}w=G_{l_1}\left(u\right),\mathit{n}·\nabla z+L_{2}z=G_{l_2}\left(v\right),\hfill & (x,t)\in S_T,\hfill \\ w(x,0)=u_0\left(x\right),z(x,0)=v_0\left(x\right),\hfill & x\in \mathsf{\Omega },\hfill \end{array}\right.$$

(22)

where $u,v\in C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right)$, $0<T\le +\infty$ are two nonnegative functions. The auxiliary problem (22) has Robin boundary conditions, which means that there exists a unique solution $(w,z)$ to it. Define nonlinear operator $T_1:[\underline{u},\overline{u}]\to [\underline{u},\overline{u}]$ and $T_2:[\underline{v},\overline{v}]\to [\underline{v},\overline{v}]$ such that $w=T_{1}u$ and $z=T_{2}v$. Then, construct the following sequences

$$\begin{array}{cccc}{\tilde{w}}_1=T_1\overline{u},& {\tilde{w}}_2=T_1{\tilde{w}}_1,& \cdots ,& {\tilde{w}}_n=T_1{\tilde{w}}_{n-1},\\ {\widehat{w}}_1=T_1\underline{u},& {\widehat{w}}_2=T_1{\widehat{w}}_1,& \cdots ,& {\widehat{w}}_n=T_1{\widehat{w}}_{n-1};\\ {\tilde{z}}_1=T_2\overline{v},& {\tilde{z}}_2=T_2{\tilde{z}}_1,& \cdots ,& {\tilde{z}}_n=T_2{\tilde{z}}_{n-1},\\ {\widehat{z}}_1=T_1\underline{v},& {\widehat{z}}_2=T_2{\widehat{z}}_1,& \cdots ,& {\widehat{z}}_n=T_2{\widehat{z}}_{n-1}.\end{array}$$

(23)

Next, we will show that the operators $T_1$ and $T_2$ are increasing. For any $\underline{u}\le u_1\le u_2\le \overline{u}$ and $\underline{v}\le v_1\le v_2\le \overline{v}$, let $w_1=T_1{u}_1$, $w_2=T_1{u}_2$, and $z_1=T_2{v}_1$, $z_2=T_2{v}_2$, and take $W=w_2-w_1$, $Z=z_2-z_1$. Then, we have

$$\left\{\begin{array}{cc}{\displaystyle W_t-\mathsf{\Delta }W+W=k_1{\int }_{\mathsf{\Omega }}(u_2^m{v}_2^n-u_1^m{v}_1^n)dx+(u_2-u_1)\ge 0,}\hfill & (x,t)\in Q_T,\hfill \\ {\displaystyle Z_t-\mathsf{\Delta }Z+Z=k_2{\int }_{\mathsf{\Omega }}(u_2^p{v}_2^q-u_1^p{v}_1^q)dx+(v_2-v_1)\ge 0,}\hfill & (x,t)\in Q_T,\hfill \\ \mathit{n}·\nabla W+L_{1}W=G_{l_1}\left(u_2\right)-G_{l_1}\left(u_1\right)\ge 0,\hfill & (x,t)\in S_T,\hfill \\ \mathit{n}·\nabla Z+L_{2}Z=G_{l_2}\left(v_2\right)-G_{l_2}\left(v_1\right)\ge 0,\hfill & (x,t)\in S_T,\hfill \\ W(x,0)=Z(x,0)=0,\hfill & x\in \mathsf{\Omega }.\hfill \end{array}\right.$$

(24)

Applying Lemma 1 with $a_i=1$, $b_i=-1$, $c_i=d_i=0$, $h_i=L_i$, $i=1,2$, we know $W,Z\ge 0$; that is, $w_2\ge w_1$, $z_2\ge z_1$. Letting $W=\overline{u}-{\tilde{w}}_1$ and $Z=\overline{v}-{\widehat{z}}_1$, we can obtain

$$\left\{\begin{array}{cc}{\displaystyle W_t-\mathsf{\Delta }W+W=k_1{\int }_{\mathsf{\Omega }}({\overline{u}}^m{\overline{v}}^n-{\overline{u}}^m{\overline{v}}^n)dx+(\overline{u}-\overline{u})=0,}\hfill & (x,t)\in Q_T,\hfill \\ Z_t-\mathsf{\Delta }Z+Z=0,\hfill & (x,t)\in Q_T,\hfill \\ \mathit{n}·\nabla W+L_{1}W\ge G_{l_1}\left(\overline{u}\right)-G_{l_1}\left(\overline{u}\right)=0,\hfill & (x,t)\in S_T,\hfill \\ \mathit{n}·\nabla Z+L_{2}Z\ge 0,\hfill & (x,t)\in S_T,\hfill \\ W(x,0)=Z(x,0)=0,\hfill & x\in \mathsf{\Omega },\hfill \end{array}\right.$$

(25)

thus, $\overline{u}\ge {\tilde{w}}_1$ and $\overline{v}\ge {\tilde{z}}_1$ can be deduced. Similarly, ${\widehat{w}}_1\ge \underline{u}$ and ${\widehat{z}}_1\ge \underline{v}$ can be deduced, too.

By mathematical induction on n, we have

$$\begin{array}{c}\underline{u}\le {\widehat{w}}_1\le {\widehat{w}}_2\le \cdots \le {\widehat{w}}_n\le \cdots \le {\tilde{w}}_n\le {\tilde{w}}_{n-1}\le \cdots \le {\tilde{w}}_1\le \overline{u},\hfill \\ \underline{v}\le {\widehat{z}}_1\le {\widehat{z}}_2\le \cdots \le {\widehat{z}}_n\le \cdots \le {\tilde{z}}_n\le {\tilde{z}}_{n-1}\le \cdots \le {\tilde{z}}_1\le \overline{v},\hfill \end{array}$$

(26)

which shows that the sequences $\left\{{\tilde{w}}_n\right\}$, $\left\{{\widehat{w}}_n\right\}$, $\left\{{\tilde{z}}_n\right\}$, $\left\{{\widehat{z}}_n\right\}$ are increasing and bounded. Therefore, limits

$$\begin{array}{cc}{\tilde{w}}_0=\underset{n\to \infty }{lim}{\tilde{w}}_n,& {\widehat{w}}_0=\underset{n\to \infty }{lim}{\widehat{w}}_n,\\ {\tilde{z}}_0=\underset{n\to \infty }{lim}{\tilde{z}}_n,& {\widehat{z}}_0=\underset{n\to \infty }{lim}{\widehat{z}}_n\end{array}$$

(27)

satisfying ${\tilde{w}}_0=T_1{\tilde{w}}_0$, ${\tilde{z}}_0=T_2{\tilde{z}}_0$ and ${\widehat{w}}_0=T_1{\widehat{w}}_0$, ${\widehat{z}}_0=T_2{\widehat{z}}_0$, exist. Considering the compactness of the nonlinear operators $T_1$, $T_2$ and $\left|\mathsf{\Omega }\right|<\infty$, we know that $({\tilde{w}}_0,{\tilde{z}}_0)$ and $({\widehat{w}}_0,{\widehat{z}}_0)$ are the solutions to problem (1). The local existence of the solutions to problem (1) is proved. □

3. Global Existence and Uniform Blow-Up Results

In this section, we will use the sub-and-super solution theorem and combine it with Lemma 2 to give the global existence and uniform blow-up conditions of system (1). Firstly, we define the uniform blow-up solution.

Definition 2.

The nonnegative solution $(u,v)$ to problem (1) blows up uniformly in finite time if there exists a positive real number $T<\infty$ such that

$$\underset{t\to T}{lim\; sup}\underset{x\in \overline{\mathsf{\Omega }}}{min}(u(x,t)+v(x,t))=+\infty .$$

(28)

Further, the solution $(u,v)$ of problem (1) exists globally if for all $t\in (0,+\infty )$,

$$\underset{x\in \overline{\mathsf{\Omega }}}{max}(u(x,t)+v(x,t))<+\infty .$$

(29)

Then, we refer to [8,15] to give Theorems 2 and 3, which are about global existence and blow-up, respectively. Further, the proofs are given using the sub-and-super solution theorem.

Theorem 2.

Suppose Assumptions (H1)–(H3) hold, $g_1$, $g_2$ are derivable and

$$\begin{array}{ccc}\hfill m<1,& p<1,& nq\le (1-m)(1-p).\hfill \end{array}$$

(30)

Then, the solution $(u,v)$ of this problem exists globally of system (1).

Proof. 

First, according to condition (30), we have

$$\frac{1-m}{n}·\frac{1-p}{q}\ge 1,$$

(31)

so there exist two positive constants ${\alpha }_1,{\beta }_1>1$ such that

$$\begin{array}{cc}\hfill {\displaystyle \frac{1-m}{n}\ge \frac{{\beta }_1}{{\alpha }_1},}& {\displaystyle \frac{1-p}{q}\ge \frac{{\alpha }_1}{{\beta }_1}.}\end{array}$$

(32)

Due to the continuity of functions $g_1$ and $g_2$, let ${\delta }_0=min\{min{g}_1,min{g}_2\}$ and $c_0>\frac{B}{{\delta }_0}max\{{\alpha }_1,{\beta }_1\}$. We consider the following eigenvalue problem

$$\left\{\begin{array}{cc}\mathsf{\Delta }\phi +\lambda \phi =0,\hfill & x\in \mathsf{\Omega },\hfill \\ \phi =c_0,\hfill & x\in \partial \mathsf{\Omega }.\hfill \end{array}\right.$$

(33)

The first eigenvalue of problem (33) is denoted by $\lambda$. Take $B=\underset{\overline{\mathsf{\Omega }}}{max}|\nabla \phi |$, ${\gamma }_0=\underset{\overline{\mathsf{\Omega }}}{max}\phi$ and ${\overline{k}}_1={\gamma }_0^{m+n}{k}_1\left|\mathsf{\Omega }\right|$, ${\overline{k}}_2={\gamma }_0^{p+q}{k}_2\left|\mathsf{\Omega }\right|$. Then, let $s\left(t\right)$ be the unique solution to the Cauchy problem

$$\left\{\begin{array}{c}{\displaystyle \frac{ds}{dt}=-\lambda s\left(t\right)+({\alpha }_1+{\beta }_1-2)c_0^{-2}{B}^{2}s\left(t\right)+{\overline{k}}_1{\alpha }_1^{-1}{c}_0^{-{\alpha }_1}{s}^{m{\alpha }_1+n{\beta }_1-{\alpha }_1+1}\left(t\right)}\hfill \\ +{\overline{k}}_2{\beta }_1^{-1}{c}_0^{-{\beta }_1}{s}^{p{\alpha }_1+q{\beta }_1-{\beta }_1+1}\left(t\right),\hfill & t>0,\hfill \\ {\displaystyle s\left(0\right)=\frac{1}{c_0}max\left\{{\left(\underset{\overline{\mathsf{\Omega }}}{max}{u}_0\left(x\right)\right)}^{\frac{1}{{\alpha }_1}},{\left(\underset{\overline{\mathsf{\Omega }}}{max}{v}_0\left(x\right)\right)}^{\frac{1}{{\beta }_1}}\right\}+1.}\hfill \end{array}\right.$$

where $m{\alpha }_1+n{\beta }_1-{\alpha }_1+1$, $p{\alpha }_1+q{\beta }_1-{\beta }_1+1<1$ such that $s\left(t\right)$ exists globally. Set $\overline{u}=s^{{\alpha }_1}\left(t\right){\phi }^{{\alpha }_1}\left(x\right)$, $\overline{v}=s^{{\beta }_1}\left(t\right){\phi }^{{\beta }_1}\left(x\right)$, $(x,t)\in \mathsf{\Omega }\times (0,+\infty )$. Then, we assert that $(\overline{u},\overline{v})$ is a super-solution to problem (1). In $\mathsf{\Omega }\times (0,+\infty )$, we have

$$\begin{array}{cc}\hfill \mathsf{\Delta }\overline{u}& {\displaystyle +k_1{\int }_{\mathsf{\Omega }}{\overline{u}}^m{\overline{v}}^{n}dx=s^{{\alpha }_1}\left(t\right)\mathsf{\Delta }{\phi }^{{\alpha }_1}+k_1{s}^{m{\alpha }_1+n{\beta }_1}\left(t\right){\int }_{\mathsf{\Omega }}{\phi }^{m{\alpha }_1+n{\beta }_1}dx}\hfill \\ \hfill & \le s^{{\alpha }_1}\left(t\right)\left({\alpha }_1{\phi }^{{\alpha }_1-1}\mathsf{\Delta }\phi +{\alpha }_1({\alpha }_1-1){\phi }^{{\alpha }_1-2}{(\nabla \phi )}^2\right)+{\overline{k}}_1{s}^{m{\alpha }_1+n{\beta }_1}\left(t\right)\hfill \\ \hfill & =s^{{\alpha }_1}\left(t\right)\left(-\lambda {\alpha }_1{\phi }^{{\alpha }_1}+{\alpha }_1({\alpha }_1-1){\phi }^{{\alpha }_1-2}{(\nabla \phi )}^2\right)+{\overline{k}}_1{s}^{m{\alpha }_1+n{\beta }_1}\left(t\right)\hfill \\ \hfill & \le {\alpha }_1{s}^{{\alpha }_1-1}\left(t\right){\phi }^{{\alpha }_1}\left(-\lambda +({\alpha }_1-1)c_0^{-2}{B}^2+{\overline{k}}_1{\alpha }_1^{-1}{c}_0^{-{\alpha }_1}{s}^{m{\alpha }_1+n{\beta }_1-{\alpha }_1}\left(t\right)\right)s\left(t\right)\hfill \\ \hfill & \le {\alpha }_1{s}^{{\alpha }_1-1}\left(t\right)s^{\prime }\left(t\right){\phi }^{{\alpha }_1}={\overline{u}}_t,\hfill \end{array}$$

(34)

similarly,

$$\begin{array}{cc}\hfill \mathsf{\Delta }\overline{v}& {\displaystyle +k_2{\int }_{\mathsf{\Omega }}{\overline{u}}^p{\overline{v}}^{q}dx=s^{{\beta }_1}\left(t\right)\mathsf{\Delta }{\phi }^{{\beta }_1}+k_2{s}^{p{\alpha }_1+q{\beta }_1}\left(t\right){\int }_{\mathsf{\Omega }}{\phi }^{p{\alpha }_1+q{\beta }_1}dx}\hfill \\ \hfill & \le s^{{\beta }_1}\left(t\right)\left({\beta }_1{\phi }^{{\beta }_1-1}\mathsf{\Delta }\phi +{\beta }_1({\beta }_1-1){\phi }^{{\beta }_1-2}{(\nabla \phi )}^2\right)+{\overline{k}}_2{s}^{p{\alpha }_1+q{\beta }_1}\left(t\right)\hfill \\ \hfill & =s^{{\beta }_1}\left(t\right)\left(-\lambda {\beta }_1{\phi }^{{\beta }_1}+{\beta }_1({\beta }_1-1){\phi }^{{\beta }_1-2}{(\nabla \phi )}^2\right)+{\overline{k}}_2{s}^{p{\alpha }_1+q{\beta }_1}\left(t\right)\hfill \\ \hfill & \le {\beta }_1{s}^{{\beta }_1-1}\left(t\right){\phi }^{{\beta }_1}\left(-\lambda +({\beta }_1-1)c_0^{-2}{B}^2+{\overline{k}}_2{\beta }_1^{-1}{c}_0^{-{\beta }_1}{s}^{p{\alpha }_1+q{\beta }_1-{\beta }_1}\left(t\right)\right)s\left(t\right)\hfill \\ \hfill & \le {\beta }_1{s}^{{\beta }_1-1}\left(t\right)s^{\prime }\left(t\right){\phi }^{{\beta }_1}={\overline{v}}_t.\hfill \end{array}$$

(35)

Since $\phi =c_0$ on $\partial \mathsf{\Omega }$, we have that

$$\mathit{n}·\nabla \overline{u}+g_1\left(\overline{u}\right)\overline{u}={\phi }^{{\alpha }_1-1}{s}^{{\alpha }_1}({\alpha }_1\mathit{n}·\nabla \phi +c_{0}g\left(\overline{u}\right))>0,$$

(36)

and

$$\mathit{n}·\nabla \overline{v}+g_2\left(\overline{v}\right)\overline{v}={\phi }^{{\beta }_1-1}{s}^{{\beta }_1}({\beta }_1\mathit{n}·\nabla \phi +c_{0}g\left(\overline{v}\right))>0$$

(37)

hold in $\partial \mathsf{\Omega }\times (0,+\infty )$. Considering the initial values, we have

$${\displaystyle \overline{u}(x,0)=s^{{\alpha }_1}\left(0\right){\phi }^{{\alpha }_1}>\frac{{\phi }^{{\alpha }_1}}{c_0^{{\alpha }_1}}\underset{\overline{\mathsf{\Omega }}}{max}{u}_0\ge u_0,}$$

(38)

and

$${\displaystyle \overline{v}(x,0)=s^{{\beta }_1}\left(0\right){\phi }^{{\beta }_1}>\frac{{\phi }^{{\beta }_1}}{c_0^{{\beta }_1}}\underset{\overline{\mathsf{\Omega }}}{max}{v}_0\ge v_0.}$$

(39)

Hence, $(\overline{u},\overline{v})$ is a super-solution to problem (1), and satisfies (16). Applying Lemma 2, the solution $(u,v)$ to problem (1) satisfies $u<\overline{u}$, $v<\overline{v}$. Since $\overline{u}$, $\overline{v}$ exist globally, Theorem 2 is proven. □

Theorem 3.

Suppose Assumptions (H1)–(H3) hold and $g_1$, $g_2$ are derivable.

Case (i). If one of the following conditions holds

$$\begin{array}{ccc}\hfill \left(a\right)m>1;& \left(b\right)q>1;& \left(c\right)np>(1-m)(1-q),\hfill \end{array}$$

(40)

and $u_0\left(x\right),v_0\left(x\right)$ are sufficiently large, then the solution $(u,v)$ of problem (1) blows up uniformly in a finite time.

Case (ii). If (40) is satisfied and $u_0\left(x\right),v_0\left(x\right)$ are sufficiently small, then the solution $(u,v)$ exists globally.

Proof. 

Case (i) (a). Assuming that $m>1$, we consider the eigenvalue problem (33) with $c_0=0$, and for convenience, let $\underset{\overline{\mathsf{\Omega }}}{max}\phi =\frac{1}{2}$. Take ${\alpha }_2$, ${\beta }_2>1$ such that $p{\alpha }_2+q{\beta }_2-{\beta }_2>0$ and set

$$\gamma =min\{m{\alpha }_2+n{\beta }_2-{\alpha }_2+1,p{\alpha }_2+q{\beta }_2-{\beta }_2+1\}.$$

(41)

Obviously, $\gamma >1$. Let $h\left(t\right)$ be the unique solution to the following Cauchy problem

$$\left\{\begin{array}{cc}{\displaystyle \frac{dh}{dt}=-\lambda h\left(t\right)+min\left\{{\displaystyle \frac{k_1}{{\alpha }_2}{\int }_{\mathsf{\Omega }}{\phi }^{m{\alpha }_2+n{\beta }_2}dx,\frac{k_2}{{\beta }_2}{\int }_{\mathsf{\Omega }}{\phi }^{p{\alpha }_2+q{\beta }_2}dx}\right\}{h}^{\gamma }\left(t\right),}\hfill & t>0,\hfill \\ h\left(0\right)=h_0,\hfill \end{array}\right.$$

(42)

where $h_0>0$ is sufficiently large such that the solution to (42) blows up in a finite time.

Let $u_0\left(x\right)$, $v_0\left(x\right)$ be sufficiently large such that $min\{{\left({min}_{\overline{\mathsf{\Omega }}}{u}_0\right)}^{\frac{1}{{\alpha }_2}},{\left({min}_{\overline{\mathsf{\Omega }}}{v}_0\right)}^{\frac{1}{{\beta }_2}}\}>h_0$ and $\underline{u}=h^{{\alpha }_2}\left(t\right){(\phi \left(x\right)+\delta )}^{{\alpha }_2}$, $\underline{v}=h^{{\beta }_2}\left(t\right){(\phi \left(x\right)+\delta )}^{{\beta }_2}$, $(x,t)\in \mathsf{\Omega }\times (0,T^{*}-\epsilon ]$, where $\epsilon \in (0,T^{*})$ and $\delta \in (0,\frac{1}{2})$ are arbitrarily real numbers. Then, we will show that $(\underline{u},\underline{v})$ is a sub-solution to problem (1). In $\mathsf{\Omega }\times (0,T^{*}-\epsilon ]$, we yield

$$\begin{array}{cc}\hfill \mathsf{\Delta }\underline{u}& {\displaystyle +k_1{\int }_{\mathsf{\Omega }}{\underline{u}}^m{\underline{v}}^{n}dx=h^{{\alpha }_2}\left(t\right)\mathsf{\Delta }{(\phi +\delta )}^{{\alpha }_2}+k_1{h}^{m{\alpha }_2+n{\beta }_2}\left(t\right){\int }_{\mathsf{\Omega }}{(\phi +\delta )}^{m{\alpha }_2+n{\beta }_2}dx}\hfill \\ \hfill & \ge h^{{\alpha }_2}\left(t\right)\left(-\lambda {\alpha }_2{(\phi +\delta )}^{{\alpha }_2}+{\alpha }_2({\alpha }_2-1){(\phi +\delta )}^{{\alpha }_2-2}{(\nabla \phi )}^2\right)\hfill \\ \hfill & {\displaystyle +k_1{h}^{m{\alpha }_2+n{\beta }_2}\left(t\right){\int }_{\mathsf{\Omega }}{\phi }^{m{\alpha }_2+n{\beta }_2}dx}\hfill \\ \hfill & \ge {\alpha }_2{h}^{{\alpha }_2-1}\left(t\right){(\phi +\delta )}^{{\alpha }_2}\left({\displaystyle -\lambda +\frac{k_1}{{\alpha }_2}{h}^{m{\alpha }_2+n{\beta }_2-{\alpha }_2}\left(t\right){\int }_{\mathsf{\Omega }}{\phi }^{m{\alpha }_2+n{\beta }_2}dx}\right)h\left(t\right)\hfill \\ \hfill & \ge {\alpha }_2{h}^{{\alpha }_2-1}\left(t\right)h^{\prime }\left(t\right){(\phi +\delta )}^{{\alpha }_2}={\underline{u}}_t,\hfill \end{array}$$

(43)

and

$$\begin{array}{cc}\hfill \mathsf{\Delta }\underline{v}& {\displaystyle +k_2{\int }_{\mathsf{\Omega }}{\underline{u}}^p{\underline{v}}^{q}dx=h^{{\beta }_2}\left(t\right)\mathsf{\Delta }{(\phi +\delta )}^{{\beta }_2}+k_2{h}^{p{\alpha }_2+q{\beta }_2}\left(t\right){\int }_{\mathsf{\Omega }}{(\phi +\delta )}^{p{\alpha }_2+q{\beta }_2}dx}\hfill \\ \hfill & \ge h^{{\beta }_2}\left(t\right)\left(-\lambda {\beta }_2{(\phi +\delta )}^{{\beta }_2}+{\beta }_2({\beta }_2-1){(\phi +\delta )}^{{\beta }_2-2}{(\nabla \phi )}^2\right)\hfill \\ \hfill & {\displaystyle +k_2{h}^{p{\alpha }_2+q{\beta }_2}\left(t\right){\int }_{\mathsf{\Omega }}{\phi }^{p{\alpha }_2+q{\beta }_2}dx}\hfill \\ \hfill & \ge {\beta }_2{h}^{{\beta }_2-1}\left(t\right){(\phi +\delta )}^{{\beta }_2}\left({\displaystyle -\lambda +\frac{k_2}{{\beta }_2}{h}^{p{\alpha }_2+q{\beta }_2-{\beta }_2}\left(t\right){\int }_{\mathsf{\Omega }}{\phi }^{p{\alpha }_2+q{\beta }_2}dx}\right)h\left(t\right)\hfill \\ \hfill & \ge {\beta }_2{h}^{{\beta }_2-1}\left(t\right)h^{\prime }\left(t\right){(\phi +\delta )}^{{\beta }_2}={\underline{v}}_t.\hfill \end{array}$$

(44)

On $\partial \mathsf{\Omega }\times (0,T^{*}-\epsilon ]$, we yield

$$\left\{\begin{array}{c}\mathit{n}·\nabla \underline{u}+g_1\left(\underline{u}\right)\underline{u}={\delta }^{{\alpha }_2-1}{h}^{{\alpha }_2}\left(t\right)({\alpha }_2\mathit{n}·\nabla \phi +\delta g_1\left(\underline{u}\right))<0,\hfill \\ \mathit{n}·\nabla \underline{v}+g_2\left(\underline{v}\right)\underline{v}={\delta }^{{\beta }_2-1}{h}^{{\beta }_2}\left(t\right)({\beta }_2\mathit{n}·\nabla \phi +\delta g_2\left(\underline{v}\right))<0,\hfill \end{array}\right.$$

(45)

when $\delta$ is sufficiently close to 0. Since

$$\left\{\begin{array}{cc}\underline{u}(x,0)=h_0^{{\alpha }_2}{(\phi +\delta )}^{{\alpha }_2}<u_0\left(x\right),\hfill & x\in \mathsf{\Omega },\hfill \\ \underline{v}(x,0)=h_0^{{\beta }_2}{(\phi +\delta )}^{{\beta }_2}<v_0\left(x\right),\hfill & x\in \mathsf{\Omega },\hfill \end{array}\right.$$

(46)

we can obtain that $(\underline{u},\underline{v})$ is a sub-solution to problem (1) and satisfies (17). Applying Lemma 2, we know that $u>\underline{u}$, $v>\underline{v}$ in $\mathsf{\Omega }\times (0,T^{*}-\epsilon ]$. Due to the arbitrary nature of $\epsilon$, letting $\epsilon \to 0^{+}$, $u\ge \underline{u}$, $v\ge \underline{v}$ in $\mathsf{\Omega }\times (0,T^{*})$ can be obtained.

Specifically, we have $u>\underline{u}={\delta }^{{\alpha }_2}{h}^{{\alpha }_2}\left(t\right)$ and $v>\underline{v}={\delta }^{{\beta }_2}{h}^{{\beta }_2}\left(t\right)$ on $\partial \mathsf{\Omega }\times (0,T^{*})$. Hence, the solution $(u,v)$ blows up globally when $m>1$ and $u_0\left(x\right)$, $v_0\left(x\right)$ are sufficiently large.

Case (i) (b). We omit the proof for the comparable case in which $q>1$.

Case (i) (c). When $0<m\le 1$, $0<q\le 1$ and $np>(1-m)(1-q)$, we know that

$${\displaystyle \frac{n}{1-m}-\frac{1-q}{p}>0.}$$

(47)

Take $\epsilon \in \left(0,\frac{n}{1-m}-\frac{1-q}{p}\right)$ and $\frac{{\alpha }_2}{{\beta }_2}=\frac{1-q}{p}+\epsilon$, then there exist two positive constants ${\alpha }_2$, ${\beta }_2>1$ such that

$$\begin{array}{cc}\hfill {\displaystyle \frac{1-q}{p}<\frac{{\alpha }_2}{{\beta }_2},}& {\displaystyle \frac{1-m}{n}<\frac{{\beta }_2}{{\alpha }_2},}\end{array}$$

(48)

which means that $m{\alpha }_2+n{\beta }_2-{\alpha }_2+1>1$, $p{\alpha }_2+q{\beta }_2-{\beta }_2+1>1$. When $\gamma =min\{m{\alpha }_2+n{\beta }_2-{\alpha }_2+1>1$, $p{\alpha }_2+q{\beta }_2-{\beta }_2+1\}$ is used, and the solution $(u,v)$ also blows up, as shown in Case (i).

Case (ii). By the continuity of functions $g_1$ and $g_2$, we have $min{g}_1,min{g}_2>0$. Let positive constant $\delta$ be sufficiently small such that $\delta <min\{min{g}_1,min{g}_2\}$ and $e\left(x\right)$ be the unique solution to the elliptic problem

$$\left\{\begin{array}{cc}-\mathsf{\Delta }e\left(x\right)=1,\hfill & x\in \mathsf{\Omega },\hfill \\ \mathit{n}·\nabla e\left(x\right)+\delta e\left(x\right)=0,\hfill & x\in \partial \mathsf{\Omega }\hfill \end{array}\right.$$

Then, there exists a positive constant M such that $0\le e\left(x\right)\le M$. Set

$$\begin{array}{cc}\hfill \overline{u}(x,t)={\alpha }_3(1+e\left(x\right)),& \overline{v}(x,t)={\beta }_3(1+e\left(x\right)),\end{array}$$

where

$$\begin{array}{cc}\hfill {\alpha }_3\le k_1\left|\mathsf{\Omega }\right|{\alpha }_3^m{\beta }_3^n{(1+M)}^{m+n},& {\beta }_3\le k_2\left|\mathsf{\Omega }\right|{\alpha }_3^p{\beta }_3^q{(1+M)}^{p+q}.\end{array}$$

When $x\in \partial \mathsf{\Omega }$, we have

$$\begin{array}{c}\hfill \mathit{n}·\nabla \overline{u}+g_1\left(\overline{u}\right)\overline{u}={\alpha }_3{g}_1\left(\overline{u}\right)+{\alpha }_{3}e\left(x\right)(g_1\left(\overline{u}\right)-\delta )>0,\\ \hfill \mathit{n}·\nabla \overline{v}+g_2\left(\overline{v}\right)\overline{u}={\beta }_3{g}_2\left(\overline{v}\right)+{\beta }_{3}e\left(x\right)(g_2\left(\overline{v}\right)-\delta )>0.\end{array}$$

Taking the initial values of problem (1) $u_0\left(x\right)$, $v_0\left(x\right)$ are sufficiently small such that $u_0\left(x\right)<\overline{u}(x,t)$, $v_0\left(x\right)<\overline{v}(x,t)$, we have that $(\overline{u},\overline{v})$ is a super-solution to (1), and satisfies (16). Using Lemma 2, we obtain $\overline{u}>u$, $\overline{v}>v$. Thus, u and v exist globally. Theorem 3 is then fully proved. □

4. Uniform Blow-Up Profile of the Solution

In this section, according to the ideas of [10], we discuss the uniform blow-up profile of the solution to (1).

We denote

$$\begin{array}{cc}{\displaystyle F_1\left(t\right)=k_1{\int }_{\mathsf{\Omega }}{u}^m{v}^{n}dx,}& {\displaystyle G_1\left(t\right)={\int }_0^t{F}_1\left(s\right)ds;}\\ {\displaystyle F_2\left(t\right)=k_2{\int }_{\mathsf{\Omega }}{u}^p{v}^{q}dx,}& {\displaystyle G_2\left(t\right)={\int }_0^t{F}_2\left(s\right)ds.}\end{array}$$

(49)

Lemma 3.

Assume that (H1)-(H3) hold, $\mathsf{\Delta }{u}_0$, $\mathsf{\Delta }{v}_0<0$, and $g_1$, $g_2$ can be derived. Let $(u,v)\in (C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right))\times (C^{2,1}\left(Q_T\right)\cap C^1\left({\overline{Q}}_T\right))$ be a solution to problem (1). If $u,v$ blow up at the finite time $T^{*}$ simultaneously, then we have that for all $\epsilon >0$, there exists $C_1>0$ such that

$$\begin{array}{c}{C}_1\le -\mathsf{\Delta }u\le max\left\{\underset{s\in [0,t]}{sup}{F}_1\left(s\right),C_1\right\},\\ C_1\le -\mathsf{\Delta }v\le max\left\{\underset{s\in [0,t]}{sup}{F}_2\left(s\right),C_1\right\}\end{array}$$

(50)

in $\mathsf{\Omega }\times [\frac{T^{*}}{2},T^{*}-\epsilon ]$.

Proof. 

We take the first equation in (1) as an example. Let $w=-\mathsf{\Delta }u$. Since $\mathsf{\Delta }{F}_1\left(t\right)=0$, we obtain

$$\begin{array}{cc}\hfill w_t-\mathsf{\Delta }w=0,& (x,t)\in {\displaystyle \mathsf{\Omega }\times [\frac{T^{*}}{2},T^{*}-\epsilon ]}.\hfill \end{array}$$

(51)

It is easy to see that w can obtain its maximum and minimum in $\partial \mathsf{\Omega }\times [\frac{T^{*}}{2},T^{*}-\epsilon ]$.

On the one hand, if there is a point $(x_0,t_0)$, $x_0\in \mathsf{\Omega }$, $\frac{T^{*}}{2}\le t_0\le T^{*}-\epsilon$ such that $w(x_0,t_0)={max}_{\overline{\mathsf{\Omega }}\times [\frac{T^{*}}{2},T^{*}-\epsilon ]}w(x,t)$, then according to the strong maximum principle of heat equations, we know that w is a constant when $t\in [\frac{T^{*}}{2},t_0]$.

On the other hand, when $t>t_0$, w cannot obtain its maximum and minimum in $\mathsf{\Omega }\times (t_0,T^{*}-\epsilon ]$. For $(x,t)\in \partial \mathsf{\Omega }\times (t_0,T^{*}-\epsilon ]$, set $\psi \left(u\right)=g_1^{\prime }\left(u\right)u+g_1\left(u\right)$. Obviously, $\psi \left(u\right)>0$. A straightforward computation yields

$${\displaystyle \frac{\partial }{\partial t}\frac{\partial u}{\partial \mathit{n}}=-\frac{\partial }{\partial t}\left(g_1\left(u\right)u\right)=-\psi \left(u\right)u_t.}$$

(52)

Further, according to $w=-u_t+F_1\left(t\right)$, we deduce

$${\displaystyle \frac{\partial w}{\partial \mathit{n}}=-\frac{\partial u_t}{\partial \mathit{n}}=\psi \left(u\right)u_t.}$$

(53)

Applying Theorem 6 in [20] Chap. 3, when w takes the minimum value, we have that

$${\displaystyle \frac{\partial w}{\partial \mathit{n}}=\psi \left(u\right)(F_1\left(t\right)-w)<0.}$$

(54)

Since u, v, $F_1\left(t\right)>0$ and by continuity, there exists a constant $0<C_1\le {max}_{\overline{\mathsf{\Omega }}}u(x,\frac{T^{*}}{2})$ such that

$$-\mathsf{\Delta }u\ge C_1.$$

(55)

And, when w takes the maximum value, we have that

$${\displaystyle \frac{\partial w}{\partial \mathit{n}}=\psi \left(u\right)(F_1\left(t\right)-w)>0.}$$

(56)

So we can deduce that

$$-\mathsf{\Delta }u\le \underset{s\in [0,t]}{sup}{F}_1\left(s\right)$$

(57)

for $t\in [\frac{T^{*}}{2},T^{*}-\epsilon ]$. Combining (55) and (57), we have

$${\displaystyle C_1\le -\mathsf{\Delta }u\le max\left\{\underset{s\in [0,t]}{sup}{F}_1\left(s\right),C_1\right\}.}$$

(58)

The proof of the inequality on $-\mathsf{\Delta }v$ is similar to the one on $-\mathsf{\Delta }u$, which is omitted. □

According to (50), we have

$$\begin{array}{c}{u}_t-C_1\le u_t-\mathsf{\Delta }u=F_1\left(t\right),\\ v_t-C_1\le v_t-\mathsf{\Delta }v=F_2\left(t\right).\end{array}$$

(59)

Integrating Equation (59) from $\frac{T^{*}}{2}$ to t yields the following lemma.

Lemma 4.

Under the assumptions of Lemma 3, we have that for all $\epsilon >0$

$$\begin{array}{c}{C}_2^{\prime }\le u(x,t)\le C_2+G_1\left(t\right),\\ C_2^{\prime }\le v(x,t)\le C_2+G_2\left(t\right)\end{array}$$

(60)

where $C_2^{\prime },C_2>0$ are constants and $t\in [\frac{T^{*}}{2},T^{*}-\epsilon ]$.

Proof. 

After performing the integration, we have

$$\begin{array}{c}{\displaystyle u(x,t)-u(x,\frac{T^{*}}{2})-C_1(t-\frac{T^{*}}{2})\le G_1\left(t\right)-G_1\left(\frac{T^{*}}{2}\right)\le G_1\left(t\right),}\\ {\displaystyle v(x,t)-v(x,\frac{T^{*}}{2})-C_1(t-\frac{T^{*}}{2})\le G_2\left(t\right)-G_2\left(\frac{T^{*}}{2}\right)\le G_2\left(t\right),}\end{array}$$

(61)

Taking $C_2=max\left\{\underset{x\in \mathsf{\Omega }}{max}u(x,\frac{T^{*}}{2})+\frac{T^{*}}{2}{C}_1,\underset{x\in \mathsf{\Omega }}{max}v(x,\frac{T^{*}}{2})+\frac{T^{*}}{2}{C}_1\right\}$,

$$\begin{array}{c}u(x,t)\le C_2+G_1\left(t\right),\\ v(x,t)\le C_2+G_2\left(t\right)\end{array}$$

are obtained. Since u, $v>0$ in $\overline{\mathsf{\Omega }}\times (0,T^{*})$ and due to their continuity, there exists a constant $C_2^{\prime }>0$ such that u, $v\ge C_2^{\prime }$. □

Remark 1.

An obvious conclusion deduced from Lemma 4 is that

$$\begin{array}{cc}\hfill \underset{t\to T^{*}}{lim}{G}_1\left(t\right)=+\infty ,& \underset{t\to T^{*}}{lim}{G}_2\left(t\right)=+\infty ,\end{array}$$

(62)

when u, v blow up.

Set

$$\begin{array}{cc}\hfill {\displaystyle H_1\left(t\right)={\int }_0^t{G}_1\left(s\right)ds,}& {\displaystyle H_2\left(t\right)={\int }_0^t{G}_1\left(s\right)ds,}\end{array}$$

(63)

where $t\in [0,T)$.

We consider the eigenvalue problem (33) with $c_0\ge 0$. Set $\lambda$ as the first eigenvalue of (33), and $\phi >0$ is normalized with ${\int }_{\mathsf{\Omega }}\phi dx=1$. Define

$$\begin{array}{cc}\hfill {\displaystyle K_1\left(t\right)={\int }_{\partial \mathsf{\Omega }}u\frac{\partial \phi }{\partial \mathit{n}}dS,}& {\displaystyle K_2\left(t\right)={\int }_{\partial \mathsf{\Omega }}v\frac{\partial \phi }{\partial \mathit{n}}dS,}\end{array}$$

(64)

where $t\in [0,T)$. We have $K_1\left(t\right)$, $K_2\left(t\right)<0$.

Lemma 5.

Under the assumptions of Lemma 3, letting $x\in \overline{\mathsf{\Omega }}$, and any $\rho >0$ such that (i) $B(x,\rho )\subset {\mathsf{\Omega }}^{\circ }$, if $x\in {\mathsf{\Omega }}^{\circ }$; or (ii) $B(y,\rho )\cap \partial \mathsf{\Omega }=\left\{x\right\}$, $B(y,\rho )\subset \mathsf{\Omega }$ where $y\in {\mathsf{\Omega }}^{\circ }$ is fixed, if $x\in \partial \mathsf{\Omega }$; and $C_3>0$ is a constant, it holds that

$$\begin{array}{c}{\displaystyle \underset{x\in K_{\rho }}{sup}[G_1\left(t\right)-u(x,t)]\le \frac{C_3}{{\rho }^N}(1+H_1\left(t\right)),}\\ {\displaystyle \underset{x\in K_{\rho }}{sup}[G_2\left(t\right)-v(x,t)]\le \frac{C_3}{{\rho }^N}(1+H_2\left(t\right)),}\end{array}$$

(65)

in $\mathsf{\Omega }\times [\frac{T^{*}}{2},T^{*}-\epsilon ]$, for all $\epsilon >0$, where $K_{\rho }=B(x,\rho )($or $B(y,\rho ))$.

Proof. 

Case (i). Let $z(x,t)=G_1\left(t\right)-u(x,t)$, $c_0=0$ in (33) and ${\displaystyle \beta \left(t\right)={\int }_{\mathsf{\Omega }}z(x,t)\phi \left(x\right)dx}$. By Green’s formula, we have

$$\begin{array}{cc}\hfill {\beta }^{\prime }\left(t\right)& {\displaystyle ={\int }_{\mathsf{\Omega }}(F_1\left(t\right)-u_t(x,t))\phi \left(x\right)dx=-{\int }_{\mathsf{\Omega }}\phi \left(x\right)\mathsf{\Delta }udx}\hfill \\ \hfill & {\displaystyle =-{\int }_{\mathsf{\Omega }}u(x,t)\mathsf{\Delta }\phi dx+K_1\left(t\right)}\hfill \\ \hfill & {\displaystyle =\lambda {\int }_{\mathsf{\Omega }}u(x,t)\phi \left(x\right)dx+K_1\left(t\right)}\hfill \\ \hfill & =-\lambda \beta +\lambda G_1\left(t\right)+K_1\left(t\right).\hfill \end{array}$$

(66)

Solving this ODE, we have

$$\begin{array}{cc}\hfill \beta \left(t\right)& {\displaystyle =\beta \left(0\right)e^{-\lambda t}+{\int }_0^t{e}^{-\lambda (t-s)}(K_1\left(s\right)+\lambda G_1\left(s\right))}\hfill \\ \hfill & {\displaystyle \le \beta \left(0\right)e^{-\lambda t}+\lambda {\int }_0^t{e}^{-\lambda (t-s)}{G}_1\left(s\right)ds}\hfill \\ \hfill & \le C(1+H_1\left(t\right)).\hfill \end{array}$$

(67)

On the other hand, Lemma 4 implies

$$\underset{\mathsf{\Omega }}{inf}z(x,t)\ge -C_2$$

(68)

when $t\in [\frac{T^{*}}{2},T^{*}-\epsilon ]$ for all $\epsilon >0$, which, combined with Equation (67), implies

$${\displaystyle {\int }_{\mathsf{\Omega }}\left|z(x,t)\right|\phi \left(x\right)dx\le C^{\prime }(1+H_1\left(t\right)).}$$

(69)

Further, by Lemma 3, we have

$$-\mathsf{\Delta }z\le -C_1\le 0.$$

(70)

Fixing $K_{\rho }$, whose center is noted as x, the function $z(y,t)$, $y\in K_{\rho }\subset {\mathsf{\Omega }}^{\circ }$ is a subharmonic implied by (70). Applying the mean-value inequality for subharmonic functions, it follows that

$${\displaystyle z(x,t)\le \frac{1}{|K_{\rho }|}{\int }_{K_{\rho }}z(y,t)dy\le \frac{1}{|K_{\rho }|}{\int }_{K_{\rho }}\left|z(y,t)\right|dy.}$$

(71)

We know that ${inf}_{K_{\rho }}\phi \ge c_0^{\prime }$, where $c_0^{\prime }>0$ is related to the distance from $\partial \mathsf{\Omega }$, which, together with (69) and (71), can imply that

$${\displaystyle z(x,t)\le \frac{C^{\prime }}{{\rho }^N}{\int }_{K_{\rho }}\left|z(y,t)\right|\phi \left(y\right)dy\le \frac{C^{\prime }}{{\rho }^N}(1+H_1\left(t\right)).}$$

(72)

Similarly, it follows that

$${\displaystyle G_2\left(t\right)-v(x,t)\le \frac{C^{″}}{{\rho }^N}(1+H_2\left(t\right)).}$$

(73)

Selecting $C_3\ge max\{C^{\prime },C^{″}\}$, Case (i) can be proved.

Case (ii). Letting $c_0>0$ in (33), considering the mean value theorem, (66) and (67) are transformed into

$${\beta }^{\prime }\left(t\right)=-\lambda \beta +\lambda G_1\left(t\right)+K_1\left(t\right)+c_0{\int }_{\partial \mathsf{\Omega }}\left(-\frac{\partial u}{\partial \mathit{n}}\right)dS,$$

(74)

and

$$\begin{array}{cc}\hfill \beta \left(t\right)& {\displaystyle =\beta \left(0\right)e^{-\lambda t}+{\int }_0^t{e}^{-\lambda (t-s)}\left(K_1\left(s\right)+\lambda G_1\left(s\right)+c_0{\int }_{\partial \mathsf{\Omega }}\left(-\frac{\partial u(x,s)}{\partial \mathit{n}}\right)dS\right)ds}\hfill \\ \hfill & {\displaystyle \le \beta \left(0\right)e^{-\lambda t}+{\int }_0^t{e}^{-\lambda (t-s)}\left(c_0{\int }_{\mathsf{\Omega }}(-\mathsf{\Delta }u(x,s))dx+\lambda G_1\left(s\right)\right)ds}\hfill \\ \hfill & {\displaystyle =\beta \left(0\right)e^{-\lambda t}+{\int }_0^t{e}^{-\lambda (t-s)}\left(-c_0\left|\mathsf{\Omega }\right|\mathsf{\Delta }u(x_0,s)+\lambda G_1\left(s\right)\right)ds}\hfill \\ \hfill & \le C\left({\displaystyle 1+H_1\left(t\right)-{\int }_0^t\mathsf{\Delta }u(x_0,s)ds}\right).\hfill \end{array}$$

(75)

where $x_0\in {\mathsf{\Omega }}^{\circ }$, respectively. Similarly, since ${inf}_{K_{\rho }}\ge c_0>0$ and $z(y,t)$, $y\in K_{\rho }\subset \overline{\mathsf{\Omega }}$ is a subharmonic function. Lemma 3 deduces that ${\int }_0^t\mathsf{\Delta }uds$ is bounded on $\mathsf{\Omega }\times (\frac{T^{*}}{2},T^{*}-\epsilon ]$ for all $\epsilon >0$, so it follows that

$${\displaystyle z(x,t)\le \frac{C^{\prime }}{{\rho }^N}{\int }_{K_{\rho }}\left|z(y,t)\right|\phi \left(y\right)dy\le \frac{C^{\prime }}{{\rho }^N}(1+H_1\left(t\right)),}$$

(76)

too. Choosing sufficiently large $C_3$, Lemma 5 is proved completely. □

Lemma 6.

Under the assumptions of Lemma 3, we have that

$$\begin{array}{cc}\hfill \underset{t\to T^{*}}{lim\; sup}\underset{x\in \overline{\mathsf{\Omega }}}{min}u(x,t)=+\infty ,& {\displaystyle \underset{t\to T^{*}}{lim\; sup}\underset{x\in \overline{\mathsf{\Omega }}}{min}v(x,t)=+\infty }\end{array}$$

(77)

if and only if

$$\begin{array}{cc}\hfill \underset{t\to T^{*}}{lim}{G}_1\left(t\right)=+\infty ,& {\displaystyle \underset{t\to T^{*}}{lim}{G}_2\left(t\right)=+\infty .}\end{array}$$

(78)

Further, if (77) or (78) is fulfilled, then

$$\begin{array}{c}{\displaystyle \underset{t\to T^{*}}{lim}\frac{u(x,t)}{G_1\left(t\right)}=\underset{t\to T^{*}}{lim}\frac{{\parallel u\left(t\right)\parallel }_{\infty }}{G_1\left(t\right)}=1,}\\ {\displaystyle \underset{t\to T^{*}}{lim}\frac{v(x,t)}{G_2\left(t\right)}=\underset{t\to T^{*}}{lim}\frac{{\parallel v\left(t\right)\parallel }_{\infty }}{G_2\left(t\right)}=1,}\end{array}$$

(79)

uniformly on $\overline{\mathsf{\Omega }}$.

Proof. 

(77) ⇒ (78) is a simple corollary of Lemma 4. Assuming (78) holds, we use the method in [10]. According to Lemma 5 Case (i), for any fixed $K_{\rho }\subset {\mathsf{\Omega }}^{\circ }$, combining Lemma 4 and $G_1\left(t\right),G_2\left(t\right)>0$ yields

$$\begin{array}{c}{\displaystyle -\frac{C_2}{G_1\left(t\right)}\le 1-\frac{u(x,t)}{G_1\left(t\right)}\le \frac{C_3}{{\rho }^N}\frac{1+H_1\left(t\right)}{G_1\left(t\right)},}\\ {\displaystyle -\frac{C_2}{G_2\left(t\right)}\le 1-\frac{v(x,t)}{G_2\left(t\right)}\le \frac{C_3}{{\rho }^N}\frac{1+H_2\left(t\right)}{G_2\left(t\right)}.}\end{array}$$

(80)

Since $G_1$, $G_2$ are increasing, it follows that for all $\epsilon >0$,

$$\begin{array}{c}{\displaystyle 0\le \frac{1+H_1\left(t\right)}{G_1\left(t\right)}\le \frac{{\int }_0^{T^{*}-\epsilon }{G}_1\left(s\right)ds}{G_1\left(t\right)}+\epsilon ,}\\ {\displaystyle 0\le \frac{1+H_2\left(t\right)}{G_2\left(t\right)}\le \frac{{\int }_0^{T^{*}-\epsilon }{G}_2\left(s\right)ds}{G_2\left(t\right)}+\epsilon ,}\end{array}$$

(81)

which, together with $G_1\left(t\right)$, $G_2\left(t\right)\to +\infty$ implies that $\underset{t\to T^{*}}{lim}\frac{H_i\left(t\right)}{G_i\left(t\right)}=0,i=1,2$.

$${\displaystyle \underset{t\to T^{*}}{lim}\frac{u(x,t)}{G_1\left(t\right)}=\underset{t\to T^{*}}{lim}\frac{v(x,t)}{G_2\left(t\right)}=1}$$

(82)

on $K_{\rho }$ is deduced.

Integrating the first two equations in (1) from 0 to t, we have

$$\left\{\begin{array}{cc}{\displaystyle u(x,t)-{\int }_0^t\mathsf{\Delta }u(x,s)ds-u_0\left(x\right)=G_1\left(t\right),}\hfill & (x,t)\in K_{\rho }\times [\frac{T^{*}}{2},T^{*})\hfill \\ {\displaystyle v(x,t)-{\int }_0^t\mathsf{\Delta }v(x,s)ds-v_0\left(x\right)=G_2\left(t\right),}\hfill & (x,t)\in K_{\rho }\times [\frac{T^{*}}{2},T^{*}).\hfill \end{array}\right.$$

(83)

Since (82), we know that

$${\displaystyle \underset{t\to T^{*}}{lim}\frac{{\int }_0^t\mathsf{\Delta }uds}{G_1\left(t\right)}=\underset{t\to T^{*}}{lim}\frac{{\int }_0^t\mathsf{\Delta }vds}{G_2\left(t\right)}=0.}$$

(84)

On the other hand, according to Lemma 4, it follows that $F_1\left(t\right)$, $F_2\left(t\right)>0$; that is,

$$\begin{array}{cc}\hfill u_t-\mathsf{\Delta }u>0,& v_t-\mathsf{\Delta }v>0.\end{array}$$

Applying the maximum principle, we know that the solution $(u,v)$ can take the minimum in $\partial \mathsf{\Omega }$. For all $x\in \overline{\mathsf{\Omega }}$, combining Lemmas 4 and 5 Case (ii) and $G_1\left(t\right),G_2\left(t\right)>0$, there exists a fixed $K_{\rho }\subset \overline{\mathsf{\Omega }}$ such that

$$\begin{array}{c}{\displaystyle -\frac{C_2}{G_1\left(t\right)}\le 1-\frac{u(x,t)}{G_1\left(t\right)}\le \frac{C_3}{{\rho }^N}\frac{1+H_1\left(t\right)-{\int }_0^t\mathsf{\Delta }u(x_{01},s)ds}{G_1\left(t\right)},}\\ {\displaystyle -\frac{C_2}{G_2\left(t\right)}\le 1-\frac{v(x,t)}{G_2\left(t\right)}\le \frac{C_3}{{\rho }^N}\frac{1+H_2\left(t\right)-{\int }_0^t\mathsf{\Delta }v(x_{02},s)ds}{G_2\left(t\right)}.}\end{array}$$

(85)

where $x_{01}$, $x_{02}\in {\mathsf{\Omega }}^{\circ }$. Since $\underset{t\to T^{*}}{lim}\frac{H_i\left(t\right)}{G_i\left(t\right)}=0$, $i=1,2$ and (84), (85) can imply (79) uniformly on $\overline{\mathsf{\Omega }}$. Further, we obtain

$$\begin{array}{c}\hfill {\displaystyle \underset{t\to T^{*}}{lim\; sup}\underset{x\in \overline{\mathsf{\Omega }}}{min}u(x,t)=\underset{t\to T^{*}}{lim\; sup}\underset{x\in \partial \mathsf{\Omega }}{min}u(x,t)=+\infty ,}\\ \hfill {\displaystyle \underset{t\to T^{*}}{lim\; sup}\underset{x\in \overline{\mathsf{\Omega }}}{min}v(x,t)=\underset{t\to T^{*}}{lim\; sup}\underset{x\in \partial \mathsf{\Omega }}{min}v(x,t)=+\infty .}\end{array}$$

The proof of Lemma 6 is completed. □

Using the above lemmas and corollaries, we can obtain the following theorems describing blow-up solutions by the same method as in [8,21]. Theorems 4 and 5 give the necessary and sufficient conditions that u, v blow up simultaneously. Further, Theorem 6 describes the blow-up profile of (1) when u, v blow up simultaneously.

Theorem 4.

Assuming (H1)–(H3) hold, $\mathsf{\Delta }{u}_0$, $\mathsf{\Delta }{v}_0<0$, $g_1$, $g_2$ are derivable. Let $(u,v)$ be a classical solution to problem 1. If u and v blow up in a finite time $T^{*}$ simultaneously, then (i) $p\ge m-1$ and $n\ge q-1$, or (ii) $p<m-1$ and $n<q-1$ must be satisfied.

Theorem 5.

Under the assumption of Theorem 4. Let $(u,v)$ be a classical blow-up solution to problem 1. If $p\ge m-1>0$ and $n\ge q-1>0$, then u and v blow up simultaneously and uniformly.

Theorem 6.

Under the assumption of Theorem 4, the following results hold uniformly on $\overline{\mathsf{\Omega }}$:

(i) 

if (a) $n>q-1$, $p>m-1$ or (b) $n<q-1$, $p<m-1$, then we have

$$\left\{\begin{array}{c}{\displaystyle \underset{t\to T^{*}}{lim}u(x,t){(T^{*}-t)}^{\theta }=\underset{t\to T^{*}}{lim}{\parallel u\left(t\right)\parallel }_{\infty }{(T^{*}-t)}^{\theta }={\left(\frac{k_1\left|\mathsf{\Omega }\right|}{\theta }{\left(\frac{k_2}{k_1}\frac{\theta }{\sigma }\right)}^{\frac{n}{n+1-q}}\right)}^{-\theta },}\hfill \\ {\displaystyle \underset{t\to T^{*}}{lim}v(x,t){(T^{*}-t)}^{\sigma }=\underset{t\to T^{*}}{lim}{\parallel v\left(t\right)\parallel }_{\infty }{(T^{*}-t)}^{\sigma }={\left(\frac{k_2\left|\mathsf{\Omega }\right|}{\sigma }{\left(\frac{k_1}{k_2}\frac{\sigma }{\theta }\right)}^{\frac{p}{p+1-m}}\right)}^{-\sigma },}\hfill \end{array}\right.$$

where

$$\begin{array}{cc}\hfill {\displaystyle \theta =\frac{n+1-q}{np-(m-1)(q-1)},}& {\displaystyle \sigma =\frac{p+1-m}{np-(m-1)(q-1)};}\end{array}$$

(ii) 

if $p=m-1>0$ and $n>q-1>0$, then we have

$$\left\{\begin{array}{c}{\displaystyle \underset{t\to T^{*}}{lim}{u}^p(x,t){[lnu(x,t)]}^{\frac{n}{n+1-q}}(T^{*}-t)=(p{k}_1{\left|\mathsf{\Omega }\right|)}^{-1}{\left[\frac{k_2(n+1-q)}{k_1}\right]}^{-\frac{n}{n+1-q}},}\hfill \\ {\displaystyle \underset{t\to T^{*}}{lim}{v}^{n+1-q}{|ln(T^{*}-t)|}^{-1}=\frac{k_2}{k_1}\frac{n+1-q}{p};}\hfill \end{array}\right.$$

(iii) 

if $p>m-1>0$ and $n=q-1>0$, then we have

$$\left\{\begin{array}{c}{\displaystyle \underset{t\to T^{*}}{lim}{u}^{p+1-m}(x,t){|ln(T^{*}-t)|}^{-1}=\frac{k_1}{k_2}\frac{p+1-m}{n},}\hfill \\ {\displaystyle \underset{t\to T^{*}}{lim}{v}^n(x,t){[lnv(x,t)]}^{\frac{p}{p+1-m}}(T^{*}-t)=(n{k}_2{\left|\mathsf{\Omega }\right|)}^{-1}{\left[\frac{k_1(p+1-m)}{k_2}\right]}^{-\frac{p}{p+1-m}};}\hfill \end{array}\right.$$

(iv) 

if $p=m-1>0$ and $n=q-1>0$, then we have

$$\left\{\begin{array}{c}{\displaystyle \underset{t\to T^{*}}{lim}\frac{lnu(x,t)}{|ln(T^{*}-t\left)\right|}=\underset{t\to T^{*}}{lim}\frac{{\parallel lnu\left(t\right)\parallel }_{\infty }}{|ln(T^{*}-t\left)\right|}=\frac{k_1}{p{k}_1+n{k}_2},}\hfill \\ {\displaystyle \underset{t\to T^{*}}{lim}\frac{lnv(x,t)}{|ln(T^{*}-t\left)\right|}=\underset{t\to T^{*}}{lim}\frac{{\parallel lnv\left(t\right)\parallel }_{\infty }}{|ln(T^{*}-t\left)\right|}=\frac{k_2}{p{k}_1+n{k}_2}.}\hfill \end{array}\right.$$

(86)

The proofs of Theorems 4–6 are very similar to [8]; we only need to pay attention to the constants $k_1$, $k_2$, so we only give the proof by taking Theorem 6 Case (i) as an example, and omit the others.

Proof of Theorem 6 Case (i).

We have

$${\displaystyle G_1^{\prime }\left(t\right)=F_1\left(t\right)=k_1{\int }_{\mathsf{\Omega }}{u}^m(x,t)v^n(x,t)dx\sim k_1\left|\mathsf{\Omega }\right|G_1^m\left(t\right)G_2^n\left(t\right),}$$

(87)

$${\displaystyle G_2^{\prime }\left(t\right)=F_2\left(t\right)=k_2{\int }_{\mathsf{\Omega }}{u}^p(x,t)v^q(x,t)dx\sim k_2\left|\mathsf{\Omega }\right|G_1^p\left(t\right)G_2^q\left(t\right),}$$

(88)

it follows that

$$k_2{G}_1^{p-m}\left(t\right)d{G}_1\sim k_1{G}_2^{n-q}\left(t\right)d{G}_2.$$

(89)

When $n>q-1$ and $p>m-1$, integrating (89) from 0 to t, yields $\frac{k_2}{p+1-m}{G}_1^{p+1-m}\left(t\right)\sim \frac{k_1}{n+1-q}{G}_2^{n+1-q}\left(t\right)$. That is,

$$k_2(n+1-q)G_1^{p+1-m}\left(t\right)\sim k_1(p+1-m)G_2^{n+1-q}\left(t\right).$$

(90)

While $n<q-1$ and $p<m-1$, since $\underset{t\to T^{*}}{lim}{G}_i=+\infty$, $i=1,2$, integrating (89) from t to $T^{*}$, we have

$$k_2(n+1-q)G_1^{p+1-m}\left(t\right)\sim k_1(p+1-m)G_2^{n+1-q}\left(t\right),$$

(91)

similarly. By (87) and (90), we find

$$\begin{array}{cc}\hfill {\displaystyle G_1^{\prime }\left(t\right)}& \sim k_1\left|\mathsf{\Omega }\right|{\left[\frac{k_2(n+1-q)}{k_1(p+1-m)}\right]}^{\frac{n}{n+1-q}}{G}_1^{m+\frac{n(p+1-m)}{n+1-q}}\left(t\right)\hfill \\ \hfill & {\displaystyle =k_1\left|\mathsf{\Omega }\right|{\left(\frac{k_2}{k_1}\frac{\theta }{\sigma }\right)}^{\frac{n}{n+1-q}}{G}_1^{m+\frac{n\sigma }{\theta }}\left(t\right).}\hfill \end{array}$$

(92)

Since $1-m-\frac{n\sigma }{\theta }=-\frac{1}{\theta }<0$ and $\underset{t\to T^{*}}{lim}{G}_1\left(t\right)=+\infty$, integrating (92) from t to $T^{*}$, we obtain

$${\displaystyle G_1\left(t\right)\sim {\left(\frac{k_1\left|\mathsf{\Omega }\right|}{\theta }{\left(\frac{k_2}{k_1}\frac{\theta }{\sigma }\right)}^{\frac{n}{n+1-q}}(T^{*}-t)\right)}^{-\theta }.}$$

(93)

According to (93) and Lemma 6, it follows that uniformly on $\overline{\mathsf{\Omega }}$,

$${\displaystyle u(x,t)\sim {\parallel u\left(t\right)\parallel }_{\infty }\sim {\left(\frac{k_1\left|\mathsf{\Omega }\right|}{\theta }{\left(\frac{k_2}{k_1}\frac{\theta }{\sigma }\right)}^{\frac{n}{n+1-q}}(T^{*}-t)\right)}^{-\theta },}$$

that is,

$${\displaystyle \underset{t\to T^{*}}{lim}u(x,t){(T^{*}-t)}^{\theta }=\underset{t\to T^{*}}{lim}{\parallel u\left(t\right)\parallel }_{\infty }{(T^{*}-t)}^{\theta }={\left(\frac{k_1\left|\mathsf{\Omega }\right|}{\theta }{\left(\frac{k_2}{k_1}\frac{\theta }{\sigma }\right)}^{\frac{n}{n+1-q}}\right)}^{-\theta }}$$

holds uniformly on $\overline{\mathsf{\Omega }}$.

Combining (88) and (91), and applying the same proofs of $G_2$ and v, we obtain that

$${\displaystyle \underset{t\to T^{*}}{lim}v(x,t){(T^{*}-t)}^{\sigma }=\underset{t\to T^{*}}{lim}{\parallel v\left(t\right)\parallel }_{\infty }{(T^{*}-t)}^{\sigma }={\left(\frac{k_2\left|\mathsf{\Omega }\right|}{\sigma }{\left(\frac{k_1}{k_2}\frac{\sigma }{\theta }\right)}^{\frac{p}{p+1-m}}\right)}^{-\sigma }}$$

holds uniformly on $\overline{\mathsf{\Omega }}$. □

5. Numerical Simulations

In this section, we give numerical simulations for several specific cases to illustrate Theorems 2 and 3. All calculations are performed through Mathematica.

Firstly, letting $m=0.2$, $n=0.5$, $p=q=0.3$ and $T=10$, we obtain problem (1) of the following form

$$\left\{\begin{array}{cc}{\displaystyle u_t=\mathsf{\Delta }u+{\int }_{\mathsf{\Omega }}{u}^{0.2}(t,x,y)v^{0.5}(t,x,y)d\sigma ,}\hfill & (t,x,y)\in (0,10)\times \mathsf{\Omega },\hfill \\ {\displaystyle v_t=\mathsf{\Delta }v+{\int }_{\mathsf{\Omega }}{u}^{0.3}(t,x,y)v^{0.3}(t,x,y)d\sigma ,}\hfill & (t,x,y)\in (0,10)\times \mathsf{\Omega },\hfill \\ \mathit{n}·\nabla u+u^2=\mathit{n}·\nabla v+v^{1.5}=0,\hfill & (t,x,y)\in (0,10)\times \partial \mathsf{\Omega },\hfill \\ {\displaystyle u(0,x,y)=v(0,x,y)=1-\frac{1}{2}(x^2+y^2),}\hfill & (x,y)\in \mathsf{\Omega },\hfill \end{array}\right.$$

(94)

where $\mathsf{\Omega }=\{(x,y):x^2+y^2\le 1\}$. Because of the symmetry, we only need to simulate the values of its solution on $0\le x\le 1$ as shown below.

In this case, $g_1\left(u\right)=u$, $g_2\left(v\right)=v^{\frac{1}{2}}$ satisfies (H2) and (H3); since ${\displaystyle u_0(x,y)=v_0(x,y)=1-\frac{1}{2}(x^2+y^2)>0}$,

$${\displaystyle \frac{\partial u_0}{\partial \mathit{n}}=\frac{\partial v_0}{\partial \mathit{n}}=(x,y)·(-x,-y)=-(x^2+y^2)=-1<0,}$$

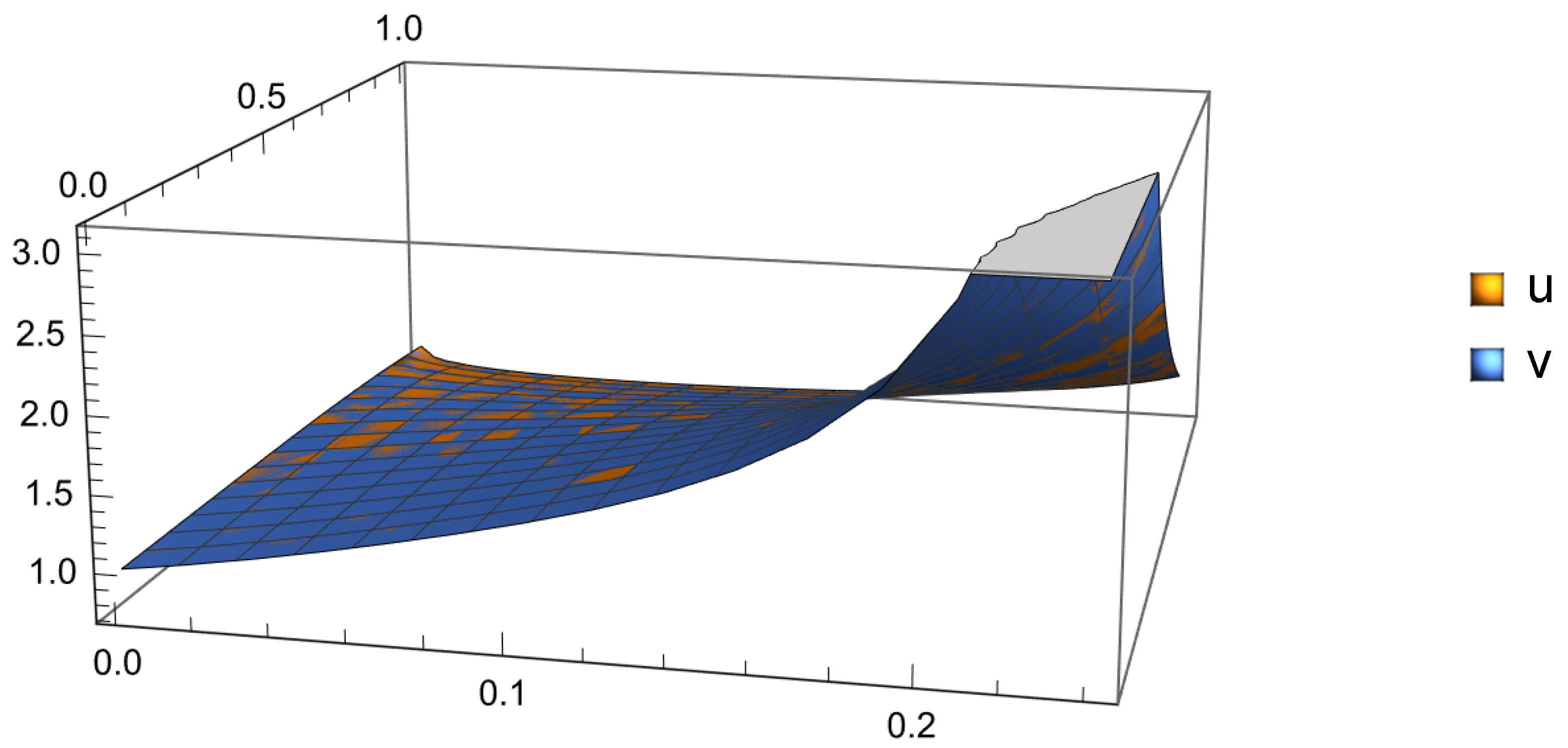
Further, (94) satisfies (H1) and $m=0.2<1$, $p=0.3<1$, $nq=0.15\le 0.56=(1-m)(1-p)$. Therefore, (94) satisfies the conditions of Theorem 2, so its solution should exist globally, which can be illustrated by Figure 1.

Next, we present a numerical simulation to illustrate the blow-up profiles using Mathematica. As stated in Theorem 3, we consider problem (1) in the following form satisfying (40):

$$\left\{\begin{array}{cc}{\displaystyle u_t=\mathsf{\Delta }u+{\int }_{\mathsf{\Omega }}{u}^{1.2}(t,x,y)v^{0.4}(t,x,y)d\sigma ,}\hfill & (t,x,y)\in (0,T^{*})\times \mathsf{\Omega },\hfill \\ {\displaystyle v_t=\mathsf{\Delta }v+{\int }_{\mathsf{\Omega }}{u}^{0.3}(t,x,y)v^{1.3}(t,x,y)d\sigma ,}\hfill & (t,x,y)\in (0,T^{*})\times \mathsf{\Omega },\hfill \\ \mathit{n}·\nabla u+u^2=\mathit{n}·\nabla v+v^{1.5}=0,\hfill & (t,x,y)\in (0,T^{*})\times \partial \mathsf{\Omega },\hfill \\ {\displaystyle u(0,x,y)=v(0,x,y)=1-\frac{1}{12}(x^4+y^4),}\hfill & (x,y)\in \mathsf{\Omega },\hfill \end{array}\right.$$

(95)

where $\mathsf{\Omega }=\{(x,y):x^2+y^2\le 1\}$ and $T^{*}$ is the blow-up time that will be given by the numerical simulation. In this case, the initial values satisfy

$${\displaystyle \frac{\partial u_0}{\partial \mathit{n}}=\frac{\partial v_0}{\partial \mathit{n}}=(x,y)·(-\frac{1}{3}{x}^3,-\frac{1}{3}{y}^3)=-\frac{1}{3}(x^4+y^4)<0}$$

and

$$\mathsf{\Delta }{u}_0=\mathsf{\Delta }{v}_0=-(x^2+y^2)<0.$$

According to Theorem 3, we know that the solution to (95) blows up in a finite time. Without loss of generality, we take as an example the value of function u when $t\in (0,0.979)$, $x\in [0,1]$, $y=0$, as in Figure 2.

As expected, Since (95) satisfies $p\ge m-1>0$ and $n\ge q-1>0$, the solution $(u,v)$ blows up at approximately $T^{*}=0.979$, simultaneously. We take m = 1.2, n = 0.5, p = 1.3, q = 0.3 and replace the initial value conditions with

$${\displaystyle u_0(x,y)=v_0(x,y)=\frac{1}{4}-\frac{1}{48}(x^4+y^4),}$$

which does not satisfy that $u_0\left(x\right),v_0\left(x\right)$ are sufficiently large in Theorem 3. We resolve the solution $(u,v)$ of problem (95) (see Figure 3).

Figure 3 shows that when the initial values are very small, the solution $(u,v)$ does not blow up even if (40) is satisfied. Then, we change the values of m, n, p and q in (95) and perform numerical simulations for the rest of the cases mentioned in Theorem 6. This is shown in Figure 4, Figure 5, Figure 6 and Figure 7.