A Novel Integrated Heuristic Optimizer Using a Water Cycle Algorithm and Gravitational Search Algorithm for Optimization Problems

Abstract

This paper presents a novel composite heuristic algorithm for global optimization by organically integrating the merits of a water cycle algorithm (WCA) and gravitational search algorithm (GSA). To effectively reinforce the exploration and exploitation of algorithms and reasonably achieve their balance, a modified WCA is first put forward to strengthen its search performance by introducing the concept of the basin, where the position of the solution is also considered into the assignment of the sea or river and its streams, and the number of the guider solutions is adaptively reduced during the search process. Furthermore, the enhanced WCA is adaptively cooperated with the gravitational search to search for new solutions based on their historical performance within a certain stage. Moreover, the binomial crossover operation is also incorporated after the water cycle search or the gravitational search to further improve the search capability of the algorithm. Finally, the performance of the proposed algorithm is evaluated by comparing with six excellent meta-heuristic algorithms on the IEEE CEC2014 test suite, and the numerical results indicate that the proposed algorithm is very competitive.

1. Introduction

With the development of science and technology, global optimization problems can be found in almost all applications, and have attracted great interest from researchers [1,2,3,4,5]. In order to deal with these real problems satisfactorily, many meta-heuristic algorithms have been presented by the inspiration of natural phenomena, animal behaviours, human activities and physical criteria, such as particle swarm optimization (PSO) [6], genetic algorithm (GA) [7], differential evolution (DE) [8], ant colony optimization [9], fireworks algorithm (FA) [10], joint operations algorithm [11], squirrel search algorithm [12], gaining–sharing knowledge-based algorithm [13], and so on. Specifically, more nature-inspired approaches can be further found in the literature [14]. As we all know, these approaches have been proved to be accurate, reasonably fast and robust optimizers, and have been applied in many fields, including pattern recognition [15], feature selection [16], image processing [17], multitask optimization [18], multimodal optimization [19], and data clustering [20]. However, they still do not guarantee the convergence to the global optimum, especially for complicated problems [21,22]. Hence, it is necessary to study more promising versions for them.

Since the performance of each heuristic optimization algorithm heavily depends on its balance between exploration and exploitation of the search space, many variants of the classical algorithms and hybrid algorithms have been developed by incorporating new mechanisms or combining with other approaches [23,24,25,26,27,28,29,30,31,32,33,34,35,36]. For example, Yan and Tian [25] presented an enhanced adaptive DE variant, with respect to the classical DE algorithm, by making full use of the information of the current individual, its best neighbour and a randomly selected neighbour to predict the promising region around it. Li et al. [26] proposed a novel integrated DE algorithm by dividing the population into the leader and adjoint sub-populations based on a leader–adjoint model and, respectively, adopting two mutation strategies for them. For the particle swarm optimization algorithm, to integrate the advantages of the update strategies from different PSO variants, Xu et al. [27] developed a strategy learning framework to learn an optimal combination of strategies. For the gravitational search algorithm, Sun et al. [23] improved its search performance by learning from the unique neighbourhood and historically global best agent to avoid premature convergence and high runtime consumption. Moreover, by integrating the benefits of the genetic algorithm and particle swarm optimization algorithm, Yu et al. [24] developed a hybrid GAPSO algorithm and applied it to the integration of process planning and scheduling. To further improve the search ability of the fireworks optimization method, Zheng et al. [29] additionally incorporated some differential evolution operators into the framework of the fireworks optimization method, and proposed a hybrid fireworks optimization method. Through properly introducing the search operations of differential evolutions in the cultural algorithm and particle swarm optimization algorithm, Awad et al. [30] and Zuo et al. [28], respectively, put forward a novel hybrid algorithm. Furthermore, by incorporating a local pattern search method into a water cycle algorithm to enhance its convergence speed, Taib et al. [34] presented a hybrid water cycle algorithm for data clustering, while by introducing a reinforcement learning technique into the framework of the particle swarm optimization algorithm, Li et al. [36] proposed an enhanced PSO variant for global optimization problems, where a neighbourhood differential mutation operator is also employed to increase the diversity of the algorithm. Thereby, designing new strategies and combining different approaches or algorithms is still an effective and popular way to enhance the performance of an algorithm.

In last decade, the gravitational search algorithm (GSA) [37] and water cycle algorithm (WCA) [38] were proposed to solve the optimization problem according to the Newton’s law of gravity and motion and the water cycle phenomenon, respectively. In particular, the particles in the population, considered as objects and their performance are evaluated as their mass, absorb each other by the gravitational force in the GSA, while the total population is divided into streams, rivers and the sea according to their fitness values in the WCA, and the rivers and the sea are regarded as leaders to guide other points towards better points, thus avoiding the search in inappropriate regions. Since they were born, they have attracted more and more attention from researchers and been applied to different fields [39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. For instance, with respect to the water cycle algorithm, to strengthen its search performance, Sadollaha et al. [39] further developed the concept of evaporation and incorporated the evaporation procedures into the original WCA, while Heidari et al. [40] adopted a chaotic mapping to set its parameters. By considering and simulating the real-world percolation process, Qiao et al. [44] designed a percolation operator and then developed an improved WCA for clustering analysis. Meanwhile, by adding the solution mapping technique in the WCA, Osaba et al. [45] put forward a discrete WCA variant to solve the symmetric and asymmetric travelling salesman problem; moreover, by introducing two different surrogate modes, Chen et al. [52] proposed a novel water cycle algorithm for high-dimensional expensive optimization. Furthermore, in order to alleviate the low precision and slow convergence of the WCA, Ye et al. [53] further presented an enhanced version of the WCA based on quadratic interpolation, where a new non-linear adjustment strategy is designed for distance control parameters, mutation operations are probabilistically performed, and the quadratic interpolation operator is introduced to improve the local exploitation capability of the algorithm. Specifically, more detailed works on the improvements and applications of the WCA can be found in [48]. On the other hand, for the gravitational search algorithm, by introducing chaotic mappings to control the gravitational constants, Mirjalili and Gandomi [41] presented a chaotic GSA version; whereas Lei et al. [43] proposed a hierarchical gravitational search algorithm by adaptively adjusting the gravitational constants and introducing the population topology. Meanwhile, to alleviate the stagnation of the GSA, Oshi [50] put forward an enhanced GSA variant by incorporating chaos-embedded opposition-based learning into the basic GSA, introducing a sine–cosine-based chaotic mapping to set the gravitational constants. More detailed descriptions of recent GSA variants can be found in [49]. Noticeably, even though the WCA and GSA variants have been proven to be more effective than their original versions, the GSA versions still easily fall into local optima and become very costly when the particles are only guided by superior agents or too many agents, respectively; while the WCA variants have a poorer exploration ability in the search space since the processes of the streams flowing to their corresponding rivers and consequent sea are similar to the mutation in differential evolution [54]. Therefore, it is necessary to develop an improved version of them to effectively balance exploration and exploitation.

Based on above discussions, this paper presents a novel hybrid heuristic algorithm (HMWCA) by combining the water cycle algorithm and the gravitational search algorithm. To effectively enhance the search capability of the algorithm and obtain a better balance between exploration and exploitation, a modified WCA was first developed by designing a crude niching technique and using it to assign the sea, rivers and their corresponding streams in the WCA, and dynamically adjusting the total number of rivers and the sea in an adaptive manner. Furthermore, the resulting water cycle search and gravitational search were organically integrated to explore or exploit the search space by making full use of their history performance within certain iterations. Moreover, in order to further improve the search effectiveness of the algorithm, the binomial crossover operation was further incorporated after the gravitational search or modified water cycle search to adjust the transmission of the search information. Then, the HMWCA could not only effectively balance the exploration and exploitation, but also save the computing resources during the search process. Finally, numerical experiments were carried out to evaluate the performance of the HMWCA by comparing with six excellent meta-heuristic algorithms on 30 CEC2014 benchmark functions [55] with different dimensions, and the experimental results showed that the proposed algorithm was very competitive. Furthermore, the HMWCA was also applied to spread-spectrum radar polyphase code design (SSRPPCD) [56].

For clarity, compared with the existing works, the main contributions and novelties of this paper are listed below.

(1)

A crude niching technique was designed and adopted to define the sea, rivers and their corresponding streams in the WCA, and a non-linear setting was introduced to adjust the total number of rivers and the sea during the search process. Thereby, a modified WCA is presented, which could possess a better balance between exploration and exploitation.

(2)

To further strengthen the adaptivity and robustness of the algorithm for various search stages and problems, the resulting water cycle search and gravitational search were further integrated according to their history performance within certain iterations.

(3)

The binomial crossover operation was additionally introduced in the proposed algorithm when the gravitational search or modified water cycle search were executed. This might further promote control over the transmission of the search information.

Therefore, the proposed algorithm could have a more promising search performance.

The reminder of this paper is organized as follows. Section 2 gives brief descriptions of the classical gravitational search algorithm and water cycle algorithm. The proposed algorithm is presented in Section 3. Section 4 provides and discusses the experimental results against benchmark functions. Finally, conclusions are drawn in Section 5.

2. The Classical GSA and WCA

In this section, we shall simply describe the classical gravitational search algorithm and water cycle algorithm.

2.1. Gravitational Search Algorithm

According to the law of gravity and mass interaction, Rashedi et al. [37] proposed a new heuristic optimization algorithm, GSA, for optimization problems. In the GSA, agents are considered as objects and their performance are measured by their masses. All objects attract each other by a gravity force, thus leading to a global movement towards objects with heavier masses. For a minimization problem, $min\left\{f\left(X\right)\right|X=(x^1,x^2,\cdots ,x^D)\in \mathsf{\Omega }\}$, the concrete steps of the GSA can be described as follows. Herein, $\mathsf{\Omega }$ is the search space, and D are the dimensions of $\mathsf{\Omega }$,

Consider a system with $N_{pop}$ objects, and $X_i=(x_i^1,x_i^2,\cdots ,x_i^D)$ ($i=1,2,\cdots ,N_{pop}$) is the position of the ith object with $x_i^d$ being its d-th dimension, the gravitational force from agent j on agent i at a specific time t is defined as:

$$\begin{array}{c}\hfill F_{ij}^d\left(t\right)=G\left(t\right)\frac{M_{pi}\left(t\right)\times M_{aj}\left(t\right)}{R_{ij}\left(t\right)+\epsilon }[x_j^d\left(t\right)-x_i^d\left(t\right)],\end{array}$$

(1)

where $M_{aj}\left(t\right)$ is the active gravitational mass related to agent j, $M_{pi}\left(t\right)$ is the passive gravitational mass related to agent i, $\epsilon >0$ is a small constant, $R_{ij}\left(t\right)$ is the Euclidean distance between the agents i and j, and $G\left(t\right)$ is the gravitational constant at time t.

The total force acting on agent i in the d-th dimension is a randomly weighted sum of d-th components of the forces exerted from other agents:

$$\begin{array}{c}\hfill F_i^d\left(t\right)=\sum _{j=1,j\ne i}^{N_{pop}}ran{d}_j{F}_{ij}^d\left(t\right),\end{array}$$

(2)

where $ran{d}_j$ is a random number in the interval [0,1]. Then, the acceleration $a_i^d\left(t\right)$ is given by

$$\begin{array}{c}\hfill a_i^d\left(t\right)=\frac{F_i^d\left(t\right)}{M_{ii}\left(t\right)}\end{array}$$

(3)

where $M_{ii}\left(t\right)$ is the mass of object i. The velocity and position of agent i are, respectively, calculated by

$$\begin{array}{c}\hfill v_i^d(t+1)=rand\times v_i^d\left(t\right)+a_i^d\left(t\right)\end{array}$$

(4)

and

$$\begin{array}{c}\hfill x_i^d(t+1)=x_i^d\left(t\right)+v_i^d(t+1)\end{array}$$

(5)

where $d=1,2,\cdots ,D$, and $rand\in [0,1]$ is a random number subjected to uniform distribution.

Moreover, the masses of objects are calculated by the following equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{M}_{aj}=M_{pi}=M_{ii}=M_i,\hfill \\ m_i\left(t\right)=\frac{fi{t}_i\left(t\right)-worst\left(t\right)}{best\left(t\right)-worst\left(t\right)},\hfill \\ M_i\left(t\right)=\frac{m_i\left(t\right)}{{\displaystyle \sum _{i=1}^N}{m}_i\left(t\right)}\hfill \end{array}\right.\end{array}$$

(6)

where $i=1,2,\cdots ,N_{pop}$, $fi{t}_i\left(t\right)$ represents the fitness value of the ith object at time t, and $best\left(t\right)$ and $worst\left(t\right)$ are defined by:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}& {\displaystyle best\left(t\right)=\underset{i=1,2,\cdots ,N_{pop}}{min}fi{t}_i\left(t\right),}\hfill \\ & {\displaystyle worst\left(t\right)=\underset{i=1,2,\cdots ,N_{pop}}{max}fi{t}_i\left(t\right).}\hfill \end{array}\right.\end{array}$$

(7)

2.2. Water Cycle Algorithm

The water cycle algorithm (WCA) is a new meta-heuristic optimizer inspired by real-world observations of the water cycle and how rivers and streams flow downhill towards the sea [38]. Same as in Section 2.1, a minimization problem $min\left\{f\left(X\right)\right|X=(x^1,x^2,\cdots ,x^D)\in \mathsf{\Omega }\}$ is considered, where $\mathsf{\Omega }$ is the search space and D is the dimensions of $\mathsf{\Omega }$. Then the main contents of the WCA can be described as follows.

In the WCA, after the initialization of the population, the best individual is chosen as the sea, and a number of better streams are chosen as rivers. Thus, the population can be redefined as

$$Total poplution=\left[\begin{array}{c}Sea\\ Rive{r}_1\\ Rive{r}_2\\ ⋮\\ Strea{m}_{Nsr+1}\\ Strea{m}_{Nsr+2}\\ ⋮\\ Strea{m}_{N_{pop}}\end{array}\right]=\left[\begin{array}{cccc}{x}_1^1& x_1^2& \cdots & x_1^D\\ x_2^1& x_2^2& \cdots & x_2^D\\ ⋮& ⋮& ⋮& ⋮& \\ x_{N_{pop}}^1& x_{N_{pop}}^2& \cdots & x_{N_{pop}}^D\end{array}\right],$$

(8)

where $N_{pop}$ is the size of population, while the total number $N_{sr}$ of rivers and the sea and the number of streams can be computed by

$$\begin{array}{c}\hfill N_{sr}=NumberofRivers+\underset{sea}{\underbrace{1}},\end{array}$$

(9)

and

$$\begin{array}{c}\hfill N_{stream}=N_{pop}-N_{sr},\end{array}$$

(10)

respectively. Moreover, the cost of a raindrop is calculated as follows:

$$\begin{array}{c}\hfill Cos{t}_i=f\left(X_i\right),i=1,2,\cdots ,N_{pop},\end{array}$$

(11)

where $X_i=(x_i^1,x_i^2,\cdots ,x_i^D)$. Then the corresponding flow intensity of rivers and the sea are calculated by

$$\begin{array}{c}\hfill C_n=Cos{t}_n-Cos{t}_{N_{sr}+1},n=1,2,\cdots ,N_{sr},\end{array}$$

(12)

$$\begin{array}{c}\hfill N{S}_n=round\left\{\left|\frac{C_n}{{\displaystyle \sum _{i=1}^{N_{sr}}}{C}_i}\right|\times N_{stream}\right\},n=1,2,\cdots ,N_{sr},\end{array}$$

(13)

where $N{S}_n$ is the number of streams flowing to a specific river or sea. During the search process, the streams flowing to the sea and rivers, and the rivers flowing to the sea are, respectively, updated by the following equations:

$$\begin{array}{c}\hfill X_{stream}(t+1)=X_{stream}\left(t\right)+rand\times C\times (X_{sea}\left(t\right)-X_{stream}\left(t\right)),\end{array}$$

(14)

$$\begin{array}{c}\hfill X_{stream}(t+1)=X_{stream}\left(t\right)+rand\times C\times (X_{river}\left(t\right)-X_{stream}\left(t\right)),\end{array}$$

(15)

$$\begin{array}{c}\hfill X_{river}(t+1)=X_{river}\left(t\right)+rand\times C\times (X_{sea}\left(t\right)-X_{river}\left(t\right)),\end{array}$$

(16)

where t represents the number of the current iteration, and $1<C<2$ is a constant. In particular, when the new position is better than its corresponding river or sea, their positions will be exchanged.

Furthermore, as one of the most important procedures in the WCA, evaporation is used to prevent the algorithm from premature convergence, and its detail procedures can be described as follows.

(a) If $∥X_{sea}-X_{river,i}∥<d_{max}$, $i=1,2,\cdots ,N_{sr}-1$, then the raining process will be executed for its corresponding streams by

$$\begin{array}{c}\hfill X_{stream,new}=\overrightarrow{LB}+rand\times (\overrightarrow{UB}-\overrightarrow{LB}),\end{array}$$

(17)

where $LB$ and $UB$ are the lower and upper bounds of the search space, respectively.

(b) If the streams flowing to the sea are satisfied the above evaporation condition, then let

$$\begin{array}{c}\hfill X_{stream,new}=X_{sea}+\sqrt{\mu }\times randn(1,D),\end{array}$$

(18)

where the coefficient $\mu$ represents the concept of variance to show the range of searching regions around the best solution, $randn$ is a normally distributed random number, and $d_{max}$ is a small number close to zero to control the search intensity. To enhance the search near the sea, $d_{max}$ adaptively decreases as follows:

$$\begin{array}{c}\hfill d_{max}(t+1)=d_{max}\left(t\right)(1-\frac{1}{T})\end{array}$$

(19)

where T is the maximum number of iterations.

Overall, even though the GSA and WCA have promising performances for optimization problems and applied in actual optimization problems [37,38], the WCA easily becomes trapped into local optima since the streams and rivers always flow to few super individuals, while the GSA requires a large amount of computing resources, since each object is attracted by the sum of the forces exerted from other objects. Thereby, it is necessary to further develop a more promising optimizer.

3. Proposed Algorithm

As mentioned above, the GSA has a strong global search ability, while the WCA performs better in local searches. Consequently, we develop a novel hybrid algorithm (HMWCA) to balance exploration and exploitation by making full use of their advantages.

3.1. Modified WCA

Although the WCA has been broadly researched and successfully adopted to solve various real-world optimization problems [33,34,35,36,38,39,40,44,45,46,47,48,52,53], it still easily falls into premature convergence, especially for complicated functions. The reasons for this might be due to the fact that the number of rivers, streams and the sea in the original WCA are fixed during the whole search process once they are formed at the start of the algorithm. Obviously, it is not suitable for the search states to change. Moreover, the fitness values of the population are only taken into account to form the sea, rivers and their streams, which might lead to premature convergence since the superior individuals are crowded in general. To overcome these shortcomings, a modified WCA (MWCA) was proposed by simultaneously considering both the fitness values and positions of the population to design the sea, rivers and streams in the WCA and adjusting the total number of rivers and the sea in an adaptive manner.

As pointed out in [57], niching techniques can divide the whole population into smaller niches according to both the fitness value and distance, and maintain the diversity of the population during the search process. Then a special niching method, named clustering for speciation [57], was considered and modified here to form the sea, rivers and their corresponding streams in the WCA. Accordingly, the intensity of the flow for the rivers and sea would be regarded as the cluster size in clustering for speciation.

To enhance the global search capability, the intensity of the flow for rivers and sea was set as follows:

$$\begin{array}{c}\hfill N{S}_n=floor\left(\frac{N_{stream}}{N_{sr}}\right),n=2,3,\cdots ,N_{sr},\end{array}$$

(20)

and

$$\begin{array}{c}\hfill N{S}_1=N_{stream}-\sum _{i=2}^{N_{sr}}N{S}_i,\end{array}$$

(21)

where $floor\left(A\right)$ returns the nearest integer less than or equal to A. For clarity, the detail procedures of the modified niching approach generating the sea, rivers and streams, are shown in Algorithm 1.

Algorithm 1 Modified niching approach.

1: Input: The population P, the fitness values of P, and the total number of rivers and the sea $N_{sr}$. 2: Calculate the intensity $N{S}_n$ ($n=1,2,\cdots ,N_{sr}$) of flow for each river and sea by Equations (20) and (21). 3: for i ← 1 to $N_{sr}$ do 4:    Find the best individual ${\mathbf{P}}_{best}$ in P as a new seed (sea or river) based on its fitness value, and delete it from P; 5:    Randomly select three indexes, named $d_1,d_2,$ and $d_3$, among $1,2,\cdots ,D$, and compute the Euclidean distance $di{s}_j$ ($j=1,2,\cdots ,\left|\mathbf{P}\right|$) between each individual $X_j$ in P and ${\mathbf{P}}_{best}$ just on the chosen three dimensions $d_1$, $d_2$ and $d_3$, where $\left|A\right|$ denotes the size of set A. 6:    Sort the individuals in P in ascending order according to their Euclidean distances; 7:    Let the first $N{S}_i$ individuals be the streams flowing to the above-chosen sea or river ${\mathit{P}}_{best}$, and delete them from P; 8: end for 9: Output: The sea, rivers and their corresponding streams.

Moreover, to enhance the exploitation at the later search stage, the total number of rivers and sea $N_{sr}$ is adjusted in an adaptive manner as follows:

$$\begin{array}{c}\hfill N_{sr}=max(round(N_{sr}^{inital}\times {(1-\frac{t}{T})}^2),1),\end{array}$$

(22)

where $round\left(A\right)$ returns the nearest integer to A, t and T are the number of the current iteration and the maximum number of iterations, respectively. Obviously, $N_{sr}$ decreases gradually as the number of iteration increases. Then, the initial total number of the sea and rivers $N_{sr}^{inital}$ plays an important role in the performance of the algorithm. A too low a value for $N_{sr}^{inital}$ would increase the chances of becoming trapped into local optima, while a too large a value might decrease the capability of the algorithm to efficiently exploit each promising region. Thus, we let $N_{sr}^{inital}=5$, and its suitability is shown in Section 4.1. More specifically, when the value of $N_{sr}$ is changed, the sea, rivers and streams will be reassigned by Algorithm 1.

By integrating the above changes within the classical WCA, a variant of the WCA (MWCA) was developed, and its framework is clearly described in Algorithm 2. Differing from the classical WCA [38], the fitness value and position of individuals are both considered to form the sea, rivers and their streams (see Steps 4–7 in Algorithm 1), and the total number of rivers and the sea are dynamically reduced during the search process. Therefore, the WCA variant is helpful for both keeping the diversity of the population and enhancing the convergence of the algorithm during the search process. Moreover, it is worth noting that the modified niching method is more close to the real river system, where the streams flow to the nearest river. Thereby, for convenience, a subpopulation consisting of the sea or rivers and its corresponding streams is called a basin in the following.

Algorithm 2 The framework of the MWCA.

1: Input: The total number of the population $N_{pop}$, the initial total number of rivers and the sea $N_{sr}^{inital}$, the predefined parameter $d_{max}$ and the maximum number of iterations T. 2: Initialize the population P by randomly generating $N_{pop}$ individuals; Calculate the fitness values (costs) of the population by Equation (11); 3: Set the current iteration $t=0$; Let $N_{sr}=N_{sr}^{inital}$; 4: Calculate the intensity $N{S}_n$ ($n=1,2,\cdots ,N_{sr}$) of flow for each river and sea by Equations (20) and (21). 5: Determine the sea, rivers and their corresponding streams by Algorithm 1; 6: while   $t\le T$  do 7:    for i ← 1 to $N_{sr}$ do 8:      for j ← 2 to $N{S}_i$ do 9:         if $i==1$ then 10:           Update the position of each stream $X_j$ by Equation (14); 11:         else 12:           Update the position of each stream $X_j$ by Equation (15); 13:         end if 14:      end for 15:    end for 16:    for i ← 1 to $N_{sr}-1$ do 17:      Update the position of each river $X_{river,i}$ by Equation (16); 18:    end for 19:    Execute the evaporation operation as same as in the original WCA; 20:    Update $d_{max}$ by Equation (19) and the total number of rivers and the sea $N_{sr}$ by Equation (22); 21:    if $N_{sr}$ is changed then 22:      Determine the sea, rivers and their corresponding streams by Algorithm 1; 23:    end if 24:    $t=t+1$; 25: end while 26: Output: The sea (global optimum).

3.2. The Hybridization of MWCA and GSA

As described in the last subsection, the MWCA can maintain the diversity of population and has a strong search capability. However, the sea, rivers and their streams are only updated by Equations (14)–(16), respectively, and these update approaches are similar to the mutation in DE, which easily leads to premature convergence [40]. To overcome this shortcoming, by properly integrating the stronger exploration of the gravitational search, a hybrid approach was designed to further enhance the search ability of the algorithm. Specifically, the concrete procedures of this hybrid method are described in the following.

In order to effectively balance the exploration and exploitation, the water cycle search and gravitational search are combined and alternatively operated to update the population based on their history performance within constant iterations $TS$. In detail, for each basin, the performance of the current operation is evaluated by the successful number $Nu{m}_{suc}$ over the $TS$ iterations. Meanwhile, similar to [58], if $Nu{m}_{suc}\ge 0.3\ast TS$, meaning that this operation has promising performance, then it continues to execute for this basin in the next stage; otherwise, another operation is conducted. Clearly, $TS$ is a key factor to the performance of the hybrid approach, and a large $TS$ will not evaluate the search stage in time, while a small $TS$ cannot precisely measure the performance. Thus, we let $TS=15$, shown to be a suitable choice from the experiments in Section 4.1.

Moreover, to save the computing costs, unlike the traditional gravitational search algorithm [37], each object is only attracted by $N_{best}$ superior objects measured by their fitness values. Furthermore, to effectively balance exploration and exploitation, and accelerate the convergence speed at the later search stage, we let

$$\begin{array}{c}\hfill N_{best}=round(N{S}_i\times {(1+e^{20\times (\frac{t}{T}-0.4)})}^{-1}+1,i=1,2,\cdots ,N_{sr}.\end{array}$$

(23)

Clearly, $N_{best}$ decreases gradually with the lapse of iterations. Then each object is absorbed by almost all objects in the previous search stage and a few superior ones in the later stage, respectively. Thus, this setting can ensure the exploration and convergence of the algorithm at different search stages.

Noticeably, compared with the original WCA and GSA [37,38], the proposed hybrid approach can not only effectively balance exploration and exploitation, but also decrease the cost of computation.

3.3. The Crossover Operation

Considering that the update approaches of the streams and rivers in the WCA are similar to the mutation in differential evolution, and the mutation operator always performs together with the crossover operation in DE, a crossover operation was added in the proposed method after the water cycle search or gravitational search.

In particular, to enhance the performance of the algorithm, the binomial crossover [54] was employed and an adaptive method [59] was also introduced to set its corresponding crossover rate. In particular, for one solution (river or stream) $X_i\left(t\right)$ at iteration t, when one new position $X_{tempt,i}\left(t\right)$ has been generated by the water cycle search or gravitational search, its new position $X_i(t+1)$ will be created by

$$\begin{array}{c}\hfill x_i^d(t+1)=\left\{\begin{array}{cc}{x}_{tempt,i}^d\left(t\right),\hfill & \mathrm{if}rand\le C{r}_i\left(t\right)ord=randn\left(i\right),\hfill \\ x_i^d\left(t\right),\hfill & \mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(24)

where $d=1,2,\cdots ,D$, $C{r}_i\left(t\right)\in [0,1]$ is the crossover rate, $x_{tempt,i}^d\left(t\right)$ denotes the d-th dimension of $X_{tempt,i}\left(t\right)$, and $randn\left(i\right)$ returns a random integer within $[1,D]$, which ensures that $X_i(t+1)$ receives at least one component from $X_{tempt,i}\left(t\right)$. Moreover, the value of $C{r}_i\left(t\right)$ can be obtained by

$$\begin{array}{c}\hfill C{r}_i\left(t\right)=ran{d}_n(C{r}_{mean}\left(t\right),0.1),\end{array}$$

(25)

where $ran{d}_n(C{r}_{mean}\left(t\right),0.1)$ is the normal distribution with standard deviation $0.1$ and mean

$$\begin{array}{c}\hfill C{r}_{mean}\left(t\right)=\left\{\begin{array}{cc}c·C{r}_{mean}(t-1)+(1-c)·mea{n}_{WA}\left(S_{Cr}(t-1)\right),\hfill & \mathrm{if}{S}_{Cr}(t-1)\ne \varnothing ,\hfill \\ 1-C{r}_{mean}(t-1),\hfill & \mathrm{otherwise}.\hfill \end{array}\right.\end{array}$$

(26)

Herein, $mea{n}_{WA}(·)$ is the weighted arithmetic mean [59], and $S_{Cr}(t-1)$ denotes the set of all successful $Cr$ values at iteration t. Furthermore, similar to [59], c is set to $0.1$, and $C{r}_{mean}$ is initialized to $0.5$.

From the above descriptions, the binomial crossover operation and an adaptive parameter setting were incorporated in the proposed algorithm to update the information of all solutions during the search process. Thereby, this operation can further adjust the search ability of the algorithm, and adaptively control the transmission of the search information during the search process.

Overall, by integrating the above-presented approaches, the framework of the proposed algorithm is described in Algorithm 3.

From Algorithm 3, we see that the population is first divided into $N_{sr}$ basins by using the modified niching method. Next, the object in each basin is updated by the hybrid approach and binomial crossover, and then the evaporation condition is judged. Finally, $N_{sr}$ is updated and the condition of forming the new basins is judged. If satisfied, then the population is divided again. Obviously, differing from the classical WCA [38], the sea, rivers and streams are formed by the modified niching method to enhance the diversity of the population, and the population is updated by the hybrid approach and binary crossover operation to balance exploration and exploitation. Therefore, the HMWCA has a promising performance to escape from local optima and find the global optima.

Algorithm 3 The framework of the HMWCA.

1: Input: The total number of the population $N_{pop}$, the initial total number of rivers and the sea $N_{sr}^{inital}$, the predefined parameter $d_{max}$, the maximum number of iterations T, and the constant iterations $TS$. 2: Initialize the population P by randomly generating $N_{pop}$ individuals; calculate the fitness values (costs) of the population by Equation (11); and initialize the crossover parameter $C{r}_{mean}$ to $0.5$; 3: Set the current iteration $t=0$; let $N_{sr}=N_{sr}^{inital}$; 4: Calculate the intensity $N{S}_n$ ($n=1,2,\cdots ,N_{sr}$) of flow for each river and sea by Equations (20) and (21). 5: Determine the sea, rivers and their corresponding streams by Algorithm 1; 6: Set the successful number $Nu{m}_{suc,i}$ for each basin $B_i$ ($i=1,2,\cdots ,N_{sr}$) to 0; 7: Set the indicator $in{d}_i$ of the adopted updating strategy for each basin $B_i$ ($i=1,2,\cdots ,N_{sr}$) to 1; 8: while  $t\le T$  do 9:    for i ← 1 to $N_{sr}$ do 10:      if $in{d}_i==1$ then 11:         Generate the corresponding crossover rate for each stream in the current basin $B_i$ by Equations (25) and (26); 12:         Update the positions of the streams in the current basin $B_i$ as the same as in Algorithm 2 and Equation (24); 13:      end if 14:      if $in{d}_i==2$ then 15:         Compute $N_{best}$ by Equation (23); 16:         Generate the corresponding crossover rate for each stream in the current basin $B_i$ by Equations (25) and (26); 17:         Update the positions of the streams in the current basin $B_i$ by Equations (5) and (24); 18:      end if 19:      if The best individual in $B_i$ is updated then 20:         $Nu{m}_{suc,i}=Nu{m}_{suc,i}+1$; 21:      end if 22:      Update the crossover parameter as the same as in [59]; 23:    end for 24:    if $mod(t,TS)==0$ then 25:      for i ← 1 to $N_{sr}$ do 26:         if $Nu{m}_{suc,i}<0.3\ast TS$ then 27:           $in{d}_i=mod(in{d}_i+1,2)+1$; 28:         end if 29:         $Nu{m}_{suc,i}=0$; 30:      end for 31:    end if 32:    Execute the evaporation operation as in the original WCA; 33:    Update $d_{max}$ by Equation (19) and the total number of rivers and the sea $N_{sr}$ by Equation (22); 34:    if $N_{sr}$ is changed then 35:      Determine the sea, rivers and their corresponding streams by Algorithm 1; 36:    end if 37:    $t=t+1$; 38: end while 39: Output: The sea (global optimum).

3.4. Complexity Analysis

In this subsection, the complexity of the HMWCA is further analysed and presented. Obviously, the main differences between the HMWCA and the original WCA [38] are the modified niching method, the hybridization of the water cycle search and gravitational search, and the binomial crossover operation. According to [38], the complexity of the original WCA is $O(N_{pop}·D·T+{log}_2{N}_{pop})$.

For the modified niching method, it must sort the population based on their fitness values and calculate the distances between the sea, rivers and the population. Moreover, note that the modified niching method is only performed $N_{sr}^{initial}$ times during the whole search process. Then their complexity are $O(N_{pop}·{log}_2{N}_{pop}·N_{sr}^{initial})$ and $O((N_{sr}^{initial}+1)/2·N_{pop}·D)$, respectively. Therefore, the complexity of the modified niching method is $O(N_{pop}·(D·(N_{sr}^{initial}+1)/2+{log}_2{N}_{pop}·N_{sr}^{initial}))$. Meanwhile, with respect to the hybridization of the water cycle search and gravitational search, according to [37,38], the complexity of the water cycle search and gravitational search are $O(N_{pop}·D·T)$ and $O(N_{pop}^2·D·T)$, respectively. In addition, the complexity of the alternate criterion between them is $O(N_{pop}·T)$. Then, the complexity of the hybridization of the water cycle search and gravitational search is $O(N_{pop}·T·(D·N_{pop}+1))$. Moreover, for the binomial crossover operation, according to [60], its complexity is $O(N_{pop}·D·T)$.

Overall, the total complexity of the HMWCA is $O(N_{pop}·(D·(N_{sr}^{initial}+1)/2+{log}_2$$N_{pop}·N_{sr}^{initial}+T·(D·N_{pop}+1+D)\left)\right)$, which can be simplified as $O(N_{pop}^2·D·T)$. Note that the gravitational search is operated in alternation during the search process in the HMWCA, and the complexity of the original GSA is $O(N_{pop}^2·D·T)$. Therefore, the HMWCA has acceptable complexity.

4. Numerical Experiments

In this section, the performance of the proposed HMWCA is evaluated on 30 well-known benchmark functions $f_1$-$f_{30}$ from the CEC2014 with both $D=30$ and $D=50$ [55]. Meanwhile, the sensitivity of the parameters in the HMWCA are discussed against eight typical functions: unimodal functions $f_1$ and $f_3$, simple multimodal functions $f_4$ and $f_9$, hybrid functions $f_{17}$ and $f_{21}$, and composition functions $f_{27}$ and $f_{29}$. Moreover, four variants of the HMWCA are designed and compared to show the effects of the proposed components. Furthermore, a comparison of the HMWCA with six well-known optimization algorithms, including the original WCA [38], two competitive variants of the WCA (the ER_WCA [39] and CWCA [40]), the original GSA [37] and two other well-known heuristic algorithms (CLPSO [22] and HSOGA [61]), was conducted to discuss the efficiency of the HMWCA.

In these experiments, the maximum number of function evaluations ($FE{S}_{max}$) was set to 60,000 for all problems with both $D=30$ and $D=50$, and all problems were independently ran 25 times. Moreover, for fair comparisons, the size of the population $N_{pop}$ was set to 50 in the HMWCA, the same as in the original WCA and its two variants, the ER_WCA and CWCA.

4.1. The Sensitivities of Parameters $N_{sr}^{initial}$ and $TS$

In this subsection, the sensitivity of parameters in HMWCA is discussed by a series of tuning experiments. In particular, to obtain the reasonable values of $N_{sr}^{initial}$ and $TS$, the HMWCA was ran on $f_1$, $f_3$, $f_4$, $f_9$, $f_{17}$, $f_{21}$, $f_{27}$ and $f_{29}$, varying $N_{sr}^{initial}$ and $TS$ from 4 to 7 and from 5 to 20 in steps of 1 and 5, respectively. Table 1 reports the experimental results, where the “Mean Error” and “Std Dev” represent the average and standard deviation of the obtained error function values from 25 runs, respectively, and the best results are marked by bold for each function (the same as below).

Table 1. Experimental results of the HMWCA with different values for $TS$ and $N_{sr}^0$.

Functions		Statistical	${\mathit{f}}_1$	${\mathit{f}}_3$	${\mathit{f}}_4$	${\mathit{f}}_9$	${\mathit{f}}_{17}$	${\mathit{f}}_{21}$	${\mathit{f}}_{27}$	${\mathit{f}}_{29}$
$\mathit{TS}$	${\mathit{N}}_{\mathit{sr}}^0$	Item
5	5	Mean Error	4.97 × 10${}^6$	4.04 × 10${}^3$	1.01 × 10${}^2$	1.39 × 10${}^2$	4.91 × 10${}^5$	2.71 × 10${}^5$	7.06 × 10${}^2$	2.17 × 10${}^2$
		Std Dev	3.31 × 10${}^6$	7.79 × 10${}^3$	4.80 × 10${}^1$	3.28 × 10${}^1$	3.19 × 10${}^5$	3.31 × 10${}^5$	3.25 × 10${}^2$	2.84 × 10${}^0$
	8	Mean Error	4.78 × 10${}^6$	2.89 × 10${}^3$	7.59 × 10${}^1$	1.22 × 10${}^2$	4.73 × 10${}^5$	2.07 × 10${}^5$	7.54 × 10${}^2$	2.22 × 10${}^2$
		Std Dev	2.78 × 10${}^6$	3.24 × 10${}^3$	3.23 × 10${}^1$	2.74 × 10${}^1$	4.15 × 10${}^5$	1.35 × 10${}^5$	3.09 × 10${}^2$	2.09 × 10${}^1$
	10	Mean Error	7.97 × 10${}^6$	2.00 × 10${}^3$	6.49 × 10${}^1$	1.33 × 10${}^2$	8.00 × 10${}^5$	2.92 × 10${}^5$	8.78 × 10${}^2$	2.44 × 10${}^2$
		Std Dev	7.17 × 10${}^6$	2.34 × 10${}^3$	3.75 × 10${}^1$	4.48 × 10${}^1$	3.46 × 10${}^5$	1.87 × 10${}^5$	1.76 × 10${}^2$	5.89 × 10${}^1$
10	5	Mean Error	6.45 × 10${}^6$	1.05 × 10${}^3$	6.25 × 10${}^1$	1.35 × 10${}^2$	4.72 × 10${}^5$	2.27 × 10${}^5$	8.21 × 10${}^2$	2.34 × 10${}^2$
		Std Dev	3.67 × 10${}^6$	2.52 × 10${}^3$	2.48 × 10${}^1$	1.99 × 10${}^1$	3.34 × 10${}^5$	2.16 × 10${}^5$	2.27 × 10${}^2$	3.80 × 10${}^1$
	8	Mean Error	5.01 × 10${}^6$	1.27 × 10${}^3$	6.95 × 10${}^1$	1.36 × 10${}^2$	4.01 × 10${}^5$	1.53 × 10${}^5$	6.21 × 10${}^2$	2.16 × 10${}^2$
		Std Dev	2.85 × 10${}^6$	2.85 × 10${}^3$	3.37 × 10${}^1$	3.03 × 10${}^1$	2.84 × 10${}^5$	1.01 × 10${}^5$	2.83 × 10${}^2$	4.54 × 10${}^0$
	10	Mean Error	4.46 × 10${}^6$	2.39 × 10${}^3$	7.63 × 10${}^1$	1.20 × 10${}^2$	4.54 × 10${}^5$	1.06 × 10${}^5$	8.03 × 10${}^2$	2.29 × 10${}^2$
		Std Dev	2.59 × 10${}^6$	1.84 × 10${}^3$	5.03 × 10${}^1$	1.62 × 10${}^1$	3.30 × 10${}^5$	4.84 × 10${}^4$	2.76 × 10${}^2$	2.93 × 10${}^1$
15	5	Mean Error	2.90 × 10${}^6$	7.61 × 10${}^2$	6.11 × 10${}^1$	1.31 × 10${}^2$	2.75 × 10${}^5$	1.00 × 10${}^5$	7.58 × 10${}^2$	2.29 × 10${}^2$
		Std Dev	1.26 × 10${}^6$	1.17 × 10${}^3$	2.12 × 10${}^1$	1.79 × 10${}^1$	1.75 × 10${}^5$	6.50 × 10${}^4$	3.14 × 10${}^2$	2.90 × 10${}^1$
	8	Mean Error	4.31 × 10${}^6$	1.29 × 10${}^3$	7.65 × 10${}^1$	1.37 × 10${}^2$	5.74 × 10${}^5$	1.38 × 10${}^5$	7.97 × 10${}^2$	2.15 × 10${}^2$
		Std Dev	1.79 × 10${}^6$	1.34 × 10${}^3$	3.07 × 10${}^1$	3.05 × 10${}^1$	5.52 × 10${}^5$	7.06 × 10${}^4$	2.82 × 10${}^2$	4.34 × 10${}^0$
	10	Mean Error	4.63 × 10${}^6$	2.18 × 10${}^3$	7.55 × 10${}^1$	1.20 × 10${}^2$	4.33 × 10${}^5$	2.03 × 10${}^5$	7.65 × 10${}^2$	2.20 × 10${}^2$
		Std Dev	2.59 × 10${}^6$	2.00 × 10${}^3$	3.97 × 10${}^1$	2.72 × 10${}^1$	2.48 × 10${}^5$	9.98 × 10${}^4$	3.14 × 10${}^2$	1.62 × 10${}^1$
20	5	Mean Error	3.72 × 10${}^6$	1.13 × 10${}^3$	8.22 × 10${}^1$	1.41 × 10${}^2$	4.80 × 10${}^5$	1.89 × 10${}^5$	6.77 × 10${}^2$	2.21 × 10${}^2$
		Std Dev	2.60 × 10${}^6$	1.75 × 10${}^3$	3.07 × 10${}^1$	2.31 × 10${}^1$	3.53 × 10${}^5$	1.10 × 10${}^5$	2.89 × 10${}^2$	2.04 × 10${}^1$
	8	Mean Error	6.91 × 10${}^6$	2.25 × 10${}^3$	8.13 × 10${}^1$	1.41 × 10${}^2$	2.87 × 10${}^5$	2.91 × 10${}^5$	8.21 × 10${}^2$	2.24 × 10${}^2$
		Std Dev	3.05 × 10${}^6$	3.72 × 10${}^3$	3.63 × 10${}^1$	2.46 × 10${}^1$	1.34 × 10${}^5$	2.62 × 10${}^5$	3.00 × 10${}^2$	2.92 × 10${}^1$
	10	Mean Error	4.29 × 10${}^6$	1.36 × 10${}^3$	7.70 × 10${}^1$	1.27 × 10${}^2$	4.46 × 10${}^5$	1.25 × 10${}^5$	7.47 × 10${}^2$	2.16 × 10${}^2$
		Std Dev	2.52 × 10${}^6$	1.17 × 10${}^3$	3.43 × 10${}^1$	1.93 × 10${}^1$	3.96 × 10${}^5$	7.27 × 10${}^4$	3.00 × 10${}^2$	2.97 × 10${}^0$

From Table 1, we see that $f_1$, $f_3$, $f_4$, $f_{17}$ and $f_{21}$ obtain the best values when $TS$ = 15 and $N_{sr}^0$ = 5, $f_9$ obtained the best values when $N_{sr}^0$ = 10, $TS$ = 10 and 15, $f_{27}$ obtains the best values when $TS$ = 10 and $N_{sr}^0$ = 8, while $f_{29}$ obtains the best values when $TS$ = 15 and $N_{sr}^0$ = 8. Moreover, it can also been seen that there is no best values when $TS$ = 5 or 20, and only two best values when $TS$ = 10, while the HMWCA obtains 4, 2 and 2 best values when $N_{sr}^0$ = 5, 8 and 10, respectively. Then, the value for $TS$ should not be too small or too large, with 15 and 5 as reasonable choices for $TS$ and $N_{sr}^0$ for most functions, respectively. Therefore, we let $TS$ = 15 and $N_{sr}^0$ = 5 in this paper.

4.2. The Effectiveness of the Proposed Components in the HMWCA

To clearly show the effects of the modified niching method, the hybridization of the water cycle search and gravitational search, and the binomial crossover operation on the performance of the HMWCA, we first designed four variants of the HMWCA as follows.

(1)

HMWCA1: the method in the original WCA [38] was used to form the sea, rivers and streams instead of the modified niching method in the HMWCA.

(2)

HMWCA2: the population was only updated by the water cycle search in the HMWCA during the whole search process.

(3)

HMWCA3: after the water cycle search or gravitational search at each generation, the binomial crossover operation is not further used in the HMWCA.

(4)

HMWCA4: the total number of and rivers and the sea is unchanged in the HMWCA during the search process. In particular, similar to the original WCA [38] and its variants [39,40], $N_{sr}$ was set to 4 in the HMWCA.

Then, a comparison of the HMWCA with the above four variants was made against all problems from the CEC2014 with D=30. The experimental results are listed in Table 2, and the rank of each algorithm against each problems was used to measure their performance.

Table 2. Experimental results of the HMWCA and its four variants on the $CEC2014$ functions with $D=30$.

Functions	HMWCA1	HMWCA2	HMWCA3	HMWCA4	HMWCA
	Mean Error ± Std Dev /Rank	Mean Error ± Std Dev /Rank	Mean Error ± Std Dev /Rank	Mean Error ± Std Dev /Rank	Mean Error ± Std Dev /Rank
$f_1$	6.34 × 106 ± 3.14 × 106 /2	7.37 × 106 ± 5.28 × 106 /3	3.04 × 107 ± 1.07 × 107 /5	1.03 × 107 ± 2.53 × 106 /4	2.90 × 106 ± 1.26 × 106 /1
$f_2$	1.47 × 10${}^4$ ± 1.52 × 10${}^4$ /3	1.54 × 10${}^3$ ± 4.94 × 10${}^3$ /1	2.36 × 10${}^7$ ± 2.68 × 10${}^7$ /5	8.03 × 10${}^5$ ± 8.77 × 10${}^5$ /4	5.80 × 10${}^3$ ± 4.72 × 10${}^3$ /2
$f_3$	2.71 × 10${}^3$ ± 3.26 × 10${}^3$ /3	5.08 × 10${}^2$ ± 8.21 × 10${}^2$ /1	2.89 × 10${}^4$ ± 7.60 × 10${}^3$ /5	1.86 × 10${}^4$ ± 8.72 × 10${}^3$ /4	7.61 × 10${}^2$ ± 1.17 × 10${}^3$ /2
$f_4$	1.20 × 10${}^2$ ± 4.56 × 10${}^1$ /3	8.12 × 10${}^1$ ± 4.56 × 10${}^1$ /2	1.91 × 10${}^2$ ± 4.55 × 10${}^1$ /4	2.14 × 10${}^2$ ± 3.35 × 10${}^1$ /5	6.11 × 10${}^1$ ± 2.12 × 10${}^1$ /1
$f_5$	2.00 × 10${}^1$ ± 4.48 × 10${}^{-4}$ /1	2.00 × 10${}^1$ ± 1.86 × 10${}^{-5}$ /1	2.00 × 10${}^1$ ± 3.35 × 10${}^{-3}$ /1	2.01 × 10${}^1$ ± 6.87 × 10${}^{-2}$ /5	2.00 × 10${}^1$ ± 2.12 × 10${}^1$ /1
$f_6$	2.64 × 10${}^1$ ± 3.60 × 10${}^0$ /3	2.61 × 10${}^1$ ± 4.05 × 10${}^0$ /2	3.04 × 10${}^1$ ± 3.32 × 10${}^0$ /4	5.27 × 10${}^1$ ± 5.90 × 10${}^0$ /5	2.42 × 10${}^1$ ± 2.93 × 10${}^0$ /1
$f_7$	8.62 × 10${}^{-2}$ ± 1.05 × 10${}^{-1}$ /3	3.52 × 10${}^{-2}$ ± 3.86 × 10${}^{-2}$ /2	1.29 × 10${}^0$ ± 3.79 × 10${}^{-1}$ /5	6.43 × 10${}^{-1}$ ± 2.87 × 10${}^{-1}$ /4	1.10 × 10${}^{-2}$ ± 1.18 × 10${}^{-2}$ /1
$f_8$	1.10 × 10${}^2$ ± 1.48 × 10${}^1$ /2	8.26 × 10${}^1$ ± 1.88 × 10${}^1$ /1	1.33 × 10${}^2$ ± 2.95 × 10${}^1$ /4	2.30 × 10${}^2$ ± 2.23 × 10${}^1$ /5	1.10 × 10${}^2$ ± 2.94 × 10${}^1$ /2
$f_9$	1.41 × 10${}^2$ ± 3.01 × 10${}^1$ /2	1.46 × 10${}^2$ ± 4.55 × 10${}^1$ /3	1.47 × 10${}^2$ ± 2.66 × 10${}^1$ /4	2.77 × 10${}^2$ ± 4.49 × 10${}^1$ /5	1.31 × 10${}^2$ ± 1.79 × 10${}^1$ /1
$f_{10}$	2.64 × 10${}^3$ ± 4.46 × 10${}^2$ /3	2.12 × 10${}^3$ ± 4.83 × 10${}^2$ /2	3.39 × 10${}^3$ ± 6.39 × 10${}^2$ /4	4.67 × 10${}^3$ ± 1.05 × 10${}^3$ /5	1.82 × 10${}^3$ ± 4.59 × 10${}^2$ /1
$f_{11}$	3.70 × 10${}^3$ ± 6.28 × 10${}^2$ /2	3.95 × 10${}^3$ ± 7.07 × 10${}^2$ /3	3.95 × 10${}^3$ ± 6.05 × 10${}^2$ /3	6.77 × 10${}^3$ ± 1.14 × 10${}^3$ /5	3.56 × 10${}^3$ ± 5.39 × 10${}^2$ /1
$f_{12}$	6.24 × 10${}^{-1}$ ± 2.83 × 10${}^{-1}$ /2	1.03 × 10${}^0$ ± 4.80 × 10${}^{-1}$ /3	1.32 × 10${}^0$ ± 6.11 × 10${}^{-1}$ /4	1.65 × 10${}^0$ ± 6.49 × 10${}^{-1}$ /5	6.21 × 10${}^{-1}$ ± 2.09 × 10${}^{-1}$ /1
$f_{13}$	4.99 × 10${}^{-1}$ ± 1.40 × 10${}^{-1}$ /3	4.80 × 10${}^{-1}$ ± 1.13 × 10${}^{-1}$ /2	5.39 × 10${}^{-1}$ ± 1.26 × 10${}^{-1}$ /4	5.77 × 10${}^{-1}$ ± 1.04 × 10${}^{-1}$ /5	4.20 × 10${}^{-1}$ ± 6.11 × 10${}^{-2}$ /1
$f_{14}$	2.85 × 10${}^{-1}$ ± 5.61 × 10${}^{-2}$ /1	3.33 × 10${}^{-1}$ ± 1.07 × 10${}^{-1}$ /5	3.04 × 10${}^{-1}$ ± 4.05 × 10${}^{-2}$ /2	3.17 × 10${}^{-1}$ ± 4.21 × 10${}^{-2}$ /4	3.05 × 10${}^{-1}$ ± 5.20 × 10${}^{-2}$ /3
$f_{15}$	5.12 × 10${}^1$ ± 2.21 × 10${}^1$ /3	3.44 × 10${}^1$ ± 1.13 × 10${}^1$ /2	5.15 × 10${}^1$ ± 1.73 × 10${}^1$ /4	1.36 × 10${}^2$ ± 2.19 × 10${}^1$ /5	3.11 × 10${}^1$ ± 9.66 × 10${}^0$ /1
$f_{16}$	1.24 × 10${}^1$ ± 6.40 × 10${}^{-1}$ /2	1.28 × 10${}^1$ ± 5.10 × 10${}^{-1}$ /4	1.27 × 10${}^1$ ± 4.50 × 10${}^{-1}$ /3	2.21 × 10${}^1$ ± 2.92 × 10${}^{-1}$ /5	1.21 × 10${}^1$ ± 5.98 × 10${}^{-1}$ /1
$f_{17}$	5.13 × 10${}^5$ ± 3.13 × 10${}^5$ /2	7.28 × 10${}^5$ ± 6.17 × 10${}^5$ /3	1.14 × 10${}^6$ ± 9.40 × 10${}^5$ /4	1.99 × 10${}^6$ ± 1.23 × 10${}^6$ /5	2.75 × 10${}^5$ ± 1.75 × 10${}^5$ /1
$f_{18}$	1.08 × 10${}^3$ ± 1.33 × 10${}^3$ /2	4.32 × 10${}^3$ ± 7.55 × 10${}^3$ /4	1.70 × 10${}^3$ ± 2.14 × 10${}^3$ /3	4.75 × 10${}^3$ ± 4.96 × 10${}^3$ /5	5.19 × 10${}^2$ ± 3.36 × 10${}^2$ /1
$f_{19}$	1.71 × 10${}^1$ ± 3.84 × 10${}^0$ /2	1.56 × 10${}^1$ ± 3.27 × 10${}^0$ /1	2.51 × 10${}^1$ ± 3.54 × 10${}^0$ /4	5.86 × 10${}^1$ ± 3.28 × 10${}^1$ /5	1.79 × 10${}^1$ ± 3.05 × 10${}^0$ /3
$f_{20}$	5.51 × 10${}^3$ ± 3.94 × 10${}^3$ /3	5.37 × 10${}^3$ ± 6.11 × 10${}^3$ /2	6.59 × 10${}^3$ ± 5.28 × 10${}^3$ /4	2.72 × 10${}^4$ ± 1.09 × 10${}^4$ /5	3.80 × 10${}^3$ ± 2.14 × 10${}^3$ /1
$f_{21}$	1.90 × 10${}^5$ ± 2.03 × 10${}^5$ /2	2.48 × 10${}^5$ ± 1.69 × 10${}^5$ /3	3.45 × 10${}^5$ ± 2.61 × 10${}^5$ /4	1.31 × 10${}^6$ ± 7.29 × 10${}^5$ /5	1.00 × 10${}^5$ ± 6.50 × 10${}^4$ /1
$f_{22}$	7.39 × 10${}^2$ ± 1.76 × 10${}^2$ /3	6.36 × 10${}^2$ ± 1.84 × 10${}^2$ /1	8.24 × 10${}^2$ ± 2.30 × 10${}^2$ /4	1.44 × 10${}^3$ ± 3.84 × 10${}^2$ /5	6.37 × 10${}^2$ ± 1.27 × 10${}^2$ /2
$f_{23}$	3.14 × 10${}^2$ ± 4.68 × 10${}^{-2}$ /1	3.14 × 10${}^2$ ± 2.00 × 10${}^{-2}$ /1	3.26 × 10${}^2$ ± 8.14 × 10${}^0$ /4	3.37 × 10${}^2$ ± 2.96 × 10${}^{-1}$ /5	3.14 × 10${}^2$ ± 5.50 × 10${}^{-3}$ /1
$f_{24}$	2.31 × 10${}^2$ ± 3.31 × 10${}^0$ /2	2.44 × 10${}^2$ ± 6.21 × 10${}^0$ /4	2.29 × 10${}^2$ ± 2.83 × 10${}^0$ /1	2.80 × 10${}^2$ ± 1.14 × 10${}^1$ /5	2.31 × 10${}^2$ ± 6.54 × 10${}^0$ /2
$f_{25}$	2.12 × 10${}^2$ ± 2.75 × 10${}^0$ /3	2.06 × 10${}^2$ ± 8.45 × 10${}^0$ /1	2.11 × 10${}^2$ ± 3.58 × 10${}^0$ /2	2.30 × 10${}^2$ ± 7.12 × 10${}^0$ /5	2.12 × 10${}^2$ ± 1.61 × 10${}^0$ /3
$f_{26}$	1.01 × 10${}^2$ ± 1.15 × 10${}^{-1}$ /2	1.01 × 10${}^2$ ± 1.62 × 10${}^{-1}$ /2	1.01 × 10${}^2$ ± 7.34 × 10${}^{-1}$ /2	1.60 × 10${}^2$ ± 5.15 × 10${}^1$ /5	1.00 × 10${}^2$ ± 1.18 × 10${}^{-1}$ /1
$f_{27}$	8.07 × 10${}^2$ ± 3.40 × 10${}^2$ /3	8.33 × 10${}^2$ ± 3.08 × 10${}^2$ /4	6.44 × 10${}^2$ ± 3.39 × 10${}^2$ /1	1.68 × 10${}^3$ ± 1.11 × 10${}^2$ /5	7.58 × 10${}^2$ ± 3.14 × 10${}^2$ /2
$f_{28}$	5.80 × 10${}^2$ ± 1.83 × 10${}^2$ /4	4.87 × 10${}^2$ ± 9.00 × 10${}^1$ /1	1.52 × 10${}^3$ ± 7.50 × 10${}^2$ /5	5.44 × 10${}^2$ ± 1.14 × 10${}^2$ /3	5.43 × 10${}^2$ ± 1.18 × 10${}^2$ /2
$f_{29}$	3.02 × 10${}^2$ ± 2.74 × 10${}^2$ /5	2.19 × 10${}^2$ ± 2.01 × 10${}^1$ /1	2.51 × 10${}^3$ ± 3.53 × 10${}^3$ /3	2.63 × 10${}^2$ ± 4.03 × 10${}^1$ /4	2.29 × 10${}^2$ ± 2.90 × 10${}^1$ /2
$f_{30}$	1.04 × 10${}^3$ ± 5.44 × 10${}^2$ /3	9.79 × 10${}^2$ ± 3.11 × 10${}^2$ /2	1.55 × 10${}^4$ ± 2.83 × 10${}^4$ /5	1.63 × 10${}^3$ ± 6.12 × 10${}^2$ /4	9.38 × 10${}^2$ ± 7.82 × 10${}^2$ /1
Sum Rank	75	67	107	141	44
Average Rank	2.5	2.23	3.57	4.7	1.47

From Table 2, we see that for unimodal functions $f_1$–$f_3$, the HMWCA obtains the best results for $f_1$ and the HMWCA2 obtains the best results for $f_2$ and $f_3$, potentially due to the fact that the gravitational search degrades the local search ability. For simple multimodal functions $f_4$–$f_{16}$, the HMWCA obtains the best results, except the HMWCA2 achieves the best results for $f_8$ and the HMWCA1 achieves the best results for $f_{14}$. In particular, the HMWCA has similar top results for $f_5$ with the HMWCA1, HMWCA2 and HMWCA3. For hybrid functions $f_{17}$–$f_{22}$, the HMWCA has the best results, except the HMWCA2 achieves the best results for $f_{19}$ and $f_{22}$. For composition functions $f_{23}$–$f_{30}$, HMWCA obtains the best values for $f_{23}$, $f_{26}$ and $f_{30}$, the HMWCA2 obtains the best values for $f_{25}$, $f_{28}$ and $f_{29}$, and the HMWCA3 attains the best values for $f_{24}$ and $f_{27}$. Furthermore, the HMWCA1, HMWCA2, HMWCA3, HMWCA4 and HMWCA obtain 75, 67, 107, 141 and 44 in terms of their total rank and $2.5$, $2.23$, $3.57$, $4.7$ and $1.47$ in terms of their average rank for all problems, respectively. Therefore, it can be noted that the modified niching method, the hybridization of the water cycle search and gravitational search, and the binomial crossover operation are helpful to enhance the search performance of the HMWCA.

4.3. Comparisons and Discussion

In this subsection, to evaluate the performance of the HMWCA, six well-known optimization algorithms including the original WCA [38], two competitive variants of the WCA (the ER_WCA [39] and CWCA [40]), the original GSA [37] and two other well-known heuristic algorithms (CLPSO [22] and HSOGA [61]) were used as a comparison with CEC2014 problems with both $D=30$ and $D=50$. Among these compared algorithms, the ER_WCA [39] is an improved version of the WCA [38] to balance exploration and exploitation by defining the new concept of the evaporation rate for different rivers and streams. The CWCA [40] is a well-known variant of the WCA incorporating chaotic patterns into the stochastic processes of the WCA. CLPSO [22] is an improved PSO using personal historical best information of all particles to update the velocity of particles [22], and the HSOGA [61] is a hybrid self-adaptive orthogonal genetic algorithm designing a self-adaptive orthogonal crossover operator.

In our experiments, to perform fair comparisons, $FE{S}_{max}$ was set to 60,000 for all the above algorithms, the size of population in the HMWCA was set to 50, consistent with the traditional WCA, ER_WCA and CWCA.The other parameters involved are listed in Table 3. The parameters of the other three algorithms, including the GSA, CLPSO and HSOGA, are the same as in their original papers.

Table 3. Parameters setting.

Algorithms	Parameter Setting
GSA	$N_{pop}=50$, $G_0=100$, $\alpha =20$
HSOGA	$N_{pop}=200$, $Q_0=D-1$, $Q=2$, $S=5$, $P_c=0.6$, $P_m=0.1$, ${\delta }_0=0.05$
CLPSO	$N_{pop}=30$, $c_1=c_2=1.494$, $w_{max}=0.9$, $w_{min}=0.4$, m = 5
WCA	$N_{pop}=50$, $N_{sr}=4$, $d_{max}=0.0001$
CWCA	$N_{pop}=50$, $N_{sr}=4$, $d_{max}=0.0001$, $C_i=1$, $C_f=2$, ${\mu }_i=0.1$, ${\mu }_f=0.8$
ER_WCA	$N_{pop}=50$, $N_{sr}=4$, $d_{max}=0.0001$
HMWCA	$N_{pop}=50$, $N_{sr}^{initial}=5$, $d_{max}=0.0001$, $G_0=100$, $\alpha =20$, $TS=15$

Furthermore, the average error (Mean Error) and standard deviation (Std Dev) of the function errors from 25 independent runs were recorded to measure their performances, and a Wilcoxon’s rank sum test ($p<0.05$) and their ranks were conducted on the experimental results draw statistically sound conclusions. Table 4 and Table 5 report the experimental results for all problems with $D=30$ and $D=50$, respectively, where the best results are marked in bold for each function, and “+”, “−” or “≈ ” to denote that the HMWCA performance was better, worse, or equivalent to the corresponding algorithms, respectively.

Table 4. Experimental results of the HMWCA and six well-known algorithms on the $CEC2014$ functions with $D=30$.

Function	Algorithm	WCA	CWCA	ER_WCA	GSA	CLPSO	HSOGA	HMWCA
$f_1$	Mean Error	2.82 × 10${}^6$ −	6.00 × 10${}^6$ +	1.32 × 10${}^6$ −	9.10 × 10${}^7$ +	1.04 × 10${}^8$ +	1.91 × 10${}^8$ +	2.90 × 10${}^6$
	Std Dev /Rank	1.05 × 10${}^6$ /2	4.88 × 10${}^6$ /4	6.07 × 10${}^5$ /1	2.37 × 10${}^7$ /5	3.12 × 10${}^7$ /6	2.49 × 10${}^7$ /7	1.26 × 10${}^6$ /3
$f_2$	Mean Error	1.07 × 10${}^4$ +	2.93 × 10${}^4$ +	1.36 × 10${}^4$ +	1.12 × 10${}^7$ +	2.93 × 10${}^7$ +	5.68 × 10${}^9$ +	5.80 × 10${}^3$
	Std Dev /Rank	1.01 × 10${}^4$ /2	2.12 × 10${}^4$ /4	1.04 × 10${}^4$ /3	3.17 × 10${}^7$ /5	7.69 × 10${}^6$ /6	1.00 × 10${}^9$ /7	4.72 × 10${}^3$ /1
$f_3$	Mean Error	3.99 × 10${}^3$ +	2.02 × 10${}^4$ +	8.53 × 10${}^2$ +	8.71 × 10${}^4$ +	6.46 × 10${}^3$ +	2.30 × 10${}^4$+	7.61 × 10${}^2$
	Std Dev /Rank	2.56 × 10${}^3$ /3	1.85 × 10${}^4$ /4	9.62 × 10${}^2$ /2	7.63 × 10${}^3$ /7	2.94 × 10${}^3$ /5	5.09 × 10${}^3$ /6	1.17 × 10${}^3$ /1
$f_4$	Mean Error	1.03 × 10${}^2$ +	1.36 × 10${}^2$ +	7.99 × 10${}^1$ +	3.92 × 10${}^2$ +	2.30 × 10${}^2$ +	5.02 × 10${}^2$ +	6.11 × 10${}^1$
	Std Dev /Rank	3.22 × 10${}^1$ /3	6.46 × 10${}^1$ /4	2.71 × 10${}^1$ /2	1.07 × 10${}^2$ /6	2.80 × 10${}^1$ /5	6.48 × 10${}^1$ /7	2.12 × 10${}^1$ /1
$f_5$	Mean Error	2.01 × 10${}^1$ +	2.01 × 10${}^1$ +	2.01 × 10${}^1$ +	2.00 × 10${}^1$ ≈	2.07 × 10${}^1$ +	2.10 × 10${}^1$ +	2.00 × 10${}^1$
	Std Dev /Rank	8.27 × 10${}^{-2}$ /3	6.84 × 10${}^{-2}$ /3	9.23 × 10${}^{-2}$ /3	5.71 × 10${}^{-4}$ /1	5.05 × 10${}^{-2}$ /6	5.92 × 10${}^{-2}$ /7	2.73 × 10${}^{-4}$ /1
$f_6$	Mean Error	3.10 × 10${}^1$ +	2.52 × 10${}^1$ +	3.03 × 10${}^1$ +	2.47 × 10${}^1$ +	2.30 × 10${}^1$ −	3.17 × 10${}^1$ +	2.42 × 10${}^1$
	Std Dev /Rank	3.45 × 10${}^0$ /6	3.28 × 10${}^0$ /4	3.55 × 10${}^0$ /5	2.11 × 10${}^0$ /3	1.61 × 10${}^0$ /1	1.86 × 10${}^0$ /7	2.93 × 10${}^0$ /2
$f_7$	Mean Error	2.19 × 10${}^{-2}$ +	9.12 × 10${}^{-2}$ +	1.13 × 10${}^{-2}$ +	1.33 × 10${}^0$ +	1.19 × 10${}^0$ +	4.27 × 10${}^1$ +	1.10 × 10${}^{-2}$
	Std Dev /Rank	1.90 × 10${}^{-2}$ /3	4.97 × 10${}^{-2}$ /4	1.30 × 10${}^{-2}$ /2	1.69 × 10${}^0$ /6	6.56 × 10${}^{-2}$ /5	6.12 × 10${}^0$ /7	1.18 × 10${}^{-2}$ /1
$f_8$	Mean Error	1.51 × 10${}^2$ +	7.45 × 10${}^1$ −	1.73 × 10${}^2$ +	1.41 × 10${}^2$ +	1.80 × 10${}^1$ −	1.36 × 10${}^2$ +	1.10 × 10${}^2$
	Std Dev /Rank	2.99 × 10${}^1$ /6	2.68 × 10${}^1$ /2	4.28 × 10${}^1$ /7	1.22 × 10${}^1$ /5	3.23 × 10${}^0$ /1	1.04 × 10${}^1$ /4	2.94 × 10${}^1$ /3
$f_9$	Mean Error	1.82 × 10${}^2$ +	2.39 × 10${}^2$ +	1.82 × 10${}^2$ +	1.65 × 10${}^2$ +	1.43 × 10${}^2$ +	2.28 × 10${}^2$ +	1.31 × 10${}^2$
	Std Dev /Rank	4.10 × 10${}^1$ /4	5.35 × 10${}^1$ /7	4.93 × 10${}^1$ /4	2.11 × 10${}^1$ /3	1.22 × 10${}^1$ /2	1.88 × 10${}^1$ /6	1.79 × 10${}^1$ /1
$f_{10}$	Mean Error	4.00 × 10${}^3$ +	1.84 × 10${}^3$ +	3.64 × 10${}^3$ +	3.85 × 10${}^3$ +	3.71 × 10${}^2$ +	1.89 × 10${}^3$ +	1.82 × 10${}^3$
	Std Dev /Rank	8.84 × 10${}^2$ /7	6.25 × 10${}^2$ /2	6.58 × 10${}^2$ /4	4.76 × 10${}^2$ /6	1.02 × 10${}^2$ /5	1.85 × 10${}^2$ /3	4.59 × 10${}^2$ /1
$f_{11}$	Mean Error	4.23 × 10${}^3$ +	3.72 × 10${}^3$ +	4.55 × 10${}^3$ +	4.48 × 10${}^3$ +	4.44 × 10${}^3$ +	7.22 × 10${}^3$ +	3.56 × 10${}^3$
	Std Dev /Rank	1.02 × 10${}^3$ /3	6.81 × 10${}^2$ /2	7.33 × 10${}^2$ /6	6.12 × 10${}^2$ /5	2.79 × 10${}^2$ /4	3.29 × 10${}^2$ /7	5.39 × 10${}^2$ /1
$f_{12}$	Mean Error	1.40 × 10${}^0$ +	3.60 × 10${}^{-1}$ −	1.51 × 10${}^0$ +	5.59 × 10${}^{-3}$ −	9.08 × 10${}^{-1}$ +	2.61 × 10${}^0$ +	6.21 × 10${}^{-1}$
	Std Dev /Rank	5.34 × 10${}^{-1}$ /5	1.08 × 10${}^{-1}$ /2	5.67 × 10${}^{-1}$ /6	4.62 × 10${}^{-3}$ /1	1.52 × 10${}^{-1}$ /4	4.56 × 10${}^{-1}$ /7	2.09 × 10${}^{-1}$ /3
$f_{13}$	Mean Error	5.41 × 10${}^{-1}$ +	7.67 × 10${}^{-1}$ +	5.62 × 10${}^{-1}$ +	3.66 × 10${}^{-1}$ −	3.89 × 10${}^{-1}$ −	9.30 × 10${}^{-1}$ +	4.20 × 10${}^{-1}$
	Std Dev /Rank	1.19 × 10${}^{-1}$ /4	1.31 × 10${}^{-1}$ /6	1.56 × 10${}^{-1}$ /5	6.61 × 10${}^{-2}$ /1	4.75 × 10${}^{-2}$ /2	1.77 × 10${}^{-1}$ /7	6.11 × 10${}^{-2}$ /3
$f_{14}$	Mean Error	3.46 × 10${}^{-1}$ +	9.83 × 10${}^{-1}$ +	4.69 × 10${}^{-1}$ +	5.43 × 10${}^{-1}$ +	3.43 × 10${}^{-1}$ +	1.43 × 10${}^1$ +	3.05 × 10${}^{-1}$
	Std Dev /Rank	1.32 × 10${}^{-1}$ /3	3.64 × 10${}^{-1}$ /6	2.33 × 10${}^{-1}$ /4	1.50 × 10${}^0$ /5	3.30 × 10${}^{-2}$ /2	3.63 × 10${}^0$ /7	5.20 × 10${}^{-2}$ /1
$f_{15}$	Mean Error	3.24 × 10${}^1$ +	2.65 × 10${}^1$ −	4.88 × 10${}^1$ +	3.28 × 10${}^1$ +	2.65 × 10${}^1$ −	7.75 × 10${}^2$ +	3.11 × 10${}^1$
	Std Dev /Rank	1.19 × 10${}^1$ /4	1.41 × 10${}^1$ /1	3.34 × 10${}^1$ /6	1.37 × 10${}^1$ /5	2.92 × 10${}^0$ /1	4.76 × 10${}^2$ /7	9.66 × 10${}^0$ /3
$f_{16}$	Mean Error	1.27 × 10${}^1$ +	1.21 × 10${}^1$ ≈	1.29 × 10${}^1$ +	1.37 × 10${}^1$ +	1.19 × 10${}^1$ −	1.31 × 10${}^1$ +	1.21 × 10${}^1$
	Std Dev /Rank	4.62 × 10${}^{-1}$ /4	5.50 × 10${}^{-1}$ /2	4.58 × 10${}^{-1}$ /5	2.02 × 10${}^{-1}$ /7	3.18 × 10${}^{-1}$ /1	2.63 × 10${}^{-1}$ /6	5.98 × 10${}^{-1}$ /2
$f_{17}$	Mean Error	2.91 × 10${}^5$ +	6.40 × 10${}^5$ +	9.12 × 10${}^4$ −	7.50 × 10${}^6$ +	6.60 × 10${}^6$ +	2.24 × 10${}^6$ +	2.75 × 10${}^5$
	Std Dev /Rank	1.75 × 10${}^5$ /3	5.92 × 10${}^5$ /4	5.37 × 10${}^4$ /1	2.83 × 10${}^6$ /7	3.85 × 10${}^6$ /6	8.12 × 10${}^5$ /5	1.75 × 10${}^5$ /2
$f_{18}$	Mean Error	5.26 × 10${}^3$ +	1.33 × 10${}^4$ +	5.01 × 10${}^3$ +	5.24 × 10${}^2$ +	5.31 × 10${}^5$ +	2.04 × 10${}^7$ +	5.19 × 10${}^2$
	Std Dev /Rank	6.44 × 10${}^3$ /4	1.04 × 10${}^4$ /5	6.27 × 10${}^3$ /3	4.55 × 10${}^2$ /2	4.55 × 10${}^5$ /6	7.96 × 10${}^6$ /7	3.36 × 10${}^2$ /1
$f_{19}$	Mean Error	3.99 × 10${}^1$ +	4.75 × 10${}^1$ +	2.38 × 10${}^1$ +	1.32 × 10${}^2$ +	2.78 × 10${}^1$ +	5.15 × 10${}^1$ +	1.79 × 10${}^1$
	Std Dev /Rank	4.12 × 10${}^1$ /4	4.52 × 10${}^1$ /5	2.31 × 10${}^5$ /2	3.63 × 10${}^1$ /7	1.04 × 10${}^1$ /3	1.17 × 10${}^1$ /6	3.05 × 10${}^0$ /1
$f_{20}$	Mean Error	4.46 × 10${}^3$ +	2.57 × 10${}^4$ +	1.04 × 10${}^3$ −	2.48 × 10${}^5$ +	1.11 × 10${}^4$ +	1.64 × 10${}^4$ +	3.80 × 10${}^3$
	Std Dev /Rank	3.42 × 10${}^3$ /3	1.66 × 10${}^4$ /6	7.08 × 10${}^2$ /1	1.21 × 10${}^5$ /7	4.72 × 10${}^3$ /4	5.58 × 10${}^3$ /5	2.14 × 10${}^3$ /2
$f_{21}$	Mean Error	1.03 × 10${}^5$ +	2.34 × 10${}^5$ +	4.19 × 10${}^4$ +	2.74 × 10${}^6$ +	8.31 × 10${}^5$ +	5.99 × 10${}^5$ +	1.00 × 10${}^5$
	Std Dev /Rank	6.59 × 10${}^4$ /2	1.62 × 10${}^5$ /3	1.66 × 10${}^4$ /4	1.35 × 10${}^6$ /7	4.29 × 10${}^5$ /6	1.89 × 10${}^5$ /5	6.50 × 10${}^4$ /1
$f_{22}$	Mean Error	6.43 × 10${}^2$ +	6.81 × 10${}^2$ +	6.66 × 10${}^2$ +	1.17 × 10${}^3$ +	4.01 × 10${}^2$ −	6.38 × 10${}^2$ +	6.37 × 10${}^2$
	Std Dev /Rank	2.50 × 10${}^2$ /4	2.46 × 10${}^2$ /6	1.98 × 10${}^2$ /5	3.02 × 10${}^2$ /7	1.07 × 10${}^2$ /1	1.32 × 10${}^2$ /3	1.27 × 10${}^2$ /2
$f_{23}$	Mean Error	3.15 × 10${}^2$ +	3.16 × 10${}^2$ +	3.15 × 10${}^2$ +	2.69 × 10${}^2$ −	3.20 × 10${}^2$ +	3.45 × 10${}^2$ +	3.14 × 10${}^2$
	Std Dev /Rank	1.70 × 10${}^{-2}$ /3	1.67 × 10${}^0$ /5	9.38 × 10${}^{-4}$ /3	7.39 × 10${}^1$ /1	1.59 × 10${}^0$ /6	2.54 × 10${}^1$ /7	5.50 × 10${}^{-3}$ /2
$f_{24}$	Mean Error	2.43 × 10${}^2$ +	2.45 × 10${}^2$ +	2.43 × 10${}^2$ +	2.03 × 10${}^2$ −	2.35 × 10${}^2$ +	2.09 × 10${}^2$ −	2.31 × 10${}^2$
	Std Dev /Rank	1.02 × 10${}^1$ /5	6.35 × 10${}^0$ /7	1.07 × 10${}^1$ /5	6.21 × 10${}^0$ /1	3.03 × 10${}^0$ /4	3.45 × 10${}^0$ /2	6.54 × 10${}^0$ /3
$f_{25}$	Mean Error	2.21 × 10${}^2$ +	2.12 × 10${}^2$ ≈	2.24 × 10${}^2$ +	2.02 × 10${}^2$ −	2.17 × 10${}^2$ +	2.04 × 10${}^2$ −	2.12 × 10${}^2$
	Std Dev /Rank	1.02 × 10${}^1$ /6	7.77 × 10${}^0$ /3	9.17 × 10${}^0$ /7	3.38 × 10${}^0$ /1	2.58 × 10${}^0$ /5	2.09 × 10${}^0$ /2	1.61 × 10${}^0$ /3
$f_{26}$	Mean Error	1.13 × 10${}^2$ +	1.01 × 10${}^2$ +	1.09 × 10${}^2$ +	1.98 × 10${}^2$ +	1.01 × 10${}^2$ +	1.01 × 10${}^2$ +	1.00 × 10${}^2$
	Std Dev /Rank	3.30 × 10${}^1$ /6	2.15 × 10${}^{-1}$ /2	2.75 × 10${}^1$ /5	1.19 × 10${}^1$ /7	7.98 × 10${}^{-1}$ /2	3.53 × 10${}^{-1}$ /2	1.18 × 10${}^{-1}$ /1
$f_{27}$	Mean Error	9.20 × 10${}^2$ +	9.36 × 10${}^2$ +	1.04 × 10${}^3$ +	1.81 × 10${}^3$ +	4.94 × 10${}^2$ −	1.07 × 10${}^3$ +	7.58 × 10${}^2$
	Std Dev /Rank	3.69 × 10${}^2$ /3	2.75 × 10${}^2$ /4	3.34 × 10${}^2$ /5	4.19 × 10${}^2$ /7	4.79 × 10${}^1$ /1	3.53 × 10${}^1$ /6	3.14 × 10${}^2$ /2
$f_{28}$	Mean Error	1.89 × 10${}^3$ +	1.39 × 10${}^3$ +	1.82 × 10${}^3$ +	2.52 × 10${}^3$ +	1.51 × 10${}^3$ +	8.46 × 10${}^2$ +	5.43 × 10${}^2$
	Std Dev /Rank	5.19 × 10${}^2$ /6	4.32 × 10${}^2$ /3	6.15 × 10${}^2$ /5	8.18 × 10${}^2$ /7	2.96 × 10${}^2$ /4	1.14 × 10${}^2$ /2	1.18 × 10${}^2$ /1
$f_{29}$	Mean Error	5.44 × 10${}^6$ +	7.23 × 10${}^5$ +	8.48 × 10${}^6$ +	1.44 × 10${}^5$ +	9.69 × 10${}^4$ +	8.30 × 10${}^2$ +	2.29 × 10${}^2$
	Std Dev /Rank	9.48 × 10${}^6$ /6	2.49 × 10${}^6$ /5	8.97 × 10${}^6$ /7	7.19 × 10${}^5$ /4	5.71 × 10${}^4$ /3	2.40 × 10${}^2$ /2	2.90 × 10${}^1$ /1
$f_{30}$	Mean Error	1.82 × 10${}^4$ +	6.71 × 10${}^3$ +	6.51 × 10${}^3$ +	2.28 × 10${}^5$ +	4.04 × 10${}^4$ +	2.19 × 10${}^3$ +	9.38 × 10${}^2$
	Std Dev /Rank	1.75 × 10${}^4$ /5	9.54 × 10${}^3$ /4	3.24 × 10${}^3$ /3	1.09 × 10${}^5$ /7	1.46 × 10${}^4$ /6	4.75 × 10${}^2$ /2	7.82 × 10${}^2$ /1
Average Rank		4.07	3.97	4.37	4.77	3.77	5.27	1.7
+		29	25	27	24	23	29
-		1	3	3	5	7	1
≈		0	2	0	1	0	0

Table 5. Experimental results of the HMWCA and six well-known algorithms on the $CEC2014$ functions with $D=50$.

Function	Algorithm	WCA	CWCA	ER_WCA	GSA	CLPSO	HSOGA	HMWCA
$f_1$	Mean Error	7.78 × 10${}^6$ +	2.38 × 10${}^7$ +	5.50 × 10${}^6$ −	3.93 × 10${}^8$ +	2.37 × 10${}^8$ +	7.62 × 10${}^8$ +	6.76 × 10${}^6$
	Std Dev /Rank	1.84 × 10${}^6$ /3	1.18 × 10${}^7$ /4	1.41 × 10${}^6$ /1	3.05 × 10${}^8$ /6	6.61 × 10${}^7$ /5	1.24 × 10${}^8$ /7	2.17 × 10${}^6$ /2
$f_2$	Mean Error	1.31 × 10${}^4$ −	1.16 × 10${}^9$ +	8.17 × 10${}^3$ −	2.04 × 10${}^{10}$ +	1.25 × 10${}^9$ +	5.15 × 10${}^{10}$ +	3.93 × 10${}^5$
	Std Dev /Rank	8.55 × 10${}^3$ /2	2.61 × 10${}^9$ /4	9.44 × 10${}^3$ /1	3.40 × 10${}^9$ /6	2.83 × 10${}^8$ /4	5.66 × 10${}^9$ /7	2.58 × 10${}^5$ /3
$f_3$	Mean Error	1.07 × 10${}^4$ −	1.05 × 10${}^5$ +	5.07 × 10${}^3$ −	1.56 × 10${}^5$ +	6.01 × 10${}^4$ +	1.67 × 10${}^5$ +	1.50 × 10${}^4$
	Std Dev /Rank	4.72 × 10${}^3$ /2	3.77 × 10${}^4$ /4	3.33 × 10${}^3$ /1	9.58 × 10${}^3$ /6	1.15 × 10${}^4$ /4	1.73 × 10${}^4$ /7	6.75 × 10${}^3$ /3
$f_4$	Mean Error	1.40 × 10${}^2$ −	4.81 × 10${}^2$ +	1.04 × 10${}^2$ −	2.91 × 10${}^3$ +	7.83 × 10${}^2$ +	7.37 × 10${}^3$ +	2.03 × 10${}^2$
	Std Dev /Rank	5.19 × 10${}^1$ /2	2.94 × 10${}^2$ /4	4.73 × 10${}^1$ /1	6.40 × 10${}^2$ /6	8.79 × 10${}^1$ /5	1.28 × 10${}^3$ /7	3.04 × 10${}^1$ /3
$f_5$	Mean Error	2.01 × 10${}^1$ +	2.03 × 10${}^1$ +	2.01 × 10${}^1$ +	2.00 × 10${}^1$ ≈	2.08 × 10${}^1$ +	2.12 × 10${}^1$ +	2.00 × 10${}^1$
	Std Dev /Rank	1.35 × 10${}^{-1}$ /3	9.38 × 10${}^{-2}$ /5	9.13 × 10${}^{-2}$ /3	1.06 × 10${}^{-4}$ /1	3.21 × 10${}^{-2}$ /6	5.27 × 10${}^{-2}$ /7	3.58 × 10${}^{-3}$ /1
$f_6$	Mean Error	5.91 × 10${}^1$ +	4.91 × 10${}^1$ −	5.84 × 10${}^1$ +	5.30 × 10${}^1$ +	5.14 × 10${}^1$ −	6.71 × 10${}^1$ +	5.16 × 10${}^1$
	Std Dev /Rank	4.80 × 10${}^0$ /6	4.63 × 10${}^0$ /1	7.92 × 10${}^0$ /5	2.74 × 10${}^0$ /4	2.27 × 10${}^0$ /2	1.86 × 10${}^0$ /7	3.18 × 10${}^0$ /3
$f_7$	Mean Error	4.30 × 10${}^{-2}$ −	1.01 × 10${}^1$ +	8.53 × 10${}^{-3}$ −	2.02 × 10${}^2$ +	1.09 × 10${}^1$ +	5.09 × 10${}^2$ +	4.64 × 10${}^{-1}$
	Std Dev /Rank	2.06 × 10${}^{-2}$ /2	2.74 × 10${}^1$ /4	7.12 × 10${}^{-3}$ /1	3.14 × 10${}^1$ /6	2.70 × 10${}^0$ /5	6.57 × 10${}^1$ /7	1.93 × 10${}^{-1}$ /3
$f_8$	Mean Error	3.00 × 10${}^2$ +	2.21 × 10${}^2$ +	3.03 × 10${}^2$ +	2.77 × 10${}^2$ +	9.14 × 10${}^1$ −	3.97 × 10${}^2$ +	1.93 × 10${}^2$
	Std Dev /Rank	3.96 × 10${}^1$ /5	4.77 × 10${}^1$ /3	6.53 × 10${}^1$ /6	1.80 × 10${}^1$ /4	8.54 × 10${}^0$ /1	2.59 × 10${}^1$ /7	2.86 × 10${}^1$ /2
$f_9$	Mean Error	4.01 × 10${}^2$ +	5.14 × 10${}^2$ +	3.94 × 10${}^2$ +	3.55 × 10${}^2$ +	3.76 × 10${}^2$ +	5.54 × 10${}^2$ +	2.58 × 10${}^2$
	Std Dev /Rank	7.32 × 10${}^1$ /5	7.88 × 10${}^1$ /6	5.73 × 10${}^1$ /4	2.82 × 10${}^1$ /2	2.54 × 10${}^1$ /3	3.21 × 10${}^1$ /7	6.46 × 10${}^1$ /1
$f_{10}$	Mean Error	7.29 × 10${}^3$ +	4.26 × 10${}^3$ −	6.93 × 10${}^3$ +	7.52 × 10${}^3$ +	2.49 × 10${}^3$ −	7.41 × 10${}^3$ +	4.72 × 10${}^3$
	Std Dev /Rank	8.50 × 10${}^2$ /5	1.10 × 10${}^3$ /2	8.71 × 10${}^2$ /4	7.19 × 10${}^2$ /7	2.68 × 10${}^2$ /1	5.42 × 10${}^2$ /6	8.04 × 10${}^2$ /3
$f_{11}$	Mean Error	8.08 × 10${}^3$ +	7.19 × 10${}^3$ +	7.80 × 10${}^3$ +	8.17 × 10${}^3$ +	9.29 × 10${}^3$ +	1.39 × 10${}^4$ +	6.88 × 10${}^3$
	Std Dev /Rank	1.40 × 10${}^3$ /4	6.86 × 10${}^2$ /2	1.03 × 10${}^3$ /3	8.54 × 10${}^2$ /5	4.63 × 10${}^2$ /6	4.12 × 10${}^2$ /7	5.96 × 10${}^2$ /1
$f_{12}$	Mean Error	2.16 × 10${}^0$ +	6.29 × 10${}^{-1}$ −	2.13 × 10${}^0$ +	1.28 × 10${}^{-2}$ −	1.18 × 10${}^0$ −	4.07 × 10${}^0$ +	1.24 × 10${}^0$
	Std Dev /Rank	6.70 × 10${}^{-1}$ /6	1.85 × 10${}^{-1}$ /2	8.20 × 10${}^{-1}$ /5	6.79 × 10${}^{-3}$ /1	1.34 × 10${}^{-1}$ /3	3.90 × 10${}^{-1}$ /7	2.90 × 10${}^{-1}$ /4
$f_{13}$	Mean Error	6.25 × 10${}^{-1}$ +	8.01 × 10${}^{-1}$ +	6.31 × 10${}^{-1}$ +	2.87 × 10${}^0$ +	5.36 × 10${}^{-1}$ −	4.98 × 10${}^0$ +	5.81 × 10${}^{-1}$
	Std Dev /Rank	8.50 × 10${}^{-2}$ /3	1.40 × 10${}^{-1}$ /5	1.50 × 10${}^{-1}$ /4	5.98 × 10${}^{-1}$ /6	7.86 × 10${}^{-2}$ /1	3.24 × 10${}^{-1}$ /7	5.33 × 10${}^{-2}$ /2
$f_{14}$	Mean Error	4.15 × 10${}^{-1}$ +	2.62 × 10${}^0$ +	3.84 × 10${}^{-1}$ +	4.33 × 10${}^1$ +	4.88 × 10${}^{-1}$ +	1.18 × 10${}^2$ +	3.30 × 10${}^{-1}$
	Std Dev /Rank	1.92 × 10${}^{-1}$ /3	5.25 × 10${}^0$ /5	1.32 × 10${}^{-1}$ /2	7.20 × 10${}^0$ /6	8.13 × 10${}^{-2}$ /4	1.33 × 10${}^1$ /7	3.79 × 10${}^{-2}$ /1
$f_{15}$	Mean Error	8.77 × 10${}^1$ −	1.05 × 10${}^5$ +	1.26 × 10${}^2$ +	9.76 × 10${}^3$ +	7.27 × 10${}^2$ +	2.16 × 10${}^5$ +	1.07 × 10${}^2$
	Std Dev /Rank	2.33 × 10${}^1$ /1	3.36 × 10${}^5$ /6	4.38 × 10${}^1$ /3	6.07 × 10${}^3$ /5	3.30 × 10${}^2$ /4	7.80 × 10${}^4$ /7	1.84 × 10${}^1$ /2
$f_{16}$	Mean Error	2.24 × 10${}^1$ +	2.14 × 10${}^1$ −	2.24 × 10${}^1$ +	2.26 × 10${}^1$ +	2.14 × 10${}^1$ −	2.30 × 10${}^1$ +	2.16 × 10${}^1$
	Std Dev /Rank	6.51 × 10${}^{-1}$ /4	5.88 × 10${}^{-1}$ /1	5.65 × 10${}^{-1}$ /4	3.45 × 10${}^{-1}$ /6	3.12 × 10${}^{-1}$ /1	1.55 × 10${}^{-1}$ /7	9.07 × 10${}^{-1}$ /3
$f_{17}$	Mean Error	7.90 × 10${}^5$ −	4.06 × 10${}^6$ +	3.34 × 10${}^5$ −	2.69 × 10${}^7$ +	4.03 × 10${}^7$ +	7.84 × 10${}^7$ +	1.73 × 10${}^6$
	Std Dev /Rank	2.82 × 10${}^5$ /2	2.50 × 10${}^6$ /4	1.55 × 10${}^5$ /1	1.07 × 10${}^7$ /5	1.36 × 10${}^7$ /6	1.69 × 10${}^7$ /7	5.87 × 10${}^5$ /3
$f_{18}$	Mean Error	2.77 × 10${}^3$ +	5.49 × 10${}^3$ +	2.92 × 10${}^3$ +	3.16 × 10${}^8$ +	9.25 × 10${}^6$ +	8.58 × 10${}^8$ +	2.13 × 10${}^3$
	Std Dev /Rank	1.92 × 10${}^3$ /2	2.22 × 10${}^3$ /4	2.07 × 10${}^3$ /3	6.70 × 10${}^8$ /6	4.50 × 10${}^6$ /5	1.70 × 10${}^8$ /7	1.15 × 10${}^3$ /1
$f_{19}$	Mean Error	6.39 × 10${}^1$ +	6.91 × 10${}^1$ +	7.20 × 10${}^1$ +	1.72 × 10${}^2$ +	9.43 × 10${}^1$ +	3.85 × 10${}^2$ +	5.22 × 10${}^1$
	Std Dev /Rank	3.00 × 10${}^1$ /2	3.31 × 10${}^1$ /3	2.59 × 10${}^1$ /4	3.22 × 10${}^1$ /6	1.20 × 10${}^1$ /5	5.60 × 10${}^1$ /7	3.23 × 10${}^1$ /1
$f_{20}$	Mean Error	6.07 × 10${}^3$ −	7.20 × 10${}^4$ +	2.53 × 10${}^3$ −	1.99 × 10${}^5$ +	4.90 × 10${}^4$ +	7.17 × 10${}^4$ +	1.81 × 10${}^4$
	Std Dev /Rank	3.89 × 10${}^3$ /2	3.24 × 10${}^4$ /6	1.67 × 10${}^3$ /1	8.45 × 10${}^4$ /7	1.00 × 10${}^4$ /4	2.48 × 10${}^4$ /5	1.34 × 10${}^4$ /3
$f_{21}$	Mean Error	4.71 × 10${}^5$ −	1.83 × 10${}^6$ +	2.03 × 10${}^5$ −	4.58 × 10${}^6$ +	1.21 × 10${}^7$ +	1.65 × 10${}^7$ +	9.98 × 10${}^5$
	Std Dev /Rank	2.64 × 10${}^5$ /2	1.16 × 10${}^6$ /4	1.16 × 10${}^5$ /1	1.08 × 10${}^6$ /5	4.48 × 10${}^6$ /6	6.04 × 10${}^6$ /7	5.53 × 10${}^5$ /3
$f_{22}$	Mean Error	1.50 × 10${}^3$ +	1.51 × 10${}^3$ +	1.55 × 10${}^3$ +	2.15 × 10${}^3$ +	1.48 × 10${}^3$ +	2.25 × 10${}^3$ +	1.13 × 10${}^3$
	Std Dev /Rank	3.82 × 10${}^2$ /3	3.31 × 10${}^2$ /4	3.86 × 10${}^2$ /5	3.95 × 10${}^2$ /6	2.17 × 10${}^2$ /2	1.88 × 10${}^2$ /7	2.89 × 10${}^2$ /1
$f_{23}$	Mean Error	3.45 × 10${}^2$ +	3.59 × 10${}^2$ +	3.44 × 10${}^2$ +	2.55 × 10${}^2$ −	3.92 × 10${}^2$ +	3.31 × 10${}^2$ −	3.37 × 10${}^2$
	Std Dev /Rank	1.28 × 10${}^0$ /5	1.39 × 10${}^1$ /6	2.69 × 10${}^{-2}$ /4	1.52 × 10${}^2$ /1	1.08 × 10${}^1$ /7	7.84 × 10${}^1$ /2	1.70 × 10${}^{-1}$ /3
$f_{24}$	Mean Error	3.00 × 10${}^2$ +	2.97 × 10${}^2$ +	3.08 × 10${}^2$ +	2.40 × 10${}^2$ −	2.93 × 10${}^2$ +	2.17 × 10${}^2$ −	2.84 × 10${}^2$
	Std Dev /Rank	9.52 × 10${}^0$ /6	1.63 × 10${}^1$ /5	1.16 × 10${}^1$ /7	1.66 × 10${}^1$ /2	1.91 × 10${}^0$ /4	6.62 × 10${}^0$ /1	1.13 × 10${}^1$ /3
$f_{25}$	Mean Error	2.45 × 10${}^2$ +	2.24 × 10${}^2$ −	2.44 × 10${}^2$ +	2.04 × 10${}^2$ −	2.54 × 10${}^2$ +	2.03 × 10${}^2$ −	2.27 × 10${}^2$
	Std Dev /Rank	1.03 × 10${}^1$ /6	9.48 × 10${}^0$ /3	1.11 × 10${}^1$ /5	5.55 × 10${}^0$ /2	7.41 × 10${}^0$ /7	1.69 × 10${}^0$ /1	1.25 × 10${}^1$ /4
$f_{26}$	Mean Error	1.75 × 10${}^2$ +	1.25 × 10${}^2$ +	2.32 × 10${}^2$ −	2.00 × 10${}^2$ +	1.24 × 10${}^2$ −	1.07 × 10${}^2$ −	1.50 × 10${}^2$
	Std Dev /Rank	7.59 × 10${}^1$ /5	6.78 × 10${}^1$ /7	1.01 × 10${}^2$ /3	1.00 × 10${}^{-1}$ /6	3.78 × 10${}^1$ /2	5.61 × 10${}^{-1}$ /1	5.27 × 10${}^1$ /4
$f_{27}$	Mean Error	1.87 × 10${}^3$ +	1.62 × 10${}^3$ −	1.85 × 10${}^3$ +	3.25 × 10${}^3$ +	1.63 × 10${}^3$ −	2.00 × 10${}^3$ +	1.67 × 10${}^3$
	Std Dev /Rank	1.26 × 10${}^2$ /5	1.07 × 10${}^2$ /1	1.28 × 10${}^2$ /4	4.99 × 10${}^2$ /7	1.80 × 10${}^2$ /2	4.42 × 10${}^1$ /6	1.62 × 10${}^2$ /3
$f_{28}$	Mean Error	3.64 × 10${}^3$ +	2.81 × 10${}^3$ +	3.65 × 10${}^3$ +	5.93 × 10${}^3$ +	4.24 × 10${}^3$ +	8.26 × 10${}^2$ +	4.74 × 10${}^2$
	Std Dev /Rank	1.03 × 10${}^3$ /4	6.16 × 10${}^2$ /3	9.26 × 10${}^2$ /5	1.41 × 10${}^3$ /7	8.98 × 10${}^2$ /6	1.17 × 10${}^3$ /2	4.71 × 10${}^1$ /1
$f_{29}$	Mean Error	1.23 × 10${}^8$+	9.22 × 10${}^6$ +	1.08 × 10${}^8$ +	2.02 × 10${}^2$ −	5.93 × 10${}^6$ +	5.19 × 10${}^4$ +	2.37 × 10${}^2$
	Std Dev /Rank	1.06 × 10${}^8$ /7	1.88 × 10${}^7$ /5	7.85 × 10${}^7$ /6	3.72 × 10${}^{-1}$ /1	2.02 × 10${}^6$ /4	2.06 × 10${}^4$ /3	1.73 × 10${}^1$ /2
$f_{30}$	Mean Error	4.31 × 10${}^4$ +	1.65 × 10${}^4$ +	1.88 × 10${}^4$ +	3.17 × 10${}^6$ +	2.41 × 10${}^5$ +	7.38 × 10${}^4$ +	1.91 × 10${}^3$
	Std Dev /Rank	5.51 × 10${}^4$ /4	3.71 × 10${}^3$ /2	4.31 × 10${}^3$ /3	3.72 × 10${}^6$ /7	8.66 × 10${}^4$ /6	7.47 × 10${}^4$ /5	4.21 × 10${}^2$ /1
Average Rank		3.7	3.83	3.33	4.77	4.03	5.73	2.33
+		22	24	21	24	22	26
-		8	6	9	5	8	4
≈		0	0	0	1	0	0

From Table 4, we can see that for unimodal functions $f_1$–$f_3$, the HMWCA obtains the best results for all functions, except the ER_WCA has the best results for $f_1$, where the HMWCA is significantly better than the CWCA, GSA, CLPSO and HSOGA achieving 3 in terms of its rank. For simple multimodal functions $f_4$–$f_{16}$, the HMWCA obtains the best results for most functions, including $f_4$, $f_5$, $f_7$, $f_9$–$f_{11}$ and $f_{14}$, while CLPSO attains the best results for $f_6$, $f_8$, $f_{15}$ and $f_{16}$, the GSA achieves the best results for $f_5$, $f_{12}$ and $f_{13}$, while the CWCA has the best results for $f_{15}$. For hybrid functions $f_{17}$–$f_{22}$, the HMWCA obtains the best results for $f_{18}$, $f_{19}$ and $f_{21}$, the ER_WCA has the best results for $f_{17}$ and $f_{20}$, and CLPSO has the best results for $f_{22}$. For composition functions $f_{23}$–$f_{30}$, the HMWCA obtains the best results for $f_{26}$ and $f_{28}$–$f_{30}$, the GSA obtains the best results for $f_{23}$–$f_{25}$, and CLPSO achieves the best results for $f_{27}$. In summary, according to the results of the Wilcoxon’s rank sum tests reported in Table 4, the HMWCA is better than the WCA, CWCA, ER_WCA, GSA, CLPSO and HSOGA on the 29, 25, 27, 24, 23, and 29 test functions, respectively, equivalent on the 0, 2, 0, 1, 0, and 0 test functions, respectively, and slightly worse on the 1, 3, 3, 5, 7, and 1 test functions, respectively. Moreover, the WCA, CWCA, ER_WCA, GSA, CLPSO, HSOGA and HMWCA obtain $4.07$, $3.97$, $4.37$, $4.77$, $3.77$, $5.27$ and $1.7$ in terms of their average rank for all functions, respectively.

For clarity, the evolution curves of these compared algorithms on ten functions, including $f_1$, $f_2$, $f_3$, $f_4$, $f_9$, $f_{17}$, $f_{19}$, $f_{21}$, $f_{28}$ and $F_{30}$, are plotted in Figure 1 and Figure 2, and their results from 25 independent runs are compared in Figure 3 and Figure 4. From Figure 1, Figure 2, Figure 3 and Figure 4, we can see that the HMWCA has a more promising performance than others. In detail, for unimodal functions $f_1$ and $f_2$, the HMWCA has a better exploration ability than the WCA and ER_WCA, and worse than the GSA. Meanwhile, for complex functions, the HMWCA has a better performance for most functions, especially for $f_9$, $f_{19}$, $f_{28}$ and $f_{30}$. Therefore, the HMWCA has an effective performance.

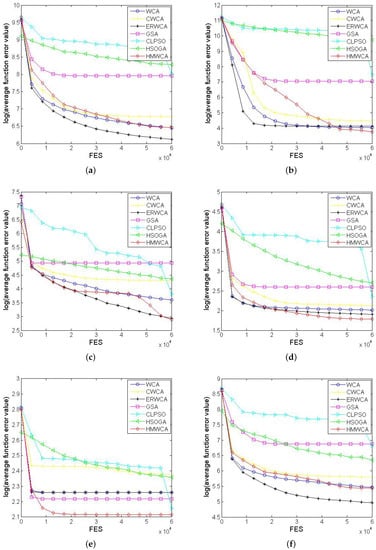
Figure 1. The evolution curves of the seven studied algorithms for functions (a) $f_1$, (b) $f_2$, (c) $f_3$, (d) $f_4$, (e) $f_9$ and (f) $f_{17}$ with $D=30$.

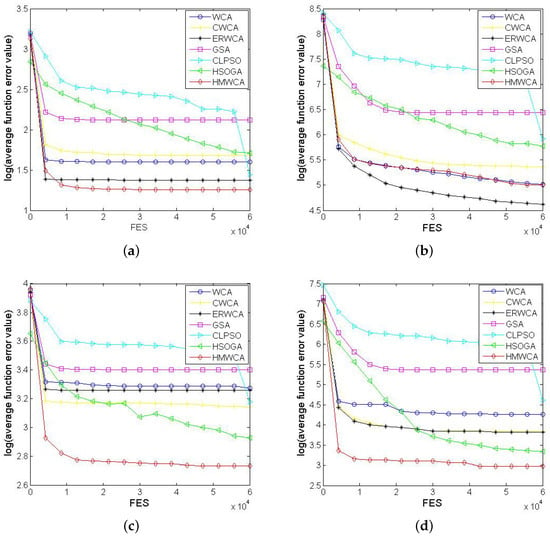
Figure 2. The evolution curves of the seven studied algorithms for functions (a) $f_{19}$, (b) $f_{21}$, (c) $f_{28}$, (d) $f_{30}$ with $D=30$.

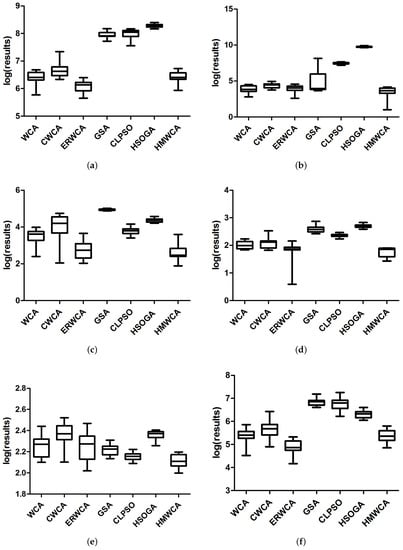
Figure 3. The comparisons of the results of the seven studied algorithms for the functions (a) $f_1$, (b) $f_2$, (c) $f_3$, (d) $f_4$, (e) $f_9$ and (f) $f_{17}$ with $D=30$.

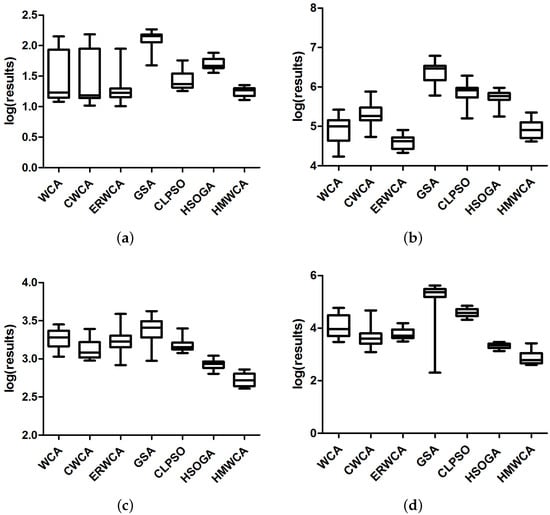
Figure 4. The comparisons of the results of the seven studied algorithms for the functions (a) $f_{19}$, (b) $f_{21}$, (c) $f_{28}$, (d) $f_{30}$ with $D=30$.

From Table 5, we can see that for unimodal functions $f_1$–$f_3$, the HMWCA is significantly better than the CWCA, GSA, CLPSO and HSOGA, while the ER_WCA achieves the best results for all functions. This might be because the gravitational search reduces the exploitation ability of the HMWCA. For simple multimodal functions $f_4$–$f_{16}$, the HMWCA obtains the best results for $f_9$, $f_{11}$ and $f_{14}$, the ER_WCA obtains the best results for $f_4$ and $f_7$, while the CWCA, GSA and WCA have the best results for $f_6$, $f_{12}$ and $f_{15}$, respectively, and CLPSO obtains the best results for $f_8$, $f_{10}$ and $f_{13}$. In particular, the HMWCA and GSA obtain the best results for $f_5$, while the CWCA and CLPSO have the best results for $f_{16}$. For hybrid functions $f_{17}$–$f_{22}$, the HMWCA obtains the results for $f_{18}$, $f_{19}$ and $f_{22}$, while the ER_WCA has the best results for $f_{17}$, $f_{20}$ and $f_{21}$. For composition functions $f_{23}$–$f_{30}$, the HMWCA obtains the best results for $f_{28}$ and $f_{30}$, the GSA has the best results for $f_{23}$ and $f_{29}$, the HSOGA obtains the best results for $f_{24}$–$f_{26}$, and the CWCA obtains the best results for $f_{27}$. According to the statistical results of the Wilcoxon’s rank sum test reported in Table 5, the HMWCA is better than the WCA, CWCA, ER_WCA, GSA, CLPSO and HSOGA for the 22, 24, 21, 24, 22, and 26 test functions, respectively, equivalent on 0, 0, 0, 1, 0, and 0 test functions, respectively, and slightly worse on 8, 6, 9, 5, 8, and 4 test functions, respectively. Furthermore, in terms of their average rank, the WCA, CWCA, ER_WCA, GSA, CLPSO, HSOGA and HMWCA obtain $3.7$, $3.83$, $3.33$, $4.77$, $4.03$, $5.73$ and $2.33$ for all functions, respectively. Therefore, the HMWCA is a more promising optimizer.

4.4. Algorithm Efficiency

In this subsection, a comparisons of the HMWCA with the WCA and GSA are conducted to show the running efficiency of the HMWCA on six typical functions, including $f_1$, $f_3$, $f_4$, $f_9$, $f_{17}$ and $f_{21}$. This experiment was conducted in MATLAB 2015a on a personal computer (Pentium(R) Dual-Core CPU at 3.06 GHz and 4 GB memory), and the average running time of 25 independent runs was recorded to evaluate their efficiencies. The maximum number of function evaluations $FE{S}_{max}$ was considered as the termination condition and set to 60,000 for all algorithms. Table 6 reports their numerical results, where the time represents the CPU time when $FE{S}_{max}$ is met.

Table 6. The average CPU time of the HMWCA, WCA and GSA.

Function	${\mathit{f}}_1$	${\mathit{f}}_3$	${\mathit{f}}_4$	${\mathit{f}}_9$	${\mathit{f}}_{17}$	${\mathit{f}}_{21}$
HMWCA	54.22 s	55.87 s	53.23 s	54.98 s	59.72 s	56.70 s
WCA	30.70 s	24.16 s	31.03 s	25.37 s	29.44 s	28.16 s
GSA	116.60 s	115.87 s	115.40 s	116.58 s	115.99 s	116.55 s

From Table 6, we can see that the HMWCA is faster than the GSA and slower than the WCA. It should be noted that the water cycle search and gravitational search are alternatively operated during the search process according to their performances. This determines that the HMWCA cost more than the WCA but less than the GSA. Thus, the HMWCA has acceptable complexity.

4.5. Application

Herein, the HMWCA is further applied to solve a practical problem, named the spread-spectrum radar polyphase code design (SSRPPCD) [56]. This problem aims to select an appropriate waveform, and can be modelled as the following min–max non-linear non-convex optimization problem.

$$\begin{array}{c}\hfill \underset{x\in X}{min}f\left(x\right)=max\{{\varphi }_1\left(x\right),\cdots ,{\varphi }_{2m}\left(x\right)\},\end{array}$$

where $X=\{(x_1,\cdots ,x_n)\in R^n|0\le x_j\le 2\pi$ for $j=1,\cdots ,n\}$, $m=2n-1$, ${\varphi }_{m+i}\left(x\right)=-{\varphi }_i\left(x\right)$ for $i=1,\cdots ,m$ and

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}{\varphi }_{2i-1}\left(x\right)={\displaystyle \sum _{j=1}^n}cos\left({\displaystyle \sum _{k=|2i-j-1|+1}^j}{x}_k\right),\hfill & i=1,\cdots ,n\hfill \\ {\varphi }_{2i}\left(x\right)=0.5+{\displaystyle \sum _{j=i+1}^n}cos\left({\displaystyle \sum _{k=|2i-j|+1}^j}{x}_k\right),\hfill & i=1,\cdots ,n-1.\hfill \end{array}\right.\end{array}$$

Clearly, the objective function is piecewise smooth and has numerous local optima. Table 7 lists the numerical results of the HMWCA, WCA, CWCA and ER_WCA over 25 runs with n = 30 and $FE{S}_{max}$ = 60,000, where the best algorithm among them is marked in bold. From Table 7 one can see that the HMWCA has the best results in terms of the “Best” result, “Worse” result and “Average” value, while it has a poorer performance than the CWCA and ER_WCA in term of the standard deviation. Therefore, the HMWCA’s performance is more promising for this problem.

Table 7. Numerical results of the HMWCA on the SSRPPCD.

Algorithm	Best (Result)	Worse (Result)	Average Value	Standard Deviation
WCA	3.62 × 10${}^0$	2.57 × 10${}^0$	3.09 × 10${}^0$	4.00 × 10${}^{-1}$
CWCA	3.35 × 10${}^0$	2.46 × 10${}^0$	3.02 × 10${}^0$	3.14 × 10${}^{-1}$
ER_WCA	3.44 × 10${}^0$	2.68 × 10${}^0$	2.93 × 10${}^0$	2.34 × 10${}^{-1}$
HMWCA	3.27 $n.\times$ 10${}^0$ is versio	2.29 × 10${}^0$	2.77 × 10${}^0$	3.16 × 10${}^{-1}$

5. Conclusions

To integrate the advantages of the WCA and GSA, this paper proposed the HMWCA with the GSA for global optimization. To effectively balance exploitation and exploration, a modified niching technique was first designed and used to assign the sea, rivers and their corresponding streams in the WCA, and the total number of rivers and the sea were adjusted in an adaptive manner during the search process. Moreover, the gravitational search and water cycle search were combined and alternatively operated to explore or exploit the search space according to their performances within certain iterations. Furthermore, to improve the search capability, the binomial crossover operation was also employed and operated after the water cycle search or gravitational search, and an adaptive method was used to set its parameter. Finally, the HMWCA was compared with six well-known optimization algorithms to evaluate its performance on 30 IEEE CEC2014 benchmark functions with different dimensions, and applied to the spread-spectrum radar polyphase code design (SSRPPCD). The experimental results show that the proposed algorithm is very competitive.

Further research should focus on the application of the HMWCA to constrained optimization problems as well as real-world optimization problems to further test its performance. Furthermore work should be conducted to design other improved optimization approaches by hybridising the WCA with other heuristic algorithms.