An Alternated Inertial Projection Algorithm for Multi-Valued Variational Inequality and Fixed Point Problems

Abstract

In this paper, we propose an alternated inertial projection algorithm for solving multi-valued variational inequality problem and fixed point problem of demi-contractive mapping. On one hand, this algorithm only requires the mapping is pseudo-monotone. On the other hand, this algorithm is combined with the alternated inertial method to accelerate the convergence speed. The global convergence of the algorithm can be obtained under mild conditions. Preliminary numerical results show that the convergence speed of our algorithm is faster than some existing algorithms.

1. Introduction and Preliminaries

Let C be a nonempty closed convex subset of $R^n$ and $F:R^n\to 2^{R^n}$ be a set-valued mapping with nonempty compact and convex values, $R^n$ is n-dimensional Euclidean space. We consider the following multi-valued variational inequality problem (MVIP):

find a vector $x\in C$ and a vector $t\in F\left(x\right)$ such that

$$⟨t,y-x⟩\ge 0,\mathrm{for}\mathrm{all}y\in C.$$

We denote the solution set of problem (MVIP) is S, $S_D$ is the solution set of the dual multi-valued variational inequality: find a vector $x\in C$ that satisfies

$$⟨u,y-x⟩\ge 0,\mathrm{for}\mathrm{all}y\in C,\mathrm{all}u\in F\left(y\right).$$

When F is continuous, we have

$$S_D\subseteq S.$$

When the mapping F is single-valued, problem (MVIP) reduces to problem (VIP), i.e., find a vector $x\in C$ that satisfies

$$⟨F\left(x\right),y-x⟩\ge 0,\mathrm{for}\mathrm{all}y\in C.$$

It is not difficult to see from the above definitions that the multi-valued variational inequality is a more general variational inequality. Therefore, it is of great significance to study the multi-valued variational inequality.

In recent years, multi-valued variational inequality has attracted extensive attention from scholars. In 2018, Ye [1] proposed an algorithm for solving multi-valued variational inequality problem, this algorithm requires the mapping F has pseudo-monotonicity and $S\ne Ø$. Chen [2] proposed an inertial Popov extragradient projection algorithm for solving multi-valued variational inequality problem, and this algorithm only needs one value of the mapping F. Thus, the computation amount of the algorithm reduces, but it requires that the mapping F is pseudo-monotone and Lipschitz continuous. He [3] proposed a new algorithm for variational inequality problem without monotonicity. However, the next iteration point $x^{k+1}$ is generated by projecting a vector onto the intersection of the feasible set C and $k+1$ half-spaces. Hence, the computational cost of computing $x^{k+1}$ will increase as k increases.

Next, we introduce the fixed point problem (FFP) [4].

Let $T:R^n\to R^n$ be a mapping and $Fix\left(T\right)$ be the set of the fixed points of T, that is,

$$Fix\left(T\right)=\{x\in R^n:T\left(x\right)=x\}.$$

(1)

With the development of variational inequality algorithm, the common solutions of variational inequality and fixed point problems have been widely studied, for example, [5,6,7,8,9,10,11,12,13,14,15]. The reason for studying this kind of problems is that some constraints in mathematical models can be expressed as variational inequality problems or fixed point problems, especially in practical problems, such as signal processing, network resource allocation, image restoration, etc. The multi-valued variational inequality problem generalizes single-valued to multi-valued, which makes the structure of variational inequality complicated. Based on the above, the research on the common solutions of multi-valued variational inequality and fixed point problems is not deep enough, compared with classical variational inequality.

In 2015, Tu [16] introduced an algorithm to solve multi-valued variational inequality problem and fixed point problem of nonexpansive mapping, which requires that the mapping F must be pseudo-monotone. In addition, as we are all known, nonexpansive mapping is not a very generalized mapping as compared to quasi-nonexpansive mapping, strictly pseudo-contractive, demi-contractive mapping, etc. Therefore, it is very interesting to study the common solution of variational inequality problem and fixed point problem of these classes of mappings. In 2018, Zhang [17] proposed an algorithm to solve multi-valued variational inequality problem and fixed point problem of strictly pseudo-contractive mappings. Compared with the algorithm in [16], this algorithm does not require any monotonicity of the mapping F, and this algorithm solves the fixed point problem of a class of strictly pseudo-contractive mappings. Therefore, it is suitable for more common solutions of variational inequalities and fixed points problem. However, similar to the algorithm in [3], this algorithm needs to calculate the projection to the intersection of $k+1$ half spaces and C once in each iteration, computational amount will increase with the growth of the number of iterations increases unceasingly, the convergence speed of the algorithm is seriously affected.

In order to improve the convergence speed of algorithm, scholars have done extensive research [18,19,20,21]. Utilizing inertial technique can accelerate the convergence speed of the algorithm. For general inertial technique, the Fejér monotonicity of $\{\parallel x_n-x^{*}\parallel \}(x\in S)$ is lost and this makes the inertial technique ineffective in speeding up the algorithm in some cases. In order to overcome this shortcoming, in 2015, Mu [22] proposed an alternated inertial method, to some extent, which ensured Fejér monotonicity of $\{\parallel x_{2n}-x^{*}\parallel \}(x\in S)$, see [23,24,25].

Inspired by the above work, this paper proposes an improved alternated inertial projection algorithm for solving the common solution of multi-valued variational inequality and fixed point problems. Our algorithm combines the alternated inertial technique to ensure the Fejér monotonicity of $\{\parallel x_n-x^{*}\parallel \}(x\in S)$, thus improves the convergence rate of the algorithm. In addition, under some mild conditions, we prove that the sequence generated by the algorithm is globally convergent.

The paper is structured as follows: In Section 1, we give some theorems and lemmas, and Section 2 introduces our algorithm and prove a strong convergence result of it. In Section 3, two numerical experiments are given to prove the effectiveness of the algorithm. The conclusion is given in Section 4.

For the completeness of next section, we give the following definitions.

The inner product in $R^n$ is denoted by $⟨·,·⟩$ and its norm by $\parallel ·\parallel$. The weak convergence of $x_n$ to x represented by $x_n\rightharpoonup x$.

Definition 1 ([26]). 

Let $F:R^n\to 2^{R^n}$ be multi-valued mapping, $C\subset R^n$ be a nonempty closed convex set. We say

(i) F is said to be outer-semicontinuous, if and only if, the graph of F is closed.

(ii) F is said to be inner-semicontinuous at $x\in C$, if and only if, for any $y\in F\left(x\right)$ and for any sequence ${\left(x_k\right)}_{k\in N}$ such that $x_k\to x$, there exists a sequence ${\left(y_k\right)}_{k\in N}$ satisfies $y_k\in F\left(x_{{}_k}\right)$ for all $k\in N$, $y_k\to y$.

(iii) F is said to be continuous if and only if it is both outer-semicontinuous and inner-semicontinuous.

Definition 2. 

Let $C\subset R^n$ be a nonempty closed convex set, a mapping $F:R^n\to 2^{R^n}$ is called

(i) pseudo-monotone on C if and only if for all $x,y\in C$ and $t_x\in F\left(x\right)$

$$⟨t_x,y-x⟩\ge 0 implies ⟨t_y,y-x⟩\ge 0 for all t_y\in F\left(y\right).$$

A mapping $T:R^n\to R^n$ is called

(ii) nonexpansive if and only if

$$\parallel T\left(x\right)-T\left(y\right)\parallel \le \parallel x-y\parallel ,for all x,y\in R^n.$$

(iii) ρ-demi-contractive with $0\le \rho <1$ if and only if

$${\parallel T\left(x\right)-z\parallel }^2\le {\parallel x-z\parallel }^2+\rho {\parallel x-T\left(x\right)\parallel }^2,\mathit{for}\mathit{all}z\in Fix\left(T\right),x\in R^n.$$

(2)

or equivalently

$$⟨Tx-x,x-z⟩\le \frac{\rho -1}{2}{\parallel x-Tx\parallel }^2,\mathit{for}\mathit{all}z\in Fix\left(T\right),x\in R^n.$$

(3)

(iv) ρ-strict pseudo-contractive mapping if and only if there exists $\rho \in [0,1)$ satisfying

$${\parallel T\left(x\right)-T\left(y\right)\parallel }^2\le {\parallel x-y\parallel }^2+\rho {\parallel (I-T)x-(I-T)y\parallel }^2,\mathit{for}\mathit{all}x,y\in R^n.$$

or equivalently

$${\displaystyle ⟨Tx-Ty,x-z⟩\le {\parallel x-y\parallel }^2-\frac{1-\rho }{2}{\parallel (I-T)x-(I-T)y\parallel }^2,\mathit{for}\mathit{all}x,y\in R^n.}$$

Remark 1. 

We can easily seen from the above definition that:

T is nonexpansive mapping implies T is ρ-strict pseudo-contractive mapping, and T is ρ-strict pseudo-contractive mapping implies T is ρ-demi-contractive mapping. The converse is not necessarily true.

Example 1. 

Let the mapping $T:[-2,1]\to [-2,1]$ such that

$$Tx=-x^2-x.$$

We can see that T is a demi-contractive mapping, but not a nonexpansive or strictly pseudo-contractive mapping, so the demi-contractive mapping is more generalized than nonexpansive and strictly pseudo-contractive mapping.

Definition 3 ([27]). 

Assume that the mapping T such that $Fix\left(T\right)\ne Ø$. Then T is said to be demiclosed at zero if for any sequence $\left\{x_n\right\}$ in $R^n$, the following implication holds:

$$x_n\rightharpoonup x \mathit{and} (I-T)x_n\to 0 \mathit{implies} x\in Fix\left(T\right).$$

Lemma 1 ([28]). 

For a given multi-valued variational inequality problem (MVIP(F,C)), we let its residual function be $r(x,\mu ,\xi )=x-P_C(x-\mu \xi )$, $\xi \in F\left(x\right)$. Then

x is a solution to the (MVIP(F,C)) if and only if $r(x,\mu ,\xi )=0$, for all $\mu >0$.

Lemma 2 ([1]). 

Let $C\subset R^n$ be a nonempty closed convex set. Then, we have

(i) $⟨P_C\left(x\right)-x,y-P_C\left(x\right)⟩\ge 0$, for all $y\in C$, all $x\in R^n$.

(ii) $\parallel P_C\left(x\right)-P_C\left(y\right)\parallel \le \parallel x-y\parallel$, for all $x,y\in R^n$.

(iii) $\parallel P_C{\left(x\right)-z\parallel }^2\le {\parallel x-z\parallel }^2-{\parallel P_C\left(x\right)-x\parallel }^2$, for all $x\in R^n$, all $z\in C$.

Lemma 3 ([29]). 

The following equalities are true:

(i) $2⟨x,y⟩={\parallel x\parallel }^2+{\parallel y\parallel }^2-{\parallel x-y\parallel }^2$, for all $x,y\in H$.

(ii) $2⟨x-y,x-z⟩={\parallel x-y\parallel }^2{+\parallel x-z\parallel }^2-{\parallel y-z\parallel }^2$, for all $x,y,z\in R^n$.

(iii) For $\forall x,y\in H$, $\alpha ,\beta \in [0,1]$ and $\alpha +\beta =1$, then

$${\parallel \alpha x+\beta y\parallel }^2={\alpha \parallel x\parallel }^2+{\beta \parallel y\parallel }^2-\alpha \beta {\parallel x-y\parallel }^2.$$

(iv) For all $x,y\in H$, we have

$${\parallel (1+\theta )x-\theta y\parallel }^2={(1+\theta )\parallel x\parallel }^2-{\theta \parallel y\parallel }^2+\theta (1+\theta ){\parallel x-y\parallel }^2.$$

Lemma 4 ([1]). 

Let $x\in R^n$, $\xi \in F\left(x\right)$, then the following sentences are true

(i) $\parallel r(x,\alpha ,\xi )\parallel$ is nondecreasing, for all $\alpha >0$;

(ii) ${\displaystyle \frac{\parallel r(x,\alpha ,\xi )\parallel }{\alpha }}$ is nonincreasing, for all $\alpha >0$.

Lemma 5 ([30]). 

Let C be a closed convex subset of $R^n$, h be a real-valued function on $R^n$, and $K=\{x\in C:h(x)\le 0\}$. If K is nonempty and h is Lipschitz continuous on C with modulus $\theta >0$, then

$$\mathrm{dist}(x,K)\ge {\theta }^{-1}\max \left\{h\right(x),0\},\mathit{for} \mathit{all} x\in C.$$

2. Main Results

In this section, we introduce an alternated inertial projection algorithm for the common solution of multi-valued variational inequality and fixed points problem. The algorithm only requires the following mild assumptions:

Assumption 1. 

$S\cap Fix\left(T\right)\ne Ø$.

Assumption 2. 

The multi-valued mapping F is continuous on $R^n$ with nonempty compact convex values, and is pseudo-monotone on C. The mapping $T:R^n\to R^n$ is ρ-demi-contractive mapping, and demiclosed at zero, $\rho \in \left({\displaystyle 0,1-\frac{\sqrt{2}}{2}}\right)$.

Assumption 3. 

$\theta \in \left({\displaystyle 0,\frac{2{(1-\rho )}^2-1}{2{(1-\rho )}^2+1}}\right)$, ${\displaystyle \frac{1+\theta }{2(1-\rho )}<{\beta }_n<\sqrt{{\displaystyle \frac{1-{\theta }^2}{2}}}}$.

Remark 2. 

In Algorithm 1, if $\theta =0$ and the mapping T is the identity mapping $(i.e.,T(x)=x)$, then Algorithm 1 reduces to He’s algorithm proposed in [3].

Lemma 6 ([1]). 

For any ${\xi }_n\in F\left({\omega }_n\right)$, the step size can be clearly defined, that is, there must be a nonnegative integer m satisfies the following inequality

$$l^m⟨{\xi }_n-t_n\left(m\right),{\omega }_n-y_n\left(m\right)⟩\le \sigma {\parallel {\omega }_n-y_n\left(m\right)\parallel }^2.$$

Lemma 7. 

Let $\overline{x}\in S$, and $\left\{x_n\right\}$ be the sequence generated by Algorithm 1, then

$$h_n\left(\overline{x}\right)\le 0 \mathit{and} h_n\left(x_n\right)\ge (1-\sigma ){\parallel r({\omega }_n,{\alpha }_n,{\xi }_n)\parallel }^2.$$

Algorithm 1 Choose parameters $\sigma ,l\in (0,1)$, $x_0,x_1\in C$ as initial points.

Step 1 Take arbitrarily ${\xi }_n\in F\left({\omega }_n\right)$, if ${\omega }_n-P_C({\omega }_n-{\xi }_n)=0$ and $T\left({\omega }_n\right)={\omega }_n$, then stop, otherwise, go to step 2, where $$\begin{array}{c}\hfill {\omega }_n=\left\{\begin{array}{ccc}& x_n,\hspace{1em}\hspace{1em}n\hspace{1em}\hspace{1em}\mathrm{is}\hspace{1em}\hspace{1em}\mathrm{even};\hfill & \\ & x_n+\theta (x_n-x_{n-1}),\hspace{1em}\hspace{1em}n\hspace{1em}\hspace{1em}\mathrm{is}\hspace{1em}\hspace{1em}\mathrm{odd}.\hfill & \end{array}\right.\end{array}$$

Step 2 Let $m_n$ is the smallest nonegative integer m such that $$l^m⟨{\xi }_n-t_n\left(m\right),{\omega }_n-y_n\left(m\right)⟩\le \sigma {\parallel {\omega }_n-y_n\left(m\right)\parallel }^2,$$

where $y_n\left(m\right)=P_C({\omega }_n-l^m{\xi }_n)$, $t_n\left(m\right)=P_{F\left(y_n\left(m\right)\right)}\left({\xi }_n\right)$, $t_n=t_n\left(m_n\right)$ and $y_n=y_n\left(m_n\right)$, ${\alpha }_n=l^{m_n}.$

Step 3 Compute $d_n=P_{H_n}\left({\omega }_n\right)$, where $$h_n\left(v\right)=⟨{\omega }_n-y_n-{\alpha }_n({\xi }_n-t_n),v-y_n⟩,$$ $$H_n=\{v:h_n\left(v\right)\le 0\}.$$

Step 4 Compute $x_{n+1}=(1-{\beta }_n)d_n+{\beta }_{n}T{d}_n$. Set $n=n+1$ and go to Step 1.

Proof. 

By the definition of $h_n$ and step size, the following is true

$$\begin{array}{cc}\hfill h_n\left({\omega }_n\right)& =⟨{\omega }_n-y_n-{\alpha }_n({\xi }_n-t_n),{\omega }_n-y_n⟩\hfill \\ & =\parallel {\omega }_n-y_n{\parallel }^2-{\alpha }_n⟨{\xi }_n-t_n,{\omega }_n-y_n⟩\hfill \\ & \ge \parallel {\omega }_n-y_n{\parallel }^2-\sigma {\parallel {\omega }_n-y_n\parallel }^2\hfill \\ & =(1-\sigma )\parallel {\omega }_n-y_n{\parallel }^2\hfill \\ & =(1-\sigma )\parallel r({\omega }_n,{\alpha }_n,{\xi }_n){\parallel }^2.\hfill \end{array}$$

(4)

In addition, according to the pseudo-monotonicity of F, $\overline{x}\in S$ and $t_n\in F\left(y_n\right)$, we can obtain

$$⟨t_n,\overline{x}-y_n⟩\le 0.$$

(5)

From (5) and Lemma 2, we have

$$\begin{array}{cc}\hfill h_n\left(\overline{x}\right)& =⟨{\omega }_n-y_n-{\alpha }_n({\xi }_n-t_n),\overline{x}-y_n⟩\hfill \\ & =⟨{\omega }_n-y_n-{\alpha }_n{\xi }_n,\overline{x}-y_n⟩+{\alpha }_n⟨t_n,\overline{x}-y_n⟩\hfill \\ & \le ⟨{\omega }_n-y_n-{\alpha }_n{\xi }_n,\overline{x}-y_n⟩\le 0.\hfill \end{array}$$

(6)

□

Remark 3. 

For all $\overline{x}\in S$, we can obtain $h_n\left(\overline{x}\right)\le 0$, then $\overline{x}\in H_n$, for all $n\in N$.

Lemma 8. 

Let $\left\{x_n\right\}$ be a sequence generated by Algorithm 1, $p\in S\cap Fix\left(T\right)$, then

$$\parallel x_{n+1}{-p\parallel }^2\le \parallel d_n{-p\parallel }^2-{\beta }_n(1-\rho -{\beta }_n){\parallel d_n-T{d}_n\parallel }^2.$$

Proof. 

From the definition of $x_{n+1}$ and (2), (3), we get

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-p\parallel }^2& =\parallel {\beta }_{n}T{d}_n+(1-{\beta }_n)d_n{-p\parallel }^2\hfill \\ & =\parallel {\beta }_n(T{d}_n-p)+(1-{\beta }_n)(d_n-p){\parallel }^2\hfill \\ & ={\beta }_n^2\parallel T{d}_n{-p\parallel }^2+{(1-{\beta }_n)}^2{\parallel d_n-p\parallel }^2+2{\beta }_n(1-{\beta }_n)⟨T{d}_n-p,d_n-p⟩\hfill \\ & ={\beta }_n^2{\parallel T{d}_n-p\parallel }^2+2{\beta }_n(1-{\beta }_n)⟨T{d}_n-d_n,d_n-p⟩\hfill \\ & +2{\beta }_n(1-{\beta }_n)\parallel d_n{-p\parallel }^2+{(1-{\beta }_n)}^2{\parallel d_n-p\parallel }^2\hfill \\ & \le {(1-{\beta }_n)}^2\parallel d_n{-p\parallel }^2+{\beta }_n^2\parallel d_n{-p\parallel }^2+{\beta }_n^2\rho {\parallel T{d}_n-d_n\parallel }^2\hfill \\ & +{\beta }_n(1-{\beta }_n)(\rho -1)\parallel T{d}_n-d_n{\parallel }^2+2{\beta }_n(1-{\beta }_n){\parallel d_n-p\parallel }^2\hfill \\ & \le \parallel d_n{-p\parallel }^2-{\beta }_n(1-\rho -{\beta }_n){\parallel T{d}_n-d_n\parallel }^2.\hfill \end{array}$$

The proof is completed.   □

Lemma 9. 

The sequence $\left\{x_{2n}\right\}$ generated by Algorithm 1 is bounded.

Proof. 

By Lemmas 2 and 3 and the definition of $d_n$, for all $p\in S\cap Fix\left(T\right)$, we have

$$\begin{array}{cc}\hfill \parallel x_{2n+2}{-p\parallel }^2\le & \parallel d_{2n+1}{-p\parallel }^2-{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ \hfill =& \parallel P_{H_{2n+1}}\left({\omega }_{2n+1}\right){-p\parallel }^2-{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ \hfill \le & \parallel {\omega }_{2n+1}{-p\parallel }^2-{\parallel {\omega }_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ & -{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ \hfill =& \parallel (1+\theta )(x_{2n+1}-p)-\theta (x_{2n}-p){\parallel }^2-{\parallel {\omega }_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ & -{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ \hfill \le & (1+\theta )\parallel x_{2n+1}{-p\parallel }^2-\theta \parallel x_{2n}{-p\parallel }^2+\theta (1+\theta ){\parallel x_{2n+1}-x_{2n}\parallel }^2\hfill \\ & -\parallel {\omega }_{2n+1}-d_{2n+1}{\parallel }^2-{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2.\hfill \end{array}$$

Again, by Lemma 8 and the fact ${\omega }_{2n}=x_{2n}$, we obtain

$$\begin{array}{cc}\hfill \parallel x_{2n+2}{-p\parallel }^2\le & (1+\theta )[\parallel d_{2n}{-p\parallel }^2-{\beta }_{2n}(1-\rho -{\beta }_{2n})\parallel T{d}_{2n}-d_{2n}{\parallel }^2]-\theta \parallel x_{2n}{-p\parallel }^2\hfill \\ & +\theta (1+\theta )\parallel x_{2n+1}-x_{2n}{\parallel }^2-{\parallel {\omega }_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ & -{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ \hfill =& (1+\theta )\parallel P_{H_{2n}}\left(x_{2n}\right){-p\parallel }^2-(1+\theta ){\beta }_{2n}(1-\rho -{\beta }_{2n}){\parallel T{d}_{2n}-d_{2n}\parallel }^2\hfill \\ & -\theta \parallel x_{2n}{-p\parallel }^2+\theta (1+\theta )\parallel x_{2n+1}-x_{2n}{\parallel }^2-{\parallel {\omega }_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ & -{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ \hfill \le & (1+\theta )[\parallel x_{2n}-p{\parallel }^2-\parallel x_{2n}-d_{2n}{\parallel }^2]\hfill \\ & -(1+\theta ){\beta }_{2n}(1-\rho -{\beta }_{2n})\parallel T{d}_{2n}-d_{2n}{\parallel }^2-\theta {\parallel x_{2n}-p\parallel }^2\hfill \\ & +\theta (1+\theta )\parallel x_{2n+1}-x_{2n}{\parallel }^2-{\parallel {\omega }_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ & -{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ \hfill =& \parallel x_{2n}{-p\parallel }^2-(1+\theta )\parallel x_{2n}-d_{2n}{\parallel }^2+\theta (1+\theta ){\parallel x_{2n+1}-x_{2n}\parallel }^2\hfill \\ & -(1+\theta ){\beta }_{2n}(1-\rho -{\beta }_{2n})\parallel T{d}_{2n}-d_{2n}{\parallel }^2-{\parallel {\omega }_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ & -{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2.\hfill \end{array}$$

(7)

By the definition of $x_{2n+1}$, we have

$$\begin{array}{cc}\hfill (1+\theta )\parallel x_{2n}-d_{2n}{\parallel }^2=& (1+\theta )\parallel x_{2n}-x_{2n+1}+{\beta }_{2n}(T{d}_{2n}-d_{2n}){\parallel }^2\hfill \\ \hfill =& (1+\theta )\parallel x_{2n}-x_{2n+1}{\parallel }^2+(1+\theta ){\beta }_{2n}^2{\parallel T{d}_{2n}-d_{2n}\parallel }^2\hfill \\ & -2(1+\theta ){\beta }_{2n}⟨d_{2n}-T{d}_{2n},x_{2n}-x_{2n+1}⟩\hfill \\ \hfill \ge & (1+\theta )\parallel x_{2n}-x_{2n+1}{\parallel }^2+(1+\theta ){\beta }_{2n}^2{\parallel T{d}_{2n}-d_{2n}\parallel }^2\hfill \\ & -2(1+\theta ){\beta }_{2n}\parallel d_{2n}-T{d}_{2n}\parallel \parallel x_{2n}-x_{2n+1}\parallel \hfill \\ \hfill \ge & (1+\theta )\parallel x_{2n}-x_{2n+1}{\parallel }^2+(1+\theta ){\beta }_{2n}^2{\parallel T{d}_{2n}-d_{2n}\parallel }^2\hfill \\ & -\frac{{(1+\theta )}^2}{2}\parallel d_{2n}-T{d}_{2n}{\parallel }^2-2{\beta }_{2n}^2\parallel x_{2n}-x_{2n+1}\parallel .\hfill \end{array}$$

(8)

Substituting (8) into (7), we obtain

$$\begin{array}{cc}\hfill \parallel x_{2n+2}{-p\parallel }^2\le & \parallel x_{2n}{-p\parallel }^2-[(1+\theta )\parallel x_{2n}-x_{2n+1}{\parallel }^2+(1+\theta ){\beta }_{2n}^2{\parallel T{d}_{2n}-d_{2n}\parallel }^2\hfill \\ & -\frac{{(1+\theta )}^2}{2}\parallel d_{2n}-T{d}_{2n}{\parallel }^2-2{\beta }_{2n}^2\parallel x_{2n}-x_{2n+1}\parallel ]\hfill \\ & -(1+\theta ){\beta }_{2n}(1-\rho -{\beta }_{2n})\parallel T{d}_{2n}-d_{2n}{\parallel }^2+\theta (1+\theta ){\parallel x_{2n+1}-x_{2n}\parallel }^2\hfill \\ & -\parallel {\omega }_{2n+1}-d_{2n+1}{\parallel }^2-{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ \hfill =& \parallel x_{2n}{-p\parallel }^2-(1-{\theta }^2)\parallel x_{2n}-x_{2n+1}{\parallel }^2+\frac{{(1+\theta )}^2}{2}{\parallel d_{2n}-T{d}_{2n}\parallel }^2\hfill \\ & -(1+\theta )({\beta }_{2n}-\rho {\beta }_{2n})\parallel d_{2n}-T{d}_{2n}{\parallel }^2+2{\beta }_{2n}^2{\parallel x_{2n+1}-x_{2n}\parallel }^2\hfill \\ & -\parallel {\omega }_{2n+1}-d_{2n+1}{\parallel }^2-{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ \hfill =& \parallel x_{2n}{-p\parallel }^2-(1-{\theta }^2-2{\beta }_{2n}^2)\parallel x_{2n}-x_{2n+1}{\parallel }^2-{\parallel {\omega }_{2n+1}-d_{2n+1}\parallel }^2\hfill \\ & -(1+\theta )[{\beta }_{2n}-\rho {\beta }_{2n}-\frac{(1+\theta )}{2}]{\parallel d_{2n}-T{d}_{2n}\parallel }^2\hfill \\ & -{\beta }_{2n+1}(1-\rho -{\beta }_{2n+1}){\parallel T{d}_{2n+1}-d_{2n+1}\parallel }^2.\hfill \end{array}$$

(9)

According to $\theta \in \left({\displaystyle 0,\frac{2{(1-\rho )}^2-1}{2{(1-\rho )}^2+1}}\right)$, ${\displaystyle \frac{1+\theta }{2(1-\rho )}<{\beta }_n<\sqrt{{\displaystyle \frac{1-{\theta }^2}{2}}}}$, we get the sequence $\{\parallel x_{2n}-p\parallel \}$ is decreasing, hence $\{\parallel x_{2n}-p\parallel \}$ is convergent, further, $\left\{x_{2n}\right\}$ is bounded.    □

Lemma 10. 

Let $\left\{x_{2n}\right\}$ be the sequence generated by Algorithm 1, $x^{*}$ be any cluster point of sequence $\left\{x_{2n}\right\}$, then $x^{*}\in Fix\left(T\right)$.

Proof. 

Since $x^{*}$ is a cluster point of sequence $\left\{x_{2n}\right\}$, then there exists a subsequence $\left\{x_{2n_k}\right\}\subset \left\{x_{2n}\right\}$ satisfying

$$x_{2n_k}\to x^{*}.$$

From (9) and the convergence of $\{\parallel x_{2n}-p\parallel \}$, we can deduce that

$$\parallel x_{2n}-x_{2n+1}\parallel \to 0,\parallel d_{2n}-T{d}_{2n}\parallel \to 0,$$

(10)

$$\parallel d_{2n+1}-T{d}_{2n+1}\parallel \to 0,\parallel {\omega }_{2n+1}-d_{2n+1}\parallel \to 0,\mathrm{as}n\to +\infty .$$

(11)

By the definition of $x_{2n+1}$, we have

$$\begin{array}{cc}\hfill \parallel x_{2n}-d_{2n}\parallel & =\parallel x_{2n}-x_{2n+1}-{\beta }_{2n}{d}_{2n}+{\beta }_{2n}T{d}_{2n}\parallel \hfill \\ & \le \parallel x_{2n}-x_{2n+1}\parallel +{\beta }_{2n}\parallel d_{2n}-T{d}_{2n}\parallel ,\hfill \end{array}$$

then

$$\parallel x_{2n}-d_{2n}\parallel \to 0.$$

(12)

It implies

$$\underset{n\to +\infty }{\lim }\mathrm{dist}(x_{2n},H_{2n})=0.$$

(13)

Next, it suffices to prove that $x^{*}\in Fix\left(T\right)$, by (12) and $x_{2n_k}\to x^{*}$, then we get

$$d_{2n_k}\to x^{*}.$$

(14)

Since T is demiclosed at zero, Definition 3, (10) and (14) imply

$$x^{*}\in Fix\left(T\right).$$

The proof is completed.   □

Lemma 11. 

Assume that Assumption 1–3 hold, and let $\left\{x_{2n}\right\}$ be the sequence generated by Algorithm 1, $x^{*}$ be any cluster point of sequence $\left\{x_{2n}\right\}$, then $x^{*}\in S$.

Proof. 

Since $\left\{x_{2n}\right\}$ is bounded, F and $r(·)$ are continuous, then we conclude that $\left\{y_{2n}\right\}$, $\left\{{\xi }_{2n}\right\}$ and $\left\{t_{2n}\right\}$ are bounded, therefore, $\{{\omega }_{2n}-y_{2n}-{\alpha }_{2n}({\xi }_{2n}-t_{2n})\}$ is bounded, then there exists a constant $M>0$ satisfying

$$\parallel {\omega }_{2n}-y_{2n}-{\alpha }_{2n}({\xi }_{2n}-t_{2n})\parallel \le M.$$

By the definition of $h_{2n}$, then for all $x,y\in R^n$, we have

$$\begin{array}{cc}\hfill \parallel h_{2n}\left(x\right)-h_{2n}\left(y\right)\parallel & =\parallel ⟨{\omega }_{2n}-y_{2n}-{\alpha }_{2n}({\xi }_{2n}-t_{2n}),x-y⟩\parallel \hfill \\ & \le \parallel {\omega }_{2n}-y_{2n}-{\alpha }_{2n}({\xi }_{2n}-t_{2n})\parallel \parallel x-y\parallel \hfill \\ & \le M\parallel x-y\parallel .\hfill \end{array}$$

It implies $h_{2n}(·)$ is M-Lipschitz continuous. From Lemma 5 and Lemma 7, we have

$$\begin{array}{cc}\hfill \mathrm{dist}(x_{2n},H_{2n})& \ge M^{-1}{h}_{2n}\left(x_{2n}\right)\hfill \\ & \ge M^{-1}(1-\sigma ){\parallel r(x_{2n},{\alpha }_{2n},{\xi }_{2n})\parallel }^2.\hfill \end{array}$$

Let $n\to +\infty$ on both sides of this inequality, (13) implies

$$\underset{n\to +\infty }{\lim }\parallel r(x_{2n},{\alpha }_{2n},{\xi }_{2n})\parallel =0.$$

Since $\left\{x_{2n}\right\}$ and $\left\{{\xi }_{2n}\right\}$ are bounded, we let $x^{*}$ and $\overline{\xi }$ be cluster points of $\left\{x_{2n}\right\}$ and $\left\{{\xi }_{2n}\right\}$, then there exist subsequences $\left\{x_{2n_k}\right\}\subset \left\{x_{2n}\right\}$, $\left\{{\xi }_{2n_k}\right\}\subset \left\{{\xi }_{2n}\right\}$ such that

$$x_{2n_k}\to x^{*},{\xi }_{2n_k}\to \overline{\xi }.$$

Since F is an outer-semicontinuous mapping, we can deduced that F is closed from Definition 1. In addition, this together with the fact $x_{2n_k}\to x^{*}$, ${\xi }_{2n_k}\to \overline{\xi }$ and the fact ${\xi }_{2n_k}\in F\left(x_{2n_k}\right)$, we have

$$\overline{\xi }\in F\left(x^{*}\right).$$

Next, we prove it in two cases:

Case 1. $\underset{k\to +\infty }{\lim \sup } {\alpha }_{2n_k}>b>0$, there exists $\{{\alpha }_{2n_{k_j}}\}\subset \{{\alpha }_{2n_k}\}$ such that $\underset{j\to +\infty }{\lim }{\alpha }_{2n_{k_j}}>b$. Therefore there exists $N>0$, for all $j\ge N$, ${\alpha }_{2n_{k_j}}>b$.

Then by Lemma 4, we have

$${\displaystyle 0\le \parallel r(x_{2n_{k_j}},1,{\xi }_{2n_{k_j}})\parallel \le \frac{\parallel r(x_{2n_{k_j}},\min \{{\alpha }_{2n_{k_j}},1\},{\xi }_{2n_{k_j}})\parallel }{\min \{{\alpha }_{2n_{k_j}},1\}}\le \frac{\parallel r(x_{2n_{k_j}},{\alpha }_{2n_{k_j}},{\xi }_{2n_{k_j}})\parallel }{\min \{b,1\}}.}$$

Taking $j\to +\infty$, we have

$$r(x^{*},1,\overline{\xi })=0.$$

Case 2. $\underset{k\to +\infty }{\lim \sup } {\alpha }_{2n_k}=0$, then

$$\underset{k\to +\infty }{\lim }{\alpha }_{2n_k}=0.$$

$\underset{j\to +\infty }{\lim }\parallel r(x_{2n_k},{\alpha }_{2n_k},t_{2n_k})\parallel =0$ and $\underset{j\to +\infty }{\lim }{\alpha }_{2n_k}=0$ imply

$$\begin{array}{cc}\hfill \parallel x_{2n_k}-y_{2n_k}(m_{2n_k}-1)\parallel \le & \parallel x_{2n_k}-y_{2n_k}\parallel +\parallel y_{2n_k}-y_{2n_k}(m_{2n_k}-1)\parallel \hfill \\ \hfill =& \parallel r(x_{2n_k},{\alpha }_{2n_k},t_{2n_k})\parallel \hfill \\ & +\parallel P_C(x_{2n_k}-{\alpha }_{2n_k}{\xi }_{2n_k})-P_C(x_{2n_k}-l^{-1}{\alpha }_{2n_k}{\xi }_{2n_k})\parallel \hfill \\ \hfill \le & \parallel r(x_{2n_k},{\alpha }_{2n_k},t_{2n_k})\parallel +\parallel x_{2n_k}-{\alpha }_{2n_k}{\xi }_{2n_k}-(x_{2n_k}-l^{-1}{\alpha }_{2n_k}{\xi }_{2n_k})\parallel \hfill \\ \hfill =& \parallel r(x_{2n_k},{\alpha }_{2n_k},t_{2n_k})\parallel +{\alpha }_{2n_k}(l^{-1}-1)\parallel {\xi }_{2n_k}\parallel \to 0,\mathrm{as}k\to +\infty .\hfill \end{array}$$

Combining $\parallel x_{2n_k}-y_{2n_k}(m_{2n_k}-1)\parallel \to 0$ with $x_{2n_k}\to x^{*}$, we have

$$y_{2n_k}(m_{2n_k}-1)\to x^{*},$$

and together with $\overline{\xi }\in F\left(x^{*}\right)$ and F is inner-semicontinuous, we can deduced that there exists a sequence $v_{2n_k}(m_{2n_k}-1)\in F\left(y_{2n_k}(m_{2n_k}-1)\right)$ such that

$$v_{2n_k}(m_{2n_k}-1)\to \overline{\xi }.$$

Further, from $t_{2n_k}(m_{2n_k}-1)=P_{F(y_{2n_k}(m_{2n_k}-1))}\left({\xi }_{2n_k}\right)$, we can obtain

$$\begin{array}{cc}\hfill 0& \le \parallel t_{2n_k}(m_{2n_k}-1)-{\xi }_{2n_k}\parallel \hfill \\ & \le \parallel v_{2n_k}(m_{2n_k}-1)-{\xi }_{2n_k}\parallel \hfill \\ & \le \parallel v_{2n_k}(m_{2n_k}-1)-\overline{\xi }\parallel +\parallel \overline{\xi }-{\xi }_{2n_k}\parallel ,\hfill \end{array}$$

it implies

$$\parallel t_{2n_k}(m_{2n_k}-1)-{\xi }_{2n_k}\parallel \to 0.$$

(15)

In addition, by the definition of step size ${\alpha }_{2n_k}$, we have

$${\alpha }_{2n_k}{l}^{-1}⟨{\xi }_{2n_k}-t_{2n_k}(m_{2n_k}-1),x_{2n_k}-y_{2n_k}(m_{2n_k}-1)⟩>\sigma {\parallel x_{2n_k}-y_{2n_k}(m_{2n_k}-1)\parallel }^2,$$

and there exists a positive integer N, for all $k\ge N$, ${\alpha }_{2n_k}{l}^{-1}\le 1$, Lemma 4 implies

$${\displaystyle \parallel {\xi }_{2n_k}-t_{2n_k}(m_{2n_k}-1)\parallel >\frac{\sigma r(x_{2n_k},{\alpha }_{2n_k}{l}^{-1},{\xi }_{2n_k})}{{\alpha }_{2n_k}{l}^{-1}}\ge \frac{\sigma r(x_{2n_k},1,{\xi }_{2n_k})}{1},\mathrm{for}\mathrm{all}k\ge N.}$$

Let $k\to +\infty$ on both sides of this inequality, combining with (15), we get

$$\underset{k\to +\infty }{\lim }\parallel r(x_{2n_k},1,{\xi }_{2n_k})\parallel =0,$$

it implies

$$r(x^{*},1,\overline{\xi })=0.$$

Therefore, $x^{*}\in S$.    □

Theorem 1. 

Let $\left\{x_n\right\}$ be the sequence generated by Algorithm 1, then $\left\{x_n\right\}$ strongly converges to a point of $S\cap Fix\left(T\right)$.

Proof. 

Let $x^{*}$ be any cluster point of the sequence $\left\{x_{2n}\right\}$, then Lemmas 10 and 11 imply

$$x^{*}\in S\cap Fix\left(T\right).$$

According to Lemma 9, we can obtain $\{\parallel x_{2n}-x^{*}\parallel \}$ is convergent. Further, $x^{*}$ is a cluster point of the sequence $\left\{x_{2n}\right\}$ implies $\left\{x_{2n}\right\}$ converges to $x^{*}$, i.e.,

$$x_{2n}\to x^{*}.$$

(16)

In addition, by (10) and (16), we get

$$\parallel x_{2n+1}-x^{*}\parallel \le \parallel x_{2n+1}-x_{2n}\parallel +\parallel x_{2n}-x^{*}\parallel \to 0,\mathrm{as}n\to +\infty ,$$

Therefore, $\left\{x_{2n+1}\right\}$ converges to $x^{*}$, then, $\left\{x_n\right\}$ converges globally to a point $x^{*}\in S\cap Fix\left(T\right)$.    □

Remark 4. 

Our algorithm has the following advantages over the existing algorithms:

(i) Compared with [1,31], we extend the multi-valued variational inequality problem to the common solution of multi-valued variational inequality and fixed point problem.

(ii) Compared with [3], this algorithm does not require the Lipschitz continuity of the mapping and can get strong convergence results under the condition of continuous mapping.

(iii) Compared with [16,17]. On one hand, our proposed algorithm for solving multi-valued variational inequality problem and fixed point problem of demi-contractive mapping, and demi-contractive mapping is more generalized than strictly pseudo-contractive mapping and nonexpansive mapping. On the other hand, we use the alternated inertial technique to accelerate the convergence speed of the algorithm.

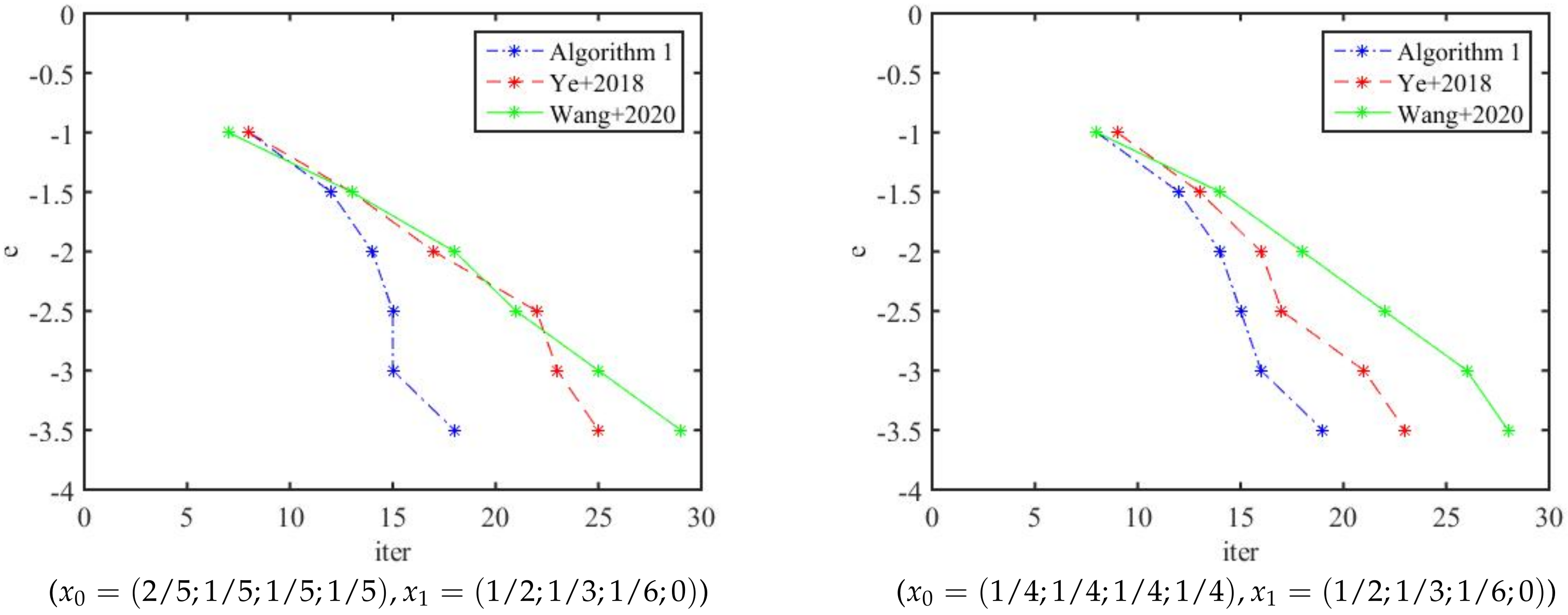
3. Numerical Examples

In this section, several examples are given to prove the effectiveness of Algorithm 3.1, and Algorithm 1 is compared with Algorithm 1 [1] (shortly, Ye+2018) and Algorithm 3.1 [31] (shortly, Wang+2020), which proves that Algorithm 1 is better than other algorithms in terms of convergence speed and iteration times. The tolerance e means that when $r(x,\xi )\le e$, the procedure stops.

In our experiment, the parameters in each algorithm are as follows:

For our Algorithm 1 and Algorithm 1 [1], $\sigma =0.9$, $l=0.5$; in Algorithm 3.1 [31], $r=0.55$, $\sigma =0.2$, $\rho =3$.

Example 2. 

Let C be a nonempty closed convex sets, and $C=\{x\in R_{+}^n:{\sum }_{i=1}^n{x}_i=1\}$, $F:C\to 2^{R^n}$ such that

$$F\left(x\right)=\{(t;t+2x_2;t+3x_3;t+4x_4):t\in [0,1]\},$$

and the mapping $T_1:R^n\to R^n$ satisfies $T_1\left(x\right)=(x_1;x_4;x_3;x_2)$, $T_2=I$ (I is the identity mapping). It is obvious that mapping F has pesdo-monotonicity and $T_1$ is a demi-contractive mapping. $x^{*}=(1;0;0;0)\in S\cap Fix\left(T\right)$, in our Algorithm 1, we let $\theta =0.1$, $\beta =0.6$. Numerical observations for Example 2 are shown in Table 1 and Table 2, Figure 1.

Table 1. The numerical result under $T=T_1$ in Example 2.

Algorithm 1
e	iter	Cpu	$x^{*}$
${10}^{-1}$	7	2.1875	(0.8854; 0.0465; 0.0215; 0.0463)
${10}^{-2}$	17	2.9218	(0.9891; 0.0052; 0.0004; 0.0051)
${10}^{-3}$	26	3.4218	(0.9989; 0.0005; 7.6653$\times {10}^{-6}$; 0.0005)
${10}^{-3.5}$	30	3.7500	(0.9994; 0.0002; 9.3523$\times {10}^{-5}$; 0.0002)

Table 2. Comparison of numerical results of Algorithm 1, Algorithm 1 [1] and Algorithm 3.1 [31] at different initial points under $T=T_2$ in Example 2.

		Algorithm 1	Algorithm 1 [1]	Algorithm 3.1 [31]
Case I	iter	15	23	29
	Cpu	2.7340	3.1093	3.3656
Case II	iter	16	21	28
	Cpu	2.7968	3.0781	3.9218

Figure 1. Comparison of iteration times of Algorithm 1, Algorithm 1 [1] and Algorithm 3.1 [31] at different initial points under $T=T_2$ in Example 2.

When $T=T_1$, let $x_0=(2/5;1/5;1/5;1/5),x_1=(1/2;1/3;1/6;0)$ be initial values.

When $T=T_2=I$, $S=S\cap Fix\left(T\right)$, let $e={10}^{-3}$, and take the following different initial values for the numerical experiment:

(i) $x_0=(2/5;1/5;1/5;1/5),x_1=(1/2;1/3;1/6;0)$;

(ii) $x_0=(1/4;1/4;1/4;1/4),x_1=(1/2;1/3;1/6;0)$.

Example 3. 

Let feasible set C be $[-1,1]\times [-1,1]$. The mapping $F:R^2\to R^2$ defined by

$$F(x_1,x_2)=(x_1+x_2+\sin \left(x_1\right);-x_1+x_2+\sin \left(x_2\right)),$$

we see that the mapping F satisfies Assumption 1–3. Let $x_0=(-1;1),x_1=(1;1)$ be initial values for Algorithm 1, $x_0=(-1;1)$ be initial value for Algorithm 1 [1] and Algorithm 3.1 [31]. Numerical observations for Example 3 are shown in Table 3.

Table 3. Comparison of numerical results of Algorithm 1, Algorithm 1 [1], Algorithm 3.1 [31] in Example 3.

e		Algorithm 1	Algorithm 1 [1]	Algorithm 3.1 [31]
${10}^{-1}$	iter	5	6	9
	cpu	1.5625	1.7031	1.8750
${10}^{-2}$	iter	8	9	15
	cpu	1.7812	1.8281	2.0000
${10}^{-3}$	iter	12	12	20
	cpu	1.8750	2.3125	2.2343
${10}^{-3}$	iter	15	16	33
	cpu	1.9375	2.4218	2.4843
${10}^{-5}$	iter	18	19	52
	cpu	2.1406	2.4687	3.0468
${10}^{-6}$	iter	21	22	-
	cpu	2.2343	2.5156	-
${10}^{-7}$	iter	24	25	-
	cpu	2.4062	2.5468	-

4. Conclusions

Algorithm 1 proposed in this paper is designed to solve multi-valued variational inequality problem and fixed point problem of demi-contractive mappings. It is worth noting that we combined alternated inertial technique to accelerate the convergence rate of the algorithm and to some extent ensure the Fejér monotonicity of $\{\parallel x_{2n}-x^{*}\parallel \}$. Different from algorithm [31], this algorithm study the fixed point problem of demi-contractive mapping, which is more generalized than strictly pseudo-contractive mapping. In addition, the experiments show that the effectiveness of Algorithm 1.