Shunting Inhibitory Cellular Neural Networks with Compartmental Unpredictable Coefficients and Inputs

Abstract

Shunting inhibitory cellular neural networks with compartmental periodic unpredictable coefficients and inputs is the focus of this research. A new algorithm is suggested, to enlarge the set of known unpredictable functions by applying diagonalization in arguments of functions of several variables. Sufficient conditions for the existence and uniqueness of exponentially stable unpredictable and Poisson stable outputs are obtained. To attain theoretical results, the included intervals method and the contraction mapping principle are used. Appropriate examples with numerical simulations that support the theoretical results are provided. It is shown how dynamics of the neural network depend on a new numerical characteristic, the degree of periodicity.

1. Introduction

In 1988 [1], Chua and Yang introduced the concept of cellular neural networks (CNNs), which are arrays of dynamical systems. The authors used CNNs for image processing problems and solving partial differential equations [2]. These publications sparked widespread interest in CNNs among researchers, and since then, many new applications of CNNs have been introduced.

A class of CNNs, shunting inhibitory cellular neural networks (SICNNs), was proposed by Bouzerdoum and Pinter in 1993 [3]. They are biologically inspired networks in which the synaptic interactions among neurons are mediated via a nonlinear mechanism called shunting inhibition. In the Ref. [4], the application of SICNNs for medical diagnosis, which is based on some given symptoms and initial data, was shown. SICNNs are very useful for image processing since they can provide contrast and edge enhancement. The SICNNs algorithm allows to achieve a balance between enhancing the dark region, and at the same time retaining the colours in the bright [5,6]. The neural networks have been widely applied in various fields such as psychophysics, robotics, perception, and adaptive pattern recognition [7,8,9]. The variable and continuous-time excitatory inputs guarantee rich dynamics for SICNNs, as well as for shunting inhibitory artificial neural networks [4,5]. Exceptionally, if they are chaotic, the case will be under investigation of the present research.

It is known that dynamics of the neural networks is very complex, and play an important role in applications. Thus, many studies have been devoted to the study of SICNNs. In particular, the existence and stability of periodic [10,11], anti-periodic [12,13,14], almost periodic [15,16,17] and pseudo-periodic solutions [18,19] have been investigated.

In its original formulation [3], the model of SICNNs is as follows. Consider a two-dimensional grid of cells, and denote by $C_{ij},$ $i=1,\dots ,m,$ $j=1,\dots ,n,$ the cell at the $(i,j)$ position of the mesh. In SICNNs, neighboring cells exert shunting-type mutual inhibitory interactions. The following differential equation describes the dynamics of the cell $C_{ij},$

$$\begin{array}{ccc}\hfill & & x_{ij}^{\prime }\left(t\right)=-a_{ij}{x}_{ij}\left(t\right)-\sum _{C_{kl}\in N_r(i,j)}{C}_{ij}^{kl}f\left(x_{kl}\left(t\right)\right)x_{ij}\left(t\right)+v_{ij}\left(t\right),\hfill \end{array}$$

(1)

where $x_{ij}$ is the activity of the cell $C_{ij};$ $a_{ij}$ is the passive decay rate of the cell activity; $C_{ij}^{kl}\ge 0$ is the connection of postsynaptic activity of the cell $C_{kl}$ transmitted to the cell $C_{ij};$ $f\left(s\right)$ is the activation function; $v_{ij}\left(t\right)$ is the external input to cell $C_{ij};$ and the r-neighborhood $N_r(i,j)$ of $C_{ij}$ is

$$\begin{array}{ccc}& & N_r(i,j)= \{C_{kl}:max\left(\right|k-i|,|l-j\left|\right)\le r,1\le k\le m,1\le l\le n\},\hfill \end{array}$$

with fixed natural numbers m and $n.$

Currently, only a few studies have investigated the Poisson stable and unpredictable motions of shunting-type cellular neural networks. For instance, the dynamics of the SICNNs (1), where the inputs $v_{ij}\left(t\right)$ are unpredictable, was investigated in [20]. Unpredictable oscillations of SICNNs with delay,

$$\begin{array}{ccc}\hfill & & x_{ij}^{\prime }\left(t\right)=-a_{ij}{x}_{ij}\left(t\right)-\sum _{C_{kl}\in N_r(i,j)}{C}_{ij}^{kl}f\left(x_{kl}(t-\tau )\right)x_{ij}\left(t\right)+L_{ij}\left(t\right),\hfill \end{array}$$

(2)

were considered in the Ref. [21]. In system (2), inputs $L_{ij}\left(t\right)$ are piecewise constant functions, which have not been approved for unpredictability, while in our research they are continuous unpredictable functions obtained through the compartmental algorithm.

In the Ref. [22], the following symmetrical impulsive SICNNs with a generalized piecewise constant argument,

$$\begin{array}{ccc}\hfill & & x_{ij}^{\prime }\left(t\right)=a_{ij}\left(t\right)x_{ij}\left(t\right)-\sum _{C_{hl}\in N_r(i,j)}{C}_{ij}^{hl}\left(t\right)f\left(x_{hl}\left(\gamma \left(t\right)\right)\right)x_{ij}\left(t\right)+v_{ij}\left(t\right),t\ne {\theta }_k,\hfill \\ & & \Delta x_{ij}\left(t\right){\mid }_{t={\theta }_k}=b_{ij}\left(t\right)x_{ij}\left({\theta }_k\right)-\sum _{D_{hl}\in N_r(i,j)}{C}_{ij}^{hl}\left(t\right)g\left(x_{hl}\left({\theta }_k\right)\right)x_{ij}\left({\theta }_k\right)+h_{ijk},\hfill \end{array}$$

(3)

was considered, and sufficient conditions for the existence and uniqueness of Poisson stable solutions were obtained.

The following neural model is in the focus of our study,

$$\begin{array}{ccc}\hfill & & x_{ij}^{\prime }\left(t\right)=-(a_{ij}\left(t\right)+b_{ij}\left(t\right))x_{ij}\left(t\right)-\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(t\right)f\left(x_{kl}\left(t\right)\right)x_{ij}\left(t\right)+v_{ij}\left(t\right),\hfill \end{array}$$

(4)

where the coefficients $a_{ij}\left(t\right)$ are continuous periodic functions; the components $b_{ij}\left(t\right),$ connection weights $c_{ij}^{kl}\left(t\right)$ and inputs $v_{ij}\left(t\right)$ are compartmental periodic unpredictable functions; the activation function $f\left(s\right)$ is continuous.

The dynamics of SICNNs (4), where the functions $a_{ij}\left(t\right)$ are periodic, $b_{ij}\left(t\right),$ $v_{ij}\left(t\right)$ are Poisson stable, and connection weights $c_{ij}^{kl}$ are constants, were investigated in the Ref. [23]. This time, all coefficients are time-varying functions, and have a more complex structure that combines periodicity and unpredictability. The Poisson stable and unpredictable solutions of the neural network (4) are under investigation.

It is indisputable that any theory of functions with applications should be accompanied by a number of methods of construction as well as numerical presentations of the functions. They can be simple algebraic operations, Fourier series and results of theory of operators. The methods of construction as well as numerical analysis of the unpredictable solutions are also on the agenda. A novel way to determine unpredictable functions is suggested, which is rooted at the compartmental paradigm. We start with functions of two variables, which are unpredictable in one of them, and in another are periodic. The domains of the functions are narrowed to diagonals of the argument spaces. The method of diagonals is known for quasi-periodic functions or almost periodic functions [24,25]. In the present study, the diagonalization is made on an essentially new level, since dependence on the two variables is significantly different. This is why it is of large interest to look for conditions such that functions on diagonals admit the unpredictability.

Despite many papers on almost periodic and Poisson stable functions, there are no numerical examples, neither for the functions nor solutions, if they are not quasi-periodic. However, the needs of the industry and particularly neuroscience and other modern areas demand numerical presentation of dynamics to support theories. Our study meets the challenges, since we construct several Poisson stable and unpredictable functions numerically, utilizing the merits of the logistic equation. One can emphasise that even for Poisson stable functions, which have been researched for about a century, the concrete samples of functions appeared for the first time in our papers [26,27]. The numerical experiments are advantageous, since they are accompanied by newly developed strong instruments of the functions simulations. They are convenient for synchronization of chaos. Delta synchronization has been introduced, which works for gas discharge-semiconductor systems [28,29], where even the generalized synchronization [30] is not effective. A numerical test for the unpredictable dynamics was suggested in the Ref. [31], and strange attractors were discovered [32]. Moreover, we constructed algorithms which allow to see the contribution of periodicity and the unpredictability for the compartmental dynamics [33]. They are based on the concept of the degree of periodicity. It was learnt that very similar time series can be seen in industrial experiments [34,35,36,37,38], and this is a strong argument for the application of our results. We believe that the study of the compartmental functions will shed more light on the problem of the transition from quasi-periodicity to chaos [39,40].

The rest of the paper is organized as follows. In Section 2, the basic and novel definitions are presented. Special relations between periodicity and unpredictability in compartmental arguments are determined to establish the unpredictability of compartmental functions. They are formulated in terms of time sequences. The lemma on the existence of an equivalent integral equation is provided as a key technical step in the analysis. The conditions for neural networks that are sufficient to obtain the results of the article are announced. Section 3 contains the main results of our study. Using the method of included intervals [26,27] and a contraction mapping principle, it is strictly proved that the Poisson stable and unpredictable motions, which are exponentially stable, are present in the dynamics of the SICNNs (4). In Section 4, discontinuous and continuous unpredictable functions are defined through the solution of the logistic map. A parameter, the degree of periodicity, which strongly affects the behaviour of the neural network is introduced. Numerical examples with illustrations confirming the feasibility of theoretical results are given. Finally, prospects of the obtained results for chaos control and synchronization in neural networks are discussed in Section 5.

2. Preliminaries

The definitions of the Poisson stable and unpredictable function are as follows.

Definition 1 

([41]). A bounded function $g\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is called Poisson stable if there exists a sequence $t_p,$ $t_p\to \infty$ as $p\to \infty ,$ such that the sequence of functions $g(t+t_p)$ converges to $g\left(t\right)$ uniformly on each bounded interval of $\mathbb{R}.$

Definition 2 

([42]). A bounded function $g:\mathbb{R}\to {\mathbb{R}}^n$ is said to be unpredictable if there exist positive numbers ${ϵ}_0,\delta$ and sequences $t_p\to \infty ,$ $s_p\to \infty$ as $p\to \infty ,$ such that $\parallel g(t+t_p)-g\left(t\right)\parallel \to 0$ uniformly on compact subsets of $\mathbb{R}$ and $\parallel g(t+t_p)-g\left(t\right)\parallel >{ϵ}_0$ for each $t\in [s_p-\delta ,s_p+\delta ]$ and $p\in \mathbb{N}$.

The sequence $t_p,p=1,2,\dots ,$ is called the convergence sequence in Definitions 1, 2, and correspondingly, we shall say about the convergence property, while the existence of positive numbers ${ϵ}_0,\delta$ and sequence $s_p$ is said to be the separation property.

It is easily seen, reading the last two definitions, that all unpredictable functions make a subset of Poisson stable functions specified with an additional property of separation. It was proved in our studies [42] that the property guarantees chaotic dynamics of the unpredictable motion. Loosely speaking, one can say that an unpredictable function is a Poisson stable function with assigned chaotic behaviour.

Definition 3 

([33]). A function $g\left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is called a compartmental periodic unpredictable function, if $g\left(t\right)=G(t,t),$ where $G(u,v)$ is a bounded continuous function, periodic in u uniformly with respect to $v,$ and unpredictable in v uniformly with respect to $u,$ that is, there exist positive numbers $\omega ,$ ${ϵ}_0$, δ and sequences $t_p\to \infty ,$ $s_p\to \infty$ as $p\to \infty ,$ such that ${\displaystyle G(u+\omega ,v)=G(u,v)}$ for all $u,v\in \mathbb{R},$ ${\displaystyle \underset{u\in \mathbb{R}}{sup}\parallel G(u,v+t_p)-G(u,v)\parallel \to 0}$ uniformly on bounded intervals of $v,$ and ${\displaystyle \parallel G(u,v+t_p)-G(u,v)\parallel >{ϵ}_0}$ for $v\in [s_p-\delta ,s_p+\delta ],$ $u\in \mathbb{R}$ and $p\in \mathbb{N}$.

Remark 1. 

To say that function $g\left(t\right)$ in the last definition is a compartmental periodic unpredictable function does not mean that it is unpredictable in the sense of Definition 2. The question of whether the function on the diagonal is unpredictable will be answered under the conditions of Lemma 1.

Let us consider the convergence sequence $t_p,p=1,2,\dots ,$ and a fixed positive number $\omega .$ One can write that $t_p={\theta }_p\left(mod\omega \right),$ where $0\le {\theta }_p<\omega ,$ $p=1,2,\dots .$ There exists a subsequence ${\theta }_{p_l},$ $l=1,2,\cdots ,$ which tends to a real number ${\theta }_{\omega }.$ Consequently, one can find a subsequence $t_{p_l},$ $l=1,2,\cdots ,$ such that $t_{p_l}\to {\theta }_{\omega }\left(mod\omega \right)$ as $l\to \infty .$ The number ${\theta }_{\omega }$ is called a Poisson shift for the convergence sequence $t_p.$ Denote by $\mathcal{T}$ ${}_{\omega }$ the set of all Poisson shifts. The number ${\kappa }_{\omega }=inf\mathcal{T}$ ${}_{\omega },$ $0\le {\kappa }_{\omega }<\omega ,$ is said to be the Poisson number for $t_p,$ $p=1,2,\cdots .$ We say that the convergence sequence satisfies kappa property with respect to the $\omega$ if ${\kappa }_{\omega }=0.$

The following lemma is a main auxiliary result of the paper.

Lemma 1. 

Let a bounded function $F(u,v):\mathbb{R}\times \mathbb{R}\to {\mathbb{R}}^n,$ is $\omega -$periodic in $u.$ The function $f\left(t\right)=F(t,t)$ is unpredictable if the following conditions are valid:

(i) 

For each $ϵ>0$ there exists a positive number η such that $\parallel F(t+s,t)-F(t,t)\parallel <ϵ$ if $\left|s\right|<\eta ,t\in \mathbb{R};$

There exist positive numbers ${ϵ}_0,\delta$ and sequences $t_p,$ $s_p$ both of which diverges to infinity as $p\to \infty ,$ such that

(ii) 

The sequence $t_p$ satisfies kappa property with respect to the $\omega ;$

(iii) 

$\parallel F(t,t+t_p)-F(t,t)\parallel \to 0,$ uniformly on each bounded interval $I\subset R$ of $t;$

(iv) 

 ${\displaystyle \underset{[s_p-\delta ,s_p+\delta ]}{inf}\parallel F(t,t+t_p)-F(t,t)\parallel >{ϵ}_0,}$  $p\in \mathbb{N}.$

Proof. 

Let us fix a bounded interval $I\in \mathbb{R},$ and a positive number $ϵ.$ By assumption $\left(ii\right),$ one can write, without loss of generality, that $t_p\to 0\left(mod\omega \right)$ as $p\to \infty .$ Therefore, conditions $\left(i\right)$ and $\left(iii\right)$ imply that the following inequalities are valid:

$$\begin{array}{c}\hfill \underset{\mathbb{R}\times \mathbb{R}}{sup}\parallel F(t+t_p,t)-F(t,t)\parallel <\frac{ϵ}{2}\end{array}$$

(5)

and

$$\begin{array}{c}\hfill \underset{\mathbb{R}\times I}{sup}\parallel F(t,t+t_p)-F(t,t)\parallel <\frac{ϵ}{2},\end{array}$$

(6)

for sufficiently large $p.$

Using inequalities (5) and (6), we obtain that

$$\begin{array}{ccc}& & \parallel f(t+t_p)-f\left(t\right)\parallel = \parallel F(t+t_p,t+t_p)-F(t,t)\parallel \le \hfill \\ & & \parallel F(t+t_p,t+t_p)-F(t,t+t_p)\parallel +\parallel F(t,t+t_p)-F(t,t)\parallel <\frac{ϵ}{2}+\frac{ϵ}{2}=ϵ,\hfill \end{array}$$

for all $t\in I.$ That is, $f(t+t_p)$ converges to $f\left(t\right)$ on each arbitrary bounded time interval uniformly, and the function $f\left(t\right)$ satisfies the convergence property.

Conditions $\left(i\right)$ and $\left(ii\right)$ imply that ${\displaystyle \underset{\mathbb{R}}{sup}\parallel F(t+t_p,t)-F(t,t)\parallel <\frac{{ϵ}_0}{2}}$ for sufficiently large $p.$ Applying assumption $\left(iv\right),$ one can obtain that

$$\begin{array}{ccc}& & \parallel f(t+t_p)-f\left(t\right)\parallel = \parallel F(t+t_p,t+t_p)-F(t,t)\parallel \ge \hfill \\ & & \parallel F(t+t_p,t+t_p)-F(t+t_p,t)\parallel -\parallel F(t+t_p,t)-F(t,t)\parallel >{ϵ}_0-\frac{{ϵ}_0}{2}=\frac{{ϵ}_0}{2},\hfill \end{array}$$

for all $t\in [s_p-\delta ,s_p+\delta ],$ $p\in \mathbb{N}.$ Thus, the separation property is valid. The lemma is proved. □

Remark 2. 

If the conditions of Lemma 1 are valid, then function $F(u,v)$ admits properties of Definition 3. This is why the lemma provides conditions for unpredictability of a compartmental periodic function.

Using the theory of differential equations [43], one can verify that the following lemma is true.

Lemma 2. 

In order for a bounded on $\mathbb{R}$ function $y\left(t\right)=\left(y_{ij}\left(t\right)\right),$ $i=1,\dots ,m,j=1,\dots ,n,$ to be a solution of (4), it is necessary and sufficient that it satisfies the integral equation

$$\begin{array}{c}\hfill {\displaystyle y_{ij}\left(t\right)=-{\int }_{-\infty }^t{e}^{-{\int }_s^t{a}_{ij}\left(u\right)du}\left(b_{ij}\left(s\right)y_{ij}\left(s\right)+\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(y_{kl}\left(s\right)\right)y_{ij}\left(s\right)-v_{ij}\left(s\right)\right)ds,}\end{array}$$

(7)

for all $i=1,\dots ,m,j=1,\dots ,n.$

Throughout the paper, we will use the norm ${\displaystyle ∥v∥=\underset{(i,j)}{max}\left|v_{ij}\right|,}$ $i=1,\dots ,m,j=1,\dots ,n,$ where $\left|·\right|$ is the absolute value. In what follows, we consider the activation function f in the domain $(-H,H),$ where H is a fixed positive number.

Suppose that $\mathcal{Q}$ is a set of functions $\varphi \left(t\right)=\left({\varphi }_{ij}\left(t\right)\right),$ $i=1,2,\cdots ,m,j=1,2,\cdots ,n,$ with the norm ${\parallel \varphi \left(t\right)\parallel }_0={max}_{i,j}\parallel {\varphi }_{ij}\left(t\right)\parallel ,$ such that all ${\varphi }_{ij}\left(t\right)$ are Poisson stable with a common convergence sequence $t_p,p=1,2,\dots ,$ and $|{\varphi }_{ij}\left(t\right)|<H,$ $i=1,2,\cdots ,m,j=1,2,\cdots ,n.$

Define on $\mathcal{Q}$ the operator T as $T\varphi \left(t\right)=\left(T_{ij}\varphi \left(t\right)\right),$ $i=1,\dots ,m,j=1,\dots ,n,$ where

$$\begin{array}{c}\hfill T_{ij}\varphi \left(t\right)\equiv -{\int }_{-\infty }^t{e}^{-{\int }_s^t{a}_{ij}\left(u\right)du}\left(b_{ij}\left(s\right){\varphi }_{ij}\left(s\right)+\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left({\varphi }_{kl}\left(s\right)\right){\varphi }_{ij}\left(s\right)-v_{ij}\left(s\right)\right)ds.\end{array}$$

(8)

The following assumptions are needed for system (4):

(C1)

functions $a_{ij}\left(t\right),$ $i=1,\dots ,m,$ $j=1,\dots ,n,$ are $\omega$-periodic, and ${\int }_0^{\omega }{a}_{ij}\left(s\right)ds>0;$

(C2)

functions $b_{ij}\left(t\right),$ $c_{ij}^{kl}\left(t\right)$ and $v_{ij}\left(t\right)$ are compartmental periodic unpredictable such that $b_{ij}\left(t\right)=B_{ij}(t,t),$ $c_{ij}^{kl}\left(t\right)=C_{ij}^{kl}(t,t),$ $v_{ij}\left(t\right)=V_{ij}(t,t),$ where the functions $B_{ij}(u,v),$ $C_{ij}^{kl}(u,v)$ and $V_{ij}(u,v)$ are $\omega -$periodic in u uniformly with respect to $v,$ and unpredictable in v with common sequences $t_p,$ $s_p,$ $p=1,2,\dots ,$ uniformly with respect to $u;$

(C3)

convergence sequence $t_p,p=1,2,\dots ,$ satisfies the kappa property;

(C4)

${sup}_{\left|s\right|<H}\left|f\left(s\right)\right|=m_f,$ where $m_f$ is a positive number;

(C5)

there exists a constant $L>0$ such that $|f\left(s_1\right)-f\left(s_2\right)|\le L|s_1-s_2|$ if $|s_1|<H,|s_2|<H.$

Condition (C1) implies that there exist constants $K_{ij}\ge 1$ and ${\lambda }_{ij}>0,$ which satisfy

$$\begin{array}{c}\hfill {\displaystyle e^{-{\int }_s^t{a}_{ij}\left(u\right)du}\le K_{ij}{e}^{-{\lambda }_{ij}(t-s)},t\ge s,}\end{array}$$

for all $i=1,\dots ,m,j=1,\dots ,n.$

For the sake of simplicity, the following notations will be used.

$$\begin{array}{c}\hfill {\displaystyle m_{ij}^b=\underset{t\in \mathbb{R}}{sup}|b_{ij}\left(t\right)|,m_{ij}^c=\sum _{C_{kl}\in N_r(i,j)}\underset{t\in \mathbb{R}}{sup}|c_{ij}^{kl}\left(t\right)|,m_{ij}^v=\underset{t\in \mathbb{R}}{sup}|v_{ij}\left(t\right)|,}\end{array}$$

for each $i=1,2,\dots ,m,j=1,2,\dots ,n.$

We assume that the following conditions are satisfied.

(C6)

${\displaystyle \frac{K_{ij}{m}_{ij}^v}{{\lambda }_{ij}-K_{ij}{m}_{ij}^b-K_{ij}{m}_{ij}^c{m}_f}<H,}$  $i=1,\dots ,m,j=1,\dots ,n;$

(C7)

$K_{ij}(m_{ij}^b+m_{ij}^c(m_f+LH))<{\lambda }_{ij},$  $i=1,\dots ,m,j=1,\dots ,n.$

3. Main Results

This part of the manuscript considers the existence of the dynamics, which is described in the Preliminary section. The discussion is fulfilled by researching dynamics of operator T in the space $\mathcal{Q}.$ We will show that it is invariant and contractive in the set, and prove the existence of Poisson stable dynamics for the neural networks. Next, the existence of the unpredictable solution is approved, to guarantee chaotic features in the dynamics. The exponential stability of the solution is verified under suggested conditions.

Lemma 3. 

Assume that conditions (C1)–(C6) are valid. Then T is an invariant operator in $\mathcal{Q}.$

Proof. 

Let $\varphi \left(t\right)\in \mathcal{Q}.$ We have that

$$\begin{array}{ccc}& & |T_{ij}\varphi \left(t\right)|\le |{\int }_{-\infty }^t{e}^{-{\int }_s^t{a}_{ij}\left(u\right)du}\left(b_{ij}\left(s\right){\varphi }_{ij}\left(s\right)+\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left({\varphi }_{kl}\right)\left(s\right){\varphi }_{ij}\left(s\right)-v_{ij}\left(s\right)\right)ds|\le \hfill \\ & & {\int }_{-\infty }^t{K}_{ij}{e}^{-{\lambda }_{ij}(t-s)}\left(|b_{ij}\left(s\right)||{\varphi }_{ij}\left(s\right)|+\sum _{c_{kl}\in N_r(i,j)}|c_{ij}^{kl}\left(s\right)||f\left({\varphi }_{kl}\right)\left(s\right)\left|\right|{\varphi }_{ij}\left(s\right)|+|v_{ij}\left(s\right)|\right)ds\le \hfill \\ & & \frac{K_{ij}}{{\lambda }_{ij}}(m_{ij}^{b}H+m_{ij}^c{m}_{f}H+m_{ij}^v),\hfill \end{array}$$

for all $i=1,2,\cdots ,m,j=1,2,\cdots ,n.$ By condition (C6), we obtain that $|T_{ij}\varphi \left(t\right)|<H,$ $i=1,2,\cdots ,m,j=1,2,\cdots ,n.$

Next, we prove that the sequence of the functions $T_{ij}\varphi (t+t_p),$ $i=1,2,\cdots ,m,$ $j=1,2,\cdots ,n,$ uniformly converges to $T_{ij}\varphi \left(t\right)$ on each bounded interval of $\mathbb{R}.$ Let us fix a bounded interval $[\alpha ,\beta ]\subset \mathbb{R},$ and a positive number $ϵ.$ There exist numbers $\xi >0$ and $\gamma <\alpha ,$ such that the following inequalities are valid for all $i=1,2,\cdots ,m,$ $j=1,2,\cdots ,n,$

$$\begin{array}{c}\hfill \frac{2K_{ij}}{{\lambda }_{ij}}{e}^{-{\lambda }_{ij}(\alpha -\gamma )}\left(3m_{ij}^{b}H+3m_{ij}^c{m}_{f}H+m_{ij}^{c}L{H}^2+2m_{ij}^v\right)<\frac{ϵ}{2},\end{array}$$

(9)

$$\begin{array}{c}\hfill \frac{K_{ij}}{{\lambda }_{ij}}(e^{\xi (\beta -\gamma )}-1)\left(2m_{ij}^{b}H+m_{ij}^c{m}_{f}H+m_{ij}^v\right)<\frac{ϵ}{4},\end{array}$$

(10)

$$\begin{array}{c}\hfill \frac{K_{ij}\xi }{{\lambda }_{ij}}\left(m_{ij}^b+H+m_{ij}^c{m}_f+m_{ij}^{c}LH+mn{m}_{f}H+1\right)<\frac{ϵ}{4}.\end{array}$$

(11)

The proof technique given below is called the method of included intervals, since the interval $[\alpha ,\beta ]$ is contained in $[\gamma ,\beta ]$ [26].

Applying condition (C3), one can take a sufficiently large number p such that $|b_{ij}(t+t_p)-b_{ij}\left(t\right)|<\xi ,$ $|c_{ij}(t+t_p)-c_{ij}\left(t\right)|<\xi ,$ $|v_{ij}(t+t_p)-v_{ij}\left(t\right)|<\xi ,$ $|{\varphi }_{ij}(t+t_p)-{\varphi }_{ij}\left(t\right)|<\xi ,$ $i=1,2,\cdots ,m,$ $j=1,2,\cdots ,n,$ for $t\in [\gamma ,\beta ].$ Moreover, due to condition (C1), it is correct that $|a_{ij}(t+t_p)-a_{ij}\left(t\right)|<\xi$ for all $t\in \mathbb{R}.$ We have that

$$\begin{array}{ccc}& & |T_{ij}\varphi (t+t_p)-T_{ij}\varphi \left(t\right)|\le |{\int }_{-\infty }^t{e}^{-{\int }_s^t{a}_{ij}(u+t_p)du}(b_{ij}(s+t_p)\varphi (s+t_p)+\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}(s+t_p)f\left({\varphi }_{kl}(s+t_p)\right){\varphi }_{ij}(s+t_p)-v_{ij}(s+t_p))ds+\hfill \\ & & {\int }_{-\infty }^t{e}^{-{\int }_s^t{a}_{ij}\left(u\right)du}\left(b_{ij}\left(s\right)\varphi \left(s\right)+\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left({\varphi }_{kl}\left(s\right)\right){\varphi }_{ij}\left(s\right)-v_{ij}\left(s\right)\right)ds|\le \hfill \\ & & {\displaystyle {\int }_{-\infty }^t|e^{-{\int }_s^t{a}_{ij}(u+t_p)du}-e^{-{\int }_s^t{a}_{ij}\left(u\right)du}||b_{ij}(s+t_p)\varphi (s+t_p)+}\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}(s+t_p)f\left({\varphi }_{kl}(s+t_p)\right){\varphi }_{ij}(s+t_p)-v_{ij}(s+t_p)|ds+\hfill \\ & & {\int }_{-\infty }^t{e}^{-{\int }_s^t{a}_{ij}\left(u\right)du}|b_{ij}(s+t_p)\varphi (s+t_p)-b_{ij}\left(s\right)\varphi \left(s\right)+\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}(s+t_p)f\left({\varphi }_{kl}(s+t_p)\right){\varphi }_{ij}(s+t_p)-\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left({\varphi }_{kl}\left(s\right)\right){\varphi }_{ij}\left(s\right)-v_{ij}(s+t_p)+v_{ij}\left(s\right)|ds.\hfill \end{array}$$

Consider the last inequality separately on intervals $(-\infty ,\gamma ]$ and $(\gamma ,t].$ Applying inequalities (9)–(11), we obtain

$$\begin{array}{ccc}\hfill & & {\displaystyle I_1={\int }_{-\infty }^{\gamma }|e^{-{\int }_s^t{a}_{ij}(u+t_p)du}-e^{-{\int }_s^t{a}_{ij}\left(u\right)du}||b_{ij}(s+t_p)\varphi (s+t_p)+}\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}(s+t_p)f\left({\varphi }_{kl}(s+t_p)\right){\varphi }_{ij}(s+t_p)-v_{ij}(s+t_p)|ds+\hfill \\ & & {\int }_{-\infty }^{\gamma }{e}^{-{\int }_s^t{a}_{ij}\left(u\right)du}|b_{ij}(s+t_p)\varphi (s+t_p)-b_{ij}\left(s\right)\varphi \left(s\right)+\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}(s+t_p)f\left({\varphi }_{kl}(s+t_p)\right){\varphi }_{ij}(s+t_p)-\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left({\varphi }_{kl}\left(s\right)\right){\varphi }_{ij}\left(s\right)-v_{ij}(s+t_p)+v_{ij}\left(s\right)|ds\le \hfill \\ & & {\int }_{-\infty }^{\gamma }2K_{ij}{e}^{-{\lambda }_{ij}(t-s)}\left(m_{ij}^{b}H+m_{ij}^c{m}_{f}H+m_{ij}^v\right)ds+\hfill \\ & & {\int }_{-\infty }^{\gamma }{K}_{ij}{e}^{-{\lambda }_{ij}(t-s)}\left(4m_{ij}^{b}H+2H{m}_f{m}_{ij}^c+2m_{ij}^{c}L{H}^2+2m_{ij}^{c}H{m}_f+2m_{ij}^v\right)ds\le \hfill \\ & & \frac{2K_{ij}}{{\lambda }_{ij}}{e}^{-{\lambda }_{ij}(\alpha -\gamma )}\left(3m_{ij}^{b}H+3m_{ij}^c{m}_{f}H+m_{ij}^{c}L{H}^2+2m_{ij}^v\right)<\frac{ϵ}{2}\hfill \end{array}$$

(12)

and

$$\begin{array}{ccc}\hfill & & {\displaystyle I_2={\int }_{-\gamma }^t|e^{-{\int }_s^t{a}_{ij}(u+t_p)du}-e^{-{\int }_s^t{a}_{ij}\left(u\right)du}||b_{ij}(s+t_p)\varphi (s+t_p)+}\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}(s+t_p)f\left({\varphi }_{kl}(s+t_p)\right){\varphi }_{ij}(s+t_p)-v_{ij}(s+t_p)|ds+\hfill \\ & & {\int }_{\gamma }^t{e}^{-{\int }_s^t{a}_{ij}\left(u\right)du}|b_{ij}(s+t_p)\varphi (s+t_p)-b_{ij}\left(s\right)\varphi \left(s\right)+\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}(s+t_p)f\left({\varphi }_{kl}(s+t_p)\right){\varphi }_{ij}(s+t_p)-\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left({\varphi }_{kl}\left(s\right)\right){\varphi }_{ij}\left(s\right)-v_{ij}(s+t_p)+v_{ij}\left(s\right)|ds\le \hfill \\ & & \le {\int }_{\gamma }^t{K}_{ij}{e}^{-{\lambda }_{ij}(t-s)}(e^{\xi (\beta -\gamma )}-1)\left(2m_{ij}^{b}H+m_{ij}^c{m}_{f}H+m_{ij}^v\right)ds+\hfill \\ & & {\int }_{\gamma }^t{K}_{ij}{e}^{-\lambda (t-s)}\left(m_{ij}^b\xi +H\xi +m_{ij}^c{m}_f\xi +m_{ij}^{c}LH\xi +mn\xi m_{f}H+\xi \right)ds\le \hfill \\ & & \frac{K_{ij}}{{\lambda }_{ij}}(e^{\xi (\beta -\gamma )}-1)\left(2m_{ij}^{b}H+m_{ij}^c{m}_{f}H+m_{ij}^v\right)+\hfill \\ & & \frac{K_{ij}}{{\lambda }_{ij}}\xi \left(m_{ij}^b+H+m_{ij}^c{m}_f+m_{ij}^{c}LH+mn{m}_{f}H+1\right)<\frac{ϵ}{4}+\frac{ϵ}{4}=\frac{ϵ}{2}.\hfill \end{array}$$

(13)

Inequalities (12) and (13) give that $|T_{ij}\varphi (t+t_p)-T_{ij}\varphi \left(t\right)|\le I_1+I_2<ϵ$ for all $i=1,2,\cdots ,m,j=1,2,\cdots ,n,$ if $t\in [\alpha ,\beta ].$ Therefore, $T\mathcal{Q}\subseteq \mathcal{Q}.$  □

Lemma 4. 

Conditions (C1)–(C7) imply that T is a contraction operator in $\mathcal{Q}$.

Proof. 

Let $\phi$ and $\psi$ be members of $\mathcal{Q}.$ It is true that the inequality

$$\begin{array}{ccc}& & |T_{ij}\phi \left(t\right)-T_{ij}\psi \left(t\right)|\le {\int }_{-\infty }^t{e}^{-{\int }_s^t{a}_{ij}\left(u\right)du}(\left|b_{ij}\left(s\right)(\phi \left(s\right)-\psi \left(s\right))\right|+\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)\left(\right|f\left({\phi }_{kl}\left(s\right)\right){\phi }_{ij}\left(s\right)-f\left({\phi }_{kl}\left(s\right)\right){\psi }_{ij}\left(s\right)|+\hfill \\ & & |f\left({\phi }_{kl}\left(s\right)\right){\psi }_{ij}\left(s\right)-f\left({\psi }_{kl}\left(s\right)\right){\psi }_{ij}\left(s\right)\left)\right|)ds\le \frac{K_{ij}}{{\lambda }_{ij}}\left(m_{ij}^b+m_{ij}^c(m_f+LH)\right){\parallel \phi -\psi \parallel }_0\hfill \end{array}$$

is valid for all $i=1,2,\cdots ,m,j=1,2,\cdots ,n.$ Therefore, it is true that ${\displaystyle {\parallel T\phi -T\psi \parallel }_0\le \frac{K_{ij}(m_{ij}^b+m_{ij}^c(m_f+LH))}{{\lambda }_{ij}}{∥\phi -\psi ∥}_0}$, and by condition $\left(C7\right)$, operator T is contractive in $\mathcal{Q}$. □

Theorem 1. 

If the assumptions $\left(C1\right)$–$\left(C7\right)$ are valid, then the neural network (4) has a unique, exponentially stable Poisson stable solution.

Proof. 

Let us show that the set $\mathcal{Q}$ is complete. Consider a sequence ${\varphi }^k\left(t\right)$ in $\mathcal{Q},$ which converges on $\mathbb{R}$ to a limit function $\varphi \left(t\right).$ Fix a section $I\subset \mathbb{R}.$ We have that

$$\begin{array}{c}\hfill \parallel \varphi (t+t_p)-\varphi \left(t\right)\parallel \le \parallel \varphi (t+t_p)-{\varphi }^k(t+t_p)\parallel +\parallel {\varphi }^k(t+t_p)-{\varphi }^k\left(t\right)\parallel +\parallel {\varphi }^k\left(t\right)-\varphi \left(t\right)\parallel .\end{array}$$

(14)

One can take sufficiently large numbers p and k such that each term on the right-hand-side of (14) is smaller than $\frac{ϵ}{3}$ for an arbitrary $ϵ>0$ and $t\in I$. The inequality (14) implies that $\varphi (t+t_p)$ converges to $\varphi \left(t\right)$ uniformly on $I.$ That is, the set $\mathcal{Q}$ is complete.

By the contraction mapping principle, duo to Lemmas 3 and 4, there exists a unique Poisson stable solution, $z\left(t\right)\in \mathcal{Q}$ of the system (4), such that the sequences $z(t+t_p)$ converges to $z\left(t\right)$ uniformly on each of the bounded intervals of $\mathbb{R}.$

Now, let us discuss the stability of the solution $z\left(t\right).$ It is true that

$$\begin{array}{c}\hfill {\displaystyle z_{ij}\left(t\right)=e^{-{\int }_{t_0}^t{a}_{ij}\left(u\right)du}{z}_{ij}\left(t_0\right)-{\int }_{t_0}^t{e}^{-{\int }_s^t{a}_{ij}\left(u\right)du}\left(b_{ij}\left(s\right)z_{ij}\left(s\right)+\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(z_{kl}\left(s\right)\right)z_{ij}\left(s\right)-v_{ij\left(s\right)}\right)ds,}\end{array}$$

for all $i=1,\dots ,m$, $j=1,\dots ,n.$

If $x\left(t\right)=\left(x_{ij}\left(t\right)\right),$ $i=1,\dots ,m,j=1,\dots ,n,$ is another solution of the neural network (4), then

$$\begin{array}{c}\hfill {\displaystyle x_{ij}\left(t\right)=e^{-{\int }_{t_0}^t{a}_{ij}\left(u\right)du}{x}_{ij}\left(t_0\right)-{\int }_{t_0}^t{e}^{-{\int }_s^t{a}_{ij}\left(u\right)du}\left(b_{ij}\left(s\right)x_{ij}\left(s\right)+\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(x_{kl}\left(s\right)\right)x_{ij}\left(s\right)-v_{ij\left(s\right)}\right)ds.}\end{array}$$

Using the formula

$$\begin{array}{ccc}& & x_{ij}\left(t\right)-z_{ij}\left(t\right)=e^{-{\int }_{t_0}^t{a}_{ij}\left(u\right)du}\left(x_{ij}\left(t_0\right)-z_{ij}\left(t_0\right)\right)-{\int }_{t_0}^t{e}^{-{\int }_{t_0}^t{a}_{ij}\left(u\right)du}\times \hfill \\ & & \left(\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(x_{kl}\left(s\right)\right)x_{ij}\left(s\right)-\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(z_{kl}\left(s\right)\right)z_{ij}\left(s\right)\right)ds=\hfill \\ & & e^{-{\int }_{t_0}^t{a}_{ij}\left(u\right)du}\left(x_{ij}\left(t_0\right)-z_{ij}\left(t_0\right)\right)-{\int }_{t_0}^t{e}^{-{\int }_{t_0}^t{a}_{ij}\left(u\right)du}(\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(x_{kl}\left(s\right)\right)x_{ij}\left(s\right)-\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(z_{kl}\left(s\right)\right)x_{ij}\left(s\right)+\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(z_{kl}\left(s\right)\right)x_{ij}\left(s\right)-\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(z_{kl}\left(s\right)\right)z_{ij}\left(s\right))ds,\hfill \end{array}$$

we obtain that

$$\begin{array}{ccc}& & |x_{ij}\left(t\right)-z_{ij}\left(t\right)|\le e^{-{\int }_{t_0}^t{a}_{ij}\left(u\right)du}|x_{ij}\left(t_0\right)-z_{ij}\left(t_0\right)|+{\int }_{t_0}^t{e}^{-{\int }_{t_0}^t{a}_{ij}\left(u\right)du}(b_{ij}\left(s\right)(x_{ij}\left(s\right)-z_{ij}\left(s\right))+\hfill \\ & & \sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)|f\left(x_{kl}\left(s\right)\right)-f\left(z_{kl}\left(s\right)\right)\left|\right|x_{ij}\left(s\right)|ds+\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)|f\left(z_{kl}\left(s\right)\right)\left|\right|x_{ij}\left(s\right)-z_{ij}\left(s\right)\left|\right)ds\le \hfill \\ & & K_{ij}{e}^{-{\lambda }_{ij}(t-t_0)}|x_{ij}\left(t_0\right)-z_{ij}\left(t_0\right)|+{\int }_{t_0}^t{K}_{ij}{e}^{-{\lambda }_{ij}(t-t_0)}(m_{ij}^b+m_{ij}^c(LH+m_f))|x_{ij}\left(s\right)-z_{ij}\left(s\right)|ds,\hfill \end{array}$$

is valid for all $i=1,2,\cdots ,m,j=1,2,\cdots ,n.$

Applying the Gronwall–Bellman lemma, one can attain that

$$\begin{array}{ccc}& & |x_{ij}\left(t\right)-z_{ij}\left(t\right)|\le K_{ij}|x_{ij}\left(t_0\right)-z_{ij}\left(t_0\right)|e^{(K_{ij}(m_{ij}^b+m_{ij}^c(LH+m_{f}H))-{\lambda }_{ij})(t-t_0)},t>t_0.\hfill \end{array}$$

Consequently, $z\left(t\right)$ is exponentially stable in accordance with condition (C7). □

Theorem 2. 

Assume that conditions $\left(C1\right)$–$\left(C7\right)$ are fulfilled. Then the neural network (4) possesses a unique exponentially stable unpredictable solution.

Proof. 

According to Theorem 1, under conditions $\left(C1\right)$–$\left(C7\right)$ there exists a unique exponentially stable solution $z\left(t\right),$ which satisfies the convergence property. Now, we will prove that the separation property for the solution $z\left(t\right)$ is true. Condition $\left(C2\right)$ implies that for functions $v_{ij}\left(t\right),$ $i=1,\dots ,m$, $j=1,\dots ,n,$ there exists a sequence $s_p$ and positive numbers ${ϵ}_0,\delta$ such that $|v_{ij}(t+t_p)-v_{ij}\left(t\right)|>{ϵ}_0$ for each $t\in [s_p-\delta ,s_p+\delta ]$ and $p\in \mathbb{N}.$

It is true that

$$\begin{array}{ccc}& & {\displaystyle z_{ij}\left(t\right)=z_{ij}\left(s_p\right)-{\int }_{s_p}^t{a}_{ij}\left(s\right)z_{ij}\left(s\right)ds-{\int }_{s_p}^t{b}_{ij}\left(s\right)z_{ij}\left(s\right)ds-}\hfill \\ & & {\displaystyle {\int }_{s_p}^t\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kp}\left(s\right)f\left(z_{kp}\left(s\right)\right){\omega }_{ij}\left(s\right)ds+{\int }_{s_p}^t{v}_{ij}\left(s\right)ds}\hfill \end{array}$$

and

$$\begin{array}{ccc}& & {\displaystyle z_{ij}(t+t_p)=z_{ij}(t_p+s_p)-{\int }_{s_p}^t{a}_{ij}(s+t_p)z_{ij}(s+t_p)ds-{\int }_{s_p}^t{b}_{ij}(s+t_p)z_{ij}(s+t_p)ds-}\hfill \\ & & {\displaystyle {\int }_{s_p}^t\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}(s+t_p)f\left(z_{kl}(s+t_p)\right){\omega }_{ij}(s+t_p)ds+{\int }_{s_s}^t{v}_{ij}(s+t_p)ds.}\hfill \end{array}$$

Therefore, we have that

$$\begin{array}{ccc}& & {\displaystyle z_{ij}(t+t_p)-z_{ij}\left(t\right)=z_{ij}(t_p+s_p)-z_{ij}\left(s_p\right)-{\int }_{s_p}^t{a}_{ij}{(s+t_p)}_{ij}(s+t_p)ds+}\hfill \\ & & {\displaystyle {\int }_{s_p}^t{a}_{ij}\left(s\right)z_{ij}\left(s\right)ds-{\int }_{s_p}^t{b}_{ij}(s+t_p)z_{ij}(s+t_p)ds+{\int }_{s_p}^t{b}_{ij}\left(s\right)z_{ij}\left(s\right)ds-}\hfill \\ & & {\displaystyle {\int }_{s_p}^t\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}(s+t_p)f\left(z_{kl}(s+t_p)\right){\omega }_{ij}(s+t_p)ds+}\hfill \\ & & {\displaystyle {\int }_{s_p}^t\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(z_{kl}\left(s\right)\right){\omega }_{ij}\left(s\right)ds-{\int }_{s_s}^t{v}_{ij}(s+t_p)ds+{\int }_{s_p}^t{v}_{ij}\left(s\right)ds.}\hfill \end{array}$$

Denote ${\displaystyle m_{ij}^a=\underset{t\in \mathbb{R}}{sup}\left|a_{ij}\left(t\right)\right|.}$ One can fix positive numbers $l,k$ and ${\delta }_1$ such that the following inequalities are satisfied:

$${\delta }_1<\delta ;$$

(15)

$$|a_{ij}(t+s)-a_{ij}\left(s\right)|<{ϵ}_0(\frac{1}{l}+\frac{2}{k}),t\in \mathbb{R},$$

(16)

$$|c_{ij}(t+s)-c_{ij}\left(s\right)|<{ϵ}_0(\frac{1}{l}+\frac{2}{k}),t\in \mathbb{R},$$

(17)

$${\delta }_1\left. [{ϵ}_0\left(1-(\frac{1}{l}+\frac{2}{k})(m_{ij}^a+H+m_{ij}^b+LH+m_{ij}^c{m}_f+mn{m}_{f}H)\right)-2H(m_{ij}^b+m_{ij}^c{m}_f)\right]>\frac{3{ϵ}_0}{2l},$$

(18)

$$|z_{ij}(t+s)-z_{ij}\left(t\right)|<{ϵ}_{0}min(\frac{1}{k},\frac{1}{4l}),t\in \mathbb{R},\left|s\right|<{\delta }_1.$$

(19)

Consider the following two alternatives: (i) $|z_{ij}(t_p+s_p)-z_{ij}\left(s_p\right)|<{ϵ}_0/l;$  (ii) $|z_{ij}(t_p+s_p)-z_{ij}\left(s_p\right)|\ge {ϵ}_0/l.$

(i) Using (19), for each $i=1,2,\cdots ,m,j=1,2,\cdots ,n,$ one can show that

$$\begin{array}{ccc}\hfill & & |z_{ij}(t+t_p)-z_{ij}\left(t_p\right)|\le |z_{ij}(t+t_p)-z_{ij}(s_p+t_p)|+|z_{ij}(s_p+t_p)-z_{ij}\left(s_p\right)|+\hfill \\ & & |z_{ij}\left(s_p\right)-z_{ij}\left(t\right)|<\frac{{ϵ}_0}{l}+\frac{{ϵ}_0}{k}+\frac{{ϵ}_0}{k}={ϵ}_0(\frac{1}{l}+\frac{2}{k}),\hfill \end{array}$$

(20)

if $t\in [s_p,s_p+{\delta }_1].$ Therefore, the condition (C4) and inequalities (15)–(19) imply that

$$\begin{array}{ccc}& & {\displaystyle |z_{ij}(t+t_p)-z_{ij}\left(t\right)|\ge {\int }_{s_p}^t|v_{ij}(s+t_p)-v_{ij}\left(s\right)|ds-|z_{ij}(t_p+s_p)-z_{ij}\left(s_p\right)|-}\hfill \\ & & {\int }_{s_p}^t|a_{ij}(s+t_p)z_{ij}(s+t_p)|ds+{\int }_{s_p}^t|a_{ij}{\left(s\right)}_{ij}{z}_{ij}\left(s\right)|ds-{\int }_{s_p}^t|b_{ij}(s+t_p)z_{ij}(s+t_p)|ds+\hfill \\ & & {\int }_{s_p}^t|b_{ij}{\left(s\right)}_{ij}{z}_{ij}\left(s\right)|ds-{\int }_{s_p}^t|\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}(s+t_p)f\left(z_{kl}(s+t_p)\right)z_{ij}(s+t_p)|ds+\hfill \\ & & {\int }_{s_p}^t|\sum _{c_{kl}\in N_r(i,j)}{c}_{ij}^{kl}\left(s\right)f\left(z_{kl}\left(s\right)\right)z_{ij}\left(s\right)|ds>{ϵ}_0{\delta }_1-\frac{{ϵ}_0}{l}-{ϵ}_0{\delta }_1(\frac{1}{l}+\frac{2}{k})(m_{ij}^a+H)-\hfill \\ & & 2{\delta }_1{m}_{ij}^{b}H-{ϵ}_0{\delta }_1(\frac{1}{l}+\frac{2}{k})m_{ij}^b-2{\delta }_1{m}_{ij}^c{m}_{f}H-{ϵ}_0{\delta }_1(\frac{1}{l}+\frac{2}{k})(LH+m_{ij}^c{m}_f+mn{m}_{f}H)=\hfill \\ & & {\delta }_1\left({ϵ}_0-2m_{ij}^{b}H-2m_{ij}^c{m}_{f}H-{ϵ}_0(\frac{1}{l}+\frac{2}{k})(m_{ij}^a+H+m_{ij}^b+LH+m_{ij}^c{m}_f+mn{m}_{f}H)\right)\hfill \\ & & -\frac{{ϵ}_0}{l}\ge \frac{{ϵ}_0}{2l},\hfill \end{array}$$

for $t\in [s_p,s_p+{\delta }_1].$

(ii) If $|z_{ij}(t_p+s_p)-z_{ij}\left(s_p\right)|\ge {ϵ}_0/l$, it is not difficult to find that (18) implies:

$$\begin{array}{ccc}& & |z_{ij}(t+t_p)-z_{ij}\left(t\right)|\ge |z_{ij}(t_p+s_p)-z_{ij}\left(s_p\right)|-|z_{ij}\left(s_p\right)-z_{ij}\left(t\right)|-\hfill \\ & & |z_{ij}(t+t_p)-z_{ij}(t_p+s_p)|>\frac{{ϵ}_0}{l}-\frac{{ϵ}_0}{4l}-\frac{{ϵ}_0}{4l}=\frac{{ϵ}_0}{2l},\hfill \end{array}$$

for $t\in [s_p-{\delta }_1,s_p+{\delta }_1]$ and $p\in \mathbb{N}.$ Thus, we can conclude that $z\left(t\right)$ is an unpredictable solution with positive numbers $\frac{{\delta }_1}{2},$ $\frac{{ϵ}_0}{2l}$ and sequences $t_p,$ $s_p.$  □

4. Degree of Periodicity and Numerical Simulations

This part of the article emphasises application significance of the theoretical achievements in the Section 3. Unpredictable continuous and discontinuous functions are constructively determined through discrete Poisson stable and unpredictable motions of the logistic equation. A special technical characteristic, the degree of periodicity, is introduced, which allows to estimate contributions of periodic and unpredictable arguments to the behaviour of the neural network. This can be useful for analysis of experimental data in industries [34,35,36,37,38], and this is a strong argument for the application of our results. Finally, two numerical examples with sophisticated dynamics can be seen below.

In the Ref. [42], it was proved that the logistic map

$${\lambda }_{i+1}=\nu {\lambda }_i(1-{\lambda }_i),i\in \mathbb{Z}.$$

(21)

admits an unpredictable solution ${\mu }_i,$ $i\in \mathbb{Z},$ if $\nu \in [3+{(2/3)}^{1/2},4].$ That is, there exist sequences ${\zeta }_p\to \infty ,$ ${\eta }_p\to \infty$ as $p\to \infty ,$ and a positive number ${ϵ}_0$ such that ${\mu }_{i+{\zeta }_p}$ tends to ${\mu }_i$ for each i in a bounded interval of integers and $|{\mu }_{{\zeta }_p+{\eta }_p}-{\mu }_{{\eta }_p}|>{ϵ}_0$ for $p\in \mathbb{N}.$

Discontinuous unpredictable function. Consider the function $\pi \left(t\right)={\mu }_i\xi (t-ih),$ $t\in (ih,(i+1\left)h\right],$ $i\in \mathbb{Z},$ where ${\mu }_i$ is an unpredictable solution of the logistic Equation (21), $\xi \left(t\right):(0,h]\to {\mathbb{R}}^n,n\in \mathbb{N},$ is a continuous function, and h is a positive number. Assume that there exist positive numbers $\delta ,s$ and ${ϵ}_1$ such that $[s-\delta ,s+\delta ]\subset (0,h]$ and $\parallel \xi \left(t\right)\parallel >{ϵ}_1$ for each $t\in [s-\delta ,s+\delta ].$

Let us show that the function $\pi \left(t\right)$ is unpredictable. Fix an interval of real numbers $(\alpha ,\beta )$ and a number $i\in \mathbb{Z}$ such that $(\alpha ,\beta )\subset \left[\right(i-1)h,(i+s+1\left)h\right],$ where s is a natural number. Then for $t_p={\zeta }_{p}h,$ $p\in \mathbb{N},$ and $t\in (jh,(j+1\left)h\right],$ $i-1\le j\le i+s,$ we have that $t+{\zeta }_{p}h\in ((j+{\zeta }_p)h,(j+{\zeta }_p+1)h],$ and $\xi (t-(j+{\zeta }_p)h)=\xi (t-jh).$

Denote $M={sup}_{t\in (0,h]}\parallel \xi \left(t\right)\parallel .$ For a fixed positive number $ϵ,$ and sufficiently large number p, it is true that $|{\mu }_{j+{\zeta }_p}-{\mu }_j|<\frac{ϵ}{M},$ $i-1\le j\le i+s.$ Therefore, for $t\in (lh,(l+1\left)h\right],$ where l is a fixed integer number from $i-1$ to $i+s,$ one can obtain that

$$\begin{array}{ccc}\hfill & & \parallel \pi (t+t_p)-\pi \left(t\right)\parallel = \parallel \pi (t+{\zeta }_{p}h)-\pi \left(t\right)\parallel = \parallel {\mu }_{l+{\zeta }_p}\xi (t-(l+{\zeta }_p)h)-{\mu }_l\xi (t-lh)\parallel =\hfill \\ & & |{\mu }_{l+{\zeta }_p}-{\mu }_j|\parallel \xi (t-lh)\parallel \le |{\mu }_{l+{\zeta }_p}-{\mu }_l|M<ϵ.\hfill \end{array}$$

The last inequality is valid for all $i-1\le l\le i+s.$ Consequently, $\parallel \pi (t+t_p)-\pi \left(t\right)\parallel <ϵ$ if $t\in (\alpha ,\beta ).$ Thus, the function $\pi \left(t\right)$ satisfies the convergence property.

We have that there exists a positive number ${ϵ}_0,$ and the sequence ${\eta }_p,$ ${\eta }_p\to \infty$ as $p\to \infty ,$ such that $|{\mu }_{{\zeta }_p+{\eta }_p}-{\mu }_{{\eta }_p}|>{ϵ}_0$ for each $p\in \mathbb{N}.$

From $t_p={\zeta }_{p}h,$ $p=1,2,\cdots ,$ and $t\in ({\eta }_{p}h+s-\delta ,{\eta }_{p}h+s+\delta ]$ it follows that $t+t_p=t+{\zeta }_{p}h\in (({\zeta }_p+{\eta }_p)h+s-\delta ,({\zeta }_p+{\eta }_p)h+s+\delta ].$ Therefore, $\xi (t+t_p)=\xi (t-({\zeta }_p+{\eta }_p)h)=\xi (t-{\eta }_{p}h),$ $p=1,2,\cdots .$ We obtain that

$$\begin{array}{ccc}\hfill & & \parallel \pi (t+t_p)-\pi \left(t\right)\parallel = \parallel {\mu }_{{\zeta }_p+{\eta }_p}\xi (t-({\zeta }_p+{\eta }_p)h)-{\mu }_{{\eta }_p}\xi (t-{\zeta }_{p}h)\parallel =\hfill \\ & & |{\mu }_{{\zeta }_p+{\eta }_p}-{\mu }_{{\eta }_p}|\parallel \xi (t-{\eta }_{p}h)\parallel >{ϵ}_0{ϵ}_1>0,\hfill \end{array}$$

(22)

for all $t\in ({\eta }_{p}h+s-\delta ,{\eta }_{p}h+s+\delta ],$ $p=1,2,\cdots .$ Thus, the function $\pi \left(t\right)$ satisfies separation property, and one can conclude that it is unpredictable with positive numbers ${ϵ}^{*}={ϵ}_0{ϵ}_1,$ $\delta ,$ and sequences $t_p={\zeta }_{p}h,$ $s_p={\eta }_{p}h+s,$ $p=1,2,\cdots .$

Continuous unpredictable function. Using the function $\pi \left(t\right),$ we construct an integral function $\Xi \left(t\right)={\int }_{-\infty }^t{e}^{-\alpha (t-s)}\pi \left(s\right)ds,$ where $\alpha$ is a positive real number. The function $\Xi \left(t\right)$ is bounded on $\mathbb{R}$ such that ${sup}_{t\in \mathbb{R}}\parallel \Xi \left(t\right)\parallel \le \frac{M_{\pi }}{\alpha },$ where $M_{\pi }={sup}_{t\in \mathbb{R}}\parallel \pi \left(t\right)\parallel .$

Let us discuss the unpredictability of the function $\Xi \left(t\right).$ Firstly, we shall approve the convergence property. Fix an interval $[a,b]\subset \mathbb{R}$ and a number $ϵ>0.$ Applying the method of included intervals [26], we will show that $\Xi (t+t_p)\to \Xi \left(t\right)$ uniformly on $[a,b].$ There exist numbers $\xi >0$ and $c<a,$ such that the following inequalities are valid, $\frac{2M_{\pi }}{\alpha }{e}^{-\alpha (a-c)}<\frac{ϵ}{2}$ and $\frac{\xi }{\alpha }[1-e^{-\alpha (b-c)}]<\frac{ϵ}{2}.$ Let p be a large enough number, such that ${\displaystyle \parallel \pi (t+t_p)-\pi \left(t\right)\parallel <\xi }$ on $[c,b].$ We obtain that

$$\begin{array}{ccc}& & \parallel \Xi (t+t_p)-\Xi \left(t\right)\parallel = \parallel {\int }_{-\infty }^t{e}^{-\alpha (t-s)}(\pi (s+t_p)-\pi \left(s\right))ds\parallel =\hfill \\ & & \parallel {\int }_{-\infty }^c{e}^{-\alpha (t-s)}(\pi (s+t_p)-\pi \left(s\right))ds+{\int }_c^t{e}^{-\alpha (t-s)}(\pi (s+t_p)-\pi \left(s\right))ds\parallel \le \hfill \\ & & {\int }_{-\infty }^c{e}^{-\alpha (t-s)}2M_{\pi }ds+{\int }_c^t{e}^{-\alpha (t-s)}\xi ds\le \frac{2M_{\pi }}{\alpha }{e}^{-\alpha (a-c)}+\frac{\xi }{\alpha }[1-e^{-\alpha (b-c)}]<\frac{ϵ}{2}+\frac{ϵ}{2}=ϵ,\hfill \end{array}$$

for all $t\in [a,b].$ Thus, $\parallel \Xi (t+t_k)-\Xi \left(t\right)\parallel \to 0$ as $k\to \infty$ uniformly on the interval $[a,b],$ and the convergence property is fulfilled.

Next, we verify that the separation property is correct. Due to the unpredictability of the function $\pi \left(t\right),$ we have that $\parallel \pi (t+t_p)-\pi \left(t\right)\parallel >{ϵ}^{*}$ for $t\in [s_p-\delta ,s_p+\delta ].$ Fix a natural number p and positive ${\delta }_1<\delta$ such that $\frac{2M_{\pi }{\delta }_1}{\alpha }[1-e^{-\alpha {\delta }_1}]<\frac{{ϵ}^{*}}{3\alpha }.$ Consider two alternative cases: (i) $\parallel \Xi (t_p+s_p)-\Xi \left(s_p\right)\parallel <\frac{2{\delta }_1{ϵ}^{*}}{3\alpha },$  (ii) $\parallel \Xi (t_p+s_p)-\Xi \left(s_p\right)\parallel \ge \frac{2{\delta }_1{ϵ}^{*}}{3\alpha }.$

It is easily seen that the following relation holds

$$\begin{array}{ccc}\hfill & & {\displaystyle \Xi (t+t_p)-\Xi \left(t\right)=\Xi (t_p+s_p)-\Xi \left(s_p\right)+{\int }_{s_p}^t{e}^{-\alpha (t-s)}(\pi (s+t_p)-\pi \left(s\right))ds.}\hfill \end{array}$$

(23)

(i) From the last relation, we obtain that

$$\begin{array}{ccc}\hfill & & {\displaystyle \parallel \Xi (t+t_p)-\Xi \left(t\right)\parallel \ge \parallel {\int }_{s_p}^t{e}^{-\alpha (t-s)}(\pi (s+t_p)-\pi \left(s\right))ds\parallel -\parallel \Xi (t_p+s_p)-\Xi \left(s_p\right)\parallel >}\hfill \\ & & {\int }_{s_p}^t{e}^{-\alpha (t-s)}{ϵ}^{*}ds-\frac{2{\delta }_1{ϵ}^{*}}{3\alpha }\ge \frac{{\delta }_1{ϵ}^{*}}{\alpha }-\frac{2{\delta }_1{ϵ}^{*}}{3\alpha }=\frac{{\delta }_1{ϵ}^{*}}{3\alpha }\hfill \end{array}$$

(24)

for $t\in [s_p-{\delta }_1,s_p+{\delta }_1].$

(ii) Using the relation (23), we obtain that

$$\begin{array}{ccc}\hfill & & {\displaystyle \parallel \Xi (t+t_p)-\Xi \left(t\right)\parallel \ge \parallel \Xi (t_p+s_p)-\Xi \left(s_p\right)\parallel -\parallel {\int }_{s_p}^t{e}^{-\alpha (t-s)}(\pi (s+t_p)-\pi \left(s\right))ds\parallel >}\hfill \\ & & \frac{2{\delta }_1{ϵ}^{*}}{3\alpha }-{\int }_{s_p}^t{e}^{-\alpha (t-s)}2M_{\pi }ds\ge \frac{2{\delta }_1{ϵ}^{*}}{3\alpha }-\frac{2M_{\pi }{\delta }_1}{\alpha }[1-e^{-\alpha {\delta }_1}]>\frac{{\delta }_1{ϵ}^{*}}{3\alpha }\hfill \end{array}$$

(25)

for $t\in [s_p-{\delta }_1,s_p+{\delta }_1].$ The inequalities (24) and (25) prove that the separation property is valid. Thus, the function $\Xi \left(t\right)$ is unpredictable with positive numbers ${ϵ}_1=\frac{{\delta }_1{ϵ}^{*}}{3\alpha },$ ${\delta }_1$ and sequences $t_p,$ $s_p.$

Below, we will use the continuous unpredictable function $\Xi \left(t\right)={\int }_{-\infty }^t{e}^{-3(t-s)}\pi \left(s\right)ds,$ where $\pi \left(t\right)={\mu }_{i}cos(t-ih),$ $t\in (ih,(i+1\left)h\right],$ $i\in \mathbb{Z},$ as a component of compartmental periodic unpredictable coefficients. The number h is said to be the length of step of functions $\pi \left(t\right)$ and $\Xi \left(t\right).$ For compartmental periodic unpredictable functions, the number $\nabla =\omega /h,$ is called the degree of periodicity.

Let us consider the following compartmental periodic unpredictable function $f\left(t\right)=G(t,t)=2cos\left(0.1t\right)\Xi \left(t\right)+sin\left(0.2t\right).$ The function $G(u,v)$ is $20\pi -$periodic in u uniformly with respect to $v,$ and unpredictable in v uniformly with respect to $u.$ For the function $f\left(t\right)$ the degree of periodicity is equal to 200. In Figure 1 the graph of function $f\left(t\right)$ is shown.

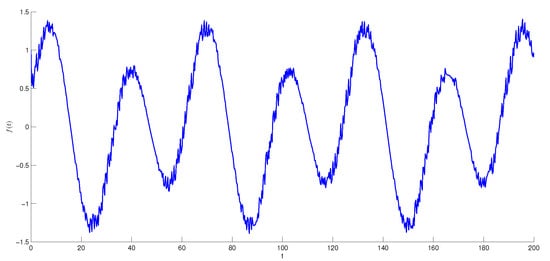
Figure 1. The graph of compartmental periodic unpredictable function $f\left(t\right).$ The length of step $h=0.1\pi ,$ and degree of periodicity $\nabla =200.$

The following lemma is used in the examples.

Lemma 5 

([33]). Assume that bounded function $g\left(u\right):{\mathbb{R}}^n\to {\mathbb{R}}^n,$ satisfies the inequalities $L_1∥u_1-u_2∥\le ∥g\left(u_1\right)-g\left(u_2\right)∥\le L_2∥u_1-u_2∥,$ where $L_1,L_2$ are positive constants, for all $u_1,u_2\in {\mathbb{R}}^n.$ Then the function $g\left(\psi \right(t\left)\right)$ is unpredictable, provided that $\psi \left(t\right):\mathbb{R}\to {\mathbb{R}}^n$ is an unpredictable function.

Example 1. 

Let us consider the system:

$$\begin{array}{c}\hfill \frac{d{x}_{ij}\left(t\right)}{dt}=-(a_{ij}\left(t\right)+b_{ij}\left(t\right))x_{ij}\left(t\right)-\sum _{c_{kl}\in N_1(i,j)}{c}_{ij}^{kl}\left(t\right)f\left(x_{kl}\left(t\right)\right)x_{ij}\left(t\right)+v_{ij}\left(t\right),\end{array}$$

(26)

with $i=1,2,$ $j=1,2,3,$ and $f\left(s\right)=0.25tanh\left(s\right).$ The functions $c_{ij}^{11}\left(t\right)=0.2sin\left(2t\right)\Xi \left(t\right),$ $c_{ij}^{12}\left(t\right)=0.1sin\left(t\right)\Xi \left(t\right),$ $c_{ij}^{13}\left(t\right)=0.3cos\left(2t\right)\Xi \left(t\right),$ $c_{ij}^{21}\left(t\right)=0.3sin\left(2t\right)\Xi \left(t\right),$ $c_{ij}^{22}\left(t\right)=0.1cos\left(t\right)\Xi \left(t\right)$ and $c_{ij}^{23}\left(t\right)=0.2sin\left(t\right)\Xi \left(t\right)$ are compartmental periodic unpredictable. The functions $a_{ij}\left(t\right),$ $i=1,2,$ $j=1,2,3,$ are $2\pi -$periodic: $a_{11}\left(t\right)=3+sin\left(t\right),$ $a_{12}\left(t\right)=2+cos\left(t\right),$ $a_{13}\left(t\right)=4+sin\left(2t\right),$ $a_{21}\left(t\right)=5+cos\left(4t\right),$ $a_{22}\left(t\right)=3+cos\left(2t\right),$ $a_{23}\left(t\right)=2+sin\left(t\right).$ According Lemma 5, the functions $b_{ij}\left(t\right)$ and perturbation $v_{ij}\left(t\right)$ are compartmental periodic unpredictable: $b_{11}\left(t\right)=cos\left(4t\right)\Xi \left(t\right),$ $b_{12}\left(t\right)=sin\left(2t\right)tanh(\Xi \left(t\right)),$ $b_{13}\left(t\right)=sin\left(4t\right)\Xi \left(t\right),$ $b_{21}\left(t\right)=cos\left(2t\right)arctan(\Xi \left(t\right)),$ $b_{22}\left(t\right)=sin\left(t\right)\Xi \left(t\right),$ $b_{23}\left(t\right)=cos\left(4t\right)\Xi \left(t\right),$ $v_{11}\left(t\right)=3sin\left(2t\right)\Xi \left(t\right),$ $v_{12}\left(t\right)=arctan(\Xi \left(t\right))+0.5cos\left(2t\right),$ $v_{13}\left(t\right)=4sin\left(t\right)\Xi \left(t\right),$ $v_{21}\left(t\right)=3sin\left(t\right)arctan(\Xi \left(t\right)),$ $v_{22}\left(t\right)=0.4cos\left(2t\right)\Xi \left(t\right),$ $v_{23}\left(t\right)=cos\left(2t\right)\Xi \left(t\right).$ Condition (C1) is satisfied, and $K_{ij}=1.5,$ $i=1,2,$ $j=1,2,3,$ ${\lambda }_{11}=6\pi ,$ ${\lambda }_{12}=4\pi ,$ ${\lambda }_{13}=8\pi ,$ ${\lambda }_{21}=10\pi ,$ ${\lambda }_{22}=6\pi ,$ ${\lambda }_{23}=4\pi .$ Condition (C3) is valid since the elements of the convergence sequence $t_p$ are multiples of the length of step h and the period ω is equal to $2\pi .$ Conditions (C4)–(C7) are satisfied with $H=0.8,$ $m_f=\pi /8,$ $L=0.25,$ ${max}_{(i,j)}{m}_{ij}^c=2/15,$ ${max}_{(i,j)}{m}_{ij}^b=1/3,$ $m_{11}^v=1,$ $m_{12}^v=5/6,$ $m_{13}^v=4/3,$ $m_{21}^v=1,$ $m_{22}^v=2/15$ and $m_{23}^v=1/3.$

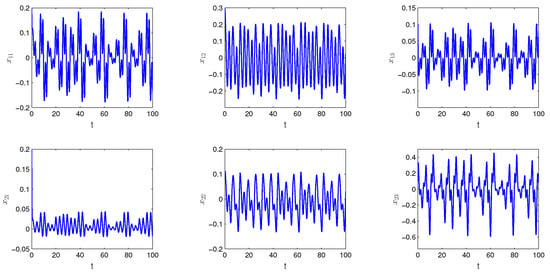
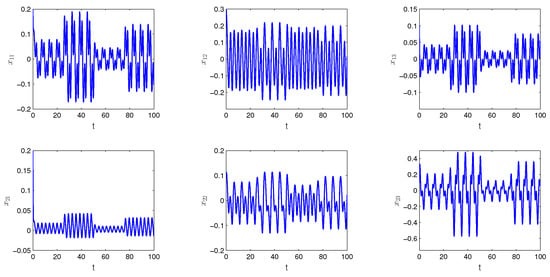
By Theorem 2, the neural network (26) has a unique exponentially stable unpredictable solution $z\left(t\right)=\left(z_{ij}\left(t\right)\right),$ $i=1,2,$ $j=1,2,3.$ Figure 2 and Figure 3 show the solution $x\left(t\right)=\left(x_{ij}\left(t\right)\right),$ $i=1,2,$ $j=1,2,3,$ with the length of step $h=2\pi$ and $h=8\pi ,$ respectively. The solution $x\left(t\right)$ exponentially converges to the unpredictable solution $z\left(t\right).$

Figure 2. The time series of the solution $x\left(t\right)=\left(x_{ij}\left(t\right)\right),$ $i=1,2,$ $j=1,2,3,$ of the system (26) with initial values $x_{11}\left(0\right)=0.2,$ $x_{12}\left(0\right)=0.3,$ $x_{13}\left(0\right)=0.1,$ $x_{21}\left(0\right)=0.2,$ $x_{22}\left(0\right)=0.1,$ $x_{23}\left(0\right)=0.1,$ and the degree of periodicity $\nabla =1.$

Figure 3. The graph of the solution $x\left(t\right)=\left(x_{ij}\left(t\right)\right),$ $i=1,2,$ $j=1,2,3,$ of SICNNs (26) with the initial values $x_{11}\left(0\right)=0.2,$ $x_{12}\left(0\right)=0.3,$ $x_{13}\left(0\right)=0.1,$ $x_{21}\left(0\right)=0.2,$ $x_{22}\left(0\right)=0.1,$ $x_{23}\left(0\right)=0.1,$ and the degree of periodicity $\nabla =1/4.$

Example 2. 

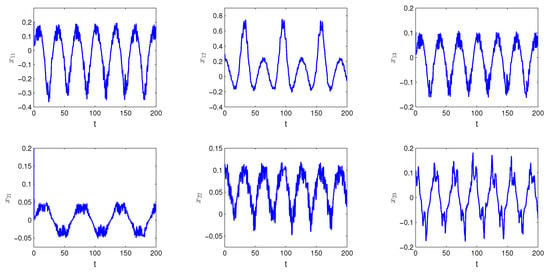
Let us take into account the SICNNs (26) with $a_{11}\left(t\right)=3+sin\left(0.1t\right),$ $a_{12}\left(t\right)=2+cos\left(0.1t\right),$ $a_{13}\left(t\right)=4+sin\left(0.2t\right),$ $a_{21}\left(t\right)=5+cos\left(0.4t\right),$ $a_{22}\left(t\right)=3+cos\left(0.2t\right),$ $a_{23}\left(t\right)=2+sin\left(0.1t\right),$ $v_{11}\left(t\right)=3sin\left(0.2t\right)\Xi \left(t\right),$ $v_{12}\left(t\right)=arctan(\Xi \left(t\right))+0.5cos\left(0.2t\right),$ $v_{13}\left(t\right)=4sin\left(0.1t\right)\Xi \left(t\right),$ $v_{21}\left(t\right)=3sin\left(0.1t\right)arctan(\Xi \left(t\right)),$ $v_{22}\left(t\right)=0.4cos\left(0.2t\right)\Xi \left(t\right),$ $v_{23}\left(t\right)=cos\left(0.2t\right)\Xi \left(t\right).$ The functions $b_{ij}\left(t\right)$ and $c_{ij}^{kl}\left(t\right)$ are the same as in Example 1. The period ω is equal to $20\pi .$ In Figure 4, the graph of the solution of SICNNs (26) with the length of step $h=0.2\pi$ and the degree of periodicity $\nabla =100$ is demonstrated.

Figure 4. The graph of the solution $x\left(t\right)=\left(x_{ij}\left(t\right)\right),$ $i=1,2,$ $j=1,2,3,$ of SICNNs (26) with the initial values $x_{11}\left(0\right)=0.2,$ $x_{12}\left(0\right)=0.3,$ $x_{13}\left(0\right)=0.1,$ $x_{21}\left(0\right)=0.2,$ $x_{22}\left(0\right)=0.1,$ $x_{23}\left(0\right)=0.1,$ and the degree of periodicity $\nabla =100.$

Analysing the numerical simulations above, one can make interesting observations concerning dominance of periodicity and unpredictability in compartmental functions. Figure 2 and Figure 3 show that the unpredictability prevails if $\nabla \le 1.$ More precisely, periodicity is not seen if $\nabla =1$ at all, and it appears only locally on isolated intervals, if $\nabla <1.$ In contrast, if $\nabla >1,$ one can see in Figure 1 and Figure 4 that the graphs admit a clear periodic shape, which is enveloped by the unpredictability.

5. Conclusions

In this paper, we considered SICNNs with variable compartmental unpredictable coefficients and inputs. Sufficient conditions were obtained to ensure the existence of exponentially stable unpredictable and Poisson stable solutions. Effectiveness of neural networks strongly depend on the selection of the right inputs [7,8,9]. Obviously, one can consider them not to be constant, but variable. In this case, there are two significantly different sorts of continuous-type inputs, regular (such as periodic, almost periodic, and recurrent) [10,11,12,13,14,15,16,17], and irregular or chaotic [44,45]. The choice of chaotic bias is an effective approach, since it is rich for infinitely many various motions, and periodic and almost periodic [46] are among them. The motions can be stabilized by different methods of control [47]. Recently, we have started to work with chaotic dynamics being focused on a single motion, the unpredictable point. The point is an unpredictable function [42], if the space is a functional one. The dynamics on the closure of the trajectory was named Poincaré chaos. Thus, all benefits of neural networks with chaotic inputs are also valid for the unpredictable dynamics in neuroscience. Additionally, new characteristics to synchronize have been determined [28,29], the convergence and divergence sequences. The characteristics make convenient circumstances for collective analysis of the neural networks. It deserves to be mentioned that the reduction in chaotic analysis to a single motion provides new possibilities for numerical simulations of neural networks, and this was seen in the present paper. We compared Figure 1, Figure 2, Figure 3 and Figure 4 with experimental data in the Refs. [34,35,36,37,38], and it was found that they are surprisingly similar. It means that the compartmental motions can find applications in solutions of industrial problems. Finally, the effectiveness of the compartmental approach to the unpredictability was shown by analysis of contributions of periodicity and unpredictability in the outputs, and it was just the first step in the direction of application of the research, since the next ones will be connected to control of chaos, which will be applied to the compartments’ parameters separately. Moreover, it will be productive if the compartmental nature of the dynamics will be taken into account for synchronization research [28,29,47,48,49].