Multi de Bruijn Sequences and the Cross-Join Method

Abstract

We show a method to construct binary multi de Bruijn sequences using the cross-join method. We extend the proof given by Alhakim for ordinary de Bruijn sequences to the case of multi de Bruijn sequences. In particular, we establish that all multi de Bruijn sequences can be obtained by cross-joining an ordinary de Bruijn sequence concatenated with itself an appropriate number of times. We implemented the generation of all multi de Bruijn sequences of type $C(2,2,2)$ and $C(3,2,2).$ We experimentally confirm that some multi de Bruijn sequences can be generated by Galois Nonlinear Feedback Shift Registers (NLFSRs). It is supposed that all multi de Bruijn sequences can be generated using Galois NLFSRs.

1. Introduction

De Bruijn sequences have been investigated for decades [1,2,3,4]. They have many applications: in combinatorial problems, in cryptography to generate pseudo-random sequences, and in biology to investigate genome sequences [5]. It is known that binary de Bruijn sequences can be generated by Nonlinear Feedback Shift Registers (NLFSRs) [6]. NLFSRs are the main components in constructing stream ciphers. Knowing a de Bruijn sequence, one can apply the cross-join method to construct new de Bruijn sequences [3,7,8,9]. In papers [10,11] It was proved first that the cross-join method generates all de Bruijn sequences of given order. In [10], an algorithm was explicitly given that begins with an arbitrary de Bruijn sequence from a finite alphabet and outputs a Hamiltonian path in the corresponding cross-join graph.

Paper [9] generalizes the notion of de Bruijn sequences to multi de Bruijn sequences, where patterns of fixed length appear m times (m = 1 for ordinary de Bruijn sequences), that paper presents formulas for the total number of possible multi de Bruijn sequences with a specified set of parameters. However, it does not provide a method to generate any such sequence. Although the notion of multi de Bruijn sequences appears to be more complex than ordinary ones and may cater to more applications (they appear in some biological sequences investigations [5],) one important consequence of the results of this paper is that all multi de Bruijn sequences stem, simply, from any ordinary de Bruijn sequence.

Following the proof given by Alhakim [10], we prove that all multi de Bruijn sequences can be generated starting from one such sequence by using the cross-join method. The proof is non-constructive in the sense that one has to start with a particular multi de Bruijn sequence in order to apply the cross-join method. On the positive side, it is sufficient to form a trivial multi de Bruijn sequence by concatenating an ordinary de Bruijn sequence m times with itself. Ordinary de Bruijn sequences can be constructed using various methods [7,12,13,14] (see also, [3] and references therein). We implemented this method for the case of multi de Bruijn sequences of the type $C(2,2,2)$ and $C(2,2,3)$ (binary multi de Bruijn sequences of order 2 and 3 with multiplicity 2 and patterns of length 2 and 3, see below for a formal definition). The drawback of the cross-join method is that to find a cross-join pair, we potentially have to run over the whole sequence. This can still be reasonably done for sequences up to the order of 40.

Galois NLFSRs were considered in papers [15,16]. We confirmed experimentally that some sequences of type $C(2,2,3)$ can be generated by Galois NLFSRs listed in [16]. In fact, they are modified sequences where one of the patterns has a lower multiplicity. It is an open problem whether all binary multi de Bruijn sequences can be generated using suitable Galois NLFSRs.

2. Multi de Bruijn Sequences

We introduce multi de Bruijn sequences following Tesler’s paper [9]. Let $\mathsf{\Omega }$ be a totally ordered alphabet of size $q\ge 1$. A linear sequence is an ordinary sequence of elements of $\mathsf{\Omega }$ denoted $a_1{a}_2\dots a_n$. Define the cyclic shift of a linear sequence by $\rho (a_1{a}_2\dots a_n)=a_n{a}_1\dots a_{n-1}.$ In a cyclic sequence, we treat all rotations of a given linear sequence as equivalent. A k-$mer$ is a sequence of length k over $\mathsf{\Omega }$. The set of all k-$mers$ over $\mathsf{\Omega }$ is ${\mathsf{\Omega }}^k$. A de Bruijn sequence is a cyclic sequence over alphabet $\mathsf{\Omega }$ in which all k-$mers$ occur exactly once. The length of such a sequence is $N=q^k$.

Definition 1. 

A multi de Bruijn sequence is a cyclic sequence over an alphabet Ω of size q in which each k-$mer$ occurs exactly m-times with $m,q,k\ge 1$. k is the order of the sequence.

Let $C(m,q,k)$ denote the set of all such sequences. The length of such a sequence is $N=m{q}^k$, since each of the $q^k$k-$mers$ accounts for m starting positions. Tesler [9] derived the formula for the cardinality of $C(m,q,k)$. In the following, we consider multi de Bruijn sequences over an alphabet $\mathsf{\Omega }$ with q symbols $\{0,1\dots ,q-1\}$, addition modulo q is used.

Definition 2. 

Let a sequence $\left(x_i\right)\in C(m,q,k)$ be represented as a sequence of its states $\left(S_i\right)$, where each state is a k-mer $S_i=(x_i,x_{i+1},\dots ,x_{i+k-1})$. It is conjugate to a state $S_j=(x_j,x_{j+1},\dots ,x_{j+k-1})$ if $x_i=x_j+1$ and $(x_{i+1},\dots ,x_{i+k-1})=(x_{j+1},\dots ,x_{j+k-1})$. We denote this $S_i=\widehat{S_j}$. The state $S_i$ is a companion of the state $S_j$ if $x_{i+k-1}=x_{j+k-1}+1$ and $(x_i,x_{i+1},\dots ,x_{i+k-2})=(x_j,x_{j+1},\dots ,x_{j+k-2}).$

Definition 3. 

Two pairs of vertices that allow the transformation of a de Bruijn cycle to another de Bruijn cycle are called cross-join pairs. Let a multi de Bruijn sequence $\left(x_i\right)$ be considered a cyclic sequence and represented as a sequence of states $\left(S_i\right)$. Then the four states $(S_i,S_j,\widehat{S_i},\widehat{S_j})$, form a cross-join pair for the sequence $\left(x_i\right)$ if they occur in the sequence in the listed order.

Definition 4. 

Let $\left(x_i\right)\in C(m,q,k)$ and $(S_i,S_j,\widehat{S_i},\widehat{S_j})$ be a cross-join pair. We construct a new multi de Bruijn sequence $\left(y_i\right)$ by swapping the successors of $S_i$ and $\widehat{S_i}$ and the successors of $S_j$ and $\widehat{S_j}$. That is, by going from $S_i$ to the successor of $\widehat{S_i}$, then from $\widehat{S_j}$ to the successor of $S_j$ and so on until closing the cycle. This construction is called the cross-join method.

To be more precise, let us denote $\widehat{S_i}=S_p$ and $\widehat{S_j}=S_q$. Then the original sequence has states that proceed as:

$$S_i,S_{i+1},\dots ,S_j,S_{j+1},\dots ,S_p,S_{p+1},\dots ,S_l,S_{q+1},\dots ,S_{i-1}.$$

After the cross-join operation, the modified sequence has states that proceed as:

$$S_i,S_{p+1},\dots ,S_q,S_{j+1},\dots ,S_p,S_{i+1},\dots ,S_j,S_{q+1},\dots ,S_{i-1}.$$

The conjugate pair of states $S_i,\widehat{S_i}$ splits the full cycle into two shorter cycles after interchanging their successors. Then the states $S_j,\widehat{S_j}$ are on different cycles, and after interchanging their successors, we obtain a new de Bruijn cycle (see Figure 1).

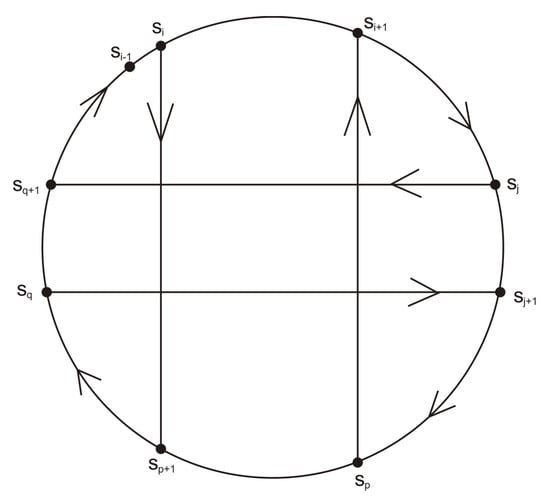
Figure 1. A geometric representation of the cross-join method.

3. The Main Theorem

Definition 5. 

Let $\left(x_i\right),\left(y_i\right)$ be two sequences from $C(m,q,k)$. The length of the sequences is $N=m{q}^k$. We take the least lexicographical representatives of both sequences and consider the length L of the longest common initial path of these sequences

$$(x_1,x_2,\dots ,x_L,\dots ,x_N),(x_1,x_2,\dots ,x_L,y_{L+1},\dots ,y_N).$$

We define the function (pseudo-distance) of the sequences as $d(x,y)=N-L$.

Proposition 1. 

The function $d(x,y)$ has the properties:

• For all $x,y$ in $\mathcal{C}(m,q,k),d(x,y)=0$ if and only if $x=y.$
• $d(x,y)=d(y,x)for allx,y\in \mathcal{C}(m,q,k).$

One can find examples of three multi de Bruijn sequences, which are concatenations of de Bruijn sequences of lower order for which the triangle inequality is not satisfied. It turns out that the pseudo-distance suffices to get our connectedness result. Unlike the case of ordinary de Bruijn cycles, the absence of the triangle inequality does not allow for the construction of a Hamiltonian path of multi de Bruijn cycles.

Definition 6. 

Let x and y be two distinct multi de Bruijn sequences. We say that y is a neighbor of x if y can be obtained from x by applying a sequence of cross-join operations.

We adapt the following proposition and its proof from the paper [10].

Proposition 2. 

Let $x=\left(x_i\right)$ and $y=\left(y_i\right)$ be two distinct multi de Bruijn sequences from the set $C(m,q,k)$. Then there exists a multi de Bruijn sequence $u\in C(m,q,k)$, which is a neighbor of x in $C(m,q,k)$ such that $d(u,y)<d(x,y)$.

Proposition 2 is crucial in the proof of following.

Theorem 1. 

Any two distinct multi de Bruijn sequences in $C(m,q,k)$ can be connected by applying a sequence of the cross-join operations.

Proof. 

Let x and y be two distinct sequences in $C(m,q,k)$. By Proposition 2, x has a neighbor $u_1$ such that $d(u_1,y)<d(x,y)$. If $u_1=y$, then we are done; otherwise, the same argument can be iterated to get a sequence $u_2$, which is a neighbor of $u_1$, with $d(u_2,y)<d(u_1,y)$. Due to the strict inequality, and since the number of sequences in $\mathcal{C}(m,q,k)$ is finite, it is evident that this iterative process must end at y after a finite number of steps l, leading to the desired path $u_0=x,u_1,\dots ,u_l=y$. □

Proof of Proposition 2. 

Let x and y be state sequences of multi de Bruijn sequences. We take the least lexicographical representatives of the sequences $x=\left(X_i\right)$ and $y=\left(Y_i\right)$, where $X_i$ and $Y_i$ are successive states of the multi de Bruijn sequences. Let $M_0$ be the maximal common initial sequence of x and y. Suppose that the sequence

$$M_0:\mathbf{0}=X_1\to X_2\to \dots \to X_{L_0}$$

is common to x and y and $L_0$ is maximal, where 0 is the state of zeros $(0,\dots ,0)$. Since $x\ne y,L_0<N$ and for the successors of $X_{L_0}$ in x and y at least one is distinct from the state 0. Let us refer to these successors as $X^{\left(1\right)}$ and $Y_{L_0+1}$. Since x is a multi de Bruijn sequence, it contains every state m times, so it must contain $Y_{L_0+1}$. The latter is at least one of the states in ${\tilde{M}}_0$, the complement of $M_0$ in x; that is, the subsequence of x that starts with $X^{\left(1\right)}$ and extends till the end of the sequence, just before cycling back to $M_0$. Let ${}^{*}{X}_0$ be the predecessor of the first occurrence of $Y_{L_0+1}$ in x. Since $Y_{L_0+1}$ belongs to ${\tilde{M}}_0$, the state ${}^{*}{X}_0$ is either in ${\tilde{M}}_0$ or it is $X_{L_0}$ itself. However, the latter would make the common initial sub-sequence of x, and y would extend to $Y_{L_0+1}$, which contradicts the maximality of $M_0$. Now $X_{L_0}$ and ${}^{*}{X}_0$ are predecessors of the same state so they form a conjugate pair. Swapping their successors, we split x into two cycles, a cycle $C_1$ that includes the initial subsequence $M_0$, and another cycle ${\tilde{C}}_1$ that includes the edge ${}^{*}{X}_0\to X^{\left(1\right)}$.

The cycle $C_1$ aligned to start with the initial subsequence $M_0$ and the multi de Bruijn cycle y have a maximal common initial sequence of states

$$M_1:\mathbf{0}=X_1\to X_2\to \dots \to X_{L_0}\to \dots \to X_{L_1}$$

where $L_1\ge L_0+1$. Let ${\tilde{M}}_1$ be a complement of $M_1$ in $C_1$. The rest of the proof depends on establishing the following. □

Claim 1. 

It is possible to join $C_1$ and ${\tilde{C}}_1$ by using a state in ${\tilde{M}}_1$ and a conjugate state in ${\tilde{C}}_1$, i.e., there is a state in ${\tilde{M}}_1$ that has a conjugate in ${\tilde{C}}_1.$

To show this, suppose we cannot. Then let the successors of $X_{L_1}$ in y and $C_1$ be $Y_{L_1+1}$ and $X^{\left(2\right)}$, respectively. Obviously, since $M_1$ is common to y and $C_1$ and since $Y_{L_1+1}$ is not on the path $M_1$ of y, there is at least one occurrence of the word $Y_{L_1+1}$ in ${\tilde{M}}_1$, the complement of $M_1$ in $C_1$, as it cannot be on ${\tilde{C}}_1$, by our assumption. Let ${}^{*}{X}_1$ be the predecessor of $Y_{L_1+1}$ in $C_1$. As before, we can argue that ${}^{*}{X}_1$ is in ${\tilde{M}}_1$.

Interchanging the successors of $X_{L_1}$ and ${}^{*}{X}_1$, we further split the cycle $C_1$ into two cycles $C_2$ and ${\tilde{C}}_2$ with the former being the cycle that includes the initial subsequence $M_0$ and that shares a larger still initial path with y:

$$M_2:\mathbf{0}=X_1\to X_2\to \dots \to X_{L_2},L_2>L_1.$$

In essence, this process can be iterated, arranging and re-arranging vertices on the initial cycle $C_1$ but without using vertices ${\tilde{C}}_1$, only a finite number of times. Let k be the maximal number of iterations and let $C_k$ be the resulting cycle that includes $M_0$ with maximal initial path

$$M_k:\mathbf{0}=X_1\to X_2\to \dots \to X_{L_k}{L}_k>L_{k-1}$$

that is common with the multi de Bruijn sequence y. Under the assumption that the above claim is not valid, we prove the following: the sub-path of the cycle $C_k$ that begins with $X_{L_k}$ and ends with 0 is simply an edge $(X_{L_k},\mathbf{0})$. That is, $X_{L_k}$ is the last vertex before rounding back to $M_k$.

To see this, suppose that $X^{(k+1)}\ne \mathbf{0}$ is the successor of $X_{L_k}$ in $C_k$. Let $Y_{L_k+1}$ be the successor of $X_{L_k}$ in y, so that $Y_{L_k+1}$ and $X^{(k+1)}$ are companion vertices. We then see that $X_{L_k}$ is not the last vertex in y for otherwise, the multi de Bruijn sequence y would be shorter than $C_k$. Hence, $Y_{L_k+1}$ is not the initial $\mathbf{0}$ of $M_k$. Consequently, one occurrence of $Y_{L_k+1}$ is either in ${\tilde{C}}_1$ or in the part ${\tilde{M}}_1$ of $C_1$. If the first case is true, swapping the predecessor of $Y_{L_k+1}$ in ${\tilde{C}}_1$ with the predecessor of $X^{(k+1)}$ (which is evidently one of the vertices of ${\tilde{M}}_1$) shows that $C_1$ and ${\tilde{C}}_1$ can be joined into multi de Bruijn sequence using a vertex outside $M_1$, contradicting the original assumption of the Claim.

If the second case is true, that is, if $Y_{L_k+1}$ belongs to ${\tilde{M}}_k$ or any of the cycles made by the previous iteration and that are at most $C_2,\dots ,C_{k-1},{\tilde{C}}_2,\dots ,{\tilde{C}}_{k-1}$ (equivalently, it is one of the vertices of ${\tilde{M}}_1$), then we can swap the predecessors of $X^{(k+1)}$ and $Y_{L_k+1}$ to get yet another cycle $C_{k+1}$ that shares a longer initial segment with y, contradicting the maximality of $C_k$. It follows that $X_{L_k}$ is the last vertex in $C_k$.

We now prove the following: $C_k$ includes all predecessors of 0. We prove this in a way similar to the proof of the previous statement. In effect, suppose that U is a predecessor of 0 that is not on $C_k$. If U belongs to ${\tilde{C}}_1$, we get a contradiction because we could have joined $C_1$ and ${\tilde{C}}_1$ by swapping, for example, the successors of U and the last vertex in $C_1$ before the initial subsequence $M_1$, which is, of course, in ${\tilde{M}}_1$. Likewise, the presence of U on any of the intermediate cycles $C_2,\dots ,C_{k-1},{\tilde{C}}_2,\dots ,{\tilde{C}}_{k-1}$ contradicts the maximality of k.

The validity of this last means that the sequence $M_k$ cannot be continued into a multi de Bruijn sequence as it cannot cycle back to 0 without using one of the predecessors of zero. This, of course, is not true because $M_k$ is already the initial path of the multi de Bruijn sequence y. This contradiction means that the Claim must be true.

We have thus proven that $C_1$ and ${\tilde{C}}_1$ can be joined by swapping the successors of a vertex in ${\tilde{M}}_1$ with that of a conjugate vertex in ${\tilde{C}}_1$. This makes a new multi de Bruijn sequence z which is a neighbor of x. Since $L_0<L_1,N-L_1<N-L_0$ and z satisfies the inequality

$$d(z,y)<d(x,y)$$

as desired.

Proposition 3. 

Starting with a multi de Bruijn sequence in $C(m,q,k)$ and applying the cross-join method generates all sequences in $C(m,q,k)$.

We present now the formula for the number of elements of $C(m,q,k)$ [9].

$$\left|C(m,q,k)\right|=\frac{1}{m{q}^k}\sum _{r|m}\varphi (m/r)·W(r,q,k)$$

where $\varphi$ is the Euler totient function and

$$W(r,q,k)={\left(\frac{\left(rq\right)!}{r{!}^q}\right)}^{q^{k-1}}={\left(\genfrac{}{}{0pt}{}{mq}{\underbrace{m,\dots ,m}}\right)}^{q^{k-1}},$$

where m is repeated m times. We calculate

$$\left|C(2,2,2)\right|=\frac{1}{2·2}\sum _{r|2}\varphi (2/r){\left(\genfrac{}{}{0pt}{}{2r}{r,r}\right)}^{2^1}=\frac{1}{8}{\left(\varphi \left(1\right){\left(\genfrac{}{}{0pt}{}{2·2}{2,2}\right)}^2+\varphi \left(2\right)\left(\genfrac{}{}{0pt}{}{2·1}{1,1}\right)\right)}^2$$

$$=\frac{1}{8}\left(1·{\left(\genfrac{}{}{0pt}{}{4}{1,1}\right)}^2+1·{\left(\genfrac{}{}{0pt}{}{2}{1,1}\right)}^2\right)=\frac{1}{8}(6^2+2)=\frac{40}{8}=5.$$

Next we calculate

$$\left|C\right(2,2,3\left)\right|=\frac{1}{2·2^3}\sum _{r|2}\varphi (2/r)W(r,2,3)=\frac{1}{16}(\varphi \left(2\right)W(1,2,3)+W(2,2,3))$$

$$=\frac{1}{16}\left({\left(\genfrac{}{}{0pt}{}{2·2}{2,2}\right)}^{2^2}+{\left(\genfrac{}{}{0pt}{}{2·2}{2,2}\right)}^{2^2}\right)=\frac{1}{16}(2^4+6^4)=\frac{1}{16}(16+1292)=\frac{1312}{16}=82.$$

We have implemented the cross-join method for the multi de Bruijn sequences of the type $C(2,2,2)$ and $C(2,2,3)$. The implementation has been done in SAGE [17]. For each sequence, the succeeded states are represented as decimals, and the sequence representative is the least lexicographical one. We have started from the first sequences in the list in Table 1 and generated all sequences. First, we find the cross-join pairs from the chosen sequence and generate the corresponding sequences. Then we choose a new de Bruijn sequence and repeat the process. We then check whether all the sequences are different and throw away the repeated ones. After a few steps of this process, we find all sequences of a given type.

Table 1. The sequences $C(2,2,3),\left|C\right(2,2,3\left)\right|=82$. (Tesler [9]). The green and the red sequences are the concatenation of de Bruijn sequences of $C(1,2,3)$. Changing from decimal representation to binary representation is descibed after Table 2.

(0425210463567731)	(0425635210467731)	(0425631042567731)
(0421042563567731)	(0042521463567731)	(0042563521467731)
(0042563142567731)	(0042563567731421)	(0046314252567731)
(0046314252567731)	(0046352521467731)	(0046352142567731)
(0046356773521421)	(0046773142563521)	(0046773563521421)
(0046735214256731)	(0046773521425631)	(0042525631467731)
(0042567735631421)	(0042567314256731)	(0042567731425631)
(0042146352567731)	(0042146356773521)	(0042146773563521)
(0042146735256731)	(0042146773525631)	(0042142567356731)
(0042142567735631)	(0046352567731421)	(0046773146352521)
(0046735256731421)	(0046773525631421)	(0046773142525631)
(0042567731463521)	(0042567356731421)	(0042525677314631)
(0042567314673521)	(0042563146773521)	(0421046352567731)
(0421046356773521)	(0463521046773521)	(0463525210467731)
(0467310467352521)	(0463104677352521)	(0425677310463521)
(0425673521046731)	(0425677352104631)	(0425256310467731)
(0425256731046731)	(0425256773104631)	(0425210467356731)
(0425210467735631)	(0421046773563521)	(0421046735256731)
(0421046773525631)	(0425673104673521)	(0425631046773521)
(0421042567735631)	(0421042567356731)	(0425673104256731)
(0046735252146731)	(0046773525214631)	(0042567352146731)
(0042567735214631)	(0042525673146731)	(0042521467356731)
(0042521467735631)	(0046352146773521)	(0046314256773521)
(0046773563142521)	(0046731425256731)	(0046735673142521)
(0046314677352521)	(0046731425673521)	(0046731467352521)
(0046735214673521)	(0046773521463521)	(0046735673521421)
(0042146735673521)	(0042142563567731)	(0467352104673521)
	(0421046735673521)

The List. The feedback functions of NLFSRs generated the sequences shown in Table 2. + is understood as modulo 2 addition. This table is a part of the Table 3 of Dubrova et al. [16].

#	$f_3$	$f_2$	$f_1$	$f_0$
1	$x_0$	$1+x_0+x_1+x_3+x_0{x}_1$	$1+x_1+x_2+x_3$	$1+x_0+x_1+x_2+x_0{x}_2$
2	$x_0$	$x_3+x_0{x}_2$	$x_2+x_3+x_1$	$x_1+x_0+x_0{x}_2$
3	$x_0$	$x_3+x_0{x}_2$	$x_2+1+x_3+x_0{x}_3$	$x_1+1+x_2+x_0+x_2{x}_0$
4	$x_0$	$x_3+x_0{x}_2$	$x_2+1+x_0+x_1{x}_0$	$x_1+1+x_2+x_0{x}_2$
5	$x_0$	$x_3+1+x_1+x_2+x_1{x}_2$	$x_2+x_1+x_0{x}_1$	$x_1+1+x_0+x_0{x}_2$
6	$x_0$	$x_3+x_1{x}_2$	$x_2+x_1+x_1{x}_0$	$x_1+x_2{x}_0$
7	$x_0$	$x_3+x_1{x}_2$	$x_2+1+x_0$	$x_1+1+x_2+x_3+x_2{x}_3$
8	$x_0$	$x_3+x_1+x_0{x}_1$	$x_2+1+x_3+x_1$	$x_1+x_2+x_0{x}_2$
9	$x_0$	$x_3+x_2+x_0{x}_2$	$x_2+1+x_0+x_1+x_0{x}_1$	$x_1+1+x_0+x_0{x}_2$
10	$x_0$	$x_3+x_2+x_1{x}_2$	$x_2+x_3{x}_1$	$x_1+x_2+x_3+x_2{x}_3$
11	$x_0$	$x_3+x_2+x_1{x}_2$	$x_2+x_0{x}_1$	$x_1+x_2+x_0{x}_2$
12	$x_0$	$x_3+x_2+x_1{x}_2$	$x_2+x_0$	$x_1+x_2+x_0{x}_2$
13	$x_0$	$x_3+x_2+x_2{x}_0$	$x_2$	$x_1+x_2{x}_0$
14	$x_0$	$x_3+1+x_1+x_2+x_1{x}_2$	$x_2+1+x_0+x_1{x}_0$	$x_1+1+x_0+x_2+x_2{x}_0$
15	$x_0+x_1{x}_2$	$x_3+x_0{x}_2$	$x_2$	$x_1+1+x_0+x_2+x_2{x}_0$
16	$x_0+1+x_1+x_2+x_1{x}_2$	$x_3+1+x_1+x_2+x_1{x}_2$	$x_2$	$x_1+x_2$
17	$x_0+1+x_1+x_3+x_1{x}_3$	$x_3+x_0{x}_1$	$x_2+1+x_0$	$x_1+1+x_2+x_0$
18	$x_0+x_2{x}_3$	$x_3+x_1+x_2+x_1{x}_2$	$x_2+x_1+x_1{x}_3$	$x_1+x_0$

Table 2. The sequences generated by Galois NLFSRs from the List above.

	Decimal	Binary
1	(046773525214631)	(000111101010011)
2	(042525631467731)	(000101011001111)
3	(046773563521421)	(000111101101001)
4	(042146773563521)	(000100111101101)
5	(046773146352521)	(000111100110101)
6	(046314677352521)	(000110011110101)
7	(042142567735631)	(000100101111011)
8	(042142563567731)	(000100101101111)
9	(046352521467731)	(000110101001111)
10	(042563567731421)	(000101101111001)
11	(042146356773521)	(000100110111101)
12	(042525677314631)	(000101011110011)
13	(042567735631421)	(000101111011001)
14	(046356773521421)	(000110111101001)
15	(004252567314631)	(000010101110011)
16	(042563142567731)	(000101100101111)
17	(042567731425631)	(000101111001011)
18	(046352146773521)	(000110100111101)

Table 3. The sequences $C(2,2,2),\left|C\right(2,2,2\left)\right|=5.$ (Tesler [9]).

	Decimal	Binary
1	(04256731)	(00010111)
2	(04635631)	(00011011)
3	(04673521)	(00011101)
4	(42146731)	(00100111)
5	(46314631)	(00110011)

4. Galois NLFSRs

Following Dubrova et al. [16] and Dubrova [15], we introduce Galois NLFSRs. A Galois NLFSR is described by the set $f_0,f_1,\dots ,f_{n-1}$ of Boolean functions of n binary variables and n cells which keep bits (Figure 2). The state of an NLFSR consists of the content of n cells at a given time. After the next clock, each bit i in the state of Galois NLFSR is updated to its next-state function, which is a Boolean function of state variables.

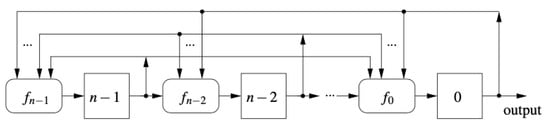
Figure 2. (Dubrova [16]). A scheme of Galois NLFSRs of order n.

We considered Galois NLFSRs of order 4 given by Dubrova ([16], Table 1) which have period 15. We checked experimentally that some of them generate modified multi de Bruijn sequences of type $C(2,2,3)$. In Table 2 at all sequences, state 000 appears once, and other states appear twice beyond line 15, where state 000 appears twice, and state 111 appears once.

Conjecture: All binary multi de Bruijn sequences can be generated by some Galois NLFSRs.

The digital numbers in Table 2 are the states of NLFSRs regarded as generating sequences from $C(2,2,3)$. Each $d\in \{0,1,\dots ,7\}$ can be represented as $d=c_0+c_1·2+c_3·4$. We explain the representation in the example. Let us take the first line in Table 2. The digit 0 from the left-hand side of the Decimal column is represented as the binary 000, and they are the first digitals in Binary. Then we take the decimal 4 and represent it as 001, and we add 1 to the sequence 000. Then we take 6 and represent it as 011 and add 1 to the sequence 0001. This way, each triple of binary digits from Binary, taking it from Decimal and going with one position from left to right, is a representation of a decimal digit from Decimal. The binary representation is treated as a cycle. The same representation can be done in Table 1 and Table 3.

5. Conclusions

We have extended the Alhakim proof [10] to the case of multi de Bruijn sequences. Specifically, we have shown that any multi de Bruijn sequence can be obtained using a sequence of cross-joins of an ordinary de Bruijn sequence concatenated m times with itself. Additionally, we have generated the $C(2,2,2)$ and $C(2,2,3)$ sequences. We have experimentally found that some Galois NLFSRs generate the multi de Bruijn sequences of type $C(2,2,3).$