On the Construction of Pandiagonal Magic Cubes

Abstract

This paper investigates the construction method of pandiagonal magic cube. First, we define a pandiagonal Latin cube. According to this definition, the cube can be constructed by simple methods. After designing a set of orthogonal pandiagonal Latin cubes, the corresponding order pandiagonal magic cube can be constructed. In addition, we give the algebraic conditions of the universal diagonal Latin cube orthogonality and the strict theoretical proof. Based on the proposed method, it can be shown that at least $6{(n!)}^3$ pandiagonal magic cubes of order n is formed through a pandiagonal Latin cube. Moreover, our method is easy to implement by computer program.

1. Introduction

A square matrix of order n, composed of continuous natural numbers from 1 to $n^2$, is called the magic square of order n if the sums of elements in each row, column and diagonal are the same. This sum is called magic sum, and it is equal to $\frac{n(1+n^2)}{2}$ [1]. Magic square is one of the important research objects of combinatorial design. It is applied in the fields of image processing, computer science, and cryptography [2,3,4]. The study of magic squares can be traced back to ancient China. The “Luoshu” discovered 4000 years ago is a magic square of order three [5]. Thereafter, there has been a lot of research on magic squares, and magic squares in these studies have different characteristics [6,7,8]. If the sums of the numbers on each pandiagonal are the same in a magic square, this magic square is called pandiagonal magic square. The so-called pandiagonal refers to the “broken diagonal” paralleled to the diagonal, and wrap round at the edges of the square [9,10]. For example, let a magic square be ${\left(a_{ij}\right)}_{n\times n}$, then $a_{12}$, $a_{23}$, ⋯, $a_{n-1,n}$, $a_{n,1}$ are elements of a pandiagonal. There are also other pandiagonals. After extending a magic square to the three-dimensional, a magic cube is obtained. An integer magic cube of order n is a three-dimensional array $A=\left(a_{ijk}\right)$ which consists of the numbers $1,2,\cdots ,n^3$, with each section and six diagonal planes being magic squares. Previous studies have given the construction methods of concrete magic cubes with various characteristics [11,12,13]. If every cross section, every diagonal and every pandiagonal of the magic cube is a pandiagonal magic square, it is called a pandiagonal magic cube. The relevant concepts are strictly defined below.

An integer cube of order n is a three-dimensional array $A=\left(a_{ijk}\right)$ which consists of the numbers 1, 2, ⋯, $n^3$. Matrices ${\left(a_{ijk}\right)}_{i,j=1,2,\cdots ,n}$, ${\left(a_{ijk}\right)}_{i,k=1,2,\cdots ,n}$, ${\left(a_{ijk}\right)}_{j,k=1,2,\cdots ,n}$ are called cross sections. In particular, ${\left(a_{ij1}\right)}_{i,j=1,2,\cdots ,n}$, ${\left(a_{i1k}\right)}_{i,k=1,2,\cdots ,n}$, ${\left(a_{1jk}\right)}_{j,k=1,2,\cdots ,n}$ are called surfaces. Similarly, matrices ${\left(a_{ijj}\right)}_{i,j=1,2,\cdots ,n}$, ${\left(a_{i,n-j+1,j}\right)}_{i,j=1,2,\cdots ,n}$, ${\left(a_{iji}\right)}_{i,j=1,2,\cdots ,n}$, ${\left(a_{i,j,n-i+1}\right)}_{i,j=1,2,\cdots ,n}$, ${\left(a_{iij}\right)}_{i,j=1,2,\cdots ,n}$, ${\left(a_{i,n-i+1,j}\right)}_{i,j=1,2,\cdots ,n}$ are called diagonal planes.

 Definition 1. 

An integer cube is called a pandiagonal magic cube, if all of its cross sections and diagonal planes are pandiagonal magic squares.

The concept of pandiagonal magic square can be found in [6,7,8,14]. Because a line parallel to an edge of an integer cube is a row or a column of a cross section, a great diagonal is a diagonal of a diagonal plane, so that a pandiagonal magic cube is certainly a magic cube [15].

The studies of magic squares and magic cubes have made relatively rich achievements. Cammann and Andrews introduced the early research results of magic squares and magic cubes [12,16]. Abe put forward 23 questions about magic squares, involving basic magic squares, pandiagonal magic squares, sparse magic squares, anti-magic squares, etc., which promoted the study of magic squares [17]. Loly et al. [18], Lee et al. [19], Nordgren et al. [20], and Hou et al. [21] discussed the algebraic properties of magic squares. Trenkler proposed an algorithm for making magic cubes [22]. However, the study on pandiagonal magic cubes is rare.

In this paper, we will study the existence and construction of pandiagonal magic cubes of order n based on the pandiagonal magic square idea in [6]. The following is the outline of this paper. First, a three-dimensional auxiliary cube is defined and its properties are discussed. Then, based on the discussion of Latin cube and pandiagonal Latin cube, the design method of the pandiagonal Latin cube is given. At the same time, we give the necessary and sufficient conditions for the orthogonality of three pandiagonal Latin cubes. Finally, by using the orthogonal pandiagonal Latin cubes, the construction method of pandiagonal magic cubes is obtained. In addition, we give a method to find another two pandiagonal Latin cubes orthogonal to one known pandiagonal Latin cube.

2. Auxiliary Cube and Its Properties

In this section, the definition and properties of the auxiliary cube are shown.

 Definition 2. 

A cube $A=\left(a_{ijk}\right)$ which consists of consecutive integers from 1 to $n^3$ is called an Auxiliary Cube (hereafter written as Aux Cube) if it satisfies the following conditions:

(1) The top surface $\left(a_{ij1}\right)$ is an auxiliary matrix [6], namely $\left(a_{ij1}\right)$ satisfies

$$a_{i11}-a_{111}=a_{i21}-a_{121}=\cdots =a_{in1}-a_{1n1}(i=1,2,\cdots ,n)$$

(2) The cross sections ${\left(a_{ijk}\right)}_{i,j=1,2,\cdots ,n}$ and ${\left(a_{ij1}\right)}_{i,j=1,2,\cdots ,n}$ satisfy

$$a_{ijk}-a_{ij1}={\beta }_k(k=1,2,\cdots ,n)$$

where ${\beta }_k$ is independent of i and j.

The preceding conditions (1) and (2) are equivalent to the fact that each cross section is an auxiliary matrix [6].

Let

$$a_{ijk}=n(i-1)+j+n^2(k-1)$$

then $A=\left(a_{ijk}\right)$ is called Natural Auxiliary Cube. Clearly, by interchanging two parallel cross sections of an Aux Cube A, we can form other Aux Cubes. A is an Aux Cube if, and only if, A can be obtained from Natural Aux Cube through finite interchanges of parallel cross sections in succession. Because there are $n!$ permutations of $1,2,\cdots ,n$, we can create ${(n!)}^3$ Aux Cubes from Natural Aux Cube by interchanging parallel cross sections.

 Lemma 1. 

Let A be an Aux Cube of order n, then the sum of any n entries in different rows, different columns and different levels is the same. Namely, if $A=\left(a_{ijk}\right)$, $i_1,i_2,\cdots ,i_n$, $j_1,j_2,\cdots ,j_n$, $k_1,k_2,\cdots ,k_n$ are all permutations of $1,2,\cdots ,n$, then

$$\begin{array}{c}\hfill \sum _{s=1}^n{a}_{i_s{j}_s{k}_s}=\mathrm{constant}\end{array}$$

 Proof. 

Assume

$$a_{i11}-a_{111}=a_{i21}-a_{121}=\cdots =a_{in1}-a_{1n1}={\alpha }_i$$

Then we have

$$a_{ijk}=a_{ij1}+{\beta }_k{a}_{ij1}=a_{1j1}+{\alpha }_i$$

Suppose that

$$a_{i_1{j}_1{k}_1},\cdots ,a_{i_n{j}_n{k}_n}$$

are n entries in different rows, different columns, and different levels of A. This is equivalent to the fact that “$i_1,i_2,\cdots ,i_n$”, “$j_1,j_2,\cdots ,j_n$”, “$k_1,k_2,\cdots ,k_n$” are all permutations of $1,2,\cdots ,n$. The sum of these entries is given by

$$\begin{array}{ccc}\hfill \sum _{s=1}^n{a}_{i_s{j}_s{k}_s}& =& \sum _{s=1}^n(a_{1j_{s}1}+{\alpha }_{i_s}+{\beta }_{k_s})\hfill \\ & =& \sum _{s=1}^n{a}_{1j_{s}1}+\sum _{s=1}^n{\alpha }_{i_s}+\sum _{s=1}^n{\beta }_{k_s}\hfill \\ & =& \sum _{s=1}^n{a}_{1s1}+\sum _{s=1}^n{\alpha }_s+\sum _{s=1}^n{\beta }_s\hfill \end{array}$$

The last three terms are independent of “$i_1,i_2,\cdots ,i_n$”, “$j_1,j_2,\cdots ,j_n$”, “$k_1,k_2,\cdots ,k_n$”. This completes the proof. □

Let A be an Aux Cube. From Lemma 1, a pandiagonal magic cube can be obtained by adjusting the entries of A so that its each row, each column and each pandiagonal of its each cross section and each diagonal plane consists of entries in distinct rows, distinct columns and distinct levels of A, respectively.

 Definition 3. 

The integer cube A of order n consisting of $1,2,\cdots ,n$ is said to be a pandiagonal Latin cube if all of its cross sections and diagonal planes are pandiagonal Latin squares [6].

 Definition 4. 

A set of pandiagonal Latin cubes $L_1=\left(l_{ijk}^1\right)$, $L_2=\left(l_{ijk}^2\right)$, $L_3=\left(l_{ijk}^3\right)$ is called orthogonal if entries of the cube

$$L=\left((l_{ijk}^1,l_{ijk}^2,l_{ijk}^3)\right)$$

run through all ordered three-tuples $(1,1,1)$ to $(n,n,n)$ [8,23].

For an integer cube $A=\left(a_{ijk}\right)$, its entries have three subscripts i, j and k. The set of first integers, i.e., i’s, form another integer cube, and similarly for the second and third ones. It is not difficult to understand the following fact. If $A=\left(a\right(i,j,k\left)\right)$ is an Aux Cube, $L_1=\left(l_{ijk}^1\right)$, $L_2=\left(l_{ijk}^2\right)$, $L_3=\left(l_{ijk}^3\right)$ are orthogonal pandiagonal Latin cubes. Define $B=\left(b_{suv}\right)$ as

$$b_{suv}=a(l_{suv}^1,l_{suv}^2,l_{suv}^3)(s,u,v=1,2,\cdots ,n)$$

Then B is a pandiagonal magic cube. Therefore, we can construct a pandiagonal magic cube as follows. First, construct a set of orthogonal pandiagonal Latin cubes, and join them into a cube of 3-tuples, and then change entries into entries of some auxiliary cube so that the subscripts are these three-tuples. This provides a pandiagonal magic cube.

If we use the first, second and third subscripts of each element in a pandiagonal magic cube to form a number cube in the original order, respectively, three orthogonal pandiagonal Latin cubes can be obtained.

In this paper, we will use a transformation $T_s$, whose definition can be found in [6]. Let $i_1,i_2,\cdots ,i_n$ be a permutation of $1,2,\cdots ,n$. $T_s(i_1,i_2,\cdots ,i_n)$$(3\le s\le n-1)$ is a square matrix such that the first row is

$$i_1,\cdots ,i_{s-1},i_s,i_{s+1},\cdots ,i_n$$

and the second row is

$$i_s,i_{s+1},\cdots ,i_n,i_1,\cdots ,i_{s-1}$$

By using the same rule, we form third row, and so on, to obtain $T_s(i_1,i_2,\cdots ,i_n)$, which is written as

$$\left.\left[\begin{array}{ccccccc}{i}_1& i_2& \cdots & i_s& i_{s+1}& \cdots & i_n\\ i_s& i_{s+1}& \cdots & \cdots & \cdots & \cdots & i_{s-1}\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right]\right\}n\mathrm{rows}$$

For example, $T_3(1,2,3,4,5)$ is given by

$$\left[\begin{array}{ccccc}1& 2& 3& 4& 5\\ 3& 4& 5& 1& 2\\ 5& 1& 2& 3& 4\\ 2& 3& 4& 5& 1\\ 4& 5& 1& 2& 3\end{array}\right]$$

3. Special Case: A Pandiagonal Magic Cube of Order 11

In this section, an example of a pandiagonal magic cube of order 11 is revealed.

First, we construct a pandiagonal Latin cube of order 11. Let Figure 1 represent the integer cube. Let the first row of top surface, namely $DC$ be

$$\begin{array}{ccccccccccc}1& 2& 3& 4& 5& 6& 7& 8& 9& 10& 11\end{array}$$

Figure 1. A Integer Cube.

From [6], in order that $DCGH$ is a pandiagonal Latin square, it suffices to select some k, $3\le k\le n-1$, such that $DCGH=T_k(1,2,\cdots ,11)$ (because $n=11$ is a prime number). Let k = 7, i.e., let the back surface $DCGH$ be $T_3(1,2,\cdots ,11)$:

$$\boxed{\begin{array}{ccccccccccc}1& 2& 3& 4& 5& 6& 7& 8& 9& \hfill 10& \hfill 11\\ 3& 4& 5& 6& 7& 8& 9& 10& 11& \hfill 1& \hfill 2\\ 5& 6& 7& 8& 9& 10& 11& 1& 2& \hfill 3& \hfill 4\\ 7& 8& 9& 10& 11& 1& 2& 3& 4& \hfill 5& \hfill 6\\ 9& 10& 11& 1& 2& 3& 4& 5& 6& \hfill 7& \hfill 8\\ 11& 1& 2& 3& 4& 5& 6& 7& 8& \hfill 9& \hfill 10\\ 2& 3& 4& 5& 6& 7& 8& 9& 10& \hfill 11& \hfill 1\\ 4& 5& 6& 7& 8& 9& 10& 11& 1& \hfill 2& \hfill 3\\ 6& 7& 8& 9& 10& 11& 1& 2& 3& \hfill 4& \hfill 5\\ 8& 9& 10& 11& 1& 2& 3& 4& 5& \hfill 6& \hfill 7\\ 10& 11& 1& 2& 3& 4& 5& 6& 7& \hfill 8& \hfill 9\end{array}}$$

Then take s, $3\le s\le n-1$, $s\ne k$, for example, $s=5$. Apply $T_5$ to each row of $DCGH$ to obtain 11 horizontal cross sections. They form the integer cube $ABCD$-$EFGH$, the top surface of which is $T_5(1,2,\cdots ,11)$:

$$\boxed{\begin{array}{ccccccccccc}\hfill 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& \hfill 11\\ \hfill 5& 6& 7& 8& 9& 10& 11& 1& 2& 3& \hfill 4\\ \hfill 9& 10& 11& 1& 2& 3& 4& 5& 6& 7& \hfill 8\\ \hfill 2& 3& 4& 5& 6& 7& 8& 9& 10& 11& \hfill 1\\ \hfill 6& 7& 8& 9& 10& 11& 1& 2& 3& 4& \hfill 5\\ \hfill 10& 11& 1& 2& 3& 4& 5& 6& 7& 8& \hfill 9\\ \hfill 3& 4& 5& 6& 7& 8& 9& 10& 11& 1& \hfill 2\\ \hfill 7& 8& 9& 10& 11& 1& 2& 3& 4& 5& \hfill 6\\ \hfill 11& 1& 2& 3& 4& 5& 6& 7& 8& 9& \hfill 10\\ \hfill 4& 5& 6& 7& 8& 9& 10& 11& 1& 2& \hfill 3\\ \hfill 8& 9& 10& 11& 1& 2& 3& 4& 5& 6& \hfill 7\end{array}}$$

The second cross section under the top surface is $T_5(3,4,5,6,7,8,9,10,11,1,2)$:

$$\boxed{\begin{array}{ccccccccccc}\hfill 3& 4& 5& 6& 7& 8& 9& 10& 11& 1& \hfill 2\\ \hfill 7& 8& 9& 10& 11& 1& 2& 3& 4& 5& \hfill 6\\ \hfill 11& 1& 2& 3& 4& 5& 6& 7& 8& 9& \hfill 10\\ \hfill 4& 5& 6& 7& 8& 9& 10& 11& 1& 2& \hfill 3\\ \hfill 8& 9& 10& 11& 1& 2& 3& 4& 5& 6& \hfill 7\\ \hfill 1& 2& 3& 4& 5& 6& 7& 8& 9& 10& \hfill 11\\ \hfill 5& 6& 7& 8& 9& 10& 11& 1& 2& 3& \hfill 4\\ \hfill 9& 10& 11& 1& 2& 3& 4& 5& 6& 7& \hfill 8\\ \hfill 2& 3& 4& 5& 6& 7& 8& 9& 10& 11& \hfill 1\\ \hfill 6& 7& 8& 9& 10& 11& 1& 2& 3& 4& \hfill 5\\ \hfill 10& 11& 1& 2& 3& 4& 5& 6& 7& 8& \hfill 9\end{array}}$$

etc. We denote the cube $ABCD$-$EFGH$ as $T_{3,5}(1,2,\cdots ,11)$, since the above cube is constructed by $T_3$ and $T_5$.

Now, we turn to prove that the cube $T_{3,5}(1,2,\cdots ,11)$ is a pandiagonal Latin cube of order 11. First, it should be noted that cross sections parallel to the top surface are all pandiagonal Latin squares. The back surface $DCGH$ is also a pandiagonal Latin square. It follows from symmetry of the top and back surfaces that cross sections parallel to back surface $DCGH$ are also pandiagonal Latin squares. We have to prove that cross sections parallel to $DAEH$ and the six diagonal planes are pandiagonal magic squares. The surface $DAEH$ is given by

$$\boxed{\begin{array}{ccccccccccc}1& 5& 9& 2& 6& 10& 3& 7& 11& 4& \hfill 8\\ 3& 7& 11& 4& 8& 1& 5& 9& 2& 6& \hfill 10\\ 5& 9& 2& 6& 10& 3& 7& 11& 4& 8& \hfill 1\\ 7& 11& 4& 8& 1& 5& 9& 2& 6& 10& \hfill 3\\ 9& 2& 6& 10& 3& 7& 11& 4& 8& 1& \hfill 5\\ 11& 4& 8& 1& 5& 9& 2& 6& 10& 3& \hfill 7\\ 2& 6& 10& 3& 7& 11& 4& 8& 1& 5& \hfill 9\\ 4& 8& 1& 5& 9& 2& 6& 10& 3& 7& \hfill 11\\ 6& 10& 3& 7& 11& 4& 8& 1& 5& 9& \hfill 2\\ 8& 1& 5& 9& 2& 6& 10& 3& 7& 11& \hfill 4\\ 10& 3& 7& 11& 4& 8& 1& 5& 9& 2& \hfill 6\end{array}}$$

This is just right $T_7(1,5,9,2,6,10,3,7,11,4,8)$. Similarly, we can prove that all cross sections parallel to $DAEH$ are created through applying $T_7$ to some column of top surface. Thus they are all pandiagonal Latin squares. The diagonal plane $DCFE$ is given by

$$\boxed{\begin{array}{ccccccccccc}1& 2& 3& 4& 5& 6& 7& 8& 9& 10& \hfill 11\\ 7& 8& 9& 10& 11& 1& 2& 3& 4& 5& \hfill 6\\ 2& 3& 4& 5& 6& 7& 8& 9& 10& 11& \hfill 1\\ 8& 9& 10& 11& 1& 2& 3& 4& 5& 6& \hfill 7\\ 3& 4& 5& 6& 7& 8& 9& 10& 11& 1& \hfill 2\\ 9& 10& 11& 1& 2& 3& 4& 5& 6& 7& \hfill 8\\ 4& 5& 6& 7& 8& 9& 10& 11& 1& 2& \hfill 3\\ 10& 11& 1& 2& 3& 4& 5& 6& 7& 8& \hfill 9\\ 5& 6& 7& 8& 9& 10& 11& 1& 2& 3& \hfill 4\\ 11& 1& 2& 3& 4& 5& 6& 7& 8& 9& \hfill 10\\ 6& 7& 8& 9& 10& 11& 1& 2& 3& 4& \hfill 5\end{array}}$$

which is $T_7(1,2,\cdots ,11)$, a pandiagonal Latin square. The diagonal plane $ABGH$ is

$$\boxed{\begin{array}{ccccccccccc}\hfill 8& 9& 10& 11& 1& 2& 3& 4& 5& \hfill 6& \hfill 7\\ \hfill 6& 7& 8& 9& 10& 11& 1& 2& 3& \hfill 4& \hfill 5\\ \hfill 4& 5& 6& 7& 8& 9& 10& 11& 1& \hfill 2& \hfill 3\\ \hfill 2& 3& 4& 5& 6& 7& 8& 9& 10& \hfill 11& \hfill 1\\ \hfill 11& 1& 2& 3& 4& 5& 6& 7& 8& \hfill 9& \hfill 10\\ \hfill 9& 10& 11& 1& 2& 3& 4& 5& 6& \hfill 7& \hfill 8\\ \hfill 7& 8& 9& 10& 11& 1& 2& 3& 4& \hfill 5& \hfill 6\\ \hfill 5& 6& 7& 8& 9& 10& 11& 1& 2& \hfill 3& \hfill 4\\ \hfill 3& 4& 5& 6& 7& 8& 9& 10& 11& \hfill 1& \hfill 2\\ \hfill 1& 2& 3& 4& 5& 6& 7& 8& 9& \hfill 10& \hfill 11\\ \hfill 10& 11& 1& 2& 3& 4& 5& 6& 7& \hfill 8& \hfill 9\end{array}}$$

We see that the above square is $T_{10}(8,9,10,1,2,3,4,5,6,7)$, a pandiagonal Latin square. The diagonal planes $ADGF$, $CBEH$, $DHFB$, and $CGEA$ are, respectively, given by

$$T_7(1,5,9,2,6,10,3,7,11,4,8)$$

$$T_4(11,4,8,1,5,9,2,6,10,3,7)$$

$$T_9(1,3,5,7,9,11,2,4,6,8,10)$$

$$T_8(11,2,4,6,8,10,1,3,5,7,9)$$

They are all pandiagonal Latin squares.

The preceding facts make clear that the cube $T_{3,5}(1,2,\cdots ,11)$ is a pandiagonal Latin cube.

By the same method, we can construct $T_{6,9}(1,2,\cdots ,11)$ and $T_{4,7}(1,2,\cdots ,11)$. It can be shown that they are all pandiagonal Latin cubes, and that $T_{3,5}(1,2,\cdots ,11)$, $T_{6,9}(1,2,\cdots ,11)$, $T_{4,7}(1,2,\cdots ,11)$ are orthogonal.

Now we construct cube of three-tuple $L={\left(l_{ijk}^1,l_{ijk}^2,l_{ijk}^3\right)}_{i,j,k=1,2,\cdots ,11}$, where $l_{ijk}^1\in T_{3,5}(1,2,\cdots ,11)$, $l_{ijk}^2\in T_{6,9}(1,2,\cdots ,11)$, $l_{ijk}^3\in T_{4,7}(1,2,\cdots ,11)$. For example, the top surface of L is given by

$$\boxed{\begin{array}{ccccccccccc}(1,1,1)& (2,2,2)& (3,3,3)& (4,4,4)& (5,5,5)& (6,6,6)& (7,7,7)& (8,8,8)& (9,9,9)& (10,10,10)& (11,11,11)\\ (5,9,7)& (6,10,8)& (7,11,9)& (8,1,10)& (9,2,11)& (10,3,1)& (11,4,2)& (1,5,3)& (2,6,4)& (3,7,5)& (4,8,6)\\ (9,6,2)& (10,7,3)& (11,8,4)& (1,9,5)& (2,10,6)& (3,11,7)& (4,1,8)& (5,2,9)& (6,3,10)& (7,4,11)& (8,5,1)\\ (2,3,8)& (3,4,9)& (4,5,10)& (5,6,11)& (6,7,1)& (7,8,2)& (8,9,3)& (9,10,4)& (10,11,5)& (11,1,6)& (1,2,7)\\ (6,11,3)& (7,1,4)& (8,2,5)& (9,3,6)& (10,4,7)& (11,5,8)& (1,6,9)& (2,7,10)& (3,8,11)& (4,9,1)& (5,10,2)\\ (10,8,9)& (11,9,10)& (1,10,11)& (2,11,1)& (3,1,2)& (4,2,3)& (5,3,4)& (6,4,5)& (7,5,6)& (8,6,7)& (9,7,8)\\ (3,5,4)& (4,6,5)& (5,7,6)& (6,8,7)& (7,9,8)& (8,10,9)& (9,11,10)& (10,1,11)& (11,2,1)& (1,3,2)& (2,4,3)\\ (7,2,10)& (8,3,11)& (9,4,1)& (10,5,2)& (11,6,3)& (1,7,4)& (2,8,5)& (3,9,6)& (4,10,7)& (5,11,8)& (6,1,9)\\ (11,10,5)& (1,11,6)& (2,1,7)& (3,2,8)& (4,3,9)& (5,4,10)& (6,5,11)& (7,6,1)& (8,7,2)& (9,8,3)& (10,9,4)\\ (4,7,11)& (5,8,1)& (6,9,2)& (7,10,3)& (8,11,4)& (9,1,5)& (10,2,6)& (11,3,7)& (1,4,8)& (2,5,9)& (3,6,10)\\ (8,4,6)& (9,5,7)& (10,6,8)& (11,7,9)& (1,8,10)& (2,9,11)& (3,10,1)& (4,11,2)& (5,1,3)& (6,2,4)& (7,3,5)\end{array}}$$

By using this cube of 3-tuple L, we construct the integer cube $C=\left(c_{ijk}\right)$ with

$$c_{ijk}=11\left(l_{ijk}^1-1\right)+l_{ijk}^2+{11}^2\left(l_{ijk}^3-1\right),i,j,k=1,2,\cdots ,n.$$

Then C is a pandiagonal magic cube which is shown in Appendix A.

4. Main Results and Their Proofs

Our purpose is for any integer n to derive existence conditions of pandiagonal magic cubes of order n and to study a construction method by using the approach developed in Section 3. First, we construct three orthogonal pandiagonal Latin cubes, and then join them into a cube of ordered three-tuples. By replacing elements of the cube into elements of some auxiliary cube, we obtain a pandiagonal magic cube.

Let $i_1,i_2,\cdots ,i_n$ be any permutation of $1,2,\cdots ,n$. Without loss of generality let it just be $1,2,\cdots ,n$. Otherwise, it suffices to prove the result for $1,2,\cdots ,n$ first, then change j into $i_j$$(j=1,2,\cdots ,n)$. Since this transformation changes a permutation of $1,2,\cdots ,n$ into another permutation of $1,2,\cdots ,n$, the following discussion is valid in general.

Taking $1,2,\cdots ,n$ as an edge, we construct an integer cube $ABCD$-$EFGH$ as follows (see Figure 1). Assume $3\le k\le n-1$, $3\le s\le n-1$. Let the back plane $DCGH$ be $T_k(1,2,\cdots ,n)$. Apply $T_s$ to each row of $DCGH$ to obtain n horizontal cross sections. They form the integer cube $ABCD$-$EFGH$. Denote it by $T_{k,s}(1,2,\cdots ,n)$ or briefly $T_{k,s}$.

Now let us study sufficient conditions such that $T_{k,s}$ is a pandiagonal Latin cube. By using the same method as in Section 3, we easily follows that parallel cross sections of the cube $T_{k,s}$ have identical generating transformation $T_t$ for some t. Sections parallel to pandiagonal sections of $T_{k,s}$ also have identical generating transformation $T_{t^{\prime }}$ for some $t^{\prime }$. Therefore it suffices to find conditions, such that $ABCD$, $DCGH$, $ADHE$, and six diagonal sections are pandiagonal Latin squares. For pandiagonal Latin squares, we have the following theorem.

 Theorem 1. 

Let n and k be integers with $3\le k\le n-1$. Then $T_k(1,2,\cdots ,n)$ is a pandiagonal Latin square of order n if, and only if,

$$(k,n)=1,(k-1,n)=1,(k-2,n)=1$$

Here, $(i,j)=1$ means that i and j are mutually prime, namely, the maximum common factor of i and j is equal to 1.

When n is a prime number, the proof of this theorem can be found in [6]. The proof of general situation requires the following two preliminary facts.

 Lemma 2. 

If the first column of $T_k(1,2,\cdots ,n)$ is a permutation of $1,2,\cdots ,n$, so is every column of  $T_k(1,2,\cdots ,n)$.

 Proof. 

We regard an element of $T_k(1,2,\cdots ,n)$ as itself modulo n, then $\left[i\right]=[jn+i]$ (j is an integer. We choose representative elements of congruence group of modulo n as $1,2,\cdots ,n$. Hereafter suppose just so). Consider numbers in the bracket [ ]. Since

$$T_k(1,2,\cdots ,n)=\left[\begin{array}{cccc}1& 2& \cdots & n\\ \left[1+(k-1)\right]& [2+(k-1\left)\right]& \cdots & [n+(k-1\left)\right]\\ \cdots & \cdots & \cdots & \cdots \\ \left[1+(n-1)(k-1)\right]& [2+(n-1\left)\right(k-1\left)\right]& \cdots & [n+(n-1\left)\right(k-1\left)\right]\end{array}\right]$$

it is clear that if 1, $\left[1+(k-1)\right]$, ⋯, $\left[1+(n-1)(k-1)\right]$ is a permutation of $1,2,\cdots ,n$, so are i, $\left[i+(k-1)\right]$, ⋯, $\left[i+(n-1)(k-1)\right]$ ($i=1$, 2, ⋯, n). This proves the Lemma. □

 Lemma 3. 

If some diagonal of $T_k(1,2,\cdots ,n)$ is a permutation of $1,2,\cdots ,n$, so is each pandiagonal which is parallel to the diagonal. If some pandiagonal of $T_k(1,2,\cdots ,n)$ is a permutation of $1,2,\cdots ,n$, so is each pandiagonal which is parallel to the pandiagonal.

 Proof. 

Since $\left[i\right]=[jn+i]$, we can substitute i for $[jn+i]$ for some j. The following are the first n rows of $T_k(1,2,\cdots ,2n)$

$$\left[\begin{array}{ccccccc}\left[1\right]& \left[2\right]& \cdots & \left[n\right]& [n+1]& \cdots & \left[2n\right]\\ \left[2n+k\right]& [2n+k+1]& \cdots & [2n+k+(n-1\left)\right]& [2n+k+n]& \cdots & [2n+k+2n-1]\\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ b_1& b_2& \cdots & b_n& b_{n+1}& \cdots & b_{2n}\end{array}\right]$$

From the generating rule, we see that the first n columns just form $T_k(1,2,\cdots ,n)$. Since $\left[i\right]=[n+i]$, $[2n+k+i]=[2n+k+i+n]$, the last n columns also form $T_k(1,2,\cdots ,n)$. Hence the line from $b_1$ to $\left[n\right]$ is a diagonal. The line from $b_2$ to $[n+1]$ stands for the pandiagonal $\left[1\right]b_2\cdots [2n+k+(n-1)]$, and the line from $b_n$ to $[2n-1]$ stands for the pandiagonal $[n-1][2n+k+n-2]\cdots b_n$. Since $b_1\cdots \left[n\right]$ is a diagonal, $(b_1+i)\cdots [n+i]$ $(i=1,\cdots ,n-1)$ are all pandiagonals which parallel to line $b_1\cdots \left[n\right]$. Thus, if one of them is a permutation of $1,2,\cdots ,n$, then so are others. The proof for pandiagonals which are parallel to diagonal $\left[1\right]\cdots b_n$ is the same. This completes the proof of Lemma 3. □

 (Proof of Theorem 1). 

Sufficiency. Suppose the conditions hold. From Lemmas 2 and 3, it suffices to prove that the first column and two diagonals are permutations of $1,2,\cdots ,n$. From the definition of $T_k(1,2,\cdots ,n)$, its first column is

$$\left[1\right],[1+(k-1\left)\right],\cdots ,[1+(n-1\left)\right(k-1\left)\right]$$

i.e., the difference of two successive elements is $k-1$. Since $(k-1,n)=1$, if $3\le k\le n-1$, the first column is a permutation of $1,2,\cdots ,n$.

Similarly, the difference of two elements of the diagonal starting from $\left[1\right]$ is $\left[\right(2n+k+1)-1]=\left[k\right]=k$. It follows at once from $(k,n)=1$ that the diagonal is a permutation of $1,2,\cdots ,n$. Similar proof is applicable to another diagonal because $\left[\right(2n+k+2n-2)-2n]=k-2$ and $(k-2,n)=1$.

Necessity. Suppose one of the conditions $(k,n)=1,(k-1,n)=1,(k-2,n)=1$ does not hold. For example, let $(k-1,n)=d\ne 1$. So there exists integers p and q, such that $k-1=dq$, $n=dp$, $(p,q)=1$. Thus the first column of $T_k(1,2,\cdots ,n)$ is $\left[1\right][1+(k-1\left)\right]\cdots [1+p(k-1\left)\right]\cdots [1+(n-1\left)\right(k-1\left)\right]$. Since $[1+p(k-1\left)\right]=[1+n/d·dq]=[1+nq]=\left[1\right]$, the pth element is equal to the first element. This implies that the first column is not a permutation of $1,2,\cdots ,n$, which is a contradiction. The other cases are treated similarly. This completes the proof of Theorem 1. □

The following is one of the main theorems of this paper.

 Theorem 2. 

Let $3\le k\le n-1$, $3\le s\le n-1$. Suppose that the following conditions are satisfied

(1) $(k,n)=1$, $(k-1,n)=1$, $(k-2,n)=1$;

(2) $(s,n)=1$, $(s-1,n)=1$, $(s-2,n)=1$;

(3) $(k-s,n)=1$, $(s-k+1,n)=1$, $(k-s+1,n)=1$;

(4) $(k+s-1,n)=1$, $(k+s-2,n)=1$, $(k+s-3,n)=1$.

Then the preceding $T_{k,s}(i_1,i_2,\cdots ,i_n)$ is a pandiagonal Latin cube, where $i_1,i_2,\cdots ,i_n$ is a permutation of $1,2,\cdots ,n$, and vice versa.

 Proof. 

We show that the conditions $\left(1\right)$–$\left(4\right)$ are necessary and sufficient so that each surface and each diagonal section is a pandiagonal Latin square.

Because the surface $DCGH$ is $T_k(1,2,\cdots ,n)$, $\left(1\right)$ is a necessary and sufficient condition such that $DCGH$ is a pandiagonal Latin square. Similarly, $\left(2\right)$ is a necessary and sufficient condition such that $ABCD$ is a pandiagonal Latin square.

The left surface $ADHE$ is given by

$$\left[\begin{array}{ccccc}1& n+s& 2n+(2s-1)& \cdots & (n-1)n+(n-1)s-(n-2)\\ n+k& n+k+(s-1)& n+k+2(s-1)& \cdots & n+k+(n-1)(s-1)\\ \cdots & \cdots & \cdots & \cdots & \cdots \end{array}\right]$$

From Theorem 1, in order that this surface be a pandiagonal Latin square, necessary and sufficient conditions are

$$(s-1,n)=1,(k-1,n)=1,(k+s-2,n)=1,(s-k,n)=1.$$

These are included in $\left(1\right)$–$\left(4\right)$.

The diagonal section $DCFE$ is $T_{[k+s-1]}(1,2,\cdots ,n)$. It is a pandiagonal Latin square if, and only if,

$$(k+s-1,n)=1,(k+s-2,n)=1,(k+s-3,n)=1.$$

These are exactly conditions in $\left(4\right)$.

The diagonal section $ABGH$ is given by

$$\left[\begin{array}{cccc}(n-1)n+(n-1)s-(n-2)& (n-1)n+(n-1)s-(n-2)+1& \cdots & n^2-(n-1)+(n-1)s\\ n+k+(n-2)(s-1)& n+k+(n-2)(s-1)+1& \cdots & 2n-1+k+(n-2)(s-1)\\ \cdots & \cdots & \cdots & \cdots \end{array}\right]$$

i.e.,

$$\left[\begin{array}{cccc}n+2-s& n+3-s& \cdots & n+1-s\\ k-2s+2& k-2s+3& \cdots & k-2s+1\\ \cdots & \cdots & \cdots & \cdots \end{array}\right]$$

It is a pandiagonal Latin square if, and only if,

$$\left(\right(k-2s+2)-(n+2-s),n)=1,$$

$$\left(\right(k-2s+2)-(n+3-s),n)=1,$$

$$\left(\right(k-2s+3)-(n+2-s),n)=1,$$

i.e.,

$$(k-s,n)=1,(s-k+1,n)=1,(k-s+1,n)=1.$$

These conditions are also included in $\left(1\right)$–$\left(4\right)$.

The diagonal section $BCHE$ is

$$\left[\begin{array}{cccc}n& s-1& \cdots & (n-1)(s-1)\\ k-2& k+s-3& \cdots & k-2+(n-1)(s-1)\\ \cdots & \cdots & \cdots & \cdots \end{array}\right]$$

In order that this section be a pandiagonal Latin square, necessary and sufficient conditions are

$$(n-s+1,n)=1,(n-k+2,n)=1,(k-s-1,n)=1,(n-k-s+3,n)=1.$$

i.e.,

$$(s-1,n)=1,(k-2,n)=1,(s-k+1,n)=1,(k+s-3,n)=1.$$

These conditions are included in $\left(1\right)$–$\left(4\right)$.

The diagonal section $DHFB$ is

$$\left[\begin{array}{cccc}1& n+k& \cdots & (n-1)n+(n-1)k-(n-2)\\ n+s+1& n+s+k& \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots \end{array}\right]$$

It is a pandiagonal Latin square if, and only if,

$$(n+s+1-1,n)=1,(n+k-1,n)=1,(s+1-k,n)=1,(n+s+k-1,n)=1.$$

i.e.,

$$(s,n)=1,(k-1,n)=1,(s-k+1,n)=1,(s+k-1,n)=1.$$

These conditions are also included in $\left(1\right)$–$\left(4\right)$.

The diagonal section $CGEA$ is

$$\left[\begin{array}{cccc}n& 2n-1+k& \cdots & n^2-(n-1)+(n-1)k\\ 2n-2+s& 2n-2+(s-1)+k& \cdots & \cdots \\ \cdots & \cdots & \cdots & \cdots \end{array}\right]$$

It is a pandiagonal Latin square if, and only if,

$$(k-1,n)=1,(s-2,n)=1,(k-s+1,n)=1,(s+k-3,n)=1.$$

These conditions are also included in $\left(1\right)$–$\left(4\right)$.

The diagonal section $ABGH$ is

$$\left[\begin{array}{cccc}(n-1)n+(n-1)s-(n-2)& (n-1)n+(n-1)s-(n-2)+1& \cdots & n^2-(n-1)+(n-1)s\\ n+k+(n-2)(s-1)& n+k+(n-2)(s-1)+1& \cdots & 2n-1+k+(n-2)(s-1)\\ \cdots & \cdots & \cdots & \cdots \end{array}\right]$$

It is a pandiagonal Latin square if, and only if,

$$(k-s,n)=1,(s-k+1,n)=1,(k-s+1,n)=1.$$

This is the condition $\left(3\right)$.

The diagonal section $ADGF$ is

$$\left[\begin{array}{cccc}1& 1+(s-1)& \cdots & 1+(n-1)(s-1)\\ k+1& k+1+(s-1)& \cdots & k+1+(n-1)(s-1)\\ \cdots & \cdots & \cdots & \cdots \end{array}\right]$$

It is a pandiagonal Latin square if, and only if,

$$(s-1,n)=1,(k,n)=1,(k-s+1,n)=1,(k+s-1,n)=1.$$

These conditions are included in $\left(1\right)$–$\left(4\right)$. The proof is completed. □

 Remark 1. 

We observe that if $T_{k,s}(i_1,i_2,\cdots ,i_n)$ is a pandiagonal Latin cube, so is $T_{s,k}(i_1,i_2,\cdots ,i_n)$. Since conditions $\left(1\right)$–$\left(4\right)$ of Theorem 2 are symmetric with respect to s, k.

 Corollary 1. 

Let n be a prime number. Then if

$$3\le k\le n-1,3\le s\le n-1;$$

$$k\ne s,k\ne s+1,s\ne k+1;$$

$$k+s-1\ne n,k+s-2\ne n,k+s-3\ne n,$$

are satisfied, $T_{k,s}(i_1,i_2,\cdots ,i_n)$ is a pandiagonal Latin cube.

 Proof. 

Immediate from Theorem 2. □

Now we give the second main theorem of this paper.

 Theorem 3. 

Suppose $T_{k_i,s_i}(j_1,j_2,\cdots ,j_n)(i=1,2,3)$ are pandiagonal Latin cubes. They are orthogonal if, and only if, the determinant

$$\Delta =\left|\begin{array}{ccc}{s}_1& k_1& 1\\ s_2& k_2& 1\\ s_3& k_3& 1\end{array}\right|$$

and n are coprime, i.e., $(\Delta ,n)=1$.

 Proof. 

Without loss of generality it suffices to prove that $(\Delta ,n)=1$ if, and only if, number 1, which is on the common vertex $(1,1,1)$ of $T_{k_i,s_i}(1,2,\cdots ,n)(i=1,2,3)$, cannot appear on another common place. Indeed, if 1 appears again on common place $(i,j,r)$, then there are relations

$$1+(i-1)(s_i-1)+(r-1)(k_i-1)+(j-1)\equiv 1\left(modn\right)(i=1,2,3)$$

Thus there exist integers $u_1,u_2,u_3$, such that

$$\begin{array}{c}\hfill (i-1)(s_i-1)+(r-1)(k_i-1)+(j-1)=u_{i}n(i=1,2,3)\end{array}$$

(1)

This is a system of linear equations for $(i-1),(j-1),(r-1)$. The determinant of coefficient matrix is

$$\left|\begin{array}{ccc}{s}_1-1& k_1-1& 1\\ s_2-1& k_2-1& 1\\ s_3-1& k_3-1& 1\end{array}\right|=\left|\begin{array}{ccc}{s}_1& k_1& 1\\ s_2& k_2& 1\\ s_3& k_3& 1\end{array}\right|=\Delta$$

From cyclic group theory [24], $(\Delta ,n)=1$ if, and only if, there is a unique solution of system (1) with $1\le i\le n$, $1\le j\le n$, $1\le r\le n$. Since $(i,j,k)=(1,1,1)$ is a solution, there is no other solution. The proof is complete. □

From this theorem we obtain the following result.

 Corollary 2. 

Let $T_{k_i,s_i}(1,2,\cdots ,n)(i=1,2,3)$ be three pandiagonal Latin cubes of order n. In order that they are orthogonal, two necessary conditions are

$\left(i\right)$ Not all of $s_i+k_i(i=1,2,3)$ are the same;

$\left(ii\right)$ Not all of $s_i-k_i(i=1,2,3)$ are the same.

We prove $\left(i\right)$. If $s_1+k_1=s_2+k_2=s_3+k_3$, then

$$\Delta =\left|\begin{array}{ccc}{s}_1& k_1& 1\\ s_2& k_2& 1\\ s_3& k_3& 1\end{array}\right|=0$$

It is not coprime with n. The proof of $\left(ii\right)$ is similar.

The following theorem give a method of generating orthogonal pandiagonal Latin cubes from a given pandiagonal Latin cube.

 Theorem 4. 

Suppose $T_{k,s}(i_1,i_2,\cdots ,i_n)$ is a pandiagonal Latin cube. Choose integers α, β, $3\le \alpha \le n-1$, $3\le \beta \le n-1$, such that

$$\begin{array}{c}\hfill 1+\alpha (s-1)\equiv k\left(modn\right)\end{array}$$

(2)

$$\begin{array}{c}\hfill 1+\beta (s-1)\equiv 2\left(modn\right)\end{array}$$

(3)

Then $T_{k,s}(i_1,i_2,\cdots ,i_n),T_{s,k}(j_1,j_2,\cdots ,j_n),T_{\alpha +1,\beta +1}(k_1,k_2,\cdots ,k_n)$ are orthogonal pandiagonal Latin cubes.

 Proof. 

The proof is performed in five steps. Steps (a) to (d) show that $T_{\alpha +1,\beta +1}$ is a pandiagonal Latin cube. Step (e) shows that $T_{k,s},T_{s,k},T_{\alpha +1,\beta +1}$ are orthogonal. For convenience we denote $\alpha +1$, $\beta +1$ by ${\alpha }^{\prime }$, ${\beta }^{\prime }$, respectively.

(a) We prove $\left(1\right)$ of Theorem 2, i.e.,

$$({\alpha }^{\prime },n)=1,({\alpha }^{\prime }-1,n)=1,({\alpha }^{\prime }-2,n)=1$$

1. If $({\alpha }^{\prime },n)\ne 1$, i.e., ${\alpha }^{\prime }$ and n have a common factor d which is larger than 1:

$$\begin{array}{ccc}& & \alpha +1={\alpha }^{\prime }=pd\hfill \end{array}$$

(4)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(5)

where p and q are positive integer, $(p,q)=1$. Substituting (4) into (2) yields

$$\begin{array}{c}\hfill k\equiv (pd-1)(s-1)+1\left(modn\right)\end{array}$$

i.e.,

$$k\equiv pd(s-1)-s+2\left(modn\right)$$

This can be written as

$$k+s-2\equiv pd(s-1)\left(modn\right)$$

This means d is a common factor of $k+s-2$ and n, i.e., $(k+s-2,n)\ne 1$. This contradicts assumptions. Thus, the relation $({\alpha }^{\prime },n)=1$ is true.

2. If $({\alpha }^{\prime }-1,n)\ne 1$, then there is $d>1$ which is a common factor of ${\alpha }^{\prime }-1$ and n. So we obtain

$$\begin{array}{ccc}& & \alpha ={\alpha }^{\prime }-1=pd\hfill \end{array}$$

(6)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(7)

Substituting (6) into (2) we obtain

$$\begin{array}{c}\hfill k\equiv pd(s-1)+1\left(modn\right)\end{array}$$

i.e.,

$$k-1\equiv pd(s-1)\left(modn\right)$$

Therefore, $(k-1,n)\ne 1$. This contradicts assumptions, so that we have $({\alpha }^{\prime }-1,n)=1$.

3. If $({\alpha }^{\prime }-2,n)\ne 1$, then there exists an integer $d>1$, such that

$$\begin{array}{ccc}& & \alpha -1={\alpha }^{\prime }-2=pd\hfill \end{array}$$

(8)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(9)

Substituting (8) into (2) yields

$$\begin{array}{c}\hfill k\equiv (pd+1)(s-1)+1\left(modn\right)\end{array}$$

i.e.,

$$k-s\equiv pd(s-1)\left(modn\right)$$

So $(k-s,n)\ne 1$. This is a contradiction. Thus $({\alpha }^{\prime }-2,n)=1$.

(b) We prove $\left(2\right)$ of Theorem 2, i.e.,

$$({\beta }^{\prime },n)=1,({\beta }^{\prime }-1,n)=1,({\beta }^{\prime }-2,n)=1$$

1. If $({\beta }^{\prime },n)\ne 1$, then there exists $d>1$ which is a common factor of ${\beta }^{\prime }$ and n:

$$\begin{array}{ccc}& & \beta +1={\beta }^{\prime }=pd\hfill \end{array}$$

(10)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(11)

Substituting (10) into (3), we obtain

$$\begin{array}{c}\hfill 2\equiv (pd-1)(s-1)+1\left(modn\right)\end{array}$$

i.e.,

$$s\equiv pd(s-1)\left(modn\right)$$

This means $(s,n)\ne 1$. This is a contradiction. So $({\beta }^{\prime },n)=1$.

2. If $({\beta }^{\prime }-1,n)\ne 1$, then there exists $d>1$ which is a common factor of ${\beta }^{\prime }-1$ and n:

$$\begin{array}{ccc}& & \beta ={\beta }^{\prime }=pd\hfill \end{array}$$

(12)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(13)

Substituting (12) into (3) we obtain

$$\begin{array}{c}\hfill 2\equiv pd(s-1)+1\left(modn\right)\end{array}$$

i.e.,

$$1\equiv pd(s-1)\left(modn\right)$$

This means d is a factor of number 1, a contradiction. So $({\beta }^{\prime }-1,n)=1$.

3. If $({\beta }^{\prime }-2,n)\ne 1$, then ${\beta }^{\prime }-2$ and n have a common factor $d>1$:

$$\begin{array}{ccc}& & \beta -1={\beta }^{\prime }-2=pd\hfill \end{array}$$

(14)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(15)

Substituting (14) into (3) yields

$$\begin{array}{c}\hfill 2\equiv (pd+1)(s-1)+1\left(modn\right)\end{array}$$

i.e.,

$$-s\equiv pd(s-1)\left(modn\right)$$

So $(s,n)\ne 1$. This is a contradiction. Thus $({\beta }^{\prime }-2,n)=1$.

(c) We prove $\left(3\right)$ of Theorem 2, i.e.,

$$({\alpha }^{\prime }-{\beta }^{\prime },n)=1,({\alpha }^{\prime }-{\beta }^{\prime }+1,n)=1,({\beta }^{\prime }-{\alpha }^{\prime }+1,n)=1$$

1. If $({\alpha }^{\prime }-{\beta }^{\prime },n)\ne 1$, then there exists $d>1$ which is a common factor of ${\alpha }^{\prime }-{\beta }^{\prime }$ and n:

$$\begin{array}{ccc}& & \alpha -\beta ={\alpha }^{\prime }-{\beta }^{\prime }=pd\hfill \end{array}$$

(16)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(17)

Substituting (16) into (2) we obtain

$$\begin{array}{c}\hfill k\equiv (\beta +pd)(s-1)+1\left(modn\right)\end{array}$$

i.e.,

$$\begin{array}{c}\hfill k\equiv \left[\beta \right(s-1)+1]+pd(s-1)\left(modn\right)\end{array}$$

By applying (3), we obtain

$$\begin{array}{c}\hfill k-2\equiv pd(s-1)\left(modn\right)\end{array}$$

This means $(k-2,n)\ne 1$. This is a contradiction. So $({\alpha }^{\prime }-{\beta }^{\prime },n)=1$.

2. If $({\alpha }^{\prime }-{\beta }^{\prime }+1,n)\ne 1$, then there exists $d>1$ which is a common factor of ${\alpha }^{\prime }-{\beta }^{\prime }+1$ and n:

$$\begin{array}{ccc}& & \alpha -\beta +1={\alpha }^{\prime }-{\beta }^{\prime }+1=pd\hfill \end{array}$$

(18)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(19)

Substituting (18) into (2) yields

$$\begin{array}{c}\hfill k\equiv (\beta +pd-1)(s-1)+1\left(modn\right)\end{array}$$

i.e.,

$$\begin{array}{c}\hfill k\equiv \left[\beta \right(s-1)+1]+pd(s-1)-(s-1)\left(modn\right)\end{array}$$

Because of (3), this can be written as

$$k\equiv 2+pd(s-1)-(s-1)\left(modn\right)$$

i.e.,

$$\begin{array}{c}\hfill k+s-3\equiv pd(s-1)\left(modn\right)\end{array}$$

This means $(k+s-3,n)\ne 1$. This contradicts the assumption. So $({\alpha }^{\prime }-{\beta }^{\prime }+1,n)=1$.

3. If $({\beta }^{\prime }-{\alpha }^{\prime }+1,n)\ne 1$, then there exists $d>1$ which is a common factor of ${\beta }^{\prime }-{\alpha }^{\prime }+1$ and n such that

$$\begin{array}{ccc}& & \beta -\alpha +1={\beta }^{\prime }-{\alpha }^{\prime }+1=pd\hfill \end{array}$$

(20)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(21)

Substituting (20) into (2) yields

$$\begin{array}{c}\hfill k\equiv (\beta -pd+1)(s-1)+1\left(modn\right)\end{array}$$

i.e.,

$$\begin{array}{c}\hfill k\equiv \left[\beta \right(s-1)+1]-pd(s-1)+(s-1)\left(modn\right)\end{array}$$

Because of (3), this can be written as

$$\begin{array}{c}\hfill k\equiv 2-pd(s-1)+(s-1)\left(modn\right)\end{array}$$

i.e.,

$$\begin{array}{c}\hfill s-k+1\equiv pd(s-1)\left(modn\right)\end{array}$$

This means $(s-k+1,n)\ne 1$. This contradicts assumption. So $({\beta }^{\prime }-{\alpha }^{\prime }+1,n)=1$.

(d) We prove $\left(4\right)$ of Theorem 2, i.e.,

$$({\alpha }^{\prime }+{\beta }^{\prime }-1,n)=1,({\alpha }^{\prime }+{\beta }^{\prime }-2,n)=1,({\alpha }^{\prime }+{\beta }^{\prime }-3,n)=1$$

1. If $({\alpha }^{\prime }+{\beta }^{\prime }-1,n)\ne 1$, then ${\alpha }^{\prime }+{\beta }^{\prime }-1$ and n have a common factor $d>1$:

$$\begin{array}{ccc}& & \alpha +\beta +1={\alpha }^{\prime }+{\beta }^{\prime }-1=pd\hfill \end{array}$$

(22)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(23)

Substituting (22) into (2) yields

$$\begin{array}{c}\hfill k\equiv (pd-\beta -1)(s-1)+1\left(modn\right)\end{array}$$

i.e.,

$$\begin{array}{c}\hfill k\equiv pd(s-1)-\beta (s-1)-(s-1)+1\left(modn\right)\end{array}$$

From (3), we obtain

$$\begin{array}{c}\hfill k+s-1\equiv pd(s-1)\left(modn\right)\end{array}$$

So $(k+s-1,n)\ne 1$. This is a contradiction. Thus $({\alpha }^{\prime }+{\beta }^{\prime }-1,n)=1$.

2. If $({\alpha }^{\prime }+{\beta }^{\prime }-2,n)\ne 1$, then ${\alpha }^{\prime }+{\beta }^{\prime }-2$ and n have a common factor $d>1$:

$$\begin{array}{ccc}& & \alpha +\beta ={\alpha }^{\prime }+{\beta }^{\prime }-2=pd\hfill \end{array}$$

(24)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(25)

Substituting (24) into (2) yields

$$k\equiv (pd-\beta )(s-1)+1\left(modn\right)$$

i.e.,

$$\begin{array}{c}\hfill k\equiv pd(s-1)-\beta (s-1)+1\left(modn\right)\end{array}$$

Using (3), we obtain

$$k\equiv pd(s-1)\left(modn\right)$$

So $(k,n)\ne 1$. This is a contradiction. Thus $({\alpha }^{\prime }+{\beta }^{\prime }-2,n)=1$.

3. If $({\alpha }^{\prime }+{\beta }^{\prime }-3,n)\ne 1$, then ${\alpha }^{\prime }+{\beta }^{\prime }-3$ and n have a common factor $d>1$:

$$\begin{array}{ccc}& & \alpha +\beta -1={\alpha }^{\prime }+{\beta }^{\prime }-3=pd\hfill \end{array}$$

(26)

$$\begin{array}{ccc}& & n=qd\hfill \end{array}$$

(27)

Substituting (26) into (2) yields

$$k\equiv (pd-\beta +1)(s-1)+1\left(modn\right)$$

i.e.,

$$k\equiv pd(s-1)-\beta (s-1)+(s-1)+1\left(modn\right)$$

It follows from (3) that

$$k-s+1\equiv pd(s-1)\left(modn\right)$$

So $(k-s+1,n)\ne 1$. This is a contradiction. Thus $({\alpha }^{\prime }+{\beta }^{\prime }-3,n)=1$.

(a), (b), (c), and (d) above show that $\alpha +1,\beta +1$ satisfy the conditions of Theorem 2, so that $T_{\alpha +1,\beta +1}$ is a pandiagonal magic cube. Now we have three pandiagonal magic cubes $T_{k,s},T_{s,k},T_{\alpha +1,\beta +1}$.

(e) We now turn to prove the orthogonality of $T_{k,s},T_{s,k},T_{\alpha +1,\beta +1}$. First, construct three determinants:

$$\Delta =\left|\begin{array}{ccc}s& k& 1\\ k& s& 1\\ \alpha +1& \beta +1& 1\end{array}\right|=\left|\begin{array}{ccc}s-1& k-1& 1\\ k-1& s-1& 1\\ \alpha & \beta & 1\end{array}\right|$$

$$\Delta (s-1)=\left|\begin{array}{ccc}s-1& k-1& 1\\ k-1& s-1& 1\\ \alpha (s-1)& \beta (s-1)& s-1\end{array}\right|$$

$${\Delta }^{\prime }=\left|\begin{array}{ccc}s-1& k-1& 1\\ k-1& s-1& 1\\ k-1& 1& s-1\end{array}\right|=(s-k)[(s+k-2)(s-1)-k]$$

From assumptions of (2), (3), we have $(s-1,n)=1$. Therefore, we obtain

$$(\Delta ,n)=1⟺(\Delta (s-1),n)=1⟺({\Delta }^{\prime },n)=1$$

Note that $(s+k-2)(s-1)-k=(s-2)(k+s-1)$, so $\left(\right(s+k-2\left)\right(s-1)-k,n)=1$. Because $T_{k,s}(1,2,\cdots ,n)$ is a pandiagonal Latin square (third condition (2) and first condition (4) in Theorem 2), $\left(\right(s+k-2\left)\right(s-1)-k,n)=1$. Compounded with $(s-k,n)=1$, we have $({\Delta }^{\prime },n)=1$, so $(\Delta ,n)=1$. From Theorem 3 it follows that $T_{k,s},T_{s,k},T_{\alpha +1,\beta +1}$ are orthogonal. This completes the proof. □

The following theorem give another method to construct orthogonal pandiagonal Latin cubes.

 Theorem 5. 

Suppose $3\le k\le n-1$, $3\le s\le n-1$. If the conditions

(1) $(k+i,n)=1$$(i=-2,-1,0,1,2)$;

(2) $(s+i,n)=1$$(i=-2,-1,0,1,2)$;

(3) $(k-s,n)=1$$(s-k+1,n)=1$, $(k-s+1,n)=1$;

(4) $(k+s+i,n)=1$$(i=-3,-2,-1,0,1,2,3)$

are satisfied, then $T_{k,s}$, $T_{s,k}$, $T_{n-k,n-s}$, $T_{n-s,n-k}$ are all pandiagonal Latin cubes and three of them are orthogonal.

 Proof. 

For $\{s,k\}$ or $\{n-k,n-s\}$, the conditions of Theorem 2 are satisfied. Then $T_{k,s}$, $T_{s,k}$, $T_{n-k,n-s}$, $T_{n-s,n-k}$ are all pandiagonal Latin cubes.

In addition,

$$\Delta =\left|\begin{array}{ccc}s& k& 1\\ k& s& 1\\ n-s& n-k& 1\end{array}\right|=2n(k-s)-2(k-s)(k+s),$$

and n are coprime if, and only if, $\left(2\right(k-s\left)\right(k+s),n)=1$. However, this is true because $(2,n)=1$, $(k-s,n)=1$, $(k+s,n)=1$.

Hence from Theorem 3, any three of them are orthogonal. This completes the proof. □

Now, we can construct a pandiagonal magic cube by using Natural Aux Cube. We obtain the following theorem.

 Theorem 6. 

Let $T_{k_i,s_i}(j_1^{\left(i\right)},j_2^{\left(i\right)},\cdots ,j_n^{\left(i\right)})=\left(l_{tuv}^{\left(i\right)}\right)(i=1,2,3)$ be orthogonal pandiagonal Latin cubes. Construct integers cube $C=\left(c_{tuv}\right)$, where

$$c_{tuv}=n(l_{tuv}^{\left(1\right)}-1)+l_{tuv}^{\left(2\right)}+n^2(l_{tuv}^{\left(3\right)}-1)(t,u,v=1,2,\cdots ,n)$$

Then C is a pandiagonal magic cube.

 Proof. 

Consider any section or diagonal S of C. According to the properties of pandiagonal Latin cubes, $l_{tuv}^{\left(1\right)},l_{tuv}^{\left(2\right)},l_{tuv}^{\left(3\right)}$ take the complete permutation of $1,2,\cdots ,n$ on any row, column or pandiagonal line of S. When adding the elements of C on such a row, column, or pandiagonal, there is

$$\begin{array}{cc}\hfill \sum c_{tuv}& =n\left(\sum l_{tuv}^{\left(1\right)}-\sum 1\right)+\sum l_{tuv}^{\left(2\right)}+n^2\left(\sum l_{tuv}^{\left(3\right)}-\sum 1\right)\hfill \\ & =n\left(\sum _{i=1}^{n}i-n\right)+\sum _{i=1}^{n}i+n^2\left(\sum _{i=1}^{n}i-n\right)\hfill \\ & =\frac{n^2(n-1)}{2}+\frac{n(n+1)}{2}+\frac{n^3(n-1)}{2}\hfill \\ & =\frac{n\left(1+n^3\right)}{2}\hfill \end{array}$$

They are all equal to magic sum, so C is a pandiagonal magic cube. □

If a set of orthogonal pandiagonal Latin cubes is given, we can construct 6${(n!)}^3$ pandiagonal magic squares. This is because there exist six arrangements of three pandiagonal Latin squares and there are $n!$ permutations of $1,2,\cdots ,n$.

Next, we give some examples of satisfying the Theorems and Corollaries.

 Example 1. 

For n = 11, computer studies show that there exist 23 pandiagonal Latin cubes which satisfy the conditions of Corollary 1, and there are 9870 orthogonal sets. For example, three orthogonal pandiagonal Latin cube sets are $\{T_{3,5},T_{6,9},T_{4,7}\}$, $\{T_{6,10},T_{3,8},T_{5,10}\}$, $\{T_{6,10},T_{3,8},T_{6,3}\}$.

 Example 2. 

Suppose n = 143.

Let $k_1=67$, $s_1=4$, $k_2=96$, $s_2=5$, $k_3=120$, $s_3=8$.

Then they satisfy the conditions of Theorem 3.

 Example 3. 

For n = 121, let

$k=29$, $s=21$, $\alpha +1=75$, $\beta +1=116$.

$k=21$, $s=29$, $\alpha +1=19$, $\beta +1=14$

$k=5$, $s=109$, $\alpha +1=28$, $\beta +1=97$

These are three sets of parameters such that orthogonal pandiagonal Latin cubes satisfy the conditions of Theorem 4.

5. Further Property

The pandiagonal magic cube considered in the foregoing sections has further interesting properties.

Let $ABCD$-$EFGH$ in Figure 2 be an integer cube, and $NM$-$KL$ be a pandiagonal line on the top surface $ABCD$. Using two planes which are parallel to the edge $DH$, we can cut $ABCD$-$EFGH$ into three parts. Let cross sections be $NM{M}^{\prime }{N}^{\prime }$ and $KL{L}^{\prime }{K}^{\prime }$. Through parallel translation, we obtain a square matrix $NMKL{L}^{\prime }{K}^{\prime }{M}^{\prime }{N}^{\prime }$ (or $KLNM{M}^{\prime }{N}^{\prime }{L}^{\prime }{K}^{\prime }$), which is called a pandiagonal plane. There are six sets of such planes, where each set has n pandiagonal planes which are parallel to each other.

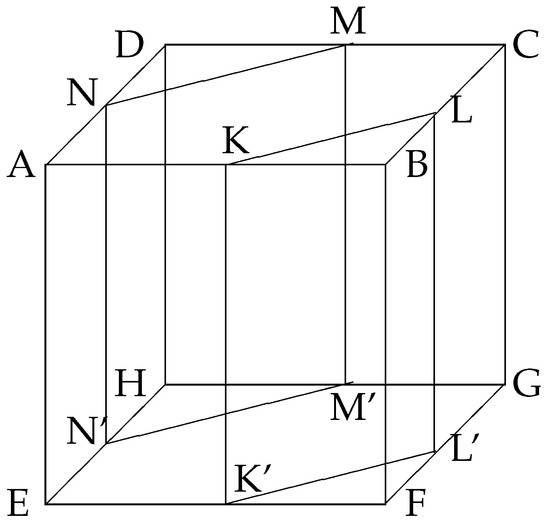
Figure 2. The Integer Cube-$ABCD$-$EFGH$.

A pandiagonal plane of a pandiagonal magic cube is also a pandiagonal magic square. In fact, let us begin with a pandiagonal Latin cube. Let $ABCD$-$EFGH$ be a pandiagonal Latin cube, then its each pandiagonal plane has the same generating transformation with the diagonal plane parallel to itself. For example, the diagonal plane $ACGE$ of $T_{3,5}(1,2,\cdots ,11)$ of Section 3 is given by

$$\boxed{\begin{array}{ccccccccccc}8& 5& 2& 10& 7& 4& 1& 9& 6& \hfill 3& \hfill 11\\ 10& 7& 4& 1& 9& 6& 3& 11& 8& \hfill 5& \hfill 2\\ 1& 9& 6& 3& 11& 8& 5& 2& 10& \hfill 7& \hfill 4\\ 3& 11& 8& 5& 2& 10& 7& 4& 1& \hfill 9& \hfill 6\\ 5& 2& 10& 7& 4& 1& 9& 6& 3& \hfill 11& \hfill 8\\ 7& 4& 1& 9& 6& 3& 11& 8& 5& \hfill 2& \hfill 10\\ 9& 6& 3& 11& 8& 5& 2& 10& 7& \hfill 4& \hfill 1\\ 11& 8& 5& 2& 10& 7& 4& 1& 9& \hfill 6& \hfill 3\\ 2& 10& 7& 4& 1& 9& 6& 3& 11& \hfill 8& \hfill 5\\ 4& 1& 9& 6& 3& 11& 8& 5& 2& \hfill 10& \hfill 7\\ 6& 3& 11& 8& 5& 2& 10& 7& 4& \hfill 1& \hfill 9\end{array}}$$

A pandiagonal plane parallel to $ACGE$ is

$$\boxed{\begin{array}{ccccccccccc}6& 3& 11& 8& 5& 2& 10& 7& 4& 1& \hfill 9\\ 8& 5& 2& 10& 7& 4& 1& 9& 6& 3& \hfill 11\\ 10& 7& 4& 1& 9& 6& 3& 11& 8& 5& \hfill 2\\ 1& 9& 6& 3& 11& 8& 5& 2& 10& 7& \hfill 4\\ 3& 11& 8& 5& 2& 10& 7& 4& 1& 9& \hfill 6\\ 5& 2& 10& 7& 4& 1& 9& 6& 3& 11& \hfill 8\\ 7& 4& 1& 9& 6& 3& 11& 8& 5& 2& \hfill 10\\ 9& 6& 3& 11& 8& 5& 2& 10& 7& 4& \hfill 1\\ 11& 8& 5& 2& 10& 7& 4& 1& 9& 6& \hfill 3\\ 2& 10& 7& 4& 1& 9& 6& 3& 11& 8& \hfill 5\\ 4& 1& 9& 6& 3& 11& 8& 5& 2& 10& \hfill 7\end{array}}$$

They are all generated by $T_4$. This fact can be proved in general. Because of this and the fact that all of diagonal planes are pandiagonal magic squares, pandiagonal planes are all pandiagonal magic squares for a pandiagonal magic cube.

As an example, in Appendix B, we give a set of pandiagonal planes of the pandiagonal magic cube shown in Appendix A. They are cross sections of another pandiagonal magic cube. In other words, if $A=\left(a_{ijk}\right)$ is a pandiagonal magic cube, then $B=\left(b_{ijk}\right)=\left(a_{j[k-j+1]i}\right)$ (here [ ] expresses modulo n, we define that [0] = n) is also a pandiagonal magic cube. Similarly, $\left(b_{ijk}\right)=\left(a_{j[k+j-1]i}\right)$, $\left(b_{ijk}\right)=\left(a_{[k-j+1]ij}\right)$, $B=\left(b_{ijk}\right)=\left(a_{ij[k-j+1]}\right)$, $\left(b_{ijk}\right)=\left(a_{[k+j-1]ij}\right)$, $\left(b_{ijk}\right)=\left(a_{ij[k+j-1]}\right)$ are all pandiagonal magic cubes. Appendix B shows $B=\left(b_{ijk}\right)=\left(a_{j[k-j+1]i}\right)$.

6. Conclusions

In this paper, we have defined a kind of magic cube called pandiagonal magic cube, whose cross sections and diagonal planes are pandiagonal magic squares. We have given a construction method for this pandiagonal magic cube. First, we construct three orthogonal pandiagonal Latin cubes, join them into a cube of three-tuples, and then replace entries by entries of some auxiliary cube so that the subscripts are these three-tuple. The last cube is a pandiagonal magic cube. If we have a pandiagonal Latin cube, Theorems 4 and 5 tell us how to construct a set of orthogonal pandiagonal Latin cubes. Some examples are also included. The construction method of pandiagonal magic cubes proposed in this paper can be extended to higher dimensions.