Research Trend, Logical Structure and Outlook on Complex Economic Game
Abstract
:1. Introduction
2. Research Framework
3. Cluster Analysis, Hotspots Analysis, and Research Logic Analysis
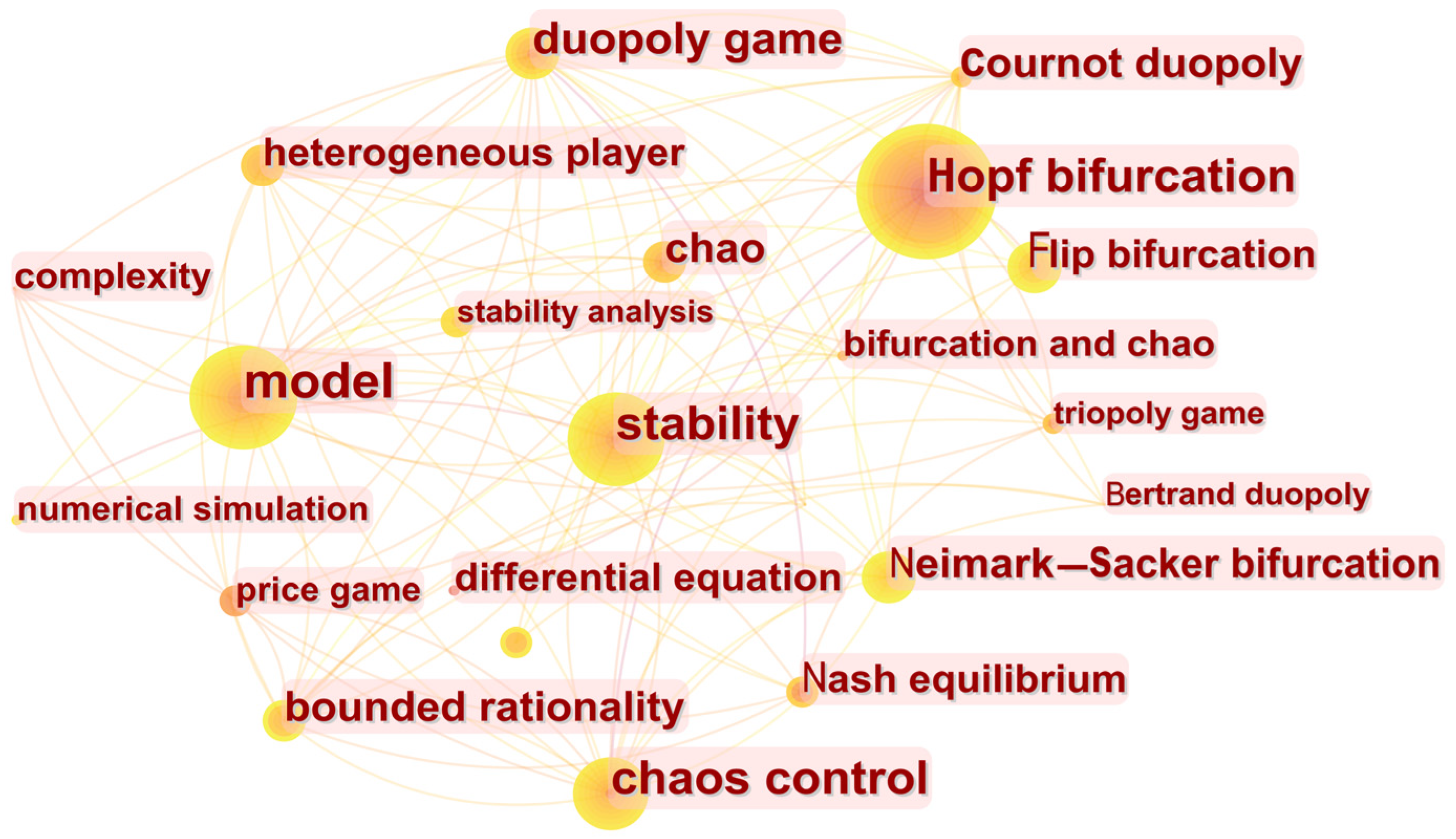
3.1. Cluster Analysis and Research Logic Analysis
- (1)
- Cluster Analysis
- (2)
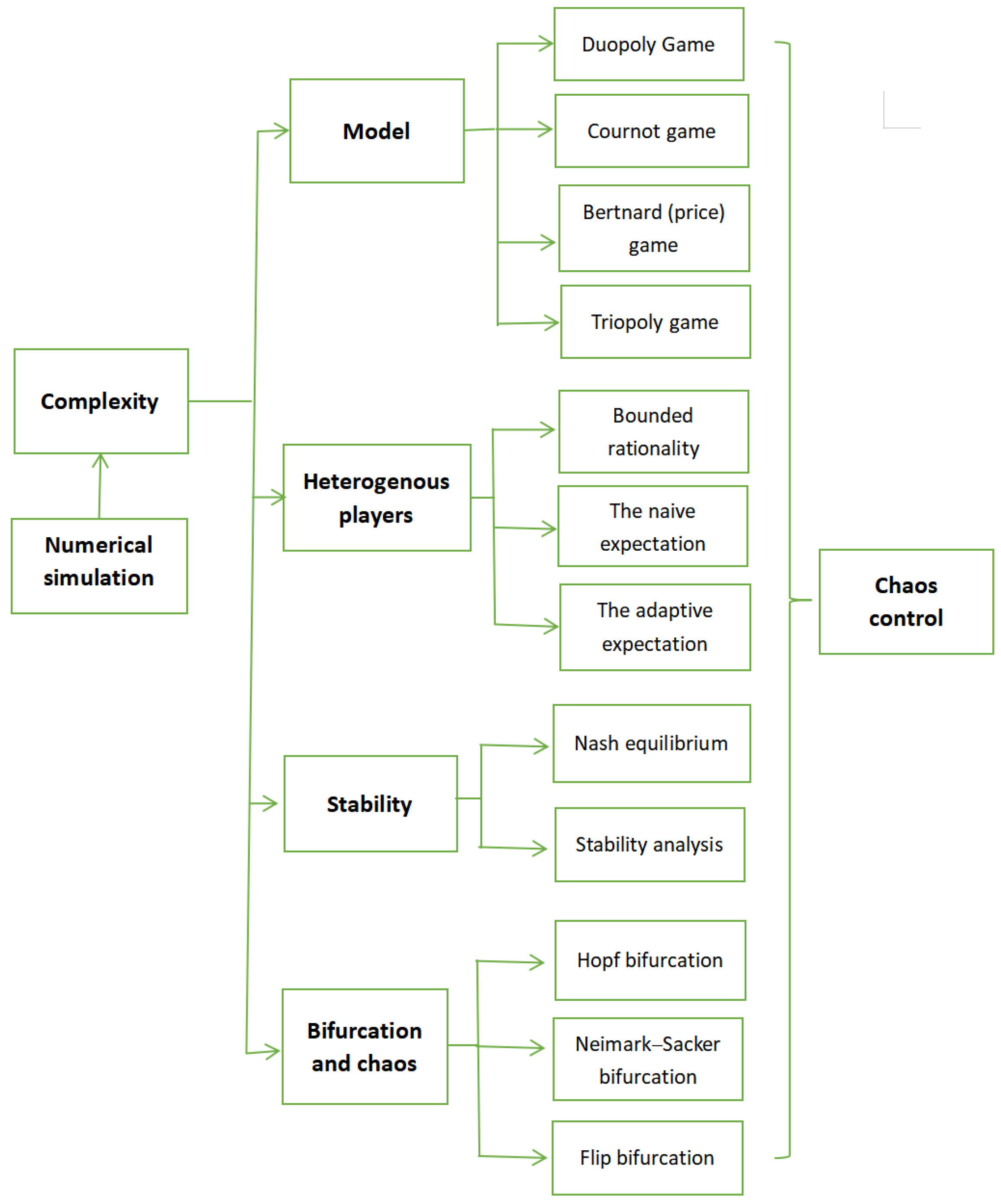
- Research Logic Analysis
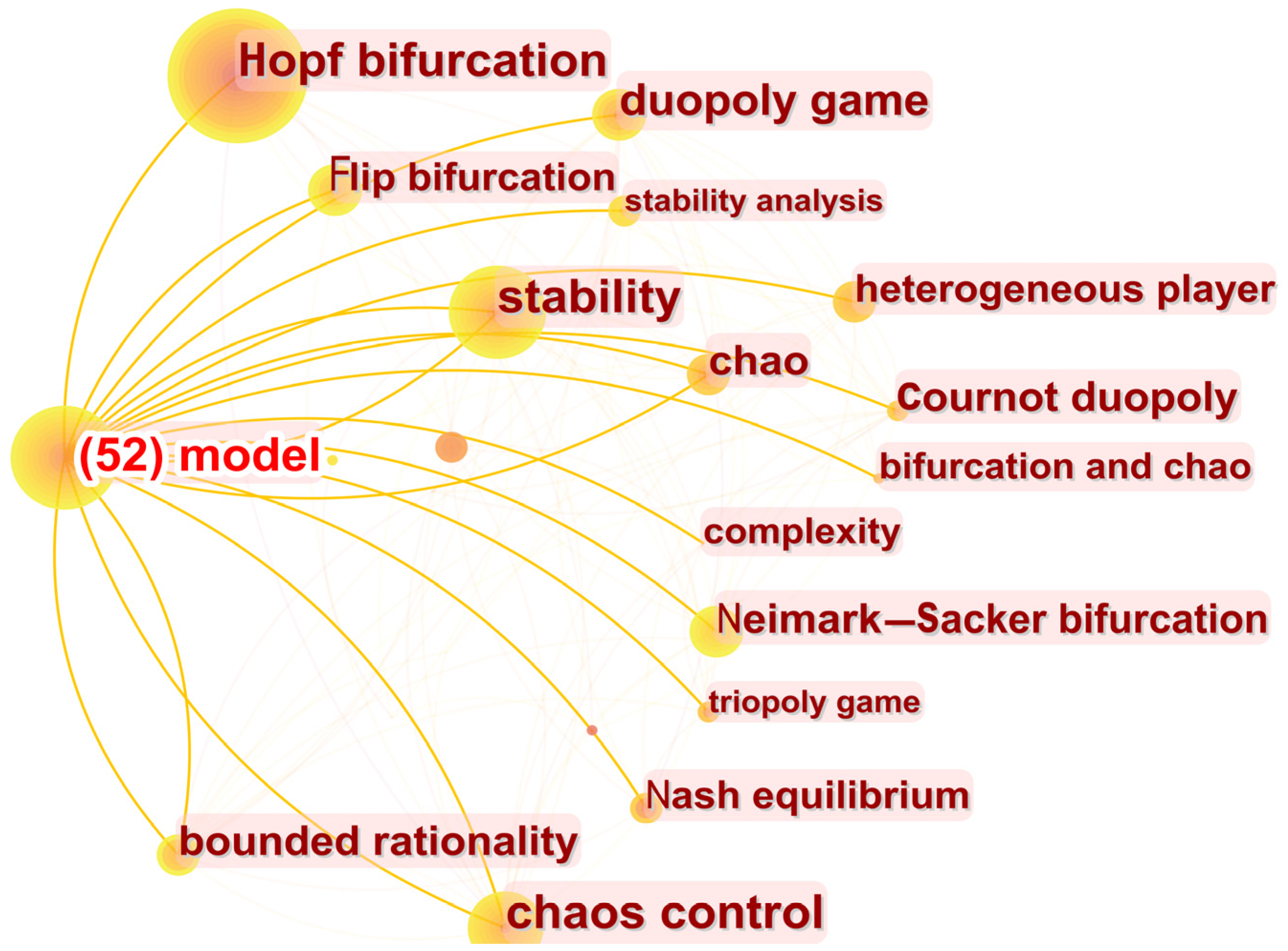
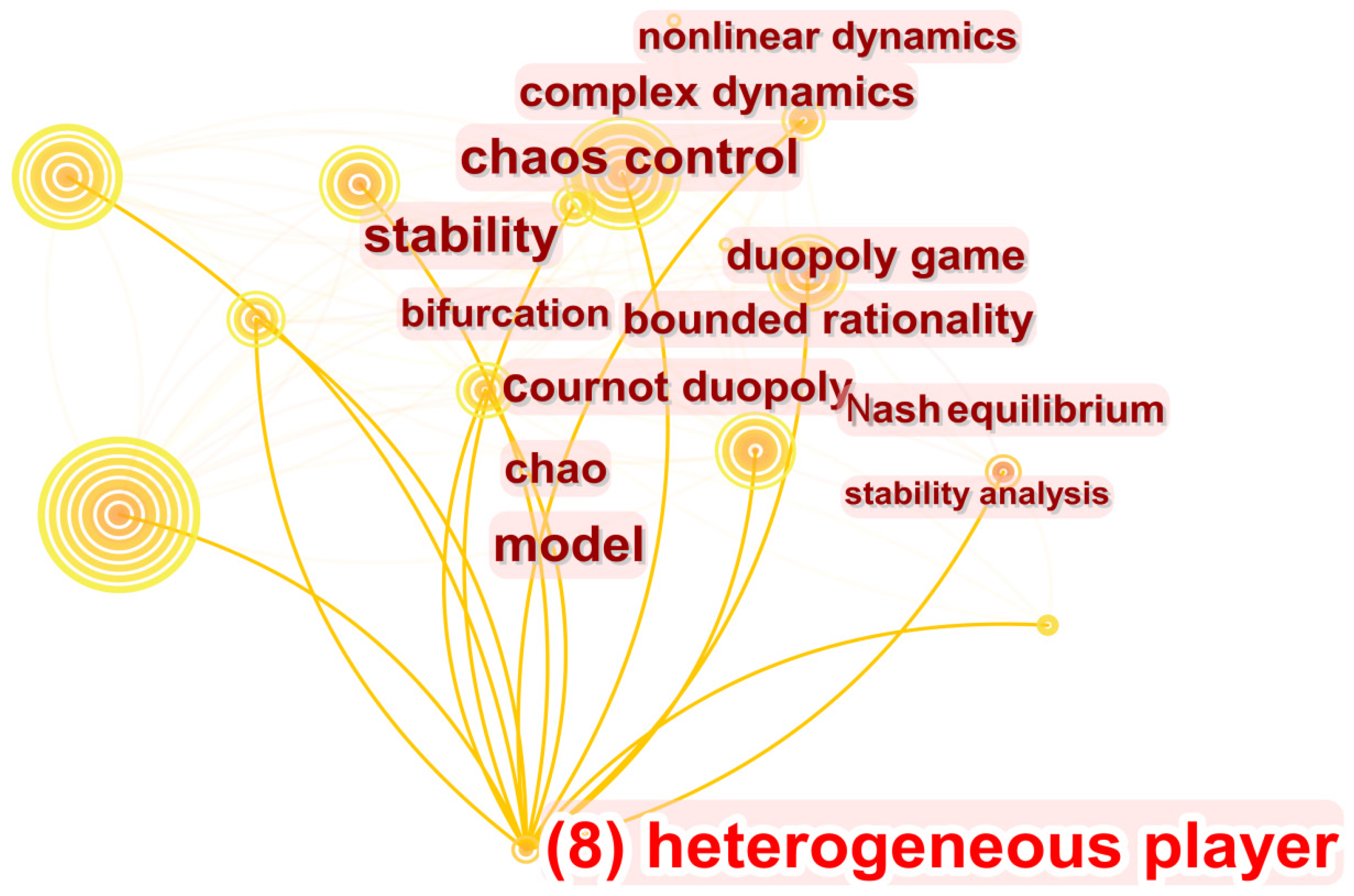
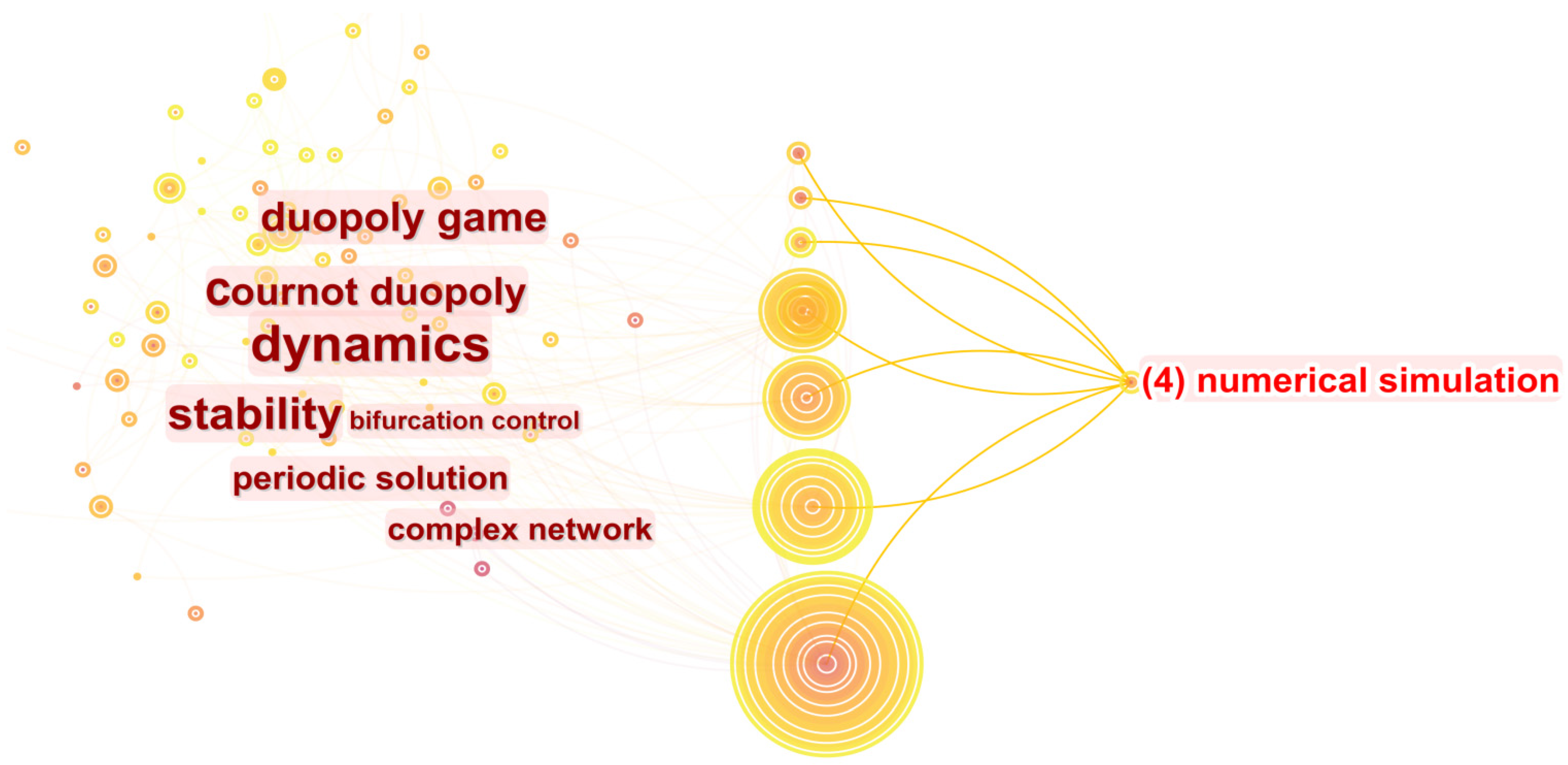
3.2. Hotspots Analysis and Research Logic Analysis
- (1)
- Hotspots Analysis by CiteSpace
- (2)
- Research Logic Analysis of Hot Keywords
4. Related Research
4.1. The Complexity
4.2. The Model
4.3. Heterogenous Player
4.4. Stability
4.5. Numerical Simulation
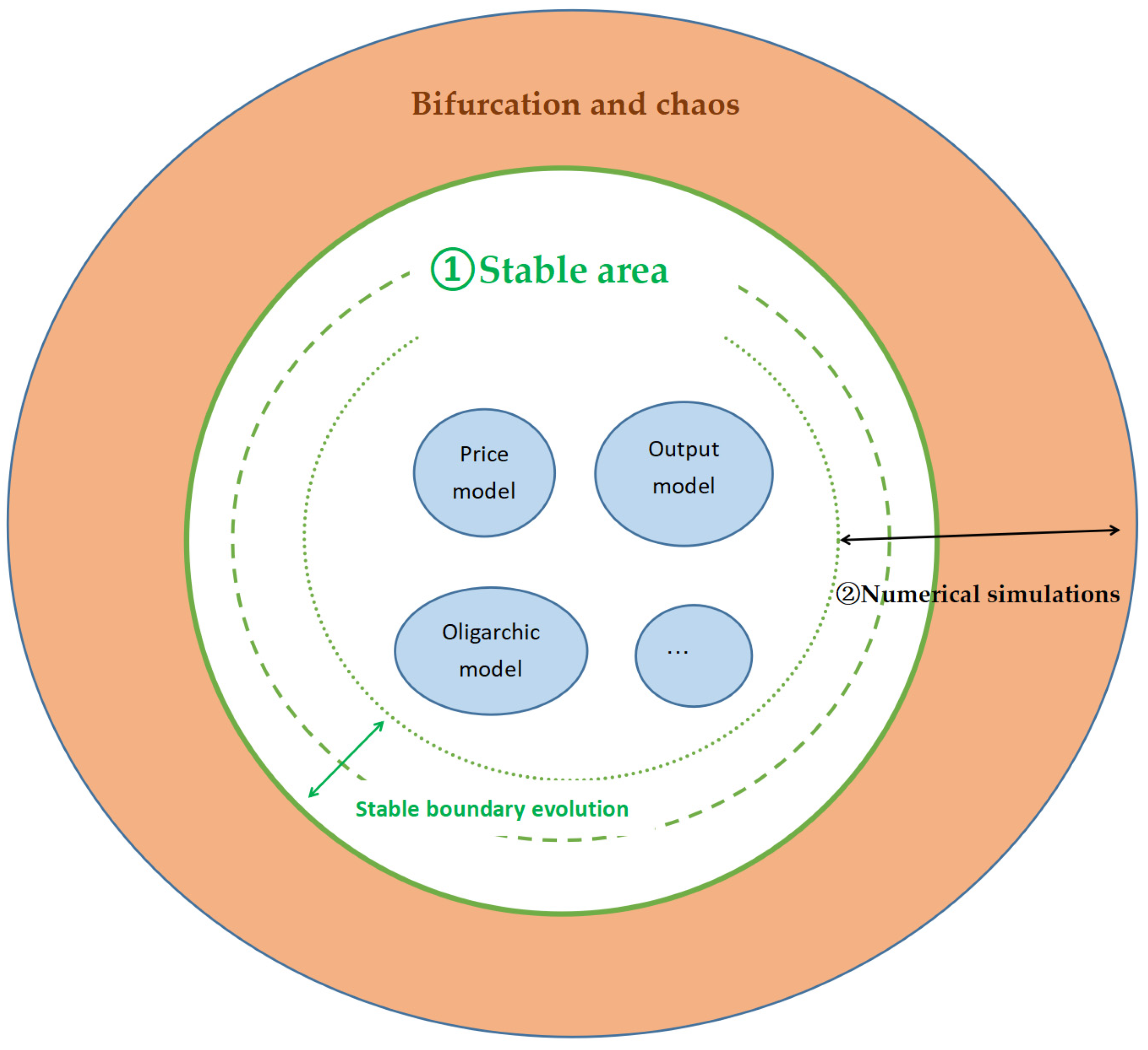
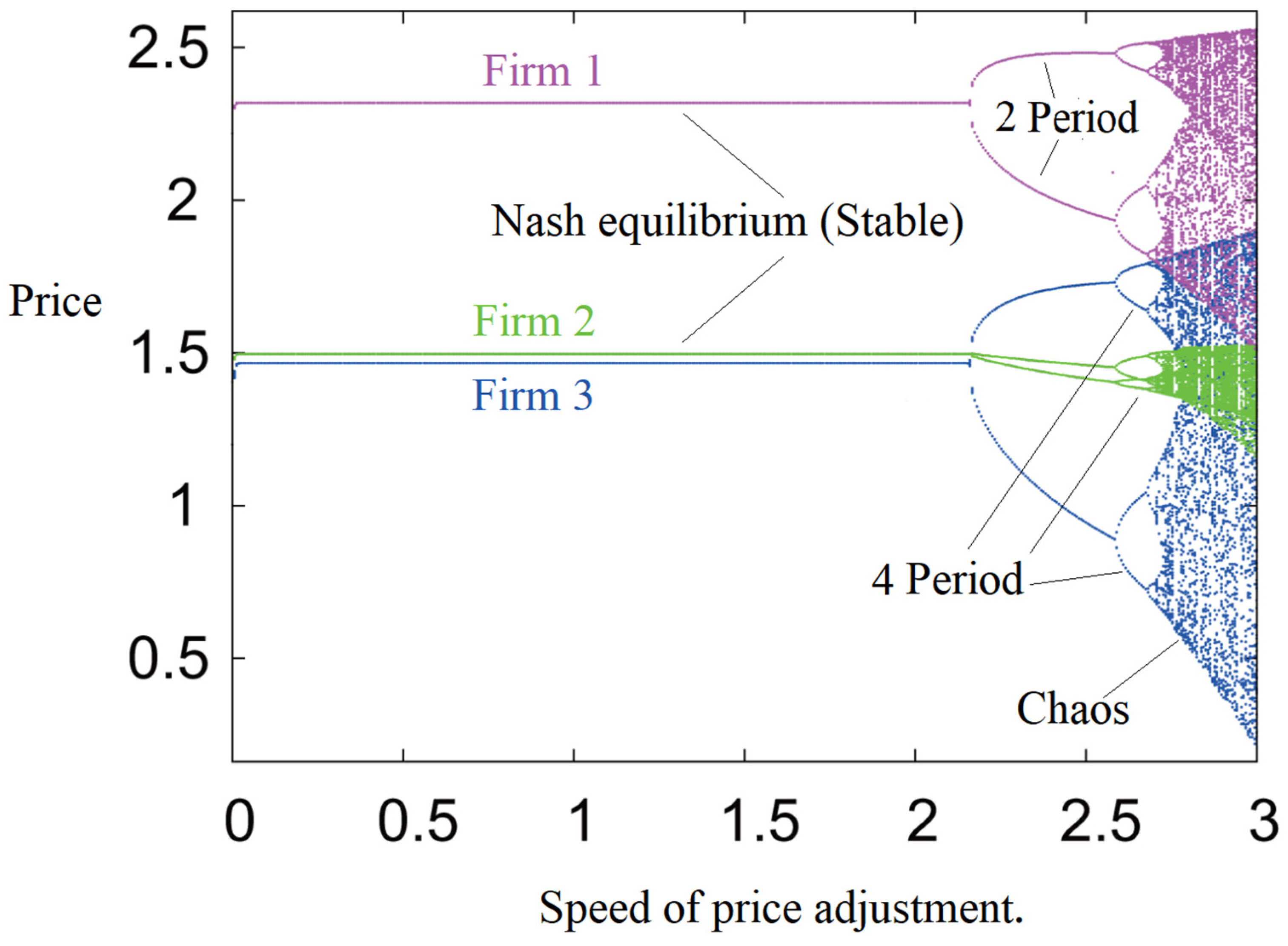
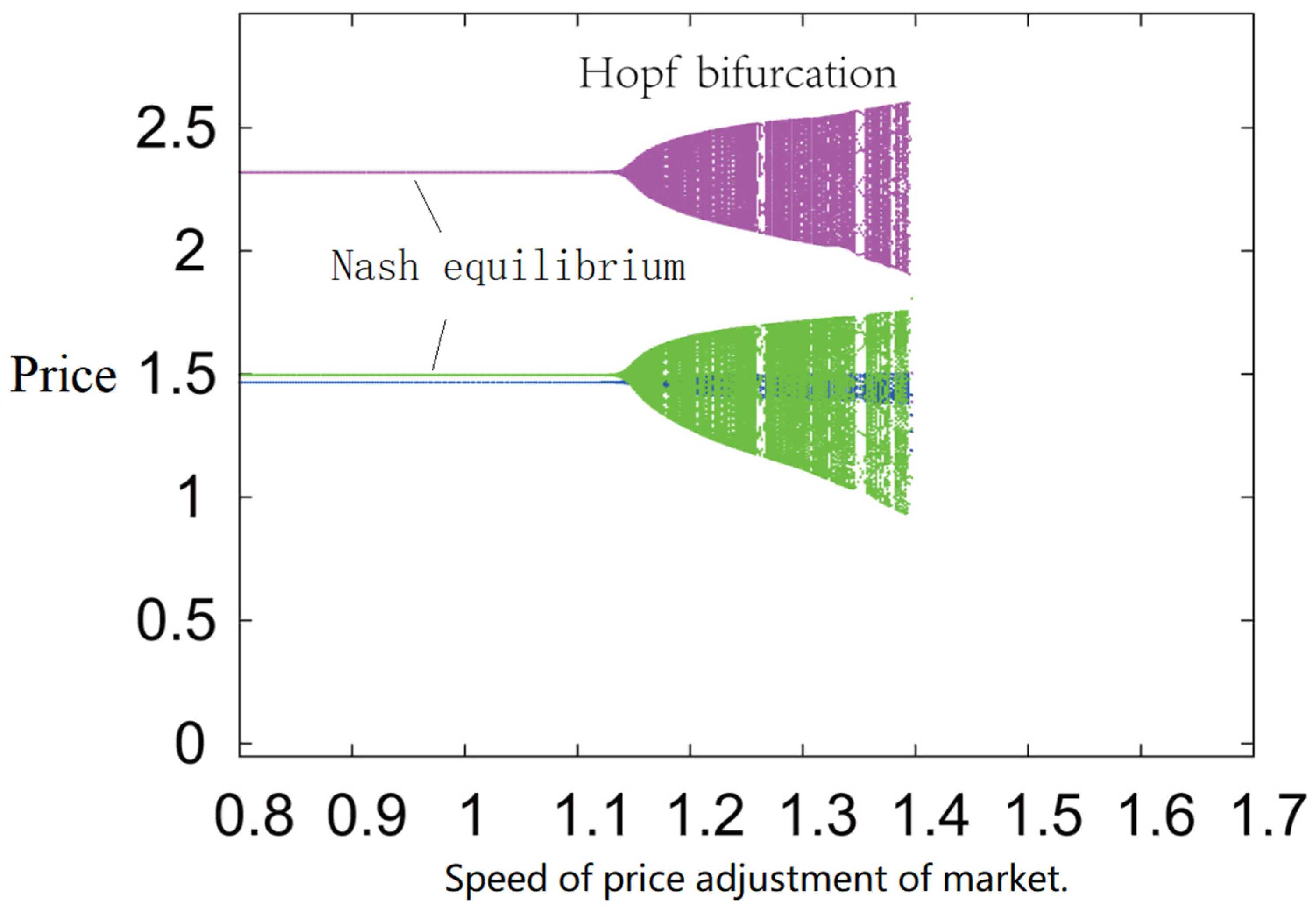
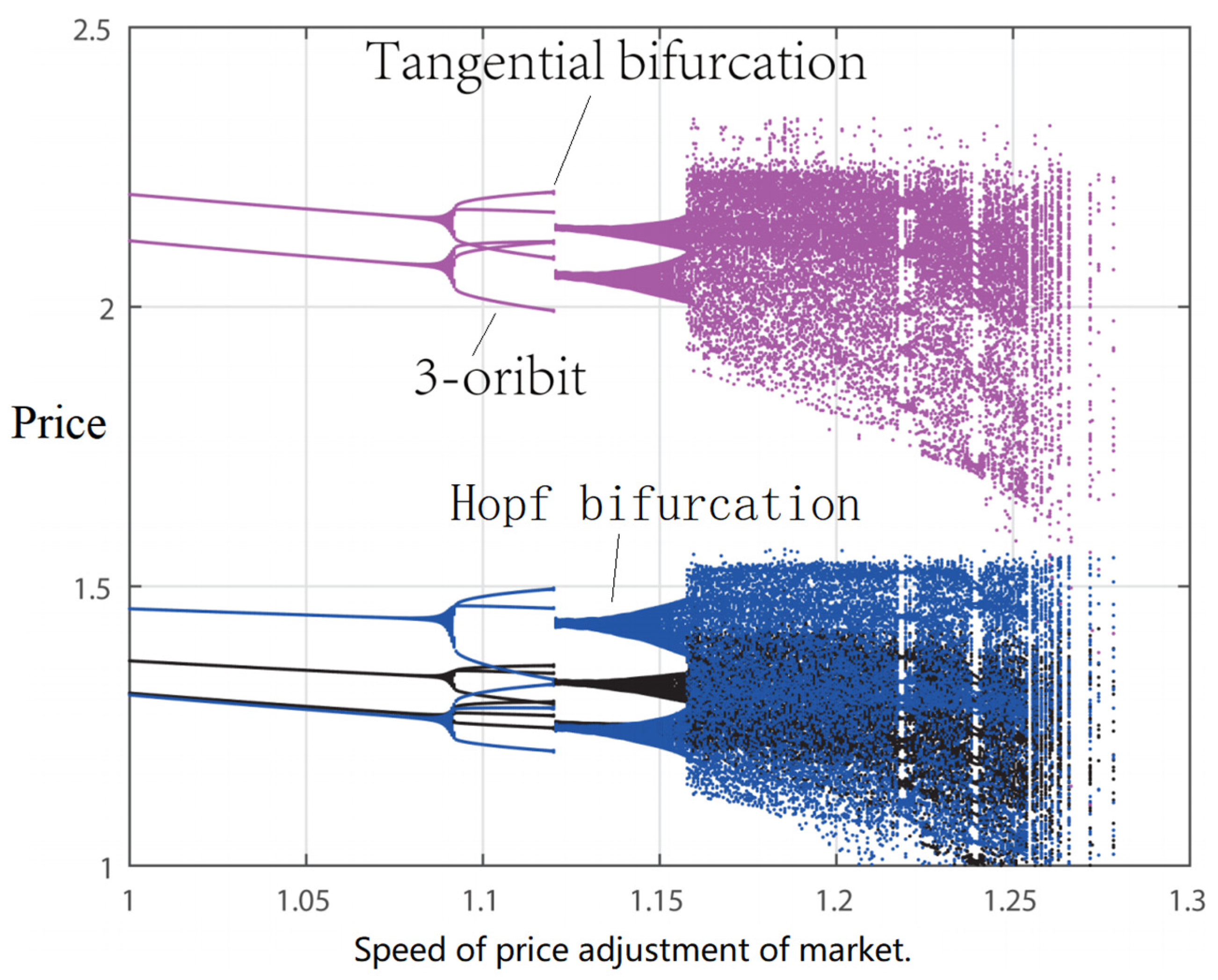
4.6. Bifurcation, Chaos, and Control
4.6.1. Bifurcation and Chaos
4.6.2. Chaos Control
5. Research Outlook
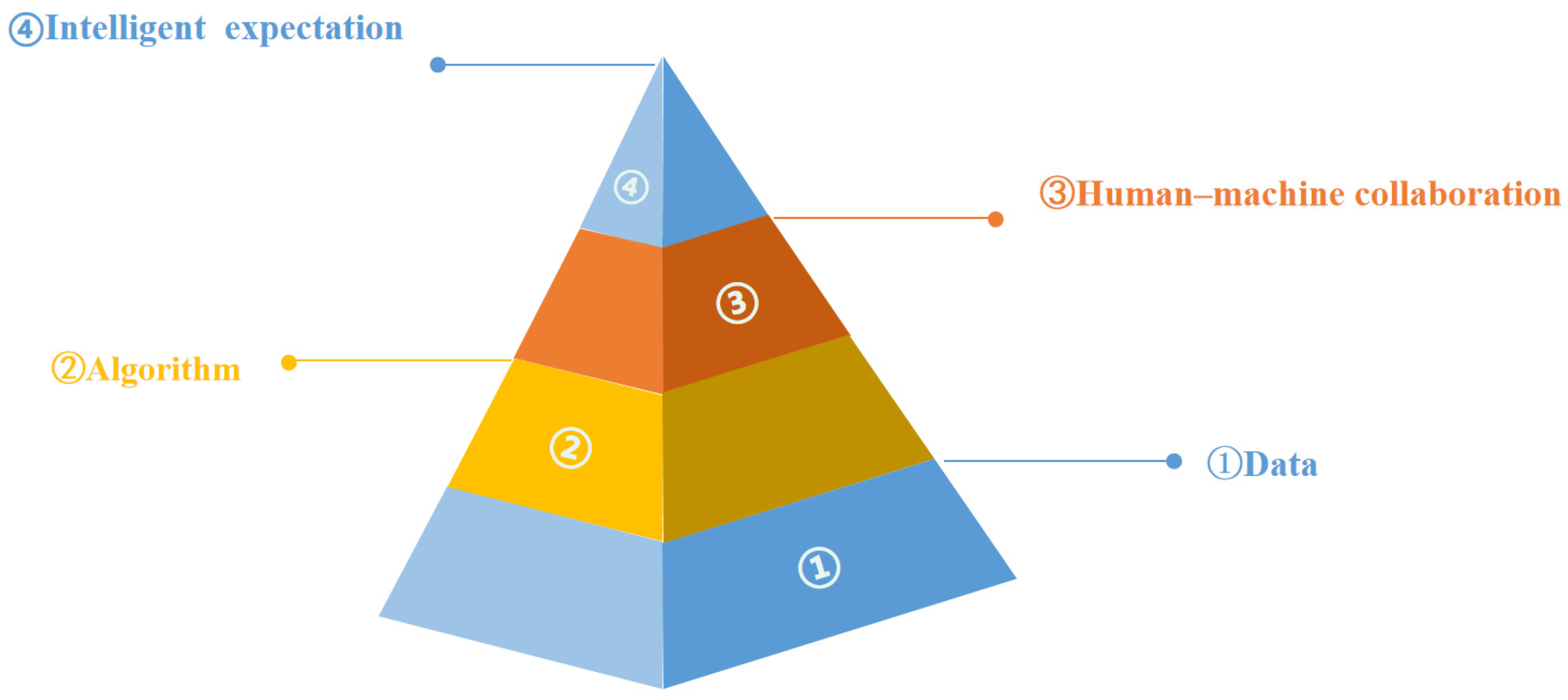
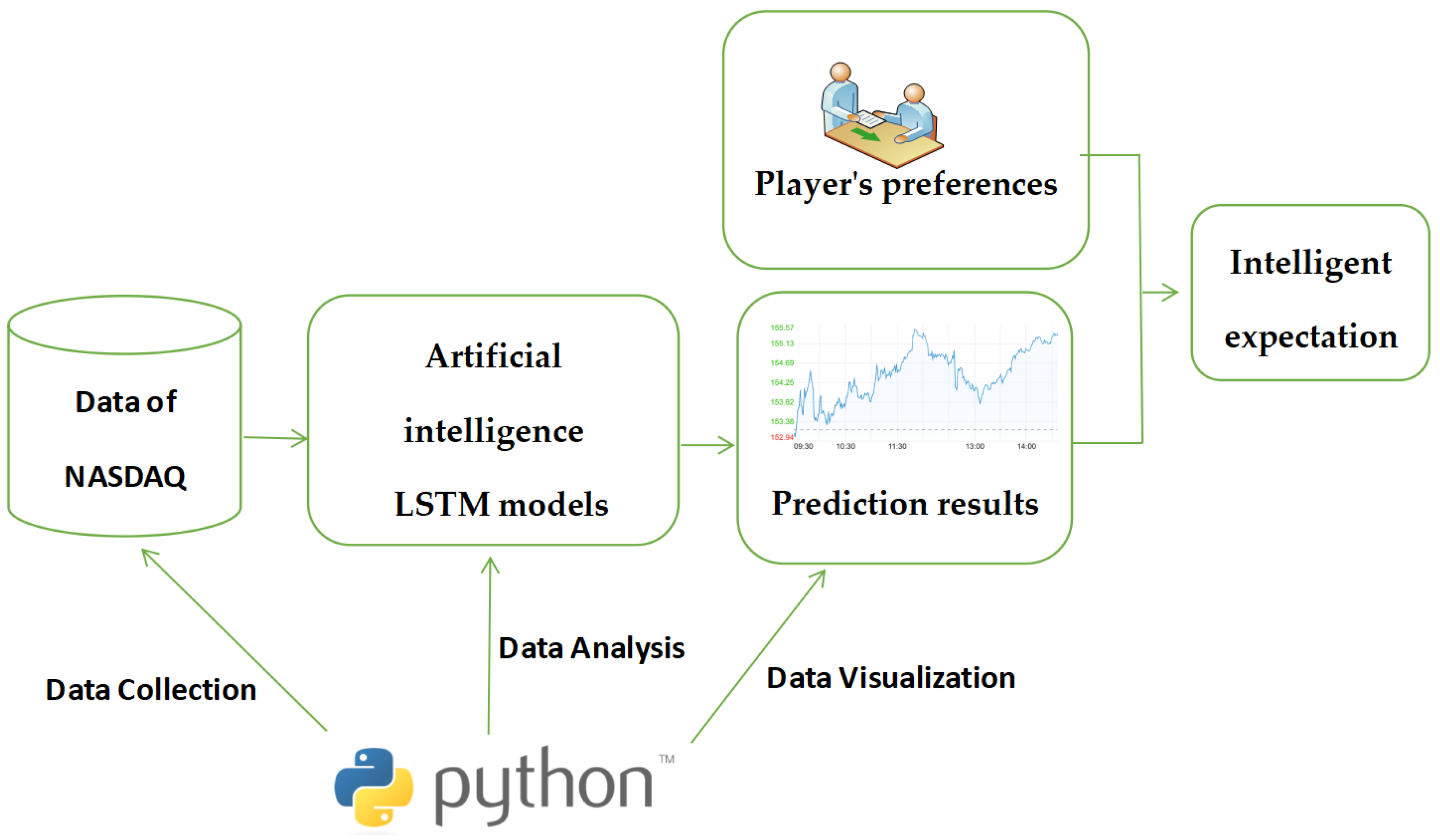
5.1. Market Expectations Based on Big Data and Artificial Intelligence
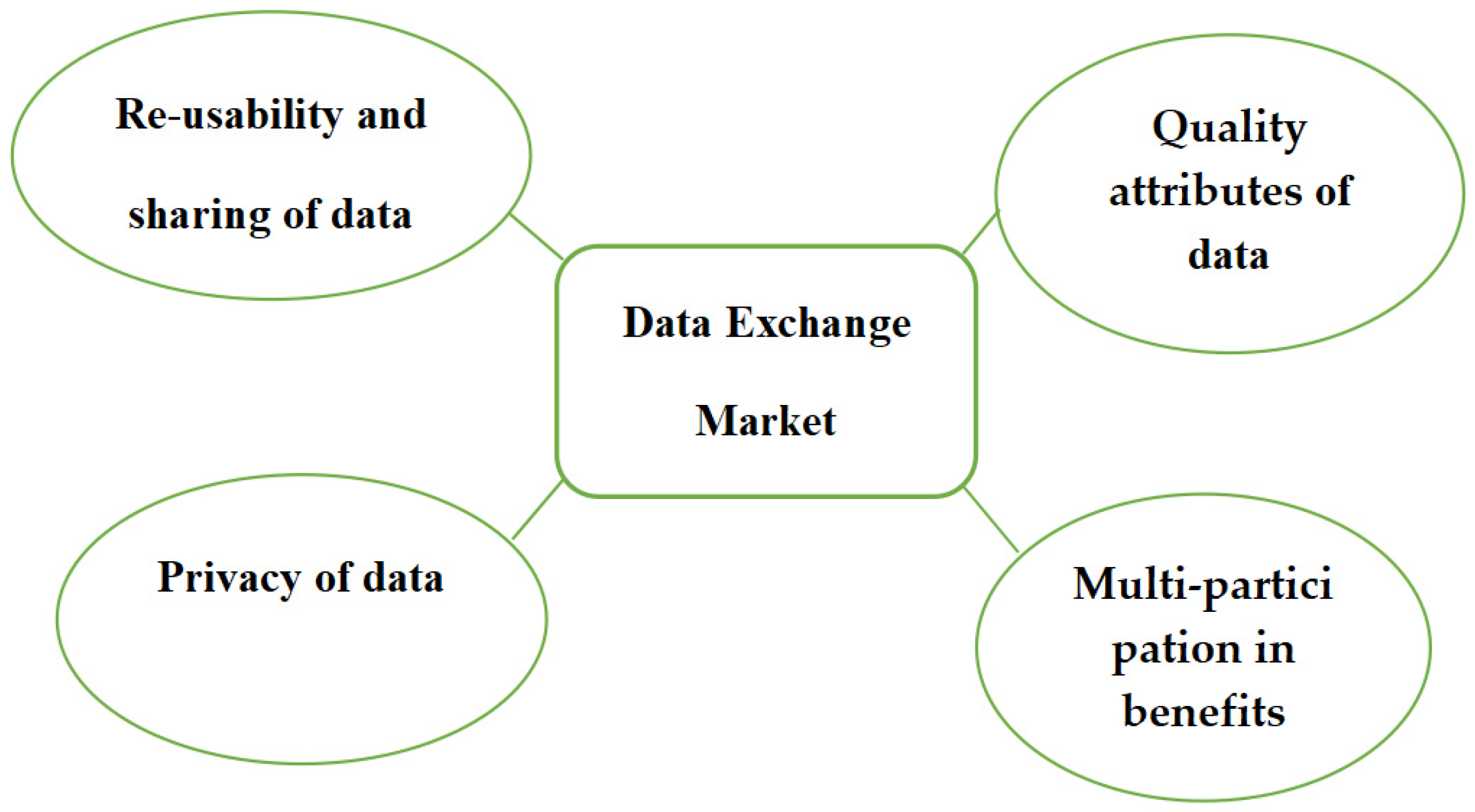
5.2. Complex Risk of Data Trading
5.3. Emergency Warning Based on Complexity Theory
6. The Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- Ball, P. Social science goes virtual. Nature 2007, 448, 647–648. [Google Scholar] [CrossRef] [Green Version]
- Arthur, W.B. Foundations of complexity economics. Nat. Rev. Phys. 2021, 3, 136–145. [Google Scholar] [CrossRef]
- Arthur, W.B. Complexity and the Economy. Science 1999, 284, 107–109. [Google Scholar] [CrossRef]
- Lampart, M.; Lampartova, A. Chaos control and anti-control of the heterogeneous cournot oligopoly model. Mathematics 2020, 8, 1670. [Google Scholar] [CrossRef]
- Ma, J.H.; Zhang, J.L. Price game and chaos control among three oligarchs with different rationalities in property insurance market. Chao 2012, 22, 043120. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.H.; Wu, F. The application and complexity analysis about a high-dimension discrete dynamical system based on heterogeneous triopoly game with multi-product. Nonlinear Dyn. 2014, 77, 781–792. [Google Scholar] [CrossRef]
- Wu, F.; Ma, J. The chaos dynamic of multiproduct Cournot duopoly game with managerial delegation. Discret. Dyn. Nat. Soc. 2014, 2014, 206961. [Google Scholar] [CrossRef] [Green Version]
- Wu, F.; Ma, J. The equilibrium, complexity analysis and control in epiphytic supply chain with product horizontal diversification. Nonlinear Dyn. 2018, 93, 2145–2158. [Google Scholar] [CrossRef]
- Xin, B.; Peng, W.; Guerrini, L. A continuous time Bertrand duopoly game with fractional delay and conformable derivative: Modeling, discretization process, Hopf bifurcation, and chaos. Front. Phys. 2019, 7, 00084. [Google Scholar] [CrossRef]
- Zhou, W.; Cao, Y.; Elsonbaty, A.; Elsadny, A.; Chu, T. Bifurcation analysis of a bounded rational duopoly game with consumer surplus. Int. J. Bifurc. Chaos 2021, 31. [Google Scholar] [CrossRef]
- Wu, F.; Ma, J.; Li, Y. Complex fluctuation of power price in dual-channel and multienergy supply chain based on sticky expectation. Int. J. Bifurc. Chaos 2021, 31, 206–215. [Google Scholar] [CrossRef]
- Forrester, J.W. System dynamics, system thinking and soft OR. Syst. Dyn. Rev. 1994, 10, 1–14. [Google Scholar] [CrossRef]
- Holland, J. Adaptation in Natural and Artificial Systems: An Introductory Analysis with Application to Biology, Control, and Artificial Intelligence; University of Michigan Press: Michigan, USA, 1975; pp. 1–20. [Google Scholar]
- Warfield, J.N. Societal systems planning, policy and complexity. J. Cybern. 1978, 8, 113–115. [Google Scholar] [CrossRef]
- Magda, F. The Santa Fe Perspective on Economics: Emerging patterns in the science of complexity. Cesmep Work. Pap. 2009, 18, 183–212. [Google Scholar] [CrossRef]
- Xin, B.G.; Peng, W.; Kwon, Y. A discrete fractional-order Cournot duopoly game. Phys. -Stat. Mech. Its Appl. 2020, 558, 124993. [Google Scholar] [CrossRef]
- Ledvina, A.; Sircar, R. Dynamic Bertrand oligopoly. Appl. Math. Optim. 2011, 63, 11–44. [Google Scholar] [CrossRef] [Green Version]
- Askar, S.S. Tripoly Stackelberg game model: One leader versus two followers. Appl. Math. Comput. 2018, 328, 301–311. [Google Scholar] [CrossRef]
- Xin, B.G.; Chen, T. On a master-slave Bertrand game model. Econ. Model. 2011, 28, 1864–1870. [Google Scholar] [CrossRef]
- Cavalli, F.; Naimzada, A. Complex dynamics and multistability with increasing rationality in market games. Chaos Solitons Fractals 2016, 93, 151–161. [Google Scholar] [CrossRef]
- Elsadany, A.A.; Awad, A.M. Dynamical analysis and chaos control in a heterogeneous Kopel duopoly game. Indian J. Pure Appl. Math. 2016, 47, 617–639. [Google Scholar] [CrossRef]
- Si, F.; Ma, J. Complex dynamics in a triopoly game with multiple delays in the competition of green product level. Int. J. Bifurc. Chaos 2018, 28, 1850027. [Google Scholar] [CrossRef]
- Ma, J.; Ren, W. Complexity and Hopf bifurcation analysis on a kind of fractional-order IS-LM macroeconomic system. Int. J. Bifurc. Chaos 2016, 26, 1650181. [Google Scholar] [CrossRef] [Green Version]
- Ma, J.; Tu, H. Analysis of the stability and Hopf bifurcation of money supply delay in complex macroeconomic models. Nonlinear Dyn. 2013, 76, 497–508. [Google Scholar] [CrossRef]
- Yang, H.; Yang, S.; Zhao, J.; Dong, Z. Complex dynamics and chaos control of electricity markets with heterogeneous expectations. Int. Trans. Electr. Energy Syst. 2013, 24, 1047–1064. [Google Scholar] [CrossRef]
- Wu, F.; Ma, J. Evolution dynamics of agricultural internet of things technology promotion and adoption in China. Discret. Dyn. Nat. Soc. 2020, 2020, 1854193. [Google Scholar] [CrossRef]
- Garmani, H.; Omar, D.A.; El Amrani, M.; Baslam, M.; Jourhmane, M. A dynamic duopoly game with content providers bounded rationality. Int. J. Bifurc. Chaos 2020, 30, 2050095. [Google Scholar] [CrossRef]
- Zhou, W.; Li, H. Complex dynamical behaviors in a Bertrand game with service factor and differentiated products. Nonlinear Dyn. 2021, 106, 2739–2759. [Google Scholar] [CrossRef]
- Peng, Y.; Xiao, Y.; Lu, Q.; Wu, X.; Zhao, Y. Chaotic dynamics in Cournot duopoly model with bounded rationality based on relative profit delegation maximization. Phys. A Stat. Mech. Appl. 2020, 560, 125174. [Google Scholar] [CrossRef]
- Xiao, Y.; Peng, Y.; Lu, Q.; Wu, X. Chaotic dynamics in nonlinear duopoly Stackelberg game with heterogeneous players. Phys. A: Stat. Mech. Its Appl. 2018, 492, 1980–1987. [Google Scholar] [CrossRef]
- Sun, Z.; Ma, J. Complexity of triopoly price game in Chinese cold rolled steel market. Nonlinear Dyn. 2011, 67, 2001–2008. [Google Scholar] [CrossRef]
- Rump, C.M.; Stidham, S. Stability and Chaos in input pricing for a service facility with adaptive customer response to congestion. Manag. Sci. 1998, 44, 246–261. [Google Scholar] [CrossRef]
- Ilk, N.; Shang, G.; Fan, S.; Zhao, J.L. Stability of transaction fees in Bitcoin: A supply and demand perspective. MIS Q. 2021, 45, 563–692. [Google Scholar] [CrossRef]
- Sarafopoulos, G.; Papadopoulos, K. Complexity of a Bertrand duopoly game with homogeneous expectations, quadratic cost functions and chaos control. IFAC-Papers OnLine 2021, 54, 41–46. [Google Scholar] [CrossRef]
- Askar, S.S.; Al-Khedhairi, A. A Remanufacturing duopoly game based on a piecewise nonlinear map: Analysis and Investigations. Int. J. Nonlin. Sci. Num. 2020, 21, 549–561. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Zhou, W.; Chu, T.; Chu, Y.D.; Yu, J.N. Complex dynamics analysis for a two-stage Cournot duopoly game of semi-collusion in production. Nonlinear Dyn. 2018, 91, 819–835. [Google Scholar] [CrossRef]
- Long, J.; Zhao, H. Stability of equilibrium prices in a dynamic duopoly Bertrand game with asymmetric information and cluster spillovers. Int. J. Bifurcat. Chaos 2021, 31, 2150240. [Google Scholar] [CrossRef]
- Li, W.N.; Elsadany, A.; Zhou, W.; Zhu, Y.-L. Global analysis, multi-stability and synchronization in a competition model of public enterprises with consumer surplus. Chaos Solitons Fractals 2021, 143, 110604. [Google Scholar] [CrossRef]
- Li, H.; Zhou, W.; A Elsadany, A.; Chu, T. Stability, multi-stability and instability in Cournot duopoly game with knowledge spillover effects and relative profit maximization. Chaos Solitons Fractals 2021, 146, 110936. [Google Scholar] [CrossRef]
- Awad, A.M.; Askar, S.S.; Elsadany, A.A. Complex dynamics investigations of a mixed Bertrand duopoly game: Synchronization and global analysis. Nonlinear Dyn. 2022, 107, 3983–3999. [Google Scholar] [CrossRef]
- Kabir, K.M.A.; Kuga, K.; Tanimoto, J. The impact of information spreading on epidemic vaccination game dynamics in a heterogeneous complex network-A theoretical approach. Chaos Solitons Fractals 2019, 132, 960–979. [Google Scholar] [CrossRef]
- Gao, Q.; Ma, J.H. Chaos and Hopf bifurcation of a finance system. Nonlinear Dyn. 2009, 58, 209–216. [Google Scholar] [CrossRef]
- Shi, J.; He, K.; Fang, H. Chaos, Hopf bifurcation and control of a fractional-order delay financial system. Math. Comput. Simul. 2022, 194, 248–364. [Google Scholar] [CrossRef]
- Li, P.; Yan, J.; Xu, C.; Gao, R.; Li, Y. Understanding dynamics and bifurcation control mechanism for a fractional-order delayed duopoly game model in insurance market. Fractal Fract. 2022, 6, 270. [Google Scholar] [CrossRef]
- Peng, Y.; Lu, Q. Complex dynamics analysis for a duopoly Stackelberg game model with bounded rationality. Appl. Math. Comput. 2015, 271, 259–268. [Google Scholar] [CrossRef]
- Global IT Industry Outlook 2020. Available online: http://m.thepaper.cn/baijiahao_4917518 (accessed on 8 November 2019).


| Step | Details |
|---|---|
| ① Data Format | Data from Web of Science is exported as “text file”. |
| ② Data pre-processing | Delete duplicate literature. |
| ③ Data conversion | Import data to “CiteSpace 6.1.R6” software, and execute “conversion” command. |
| ④ Data analysis, data visualization, manual summarization | Clustering, hot keywords and their co-occurrence keywords, research logic analysis. |
| Cluster Label | Cluster Explanation |
|---|---|
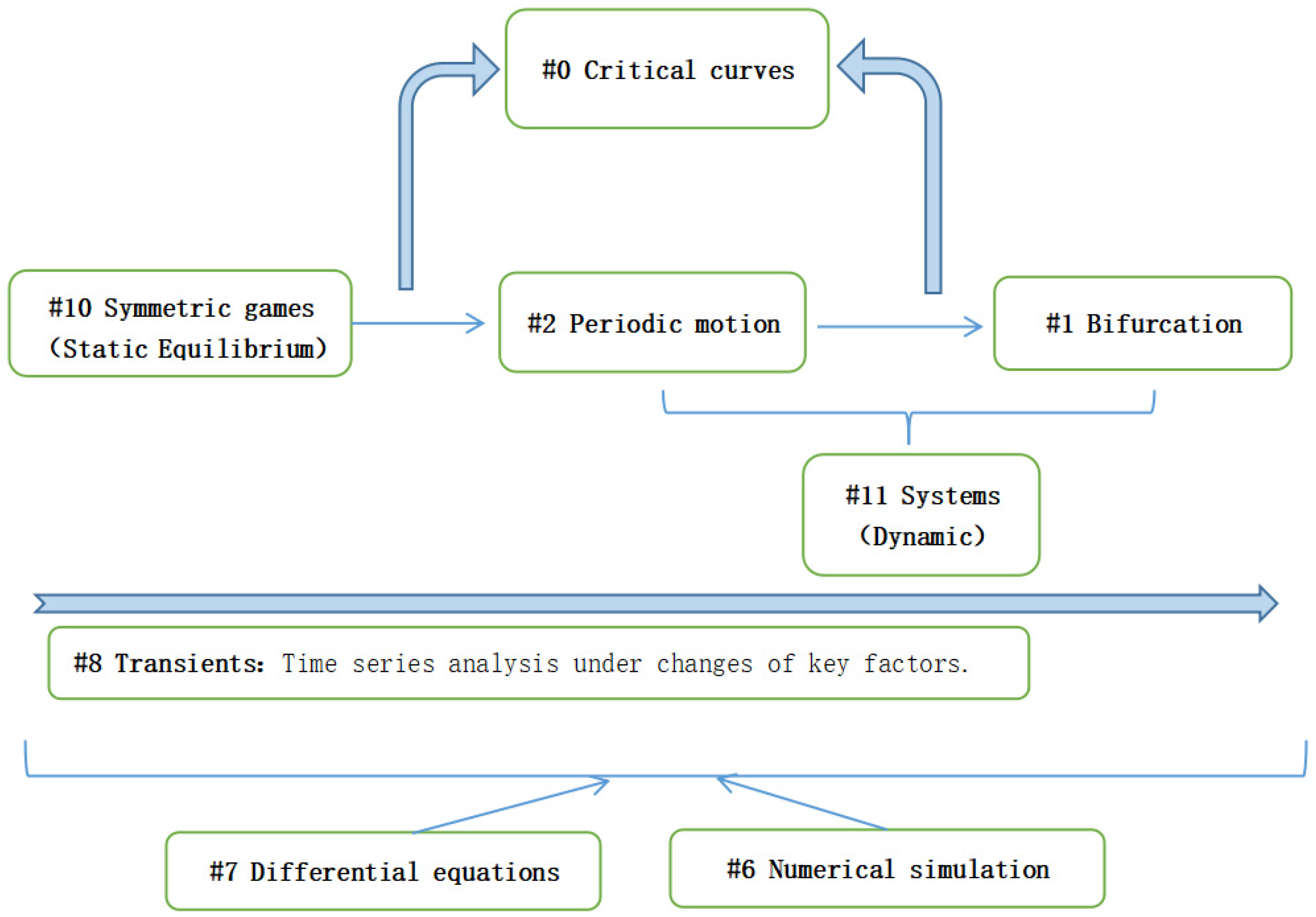
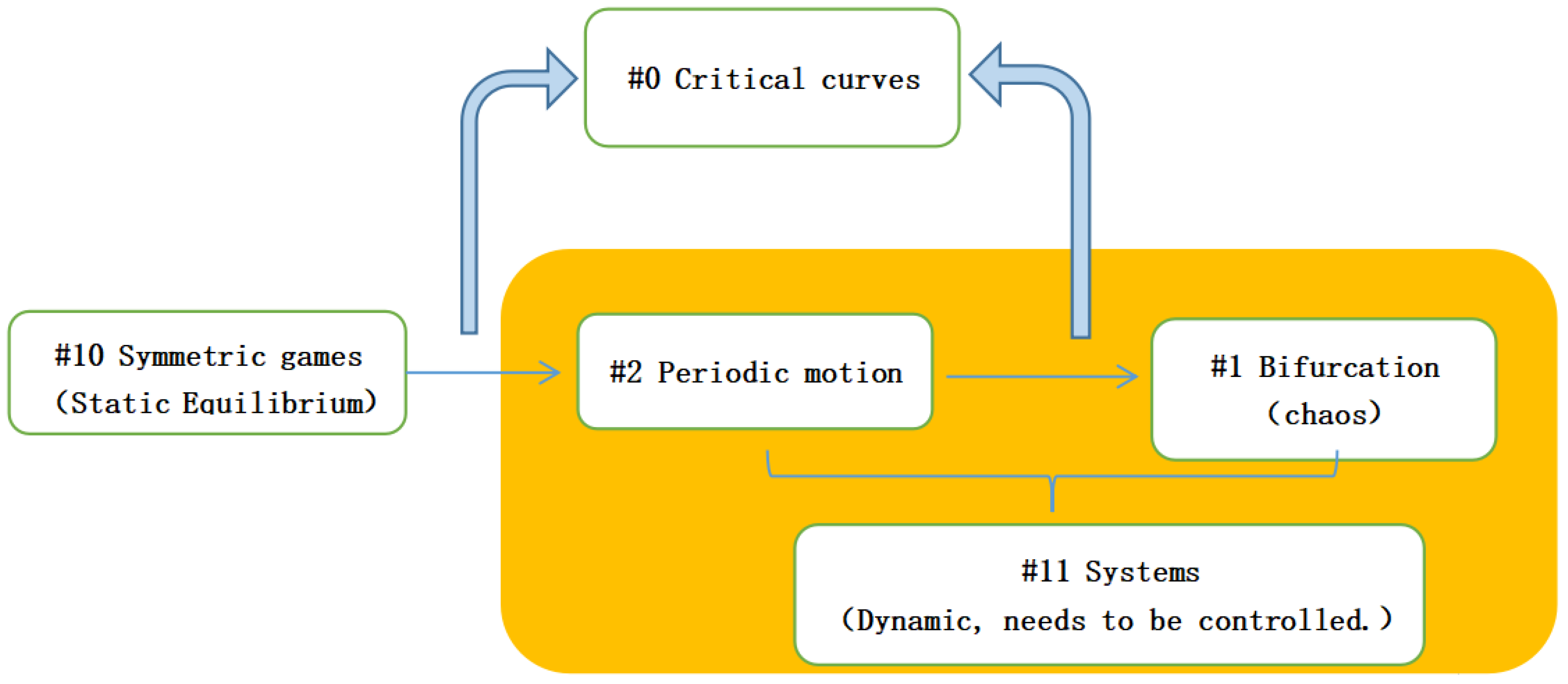
| #0 Critical curves | Calculate the boundaries of equilibrium, period, and chaos. |
| #1 Bifurcation | #3 Neimark–Sacker bifurcation#5 bifurcation and chaos#4 Hopf bifurcation |
| #2 Periodic motion | Periodic characteristics of economic fluctuations. |
| #6 Numerical simulation | Dynamic systems, periodic fluctuations, bifurcation, and chaos were analyzed by numerical simulation. |
| #7 Differential equations | The economic iterative models were built through differential equations. |
| #8 Transients | Instantaneous dynamics of system through time series methods. |
| #10 Symmetric games | Calculating static Nash equilibrium through symmetry games. |
| #11 Systems | Dynamic Systems. |
| Type | Application Fields |
|---|---|
| Hopf bifurcation | Finance system [42]; Macroeconomics ISLM model [23]; Money supply [24]; Delay, Price game [9]; Financial Risks [43]; Insurance industry [44]. |
| Flip bifurcation | Oligopoly game of semi-collusion in production [36]; The oligopoly game considering consumer surplus [10]; Stackelberg game [45]. |
| Tangential bifurcation | Sticky price [11]. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, F.; Ma, J. Research Trend, Logical Structure and Outlook on Complex Economic Game. Mathematics 2023, 11, 1179. https://doi.org/10.3390/math11051179
Wu F, Ma J. Research Trend, Logical Structure and Outlook on Complex Economic Game. Mathematics. 2023; 11(5):1179. https://doi.org/10.3390/math11051179
Chicago/Turabian StyleWu, Fang, and Junhai Ma. 2023. "Research Trend, Logical Structure and Outlook on Complex Economic Game" Mathematics 11, no. 5: 1179. https://doi.org/10.3390/math11051179
APA StyleWu, F., & Ma, J. (2023). Research Trend, Logical Structure and Outlook on Complex Economic Game. Mathematics, 11(5), 1179. https://doi.org/10.3390/math11051179







