Investigation of Size-Dependent Vibration Behavior of Piezoelectric Composite Nanobeams Embedded in an Elastic Foundation Considering Flexoelectricity Effects
Abstract
1. Introduction
2. Theory and Mathematical Formulation
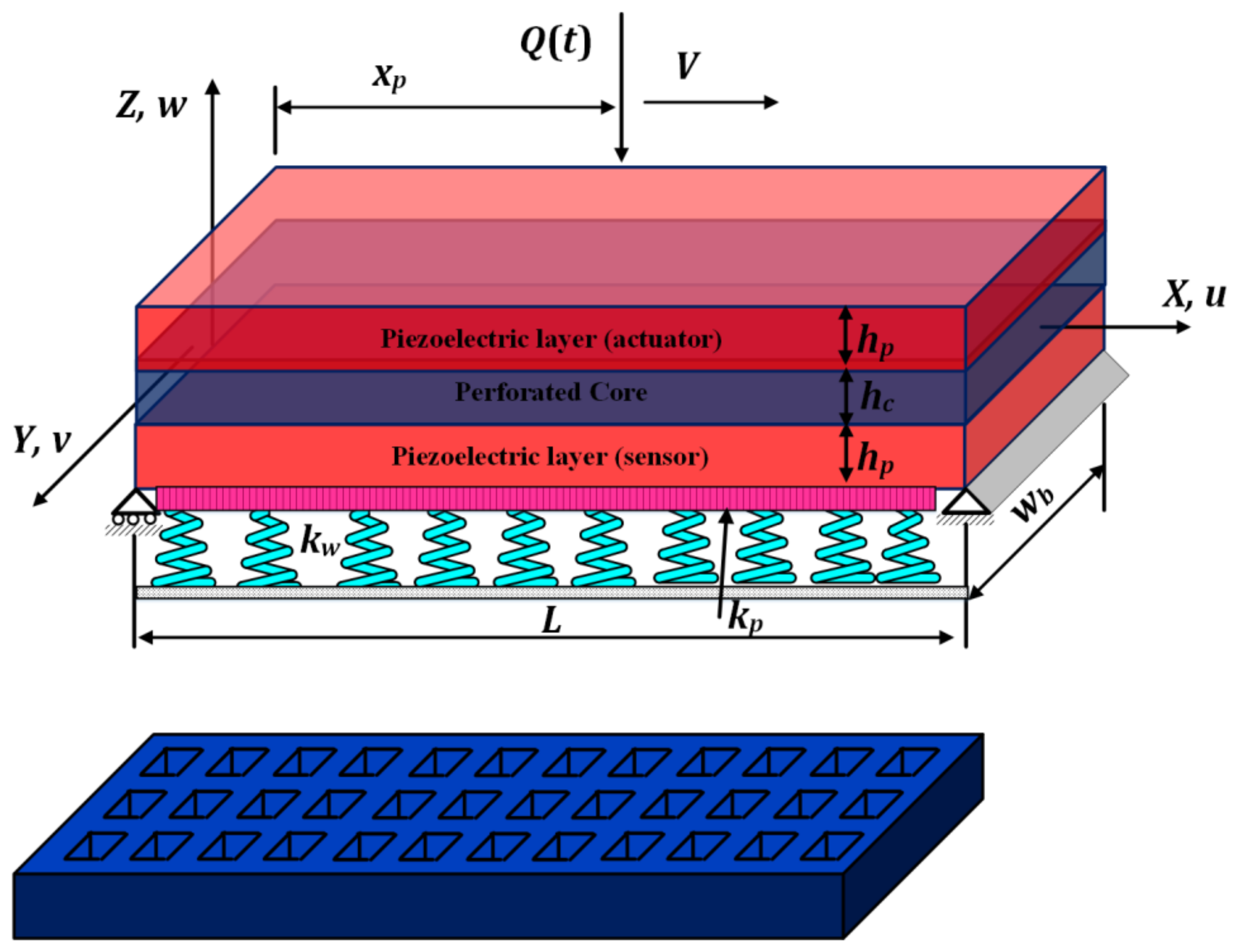
2.1. Geometrical Model for Regular Squared Cutouts
2.2. Basic Elastic and Flexoelectric Kinematic Relations
2.3. The Modified Nonlocal Strain Gradient Theory with Flexoelectricity Effect
3. Dynamic Equation of Motion of Piezoelectric Composite Nanobeam
4. Analytical Solution Methodology
5. Numerical Results and Discussion
5.1. Verification of the Developed Methodology for Free Vibration Analysis
5.2. Parametric Studies
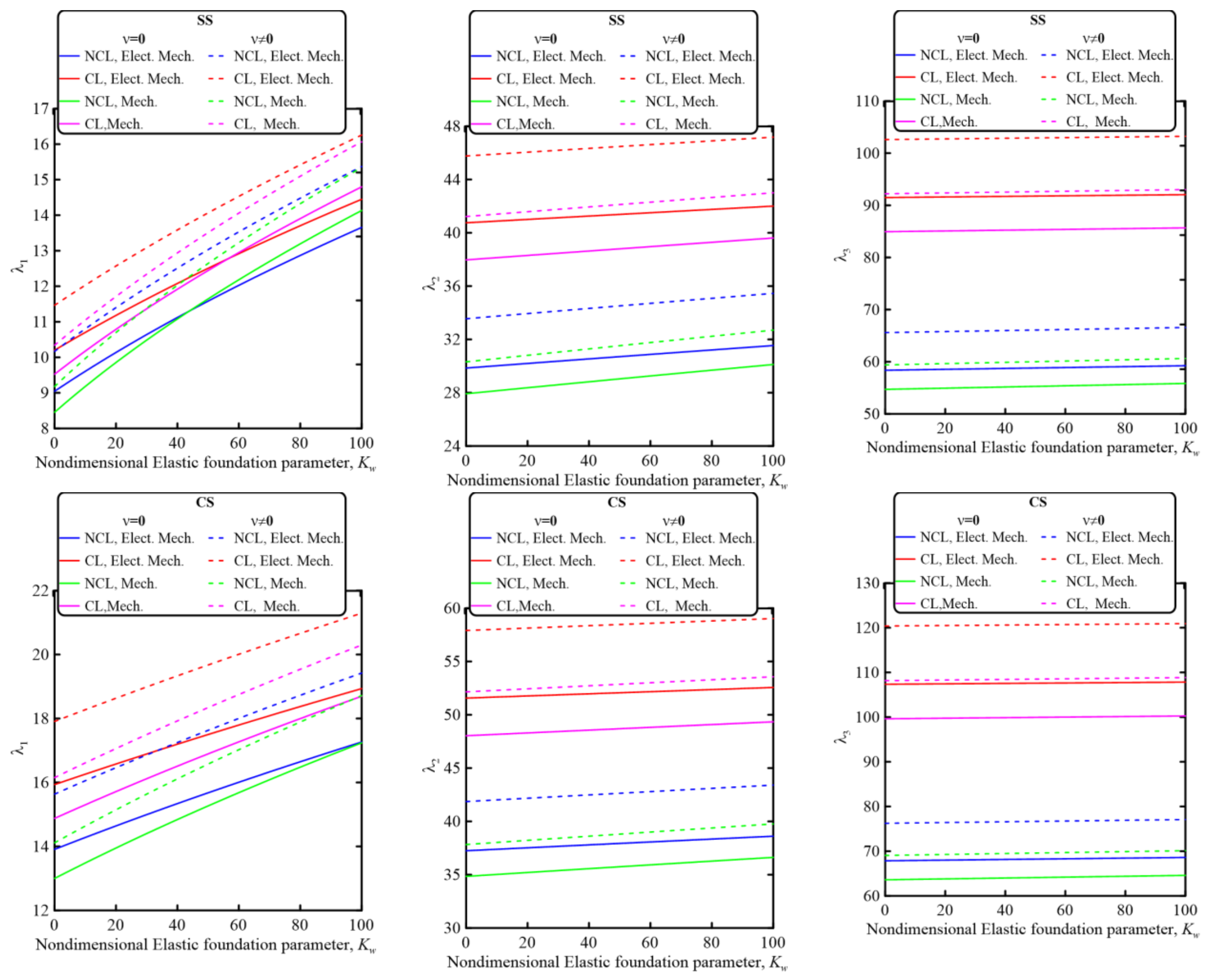
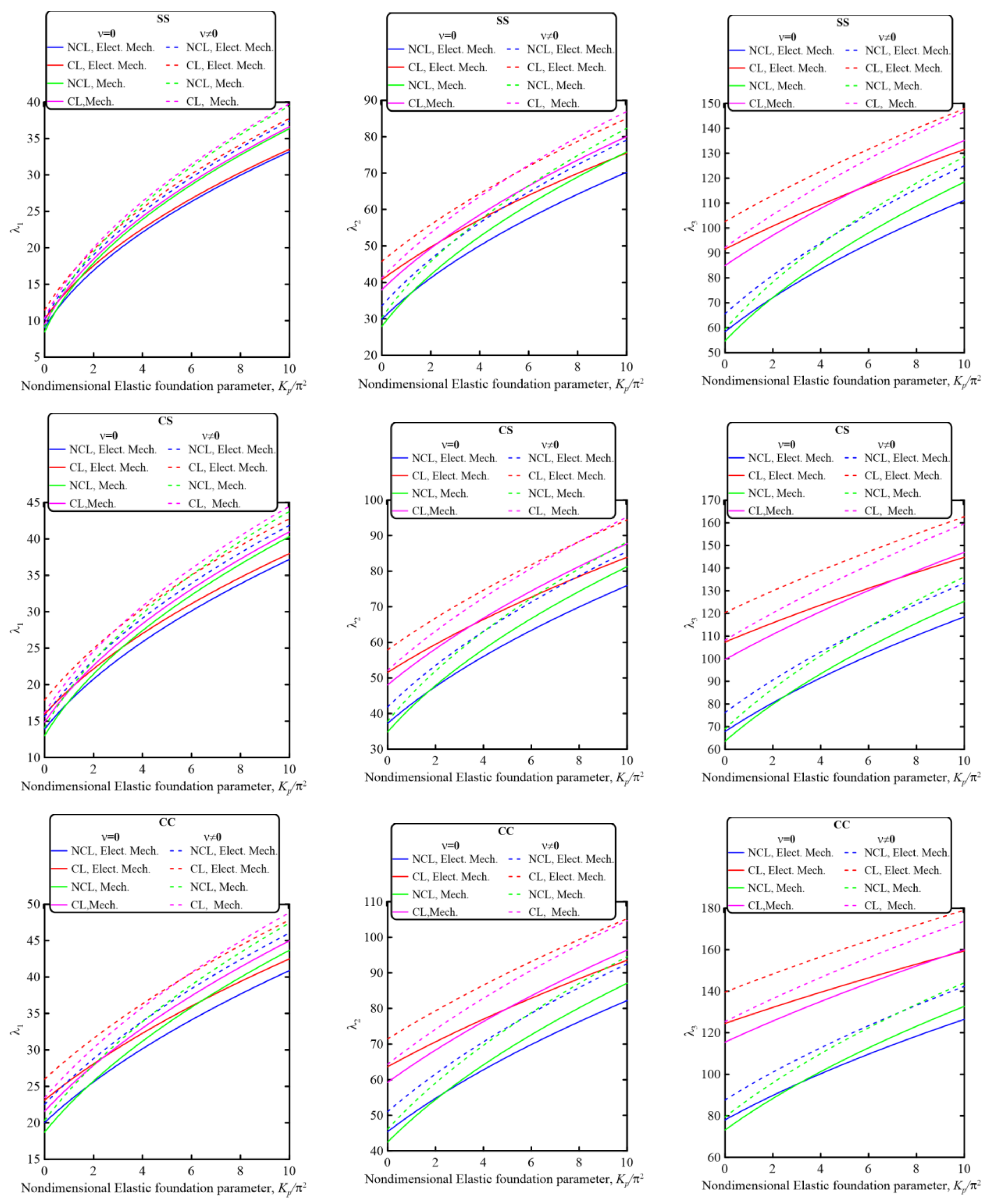
5.2.1. Effect of the Nondimensional Elastic Foundation Parameters, Kw and Kp
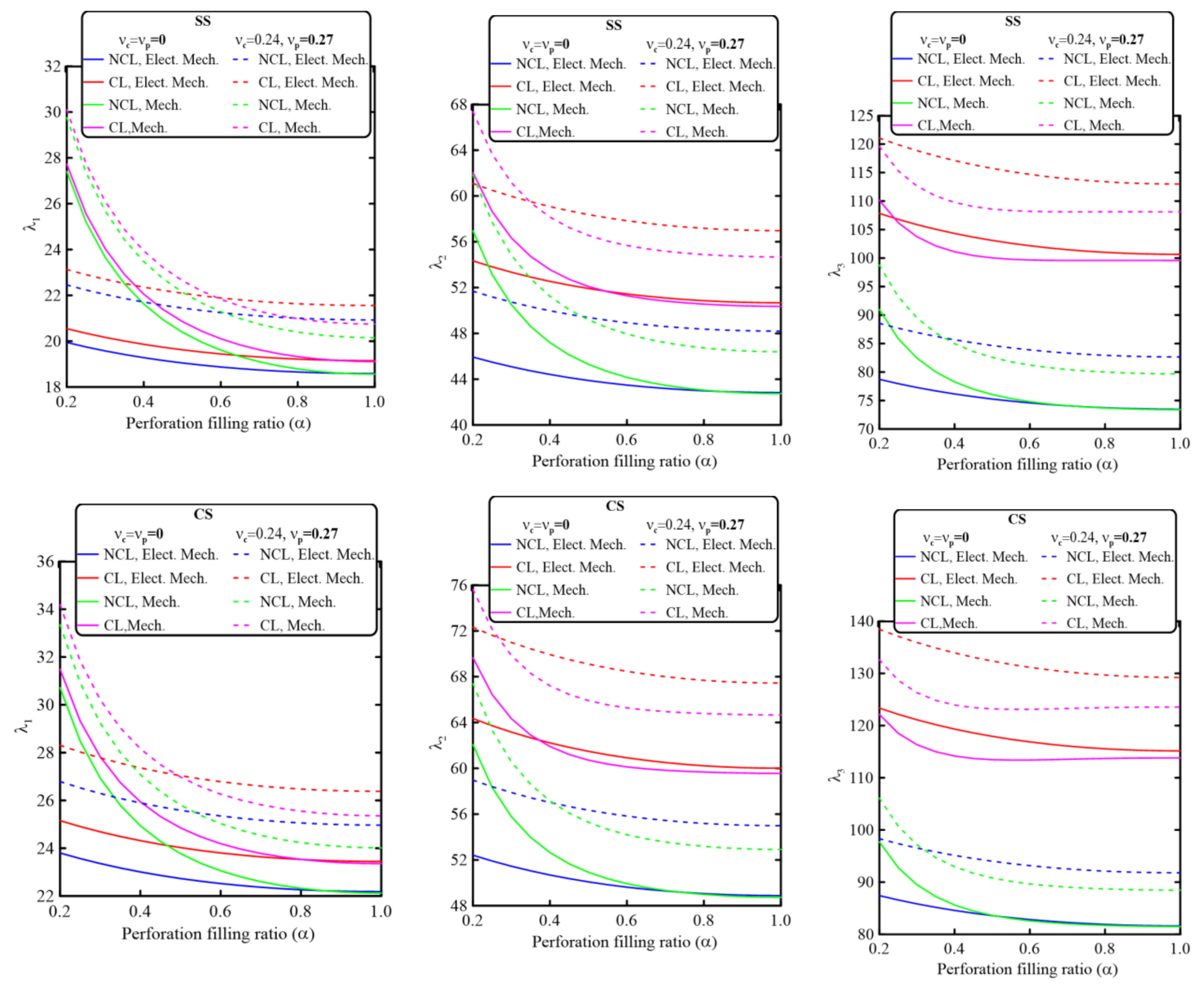
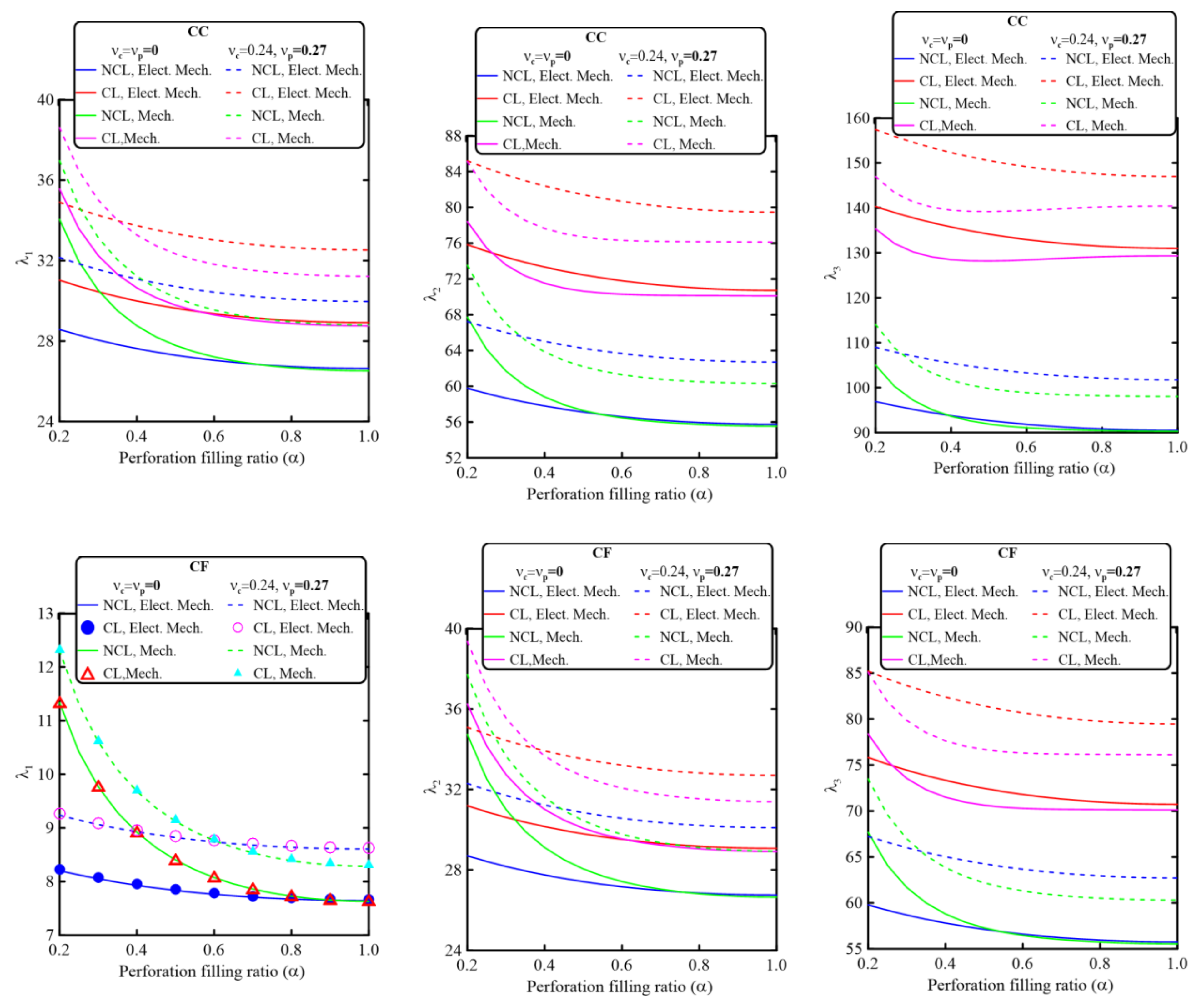
5.2.2. Effect of the Perforation Filling Ratio, α
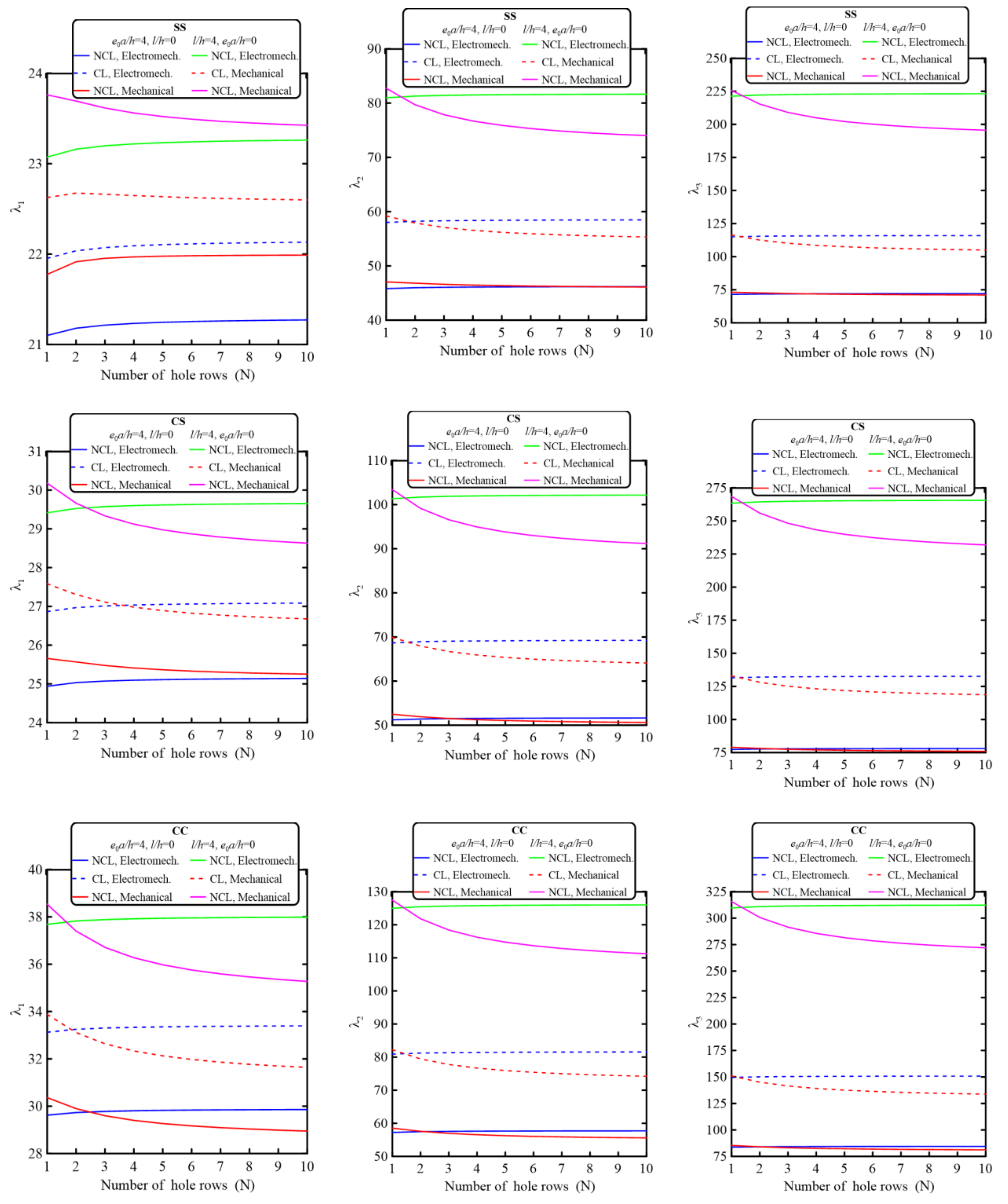
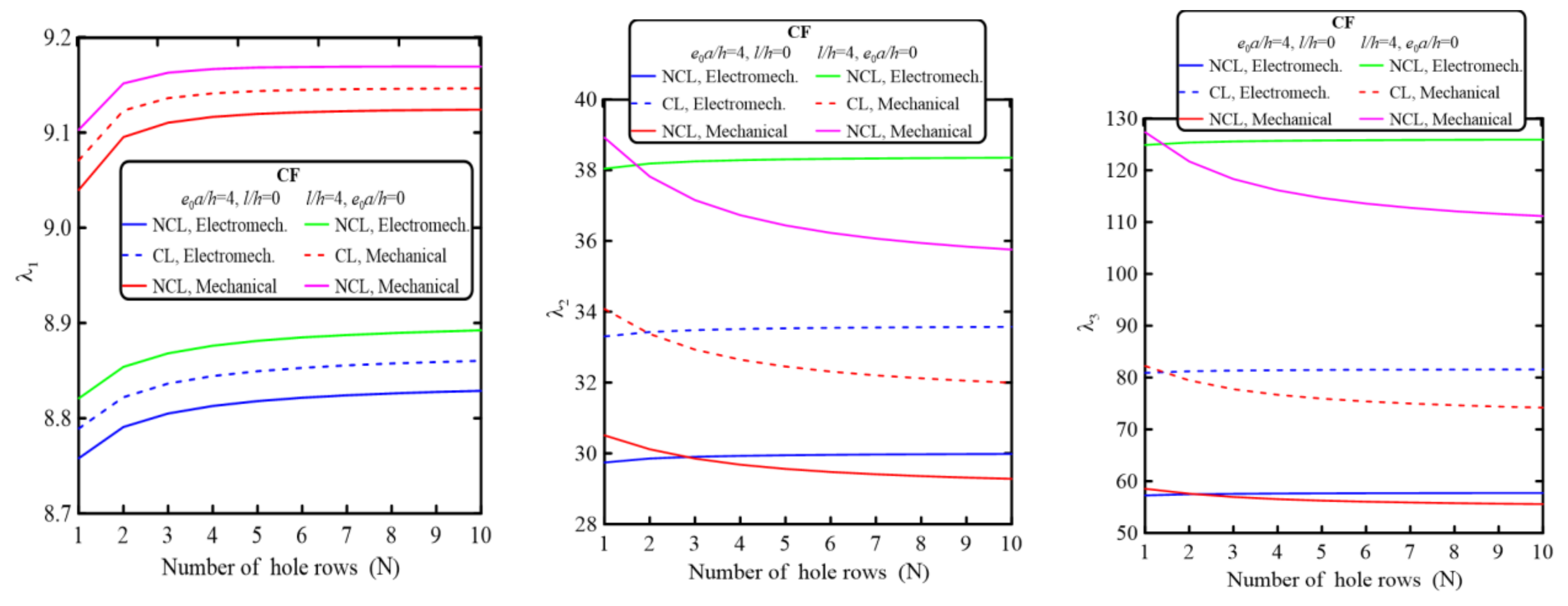
5.2.3. Effect of the Number of Hole Rows, N
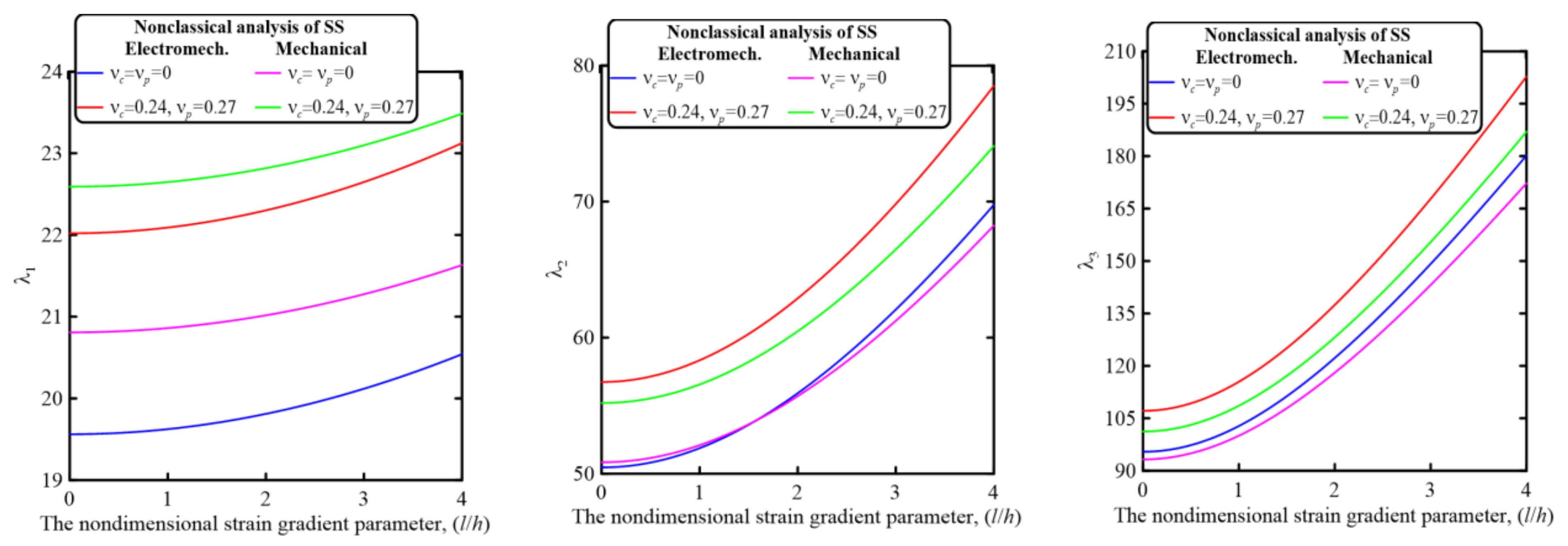
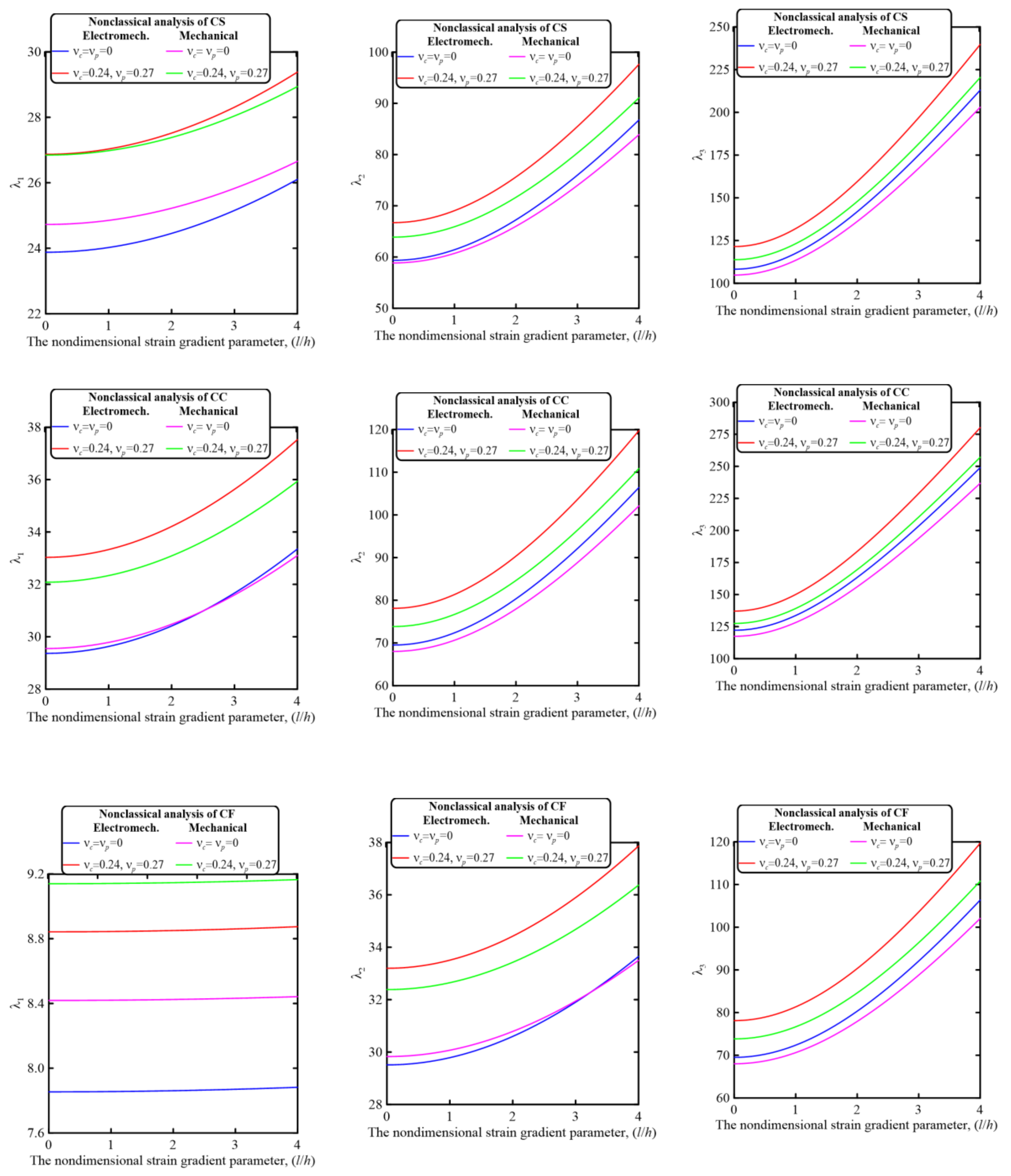
5.2.4. Effect of the Nondimensional Strain Gradient Parameter, (l/h)
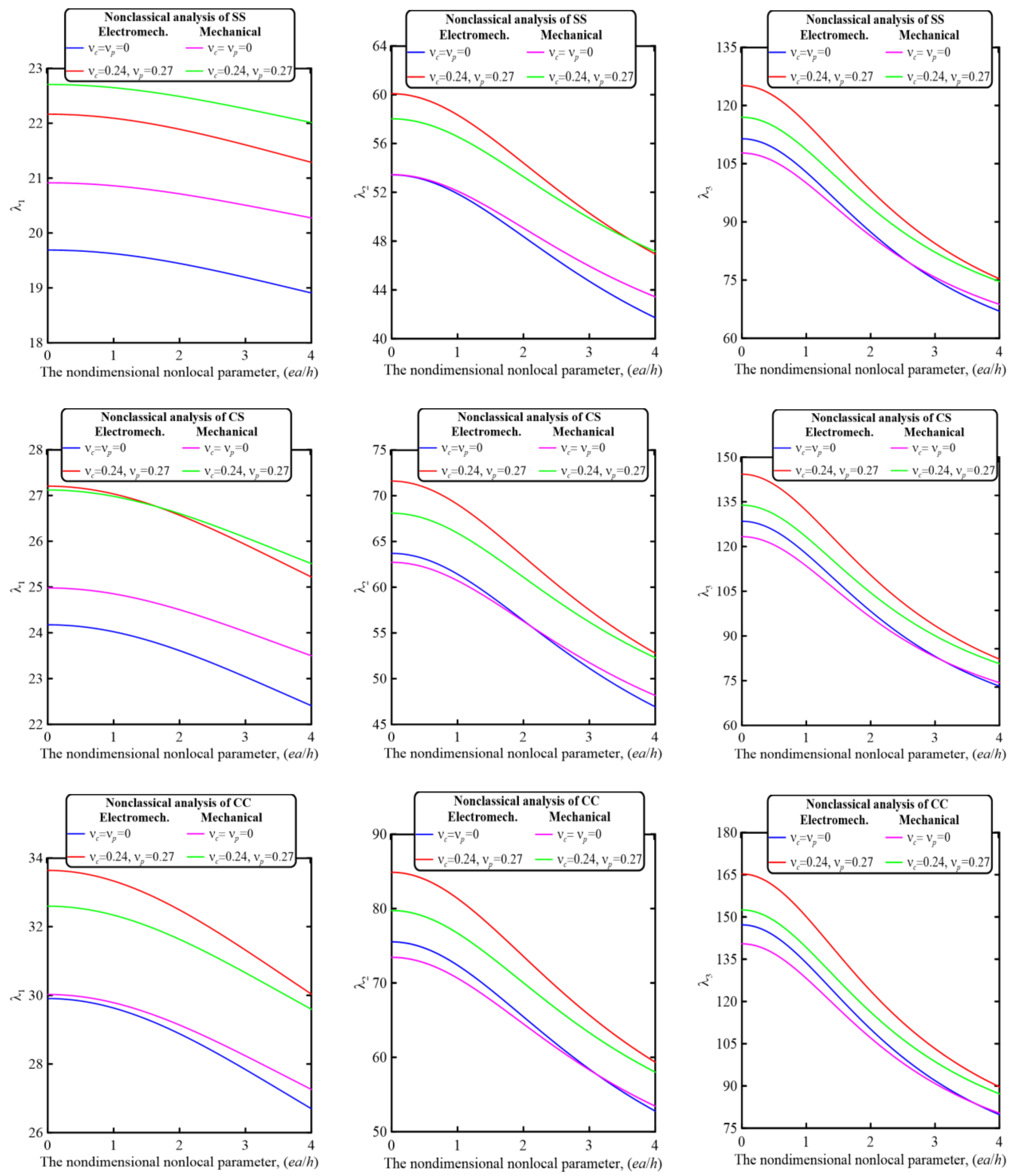
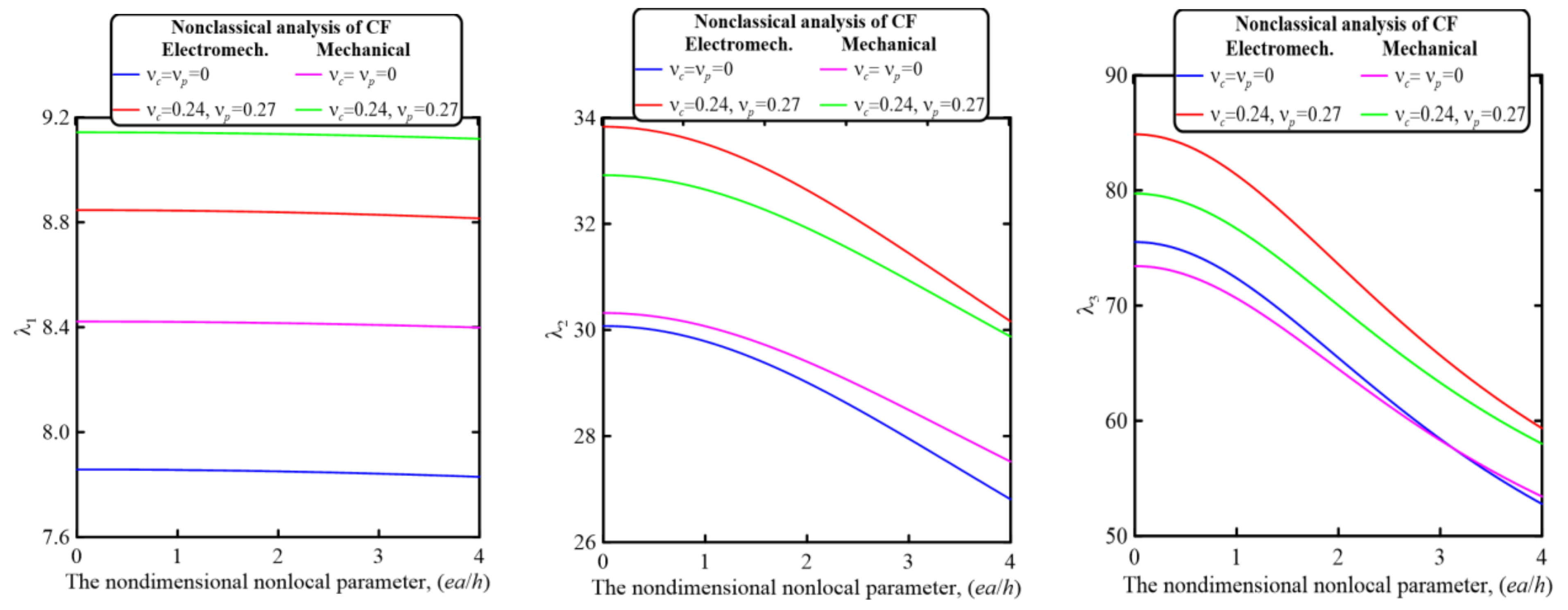
5.2.5. Effect of the Nondimensional Nonlocal Parameter, (ea/h)
5.2.6. Effect of the Piezoelectric Coefficient, (e311)
5.2.7. Effect of Electric Field Strain Gradient Coupling Coefficient, (μ3111)
6. Conclusions
- ➢
- The elastic foundation significantly affects the electromechanical as well as the mechanical dynamic behavior of piezoelectrically layered perforated nanobeams embedded in an elastic media. The resonant frequencies and, consequently, the dynamic behavior could be controlled by controlling the elastic foundation parameters.
- ➢
- The electromechanical resonant frequencies of piezoelectrically layered perforated nanobeams are increased with increasing the elastic foundation parameters due to increasing the overall system stiffness.
- ➢
- The electromechanical vibration behavior is more sensitive to increasing the elastic foundation parameter, Kp, compared with increasing Kw.
- ➢
- The electromechanical and mechanical dynamic behaviors of piezoelectric composite nanobeams are significantly affected by the material Poisson’s ratio. Ignoring the effect of the material Poisson’s ratio leads to underestimates of the nondimensional frequency parameters.
- ➢
- Perforation configuration and parameters have significant effects on the electromechanical and mechanical dynamic behavior of piezoelectrically layered perforated nanobeams. Both electromechanical and mechanical vibration behaviors could be controlled by controlling the geometrical parameters of the perforation configuration.
- ➢
- The nonclassical material parameters significantly affect the electromechanical as well as mechanical vibration behavior of piezoelectrically layered perforated nanobeam embedded in an elastic media. Both softening and stiffening effects could be incorporated by applying the modified nonlocal strain gradient theory. Incorporation of the strain gradient effect produces a stiffening effect, while the introduction of the nonlocality effect results in a softening effect.
- ➢
- The electromechanical vibration behavior could be controlled by controlling the piezoelectricity as well as flexoelectricity parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bagheri, R.; Tadi Beni, Y. On the size-dependent nonlinear dynamics of viscoelastic/flexoelectric nanobeams. J. Vib. Control 2021, 27, 2018–2033. [Google Scholar] [CrossRef]
- Liang, X.; Hu, S.; Shen, S. Effects of surface and flexoelectricity on a piezoelectric nanobeam. Smart Mater. Struct. 2014, 23, 035020. [Google Scholar] [CrossRef]
- Bhaskar, U.K.; Banerjee, N.; Abdollahi, A.; Wang, Z.; Schlom, D.G.; Rijnders, G.; Catalan, G. A flexoelectric microelectromechanical system on silicon. Nat. Nanotechnol. 2016, 11, 263–266. [Google Scholar] [CrossRef] [PubMed]
- Baroudi, S.; Najar, F.; Jemai, A. Static and dynamic analytical coupled field analysis of piezoelectric flexoelectric nanobeams: A strain gradient theory approach. Int. J. Solids Struct. 2018, 135, 110–124. [Google Scholar] [CrossRef]
- Chu, L.; Dui, G.; Ju, C. Flexoelectric effect on the bending and vibration responses of functionally graded piezoelectric nanobeams based on general modified strain gradient theory. Compos. Struct. 2018, 186, 39–49. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Karimiasl, M. Nonlocal and surface effects on the buckling behavior of flexoelectric sandwich nanobeams. Mech. Adv. Mater. Struct. 2018, 25, 943–952. [Google Scholar] [CrossRef]
- Wang, K.F.; Wang, B.L.; Zeng, S. Analysis of an array of flexoelectric layered nanobeams for vibration energy harvesting. Compos. Struct. 2018, 187, 48–57. [Google Scholar] [CrossRef]
- Shijie, Z.; Xie, Z.; Wang, H. Theoretical and finite element modeling of piezoelectric nanobeams with surface and flexoelectricity effects. Mech. Adv. Mater. Struct. 2019, 26, 1261–1270. [Google Scholar] [CrossRef]
- Basutkar, R. Analytical modelling of a nanoscale series-connected bimorph piezoelectric energy harvester incorporating the flexoelectric effect. Int. J. Eng. Sci. 2019, 139, 42–61. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Omar, F.A.; Abdalla, W.S.; Kabeel, A.M.; Alshorbagy, A.E. Mechanical analysis of cutout piezoelectric nonlocal nanobeam including surface energy effects. Struct. Eng. Mech. 2020, 76, 141–151. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Omar, F.A.; Abdraboh, A.M.; Abdalla, W.S.; Alshorbagy, A.E. Mechanical behaviors of piezoelectric nonlocal nanobeam with cutouts. Smart Struct. Syst. 2020, 25, 219–228. [Google Scholar] [CrossRef]
- Zhao, X.; Zheng, S.; Li, Z. Effects of porosity and flexoelectricity on static bending and free vibration of AFG piezoelectric nanobeams. Thin-Walled Struct. 2020, 151, 106754. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. On the dynamics of a visco–piezo–flexoelectric nanobeam. Symmetry 2020, 12, 643. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. On nonlinear bending study of a piezo-flexomagnetic nanobeam based on an analytical-numerical solution. Nanomaterials 2020, 10, 1762. [Google Scholar] [CrossRef]
- Malikan, M. Electro-mechanical shear buckling of piezoelectric nanoplate using modified couple stress theory based on simplified first order shear deformation theory. Appl. Math. Model. 2017, 48, 196–207. [Google Scholar] [CrossRef]
- Malikan, M.; Eremeyev, V.A. Flexomagnetic response of buckled piezomagnetic composite nanoplates. Compos. Struct. 2021, 267, 113932. [Google Scholar] [CrossRef]
- Esen, I.; Abdelrhmaan, A.A.; Eltaher, M.A. Free vibration and buckling stability of FG nanobeams exposed to magnetic and thermal fields. Eng. Comput. 2022, 38, 3463–3482. [Google Scholar] [CrossRef]
- Esen, I.; Özarpa, C.; Eltaher, M.A. Free vibration of a cracked FG microbeam embedded in an elastic matrix and exposed to magnetic field in a thermal environment. Compos. Struct. 2021, 261, 113552. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Liu, Y.F.; Yang, T.H. Nonlinear thermo-electro-mechanical vibration of functionally graded piezoelectric nanoshells on Winkler–Pasternak foundations via nonlocal Donnell’s nonlinear shell theory. Int. J. Struct. Stab. Dyn. 2019, 19, 1950100. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Chu, F. Nonlinear forced vibrations of functionally graded piezoelectric cylindrical shells under electric-thermo-mechanical loads. Int. J. Mech. Sci. 2021, 201, 106474. [Google Scholar] [CrossRef]
- Liu, Y.; Qin, Z.; Chu, F. Nonlinear forced vibrations of FGM sandwich cylindrical shells with porosities on an elastic substrate. Nonlinear Dyn. 2021, 104, 1007–1021. [Google Scholar] [CrossRef]
- Gao, W.; Liu, Y.; Qin, Z.; Chu, F. Wave propagation in smart sandwich plates with functionally graded nanocomposite porous core and piezoelectric layers in multi-physics environment. Int. J. Appl. Mech. 2022, 14, 2250071. [Google Scholar] [CrossRef]
- Melaibari, A.; Abdelrahman, A.A.; Hamed, M.A.; Abdalla, A.W.; Eltaher, M.A. Dynamic Analysis of a Piezoelectrically Layered Perforated Nonlocal Strain Gradient Nanobeam with Flexoelectricity. Mathematics 2022, 10, 2614. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S.; Mahesh, V.; Harursampath, D.; Sedighi, H.M. A novel numerical approach for the stability of nanobeam exposed to hygro-thermo-magnetic environment embedded in elastic foundation. ZAMM-J. Appl. Math. Mech. 2022, 102, e202100380. [Google Scholar] [CrossRef]
- Sun, R.; Liu, D.; Yan, Z. A finite element approach for flexoelectric nonuniform nanobeam energy harvesters. Mech. Adv. Mater. Struct. 2022, 1–12. [Google Scholar] [CrossRef]
- Thai, T.Q.; Zhuang, X.; Rabczuk, T. Curved flexoelectric and piezoelectric micro-beams for nonlinear vibration analysis of energy harvesting. Int. J. Solids Struct. 2023, 264, 112096. [Google Scholar] [CrossRef]
- Momeni-Khabisi, H.; Tahani, M. Coupled thermal stability analysis of piezomagnetic nano-sensors and nano-actuators considering the flexomagnetic effect. Eur. J. Mech. A/Solids 2023, 97, 104773. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S.; Tornabene, F. Dynamical behavior of nanobeam embedded in constant, linear, parabolic, and sinusoidal types of Winkler elastic foundation using first-order nonlocal strain gradient model. Mater. Res. Express 2019, 6, 0850f2. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S. Dynamic analysis of single-layered graphene nano-ribbons (SLGNRs) with variable cross-section resting on elastic foundation. Curved Layer. Struct. 2019, 6, 132–145. [Google Scholar] [CrossRef]
- Jena, S.K.; Chakraverty, S.; Malikan, M.; Mohammad-Sedighi, H. Hygro-magnetic vibration of the single-walled carbon nanotube with nonlinear temperature distribution based on a modified beam theory and nonlocal strain gradient model. Int. J. Appl. Mech. 2020, 12, 2050054. [Google Scholar] [CrossRef]
- Malikan, M.; Krasheninnikov, M.; Eremeyev, V.A. Torsional stability capacity of a nano-composite shell based on a nonlocal strain gradient shell model under a three-dimensional magnetic field. Int. J. Eng. Sci. 2020, 148, 103210. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Rabczuk, T. Dynamics of two-dimensional functionally graded tapered Timoshenko nanobeam in thermal environment using nonlocal strain gradient theory. Compos. Part B Eng. 2020, 182, 107622. [Google Scholar] [CrossRef]
- Chakraverty, S.; Jena, S.K. Free vibration of single walled carbon nanotube resting on exponentially varying elastic foundation. Curved Layer. Struct. 2018, 5, 260–272. [Google Scholar] [CrossRef]
- Abdelrahman, A.A.; Esen, I.; Daikh, A.A.; Eltaher, M.A. Dynamic analysis of FG nanobeam reinforced by carbon nanotubes and resting on elastic foundation under moving load. Mech. Based Des. Struct. Mach. 2021, 1–24. [Google Scholar] [CrossRef]
- Tocci Monaco, G.; Fantuzzi, N.; Fabbrocino, F.; Luciano, R. Trigonometric solution for the bending analysis of magneto-electro-elastic strain gradient nonlocal nanoplates in hygro-thermal environment. Mathematics 2021, 9, 567. [Google Scholar] [CrossRef]
- Ghandourah, E.E.; Daikh, A.A.; Alhawsawi, A.M.; Fallatah, O.A.; Eltaher, M.A. Bending and Buckling of FG-GRNC Laminated Plates via Quasi-3D Nonlocal Strain Gradient Theory. Mathematics 2022, 10, 1321. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Esen, I.; Abdelrahman, A.A.; Abdraboh, A.M.; Eltaher, M.A. Dynamic analysis of functionally graded (FG) nonlocal strain gradient nanobeams under thermo-magnetic fields and moving load. Adv. Nano Res. 2022, 12, 231–251. [Google Scholar] [CrossRef]
- Alam, M.; Mishra, S.K. A boundary layer solution for the post-critical thermo-electro-mechanical stability of nonlocal-strain gradient Functionally Graded Piezoelectric cylindrical shells. Eur. J. Mech. A/Solids 2023, 97, 104836. [Google Scholar] [CrossRef]
- Boyina, K.; Piska, R. Wave propagation analysis in viscoelastic Timoshenko nanobeams under surface and magnetic field effects based on nonlocal strain gradient theory. Appl. Math. Comput. 2023, 439, 127580. [Google Scholar] [CrossRef]
- Luschi, L.; Pieri, F. An analytical model for the determination of resonance frequencies of perforated beams. J. Micromech. Microeng. 2014, 24, 055004. [Google Scholar] [CrossRef]
- Abdelrahman, A.A.; Eltaher, M.A. On bending and buckling responses of perforated nanobeams including surface energy for different beams theories. Eng. Comput. 2022, 38, 2385–2411. [Google Scholar] [CrossRef]
- Zeng, S.; Wang, K.; Wang, B.; Wu, J. Vibration analysis of piezoelectric sandwich nanobeam with flexoelectricity based on nonlocal strain gradient theory. Appl. Math. Mech. 2020, 41, 859–880. [Google Scholar] [CrossRef]
- Eftekhari, S.A.; Toghraie, D. Vibration and dynamic analysis of a cantilever sandwich microbeam integrated with piezoelectric layers based on strain gradient theory and surface effects. Appl. Math. Comput. 2022, 419, 126867. [Google Scholar] [CrossRef]
- Abdelrahman, A.A.; Mohamed, N.A.; Eltaher, M.A. Static bending of perforated nanobeams including surface energy and microstructure effects. Eng. Comput. 2022, 38, 415–435. [Google Scholar] [CrossRef]
- Mehralian, F.; Beni, Y.T. Vibration analysis of size-dependent bimorph functionally graded piezoelectric cylindrical shell based on nonlocal strain gradient theory. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 1–15. [Google Scholar] [CrossRef]
- Abdelrahman, A.A.; Eltaher, M.A.; Kabeel, A.M.; Abdraboh, A.M.; Hendi, A.A. Free and forced analysis of perforated beams. Steel Compos. Struct. 2019, 31, 489–502. [Google Scholar] [CrossRef]
- Eltaher, M.A.; Mohamed, N.; Mohamed, S.A.; Seddek, L.F. Periodic and nonperiodic modes of postbuckling and nonlinear vibration of beams attached to nonlinear foundations. Appl. Math. Model. 2019, 75, 414–445. [Google Scholar] [CrossRef]
- Chanthanumataporn, S.; Watanabe, N. Free vibration of a light sandwich beam accounting for ambient air. J. Vib. Control 2018, 24, 3658–3675. [Google Scholar] [CrossRef]
- Ke, L.L.; Wang, Y.S.; Wang, Z.D. Nonlinear vibration of the piezoelectric nanobeams based on the nonlocal theory. Compos. Struct. 2012, 94, 2038–2047. [Google Scholar] [CrossRef]
- Chen, W.Q.; Lü, C.F.; Bian, Z.G. A mixed method for bending and free vibration of beams resting on a Pasternak elastic foundation. Appl. Math. Model. 2004, 28, 877–890. [Google Scholar] [CrossRef]
- De Rosa, M.A.; Maurizi, M.J. The influence of concentrated masses and Pasternak soil on the free vibrations of Euler beams—Exact solution. J. Sound Vib. 1998, 212, 573–581. [Google Scholar] [CrossRef]



| L/ht | Kw | SS | CC | CS | CF | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Present | Ref [49] | Ref [44] | Present | Ref [44] | Present | Ref [49] | Ref [44] | Present | Ref [44] | ||
| 6 | 0 | 0.4519 | 0.4570 | 0.4571 | 1.0149 | 1.0245 | 0.7012 | 0.7077 | 0.7087 | 0.1699 | 0.1714 |
| 102 | 0.6562 | -------- | -------- | -------- | -------- | 0.8454 | -------- | -------- | 0.5098 | -------- | |
| 104 | 4.7786 | -------- | -------- | -------- | -------- | 4.7996 | -------- | -------- | 4.8095 | -------- | |
| 8 | 0 | 0.3406 | 0.3428 | 0.3428 | 0.7644 | 0.7684 | 0.5284 | 0.5310 | 0.5315 | 0.1274 | 0.1285 |
| 102 | 0.4945 | -------- | -------- | 0.8424 | -------- | 0.6377 | -------- | -------- | 0.3825 | -------- | |
| 104 | 3.6016 | -------- | -------- | 3.6602 | -------- | 3.6203 | -------- | -------- | 3.6087 | -------- | |
| 10 | 0 | 0.2731 | 0.2742 | 0.2742 | 0.6127 | 0.6167 | 0.4236 | 0.4250 | 0.4252 | 0.1020 | 0.1028 |
| 102 | 0.3965 | -------- | -------- | 0.6758 | -------- | 0.5115 | -------- | -------- | 0.306 | -------- | |
| 104 | 2.8879 | -------- | -------- | 2.9365 | -------- | 2.904 | -------- | -------- | 2.8875 | -------- | |
| 16 | 0 | 0.1711 | 0.1714 | 0.1714 | 0.3838 | 0.3842 | 0.2654 | 0.2658 | 0.2658 | 0.0637 | 0.0643 |
| 102 | 0.2485 | -------- | -------- | 0.4237 | -------- | 0.3206 | -------- | -------- | 0.1913 | -------- | |
| 104 | 1.8094 | -------- | -------- | 1.841 | -------- | 1.8203 | -------- | -------- | 1.8051 | -------- | |
| 20 | 0 | 0.1370 | 0.1371 | 0.1371 | 0.3072 | 0.3073 | 0.2124 | 0.2127 | 0.2126 | 0.0510 | 0.0514 |
| 102 | 0.1989 | ------- | -------- | 0.3392 | -------- | 0.2567 | -------- | -------- | 0.1531 | -------- | |
| 104 | 1.4484 | ------- | -------- | 1.4739 | -------- | 1.4572 | -------- | -------- | 1.4441 | -------- | |
| 30 | 0 | 0.0914 | 0.0914 | 0.0914 | 0.2049 | 0.2049 | 0.1417 | 0.1420 | 0.1417 | 0.0340 | 0.0343 |
| 102 | 0.1327 | ------- | -------- | 0.2263 | -------- | 0.1712 | -------- | -------- | 0.102 | -------- | |
| 104 | 0.9661 | ------- | -------- | 0.9833 | -------- | 0.9721 | -------- | -------- | 0.9628 | -------- | |
| Foundation Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Kw | Present | Ref [50] | Analytical, Ref [50] | Ref [51] | % Error | Present | Ref [50] | Analytical, Ref [50] | % Error | |
| 0 | 0 | 3.141548 | 3.141434 | 3.141417 | 3.1415 | 0.0042 | 3.1387282 | 3.1302472 | 3.1302475 | 0.270927 |
| 0.5 | 3.476694 | 3.476594 | 3.476589 | 3.4767 | 0.0030 | 3.4735738 | 3.4667120 | 3.4667123 | 0.197925 | |
| 1.0 | 3.735951 | 3.735876 | 3.735859 | 3.7360 | 0.0025 | 3.732598 | 3.7265663 | 3.7265663 | 0.161857 | |
| 2.5 | 4.296954 | 4.296866 | 4.296879 | 4.2970 | 0.0017 | 4.2930972 | 4.2880927 | 4.2880929 | 0.116702 | |
| 102 | 0 | 3.748311 | 3.748233 | 3.748219 | 3.7483 | 0.0025 | 3.7449466 | 3.7389476 | 3.7389477 | 0.160444 |
| 0.5 | 3.960753 | 3.960677 | 3.960669 | 3.9608 | 0.0021 | 3.9571978 | 3.9516805 | 3.9516807 | 0.139614 | |
| 1.0 | 4.143643 | 4.143563 | 4.143565 | 4.1437 | 0.0019 | 4.1399244 | 4.1347186 | 4.1347188 | 0.12590 | |
| 2.5 | 4.582333 | 4.582266 | 4.582264 | 4.5824 | 0.0015 | 4.5782205 | 4.5734720 | 4.5734720 | 0.103827 | |
| 104 | 0 | 10.024121 | 10.02403 | 10.02404 | 10.024 | 0.0008 | 10.015124 | 9.9958218 | 9.9958219 | 0.193102 |
| 0.5 | 10.036187 | 10.03610 | 10.03610 | 10.036 | 0.0009 | 10.0271791 | 10.007782 | 10.007782 | 0.19382 | |
| 1.0 | 10.048209 | 10.04813 | 10.04813 | 10.048 | 0.0008 | 10.0391909 | 10.019699 | 10.019699 | 0.194536 | |
| 2.5 | 10.08402 | 10.08394 | 10.08394 | 10.084 | 0.0008 | 10.07497 | 10.055193 | 10.055193 | 0.196684 | |
| Foundation Parameters | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Kw | Present | Ref [50] | Ref [51] | Present | Ref [50] | Ref [51] | Present | Ref [50] | Ref [51] | |
| 0 | 0 | 4.7299 | 4.7314 | 4.73 | 7.8527 | 7.8533 | 7.854 | 10.9940 | 10.9908 | 10.996 |
| 0.5 | 4.8672 | 4.8683 | 4.869 | 7.9674 | 7.9680 | 7.968 | 11.0847 | 11.0815 | 11.086 | |
| 1.0 | 4.9938 | 4.9938 | 4.994 | 8.0774 | 8.0777 | 8.078 | 11.1732 | 11.1700 | 11.174 | |
| 2.5 | 5.3250 | 5.3195 | 5.32 | 8.3830 | 8.3812 | 8.38 | 11.4267 | 11.4233 | 11.43 | |
| 102 | 0 | 4.9503 | 4.9515 | 4.95 | 7.9038 | 7.904 | 7.904 | 11.0128 | 11.0096 | 11.014 |
| 0.5 | 5.0709 | 5.0718 | 5.071 | 8.0164 | 8.0169 | 8.017 | 11.1030 | 11.0998 | 11.104 | |
| 1.0 | 5.1835 | 5.1834 | 5.182 | 8.1244 | 8.1247 | 8.124 | 11.1910 | 11.1878 | 11.192 | |
| 2.5 | 5.4834 | 5.4783 | 5.477 | 8.4251 | 8.4234 | 8.423 | 11.4434 | 11.4400 | 11.444 | |
| 104 | 0 | 10.1227 | 10.1227 | 10.123 | 10.8385 | 10.8384 | 10.839 | 12.5242 | 12.5216 | 12.526 |
| 0.5 | 10.1373 | 10.1373 | 10.137 | 10.8828 | 10.8827 | 10.883 | 12.5858 | 12.5832 | 12.588 | |
| 1.0 | 10.1518 | 10.1517 | 10.152 | 10.9266 | 10.9264 | 10.927 | 12.6465 | 12.6439 | 12.648 | |
| 2.5 | 10.1951 | 10.1942 | 10.194 | 11.0550 | 11.0539 | 11.055 | 12.8237 | 12.8209 | 12.825 | |
| for L/H = 15 | ||||||||||
| 0 | 0 | 4.7246271 | 4.66554 | ----- | 7.8200665 | 7.61037 | ----- | 10.8971419 | 10.42711 | ----- |
| 0.5 | 4.8618011 | 4.80385 | ----- | 7.9343451 | 7.72927 | ----- | 10.9869929 | 10.52435 | ----- | |
| 1.0 | 4.9882582 | 4.93027 | ----- | 8.0438889 | 7.84259 | ----- | 11.0746921 | 10.61889 | ----- | |
| 2.5 | 5.3190604 | 5.25671 | ----- | 8.3481637 | 8.15441 | ----- | 11.3259972 | 10.88791 | ----- | |
| 102 | 0 | 4.9447357 | 4.89268 | ----- | 7.8709675 | 7.66521 | ----- | 10.9157313 | 10.44810 | ----- |
| 0.5 | 5.0652311 | 5.01352 | ----- | 7.9831048 | 7.78165 | ----- | 11.0051315 | 10.54476 | ----- | |
| 1.0 | 5.1776934 | 5.12542 | ----- | 8.0907063 | 7.89277 | ----- | 11.0924046 | 10.63876 | ----- | |
| 2.5 | 5.4772355 | 5.41981 | ----- | 8.3900963 | 8.19912 | ----- | 11.3425599 | 10.90635 | ----- | |
| 104 | 0 | 10.1113553 | 10.04899 | ----- | 10.7934756 | 10.70252 | ----- | 12.4138087 | 12.08187 | ----- |
| 0.5 | 10.1259392 | 10.0640 | ----- | 10.8376283 | 10.7461 | ----- | 12.4748902 | 12.14487 | ----- | |
| 1.0 | 10.1404604 | 10.07881 | ----- | 10.8812478 | 10.78903 | ----- | 12.5350874 | 12.20684 | ----- | |
| 2.5 | 10.1836536 | 10.12225 | ----- | 11.0090521 | 10.91414 | ----- | 12.710659 | 12.38693 | ----- | |
| Parameters | Thickness (nm) | Length (nm) | Width (nm) | Young’s Modulus (GPa) | Mass Density (Kg/m3) | Poisson’s Ratio | e311 (C/m2) | μ3111 (C/m) | a33 N/(m2.K) | l |
|---|---|---|---|---|---|---|---|---|---|---|
| Elastic core | 3 | 100 | 5 | 0.130 | 1380 | 0.24 | ---- | ---- | ------ | h |
| Piezoelectric Layer | 1 | 100 | 5 | 132 | 7500 | 0.27 | −4.1 | 5 × 10−8 | 7.124 × 10−9 | h |
| CC | CF | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kw | NCL_Elect | %E | NCL_Mech | %E | NCL_Elect | %E | NCL_Mech | %E | ||||
| ν = 0 | ν ≠ 0 | ν = 0 | ν ≠ 0 | ν = 0 | ν ≠ 0 | ν = 0 | ν ≠ 0 | |||||
| λ1 | ||||||||||||
| 0 | 20.0360 | 22.5228 | 12.4117 | 18.7259 | 20.3300 | 8.5662 | 3.5897 | 4.0356 | 12.4217 | 3.3542 | 3.6415 | 8.5654 |
| 5 | 20.1661 | 22.6696 | 12.4144 | 18.8963 | 20.5150 | 8.5662 | 4.2587 | 4.7903 | 12.4827 | 4.2045 | 4.5647 | 8.5670 |
| 25 | 20.6783 | 23.2476 | 12.4251 | 19.5630 | 21.2388 | 8.5662 | 6.2562 | 7.0421 | 12.5619 | 6.5869 | 7.1511 | 8.5655 |
| 50 | 21.3012 | 23.9504 | 12.4369 | 20.3657 | 22.1102 | 8.5659 | 8.0867 | 9.1048 | 12.5898 | 8.6904 | 9.4348 | 8.5658 |
| 100 | 22.4953 | 25.2976 | 12.4573 | 21.8829 | 23.7574 | 8.5660 | 10.8583 | 12.2274 | 12.6088 | 11.8235 | 12.8364 | 8.5668 |
| λ2 | ||||||||||||
| 0 | 45.4108 | 51.0377 | 12.3911 | 42.4857 | 46.1251 | 8.5662 | 19.5591 | 21.9865 | 12.4106 | 18.2806 | 19.8466 | 8.5665 |
| 5 | 45.4677 | 51.1019 | 12.3917 | 42.5605 | 46.2063 | 8.5662 | 19.6923 | 22.1369 | 12.4140 | 18.4551 | 20.0359 | 8.5657 |
| 25 | 45.6945 | 51.3579 | 12.3941 | 42.8583 | 46.5296 | 8.5661 | 20.2163 | 22.7282 | 12.4251 | 19.137 | 20.7763 | 8.5661 |
| 50 | 45.9764 | 51.6761 | 12.3970 | 43.2277 | 46.9306 | 8.5660 | 20.8528 | 23.4463 | 12.4372 | 19.9566 | 21.6661 | 8.5661 |
| 100 | 46.5351 | 52.3067 | 12.4027 | 43.9571 | 47.7225 | 8.5661 | 22.0708 | 24.8204 | 12.4581 | 21.5024 | 23.3443 | 8.5660 |
| λ3 | ||||||||||||
| 0 | 78.0220 | 87.6756 | 12.3729 | 73.1538 | 79.4202 | 8.5661 | 45.4547 | 51.087 | 12.3910 | 42.5265 | 46.1694 | 8.5662 |
| 5 | 78.0546 | 87.7123 | 12.3730 | 73.1967 | 79.4668 | 8.5661 | 45.5115 | 51.1511 | 12.3916 | 42.6012 | 46.2505 | 8.5662 |
| 25 | 78.1845 | 87.8591 | 12.3741 | 73.3681 | 79.6529 | 8.5661 | 45.7381 | 51.4069 | 12.3940 | 42.8987 | 46.5735 | 8.5662 |
| 50 | 78.3467 | 88.0421 | 12.3750 | 73.5819 | 79.8850 | 8.5661 | 46.0198 | 51.7248 | 12.3968 | 43.2678 | 46.9741 | 8.5660 |
| 100 | 78.6700 | 88.4071 | 12.3771 | 74.0075 | 80.3471 | 8.5662 | 46.578 | 52.3549 | 12.4026 | 43.9966 | 47.7654 | 8.5661 |
| CS | SS | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Kp/π2 | NCL_Elect | %E | NCL_Mech | %E | NCL_Elect | %E | NCL_Mech | %E | ||||
| ν = 0 | ν ≠ 0 | ν = 0 | ν ≠ 0 | ν = 0 | ν ≠ 0 | ν = 0 | ν ≠ 0 | |||||
| λ1 | ||||||||||||
| 0 | 13.9087 | 15.6351 | 12.4124 | 12.999 | 14.1125 | 8.5660 | 9.0454 | 10.1683 | 12.4140 | 8.4535 | 9.1776 | 8.5657 |
| 0.5 | 15.9026 | 17.8847 | 12.4640 | 15.5506 | 16.8827 | 8.5662 | 11.5242 | 12.9644 | 12.4972 | 11.5731 | 12.5644 | 8.5656 |
| 2.5 | 22.1508 | 24.9297 | 12.5454 | 23.0914 | 25.0695 | 8.5664 | 18.3509 | 20.6592 | 12.5787 | 19.5917 | 21.27 | 8.5664 |
| 5 | 28.069 | 31.5995 | 12.5779 | 29.9575 | 32.5237 | 8.5661 | 24.3247 | 27.39 | 12.6016 | 26.3858 | 28.646 | 8.5660 |
| 10 | 37.1791 | 41.8641 | 12.6012 | 40.3229 | 43.777 | 8.5661 | 33.1898 | 37.3769 | 12.6156 | 36.345 | 39.4584 | 8.5662 |
| λ2 | ||||||||||||
| 0 | 37.2447 | 41.8602 | 12.3924 | 34.8416 | 37.8262 | 8.5662 | 29.8496 | 33.5493 | 12.3945 | 27.9204 | 30.3121 | 8.5661 |
| 0.5 | 40.0778 | 45.0576 | 12.4253 | 38.5146 | 41.8138 | 8.5661 | 33.0584 | 37.1703 | 12.4383 | 32.0581 | 34.8042 | 8.5660 |
| 2.5 | 49.8247 | 56.0519 | 12.4982 | 50.6075 | 54.9426 | 8.5661 | 43.5923 | 49.0502 | 12.5203 | 44.949 | 48.7994 | 8.5662 |
| 5 | 59.815 | 67.3153 | 12.5392 | 62.5164 | 67.8716 | 8.5661 | 53.9404 | 60.7149 | 12.5592 | 57.1076 | 61.9995 | 8.5661 |
| 10 | 75.9507 | 85.501 | 12.5743 | 81.2568 | 88.2173 | 8.5661 | 70.2007 | 79.0382 | 12.5889 | 75.7826 | 82.2743 | 8.5662 |
| λ3 | ||||||||||||
| 0 | 67.8433 | 76.2383 | 12.3741 | 63.5966 | 69.0443 | 8.5660 | 58.3649 | 65.5879 | 12.3756 | 54.6992 | 59.3848 | 8.5661 |
| 0.5 | 71.2365 | 80.0685 | 12.3981 | 68.0314 | 73.859 | 8.5660 | 62.0726 | 69.7729 | 12.4053 | 59.5318 | 64.6314 | 8.5662 |
| 2.5 | 83.4407 | 93.8387 | 12.4615 | 83.4461 | 90.5942 | 8.5661 | 75.0946 | 84.4642 | 12.4771 | 75.843 | 82.3398 | 8.5661 |
| 5 | 96.5505 | 108.6238 | 12.5046 | 99.4081 | 107.9235 | 8.5661 | 88.7239 | 99.833 | 12.5210 | 92.2623 | 100.1655 | 8.5660 |
| 10 | 118.4959 | 133.3641 | 12.5474 | 125.3771 | 136.1171 | 8.5662 | 111.0738 | 125.0259 | 12.5611 | 118.4595 | 128.6068 | 8.5661 |
| SS | CC | CF | CS | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NCL | CL | NCL | CL | NCL | CL | NCL | CL | |||||||||
| νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | |
| e311 | λ1 | |||||||||||||||
| −12 | 20.8663 | 23.4133 | 19.9738 | 22.4019 | 34.3647 | 38.4291 | 30.8067 | 34.3799 | 7.9924 | 8.9723 | 7.9665 | 8.943 | 26.7242 | 29.9311 | 24.7164 | 27.6506 |
| −8 | 20.6624 | 23.2319 | 19.7555 | 22.2075 | 33.7303 | 37.8628 | 30.0753 | 33.726 | 7.9232 | 8.9107 | 7.8969 | 8.8811 | 26.3367 | 29.5856 | 24.2847 | 27.2654 |
| −4 | 20.5392 | 23.1223 | 19.6234 | 22.09 | 33.3438 | 37.519 | 29.6278 | 33.3276 | 7.8813 | 8.8735 | 7.8549 | 8.8437 | 26.1014 | 29.3764 | 24.022 | 27.0317 |
| 0 | 20.4979 | 23.0857 | 19.5791 | 22.0507 | 33.214 | 37.4037 | 29.4771 | 33.1937 | 7.8673 | 8.8611 | 7.8408 | 8.8312 | 26.0225 | 29.3063 | 23.9338 | 26.9533 |
| 4 | 20.5392 | 23.1223 | 19.6234 | 22.09 | 33.3438 | 37.519 | 29.6278 | 33.3276 | 7.8813 | 8.8735 | 7.8549 | 8.8437 | 26.1014 | 29.3764 | 24.022 | 27.0317 |
| 8 | 20.6624 | 23.2319 | 19.7555 | 22.2075 | 33.7303 | 37.8628 | 30.0753 | 33.726 | 7.9232 | 8.9107 | 7.8969 | 8.8811 | 26.3367 | 29.5856 | 24.2847 | 27.2654 |
| 12 | 20.8663 | 23.4133 | 19.9738 | 22.4019 | 34.3647 | 38.4291 | 30.8067 | 34.3799 | 7.9924 | 8.9723 | 7.9665 | 8.943 | 26.7242 | 29.9311 | 24.7164 | 27.6506 |
| λ2 | ||||||||||||||||
| −12 | 71.1768 | 79.7641 | 53.9823 | 60.215 | 108.646 | 121.7285 | 76.0412 | 84.6213 | 34.6209 | 38.7283 | 30.9233 | 34.5215 | 88.5533 | 99.2212 | 64.2624 | 71.5872 |
| −8 | 70.2932 | 78.9766 | 52.6948 | 59.0636 | 107.257 | 120.4904 | 73.8096 | 82.6218 | 34.012 | 38.185 | 30.2171 | 33.8904 | 87.4255 | 98.2161 | 62.5293 | 70.0356 |
| −4 | 69.7576 | 78.5004 | 51.907 | 58.3618 | 106.415 | 119.7414 | 72.4376 | 81.3984 | 33.6414 | 37.8552 | 29.7853 | 33.506 | 86.7418 | 97.608 | 61.466 | 69.0879 |
| 0 | 69.5782 | 78.341 | 51.6417 | 58.126 | 106.132 | 119.4907 | 71.9744 | 80.9865 | 33.517 | 37.7447 | 29.64 | 33.3769 | 86.5127 | 97.4045 | 61.1075 | 68.7691 |
| 4 | 69.7576 | 78.5004 | 51.907 | 58.3618 | 106.415 | 119.7414 | 72.4376 | 81.3984 | 33.6414 | 37.8552 | 29.7853 | 33.506 | 86.7418 | 97.608 | 61.466 | 69.0879 |
| 8 | 70.2932 | 78.9766 | 52.6948 | 59.0636 | 107.257 | 120.4904 | 73.8096 | 82.6218 | 34.012 | 38.185 | 30.2171 | 33.8904 | 87.4255 | 98.2161 | 62.5293 | 70.0356 |
| 12 | 71.1768 | 79.7641 | 53.9823 | 60.215 | 108.646 | 121.7285 | 76.0412 | 84.6213 | 34.6209 | 38.7283 | 30.9233 | 34.5215 | 88.5533 | 99.2212 | 64.2624 | 71.5872 |
| λ3 | ||||||||||||||||
| −12 | 182.660 | 204.974 | 108.2391 | 120.337 | 252.201 | 283.0483 | 141.4364 | 157.043 | 108.590 | 121.6653 | 76.0419 | 84.6215 | 215.829 | 242.2106 | 124.1121 | 137.886 |
| −8 | 181.122 | 203.605 | 105.0337 | 117.462 | 250.187 | 281.255 | 136.9017 | 152.971 | 107.199 | 120.425 | 73.8083 | 82.6201 | 214.059 | 240.6345 | 120.2659 | 134.435 |
| −4 | 180.194 | 202.779 | 103.0627 | 115.703 | 248.970 | 280.1736 | 134.1074 | 150.476 | 106.355 | 119.6747 | 72.4351 | 81.3957 | 212.989 | 239.6839 | 117.898 | 132.321 |
| 0 | 179.883 | 202.503 | 102.3972 | 115.111 | 248.563 | 279.8121 | 133.1629 | 149.634 | 106.073 | 119.4236 | 71.9716 | 80.9835 | 212.632 | 239.3661 | 117.098 | 131.608 |
| 4 | 180.194 | 202.779 | 103.0627 | 115.703 | 248.970 | 280.1736 | 134.1074 | 150.476 | 106.355 | 119.6747 | 72.4351 | 81.3957 | 212.989 | 239.6839 | 117.898 | 132.321 |
| 8 | 181.122 | 203.605 | 105.0337 | 117.462 | 250.187 | 281.255 | 136.9017 | 152.971 | 107.199 | 120.425 | 73.8083 | 82.6201 | 214.059 | 240.6345 | 120.2659 | 134.435 |
| 12 | 182.660 | 204.974 | 108.2391 | 120.337 | 252.201 | 283.0483 | 141.4364 | 157.043 | 108.590 | 121.6653 | 76.0419 | 84.6215 | 215.829 | 242.2106 | 124.1121 | 137.886 |
| μ3111 × 108 | SS | CC | CF | CS | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| NCL | CL | NCL | CL | NCL | CL | NCL | CL | |||||||||
| νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | νc = νp = 0 | νc = 0.24 νp = 0.27 | |
| λ1 | ||||||||||||||||
| −5 | 20.5413 | 23.1242 | 19.6256 | 22.092 | 33.3504 | 37.5248 | 29.6354 | 33.3344 | 7.882 | 8.8741 | 7.8556 | 8.8443 | 26.1054 | 29.3799 | 24.0265 | 27.0356 |
| −2.5 | 20.5365 | 23.1199 | 19.6205 | 22.0874 | 33.3317 | 37.5082 | 29.6137 | 33.3151 | 7.8819 | 8.874 | 7.8554 | 8.8442 | 26.0948 | 29.3705 | 24.0146 | 27.0251 |
| −1.25 | 20.5353 | 23.1189 | 19.6192 | 22.0863 | 33.327 | 37.5041 | 29.6083 | 33.3103 | 7.8819 | 8.874 | 7.8554 | 8.8442 | 26.0921 | 29.3681 | 24.0116 | 27.0224 |
| 0 | 20.5349 | 23.1185 | 19.6188 | 22.0859 | 33.3255 | 37.5027 | 29.6065 | 33.3087 | 7.8819 | 8.874 | 7.8554 | 8.8442 | 26.0912 | 29.3673 | 24.0106 | 27.0215 |
| 1.25 | 20.5353 | 23.1189 | 19.6192 | 22.0863 | 33.327 | 37.5041 | 29.6083 | 33.3103 | 7.8819 | 8.874 | 7.8554 | 8.8442 | 26.0921 | 29.3681 | 24.0116 | 27.0224 |
| 2.5 | 20.5365 | 23.1199 | 19.6205 | 22.0874 | 33.3317 | 37.5082 | 29.6137 | 33.3151 | 7.8819 | 8.874 | 7.8554 | 8.8442 | 26.0948 | 29.3705 | 24.0146 | 27.0251 |
| 5 | 20.5413 | 23.1242 | 19.6256 | 22.092 | 33.3504 | 37.5248 | 29.6354 | 33.3344 | 7.882 | 8.8741 | 7.8556 | 8.8443 | 26.1054 | 29.3799 | 24.0265 | 27.0356 |
| λ2 | ||||||||||||||||
| −5 | 69.7667 | 78.5084 | 51.9204 | 58.3737 | 106.429 | 119.754 | 72.461 | 81.4192 | 33.6477 | 37.8608 | 29.7926 | 33.5125 | 86.7534 | 97.6183 | 61.4841 | 69.104 |
| −2.5 | 69.6838 | 78.4347 | 51.7979 | 58.2648 | 106.277 | 119.619 | 72.2115 | 81.1973 | 33.6284 | 37.8436 | 29.7701 | 33.4925 | 86.6384 | 97.516 | 61.3042 | 68.944 |
| −1.25 | 69.663 | 78.4163 | 51.7672 | 58.2375 | 106.239 | 119.585 | 72.149 | 81.1417 | 33.6235 | 37.8393 | 29.7644 | 33.4874 | 86.6096 | 97.4905 | 61.2592 | 68.9039 |
| 0 | 69.6561 | 78.4101 | 51.757 | 58.2284 | 106.226 | 119.574 | 72.1281 | 81.1231 | 33.6219 | 37.8379 | 29.7625 | 33.4858 | 86.6 | 97.4819 | 61.2441 | 68.8906 |
| 1.25 | 69.663 | 78.4163 | 51.7672 | 58.2375 | 106.239 | 119.585 | 72.149 | 81.1417 | 33.6235 | 37.8393 | 29.7644 | 33.4874 | 86.6096 | 97.4905 | 61.2592 | 68.9039 |
| 2.5 | 69.6838 | 78.4347 | 51.7979 | 58.2648 | 106.277 | 119.619 | 72.2115 | 81.1973 | 33.6284 | 37.8436 | 29.7701 | 33.4925 | 86.6384 | 97.516 | 61.3042 | 68.944 |
| 5 | 69.7667 | 78.5084 | 51.9204 | 58.3737 | 106.429 | 119.754 | 72.461 | 81.4192 | 33.6477 | 37.8608 | 29.7926 | 33.5125 | 86.7534 | 97.6183 | 61.4841 | 69.104 |
| λ3 | ||||||||||||||||
| −5 | 180.209 | 202.793 | 103.096 | 115.733 | 248.991 | 280.192 | 134.155 | 150.518 | 106.370 | 119.687 | 72.4585 | 81.4165 | 213.007 | 239.70 | 117.938 | 132.357 |
| −2.5 | 179.886 | 202.506 | 102.4037 | 115.117 | 248.519 | 279.773 | 133.06 | 149.543 | 106.218 | 119.552 | 72.2096 | 81.1951 | 212.613 | 239.350 | 117.057 | 131.572 |
| −1.25 | 179.805 | 202.434 | 102.2298 | 114.962 | 248.401 | 279.668 | 132.785 | 149.298 | 106.180 | 119.519 | 72.1472 | 81.1396 | 212.515 | 239.262 | 116.835 | 131.375 |
| 0 | 179.778 | 202.410 | 102.1718 | 114.911 | 248.362 | 279.633 | 132.693 | 149.216 | 106.167 | 119.507 | 72.1264 | 81.1212 | 212.482 | 239.233 | 116.761 | 131.309 |
| 1.25 | 179.805 | 202.434 | 102.2298 | 114.962 | 248.401 | 279.668 | 132.785 | 149.298 | 106.180 | 119.519 | 72.1472 | 81.1396 | 212.515 | 239.262 | 116.835 | 131.375 |
| 2.5 | 179.886 | 202.506 | 102.4037 | 115.117 | 248.519 | 279.773 | 133.06 | 149.543 | 106.218 | 119.552 | 72.2096 | 81.1951 | 212.613 | 239.350 | 117.057 | 131.572 |
| 5 | 180.209 | 202.793 | 103.0962 | 115.733 | 248.991 | 280.192 | 134.155 | 150.518 | 106.370 | 119.687 | 72.4585 | 81.4165 | 213.007 | 239.70 | 117.938 | 132.357 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdelrahman, A.A.; Abdelwahed, M.S.; Ahmed, H.M.; Hamdi, A.; Eltaher, M.A. Investigation of Size-Dependent Vibration Behavior of Piezoelectric Composite Nanobeams Embedded in an Elastic Foundation Considering Flexoelectricity Effects. Mathematics 2023, 11, 1180. https://doi.org/10.3390/math11051180
Abdelrahman AA, Abdelwahed MS, Ahmed HM, Hamdi A, Eltaher MA. Investigation of Size-Dependent Vibration Behavior of Piezoelectric Composite Nanobeams Embedded in an Elastic Foundation Considering Flexoelectricity Effects. Mathematics. 2023; 11(5):1180. https://doi.org/10.3390/math11051180
Chicago/Turabian StyleAbdelrahman, Alaa A., Mohamed S. Abdelwahed, Hani M. Ahmed, Amin Hamdi, and Mohamed A. Eltaher. 2023. "Investigation of Size-Dependent Vibration Behavior of Piezoelectric Composite Nanobeams Embedded in an Elastic Foundation Considering Flexoelectricity Effects" Mathematics 11, no. 5: 1180. https://doi.org/10.3390/math11051180
APA StyleAbdelrahman, A. A., Abdelwahed, M. S., Ahmed, H. M., Hamdi, A., & Eltaher, M. A. (2023). Investigation of Size-Dependent Vibration Behavior of Piezoelectric Composite Nanobeams Embedded in an Elastic Foundation Considering Flexoelectricity Effects. Mathematics, 11(5), 1180. https://doi.org/10.3390/math11051180










