High Order Energy Preserving Composition Method for Multi-Symplectic Sine-Gordon Equation

Abstract

A fourth-order energy preserving composition scheme for multi-symplectic structure partial differential equations have been proposed. The accuracy and energy conservation properties of the new scheme were verified. The new scheme is applied to solve the multi-symplectic sine-Gordon equation with periodic boundary conditions and compared with the corresponding second-order average vector field scheme and the second-order Preissmann scheme. The numerical experiments show that the new scheme has fourth-order accuracy and can preserve the energy conservation properties well.

1. Introduction

The symplectic geometric algorithm for the Hamiltonian system can accurately simulate the evolution of the system over a long period, which preserves the energy conservation of the system [1,2,3,4,5,6]. Marsden et al. [7,8,9] proposed the multi-symplectic method of the partial differential equations (PDE) with the multi-symplectic structure, which can also calculate the equations accurately for a long time and approximately preserve the energy conservation property. Multi-symplectic algorithm has been successfully applied to solve several important equations [10,11,12,13]. Recently, energy-preserving methods for Hamiltonian systems and multi-symplectic structure PDE have received much attention. Celledoni et al. proposed the second-order and higher-order average vector field (AVF) method to the Hamiltonian system, which can preserve the energy conservation of the Hamiltonian system exactly [14,15,16]. At the same time, the second order AVF method has also been proposed to solve the multi-symplectic structure PDE, which can also preserve the energy conservation [17]. However, few people study the high order energy preserving method of the multi-symplectic PDE structures.

Composition method is a class of important method to construct high order scheme of the differential equation. The method of forming multi-level high order schemes with the combination of low order invertible schemes was proposed by Ruth and Yoshida [18,19]. Ruth constructed three order three level composition schemes for the separate Hamiltonian system. Yoshida constructed the high order explicit difference scheme of separable Hamiltonian system. Qin extended the Yoshida’s composition method to the general non-Hamiltonian systems [20,21]. In this paper, we propose a fourth order energy preserving scheme of the multi-symplectic structure PDE by the composition method based on the second order energy preserving average vector field scheme of the multi-symplectic PDE. The new fourth order energy preserving composition scheme is applied to solve the sine-Gordon equation.

This paper is organized as following. In Section 2, the second order multi-symplectic energy-preserving scheme and the fourth order multi-symplectic energy preserving composition scheme are proposed. In Section 3, the sine-Gordon equation is discretizated in spacial direction by the pseudo-spectral method. Then the two energy preserving schemes for the multi-symplectic sine-Gordon equation are proposed by applying the second order AVF method and the fourth order composition AVF method, respectively. In Section 4, the numerical experiments are reported. The accuracy and energy conservation property of the second order AVF scheme and the fourth order composition AVF scheme of the multi-symplectic sine-Gordon equations are investigated compared with the corresponding second order multi-symplectic scheme. At last, we finish the paper with conclusive remarks in Section 5.

2. Multi-Symplectic Discretization for the Partial Differential Equations

Many partial differential equations can be written as the following multi-symplectic structure

$$\begin{array}{c}\hfill {\mathbf{M}}_1{\mathbf{z}}_t+{\mathbf{K}}_1{\mathbf{z}}_x={\nabla }_{\mathbf{z}}{S}_1(\mathbf{z}),\mathbf{z}\in {\mathbb{R}}^d,(x,t)\in {\mathbb{R}}^2,\end{array}$$

(1)

where ${\mathbf{M}}_1$ and ${\mathbf{K}}_1$ are skew symmetric matrices, $S_1:{\mathbb{R}}^d\to \mathbb{R}$ is a scalar smooth function and $d\ge 1$, ∇ is the gradient of a function [7,8].

2.1. Spatial Discretization for the Partial Differential Equations

Equation (1) can be discretizated in spatial direction by the Fourier pseudo-spectral method [22]. Suppose $u(x,t)$ is a function with $x\in [a,b]$, the interval $\mathsf{\Omega }=[a,b]$ is divided into N equal subintervals, where the integer N is an even number. Denoting $L=b-a$, the spatial collocation nodes are given by $x_j=a+(j-1)h,j=1,\cdots ,N,$ where $h=L/N$ is the space step. Let $u_j$ be the approximation of $u(x_j,t)$.

Let $S^{\prime }=\{g_j(x);1\le j\le N\}$ be the interpolation space. The function $g_j(x)$ is the trigonometric polynomial explicitly given by

$$\begin{array}{c}\hfill g_j(x)=\frac{1}{N}\sum _{k=-N/2}^{N/2}\frac{1}{c_k}{exp}^{\mathrm{i}k\mu (x-x_j)},\end{array}$$

(2)

where $c_k=1(|k|\ne N/2),c_{-N/2}=c_{N/2}=2$ and $\mu =\frac{2\pi }{L}$. The interpolation operator $I_N:L^2(\mathsf{\Omega })\to S_N^{{}^{\prime }}$ is defined as

$$\begin{array}{c}\hfill I_{N}u(x,t)=\sum _{m=1}^N{u}_m{g}_m(x).\end{array}$$

(3)

Therefore, we have

$$\begin{array}{c}\hfill I_{N}u(x_j,t)=\sum _{m=1}^N{u}_m{g}_m(x_j)=u(x_j),\end{array}$$

(4)

where $j=1,\cdots ,N.$

By differentiating (3), the k order derivative of the operator $I_{N}u(x,t)$ at nodes $x_j$ reads

$$\begin{array}{c}\hfill \frac{{\partial }^k}{\partial x^k}{I}_N{u(x,t)|}_{x=x_j}=\sum _{m=1}^N{u}_m\frac{d^k{g}_m(x_j)}{d{x}^k}={({\mathbf{D}}_k\mathbf{u})}_j,j=1,\cdots ,N.\end{array}$$

(5)

where ${\mathbf{D}}_k\in {\mathbb{R}}^{N\times N}$ is a spectral differential matrix with elements

$$\begin{array}{c}\hfill {({\mathbf{D}}_k)}_{j,n}=\frac{d^k{g}_n(x_j)}{d{x}^k},\end{array}$$

(6)

and $\mathbf{u}={(u_1,u_2,\cdots ,u_N)}^T$.

We can obtain explicitly ${\mathbf{D}}_1$

$${({\mathbf{D}}_1)}_{i,j}=\{\begin{array}{c}\frac{1}{2}\mu {(-1)}^{i+j}cot\left(\mu \frac{x_i-x_j}{2}\right),i\ne j,\hfill \\ 0,i=j.\hfill \end{array}$$

(7)

In particular, ${\mathbf{D}}_k={({\mathbf{D}}_1)}^k$, if k is an odd number.

Applying the Fourier pseudo-spectral method to Equation (1) in spatial direction, we can obtain

$$\begin{array}{c}\hfill \mathbf{M}{\mathbf{Z}}_t+\mathbf{K}\mathbf{D}\mathbf{Z}={\nabla }_{\mathbf{Z}}S(\mathbf{Z}),\end{array}$$

(8)

where $\mathbf{M},\mathbf{K}\in R^{Nd}$ are skew symmetric matrices, $\mathbf{Z}={(z_{1,1},\dots ,z_{N,1},\dots ,z_{1,d},\dots ,z_{N,d})}^T$, $S:{\mathbb{R}}^{Nd}\to \mathbb{R}$ is a scalar smooth function. $\mathbf{D}$ is a matrix with ${\mathbf{D}}_{\mathbf{1}}$. Equation (8) can be written as

$$\begin{array}{c}\hfill \mathbf{M}\frac{d\mathbf{Z}}{dt}={\nabla }_{\mathbf{Z}}E(\mathbf{Z})=f(\mathbf{Z}),\end{array}$$

(9)

where $E(\mathbf{Z})=S(\mathbf{Z})-\frac{1}{2}{\mathbf{Z}}^T\mathbf{K}\mathbf{D}\mathbf{Z}$.

2.2. Second Order Energy-Preserving Scheme for Multi-Symplectic PDE

Applying the second order AVF method to Equation (9), we can obtain that

$$\begin{array}{c}\hfill \mathbf{M}\frac{{\mathbf{Z}}^{n+1}-{\mathbf{Z}}^n}{\tau }={\int }_0^1{\nabla }_{\mathbf{Z}}E((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n+1})d\xi ={\int }_0^{1}f((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n+1})d\xi ,\end{array}$$

(10)

where $\tau$ is the time step. It can also be written as

$$\begin{array}{c}\hfill \mathbf{M}\frac{{\mathbf{Z}}^{n+1}-{\mathbf{Z}}^n}{\tau }+\mathbf{K}\mathbf{D}\frac{{\mathbf{Z}}^n+{\mathbf{Z}}^{n+1}}{2}={\int }_0^1{\nabla }_{\mathbf{Z}}S((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n+1})d\xi .\end{array}$$

(11)

The scheme (11) is consistent with the second order global energy preserving scheme [17]. However, the accuracy of the scheme has not been proved. We prove the accuracy and energy conservation property of the scheme in a new way.

Theorem 1.

Scheme (10) has second order accuracy.

Proof. 

Let $s=Nd$, $\mathbf{Z}\in {\mathbb{R}}^s$, the skew symmetric matrix $\mathbf{M}$ can be transformed into a diagonal matrix $\mathbf{G}$ with diagonal element 1 and 0 on diagonal line by a similar transformation [23]. We can get ${\mathbf{P}}^T\mathbf{M}\mathbf{P}=\mathbf{G}$, $\mathbf{P}$ is a invertible matrix. Equation (9) is equivalent to

$$\begin{array}{c}\hfill {\mathbf{P}}^T\mathbf{M}\mathbf{P}\frac{d{\mathbf{P}}^{-1}\mathbf{Z}}{dt}={\mathbf{P}}^T{\nabla }_{\mathbf{Z}}E(\mathbf{Z})={\mathbf{P}}^T{\nabla }_{\mathbf{Z}}E(\mathbf{P}{\mathbf{P}}^{-1}\mathbf{Z}).\end{array}$$

(12)

Let ${\mathbf{P}}^{-1}\mathbf{Z}=\mathbf{Y}$, ${\mathbf{P}}^T{\nabla }_{\mathbf{Z}}E(\mathbf{Z})=h(\mathbf{Z})=g(\mathbf{Y})$, so Equation (12) is equivalent to

$$\begin{array}{c}\hfill \mathbf{G}\frac{d\mathbf{Y}}{dt}=g(\mathbf{Y}),\end{array}$$

(13)

where $g(\mathbf{Y})=({\mathbf{g}}^{\mathbf{1}},{\mathbf{g}}^{\mathbf{2}},\cdots ,{\mathbf{g}}^{\mathbf{s}}).$ Equation (13) is equivalent to Equation (9). So Equation (10) can be written as

$$\begin{array}{cc}\hfill \mathbf{G}\frac{{\mathbf{Y}}^{n+1}-{\mathbf{Y}}^n}{\tau }& ={\int }_0^1{\mathbf{P}}^T{\nabla }_{\mathbf{Z}}E((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n+1})d\xi \hfill \\ \hfill & ={\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n+1})d\xi .\hfill \end{array}$$

(14)

Equations (10) and (14) have the same accuracy. So we can only prove Equation (14) has the second order accuracy.

We give the following partial derivatives definition

$$\begin{array}{cc}\hfill & [g_k^i{g}^k]={(g_k^1{g}^k,\cdots ,g_k^i{g}^k,\cdots ,g_k^s{g}^k)}^T,\hfill \\ & [g_k^i{g}_m^k{g}^m]={(g_k^1{g}_m^k{g}^m,\cdots ,g_k^i{g}_m^k{g}^m,\cdots ,g_k^s{g}_m^k{g}^m)}^T,\hfill \\ & [g_{kj}^i{g}^k{g}^j]={(g_{kj}^1{g}^k{g}^j,\cdots ,g_{kj}^i{g}^k{g}^j,\cdots ,g_{kj}^s{g}^k{g}^j)}^T,\hfill \\ & [g_{kjm}^i{g}^k{g}^j{g}^m]={(g_{kjm}^1{g}^k{g}^j{g}^m,\cdots ,g_{kjm}^i{g}^k{g}^j{g}^m,\cdots ,g_{kjm}^s{g}^k{g}^j{g}^m)}^T,\hfill \\ & [g_{kj}^i{g}_m^k{g}^j{g}^m]={(g_{kj}^1{g}_m^k{g}^j{g}^m,\cdots ,g_{kj}^i{g}_m^k{g}^j{g}^m,\cdots ,g_{kj}^s{g}_m^k{g}^j{g}^m)}^T,\hfill \\ & [g_k^i{g}_{mj}^k{g}^j{g}^m]={(g_k^1{g}_{mj}^k{g}^j{g}^m,\cdots ,g_k^i{g}_{mj}^k{g}^j{g}^m,\cdots ,g_k^s{g}_{mj}^k{g}^j{g}^m)}^T,\hfill \\ & [g_k^i{g}_m^k{g}_j^m{g}^j]={(g_k^1{g}_m^k{g}_j^m{g}^j,\cdots ,g_k^i{g}_m^k{g}_j^m{g}^j,\cdots ,g_k^s{g}_m^k{g}_j^m{g}^j)}^T,\hfill \end{array}$$

(15)

where

$$\begin{array}{cc}\hfill & g_k^i{g}^k=\sum _{k=1}^s\frac{\partial g^i}{\partial y_k}{g}^k,\hfill \\ & g_k^i{g}_m^k{g}^m=\sum _{k=1}^s\sum _{m=1}^s\frac{\partial g^i}{\partial y_k}\frac{\partial g^k}{\partial y_m}{g}^m,\hfill \\ & g_{kj}^i{g}^k{g}^j=\sum _{k=1}^s\sum _{j=1}^s\frac{\partial }{\partial y_k}(\frac{\partial g^i}{\partial y_j})g^k{g}^j,\hfill \\ & g_{kjm}^i{g}^k{g}^j{g}^m=\sum _{k=1}^s\sum _{m=1}^s\sum _{j=1}^s\frac{\partial }{\partial y_k}(\frac{\partial }{\partial y_j}(\frac{\partial g^i}{\partial y_m}))g^k{g}^m{g}^j,\hfill \\ & g_{kj}^i{g}_m^k{g}^j{g}^m=\sum _{k=1}^s\sum _{j=1}^s\sum _{m=1}^s\frac{\partial }{\partial y_k}(\frac{\partial g^i}{\partial y_j})\frac{\partial g^k}{\partial y_m}{g}^m{g}^j,\hfill \\ & g_k^i{g}_{mj}^k{g}^j{g}^m=\sum _{k=1}^s\sum _{j=1}^s\sum _{m=1}^s\frac{\partial g^i}{\partial y_k}\frac{\partial }{\partial y_j}(\frac{\partial g^k}{\partial y_m})g^m{g}^j,\hfill \\ & g_k^i{g}_m^k{g}_j^m{g}^j=\sum _{k=1}^s\sum _{m=1}^s\sum _{j=1}^s\frac{\partial g^i}{\partial y_k}\frac{\partial g^k}{\partial y_m}\frac{\partial g^m}{\partial y_j}{g}^j.\hfill \end{array}$$

(16)

The corresponding Taylor expansion of $\mathbf{Y}(t_{n+1})$ can be written as

$$\begin{array}{c}\hfill \mathbf{Y}(t_{n+1})=\mathbf{Y}(t_n)+\frac{d\mathbf{Y}(t_n)}{dt}\tau +\frac{1}{2}\frac{d^2\mathbf{Y}(t_n)}{d{t}^2}{\tau }^2+O({\tau }^3).\end{array}$$

(17)

Multiplying ${\mathbf{G}}^2$ to both side of Equation (17), we can obtain that

$$\begin{array}{cc}\hfill {\mathbf{G}}^2\mathbf{Y}(t_{n+1})& ={\mathbf{G}}^2\mathbf{Y}(t_n)+{\mathbf{G}}^2\frac{d\mathbf{Y}(t_n)}{dt}\tau +{\mathbf{G}}^2\frac{1}{2}\frac{d^2\mathbf{Y}(t_n)}{d{t}^2}{\tau }^2+O({\tau }^3)\hfill \\ & ={\mathbf{G}}^2\mathbf{Y}(t_n)+\mathbf{G}g(\mathbf{Y}(t_n))\tau +\frac{1}{2}\mathbf{G}\frac{d}{dt}(g(\mathbf{Y}(t_n))){\tau }^2+O({\tau }^3),\hfill \end{array}$$

(18)

where

$$\begin{array}{c}\hfill \mathbf{G}\frac{d}{dt}(g(\mathbf{Y}(t_n)))=\frac{\partial g(\mathbf{Y}(t_n))}{\partial \mathbf{Y}}\mathbf{G}\frac{d\mathbf{Y}}{dt}=\frac{\partial g(\mathbf{Y}(t_n))}{\partial \mathbf{Y}}g(\mathbf{Y})=[g_k^i{g}^k],\end{array}$$

(19)

so Equation (18) can be written as

$$\begin{array}{cc}\hfill {\mathbf{G}}^2\mathbf{Y}(t_{n+1})& ={\mathbf{G}}^2\mathbf{Y}(t_n)+\mathbf{G}g(\mathbf{Y}(t_n))\tau +\frac{1}{2}[g_k^i{g}^k]{\tau }^2+O({\tau }^3).\hfill \end{array}$$

(20)

Equation (14) can be written as

$$\begin{array}{c}\hfill \mathbf{G}{\mathbf{Y}}^{n+1}=\mathbf{G}{\mathbf{Y}}^n+\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n+1})d\xi ,\end{array}$$

(21)

multiplying $\mathbf{G}$ to both side of the equal sign and expanding ${\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n+1})d\xi$. We will obtain that

$$\begin{array}{cc}\hfill & {\mathbf{G}}^2{\mathbf{Y}}^{n+1}={\mathbf{G}}^2{\mathbf{Y}}^n+\tau \mathbf{G}{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n+1})d\xi \hfill \\ & ={\mathbf{G}}^2{\mathbf{Y}}^n+\tau \mathbf{G}{\int }_0^1(g({\mathbf{Y}}^n)+\xi \frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}({\mathbf{Y}}^{n+1}-{\mathbf{Y}}^n)+O({\tau }^2))d\xi \hfill \\ \hfill & ={\mathbf{G}}^2{\mathbf{Y}}^n+\tau \mathbf{G}g({\mathbf{Y}}^n)+\frac{{\tau }^2}{2}[g_k^i{g}^k]+O({\tau }^3),\hfill \end{array}$$

(22)

where $\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}=\frac{\partial g(\mathbf{Y})}{\partial \mathbf{Y}}{|}_{\mathbf{Y}={\mathbf{Y}}^n}$, suppose $\mathbf{Y}(t_n)={\mathbf{Y}}^n$, we can get ${\mathbf{G}}^2(\mathbf{Y}(t_{n+1})-{\mathbf{Y}}^{n+1})=O({\tau }^3)$, that is $\mathbf{Y}(t_{n+1})-{\mathbf{Y}}^{n+1}=O({\tau }^3)$. Scheme (14) has the second order accuracy, so scheme (10) has the second order accuracy. □

Theorem 2.

Equation (10) can preserve the energy conservation property.

Proof. 

Since $\mathbf{M}$ is a skew symmetric matrix, it is obvious that

$$\begin{array}{cc}\hfill \frac{E({\mathbf{Z}}^{n+1})-E({\mathbf{Z}}^n)}{\tau }& =\frac{1}{\tau }{\int }_0^1\frac{d}{d\xi }E((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n+1})d\xi \hfill \\ & =({\int }_0^1{({\nabla }_{\mathbf{Z}}E((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n+1})d\xi )}^T\frac{{\mathbf{Z}}^{n+1}-{\mathbf{Z}}^n}{\tau }\hfill \\ & =-{(\frac{{\mathbf{Z}}^{n+1}-{\mathbf{Z}}^n}{\tau })}^T\mathbf{M}\frac{{\mathbf{Z}}^{n+1}-{\mathbf{Z}}^n}{\tau }\hfill \\ & =0.\hfill \end{array}$$

(23)

So Equation (10) can preserve the energy conservation property. □

2.3. Fourth Order Energy Preserving Schemes for Multi-Symplectic PDE

To the ordinary differential equations

$$\begin{array}{c}\hfill \frac{d\mathbf{Z}}{dt}=f(\mathbf{Z}),\mathbf{Z}\in {\mathbb{R}}^s,s\ge 1,\end{array}$$

(24)

the trapezoidal scheme of Equation (24) can be written as

$$\begin{array}{c}\hfill \frac{{\mathbf{Z}}^{n+1}-{\mathbf{Z}}^n}{\tau }=\frac{f({\mathbf{Z}}^n)+f({\mathbf{Z}}^{n+1})}{2}.\end{array}$$

(25)

The scheme (25) has second order accuracy.

Qin et al. [20] proposed the following composition scheme

$$\begin{array}{cc}\hfill & {\mathbf{Z}}_1={\mathbf{Z}}_0+c_1\tau (f({\mathbf{Z}}_0)+f({\mathbf{Z}}_1)),\hfill \\ & {\mathbf{Z}}_2={\mathbf{Z}}_1+c_2\tau (f({\mathbf{Z}}_1)+f({\mathbf{Z}}_2)),\hfill \\ & {\mathbf{Z}}_3={\mathbf{Z}}_2+c_3\tau (f({\mathbf{Z}}_2)+f({\mathbf{Z}}_3)).\hfill \end{array}$$

(26)

When the coefficients $c_1=c_3=\frac{1}{2-2^{\frac{1}{3}}}$, $c_2=\frac{-2^{\frac{1}{3}}}{2-2^{\frac{1}{3}}}$ is satisfied, it is proved that the scheme (26) has the fourth order accuracy [20].

We propose a new fourth order energy preserving scheme of Equation (9) based on the second order scheme (10) by the composition method

$$\begin{array}{cc}\hfill & \mathbf{M}\frac{{\mathbf{Z}}^{n,1}-{\mathbf{Z}}^n}{\tau }=c_1{\int }_0^1{\nabla }_{\mathbf{Z}}E((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n,1})d\xi =c_1{\int }_0^{1}f((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n,1})d\xi ,\hfill \\ & \mathbf{M}\frac{{\mathbf{Z}}^{n,2}-{\mathbf{Z}}^{n,1}}{\tau }=c_2{\int }_0^1{\nabla }_{\mathbf{Z}}E((1-\xi ){\mathbf{Z}}^{n,1}+\xi {\mathbf{Z}}^{n,2})d\xi =c_2{\int }_0^{1}f((1-\xi ){\mathbf{Z}}^{n,1}+\xi {\mathbf{Z}}^{n,2})d\xi ,\hfill \\ & \mathbf{M}\frac{{\mathbf{Z}}^{n+1}-{\mathbf{Z}}^{n,2}}{\tau }=c_3{\int }_0^1{\nabla }_{\mathbf{Z}}E((1-\xi ){\mathbf{Z}}^{n,2}+\xi {\mathbf{Z}}^{n+1})d\xi =c_3{\int }_0^{1}f((1-\xi ){\mathbf{Z}}^{n,2}+\xi {\mathbf{Z}}^{n+1})d\xi ,\hfill \end{array}$$

(27)

where $c_1=c_3=\frac{1}{2-2^{\frac{1}{3}}}$, $c_2=\frac{-2^{\frac{1}{3}}}{2-2^{\frac{1}{3}}}$.

According to Equation (21), Equation (27) can be transformed into the same form. We can obtain that

$$\begin{array}{cc}\hfill & \mathbf{G}{\mathbf{Y}}^{n,1}=\mathbf{G}{\mathbf{Y}}^n+\tau c_1{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi ,\hfill \\ & \mathbf{G}{\mathbf{Y}}^{n,2}=\mathbf{G}{\mathbf{Y}}^{n,1}+\tau c_2{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi ,\hfill \\ & \mathbf{G}{\mathbf{Y}}^{n+1}=\mathbf{G}{\mathbf{Y}}^{n,2}+\tau c_3{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,2}+\xi {\mathbf{Y}}^{n+1})d\xi ,\hfill \end{array}$$

(28)

The function $\mathbf{Y}(t_{n+1})$ is expanded at $\mathbf{Y}(t_n)$, the Taylor expansion is obtained,

$$\begin{array}{c}\hfill \mathbf{Y}(t_{n+1})=\mathbf{Y}(t_n)+\frac{d\mathbf{Y}(t_n)}{dt}\tau +\frac{{\tau }^2}{2}\frac{d^2\mathbf{Y}(t_n)}{d{t}^2}+\frac{{\tau }^3}{3!}\frac{d^3\mathbf{Y}(t_n)}{d{t}^3}+\frac{{\tau }^4}{4!}\frac{d^4\mathbf{Y}(t_n)}{d{t}^4}+O({\tau }^5).\end{array}$$

(29)

Multiplying ${\mathbf{G}}^4$ to both side of the Equation (29), we can obtain that

$$\begin{array}{cc}\hfill {\mathbf{G}}^4\mathbf{Y}(t_{n+1})& ={\mathbf{G}}^4\mathbf{Y}(t_n)+{\mathbf{G}}^4\frac{d\mathbf{Y}(t_n)}{dt}\tau +\frac{{\tau }^2}{2}{\mathbf{G}}^4\frac{d^2\mathbf{Y}(t_n)}{d{t}^2}+\frac{{\tau }^3}{3!}{\mathbf{G}}^4\frac{d^3\mathbf{Y}(t_n)}{d{t}^3}\hfill \\ & +\frac{{\tau }^4}{4!}{\mathbf{G}}^4\frac{d^4\mathbf{Y}(t_n)}{d{t}^4}+O({\tau }^5)\hfill \end{array}$$

(30)

where

$$\begin{array}{cc}\hfill & {\mathbf{G}}^4\frac{d^2\mathbf{Y}(t_n)}{d{t}^2}={\mathbf{G}}^3\frac{d}{dt}(g(\mathbf{Y}(t_n)))={\mathbf{G}}^3\frac{\partial g(\mathbf{Y}(t_n))}{\partial \mathbf{Y}}\frac{d\mathbf{Y}}{dt}={\mathbf{G}}^2[g_k^i{g}^k],\hfill \\ & {\mathbf{G}}^4\frac{d^3\mathbf{Y}(t_n)}{d{t}^3}={\mathbf{G}}^2\frac{d}{dt}([g_k^i{g}^k])=\mathbf{G}([g_k^i{g}_m^k{g}^m]+[g_{kj}^i{g}^k{g}^j])\hfill \\ & {\mathbf{G}}^4\frac{d^4\mathbf{Y}(t_n)}{d{t}^4}=\mathbf{G}\frac{d}{dt}([g_k^i{g}_m^k{g}^m]+[g_{kj}^i{g}^k{g}^j])=[g_{kjm}^i{g}^k{g}^j{g}^m]+3[g_{kj}^i{g}_m^k{g}^j{g}^m]\hfill \\ & +[g_k^i{g}_{mj}^k{g}^j{g}^m]+[g_k^i{g}_m^k{g}_j^m{g}^j].\hfill \end{array}$$

(31)

So Equation (30) can be written as

$$\begin{array}{cc}\hfill {\mathbf{G}}^4\mathbf{Y}(t_{n+1})& ={\mathbf{G}}^4\mathbf{Y}(t_n)+{\mathbf{G}}^{3}g(\mathbf{Y}(t_n))\tau +\frac{{\tau }^2}{2}{\mathbf{G}}^2[g_k^i{g}^k]+\frac{{\tau }^3}{3!}\mathbf{G}([g_k^i{g}_m^k{g}^m]+\hfill \\ & [g_{kj}^i{g}^k{g}^j])+\frac{{\tau }^4}{4!}([g_{kjm}^i{g}^k{g}^j{g}^m]+3[g_{kj}^i{g}_m^k{g}^j{g}^m]+[g_k^i{g}_{mj}^k{g}^j{g}^m]\hfill \\ & +[g_k^i{g}_m^k{g}_j^m{g}^j])+O({\tau }^5)\hfill \end{array}$$

(32)

Theorem 3.

Scheme (28) has the fourth order accuracy.

Proof. 

The composition scheme (28) can be written as

$$\begin{array}{cc}\hfill \mathbf{G}{\mathbf{Y}}^{n+1}& =\mathbf{G}{\mathbf{Y}}^n+(c_1\tau {\int }_0^{1}g({\mathbf{Y}}^n+\xi ({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n))d\xi +c_2\tau {\int }_0^{1}g({\mathbf{Y}}^{n,1}\hfill \\ & +\xi ({\mathbf{Y}}^{n,2}-{\mathbf{Y}}^{n,1}))d\xi +c_3\tau {\int }_0^{1}g({\mathbf{Y}}^{n,2}+\xi ({\mathbf{Y}}^{n+1}-{\mathbf{Y}}^{n,2}))d\xi ),\hfill \end{array}$$

(33)

Multiplying ${\mathbf{G}}^3$ to both side of the equation, we will obtain

$$\begin{array}{cc}\hfill {\mathbf{G}}^4{\mathbf{Y}}^{n+1}& ={\mathbf{G}}^4{\mathbf{Y}}^n+{\mathbf{G}}^3(c_1\tau {\int }_0^{1}g({\mathbf{Y}}^n+\xi ({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n))d\xi +c_2\tau {\int }_0^{1}g({\mathbf{Y}}^{n,1}\hfill \\ & +\xi ({\mathbf{Y}}^{n,2}-{\mathbf{Y}}^{n,1}))d\xi +c_3\tau {\int }_0^{1}g({\mathbf{Y}}^{n,2}+\xi ({\mathbf{Y}}^{n+1}-{\mathbf{Y}}^{n,2}))d\xi ),\hfill \end{array}$$

(34)

expand to $\tau$s fourth order to calculate their Taylor expansion

$$\begin{array}{cc}\hfill & {\mathbf{G}}^3{\int }_0^{1}g({\mathbf{Y}}^n+\xi ({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n))d\xi \hfill \\ & ={\int }_0^1({\mathbf{G}}^{3}g({\mathbf{Y}}^n)+{\mathbf{G}}^3\xi \frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n)+{\mathbf{G}}^3\frac{{\xi }^2}{2!}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}){({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n)}^2\hfill \\ & +{\mathbf{G}}^3\frac{{\xi }^3}{3!}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}})){({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n)}^3)d\xi +O({\tau }^4)\hfill \\ & ={\int }_0^1({\mathbf{G}}^{3}g({\mathbf{Y}}^n)+{\mathbf{G}}^2\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}{c}_1\tau \xi {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi +\hfill \\ & \frac{1}{2!}\mathbf{G}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}})(\xi c_1\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi {)}^2+\frac{1}{3!}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}))\hfill \\ & (\xi c_1\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi {)}^3)d\xi +O({\tau }^4).\hfill \end{array}$$

(35)

The integral ${\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi$ appears on the right part of (35), so it should be replaced by its Taylor expansion until it does not appear on the right part. So

$$\begin{array}{cc}\hfill & {\mathbf{G}}^3{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi \hfill \\ & ={\int }_0^1({\mathbf{G}}^{3}g({\mathbf{Y}}^n)+\xi {\mathbf{G}}^2\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}{c}_1\tau {\int }_0^1(g({\mathbf{Y}}^n)+\xi \frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n)+\hfill \\ & \frac{{\xi }^2}{2!}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}){({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n)}^2)d\xi +\frac{1}{2!}\mathbf{G}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}})(\xi c_1\tau {\int }_0^1(g({\mathbf{Y}}^n)\hfill \\ & +\xi \frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n){)d\xi )}^2+\frac{1}{3!}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}))(\xi c_1\tau {\int }_0^{1}g({\mathbf{Y}}^n)d\xi {)}^3)d\xi \hfill \\ & +O({\tau }^4)\hfill \\ & ={\mathbf{G}}^{3}g({\mathbf{Y}}^n)+\frac{c_1}{2}\tau {\mathbf{G}}^2[g_k^i{g}^k]+{(c_1\tau )}^2(\frac{1}{4}\mathbf{G}[g_k^i{g}_m^k{g}^m]+\frac{1}{6}\mathbf{G}[g_{kj}^i{g}^k{g}^j])+\hfill \\ & {(c_1\tau )}^3(\frac{1}{8}[g_k^i{g}_m^k{g}_j^m{g}^j]+\frac{1}{12}[g_k^i{g}_{mj}^k{g}^j{g}^m]+\frac{1}{6}[g_{kj}^i{g}_m^k{g}^j{g}^m]+\frac{1}{24}[g_{kjm}^i{g}^k{g}^j{g}^m])+O({\tau }^4).\hfill \end{array}$$

(36)

The integral ${\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi$ and ${\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,2}+\xi {\mathbf{Y}}^{n+1})d\xi$ can be expanded by the same method. So

$$\begin{array}{cc}\hfill & {\mathbf{G}}^3{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi \hfill \\ & ={\int }_0^1({\mathbf{G}}^{3}g({\mathbf{Y}}^n)+{\mathbf{G}}^3\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}(({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n)+\xi ({\mathbf{Y}}^{n,2}-{\mathbf{Y}}^{n,1}))+\frac{1}{2!}{\mathbf{G}}^3\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}})\hfill \\ & {(({\mathbf{Y}}^{n,1}-{\mathbf{Z}}^n)+\xi ({\mathbf{Y}}^{n,2}-{\mathbf{Y}}^{n,1}))}^2+\frac{1}{3!}{\mathbf{G}}^3\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}))(({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n)+\hfill \\ & \xi ({\mathbf{Y}}^{n,2}-{\mathbf{Y}}^{n,1}){)}^3)d\xi +O({\tau }^4)\hfill \\ & ={\int }_0^1({\mathbf{G}}^{3}g({\mathbf{Y}}^n)+{\mathbf{G}}^2\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}(c_1\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi +\xi c_2\tau {\int }_0^{1}g((1-\hfill \\ & \xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi )+\frac{1}{2!}\mathbf{G}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}})(c_1\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi \hfill \\ & +\xi c_2\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2}){d\xi )}^2+\frac{1}{3!}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}))(c_1\tau {\int }_0^{1}g((1-\hfill \\ & \xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi +\xi c_2\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi {)}^3)d\xi +O({\tau }^4).\hfill \end{array}$$

(37)

The integral ${\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi$ in (37) can be replaced by its Taylor expansion. The final solution is

$$\begin{array}{cc}\hfill & {\mathbf{G}}^3{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi \hfill \\ & ={\mathbf{G}}^{3}g({\mathbf{Y}}^n)+\tau ((c_1+\frac{c_2}{2}){\mathbf{G}}^2[g_k^i{g}^k])+{\tau }^2((\frac{c_1^2}{2}+\frac{c_1{c}_2}{2}+\frac{c_2^2}{4})\mathbf{G}[g_k^i{g}_m^k{g}^m]+(\frac{c_1^2}{2}+\frac{c_2^2}{6}+\hfill \\ & \frac{c_1{c}_2}{2})\mathbf{G}[g_{kj}^i{g}^k{g}^j])+{\tau }^3((\frac{c_1^3}{4}+\frac{c_1^2{c}_2}{4}+\frac{c_1{c}_2^2}{4}+\frac{c_2^3}{8})[g_k^i{g}_m^k{g}_j^m{g}^j]+(\frac{c_1^3}{6}+\frac{c_1^2{c}_2}{4}+\frac{c_2^3}{12}\hfill \\ & +\frac{c_1{c}_2^2}{4})[g_k^i{g}_{mj}^k{g}^j{g}^m]+(\frac{c_1^3}{2}+\frac{3c_1^2{c}_2}{4}+\frac{c_2^3}{6}+\frac{7c_1{c}_2^2}{12})[g_{kj}^i{g}_m^k{g}^j{g}^m]+(\frac{c_1^3}{6}+\frac{c_2^3}{24}+\hfill \\ & \frac{c_1^2{c}_2}{4}+\frac{c_1{c}_2^2}{6})[g_{kjm}^i{g}^k{g}^j{g}^m])+O({\tau }^4).\hfill \end{array}$$

(38)

The integral ${\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,2}+\xi {\mathbf{Y}}^{n+1})d\xi$ can be calculated by the same method, the solution is

$$\begin{array}{cc}\hfill & {\mathbf{G}}^3{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,2}+\xi {\mathbf{Y}}^{n+1})d\xi \hfill \\ & ={\int }_0^1({\mathbf{G}}^{3}g({\mathbf{Y}}^n)+{\mathbf{G}}^3\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}(({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n)+({\mathbf{Y}}^{n,2}-{\mathbf{Y}}^{n,1})+\xi ({\mathbf{Y}}^{n+1}-{\mathbf{Y}}^{n,2}))\hfill \\ & +\frac{1}{2!}{\mathbf{G}}^3\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}){(({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n)+({\mathbf{Y}}^{n,2}-{\mathbf{Z}}^{n,1})+\xi ({\mathbf{Y}}^{n+1}-{\mathbf{Y}}^{n,2}))}^2+\hfill \\ & \frac{1}{3!}{\mathbf{G}}^3\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}})){(({\mathbf{Y}}^{n,1}-{\mathbf{Y}}^n)+({\mathbf{Y}}^{n,2}-{\mathbf{Y}}^{n,1})+\xi ({\mathbf{Y}}^{n+1}-{\mathbf{Y}}^{n,2}))}^3)d\xi \hfill \\ & +O({\tau }^4)\hfill \\ & ={\int }_0^1({\mathbf{G}}^{3}g({\mathbf{Y}}^n)+{\mathbf{G}}^2\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}(c_1\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi +c_2\tau {\int }_0^{1}g((1-\hfill \\ & \xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi +\xi c_3\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,2}+\xi {\mathbf{Y}}^{n+1})d\xi )+\frac{1}{2!}\mathbf{G}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}})\hfill \\ & (c_1\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi +c_2\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi +\hfill \\ & \xi c_3\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,2}+\xi {\mathbf{Y}}^{n+1}){d\xi )}^2+\frac{1}{3!}\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial }{\partial \mathbf{Y}}(\frac{\partial g({\mathbf{Y}}^n)}{\partial \mathbf{Y}}))({\mathbf{Y}}^n)(c_1\tau {\int }_0^{1}g((1-\hfill \\ & \xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi +c_2\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi +\xi c_3\tau {\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,2}+\hfill \\ & \xi {\mathbf{Y}}^{n+1}{)d\xi )}^3)d\xi +O({\tau }^4).\hfill \end{array}$$

(39)

The integral ${\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi$ and ${\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi$ in (39) can be replaced by its Taylor expansion. The final solution is

$$\begin{array}{cc}\hfill & {\mathbf{G}}^3{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,2}+\xi {\mathbf{Y}}^{n+1})d\xi \hfill \\ & ={\mathbf{G}}^{3}g({\mathbf{Y}}^n)+\tau (c_1+c_2+\frac{c_3}{2}){\mathbf{G}}^2[g_k^i{g}^k]+{\tau }^2((\frac{c_1^2}{2}+c_1{c}_2+\frac{c_2^2}{2}+\frac{c_1{c}_3}{2}+\frac{c_2{c}_3}{2}\hfill \\ & +\frac{c_3^2}{4})\mathbf{G}[g_k^i{g}_m^k{g}^m]+(\frac{c_1^2}{2}+\frac{c_2^2}{2}+\frac{c_3^2}{6}+c_1{c}_2+\frac{c_1{c}_3}{2}+\frac{c_2{c}_3}{2})\mathbf{G}[g_{kj}^i{g}^k{g}^j])\hfill \\ & +{\tau }^3((\frac{c_1^3}{4}+\frac{c_1^2{c}_2}{2}+\frac{c_1{c}_2^2}{2}+\frac{c_2^3}{4}+\frac{c_1^2{c}_3}{4}+\frac{c_1{c}_2{c}_3}{2}+\frac{c_2^2{c}_3}{4}+\frac{c_1{c}_3^2}{4}+\frac{c_2{c}_3^2}{4}\hfill \\ & +\frac{c_3^3}{8})[g_k^i{g}_m^k{g}_j^m{g}^j]+(\frac{c_1^3}{6}+\frac{c_1^2{c}_2}{2}+\frac{c_2^3}{6}+\frac{c_1{c}_2^2}{2}+\frac{c_1^2{c}_3}{4}+\frac{c_2^2{c}_3}{4}+\frac{c_3^3}{12}+\hfill \\ & \frac{c_1{c}_2{c}_3}{2}+\frac{c_1{c}_3^2}{4}+\frac{c_2{c}_3^2}{4})[g_k^i{g}_{mj}^k{g}^j{g}^m]+(\frac{c_1^3}{2}+\frac{3c_1^2{c}_2}{2}+\frac{c_2^3}{2}+\frac{3c_1{c}_2^2}{2}+\frac{3c_1^2{c}_3}{4}\hfill \\ & +\frac{3c_2^2{c}_3}{4}+\frac{c_3^3}{6}+\frac{3c_1{c}_2{c}_3}{2}+\frac{7c_1{c}_3^2}{12}+\frac{7c_2{c}_3^2}{12})[g_{kj}^i{g}_m^k{g}^j{g}^m]+(\frac{c_1^3}{6}+\frac{c_2^3}{6}+\hfill \\ & \frac{c_3^3}{24}+\frac{c_1^2{c}_2}{2}+\frac{c_1^2{c}_3}{4}+\frac{c_2^2{c}_3}{4}+\frac{c_1{c}_2^2}{2}+\frac{c_1{c}_3^2}{6}+\frac{c_2{c}_3^2}{6}+\frac{c_1{c}_2{c}_3}{2})[g_{kjm}^i{g}^k{g}^j{g}^m])\hfill \\ & +O({\tau }^4).\hfill \end{array}$$

(40)

Let Equations (36), (38) and (40) replace ${\mathbf{G}}^3{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^n+\xi {\mathbf{Y}}^{n,1})d\xi$, ${\mathbf{G}}^3{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,1}+\xi {\mathbf{Y}}^{n,2})d\xi$ and ${\mathbf{G}}^3{\int }_0^{1}g((1-\xi ){\mathbf{Y}}^{n,2}+\xi {\mathbf{Y}}^{n+1})d\xi$ in Equation (34).

Suppose $\mathbf{Y}(t_n)={\mathbf{Y}}^n$ and Equation (33) is compared with Equation (32), if the following equations are satisfied, Equation (33) can have the fourth order accuracy.

$$\begin{array}{cc}\hfill & \tau {\mathbf{G}}^{3}g({\mathbf{Y}}^n):c_1+c_2+c_3=1,\hfill \\ \hfill & {\tau }^2{\mathbf{G}}^2[g_k^i{g}^k]:\frac{c_1^2}{2}+c_1{c}_2+\frac{c_2^2}{2}+c_1{c}_3+c_2{c}_3+\frac{c_3^2}{2}=\frac{1}{2},\hfill \\ \hfill & {\tau }^3\mathbf{G}[g_k^i{g}_m^k{g}^m]:\frac{c_1^3}{4}+\frac{c_1^2{c}_2}{2}+\frac{c_1{c}_2^2}{2}+\frac{c_2^3}{4}+\frac{c_1^2{c}_3}{2}+c_1{c}_2{c}_3+\frac{c_2^2{c}_3}{2}+\frac{c_3^3}{4}\hfill \\ & +\frac{c_1{c}_3^2}{2}+\frac{c_2{c}_3^2}{2}=\frac{1}{6},\hfill \\ \hfill & {\tau }^3\mathbf{G}[g_{kj}^i{g}^k{g}^j]:\frac{c_1^3}{6}+\frac{c_1^2{c}_2}{2}+\frac{c_2^3}{6}+\frac{c_1{c}_2^2}{2}+\frac{c_2^2{c}_3}{2}+\frac{c_3^3}{6}+c_1{c}_2{c}_3+\frac{c_1{c}_3^2}{2}\hfill \\ & +\frac{c_2{c}_3^2}{2}+\frac{c_1^2{c}_3}{2}=\frac{1}{6},\hfill \\ \hfill & {\tau }^4[g_k^i{g}_m^k{g}_j^m{g}^j]:\frac{c_1^4}{8}+\frac{c_1^3{c}_2}{4}+\frac{c_1^2{c}_2^2}{4}+\frac{c_1{c}_2^3}{4}+\frac{c_2^4}{8}+\frac{c_1^2{c}_2{c}_3}{2}+\frac{c_1{c}_2^2{c}_3}{2}+\frac{c_2^3{c}_3}{4}\hfill \\ & +\frac{c_1^2{c}_3^2}{4}+\frac{c_1{c}_2{c}_3^2}{2}+\frac{c_2^2{c}_3^2}{4}+\frac{c_1{c}_3^3}{4}+\frac{c_2{c}_3^3}{4}+\frac{c_1^3{c}_3}{4}+\frac{c_3^4}{8}=\frac{1}{24},\hfill \\ \hfill & {\tau }^4[g_k^i{g}_{mj}^k{g}^j{g}^m]:\frac{c_1^4}{12}+\frac{c_1^3{c}_2}{6}+\frac{c_1^2{c}_2^2}{4}+\frac{c_2^4}{12}+\frac{c_1{c}_2^3}{4}+\frac{c_1^3{c}_3}{6}+\frac{c_1^2{c}_2{c}_3}{2}+\frac{c_2^3{c}_3}{6}\hfill \\ & +\frac{c_3^4}{12}+\frac{c_1{c}_2^2{c}_3}{2}+\frac{c_1^2{c}_3^2}{4}+\frac{c_2^2{c}_3^2}{4}+\frac{c_1{c}_2{c}_3^2}{2}+\frac{c_1{c}_3^3}{4}+\frac{c_2{c}_3^3}{4}=\frac{1}{24},\hfill \\ \hfill & {\tau }^4[g_{kj}^i{g}_m^k{g}^j{g}^m]:\frac{c_1^4}{6}+\frac{c_1^3{c}_2}{2}+\frac{3c_1^2{c}_2^2}{4}+\frac{c_2^4}{6}+\frac{7c_1{c}_2^3}{12}+\frac{c_1^3{c}_3}{2}+\frac{3c_1^2{c}_2{c}_3}{2}+\frac{c_2^3{c}_3}{2}\hfill \\ & +\frac{c_3^4}{6}+\frac{3c_1{c}_2^2{c}_3}{2}+\frac{3c_1^2{c}_3^2}{4}+\frac{3c_2^2{c}_3^2}{4}+\frac{3c_1{c}_2{c}_3^2}{2}+\frac{7c_1{c}_3^3}{12}+\frac{7c_2{c}_3^3}{12}=\frac{1}{8},\hfill \\ \hfill & {\tau }^4[g_{kjm}^i{g}^k{g}^j{g}^m]:\frac{c_1^4}{24}+\frac{c_1^3{c}_2}{6}+\frac{c_2^4}{24}+\frac{c_1^2{c}_2^2}{4}+\frac{c_1{c}_2^3}{6}+\frac{c_1^3{c}_3}{6}+\frac{c_2^3{c}_3}{6}+\frac{c_3^4}{24}+\frac{c_1^2{c}_2{c}_3}{2}\hfill \\ & +\frac{c_1^2{c}_3^2}{4}+\frac{c_2^2{c}_3^2}{4}+\frac{c_1{c}_2^2{c}_3}{2}+\frac{c_1{c}_3^3}{6}+\frac{c_2{c}_3^3}{6}+\frac{c_1{c}_2{c}_3^2}{2}=\frac{1}{24}.\hfill \end{array}$$

(41)

When $c_1=c_3,$ the above Equations (41) are equivalent to

$$\begin{array}{cc}\hfill & 2c_1+c_2=1,\hfill \\ \hfill & -2c_1^3+4c_1^2-2c_1+\frac{1}{3}=0.\hfill \end{array}$$

(42)

We can obtain that $c_1=c_3=\frac{1}{2-2^{\frac{1}{3}}}$, $c_2=\frac{-2^{\frac{1}{3}}}{2-2^{\frac{1}{3}}}$.

The coefficients are the same as the coefficients of the Qin composition method. So

$$\begin{array}{cc}\hfill {\mathbf{G}}^4{\mathbf{Y}}^{n+1}& ={\mathbf{G}}^4{\mathbf{Y}}^n+{\mathbf{G}}^{3}g({\mathbf{Y}}^n)\tau +\frac{{\tau }^2}{2}{\mathbf{G}}^2[g_k^i{g}^k]+\frac{{\tau }^3}{3!}\mathbf{G}([g_k^i{g}_m^k{g}^m]+\hfill \\ & [g_{kj}^i{g}^k{g}^j])+\frac{{\tau }^4}{4!}([g_{kjm}^i{g}^k{g}^j{g}^m]+3[g_{kj}^i{g}_m^k{g}^j{g}^m]+[g_k^i{g}_{mj}^k{g}^j{g}^m]\hfill \\ & +[g_k^i{g}_m^k{g}_j^m{g}^j])+O({\tau }^5).\hfill \end{array}$$

(43)

We can get ${\mathbf{G}}^4(\mathbf{Y}(t_{n+1})-{\mathbf{Y}}^{n+1})=O({\tau }^5)$, that is $\mathbf{Y}(t_{n+1})-{\mathbf{Y}}^{n+1}=O({\tau }^5)$.

Scheme (28) has the fourth order accuracy. So Scheme (27) has the fourth order accuracy □

Theorem 4.

Scheme (27) can preserve the energy conservation property.

Proof. 

We only consider the first equation of scheme (27). Since $\mathbf{M}$ is a skew symmetric matrix, it is obvious that

$$\begin{array}{cc}\hfill \frac{E({\mathbf{Z}}^{n,1})-E({\mathbf{Z}}^n)}{\tau }& =\frac{1}{\tau }{\int }_0^1\frac{d}{d\xi }E((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n,1})d\xi \hfill \\ & =({\int }_0^1{({\nabla }_{\mathbf{Z}}E((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n,1})d\xi )}^T\frac{{\mathbf{Z}}^{n,1}-{\mathbf{Z}}^n}{\tau }\hfill \\ & =-{(\frac{{\mathbf{Z}}^{n,1}-{\mathbf{Z}}^n}{c_1\tau })}^T\mathbf{M}\frac{{\mathbf{Z}}^{n,1}-{\mathbf{Z}}^n}{\tau }\hfill \\ & =0.\hfill \end{array}$$

(44)

So the first equation of scheme (27) can have the energy conservation property $E({\mathbf{Z}}^{n,1})=E({\mathbf{Z}}^n)$. In the same way, we can obtain that $E({\mathbf{Z}}^{n,1})=E({\mathbf{Z}}^{n,2})=E({\mathbf{Z}}^{n+1})$. Thus, the new composition scheme (27) satisfy the energy conservation $E({\mathbf{Z}}^n)=E({\mathbf{Z}}^{n+1})$. □

3. Discrete Schemes of Multi-Symplectic Sine-Gordon Equation

The sine-Gordon equation is an important nonlinear equation of mathematical physics discovered in the 19th century. It has multiple soliton solutions and preserves the energy conservation of the system. The sine-Gordon solitary wave equation is widely used in scientific and engineering problems, such as the motion of a rapid pendulum attached to a stretched wire, nonlinear optics, and can be used to describe many physical phenomena in fields of fluid mechanics, meteorology, and field theory [24,25]. Many scholars applied the numerical methods to solve sine-Gordon equation [26]. Vu-Quoc et al. [27,28] proposed the finite difference scheme of energy momentum conservation of wave equations. McLachlan et al. simulated the evolution of wave equations by symplectic geometry algorithm [29]. We consider the sine-Gordon equation

$$\begin{array}{c}\hfill u_{tt}-u_{xx}+sin(u)=0.\end{array}$$

(45)

Let $v=u_t$, $w=u_x$, the equation satisfies the following energy conservation law [26]

$$\begin{array}{c}\hfill I={\int }_a^b(\frac{1}{2}(v^2-w^2)-cos(u))dx=c,\end{array}$$

(46)

where I stands for energy, c is a constant. Additionally, the equation is equivalent to

$$\begin{array}{cc}\hfill & -v_t+w_x=sin(u),\hfill \\ & u_t=v,\hfill \\ & -u_x=-w.\hfill \end{array}$$

(47)

Equation (47) can be written as a multi-symplectic structure

$$\begin{array}{c}\hfill {\mathbf{M}}_1{\mathbf{z}}_t+{\mathbf{K}}_1{\mathbf{z}}_x={\nabla }_{\mathbf{z}}{S}_1(\mathbf{z}),\end{array}$$

(48)

where $\mathbf{z}={(u,v,w)}^T\in {\mathbb{R}}^3$, $S_1=\frac{1}{2}(v^2-w^2)-cos(u)$,

$$\begin{array}{c}\hfill {\mathbf{M}}_1=\left(\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 0\end{array}\right),{\mathbf{K}}_1=\left(\begin{array}{ccc}0& 0& 1\\ 0& 0& 0\\ -1& 0& 0\end{array}\right).\end{array}$$

(49)

${\mathbf{M}}_1$ and ${\mathbf{K}}_1$ are skew symmetric matrices, $S:{\mathbb{R}}^3\to \mathbb{R}$ is a scalar smooth function. Equation (45) satisfies the following multi-symplectic conservation law

$$\begin{array}{c}\hfill \frac{\partial }{\partial t}\omega +\frac{\partial }{\partial x}\kappa =0,\end{array}$$

(50)

where $\omega =du\wedge d\psi +\delta dv\wedge du$, $\kappa =dp\wedge d\psi +\delta dw\wedge du$, and ∧ is the exterior product.

Suppose two functions $u_1$ and $u_2\in {\bigwedge }^1(R^n)$, the exterior product of $u_1$ and $u_2$ is defined as

$$(u_1\wedge u_2)({\eta }_1,{\eta }_2)==\left|\begin{array}{cc}{u}_1({\eta }_1)& u_2({\eta }_1)\\ u_1({\eta }_2)& u_2({\eta }_2)\end{array}\right|,{\eta }_1,{\eta }_2\in R^n,$$

which is the orient area of the image of the parallelogram with sides $u({\eta }_1)$ and $u({\eta }_2)$ on the $u_1$, $u_2$ plane. The exterior product of the differential form is defined in the same way. The detailed property of the exterior product can be found in [30].

Applying the Fourier pseudo-spectral method to Equation (48) in spatial direction, the interval $[a,b]$ is divided into N equal subintervals, we can obtain

$$\begin{array}{c}\hfill \mathbf{M}{\mathbf{Z}}_t+\mathbf{K}\mathbf{D}\mathbf{Z}={\nabla }_{\mathbf{Z}}S(\mathbf{Z}),\end{array}$$

(51)

where $\mathbf{Z}={(\mathbf{U},\mathbf{V},\mathbf{W})}^T$, $\mathbf{U}={(u_1,\cdots ,u_N)}^T$, $\mathbf{V}$, $\mathbf{W}$ are similar as $\mathbf{U}$, $S={\displaystyle \sum _{i=1}^N}(\frac{1}{2}(v_i^2-w_i^2)-cos(u_i))$,

$$\begin{array}{c}\hfill \mathbf{M}=\left(\begin{array}{ccc}\mathbf{O}& -\mathbf{I}& \mathbf{O}\\ \mathbf{I}& \mathbf{O}& \mathbf{O}\\ \mathbf{O}& \mathbf{O}& \mathbf{O}\end{array}\right),\mathbf{K}=\left(\begin{array}{ccc}\mathbf{O}& \mathbf{O}& \mathbf{I}\\ \mathbf{O}& \mathbf{O}& \mathbf{O}\\ -\mathbf{I}& \mathbf{O}& \mathbf{O}\end{array}\right),\end{array}$$

(52)

$$\begin{array}{c}\hfill \mathbf{D}=\left(\begin{array}{ccc}{\mathbf{D}}_{\mathbf{1}}& \mathbf{O}& \mathbf{O}\\ \mathbf{O}& {\mathbf{D}}_{\mathbf{1}}& \mathbf{O}\\ \mathbf{O}& \mathbf{O}& {\mathbf{D}}_{\mathbf{1}}\end{array}\right).\end{array}$$

$\mathbf{I}$ is a N-th identity matrix, $\mathbf{O}$ is a N-th zero matrix, ${\mathbf{D}}_{\mathbf{1}}$ is a N-th spectral differential matrix, ${({\mathbf{D}}_{\mathbf{1}}\mathbf{U})}_j={\displaystyle \sum _{k=1}^N}{({\mathbf{D}}_{\mathbf{1}})}_{j,k}{u}_k$.

3.1. Second Order AVF Scheme for Sine-Gordon Equation

Applying the second order AVF method to Equation (51) in time direction, we can obtain the discrete scheme of Equation (45), that is

$$\begin{array}{c}\hfill \mathbf{M}\frac{{\mathbf{Z}}^{n+1}-{\mathbf{Z}}^n}{\tau }+\mathbf{K}\mathbf{D}\frac{{\mathbf{Z}}^{n+1}+{\mathbf{Z}}^n}{2}={\int }_0^1{\nabla }_{\mathbf{Z}}S((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n+1})d\xi \end{array}$$

(53)

where $\tau$ is the time step. The scheme (53) can maintain global energy conservation of Equation (45). Equation (53) produces the following singular integrals in the calculation

$$\begin{array}{c}\hfill {\int }_0^{1}sin((1-\xi )u^n+\xi u^{n+1})d\xi =\frac{cos(u^n)-cos(u^{n+1})}{u^{n+1}-u^n}.\end{array}$$

(54)

In 2007, Iavernaro et al. [31] proposed Boole discrete line integral method based on AVF method of the Hamilton system. The AVF scheme can be written as

$$\begin{array}{c}\hfill \frac{{\mathbf{z}}^{n+1}-{\mathbf{z}}^n}{\tau }={\int }_0^{1}f((1-\xi ){\mathbf{z}}^n+\xi {\mathbf{z}}^{n+1})d\xi =\mathbf{S}{\int }_0^1\nabla H((1-\xi ){\mathbf{z}}^n+\xi {\mathbf{z}}^{n+1})d\xi ,\end{array}$$

(55)

where $\tau$ is the time step, $\mathbf{z}\in {\mathbb{R}}^N$. Suppose the initial value at $t=n\tau$ is ${\mathbf{z}}^n$, the numerical solution at $t=(n+1)\tau$ is ${\mathbf{z}}^{n+1}$, and the simplest path to connect ${\mathbf{z}}^n$ and ${\mathbf{z}}^{n+1}$ is

$$\begin{array}{c}\hfill \sigma (c\tau )=c{\mathbf{z}}^{n+1}+(1-c){\mathbf{z}}^n,c\in [0,1].\end{array}$$

(56)

Applying the Boole integral to the integral term on format (55), let $\mathbf{z}=c_i{\mathbf{z}}^{n+1}+(1-c_i){\mathbf{z}}^n$, we can obtain the following Boole discrete line integral scheme

$$\begin{array}{c}\hfill {\mathbf{z}}^{n+1}={\mathbf{z}}^n+\tau \sum _{i=1}^v{\beta }_i\mathbf{S}\nabla H(c_i{\mathbf{z}}^{n+1}+(1-c_i){\mathbf{z}}^n)\equiv {\mathbf{z}}^n+\tau \sum _{i=1}^v{b}_{i}f(\mathbf{z}),\end{array}$$

(57)

where $c_i=\frac{i-1}{v-1}$, $b_i={\int }_0^1{\displaystyle \prod _{j=1,j\ne i}^v}\frac{t-c_j}{c_i-c_j}dt,i=1,\dots ,v$. $H\in {\prod }_v$ (${\prod }_v$ is the set of polynomials whose highest degree is less than v). So the integrand of the format (57) has $v-1$ degrees. It can calculate the format (57) exactly. In this case, it is equivalent to a Newton–Coates formula based on the equal distance abscissa of v on the interval of $[0,1]$. When $v=5$, the Boole discrete line integral format can be obtained that

$$\begin{array}{cc}\hfill {\mathbf{z}}^{n+1}& ={\mathbf{z}}^n+\frac{\tau }{90}\mathbf{S}(7\nabla H({\mathbf{z}}^n)+32\nabla H(\frac{3{\mathbf{z}}^n+{\mathbf{z}}^{n+1}}{4})+12\nabla H(\frac{{\mathbf{z}}^n+{\mathbf{z}}^{n+1}}{2})\hfill \\ & +32\nabla H(\frac{{\mathbf{z}}^n+3{\mathbf{z}}^{n+1}}{4})+7\nabla H({\mathbf{z}}^{n+1})).\hfill \end{array}$$

(58)

Applying the Bool discrete integral scheme (58) to Equation (51), we can obtain

$$\begin{array}{cc}\hfill & -\frac{v_j^{n+1}-v_j^n}{\tau }+{({\mathbf{D}}_1\frac{{\mathbf{W}}^{n+1}+{\mathbf{W}}^n}{2})}_j=\frac{1}{90}(7sin(u_j^n)+32sin(\frac{3u_j^n+u_j^{n+1}}{4})\hfill \\ & +12sin(\frac{u_j^n+u_j^{n+1}}{2})+32sin(\frac{u_j^n+3u_j^{n+1}}{4})+7sin(u_j^{n+1})),\hfill \\ & \frac{u_j^{n+1}-u_j^n}{\tau }=\frac{1}{90}(7v_j^n+32\frac{3v_j^n+v_j^{n+1}}{4}+12\frac{v_j^n+v_j^{n+1}}{2}+32\frac{v_j^n+3v_j^{n+1}}{4}+7v_j^{n+1}),\hfill \\ & -{({\mathbf{D}}_1\frac{{\mathbf{U}}^n-{\mathbf{U}}^{n+1}}{2})}_j=-\frac{1}{90}(7w_j^n+32\frac{3w_j^n+w_j^{n+1}}{4}+12\frac{w_j^n+w_j^{n+1}}{2}+\hfill \\ & 32\frac{w_j^n+3w_j^{n+1}}{4}+7w_j^{n+1}).\hfill \end{array}$$

(59)

The discrete scheme (59) is equivalent to the following scheme

$$\begin{array}{cc}\hfill & -\frac{v_j^{n+1}}{\tau }+{(\frac{{\mathbf{D}}_1{\mathbf{W}}^{n+1}}{2})}_j=-\frac{v_j^n}{\tau }-{(\frac{{\mathbf{D}}_1{\mathbf{W}}^n}{2})}_j+\frac{1}{90}(7sin(u_j^n)+32sin(\frac{3u_j^n+u_j^{n+1}}{4})\hfill \\ & +12sin(\frac{u_j^n+u_j^{n+1}}{2})+32sin(\frac{u_j^n+3u_j^{n+1}}{4})+7sin(u_j^{n+1})),\hfill \\ & \frac{u_j^{n+1}}{\tau }-\frac{v_j^{n+1}}{2}=\frac{u_j^n}{\tau }+\frac{v_j^n}{2},\hfill \\ & -{(\frac{{\mathbf{D}}_1{\mathbf{U}}^{n+1}}{2})}_j+\frac{w_j^{n+1}}{2}={(\frac{{\mathbf{D}}_1{\mathbf{U}}^n}{2})}_j-\frac{w_j^n}{2}.\hfill \end{array}$$

(60)

Equation (60) can be written as

$$\begin{array}{c}\hfill \mathbf{A}{\mathbf{Z}}^{n+1}=\mathbf{B}{\mathbf{Z}}^n+\mathbf{F},\end{array}$$

(61)

where

$$\begin{array}{c}\hfill \mathbf{A}=\left(\begin{array}{ccc}\mathbf{O}& -\frac{\mathbf{I}}{\tau }& \frac{{\mathbf{D}}_1}{2}\\ \frac{\mathbf{I}}{\tau }& -\frac{\mathbf{I}}{2}& \mathbf{O}\\ -\frac{{\mathbf{D}}_1}{2}& \mathbf{O}& \frac{\mathbf{I}}{2}\end{array}\right),\mathbf{B}=\left(\begin{array}{ccc}\mathbf{O}& -\frac{\mathbf{I}}{\tau }& -\frac{{\mathbf{D}}_1}{2}\\ \frac{\mathbf{I}}{\tau }& \frac{\mathbf{I}}{2}& \mathbf{O}\\ \frac{{\mathbf{D}}_1}{2}& \mathbf{O}& -\frac{\mathbf{I}}{2}\end{array}\right),\end{array}$$

$\mathbf{F}=(\frac{1}{90}(7sin(u_1^n)+32sin(\frac{3u_1^n+u_1^{n+1}}{4})+12sin(\frac{u_1^n+u_1^{n+1}}{2})+32sin(\frac{u_1^n+3u_1^{n+1}}{4})+$

$7sin(u_1^{n+1})),\cdots ,\frac{1}{90}(7sin(u_N^n)+32sin(\frac{3u_N^n+u_N^{n+1}}{4})+12sin(\frac{u_N^n+u_N^{n+1}}{2})$

$+32sin(\frac{u_N^n+3u_N^{n+1}}{4})+7sin(u_N^{n+1}){),0,\cdots ,0,0,\cdots ,0)}^T$.

3.2. Fourth Order Composition AVF Scheme for Sine-Gordon Equation

Applying the fourth order composition AVF method to Equation (51) in time direction, we can obtain the discrete scheme of Equation (45), that is

$$\begin{array}{cc}\hfill & \mathbf{M}\frac{{\mathbf{Z}}^{n,1}-{\mathbf{Z}}^n}{\tau }+c_1\mathbf{K}\mathbf{D}\frac{{\mathbf{Z}}^{n,1}+{\mathbf{Z}}^n}{2}=c_1{\int }_0^1{\nabla }_{\mathbf{Z}}S((1-\xi ){\mathbf{Z}}^n+\xi {\mathbf{Z}}^{n,1})d\xi ,\hfill \\ & \mathbf{M}\frac{{\mathbf{Z}}^{n,2}-{\mathbf{Z}}^{n,1}}{\tau }+c_2\mathbf{K}\mathbf{D}\frac{{\mathbf{Z}}^{n,2}+{\mathbf{Z}}^{n,1}}{2}=c_2{\int }_0^1{\nabla }_{\mathbf{Z}}S((1-\xi ){\mathbf{Z}}^{n,1}+\xi {\mathbf{Z}}^{n,2})d\xi ,\hfill \\ & \mathbf{M}\frac{{\mathbf{Z}}^{n+1}-{\mathbf{Z}}^{n,2}}{\tau }+c_3\mathbf{K}\mathbf{D}\frac{{\mathbf{Z}}^{n+1}+{\mathbf{Z}}^{n,2}}{2}=c_3{\int }_0^1{\nabla }_{\mathbf{Z}}S((1-\xi ){\mathbf{Z}}^{n,2}+\xi {\mathbf{Z}}^{n+1})d\xi .\hfill \end{array}$$

(62)

Using the Boole discrete line integral method, the discrete scheme (62) is equivalent to the following scheme

$$\begin{array}{cc}\hfill & -\frac{v_j^{n,1}-v_j^n}{\tau }+c_1{({\mathbf{D}}_1\frac{{\mathbf{W}}^{n,1}+{\mathbf{W}}^n}{2})}_j=\frac{c_1}{90}(7sin(u_j^n)+32sin(\frac{3u_j^n+u_j^{n,1}}{4})\hfill \\ & +12sin(\frac{u_j^n+u_j^{n,1}}{2})+32sin(\frac{u_j^n+3u_j^{n,1}}{4})+7sin(u_j^{n,1})),\hfill \\ & \frac{u_j^{n,1}-u_j^n}{\tau }=\frac{c_1}{90}(7v_j^n+32\frac{3v_j^n+v_j^{n,1}}{4}+12\frac{v_j^n+v_j^{n,1}}{2}+32\frac{v_j^n+3v_j^{n,1}}{4}+7v_j^{n,1}),\hfill \\ & -c_1{({\mathbf{D}}_1\frac{{\mathbf{U}}^n+{\mathbf{U}}^{n,1}}{2})}_j=-\frac{c_1}{90}(7w_j^n+32\frac{3w_j^n+w_j^{n,1}}{4}+12\frac{w_j^n+w_j^{n,1}}{2}+\hfill \\ & 32\frac{w_j^n+3w_j^{n,1}}{4}+7w_j^{n,1}),\hfill \\ & -\frac{v_j^{n,2}-v_j^{n,1}}{\tau }+c_2{({\mathbf{D}}_1\frac{{\mathbf{W}}^{n,2}+{\mathbf{W}}^{n,1}}{2})}_j=\frac{c_2}{90}(7sin(u_j^{n,1})+32sin(\frac{3u_j^{n,1}+u_j^{n,2}}{4})\hfill \\ & +12sin(\frac{u_j^{n,1}+u_j^{n,2}}{2})+32sin(\frac{u_j^{n,1}+3u_j^{n,2}}{4})+7sin(u_j^{n,2})),\hfill \\ & \frac{u_j^{n,2}-u_j^{n,1}}{\tau }=\frac{c_2}{90}(7v_j^{n,1}+32\frac{3v_j^{n,1}+v_j^{n,2}}{4}+12\frac{v_j^{n,1}+v_j^{n,2}}{2}+32\frac{v_j^{n,1}+3v_j^{n,2}}{4}+7v_j^{n,2}),\hfill \\ & -c_2{({\mathbf{D}}_1\frac{{\mathbf{U}}^{n,1}+{\mathbf{U}}^{n,2}}{2})}_j=-\frac{c_2}{90}(7w_j^{n,1}+32\frac{3w_j^{n,1}+w_j^{n,2}}{4}+12\frac{w_j^{n,1}+w_j^{n,2}}{2}+\hfill \\ & 32\frac{w_j^{n,1}+3w_j^{n,2}}{4}+7w_j^{n,2}),\hfill \\ & -\frac{v_j^{n+1}-v_j^{n,2}}{\tau }+c_3{({\mathbf{D}}_1\frac{{\mathbf{W}}^{n+1}+{\mathbf{W}}^{n,2}}{2})}_j=\frac{c_3}{90}(7sin(u_j^{n,2})+32sin(\frac{3u_j^{n,2}+u_j^{n+1}}{4})\hfill \\ & +12sin(\frac{u_j^{n,2}+u_j^{n+1}}{2})+32sin(\frac{u_j^{n,2}+3u_j^{n+1}}{4})+7sin(u_j^{n+1})),\hfill \\ & \frac{u_j^{n+1}-u_j^{n,2}}{\tau }=\frac{c_3}{90}(7v_j^{n,2}+32\frac{3v_j^{n,2}+v_j^{n+1}}{4}+12\frac{v_j^{n,2}+v_j^{n+1}}{2}+32\frac{v_j^{n,2}+3v_j^{n+1}}{4}+7v_j^{n+1}),\hfill \\ & -c_3{({\mathbf{D}}_1\frac{{\mathbf{U}}^{n,2}+{\mathbf{U}}^{n+1}}{2})}_j=-\frac{c_3}{90}(7w_j^{n,2}+32\frac{3w_j^{n,2}+w_j^{n+1}}{4}+12\frac{w_j^{n,2}+w_j^{n+1}}{2}+\hfill \\ & 32\frac{w_j^{n,2}+3w_j^{n+1}}{4}+7w_j^{n+1}).\hfill \end{array}$$

(63)

Equation (63) can be written as

$$\begin{array}{cc}\hfill & {\mathbf{A}}_1{\mathbf{Z}}^{n,1}={\mathbf{B}}_1{\mathbf{Z}}^n+{\mathbf{F}}_1,\hfill \\ & {\mathbf{A}}_2{\mathbf{Z}}^{n,2}={\mathbf{B}}_2{\mathbf{Z}}^{n,1}+{\mathbf{F}}_2,\hfill \\ & {\mathbf{A}}_3{\mathbf{Z}}^{n+1}={\mathbf{B}}_3{\mathbf{Z}}^{n,2}+{\mathbf{F}}_3,\hfill \end{array}$$

(64)

where

$$\begin{array}{cc}\hfill & {\mathbf{A}}_1=\left(\begin{array}{ccc}\mathbf{O}& -\frac{\mathbf{I}}{\tau }& \frac{c_1{\mathbf{D}}_1}{2}\\ \frac{\mathbf{I}}{\tau }& -\frac{c_1\mathbf{I}}{2}& \mathbf{O}\\ -\frac{c_1{\mathbf{D}}_1}{2}& \mathbf{O}& \frac{c_1\mathbf{I}}{2}\end{array}\right),{\mathbf{B}}_1=\left(\begin{array}{ccc}\mathbf{O}& -\frac{\mathbf{I}}{\tau }& -\frac{c_1{\mathbf{D}}_1}{2}\\ \frac{\mathbf{I}}{\tau }& \frac{c_1\mathbf{I}}{2}& \mathbf{O}\\ \frac{c_1{\mathbf{D}}_1}{2}& \mathbf{O}& -\frac{c_1\mathbf{I}}{2}\end{array}\right),\hfill \\ & {\mathbf{A}}_2=\left(\begin{array}{ccc}\mathbf{O}& -\frac{\mathbf{I}}{\tau }& \frac{c_2{\mathbf{D}}_1}{2}\\ \frac{\mathbf{I}}{\tau }& -\frac{c_2\mathbf{I}}{2}& \mathbf{O}\\ -\frac{c_2{\mathbf{D}}_1}{2}& \mathbf{O}& \frac{c_2\mathbf{I}}{2}\end{array}\right),{\mathbf{B}}_2=\left(\begin{array}{ccc}\mathbf{O}& -\frac{\mathbf{I}}{\tau }& -\frac{c_2{\mathbf{D}}_1}{2}\\ \frac{\mathbf{I}}{\tau }& \frac{c_2\mathbf{I}}{2}& \mathbf{O}\\ \frac{c_2{\mathbf{D}}_1}{2}& \mathbf{O}& -\frac{c_2\mathbf{I}}{2}\end{array}\right),\hfill \\ & {\mathbf{A}}_3=\left(\begin{array}{ccc}\mathbf{O}& -\frac{\mathbf{I}}{\tau }& \frac{c_3{\mathbf{D}}_1}{2}\\ \frac{\mathbf{I}}{\tau }& -\frac{c_3\mathbf{I}}{2}& \mathbf{O}\\ -\frac{c_3{\mathbf{D}}_1}{2}& \mathbf{O}& \frac{c_3\mathbf{I}}{2}\end{array}\right),{\mathbf{B}}_3=\left(\begin{array}{ccc}\mathbf{O}& -\frac{\mathbf{I}}{\tau }& -\frac{c_3{\mathbf{D}}_1}{2}\\ \frac{\mathbf{I}}{\tau }& \frac{c_3\mathbf{I}}{2}& \mathbf{O}\\ \frac{c_3{\mathbf{D}}_1}{2}& \mathbf{O}& -\frac{c_3\mathbf{I}}{2}\end{array}\right),\hfill \end{array}$$

${\mathbf{F}}_1={(\frac{c_1}{90}(7sin(u_1^n)+32sin(\frac{3u_1^n+u_1^{n+1}}{4})+12sin(\frac{u_1^n+u_1^{n+1}}{2})+32sin(\frac{u_1^n+3u_1^{n+1}}{4})+7sin(u_1^{n+1})),\cdots ,\frac{c_1}{90}(7sin(u_N^n)+32sin(\frac{3u_N^n+u_N^{n+1}}{4})+12sin(\frac{u_N^n+u_N^{n+1}}{2})+32sin(\frac{u_N^n+3u_N^{n+1}}{4})+7sin(u_N^{n+1})),0,\cdots ,0,0,\cdots ,0)}^T$. ${\mathbf{F}}_2$, ${\mathbf{F}}_3$ are similar as ${\mathbf{F}}_1$.

The corresponding second order Preissmann scheme of sine-Gordon equation is also given. That is

$$\begin{array}{cc}\hfill & -\frac{v_j^{n+1}-v_j^n}{\tau }+{({\mathbf{D}}_1\frac{{\mathbf{W}}^n+{\mathbf{W}}^{n+1}}{2})}_j=sin(\frac{u_j^{n+1}+u_j^n}{2}),\hfill \\ & \frac{u_j^{n+1}-u_j^n}{\tau }=\frac{v_j^n+v_j^{n+1}}{2},\hfill \\ & -{({\mathbf{D}}_1\frac{{\mathbf{U}}^n+{\mathbf{U}}^{n+1}}{2})}_j=-\frac{w_j^n+w_j^{n+1}}{2}.\hfill \end{array}$$

(65)

4. Numerical Experiments

In this section, numerical experiments for the sine-Gordon equation with periodic boundary conditions are presented to investigate the relative energy error and accuracy of convergence. The discrete energy corresponding to (46) can be expressed as $\overline{\mathtt{I}}$.

$$\begin{array}{c}\hfill \overline{\mathtt{I}}=\Delta x(\sum _{i=0}^{N-1}(\frac{1}{2}({(v_{i+1}^k)}^2-{(w_{i+1}^k)}^2)-cos(u_{i+1}^k)).\end{array}$$

(66)

The energy error at $t=n\tau$ is defined as

$$\begin{array}{c}\hfill \mathtt{Error}(t)=|\frac{\overline{\mathtt{I}}({\mathbf{Z}}^n)-\overline{\mathtt{I}}({\mathbf{Z}}^0)}{\overline{\mathtt{I}}({\mathbf{Z}}^0)}|,\end{array}$$

(67)

where $\overline{\mathtt{I}}({\mathbf{Z}}^0)$ is the initial energy, $\overline{\mathtt{I}}({\mathbf{Z}}^n)$ is the energy value at $t=n\tau$. The maximal module error of numerical solution and exact solution is defined as

$$\begin{array}{c}\hfill {\mathrm{Ł}}^{\infty }(\tau )=\underset{1\le j\le N}{max}|u_j^n-u(x_j,t_n)|.\end{array}$$

(68)

The order of convergence is defined as

$$\begin{array}{c}\hfill \mathtt{Ratio}=\frac{log(\frac{{\mathrm{Ł}}^{\infty }(\tau )}{{\mathrm{Ł}}^{\infty }(\frac{\tau }{2})})}{log(2)}.\end{array}$$

(69)

4.1. Numerical Experiments for Single Solitary Wave

Firstly, we consider the motion of single solitary wave. Equation (45) has the exact solution [32,33]

$$\begin{array}{c}\hfill u(x,t)=4{\mathtt{tan}}^{-1}(t\mathtt{sech}(x)),\end{array}$$

(70)

where $x\in [-20,20]$, $N=100$, $\tau =0.02$, the initial condition is obtained when $t=0$ in Equation (70).

Table 1 shows the maximal module error of numerical solution and exact solution and the order of convergence of the different schemes with different time steps at $t=0.25$. It is easy to see that the orders of convergence of fourth order energy preserving composition AVF scheme is almost equal to 4, and the orders of convergence of second order AVF scheme and second order Preissman method are almost equal to 2. The fourth order energy preserving composition AVF scheme is more accurate than the second order AVF scheme and second order Preissman method, this result is consistent with the theory.

Table 1. The ${\mathtt{L}}^{\infty }$ errors and the order of convergence of three different schemes with $h=0.16$ and different time steps at $t=0.25$.

$\mathit{t}=0.25$	Scheme 1	Order	Scheme 2	Order	Scheme 3	Order
$\tau =0.05$	3.5408 × 10${}^4$	–	3.3818 × 10${}^4$	–	2.2893 × 10${}^6$	–
$\tau =0.025$	8.8508 × 10${}^5$	2.0003	8.4576 × 10${}^5$	1.9995	1.4431 × 10${}^7$	3.9876
$\tau =0.0125$	2.2126 × 10${}^5$	2.0002	2.1146 × 10${}^5$	1.9999	9.0375 × 10${}^9$	3.9971
$\tau =0.00625$	5.5315 × 10${}^6$	2.0001	5.2866 × 10${}^6$	2.0000	5.6367 × 10${}^{10}$	4.0030

Scheme 1 is the second order Preissman scheme, Scheme 2 is the second order AVF scheme, and Scheme 3 is the fourth order composition AVF scheme.

Figure 1 shows the evolution of single solitary waves in $t\in [0,100]$. The numerical solution obtained from the fourth order energy-preserving composition AVF scheme can well simulate the single solitary wave. Figure 2a shows the energy error obtained from the second order AVF scheme. Figure 2b shows the energy error obtained from the fourth order composition AVF scheme. Figure 2c shows the energy error obtained from the second order Preissman scheme. It is obvious that the second order AVF scheme and the fourth order composition AVF scheme can preserve the energy conservation accurately, the second order Preissman scheme only can preserve the energy conservation approximatively.

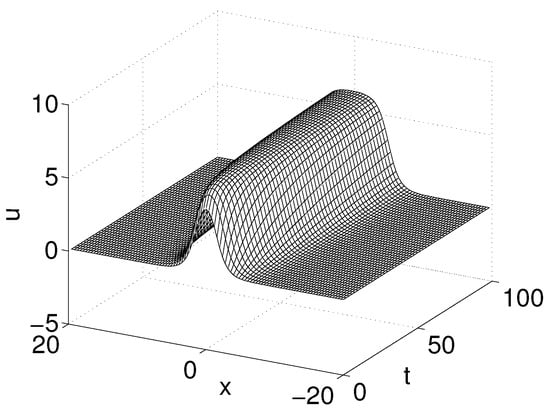
Figure 1. The numerical solutions from $t=0$ to $t=100$ with $\tau =0.02$ and $h=0.4$.

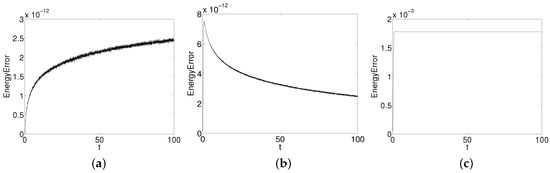
Figure 2. The double solitary wave’s energy error of second order AVF method, fourth order composition method and second order Preissman method in $t\in [0,100]$ with $\tau =0.02$, $h=0.4$. (a) AVF method; (b) composition method; and (c) Preissman method.

4.2. Numerical Experiments for Kink and Anti-Kink Solitary Waves

In this section, we consider the collision behavior of kink and anti-kink solitary waves. Equation (45) has the exact solution

$$\begin{array}{c}\hfill u(x,t)=4arctan(exp(\frac{x+x_0-\beta t}{\sqrt{1-{\beta }^2}}))+4arctan(exp(\frac{-x+x_0-\beta t}{\sqrt{1-{\beta }^2}})),\end{array}$$

(71)

where $x\in [-30,30]$, $N=300$, $\tau =0.02$, $x_0=10$, $\beta =0.5$, the initial condition is obtained when $t=0$ in Equation (71).

Table 2 shows the maximal module error of numerical solution and exact solution and the order of convergence of the different schemes with different time steps at $t=0.2$. It is easy to see that the orders of convergence of fourth order energy preserving composition AVF scheme is close to 4, and the orders of convergence of second order AVF scheme and second order Preissman method are almost equal to 2. The fourth order energy preserving composition AVF scheme is more accurate than the second order AVF scheme and second order Preissman method, this result is consistent with the theory.

Table 2. The ${\mathtt{L}}^{\infty }$ errors and the order of convergence of three different schemes with $h=0.2$ and different time steps at $t=0.2$.

$\mathit{t}=0.2$	Scheme 1	Order	Scheme 2	Order	Scheme 3	Order
$\tau =0.04$	1.5178 × 10${}^5$	–	1.0912 × 10${}^5$	–	7.4527 × 10${}^8$	–
$\tau =0.025$	2.8834 × 10${}^6$	1.9981	2.7312 × 10${}^6$	1.9983	4.7887 × 10${}^9$	3.9601
$\tau =0.0125$	7.2113 × 10${}^7$	1.9994	6.8304 × 10${}^7$	1.9995	3.5881 × 10${}^{10}$	3.7383
$\tau =0.00625$	1.8034 × 10${}^7$	1.9995	1.7082 × 10${}^7$	1.9995	2.7656 × 10${}^{11}$	3.6987

Scheme 1 is the second order Preissman scheme. Scheme 2 is the second order AVF scheme. Scheme 3 is the fourth order composition AVF scheme.

Figure 3 shows the collision behavior of kink and anti-kink solitary waves with time, the fourth order composition AVF scheme can simulate the waves well. As can be seen from Figure 4a, the error of energy is very small, almost close to zero, the second order AVF scheme can preserve the energy conservation well. Figure 4b shows the error of energy from fourth order composition scheme, we can see that the scheme can preserve the energy accurately. From Figure 4c, the error of energy is ${10}^{-4}$. This shows that the second order Preissman scheme can only approximately maintain the energy conservation of the equation.

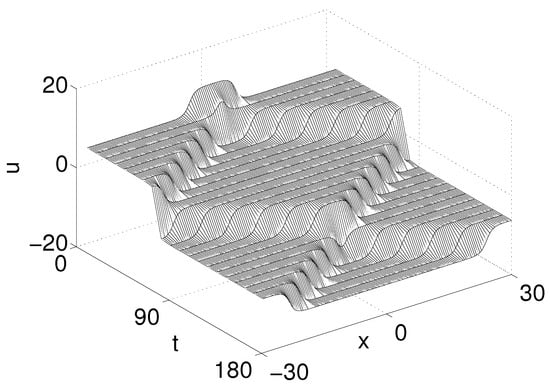
Figure 3. The numerical solutions from $t=0$ to $t=200$ with $\tau =0.02$ and $h=0.2$.

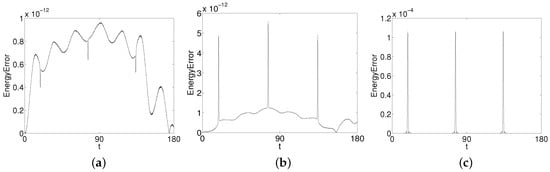
Figure 4. The kink and anti-kink solitary waves energy error of second order AVF method, fourth order composition method and second order Preissman method in $t\in [0,200]$ with $\tau =0.02$, $h=0.2$. (a) AVF method; (b) composition method; and (c) Preissman method.

5. Concluding Remarks

In this paper, a new fourth order energy preserving composition scheme for the multi-symplectic structure PDE is proposed based on the second other AVF method. The new fourth order composition AVF scheme of sine-Gordon equation is compared with the corresponding second order AVF scheme and the second order Preissman scheme. Numerical results showed that the fourth order composition AVF scheme of sine-Gordon equation can have the fourth order accuracy and preserve the energy conservation property. The fourth order energy preserving scheme of the multi-symplectic structure PDE can also be applied to other multi-symplectic structure PDE.