Non-Identical Inverter Rings as an Entropy Source: NIST-90B-Verified TRNG Architecture on FPGAs for IoT Device Integrity

Abstract

True random key generator (TRNG) architectures play a notable role in strengthening information security infrastructure. The development of new entropy sources based on reconfigurable hardware is always in demand, especially for the integrity of devices in IoT applications. TRNGs can be adopted for generating unique device IDs that form the data network in the IoT. A ring oscillator (RO) is an efficient entropy source which can be implemented on FPGAs or realised as ASIC hardware. This work proposes a non-identical RO array as an entropy source. The TRNG architecture, based on an increasing odd number of inverters per ring, was extensively studied. The various statistical and hardware analyses provided encouraging results for this reliable entropy unit. The suggested device-independent non-identical RO structure was implemented on five different types of FPGA hardware belonging to the Xilinx and Intel families, consuming 13 registers and nearly 15 combinational functions. This TRNG achieved a throughput of 3.5 Mbps. While the emergence of the Gaussian response evaluated true randomness, the NIST 800-90B and NIST 800-22 tests yielded good results in terms of the justification of randomness evolving from the proposed TRNG architecture.

1. Introduction

There is an increasing trend towards the IoT in many applications that are automation-centric. The IoT introduced the interconnectivity of threats because of its heterogeneity. Hence, it is essential to safeguard the data acquired or processed by one node from the other nodes. Cryptographic primitives play a large role in data confidentiality, requiring a key generation module to function. The key generation module must be an independent module which generates random numbers for the cryptographic operations [1,2]. This architecture can be utilised along with a data-logging unit and other data processing units for multiple operations, namely one-time pad generation, dynamic IP address generation, session key generation, nonce generation and initialization vector generation for secure communication between devices [3,4]. True random number generators (TRNGs) are crucial components for key generation because of their vast unpredictability [5]. Hence, this work focused on developing a TRNG architecture based on a ring oscillator structure on a reconfigurable hardware platform for continuously producing n-bit non-reversible random numbers. The initial studies have produced good statistical results with limited resource utilisation, ensuring the lightweight property required by resource-constrained IoT devices. Noticeably, any FPGA architecture can include this architecture, making it device-independent.

In general, RNGs can be classified into two types, namely, pseudo-random number generators (PRNGs) and true random number generators (TRNGs) [6,7,8]. However, because of the merits of TRNGs in terms of unpredictability, they have been preferred over PRNG in many more cases including, but not restricted to, cryptographic key generation, nonce generation, one-time pads, random simulations, gaming, test pattern generators and device authentication [9,10].

The National Institute of Standards and Technology (NIST) has released a standard called NIST SP 800-90B, which comprises the design principles for every TRNG source. According to this compilation, any TRNG must have a noise source, a harvesting mechanism and post-processing units to generate true random bits. In addition, the conditioning circuit can optionally be used for processing the results of the TRNG. It may reduce or enhance the randomness of the obtained bits based on the conditioning operation used [11].

TRNGs incorporate live noise sources, the response of which changes continuously over time. FPGAs are the most widely preferred choice among all the hardware options for the development of TRNGs because of their algorithms’ upgradability, agility, reconfigurability, easy prototyping and faster time to market [12]. FPGA-based TRNG implementations have attracted researchers to develop novel TRNGs. Clock jitters are the supreme source of randomness extraction for TRNGs in FPGAs, where the tiny aberration in the oscillation frequency has attracted considerable attention. Jitters are a live phenomenon in which the edges of the clock deviate from their ideal position. Hence, they can be used as a source of randomness in TRNGs [13].

This work aimed to generate true random bits by adopting a novel entropy source, namely a non-identical inverter-based ring oscillator (RO) structure. The focus, highlights and verification methodologies are listed below:

• A non-identical entropy source was designed with ROs;
• Lightweight post-processing of the XOR corrector was used for the extraction of the randomness;
• The design consumed only 80 inverters to accomplish random number generation;
• The device’s independence from the proposed TRNG design was verified by implementing it on two different vendors of FPGAs, namely Intel and Xilinx-AMD.

Different analyses were carried out, such as Gaussian jitters estimation, Hamming distance, equidistribution, hardware utility and timing analysis. From the observations, the following results have been found:

• Evidence of Gaussian jitter has been found through Keysight Logic Analyzer, and the standard deviation of the jitter is calculated as 24.010 ns;
• An equidistribution of 0.99999 is achieved without any post-processing;
• The TRNG design consumed only 15 LUTs and 13 registers to accommodate the TRNG on Intel FPGAs, which is <1% of its total hardware footprint;
• 296 ms was taken for the TRNG to generate 10,48,576 bits with the 25 MHz of the sampling clock;
• Validation of the true randomness was carried out through batteries of NIST SP 800-90B and -22 tests;
• The proposed TRNG design does not require any post-processing mechanism to enhance the randomness.

The proposed work was verified by passing standard test suites such as NIST SP 800-90B and NIST SP 800-22. Also, a minimum of 64-bit change was identified in Hamming distance calculation, ensuring the minimum switching activity for an RNG. Furthermore, the Restart experiment was conducted to verify the true randomness of the proposed TRNG.

2. Related Work

Many TRNG architectures have been realised on reconfigurable hardware platforms. Fischer and Drutarovsky proposed one such work, wherein the TRNG uses an on-chip analogue phase-locked loop (PLL) on Altera APEX EP20K200-2X FPLDs. This method utilises intrinsic randomness from the jitters generated by the on-chip PLLs. An XOR decimator was used in this work to extract the randomness. This design consumed 121 logic cells and four embedded system blocks to generate 8 × 1024 true random bits. NIST tests have been performed to test the statistical properties of TRNGs [14]. Dejun and Zhen suggested another work based on a PLL, which extracted the true randomness from the embedded analogue PLL. The proposed TRNG design was implemented on an APEX EP20K200-2X device occupying 150 logic elements [15].

Johnson et al. recommended an approach for a TRNG only for Xilinx FPGAs using beat frequency detection from digital clock managers (DCM) as a source of randomness. Tenability was achieved on the fly through dynamic partial reconfiguration of the TRNG on a Xilinx Virtex-V FPGA. This design used 19 LUTs and 34 global buffers, and consumed 1.470 W of power to accommodate the TRNG [16]. Unfortunately, though TRNGs, as mentioned earlier, have excellent statistical properties, they are device-dependent because of their on-chip utilisation of the unique components on FPGAs, making them unsuitable for other families of FPGA.

To make the TRNG design a generic one, ROs can be adopted. An RO can be constructed from a series of inverters connected via feedback to form an oscillator, which generates the required frequency with jitters. Kohlbrenner and Gaj introduced an RO-based TRNG with identical lengths of inverter chains in which the frequencies were relatively the same. Therefore, the deviations caused by the placement of ROs play an important role in exploiting jitters. This TRNG scheme was implemented on a Xilinx XCV1000 FPGA, which utilised one configurable logic block (CLB) with self-testing capability. It achieved a throughput of 0.5 Mbps with excellent statistical characteristics that were verified through Gaussian analysis and the NIST test suite [17].

To the best of our knowledge, the very first multi-event RO-based TRNG was proposed by Sunar et al. [18]. They proposed a mathematical model of an RO-based TRNG wherein the phase jitters produced by the ROs were taken as the origin of true randomness. This TRNG architecture encompassed four parts: the oscillator rings, the XOR tree, the sampler, and a resilient function as the post-processor. It deployed the XOR tree with a D flip-flop and simple resilient functions. The “coupon collector” problem was discussed in this work, in which the TRNG’s design was driven through an identical inverter ring. The true random bits were produced at a speed of 2.5 Mbps, with a maximum achievable entropy of 0.97 [18]. Further, Schellekens et al. performed a continuation of Sunar et al.’s work on a Xilinx Virtex XC2VP30 FPGA where the TRNG’s design required 1664 slices. The TRNG proposed in [13] was modified with 210 rings which consumed 973 slices, and this design yielded a speed of more than 2 Mbps with a 40 MHz sampling frequency [19].

Jessa and Matuszewkski prescribed an RO-based TRNG in which the combined independent jitters were the entropy source. A desynchronisation technique (an XOR tree) was adopted to harvest the true randomness from the independent entropy sources. The enhancement of the entropy was accomplished using an auxiliary source of randomness (ASR) with ROs. A Xilinx Virtex–5 FPGA was the target platform for implementing this TRNG, with which the random bits were acquired for different sampling frequencies, such as 100, 150, 200 and 250 MHz. The maximum throughput achieved by this TRNG was 20 Mbps [20]. To enable this work to obtain better statistical properties, an additional delay path was included with an RO-based combined TRNG. Carry4 logic (a carry chain primitive) in the Virtex-5 FPGA was used to improve the design. The Carry4 primitive belongs to the Virtex-5 FPGA, which shows the device-dependent nature of the proposed work. However, it strengthened the TRNG’s design by offering resistance against frequency injection attacks. NIST tests and restart experiments were conducted for this TRNG designed with 50 rings, achieving a maximum throughput of 12.5 Mbps at an operating sampling frequency of 100 MHz [21].

Furthermore, Łoza and Matuszewski presented an RO-governed TRNG architecture with SHA–256 as a post-processing schema. This method was free from biasing issues and correlation between adjacent bits. In this work, an eight-stage RO was developed and implemented on a Xilinx Virtex–5 FPGA device to experiment with and evaluate the architecture. The design occupied 2540 slice registers and 2467 slice LUTs. This design’s maximum frequency was 263 MHz, achieving a throughput of 36 Mbps [22].

Wold and Chik improved the RO TRNG proposed by Sunar et al. [15], using an Altera Cyclone II FPGA and applying a 100 MHz frequency to achieve a throughput of 100 Mbps [23]. A D flip-flop was also added at each output stage of the ROs, through which the high transition effects of the RO and the metastability induced in the D flip-flop were controlled. In this work, two different modalities of TRNGs were constructed. The first one had 25 rings of ROs that occupied 83 logic elements, and the second one had 50 rings of ROs which occupied 167 logic elements. True randomness was confirmed through a restart experiment.

Recently, a few studies of TRNGs on different implementation platforms other than FPGAs have been reported [24,25,26]. One such work was caried out by Fazili et al., namely, the quantum dot cellular automata (QCA). This work combined feedback and feed-forward D flip-flops in a certain arrangement, which consumed 25 cells on the QCA platform. NIST SP 800-22 batteries of tests were performed to validate the design. However, the true core randomness was not evaluated with min entropy, which is a primary concern of TRNGs. Moreover, this QCA was a simulation, which is likely to be different from real-time implementations. Moreover, the speed of the TRNG was not discussed [24]. Morsali et al. proposed a TRNG governed by spin transfer torque magnetic tunnel junction (STT-MTJ) technology. A simulation was carried out and it showed that this proposed TRNG had good stochastic properties that were verified by the NIST test suite. Moreover, this TRNG had a low power consumption rate of 53% compared with the earlier works reported [24].

Saranya et al. carried out research on a programmable delay line (PDL) inverter-based TRNG, focusing only on synthesis rather than true random acquisition in real time [26]. Dong et al. proposed an application-specific integrated circuit (ASIC) type of TRNG, which used the Bernoulli map with a reduced operational amplifier stage. The standard of 180 nm was adopted for the experiment, in which the TRNG design achieved a speed of 500 kbps with 4.68 µW of power consumption. Furthermore, the randomness was validated using NIST SP 800-22 tests. However, the raw true random bits were not evaluated with min-entropy estimations [27]. Teh et al. presented a hyperchaos-based post-processor for software-based TRNGs, improving the randomness. Hyperchaos can be used as a driver circuit to obtain the chaotic parameters from the quantised bits of software-based TRNGs. Hence, the TRNG’s bits were driven to boost their randomness [28]. Seranao et al. proposed a multimodal RO-based TRNG which uses the collapsed natured on multimodal to generate high-quality true random bits. This TRNG was implemented on Xilinx Artix-7 FPGA in which the design occupies <1% of the total hardware and yields 9.1 Mbps as throughput. True randomness was evaluated through NIST batteries of tests [29].

Though the works mentioned earlier illustrated different TRNG structures, the RO-based TRNGs have been preferred because of their ability for hardware realisation, portability and feasibility. Moreover, FPGAs are a fruitful and immediate platform for easy prototyping that is very near to the ASIC implementations.

So far, ROs with identical structure have played an immense role in the entropy sources of TRNGs. However, though the TRNGs [30,31,32,33,34,35,36,37,38,39,40,41,42,43,44] offer agreeable statistical properties, the designs consume a large number of hardware resources with reduced throughput, which may not make them suitable as part of time-critical cryptographic architectures. In this work, we propose a non-identical structure of RO as a new entropy element which was verified and validated through standard metrics, including the NIST SP 800-90B battery of tests. Furthermore, this structure consumed only 80 inverters and fewer hardware resources. Finally, its device-independent nature was verified by implementing the design on different FPGA configurations. The cumulative limitations of the works are listed in Table 1.

Table 1. TRNGs and its limitations.

References	TRNG Source	Limitations
Refs. [14,15]	Phase Locked Loop	Device-dependent; synchronization of jitter clocks is difficult; low throughput
Ref. [17]	Identical Ring Oscillator	Frequencies were relatively the same; the placement of ROs plays an essential role in exploiting jitters; low throughput
Ref. [19]	Identical Ring Oscillator	Suffers from coupon collector problem; frequencies were relatively the same; low throughput
Ref. [21]	Identical Ring Oscillator + Carry4 Chain Logic	Device dependent; more rings of ring oscillators were used
Ref. [22]	Identical Ring Oscillator + SHA 256	Consumes high volume hardware footprint

This article is structured as follows. Section 3 deals with the architecture of the proposed TRNG. Next, the experimental results are presented in Section 4 and the proposed TRNG is compared with the existing TRNGs. Finally, Section 5 summarises the work and gives future research directions in line with the proposed work.

3. Proposed Architecture

The architecture presented here was inspired by the TRNG design proposed by Sunar et al. [18]. Although this work adopted the same concept of utilising clock jitters, the true randomness was extracted by ROs with a non-identical structure. A pictorial representation of the proposed architecture is shown in Figure 1. It comprises four major blocks: a noise source, randomness extraction, post-processing and a health test. Additionally, the conditioning circuit is preferred for enhancing the randomness.

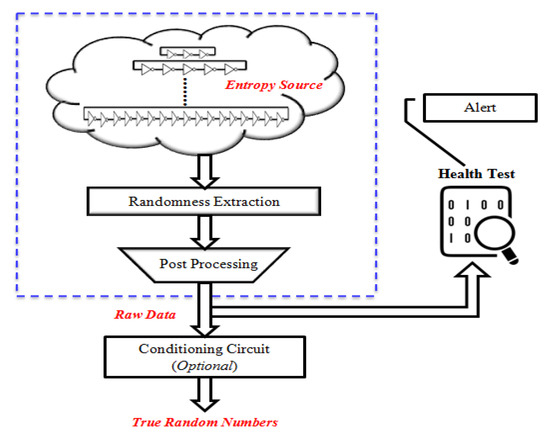
Figure 1. Pictorial representation of the proposed TRNG.

The jitters were generated by the ROs, after which they were fused with one another by the XOR operation to harvest the true randomness. Next, post-processing was applied to the extracted bits to remove the bias in the random sequence. Finally, sampling was carried out to generate the raw true random numbers. Conditioning and a health test were also applied to strengthen the process of true random number generation.

3.1. Source of Entropy

ROs were the source of entropy through which the jitters emanating from the toggling of the clock were generated. This work utilised an RO-based entropy source with a non-identical structure. A structure comprising 8 ROs with 80 inverters was constructed to form an entropy source, as shown in Figure 2.

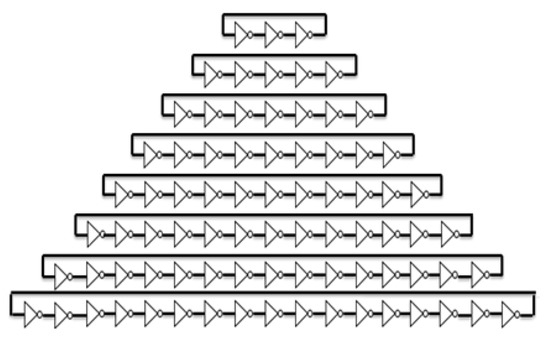
Figure 2. Entropy source of the proposed TRNG with RO-based non-identical rings.

As per the theoretical understanding, an RO can be described as a free-running oscillator with an odd number of inverters. In an RO, each inverter propagates the rising and falling edges of the generated clock signal in consecutive half-periods. The half-period of clock q, generated by an RO with 3 inverters, can be expressed as

$${\mathrm{H}}_{\mathrm{q}}={\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{r}}{\mathrm{d}}_{\mathrm{pq}}},$$

(1)

where r = {3, 5, 7, …, n} denotes the number of delay elements and d_pq is the individual delay of the p-th gate (the delay element). According to the theory of jitters in FPGAs, the origin of the jitters can be defined as

d_pq = D_p + Δd_pq
= D_p + ΔdL_pq + ΔdG_pq

(2)

In Equation (2), D_p represents the constant delay of the p-th gate, where ΔdLpq is referred to as a variation in the delay caused by the local source, and ΔdG_pq is the variation in the delay caused by the common global source. Hence, the local variation is given by

ΔdL_pq = ΔdLG_pq + ΔdLD_pq,

(3)

where ΔdLG_pq is the Gaussian jitter from an independent local source, and ΔdLD_pq is the local deterministic jitter emerging from the crosstalk. Hence, the global variation of RO in the FPGA can be expressed as

ΔdG_pq = ɸp (Δ_D + ΔdGG_q + ΔdGD_q),

(4)

where Δ_D denotes the variations in the delay that arise from variations in the temperature and/or supply voltage, ΔdGG_q is the Gaussian noise of the power supply, ΔdGD_q describes the global deterministic jitter from high-speed variations in the supply voltage, and ɸp is the global jitter coefficient. Since the Gaussian jitter from each independent element forms the source of true randomness, other jitter phenomena are ignored for assessments of the TRNG’s entropy. In addition, ΔdGD_q plays an important role in this case, since it can be controlled or manipulated by the environment, which disrupts the performance of the TRNG. The amount of the RO’s clock jitter can be calculated as follows:

Δdp = ΔdLG_q + ɸpΔdGD.

(5)

Hence, the jitter from the FPGA is a combination of the local Gaussian jitter and the global deterministic jitter of each RO. The generated jitters are accumulated to yield the cumulative entropy. Thus, jitter extraction is a vital part of the TRNG, and can be derived using Equations (1) and (3), and the RO’s half-period can be expressed as

$$\begin{array}{l}\mathrm{H}={\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{r}}{(\mathrm{D}}_{\mathrm{p}}{+\mathsf{\Delta }\mathrm{dLG}}_{\mathrm{p}}{+\mathsf{\Phi }}_{\mathrm{p}}\mathsf{\Delta }\mathrm{dGD})}\\ ={\displaystyle \sum _{\mathrm{p}=1}^{\mathrm{r}}{(\mathrm{D}}_{\mathrm{p}}{+\mathsf{\Delta }\mathrm{HLG}}_{\mathrm{accum}}{+\mathsf{\Delta }\mathrm{HGD}}_{\mathrm{accum}}})\end{array}$$

(6)

where ΔHLG_accum is the local Gaussian jitter with the probability distribution N (0, σ2accum) accumulated in one half-period H in r gates of the RO.

3.2. Extraction of Randomness

In this work, the XOR structure was adopted for extracting the true randomness from the entropy source. Let L1, L2, …, L8 be the jitter clocks from the non-identical RO entropy source. A lightweight logical operation is sufficient to create a diffused bit of individual jitter from the ROs. Hence, f(L1, L2,…L8) = L1 (*) L2 (*) ……(*) L8, where (*) may be logical operations such as AND(&), OR(|), NAND(~&), NOR(~|), XOR(^), XNOR(~^), etc. Because of its functionalities and utility in RNGs, the XOR function was adopted for harvesting the true randomness owing to its complete dependence on the logic levels of all the latches.

Let the local Gaussian jitter of Ring 1 (R1) be (ΔdLG1p1 + ΔdLG1p2 + ΔdLG1p3), where R1 has three inverters. Since the extraction of randomness happens for any of the edges of the operational clock, three half-periods of the R1 were considered for jitter accumulation. Similarly, for R2 with five inverters, the accumulation of the local Gaussian jitters will be (ΔdLG2p1 + ΔdLG2p2 + ΔdLG2p3 + ΔdLG2p4 + ΔdLG2p5). This jitter accumulation will be continued for the remaining rings of the entropy source. By applying the XOR (*) diffusion on the entropy source, the randomness extraction function can be modelled as

JEntropy = R1(ΔdLG1p) * R2(ΔdLG2p) * R3(ΔdLG3p) * R4(ΔdLG4p) * R5(ΔdLG5p) * R6(ΔdLG6p) * R7(ΔdLG7p) * R8(ΔdLG8p).

(7)

The output of the extraction process produces true random sequences. However, TRNGs have more unpredictability and poor randomness because of their unbounded physical variations. In this work, jitters were caused by variations in delays of the hardware modules of the FPGAs. These asymmetric delays introduced bias in the random sequence, resulting in the non-equidistribution of the bits’ levels. This phenomenon achieved poor data randomness, which required proper post-processing mechanisms to be used.

3.3. Post-Processing

The Von Neumann corrector (VNC) is a simple and lightweight post-processor suggested by NIST 800-90B [11]. It is a well-known compression function performing de-biasing operations for generating true random sequences. This method operates on raw true random sequences and converts them to unbiased or equally distributed random sequences. The corrector processes the given stream of bits as a stream of non-overlapping pairs of consecutive bits, and generates a single bit for every pair based on the following conditions:

If the input is “00” or “11”, then the corrector discards it (no output bit will be produced);

If the input is “01” or “10”, then the corrector provides “0” or “1”, respectively.

Similarly to the VNC, many correctors, such as XOR, linear codes, etc., have been suggested by NIST 800-90B. However, only the VNC produces bit sequences with zero bias among all the other correctors. To prove this, let us consider j to be the bias of input bit X.

Hence, P (X = 0) = (½) + j and P (X = 1) = (½) − j.

For a given output bit K,

$$\begin{array}{l}\frac{\mathrm{P}(“01”)}{\mathrm{P}(“01”\mathrm{or}“10”)} = \frac{(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right. - \mathrm{j}\left)\right(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+ \mathrm{j})}{(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+ \mathrm{j}\left)\right(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right. - \mathrm{j}) + (\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right. - \mathrm{j}\left)\right(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right. + \mathrm{j})}\\ (\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.-\mathrm{j}\left)\right(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.+ \mathrm{j}) = \frac{1}{2}\end{array}$$

(8)

Thus, we can prove that the VNC produces an output with zero bias. However, it is essential to monitor the activities of the TRNG in the case of environmental disturbances and failures of functionality. To achieve this, a health test has to be deployed in the TRNG architecture as an inbuilt function, through which the status of the TRNG can be checked periodically. In this work, the NIST 800-90B and FIPS-approved repetition count test were incorporated as health tests. This instantaneously detects the fatal failure caused by the entropy source, which can make the generator become stuck on one single output for a long period. It also generates an alert whenever the entropy source is disturbed.

As an experiment, a conditioning circuit was utilised in this work to compare the effects of the statistical properties between the raw and conditioned true random sequences [32]. According to NIST 800-90B, a conditioning circuit is an optional unit which can be used whenever the statistical properties of a TRNG need to be improved. Here, the AES–128-bit ciphering algorithm was utilised for conditioning the raw true random bits. AES undergoes 10 operation rounds with sub-bytes, ShiftRows, MixColumns and AddRoundKeys, along with a key expansion process [33]. This AES–128 encryption process implemented on FPGAs required 300 nS to process 128 bits of a raw random sequence.

4. Characterisation and Results

The proposed TRNG architecture was designed using VHDL and implemented on a Cyclone IV E FPGA using the Quartus 13.0 EDA tool. This entropy source has an architecture that makes it generic enough to be implemented on any category of FPGA. To test its generic characteristics, the proposed entropy source was implemented on two different FPGA vendors of various families, namely the Cyclone II EP2C35F672C6, the Cyclone IV E EP4CE115F29CN, the Stratix III EP3SL340H1152C3 from Intel Altera, and Artix 7 7a100tcsg324-3 and ZYNQ 7z020clg484-1 from Xilinx. Similar results were obtained by all the implementations, demonstrating the structure’s independent nature. Furthermore, the true randomness of the proposed design was evaluated through a restart experiment and the NIST 800-90B entropy estimation tool, and the hardware resources were considered to estimate the performance of the TRNG.

4.1. Evaluation of True Randomness

The quality of the TRNG was evaluated in terms of its randomness and statistical properties. Following the standard practices in the field, the initial test on randomness was to analyse the presence of Gaussian jitters [32]. To show the presence of Gaussian jitters in the output of the TRNG, the random sequences were analysed by Gaussian analysis through the Keysight digital oscilloscope. For this analysis, approximately 32,000 samples were captured from the TRNG’s output. The distribution of the random samples had a standard deviation of 24.010 nS and exhibited a normal distribution in the jitter analysis depicted in Figure 3. According to the results, it can be inferred that the presence of Gaussian jitter is visible.

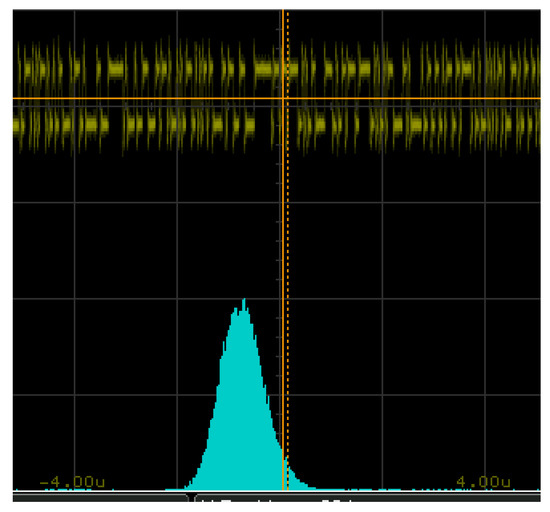
Figure 3. Evidence of Gaussian jitter captured by the digital oscilloscope from the TRNG implemented on an FPGA.

(i)

Restart experiment

Restart experiments are a primary analysis to differentiate between true randomness and pseudo-randomness. The randomness exhibited by the pseudo-random sequences will generally be the same for every iteration until the initial condition and/or seed is changed. On the contrary, in the case of a truly random sequence, the amount of randomness will be continuously varied for every iteration, indicating true randomness. This work conducted a restart experiment, following the procedures adopted by Wold and Tan [23], and Dichtl and Golić [34]. This experiment was carried out 100 times by analysing the first 100 random bits of the TRNG. As a result, the bits’ distribution pattern was different when we compared one sequence with another. Figure 4 shows the results of the restart experiment for five iterations, through which the true randomness of the proposed work was confirmed.

Figure 4. Restart experiment with 100 initial values captured through a logic analyser interfaced with an FPGA.

(ii)

Calculation of the Hamming Distance (HD)

The Hamming distance is another metric used to confirm the true randomness, which examines the zero-to-one transitions between two consecutive real random numbers. It was carried out for the 128-bit TRNG, as per the procedures given in [35]. The results are presented in Figure 5.

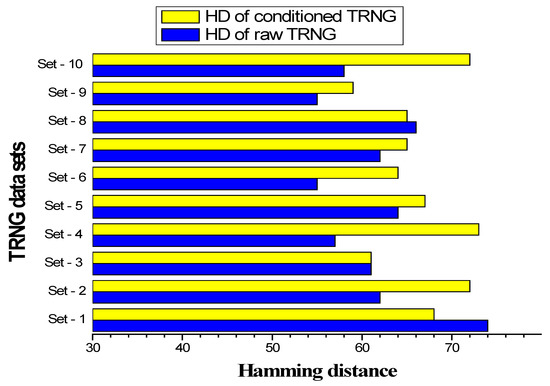
Figure 5. Average Hamming distance of the samples from the TRNG.

In Figure 5, it can be seen that the Hamming distance of the true random numbers had random variations. In addition, the HD of the post-processed bits was comparatively higher than that of the raw bits, thus illustrating the increase in randomness.

4.2. Evaluation of the Statistical Properties

Every random sequence should possess three basic properties:

(i)

It must have an equal distribution of 0 s and 1 s;

(ii)

It must be unpredictable;

(iii)

It should not produce any pattern.

Equidistribution and NIST 800-90B entropy estimation analyses were performed to analyse these properties.

(i)

Equidistribution analysis

Equidistribution is a metric of randomness. It describes the probability of the equidistribution of 0 s and 1 s within random sequences. It is a test that confirms the equal probability of distribution, which can then lead to further exploration of the TRNG’s statistics. For example, for a strong random number generator, the probabilities of the occurrence of 0 s and 1 s must ideally be equal to 0.5. This analysis was conducted to analyse the equidistribution property, and the results are presented in Table 2.

Table 2. Equidistribution analysis.

TRNG Datasets	Probability of Raw True Random Bits			Probability of Conditioned True Random Bits
	Ones	Zeros	Total	Ones	Zeros	Total
Set 1	0.500702	0.4999298	0.999999	0.499504	0.500496	0.999999
Set 2	0.499245	0.500755	0.999998	0.498688	0.501312	0.999995
Set 3	0.501144	0.498856	0.999996	0.500626	0.499374	0.999999
Set 4	0.498268	0.501732	0.999991	0.496803	0.503197	0.999971
Set 5	0.500793	0.499207	0.999998	0.497917	0.502083	0.999987
Set 6	0.500122	0.499878	1	0.499634	0.500366	1
Set 7	0.504341	0.495659	0.999946	0.499069	0.500931	0.999998
Set 8	0.499725	0.500275	1	0.500534	0.499466	0.999999
Set 9	0.501877	0.498123	0.999999	0.499321	0.500679	0.999999
Set 10	0.501282	0.498718	0.999995	0.499603	0.500397	1

Here, 100 iterations of 107 bits were generated for performing this test, and 10 sets of results are presented in Table 1. According to this table, the proposed TRNG yielded average values of 0.9999922 for the raw true random bits and 0.9999947 for the conditioned true random bits, which are close to the ideal value.

(ii)

NIST 800-90B: min-entropy estimation

NIST has released a test suite for estimating the entropy of true random number generators. NIST 800-90B estimates the entropy in two ways: independent and identically distributed (IID) and non-IID [11]. Whenever the TRNG generates output from an independent source, IID estimation is adopted, whereas non-IID estimation is preferred when the TRNG is dependent. In this work, we performed non-IID estimation for the raw and conditioned true random bits. The aim and focus of the test suite are presented in Table 3. Table 4, Table 5 and Table 6 present the min-entropy estimation of 10 consecutive samples containing 107 bits.

Table 3. List of NIST SP 800-90B estimators and their explanations [11].

Estimation Methods		Theme of Estimation	Test Definition
Entropic statistic estimates	Most common value	Number of occurrences	Works based on the frequency of the most common values in the dataset
	Collision	Repeatability checking	Counts the number of successive samples until a duplicate is found
	Markov	Dependency checking	Finds the probability of samples in which the next sample depends on the latest observed sample’s value (first-order Markov model)
	Compression	Redundancy checking	Computes the redundancy rate of a dataset based on how much the dataset can be compressed
Tuple estimates	T-Tuple	Pattern recognition	An extension of the most common value test. Examines the frequency of t–tuples (pairs, triples, etc.) in the input dataset
	LRS	Longest run checking	T-tuples with a large size. It should not be ≥35
Predictor estimates	MultiMCW Prediction	Prediction of the next values from the observed values. It has sub-predictors	Includes a sliding window to record the t most recently observed samples. It predicts the subsequent output based on the most common value in the window. The window size should be 63, 255, 1023 or 4095
	Lag prediction		Detect the correlation and prediction value.
	MultiMMC Prediction		Records the occurrences of transitions from a pattern with a fixed length to the subsequent output and predicts the most frequently observed transition from the current outputs
	LZ78Y Prediction		Keeps a dictionary to record the tuples that have appeared in the previous outputs. It is based on the LZ78Y algorithm, and the dictionary has a fixed size of 65,536

Table 4. Entropy rate of the raw true random bits.

Estimation Methods		Sample 1	Sample 2	Sample 3	Sample 4	Sample 5
Entropic statistic estimates	Most common value	0.776303	0.772829	0.774081	0.774165	0.773862
	Collision	0.582513	0.576817	0.573787	0.575271	0.576649
	Markov	0.680329	0.677495	0.677831	0.678172	0.680321
	Compression	0.43252	0.428203	0.428726	0.429465	0.428224
Tuple estimates	T-tuple	0.518165	0.503875	0.505944	0.507008	0.503875
	LRS	0.60223	0.618924	0.610076	0.612304	0.609408
Predictor estimates	MultiMCW prediction	0.776393	0.773231	0.774735	0.774728	0.77422
	Lag prediction	0.646158	0.74279	0.74279	0.580808	0.72061
	MultiMMC prediction	0.599104	0.611752	0.610858	0.614122	0.611521
	LZ78Y prediction	0.776305	0.772844	0.774106	0.774192	0.773948
Estimation Methods		Sample 6	Sample 7	Sample 8	Sample 9	Sample 10
Entropic statistic estimates	Most common value	0.773692	0.774377	0.77433	0.773578	0.773112
	Collision	0.576271	0.578065	0.577006	0.572076	0.577741
	Markov	0.678259	0.678628	0.679594	0.676664	0.678986
	Compression	0.431527	0.430099	0.429395	0.427392	0.429304
Tuple estimates	T-tuple	0.506473	0.499956	0.502869	0.503875	0.502373
	LRS	0.617982	0.618924	0.595495	0.623257	0.598258
Predictor estimates	MultiMCW prediction	0.774124	0.774787	0.774876	0.774023	0.773554
	Lag prediction	0.74279	0.72061	0.699677	0.766341	0.766341
	MultiMMC prediction	0.612737	0.611371	0.614493	0.611618	0.611666
	LZ78Y prediction	0.773766	0.774414	0.77434	0.773596	0.773135

Table 5. Entropy rate of the conditioned true random bits.

Estimation Methods		Sample 1	Sample 2	Sample 3	Sample 4	Sample 5
Entropic statistic estimates	Most common value	0.774076	0.774325	0.774639	0.772213	0.77258
	Collision	0.578074	0.574828	0.576665	0.574045	0.575295
	Markov	0.679357	0.678501	0.680025	0.677518	0.677673
	Compression	0.430194	0.427339	0.42911	0.430075	0.429719
Tuple estimates	T-tuple	0.505419	0.507008	0.5049	0.505419	0.505419
	LRS	0.625161	0.588358	0.607403	0.623526	0.585284
Predictor estimates	Multi MCW prediction	0.774649	0.774807	0.775148	0.77265	0.773064
	Lag prediction	0.766341	0.766341	0.580808	0.72061	0.72061
	Multi MMC prediction	0.613211	0.611999	0.612475	0.595327	0.612614
	LZ78Y prediction	0.774091	0.774363	0.774651	0.77224	0.772602
Estimation Methods		Sample 6	Sample 7	Sample 8	Sample 9	Sample 10
Entropic statistic estimates	Most common value	0.774787	0.774039	0.773443	0.773995	0.77494
	Collision	0.574717	0.575746	0.576025	0.576875	0.577158
	Markov	0.679194	0.679647	0.678308	0.678776	0.680344
	Compression	0.427999	0.428678	0.428281	0.428645	0.430835
Tuple estimates	T-tuple	0.50337	0.501881	0.505419	0.504385	0.504385
	LRS	0.622209	0.601729	0.589705	0.600017	0.622063
Predictor estimates	Multi MCW prediction	0.775268	0.774444	0.773912	0.774496	0.775303
	Lag prediction	0.813036	0.626573	0.679894	0.595327	0.766341
	Multi MMC prediction	0.61363	0.612777	0.614747	0.613002	0.614718
	LZ78Y prediction	0.774829	0.774054	0.773463	0.774002	0.77496

Table 6. Min entropy of the raw and conditioned true random bits.

TRNG	Sample 1	Sample 2	Sample 3	Sample 4	Sample 5
Raw bits	0.43252	0.428203	0.428726	0.429465	0.428224
Conditioned bits	0.430194	0.427339	0.42911	0.430075	0.429719
TRNG	Sample 6	Sample 7	Sample 8	Sample 9	Sample 10
Raw bits	0.431527	0.430099	0.429395	0.427392	0.429304
Conditioned bits	0.427999	0.428678	0.428281	0.428645	0.430835

According to Equation (5), the proposed RO entropy source has two components pf jitter: local Gaussian jitter and global deterministic jitter, for every half-period of the clock. Since the clock’s jitters are the source of the TRNG, true randomness is the combination of the local Gaussian and global deterministic jitters. Moreover, the local Gaussian jitter is an independent phenomenon involving the inverters, whereas the global deterministic jitter depends on the power supply. Hence, the entropy source is the cumulative sum of both types of jitter and falls into the category of non-IID.

The results proved that the proposed TRNG had an adequate amount of true randomness from all the estimators; notably, it had min-entropy values of 0.429486 for the raw bits and 0.429088 for the conditioned bits. Moreover, according to Table 4, not much difference was observed between the raw and conditioned bits, which shows that the conditioning circuit is optional for the proposed TRNG to achieve satisfactory results.

(iii)

NIST 800-22 batteries of tests

NIST has a widely used test suite that includes several tests for assessing random number generators [36,37,38,39,40]. The test suite examines the statistical characteristics of the generated random bits in terms of randomness, probability distribution and unpredictability. The probability values (p-values) in the table, which were assigned for each of the 15 NIST tests, range from 0 to 1. Low p-values demonstrate the absence of unpredictability in the bit stream. If the p-value is more than 0.001, the NIST SP 800-22 standard indicates that the bits are cryptographically strong and have passed the tests.

NIST SP 800-22 has 14 tests, namely Frequency (T1), Block Frequency (T2), Cumulative Sums I (T3), Cumulative Sums II (T4), Runs (T5), Longest Run (T6), Rank (T7), FFT (T8), Non-overlapping Template (T9), Overlapping Template (T10), Approximate Entropy (T11), Serial I (T12), Serial II (T13) and Linear Complexity (T14). Figure 6 and Figure 7 show the box chart plots of the p-values for 107 raw and conditioned true random bits samples. The proposed TRNG passed all the tests, proving that the TRNG has good statistical properties and is cryptographically strong.

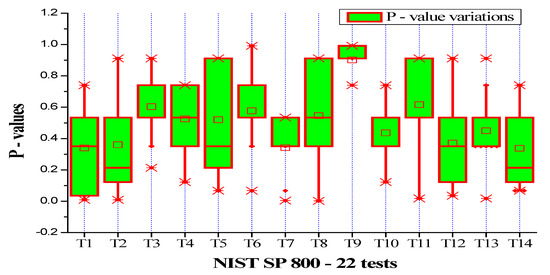
Figure 6. Box chart plot of the p values of the raw true random bits.

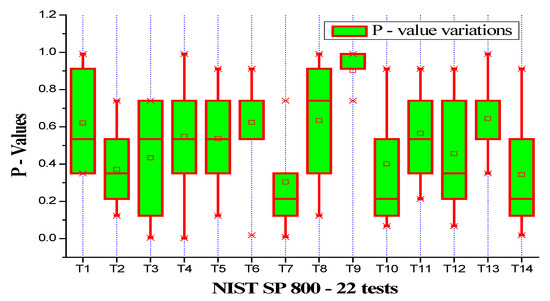
Figure 7. Box chart plot of the p-values of the conditioned true random bits.

Additionally, the Linear Complexity Test was estimated through the TestU01 test suite. This test aims to identify whether the sequence is complex enough to be considered as random or non-random. In this test, random sequences are characterized by the polynomials of LFSR. It performs jump complexity and size tests on random numbers to determine their linear complexity. For each z, 1 ≤ z ≤ n, the linear complexity of the sequence formed by the first z bits by computing the Berlekamp–Massey algorithm [41]. The following table presents the results of the linear complexity test from the TestU01 test suite, which shows that the random numbers generated from the proposed TRNG are random and complex enough. Table 7 presents the results of TestU01—Linear Complexity analyses.

Table 7. TestU01—Linear Complexity Analysis.

Test with Parameters	p-Value		Result
Linear Complexity (N =1, n = 2, 56, 00, 000 bits, r = 0, s = 1)	Normal statistic	0.89	Pass
	Chi2 statistics	0.72
Linear Complexity (N =1, n = 2, 56, 00, 000 bits, r = 29, s = 1)	Normal statistic	0.9905	Pass
	Chi2 statistics	0.18

4.3. Evaluation of the Hardware Resources

The hardware resources of any FPGA-based digital system can be analysed through its consumption of logic elements and throughput. The results shown in this section correspond to the implementation of the TRNG on a Cyclone IV E EP4CE115F29C7 FPGA. Table 8 presents the hardware resources of the proposed TRNG in terms of look-up tables (LUTs) and logic registers for implementing the TRNG on various FPGAs.

Table 8. Hardware resources of the proposed TRNG.

FPGA Vendor	Target FPGA	Consumption of Logic Elements
Intel (Altera)	Cyclone IV E (EP4CE115F29CN)	15 LUTs and 13 registers
	Cyclone II (EP2C35F672C6)	15 LUTs and 13 registers
	Stratix III (EP3SL340H1152C3)	14 LUTs and 13 registers
Xilinx	Artix-7 (7a100tcsg324-3)	10 LUTs and 13 registers
	ZYNQ 7000 (7z020clg484-1)	10 LUTs and 13 registers

The power dissipation analysis (Shown in Table 9) was carried out by the Power Play Power analyzer tool in the Quartus II Electronic Design Automation (EDA) tool. The power computation is accomplished by monitoring the switching activity of each net (signal). The switching activity comprises two parameters: (a) Static probability (b) Transition rate.

Table 9. Power dissipation analysis of the proposed TRNG.

Static Power (mW)	98.49
Dynamic Power (mW)	1.28
IO Power (mW)	41.09
Total Power (mW)	140.86

(a)

Static probability: the expected state of the signal.

(b)

Transition rate: the number of transitions per unit of time. The transition rate is also referred to as the toggle rate.

For periodic signals such as clocks having the signal’s frequency specified, the transition rate is twice the signal’s frequency (since there are two transitions—rising and falling—within each cycle). The power analysis utilizes the design’s switching activity (static probability and transition rate) for each signal. The power dissipation is calculated through Equation (9),

$$\mathrm{P}=\frac{1}{2}\mathrm{C}\times {\mathrm{Vdd}}^2\times \mathrm{Togglerate},$$

(9)

where P is the power, C is the capacitance, Vdd is the supply voltage, and Toggle rate is the switching activity of the signal. For example, consider C = 20fF (capacitor connected to the supply pin of the Cyclone FPGA) and Vdd = 1.2 V [42,43,44].

Table 9 shows that the total power dissipation is 140.86 mW, including the three components: static, dynamic and I/O power. The IoT node will generally be driven through an embedded device such as a Microcontroller/CPLD/FPGA, which requires a minimum of 1.2 core operating voltage to drive the task. In this regard, the dissipation of 140.86 mW is much less dissipation to perform the PUF. However, it is an open option that the power dissipation can be reduced to µW level upon adopting a manual placement of LUTs, which is one of the future concerns of this work.

According to Table 8, the proposed TRNG utilised only 15 LUTs in the Intel FPGAs and 10 LUTs in the Xilinx FPGAs. As a result, the proposed TRNG consumed a smaller hardware footprint (<1%), consuming 41.26 mW of power to achieve high randomness. A sampling clock of 25 MHz was utilised to generate true random sequences. The TRNG required 296 milliseconds to generate 8192 × 128 bits at a throughput of 3.5 Mbps. Timing analysis was carried out with the ZeroPlus logic analyser, and Figure 8 shows the total time taken for the TRNG to generate 10,48,576 bits.

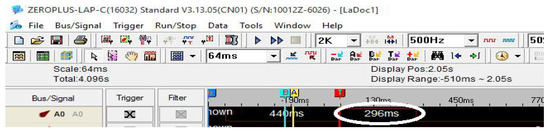
Figure 8. Timing analysis.

4.4. Performance Comparison

Most TRNG designs described in the literature include ROs as a key component to regulate the proposed TRNG. With eight rings and three inverters in each, the entropy unit of the proposed work was updated variably, going from 8 to 17 in each ring. The Quartus EDA tool was used to carry out the placement and routing for accommodating the entropy source without any temporal or physical restrictions.

The suggested TRNG’s computed throughput at a sampling frequency of 25 MHz was 3.5 Mbps, more than the earlier works listed in Table 10. Additionally, this suggested TRNG used just 80 inverters, and Figure 9 shows the comparison, demonstrating the proposed TRNG design’s compactness in terms of the inverter count. Moreover, the proposed TRNG had a keyspace of 2¹²⁸, since 128 bits were considered for testing. Hence, the proposed TRNG-based key generator is resistant to brute-force attacks. Furthermore, the number of bits of true random numbers can be expanded to any size, since the true random sequence can be packed into any n-bit number.

Table 10. Performance comparison: Hardware resources.

Reference	TRNG Design Technique	FPGA for Implementation	Hardware Resources	Frequency	Throughput
Fischer et al. [14]	PLL/DLL	Altera APEX EP20K200EFC484-2X	121 LCs, 4 ESB and 1 PLL	33.3 MHz	69 Kbps
Kohlbrenner and Gaj [17]	Free-running oscillator	Xilinx XC2VP30	12LUTs and 24 registers	150 MHz	300 Kbps
Valchanov et al. [30]	RO–RO	Xilinx XC3S500E	15 LUTs, 4 registers		2 Mbps
	RO–PLL		12 LUTs, 4 registers and 1 PLL	65 MHz	2 Mbps
	RO–DFS		11 LUTs, 6 registers and 2 DFS		2 Mbps
Schellekens et al. [19]	Free-running oscillator	Xilinx XC2VP30	973 Slices	40 MHz	2.5 Mbps
Proposed	Non-identical ROs	Cyclone IV E EP4CE115F29CN	15 LUTs and 13 registers	25 MHz	3.5 Mbps

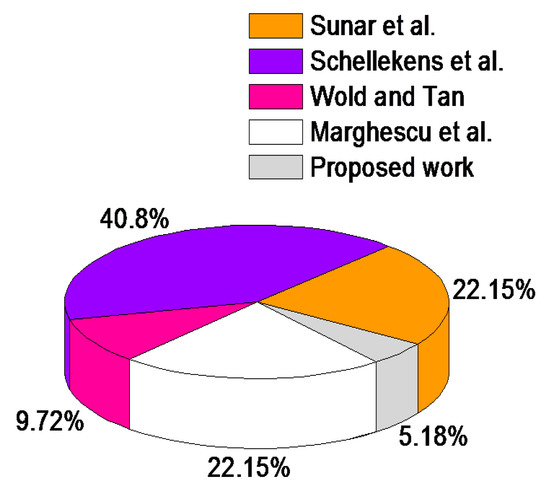
Figure 9. Performance comparison: Number of inverters [18,19,23,30].

5. Conclusions

TRNGs have a significant role in secure modern communication devices. There is a growing need to develop architectures that are part of the IoT’s hardware units or mobile devices for unique device identification. Apart from nonce generation, generic TRNGs such as the one proposed in this work will play an important role in creating unique n-bit IDs for IoT applications. The proposed TRNG was based on a group of rings comprising an odd number of inverters in each ring with increasing order. The design utilised 15 LUTs and 13 registers when realised on a Cyclone IVE FPGA. The power consumption of the architecture was 41.26 mW, with a throughput of 3.5 Mbps. The NIST 800-90B test suite was applied to the true random bits, producing satisfactory results for the various tests. The Gaussian pulse was observed through a digital oscilloscope. The Hamming distance and restart analyses proved the existence of true randomness. This proposed TRNG has a variety of application scopes, as listed below:

• Used as a session key generator in online transactions;
• Adopted as initialization vectors for rounds-based crypto-systems;
• Used as NONCE (Number Only Used Once) for mission-critical applications;
• Used as an integral part of the embedded devices for symmetric key generation;
• Used as a padding vector generator in encoding schemes;
• Used as a Physically Unclonable Function (PUF) with a slight hardware modification to verify the trustworthiness of the device in a network environment.