Convergence Analysis for Yosida Variational Inclusion Problem with Its Corresponding Yosida Resolvent Equation Problem through Inertial Extrapolation Scheme

Abstract

In this paper, we study a Yosida variational inclusion problem with its corresponding Yosida resolvent equation problem. We mention some schemes to solve both the problems, but we focus our study on discussing convergence criteria for the Yosida variational inclusion problem in real Banach space and for the Yosida resolvent equation problem in q-uniformly smooth Banach space. For faster convergence, we apply an inertial extrapolation scheme for both the problems. An example is provided.

1. Introduction

Variational inclusions are the generalized forms of variational inequalties introduced by Hassouni and Moudafi [1]. Many interrelated and unrelated problems of basic and applied sciences can be easily studied via variational inclusions, such as the problems arising in elasticity, structural analysis, oceanography, image processing, physics and engineering sciences, etc., see for example [2,3,4,5,6,7,8].

The concept of resolvent equations was introduced by Noor [9,10]. Resolvent equations are generalized forms of Wiener–Hopf equations. The equivalence between the variational inclusions and resolvent equations was shown by many authors. The resolvent operator technique is useful to solve variational inclusion problems, as projection methods fail to solve them. Various generalized resolvent operators involving different monotone operators are available in the literature.

It is a fact that maximal monotone operators are fundamental objects in modern optimization. In addition, set-valued monotone operators can be regularized into a single-valued monotone operator by a process called Yosida approximation. Applications of Yosida approximation operator can be found in a heat equation that describes the distribution of heat over time in a fixed region of space, an initial value problem for the linearized equations of coupled sound and heat flow, and a wave equation in the form of second-order partial differential equation used for the description of waves, see for example [11,12,13,14,15].

Many iterative algorithms were developed using generalized resolvent operators, but it is always beneficial to use an algorithm which accelerates the fast convergence for the sequence generated by the algorithm. Inertial extrapolation schemes are developed by using the inertial extrapolation term $\left\{\nu (x_n-x_{n-1})\right\}$ by several authors, where $\nu$ is an extrapolating factor that speeds up the convergence rate of the method. Polyak [16] first introduced the inertial-type iterative algorithm to deal with the heavy ball method. The inertial-type iterative algorithm has two steps in which the consecutive iterations are gained by using the former two terms, see for example [17,18,19,20].

In view of the above important discussion, in this paper, we consider a Yosida variational inclusion problem with its corresponding Yosida resolvent equation problem. We mention some schemes for solving Yosida variational inclusion as well as the Yosida resolvent equation problem. We concentrate our study on convergence analysis of both the problems through inertial extrapolation schemes. An example is provided through MATLAB 2015a with a computation table and a convergence graph.

2. Fundamental Tools and Concepts

Suppose that $\tilde{E}$ is a real Banach space and ${\tilde{E}}^{*}$ is its topological dual equipped with norm $\parallel ·\parallel$ and duality pairing $⟨·,·⟩$ between $\tilde{E}$ and ${\tilde{E}}^{*}$. By $2^{\tilde{E}}$, we denote the set of all non-empty subsets of $\tilde{E}$.

For $q>1$, the generalized duality mapping $J_q:\tilde{E}\to {\tilde{E}}^{*}$ is defined by

$$J_q\left(e\right)=\left\{f\in {\tilde{E}}^{*}:⟨e,f⟩={\parallel e\parallel }^q\mathrm{and}\parallel f\parallel ={\parallel e\parallel }^{q-1}\right\},\mathit{for}\mathit{all}e\in \tilde{E}.$$

For $q=2$, $J_q$ becomes normalized duality mapping. Particularly, $J:=J_2$ is called normalized duality mapping on $\tilde{E}$. It is well known that $J_q\left(e\right)={\parallel e\parallel }^{q-2}{J}_2\left(e\right)$ for $e\ne 0$ and $J_q\left(e\right)$ is the subdifferential of functional ${(1/q)\parallel ·\parallel }^q$ at e, see [21]. The mapping $J_q$ is single-valued if $\tilde{E}$ is uniformly smooth.

The definition of uniformly smooth Banach space, modulus of smoothness and the following important Lemma can be found in Xu [21].

Lemma 1. 

A real uniformly smooth Banach space $\tilde{E}$ is q-uniformly smooth if and only if there exists a constant $C_q>0$ such that for all $e,f\in \tilde{E}$, the following inequality holds:

$${\parallel e+f\parallel }^q\le {\parallel e\parallel }^q+q⟨f,J_q\left(e\right)⟩+C_q{\parallel f\parallel }^q.$$

Before providing essential definitions for the presentation of this paper and for the convenience of readers, we mention the following well-known definitions. For this purpose, we take $\tilde{E}=H$, a real Hilbert space.

Definition 1. 

A single-valued mapping $\tilde{A}:H\to H$ is called

(i)

Monotone if

$$⟨\tilde{A}\left(e\right)-\tilde{A}\left(f\right),e-f⟩\ge 0,\mathit{for}\mathit{all}e,f\in H;$$

(ii)

Strongly monotone if there exists a constant ${\delta }_{\tilde{A}}>0$ such that

$$⟨\tilde{A}\left(e\right)-\tilde{A}\left(f\right),e-f⟩\ge {\delta }_{\tilde{A}}{\parallel e-f\parallel }^2,\mathit{for}\mathit{all}e,f\in H.$$

Definition 2. 

A set-valued mapping $M:H\to 2^H$ is called monotone, if

$$⟨u-v,e-f⟩\ge 0,\mathit{for}\mathit{all}e,f\in H,u\in M\left(e\right),v\in M\left(f\right).$$

Definition 3. 

Let $\tilde{A}:H\to H$ be a mapping. A set-valued mapping $M:H\to 2^H$ is called $\tilde{A}$-monotone if M is monotone and

$$[\tilde{A}+\xi M]\left(H\right)=H,\xi >0\mathrm{is}\mathrm{a}\mathrm{constant}.$$

The generalizations of above Definitions 1–3 in q-uniformly smooth Banach space are as follows, which are needed for the presentation of this paper.

Definition 4. 

A single-valued mapping $\tilde{A}:\tilde{E}\to \tilde{E}$ is called

(i)

Accretive if

$$⟨\tilde{A}\left(e\right)-\tilde{A}\left(f\right),J_q(e-f)⟩\ge 0,\mathit{for}\mathit{all}e,f\in \tilde{E};$$

(ii)

Strongly accretive if there exists a constant ${\delta }_{\tilde{A}}>0$ such that

$$⟨\tilde{A}\left(e\right)-\tilde{A}\left(f\right),J_q(e-f)⟩\ge {\delta }_{\tilde{A}}{\parallel e-f\parallel }^q,\mathit{for}\mathit{all}e,f\in \tilde{E};$$

(iii)

Lipschitz continuous if there exists a constant ${\lambda }_{\tilde{A}}>0$ such that

$$\parallel \tilde{A}\left(e\right)-\tilde{A}\left(f\right)\parallel \le {\lambda }_{\tilde{A}}\parallel e-f\parallel ,\mathit{for}\mathit{all}e,f\in \tilde{E}.$$

Definition 5. 

A set-valued mapping $M:\tilde{E}\to 2^{\tilde{E}}$ is called accretive if

$$⟨u-v,J_q(e-f)⟩\ge 0,\mathit{for}\mathit{all}e,f\in \tilde{E},u\in M\left(e\right),v\in M\left(f\right).$$

Definition 6. 

Let $\tilde{A}:\tilde{E}\to \tilde{E}$ be a mapping. The set-valued mapping $M:\tilde{E}\to 2^{\tilde{E}}$ is called $\tilde{A}$-accretive if M is accretive and

$$\left[\tilde{A}+\xi M\right]\left(\tilde{E}\right)=\tilde{E},\xi >0\mathit{is}\mathit{a}\mathit{constant}.$$

It is well known that all the splitting methods are based on the resolvent operator of the form ${[I+\xi M]}^{-1}$, where M is a set-valued monotone mapping, $\xi$ is a positive constant and I is the identity mapping.

Definition 7. 

The resolvent operator $R_{I,\xi }^M:H\to H$, where H is a Hilbert space, is defined as

$$R_{I,\xi }^M\left(e\right)={[I+\xi M]}^{-1}\left(e\right),\mathit{for}\mathit{all}e\in H.$$

Definition 8. 

The Yosida approximation operator $Y_{I,\xi }^M:H\to H$, where H is a Hilbert space, is defined as

$$Y_{I,\xi }^M\left(e\right)=\frac{1}{\xi }[I-R_{I,\xi }^M]\left(e\right),\mathit{for}\mathit{all}e\in H.$$

The generalized forms of Definitions 7 and 8 are mentioned below.

Definition 9. 

Let $\tilde{A}:\tilde{E}\to \tilde{E}$ be a mapping and $M:\tilde{E}\to 2^{\tilde{E}}$ be a set-valued mapping. The generalized resolvent operator $R_{\tilde{A},\xi }^M:\tilde{E}\to \tilde{E}$ associated with $\tilde{A}$ and M is defined as:

$$R_{\tilde{A},\xi }^M\left(e\right)={\left[\tilde{A}+\xi M\right]}^{-1}\left(e\right),\mathit{for}\mathit{all}e\in \tilde{E}\mathit{and}\xi >0.$$

Definition 10. 

The generalized Yosida approximation operator $Y_{\tilde{A},\xi }^M:\tilde{E}\to \tilde{E}$ is defined as:

$$Y_{\tilde{A},\xi }^M\left(e\right)=\frac{1}{\xi }\left[\tilde{A}-R_{\tilde{A},\xi }^M\right]\left(e\right),\mathit{for}\mathit{all}e\in \tilde{E}\mathit{and}\xi >0.$$

Note that if $A\equiv I$, the identity mapping, then from Definitions 9 and 10, one can obtain Definitions 7 and 8, respectively.

Proposition 1. 

[22] Let $\tilde{A}:\tilde{E}\to \tilde{E}$ be strongly accretive mapping with constant r and $M:\tilde{E}\to 2^{\tilde{E}}$ be an $\tilde{A}$-accretive set-valued mapping. Then, the generalized resolvent operator $R_{\tilde{A},\xi }^M:\tilde{E}\to \tilde{E}$ is Lipschitz continuous with constant $\frac{1}{r}$, that is

$$\parallel R_{\tilde{A},\xi }^M\left(e\right)-R_{\tilde{A},\xi }^M\left(f\right)\parallel \le \frac{1}{r}\parallel e-f\parallel ,\mathit{for}\mathit{all}e,f\in \tilde{E}.$$

Lemma 2. 

[23] Let $\left\{S_n\right\}$ be a sequence of non-negative real numbers such that

$$\begin{array}{c}{S}_{n+1}\le (1-{\beta }_n)S_n+{\beta }_n{\sigma }_n+{\widehat{\xi }}_n,\mathit{for}\mathit{all}n\ge 1,\hfill \end{array}$$

where

(i)

$\left\{{\beta }_n\right\}\subset [0,1],{\displaystyle \sum _{n=1}^{\infty }}{\beta }_n=\infty ;$

(ii)

$\mathrm{lim\; sup} {\sigma }_n\le 0;$

(iii)

${\widehat{\xi }}_n\ge 0(n\ge 1),{\displaystyle \sum _{n=1}^{\infty }}{\widehat{\xi }}_n<\infty .$

Then,$S_n\to 0$, as $n\to \infty$.

Proposition 2. 

(i) If $\tilde{A}:\tilde{E}\to \tilde{E}$ is r-strongly accretive, ${\beta }_{\tilde{A}}$-expansive, ${\lambda }_{\tilde{A}}$-Lipschitz continuous and generalized resolvent operator $R_{\tilde{A},\xi }^M:\tilde{E}\to \tilde{E}$ is $\frac{1}{r}$-Lipschitz continuous, then the generalized Yosida approximation operator $Y_{\tilde{A},\xi }^M:\tilde{E}\to \tilde{E}$ is ${\theta }_Y$-strongly accretive with respect to $\tilde{A}$, that is

$$⟨Y_{\tilde{A},\xi }^M\left(e\right)-Y_{\tilde{A},\xi }^M\left(f\right),J_q\left(\tilde{A}\left(e\right)-\tilde{A}\left(f\right)\right)⟩\ge {\theta }_Y{\parallel e-f\parallel }^q,$$

where ${\theta }_Y=\frac{{\beta }_{\tilde{A}}^{q}r-{\lambda }_{\tilde{A}}^{q-1}}{\xi r},\xi r\ne 0,{\beta }_{\tilde{A}}^{q}r>{\lambda }_{\tilde{A}}^{q-1},$ and all the constants are positive.

(ii) If $\tilde{A}$ is ${\lambda }_{\tilde{A}}$-Lipschitz continuous, r-strongly accretive and $R_{\tilde{A},\xi }^M$ is $\frac{1}{r}$-Lipschitz continuous, then the generalized Yosida approximation operator is ${\lambda }_Y$-Lipschitz continuous, that is

$$\parallel Y_{\tilde{A},\xi }^M\left(e\right)-Y_{\tilde{A},\xi }^M\left(f\right)\parallel \le {\lambda }_Y\parallel e-f\parallel ,$$

where ${\lambda }_Y=\frac{{\lambda }_{\tilde{A}}r+1}{\xi r}$.

Proof. 

(i)   Using the definition of generalized duality mapping, expansiveness and Lipschitz continuity of $\tilde{A}$ and Lipschitz continuity of $R_{\tilde{A},\xi }^M$, we evaluate

$$\begin{array}{cc}\hfill ⟨Y_{\tilde{A},\xi }^M\left(e\right)-Y_{\tilde{A},\xi }^M\left(f\right),& J_q\left(\tilde{A}\left(e\right)-\tilde{A}\left(f\right)\right)⟩\hfill \\ \hfill & =\frac{1}{\xi }⟨\tilde{A}\left(e\right)-R_{\tilde{A},\xi }^M\left(e\right)-\left[\tilde{A}\left(f\right)-R_{\tilde{A},\xi }^M\left(f\right)\right],J_q\left(\tilde{A}\left(e\right)-\tilde{A}\left(f\right)\right)⟩\hfill \\ \hfill & =\frac{1}{\xi }⟨\tilde{A}\left(e\right)-\tilde{A}\left(f\right),J_q\left(\tilde{A}\left(e\right)-\tilde{A}\left(f\right)\right)⟩\hfill \\ \hfill & -\frac{1}{\xi }⟨R_{\tilde{A},\xi }^M(\left(e\right)-R_{\tilde{A},\xi }^M\left(f\right),J_q\left(\tilde{A}\left(e\right)-\tilde{A}\left(f\right)\right)⟩\hfill \\ \hfill & \ge \frac{1}{\xi }\parallel \tilde{A}\left(e\right)-\tilde{A}{\left(f\right)\parallel }^q-\frac{1}{\xi }\parallel R_{\tilde{A},\xi }^M\left(e\right)-R_{\tilde{A},\xi }^M\left(f\right)\parallel \parallel \tilde{A}\left(e\right)-\tilde{A}{\left(f\right)\parallel }^{q-1}\hfill \\ \hfill & \ge \frac{1}{\xi }{\beta }_{\tilde{A}}^q{\parallel e-f\parallel }^q-\frac{1}{\xi }\frac{1}{r}\parallel e-f\parallel \parallel \tilde{A}\left(e\right)-\tilde{A}{\left(f\right)\parallel }^{q-1}\hfill \\ \hfill & \ge \frac{1}{\xi }{\beta }_{\tilde{A}}^q{\parallel e-f\parallel }^q-\frac{1}{\xi r}{\lambda }_{\tilde{A}}^{q-1}{\parallel e-f\parallel \parallel e-f\parallel }^{q-1}\hfill \\ \hfill & =\left[\frac{1}{\xi }{\beta }_{\tilde{A}}^q-\frac{{\lambda }_{\tilde{A}}^{q-1}}{\xi r}\right]{\parallel e-f\parallel }^q\hfill \\ \hfill & ={\theta }_Y{\parallel e-f\parallel }^q.\hfill \end{array}$$

That is,

$$\begin{array}{cc}\hfill ⟨Y_{\tilde{A},\xi }^M\left(e\right)-Y_{\tilde{A},\xi }^M\left(f\right),J_q\left(\tilde{A}\left(e\right)-\tilde{A}\left(f\right)\right)⟩\ge {\theta }_Y{\parallel e-f\parallel }^q.& \end{array}$$

Thus, the generalized Yosida approximation operator $Y_{\tilde{A},\xi }^M$ is ${\theta }_Y$-strongly accretive with respect to $\tilde{A}$.

(ii)   Using Lipschitz continuity of $\tilde{A}$ and $R_{\tilde{A},\xi }^M$, we evaluate

$$\begin{array}{cc}\hfill \parallel Y_{\tilde{A},\xi }^M\left(e\right)-Y_{\tilde{A},\xi }^M\left(f\right)\parallel & =\parallel \frac{1}{\xi }\left(\tilde{A}\left(e\right)-R_{\tilde{A},\xi }^M\left(e\right)\right)-\frac{1}{\xi }\left(\tilde{A}\left(f\right)-R_{\tilde{A},\xi }^M\left(f\right)\right)\parallel \hfill \\ \hfill & =\frac{1}{\xi }\parallel \tilde{A}\left(e\right)-\tilde{A}\left(f\right)-\left[R_{\tilde{A},\xi }^M\left(e\right)-R_{\tilde{A},\xi }^M\left(f\right)\right]\parallel \hfill \\ \hfill & \le \frac{1}{\xi }\parallel \tilde{A}\left(e\right)-\tilde{A}\left(f\right)\parallel +\frac{1}{\xi }\parallel R_{\tilde{A},\xi }^M\left(e\right)-R_{\tilde{A},\xi }^M\left(f\right)\parallel \hfill \\ \hfill & \le \frac{1}{\xi }{\lambda }_{\tilde{A}}\parallel e-f\parallel +\frac{1}{\xi }\frac{1}{r}\parallel e-f\parallel \hfill \\ \hfill & =\left[\frac{{\lambda }_{\tilde{A}}}{\xi }+\frac{1}{\xi r}\right]\parallel e-f\parallel \hfill \\ \hfill & ={\lambda }_Y\parallel e-f\parallel .\hfill \end{array}$$

That is,

$$\begin{array}{cc}\hfill \parallel Y_{\tilde{A},\xi }^M\left(e\right)-Y_{\tilde{A},\xi }^M\left(f\right)\parallel \le {\lambda }_Y\parallel e-f\parallel .& \end{array}$$

Thus, the genearlized Yosida approximation operator $Y_{\tilde{A},\xi }^M$ is ${\lambda }_Y$-Lipschitz continuous. □

3. Yosida Variational Inclusion Problem and Yosida Resolvent Equation Problem

Let $\tilde{A}:\tilde{E}\to \tilde{E}$ be single-valued mapping and $M:\tilde{E}\to 2^{\tilde{E}}$ be set-valued mapping. Let $Y_{\tilde{A},\xi }^M$ be a generalized Yosida approximation operator. We consider the following Yosida variational inclusion problem.

Find $e\in \tilde{E}$ such that

$$\begin{array}{c}\hfill 0\in Y_{\tilde{A},\xi }^M\left(e\right)+M\left(e\right).\end{array}$$

(1)

If $Y_{\tilde{A},\xi }^M\left(e\right)=0$, then problem (1) reduces to the problem of finding $e\in \tilde{E}$ such that

$$0\in M\left(e\right),$$

which is a fundamental problem of analysis that has been considered by Rockafellar [24].

Lemma 3. 

The Yosida variational inclusion problem (1) has a solution $e\in \tilde{E}$ if and only if the following equation is satisfied:

$$\begin{array}{c}\hfill e=R_{\tilde{A},\xi }^M\left[\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right)\right].\end{array}$$

(2)

Proof. 

One can prove it easily by using the definition of generalized resolvent operator $R_{\tilde{A},\xi }^M$. □

Based on Lemma 3, we mention an iterative scheme as well as an inertial extrapolation scheme for solving Yosida variational inclusion problem (1).

Iterative Scheme 1. 

For any $e_0\in \tilde{E}$, compute the sequence $\left\{e_n\right\}$ by the following scheme:

$$\begin{array}{c}\hfill e_{n+1}=R_{\tilde{A},\xi }^M\left[\tilde{A}\left(e_n\right)-\xi Y_{\tilde{A},\xi }^M\left(e_n\right)\right],\mathit{where}n=0,1,2,\cdots \end{array}$$

(3)

and $\xi >0$ is a constant.

Equation (2) can also be written as

$$\begin{array}{c}\hfill e=R_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e\right)+\tilde{A}\left(e\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(e\right)\right].\end{array}$$

(4)

Based on (4), we suggest the following iterative scheme.

Iterative Scheme 2. 

For any $e_0\in \tilde{E}$, compute $e_{n+1}$ by the recurrance relation,

$$\begin{array}{c}\hfill e_{n+1}=(1-{\alpha }_n)e_n+{\alpha }_n{R}_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e_n\right)+\tilde{A}\left(e_{n+1}\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(e_{n+1}\right)\right],\mathit{where}n=0,1,2,\cdots ,\end{array}$$

(5)

${\alpha }_n\in [0,1]$ and $\xi >0$ is a constant.

We mention the following inertial extrapolation scheme using the predictor–corrector approach.

Iterative Scheme 3. 

For any $e_0\in \tilde{E}$, compute $e_{n+1}$ by the recurrance relation,

$$\begin{array}{cc}\hfill w_n& =e_n+{\nu }_n(e_n-e_{n-1}),\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill e_{n+1}=(1-{\alpha }_n)e_n+& {\alpha }_n{R}_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e_n\right)+\tilde{A}\left(w_n\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(w_n\right)\right],\hfill \end{array}$$

(7)

where ${\alpha }_n,{\nu }_n\in [0,1]$, ${\nu }_n$ is the extrapolating term for all $n\ge 1$ and $\xi >0$ is a constant.

Note that one can use the above-mentioned schemes 1 and 2 to obtain the existence and convergence result for Yosida variational inclusion problem (1). Using inertial extrapolation scheme 3, we prove a convergence result for Yosida variational inclusion problem (1) in the sequel.

In connection with Yosida variational inclusion problem (1), we state the following Yosida resolvent equation problem.

Find $e,\widehat{z}\in \tilde{E}$, such that

$$\begin{array}{c}\hfill Y_{\tilde{A},\xi }^M\left(e\right)+{\xi }^{-1}{T}_{\tilde{A},\xi }^M\left(\widehat{z}\right)=0,\end{array}$$

(8)

where $T_{\tilde{A},\xi }^M\left(\widehat{z}\right)=\left[I-\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]\left(\widehat{z}\right)$ and $\tilde{A}\left[R_{\tilde{A},\xi }^M\left(\widehat{z}\right)\right]=\left[\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]\left(\widehat{z}\right)$.

The following Lemma ensures that Yosida variational inclusion problem (1) is equivalent to Yosida resolvent equation problem (8).

Lemma 4. 

The Yosida variational inclusion problem (1) has a solution $e\in \tilde{E}$ if and only if Yosida resolvent equation problem (8) has a solution $e,\widehat{z}\in \tilde{E}$, provided $\tilde{A}$ is one-one and

$$\begin{array}{cc}\hfill & e=R_{\tilde{A},\xi }^M\left(\widehat{z}\right),\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill & \widehat{z}=\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right),\hfill \end{array}$$

(10)

where $\xi >0$ is a constant.

Proof. 

Let $e\in \tilde{E}$ be a solution of Yosida variational inclusion problem (1). Then, by Lemma 3, it satisfies the equation:

$$\begin{array}{cc}\hfill e& =R_{\tilde{A},\xi }^M\left[\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right)\right].\hfill \\ \hfill e& =R_{\tilde{A},\xi }^M\left(\widehat{z}\right),\mathrm{since} \widehat{z}=\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right).\hfill \end{array}$$

Using (9), (10) becomes

$$\begin{array}{cc}\hfill \widehat{z}=& \tilde{A}\left(R_{\tilde{A},\xi }^M\left(\widehat{z}\right)\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right),\hfill \\ \hfill \widehat{z}-& \tilde{A}\left(R_{\tilde{A},\xi }^M\left(\widehat{z}\right)\right)=-\xi Y_{\tilde{A},\xi }^M\left(e\right),\hfill \\ \hfill \widehat{z}-& \left[\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]\left(\widehat{z}\right)=-\xi Y_{\tilde{A},\xi }^M\left(e\right),\hfill \\ \hfill [I-& \left[\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]]\left(\widehat{z}\right)=-\xi Y_{\tilde{A},\xi }^M\left(e\right),\hfill \\ \hfill & T_{\tilde{A},\xi }^M\left(\widehat{z}\right)=-\xi Y_{\tilde{A},\xi }^M\left(e\right),\mathrm{since} I-\tilde{A}\left(R_{\tilde{A},\xi }^M\right)=T_{\tilde{A},\xi }^M.\hfill \end{array}$$

Thus, we have

$$\begin{array}{c}\hfill Y_{\tilde{A},\xi }^M\left(e\right)+{\xi }^{-1}{T}_{\tilde{A},\xi }^M\left(\widehat{z}\right)=0,\end{array}$$

which is required for Yosida resolvent equation problem (8).

Conversely, let $e,\widehat{z}$ be the solution of Yosida resolvent equation problem (8). Then, we have

$$\begin{array}{cc}\hfill \xi Y_{\tilde{A},\xi }^M\left(e\right)& =-T_{\tilde{A},\xi }^M\left(\widehat{z}\right)\hfill \\ \hfill & =-\left[I-\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]\left(\widehat{z}\right)\hfill \\ \hfill & =\left[\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]\left(\widehat{z}\right)-\widehat{z}\hfill \\ \hfill & =\tilde{A}\left[R_{\tilde{A},\xi }^M\left(\widehat{z}\right)\right]-\widehat{z}\hfill \\ \hfill & =\tilde{A}\left[R_{\tilde{A},\xi }^M\left(\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right)\right)\right]-\left[\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right)\right],\hfill \\ \hfill \mathrm{which}\mathrm{implies}\mathrm{that}& \\ \hfill \tilde{A}\left(e\right)& =\tilde{A}\left[R_{\tilde{A},\xi }^M\left(\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right)\right)\right].\hfill \end{array}$$

Since $\tilde{A}$ is one–one, we have

$$e=R_{\tilde{A},\xi }^M\left(\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right)\right).$$

By Lemma 3, it follows that $e\in \tilde{E}$ is the solution of Yosida variational inclusion problem (1). □

Alternative Proof. 

Let

$$\widehat{z}=\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right).$$

Using (9), we have

$$\widehat{z}=\tilde{A}\left(R_{\tilde{A},\xi }^M\left(\widehat{z}\right)\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right),$$

which implies that

$$Y_{\tilde{A},\xi }^M\left(e\right)+{\xi }^{-1}{T}_{\tilde{A},\xi }^M\left(\widehat{z}\right)=0,$$

the required Yosida resolvent equation problem (8). □

Based on Lemma 4, we state the following scheme for solving Yosida resolvent equation problem (8).

Iterative Scheme 4. 

For any $e_0,{\widehat{z}}_0\in \tilde{E}$, compute the sequences $\left\{e_n\right\}$ and $\left\{z_n\right\}$ by the following scheme:

$$\begin{array}{cc}\hfill & e_n=R_{\tilde{A},\xi }^M\left({\widehat{z}}_n\right),\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill & {\widehat{z}}_{n+1}=\tilde{A}\left(e_n\right)-\xi Y_{\tilde{A},\xi }^M\left(e_n\right),\hfill \end{array}$$

(12)

where $n=0,1,2,\cdots$ and $\xi >0$ is a constant. □

The Yosida resolvent equation problem (8) can be restated as:

$$\begin{array}{c}\hfill \widehat{z}=\tilde{A}\left(e\right)-Y_{\tilde{A},\xi }^M\left(e\right)+(I-{\xi }^{-1})T_{\tilde{A},\xi }^M\left(\widehat{z}\right).\end{array}$$

(13)

Verification. 

Using (9)

$$\begin{array}{cc}\hfill \widehat{z}=\tilde{A}\left(R_{\tilde{A},\xi }^M\left(\widehat{z}\right)\right)& -Y_{\tilde{A},\xi }^M\left(e\right)+T_{\tilde{A},\xi }^M\left(\widehat{z}\right)-{\xi }^{-1}{T}_{\tilde{A},\xi }^M\left(\widehat{z}\right)\hfill \\ \hfill \left[I-\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]\left(\widehat{z}\right)& =-Y_{\tilde{A},\xi }^M\left(e\right)+T_{\tilde{A},\xi }^M\left(\widehat{z}\right)-{\xi }^{-1}{T}_{\tilde{A},\xi }^M\left(\widehat{z}\right).\hfill \end{array}$$

Since $\left[I-\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]=T_{\tilde{A},\xi }^M$, we have

$$\begin{array}{cc}\hfill T_{\tilde{A},\xi }^M\left(\widehat{z}\right)& =-Y_{\tilde{A},\xi }^M\left(e\right)+T_{\tilde{A},\xi }^M\left(\widehat{z}\right)-{\xi }^{-1}{T}_{\tilde{A},\xi }^M\left(\widehat{z}\right).\hfill \end{array}$$

It follows that

$$Y_{\tilde{A},\xi }^M\left(e\right)+{\xi }^{-1}{T}_{\tilde{A},\xi }^M\left(\widehat{z}\right)=0.$$

□

Using fixed point formulation (13), we suggest the following iterative scheme.

Iterative Scheme 5. 

For given $e_0,{\widehat{z}}_0\in \tilde{E}$, compute the sequences $\left\{e_n\right\}$ and $\left\{z_n\right\}$ by the following scheme:

$$\begin{array}{cc}\hfill e_n& =R_{\tilde{A},\xi }^M\left({\widehat{z}}_n\right),\hfill \\ \hfill {\widehat{z}}_{n+1}=\tilde{A}\left(e_n\right)-& Y_{\tilde{A},\xi }^M\left(e_n\right)+(I-{\xi }^{-1})T_{\tilde{A},\xi }^M\left({\widehat{z}}_n\right),\hfill \end{array}$$

where $n=0,1,2,\cdots$ and $\xi >0$ is a constant. □

For positive step size $\delta$, the Yosida resolvent equation problem (8) can also be written as:

$$\begin{array}{c}\hfill e=e-\delta \left[\widehat{z}-\tilde{A}\left(R_{\tilde{A},\xi }^M\left(\widehat{z}\right)\right)+\xi Y_{\tilde{A},\xi }^M\left(e\right)\right].\end{array}$$

(14)

Verification. 

$$\begin{array}{cc}\hfill e& =e-\delta \left[\left[I-\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]\left(\widehat{z}\right)+\xi Y_{\tilde{A},\xi }^M\left(e\right)\right],\hfill \\ \hfill e& =e-\delta \left[T_{\tilde{A},\xi }^M\left(\widehat{z}\right)+\xi Y_{\tilde{A},\xi }^M\left(e\right)\right]\hfill \\ \hfill e& =e-\delta \left[Y_{\tilde{A},\xi }^M\left(e\right)+{\xi }^{-1}{T}_{\tilde{A},\xi }^M\left(\widehat{z}\right)\right],\hfill \end{array}$$

which gives

$$\begin{array}{cc}\hfill Y_{\tilde{A},\xi }^M\left(e\right)+{\xi }^{-1}{T}_{\tilde{A},\xi }^M\left(\widehat{z}\right)=0.& \end{array}$$

□

The fixed point formulation (14) enables us to suggest the following iterative scheme.

Iterative Scheme 6. 

For $e_0,{\widehat{z}}_0\in \tilde{E}$, compute the sequences $\left\{e_n\right\}$ and $\left\{{\widehat{z}}_n\right\}$ by the following scheme:

$$e_{n+1}=e_n-\delta \left[{\widehat{z}}_n-\tilde{A}\left(R_{\tilde{A},\xi }^M\left(\widehat{z_n}\right)\right)+\xi Y_{\tilde{A},\xi }^M\left(e_n\right)\right],$$

where$\xi ,\delta >0$ are constants and $n=0,1,2,\cdots$.

One can apply schemes 4–6 to obtain existence and convergence results for Yosida resolvent equation problem (8).

In order to accelerate the convergence rate, we suggest the following inertial extrapolation scheme for solving Yosida resolvent equation problem (8).

Equation (10) can also be written as

$$\begin{array}{c}\hfill \widehat{z}=\frac{\tilde{A}\left(e\right)+\tilde{A}\left(e\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(e\right).\end{array}$$

(15)

Based on (15), we establish the following implicit scheme for solving Yosida resolvent equation problem (8).

Iterative Scheme 7. 

For $e_0\in \tilde{E}$, compute the sequences $\left\{e_n\right\}$ and $\left\{{\widehat{z}}_n\right\}$ by the recurrance relation

$$\begin{array}{cc}\hfill e_n& =R_{\tilde{A},\xi }^M\left({\widehat{z}}_n\right),\hfill \\ \hfill {\widehat{z}}_{n+1}=(1-{\alpha }_n){\widehat{z}}_n+{\alpha }_n& \left[\frac{\tilde{A}\left(e_n\right)+\tilde{A}\left(e_{n+1}\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(e_{n+1}\right)\right],\hfill \end{array}$$

where $n=0,1,2,\cdots$ and ${\alpha }_n\in [0,1]$.

We design the following inertial extrapolation scheme for solving Yosida resolvent equation problem (8) applying the predictor–corrector technique.

Iterative Scheme 8. 

For $e_0,{\widehat{z}}_0\in \tilde{E}$, compute sequences $\left\{e_n\right\}$ and $\left\{z_n\right\}$ by the recurrance relation:

$$\begin{array}{cc}\hfill & w_n={\widehat{z}}_n+{\nu }_n\left({\widehat{z}}_n-{\widehat{z}}_{n-1}\right),\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill {\widehat{z}}_{n+1}=(1-{\alpha }_n){\widehat{z}}_n& +{\alpha }_n\left[\frac{\tilde{A}\left({\widehat{z}}_n\right)+\tilde{A}\left(w_n\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(w_n\right)\right],\hfill \end{array}$$

(17)

where $\xi >0$ is a constant, ${\alpha }_n,{\nu }_n\in [0,1]$ such that ${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty$ and ${\nu }_n$ is an extrapolating term for all $n\ge 1$.

4. Convergence Analysis

First, we discuss the convergence of scheme 3 for Yosida variational inclusion problem (1) in real Banach space. Thenceforth, we demonstrate convergence of scheme 8 for Yosida resolvent equation problem (8) in real q-uniformly smooth Banach space.

Theorem 1. 

Let $\tilde{E}$ be real Banach space and $\tilde{A}:\tilde{E}\to \tilde{E}$ be single-valued mapping such that $\tilde{A}$ is r-strongly accretive and ${\lambda }_{\tilde{A}}$-Lipschitz continuous. Let $M:\tilde{E}\to 2^{\tilde{E}}$ be $\tilde{A}$-accretive set-valued mapping. Suppose that $R_{\tilde{A},\xi }^M:\tilde{E}\to \tilde{E}$ is a generalized resolvent operator such that $R_{\tilde{A},\xi }^M$ is $\frac{1}{r}$-Lipschitz continuous and $Y_{\tilde{A},\xi }^M:\tilde{E}\to \tilde{E}$ is a generalized Yosida approximation operator such that $Y_{\tilde{A},\xi }^M$ is ${\lambda }_Y$-Lipschitz continuous. Suppose that the following conditions are satisfied:

$$\begin{array}{cc}\hfill \left|r-\frac{3{\lambda }_{\tilde{A}}}{4}\right|& >\frac{\sqrt{9{\lambda }_{\tilde{A}}^2+16}}{4},\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \left|r-{\lambda }_{\tilde{A}}\right|& >\sqrt{{\lambda }_{\tilde{A}}^2+1},\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill {\lambda }_{\tilde{A}}& <r+\xi {\lambda }_Y,\hfill \end{array}$$

(20)

where ${\lambda }_Y=\frac{{\lambda }_{\tilde{A}}r+1}{\xi r},r\ne 0,\xi r\ne 0$.

Let ${\alpha }_n,{\nu }_n\in [0,1]$, for all $n\ge 1$ such that

$$\begin{array}{c}\hfill \sum _{n=1}^{\infty }{\alpha }_n=\infty \mathit{as}\mathit{well}\mathit{as}\sum _{n=1}^{\infty }{\nu }_n(e_n-e_{n-1})<\infty ,\end{array}$$

(21)

where all contants are positive and ${\nu }_n$ is an extrapolating term.

Then, sequence $\left\{e_n\right\}$ generated by the scheme 3 strongly converges to the unique solution $e^{*}\in \tilde{E}$ of Yosida variational inclusion problem (1).

Proof. 

Let $e\in \tilde{E}$ be the solution of Yosida variational inclusion problem (1). Using (4), we have

$$\begin{array}{c}\hfill e^{*}=(1-{\alpha }_n)e^{*}+{\alpha }_n{R}_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e^{*}\right)+\tilde{A}\left(e^{*}\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(e^{*}\right)\right],\end{array}$$

(22)

where ${\alpha }_n\in [0,1]$, for all $n\ge 1$. Using (7) and (22), we evaluate

$$\begin{array}{cccc}\hfill \parallel e_{n+1}-e^{*}\parallel & =\parallel (1-{\alpha }_n)e_n+{\alpha }_n{R}_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e_n\right)+\tilde{A}\left(w_n\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(w_n\right)\right]\hfill & & \hfill \\ & -(1-{\alpha }_n)e^{*}+{\alpha }_n{R}_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e^{*}\right)+\tilde{A}\left(e^{*}\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(e^{*}\right)\right]\parallel \hfill \\ & =\parallel (1-{\alpha }_n)(e_n-e^{*})+{\alpha }_n[R_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e_n\right)+\tilde{A}\left(w_n\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(w_n\right)\right]\hfill \\ & -R_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e^{*}\right)+\tilde{A}\left(e^{*}\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(e^{*}\right)\right]]\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel e_n-e^{*}\parallel +{\alpha }_n\parallel R_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e_n\right)+\tilde{A}\left(w_n\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(w_n\right)\right]\hfill \\ & -R_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e^{*}\right)+\tilde{A}\left(e^{*}\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(e^{*}\right)\right]\parallel .\hfill \end{array}$$

(23)

Applying the Lipschitz continuity of generalized resolvent operator $R_{\tilde{A},\xi }^M,\tilde{A}$ and generalized Yosida approximation operator $Y_{\tilde{A},\xi }^M$, from (23), we obtain

$$\begin{array}{cccc}\hfill \parallel e_{n+1}-e^{*}\parallel & \le (1-{\alpha }_n)\parallel e_n-e^{*}\parallel +\frac{{\alpha }_n}{r}\parallel \left[\frac{\tilde{A}\left(e_n\right)+\tilde{A}\left(w_n\right)}{2}\right]-\left[\frac{\tilde{A}\left(e^{*}\right)-\tilde{A}\left(e^{*}\right)}{2}\right]\hfill & & \hfill \\ & -\xi \left[Y_{\tilde{A},\xi }^M\left(w_n\right)-Y_{\tilde{A},\xi }^M\left(e^{*}\right)\right]\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel e_n-e^{*}\parallel +\frac{{\alpha }_n}{2r}\parallel \tilde{A}\left(e_n\right)-\tilde{A}\left(e^{*}\right)\parallel +\frac{{\alpha }_n}{2r}\parallel \tilde{A}\left(w_n\right)-\tilde{A}\left(e^{*}\right)\parallel \hfill \\ & +\frac{{\alpha }_n}{r}\xi \parallel Y_{\tilde{A},\xi }^M\left(w_n\right)-Y_{\tilde{A},\xi }^M\left(e^{*}\right)\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel e_n-e^{*}\parallel +\frac{{\alpha }_n}{2r}{\lambda }_{\tilde{A}}\parallel e_n-e^{*}\parallel +\frac{{\alpha }_n}{2r}{\lambda }_{\tilde{A}}\parallel w_n-e^{*}\parallel \hfill \\ & +\frac{{\alpha }_n}{r}\xi \parallel Y_{\tilde{A},\xi }^M\left(w_n\right)-Y_{\tilde{A},\xi }^M\left(e^{*}\right)\parallel \hfill \\ & \le (1-{\alpha }_n)\parallel e_n-e^{*}\parallel +\frac{{\alpha }_n}{2r}{\lambda }_{\tilde{A}}\parallel e_n-e^{*}\parallel +\frac{{\alpha }_n}{2r}{\lambda }_{\tilde{A}}\parallel w_n-e^{*}\parallel \hfill \\ & +\frac{{\alpha }_n}{r}\xi {\lambda }_Y\parallel w_n-e^{*}\parallel \hfill \\ & =\left[(1-{\alpha }_n)+\frac{{\alpha }_n}{2r}{\lambda }_{\tilde{A}}\right]\parallel e_n-e^{*}\parallel +\left[\frac{{\alpha }_n}{2r}{\lambda }_{\tilde{A}}+\frac{{\alpha }_n}{r}\xi {\lambda }_Y\right]\parallel w_n-e^{*}\parallel .\hfill \end{array}$$

(24)

From (6), we have

$$\begin{array}{cccc}\hfill \parallel w_n-e^{*}\parallel & =\parallel e_n-e^{*}+{\nu }_n(e_n-e_{n-1})\parallel \hfill & & \hfill \\ & \le \parallel e_n-e^{*}\parallel +{\nu }_n\parallel e_n-e_{n-1}\parallel .\hfill \end{array}$$

(25)

Combining (24) and (25), we obtain

$$\begin{array}{cccc}\hfill \parallel e_{n+1}-e^{*}\parallel & \le \left[(1-{\alpha }_n)+\frac{{\alpha }_n{\lambda }_{\tilde{A}}}{2r}\right]\parallel e_n-e^{*}\parallel +\frac{{\alpha }_n({\lambda }_{\tilde{A}}+2\xi {\lambda }_Y)}{2r}\parallel e_n-e^{*}\parallel \hfill & & \hfill \\ & +\frac{{\alpha }_n({\lambda }_{\tilde{A}}+2\xi {\lambda }_Y)}{2r}{\nu }_n\parallel e_n-e_{n-1}\parallel .\hfill \end{array}$$

Thus, we have

$$\begin{array}{cc}\hfill \parallel e_{n+1}-e^{*}\parallel & \le \left[(1-{\alpha }_n)+{\alpha }_n{P}_1+{\alpha }_n{P}_2\right]\parallel e_n-e^{*}\parallel +{\alpha }_n{P}_2{\nu }_n\parallel e_n-e_{n-1}\parallel \hfill \\ & =\left[(1-{\alpha }_n)(1-(P_1+P_2))\right]\parallel e_n-e^{*}\parallel +{\nu }_n\parallel e_n-e_{n-1}\parallel ,\hfill \end{array}$$

(26)

$$\begin{array}{ccc}\hfill \mathrm{where}{P}_1& =\frac{{\lambda }_{\tilde{A}}}{2r},\hfill & \\ \hfill P_2& =\frac{{\lambda }_{\tilde{A}}+2\xi {\lambda }_Y}{2r}<1,(\mathrm{By}\mathrm{condition}(18))\hfill & \\ \hfill P_1+P_2& =\frac{{\lambda }_{\tilde{A}}}{r}+\frac{\xi {\lambda }_Y}{r}.\hfill \end{array}$$

Letting $P=P_1+P_2$, $P<1$ from condition (19). By condition (21), we have ${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty$ and ${\displaystyle \sum _{n=1}^{\infty }}{\nu }_n\parallel e_n-e_{n-1}\parallel <\infty$. Setting ${\sigma }_n=0$ and ${\tilde{\xi }}_n={\displaystyle \sum _{n=1}^{\infty }}{\nu }_n\parallel e_n-e_{n-1}\parallel <\infty$. Then, by Lemma 2 and (26), we have $e_n\to e^{*}$, as $n\to \infty$. Thus, the sequence $\left\{e_n\right\}$ generated by scheme 3 strongly converges to the unique solution $e^{*}\in \tilde{E}$ of Yosida variational inclusion problem (1). Furthermore, we show that the solution of Yosida variational inclusion problem (1) is unique.

Let $e,e^{*}\in \tilde{E}$ be the two solutions of Yosida variational inclusion problem (1). Then, by Lemma 3, we have

$$\begin{array}{cc}\hfill e& =R_{\tilde{A},\xi }^M\left[\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right)\right]\hfill \\ \hfill \mathrm{and}{e}^{*}& =R_{\tilde{A},\xi }^M\left[\tilde{A}\left(e^{*}\right)-\xi Y_{\tilde{A},\xi }^M\left(e^{*}\right)\right].\hfill \end{array}$$

Using the Lipschitz continuity of the generalized resolvent operator $R_{\tilde{A},\xi }^M$, generalized Yosida approximation operator $Y_{\tilde{A},\xi }^M$ and mapping $\tilde{A}$, we evaluate

$$\begin{array}{cc}\hfill \parallel e-e^{*}\parallel & =\parallel R_{\tilde{A},\xi }^M\left[\tilde{A}\left(e\right)-\xi Y_{\tilde{A},\xi }^M\left(e\right)\right]-R_{\tilde{A},\xi }^M\left[\tilde{A}\left(e^{*}\right)-\xi Y_{\tilde{A},\xi }^M\left(e^{*}\right)\right]\parallel \hfill \\ \hfill & \le \frac{1}{r}\parallel \tilde{A}\left(e\right)-\tilde{A}\left(e^{*}\right)-\xi \left[Y_{\tilde{A},\xi }^M\left(e\right)-Y_{\tilde{A},\xi }^M\left(e^{*}\right)\right]\parallel \hfill \\ \hfill & \le \frac{1}{r}{\lambda }_{\tilde{A}}\parallel e-e^{*}\parallel +\frac{\xi {\lambda }_Y}{r}\parallel e-e^{*}\parallel \hfill \\ \hfill & =\left(\frac{{\lambda }_{\tilde{A}}}{r}-\frac{\xi {\lambda }_Y}{r}\right)\parallel e-e^{*}\parallel \hfill \\ \hfill & =A\left(\theta \right)\parallel e-e^{*}\parallel ,\hfill \end{array}$$

(27)

where $A\left(\theta \right)=\left(\frac{{\lambda }_{\tilde{A}}}{r}-\frac{\xi {\lambda }_Y}{r}\right),{\lambda }_Y=\left(\frac{{\lambda }_{\tilde{A}}r+1}{\xi r}\right)$. It follows from condition (20) that $0<A\left(\theta \right)<1$. Thus, from (27), we have $e=e^{*}$. That is, $e^{*}$ is the unique solution of Yosida variational inclusion problem (1). □

Now, we study the convergence analysis of scheme 8 for Yosida resolvent equation problem (8) in the setting of q-uniformly smooth Banach space. Note that by Lemma 4, Yosida variational inclusion problem (1) is equivalent to Yosida resolvent equation problem (8). As Yosida variational inclusion problem (1) admits a unique solution, Yosida resolvent equation problem (8) also admits a unique solution.

Theorem 2. 

Let $\tilde{E}$ be q-uniformly smooth Banach space and $\tilde{A}:\tilde{E}\to \tilde{E}$ be single-valued mapping such that $\tilde{A}$ is one–one, ${\lambda }_{\tilde{A}}$-Lipschitz continuous, ${\beta }_{\tilde{A}}$-expansive and r-strongly accretive.

Let $M:\tilde{E}\to \tilde{E}$ be $\tilde{A}$-accretive set-valued mapping and $R_{\tilde{A},\xi }^M:\tilde{E}\to \tilde{E}$ be a generalized resolvent operator such that $R_{\tilde{A},\xi }^M$ is $\frac{1}{r}$-Lipschitz continuous. Let $Y_{\tilde{A},\xi }^M:\tilde{E}\to \tilde{E}$ be a generalized Yosida approximation operator such that $Y_{\tilde{A},\xi }^M$ is ${\theta }_Y$-strongly accretive with respect to $\tilde{A}$ and ${\lambda }_Y$-Lipschitzcontinuous. Let $T_{\tilde{A},\xi }^M\left(\widehat{z}\right)=\left[I-\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]\left(\widehat{z}\right)$, where $\tilde{A}\left(R_{\tilde{A},\xi }^M\left(\widehat{z}\right)\right)=\left[\tilde{A}\left(R_{\tilde{A},\xi }^M\right)\right]\left(\widehat{z}\right),\widehat{z}\in \tilde{E}$. Suppose that the following conditions are satisfied.

$$\begin{array}{cc}\hfill \left({\lambda }_{\tilde{A}}^q-2q\xi {\theta }_Y+2^q{\xi }^q{C}_q{\lambda }_Y^q\right)& <2^q,\hfill \end{array}$$

(28)

$$\begin{array}{c}\hfill {\lambda }_{\tilde{A}}<2.\end{array}$$

(29)

Let ${\alpha }_n,{\nu }_n\in [0,1]$, for all $n\ge 1$ such that

$$\begin{array}{cc}\hfill \sum _{n=1}^{\infty }{\alpha }_n=\infty \mathrm{and}\sum _{n=1}^{\infty }\left(\parallel {\tilde{z}}_n-w^{*}\parallel +{\nu }_n\parallel {\widehat{z}}_n-{\widehat{z}}_{n-1}\parallel \right)<\infty ,& \hfill \end{array}$$

(30)

where $\xi >0$ is a constant, $C_q$ is the same as in Lemma 1, ${\theta }_Y=\frac{{\beta }_{\tilde{A}}^{q}r-{\lambda }_{\tilde{A}}^{q-1}}{\xi r}$ and ${\lambda }_Y=\frac{{\lambda }_{\tilde{A}}r+1}{\xi r},\xi r\ne 0,r\ne 0,{\beta }_{\tilde{A}}^{q}r>{\lambda }_{\tilde{A}}^{q-1}$, and all the constants are positive.

Then, sequences $\left\{e_n\right\}$ and $\left\{{\widehat{z}}_n\right\}$ generated by scheme 8 strongly converge to the unique solution $e^{*}$ and $z^{*}$ of Yosida resolvent equation problem (8).

Proof. 

Applying (17) of scheme 8 and Lipschitz continuity of $\tilde{A}$, we evaluate

$$\begin{array}{cc}\hfill \parallel {\widehat{z}}_{n+1}-\widehat{z^{*}}\parallel & =\parallel (1-{\alpha }_n){\widehat{z}}_n+{\alpha }_n\left[\frac{\tilde{A}\left({\widehat{z}}_n\right)+\tilde{A}\left(w_n\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(w_n\right)\right]\hfill \\ \hfill & -\left[(1-{\alpha }_n)z^{*}+{\alpha }_n\left[\frac{\tilde{A}\left(\widehat{z^{*}}\right)+\tilde{A}\left(w^{*}\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(w^{*}\right)\right]\right]\parallel \hfill \\ \hfill & =\parallel (1-{\alpha }_n)({\widehat{z}}_n-\widehat{z^{*}})+{\alpha }_n[\frac{\tilde{A}\left({\widehat{z}}_n\right)-\tilde{A}\left(\widehat{z^{*}}\right)}{2}+\frac{\tilde{A}\left(w_n\right)-\tilde{A}\left(w^{*}\right)}{2}\hfill \\ \hfill & -\xi \left[Y_{\tilde{A},\xi }^M\left(w_n\right)-Y_{\tilde{A},\xi }^M\left(w^{*}\right)\right]]\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel {\widehat{z}}_n-\widehat{z^{*}}\parallel +\frac{{\alpha }_n}{2}\parallel \tilde{A}\left({\widehat{z}}_n\right)-\tilde{A}\left(\widehat{z^{*}}\right)\parallel \hfill \\ \hfill & +\frac{{\alpha }_n}{2}\parallel \tilde{A}\left(w_n\right)-\tilde{A}\left(w^{*}\right)-2\xi \left[Y_{\tilde{A},\xi }^M\left(w_n\right)-Y_{\tilde{A},\xi }^M\left(w^{*}\right)\right]\parallel \hfill \\ \hfill & \le (1-{\alpha }_n)\parallel {\widehat{z}}_n-\widehat{z^{*}}\parallel +\frac{{\alpha }_n}{2}{\lambda }_{\tilde{A}}\parallel {\widehat{z}}_n-\widehat{z^{*}}\parallel \hfill \\ \hfill & +\frac{{\alpha }_n}{2}\parallel \tilde{A}\left(w_n\right)-\tilde{A}\left(w^{*}\right)-2\xi \left[Y_{\tilde{A},\xi }^M\left(w_n\right)-Y_{\tilde{A},\xi }^M\left(w^{*}\right)\right]\parallel .\hfill \end{array}$$

(31)

Using Lemma 1, Lipschitz continuity of $\tilde{A}$, strong accretiveness of $Y_{\tilde{A},\xi }^M$ with respect to $\tilde{A}$ and Lipschitz continuity of $Y_{\tilde{A},\xi }^M$, we have

$$\begin{array}{cc}\hfill \parallel \tilde{A}\left(w_n\right)-\tilde{A}\left(w^{*}\right)-& 2\xi \left[Y_{\tilde{A},\xi }^M\left(w_n\right)-Y_{\tilde{A},\xi }^M\left(w^{*}\right)\right]{\parallel }^q\hfill \\ \hfill & \le \parallel \tilde{A}\left(w_n\right)-\tilde{A}\left(w^{*}\right){\parallel }^q-q2\xi ⟨Y_{\tilde{A},\xi }^M\left(w_n\right)-Y_{\tilde{A},\xi }^M\left(w^{*}\right),J_q(\tilde{A}\left(w_n\right)-\tilde{A}\left(w^{*}\right)⟩\hfill \\ \hfill & +2^q{\xi }^q{C}_q\parallel Y_{\tilde{A},\xi }^M\left(w_n\right)-Y_{\tilde{A},\xi }^M\left(w^{*}\right){\parallel }^q\hfill \\ \hfill & \le {\lambda }_{\tilde{A}}^q\parallel w_n-w^{*}{\parallel }^q-2q\xi {\theta }_Y\parallel w_n-w^{*}{\parallel }^q+2^q{\xi }^q{C}_q{\lambda }_Y^q{\parallel w_n-w^{*}\parallel }^q\hfill \\ \hfill & \le \left[{\lambda }_{\tilde{A}}^q-2q\xi {\theta }_Y+2^q{\xi }^q{C}_q{\lambda }_Y^q\right]{\parallel w_n-w^{*}\parallel }^q,\hfill \end{array}$$

(32)

where ${\theta }_Y=\frac{{\beta }_{\tilde{A}}^{q}r-{\lambda }_{\tilde{A}}^{q-1}}{\xi r},\xi r\ne 0,{\lambda }_Y=\frac{{\lambda }_{\tilde{A}}r+1}{\xi r}$ and ${\lambda }_{\tilde{A}}+2^q{\xi }^q{C}_q{\lambda }_Y^q>2q\xi {\theta }_Y$.

It follows from (32) that

$$\begin{array}{c}\hfill \parallel \tilde{A}\left(w_n\right)-\tilde{A}\left(w^{*}\right)-2\xi \left[Y_{\tilde{A},\xi }^M\left(w_n\right)-Y_{\tilde{A},\xi }^{M}x\left(w^{*}\right)\right]\parallel \le \sqrt[q]{{\lambda }_{\tilde{A}}^q-2q\xi {\theta }_Y+2^q{\xi }^q{C}_q{\lambda }_Y^q}\parallel w_n-w^{*}\parallel .\end{array}$$

(33)

Combining (31) and (33), we obtain

$$\begin{array}{c}\hfill \parallel {\widehat{z}}_{n+1}-\widehat{z^{*}}\parallel \le (1-{\alpha }_n)\parallel {\widehat{z}}_n-\widehat{z^{*}}\parallel +\frac{{\alpha }_n}{2}{\lambda }_{\tilde{A}}\parallel {\widehat{z}}_n-\widehat{z^{*}}\parallel +\frac{{\alpha }_n}{2}\sqrt[q]{{\lambda }_{\tilde{A}}^q-2q\xi {\theta }_Y+2^q{\xi }^q{C}_q{\lambda }_Y^q}\parallel w_n-w^{*}\parallel .\end{array}$$

(34)

Applying (16) of scheme 8, we have

$$\begin{array}{cc}\hfill \parallel w_n-w^{*}\parallel & =\parallel {\widehat{z}}_n-w^{*}+{\nu }_n({\widehat{z}}_n-{\widehat{z}}_{n-1}\parallel \hfill \\ \hfill & \le \parallel {\widehat{z}}_n-w^{*}\parallel +{\nu }_n\parallel {\widehat{z}}_n-{\widehat{z}}_{n-1}\parallel .\hfill \end{array}$$

(35)

Combining (34) with (35), we have

$$\begin{array}{cc}\hfill \parallel {\widehat{z}}_{n+1}-\widehat{z^{*}}\parallel & \le (1-{\alpha }_n)\parallel {\widehat{z}}_n-\widehat{z^{*}}\parallel +\frac{{\alpha }_n}{2}{\lambda }_{\tilde{A}}\parallel {\widehat{z}}_n-\widehat{z^{*}}\parallel \hfill \\ & +\frac{{\alpha }_n}{2}\sqrt[q]{{\lambda }_{\tilde{A}}^q-2q\xi {\theta }_Y+2^q{\xi }^q{C}_q{\lambda }_Y^q}\left[\parallel {\widehat{z}}_n-w^{*}\parallel +{\nu }_n\parallel {\widehat{z}}_n-{\widehat{z}}_{n-1}\parallel \right],\hfill \end{array}$$

that is

$$\begin{array}{cc}\hfill \parallel {\widehat{z}}_{n+1}-\widehat{z^{*}}\parallel & \le \left[(1-{\alpha }_n(1-{\widehat{\mathsf{\Pi }}}_1)\right]\parallel {\widehat{z}}_n-\widehat{z^{*}}\parallel +{\alpha }_n{\mathsf{\Pi }}_2\left[\parallel {\widehat{z}}_n-w^{*}\parallel +{\nu }_n\parallel {\widehat{z}}_n-{\widehat{z}}_{n-1}\parallel \right]\hfill \\ & \le \left[1-{\alpha }_n(1-{\widehat{\mathsf{\Pi }}}_1)\right]\parallel {\widehat{z}}_n-\widehat{z^{*}}\parallel +{\alpha }_n\left[\parallel {\widehat{z}}_n-w^{*}\parallel +{\nu }_n\parallel {\widehat{z}}_n-{\widehat{z}}_{n-1}\parallel \right],\hfill \end{array}$$

(36)

where ${\widehat{\mathsf{\Pi }}}_1=\frac{{\lambda }_{\tilde{A}}}{2}$ and ${\widehat{\mathsf{\Pi }}}_2=\frac{\sqrt[q]{{\lambda }_{\tilde{A}}^q-2q\xi {\theta }_Y+2^q{\xi }^q{C}_q{\lambda }_Y^q}}{2}$. By condition (28), ${\widehat{\mathsf{\Pi }}}_2<1$ and by condition (29), ${\widehat{\mathsf{\Pi }}}_2<1$.

Applying condition (30), we have ${\displaystyle \sum _{n=1}^{\infty }}{\alpha }_n=\infty$ and ${\displaystyle \sum _{n=1}^{\infty }}\left(\parallel {\widehat{z}}_n-w^{*}\parallel +{\nu }_n\parallel {\widehat{z}}_n-{\widehat{z}}_{n-1}\parallel \right)<\infty$. We set ${\sigma }_n=0$ and ${\widehat{\xi }}_n={\displaystyle \sum _{n=1}^{\infty }}\left(\parallel {\widehat{z}}_n-w^{*}\parallel +{\nu }_n\parallel {\widehat{z}}_n-{\widehat{z}}_{n-1}\parallel \right)<\infty$. Applying Lemma 2 and (36), we have ${\widehat{z}}_n\to \widehat{z^{*}}$, as $n\to \infty$.

In addition,

$$\begin{array}{c}\hfill \parallel e_n-e^{*}\parallel =\parallel R_{\tilde{A},\xi }^M({\widehat{z}}_n)-R_{\tilde{A},\xi }^M(\widehat{z^{*}})\parallel \le \frac{1}{r}\parallel {\widehat{z}}_n-\widehat{z^{*}}\parallel .\end{array}$$

(37)

Since ${\widehat{z}}_n\to \widehat{z^{*}}\in \tilde{E}$, it follows from (37) that $e_n\to e^{*}\in \tilde{E}$. Hence, the sequences $\left\{{\widehat{z}}_n\right\}$ and $\left\{e_n\right\}$ generated by scheme 8 converge strongly to $\widehat{z^{*}}$ and $e^{*}$, providing the unique solution of Yosida resolvent equation problem (8). □

5. Numerical Experiment

In support of Theorem 1, construct the following numerical example using MATLAB 2015a with a computation table and convergence graph.

Example 1. 

Let $\tilde{E}=\mathbb{R}$ with usual inner product and norm, $\tilde{A}:\tilde{E}\to \tilde{E}$ be single-valued mapping and $M:\tilde{E}\to 2^{\tilde{E}}$ be set-valued mapping such that

$$\begin{array}{cc}\hfill A\left(e\right)& =\frac{6}{5}e,\hfill \\ \hfill \mathit{and}M\left(e\right)& =\left\{\frac{1}{10}e\right\},\mathit{for}\mathit{all}e\in \tilde{E}.\hfill \end{array}$$

(i)   $\tilde{A}$ is r-strongly accretive and ${\lambda }_{\tilde{A}}$-Lipschtiz continuous.

$$\begin{array}{ccc}\hfill ⟨\tilde{A}\left(e\right)-\tilde{A}\left(f\right),e-f⟩& =& ⟨\frac{6}{5}e-\frac{6}{5}f,e-f⟩\hfill \\ & =& \frac{6}{5}{\parallel e-f\parallel }^2\ge \frac{11}{10}{\parallel e-f\parallel }^2.\hfill \end{array}$$

Thus, $\tilde{A}$ is $r=\frac{11}{10}$-strongly accretive mapping.

In addition,

$$\begin{array}{ccc}\hfill \parallel \tilde{A}\left(e\right)-\tilde{A}\left(f\right)\parallel & =& ∥\frac{6}{5}e-\frac{6}{5}f∥\hfill \\ & =& \frac{6}{5}∥e-f∥\le \frac{13}{10}\parallel e-f\parallel .\hfill \end{array}$$

Thus, $\tilde{A}$ is ${\lambda }_{\tilde{A}}=\frac{13}{10}$-Lipschitz continuous mapping.

(ii)   M is $\tilde{A}$-accretive.

$$\begin{array}{ccc}\hfill \parallel M\left(e\right)-M\left(f\right)\parallel & =& ∥\frac{1}{10}e-\frac{1}{10}f∥\hfill \\ & =& \frac{1}{10}∥e-f∥\ge 0.\hfill \end{array}$$

That is, M is accretive and also for $\xi =1$, it is easy to verify that

$$[\tilde{A}+\xi M]\left(\tilde{E}\right)=\tilde{E}.$$

Thus, M is $\tilde{A}$-accretive mapping.

(iii)   For $\xi =1$, we define a generalized resolvent operator

$$R_{\tilde{A},\xi }^M\left(e\right)={[\tilde{A}+\xi M]}^{-1}\left(e\right)=\frac{10}{13}e,\mathit{for}\mathit{all}e\in \tilde{E}.$$

In addition,

$$\begin{array}{ccc}\hfill \parallel R_{\tilde{A},\xi }^M\left(e\right)-R_{\tilde{A},\xi }^M\left(f\right)\parallel & =& ∥\frac{10}{13}e-\frac{10}{13}f∥\hfill \\ & =& \frac{10}{13}∥e-f∥\le \frac{1}{(11/10)}\parallel e-f\parallel .\hfill \end{array}$$

Thus, the generalized resolvent operator $R_{\tilde{A},\xi }^M$ is $\frac{1}{r}=\frac{1}{(11/10)}$-Lipschitz continuous.

(iv)   Based on step (iii), we calculate the generalized Yosida approximation operator

$$Y_{\tilde{A},\xi }^M\left(e\right)=\frac{1}{\xi }[\tilde{A}-R_{\tilde{A},\xi }^M]\left(e\right)=\frac{28}{65}e,\mathit{for}\mathit{all}e\in \tilde{E}.$$

In addition,

$$\begin{array}{ccc}\hfill \parallel Y_{\tilde{A},\xi }^M\left(e\right)-Y_{\tilde{A},\xi }^M\left(f\right)\parallel & =& ∥\frac{28}{65}e-\frac{28}{65}f∥\hfill \\ & =& \frac{28}{65}∥e-f∥\le \frac{243}{110}\parallel e-f\parallel ,\hfill \end{array}$$

Thus, the generalized Yosida approximation operator $Y_{\tilde{A},\xi }^M$ is ${\lambda }_Y=\frac{{\lambda }_{\tilde{A}}r+1}{\xi r}=\frac{243}{110}$-Lipschitz continuous.

(v)   In view of constants calculated above, the conditions (18)–(20) of Theorem 1 are fulfilled.

(vi)   For ${\alpha }_n=\frac{5}{n+1}$ and ${\nu }_n=\frac{1}{n}$, inertial extrapolation scheme 8 has the following model:

$$\begin{array}{cc}\hfill w_n& =e_n+{\nu }_n(e_n-e_{n-1})\hfill \\ \hfill e_{n+1}& =(1-{\alpha }_n)e_n+{\alpha }_n{R}_{\tilde{A},\xi }^M\left[\frac{\tilde{A}\left(e_n\right)+\tilde{A}\left(w_n\right)}{2}-\xi Y_{\tilde{A},\xi }^M\left(w_n\right)\right]\hfill \\ \hfill & =(1-{\alpha }_n)e_n+{\alpha }_n{R}_{\tilde{A},\xi }^M\left[\frac{3}{5}{e}_n+\frac{11}{65}{w}_n\right]\hfill \\ \hfill & =(1-{\alpha }_n)e_n+{\alpha }_n\left[\frac{6}{13}{e}_n+\frac{110}{845}{w}_n\right].\hfill \end{array}$$

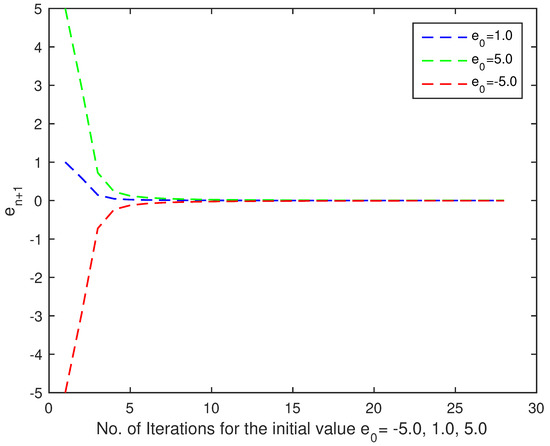
It is shown through a computation table (Table 1) and convergence graph (Figure 1) that for different initial values $e_0=1,-5.0,5.0$, the sequence $\left\{e_n\right\}$ converges to $e^{*}=0$, which is the solution of Yosida variational inclusion problem (1). For the composition of a computation table and convergence graph, we use the tools of MATLAB 2015a.

Table 1. Computation outputs for different initial values $e_0=1,-5.0$ and $5.0$.

No. of Iterations	${\mathit{e}}_0=1.0$ en	No. of Iterations	${\mathit{e}}_0=-5.0$ en	No. of Iterations	${\mathit{e}}_0=5.0$ en
1	0.5917	1	−2.9586	1	2.9586
2	0.1448	2	−0.7239	2	0.7239
3	0.0466	3	−0.2332	3	0.2332
4	0.0244	4	−0.1220	4	0.1220
5	0.0156	5	−0.0781	5	0.0781
15	0.0018	15	0.0000	15	0.0000
20	0.0010	20	0.0000	20	0.0000
25	6.4947$\times {10}^{-04}$	25	0.0000	25	0.0000
26	6.0032$\times {10}^{-04}$	26	0.0000	26	0.0000
27	5.5651$\times {10}^{-04}$	27	0.0000	27	0.0000
28	5.1730$\times {10}^{-04}$	28	0.0000	28	0.0000
29	4.8207$\times {10}^{-04}$	29	0.0000	29	0.0000
30	4.1327$\times {10}^{-04}$	30	0.0000	30	0.0000

Figure 1. Graphical representation of convergence of sequence $\left\{e_n\right\}$ with different initial values $e_0=1,-5.0$ and $5.0$.

6. Conclusions

In this paper, we have considered and studied a Yosida variational inclusion problem with its corresponding Yosida resolvent equation problem. Using the resolvent operator technique, it is shown that both the problems are equivalent under appropriate conditions. We mention the number of iterative schemes for solving both the problems. We concentrate our study on the convergence analysis of both the problems applying an inertial extrapolation scheme. For illustration, an example is constructed.

One can extend our results in higher-dimensional spaces. Engineers, physicists and other scientists may use our result for their practical purposes.