Abstract
Optimizing large-scale numerical problems is a significant challenge with numerous real-world applications. The optimization process is complex due to the multi-dimensional search spaces and possesses several locally optimal regions. In response to this issue, various metaheuristic algorithms and variations have been developed, including evolutionary and swarm intelligence algorithms and hybrids of different artificial intelligence techniques. Previous studies have shown that swarm intelligence algorithms like PSO perform poorly in high-dimensional spaces, even with algorithms focused on reducing the search space. However, we propose a modified version of the PSO algorithm called Dynamical Sphere Regrouping PSO (DSRegPSO) to avoid stagnation in local optimal regions. DSRegPSO is based on the PSO algorithm and modifies inertial behavior with a regrouping dynamical sphere mechanism and a momentum conservation physics effect. These behaviors maintain the swarm’s diversity and regulate the exploration and exploitation of the search space while avoiding stagnation in optimal local regions. The DSRegPSO mechanisms mimic the behavior of birds, moving particles similar to birds when they look for a new food source. Additionally, the momentum conservation effect mimics how birds react to collisions with the boundaries in their search space or when they are looking for food. We evaluated DSRegPSO by testing 15 optimizing functions with up to 1000 dimensions of the CEC’13 benchmark, a standard for evaluating Large-Scale Global Optimization used in Congress on Evolutionary Computation, and several journals. Our proposal improves the behavior of all variants of PSO registered in the toolkit of comparison for CEC’13 and obtains the best result in the non-separable functions against all the algorithms.
MSC:
68T20
1. Introduction
Complex real-world problems with several numerical parameters and incomplete or noisy data require global optimization in multi-dimensional search spaces. Epigenesis, Phylogeny, and Ontogeny are three optimization approaches commonly used in artificial intelligence, each with its unique characteristics and applications. Artificial neural networks utilize tentative learning in Epigenesis, while evolutionary algorithms rely on competition and survival of the fittest in Phylogeny. Swarm intelligence algorithms adopt cooperative learning in their environment in Ontogeny [1,2,3]. In complex search spaces, locating the global optimum or a suitable solution can prove to be a formidable task, as the likelihood of encountering local optimal regions tends to increase with higher dimensions [4]. Advancements in technology have made solving Large-Scale Global Optimization (LSGO) more feasible, resulting in the creation of specialized algorithms. However, a standard evaluation method for comparison is necessary [5]. The IEEE Congress on Evolutionary Computation (CEC) tool is a widely used benchmark for LSGO problems. It includes optimization functions that simulate real-world problems and has been used to evaluate algorithms in [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19]. Several metaheuristics have been applied to address the challenges associated with solving Large-Scale Global Optimization (LSGO) problems. These metaheuristics include Genetic Algorithms (GAs), Evolutionary Strategies (ES), Evolutionary Programming (EP), Memetic Algorithms (MAs), and Differential Evolution (DE), among others [1,5,6,20]. In the field of numerical optimization, swarm intelligence (SI) is considered a strong competitor to evolutionary algorithms (EAs) due to its relatively lower complexity and smaller input parameter sizes. However, in the context of Large-Scale Global Optimization (LSGO), SI algorithms tend to experience stagnation due to the presence of multiple local optimal regions [5]. Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), and Artificial Bee Colony (ABC) are among the widely used SI algorithms. Some other alternatives that have shown good results in various applications are the Wolf Algorithm (WA), Butterfly Algorithm (BA), Krill Algorithm (KA), and Moth Search Algorithm (MSA) [1,5,6]. The Particle Swarm Optimization (PSO) algorithm, proposed by Kennedy and Eberhart in 1995, is widely used for numerical optimization. It is based on the behavior of flocks of birds [21]. While the Particle Swarm Optimization (PSO) algorithm produces commendable outcomes in uncomplicated search spaces, it faces challenges when it comes to optimization in the presence of multiple local optimal regions [19,22,23,24,25,26,27,28]. Many researchers have put forth different versions of the PSO algorithm to tackle LSGO. One such variation is the GPSO, introduced in 1998 by Yuhui Shi and Russell Eberhart. The GPSO incorporates an inertial parameter that facilitates quick convergence and enhances the algorithm’s ability to resist local optima by promoting exploration. However, all the particles continue to share the best position, which can potentially result in being stuck around the global best position [24,29]. GEPSO is a PSO variant that uses three inertial weights and a new speed equation with two parameters to improve swarm convergence. It has been successfully tested in 50-dimensional optimization problems [1]. In the work presented by [16], Particle Swarm Optimization (PSO) is designed to circumvent stagnation by iteratively shifting particles toward the boundaries of the search space. Regrouping PSO (RegPSO) overcomes stagnation by resetting the position of particles and redefining the search space after detecting minimal separation between all positions within the swarm. This approach offers an effective means of addressing the issue of stagnation in PSO algorithms [30]. Canonical Deterministic PSO (CD-PSO) detects stagnation in iterations and re-energizes the swarm for better search space exploration [31]. IAPSO is an accelerated version of the PSO that uses entropy analysis to detect stagnation [32]. Intrinsic Dimension and Concise PSO use time steps to detect stagnation [33]. Multiple-strategy learning PSO (MSL-PSO) uses memorization to balance exploration and exploitation during learning [27]. PSO also incorporates the concept of memory forgetting observed in biological systems. This allows the algorithm to efficiently explore the search space and improve the quality of the solutions obtained [15]. Utilizing cooperative and competitive mechanisms, as detailed in [25], presents feasible alternatives for preventing stagnation. Multi-swarm PSO (MSPSO) utilizes multiple groups of particles to search and exploit the space with variations in topology, communication, and movement to adapt to an optimization problem [34,35,36]. The MSPSO algorithm divides a swarm into sub-swarms for exploring and exploiting multiple locations in search space. Dynamical topology and gradual reduction in particles per sub-swarm produce varied results [22]. There are also multi-swarm alternatives that even consider the problem of stagnation in PSO, including stagnation detection mechanisms like those in [36]. Although the particles in a swarm algorithm continue to update their position based on the best global position, they may still converge in local optimal regions. Subdividing the swarm can prevent stagnation but requires more function evaluations, which increases the algorithm’s running time [22,34,37,38]. PSO also hybridizes with other algorithms to improve its results similar to Multi-gradient PSO in [24], Fuzzy Self-Tuning PSO in [19], PSO with artificial neural networks in [39], Global Genetic Learning PSO in [21], Multi-swarm PSO with evolutionary algorithms [40], Multi-chaotic PSO with deterministic chaos and evolutionary computation techniques [18], and PSO with reinforced learning and a multi-swarm approach [17].
The enhancement of the Particle Swarm Optimization (PSO) algorithm for solving Large-Scale Global Optimization (LSGO) problems with lower computational complexity, without compromising its parallel structure, can have a significant impact on the field of multi-dimensional optimization.
This paper proposes a new method called DSRegPSO, which is a variation of PSO. It uses dynamic sphere regrouping and momentum conservation to prevent position stagnation, regulate exploration and exploitation of the search space, and maximize exploration when particles travel outside the position limits. The proposed method maintains the parallel structure of PSO and could have significant implications for multi-dimensional optimization.
Contribution
DSRegPSO is a novel optimization algorithm that makes use of a regrouping dynamical sphere mechanism and momentum conservation effect to deal with LSGO problems. These mechanisms are designed to prevent the swarm from getting stuck in local optima by continuously rejuvenating the swarm and balancing the trade-off between exploration and exploitation of the search space. The dynamical sphere mechanism mimics the foraging behavior of birds when looking for food, while the momentum mechanism emulates how birds interact with their surroundings.
To evaluate the effectiveness of the DSRegPSO algorithm, we used the CEC’13 benchmark functions, which are widely used in similar works like those in [41,42,43,44,45,46,47] as a standard test suite for LSGO problems. The CEC’13 test is composed of 15 optimization functions, including the Sphere Function, Elliptic Function, Rastrigin’s Function, Ackley’s Function, Schwefel’s Problem 1.2 Function, Rosenbrock’s Function, and their variants [44]. These functions are designed to challenge algorithms in solving complex LSGO problems. The CEC’13 test is also used by several well-recognized journals and is the same benchmark used in the annual Special Session and Competition on Large-Scale Global Optimization (SSCLSGO), organized by the IEEE World Congress on Computational Intelligence (WCCI) [16].
2. Materials and Methods
In this section, we will discuss the biological inspiration behind the PSO algorithm. We will also cover the most commonly used variant of PSO, the GPSO, as well as the techniques used to tackle local optima in PSO. Additionally, we will introduce the original RegPSO algorithm, which is the variant that most closely resembles our proposed DSRegPSO algorithm.
2.1. Biological Inspiration
PSO is inspired by bird flocking or fish schooling. In this algorithm, birds search for a single food source in a defined area. PSO particles represent birds that seek the global optimum or the position of the food in the search space. During the search, birds adjust their position by following the current optimum or the one nearest to the food. Birds also adjust their speed depending on the distance between themselves and the best position of the swarm or its best-known position [48].
2.2. GPSO
GPSO is a Particle Swarm Optimization technique that leverages the behavior of particles. The position of every particle is defined by a vector, , which consists of dimensions. The initial position of each particle is determined by a random array, , within the position bounds of a lower limit and an upper limit . The velocity of every particle, represented by , is used to update the position of each particle during the entire run. The cost of each particle, , is determined by evaluating the cost function for each . The positions that yield the best cost are identified as the global best position , which is the position of the particle with the best cost, and the best position of each particle , which is the position where the best cost was obtained for each particle.
During each iteration, the speed of every particle is updated using Equation (1), ensuring that it stays within the lower and upper speed limits [21].
The parameter is an inertial coefficient that ranges between 0.9 and 1.2, as proposed in the original algorithm in [29]. The parameters and represent personal and social coefficients, respectively, and their values are either user-defined or typically set to their upper limit of 2. Additionally, the arrays and are random arrays with a size of and values in the range of . The position of particles is updated every iteration using Equation (2) while being constrained within the minimum and maximum position limits .
The particles’ positions are updated using Equation (2) in each iteration of the GPSO algorithm until it meets either the specified cost value or the maximum number of iterations [27]. The objective function is used to determine and the positions of and . The velocity is determined using Equation (1) in each iteration, and then Equation (2) updates the position . The GPSO algorithm continues to calculate new global best positions and in every iteration. Algorithm 1 provides a complete description of the GPSO for each iteration.

2.3. Dealing with Local Optimums in PSO
One of the key issues with the basic formulation of PSO is that it’s possible for all particles to be attracted to a local optimum, which can lead to stagnation. For instance, in the context of biology, birds tend to fly toward the nearest food source, even if it is not the best one, which can cause stagnation [30].
There are several alternatives explored when PSO gets stuck in optimal local regions, including [30]:
- Stop the search and accept the result.
- Continue the search while hoping to find a better solution.
- Restart the swarm from new locations and search again.
- Mark the areas in the search space that lead to a local optimum and avoid them.
- Reinvigorate the swarm to maintain diversity.
2.4. Regrouping PSO
Stagnation in a PSO algorithm happens when particles’ positions have converged prematurely to a local optimum, keeping them in a nearby area in the search space [30].
To avoid stagnation in the swarm, RegPSO, a variation of PSO, measures the maximum Euclidean distance between each particle and the global best position for each iteration using Equation (3) [30].
Stagnation is confirmed when the distance between particles and around the diameter of the search space is below the user-selected stagnation threshold. Ref. [30] suggests using for its regrouping mechanism in Equation (4).
RegPSO reorganizes the swarm around the global best in case of stagnation or when a maximum number () of evaluations per grouping () is reached. This reorganization takes place between the minimum of the original range of the search space in dimension and the product of a regrouping factor times the maximum distance along dimension of any particle compared with the global best position , as shown in Equation (5).
where the regrouping factor proposed in [30] is .
The position regrouping re-initializes the position of particles using Equation (6).
With its respective lower and upper bounds, is the regrouping index starting at 0 and increasing by one with each regrouping.
According to this new range obtained, the algorithm sets a new maximum velocity with each regrouping, i.e., there are upper limits determined depending on the search space dimension, as in Equation (7).
where is a percentage that maintains speed under its limits .
The algorithm’s loop continues until it meets a stop criterion, such as achieving the desired cost value () or completing a specific number of iterations () [30]. Figure 1 presents an example of the effects of regrouping in throughout iterations.
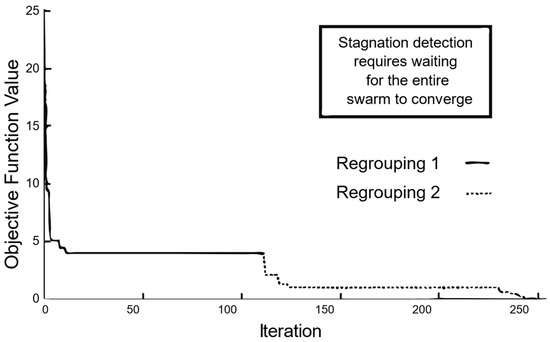
Figure 1.
Regrouping behavior of cost value across iterations with the RegPSO algorithm [30].
Algorithm 2 contains a comprehensive explanation of RegPSO.

2.5. Dynamical Sphere Regrouping PSO (DSRegPSO)
In this section, we will explore the inspirations behind the proposed DSRegPSO algorithm, as well as the algorithm itself. We aim to provide a comprehensive understanding of the development and implementation of DSRegPSO.
2.5.1. DSRegPSO Inspiration
Similar to other heuristics, PSO strives to enhance a cost function that is depicted as a mathematical expression. Achieving this objective involves multiple assessments that adjust the numerical parameters optimized either using Algorithm 1, Algorithm 2, the novel algorithm presented in this research, Algorithm 3, or alternative optimization methodologies.
The PSO algorithm involves birds or particles that continuously move toward the position with the best cost evaluation, denoted as , or the position closest to 0 in a minimizing problem. The algorithm tests trajectories every iteration, with particles searching for the optimal point where the cost function converges to 0, as shown in Equation (8).
To establish the validity of the limit, it is necessary to demonstrate its existence using the epsilon–delta definition, which has been adapted from reference [49]. This can be achieved by defining the particle’s position as , the cost function as , the global best cost as , and the best global position as , as outlined in Definition 1.
Definition 1.
Let
be a function defined on an open interval around
. The limit of
as
approaches
is
, i.e.,
. If for every
there exists a
such that for all
, Equation (9) is satisfied.
Definition 1 considers a hyper-sphere delimited by diameter that approximates the difference to a value when , i.e., , but if , then and ; therefore, . In other words, if , then and , which support that stagnation problems occur when all particles remain in approximately the same position, with almost the same cost.
Based on Definition 1, an alternative approach for revitalizing the swarm is to adjust the position of particles within a hypersphere that has an acceptable diameter of . This adjustment limits the approximation of vector to vector . Particles under this diameter can be repositioned to enhance the possibility of discovering a new cost that may be superior to with the new approximation trajectories. The swarm can avoid a local optimal region in the green function that has multiple possible local optimums by repositioning particles inside the hypersphere in red, as illustrated in Figure 2.
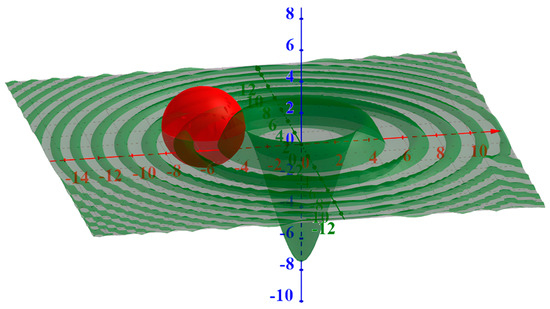
Figure 2.
Hypersphere controlling repositioning of particles to avoid stagnation.
According to [49], it is possible that trajectories may lead to a different value of in when the dimension of position is greater than 1. Therefore, it is recommended to establish a boundary or the maximum diameter for approximation to determine when to relocate a particle in the search space to preserve the diversity of the swarm.
In a biological context, represents the situation when birds have visited and exhausted several locations with less food than the position with the most food (). In this case, the birds could return to eat at while there is enough food for them (their position is outside the diameter ). If the food is exhausted, the remaining birds without food continue flying from their current location to a different one or the algorithm repositions the particles outside .
The new position updating uses a random speed array , generated when the distance between the position of particle and is under the desired diameter. This change in position means that particles too near to do not spend time exploiting this search space region. Allowing to be a dynamic parameter that increases and decreases the hyper-sphere diameter changes the swarm behavior for exploring or exploiting during the entire run.
When is greater, particles explore a more extensive region, and when it is smaller, particles exploit a smaller region. Furthermore, in this proposal, the delta value increases each iteration that remains under the desired percentage of change , allowing the algorithm to automatically change from the exploration to exploitation stage as the global best improves.
This behavior resembles the number of birds allowed given the amount of food and how fewer birds are admitted over time while food decreases in that location, forcing them to leave their current position and look for more food.
Since particles are repositioned when is less than , particles are repositioned with when reaches its maximum value due to minor improvements in . The main improvement in GPSO is the use of the previous speed with inertial momentum, allowing exploration at the beginning of the run, but its effect diminishes as the speed is approximated to 0 because and are near 0.
The inertial momentum varies depending on delta because it already controls exploration and exploitation. Thus, the inertial momentum increases when reaches a higher value or remains with minor changes, i.e., when particles are more likely to converge. On the other hand, the inertial momentum decreases, maximizing exploitation when reaches a lower value because improved more than .
In DSRegPSO, the maximum allowed velocity is controlled depending on the speed of hyper-sphere expansion , or the parameter that controls how fast we change each iteration, and the improvement is lower than . The update mechanism for increases it every time reaches its maximum value . Similar to delta, has boundaries: a maximum speed of expansion and a minimum one . When the algorithm reaches , restarts to the value .
Several researchers have controlled the maximum velocity since they found that unlimited velocity produces divergence in the algorithm [50]. Thus, when the max velocity is higher, there is more exploration or divergence; when it is lower, more exploitation occurs.
Considering the effect of velocity in exploration and exploitation, in DSRegPSO, we control the maximum allowed velocity depending on the speed of hyper-sphere expansion , or the parameter that controls how fast we change each iteration, and the improvement is lower than .
Biologically, suppose birds are repeatably attracted to the same position without finding more food. In that case, it is as if they suffer desperation to find it, causing an increment in their speed while their energy reserves allow it. The desperate situation of food about to end makes birds travel faster and more vaguely.
Thus, the higher the , the more vagueness of particles maximizing exploration. Additionally, we also maximize exploration in the inertial momentum by including and in its update.
2.5.2. The DSRegPSO Algorithm
The DSRegPSO algorithm’s initialization process involves the GPSO initialization parameters outlined in Algorithm 1, with the exception of parameter . In its place, Equation (10) utilizes parameter . This parameter uniformly distributes the maximum inertial momentum () across its dependencies, and , both of which fall within the range of .
In DSRegPSO, a new updating speed equation is defined for each iteration in Equation (11), taking into account the hyper-sphere diameter and its expansion speed. The inertial momentum component varies based on these factors. This approach is described in detail in Section 2.5.1.
The initialization of and involves determining using Equation (12). is assigned the value of (Equation (13)), and is obtained using Equation (14).
The coefficient modifies the starting limits of speed depending on the size of the search space, then speed limits and change according to the speed of expansion , obtaining the maximum velocity allowed when .
DSRegPSO recalculates and each iteration because maximum velocities vary during the algorithm depending on (birds’ desperation for food or the expansion speed described in Section 2.5.1), allowing it to break barriers in local optimums. After all, more significant speeds increase the exploration range while lower speeds increase exploitation, as described in [51]. Thus, and are updated with Equations (14) and (15), respectively.
Once DSRegPSO recalculates the speeds of the particles and retains them under its limits, Equation (16) updates the position of particles, randomly varying the components of the particles upper the hyper-sphere diameter .
is a random array under the limits of position . reinvigorates the swarm by changing the components in the position vector according to , which indicates if a particle is too near to , depending on the hyper-sphere diameter , as in Equation (17).
with the distance between the particle and the best position () determined with Equation (18).
The sphere diameter is determined in each iteration using Equation (19) when there is insufficient improvement in at that iteration; in other words, , with as the improvement factor. Additionally, if has reached its maximum, i.e., if , then we set and obtains its value according to Equation (20). In the case that there is enough improvement, then we set and to maximize exploitation.
After obtaining all the parameters in Equations (15) to (20) and the speed of particles in Equation (11), then Equation (21) updates the position of particles with the proposed conservation of momentum to retain all positions under the limits . In GPSO, rearrangement of position sets the position value to either , if crossing the lower boundary, or if crossing the upper boundary. However, in this work, we propose the conservation of momentum principle for PSO, making particles change their direction backward when crossing the boundaries. This conservational momentum maximizes exploration by returning particles to different positions in the search space if the speed vector makes them travel beyond the search space boundaries.
We let and vary depending on , progressively reducing the size of the search space around the best position since the components of a position refine across iterations, and then we reduce the search space based on that value. However, we let the user control that refinement with and , as in Equations (22) and (23).
Finally, we update the new speed limits with Equations (24) and (25), and the process iterates continually while or .

The DSRegPSO technique is presented in Algorithm 3, which applies the previous formulas while incorporating additional input parameters, namely, , , , , and . Unlike the original PSO approach, and do not need to be specified as input parameters.
3. Results and Discussion
In this section, the proposed algorithm’s performance is evaluated by testing it on the 15 functions in benchmark CEC’13, as specified in [52]. The aim of the tests is to verify the algorithm’s convergence capabilities and robustness by performing several runs for every function optimized, as described in [52]. The leading convergence indicator in the CEC’13 test is the mean of the best costs, while the Standard Deviation (SD) indicates the robustness. The benchmark runs 25 times during 3.0E+06 function evaluations, and each function has 1000 dimensions. To compare DSRegPSO with other heuristics, we used the Toolkit for Automatic Comparison of Optimizers (TACO), which is also distributed by CEC and described in [53]. The comparison is based on the mean cost obtained after 25 runs of 3.0E+06 function evaluations of the 15 functions in the benchmark.
We set the DSRegPSO (Algorithm 3) decision variables or input parameters depending on the optimization requirements for each test, and the best performance obtained according to:
- , , , , and were specified by the requirements for the optimized functions in each function of CEC’13.
- We assumed that the remaining input parameters are linearly independent. Based on this assumption, we chose the values that resulted in the best cost for each benchmark by varying them heuristically within the ranges specified in Section 3.1.
Additionally, we tested the original GPSO in Algorithm 2 with CEC’13. Again, we used the same process to select the best input parameters heuristically. Then, we included the results in the comparison.
The computer used for data analysis and result generation was an Alienware m17 R2 running Microsoft Windows 10 Home, version 10.0.19045, build 19045. The system was configured with an Intel(R) Core(TM) i7-9750H CPU @ 2.60 GHz, 16.0 GB of physical RAM, and a total of 39.8 GB of virtual memory
3.1. Results of the CEC’13 Test
The 15 functions utilized for testing in CEC’13 are categorized as fully separable, partially additively separable, overlapping, or non-separable. Each function boasts a unique domain and global optimum. To ensure accuracy, CEC’13 applies transformations such as position translation, rotation, and disturbance operations to the objective function prior to evaluation, as noted in [52].
- Fully separable functions:
- Elliptic with and .
- Rastrigin with and .
- Ackley with and .
- Partially Additively Separable Functions:
- Functions with a separable subcomponent:
- Elliptic with and .
- Rastrigin with and .
- Ackley with and .
- Schwefels Problem 1.2 with and .
- Functions with no separable subcomponents:
- Elliptic with and .
- Rastrigin with and .
- Ackley with and .
- Schwefels Problem 1.2 with and .
- Overlapping Functions:
- Rosenbrock’s with and .
- Schwefels with Conforming Overlapping Subcomponents with and .
- Schwefels with Conflicting Overlapping Subcomponents with and .
- Non-separable Functions:
- Schwefels Problem 1.2 with and .
The DSRegPSO algorithm can use a heuristic approach to find values for , , , , , , , , and . The values that were heuristically tested are provided below. The limits of the parameters related to DSRegPSO: , , , , and were determined by increasing or decreasing those limits in order to achieve better results. For the parameters related to PSO: , , , and , we used limits that were recommended in the literature, specifically in [54,55].
- .
- .
- .
- .
- .
- .
- .
- .
- .
Table 1 displays the optimal parameters for the DSRegPSO algorithm based on the average best cost after being heuristically evaluated for five runs of 5.0E+05 function evaluations per CEC’13 function, in order to obtain the best possible cost per function. We tested the algorithm parameters using 5.0E+05 function evaluations instead of 3.0E+06, as the latter would not be feasible due to the complexity of the CEC’13 test.

Table 1.
DSRegPSO parameters determined with heuristic selection in the CEC’13 test.
Similarly, we select the , , , , and input parameters of the GPSO with a heuristic approach. The values heuristically tested are below. Again, in the case that the best parameter found corresponds to the lower or upper value, we tested extra values by increasing or decreasing those limits with the same step:
- .
- .
- .
- .
- .
Table 2 shows the best parameters for GPSO based on the mean best cost after heuristically testing them against five runs of function evaluations for each CEC’13 function.

Table 2.
GPSO parameters determined with heuristic selection in the CEC’13 test.
The results obtained using the DSRegPSO and the GPSO using the selected input parameters in the CEC’13 benchmark with 1000 dimensions for function evaluations and 25 runs are shown below in Table 3. The average time per iteration varies depending on the functions and the algorithm. Despite the proposed modifications to PSO, the time per iteration remains below 100 µs.

Table 3.
DSRegPSO mean, SD, worst, and best results using the CEC’13 benchmark.
According to the results presented in Table 3, DSRegPSO outperforms GPSO in terms of both achieving the best cost for each function and demonstrating higher stability. This is evident from the fact that DSRegPSO has the best mean, best, SD, and worst values among the two algorithms, and it shows lower SD values in 14 out of the total 15 functions of the CEC’13 test.
Figure 3 shows the performance in the first 25,000 function evaluations for the proposed DSRegPSO in the optimization of of CEC’13. Figure 4 shows the performance in the entire run with function evaluations on a logarithmic scale. The behaviors of the DSRegPSO in Figure 3 and Figure 4 show that the proposed algorithm continually improves and resets the particle’s position without requiring stagnation to reinvigorate the swarm similar to RegPSO (Figure 1).
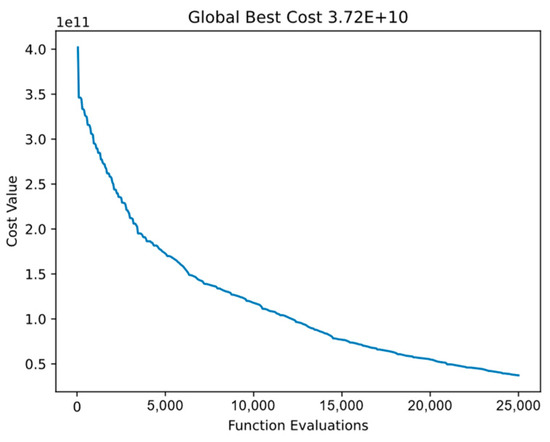
Figure 3.
Cost value for the first 25,000 function evaluations with DSRegPSO and of CEC’13.
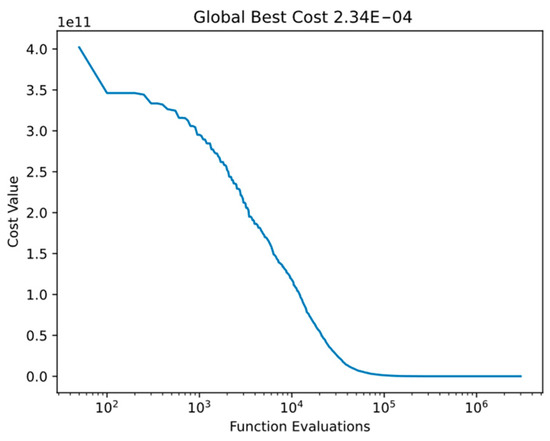
Figure 4.
Cost value with the x-axis on a logarithmic scale for the DSRegPSO in of CEC’13.
We also used Principal Component Analysis (PCA) to condense the particle position data from 1000 to 3 dimensions. This allowed us to create 3D position plots, which helped us visualize the revival of the swarm and prevent stagnation. Analyzing the three principal components provided us with valuable insights into particle behavior and optimized the swarm. Additionally, we have included convergence diagrams for functions 1 to 15 of CEC’13 for DSRegPSO to assess the convergence and stagnation of our proposal. These diagrams show a comparison per run for the 3.00E+06 function evaluations with checkpoints registered at 1.20E+05, 3.00E+05, 6.00E+05, 9.00E+05, 1.20E+06, 1.50E+06, 1.80E+06, 2.10E+06, 2.40E+06, 2.70E+06, and 3.00E+06 function evaluations, as per the default configuration of CEC’13.
Figure 5 and Figure 6 display the convergence and PCA of Function 1 of CEC’13. As depicted in the figures, the algorithm continues to improve even after 3.00E+06 function evaluations and does not converge. Additionally, the comparison among the runs demonstrates the level of stability in the algorithm for this function.
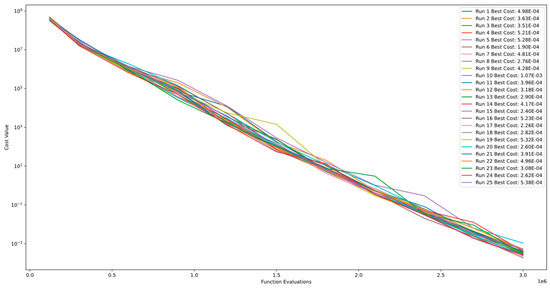
Figure 5.
Convergence diagram of Function 1 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 6.
PCA of 50 particle positions in Function 1 of CEC’13 for DSRegPSO.
Figure 7 and Figure 8 showcase the convergence and PCA of Function 2 of CEC’13. As seen in the figures, the algorithm shows continual improvement even after 3.00E+06 function evaluations and does not converge. Moreover, the comparison between runs illustrates the algorithm’s stability level for this function.
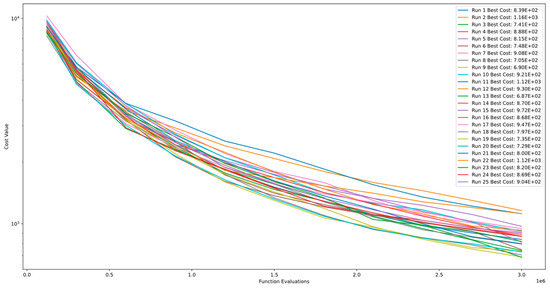
Figure 7.
Convergence diagram of Function 2 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.
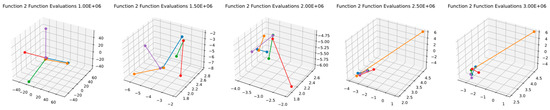
Figure 8.
PCA of 5 particle positions in Function 2 of CEC’13 for DSRegPSO.
Figure 9 and Figure 10 presented in CEC’13 highlight the convergence and PCA of Function 3. Figure 9 demonstrates the early convergence of the global best cost, and a comparison between the runs reveals stagnation caused by Function 3 being a pinhole function that cannot be solved with PSO. However, Figure 10 depicts that particles never encounter stagnation or convergence, as indicated by the PCA.
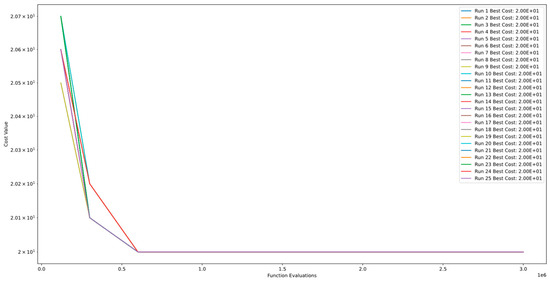
Figure 9.
Convergence diagram of Function 3 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 10.
PCA of 20 particle positions in Function 3 of CEC’13 for DSRegPSO.
Figure 11 and Figure 12 demonstrate the convergence and PCA of Function 4 of CEC’13. The figures show that the algorithm exhibits continuous improvement even after 3.00E+06 function evaluations and does not converge. Additionally, the comparison between runs indicates the algorithm’s level of stability for this function.
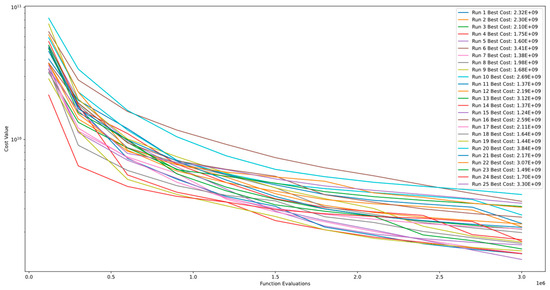
Figure 11.
Convergence diagram of Function 4 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 12.
PCA of 20 particle positions in Function 4 of CEC’13 for DSRegPSO.
Figure 13 and Figure 14 showcase the convergence and PCA of Function 5 of CEC’13. These figures indicate that the algorithm continues to improve even after 3.00E+06 function evaluations and does not converge. However, comparing the results of multiple runs highlights that the algorithm’s stability level is poor for this function.
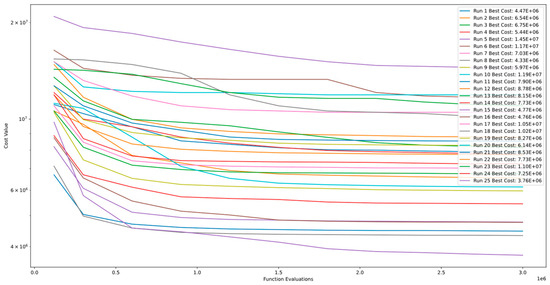
Figure 13.
Convergence diagram of Function 5 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 14.
PCA of 40 particle positions in Function 5 of CEC’13 for DSRegPSO.
Figure 15 and Figure 16 demonstrate the convergence and PCA of Function 6 of CEC’13. The figures show that the algorithm exhibits continuous improvement even after 3.00E+06 function evaluations and does not converge. However, comparing the results of multiple runs highlights that the algorithm’s stability level is poor.
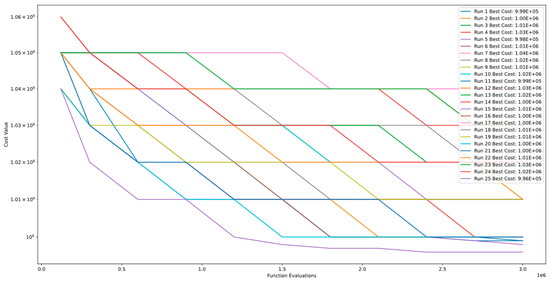
Figure 15.
Convergence diagram of Function 6 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 16.
PCA of 50 particle positions in Function 6 of CEC’13 for DSRegPSO.
Figure 17 and Figure 18 demonstrate the convergence and PCA of Function 7 of CEC’13. The figures show that the algorithm exhibits continuous improvement even after 3.00E+06 function evaluations and does not converge. Additionally, the comparison between runs indicates the algorithm’s level of stability for this function.
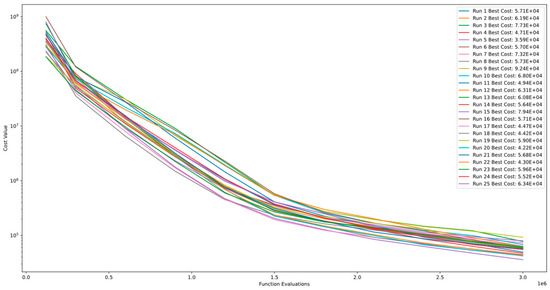
Figure 17.
Convergence diagram of Function 7 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 18.
PCA of 30 particles’ positions in Function 7 of CEC’13 for DSRegPSO.
Figure 19 and Figure 20 demonstrate the convergence and PCA of Function 8 of CEC’13. The figures show that the algorithm exhibits continuous improvement even after 3.00E+06 function evaluations and does not converge. However, the comparison between runs indicates that the algorithm’s level of stability is poor.
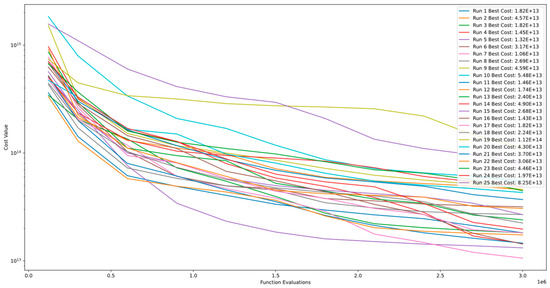
Figure 19.
Convergence diagram of Function 8 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 20.
PCA of 50 particle positions in Function 8 of CEC’13 for DSRegPSO.
Figure 21 and Figure 22 showcase the convergence and PCA of Function 9 of CEC’13. These figures indicate that the algorithm continues to improve even after 3.00E+06 function evaluations and does not converge. However, comparing the results of multiple runs highlights that the algorithm’s stability level is poor in this function.
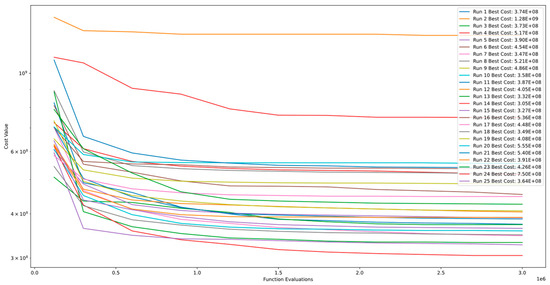
Figure 21.
Convergence diagram of Function 9 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 22.
PCA of 30 particle positions in Function 9 of CEC’13 for DSRegPSO.
Figure 23 and Figure 24 demonstrate the convergence and PCA of Function 10 of CEC’13. The figures show that the algorithm exhibits continuous improvement even after 3.00E+06 function evaluations and does not converge. However, the comparison between runs indicates that the algorithm’s level of stability is poor.
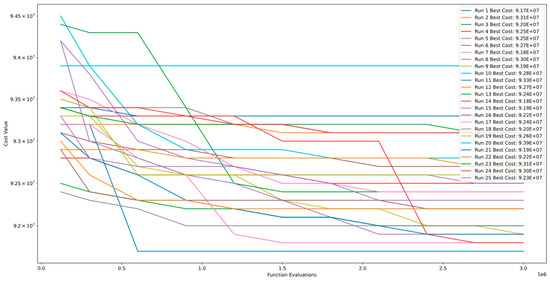
Figure 23.
Convergence diagram of Function 10 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 24.
PCA of 50 particle positions in Function 10 of CEC’13 for DSRegPSO.
Figure 25 and Figure 26 demonstrate the convergence and PCA of Function 11 of CEC’13. The figures show that the algorithm exhibits continuous improvement even after 3.00E+06 function evaluations and does not converge. Additionally, the comparison between runs indicates the algorithm’s level of stability for this function.
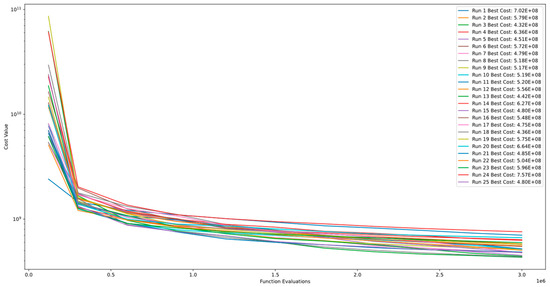
Figure 25.
Convergence diagram of Function 11 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 26.
PCA of 30 particle positions in Function 11 of CEC’13 for DSRegPSO.
From Figure 27 and Figure 28, it is evident that Function 12 of CEC’13 does not converge even after 3.00E+06 function evaluations. The PCA was conducted on the results obtained after setting the number of particles to five, as PCA cannot be performed with only one particle. It is worth noting that the algorithm shows continuous improvement, and comparing the runs indicates the stability level of the algorithm for this specific function.
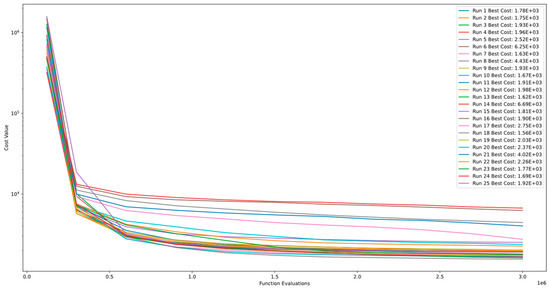
Figure 27.
Convergence diagram of Function 12 of CEC’13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 28.
PCA of 5 particle positions in Function 12 of CEC’13 for DSRegPSO.
Figure 29 and Figure 30 demonstrate the convergence and PCA of Function 13 of CEC’13. The figures show that the algorithm exhibits continuous improvement even after 3.00E+06 function evaluations and does not converge. Additionally, the comparison between runs indicates the algorithm’s level of stability for this function.
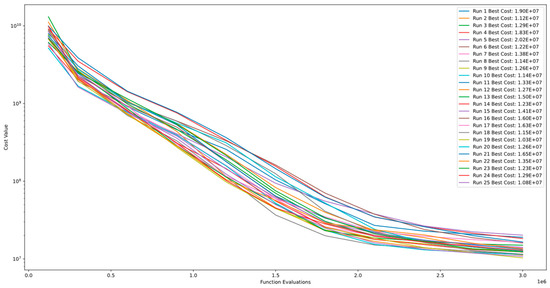
Figure 29.
Convergence diagram of Function 13 of CEC´13 for DSRegPSO with 25 runs and 3.00+E06 function evaluations.

Figure 30.
PCA of 40 particle positions in Function 13 of CEC’13 for DSRegPSO.
Figure 31 and Figure 32 demonstrate the convergence and PCA of Function 14 of CEC’13. The figures show that the algorithm exhibits continuous improvement even after 3.00E+06 function evaluations and does not converge. Additionally, the comparison between runs indicates the algorithm’s level of stability for this function.
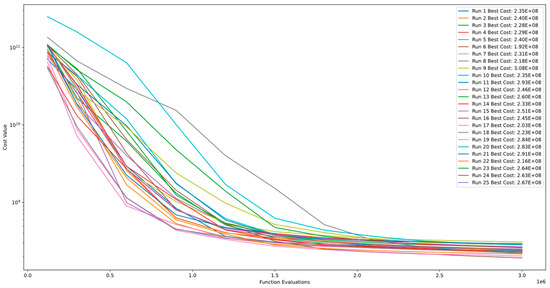
Figure 31.
Convergence diagram of Function 14 of CEC´13 for DSRegPSO with 25 runs and 3.00+"E" 06 function evaluations.

Figure 32.
PCA of 40 particle positions in Function 14 of CEC’13 for DSRegPSO.
Figure 33 and Figure 34 demonstrate the convergence and PCA of Function 15 of CEC’13. The figures show that the algorithm exhibits continuous improvement even after 3.00E+06 function evaluations and does not converge. Additionally, the comparison between runs indicates the algorithm’s level of stability for this function.
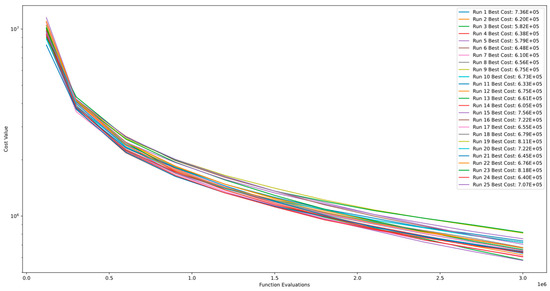
Figure 33.
Convergence diagram of Function 15 of CEC´13 for DSRegPSO with 25 runs and 3.00+"E" 06 function evaluations.

Figure 34.
PCA of 30 particle positions in Function 15 of CEC’13 for DSRegPSO.
Table 4 shows the CEC’13 TACO ranking comparison with DSRegPSO based on the best cost obtained after , , and function evaluations for the 25 runs, where the index registered is the number of functions when the algorithm obtains the best results. The proposed algorithm DSRegPSO obtains the best results in optimizing the non-separable function.

Table 4.
Ranking comparison based on mean cost with CEC’13, including the proposed DSRegPSO.
Table 5 compares the costs obtained for each algorithm registered in CEC’13 TACO in the functions of the CEC’13 benchmark against DSRegPSO and GPSO. Our proposal obtains the best value in the more complex test with the non-separable function.

Table 5.
Mean cost comparison with CEC’13, including the proposed DSRegPSO.
Additionally, we compare the results in accuracy delivered with the TACO toolkit in Figure 35. Here, we find that Shadeils—an algorithm focusing on LSGO—still has the best results across all the algorithms in the CEC’13 test. However, despite not focusing on LSGO, our proposal improves the results in several functions compared with the other algorithms and obtains the best results compared with algorithms inspired by PSO. Moreover, the cyan region in the plot is the biggest for all the algorithms since our proposal is the best one in the non-separable function.
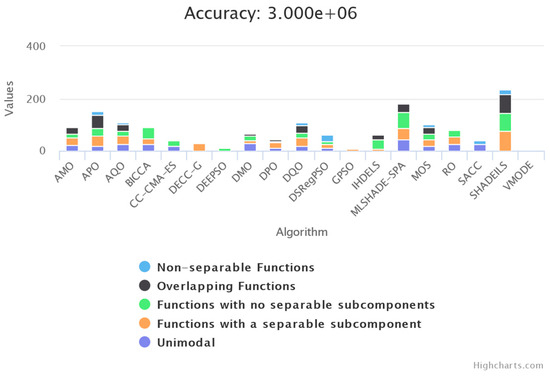
Figure 35.
TACO comparison across all algorithms, including DSRegPSO and GPSO in the CEC’13 test.
Figure 36 shows the TACO comparison, just considering the non-separable function, showing that our algorithm is the best at optimizing it.
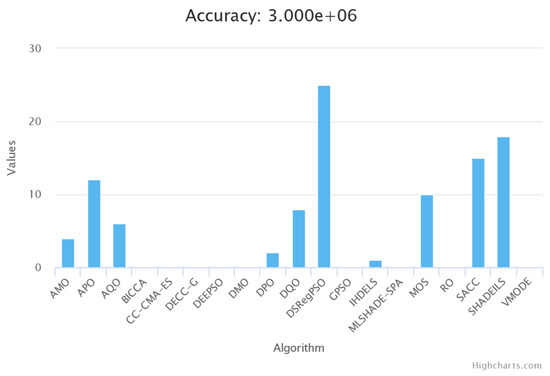
Figure 36.
TACO comparison across all algorithms, including DSRegPSO and GPSO in the non-separable CEC’13 function.
The Wilcoxon test is a non-parametric statistical test that compares the median rank of two related samples. It is proper when the normality assumption of the samples cannot be met and is a suitable alternative to the Student’s t-test [53]. Table 6 shows the results of the statistical Wilcoxon test as defined in the TACO toolkit. It compares the algorithm’s p-value in each row (first) concerning the algorithm in each column (second).

Table 6.
Wilcoxon test comparing algorithms registered in TACO in the CEC’13 test.
Blue indicates that the first algorithm is better than the second, and red indicates that the first is worse than the second, with a significance of 5%. Cyan indicates that the first algorithm is better than the second one, and yellow indicates that the first one is worse than the second. For cyan and yellow colors, there is a significance of 10%. Black means that there are no detected significant differences.
The Wilcoxon test results show that despite the limitations of PSO exploring LSGO problems, our proposal still has better results than the four algorithms with 5% significance. Furthermore, we maintain similar performance or inconclusive advantage with eight algorithms.
Table 7 shows the Wilcoxon test considering only the algorithms inspired in PSO (GPSO and DEEPSO). The results support that DSRegPSO is the best PSO-inspired algorithm with results in the CEC’13 test. Again, Blue indicates that the first algorithm is better than the second, and red indicates that the first is worse than the second, with a significance of 5%. Cyan indicates that the first algorithm is better than the second one, and yellow indicates that the first one is worse than the second. For cyan and yellow colors, there is a significance of 10%. Black means that there are no detected significant differences.

Table 7.
Wilcoxon test taking into consideration PSO-inspired algorithms.
In algorithm design, it is essential to assess both robustness and sensitivity, especially in situations where disturbances or noise are expected. Robustness refers to the ability of an algorithm to maintain its performance despite perturbations, while sensitivity measures how much these perturbations can affect the outputs of the algorithm [56,57].
A robust algorithm can handle different types of disturbances, such as input errors or process variations, and still generate consistent and reliable results. This robustness is demonstrated by the algorithm’s ability to continuously improve and converge toward a solution even when noise is present in particle positions. On the other hand, algorithm sensitivity explains how the algorithm reacts to minor variations or disturbances. A highly sensitive algorithm will produce significant variations in outcomes even with minor disturbances [57].
In our study, we evaluated the robustness and sensitivity of DSRegPSO by conducting 25 runs of CEC’13 under identical circumstances without controlling the seeds. This allowed us to generate different initial positions of particles. The results in Table 3 and the convergence diagrams demonstrate that DSRegPSO performs even better than the original PSO in terms of stability.
Additionally, as a means of testing the robustness of the DSRegPSO algorithm in the presence of noise, we carried out two experiments using the CEC’13 functions. The first experiment involved introducing random noise of varying magnitudes (1%, 5%, 10% 15%, and 20%) to the particle positions before evaluating the functions. The purpose of this experiment was to evaluate how the algorithm responds to perturbations in the search space for high-dimensional functions. Specifically, it aimed to determine whether the algorithm could still improve or converge to an optimal or near-optimal solution even when particles in a high-dimensional space are slightly displaced from their original positions due to noise.
In the second test, we introduce random noise of magnitudes (1%, 5%, 10%, 15%, and 20%) into the result of the cost function evaluation. This test assesses the algorithm’s ability to handle errors or variations in the evaluation of the objective function in high-dimensional spaces. Specifically, we investigate how the algorithm responds to the perceived “quality” of a solution (measured by its objective function) in the presence of noise. The goal is to understand how noise affects the algorithm’s ability to still improving or converge to an optimal or near-optimal solution.
Figure 37 shows a comparison between convergence diagrams with noise in particle positions and cost of Function 1 of CEC’13. Despite noise in particle positions, the algorithm continues to improve in the initial evaluations but rapidly converges to similar cost values. This could be due to the sensitivity of the cost function to small changes in particle positions. However, the algorithm still improves in tests with noise added to the cost, demonstrating the robustness of DSRegPSO.
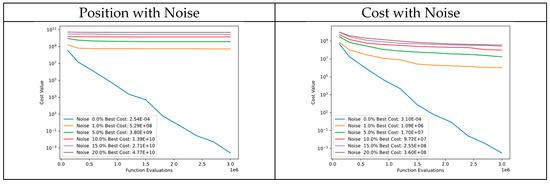
Figure 37.
Convergence diagrams of Function 1 of CEC’13 adding noise to position and cost.
In Figure 38, there is a comparison of convergence diagrams between noise in particle positions and cost of Function 2 of CEC’13. Despite the noise in particle positions, the algorithm continues to perform well in the initial evaluations and subsequently converges to similar cost values. This could be because the cost function is very sensitive to even small changes in particle positions. However, the algorithm still performs well in tests where noise is added to the cost, which demonstrates the robustness of DSRegPSO.
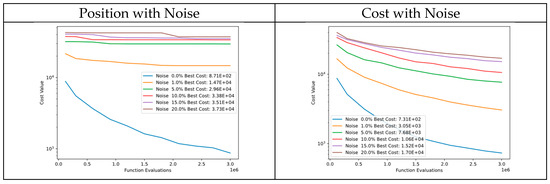
Figure 38.
Convergence diagrams of Function 2 of CEC’13 adding noise to position and cost.
In the comparison of convergence diagrams between noise in particle positions and the cost of Function 3 of CEC’13 depicted in Figure 39, adding noise to particle positions or the cost value resulted in convergence to similar cost values, with minimal improvements. This could be due to the fact that the cost function is highly sensitive to changes in position, and the cost value variation is also too small compared with the noise, as evidenced by both convergence diagrams. As a result, the algorithm showed a lack of robustness in noise tests for Function 3.
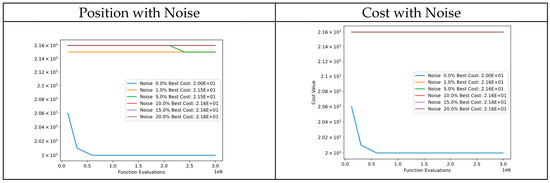
Figure 39.
Convergence diagrams of Function 3 of CEC’13 adding noise to position and cost.
Figure 40 presents a comparison of convergence diagrams between particle position noise and cost of Function 4 of CEC’13. Despite noise in particle positions, the DSRegPSO algorithm exhibits good performance in the initial evaluations and subsequently converges to similar cost values. This is due to the high sensitivity of the cost function to even minor alterations in particle positions. However, tests where noise is added to the cost indicate that DSRegPSO is robust and continues to perform well.
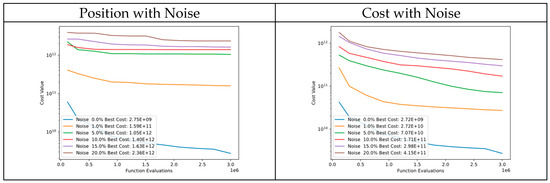
Figure 40.
Convergence diagrams of Function 4 of CEC’13 adding noise to position and cost.
Figure 41 showcases a comparison of convergence diagrams adding noise to particle position and cost of Function 5 of CEC’13. Despite the presence of noise in particle positions, the DSRegPSO algorithm exhibits commendable performance, converging to similar cost values. This can be attributed to the cost function’s high sensitivity to even minute changes in particle positions. However, tests that introduced noise to the cost indicate that DSRegPSO is robust and continues to deliver good performance.
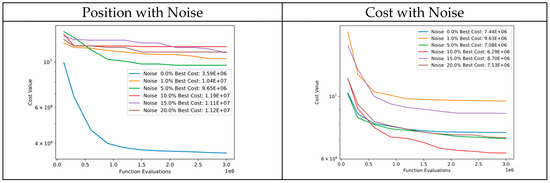
Figure 41.
Convergence diagrams of Function 5 of CEC’13 adding noise to position and cost.
When comparing convergence diagrams between noise in particle positions and cost of Function 6 of CEC’13 (Figure 42), it was found that adding noise to either the particle positions or cost value led to convergence to similar cost values, with only minimal improvements. This could be because the cost function is highly sensitive to changes in position and the cost value variation is too small compared with the noise. Consequently, the algorithm demonstrated a lack of robustness in noise tests for Function 6.
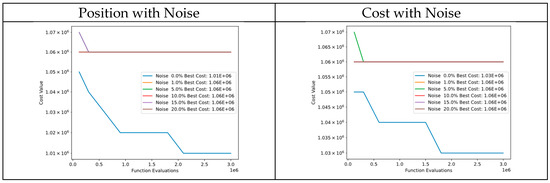
Figure 42.
Convergence diagrams of Function 6 of CEC’13 adding noise to position and cost.
In Figure 43, there is a comparison of convergence diagrams between noise in particle positions and cost of Function 7 of CEC’13. Despite the noise in particle positions, the algorithm continues to perform well in the initial evaluations and subsequently reaches similar cost values. This could be because the cost function is very sensitive to even small changes in particle positions. However, the algorithm still performs well in tests where noise is added to the cost, which demonstrates the robustness of DSRegPSO.
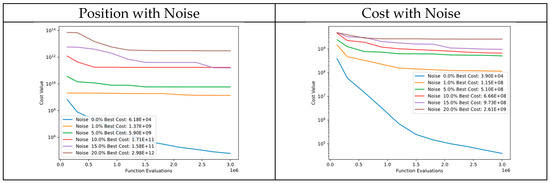
Figure 43.
Convergence diagrams of Function 7 of CEC’13 adding noise to position and cost.
Figure 44 presents a comparison of convergence diagrams between particle position noise and cost of Function 8 of CEC’13. Despite noise in particle positions, the DSRegPSO algorithm exhibits good performance in the initial evaluations and subsequently converges to similar cost values. This is due to the high sensitivity of the cost function to even minor alterations in particle positions. However, tests where noise is added to the cost indicate that DSRegPSO is robust and continues to perform well.
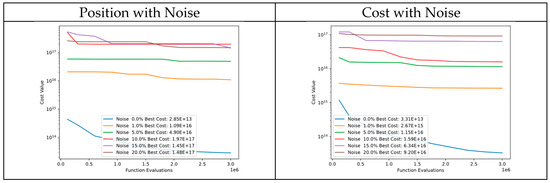
Figure 44.
Convergence diagrams of Function 8 of CEC’13 adding noise to position and cost.
Figure 45 showcases a comparison of convergence diagrams adding noise to particle position and cost of Function 9 of CEC’13. Despite the presence of noise in particle positions, the DSRegPSO algorithm exhibits commendable performance, converging to similar cost values. This can be attributed to the cost function’s high sensitivity to even minute changes in particle positions. However, tests that introduced noise to the cost indicate that DSRegPSO is robust and continues to deliver good performance.
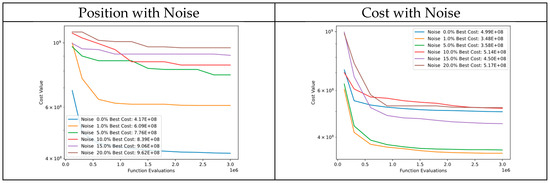
Figure 45.
Convergence diagrams of Function 9 of CEC’13 adding noise to position and cost.
Figure 46 presents a comparison of convergence diagrams between particle position noise and cost of Function 10 of CEC’13. Despite noise in particle positions, the DSRegPSO algorithm exhibits good performance in the initial evaluations and subsequently converges to similar cost values. This is due to the high sensitivity of the cost function to even minor alterations in particle positions. However, tests where noise is added to the cost indicate that DSRegPSO is robust and continues to perform well.
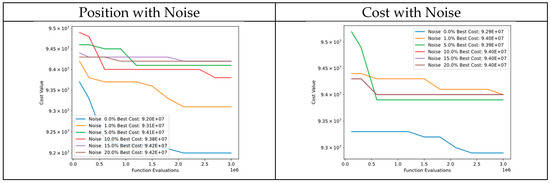
Figure 46.
Convergence diagrams of Function 10 of CEC’13 adding noise to position and cost.
In Figure 47, there is a comparison of convergence diagrams between noise in particle positions and cost of Function 11 of CEC’13. Despite the noise in particle positions, the algorithm continues to perform well in the initial evaluations and continue improving in its cost values without reaching the response without noise. This could be because the cost function is very sensitive to even small changes in particle positions. However, the algorithm still performs well in tests where noise is added to the cost, which demonstrates the robustness of DSRegPSO.
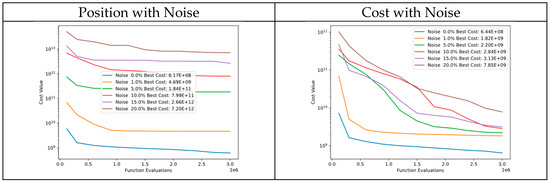
Figure 47.
Convergence diagrams of Function 11 of CEC’13 adding noise to position and cost.
Figure 48 showcases a comparison of convergence diagrams adding noise to particle position and cost of Function 12 of CEC’13. Despite the presence of noise in particle positions, the DSRegPSO algorithm exhibits commendable performance, converging to similar cost values. This can be attributed to the cost function’s high sensitivity to even minute changes in particle positions. However, tests that introduced noise to the cost indicate that DSRegPSO is robust and continues to deliver good performance.
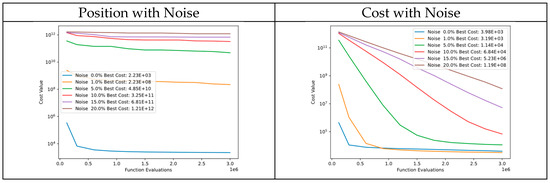
Figure 48.
Convergence diagrams of Function 12 of CEC’13 adding noise to position and cost.
In Figure 49, there is a comparison of convergence diagrams between noise in particle positions and cost of Function 13 of CEC’13. Despite the noise in particle positions, the algorithm continues to perform well in the initial evaluations and subsequently reaches similar cost values. This could be because the cost function is very sensitive to even small changes in particle positions. However, the algorithm still performs well in tests where noise is added to the cost, which demonstrates the robustness of DSRegPSO.
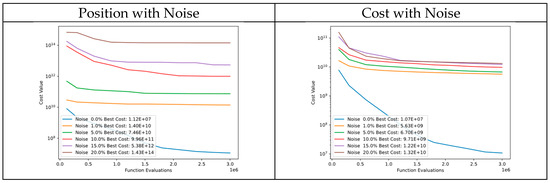
Figure 49.
Convergence diagrams of Function 13 of CEC’13 adding noise to position and cost.
Figure 50 shows convergence diagrams for noise in particle positions and the cost of Function 14 of CEC’13. Despite the noise, the algorithm performs well in initial evaluations and continues to improve cost values. The cost function is sensitive to small changes in particle positions, which may explain this. However, DSRegPSO shows better robustness in tests where noise is added to the cost instead of the position of particles.
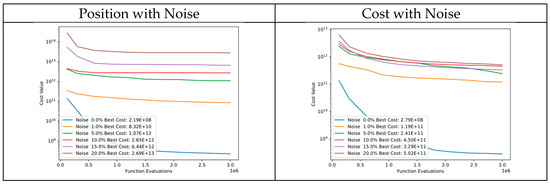
Figure 50.
Convergence diagrams of Function 14 of CEC’13 adding noise to position and cost.
In Figure 51, there is a comparison of convergence diagrams between noise in particle positions and cost of Function 15 of CEC’13. Despite the noise in particle positions, the algorithm continues to perform well in the initial evaluations and subsequently reaches similar cost values. This could be because the cost function is very sensitive to even small changes in particle positions. However, the algorithm still performs well in tests where noise is added to the cost, which demonstrates the robustness of DSRegPSO.
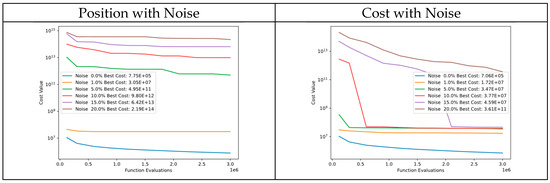
Figure 51.
Convergence diagrams of Function 15 of CEC’13 adding noise to position and cost.
4. Conclusions
In this work, we present a novel adaptation of Particle Swarm Optimization (PSO) known as Dynamical Sphere Regrouping PSO (DSRegPSO). The proposed variant addresses the issue of stagnation that commonly occurs in global optimization problems, particularly those that are large-scale. To avoid stagnation, we introduced two mechanisms.
The first mechanism involves the use of a dynamical sphere to regulate exploration and exploitation during a run, thereby preventing the particles from converging. The second mechanism is based on the conservation of physics momentum, which returns particles that travel outside the search space in the opposite direction, enabling maximum exploration of the search space.
We improved the original regrouping PSO algorithm in three main ways. Firstly, we introduced dynamical sphere regrouping, which allows the swarm to be continually reinvigorated without waiting for stagnation to be detected. This mechanism also helps regulate exploration and exploitation during a run. Secondly, we modified the inertial effects, varying them across iterations and increasing them when required for exploration. Lastly, we used momentum conservation to maintain diversity in the swarm by keeping particles within the search space when the speed equation takes them out.
Despite the existence of several variants and alternatives in the PSO algorithm, not all of them have been registered in the Toolkit of Automatic Comparison of Optimizers in CEC’13, which is a standard for LSGO evaluation. Moreover, some proposals only work with their own proposed tests or on specific problems. However, our DSRegPSO algorithm underwent testing against the CEC’13 functions for evaluating new machine learning algorithms in LSGO and achieved superior results compared with other algorithms and PSO-inspired algorithms, such as DEEPSO and GPSO.
In order to sustain our conclusion, we conducted a Wilcoxon test to compare all algorithms that use CEC’13 as support for their results. The Wilcoxon test results demonstrated that DSRegPSO is superior to DECC-G, DEEPSO, GPSO, and SACC and has similar results to APO, CCCMA-ES, DMO, DPO, IHDELS, and VMODE with a statistical significance of 5%. Additionally, our algorithm produced the best results for optimizing the non-separable function reaching a cost value of 5.79E+05, surpassing all other CEC’13 TACO registered algorithms. Thus, we recommend utilizing the proposed algorithm in applications of non-separable problems to explore the capabilities of DSRegPSO in real-world scenarios. Again, we conducted a Wilcoxon test, but based on PSO-inspired algorithms, and found that DSRegPSO outperforms GPSO and DEEPSO with 5% significance level.
In the Wilcoxon test, we also found that Shadeils, an algorithm focused on LSGO, delivered the best results in separable functions across all algorithms in the CEC’13 test. We identified that DSRegPSO did not produce the best results in separable functions because it did not prioritize detecting possible simplifications of the search space by separately optimizing dimensions, although this was not the focus of DSRegPSO in our work.
Despite not focusing on LSGO, our proposal achieved superior results in several functions compared with other algorithms and outperformed PSO-inspired algorithms.
Additionally, we used PCA to transform the particle positions from 1000 dimensions to 3 and plot 3D points with their positions across iterations. This confirms that the algorithm continuously avoids stagnation and keeps looking for better positions to improve the global best without converging in position. Although the algorithm may converge early in the global best cost of Function 3 of CEC’13, it never converges in position.
Algorithm design requires assessing robustness and sensitivity to expected disturbances or noise. Robustness ensures consistent performance despite perturbations, while sensitivity measures the impact of perturbations on an algorithm’s outputs.
We conducted 25 runs of CEC’13 without controlling the seeds to vary starting conditions and evaluate DSRegPSO’s robustness. The results show that DSRegPSO performs better than the original PSO in terms of stability, as demonstrated by the convergence diagrams in Table 3 that compare mean, best, worst, and standard deviation.
Furthermore, we conducted two experiments using CEC’13 functions to test the robustness and sensitivity of the DSRegPSO algorithm against noise and registered the convergence diagrams. The first experiment involved adding random noise (1%, 5%, 10%, 15%, and 20%) to particle positions to evaluate the algorithm’s ability to converge in a high-dimensional space. In the second experiment, we introduced random noise of varying levels (1%, 5%, 10%, 15%, and 20%) to assess the algorithm’s performance in handling errors or variations in the high-dimensional objective function evaluation. Based on our tests, we found that the DSRegPSO is a robust algorithm that can handle noise effectively. The algorithm continued to improve even in the presence of noise in 13 out of 15 functions of CEC’13. However, in all the functions, it did react to noise by modifying the reached global best. We believe that this was due to the high sensitivity of CEC’13 functions.
Future Work
The DSRegPSO algorithm has demonstrated superior performance in the non-separable function of the CEC’13 when compared with non-PSO-inspired algorithms. To further improve its utility in future versions, we propose the implementation of mechanisms for detecting separability, allowing for a simplified search space with separable functions, as seen in other LSGO algorithms.
Additionally, a thorough analysis of the parameters in the proposed algorithm is suggested to determine the optimal values for optimizing different situations. We particularly suggest focusing on the parameters related to the maximum diameter of the hyper-sphere and the expansion speed, as an optimal choice for these parameters could lead to less exploration and, consequently, fewer iterations.
Author Contributions
M.M.R., conceptualization and methodology; M.M.R. and C.G.-M., validation; formal analysis and investigation; all authors, experimentation and results; M.M.R. and C.G.-M., writing—original draft; D.L.-B., T.S.-A., M.M.R. and C.G.-M., writing—review and editing, visualization, and supervision; M.M.R. project administration. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used in this research as the support for the results in this work is publicly available and can be accessed at the following URL: https://github.com/mmrMontes/DSRegPSO.
Acknowledgments
We acknowledge the support, time, and space for experimentation in Unidad Académica de Ciencia y Tecnologia de la Luz y la Materia, Universidad Autonoma de Zacatecas, Campus Siglo XXI, Zacatecas 98160. We also thank CONAHCyT for its support in the scholarship Estancias Posdoctorales México 2022(1) (CVU: 471898).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Sedighizadeh, D.; Masehian, E.; Sedighizadeh, M.; Akbaripour, H. GEPSO: A New Generalized Particle Swarm Optimization Algorithm. Math. Comput. Simul. 2021, 179, 194–212. [Google Scholar] [CrossRef]
- Senapati, M.K.; Pradhan, C.; Calay, R.K. A Computational Intelligence Based Maximum Power Point Tracking for Photovoltaic Power Generation System with Small-Signal Analysis. Optim. Control Appl. Methods 2023, 44, 617–636. [Google Scholar] [CrossRef]
- Vahedipour-Dahraie, M.; Rashidizadeh-Kermani, H.; Anvari-Moghaddam, A. Risk-Based Stochastic Scheduling of Resilient Microgrids Considering Demand Response Programs. IEEE Syst. J. 2021, 15, 971–980. [Google Scholar] [CrossRef]
- van den Bergh, F.; Engelbrecht, A.P. A Cooperative Approach to Participle Swam Optimization. IEEE Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar] [CrossRef]
- Maučec, M.S.; Brest, J. A Review of the Recent Use of Differential Evolution for Large-Scale Global Optimization: An Analysis of Selected Algorithms on the CEC 2013 LSGO Benchmark Suite. Swarm Evol. Comput. 2018, 50, 100428. [Google Scholar] [CrossRef]
- Sun, G.; Han, R.; Deng, L.; Li, C.; Yang, G. Hierarchical Structure-Based Joint Operations Algorithm for Global Optimization. Swarm Evol. Comput. 2023, 79, 101311. [Google Scholar] [CrossRef]
- Glorieux, E.; Svensson, B.; Danielsson, F.; Lennartson, B. Constructive Cooperative Coevolution for Large-Scale Global Optimization. J. Heuristics 2017, 23, 449–469. [Google Scholar] [CrossRef]
- Jiang, R.; Shankaran, R.; Wang, S.; Chao, T. A Proportional, Integral and Derivative Differential Evolution Algorithm for Global Optimization. Expert Syst. Appl. 2022, 206, 117669. [Google Scholar] [CrossRef]
- Marcelino, C.; Almeida, P.; Pedreira, C.; Caroalha, L.; Wanner, E. Applying C-DEEPSO to Solve Large Scale Global Optimization Problems. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation, CEC, Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- Yang, S.; Jiang, J.; Yan, G. A Dolphin Partner Optimization. In Proceedings of the 2009 WRI Global Congress on Intelligent Systems, GCIS 2009, Xiamen, China, 19–21 May 2009; Volume 1, pp. 124–128. [Google Scholar] [CrossRef]
- Koçer, H.G.; Uymaz, S.A. A Novel Local Search Method for LSGO with Golden Ratio and Dynamic Search Step. Soft Comput. 2021, 25, 2115–2130. [Google Scholar] [CrossRef]
- Molina, D.; Latorre, A.; Herrera, F. SHADE with Iterative Local Search for Large-Scale Global Optimization. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation, CEC 2018—Proceedings, Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- López, E.D.; Puris, A.; Bello, R.R. Vmode: A Hybrid Metaheuristic for the Solution of Large Scale Optimization Problems. Investig. Oper. 2015, 36, 232–239. [Google Scholar]
- LaTorre, A.; Pena, J.M. A Comparison of Three Large-Scale Global Optimizers on the CEC 2017 Single Objective Real Parameter Numerical Optimization Benchmark. In Proceedings of the 2017 IEEE Congress on Evolutionary Computation, CEC 2017—Proceedings, Donostia, Spain, 5–8 June 2017; pp. 1063–1070. [Google Scholar] [CrossRef]
- Xia, X.; Gui, L.; He, G.; Wei, B.; Zhang, Y.; Yu, F.; Wu, H.; Zhan, Z.-H. An Expanded Particle Swarm Optimization Based on Multi-Exemplar and Forgetting Ability. Inf. Sci. 2020, 508, 105–120. [Google Scholar] [CrossRef]
- Pluhacek, M.; Senkerik, R.; Viktorin, A.; Kadavy, T. PSO with Attractive Search Space Border Points. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2017; Volume 10246, pp. 665–675. [Google Scholar] [CrossRef]
- Xu, Y.; Pi, D. A Reinforcement Learning-Based Communication Topology in Particle Swarm Optimization. Neural Comput. Appl. 2020, 32, 10007–10032. [Google Scholar] [CrossRef]
- Pluhacek, M.; Senkerik, R.; Viktorin, A.; Zelinka, I. Multi-Chaotic Approach for Particle Acceleration in PSO. In Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics); Springer: Cham, Switzerland, 2016; Volume 9668, pp. 75–86. [Google Scholar] [CrossRef]
- Nobile, M.S.; Cazzaniga, P.; Besozzi, D.; Colombo, R.; Mauri, G.; Pasi, G. Fuzzy Self-Tuning PSO: A Settings-Free Algorithm for Global Optimization. Swarm Evol. Comput. 2018, 39, 70–85. [Google Scholar] [CrossRef]
- Pradhan, C.; Senapati, M.K.; Malla, S.G.; Nayak, P.K.; Gjengedal, T. Coordinated Power Management and Control of Standalone PV-Hybrid System with Modified IWO-Based MPPT. IEEE Syst. J. 2020, 15, 3585–3596. [Google Scholar] [CrossRef]
- Lin, A.; Sun, W.; Yu, H.; Wu, G.; Tang, H. Global Genetic Learning Particle Swarm Optimization with Diversity Enhancement by Ring Topology. Swarm Evol. Comput. 2018, 44, 571–583. [Google Scholar] [CrossRef]
- Xia, X.; Gui, L.; Zhan, Z.-H. A Multi-Swarm Particle Swarm Optimization Algorithm Based on Dynamical Topology and Purposeful Detecting. Appl. Soft Comput. 2018, 67, 126–140. [Google Scholar] [CrossRef]
- Erskine, A.; Joyce, T.; Herrmann, J.M. Stochastic Stability of Particle Swarm Optimisation. Swarm Intell. 2017, 11, 295–315. [Google Scholar] [CrossRef]
- Al-Bahrani, L.T.; Patra, J.C. Multi-Gradient PSO Algorithm for Optimization of Multimodal, Discontinuous and Non-Convex Fuel Cost Function of Thermal Generating Units under Various Power Constraints in Smart Power Grid. Energy 2018, 147, 1070–1091. [Google Scholar] [CrossRef]
- Huang, C.; Zhou, X.; Ran, X.; Liu, Y.; Deng, W.; Deng, W. Co-Evolutionary Competitive Swarm Optimizer with Three-Phase for Large-Scale Complex Optimization Problem. Inf. Sci. 2023, 619, 2–18. [Google Scholar] [CrossRef]
- Liu, H.; Wang, Y.; Tu, L.; Ding, G.; Hu, Y. A Modified Particle Swarm Optimization for Large-Scale Numerical Optimizations and Engineering Design Problems. J. Intell. Manuf. 2018, 30, 2407–2433. [Google Scholar] [CrossRef]
- Wang, H.; Liang, M.; Sun, C.; Zhang, G.; Xie, L. Multiple-Strategy Learning Particle Swarm Optimization for Large-Scale Optimization Problems. Complex. Intell. Syst. 2021, 7, 1–16. [Google Scholar] [CrossRef]
- Al-Bahrani, L.T.; Patra, J.C. A Novel Orthogonal PSO Algorithm Based on Orthogonal Diagonalization. Swarm Evol. Comput. 2018, 40, 1–23. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R. A Modified Particle Swarm Optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings. IEEE World Congress on Computational Intelligence (Cat. No.98TH8360), Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Evers, G.I.; Ghalia, M. Ben Regrouping Particle Swarm Optimization: A New Global Optimization Algorithm with Improved Performance Consistency across Benchmarks. In Proceedings of the 2009 IEEE International Conference on Systems, Man and Cybernetics, San Antonio, TX, USA, 11–14 October 2009; pp. 3901–3908. [Google Scholar] [CrossRef]
- Li, F.; Yue, Q.; Liu, Y.; Ouyang, H.; Gu, F. A Fast Density Peak Clustering Based Particle Swarm Optimizer for Dynamic Optimization. Expert. Syst. Appl. 2024, 236, 121254. [Google Scholar] [CrossRef]
- Akan, Y.Y.; Herrmann, J.M. Stability, Entropy and Performance in PSO. In Proceedings of the GECCO 2023 Companion—Proceedings of the 2023 Genetic and Evolutionary Computation Conference Companion, Lisbon, Portugal, 15–19 July 2023; pp. 811–814. [Google Scholar] [CrossRef]
- Sun, L.; Yang, Y.; Wei, W. A Three-Stage Gene Selection Algorithm Based on Intrinsic Dimension and the Concise Particle Swarm Optimization. SSRN 2023. [CrossRef]
- Tsujimoto, T.; Shindo, T.; Jin’no, K. The Neighborhood of Canonical Deterministic PSO. In Proceedings of the Evolutionary Computation (CEC), New Orleans, LA, USA, 5–8 June 2011; pp. 1811–1817. [Google Scholar]
- Kennedy, J. Small Worlds and Mega-Minds: Effects of Neighborhood Topology on Particle Swarm Performance. In Proceedings of the 1999 Congress on Evolutionary Computation-CEC99 (Cat. No. 99TH8406), Washington, DC, USA, 6–9 July 1999; Volume 3, pp. 1931–1938. [Google Scholar]
- Yang, X.; Li, H.; Huang, Y. An Adaptive Dynamic Multi-Swarm Particle Swarm Optimization with Stagnation Detection and Spatial Exclusion for Solving Continuous Optimization Problems. Eng. Appl. Artif. Intell. 2023, 123, 106215. [Google Scholar] [CrossRef]
- Jiang, J.J.; Wei, W.X.; Shao, W.L.; Liang, Y.F.; Qu, Y.Y. Research on Large-Scale Bi-Level Particle Swarm Optimization Algorithm. IEEE Access 2021, 9, 56364–56375. [Google Scholar] [CrossRef]
- Zhao, Q.; Li, C. Two-Stage Multi-Swarm Particle Swarm Optimizer for Unconstrained and Constrained Global Optimization. IEEE Access 2020, 8, 124905–124927. [Google Scholar] [CrossRef]
- Balavalikar, S.; Nayak, P.; Shenoy, N.; Nayak, K. Particle Swarm Optimization Based Artificial Neural Network Model for Forecasting Groundwater Level in Udupi District. Proc. AIP Conf. Proc. 2018, 1952, 20021. [Google Scholar]
- Yang, X.; Li, H. Evolutionary-State-Driven Multi-Swarm Cooperation Particle Swarm Optimization for Complex Optimization Problem. Inf. Sci. 2023, 646, 119302. [Google Scholar] [CrossRef]
- Nagra, A.A.; Han, F.; Ling, Q.H.; Mehta, S. An Improved Hybrid Method Combining Gravitational Search Algorithm with Dynamic Multi Swarm Particle Swarm Optimization. IEEE Access 2019, 7, 50388–50399. [Google Scholar] [CrossRef]
- Nagra, A.A.; Han, F.; Ling, Q.H. An Improved Hybrid Self-Inertia Weight Adaptive Particle Swarm Optimization Algorithm with Local Search. Eng. Optim. 2018, 51, 1115–1132. [Google Scholar] [CrossRef]
- Vakhnin, A.V.; Sopov, E.A.; Panfilov, I.A.; Polyakova, A.S.; Kustov, D.V. A Problem Decomposition Approach for Large-Scale Global Optimization Problems. IOP Conf. Ser. Mater. Sci. Eng. 2019, 537, 052031. [Google Scholar] [CrossRef]
- Liao, T.; Stutzle, T. Benchmark Results for a Simple Hybrid Algorithm on the CEC 2013 Benchmark Set for Real-Parameter Optimization. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, CEC 2013, Cancun, Mexico, 20–23 June 2013; pp. 1938–1944. [Google Scholar] [CrossRef]
- Qu, L.; Zheng, R.; Shi, Y. BSO-CMA-ES: Brain Storm Optimization Based Covariance Matrix Adaptation Evolution Strategy for Multimodal Optimization. In Communications in Computer and Information Science; Springer: Cham, Switzerland, 2021; Volume 1454, pp. 167–174. [Google Scholar] [CrossRef]
- Lan, R.; Zhang, L.; Tang, Z.; Liu, Z.; Luo, X. A Hierarchical Sorting Swarm Optimizer for Large-Scale Optimization. IEEE Access 2019, 7, 40625–40635. [Google Scholar] [CrossRef]
- Diep, Q.B.; Zelinka, I.; Das, S. Self-Organizing Migrating Algorithm Pareto. Mendel 2019, 25, 111–120. [Google Scholar] [CrossRef]
- Zhao, D.; Yi, J.; Liu, D. Particle Swarn Optimized Adaptive Dynamic Programming. In Proceedings of the Approximate Dynamic Programming and Reinforcement Learning, ADPRL 2007, Honolulu, HI, USA, 1–5 April 2007; pp. 32–37. [Google Scholar]
- Strang, G. Calculus. In Open Textbook Library; Wellesley-Cambridge Press: Wellesley, MA, USA, 1991; ISBN 9780961408824. [Google Scholar]
- Parsopoulos, K.E.; Vrahatis, M.N. Particle Swarm Optimization and Intelligence; IGI Global: Hershey, PA, USA, 2010. [Google Scholar] [CrossRef]
- Olorunda, O.; Engelbrecht, A.P. Measuring Exploration/Exploitation in Particle Swarms Using Swarm Diversity. In Proceedings of the Evolutionary Computation, 2008. CEC 2008. (IEEE World Congress on Computational Intelligence), Hong Kong, China, 1–6 June 2008; pp. 1128–1134. [Google Scholar]
- Li, X.; Tang, K.; Omidvar, M.N.; Yang, Z.; Qin, K.; China, H. Benchmark Functions for the CEC 2013 Special Session and Competition on Large-Scale Global Optimization. Gene 2013, 7, 8. [Google Scholar]
- Molina, D.; Latorre, A. Toolkit for the Automatic Comparison of Optimizers: Comparing Large-Scale Global Optimizers Made Easy. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation, CEC 2018—Proceedings, Rio de Janeiro, Brazil, 8–13 July 2018. [Google Scholar] [CrossRef]
- Clerc, M. Particle Swarm Optimization; ISTE: London, UK, 2006; ISBN 9780470612163. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November 1995–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar] [CrossRef]
- Ferreira, S.L.C.; Caires, A.O.; Borges, T.d.S.; Lima, A.M.D.S.; Silva, L.O.B.; dos Santos, W.N.L. Robustness Evaluation in Analytical Methods Optimized Using Experimental Designs. Microchem. J. 2017, 131, 163–169. [Google Scholar] [CrossRef]
- Bonnini, S.; Chesneau, C.; Ghosh, I.; Fleming, K. On the Robustness and Sensitivity of Several Nonparametric Estimators via the Influence Curve Measure: A Brief Study. Mathematics 2022, 10, 3100. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).