Optimal Designs for Proportional Interference Models with Different Guarding Strategies

Abstract

Interference models are commonly used in agriculture, industry, and other related fields. Optimal designs for these models are important topics in block designs. In this work, we consider both direct and total effects under both guarded and unguarded proportional interference models. Some general equivalence theorems are established to characterize such efficient designs. For guarded models, we generate optimal noncircular designs for estimating both direct and total effects, respectively. Particularly, we remove the traditional circular assumption for guarded models and introduce noncircular designs which have less restriction and, more importantly, perform higher efficiency than existing circular designs. For unguarded models, we also give the construction of some optimal designs under the proportional interference model.

1. Introduction

Block designs are commonly studied in agricultural field experiments. The blocks are usually organized as rows of plots. The treatment arranged for one plot could simultaneously have direct effects on this plot and have neighbor effects over its neighboring plots in the same row. The existence of neighbor effects has been recognized in [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15] in various areas of applications such as serology, agriculture, horticulture, medical and forestry experiments. Thus, the design of such an experiment with n blocks boils down to the determination of n treatment sequences. Optimal or efficient designs for such experiments using interference models can be found in [16,17,18,19,20,21,22,23,24,25,26,27] among others.

A reasonable assumption on these interference models in many applications is neighbor effects being proportional to direct effects since effective treatments usually have large impacts on the neighboring plots. In fact, ref. [28] has proposed such a model with the same left and right neighbor effects. For a more general proportional interference model, optimal designs are constructed in [23]. The proportional assumption is also applied to the studies of crossover designs in [29,30,31,32].

In [23], the authors studied optimal designs for circular guarded designs. Guarded designs are introduced by [11] to eliminate unpredictable border effects, which are caused by uncertain environmental impacts outside the block that affect the responses of the two edge plots in each row. The authors of [33] recommended applying treatments to the two guarding plots to control the border effects. In assigning treatments to guarding plots, the circular setup has been widely applied for interference designs with guarding plots; see [19,27,33,34] for direct effects and [16,20,35] for total effects, both under the circular setup. The circular condition forces the treatments of the guarding plots to be the same as the one applied to the edge inner plots on their opposite sides. However, this condition is proposed mainly for the convenience of theoretically constructing optimal designs within a subclass of the whole design space, and it is not necessary for most applications. In practice, usually, there is no such artificial restriction on the treatments of the two guarding plots. So, we will consider the noncircular designs which remove the circular condition. Meanwhile, there are also many pieces of research assuming negligible border effects which omitted guarding plots; see [21,22,26,36] for more details.

In this manuscript, we reformulate optimal designs for proportional interference models according to different guarding strategies. $\left(i\right)$ When guarding plots are involved, we propose noncircular designs which remove the circular assumption in the existing literature. Our noncircular designs are more efficient than the optimal circular designs given in [23]. Particularly, for extremely small block sizes of 2 and 3, neither direct nor total effects are estimable using circular designs, but they are now estimable in noncircular setups. To include an intuitive comparison between circular and noncircular setups, we refer to Figure 1 as an example. The information matrix for total effects under optimal noncircular design $d_{\mathrm{NCT}}$ of Figure 1 generated in this paper is $4.5$ times that of the optimal circular design $d_{\mathrm{CT}}$ of Figure 1 generated in [23]. $\left(ii\right)$ When guarding plots are omitted, a similar theoretical framework for optimal unguarded designs is also established to make complement the theoretical results for noncircular designs. In Figure 1, $d_{\mathrm{UT}}$ is the optimal unguarded design which is equivalent to the inner plot treatments in columns 2–5 of $d_{\mathrm{NCT}}$. In brief, we generate noncircular designs to improve existing optimal circular designs when guarding plots are needed, and generate optimal unguarded designs when guarding plots can be omitted.

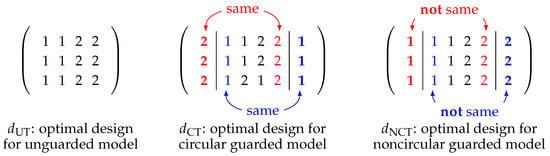
Figure 1. Optimal designs for the estimation of total effects under $\left(i\right)$ unguarded setup (left), $\left(ii\right)$ circular guarded setup (middle) and $\left(iii\right)$ noncircular guarded setup (right).

The remainder of this article is organized as follows. Section 2 provides the necessary definitions, notation, and optimality criteria. Equivalence theorems for optimal designs are given in Section 3. Section 4 gives some illustrative examples of optimal unguarded designs and compares optimal circular designs in [23] with noncircular designs. The conclusion and discussion are given in Section 5.

2. Preliminaries

2.1. Models and Notation

The well-known interference model (1) has been intensively studied in the literature such as [17,18,21,23,26,27] among many others.

$$\begin{array}{c}\hfill y_{dij}=\mu +{\beta }_i+{\tau }_{d(i,j)}+{\gamma }_{d(i,j-1)}+{\rho }_{d(i,j+1)}+{ϵ}_{ij}.\end{array}$$

(1)

For $1\le i\le n$ and $1\le j\le k$, $d(i,j)$ is the treatment index of t treatments determined by design d on the j-th plot of the i-th block. The response $y_{dij}$ is decomposed into the general mean $\mu$, the block effect ${\beta }_i$, the direct effect ${\tau }_{d(i,j)}$, the left (or right) neighbor effect ${\gamma }_{d(i,j-1)}$ (or ${\rho }_{d(i,j+1)}$). The guarding strategy depends on the setup of $d(i,0)$ and $d(i,k+1)$. The interference model is called $\left(i\right)$ unguarded if it assumes ${\gamma }_{d(i,0)}={\rho }_{d(i,k+1)}=0$ such that $d(i,0)$ and $d(i,k+1)$ can be ignored, and $\left(ii\right)$ circular guarded if it assumes $d(i,0)=d(i,k)$ and $d(i,k+1)=d(i,1)$. Besides setups $\left(i\right)$ and $\left(ii\right)$, we call a design $\left(iii\right)$ noncircular guarded if the restriction on $d(i,0)$ and $d(i,k+1)$ in $\left(ii\right)$ is removed.

The proportional interference model assumes that the neighbor effects are proportional to the direct effects, i.e., ${\gamma }_i={\lambda }_1{\tau }_i$ and ${\rho }_i={\lambda }_2{\tau }_i$ for $1\le i\le t$ with ${\lambda }_1$, ${\lambda }_2$ as two fixed parameters. To distinguish this original model from the undirectional model ([23,28,34,37]) with ${\lambda }_1={\lambda }_2=\lambda$, it is called a directional model for convenience. Let $Y_d$ be the vector of responses organized block by block. We can write these two proportional interference models in matrix form as follows.

$$\begin{array}{ccc}\hfill & & DirectionalModel:Y_d=1_{nk}\mu +U\beta +(T_d+{\lambda }_1{L}_d+{\lambda }_2{R}_d)\tau +ϵ,and\hfill \end{array}$$

(2)

$$\begin{array}{ccc}& & UndirectionalModel:Y_d=1_{nk}\mu +U\beta +(T_d+\lambda L_d+\lambda R_d)\tau +ϵ.\hfill \end{array}$$

(3)

Here, $U=I_n\otimes 1_k$, $\beta ={({\beta }_1,...,{\beta }_n)}^{\prime }$, $\tau ={({\tau }_1,...,{\tau }_t)}^{\prime }$; $I_n$ is the identity matrix of order n; ⊗ denotes the Kronecker product; ${}^{\prime }$ means the transposition; $T_d,L_d$, and $R_d$ represent the design matrices for the direct, left neighbor, and right neighbor effects, respectively. We assume that $E\left(ϵ\right)=0$ and $Var\left(ϵ\right)=I_n\otimes \Sigma$, where $\Sigma$ is an arbitrary $k\times k$ positive definite within-block covariance matrix.

Now we introduce some commonly used notation in the estimation of direct effects under the directional unguarded model. These definitions will be inherited by the analysis of other models if no change is specifically mentioned. Define $M^{-}$ as the Moore-Penrose inverse of M and $p{r}^{\perp }G=I-G{\left(G^{\prime }G\right)}^{-}{G}^{\prime }$. Let $\tilde{U}=(I_n\otimes {\Sigma }^{-1/2})U$, $\widetilde{T_d}=(I_n\otimes {\Sigma }^{-1/2})T_d$, $\widetilde{L_d}=(I_n\otimes {\Sigma }^{-1/2})L_d$, $\widetilde{R_d}=(I_n\otimes {\Sigma }^{-1/2})R_d$, $M_{x,y,z}=x\widetilde{T_d}+y\widetilde{L_d}+z\widetilde{R_d}$ for any values of x, y and z. The Fisher information matrix for the direct treatment effect $\tau$ under Model (2) is

$$\begin{array}{ccc}\hfill C_d\left(\tau \right)& =& M_{1,{\lambda }_1,{\lambda }_2}^{\prime }p{r}^{\perp }(\tilde{U}|\widetilde{L_d}\tau \left|\widetilde{R_d}\tau \right)M_{1,{\lambda }_1,{\lambda }_2}\hfill \\ & =& \sum _{i=0}^2\sum _{j=0}^2{\lambda }_i{\lambda }_j{C}_{dij}-A_d^{\prime }{\left({\tau }^{\prime }{C}_{dij}\tau \right)}_{1\le i,j\le 2}^{-}{A}_d,\hfill \end{array}$$

(4)

where ${\lambda }_0=1$, $C_{dij}=G_i^{\prime }(I_n\otimes \tilde{B})G_j$ with $G_0=T_d$, $G_1=L_d$, $G_2=R_d$, $\tilde{B}={\Sigma }^{-1}-{\Sigma }^{-1}{J}_k{\Sigma }^{-1}/1_k^{\prime }{\Sigma }^{-1}{1}_k$, $J_k=1_k{1}_k^{\prime }$, and $A_d={\left({\sum }_{i=0}^2{\lambda }_i{C}_{di1}\tau \right|{\sum }_{i=0}^2{\lambda }_i{C}_{di2}\tau )}^{\prime }$. For the case of $\Sigma =I_k$, we have $\tilde{B}=I_k-J_k/k$, and the latter is denoted by $B_k$. The information matrix for $\tau$ under Model (3) is ${\tilde{C}}_d\left(\tau \right)=M_{1,\lambda ,\lambda }^{\prime }p{r}^{\perp }\left(\tilde{U}\right|M_{0,1,1}\tau )M_{1,\lambda ,\lambda }$.

With some abuse of notation, define ${\mathbb{S}}_{k,t}$ as the set of $\left(i\right)$ all $t^k$ possible length k sequences under the unguarded model, and $\left(ii\right)$ all $t^{k+2}$ possible length $k+2$ sequences under the guarded model. A design could be considered as a result of selecting n elements from ${\mathbb{S}}_{k,t}$ with replacement. The set of all possible designs is denoted by ${\Omega }_{n,k,t}$. Let $C_{sij}$ be the matrix $C_{dij}$ when the design d is degenerated to a single sequence s for $0\le i,j\le 2$. Then we have $C_{dij}=n{\sum }_{s\in {\mathbb{S}}_{k,t}}{p}_s{C}_{sij}$, where $p_s=n_s/n$, $n_s$ is the number of times that the sequence s is selected in the design d. So, for given n, a design is determined by the measure $\xi =(p_s,s\in {\mathbb{S}}_{k,t})$. Then, for this measure, we can sequentially define

$$\begin{array}{ccc}& & C_{\xi ij}=\sum _{s\in {\mathbb{S}}_{k,t}}{p}_s{C}_{sij},A_{\xi }={\left(\sum _{i=0}^2{\lambda }_i{C}_{\xi i1}\tau \right|\sum _{i=0}^2{\lambda }_i{C}_{\xi i2}\tau )}^{\prime }\hfill \\ & & C_{\xi }\left(\tau \right)=\sum _{i=0}^2\sum _{j=0}^2{\lambda }_i{\lambda }_j{C}_{\xi ij}-A_{\xi }^{\prime }{\left({\tau }^{\prime }{C}_{\xi ij}\tau \right)}_{1\le i,j\le 2}^{-}{A}_{\xi },C_d\left(\tau \right)=n{C}_{\xi }\left(\tau \right).\hfill \end{array}$$

$C_{\xi }\left(\tau \right)$ is called the information matrix of the measure $\xi$. Similarly, we can define ${\tilde{C}}_{\xi }$ for the noncircular guarded model. If $p_s>0$, then s is called a supporting sequence of $\xi$. In approximate design theory, we search for optimal measures in the space of $P=\{\xi :\sum p_s=1,p_s\ge 0\}$. If $n\xi$ is also a vector of integers, we can naturally generate an exact design that is optimal among ${\Omega }_{n,k,t}$. Let $\mathbb{O}$ denote the set of all $t!$ permutation operators on $\{1,2,...,t\}$. For any $\sigma \in \mathbb{O}$ and $s=(t_1,...,t_k)$ with $1\le t_i\le t$, define $\sigma s=(\sigma \left(t_1\right),...,\sigma \left(t_k\right))$. A measure is symmetric if $\sigma \xi =\xi$ for all $\sigma \in \mathbb{O}$, where $\sigma \xi =(p_{{\sigma }^{-1}s},s\in \mathbb{S})$. For the guarded model, these restrictions are extended to the sequence $s=(t_0,...,t_{k+1})$.

2.2. Optimal Criterion

In this subsection, we briefly introduce optimal criteria for the unguarded model based on $C_{\xi }$. The definitions are naturally extended to guarded designs by replacing $C_{\xi }$ with ${\tilde{C}}_{\xi }$ under the noncircular guarded model. A proper criterion $\Phi$ on information matrices should satisfy (C.1) $\Phi$ is concave, (C.2) $\Phi \left(S^{\prime }CS\right)=\Phi \left(C\right)$ for any permutation matrix S, and (C.3) $\Phi \left(bC\right)$ is nondecreasing in the scalar $b>0$. Following [38,39], we call $\xi$ universally optimal if it maximizes $\Phi \left(C_{\xi }\left(\tau \right)\right)$ for all such $\Phi$. Note that the optimal design depends on $\tau$ through $C_d\left(\tau \right)$. Following [23,29,31,32], we adopt the Bayesian criterion

$$\begin{array}{c}\hfill E_g\Phi \left(C_{\xi }\left(\tau \right)\right)=\int \Phi \left(C_{\xi }\left(\tau \right)\right)g\left(\tau \right)\mathrm{d}\tau ,\end{array}$$

(5)

where g is assumed to be an exchangeable prior distribution of $\tau$ throughout the paper. A design is said to be Bayesian $\Phi$-optimal if and only if it achieves the maximum of $E_g\Phi \left(C_{\xi }\left(\tau \right)\right)$ among all designs for given g, $\Phi$, ${\lambda }_1$ and ${\lambda }_2$. For design $\xi$, let ${\eta }_1\left(C_{\xi }\right)\le {\eta }_2\left(C_{\xi }\right)\le \cdots \le {\eta }_t\left(C_{\xi }\right)$ be all the eigenvalues of $C_{\xi }$. The classical ${\Phi }_p$-criterion ${\Phi }_p\left(C_{\xi }\right)$ is defined as

$$\begin{array}{c}\hfill {\Phi }_p\left(C_{\xi }\right)={\left(\frac{1}{t}\sum _{i=1}^t{\eta }_i^{-p}\left(C_{\xi }\right)\right)}^{(-1/p)}.\end{array}$$

(6)

The ${\Phi }_p$-optimality refers to the well known T-, D-, A-, E-criteria for four specific values of $p=-1,0,1,+\infty$, respectively. A design is said to be $A_g$-optimal if it maximizes $E_g{\Phi }_1\left(C_{\xi }\left(\tau \right)\right)$. The $D_g$-, $E_g$- and $T_g$-optimality of a design are similarly defined. However, an interesting conclusion from Proposition 1–4 is that optimal designs under Bayesian ${\Phi }_p$ criterion is irrelevant to the distribution g, So we use A-, D-, E- and T- optimal in Theorems 1–4.

Since the number of blocks n is irrelevant to the search of approximate optimal designs, we focus on finding the optimal measures which maximize ${\Phi }_p\left(C_{\xi }\right)$ among P. We can easily know that an optimal measure can be found in the subclass of symmetric measures by the same proof of Proposition 1 in [23].

Define $c_{\xi ij}=tr\left(B_t{C}_{\xi ij}{B}_t\right)$, $V_{\xi }={\left(c_{\xi ij}\right)}_{0\le i,j\le 2}$, $Q_{\xi }={\left(c_{\xi ij}\right)}_{1\le i,j\le 2}$, $l={(1,{\lambda }_1,{\lambda }_2)}^{\prime }$ and $q_{\xi }^{*}=c_{\xi 00}-\left(c_{\xi 01}{c}_{\xi 02}\right)Q_{\xi }^{-}{\left(c_{\xi 01}{c}_{\xi 02}\right)}^{\prime }$. We naturally define $c_{sij}$, $V_s$, $Q_s$ by choosing $\xi$ as the Dirac measure on s. For a symmetric measure, following the similar argument as in [23], we can show that $C_{\xi ij}=c_{\xi ij}{B}_t/(t-1)+\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)J_t/t^2$, $0\le i,j\le 2$ both for the model with and without guarding plots.

3. Equivalence Theorems

Note that noncircular designs remove the restriction on the two guarding plots in circular designs discussed in [23]. Thus, the noncircular setup induces a larger experimental space which contains the experimental space for circular designs as a subset. The equivalence theorems established in [23] naturally hold under noncircular setup. The difference is that the enlarged experimental space brings in more efficient designs. This improvement will be shown in Section 4 using examples. Thus, it should be emphasized here that equivalence theorems for noncircular guarded models are not listed in this paper to avoid redundant replication. In this section, we focus on equivalence theorems for unguarded models.

3.1. Optimal Design for Direct Effects under Unguarded Model

In this subsection, we consider the estimation of direct effects under unguarded models. We can properly define $q_{\xi }^{*}=det\left(V_{\xi }\right)/det\left(Q_{\xi }\right)$ since $Q_{\xi }$ has been proved to be positive definite for any design in Lemma 2 of [26]. Proposition 1 in [23] indicates that any design can be symmetrized into a symmetric design to achieve higher or at least the same efficiency. A design is called pseudo symmetric if the corresponding information matrix is completely symmetric. The information matrix of a pseudo symmetric design $\xi$ equals to that of the symmetrized design induced by $\xi$. Thus, our discussion on optimal designs is based on pseudo symmetric designs in the rest of this manuscript.

Proposition 1. 

Under the directional unguarded model, the information matrix $C_{\xi }\left(\tau \right)$ of a pseudo symmetric measure ξ has eigenvalues of $\frac{1}{t}{\sum }_{i=0}^2{\sum }_{j=0}^2{\lambda }_i{\lambda }_j\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)$, ${(t-1)}^{-1}{q}_{\xi }^{*}$ and ${(t-1)}^{-1}{l}^{\prime }{V}_{\xi }l$ with multiplicities of 1, 1 and $t-2$, respectively. Moreover we have $q_{\xi }^{*}\le l^{\prime }{V}_{\xi }l$.

Proof. 

Note that $1_t^{\prime }\tau =0$. We have $B_t\tau =\tau$, ${\tau }^{\prime }{C}_{\xi ij}\tau =c_{\xi ij}{\tau }^{\prime }\tau /(t-1)$ and thus

$$\begin{array}{ccc}\hfill C_{\xi }\left(\tau \right)& =& \sum _{i=0}^2\sum _{j=0}^2{\lambda }_i{\lambda }_j[c_{\xi ij}{B}_t/(t-1)+\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)J_t/t^2]-a{\left({\tau }^{\prime }\tau \right)}^{-1}\tau {\tau }^{\prime }/(t-1),\hfill \\ \hfill a& =& \left(\sum _{i=0}^2{\lambda }_i{c}_{\xi i1}\right|\sum _{i=0}^2{\lambda }_i{c}_{\xi i2})Q_{\xi }^{-1}{\left(\sum _{i=0}^2{\lambda }_i{c}_{\xi i1}\right|\sum _{i=0}^2{\lambda }_i{c}_{\xi i2})}^{\prime }.\hfill \end{array}$$

Expand $1_t$ and τ into an orthogonal basis $\{1_t,\tau ,x_1,...,x_{t-2}\}$. Then, $\{1_t,\tau ,x_1,...,x_{t-2}\}$ are the eigenvectors of $C_{\xi }\left(\tau \right)$ with corresponding eigenvalues $\frac{1}{t}{\sum }_{i=0}^2{\sum }_{j=0}^2{\lambda }_i{\lambda }_j\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)$, ${(t-1)}^{-1}{q}_{\xi }^{*}$ and ${(t-1)}^{-1}{l}^{\prime }{V}_{\xi }l$ with multiplicities of 1, 1 and $t-2$, respectively. Since $a\ge 0$, and $q_{\xi }^{*}=l^{\prime }{V}_{\xi }l-a$, the proof is concluded.    □

Remark 1. 

Note that $1_t^{\prime }{C}_{\xi 0j}=0$ and $C_{\xi i0}{1}_t=0$. We can slightly simplify Proposition 1 with ${\sum }_{i=0}^2{\sum }_{j=0}^2{\lambda }_i{\lambda }_j\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)={\sum }_{i=1}^2{\sum }_{j=1}^2{\lambda }_i{\lambda }_j\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)$. Moreover, similar to Lemma 3 in [26], we know that ${\tilde{Q}}_{\xi }={\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)}_{1\le i,j\le 2}$ is a constant positive definite matrix independent of design. So, the eigenvalue $\frac{1}{t}{\sum }_{i=0}^2{\sum }_{j=0}^2{\lambda }_i{\lambda }_j\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)$ is a constant irrelevant to the design ξ.

Remark 2. 

The eigenvalues in Proposition 1 are irrelevant to the unknown direct effect τ. Thus, although we give the definition of Bayesian optimality in (5), there is no need to bring the prior distribution g of τ into the analysis of optimal designs. Actually, this conclusion holds for all models considered in this manuscript. Thus, our discussion always focuses on (6) instead of (5).

Theorem 1. 

Under the directional unguarded model, a pseudo symmetric measure ξ for estimating τ is optimal in the following cases. In each case, the $p_s$ in ξ is positive only if s reaches the maximum therein.

(1) ξ is A-optimal if and only if $det\left(V_{\xi }\right)>0$, and

$$\underset{s\in \mathbb{S}}{max}\frac{r_{s}det\left(Q_{\xi }\right)/det\left(V_{\xi }\right)+(t-2){\left(l^{\prime }{V}_{\xi }l\right)}^{-2}{l}^{\prime }{V}_{s}l}{det\left(Q_{\xi }\right)/det\left(V_{\xi }\right)+(t-2){\left(l^{\prime }{V}_{\xi }l\right)}^{-1}}=1.$$

(2) ξ is D-optimal if and only if $det\left(V_{\xi }\right)>0$, and

$$\underset{s\in \mathbb{S}}{max}\left(\frac{r_s}{t-1}+\frac{t-2}{t-1}\frac{l^{\prime }{V}_{s}l}{l^{\prime }{V}_{\xi }l}\right)=1.$$

(3) ξ is E-optimal if and only if $det\left(V_{\xi }\right)>0$, and

$$\underset{s\in \mathbb{S}}{max}{r}_s=1.$$

(4) ξ is T-optimal if and only if $det\left(V_{\xi }\right)>0$, and

$$\underset{s\in \mathbb{S}}{max}\frac{r_{s}det\left(V_{\xi }\right)/det\left(Q_{\xi }\right)+(t-2)l^{\prime }{V}_{s}l}{det\left(V_{\xi }\right)/det\left(Q_{\xi }\right)+(t-2)l^{\prime }{V}_{\xi }l}=1.$$

Here, $r_s=tr\left(V_s{V}_{\xi }^{-1}\right)-tr\left(Q_s{Q}_{\xi }^{-1}\right)$.

Proof. 

We only give the proof of Part (2) and the other cases follow similarly.

Since $det\left(Q_{\xi }\right)>0$, if $det\left(V_{\xi }\right)=0$, then $q_{\xi }^{*}=0$, ${\Phi }_{-1}\left(C_{\xi }\right)=0$, $\xi$ can not be optimal. So we only need to consider the case of $det\left(V_{\xi }\right)>0$.

According to the definition of D-optimal criterion, for any measure $\xi$, define $\varphi \left(\xi \right)=log{\left(\frac{1}{t}{\sum }_{i=0}^2{\sum }_{j=0}^2{\lambda }_i{\lambda }_j\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)\right)}^{1/t}+log{\left(\frac{1}{t-1}{q}_{\xi }^{*}\right)}^{1/t}+log{\left(\frac{1}{t-1}{l}^{\prime }{V}_{\xi }l\right)}^{\frac{t-2}{t}}$. It can be verified that $\varphi \left({\xi }^{*}\right)=\varphi \left(\xi \right)$, where ${\xi }^{*}$ is the symmetric measure defined by ${\xi }^{*}=\frac{1}{t!}{\sum }_{\sigma \in \mathbb{O}}\sigma \xi$.

For a pseudo symmetric measure $\xi$ with $det\left(V_{\xi }\right)>0$ and any measure ${\xi }_0$, $\xi$ is D-optimal if and only if

$$\begin{array}{c}\hfill \underset{\delta \to 0}{lim}\frac{\varphi ((1-\delta )\xi +\delta {\xi }_0)-\varphi \left(\xi \right)}{\delta }\le 0.\end{array}$$

(7)

Since

$$\begin{array}{c}\hfill \underset{\delta \to 0}{lim}\frac{log\left(det\left(V_{(1-\delta )\xi +\delta {\xi }_0}\right)\right)-log\left(det\left(V_{\xi }\right)\right)}{\delta }=tr\left(V_{{\xi }_0}{V}_{\xi }^{-1}\right)-3,\end{array}$$

(8)

$$\begin{array}{c}\hfill \underset{\delta \to 0}{lim}\frac{log\left(det\left(Q_{(1-\delta )\xi +\delta {\xi }_0}\right)\right)-log\left(det\left(Q_{\xi }\right)\right)}{\delta }=tr\left(Q_{{\xi }_0}{Q}_{\xi }^{-1}\right)-2.\end{array}$$

(9)

Apply (8) and (9) to (7), we have

$$\begin{array}{c}\hfill \frac{tr\left(V_{{\xi }_0}{V}_{\xi }^{-1}\right)-tr\left(Q_{{\xi }_0}{Q}_{\xi }^{-1}\right)}{t-1}+\frac{t-2}{t-1}\frac{l^{\prime }{V}_{{\xi }_0}l}{l^{\prime }{V}_{\xi }l}\le 1.\end{array}$$

(10)

Take ${\xi }_0$ as the Dirac measure on a single sequence s, we have

$$\underset{s\in S}{max}\left(\frac{tr\left(V_s{V}_{\xi }^{-1}\right)-tr\left(Q_s{Q}_{\xi }^{-1}\right)}{t-1}+\frac{t-2}{t-1}\frac{l^{\prime }{V}_{s}l}{l^{\prime }{V}_{\xi }l}\right)\le 1,$$

By taking ${\xi }_0=\xi$, we have equality in (10). Hence we have

$$\underset{s\in S}{max}\left(\frac{tr\left(V_s{V}_{\xi }^{-1}\right)-tr\left(Q_s{Q}_{\xi }^{-1}\right)}{t-1}+\frac{t-2}{t-1}\frac{l^{\prime }{V}_{s}l}{l^{\prime }{V}_{\xi }l}\right)\ge 1.$$

The proof for Part (2) is concluded.    □

To distinguish Theorem 1 from the Theorem 1 in [23], the results are simplified by removing the case that $det\left(Q_{\xi }\right)=0$ since the matrix is positive definite in our case. Propositons 2–4 and Theorems 2–4 are parallel results of Proposition 1 and Theorem 1 for other three models.

Also, the information matrix of a measure $\xi$ for $\tau$ under the undirectional unguarded model is ${\tilde{C}}_{\xi }\left(\tau \right)=n^{-1}{\tilde{C}}_d\left(\tau \right)$ and we consider only the symmetric design. Note that ${\lambda }_1={\lambda }_2=\lambda$, we have $l=(1,{\lambda }_1,{\lambda }_2)={(1,\lambda ,\lambda )}^{\prime }$. Define $l_1={(0,1,1)}^{\prime }$, $L_1=(l,l_1)$, $V_{\xi ,1}=L_1^{\prime }{V}_{\xi }{L}_1$, $Q_{\xi ,1}=l_1^{\prime }{V}_{\xi }{l}_1$, $V_{s,1}=L_1^{\prime }{V}_s{L}_1$, $Q_{s,1}=l_1^{\prime }{V}_s{l}_1$, $q_{\xi ,1}^{*}=l^{\prime }{V}_{\xi }l-l^{\prime }{V}_{\xi }{l}_1{Q}_{\xi ,1}^{-}{l}_1^{\prime }{V}_{\xi }l$. Being different from parallel analysis for the circular design in [23], $Q_{\xi ,1}$ is positive here. So, $q_{\xi ,1}^{*}$ can be written as $q_{\xi ,1}^{*}=det\left(V_{\xi ,1}\right)/Q_{\xi ,1}$.

Proposition 2. 

Under the undirectional unguarded model, the information matrix $C_{\xi }\left(\tau \right)$ of a pseudo symmetric measure ξ has eigenvalues of $\frac{{\lambda }^2}{t}{\sum }_{i=1}^2{\sum }_{j=1}^2\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)$, ${(t-1)}^{-1}{q}_{\xi ,1}^{*}$ and ${(t-1)}^{-1}{l}^{\prime }{V}_{\xi }l$ with multiplicities of 1, 1 and $t-2$, respectively. Moreover we have $q_{\xi ,1}^{*}\le l^{\prime }{V}_{\xi }l$.

Theorem 2. 

Under undirectional unguarded model, a pseudo symmetric measure ξ for estimating τ is optimal in the following cases. In each case, the $p_s$ in ξ is positive only if s reaches the maximum therein.

(1) ξ is A-optimal if and only if $det\left(V_{\xi ,1}\right)>0$, and

$$\underset{s\in \mathbb{S}}{max}\frac{r_{s,1}{Q}_{\xi ,1}/det\left(V_{\xi ,1}\right)+(t-2){\left(l^{\prime }{V}_{\xi }l\right)}^{-2}{l}^{\prime }{V}_{s}l}{Q_{\xi ,1}/det\left(V_{\xi ,1}\right)+(t-2){\left(l^{\prime }{V}_{\xi }l\right)}^{-1}}=1.$$

(2) ξ is D-optimal if and only if $det\left(V_{\xi ,1}\right)>0$, and

$$\underset{s\in \mathbb{S}}{max}\left(\frac{r_{s,1}}{t-1}+\frac{t-2}{t-1}\frac{l^{\prime }{V}_{s}l}{l^{\prime }{V}_{\xi }l}\right)=1.$$

(3) ξ is E-optimal if and only if $det\left(V_{\xi ,1}\right)>0$, and

$$\underset{s\in \mathbb{S}}{max}{r}_{s,1}=1.$$

(4) ξ is T-optimal if and only if $det\left(V_{\xi ,1}\right)>0$, and

$$\underset{s\in \mathbb{S}}{max}\frac{r_{s,1}det\left(V_{\xi ,1}\right)/det\left(Q_{\xi ,1}\right)+(t-2)l^{\prime }{V}_{s}l}{det\left(V_{\xi ,1}\right)/det\left(Q_{\xi ,1}\right)+(t-2)l^{\prime }{V}_{\xi }l}=1.$$

Here, $r_{s,1}=tr\left(V_{s,1}{V}_{\xi ,1}^{-1}\right)-Q_{s,1}{Q}_{\xi ,1}^{-1}.$

3.2. Optimal Design for Total Effects under Unguarded Model

In this subsection, we focus on optimal measures for estimating the total effects, defined by $\theta =(1+{\lambda }_1+{\lambda }_2)\tau$, under the unguarded model. For degenerated $1+{\lambda }_1+{\lambda }_2=0$ which indicates $\theta =0$, there is no need to carry out the experiment. In the rest of this section, we assume $1+{\lambda }_1+{\lambda }_2\ne 0$. The model for $\theta$ and the information matrix are

$$\begin{array}{ccc}& & Y_d=1_{nk}\mu +U\beta +{(1+{\lambda }_1+{\lambda }_2)}^{-1}(T_d+{\lambda }_1{L}_d+{\lambda }_2{R}_d)\theta +ϵ,\hfill \\ & & C_d\left(\theta \right)={(1+{\lambda }_1+{\lambda }_2)}^{-2}{M}_{1,{\lambda }_1,{\lambda }_2}^{\prime }p{r}^{\perp }(\tilde{U}|M_{-1,1+{\lambda }_2,-{\lambda }_2}\theta \left|M_{-1,-{\lambda }_1,1+{\lambda }_1}\theta \right)M_{1,{\lambda }_1,{\lambda }_2}.\hfill \end{array}$$

Similarly, the information matrix of a measure $\xi$ for $\theta$ is given by $C_{\xi }\left(\theta \right)=n^{-1}{C}_d\left(\theta \right)$ and the optimal measure can be found among symmetric measures. For convenience, we define $l_0={(-1,1+{\lambda }_2,-{\lambda }_2)}^{\prime }$, $l_2={(-1,-{\lambda }_1,1+{\lambda }_1)}^{\prime }$, $L_0=(l_0,l_2)$, $L_2=(l,L_0)$, $V_{\xi ,2}=L_2^{\prime }{V}_{\xi }{L}_2$, $Q_{\xi ,2}=L_0^{\prime }{V}_{\xi }{L}_0$, $q_{\xi ,2}^{*}=l^{\prime }{V}_{\xi }l-l^{\prime }{V}_{\xi }{L}_0{Q}_{\xi ,2}^{-}{L}_0^{\prime }{V}_{\xi }l$. Let $q_{\xi ,2}\left(x\right)=l^{\prime }{V}_{\xi }l+2l^{\prime }{V}_{\xi }{l}_{0}x+l_0^{\prime }{V}_{\xi }{l}_0{x}^2$, $x_{\xi ,2}=-l^{\prime }{V}_{\xi }{l}_0/l_0^{\prime }{V}_{\xi }{l}_0$, $q_{s,2}\left(x\right)=l^{\prime }{V}_{s}l+2l^{\prime }{V}_s{l}_{0}x+l_0^{\prime }{V}_s{l}_0{x}^2$, then $q_{\xi ,2}\left(x\right)={\sum }_s{q}_{s,2}\left(x\right)$ and $q_{\xi ,2}^{*}=q_{\xi ,2}\left(x_{\xi ,2}\right)$.

Proposition 3. 

Under the directional unguarded model, the information matrix $C_{\xi }\left(\theta \right)$ of a pseudo symmetric measure ξ has eigenvalues of ${(1+{\lambda }_1+{\lambda }_2)}^{-2}\frac{1}{t}{\sum }_{i=0}^2{\sum }_{j=0}^2{\lambda }_i{\lambda }_j\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)$, ${(1+{\lambda }_1+{\lambda }_2)}^{-2}{(t-1)}^{-1}{q}_{\xi ,2}^{*}$ and ${(1+{\lambda }_1+{\lambda }_2)}^{-2}{(t-1)}^{-1}{l}^{\prime }{V}_{\xi }l$ with multiplicities of 1, 1 and $t-2$, respectively. Moreover we have $q_{\xi ,2}^{*}\le l^{\prime }{V}_{\xi }l$.

Theorem 3. 

Under the directional unguarded model, a pseudo symmetric measure ξ for estimating θ is optimal in the following cases. In each case, the $p_s$ in ξ is positive only if s reaches the maximum therein.

(1) If $det\left(Q_{\xi ,2}\right)=0$, then ξ is A-optimal if and only if

$$\underset{s\in S}{max}\frac{q_{\xi ,2}{\left(x_{\xi ,2}\right)}^{-2}{q}_{s,2}\left(x_{\xi ,2}\right)+(t-2){\left(l^{\prime }{V}_{\xi }l\right)}^{-2}{l}^{\prime }{V}_{s}l}{q_{\xi ,2}{\left(x_{\xi ,2}\right)}^{-1}+(t-2){\left(l^{\prime }{V}_{\xi }l\right)}^{-1}}=1.$$

If $det\left(V_{\xi ,2}\right)>0$, then ξ is A-optimal if and only if

$$\underset{s\in S}{max}\frac{r_{s,2}det\left(Q_{\xi ,2}\right)/det\left(V_{\xi ,2}\right)+(t-2){\left(l^{\prime }{V}_{\xi }l\right)}^{-2}{l}^{\prime }{V}_{s}l}{det\left(Q_{\xi ,2}\right)/det\left(V_{\xi ,2}\right)+(t-2){\left(l^{\prime }{V}_{\xi }l\right)}^{-1}}=1.$$

(2) If $det\left(Q_{\xi ,2}\right)=0$, then ξ is D-optimal if and only if

$$\underset{s\in S}{max}\left(\frac{1}{t-1}\frac{q_{s,2}\left(x_{\xi ,2}\right)}{q_{\xi ,2}\left(x_{\xi ,2}\right)}+\frac{t-2}{t-1}\frac{l^{\prime }{V}_{s}l}{l^{\prime }{V}_{\xi }l}\right)=1.$$

If $det\left(V_{\xi ,2}\right)>0$, then ξ is D-optimal if and only if

$$\underset{s\in S}{max}\left(\frac{r_{s,2}}{t-1}+\frac{t-2}{t-1}\frac{l^{\prime }{V}_{s}l}{l^{\prime }{V}_{\xi }l}\right)=1.$$

(3) If $det\left(Q_{\xi ,2}\right)=0$, then ξ is E-optimal if and only if

$$\underset{s\in S}{max}\frac{q_{s,2}\left(x_{\xi ,2}\right)}{q_{\xi ,2}\left(x_{\xi ,2}\right)}=1.$$

If $det\left(V_{\xi ,2}\right)>0$, then ξ is E-optimal if and only if and

$$\underset{s\in S}{max}{r}_{s,2}=1.$$

(4) If $det\left(Q_{\xi ,2}\right)=0$, then ξ is T-optimal if and only if

$$\underset{s\in S}{max}\frac{q_{s,2}\left(x_{\xi ,2}\right)+(t-2)l^{\prime }{V}_{s}l}{q_{\xi ,2}\left(x_{\xi ,2}\right)+(t-2)l^{\prime }{V}_{\xi }l}=1.$$

If $det\left(V_{\xi ,2}\right)>0$, then ξ is T-optimal if and only if

$$\underset{s\in S}{max}\frac{r_{s,2}det\left(V_{\xi ,2}\right)/det\left(Q_{\xi ,2}\right)+(t-2)l^{\prime }{V}_{s}l}{det\left(V_{\xi ,2}\right)/det\left(Q_{\xi ,2}\right)+(t-2)l^{\prime }{V}_{\xi }l}=1.$$

Here, $r_{s,2}=tr\left(V_{s,2}{V}_{\xi ,2}^{-1}\right)-tr\left(Q_{s,2}{Q}_{\xi ,2}^{-1}\right)$.

Now we consider optimal design under undirectional model for total effects. The information matrix for $\theta$ becomes ${\tilde{C}}_d\left(\theta \right)={(1+2\lambda )}^{-2}{M}_{1,\lambda ,\lambda }^{\prime }p{r}^{\perp }\left(\tilde{U}\right|M_{2,-1,-1}\theta )M_{1,\lambda ,\lambda }$. The information matrix of a measure $\xi$ for $\theta$ is given by ${\tilde{C}}_{\xi }\left(\theta \right)=n^{-1}{\tilde{C}}_d\left(\theta \right)$. Define $l_3={(2,-1,-1)}^{\prime }$ and $L_3=(l,l_3)$. Let $V_{\xi ,3}=L_3^{\prime }{V}_{\xi }{L}_3$, $Q_{\xi ,3}=l_3^{\prime }{V}_{\xi }{l}_3$, $V_{s,3}=L_3^{\prime }{V}_s{L}_3$, $Q_{s,3}=l_3^{\prime }{V}_s{l}_3$, $q_{\xi ,3}^{*}=l^{\prime }{V}_{\xi }l-l^{\prime }{V}_{\xi }{l}_3{Q}_{\xi ,3}^{-}{l}_3^{\prime }{V}_{\xi }l$.

Proposition 4. 

Under the undirectional unguarded model, the information matrix ${\tilde{C}}_{\xi }\left(\theta \right)$ of a symmetric measure ξ has eigenvalues of ${(1+2\lambda )}^{-2}\frac{{\lambda }^2}{t}{\sum }_{i=1}^2{\sum }_{j=1}^2\left(1_t^{\prime }{C}_{\xi ij}{1}_t\right)$, ${(1+2\lambda )}^{-2}{(t-1)}^{-1}{q}_{\xi ,3}^{*}$ and ${(1+2\lambda )}^{-2}{(t-1)}^{-1}{l}^{\prime }{V}_{\xi }l$ with multiplicities of 1, 1 and $t-2$, respectively. Moreover we have $q_{\xi ,3}^{*}\le l^{\prime }{V}_{\xi }l$.

Theorem 4. 

Under undirectional unguarded model, a pseudo symmetric measure ξ for estimating θ is optimal in the following cases. In each case, the $p_s$ in ξ is positive only if s reaches the maximum therein.

(1) If $Q_{\xi ,3}=0$, then ξ is universally optimal if and only if

$$\underset{s\in S}{max}\frac{c_{s00}}{c_{\xi 00}}=1.$$

(2) If $det\left(V_{\xi ,3}\right)>0$, then ξ is A-optimal if and only if

$$\underset{s\in S}{max}\frac{r_{s,3}{Q}_{\xi ,3}/det\left(V_{\xi ,3}\right)+(t-2){\left(l^{\prime }{V}_{\xi }l\right)}^{-2}{l}^{\prime }{V}_{s}l}{Q_{\xi ,3}/det\left(V_{\xi ,3}\right)+(t-2){\left(l^{\prime }{V}_{\xi }l\right)}^{-1}}=1.$$

ξ is D-optimal if and only if

$$\underset{s\in S}{max}\left(\frac{r_{s,3}}{t-1}+\frac{t-2}{t-1}\frac{l^{\prime }{V}_{s}l}{l^{\prime }{V}_{\xi }l}\right)=1.$$

ξ is E-optimal if and only if

$$\underset{s\in S}{max}{r}_{s,3}=1.$$

ξ is T-optimal if and only if

$$\underset{s\in S}{max}\frac{r_{s,3}det\left(V_{\xi ,3}\right)/Q_{\xi ,3}+(t-2)l^{\prime }{V}_{s}l}{det\left(V_{\xi ,3}\right)/Q_{\xi ,3}+(t-2)l^{\prime }{V}_{\xi }l}=1.$$

Here $r_{s,3}=tr\left(V_{s,3}{V}_{\xi ,3}^{-1}\right)-Q_{s,3}{Q}_{\xi ,3}^{-1}.$

(3) Otherwise, ξ is not optimal.

4. Examples

Under models without guarding plots, for a sequence $s=(t_1,...,t_k)$, we define the equivalence class of s as $⟨s⟩=\{\sigma s:\sigma \in \mathbb{O}\}$. Suppose ${\mathbb{S}}_{k,t}$ is partitioned into m equivalence classes, say $⟨s_1⟩,...,⟨s_m⟩$, where $s_i$ is the representative sequence in its own class. For a measure $\xi =(p_s,s\in {\mathbb{S}}_{k,t})$, let $p_{⟨s_i⟩}={\sum }_{s\in ⟨s_i⟩}{p}_s$ and $P_{\xi }=(p_{⟨s_1⟩},...,p_{⟨s_m⟩})$. The same definitions can be similarly given under the model with guarding plots for $s=(t_0,...,t_{k+1})$. Two symmetric measures with the same $P_{\xi }$ share the same value of ${\Phi }_p\left(\xi \right)$. So, the task is simplified to finding the optimal $P_{\xi }$ which determines optimal designs.

Section 4.1 gives some examples of optimal designs for direct and total effects under model without border effects. Section 4.2 compares the optimal noncircular designs with circular designs for direct and total effects under model with border effects. We use the within-block covariance matrix to be of the form $\Sigma ={({\mathbb{I}}_{i=j}+\rho {\mathbb{I}}_{i-j=\pm 1\left(\mathrm{mod}k\right)})}_{1\le i,j\le k}$ with $\rho$ in $[-1,1]$ and let ${\lambda }_1$ and ${\lambda }_2$ be nonnegative values from $[0,1]$.

Here we provide the algorithm for deriving the optimal $P_{\xi }$ based on the theoretical results in Section 3. Suppose ${\mathbb{S}}_{k,t}$ is partitioned into m equivalence classes, say $⟨s_1⟩,...,⟨s_m⟩$, where $s_i$ is the representative sequence in its own equivalence class. We give Algorithm 1 to derive the vector $P_{\xi }$ for a symmetric measure to be E-optimal based on Theorem 1. Algorithms for other optimality criteria and noncircular designs could be dealt with similarly and so omitted to avoid redundant discussion.

Algorithm 1: For a measure $\xi$ and a sequence s, we define $\theta (P_{\xi },s)=tr\left(V_s{V}_{\xi }^{-1}\right)-tr\left(Q_s{Q}_{\xi }^{-1}\right)$, ${\theta }^{*}\left(P_{\xi }\right)={max}_{1\le i\le m}\theta (P_{\xi },s_i)$ and $e_i$ the vector of length m with ith entry as 1 and other entries 0.

Step 0.      Choose tuning parameters $ϵ>0$ and $\omega$ such that $ϵ$ is in a small neighborhood of 0 and $\omega$ is in a neighborhood of 1. Step 1.      Choose initial measure $P_0$. Put $i_0=argmi{n}_{1\le i\le m}{\theta }^{*}\left(e_i\right)$ and $n=0$, we have the initial measure $P_0=e_{i_0}$. Step 2.      If ${\theta }_n={\theta }^{*}\left(P_n\right)\ge 1+ϵ$, go to Step 3. Otherwise, we have the optimal measure $P_n$. Step 3.      Update the measure. Let $i_{n+1}=argmi{n}_{1\le i\le m}\theta (P_n,s_i)$ and the updated measure equals to $P_{n+1}={({\theta }_n-1)}^{\omega }{e}_{i_{n+1}}+(1-{({\theta }_n-1)}^{\omega })P_n$. Increase n by 1 and go to Step 2.

4.1. Optimal Unguarded Designs

This section gives some optimal designs for the model without guarding plots. The ${\Phi }_p$ value in (6) refers to the well known T-, D-, A-, E-criteria for four specific values of $p=-1,0,1,+\infty$, respectively, and are rewritten as ${\Phi }_p$

Case of $k=2$, $t=2$. The optimal measure for the direct and total effects is that with $p_{⟨12⟩}=1$. Note that when $t=2$, from the definition in (6), the A-, D-, E-, and T-criteria are the same, the optimality of a measure for direct or total effects does not depend on the values of ${\lambda }_1$ and ${\lambda }_2$ under models both with and without guarding plots.

Case of $k=3$. When $t=2$, the optimal measure for both direct and total effect is that with $p_{⟨112⟩}=p_{⟨122⟩}=0.5$ for any values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$. When $t=3$, the optimal measure for both direct and total effects is that with $p_{⟨123⟩}=1$ under the four criteria for any values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$.

Case of $k=4$.

When $t=2$, the optimal measure estimating direct effects is that with $p_{⟨1122⟩}=0.75$ and $p_{⟨1212⟩}=0.25$ for three values of $\rho$, the optimal measure for total effects is that with $p_{⟨1122⟩}=1$ for three values of $\rho$.

When $t=3$, the optimal measure for both direct and total effects is that with supporting symmetric blocks $⟨1123⟩$ and $⟨2311⟩$ for any values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$ under the four criteria. For example, when $\rho =0$, ${\lambda }_1=0.2$, ${\lambda }_2=0.3$, the optimal measure for direct effects is that with $p_{⟨1123⟩}=1$ and the optimal measure for total effects is that with $p_{⟨2311⟩}=1$ under four criteria.

When $t=4$, the supporting symmetric blocks are $⟨1122⟩$ and $⟨1123⟩$ for both direct and total effects. For example, when $\rho =0$, ${\lambda }_1=0.2$, ${\lambda }_2=0.3$, the optimal measure for direct effects is that with $p_{⟨1123⟩}=1$ under criteria A, E and T and is that with $p_{⟨1122⟩}=1$ under criterion D, the optimal measure for total effects is that with $p_{⟨1122⟩}=1$ under the four criteria.

Case of $k=5$.

When $t=2$, the optimal measure for direct effects is that with $p_{⟨11221⟩}=1$ or $p_{⟨12211⟩}=1$, and the optimal measure for total effects is that with $p_{⟨22111⟩}=1$ for any values of $\rho$.

When $t=3$, the optimal measure is different for different criterion and values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$. The supporting symmetric blocks are $⟨12123⟩$, $⟨12231⟩$, $⟨12213⟩$ for direct effect and $⟨12123⟩$, $⟨12231⟩$ for total effect. when $\rho =0$, ${\lambda }_1=0.2$, ${\lambda }_2=0.3$, for the direct effects, the optimal measure is that with $p_{⟨12231⟩}=1$ under criterion E, and $p_{⟨11223⟩}=1$ under criteria A, D and T. For the total effects, the optimal measure is that with $p_{⟨11222⟩}=1$ under criteria A and E, and $p_{⟨22211⟩}=1$ under criteria D and T. When $\rho =0.3$, ${\lambda }_1=0.2$, ${\lambda }_2=0.3$, for the direct effects, the optimal measure is that with $p_{⟨11223⟩}=1$ under four criteria. For the total effects, the optimal measure is that with $p_{⟨22211⟩}=1$ under criteria A and E, and $p_{⟨11223⟩}=1$ under criteria D and T.

When $t=4$, ${\lambda }_1=0.2$, ${\lambda }_2=0.3$. If $\rho =0$, for the direct effects, the optimal measure is that with $p_{⟨11234⟩}=1$ under four criteria. For the total effects, the optimal measure is that with $p_{⟨11234⟩}=1$ under criterion A and E, and $p_{⟨11223⟩}=1$ under criteria D and T. If $\rho =0.3$, for the direct effects, the optimal measure is that with $p_{⟨11234⟩}=1$ under four criteria. For the total effects, the optimal measure is that with $p_{⟨11234⟩}=p_{⟨23114⟩}=1/2$ under four criteria. If $\rho =-0.3$, the optimal measure for direct and total effects is that with $p_{⟨11234⟩}=1$ under four criteria.

When $t=5$, the supporting symmetric blocks for both direct and total effects are $⟨11234⟩$ and $⟨11223⟩$ for different criteria and values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$, and $⟨11234⟩$ dominates. For example, when ${\lambda }_1=0.2$, ${\lambda }_2=0.3$, $\rho =0$, for the direct effects, the optimal measure is that with $p_{⟨11234⟩}=1$ under criteria A and E, and $p_{⟨11234⟩}=0.9$, $p_{⟨11223⟩}=0.1$ under criteria D and T. For the total effects, the optimal measure is that with $p_{⟨11234⟩}=1$ under four criteria.

4.2. Optimal Noncircular Designs: In Comparison with Optimal Circular Designs

The circular designs are included in the noncircular designs since there is no restriction to the two guarding plots under noncircular setup. So, the optimal noncircular design is at least as powerful as the optimal circular design. In this section, we give examples to show that most optimal noncircular designs are strictly more efficient than optimal circular designs. However, as block size k increases, the extra benefit from using noncircular designs tends to vanish. This phenomenon has also been observed in some unreported comparisons under different k. Intuitively, As k increases, the two guarding plots play a less important role compared with these k plots and will affect the experiment less. To compare these two types of designs, we define the relative efficiency as ${\mathrm{RE}}_p={\Phi }_p\left({\xi }_2\right)/{\Phi }_p\left({\xi }_1\right)$, where ${\xi }_2$ is ${\Phi }_p$-optimal noncircular design and ${\xi }_1$ is ${\Phi }_p$-optimal circular design. In the rest of this section, we list some specific comparisons, which are concluded in Tables 2 and 3 for convenience.

Case of $k=2,3$. Both the direct and total effects are not estimable under the circular setup. See Lemma 1 in [27] for detailed proof. However, they are estimable under the noncircular setup. When $k=2$, $t=2$, the optimal noncircular measure for direct and total effects is that with $p_{⟨1122⟩}=1$ for any values of $\rho$. When $k=3$, $t=2$, the optimal noncircular measure for the direct effects is that with $p_{⟨22211⟩}=1$ for any values of $\rho$. For the total effects, when $\rho =-0.3$, the optimal noncircular measure is that with $p_{⟨21122⟩}=1$, when $\rho =0.3$, it is that with $p_{⟨11222⟩}=1$ and when $\rho =0$, it is that with $p_{⟨22211⟩}=1$.

Case of $k=4$.

When $t=2$, for the direct effects, the optimal circular measure is also optimal under noncircular setup. For the total effects, when $\rho =0$, the optimal circular measure is ${\xi }_1$ with $p_{⟨211221⟩}=2/3$ and $p_{⟨212121⟩}=1/3$. An exact circular design with three blocks is the $d_{\mathrm{CT}}$ in Figure 1. The optimal noncircular measure is ${\xi }_2$ with $p_{⟨111222⟩}=1$. An exact noncircular design with three blocks is the $d_{\mathrm{NCT}}$ in Figure 1.

When $\rho =0.3$, the optimal circular measure is ${\xi }_1$ with $p_{⟨211221⟩}=0.61$ and $p_{⟨212121⟩}=0.39$ and the optimal noncircular measure is ${\xi }_2$ with $p_{⟨112221⟩}=1$. When $\rho =-0.3$, the optimal circular measure is ${\xi }_1$ with $p_{⟨211221⟩}=0.76$ and $p_{⟨212121⟩}=0.24$ and The optimal noncircular measure is ${\xi }_2$ with $p_{⟨112221⟩}=4/5$ and $p_{⟨121221⟩}=1/5$.

The comparison between the two kinds of designs in estimating total effects with $k=4$ and $t=2$ is given in Table 1.

Table 1. Comparison of the ${\Phi }_p$ for optimal designs under circular and noncircular setups estimating total effects with $\rho =0,0.3,-0.3$ when $k=4$, $t=2$.

	$\mathit{\rho }=0$	$\mathit{\rho }=0.3$	$\mathit{\rho }=-0.3$
${\Phi }_p$ value for optimal circular design	0.2222	0.2485	0.2192
${\Phi }_p$ value for optimal noncircular design	1.0000	0.4167	0.2977
${\mathrm{RE}}_p$	4.5004	1.6769	1.3581

When $t=3$, for the direct effects, the optimal circular measure is ${\xi }_1$ with $p_{⟨311231⟩}=1$ under the four criteria given all the values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$. However, the optimal noncircular measures are different for different criteria and values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$. When $\rho =0$, ${\lambda }_1={\lambda }_2=0.1$, the optimal noncircular measure is ${\xi }_2$ with $p_{⟨122313⟩}=1$ under criteria A and E, and with $p_{⟨122133⟩}=1$ under criteria D and T. When $\rho =0.3$, ${\lambda }_1={\lambda }_2=0.1$, the optimal noncircular measure is ${\xi }_2$ with $p_{⟨112233⟩}=1$ under the four criteria. When $\rho =-0.3$, ${\lambda }_1={\lambda }_2=0.1$, the optimal noncircular measure is ${\xi }_2$ with $p_{⟨122313⟩}=1$ under the four criteria.

For the total effects, the optimal circular measures vary for different criteria and values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$. For all of them, supporting symmetric blocks are $⟨311231⟩$ and $⟨312131⟩$. However, it is different under noncircular setup. For example, when $\rho =0$, ${\lambda }_1={\lambda }_2=0.1$, the circular measure ${\xi }_1$ with $p_{⟨311231⟩}=2/3$ and $p_{⟨312131⟩}=1/3$ is E-optimal, while the optimal noncircular measure is ${\xi }_2$ with $p_{⟨122313⟩}=1$, ${\Phi }_{+\infty }\left({\xi }_1\right)=0.1389$, ${\Phi }_{+\infty }\left({\xi }_2\right)=0.3289$, the relative efficiency is ${\Phi }_{+\infty }\left({\xi }_2\right)/{\Phi }_{+\infty }\left({\xi }_1\right)=2.3679$.

When $t=4$, the optimal circular measure is ${\xi }_1$ with $p_{⟨412341⟩}=1$ for both direct and total effects under the four criteria, given all the values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$. While it is not true for the noncircular setup. For example, when $\rho =0.3$, ${\lambda }_1=0.2$, ${\lambda }_2=0.3$, the optimal noncircular measure for direct effects is ${\xi }_2$ with $p_{⟨112233⟩}=1$ under criterion T. For the direct effects, ${\Phi }_{-1}\left({\xi }_1\right)=0.3995$, ${\Phi }_{-1}\left({\xi }_2\right)=1.0452$, ${\Phi }_{-1}\left({\xi }_2\right)/{\Phi }_{-1}\left({\xi }_1\right)=2.6163$. When $\rho =-0.3$, ${\lambda }_1=0.2$, ${\lambda }_2=0.3$, the optimal noncircular measure for total effects is ${\xi }_2$ with $p_{⟨112233⟩}=0.6$ and $p_{⟨112234⟩}=0.4$ under criterion E. For the total effects, ${\Phi }_{+\infty }\left({\xi }_1\right)=0.0993$, ${\Phi }_{+\infty }\left({\xi }_2\right)=0.2040$, ${\Phi }_{+\infty }\left({\xi }_2\right)/{\Phi }_{+\infty }\left({\xi }_1\right)=2.0544$.

When $t=5$, the optimal circular measure is still ${\xi }_1$ with $p_{⟨412341⟩}=1$ for both direct and total effects under the four criteria, given all the values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$. While it is not true for the noncircular setup. For example, when $\rho =0.3$, ${\lambda }_1=0.2$, ${\lambda }_2=0.3$, the optimal noncircular measure for direct effects is ${\xi }_2$ with $p_{⟨112233⟩}=p_{⟨123455⟩}=1/2$ under criterion E. For the direct effects, ${\Phi }_{+\infty }\left({\xi }_1\right)=0.5196$, ${\Phi }_{+\infty }\left({\xi }_2\right)=0.8130$, ${\Phi }_{+\infty }\left({\xi }_2\right)/{\Phi }_{+\infty }\left({\xi }_1\right)=1.5647$. When $\rho =-0.3$, ${\lambda }_1=0.2$, ${\lambda }_2=0.3$, the optimal noncircular measure for total effects is ${\xi }_2$ with $p_{⟨123455⟩}=p_{⟨551234⟩}=1/2$ under criterion E. For the total effects, ${\Phi }_{+\infty }\left({\xi }_1\right)=0.0745$, ${\Phi }_{+\infty }\left({\xi }_2\right)=0.1828$, ${\Phi }_{+\infty }\left({\xi }_2\right)/{\Phi }_{+\infty }\left({\xi }_1\right)=2.4537$.

The comparison between the circular and noncircular designs with $k=4$ and $t=3,4,5$ are listed in Table 2 and Table 3 for the estimation of total and direct effects, respectively.

Table 2. Comparison of the ${\Phi }_p$ for optimal designs under circular and noncircular setups estimating total effects with different combinations of $(\rho ,{\lambda }_1,{\lambda }_2)$ when $k=4$.

t	$(\mathit{\rho },{\mathit{\lambda }}_1,{\mathit{\lambda }}_2)$	A	D	E	T
3	$(0,0.1,0.1)$	2.1511	1.6152	2.3679	1.2835
3	$(0.3,0.1,0.1)$	1.6474	1.3267	2.0121	1.1606
3	$(-0.3,0.1,0.1)$	2.1976	1.7487	2.5533	1.3113
4	$(0,0.2,0.3)$	1.4699	1.4211	1.6193	1.4001
4	$(0.3,0.2,0.3)$	1.2468	1.2433	1.3100	1.2768
4	$(-0.3,0.2,0.3)$	1.7360	1.5906	2.0544	1.4924
5	$(0,0.2,0.3)$	1.6108	1.4587	1.9916	1.3948
5	$(0.3,0.2,0.3)$	1.4187	1.3534	1.6081	1.3251
5	$(-0.3,0.2,0.3)$	1.7858	1.5970	2.4537	1.4853

Table 3. Comparison of the ${\Phi }_p$ for optimal designs under circular and noncircular setups estimating direct effects with different combinations of $(\rho ,{\lambda }_1,{\lambda }_2)$ when $k=4$.

t	$(\mathit{\rho },{\mathit{\lambda }}_1,{\mathit{\lambda }}_2)$	A	D	E	T
3	$(0,0.1,0.1)$	1.3048	1.1951	1.1579	1.1169
3	$(0.3,0.1,0.1)$	1.2965	1.2876	1.3778	1.2788
3	$(-0.3,0.1,0.1)$	1.0728	1.0716	1.1222	1.0704
4	$(0,0.2,0.3)$	1.2388	1.2498	1.1875	1.2660
4	$(0.3,0.2,0.3)$	2.5977	2.6053	2.5550	2.6163
4	$(-0.3,0.2,0.3)$	1.1702	1.1899	1.0483	1.2225
5	$(0,0.2,0.3)$	1.3534	1.3527	1.4376	1.3518
5	$(0.3,0.2,0.3)$	1.3642	1.3581	1.5647	1.3527
5	$(-0.3,0.2,0.3)$	1.3502	1.3516	1.3397	1.3534

Case of $k=5$.

When $t=2$, for the direct effects, the optimal circular measure is also optimal under noncircular setup. However, this is not the case for total effects. For example, when $\rho =0$, the optimal noncircular measure for total effects is ${\xi }_2$ with $p_{⟨1111222⟩}=p_{⟨2221111⟩}=1/2$, while the optimal circular measure is ${\xi }_1$ with $p_{⟨2111221⟩}=0.8$ and $p_{⟨2112121⟩}=0.2$, ${\Phi }_p\left({\xi }_1\right)=0.48$, ${\Phi }_p\left({\xi }_2\right)=1.4$, the relative efficiency is ${\Phi }_p\left({\xi }_2\right)/{\Phi }_p\left({\xi }_1\right)=2.9167$ for arbitrary p.

When $t=3$, the optimal circular measures for both direct and total effects are ${\xi }_1$ with supporting symmetric blocks $⟨3112231⟩$ and $⟨3121231⟩$ under four criteria for any values of ${\lambda }_1$, ${\lambda }_2$ and $\rho$. While the noncircular optimal measures are different. For example, when $\rho =0.3$, under criterion E, the optimal circular measure for direct effects is ${\xi }_1$ with $p_{⟨3112231⟩}=1$, while the optimal noncircular measure is ${\xi }_2$ with $p_{⟨1123321⟩}=1$ for any values of ${\lambda }_1$ and ${\lambda }_2$, ${\Phi }_{+\infty }\left({\xi }_1\right)=1.5714$, ${\Phi }_{+\infty }\left({\xi }_2\right)=1.6648$, ${\Phi }_{+\infty }\left({\xi }_2\right)/{\Phi }_{+\infty }\left({\xi }_1\right)=1.0594$.

When $t=4$, take criterion E for example. The optimal circular measure for direct effects is ${\xi }_1$ with $p_{⟨4112341⟩}=1$, the optimal noncircular measure is ${\xi }_2$ with $p_{⟨4112343⟩}=1$ for $\rho =0$ and any values of ${\lambda }_1$ and ${\lambda }_2$, ${\Phi }_{+\infty }\left({\xi }_1\right)=1.1515$, ${\Phi }_{+\infty }\left({\xi }_2\right)=1.1806$, the relative efficiency is ${\Phi }_{+\infty }\left({\xi }_2\right)/{\Phi }_{+\infty }\left({\xi }_1\right)=1.0253$.

When $t=5$, take criterion E for example. The optimal circular measure for direct effects is ${\xi }_1$ with $p_{⟨3112231⟩}=1$, the optimal noncircular measure is ${\xi }_2$ with $p_{⟨1123455⟩}=1$ for $\rho =0$ and any values of ${\lambda }_1$ and ${\lambda }_2$, ${\Phi }_{+\infty }\left({\xi }_1\right)=0.8636$, ${\Phi }_{+\infty }\left({\xi }_2\right)=1$, the relative efficiency is ${\Phi }_{+\infty }\left({\xi }_2\right)/{\Phi }_{+\infty }\left({\xi }_1\right)=1.1579$.

5. Conclusions

In this paper, we introduce the noncircular setup for proportional interference models with guarding plots. Meanwhile, equivalence theorems for addressing both unguarded and guarded optimal designs for proportional interference models are given. Both directional and undirectional models are included regarding direct and total effects. By removing circular assumptions on guarding plots, compared with the state-of-art results on circular optimal designs in [23], the efficiency of optimal designs is considerably improved using noncircular designs. Moreover, removing the circular assumption demands no extra cost and is reasonable in real-life applications.