Multi-Frequency Homotopy Analysis Method for Coupled Van der Pol-Duffing System with Time Delay

Abstract

This paper mainly studied the analytical solutions of three types of Van der Pol-Duffing equations. For a system with parametric excitation frequency, we knew that the ordinary homotopy analysis method would be unable to find the analytical solution. Thus, we primarily used the multi-frequency homotopy analysis method (MFHAM). First, the MFHAM was introduced, and the solution of the system was expressed by constructing auxiliary linear operators. Then, the method was applied to three specific systems. We compared the numerical solution obtained using the Runge–Kutta method with the analytical solution to verify the correctness of the latter. Periodic solutions, with and without time delay, were also compared under the same parameters. The results demonstrated that it was both effective and correct to use the MFHAM to find analytical solutions to Van der Pol-Duffing systems, which were classical systems. By comparison, the MFHAM proved to be effective for time delay systems.

1. Introduction

In recent years, time delay-coupled dynamical systems have become an increasingly important research object. The main reasons for this have been high-tech demands, such as precision machining, social demands, such as solving traffic jams, and scientific demands for the development of systems biology. These factors mean that time delays in the process of system coupling cannot be ignored. The dynamical behavior of differential systems with time delays has attracted the attention of researchers in many fields, such as mathematics, physics, mechanical engineering, and biology [1,2,3,4,5,6]. Hu et al. [7] emphasized singular perturbation methods. By comparing them with other methods, the authors concluded that this method could more easily calculate and accurately predict the local dynamics of systems with time delays near Hopf bifurcation. Sharma [8] studied parameter mismatch and time delay, showing that they affected the collective dynamics of nonlinear oscillation. In the context of ecology, they found that the predator–prey mechanism controlled global interactions, through appropriate time delays and parameter mismatches, to obtain constant populations. Jin et al. [9] presented an identification approach to time delays in linear systems. Ning [10] solved the problem of global adaptive control of nonlinear systems with time delay through the HOPA system method.

The Van der Pol-Duffing system has a long history of application in the physical and biological sciences [11,12,13]. For example, Fitzhugh [14] treated the equation as a model of neuronal action potentials. These equations were also used in seismology to model two plates in geological faults [15], in addition to applications in physics. In recent years, period-doubling solutions and quasi-periodic solutions of forced Van der Pol-Duffing oscillators have also received extensive attention and research. Cui et al. [16] combined the homotopy analysis method (HAM) with the multi-scale analysis method to study the analytical solution of the forced Van der Pol-Duffing oscillators.

The HAM was proposed by Liao [17,18] in 1992. Cui et al. [19] studied its stability in the Van der Pol–Duffing forced oscillator and periodic solutions. Shahram et al. [20] used the HAM to study the fourth order nonlinear free vibration of Timoshenko beams. Shukla et al. [21] proposed an improved HAM to solve quasi-periodic solutions and limit cycles in a forced Van der Pol-Duffing oscillator. Fu et al. [22] obtained a periodic solution for a coupled Duffing system using the MFHAM.

In Section 1, we introduced the systems and methods studied in this paper. In Section 2, we described the process of the MFHAM, which was used to calculate a two-degree-of-freedom coupled Duffing system. In Section 3, Section 4 and Section 5, we offered three specific examples. In Section 6, we provided our summary.

2. Multi-Frequency Homotopy Analysis Method

First, we considered the following two-degree-of-freedom Duffing system:

$$\begin{array}{c}{x}_1^{″}+c{x}_1^{\prime }+F_1\left(x_1,x_2\right)=f_{1}cos\Omega t\\ x_2^{″}+c{x}_2^{\prime }+F_2\left(x_1,x_2\right)=f_{2}cos\Omega t\end{array},$$

(1)

where $x_1\left(t\right),x_2\left(t\right)$ are unknow real functions, $F_1\left(x_1,x_2\right),F_2\left(x_1,x_2\right)$ are coupling functions, $f_1,f_2$ are the amplitudes of excitation, $\Omega$ is the frequency of the parametric excitation, and $c$ is a known physical parameter.

Based on the MFHAM, we constructed the following n-order auxiliary linear differential operator

$$\begin{array}{c}{L}_n\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{c}{x}_1^{\left(2n\right)}\\ x_2^{\left(2n\right)}\end{array}\right)+\sum _{i=1}^n{\Omega }_i^2\left(\begin{array}{c}{x}_1^{(2n-2)}\\ x_2^{(2n-2)}\end{array}\right)+\sum _{i\ne j}^n{\Omega }_i^2{\Omega }_j^2\left(\begin{array}{c}{x}_1^{(2n-4)}\\ x_2^{(2n-4)}\end{array}\right)\\ +\sum _{i\ne j\ne r}^n{\Omega }_i^2{\Omega }_j^2{\Omega }_r^2\left(\begin{array}{c}{x}_1^{(2n-6)}\\ x_2^{(2n-6)}\end{array}\right)+\dots +\prod _{i=1}^n{\Omega }_i^2\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)\end{array},$$

(2)

where ${\Omega }_i(i=\mathrm{1,2},...,n)$ are the fundamental frequencies.

The characteristic polynomial of Equation (2) is

$$P\left(\lambda \right)=\prod _{r=1}^n\left(\lambda +r\Omega i\right)\left(\lambda -r\Omega i\right).$$

(3)

The root of the characteristic polynomial in Equation (3) is the frequency under consideration multiplied by the imaginary unit $i$, so it was necessary to eliminate the long-term term formed by any sinusoidal term of the frequency under consideration on the right side of the differential operator $L_n\left(x\right)$.

When the solution of the equation contains a constant term, Equation (2) can be written as follows.

$$\begin{array}{c}{L}_{n+1}\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{c}{x}_1^{(2n+1)}\\ x_2^{(2n+1)}\end{array}\right)+\sum _{i=1}^n{\Omega }_i^2\left(\begin{array}{c}{x}_1^{(2n-1)}\\ x_2^{(2n-1)}\end{array}\right)+\sum _{i\ne j}^n{\Omega }_i^2{\Omega }_j^2\left(\begin{array}{c}{x}_1^{(2n-3)}\\ x_2^{(2n-3)}\end{array}\right)\\ +\sum _{i\ne j\ne r}^n{\Omega }_i^2{\Omega }_j^2{\Omega }_r^2\left(\begin{array}{c}{x}_1^{(2n-5)}\\ x_2^{(2n-5)}\end{array}\right)+\dots +\prod _{i=1}^n{\Omega }_i^2\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)\end{array}.$$

(4)

We constructed the following homotopy expression

$$(1-q)L_{n+1}\left(\begin{array}{c}{x}_1-g_{\mathrm{1,0}}\left(t\right)\\ x_2-g_{\mathrm{2,0}}\left(t\right)\end{array}\right)-q\hslash N\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=0,$$

(5)

where $q\in \left[\mathrm{0,1}\right]$ is the embedding variable,$g_{i,0}\left(t\right)\left(i=\mathrm{1,2}\right)$ are the intial solutions of $x_i\left(t\right)\left(i=\mathrm{1,2}\right)$ respectively, and $\hslash$ is the auxiliary parameter.

Assuming that the power series solution of Equation (1) is

$$x_i=x_{i,0}+q{x}_{i,1}+q^2{x}_{i,2}+\cdots \left(i=\mathrm{1,2}\right).$$

(6)

Substituting Equation (6) into Equation (5), and then merging the same term of $q$, we were able to obtain

$$q^0:L_{n+1}\left(\begin{array}{c}{x}_{\mathrm{1,0}}-g_{\mathrm{1,0}}\left(t\right)\\ x_{\mathrm{2,0}}-g_{\mathrm{2,0}}\left(t\right)\end{array}\right)=0,$$

(7)

$$q^1:L_{n+1}\left(\begin{array}{c}{x}_{\mathrm{1,1}}-g_{\mathrm{1,0}}\left(t\right)\\ x_{\mathrm{2,1}}-g_{\mathrm{2,0}}\left(t\right)\end{array}\right)=L_{n+1}\left(\begin{array}{c}{x}_{\mathrm{1,0}}-g_{\mathrm{1,0}}\left(t\right)\\ x_{\mathrm{2,0}}-g_{\mathrm{2,0}}\left(t\right)\end{array}\right)+\hslash N\left(\begin{array}{c}{x}_{\mathrm{1,0}}\\ x_{\mathrm{2,0}}\end{array}\right),$$

(8)

$$q^2:L_{n+1}\left(\begin{array}{c}{x}_{\mathrm{1,2}}-g_{\mathrm{1,0}}\left(t\right)\\ x_{\mathrm{2,2}}-g_{\mathrm{2,0}}\left(t\right)\end{array}\right)=L_{n+1}\left(\begin{array}{c}{x}_{\mathrm{1,1}}-g_{\mathrm{1,0}}\left(t\right)\\ x_{\mathrm{2,1}}-g_{\mathrm{2,0}}\left(t\right)\end{array}\right)+{\left.\hslash \frac{\partial N\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)}{\partial q}\right|}_{q=0}.$$

(9)

Let the solution to Equation (7) be

$$x_{i,0}(t)=g_{i,0}(t)+A_0+\sum _{l=1}{A}_{l}sin\left({\Omega }_{l}t+{\varphi }_l\right),$$

(10)

where $A_0,A_l,{\varphi }_l(l=\mathrm{1,2},...,n)$ are constants.

First, substituting Equations (7) and (10) into Equation (8), and eliminating the secular terms, we obtained $L_{n+1}\left(\genfrac{}{}{0pt}{}{x_1}{x_2}\right)$. Second, substituting $L_{n+1}\left(\genfrac{}{}{0pt}{}{x_1}{x_2}\right)$ into Equation (2) or Equation (4), $x_i\left(t\right)(i=\mathrm{1,2})$ was obtained. Finally, we obtained the value of $A_0,A_l,{\varphi }_l(l=\mathrm{1,2},...,n)$ by solving the equations consisting of secular terms.

In a similar way, $x_{i,r}\left(t\right)(i=\mathrm{1,2})$ can be determined one by one. The solution of Equation (5) was

$$x_i(t)=\underset{q\to 1}{lim}{x}_i(t,q)=x_{i,0}(t)+x_{i,1}(t)+x_{i,2}(t)+\dots .$$

(11)

3. Analyzing the Coupling Van der Pol-Duffing System with MFHAM

We considered the following system by the MFHAM

$$\begin{array}{c}{\ddot{x}}_1\left(t\right)-\mu \left(1-{x_1}^2\left(t\right)\right){\dot{x}}_1\left(t\right)+\alpha x_2\left(t\right)+\beta {x_1}^3\left(t\right)=fcos\left(\Omega t\right)\\ {\ddot{x}}_2\left(t\right)-\mu \left(1-{x_2}^2\left(t\right)\right){\dot{x}}_2\left(t\right)+\alpha x_1\left(t\right)+\beta {x_2}^3\left(t\right)=fcos\left(\Omega t\right)\end{array},$$

(12)

where the prime denotes the differential with respect to the time $t$, $x_1\left(t\right),x_2\left(t\right)$ are unknow real functions, $\Omega$ is the frequency of the parametric excitation, and $\mu >0,$ $f$ is the amplitudes of excitation.

For the single period, the characteristic polynomial is

$$p(\lambda )=\lambda {\prod }_{r=1}^3(\lambda +r\Omega i)(\lambda -r\Omega i).$$

(13)

The corresponding auxiliary linear differential operator is

$$L_4\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{c}{x}_1^{\left(7\right)}\\ x_2^{\left(7\right)}\end{array}\right)+14{\Omega }^2\left(\begin{array}{c}{x}_1^{\left(5\right)}\\ x_2^{\left(5\right)}\end{array}\right)+49{\Omega }^4\left(\begin{array}{c}{x}_1^{\left(3\right)}\\ x_2^{\left(3\right)}\end{array}\right)+36{\Omega }^6\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right).$$

(14)

Then, we constructed the homotopy expression

$$\begin{array}{c}\Gamma \left(\begin{array}{cc}{x}_1& q\\ x_2& q\end{array}\right)=L_4\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-q{L}_4\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)\\ -q\hslash \left(\begin{array}{c}{\ddot{x}}_1\left(t\right)-\mu \left(1-{x_1}^2\left(t\right)\right){\dot{x}}_1\left(t\right)+\alpha x_2\left(t\right)+\beta {x_1}^3\left(t\right)-fcos\Omega t\\ {\ddot{x}}_2\left(t\right)-\mu \left(1-{x_2}^2\left(t\right)\right){\dot{x}}_2\left(t\right)+\alpha x_1\left(t\right)+\beta {x_2}^3\left(t\right)-fcos\Omega t\end{array}\right)\end{array},$$

(15)

where $\hslash$ is the auxiliary parameter, and $q\in \left[\mathrm{0,1}\right]$ is the embedding variable.

Supposing the solution to Equation (12) was

$$x_i=x_{i,0}+q{x}_{i,1}+q^2{x}_{i,2}+\cdots (i=\mathrm{1,2}),$$

(16)

then, substituting Equation (16) into Equation (15) and merging the same power terms of $q$, we obtained

$$\begin{array}{c}{q}^0:L_4\left(\begin{array}{c}{x}_{\mathrm{1,0}}\\ x_{\mathrm{2,0}}\end{array}\right)=0\end{array},$$

(17)

$$\begin{array}{c}{q}^1:L_4\left(\begin{array}{c}{x}_{\mathrm{1,1}}\\ x_{\mathrm{2,1}}\end{array}\right)=L_4\left(\begin{array}{c}{x}_{\mathrm{1,0}}\\ x_{\mathrm{2,0}}\end{array}\right)+\hslash \left(\begin{array}{c}{\ddot{x}}_{\mathrm{1,0}}-\mu \left(1-{x_{\mathrm{1,0}}}^2\right){\dot{x}}_{\mathrm{1,0}}+\alpha x_{\mathrm{2,0}}+\beta {x_{\mathrm{1,0}}}^3-f\mathit{cos}\Omega t\\ {\ddot{x}}_{\mathrm{2,0}}-\mu \left(1-{x_{\mathrm{2,0}}}^2\right){\dot{x}}_{\mathrm{2,0}}+\alpha x_{\mathrm{1,0}}+\beta {x_{\mathrm{2,0}}}^3-f\mathit{cos}\Omega t\end{array}\right)\end{array}.$$

(18)

Assuming that the solution Equation (17) could be expressed by

$$\begin{array}{c}{x}_{\mathrm{1,0}}=a_1+b_{1}cos\left(\Omega t+{\varphi }_1\right)+b_{2}cos\left(2\Omega t+{\varphi }_2\right)+b_{3}cos\left(3\Omega t+{\varphi }_3\right)\\ x_{\mathrm{2,0}}=a_2+d_{1}cos\left(\Omega t+{\gamma }_1\right)+d_{2}cos\left(2\Omega t+{\gamma }_2\right)+d_{3}cos\left(3\Omega t+{\gamma }_3\right)\end{array},$$

(19)

where $a_1,a_2,b_i,d_i,{\varphi }_i,{\gamma }_i(i=\mathrm{1,2},3)$ are unknown parameters.

Substituting Equations (17) and (19) into Equation (18), we obtained the following equations:

$$\begin{array}{c}{L}_4\left(x_{\mathrm{1,1}}\right)=\{-fCos[t\Omega ]+\alpha \left(a_2+d_{1}Cos\left[t\Omega +{\gamma }_1\right]+d_{2}Cos\left[2t\Omega +{\gamma }_2\right]+d_{3}Cos\left[3t\Omega +{\gamma }_3\right]\right)\\ -{b_1\Omega }^{2}Cos\left[t\Omega +{\varphi }_1\right]-4{b_2\Omega }^{2}Cos\left[2t\Omega +{\varphi }_2\right]-9{b_3\Omega }^{2}Cos\left[3t\Omega +{\varphi }_3\right]+\\ \beta {\left(a_1+b_{1}Cos\left[t\Omega +{\varphi }_1\right]+b_{2}Cos\left[2t\Omega +{\varphi }_2\right]+b3Cos\left[3t\Omega +{\varphi }_3\right]\right)}^3-\\ \mu \left(1-{\left(a1+b_{1}Cos\left[t\Omega +{\varphi }_1\right]+b_{2}Cos\left[2t\Omega +{\varphi }_2\right]+b_{3}Cos\left[3t\Omega +{\varphi }_3\right]\right)}^2\right)\\ \left(-b_1\Omega Sin\left[t\Omega +{\varphi }_1\right]-2b_2\Omega Sin\left[2t\Omega +{\varphi }_2\right]-3b_3\Omega Sin\left[3t\Omega +{\varphi }_3\right]\right)\}\hslash \end{array},$$

(20)

$$\begin{array}{c}{L}_4\left(x_{\mathrm{2,1}}\right)=\{-fCos[t\Omega ]+\beta {\left(a_2+d_{1}Cos\left[t\Omega +{\gamma }_1\right]+d_{2}Cos\left[2t\Omega +{\gamma }_2\right]+d_{3}Cos\left[3t\Omega +{\gamma }_3\right]\right)}^3\\ {-\Omega }^2\left(d_{1}Cos\left[t\Omega +{\gamma }_1\right]+4d_{2}Cos\left[2t\Omega +{\gamma }_2\right]+9d_{3}Cos\left[3t\Omega +{\gamma }_3\right]\right)+\\ \alpha \left(a_1+b_{1}Cos\left[t\Omega +{\varphi }_1\right]+b_{2}Cos\left[2t\Omega +{\varphi }_2\right]+b_{3}Cos\left[3t\Omega +{\varphi }_3\right]\right)-\\ \mu \left(1-{\left(a_2+d_{1}Cos\left[t\Omega +{\gamma }_1\right]+d_{2}Cos\left[2t\Omega +{\gamma }_2\right]+d_{3}Cos\left[3t\Omega +{\gamma }_3\right]\right)}^2\right)\\ \left(-d_1\Omega Sin\left[t\Omega +{\gamma }_1\right]-2d_2\Omega Sin\left[2t\Omega +{\gamma }_2\right]-3d_3\Omega Sin\left[3t\Omega +{\gamma }_3\right]\right)\}\hslash \end{array}.$$

(21)

To eliminate the secular terms in $x_{i,1}\left(t\right)(i=\mathrm{1,2})$, we expanded the Equations (20) and (21), obtaining the equations as follows:

$$\begin{array}{c}-b_1\mu \Omega +{a_1}^2{b}_1\mu \Omega +\frac{1}{4}{b_1}^3\mu \Omega +\frac{1}{2}{b}_1{b_2}^2\mu \Omega +\frac{1}{2}{b}_1{b_3}^2\mu \Omega +a_1{b}_1{b}_2\mu \Omega Cos[2{\varphi }_1-{\varphi }_2]+\\ b_3\Omega \left(\frac{1}{4}\right.\left.{b_1}^2\mu Cos[3{\varphi }_1-{\varphi }_3]+a_1{b}_2\mu Cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]+\frac{1}{4}{b_2}^2\mu Cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]\right)+\\ d_1\alpha Sin[{\gamma }_1-{\varphi }_1]+fSin\left[{\varphi }_1\right]-3a_1{b}_1{b}_2\beta Sin[2{\varphi }_1-{\varphi }_2]-\frac{3}{4}{b_1}^2{b}_3\beta Sin[3{\varphi }_1-{\varphi }_3]-\\ 3a_1{b}_2{b}_3\beta Sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]-\frac{3}{4}{b_2}^2{b}_3\beta Sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]=0\end{array},$$

(22)

$$\begin{array}{c}-2b_2\mu \Omega +2{a_1}^2{b}_2\mu \Omega +{b_1}^2{b}_2\mu \Omega +\frac{1}{2}{b_2}^3\mu \Omega +b_2{b_3}^2\mu \Omega +a_1{b_1}^2\mu \Omega Cos[2{\varphi }_1-{\varphi }_2]+\\ 2a_1{b}_1{b}_3\mu \Omega Cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]+b_1{b}_2{b}_3\mu \Omega Cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]+d_2\alpha Sin[{\gamma }_2-{\varphi }_2]+\\ b_1\beta \left(\frac{3}{2}{a}_1{b}_{1}Sin[2{\varphi }_1-{\varphi }_2]-3a_1{b}_{3}Sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]+\frac{3}{2}{b}_2{b}_{3}Sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]\right)=0\end{array},$$

(23)

$$\begin{array}{c}-3b_3\mu \Omega +3{a_1}^{2}b3\mu \Omega +\frac{3}{2}{b_1}^2{b}_3\mu \Omega +\frac{3}{2}{b_2}^2{b}_3\mu \Omega +\frac{3}{4}{b_3}^3\mu \Omega +\frac{1}{4}{b_1}^3\mu \Omega Cos[3{\varphi }_1-{\varphi }_3]+\\ 3a_1{b}_1{b}_2\mu \Omega Cos[{\varphi }_1+\varphi 2-{\varphi }_3]+\frac{3}{4}{b}_1{b_2}^2\mu \Omega Cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]+d_3\alpha Sin[{\gamma }_3-{\varphi }_3]+\\ \frac{1}{4}{b_1}^3\beta Sin[3{\varphi }_1-{\varphi }_3]+3a_1{b}_1{b}_2\beta Sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]-\frac{3}{4}{b}_1{b_2}^2\beta Sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]=0\end{array},$$

(24)

$$\begin{array}{c}-3{a_1}^2{b}_1\beta -\frac{3b{1}^3\beta }{4}-\frac{3}{2}b1{b_2}^2\beta -\frac{3}{2}{b}_1{b_3}^2\beta +b_1{\Omega }^2-d_1\alpha Cos[{\gamma }_1-{\varphi }_1]+fCos\left[{\varphi }_1\right]-\\ 3a_1{b}_1{b}_2\beta Cos[2{\varphi }_1-{\varphi }_2]-\frac{3}{4}{b_1}^2{b}_3\beta Cos[3{\varphi }_1-{\varphi }_3]-3a_1{b}_2{b}_3\beta Cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]-\\ \frac{3}{4}{b_2}^2{b}_3\beta Cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]-a_1{b}_1{b}_2\mu \Omega Sin[2{\varphi }_1-{\varphi }_2]-\frac{1}{4}{b_1}^2{b}_3\mu \Omega Sin[3{\varphi }_1-{\varphi }_3]-\\ a_1{b}_2{b}_3\mu \Omega Sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]-\frac{1}{4}{b_2}^2{b}_3\mu \Omega Sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]=0\end{array},$$

(25)

$$\begin{array}{c}-3{a_1}^2{b}_2\beta -\frac{3}{2}{b_1}^2{b}_2\beta -\frac{3b{2}^3\beta }{4}-\frac{3}{2}{b}_{2}b{3}^2\beta +4b_2{\Omega }^2-d_2\alpha Cos[{\gamma }_2-{\varphi }_2]-\\ \frac{3}{2}{a}_1{b_1}^2\beta Cos[2{\varphi }_1-{\varphi }_2]-3a_1{b}_1{b}_3\beta Cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]-\frac{3}{2}{b}_1{b}_2{b}_3\beta Cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]+\\ \mu \Omega \left(a_1{b_1}^{2}Sin[2{\varphi }_1-{\varphi }_2]-2a_1{b}_1{b}_{3}Sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]+b_1{b}_2{b}_{3}Sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]\right)=0\end{array},$$

(26)

$$\begin{array}{c}-3{a_1}^2{b}_3\beta -\frac{3}{2}{b_1}^2{b}_3\beta -\frac{3}{2}{b_2}^2{b}_3\beta -\frac{3b{3}^3\beta }{4}+9b_3{\Omega }^2-d_3\alpha Cos[{\gamma }_3-{\varphi }_3]-\\ \frac{1}{4}{b_1}^3\beta Cos[3{\varphi }_1-{\varphi }_3]-3a_1{b}_1{b}_2\beta Cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]-\frac{3}{4}{b}_1{b_2}^2\beta Cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]+\\ \mu \Omega \left(\frac{1}{4}{b_1}^{3}S\mathrm{in}[3{\varphi }_1-{\varphi }_3]+3a_1{b}_1{b}_{2}Sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]-\frac{3}{4}{b}_1{b_2}^{2}Sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]\right)=0\end{array},$$

(27)

$$\begin{array}{c}-d_1\mu \Omega +{a_2}^{2}d1\mu \Omega +\frac{1}{4}{d_1}^3\mu \Omega +\frac{1}{2}{d}_1{d_2}^2\mu \Omega +\frac{1}{2}d1{d_3}^2\mu \Omega +a_2{d}_1{d}_2\mu \Omega Cos[2{\gamma }_1-{\gamma }_2]+\\ \frac{1}{4}{d_1}^2{d}_3\mu \Omega Cos[3{\gamma }_1-{\gamma }_3]+a2d_2{d}_3\mu \Omega Cos[{\gamma }_1+{\gamma }_2-{\gamma }_3]+\frac{1}{4}{d_2}^2{d}_3\mu \Omega Cos[{\gamma }_1-2{\gamma }_2+{\gamma }_3]+\\ \mathrm{f}\mathrm{S}\mathrm{i}\mathrm{n}\left[{\gamma }_1\right]-3a_2{d}_1{d}_2\beta Sin[2{\gamma }_1-{\gamma }_2]-\frac{3}{4}{d_1}^2{d}_3\beta Sin[3{\gamma }_1-{\gamma }_3]-\\ 3a_2{d}_2{d}_3\beta Sin[{\gamma }_1+{\gamma }_2-{\gamma }_3]-\frac{3}{4}{d_2}^2{d}_3\beta Sin[{\gamma }_1-2{\gamma }_2+{\gamma }_3]-b_1\alpha Sin[{\gamma }_1-{\varphi }_1]=0\end{array},$$

(28)

$$\begin{array}{c}-2d_2\mu \Omega +2a^2{d}_2\mu \Omega +d{1}^{2}d2\mu \Omega +\frac{1}{2}{d_2}^3\mu \Omega +d2d{3}^2\mu \Omega +a2{d_1}^2\mu \Omega Cos[2{\gamma }_1-{\gamma }_2]+\\ 2a_2{d}_1{d}_3\mu \Omega Cos[{\gamma }_1+{\gamma }_2-{\gamma }_3]+d_1{d}_2{d}_3\mu \Omega Cos[{\gamma }_1-2{\gamma }_2+{\gamma }_3]+\frac{3}{2}a2{d_1}^2\beta Sin[2{\gamma }_1-{\gamma }_2]-\\ 3a_2{d}_1{d}_3\beta Sin[{\gamma }_1+{\gamma }_2-{\gamma }_3]+\frac{3}{2}{d}_1{d}_2{d}_3\beta Sin[{\gamma }_1-2{\gamma }_2+{\gamma }_3]-b_2\alpha Sin[{\gamma }_2-{\varphi }_2]=0\end{array},$$

(29)

$$\begin{array}{c}-3d_3\mu \Omega +3{a_2}^2{d}_3\mu \Omega +\frac{3}{2}d{1}^2{d}_3\mu \Omega +\frac{3}{2}d{2}^2{d}_3\mu \Omega +\frac{3}{4}{d_3}^3\mu \Omega +\frac{1}{4}d{1}^3\mu \Omega Cos[3{\gamma }_1-{\gamma }_3]+\\ 3a_2{d}_1{d}_2\mu \Omega Cos[{\gamma }_1+{\gamma }_2-{\gamma }_3]+\frac{3}{4}{d}_1{d_2}^2\mu \Omega Cos[{\gamma }_1-2{\gamma }_2+{\gamma }_3]+\frac{1}{4}{d_1}^3\beta Sin[3{\gamma }_1-{\gamma }_3]+\\ 3a_2{d}_1{d}_2\beta Sin[{\gamma }_1+{\gamma }_2-{\gamma }_3]-\frac{3}{4}{d}_1{d_2}^2\beta Sin[{\gamma }_1-2{\gamma }_2+{\gamma }_3]-b_3\alpha Sin[{\gamma }_3-{\varphi }_3]=0\end{array},$$

(30)

$$\begin{array}{c}-\frac{3d{1}^3\beta }{4}-\frac{3}{2}{d}_1{d_2}^2\beta -\frac{3}{2}{d}_1{d_3}^2\beta +d_1{\Omega }^2+fCos\left[{\gamma }_1\right]-3a_2{d}_1{d}_2\beta Cos[2{\gamma }_1-{\gamma }_2]-\\ \frac{3}{4}{d_1}^2{d}_3\beta Cos[3{\gamma }_1-{\gamma }_3]-3a2d_2{d}_3\beta Cos[{\gamma }_1+{\gamma }_2-{\gamma }_3]-\frac{3}{4}{d_2}^2{d}_3\beta Cos[{\gamma }_1-2{\gamma }_2+{\gamma }_3]\\ -b_1\alpha Cos[{\gamma }_1-{\varphi }_1]-a_2{d}_1{d}_2\mu \Omega Sin[2{\gamma }_1-{\gamma }_2]-\frac{1}{4}{d_1}^2{d}_3\mu \Omega Sin[3{\gamma }_1-{\gamma }_3]-\\ a_2{d}_2{d}_3\mu \Omega Sin[{\gamma }_1+{\gamma }_2-{\gamma }_3]-3{a_2}^2{d}_1\beta -\frac{1}{4}{d_2}^2{d}_3\mu \Omega Sin[{\gamma }_1-2{\gamma }_2+{\gamma }_3]=0\end{array},$$

(31)

$$\begin{array}{c}-3{a_2}^2{d}_2\beta -\frac{3}{2}{d_1}^2{d}_2\beta -\frac{3d{2}^3\beta }{4}-\frac{3}{2}{d}_2{d_3}^2\beta +4d_2{\Omega }^2-\frac{3}{2}{a}_2{d_1}^2\beta Cos[2{\gamma }_1-{\gamma }_2]-\\ 3a_2{d}_1{d}_3\beta Cos\left[{\gamma }_1+{\gamma }_2-{\gamma }_3\right]-\frac{3}{2}{d}_1{d}_2{d}_3\beta Cos[{\gamma }_1-2{\gamma }_2+{\gamma }_3]-b_2\alpha Cos[{\gamma }_2-{\varphi }_2]+\\ a_2{d_1}^2\mu \Omega Sin[2{\gamma }_1-{\gamma }_2]-2a_2{d}_1{d}_3\mu \Omega Sin[{\gamma }_1+{\gamma }_2-{\gamma }_3]+d_1{d}_2{d}_3\mu \Omega Sin[{\gamma }_1-2{\gamma }_2+{\gamma }_3]=0\end{array},$$

(32)

$$\begin{array}{c}-3{a_2}^2{d}_3\beta -\frac{3}{2}{d_1}^2{d}_3\beta -\frac{3}{2}{d_2}^2{d}_3\beta -\frac{3d{3}^3\beta }{4}+9d_3{\Omega }^2-\frac{1}{4}{d_1}^3\beta Cos[3{\gamma }_1-{\gamma }_3]-\\ 3a_2{d}_1{d}_2\beta Cos[{\gamma }_1+{\gamma }_2-{\gamma }_3]-\frac{3}{4}{d}_1{d_2}^2\beta Cos[{\gamma }_1-2{\gamma }_2+{\gamma }_3]-b_3\alpha Cos[{\gamma }_3-{\varphi }_3]+\\ \frac{1}{4}{d_1}^3\mu \Omega Sin[3{\gamma }_1-{\gamma }_3]+3a_2{d}_1{d}_2\mu \Omega Sin[{\gamma }_1+{\gamma }_2-{\gamma }_3]-\frac{3}{4}{d}_1{d_2}^2\mu \Omega Sin[{\gamma }_1-2{\gamma }_2+{\gamma }_3]=0\end{array},$$

(33)

$$\begin{array}{c}-a_1\alpha -{a_2}^3\beta -\frac{3}{2}{a}_2{d_1}^2\beta -\frac{3}{2}{a}_2{d_2}^2\beta -\frac{3}{2}{a}_2{d_3}^2\beta -\frac{3}{4}{d_1}^2{d}_2\beta Cos[2{\gamma }_1-{\gamma }_2]-\\ \frac{3}{2}{d}_1{d}_2{d}_3\beta Cos[{\gamma }_1+{\gamma }_2-{\gamma }_3]=0\end{array},$$

(34)

$$\begin{array}{c}-a_2\alpha -{a_1}^3\beta -\frac{3}{2}{a}_1{b_1}^2\beta -\frac{3}{2}{a}_1{b_2}^2\beta -\frac{3}{2}{a}_1{b_3}^2\beta -\frac{3}{4}{b_1}^2{b}_2\beta Cos[2{\varphi }_1-{\varphi }_2]-\\ \frac{3}{2}{b}_1{b}_2{b}_3\beta Cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]=0\end{array}.$$

(35)

Eliminating the secular terms, we obtained $x_{\mathrm{1,1}}$ and $x_{\mathrm{2,1}}$, where the set of parameters $a_1,a_2,b_i,d_i,{\varphi }_i,{\gamma }_i(i=\mathrm{1,2},3)$ could be given by Equations (22)–(35), and the solution for $x_{\mathrm{1,1}}$ and $x_{\mathrm{2,1}}$ could be obtained.

Therefore, the first-order approximate solution of $x_1$ and $x_2$ was

$$x_i(t)=\underset{q\to 1}{lim}\left(x_0+q{x}_1\right)=x_{i,0}+x_{i,1}(i=\mathrm{1,2}).$$

(36)

Letting

$$\mu =1;\alpha =3.8;\beta =1;f=3;\Omega =2,$$

(37)

the system had a single period solution, as shown in Figure 1. This figure was a superposition of analytical solution and numerical solution. The numerical solution was obtained by directly calling the command of Mathematica 12.0 version, and the parameter values were the same as the analytical solution.

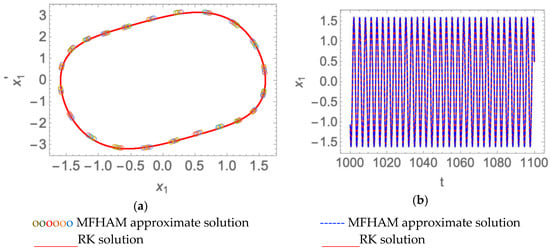
Figure 1. The single period solution of the coupling Van der Pol-Duffing system when $\tau =0$, $\mu =1$, $\alpha =4$, $\beta =1$, $f=3$, and $\Omega =2$. (a) Phase curve; (b) time history response.

For the period-doubling solution, the characteristic polynomial was

$$P\left(\lambda \right)=\lambda {\prod }_{r=1}^6\left(\lambda +\frac{r\Omega }{2}i\right)\left(\lambda -\frac{r\Omega }{2}i\right).$$

(38)

We used the following corresponding auxiliary linear differential operator

$$\begin{array}{c}{L}_7\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{c}{x}_1^{\left(13\right)}\\ x_2^{\left(13\right)}\end{array}\right)+\frac{91{\Omega }^2}{4}\left(\begin{array}{c}{x}_1^{\left(11\right)}\\ x_2^{\left(11\right)}\end{array}\right)+\frac{3003{\Omega }^4}{16}\left(\begin{array}{c}{x}_1^{\left(9\right)}\\ x_2^{\left(9\right)}\end{array}\right)+\frac{44473{\Omega }^6}{64}\left(\begin{array}{c}{x}_1^{\left(7\right)}\\ x_2^{\left(7\right)}\end{array}\right)\\ +\frac{37037{\Omega }^8}{32}\left(\begin{array}{c}{x}_1^{\left(5\right)}\\ x_2^{\left(5\right)}\end{array}\right)+\frac{48321{\Omega }^{10}}{64}\left(\begin{array}{c}{x}_1^{\left(3\right)}\\ x_2^{\left(3\right)}\end{array}\right)+\frac{2025{\Omega }^{12}}{16}\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)\end{array}.$$

(39)

Next, we constructed

$$\begin{array}{c}\Gamma \left(\begin{array}{cc}{x}_1& q\\ x_2& q\end{array}\right)=L_7\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-q{L}_7\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)\\ -q\hslash \left(\begin{array}{c}{\ddot{x}}_1\left(t\right)-\mu \left(1-{x_1}^2\left(t\right)\right){\dot{x}}_1\left(t\right)+\alpha x_2\left(t\right)+\beta {x_1}^3\left(t\right)-fcos\Omega t\\ {\ddot{x}}_2\left(t\right)-\mu \left(1-{x_2}^2\left(t\right)\right){\dot{x}}_2\left(t\right)+\alpha x_1\left(t\right)+\beta {x_2}^3\left(t\right)-fcos\Omega t\end{array}\right)\end{array},$$

(40)

where $\hslash$ is the auxiliary parameter and $q\in \left[\mathrm{0,1}\right]$ is the embedding variable.

Assuming that the solution of Equation (12) could be expressed as

$$x_i=x_{i,0}+q{x}_{i,1}+q^2{x}_{i,2}+\cdots \left(i=\mathrm{1,2}\right),$$

(41)

then, substituting Equation (41) into Equation (40) and merging the same power terms of $q$, then obtained

$$\begin{array}{c}{q}^0:L_7\left(\begin{array}{c}{x}_{\mathrm{1,0}}\\ x_{\mathrm{2,0}}\end{array}\right)=0\end{array},$$

(42)

$$\begin{array}{c}{q}^1:L_7\left(\begin{array}{c}{x}_{\mathrm{1,1}}\\ x_{\mathrm{2,1}}\end{array}\right)=L_7\left(\begin{array}{c}{x}_{\mathrm{1,0}}\\ x_{\mathrm{2,0}}\end{array}\right)+\\ \hslash \left(\begin{array}{c}{\ddot{x}}_1\left(t\right)-\mu \left(1-{x_1}^2\left(t\right)\right){\dot{x}}_1\left(t\right)+\alpha x_2\left(t\right)+\beta {x_1}^3\left(t\right)-fcos\Omega t\\ {\ddot{x}}_2\left(t\right)-\mu \left(1-{x_2}^2\left(t\right)\right){\dot{x}}_2\left(t\right)+\alpha x_1\left(t\right)+\beta {x_2}^3\left(t\right)-fcos\Omega t\end{array}\right)\end{array}.$$

(43)

The solution to Equation (42) can be expressed by

$$\begin{array}{c}{x}_{\mathrm{1,0}}=a_1+e_{1}cos\left(\frac{\Omega t}{2}+{\varphi }_0\right)+b_{1}cos\left(\Omega t+{\varphi }_1\right)+e_{2}cos\left(\frac{3\Omega t}{2}+{\varphi }_2\right)\\ +b_{2}cos\left(2\Omega t+{\varphi }_3\right)+e_{3}cos\left(\frac{5\Omega t}{2}+{\varphi }_4\right)+b_{3}cos\left(3\Omega t+{\varphi }_5\right)\end{array},$$

(44)

$$\begin{array}{c}{x}_{\mathrm{2,0}}=a_2+f_{1}cos\left(\frac{\Omega t}{2}+{\gamma }_0\right)+d_{1}cos\left(\Omega t+{\gamma }_1\right)+f_{2}cos\left(\frac{3\Omega t}{2}+{\gamma }_2\right)\\ +d_{2}cos\left(2\Omega t+{\gamma }_3\right)+f_{3}cos\left(\frac{5\Omega t}{2}+{\gamma }_4\right)+d_{3}cos\left(3\Omega t+{\gamma }_5\right)\end{array},$$

(45)

where $a_1,a_2,b_i,d_i,e_i,f_i,{\varphi }_j,{\gamma }_j(i=\mathrm{1,2},3;j=0,\mathrm{1,2},\mathrm{3,4},5)$ are unknown parameters.

Substituting Equations (42), (44), and (45) into (43), and eliminating the secular term in $x_{i,1}\left(t\right)(i=\mathrm{1,2})$, we obtained the solution of $a_1,a_2,b_i,d_i,e_i,f_i,{\varphi }_j,{\gamma }_j(i=\mathrm{1,2},3;j=\mathrm{1,2},\mathrm{3,4},5)$.

Taking $\mu =1,\alpha =3.8,\beta =1,f=3,\Omega =2$, we obtained the double period solution and found that the system had the double period of movement, as shown in Figure 2.

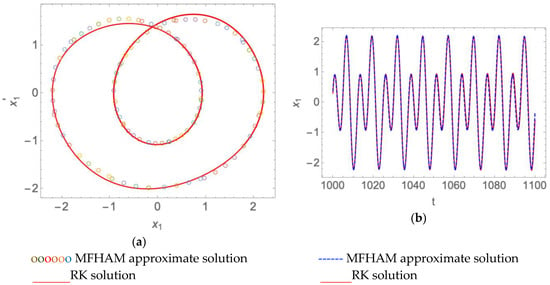
Figure 2. The double period solution of the coupling Van der Pol-Duffing system when $\tau =0$, $\mu =0.08$, $\alpha =1$, $\beta =0$, $f=0.7$ and $\Omega =0.5$. (a) Phase curve; (b) time history response.

4. Analyzing the Time Delay Van der Pol-Duffing System with MFHAM

We considered the following system by the MFHAM

$$\ddot{x}\left(t\right)-\mu \left(1-x^2\left(t\right)\right)\dot{x}\left(t\right)+\alpha x(t-\tau )+\beta x^3\left(t\right)=fcos\left(\Omega t\right),$$

(46)

where the prime denotes the differential with respect to the time $t$, $x\left(t\right)$ are unknow real functions, $\tau$ is the time delay, $\Omega$ is the frequency of the parametric excitation, and $\mu >0,$ $\alpha ,\beta ,f$ are constant physical parameters.

First, for the single period solution, we have the characteristic polynomial

$$p\left(\lambda \right)=\lambda {\prod }_{r=1}^3(\lambda +r\Omega i)(\lambda -r\Omega i).$$

(47)

Then, we obtained the corresponding auxiliary linear differential operator

$$L_4\left(x\right)=\left(x^{\left(7\right)}\right)+14{\Omega }^2\left(x^{\left(5\right)}\right)+49{\Omega }^4\left(x^{\left(3\right)}\right)+36{\Omega }^6\left(x^{\prime }\right).$$

(48)

The homotopy expression was constructed as follows:

$$\begin{array}{c}\Gamma \left(\begin{array}{cc}x,& q\end{array}\right)=L_4\left(x\right)-q{L}_4\left(x\right)-\\ q\hslash \left(\ddot{x}\left(t\right)-\mu \left(1-x^2\left(t\right)\right)\dot{x}\left(t\right)+\alpha x\left(t-\tau \right)+\beta x^3\left(t\right)-fcos\left(\Omega t\right)\right)\end{array},$$

(49)

where $q\in \left[\mathrm{0,1}\right]$ is the embedding variable and $\hslash$ is the auxiliary parameter.

We were then able to suppose that the solution to Equation (46) is

$$x=x_0+q{x}_1+q^2{x}_2+\cdots .$$

(50)

Substituting Equation (50) into Equation (49) and combining terms of the same power of q, we obtained

$$q^0:L_4\left(x_0\right)=0,$$

(51)

$$\begin{array}{c}{q}^1:L_4\left(x_1\right)=L_4\left(x_0\right)+\\ \hslash \left({\ddot{x}}_0\left(t\right)-\mu \left(1-{x_0}^2\left(t\right)\right){\dot{x}}_0\left(t\right)+\alpha x_0(t-\tau )+\beta {x_0}^3\left(t\right)-fcos\left(\Omega t\right)\right).\end{array}$$

(52)

We then supposed the solution to Equation (51) to be

$$x_0=a_1+b_{1}cos\left(\Omega t+{\varphi }_1\right)+b_{2}cos\left(2\Omega t+{\varphi }_2\right)+b_{3}cos\left(3\Omega t+{\varphi }_3\right),$$

(53)

where $a_1,b_i,{\varphi }_i(i=\mathrm{1,2},3)$ are unknown parameters.

Substituting Equation (53) into Equation (52), we obtained

$$\begin{array}{c}{L}_4\left(x_1\right)=\{\alpha \left(a_1+d_{1}Cos\left[(t-\tau )\Omega +{\varphi }_1\right]+d_{2}Cos\left[2(t-\tau )\Omega +{\varphi }_2\right]\right)+\\ d_{3}Cos\left[3(t-\tau )\Omega +{\varphi }_3\right])-4{b_2\Omega }^{2}Cos\left[2t\Omega +{\varphi }_2\right]-9{b_3\Omega }^{2}Cos\left[3t\Omega +{\varphi }_3\right]-\\ {b_1\Omega }^{2}Cos\left[t\Omega +{\varphi }_1\right]+\beta {\left(a_1+b_{1}Cos\left[t\Omega +{\varphi }_1\right]+b_{2}Cos\left[2t\Omega +{\varphi }_2\right]+b_{3}Cos\left[3t\Omega +{\varphi }_3\right]\right)}^3\\ -fCos[t\Omega ]-\mu \left(1-{\left(a1+b_{1}Cos\left[t\Omega +{\varphi }_1\right]+b_{2}Cos\left[2t\Omega +{\varphi }_2\right]+b_{3}Cos\left[3t\Omega +{\varphi }_3\right]\right)}^2\right)\\ \left(-b_1\Omega Sin\left[t\Omega +{\varphi }_1\right]-2b_2\Omega Sin\left[2t\Omega +{\varphi }_2\right]-3b_3\Omega Sin\left[3t\Omega +{\varphi }_3\right]\right)\}\hslash \end{array}.$$

(54)

Expanding Equation (54) and eliminating the secular terms in $x_1$, we obtained the following equations:

$$\begin{array}{c}3b_3\mathsf{\mu }\mathsf{\Omega }-3{a_1}^2{b}_3\mu \Omega -\frac{3}{2}{b_1}^2{b}_3\mu \Omega -\frac{3}{2}{b_2}^2{b}_3\mu \Omega -\frac{3}{4}{b_3}^3\mu \Omega -\frac{1}{4}{b_1}^3\mu \Omega cos[3{\varphi }_1-{\varphi }_3]-\\ 3a_1{b}_1{b}_2\mu \Omega cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]-\frac{3}{4}{b}_1{b_2}^2\mu \Omega cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]-\frac{1}{4}{b_1}^3\beta sin[3{\varphi }_1-{\varphi }_3]\\ -3a_1{b}_1{b}_2\beta sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]+\frac{3}{4}{b}_1{b_2}^2\beta sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]+b_3\alpha sin[3\tau \Omega ]=0\end{array},$$

(55)

$$\begin{array}{c}3a_1{b}_1{b}_3\beta sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]-{b_1}^2{b}_2\mu \Omega -\frac{1}{2}{b_2}^3\mu \Omega -b_2{b_3}^2\mu \Omega -{a_1}^2\mu \Omega cos[2{\varphi }_1-{\varphi }_2]\\ -2a_1{b}_1{b}_3\mu \Omega cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]-b_1{b}_2{b}_3\mu \Omega cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]+b_2\alpha sin[2\tau \Omega ]+\\ 2b_2\mu \Omega -2{a_1}^2{b}_2\mu \Omega -\frac{3}{2}{b}_1{b}_2{b}_3\beta sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]-\frac{3}{2}{a}_1{b_1}^2\beta sin[2{\varphi }_1-{\varphi }_2]=0\end{array},$$

(56)

$$\begin{array}{c}{b}_1\mu \Omega -{a_1}^2{b}_1\mu \Omega -\frac{1}{4}b{1}^3\mu \Omega -\frac{1}{2}{b}_1{b_2}^2\mu \Omega -\frac{1}{2}{b}_1{b_3}^2\mu \Omega -a_1{b}_1{b}_2\mu \Omega cos[2{\varphi }_1-{\varphi }_2]\\ -\frac{1}{4}{b_1}^2{b}_3\mu \Omega cos[3{\varphi }_1-{\varphi }_3]-\frac{1}{4}{b_2}^2{b}_3\mu \Omega cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]-fsin\left[{\varphi }_1\right]+\\ 3a_1{b}_1{b}_2\beta sin[2{\varphi }_1-{\varphi }_2]-a_1{b}_2{b}_3\mu cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]+\frac{3}{4}{b_1}^2{b}_3\beta sin[3{\varphi }_1-{\varphi }_3]\\ +3a_1{b}_2{b}_3\beta sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]+\frac{3}{4}{b_2}^2{b}_3\beta sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]+b_1\alpha sin[\tau \Omega ]=0,\end{array},$$

(57)

$$\begin{array}{c}\frac{3}{2}{b_2}^2{b}_3\beta +\frac{3b{3}^3\beta }{4}-9b_3{\Omega }^2+\frac{1}{4}{b_1}^3\beta cos[3{\varphi }_1-{\varphi }_3]+\frac{3}{4}{b}_1{b_2}^2\mu \Omega sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]\\ +3a_1{b}_1{b}_2\beta cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]+\frac{3}{4}{b}_1{b_2}^2\beta cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]+b_3\alpha cos[3\tau \Omega ]-\\ \frac{1}{4}{b_1}^3\mu \Omega sin[3{\varphi }_1-{\varphi }_3]-3a_1{b}_1{b}_2\mu \Omega sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]+3{a_1}^2{b}_3\beta +\frac{3}{2}{b_1}^2{b}_3\beta =0\end{array},$$

(58)

$$\begin{array}{c}3{a_1}^2{b}_2\beta +\frac{3}{2}{b_1}^2{b}_2\beta +\frac{3}{2}{b}_2{b_3}^2\beta -4b_2{\Omega }^2+\frac{3}{2}{a}_1{b_1}^2\beta cos[2{\varphi }_1-{\varphi }_2]+\\ 3a_1{b}_1{b}_3\beta cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]+\frac{3}{2}{b}_1{b}_2{b}_3\beta cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]\\ +b_2\alpha cos[2\tau \Omega ]-a_1{b_1}^2\mu \Omega sin[2{\varphi }_1-{\varphi }_2]+\frac{3b{2}^3\beta }{4}\\ +2a_1{b}_1{b}_3\mu \Omega sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]-b_1{b}_2{b}_3\mu \Omega sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]=0\end{array},$$

(59)

$$\begin{array}{c}\frac{3b{1}^3\beta }{4}+\frac{3}{2}{b}_1{b_3}^2\beta -b_1{\Omega }^2-fcos\left[{\varphi }_1\right]+\frac{3}{4}{b_1}^2{b}_3\beta cos[3{\varphi }_1-{\varphi }_3]+\\ 3a_1{b}_1{b}_2\beta cos[2{\varphi }_1-{\varphi }_2]+3a_1{b}_2{b}_{3}cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]+3{a_1}^2{b}_1\beta \\ \frac{3}{4}{b_2}^2{b}_3\beta cos[{\varphi }_1-2{\varphi }_2+{\varphi }_3]+b_1\alpha cos[\tau \Omega ]+a_1{b}_1{b}_2\mu \Omega sin[2{\varphi }_1-{\varphi }_2]\\ +\frac{1}{4}{b_1}^2{b}_3\mu \Omega sin[3{\varphi }_1-{\varphi }_3]+a_1{b}_2{b}_3\mu sin[{\varphi }_1+{\varphi }_2-{\varphi }_3]+\frac{3}{2}{b}_1{b_2}^2\beta \\ +\frac{1}{4}{b_2}^2{b}_3\mu \Omega sin[{\varphi }_1-2{\varphi }_2+{\varphi }_3]=0\end{array},$$

(60)

$$\begin{array}{c}{a}_1\alpha +{a_1}^3\beta +\frac{3}{2}{a}_1{b_1}^2\beta +\frac{3}{2}{a}_1{b_2}^2\beta +\frac{3}{2}{a}_1{b_3}^2\beta +\frac{3}{4}{b_1}^2{b}_2\beta cos[2{\varphi }_1-{\varphi }_2]\\ +\frac{3}{4}{b_1}^2{b}_2\beta cos[2{\varphi }_1-{\varphi }_2]+\frac{3}{2}{b}_1{b}_2{b}_3\beta cos[{\varphi }_1+{\varphi }_2-{\varphi }_3]=0\end{array}.$$

(61)

Eliminating the secular terms, we obtained $x_1$, where the set of parameters $a_1,b_i,{\varphi }_i(i=\mathrm{1,2},3)$ can be given by Equations (55)–(61).

Therefore, the first-order approximate solution of x was

$$x=\underset{q\to 1}{lim}\left(x_0+q{x}_1\right)=x_0+x_1.$$

(62)

Selecting a set of parameters, we obtained the periodic solution, as shown in Figure 3. We also obtained the single periodic solution for $\tau =0$ under the parameter, as shown in Figure 4.

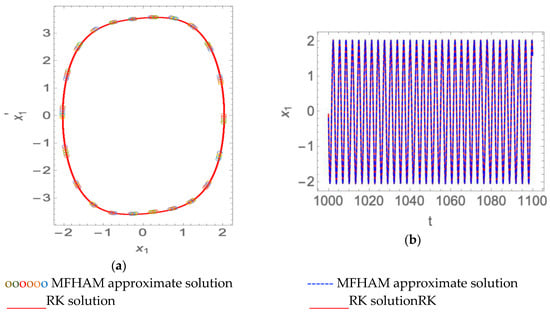
Figure 3. The single period solution of the time delay coupling Van der Pol-Duffing system when $\tau =0.01$, $\mu =0.1$, $\alpha =1$, $\beta =1$, $f=0.01$ and $\Omega =2$. (a) Phase curve; (b) time history response.

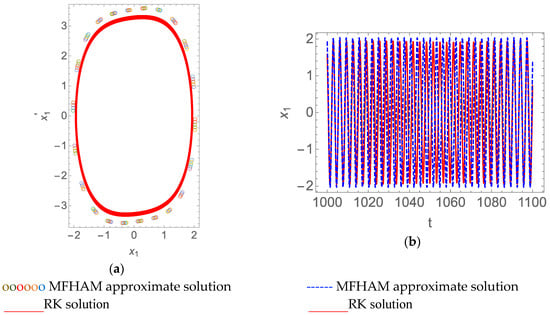
Figure 4. The single period solution of the time delay coupling Van der Pol-Duffing system when $\tau =0$, $\mu =0.1$, $\alpha =1$, $\beta =1$, $f=0.01$ and $\Omega =2$. (a) Phase curve; (b) time history response.

For the period-doubling solution, the characteristic polynomial is

$$P(\lambda )=\lambda {\prod }_{r=1}^6\left(\lambda +\frac{r\Omega }{2}i\right)\left(\lambda -\frac{r\Omega }{2}i\right).$$

(63)

We used the following corresponding auxiliary linear differential operator

$$\begin{array}{c}{L}_7\left(x\right)=\left(x^{\left(13\right)}\right)+\frac{91{\Omega }^2}{4}\left(x^{\left(11\right)}\right)+\frac{3003{\Omega }^4}{16}\left(x^{\left(9\right)}\right)+\frac{44473{\Omega }^6}{64}\left(x^{\left(7\right)}\right)\\ +\frac{37037{\Omega }^8}{32}\left(x^{\left(5\right)}\right)+\frac{48321{\Omega }^{10}}{64}\left(x^{\left(3\right)}\right)+\frac{2025{\Omega }^{12}}{16}\left(x^{\prime }\right)\end{array}.$$

(64)

Next, we constructed

$$\begin{array}{c}\Gamma \left(\begin{array}{cc}x& q\end{array}\right)=L_7\left(x\right)-q{L}_7\left(x\right)\\ -q\hslash \left(\ddot{x}\right(t)-\mu \left(1-x^2\left(t\right)\right)\dot{x}(t)+\alpha x(t-\tau )+\beta x^3(t)-fcos\left(\Omega t\right))\end{array},$$

(65)

where $\hslash$ is the auxiliary parameter, $q\in \left[\mathrm{0,1}\right]$ is the embedding variable.

We then assumed that the solution of Equation (46) could be expressed as

$$x=x_0+q{x}_1+q^2{x}_2+\cdots .$$

(66)

Substituting Equation (66) into Equation (65) and merging the same power terms of $q$, we obtained

$$q^0:L_7\left(x_0\right)=0,$$

(67)

$$\begin{array}{c}{q}^1:L_7\left(x_1\right)=L_7\left(x_0\right)+\\ \hslash \left({\ddot{x}}_0\left(t\right)-\mu \left(1-{x_0}^2\left(t\right)\right){\dot{x}}_0\left(t\right)+\alpha x_0(t-\tau )+\beta {x_0}^3\left(t\right)-fcos\left(\Omega t\right)\right)\end{array}.$$

(68)

We assumed that the solution Equation (67) could be expressed by

$$\begin{array}{c}{x}_0=a_1+e_{1}cos\left(\frac{\Omega t}{2}+{\varphi }_0\right)+b_{1}cos\left(\Omega t+{\varphi }_1\right)+e_{2}cos\left(\frac{3\Omega t}{2}+{\varphi }_2\right)\\ +b_{2}cos\left(2\Omega t+{\varphi }_3\right)+e_{3}cos\left(\frac{5\Omega t}{2}+{\varphi }_4\right)+b_{3}cos\left(3\Omega t+{\varphi }_5\right)\end{array},$$

(69)

where $a_1,b_i,e_i,{\varphi }_j(i=\mathrm{1,2},3;j=\mathrm{1,2},\mathrm{3,4},5)$ are unknown parameters.

Substituting Equations (67) and (69) into (68), and eliminating the secular term in $x_1\left(t\right)$, we obtained the solution $a_1,b_i,e_i,{\varphi }_j(i=\mathrm{1,2},3;j=\mathrm{0,1},\mathrm{2,3},\mathrm{4,5})$.

Taking $\mu =1,\alpha =3.8,\beta =1,f=3,\Omega =2,\tau =0.01$, we obtained the double period solution and found that the system had the double period of movement, as shown in Figure 5. We also obtained the double periodic solution for $\tau =0$ under this parameter, as shown in Figure 6. Therefore, we found that the existence of time delay affected the solution of the system.

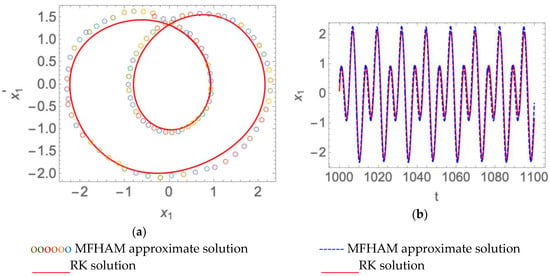
Figure 5. The double period solution of the time delay Van der Pol-Duffing system when $\tau =0.1$, $\mu =0.08$, $\alpha =1$, $\beta =0$, $f=0.71$ and $\Omega =0.5$. (a) Phase curve; (b) time history response.

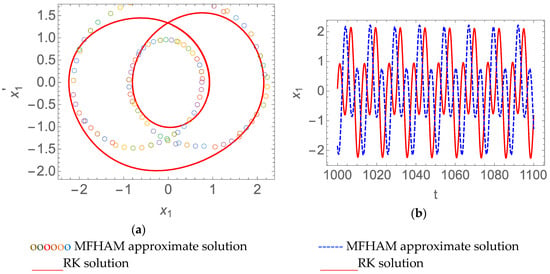
Figure 6. The double period solution of the time delay Van der Pol-Duffing system when $\tau =0$, $\mu =0.08$, $\alpha =1$, $\beta =0$, $f=0.71$ and $\Omega =0.5$. (a) Phase curve; (b) time history response.

5. Analyzing the Time Delay Coupling Van der Pol-Duffing System with MFHAM

The system was as follows

$$\begin{array}{c}{\ddot{x}}_1\left(t\right)-\mu \left(1-{x_1}^2\left(t\right)\right){\dot{x}}_1\left(t\right)+\alpha x_2(t-\tau )+\beta {x_1}^3\left(t\right)=fcos\left(\Omega t\right)\\ {\ddot{x}}_2\left(t\right)-\mu \left(1-{x_2}^2\left(t\right)\right){\dot{x}}_2\left(t\right)+\alpha x_1\left(t-\tau \right)+\beta {x_2}^3\left(t\right)=fcos\left(\Omega t\right).\end{array}$$

(70)

For the single period, the characteristic polynomial is

$$p(\lambda )=\lambda {\prod }_{r=1}^3(\lambda +r\Omega i)(\lambda -r\Omega i).$$

(71)

The corresponding auxiliary linear differential operator is

$$L_4\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{c}{x}_1^{\left(7\right)}\\ x_2^{\left(7\right)}\end{array}\right)+14{\Omega }^2\left(\begin{array}{c}{x}_1^{\left(5\right)}\\ x_2^{\left(5\right)}\end{array}\right)+49{\Omega }^4\left(\begin{array}{c}{x}_1^{\left(3\right)}\\ x_2^{\left(3\right)}\end{array}\right)+36{\Omega }^6\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right).$$

(72)

Then, we constructed the homotopy expression

$$\begin{array}{c}\Gamma \left(\begin{array}{cc}{x}_1& q\\ x_2& q\end{array}\right)=L_4\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-q{L}_4\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)\\ -q\hslash \left(\begin{array}{c}{\ddot{x}}_1\left(t\right)-\mu \left(1-{x_1}^2\left(t\right)\right){\dot{x}}_1\left(t\right)+\alpha x_2(t-\tau )+\beta {x_1}^3\left(t\right)-fcos\Omega t\\ {\ddot{x}}_2\left(t\right)-\mu \left(1-{x_2}^2\left(t\right)\right){\dot{x}}_2\left(t\right)+\alpha x_1(t-\tau )+\beta {x_2}^3\left(t\right)-fcos\Omega t\end{array}\right)\end{array},$$

(73)

where $\hslash$ is the auxiliary parameter and $q\in \left[\mathrm{0,1}\right]$ is the embedding variable.

We supposed the solution to Equation (70) to be

$$x_i=x_{i,0}+q{x}_{i,1}+q^2{x}_{i,2}+\cdots (i=\mathrm{1,2}).$$

(74)

Substituting Equation (74) into Equation (73) and merging the same power terms of $q$, we obtained

$$\begin{array}{c}{q}^0:L_4\left(\begin{array}{c}{x}_{\mathrm{1,0}}\\ x_{\mathrm{2,0}}\end{array}\right)=0\end{array},$$

(75)

$$\begin{array}{c}{q}^1:L_4\left(\begin{array}{c}{x}_{\mathrm{1,1}}\\ x_{\mathrm{2,1}}\end{array}\right)=L_4\left(\begin{array}{c}{x}_{\mathrm{1,0}}\\ x_{\mathrm{2,0}}\end{array}\right)\\ +\hslash \left(\begin{array}{c}{\ddot{x}}_1\left(t\right)-\mu \left(1-{x_1}^2\left(t\right)\right){\dot{x}}_1\left(t\right)+\alpha x_2(t-\tau )+\beta {x_1}^3\left(t\right)-fcos\Omega t\\ {\ddot{x}}_2\left(t\right)-\mu \left(1-{x_2}^2\left(t\right)\right){\dot{x}}_2\left(t\right)+\alpha x_1(t-\tau )+\beta {x_2}^3\left(t\right)-fcos\Omega t\end{array}\right)\end{array}.$$

(76)

We then assumed that the solution Equation (75) could be expressed by

$$\begin{array}{c}{x}_{\mathrm{1,0}}=a_1+b_{1}cos\left(\Omega t+{\varphi }_1\right)+b_{2}cos\left(2\Omega t+{\varphi }_2\right)+b_{3}cos\left(3\Omega t+{\varphi }_3\right)\\ x_{\mathrm{2,0}}=a_2+d_1\mathit{cos}\left(\Omega t+{\gamma }_1\right)+d_2\mathit{cos}\left(2\Omega t+{\gamma }_2\right)+d_3\mathit{cos}\left(3\Omega t+{\gamma }_3\right)\end{array},$$

(77)

where $a_1,a_2,b_i,d_i,{\varphi }_i,{\gamma }_i(i=\mathrm{1,2},3)$ are unknown parameters.

Substituting Equations (75) and (77) into Equation (76), we obtained the following equations

$$\begin{array}{c}{L}_4\left(x_{\mathrm{1,1}}\right)=\{\alpha \left(a_2+d_{1}Cos\left[(t-\tau )\Omega +{\gamma }_1\right]+d_{2}Cos\left[2(t-\tau )\Omega +{\gamma }_2\right]+d_{3}Cos\left[3(t-\tau )\Omega +{\gamma }_3\right]\right)\\ -{b_1\Omega }^{2}Cos\left[t\Omega +{\varphi }_1\right]-4{b_2\Omega }^{2}Cos\left[2t\Omega +{\varphi }_2\right]-9{b_3\Omega }^{2}Cos\left[3t\Omega +{\varphi }_3\right]-fCos[t\Omega ]+\\ \beta {\left(a_1+b_{1}Cos\left[t\Omega +{\varphi }_1\right]+b_{2}Cos\left[2t\Omega +{\varphi }_2\right]+b3Cos\left[3t\Omega +{\varphi }_3\right]\right)}^3-\\ \mu \left(1-{\left(a1+b_{1}Cos\left[t\Omega +{\varphi }_1\right]+b_{2}Cos\left[2t\Omega +{\varphi }_2\right]+b_{3}Cos\left[3t\Omega +{\varphi }_3\right]\right)}^2\right)\\ \left(-b_1\Omega Sin\left[t\Omega +{\varphi }_1\right]-2b_2\Omega Sin\left[2t\Omega +{\varphi }_2\right]-3b_3\Omega Sin\left[3t\Omega +{\varphi }_3\right]\right)\}\hslash \end{array},$$

(78)

$$\begin{array}{c}{L}_4\left(x_{\mathrm{2,1}}\right)=\{-fCos[t\Omega ]+\beta {\left(a_2+d_{1}Cos\left[t\Omega +{\gamma }_1\right]+d_{2}Cos\left[2t\Omega +{\gamma }_2\right]+d_{3}Cos\left[3t\Omega +{\gamma }_3\right]\right)}^3\\ {-\Omega }^2\left(d_{1}Cos\left[t\Omega +{\gamma }_1\right]+4d_{2}Cos\left[2t\Omega +{\gamma }_2\right]+9d_{3}Cos\left[3t\Omega +{\gamma }_3\right]\right)+\\ \alpha \left(a_1+b_{1}Cos\left[(t-\tau )\Omega +{\varphi }_1\right]+b_{2}Cos\left[2(t-\tau )\Omega +{\varphi }_2\right]+b_{3}Cos\left[3(t-\tau )\Omega +{\varphi }_3\right]\right)-\\ \mu \left(1-{\left(a_2+d_{1}Cos\left[t\Omega +{\gamma }_1\right]+d_{2}Cos\left[2t\Omega +{\gamma }_2\right]+d_{3}Cos\left[3t\Omega +{\gamma }_3\right]\right)}^2\right)\\ \left(-d_1\Omega Sin\left[t\Omega +{\gamma }_1\right]-2d_2\Omega Sin\left[2t\Omega +{\gamma }_2\right]-3d_3\Omega Sin\left[3t\Omega +{\gamma }_3\right]\right)\}\hslash \end{array}.$$

(79)

Expanding Equations (78) and (79), then eliminating the secular term in Equations (78) and (79), we obtained the Equations (A1)–(A14) in Appendix A.

Eliminating the secular terms, we obtained $x_{\mathrm{1,1}}$ and $x_{\mathrm{2,1}}$, where the set of parameters $a_1,a_2,b_i,d_i,{\varphi }_i,{\gamma }_i(i=\mathrm{1,2},3)$ can be given by Equations (A1)–(A14).

Therefore, the first-order approximate solution of $x_1$ and $x_2$ was

$$x_i(t)=\underset{q\to 1}{lim}\left(x_0+q{x}_1\right)=x_{i,0}+x_{i,1}(i=\mathrm{1,2}).$$

(80)

Selecting a set of parameters, we obtained the periodic solution, as shown in Figure 7. We also obtained the single periodic solution for $\tau =0$ under this parameter, as shown in Figure 8.

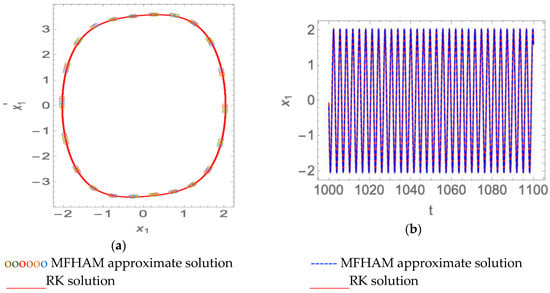
Figure 7. The single period solution of the time delay Van der Pol-Duffing system when $\tau =0.01$, $\mu =0.5$, $\alpha =4$, $\beta =1$, $f=3$ and $\Omega =2$. (a) Phase curve; (b) time history response.

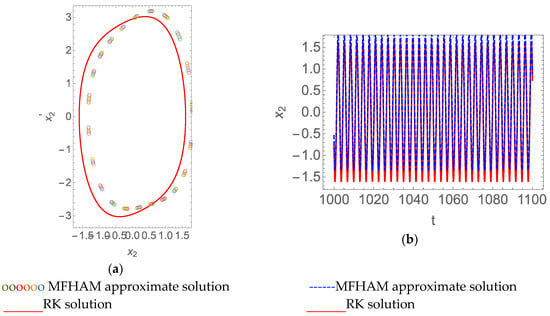
Figure 8. The single period solution of the time delay Van der Pol-Duffing system when $\tau =0$, $\mu =0.5$, $\alpha =4$, $\beta =1$, $f=3$ and $\Omega =2$. (a) Phase curve; (b) time history response.

For the period-doubling solution, the characteristic polynomial is

$$P(\lambda )=\lambda {\prod }_{r=1}^6\left(\lambda +\frac{r\Omega }{2}i\right)\left(\lambda -\frac{r\Omega }{2}i\right).$$

(81)

We used the following corresponding auxiliary linear differential operator as

$$\begin{array}{c}{L}_7\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)=\left(\begin{array}{c}{x}_1^{\left(13\right)}\\ x_2^{\left(13\right)}\end{array}\right)+\frac{91{\Omega }^2}{4}\left(\begin{array}{c}{x}_1^{\left(11\right)}\\ x_2^{\left(11\right)}\end{array}\right)+\frac{3003{\Omega }^4}{16}\left(\begin{array}{c}{x}_1^{\left(9\right)}\\ x_2^{\left(9\right)}\end{array}\right)+\frac{44473{\Omega }^6}{64}\left(\begin{array}{c}{x}_1^{\left(7\right)}\\ x_2^{\left(7\right)}\end{array}\right)\\ +\frac{37037{\Omega }^8}{32}\left(\begin{array}{c}{x}_1^{\left(5\right)}\\ x_2^{\left(5\right)}\end{array}\right)+\frac{48321{\Omega }^{10}}{64}\left(\begin{array}{c}{x}_1^{\left(3\right)}\\ x_2^{\left(3\right)}\end{array}\right)+\frac{2025{\Omega }^{12}}{16}\left(\begin{array}{c}{x}_1^{\prime }\\ x_2^{\prime }\end{array}\right)\end{array}.$$

(82)

Next, we constructed

$$\begin{array}{c}\Gamma \left(\begin{array}{cc}{x}_1& q\\ x_2& q\end{array}\right)=L_7\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-q{L}_7\left(\begin{array}{c}{x}_1\\ x_2\end{array}\right)-\\ q\hslash \left(\begin{array}{c}{\ddot{x}}_1\left(t\right)-\mu \left(1-{x_1}^2\left(t\right)\right){\dot{x}}_1\left(t\right)+\alpha x_2(t-\tau )+\beta {x_1}^3\left(t\right)-fcos\Omega t\\ {\ddot{x}}_2\left(t\right)-\mu \left(1-{x_2}^2\left(t\right)\right){\dot{x}}_2\left(t\right)+\alpha x_1(t-\tau )+\beta {x_2}^3\left(t\right)-fcos\Omega t\end{array}\right)\end{array},$$

(83)

where $\hslash$ is the auxiliary parameter and $q\in \left[\mathrm{0,1}\right]$ is the embedding variable.

We assumed that the solution of Equation (70) could be expressed as

$$x_i=x_{i,0}+q{x}_{i,1}+q^2{x}_{i,2}+\cdots \left(i=\mathrm{1,2}\right).$$

(84)

Substituting Equation (84) into Equation (83) and merging the same power terms of $q$, we obtained

$$\begin{array}{c}{q}^0:L_7\left(\begin{array}{c}{x}_{\mathrm{1,0}}\\ x_{\mathrm{2,0}}\end{array}\right)=0\end{array},$$

(85)

$$\begin{array}{c}{q}^1:L_7\left(\begin{array}{c}{x}_{\mathrm{1,1}}\\ x_{\mathrm{2,1}}\end{array}\right)=L_7\left(\begin{array}{c}{x}_{\mathrm{1,0}}\\ x_{\mathrm{2,0}}\end{array}\right)\\ +\hslash \left(\begin{array}{c}{\ddot{x}}_1\left(t\right)-\mu \left(1-{x_1}^2\left(t\right)\right){\dot{x}}_1\left(t\right)+\alpha x_2(t-\tau )+\beta {x_1}^3\left(t\right)-fcos\Omega t\\ {\ddot{x}}_2\left(t\right)-\mu \left(1-{x_2}^2\left(t\right)\right){\dot{x}}_2\left(t\right)+\alpha x_1(t-\tau )+\beta {x_2}^3\left(t\right)-fcos\Omega t\end{array}\right)\end{array}.$$

(86)

We assumed that the solution Equation (85) can be expressed by

$$\begin{array}{c}{x}_{\mathrm{1,0}}=a_1+e_{1}cos\left(\frac{\Omega t}{2}+{\varphi }_0\right)+b_{1}cos\left(\Omega t+{\varphi }_1\right)+e_{2}cos\left(\frac{3\Omega t}{2}+{\varphi }_2\right)\\ +b_{2}cos\left(2\Omega t+{\varphi }_3\right)+e_{3}cos\left(\frac{5\Omega t}{2}+{\varphi }_4\right)+b_{3}cos\left(3\Omega t+{\varphi }_5\right)\end{array},$$

(87)

$$\begin{array}{c}{x}_{\mathrm{2,0}}=a_2+f_{1}cos\left(\frac{\Omega t}{2}+{\gamma }_0\right)+d_{1}cos\left(\Omega t+{\gamma }_1\right)+f_{2}cos\left(\frac{3\Omega t}{2}+{\gamma }_2\right)\\ +d_{2}cos\left(2\Omega t+{\gamma }_3\right)+f_{3}cos\left(\frac{5\Omega t}{2}+{\gamma }_4\right)+d_{3}cos\left(3\Omega t+{\gamma }_5\right)\end{array},$$

(88)

where $a_1,a_2,b_i,d_i,e_i,f_i,{\varphi }_j,{\gamma }_j(i=\mathrm{1,2},3;j=\mathrm{1,2},\mathrm{3,4},5)$ are unknown parameters.

Substituting Equations (85), (87) and (88) into Equation (86), and eliminating the secular term in $x_{i,1}\left(t\right)(i=\mathrm{1,2})$, we obtained the solution $a_1,a_2,b_i,d_i,e_i,f_i,{\varphi }_j,{\gamma }_j(i=\mathrm{1,2},3;j=\mathrm{0,1},\mathrm{2,3},\mathrm{4,5})$. Hence, the double period solution was obtained, as shown in Figure 9. We also obtained the double periodic solution for $\tau =0$ under this parameter, as shown in Figure 10. Therefore, we found that the existence of time delay affected the solution of the system.

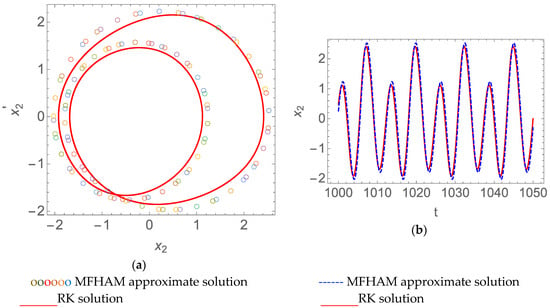
Figure 9. The double period solution of the time delay coupling Van der Pol-Duffing system when $\tau =0.01$, $\mu =0.1$, $\alpha =1$, $\beta =0$, $f=0.5$ and $\Omega =0.499$. (a) Phase curve; (b) time history response.

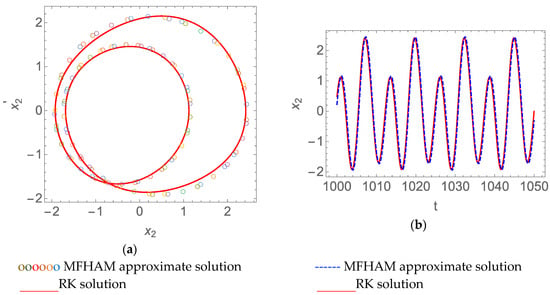
Figure 10. The double period solution of the time delay coupling Van der Pol-Duffing system when $\tau =0$, $\mu =0.1$, $\alpha =1$, $\beta =0$, $f=0.5$ and $\Omega =0.499$. (a) Phase curve; (b) time history response.

6. Conclusions

In this paper, the Van der Pol-Duffing systems contained parametric excitation frequencies. As such, the ordinary HAM was unable to solve the periodic solution of the systems. Therefore, we chose MFHAM to solve the periodic solution of the system, and applied the method to the coupled Van der Pol-Duffing system, single-degree-of-freedom delay Van der Pol-Duffing system, and Van der Pol-Duffing system with coupled time delay. Then, the solution obtained by this method was compared with the Runge–Kutta method. The results showed that the solutions obtained by the MFHAM and the Runge–Kutta method were consistent, and also showed that the time history curve obtained by the MFHAM and the Runge–Kutta method were consistent. Thus, the effectiveness of the MFHAM to study time delay-coupled nonlinear dynamical systems was demonstrated. We also compared the system with and without time delay under the same parameters, and found that the time delay affected the solution of the system and the dynamic behavior of the system. Thus, it was necessary to consider the time delay of the system.