Novel Kinds of Fractional λ–Kinetic Equations Involving the Generalized Degenerate Hypergeometric Functions and Their Solutions Using the Pathway-Type Integral

Abstract

In recent years, fractional kinetic equations (FKEs) involving various special functions have been widely used to describe and solve significant problems in control theory, biology, physics, image processing, engineering, astrophysics, and many others. This current work proposes a new solution to fractional $\lambda -$kinetic equations based on generalized degenerate hypergeometric functions (GDHFs), which has the potential to be applied to calculate changes in the chemical composition of stars such as the sun. Furthermore, this expanded form can also help to solve various problems with phenomena in physics, such as fractional statistical mechanics, anomalous diffusion, and fractional quantum mechanics. Moreover, some of the well-known outcomes are just special cases of this class of pathway-type solutions involving GDHFs, with greater accuracy, while providing an easily calculable solution. Additionally, numerical graphs of these analytical solutions, using MATLAB Software (latest version 2023b), are also considered.

1. Introduction

The calculus of derivatives and integrals of any order is the subject of fractional calculus. Because of its scientific uses over the previous three decades, its importance and appeal to researchers have grown to in this field [1,2]. Furthermore, fractional calculus has several applications in physics, finance, biology, image processing, engineering, and other disciplines. It can, for example, be used to simulate the behavior of viscoelastic materials, which have both elastic and viscous properties. Moreover, it can also solve differential equations that standard calculus cannot. We encourage readers to use the cited sources for more information on fractional calculus and its applications [3,4,5].

FKEs are types of differential equations that describe a system’s evolution over time and are based on the concept of fractional calculus [6,7]. One of the most essential applications of FKEs is modeling anomalous diffusion. Anomalous diffusion is a type of diffusion in which the mean square displacement of a particle grows sublinearly with time. This type of diffusion is observed in various systems, including turbulent fluids, porous media, and biological tissues (see, e.g., [8,9,10,11]). Furthermore, FKEs have also been used to model a variety of other systems, including, for example, the relaxation of viscoelastic materials, the spread of disease, the evolution of traffic patterns, and the behavior of financial markets [12,13,14].

Kinetic equation (KE) is defined by (cf. [1,2,3])

$$\begin{array}{c}\hfill \frac{d\mathcal{K}}{dw}=-\delta \mathcal{K},\delta \in {\mathbb{R}}^{+},\mathcal{K}\left(0\right)={\mathcal{K}}_0;\end{array}$$

(1)

The kinetic equation of fractional-order (KEFO) is presented by (see, e.g., [6,7,8,9])

$$\begin{array}{c}\hfill \mathcal{K}\left(w\right)-{\mathcal{K}}_0=-\delta {}_0{\mathbb{D}}_w^{-1}\mathcal{K}\left(w\right),\delta ,w\in {\mathbb{R}}^{+},\end{array}$$

(2)

where ${}_0{\mathbb{D}}_w^{-\alpha }$ is the fractional integral operator (cf. [1,2]) given by

$$\begin{array}{c}\hfill {}_0{\mathbb{D}}_w^{-\alpha }f\left(w\right)=\frac{1}{\Gamma \left(\alpha \right)}{\int }_0^w{(w-\tau )}^{\alpha -1}f\left(\tau \right)d\tau ,\alpha \in {\mathbb{R}}^{+}.\end{array}$$

(3)

Recently, several generalizations of the KEFO have been proposed by several researchers using various special functions. For instance, Alqarni et al. [15] introduced solutions involving the generalized incomplete Wright hypergeometric functions. Meanwhile, Khan et al. [16] considered solutions for KEFO associated with the $(p,q)-$extended $\tau -$hypergeometric and confluent hypergeometric functions, and Abubakar [17] focused on a solution for KEFO using the $(p,q;l)$-extended $\tau$-Gauss hypergeometric function. In a similar vein, Fuli He et al. [18] derived the solution of KEFO in terms of the Hadamard product of $(p,k)-$hypergeometric functions. Further, Hidan et al. [19] discussed the solution of FKEs involving extended $(k,t)-$Gauss hypergeometric matrix functions. Additionally, the general fractional kinetic model involving the hypergeometric super hyperbolic sine function via the Gauss hypergeometric series was recently presented by Geng et al. [20]. Building upon this research in this context, we present a new generalized structure of the $\lambda -$KEFO involving a degenerate generalized hypergeometric function, which was further supported by graphical presentations derived through pathway-type transform approach methodologies. Our investigation provides detailed and different results from those given in previous works and derives several special cases of known and new outcomes.

2. Some Definitions Related to the Concept of DEGENERATE

Carlitz [21,22] initiated the theory of degenerate polynomials by introducing the degenerate forms of the conventional Bernoulli and Euler polynomials. Later, mathematicians investigated degenerate versions of several special numbers and polynomials, such as degenerate Stirling numbers and polynomials [23,24], degenerate Bernoulli and Euler polynomials [25], degenerate generalized Bell polynomials [26], degenerate generalized Laguerre polynomials [27], degenerate Gould–Hopper polynomials [28], degenerate Hermite polynomials [29], and so on (see [30,31,32] and the references therein). It is also worth mentioning that the study of degenerate versions of polynomials and numbers extends to special functions, such as the Euler zeta function [33], the gamma, digamma, and polygamma functions [34,35], and degenerate hypergeometric functions [36,37]. Degenerate exponentials are especially potent tools that can be used to solve various problems in probability, statistics, and other areas of mathematics, such as differential and integral equations.

For any $\lambda \in \mathbb{R},$ the degenerate exponentials are defined in [23,24,25] by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill e_{\lambda }^{\theta }\left(w\right)=\sum _{m=0}^{\infty }{\left(\theta \right)}^{m,\lambda }\frac{w^m}{m!},\end{array}\end{array}$$

(4)

where ${\left(\theta \right)}^{m,\lambda }=\theta (\theta -\lambda )(\theta -2\lambda )\dots (\theta -(m-1)\lambda ),$ for $m\ge 1$ and ${\left(\theta \right)}^{0,\lambda }=1.$ Note that at $\lambda \to 0,$ then $e_{\lambda }^{\theta }\left(w\right)=e^{\theta w}$ and ${\left(\theta \right)}^{m,\lambda }={\theta }^m.$ In [34], Kim-Kim defined the degenerate gamma function as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\Gamma }_{\lambda }\left(w\right)=& {\int }_0^{\infty }{(1+\lambda \zeta )}^{-\frac{1}{\lambda }}{\zeta }^{w-1}d\zeta ={\int }_0^{\infty }{e}_{\lambda }^{-\zeta }{\zeta }^{w-1}d\zeta ,0<Re\left(w\right)<\frac{1}{\lambda };\lambda \in (0,1).\hfill \end{array}\end{array}$$

(5)

It is clear that ${lim}_{\lambda \to 0}{e}_{\lambda }^{\zeta }=e^{\zeta }$ and ${lim}_{\lambda \to 0}{\Gamma }_{\lambda }\left(w\right)=\Gamma \left(w\right),$ where $\Gamma \left(w\right)$ is the classical gamma function

$$\begin{array}{c}\hfill \Gamma \left(w\right)={\int }_0^{\infty }{r}^{w-1}{e}^{-r}dr,Re\left(w\right)>0.\end{array}$$

For $\lambda \in (0,1)$, we can rewrite (5) in the form

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\Gamma }_{\lambda }\left(w\right)={\lambda }^{-w}\mathbf{B}(w,\frac{1}{\lambda }-w)={\lambda }^{-w}\frac{\Gamma \left(w\right)\Gamma (\frac{1}{\lambda }-w)}{\Gamma \left(\frac{1}{\lambda }\right)}.\end{array}\end{array}$$

(6)

where

$$\begin{array}{c}\hfill \mathbf{B}(a,b)={\int }_0^1{w}^{a-1}{(1-w)}^{b-1}dw={\int }_0^{\infty }\frac{w^{a-1}}{{(1+w)}^{a+b}}dw,a>0,b>0,\end{array}$$

is the Euler beta function [33,34].

Remark 1.

Note here that (6) holds initially for $w\in \mathbb{C}$ with $0<Re\left(w\right)<\frac{1}{\lambda }$ and that it further holds for any $w\in \mathbb{C}\setminus \{0,-1,-2,\dots ,\frac{1}{\lambda },\frac{1}{\lambda }+1,\frac{1}{\lambda }+2,\dots \}$ by the analytic continuation, and defines an analytic function on $\mathbb{C}\setminus \{0,-1,-2,\dots ,\frac{1}{\lambda },\frac{1}{\lambda }+1,\frac{1}{\lambda }+2,\dots \}.$

Recently, Yağci and Şahin [37] introduced the degenerate Pochhammer symbol using the degenerate gamma function (5) as follows:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {(\varpi ;\lambda )}_{\ell }& =\frac{{\Gamma }_{\lambda }(\varpi +\ell )}{\Gamma \left(\varpi \right)}\hfill \\ & =\frac{1}{\Gamma \left(\varpi \right)}{\int }_0^{\infty }{(1+\lambda w)}^{-\frac{1}{\lambda }}{w}^{\varpi +\ell -1}dw,\lambda >Re(\varpi +\ell )>0,\hfill \end{array}\end{array}$$

(7)

where $\lambda \in (0,1)$ and ${lim}_{\lambda \to 0}{(\varpi ;\lambda )}_{\ell }={\left(\varpi \right)}_{\ell },$

$$\begin{array}{c}\hfill {\left(\varpi \right)}_{\ell }=\frac{\Gamma (\varpi +\ell )}{\Gamma \left(\varpi \right)}=\left\{\begin{array}{cc}\varpi (\varpi +1)\cdots (\varpi +\ell -1),\hfill & \ell \in \mathbb{N},\varpi \in \mathbb{C}\hfill \\ \\ 1,\hfill & \ell =0;\varpi \in \mathbb{C}\setminus \left\{0\right\},\hfill \end{array}\right.\end{array}$$

(8)

is the standard Pochhammer symbol. The degenerate Pochhammer symbol (7) satisfied several properties in [37]. Also, based on the definition (7), the GDHF is defined in [37] as

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_m{\mathbb{DH}}_n^{\lambda }\left(w\right)={}_m{\mathbb{DH}}_n^{\lambda }\left[\begin{array}{c}({\gamma }_1;\lambda )\cdots {\gamma }_m\\ \\ {\vartheta }_1\cdots {\vartheta }_n\end{array};w\right]& =\sum _{r=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_r\cdots {\left({\gamma }_m\right)}_r}{{\left({\vartheta }_1\right)}_r\cdots {\left({\vartheta }_n\right)}_r}.\frac{w^r}{r!},\hfill \end{array}\end{array}$$

(9)

where $w,{\gamma }_i\in \mathbb{C}$ for $i=1,2,3,\dots ,m,$ and ${\vartheta }_j\in \mathbb{C}\setminus {\mathbb{Z}}_0^{-}$ for $j=1,2,3,\dots ,n.$

Remark 2.

Some particular cases of (9) are as follows

(I) 

For $\lambda \to 0$ in (9), we obtain the classical generalized hypergeometric function (see, e.g., [38] [Section 1.5]))

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {}_m{\mathbf{F}}_n\left[\begin{array}{c}{\gamma }_1\dots {\gamma }_m\\ \\ {\vartheta }_1\dots {\vartheta }_n\end{array};w\right]& =\sum _{r=0}^{\infty }\frac{{\left({\gamma }_1\right)}_r\dots {\left({\gamma }_m\right)}_r}{{\left({\vartheta }_1\right)}_r\dots {\left({\vartheta }_n\right)}_r}.\frac{w^r}{r!},\hfill \end{array}\end{array}$$

(10)

where $w,{\gamma }_i\in \mathbb{C}$ for $i=1,2,3,\dots ,m,$ and ${\vartheta }_j\in \mathbb{C}\setminus {\mathbb{Z}}_0^{-}$ for $j=1,2,3,\dots ,n.$

(II) 

Taking $m=2$ and $n=1$ in (9), we have the following degenerate Gauss hypergeometric function

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {}_2{\mathbb{DH}}_1^{\lambda }\left(({\gamma }_1;\lambda ),{\gamma }_2,{\vartheta }_3;w\right)=\sum _{j=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_j{\left({\gamma }_2\right)}_j}{{\left({\vartheta }_3\right)}_j}\frac{w^j}{j!},w\in \mathbb{C},\end{array}\end{array}$$

(11)

which is absolutely and uniformly convergent if $\left|w\right|<1$, where ${\gamma }_1,{\gamma }_2,{\vartheta }_3$ are complex parameters with ${\vartheta }_3\in \mathbb{C}\setminus {\mathbb{Z}}_0^{-}.$

(III) 

Substituting $m=1$ and $n=1$ in (9), we have the following degenerate Kummer (confluent) hypergeometric function

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {}_1{\mathbb{DH}}_1^{\lambda }\left(({\gamma }_1;\lambda ),{\vartheta }_3;w\right)=\sum _{j=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_j}{{\left({\vartheta }_3\right)}_j}\frac{w^j}{j!},w\in \mathbb{C}.\end{array}\end{array}$$

(12)

(VI) 

For $\lambda \to 0,$ (11) gives the classical Gauss hypergeometric function [38]

$$\begin{array}{c}\hfill {}_2{\mathbf{F}}_1\left({\theta }_1,{\theta }_2,{\theta }_3;w\right)=\sum _{j=0}^{\infty }\frac{{\left({\theta }_1\right)}_j{\left({\theta }_2\right)}_j}{{\left({\theta }_3\right)}_j}\frac{w^j}{j!},\end{array}$$

(13)

which is absolutely and uniformly convergent if $\left|w\right|<1$, where $w,{\theta }_1,{\theta }_2$ are complex parameters with ${\theta }_3\in \mathbb{C}\setminus {\mathbb{Z}}_0^{-},$ and (12) lead to the classical Kummer (confluent) hypergeometric function [38]

$$\begin{array}{c}\hfill {}_1{\mathbf{F}}_1\left({\theta }_1,{\theta }_2;w\right)=\sum _{j=0}^{\infty }\frac{{\left({\theta }_1\right)}_j}{{\left({\theta }_2\right)}_j}\frac{w^j}{j!},\end{array}$$

(14)

where ${\theta }_1,w\in \mathbb{C}$ and ${\theta }_2\in \mathbb{C}\setminus {\mathbb{Z}}_0^{-}.$

The derivative formula of the GDHF ${}_m{\mathbb{DH}}_n^{\lambda }\left(w\right)$ is given in [37] by

$$\begin{array}{c}\hfill \begin{array}{cc}& {\left({}_m{\mathbb{DH}}_n^{\lambda }\left(w\right)\right)}^{\left(k\right)}=\frac{{\mathrm{d}}^k}{\mathrm{d}{w}^k}{}_m{\mathbb{DH}}_n^{\lambda }\left[\begin{array}{c}({\gamma }_1;\lambda )\cdots {\gamma }_m\\ \\ {\vartheta }_1,\cdots {\vartheta }_n\end{array};w\right]\hfill \\ & =\frac{{\left({\gamma }_1\right)}_k,\cdots {\left({\gamma }_m\right)}_k}{{\left({\vartheta }_1\right)}_k,\cdots {\left({\vartheta }_n\right)}_k}{}_m{\mathbb{DH}}_n^{\lambda }\left[\begin{array}{c}({\gamma }_1+k;\lambda )\cdots {\gamma }_m+k\\ \\ {\vartheta }_1+k,\cdots {\vartheta }_n+k\end{array};w\right],k\in \mathbb{N}.\hfill \end{array}\end{array}$$

(15)

3. Pathway-Type Transform

The pathway-type integral transform (${\mathit{P}}_{\varsigma }-$transform) of a function $f\left(w\right)$, of a real variable w, denoted by ${\mathit{P}}_{\varsigma }[f\left(w\right);\phi ],$ is an important concept in mathematics. It has been defined initially in [15,39,40] under certain conditions on $f\left(w\right)$, as well as the condition $\varsigma >1$. This transform can be used to convert a given function from its original domain into another domain and can thus provide insight into the properties and behavior of the original functions. Moreover, the pathway-type integral transform is regarded as one of the most helpful mathematics tools and has numerous applications (see, e.g., [41,42,43]). Indeed, the pathway-type integral transform is strongly linked to the Laplace transform, the Mellin transform, and the Fourier transform; see for example [15,43,44].

The pathway-type transform (${\mathit{P}}_{\varsigma }-$transform) is given in [15,39,40] in the form

$$\begin{array}{c}\hfill {\mathit{P}}_{\varsigma }[f\left(w\right),\phi ]=F\left(\phi \right)={\int }_0^{\infty }{[1+(\varsigma -1)\phi ]}^{\frac{-w}{\varsigma -1}}f\left(w\right)dw\varsigma >1,\end{array}$$

(16)

with

$$\begin{array}{c}\hfill \underset{\varsigma \to 1^{+}}{lim}{[1+(\varsigma -1)\phi ]}^{\frac{-w}{\varsigma -1}}=e^{-\varphi w},\end{array}$$

(17)

and

$$\begin{array}{c}\hfill \underset{\varsigma \to 1^{+}}{lim}{\mathit{P}}_{\varsigma }[f\left(w\right),\phi ]=\mathrm{L}[f\left(w\right),\phi ],\end{array}$$

(18)

where $\left(\mathrm{L}\right[.,.\left]\right)$ is the Laplace transform (see, [1,2]). Moreover, the ${\mathit{P}}_{\varsigma }$-transform of a function $f\left(w\right)$ converges under certain conditions as established in [39] by the following theorem.

Theorem 1.

If

(i) 

$f\left(w\right)$ is integrable over a finite limit $(a,b),0<a<w<b,$;

(ii) 

for arbitrary positive $a,$ the integral ${\int }_{\upsilon }^a\left|f\left(w\right)\right|dw$ resort to a finite limit as $\upsilon \to 0^{+},$;

(iii) 

$f\left(w\right)=\mathcal{O}\left(e^{\epsilon w}\right),\epsilon >0$ as $w\to \infty$ where $\mathcal{O}(.)$ is the standard big $\mathcal{O}$ notation which means $f\left(w\right)$ is of order not exceeding $e^{\epsilon w}.$

Then the ${\mathit{P}}_{\varsigma }-$ transform defined in (16) converges absolutely if $Re\left(\frac{ln(1+(\varsigma -1\left)\phi \right)}{\varsigma -1}\right)>\epsilon ,\varsigma >1.$

Some basic results of the ${\mathit{P}}_{\varsigma }-$ transform are proven in [39,40] as follows

$$\begin{array}{c}\hfill {\mathit{P}}_{\varsigma }[1,\phi ]=\frac{\varsigma -1}{ln[1+(\varsigma -1\left)\phi \right]},\end{array}$$

(19)

$$\begin{array}{c}\hfill {\mathit{P}}_{\varsigma }[w^{\upsilon },\phi ]={\left\{\frac{\varsigma -1}{ln[1+(\varsigma -1\left)\phi \right]}\right\}}^{\upsilon +1}\Gamma (\upsilon +1),\upsilon \in \mathbb{C},\end{array}$$

(20)

and

$$\begin{array}{c}\hfill {\mathit{P}}_{\varsigma }{[}_0{\mathbb{D}}_w^{-\alpha }f\left(w\right),\phi ]={\left[\frac{\varsigma -1}{ln[1+(\varsigma -1\left)\phi \right]}\right]}^{\alpha }{\mathit{P}}_{\varsigma }[f\left(w\right),\phi ],Re\left(\alpha \right)>0,\varsigma >1,\end{array}$$

(21)

where ${}_0{\mathbb{D}}_w^{-\alpha }f\left(w\right)$ is given in (3). More information about the ${\mathit{P}}_{\varsigma }-$transform and its applications may be found in [15,39,40,45,46,47,48].

4. Main Results

The purpose of this section is to study the solutions of the new generalized form of the fractional $\lambda -$kinetic equations involving GDHFs, as well as some special cases.

Theorem 2.

Let $\alpha ,\beta ,\sigma ,\wp \in {\mathbb{R}}^{+},w\in \mathbb{C},\lambda \in (0,1),{\gamma }_i\in \mathbb{C}$ for $i=1,2,3,\dots ,m$ and ${\vartheta }_j\in \mathbb{C}\setminus {\mathbb{Z}}_0^{-}$ for $j=1,2,3,\dots ,n.$ The solution of

$$\begin{array}{c}\hfill \mathcal{K}\left(w\right)-{\mathcal{K}}_0{}_m{\mathbb{DH}}_n^{\lambda }\left({\sigma }^{\beta }{w}^{\beta }\right)=-{\wp }^{\alpha }{}_0{\mathbb{D}}_w^{-\alpha }\mathcal{K}\left(w\right),\end{array}$$

(22)

is

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)={\mathcal{K}}_0\sum _{r=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_r\cdots {\left({\gamma }_m\right)}_r}{{\left({\vartheta }_1\right)}_r\cdots {\left({\vartheta }_n\right)}_r}\frac{\Gamma (\beta r+1)}{r!}{\sigma }^{\beta r}{w}^{r\beta }{\mathrm{E}}_{\alpha ,\beta r+1}(-{\wp }^{\alpha }{w}^{\alpha }),\end{array}\end{array}$$

(23)

where ${\mathrm{E}}_{\theta ,\vartheta }\left(\eta \right)$ is the generalized Mittag-Leffler function defined in [15] as

$$\begin{array}{c}\hfill \begin{array}{c}\hfill E_{\theta ,\vartheta }\left(\eta \right)=\sum _{ɩ=0}^{\infty }\frac{{\eta }^{ɩ}}{\Gamma (ɩ\theta +\vartheta )}(\theta ,\vartheta \in \mathbb{C},Re\left(\theta \right)>0,Re\left(\vartheta \right)>0).\end{array}\end{array}$$

(24)

Proof. 

Projecting the Equation (22) to the ${\mathit{P}}_{\varsigma }$-transform (16) and using the relations (20), (21), and (9), we observe that

$$\begin{array}{c}\hfill \begin{array}{cc}& \widehat{\mathcal{K}}\left(\phi \right)-{\mathcal{K}}_0\sum _{r=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_r\cdots {\left({\gamma }_m\right)}_r}{{\left({\vartheta }_1\right)}_r\cdots {\left({\vartheta }_n\right)}_r}{\sigma }^{r\beta }{\mathit{P}}_{\varsigma }\left\{\frac{w^{r\beta }}{r!}:\phi \right\}\hfill \\ & =-{\wp }^{\alpha }{\left[\frac{\varsigma -1}{ln[1+(\varsigma -1\left)\phi \right]}\right]}^{\alpha }.\hfill \end{array}\end{array}$$

Hence,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \widehat{\mathcal{K}}\left(\phi \right)& ={\mathcal{K}}_0{\left[1+{\left(\frac{\wp (\varsigma -1)}{ln[1+(\varsigma -1\left)\phi \right]}\right)}^{\alpha }\right]}^{-1}\hfill \\ & \times \sum _{r=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_r\cdots {\left({\gamma }_m\right)}_r}{{\left({\vartheta }_1\right)}_r\cdots {\left({\vartheta }_n\right)}_r}{\sigma }^{r\beta }\frac{\Gamma (r\beta +1)}{r!}{\left[\frac{\varsigma -1}{ln[1+(\varsigma -1\left)\phi \right]}\right]}^{r\beta +1},\hfill \end{array}\end{array}$$

where $\widehat{\mathcal{K}}\left(\phi \right)={\mathit{P}}_{\varsigma }\left\{{\mathit{P}}_{\varsigma }\left(w\right):\phi \right\}.$ Upon using the following geometric series

$$\begin{array}{c}\hfill \begin{array}{c}\hfill \frac{1}{\left[1+{\left\{\frac{\wp (\varsigma -1)}{ln\{1+(\varsigma -1\left)\phi \right\}}\right\}}^{\alpha }\right]}=\sum _{\ell =0}^{\infty }{(-1)}^{\ell }{\left(\frac{\wp (\varsigma -1)}{ln\{1+(\varsigma -1\left)\phi \right\}}\right)}^{\ell \alpha }\left(\left|\frac{\wp (\varsigma -1)}{ln\{1+(\varsigma -1\left)\phi \right\}}\right|<1\right),\end{array}\end{array}$$

and simple computation yields

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \widehat{\mathcal{K}}\left(\phi \right)& ={\mathcal{K}}_0\sum _{r=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_r\cdots {\left({\gamma }_m\right)}_r}{{\left({\vartheta }_1\right)}_r\cdots {\left({\vartheta }_n\right)}_r}{\sigma }^{r\beta }\frac{\Gamma (r\beta +1)}{r!}\hfill \\ & \times \sum _{\ell =0}^{\infty }{(-1)}^{\ell }{\wp }^{\ell \alpha }{(\varsigma -1)}^{r\beta +\ell \alpha +1}{\left\{ln[1+(\varsigma -1)\phi \right\}}^{-(r\beta +\ell \alpha +1)}.\hfill \end{array}\end{array}$$

(25)

Applying the inverting ${\mathcal{P}}_{\varsigma }-$transform to the last equation and making use of the relation (24), we arrive at the desired result. □

Theorem 3.

Assume that $\alpha ,\wp \in {\mathbb{R}}^{+},w\in \mathbb{C},\lambda \in (0,1),{\gamma }_i\in \mathbb{C}$ for $i=1,2,3,\dots ,m$ and ${\vartheta }_j\in \mathbb{C}\setminus {\mathbb{Z}}_0^{-}$ for $j=1,2,3,\dots ,n.$ The solution of

$$\begin{array}{c}\hfill \mathcal{K}\left(w\right)-{\mathcal{K}}_0{}_m{\mathbb{DH}}_n^{\lambda }\left(w\right)=-{\wp }^{\alpha }{}_0{\mathbb{D}}_w^{-\alpha }\mathcal{K}\left(w\right),\end{array}$$

(26)

is

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)={\mathcal{K}}_0\sum _{r=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_r\cdots {\left({\gamma }_m\right)}_r}{{\left({\vartheta }_1\right)}_r\cdots {\left({\vartheta }_n\right)}_r}{w}^r{\mathrm{E}}_{\alpha ,r+1}(-{\wp }^{\alpha }{w}^{\alpha }),\end{array}\end{array}$$

(27)

where ${\mathrm{E}}_{\theta ,\vartheta }\left(\eta \right)$ is defined in (24).

Proof. 

We obtain the required result in the same manner as provided in the proof of Theorem 2; thus, the details have been avoided. □

Theorem 4.

Suppose that $\alpha ,\wp \in {\mathbb{R}}^{+},w\in \mathbb{C},\lambda \in (0,1),{\gamma }_i\in \mathbb{C}$ for $i=1,2,3,\dots ,m$ and ${\vartheta }_j\in \mathbb{C}\setminus {\mathbb{Z}}_0^{-}$ for $j=1,2,3,\dots ,n.$ The solution of

$$\begin{array}{c}\hfill \mathcal{K}\left(w\right)-{\mathcal{K}}_0{}_m{\mathbb{DH}}_n^{\lambda }\left({\wp }^{\alpha }{w}^{\alpha }\right)=-{\wp }^{\alpha }{}_0{\mathbb{D}}_w^{-\alpha }\mathcal{K}\left(w\right),\end{array}$$

(28)

is

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)={\mathcal{K}}_0\sum _{r=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_r\cdots {\left({\gamma }_m\right)}_r}{{\left({\vartheta }_1\right)}_r\cdots {\left({\vartheta }_n\right)}_r}\frac{\Gamma (\alpha r+1)}{r!}{w}^{r\alpha }{\mathrm{E}}_{\alpha ,\alpha r+1}(-{\wp }^{\alpha }{w}^{\alpha }),\end{array}\end{array}$$

(29)

where ${\mathrm{E}}_{\theta ,\vartheta }\left(\eta \right)$ is defined in (24).

Proof. 

The proof is similar to that of Theorem 2 with choosing $\sigma =\wp$ and $\alpha =\beta .$ □

Theorem 5.

Let $\sigma ,\alpha ,\wp \in {\mathbb{R}}^{+},\sigma \ne \wp ,w\in \mathbb{C},\lambda \in (0,1),{\gamma }_i\in \mathbb{C}$ for $i=1,2,3,\dots ,m$ and ${\vartheta }_j\in \mathbb{C}\setminus {\mathbb{Z}}_0^{-}$ for $j=1,2,3,\dots ,n.$ The solution of

$$\begin{array}{c}\hfill \mathcal{K}\left(w\right)-{\mathcal{K}}_0{}_m{\mathbb{DH}}_n^{\lambda }\left({\wp }^{\alpha }{w}^{\alpha }\right)=-{\sigma }^{\alpha }{}_0{\mathbb{D}}_w^{-\alpha }\mathcal{K}\left(w\right),\end{array}$$

(30)

is given by

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)={\mathcal{K}}_0\sum _{r=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_r\cdots {\left({\gamma }_m\right)}_r}{{\left({\vartheta }_1\right)}_r\cdots {\left({\vartheta }_n\right)}_r}\frac{\Gamma (\alpha r+1)}{r!}{\left({\wp }^{\alpha }{w}^{\alpha }\right)}^r{\mathrm{E}}_{\alpha ,\alpha r+1}(-{\sigma }^{\alpha }{w}^{\alpha }).\end{array}\end{array}$$

(31)

${\mathrm{E}}_{\theta ,\vartheta }\left(\eta \right)$ is the generalized Mittag-Leffler function defined in (24).

Proof. 

The proof runs in parallel with that of Theorem 2 when $\alpha =\beta ,\sigma \ne \wp ,$ and $\sigma ⟷\wp .$ □

Theorem 6.

Let $\alpha ,\wp \in {\mathbb{R}}^{+},w\in \mathbb{C},\lambda \in (0,1)$ with ${\gamma }_i\in \mathbb{C}$ for $i=1,2,3,\dots ,m$ and ${\vartheta }_j\in \mathbb{C}\setminus {\mathbb{Z}}_0^{-}$ for $j=1,2,3,\dots ,n.$ The solution of the following equation

$$\begin{array}{c}\hfill \mathcal{K}\left(w\right)-{\mathcal{K}}_0{\left\{{}_m{\mathbb{DH}}_n^{\lambda }\left(w\right)\right\}}^{\left(k\right)}=-{\wp }^{\alpha }{}_0{\mathbb{D}}_w^{-\alpha }\mathcal{K}\left(w\right),\end{array}$$

(32)

is given by

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)& ={\mathcal{K}}_0\frac{{\left({\gamma }_1\right)}_k,\cdots {\left({\gamma }_m\right)}_k}{{\left({\vartheta }_1\right)}_k,\cdots {\left({\vartheta }_n\right)}_k}\hfill \\ & \times \sum _{r=0}^{\infty }\frac{{({\gamma }_1+k;\lambda )}_r\cdots {({\gamma }_m+k)}_r}{{({\vartheta }_1+k)}_r\cdots {({\vartheta }_n+k)}_r}{w}^r{\mathrm{E}}_{\alpha ,r+1}(-{\wp }^{\alpha }{w}^{\alpha }),\hfill \end{array}\end{array}$$

(33)

where ${\mathrm{E}}_{\theta ,\vartheta }\left(\eta \right)$ is defined in (24).

Proof. 

By taking the ${\mathcal{P}}_{\varsigma }$-transform of both sides of (30) and then using (15), we can obtain the proof as in Theorem 2. □

Special Cases

Some examples of special cases of the theorems mentioned earlier are archived as

Example 1.

By insert (10) into (22), we have

$$\begin{array}{c}\hfill \mathcal{K}\left(w\right)-{\mathcal{K}}_0{}_m{\mathbf{F}}_n\left[\begin{array}{c}{\gamma }_1\dots {\gamma }_m\\ \\ {\vartheta }_1\dots {\vartheta }_n\end{array};{\sigma }^{\beta }{w}^{\beta }\right]=-{\wp }^{\alpha }{}_0{\mathbb{D}}_w^{-\alpha }\mathcal{K}\left(w\right),\end{array}$$

(34)

the solution of which is

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)={\mathcal{K}}_0\sum _{r=0}^{\infty }\frac{{\left({\gamma }_1\right)}_r\cdots {\left({\gamma }_m\right)}_r}{{\left({\vartheta }_1\right)}_r\cdots {\left({\vartheta }_n\right)}_r}\frac{\Gamma (\beta r+1)}{r!}{\sigma }^{\beta r}{w}^{r\beta }{\mathrm{E}}_{\alpha ,\beta r+1}(-{\wp }^{\alpha }{w}^{\alpha }),\end{array}\end{array}$$

(35)

where ${\mathrm{E}}_{\theta ,\vartheta }\left(\eta \right)$ is defined in (24).

Example 2.

Upon inserting (10) into (32), we arrive at

$$\begin{array}{c}\hfill \mathcal{K}\left(w\right)-{\mathcal{K}}_0{\left\{{}_m{\mathbf{F}}_n\left(w\right)\right\}}^{\left(k\right)}=-{\wp }^{\alpha }{}_0{\mathbb{D}}_w^{-\alpha }\mathcal{K}\left(w\right),\end{array}$$

(36)

and its solution is

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)& ={\mathcal{K}}_0\frac{{\left({\gamma }_1\right)}_k,\cdots {\left({\gamma }_m\right)}_k}{{\left({\vartheta }_1\right)}_k,\cdots {\left({\vartheta }_n\right)}_k}\hfill \\ & \times \sum _{r=0}^{\infty }\frac{{({\gamma }_1+k)}_r\cdots {({\gamma }_m+k)}_r}{{({\vartheta }_1+k)}_r\cdots {({\vartheta }_n+k)}_r}{w}^r{\mathrm{E}}_{\alpha ,r+1}(-{\wp }^{\alpha }{w}^{\alpha }),\hfill \end{array}\end{array}$$

(37)

where ${\mathrm{E}}_{\theta ,\vartheta }\left(\eta \right)$ is defined in (24).

Example 3.

By invoking (11) into (22), we obtain

$$\begin{array}{c}\hfill \mathcal{K}\left(w\right)-{\mathcal{K}}_0{}_2{\mathbb{DH}}_1^{\lambda }\left({\sigma }^{\beta }{w}^{\beta }\right)=-{\wp }^{\alpha }{}_0{\mathbb{D}}_w^{-\alpha }\mathcal{K}\left(w\right),\end{array}$$

(38)

the solution of which is

$$\begin{array}{c}\hfill \begin{array}{c}\hfill {\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)={\mathcal{K}}_0\sum _{r=0}^{\infty }\frac{{({\gamma }_1;\lambda )}_r{\left({\gamma }_2\right)}_r}{{\left({\vartheta }_1\right)}_r}\frac{\Gamma (\beta r+1)}{r!}{\sigma }^{\beta r}{w}^{r\beta }{\mathrm{E}}_{\alpha ,\beta r+1}(-{\wp }^{\alpha }{w}^{\alpha }),\end{array}\end{array}$$

(39)

where ${\mathrm{E}}_{\theta ,\vartheta }\left(\eta \right)$ is defined in (24).

Remark 3.

The results already established in [6,7,8,9,15,16,17] can be easily obtained as special cases by applying the functions in Remark 2 to Theorems 2–6, which gives us a more comprehensive understanding of the topic and allows for further exploration.

5. Numerical Representations of the Solutions

In this section, we give graphical representations of the solutions discussed in the previous section for certain values of their parameters. Figure 1 depicts the plots of the solutions to Equation (23) with the chosen values for the parameters as ${\mathcal{K}}_0=1,m=2,$$n=3,$ and $w=1,2,\dots ,5$ for different values of $\lambda$ in the interval $(0,1)$. In Figure 1A–C, we set the value of $\alpha$ to $0.05$ while that for $\beta ,\sigma ,$ and ℘ equal 1. We notice that the shape of the solutions when the values of $\lambda$ in the interval $(\frac{1}{r+{\gamma }_1},\frac{1}{r+{\gamma }_1-1})$ tend to be negative because of the negative values of the degenerate gamma function (6) in this interval, as shown in Figure 1A. However, for $\lambda$ being in $(0,\frac{1}{r+{\gamma }_1})$ and $(\frac{1}{r+{\gamma }_1-1},1),$ we observe positive valued solutions, which are large for small values of $\lambda$ and smaller for its values when approaching one, as shown in Figure 1B and Figure 1C, respectively.

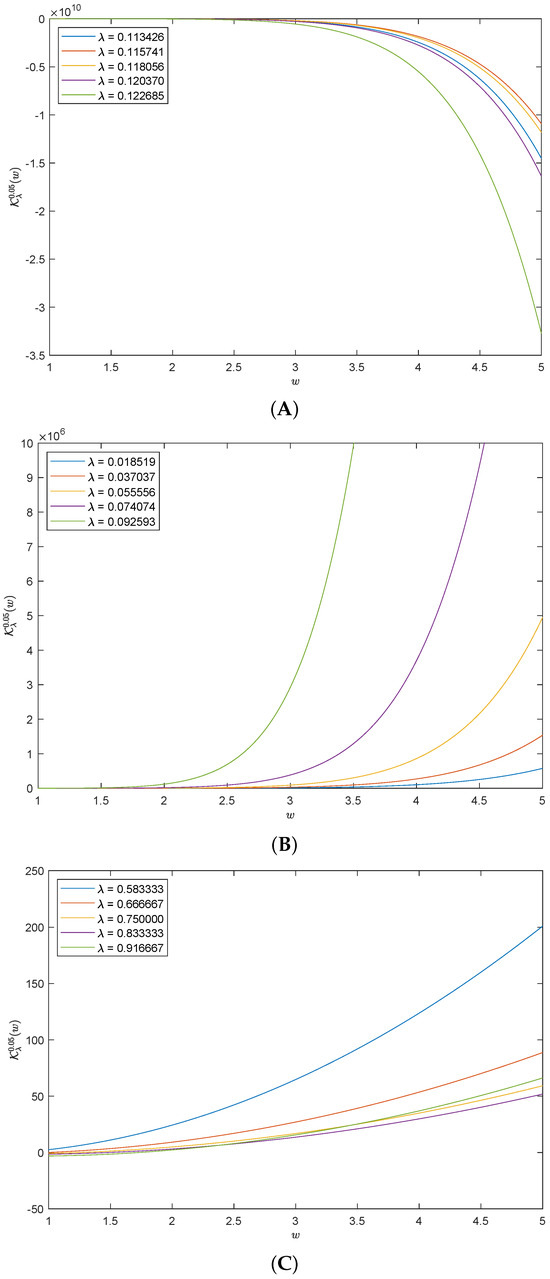
Figure 1. Solutions of (23) of ${\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)$ with different values of $\lambda$ in (A–C).

To illustrate the impact of $\alpha$ in the solutions of Equation (23), we fix the values of $\lambda$ to be $0.118,0.055,0.75$ while choosing 1 to be the values of $\beta ,\sigma ,\wp ,{\mathcal{K}}_0,$ and setting $m=2,n=3$ in Figure 2. A similar pattern to the solutions in Figure 1 can be seen clearly for various values of $\alpha$ in Figure 2A–C, with small-scale deviation in the solutions as $\alpha$ increases. Moreover, the large values of $\beta$ lead to the large solutions while the small values of $\beta$ lead to the small solutions in Figure 3, with fixed values of $\sigma =\wp ={\mathcal{K}}_0=1,\alpha =0.05,$ and $\lambda =0.055.$ Furthermore, we could change the values of $\alpha ,\beta ,$ and $\lambda$ to obtain more accurate solutions that do not appear in previous works.

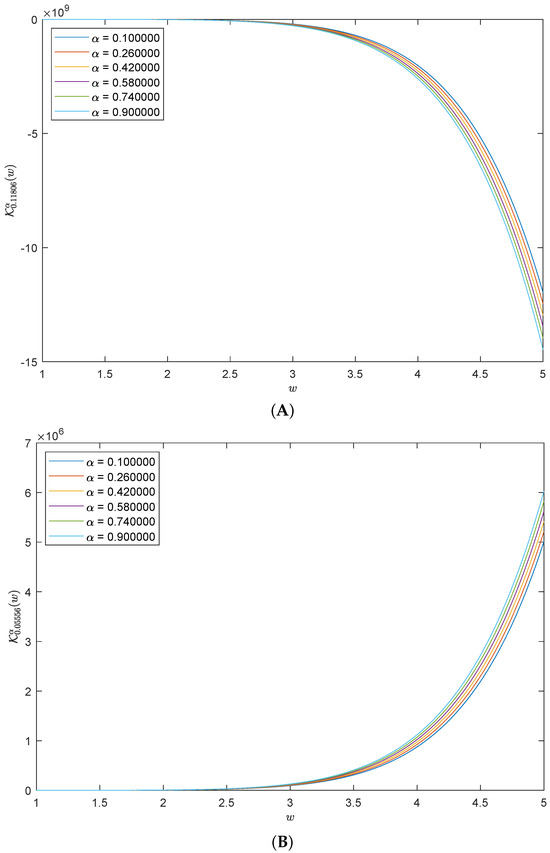
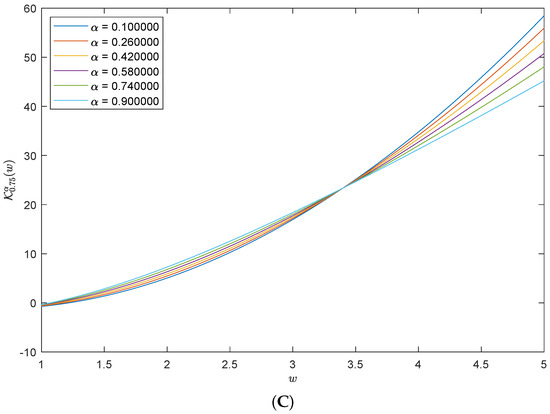
Figure 2. Solutions of (23) of ${\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)$ with different values of $\alpha$ in (A–C).

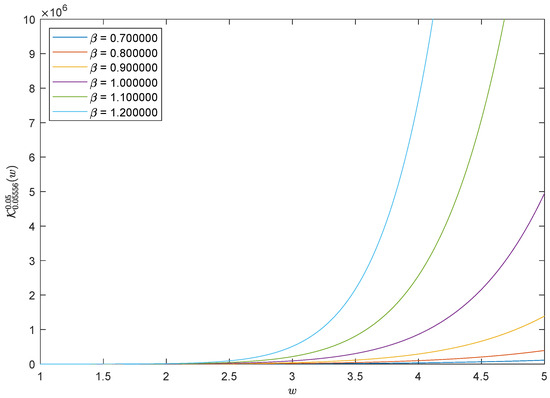
Figure 3. Solution of (23) for ${\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)$ with different values of $\beta$.

To show the significance of the derivatives of the GDHF in the solutions of Equation (33) in Figure 3, we fix the values of $\beta ,\sigma ,\wp ,{\mathcal{K}}_0$ to equal $1,$ and set $m=2,n=3$ with the different values of $\lambda$ in Figure 4A and of $\alpha$ in Figure 4B.

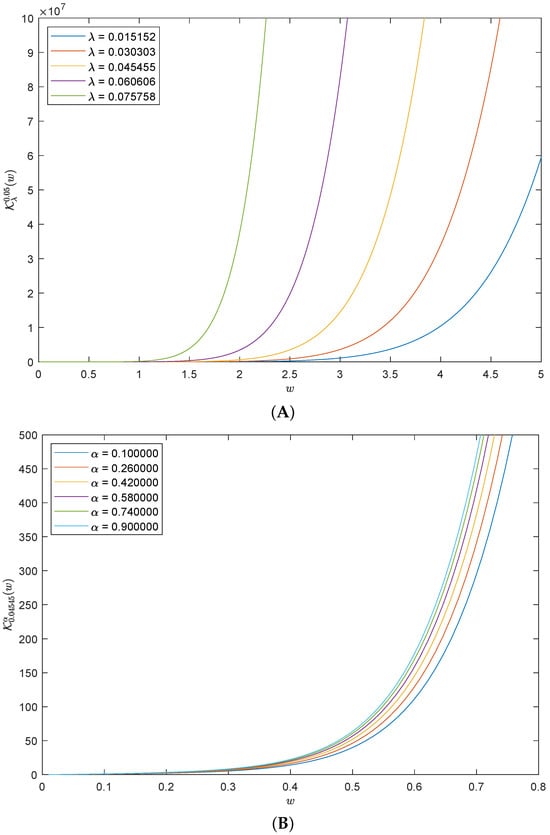
Figure 4. Solutions of (33) of ${\mathcal{K}}_{\lambda }^{\alpha }\left(w\right)$ with different values of $\lambda$ and $\alpha$ in (A,B).

6. Conclusions

The KE has been widely studied due to its usefulness in astrophysical issues and others. Recently, FKEs have been investigated to describe anomalous reactions in dynamical systems [1,2,3,4]. Various researchers have established solutions to these families of FKEs using Laplace transform [6,7,8,9], Millen transform [49], Sumudu transform [10,11], and pathway-type transform [15,39,40]. To expand upon this research base, the authors developed a new and generalized form of the $\lambda -$KEFO involving GDHFs. This new generalization can be used for computing changes in chemical composition, such as those found within stars like our sun [20,50].

Furthermore, we used the ${\mathit{P}}_{\varsigma }-$ transform approach, but other authors applied different transform techniques, and existing results are particular cases of these results, implying that the current work is a generalization. Further, our analysis yields detailed and different results from those presented in previous studies and various situations of known and new results. In addition, plotting the solutions numerically was also supplied to show their conduct and examine unique cases for FKEs.