A Novel Eighth-Order Hyperchaotic System and Its Application in Image Encryption

Abstract

With the advancement in information and communication technologies (ICTs), the widespread dissemination and sharing of digital images has raised concerns regarding privacy and security. Traditional methods of encrypting images often suffer from limitations such as a small key space and vulnerability to brute-force attacks. To address these issues, this paper proposes a novel eighth-order hyperchaotic system. This hyperchaotic system exhibits various dynamic behaviors, including hyperchaos, sub-hyperchaos, and chaos. The encryption scheme based on this system offers a key space larger than 2²³³⁸. Through a comprehensive analysis involving histogram analysis, key space analysis, correlation analysis, entropy analysis, key sensitivity analysis, differential attack analysis, and cropping attack analysis, it is demonstrated that the proposed system is capable of resisting statistical attacks, brute force attacks, differential attacks, and cropping attacks, thereby providing excellent security performance.

1. Introduction

The increasing importance of digital images across various domains has been propelled by the rapid progress of information and communication technologies (ICTs). However, the widespread dissemination and sharing of digital images on a large scale have given rise to apprehensions surrounding issues of privacy and security. In order to mitigate these concerns, image encryption technology is widely employed to ensure the confidentiality and integrity of images on diverse devices [1], such as medical, military, satellite, and Internet of Things applications [2]. As a result, addressing these issues has become a critical and urgent challenge in these fields [3].

In recent decades, numerous symmetric image encryption methods have been proposed [4]. Specifically, image encryption techniques based on the Data Encryption Standard (DES) and Advanced Encryption Standard (AES) have been extensively researched and implemented in the field of symmetric encryption. Nevertheless, the security of traditional symmetric encryption algorithms is increasingly being challenged due to the continuous enhancement of computing power and the constant development of cryptanalysis technology. Research indicates that symmetric encryption suffers from drawbacks such as a limited key space and vulnerability to brute force attacks [5].

To overcome these limitations, researchers have turned to chaotic systems that exhibit desirable properties such as high ergodicity, aperiodicity, and sensitivity to initial values [3]. Due to the fact that it is crucial to deliver messages with complete security and to execute them online [6], it is possible to employ chaotic systems to safeguard the security of data transfer and advance the “industrial 4.0 revolution” being developed [7]. Chaotic systems have also been found to be efficient and effective in image encryption. For instance, the Lorenz chaotic system has been applied to image encryption [8], providing strong security and high resistance against common attacks [9]. Another example is the 2D-SCL map, which exhibits good ergodicity and hyperchaotic behavior [10]. However, most existing chaotic systems are traditional chaotic systems that encounter issues such as a small key space and a lack of capability to resist brute force attacks, statistical attacks, and differential attacks. Particularly in light of the developing deep learning landscape [11,12,13], the capacity to analyze complex issues has grown. Therefore, the pursuit of more secure and efficient encryption schemes is an appealing research direction [14].

A hyperchaotic system is characterized by having at least two positive Lyapunov exponents, indicating that its dynamics expand in more than one direction and give rise to a more complex attractor [15]. By increasing the system dimension and incorporating nonlinear terms, the dynamics of a hyperchaotic system become more complex and unpredictable. Compared to traditional chaotic systems, hyperchaotic systems exhibit higher key sensitivity, unpredictability, and pseudo-random properties [16].

In order to establish a more secure system, this work proposes an image encryption algorithm based on a novel eighth-order hyperchaotic system. Dynamic analysis demonstrates that the hyperchaostic system has extremely rich dynamical behaviors, including hyperchaotic, sub-hyperchaotic, chaotic, and limit cycle attractors. On this basis, the image encryption scheme based on this algorithm fully guarantees the confidentiality and integrity of the image by utilizing two different states of the hyperchaotic system [1]. Additionally, it incorporates steps such as row scrambling, column scrambling, and diffusion to enhance security at a higher level. Furthermore, through various analyses of the encryption scheme, including key sensitivity, key space, image histogram, pixel correlation, and other indicators, it has been demonstrated that the proposed algorithm possesses a high level of security and robustness.

The rest of this paper is organized as follows: Section 2 introduces the novel eighth-order hyperchaotic system and analyzes its dynamic characteristics. Section 3 provides an overview of the encryption and decryption schemes based on this system. The experimental results and detailed security analysis are presented in Section 4. Finally, Section 5 concludes the paper.

2. A Novel Eighth-Order Hyperchaotic System and Its Basic Properties

2.1. Equations of a Novel Eighth-Order Hyperchaotic System

Nowadays, some researchers propose low-dimensional chaotic systems to generate pseudo-random sequences to encrypt the original image [17], which means that the encrypted scheme has a small key space and is vulnerable to attacks. Therefore, a higher-dimensional chaotic system is required. Ref. [18] proposed an nth-order chaotic system with hyperbolic sine:

$$\left\{\begin{array}{c}{\dot{x}}_1=x_2-x_1\hfill \\ {\dot{x}}_2=x_3-x_2\hfill \\ \dots \hfill \\ {\dot{x}}_{n-3}=x_{n-2}-x_{n-3}\hfill \\ {\dot{x}}_{n-2}=x_{n-1}\hfill \\ {\dot{x}}_{n-1}=x_n\hfill \\ {\dot{x}}_n=-x_n-f\left(x_{n-1}\right)-n{x}_{n-2}-n{x}_{n-3}-\dots -\frac{1}{2n}{x}_1\hfill \end{array}\right.$$

(1)

The nonlinear function in this system is $f\left(x_{n-1}\right)$, which is defined by $f\left(x_{n-1}\right)=\rho \sinh \left(\varphi x_{n-1}\right)$, where $\rho =1.2\times {10}^{-6}$ and $\varphi =\frac{1}{0.026}$. Based on Equation (1), the eighth-order chaotic system with hyperbolic sine is described by

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1& =x_2-x_1\hfill \\ \hfill {\dot{x}}_2& =x_3-x_2\hfill \\ \hfill {\dot{x}}_3& =x_4-x_3\hfill \\ \hfill {\dot{x}}_4& =x_5-x_4\hfill \\ \hfill {\dot{x}}_5& =x_6-x_5\hfill \\ \hfill {\dot{x}}_6& =x_7\hfill \\ \hfill {\dot{x}}_7& =x_8\hfill \\ \hfill {\dot{x}}_8& =-x_8-\rho \sinh \left(\varphi x_7\right)-8(x_6+x_5+x_4+x_3+x_2)-\frac{x_1}{16}\hfill \end{array}\right.$$

(2)

where $\rho$, $\varphi$ are control parameters. When ($\rho$, $\varphi$) = ($1.2\times {10}^{-6}$, $\frac{1}{0.026}$) and the initial conditions are (0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1), system (2) has a chaotic attractor, as shown in Figure 1 and the corresponding Lyapunov exponents of this chaotic attractor are (0.49, 0, − 0.60, −0.74, −0.99, −1.16, −1.38, −1.63). Moreover, system (2) has a unique stable equilibrium O(0, 0, 0, 0, 0, 0, 0, 0).

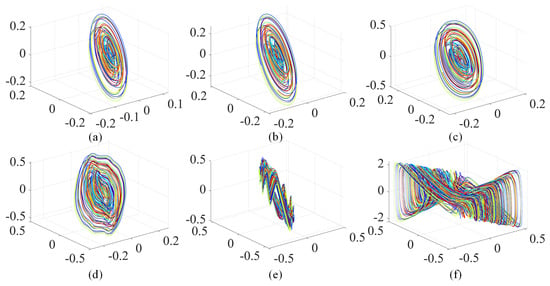
Figure 1. Chaotic attractor of system (2) with ($\rho$, $\varphi$) = ($1.2\times {10}^{-6}$, $\frac{1}{0.026}$): (a) $x_1-x_2-x_3$ phase plane; (b) $x_2-x_3-x_4$ phase plane; (c) $x_3-x_4-x_5$ phase plane; (d) $x_4-x_5-x_6$ phase plane; (e) $x_5-x_6-x_7$ phase plane; (f) $x_6-x_7-x_8$ phase plane.

By coupling a few nonlinear terms, like trigonometric and exponential functions and system (2) to increase the complexity, the following 8D chaotic system is derived:

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1& =x_2-x_1-ϵ\left(\exp \left(\varphi x_7\right)\right)+a\rho \tanh \left(x_8\right)\hfill \\ \hfill {\dot{x}}_2& =x_3-x_2+b\sin \left(x_1\right)\hfill \\ \hfill {\dot{x}}_3& =d{x}_4-x_3+\sin \left(x_5\right)\hfill \\ \hfill {\dot{x}}_4& =x_5-x_4+\sin \left(e(x_7+x_8)\right)\hfill \\ \hfill {\dot{x}}_5& =x_6-x_5-\cos \left(x_3\right)+\sin \left(x_1\right)-ϵ\left(\exp \left(\rho x_7\right)\right)\hfill \\ \hfill {\dot{x}}_6& =x_7\hfill \\ \hfill {\dot{x}}_7& =x_8+f\sin \left(x_5\right)\hfill \\ \hfill {\dot{x}}_8& =-c{x}_8-\rho \sinh \left(\varphi x_7\right)-8(x_6+x_5+x_4+x_3+x_2)-\frac{x_1}{16}\hfill \end{array}\right.$$

(3)

where $c\in [0.65,4]$; d is the constant parameter; $a,b,e,$ and f are the coupling parameters; c, $\rho$, and $\varphi$ are control parameters. When ($a,b,c,d,e,f,\rho ,\varphi$) = ($\frac{1}{2}$, 3, 1, 2, $\frac{1}{2}$, 2, $1.2\times {10}^{-6}$, $\frac{1}{0.026}$), system (3) has a unique stable equilibrium O(−0.18, −0.18, −0.35, −0.01, −0.33, 0.43, 0, 0.65) and the corresponding eight Lyapunov exponents are (0.36, 0, −0.58, −0.93, −1.04, −1.16, −1.26, 1.39). The chaotic attractor of system (3) is shown in Figure 2.

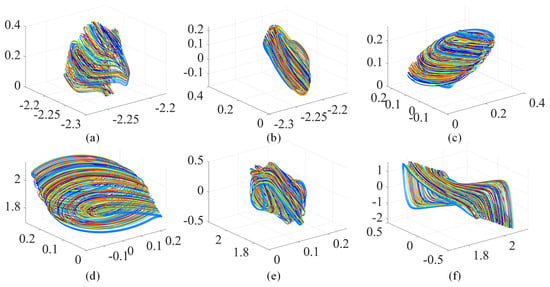
Figure 2. Chaotic attractor of system (3) with ($a,b,c,d,e,f$, $\rho$, $\varphi$) = ($\frac{1}{2}$, 3, 1, 2, $\frac{1}{2}$, 2, $1.2\times {10}^{-6}$, $\frac{1}{0.026}$): (a) $x_1-x_2-x_3$ phase plane; (b) $x_2-x_3-x_4$ phase plane; (c) $x_3-x_4-x_5$ phase plane; (d) $x_4-x_5-x_6$ phase plane; (e) $x_5-x_6-x_7$ phase plane; (f) $x_6-x_7-x_8$ phase plane.

By coupling a few linear terms and system (3) to control the scope of variables in the system and further improve the complexity [19], a novel eighth-order hyperchaotic system is proposed:

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1& =x_2-x_1-ϵ\left(\exp \left(\varphi x_7\right)\right)+a\rho \tanh \left(x_8\right)\hfill \\ \hfill {\dot{x}}_2& =x_3-x_2+b\sin \left(x_1\right)-g{x}_1\hfill \\ \hfill {\dot{x}}_3& =d{x}_4-x_3+\sin \left(x_5\right)+h{x}_7\hfill \\ \hfill {\dot{x}}_4& =x_5-x_4+\sin \left(e(x_7+x_8)\right)\hfill \\ \hfill {\dot{x}}_5& =x_6-x_5-\cos \left(x_3\right)+\sin \left(x_1\right)-ϵ\left(\exp \left(\rho x_7\right)\right)+i{x}_7\hfill \\ \hfill {\dot{x}}_6& =x_7+i{x}_8+j{x}_4\hfill \\ \hfill {\dot{x}}_7& =x_8+f\sin \left(x_5\right)+k{x}_5+l{x}_6\hfill \\ \hfill {\dot{x}}_8& =-c{x}_8-\rho \sinh \left(\varphi x_7\right)-8(x_6+x_5+x_4+x_3+x_2)\hfill \end{array}\right.$$

(4)

where $c\in [0.65,4]$; d is the constant parameter; $a,b,e,f,g,h,i,j,k,$ and l are the coupling parameters; c, $\rho$, and $\varphi$ are control parameters, determining the sub-hyperchaotic and hyperchaotic behaviors of the system [20]. Therefore, controllers c, $\rho$, and $\varphi$ and coupling parameters $a,b,e,f,g,h,i,j,k,$ and l cause the classical 8D chaotic system (2) to become a novel eighth-order hyperchaotic system (4) with two positive Lyapunov exponents [21], having eight Lyapunov exponents.

When ($a,b,c,d,e,f,g,h,i,j,k,l,\rho ,\varphi$) = ($\frac{1}{2}$, 3, 0.75, 2, $\frac{1}{2}$, 2, −1, 1, −0.01, −3, 1, $\frac{1}{2}$, $1.2\times {10}^{-6}$, $\frac{1}{0.026}$) and the initial conditions are (0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1), system (4) exhibits a hyperchaotic attractor in Figure 3, and the corresponding eight Lyapunov exponents are (0.34, 0.05, 0, −0.77, −0.96, −1.14, −1.32, −1.96).

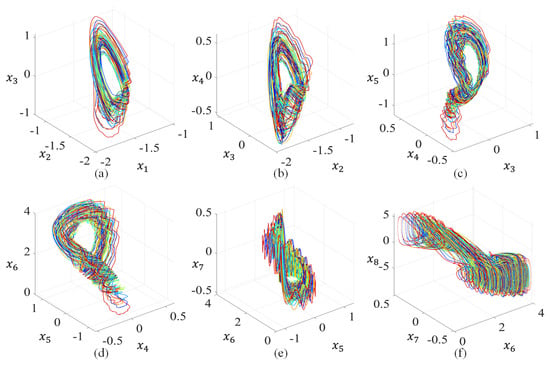
Figure 3. Hyperchaotic attractor observed from system (4) with ($a,b,c,d,e,f,g,h,i,j,k,l$, $\rho$, $\varphi$) = ($\frac{1}{2}$, 3, 0.75, 2, $\frac{1}{2}$, 2, −1, 1, −0.01, −3, 1, $\frac{1}{2}$, $1.2\times {10}^{-6}$, $\frac{1}{0.026}$): (a) $x_1-x_2-x_3$ phase plane; (b) $x_2-x_3-x_4$ phase plane; (c) $x_3-x_4-x_5$ phase plane; (d) $x_4-x_5-x_6$ phase plane; (e) $x_5-x_6-x_7$ phase plane; (f) $x_6-x_7-x_8$ phase plane.

When ($a,b,c,d,e,f,g,h,i,j,k,l,\rho ,\varphi$) = ($\frac{1}{2}$, 3, 0.945, 2, $\frac{1}{2}$, 2, −1, 1, −0.01, −3, 1, $\frac{1}{2}$, $1.2\times {10}^{-6}$, $\frac{1}{0.026}$) and the initial conditions are (0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1), system (4) exhibits a sub-hyperchaotic attractor in Figure 4, and the corresponding eight Lyapunov exponents are (0.25, 0, 0, −0.80, −0.96, −1.09, −1.36, −1.98).

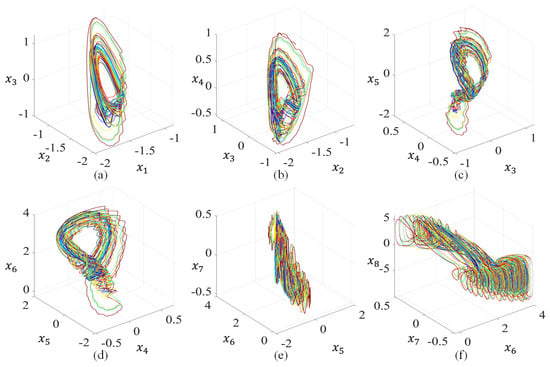
Figure 4. Sub-hyperchaotic attractor observed from system (4) with ($a,b,c,d,e,f,g,h,i,j,k,l,\rho ,\varphi$) = ($\frac{1}{2}$, 3, 0.75, 2, $\frac{1}{2}$, 2, −1, 1, −0.01, −3, 1, $\frac{1}{2}$, $1.2\times {10}^{-6}$, $\frac{1}{0.026}$): (a) $x_1-x_2-x_3$ phase plane; (b) $x_2-x_3-x_4$ phase plane; (c) $x_3-x_4-x_5$ phase plane; (d) $x_4-x_5-x_6$ phase plane; (e) $x_5-x_6-x_7$ phase plane; (f) $x_6-x_7-x_8$ phase plane.

When the novel eighth-order hyperchaotic system is applied to image encryption, it is necessary to define the default values of the constant parameter and the coupling parameters of the hyperchaotic system ($a,b,d,e,f,g,h,i,j,k,l$) as ($\frac{1}{2}$, 3, 2, $\frac{1}{2}$, 2, −1, 1, −0.01, −3, 1, $\frac{1}{2}$). The hyperchaotic system is as follows:

$$\left\{\begin{array}{cc}\hfill {\dot{x}}_1& =x_2-x_1-ϵ\left(\exp \left(\varphi x_7\right)\right)+\frac{\rho }{2}\tanh \left(x_8\right)\hfill \\ \hfill {\dot{x}}_2& =x_3-x_2+3\sin \left(x_1\right)-x_1\hfill \\ \hfill {\dot{x}}_3& =2x_4-x_3+\sin \left(x_5\right)+x_7\hfill \\ \hfill {\dot{x}}_4& =x_5-x_4+\sin \left(\frac{x_7+x_8}{2}\right)\hfill \\ \hfill {\dot{x}}_5& =x_6-x_5-\cos \left(x_3\right)+\sin \left(x_1\right)-ϵ\left(\exp \left(\rho x_7\right)\right)+\frac{x_7}{2}\hfill \\ \hfill {\dot{x}}_6& =x_7-x_8\times {10}^{-2}-3x_4\hfill \\ \hfill {\dot{x}}_7& =x_8+2\sin \left(x_5\right)+x_5+\frac{x_6}{2}\hfill \\ \hfill {\dot{x}}_8& =-c{x}_8-\rho \sinh \left(\varphi x_7\right)-8(x_6+x_5+x_4+x_3+x_2)\hfill \end{array}\right.$$

(5)

where the control parameters are $\rho =1.2\times {10}^{-6}$, $\varphi =\frac{1}{0.026}$, $ϵ=6\times {10}^{-9}$, $c\in [0.65,4]$, and the initial conditions are (0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1).

2.2. Observation of Hyperchaos and Complex Dynamics

The Lyapunov exponent of a dynamical system is a quantity that characterizes the rate of separation of infinitesimally close trajectories. Over time, two sets of initially close conditions will gradually separate due to the chaotic nature of the system. The Lyapunov exponent quantifies this exponential separation [22]. By analyzing Lyapunov exponents, valuable insights can be gained regarding a system’s sensitivity to its initial conditions, thereby aiding in the understanding and prediction of the behavior of complex systems [23].

Table 1 shows the properties of the Lyapunov exponent for an ordinary differential dynamical system.

Table 1. Properties of Lyapunov exponents for ordinary differential dynamical systems.

Dimension and Lyapunov Exponents	Symbol	State
1D ($\lambda$)	+	Divergent
1D ($\lambda$)	−	Stable fixed point
2D (${\lambda }_1$, ${\lambda }_2$)	(−, −)	Stable fixed point
2D (${\lambda }_1$, ${\lambda }_2$)	(0, −)	Limit cycle
3D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$)	(−, −, −)	Stable fixed point
3D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$)	(0, −, −)	Limit cycle
3D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$)	(0, 0, −)	2D torus
3D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$)	(+, +, 0)	Unstable limit cycle
3D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$)	(+, 0, 0)	Unstable 2D torus
3D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$)	(+, 0, −)	Chaos, strange attractor
4D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$)	(+, 0, −, −)	Chaos, strange attractor
4D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$)	(+, 0, 0, −)	Sub-hyperchaos, strange attractor
4D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$)	(+, +, 0, −)	Hyperchaos, strange attractor
…	…	…
8D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$, ${\lambda }_5$, ${\lambda }_6$, ${\lambda }_7$, ${\lambda }_8$)	(0, −, −, −, −, −, −, −)	Limit cycle
8D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$, ${\lambda }_5$, ${\lambda }_6$, ${\lambda }_7$, ${\lambda }_8$)	(0, 0, −, −, −, −, −, −)	2D torus
8D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$, ${\lambda }_5$, ${\lambda }_6$, ${\lambda }_7$, ${\lambda }_8$)	(0, 0, 0, −, −, −, −, −)	3D torus
8D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$, ${\lambda }_5$, ${\lambda }_6$, ${\lambda }_7$, ${\lambda }_8$)	(+, 0, −, −, −, −, −, −)	Chaos, strange attractor
8D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$, ${\lambda }_5$, ${\lambda }_6$, ${\lambda }_7$, ${\lambda }_8$)	(+, 0, 0, −, −, −, −, −)	Sub-hyperchaos, strange attractor
8D (${\lambda }_1$, ${\lambda }_2$, ${\lambda }_3$, ${\lambda }_4$, ${\lambda }_5$, ${\lambda }_6$, ${\lambda }_7$, ${\lambda }_8$)	(+, +, 0, −, −, −, −, −)	Hyperchaos, strange attractor

The Lyapunov exponent spectrum of the system is shown in Figure 5 for $c\in [0.65,4]$. Figure 5 shows a Lyapunov exponent spectrum, in which the eight colored lines represent the eight Lyapunov exponents, the red line represents the first Lyapunov exponent, and the green line represents the second Lyapunov exponent. When the first two Lyapunov exponents are greater than 0 and the third Lyapunov exponent is equal to 0, the system exhibits a hyperchaotic attractor. When the first Lyapunov exponent is greater than 0 and the second Lyapunov exponent is equal to 0, the system exhibits a chaotic attractor. The system exhibits hyperchaotic behavior, with the Lyapunov exponents having the signs (+, +, 0, −, −, −, −, −) when $c\in [0.65,1]$ [24]. In individual intervals, a few sub-hyperchaotic regions such as $c\in [0.69,0.695]$ and $c\in [0.94,0.945]$ can be observed, which have the sign of Lyapunov exponents as (+, 0, 0, −, −, −, −, −). In the region of $c\in [1,3.3]$, the system exhibits chaotic behavior, with the Lyapunov exponents having the signs (+, 0, −, −, −, −, −, −). In $c\in [3.3,4]$, the majority of regions exhibit periodic behavior.

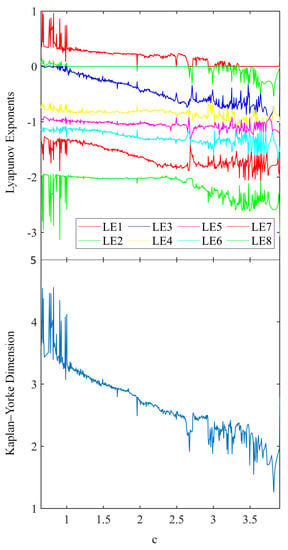
Figure 5. Lyapunov exponent map and Kaplan–Yorke dimension for a novel eighth-order hyperchaotic system.

The complexity of the attractor can be described by the Kaplan–Yorke dimension, which can be calculated using the following formula:

$$\begin{array}{cc}\hfill D_{KY}& =D+\frac{{\sum }_{i=1}^{D}L{E}_i}{\left|L{E}_D\right|}\hfill \end{array}$$

(6)

In the hyperchaotic region, which is defined as $c\in [0.65,1]$, the Kaplan–Yorke dimension falls within the approximate range of $[3.25,4.5]$. However, for  $c\in [1,4]$, the Kaplan–Yorke dimension is mostly found within the range of $[1.75,3.25]$.

Obtaining the equilibrium points is a crucial step in evaluating a new chaotic system, as it allows for the proper identification of the chaotic nature of the system [25].

Let ${\dot{x}}_1={\dot{x}}_2={\dot{x}}_3={\dot{x}}_4={\dot{x}}_5={\dot{x}}_6={\dot{x}}_7={\dot{x}}_8=0$, that is:

$$\left\{\begin{array}{cc}\hfill 0& =x_2-x_1-ϵ\left(\exp \left(\varphi x_7\right)\right)+\frac{\rho }{2}\tanh \left(x_8\right)\hfill \\ \hfill 0& =x_3-x_2+3\sin \left(x_1\right)-x_1\hfill \\ \hfill 0& =2x_4-x_3+\sin \left(x_5\right)+x_7\hfill \\ \hfill 0& =x_5-x_4+\sin \left(\frac{x_7+x_8}{2}\right)\hfill \\ \hfill 0& =x_6-x_5-\cos \left(x_3\right)+\sin \left(x_1\right)-ϵ\left(\exp \left(\rho x_7\right)\right)+\frac{x_7}{2}\hfill \\ \hfill 0& =x_7-x_8\times {10}^{-2}-3x_4\hfill \\ \hfill 0& =x_8+2\sin \left(x_5\right)+x_5+\frac{x_6}{2}\hfill \\ \hfill 0& =-c{x}_8-\rho \sinh \left(\varphi x_7\right)-8(x_6+x_5+x_4+x_3+x_2)\hfill \end{array}\right.$$

(7)

When $\rho =1.2\times {10}^{-6}$, $\varphi =\frac{1}{0.026}$, $ϵ=6\times {10}^{-9}$, $c=0.75$, the given equilibrium point (0.14, 0.17, −0.11, 0.13, −0.87, −0.18, 0.40, 2.48) has been obtained, and the Jacobian matrix can be computed at these equilibrium points. The Jacobian matrix, denoted as $f^{\prime }\left(x\right)$, represents the derivative of the multidimensional mapping:

$$\begin{array}{c}\hfill f^{\prime }\left(x\right)=\frac{\partial f}{\partial x}=\left[\begin{array}{cccc}\frac{\partial f_1}{\partial x_1}& \frac{\partial f_1}{\partial x_2}& \cdots & \frac{\partial f_1}{\partial x_8}\\ \frac{\partial f_2}{\partial x_1}& \frac{\partial f_2}{\partial x_2}& \cdots & \frac{\partial f_2}{\partial x_8}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{\partial f_8}{\partial x_1}& \frac{\partial f_8}{\partial x_2}& \cdots & \frac{\partial f_8}{\partial x_8}\end{array}\right]\end{array}$$

(8)

The eight eigenvalues calculated based on the Jacobian matrix are

$$\begin{array}{cc}\hfill {\lambda }_1& =(-0.36+13.15i),\hfill \\ \hfill {\lambda }_2& =(-0.36-13.15i),\hfill \\ \hfill {\lambda }_3& =0.52,\hfill \\ \hfill {\lambda }_4& =(0.02+1.18i),\hfill \\ \hfill {\lambda }_5& =(0.02-1.18i),\hfill \\ \hfill {\lambda }_6& =(-2.39+0.23i),\hfill \\ \hfill {\lambda }_7& =(-2.39-0.23i),\hfill \\ \hfill {\lambda }_8& =-0.80.\hfill \end{array}$$

(9)

The eigenvalues corresponding to ${\lambda }_1$ and ${\lambda }_2$, ${\lambda }_4$ and ${\lambda }_5$, and ${\lambda }_6$ and ${\lambda }_7$ exhibit a complex conjugate relationship, suggesting a characteristic oscillatory pattern. ${\lambda }_3$ has a positive real part, indicating divergence. ${\lambda }_8$ has a negative real part, indicating convergence.

Among the eight eigenvalues under consideration, it is observed that three of them exhibit instability due to the presence of eigenvalues with positive real parts. This implies that any perturbation introduced into the system will amplify over time, leading to a loss of stability at the equilibrium point. Conversely, the remaining five eigenvalues exhibit negative real components, indicating that any disturbance introduced into the system will gradually diminish, thereby preserving the stability of the equilibrium point [26].

The divergence formula for this system is as follows:

$$\begin{array}{c}\hfill \nabla ·F=\frac{\partial {\dot{x}}_1}{\partial x_1}+\frac{\partial {\dot{x}}_2}{\partial x_2}+\cdots +\frac{\partial {\dot{x}}_8}{\partial x_8}\end{array}$$

(10)

The divergence in this system is −5.74. Generally, the divergence of the hyperchaotic system is found to be negative, indicating that the system is a dissipative system.

3. Encryption and Decryption Scheme

The encryption scheme uses two chaotic sequences generated by the novel eighth-order hyperchaotic system Equation (5) when $c=1.5$ and $c=1.4$, which is used to enhance the security of images. The proposed scheme in this study involves row scrambling, column scrambling, and diffusing using chaotic sequence A ($c=1.5$), as well as diffusing, column scrambling, and row scrambling using chaotic sequence B ($c=1.4$). The encryption algorithm and decryption algorithm are shown in Algorithms 1 and 2.

• Encryption Algorithm:

• Calculate the chaotic sequence A according to the novel eighth-order hyperchaotic system when $c=1.5$ and initial values are (0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1).
• Calculate the $Key$ by the average value of a matrix generated by original image.
• Obtain the pixels of the original image and divide the original image into three channels of $R,G,B$.
• Calculate the index $s_A$ and $c_A$ from the chaotic sequence A with different keys, where

  $$\left\{\begin{array}{cc}\hfill s_i& =x_8\left(i\right)\times {10}^8-\lfloor x_8\left(i\right)\times {10}^8\rfloor \hfill \\ \hfill c_i& =mod\left(x_3\left(i\right)\times {10}^5-\lfloor x_3\left(i\right)\times {10}^5\rfloor +\left|x_3\left(i\right)\times {10}^8-round(x_3\left(i\right)\times {10}^8)\right|,256\right)\hfill \end{array}\right.$$

  (11)
• Utilize the index $s_A$ based on $2\times Key$ to perform row scrambling on the output images of the three channels from Step 3.
• Utilize the index $s_A$ based on $3\times Key$ to perform column scrambling on the output images of the three channels from Step 5.
• Perform XOR operation on the index $c_A$ and the image pixel value from Step 6.
• Calculate the chaotic sequence B according to the novel eighth-order hyperchaotic system when $c=1.4$ and initial values are (0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1).
• Calculate the index $s_B$ and $c_B$ from the chaotic sequence B with the same formula from Step 4.
• Perform XOR operation on the index $c_B$ and the image pixel value from Step 7.
• Utilize the index $s_B$ based on $3\times Key$ to perform column scrambling on the output images of the three channels in Step 10.
• Utilize the index $s_B$ based on $2\times Key$ to perform row scrambling on the output images of the three channels in Step 11.
• Merge the encrypted images of the three channels to generate the final encrypted image.

Algorithm 1 Encryption  Algorithm

Input: Original Image $(Org\_Img)$, First initial conditions, Control parameters, Output: Encrypted image $(En\_Img)$  1: $[m,n]\leftarrow \mathrm{size}(Org\_Img)$  2: $Avg\_pixel\_value\leftarrow \mathrm{mean}2(Org\_Img)\times {10}^{-9}$     ▹ mean2 is a function that returns the average value of a matrix  3: paraset($x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8$)                                                  ▹ First round of encryption  4: function seq($x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,Runge-Kutta,Avg\_pixel\_value$)  5:    $x_1\left(1\right)\leftarrow x_1\left(1\right)+Avg\_pixel\_value$  6:    for $i=1$ to $10\times m\times n$ do  7:     $[dx,dy,dz,du]\leftarrow \mathrm{Runge}-\mathrm{Kutta}\left(x\right(i),y(i),z(i),u(i\left)\right)$  8:     $x_1(i+1)\leftarrow x_1\left(i\right)+dx1$  9:     $x_2(i+1)\leftarrow x_2\left(i\right)+dx2$ 10:    $x_3(i+1)\leftarrow x_3\left(i\right)+dx3$ 11:    $x_4(i+1)\leftarrow x_4\left(i\right)+dx4$ 12:    $x_5(i+1)\leftarrow x_5\left(i\right)+dx5$ 13:    $x_6(i+1)\leftarrow x_6\left(i\right)+dx6$ 14:    $x_7(i+1)\leftarrow x_7\left(i\right)+dx7$ 15:    $x_8(i+1)\leftarrow x_8\left(i\right)+dx8$ 16:    if $\mathrm{mod}(i,10)=0$ then 17:        $s_i=x_8\left(i\right)\times {10}^8-\lfloor x_8\left(i\right)\times {10}^8\rfloor$ 18:        $t=\left|x_3\left(i\right)\times {10}^8-\mathrm{round}(x_3\left(i\right)\times {10}^8)\right|$ 19:        $c_i=\mathrm{mod}\left(x_3\left(i\right)\times {10}^5-\lfloor x_3\left(i\right)\times {10}^5\rfloor +t,256\right)$ 20:     end if 21:    end for 22:    return $s,c$ 23: end function 24: $s_1\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}1,2\times Avg\_pixel\_value)$          ▹ Using chaotic sequence A 25: $s_2\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}1,3\times Avg\_pixel\_value)$ 26: $c\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}1,Avg\_pixel\_value)$ 27: $S\_index\_1\leftarrow \mathrm{Sort}\left(s_1\right)$ 28: $S\_index\_2\leftarrow \mathrm{Sort}\left(s_2\right)$ 29: $Org\_per\_row\leftarrow \mathrm{confuse}\_\mathrm{row}$(Org_Img, S_index_1) 30: $Org\_per\_col\leftarrow \mathrm{confuse}\_\mathrm{col}$(Org_per_row, S_index_2) 31: $En\_Img1\leftarrow \mathrm{difuse}($(m, n, Org_per_col, c) 32:   33: paraset($x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8$)                                                  ▹ Second round of encryption 34: $x_1\left(1\right)\leftarrow x_1\left(1\right)+Avg\_pixel\_value$ 35: $s_1\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}2,2\times Avg\_pixel\_value)$          ▹ Using chaotic sequence B 36: $s_2\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}2,3\times Avg\_pixel\_value)$ 37: $c\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}2,Avg\_pixel\_value)$ 38: $S\_index\_1\leftarrow \mathrm{Sort}\left(s_1\right)$ 39: $S\_index\_2\leftarrow \mathrm{Sort}\left(s_2\right)$ 40: $En\_dif1\leftarrow \mathrm{difuse}$(m, n, En_Img1, c) 41: $En\_per\_col1\leftarrow \mathrm{confuse}$(n, m, En_dif1, S_index_2) 42: $En\_per\_row1\leftarrow \mathrm{confuse}$(m, n, En1_per_col1, S_index_1)

• Decryption Algorithm:

• Calculate the chaotic sequence B according to the novel eighth-order hyperchaotic system when $c=1.4$ and initial values are (0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1).
• Obtain the pixels of the original image and divide the original image into three channels of $R,G,B$.
• Calculate the index $s_B$ and $c_B$ from the chaotic sequence B with different keys.
• Utilize the index $s_B$ based on $2\times Key$ to perform row recovery on the output images of the three channels from Step 2.
• Utilize the index $s_B$ based on $3\times Key$ to perform column recovery on the output images of the three channels from Step 4.
• Perform XOR operation on the index $c_A$ and the image pixel value from Step 5.
• Calculate the chaotic sequence A according to the novel eighth-order hyperchaotic system when $c=1.5$ and initial values are (0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1).
• Calculate the index $s_A$ and $c_A$ from the chaotic sequence A with different keys.
• Perform XOR operation on the index $c_A$ and the image pixel value from Step 6.
• Utilize the index $s_A$ based on $3\times Key$ to perform column recovery on the output images of the three channels from Step 9.
• Utilize the index $s_A$ based on $2\times Key$ to perform row recovery on the output images of the three channels from Step 10.
• Merge the decrypted images of the three channels to generate the final decrypted image.

Algorithm 2 Decryption  Algorithm

Input: Encrypted Image $(En\_Img)$, First initial conditions, Control parameters, $Avg\_pixel\_value$ of $(Org\_Img)$ Output: Original image $(Org\_Img)$  1: $[m,n]\leftarrow \mathrm{size}(En\_Img)$  2: paraset($x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8$)                                                  ▹ First round of decryption  3: $x_1\left(1\right)\leftarrow x_1\left(1\right)+Avg\_pixel\_value$  4: $s_1\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}2,2\times Avg\_pixel\_value)$          ▹ Using chaotic sequence B  5: $s_2\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}2,3\times Avg\_pixel\_value)$  6: $c\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}2,Avg\_pixel\_value)$  7: $S\_index\_1\leftarrow \mathrm{Sort}\left(s_1\right)$  8: $S\_index\_2\leftarrow \mathrm{Sort}\left(s_2\right)$  9: $En\_per\_row\leftarrow \mathrm{confuse}\_\mathrm{row}$(En_Img, S_index_1) 10: $En\_per\_col\leftarrow \mathrm{confuse}\_\mathrm{col}$(En_per_row, S_index_2) 11: $En\_Img1\leftarrow \mathrm{difuse}($(m, n, En_per_col, c) 12:   13: paraset($x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8$)                                                  ▹ Second round of decryption 14: $s_1\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}1,2\times Avg\_pixel\_value)$          ▹ Using chaotic sequence A 15: $s_2\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}1,3\times Avg\_pixel\_value)$ 16: $c\leftarrow \mathrm{SEQ}(x_1,x_2,x_3,x_4,x_5,x_6,x_7,x_8,m,n,\mathrm{Runge}-\mathrm{Kutta}1,Avg\_pixel\_value)$ 17: $S\_index\_1\leftarrow \mathrm{Sort}\left(s_1\right)$ 18: $S\_index\_2\leftarrow \mathrm{Sort}\left(s_2\right)$ 19: $En\_dif1\leftarrow \mathrm{difuse}$(m, n, En_Img1, c) 20: $En\_per\_col1\leftarrow \mathrm{confuse}\_\mathrm{col}$(En_dif1, S_index_2) 21: $Org\_Img\leftarrow \mathrm{confuse}\_\mathrm{row}$(En1_per_col1, S_index_1)

The steps of the encryption and decryption scheme are shown in Figure 6 and Figure 7.

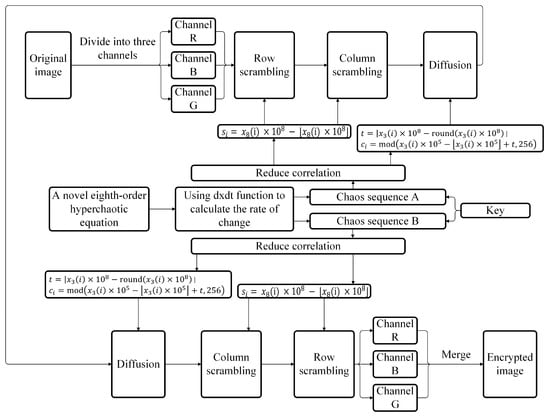
Figure 6. Scheme of image encryption.

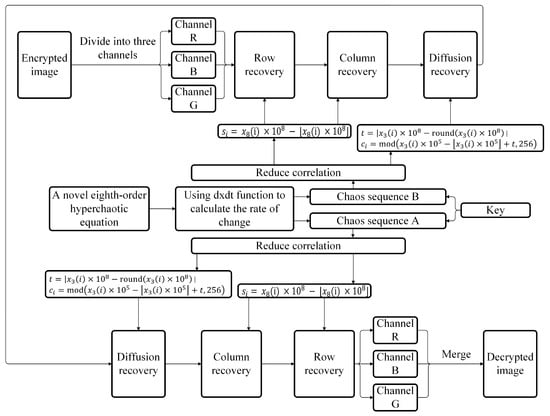
Figure 7. Scheme of image decryption.

Encryption time, particularly for chaos-based encryption algorithms, determines whether they can be employed in practice [27]. On a computer running Matlab 2022 and equipped with a 3.2 GHz Core R7-5800 U CPU, the speed of the proposed method is evaluated. This test uses a 512 × 512-pixel Lena image. Scrambling and diffusion have running times of 3.0608 and 3.1810 s, respectively. The chaotic sequence generation takes 3.0403 s to complete, while one round of encryption takes 9.5131 s. Since the proposed encryption scheme employs a serial encryption method and has a large key space, which takes longer than other references, a significant amount of effort is required to convert a serial approach to a parallel one and fully utilize the enormous processing power of GPUs [28]. The result of the experiment is that it is evident that there is still room for improvement in the encryption algorithm.

4. Experiments with Related Security Analysis

4.1. Experimental Results

The following is an experimental analysis of the image encryption algorithm proposed in this paper. The experiment involves the use of eight color images, each consisting of 512 × 512 pixels, as depicted in Figure 8. The original images are shown in (a). The encrypted images are shown in (b)–(e), and the decrypted images are shown in (f)–(i).

Figure 8. Image encryption and decryption results: (a) original image; (b–d) encrypted images of three channels of R, G, B; (e) encrypted images of three channels combined; (f–h) decrypted images of three channels of R, G, B; (i) decrypted images of three channels combined.

The result of encrypting a gray image (512 × 512 Lena) is shown in Figure 9, indicating that the image encryption algorithm is also effective for gray images.

Figure 9. Gray image encryption and decryption results: (a) original image; (b) encrypted image; (c) decrypted image.

4.2. Histogram Analysis

A histogram is a visual representation that provides an estimation of the distribution of numerical data. It involves plotting the number of pixels at each intensity level to understand the distribution of pixels in an image [29]. To ensure resistance against statistical attacks, the histograms of both the original images and encrypted images need to be described [30].

In order to quantitatively analyze histograms, the experiment uses variances of histograms to assess the uniformity of the encrypted images. Lower variance values indicate a higher level of uniformity in the encrypted images. The formula for calculating the variance of the histograms is as follows [22]:

$$\begin{array}{c}\hfill \mathrm{var}\left(\mathrm{Z}\right)=\frac{1}{n^2}\sum _{i=1}^n\sum _{j=1}^n\frac{1}{2}{(z_i-z_j)}^2\end{array}$$

(12)

where Z is the variance of the histogram, and $z_i$ and $z_j$ are the number of pixels i and j in a single channel. In the encryption experiment on the Lena image, the variance of the R channel of the plain image is 770811 and the variance of the R channel of the encrypted image is 262719; the variance of the G channel of the plain image is 490003 and the variance of the G channel of the encrypted image is 262718; the variance of the B channel of the plain image is 950821 and the variance of the B channel of the encrypted image is 262592, the variance of the gray channel of the plain image is 578833 and the variance of the gray channel of the encrypted image is 262698.

Figure 10 is the comparison of the original image and the encrypted image histogram.

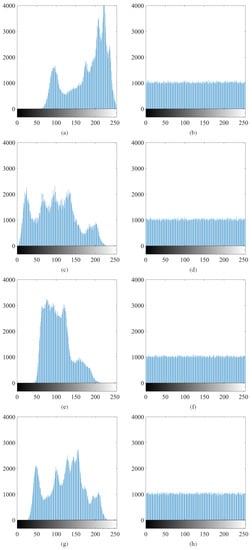
Figure 10. Comparison of the histograms of the original image and the encrypted image: (a,c,e,g) the histogram of the R, G, B, gray channel of the original image; (b,d,f,h) the histogram of the R, G, B, gray channel of the encrypted image.

Through the calculation of the variance and the analysis of the histogram, the histogram shows the distribution characteristics among the pixels. The encrypted image data of an ideal encryption scheme should be uniformly distributed, which can effectively prevent attackers from obtaining valid information from encrypted images [31], and effectively resist statistical attacks.

4.3. Key Space Analysis

The utilization of a substantial key space has the capability to effectively thwart brute force attacks, thereby mitigating the potential vulnerability of data decryption [32].

If the calculated resolution is ${10}^{15}$, for variable $x_1$, the area of attraction domain is $x_1\in [-1.88,-0.98]$, there are $0.89\times {10}^{15}=0.89\times {10}^{15}$ kinds of choices. There are $1.17\times {10}^{15}$ choices for $x_2$, $1.95\times {10}^{15}$ choices for $x_3$, $1.16\times {10}^{15}$ choices for $x_4$, $2.62\times {10}^{15}$ choices for $x_5$, $3.78\times {10}^{15}$ choices for $x_6$, $1.04\times {10}^{15}$ choices for $x_7$, and $1.41\times {10}^{16}$ choices for $x_8$. The size of the key space formed by the control variables is $0.89\times {10}^{15}\times 1.17\times {10}^{15}\times 1.95\times {10}^{15}\times 1.16\times {10}^{15}\times 2.62\times {10}^{15}\times 3.78\times {10}^{15}\times 1.04\times {10}^{15}\times 1.41\times {10}^{16}=3.45\times {10}^{123}$. Consider only one control variable c in Equation (5), the key space of the system is $3.45\times {10}^{123}\times 2.7\times {10}^{15}=9.32\times {10}^{138}$. When only the first-order term with a coefficient of 1 in the hyperchaotic equation is considered as the control variable, the key space of the system is $8.2\times {10}^{351}$. Additionally, the proposed encryption scheme involves two rounds of encryption based on the hyperchaotic system with different control variables, thus the key space is $8.2\times {10}^{351}\times 8.2\times {10}^{351}=6.72\times {10}^{703}\approx 2^{2338}$. The actual key space of this scheme will be extremely larger than that value.

4.4. Correlation Analysis

Correlation refers to a statistical association, regardless of causality, between two random variables or sets of bivariate data. In the context of encryption algorithms, it is desirable for encrypted images with low-pixel correlation to be resistant to cryptographic attacks based on statistical analysis [33]. Therefore, a comprehensive understanding of correlations is essential in order to enhance the robustness and effectiveness of image encryption techniques [34].

To calculate the correlation, the following formula is used [35]:

$$\begin{array}{c}\hfill \left\{\begin{array}{cc}\hfill \mathrm{E}\left(u\right)& =\frac{1}{N}\sum _{i=1}^N{u}_i\hfill \\ \hfill \mathrm{D}\left(u\right)& =\frac{1}{N}\sum _{i=1}^N{(u_i-E\left(u\right))}^2\hfill \\ \hfill \mathrm{cov}(u,v)& =\frac{1}{N}\sum _{i=1}^N(x_i-E\left(u\right))(y_i-E\left(v\right))\hfill \\ \hfill {\mathrm{r}}_{xy}& =\frac{\mathrm{cov}(u,v)}{\sqrt{\mathrm{D}\left(u\right)·\mathrm{D}\left(v\right)}}\hfill \end{array}\right.\end{array}$$

(13)

In order to present the importance of correlation more intuitively, Table 2 below will show the pixel value correlation analysis results of eight color images. Table 2 also displays the correlation to a gray house image, indicating that the encryption algorithm still works with gray images.

Table 2. Correlation coefficient of original images, the first round of encrypted images, and the second round of encrypted images.

Image	Original Image			First Round of Encrypted Image			Second Round of Encrypted Image
	Horiz.	Vert.	Diag.	Horiz.	Vert.	Diag.	Horiz.	Vert.	Diag.
Mandrill	R 0.9123	0.8625	0.8505	0.0097	0.0084	0.0085	0.0079	0.0113	0.0122
	G 0.8628	0.7811	0.7496	0.0149	0.0108	0.0105	0.0097	0.0126	0.0126
	B 0.8965	0.8712	0.8314	0.0100	0.0135	0.0129	0.0123	0.0131	0.0110
Lena	R 0.9808	0.9898	0.9712	0.0093	0.0090	0.0140	0.0133	0.0103	0.0120
	G 0.9695	0.9827	0.9561	0.0140	0.0095	0.0145	0.0109	0.0089	0.0091
	B 0.9352	0.9591	0.9212	0.0109	0.0069	0.0153	0.0101	0.0107	0.0120
Peppers	R 0.9650	0.9677	0.9582	0.0090	0.0115	0.0101	0.0132	0.0083	0.0117
	G 0.9813	0.9819	0.9689	0.0106	0.0102	0.0098	0.0110	0.0127	0.0096
	B 0.9668	0.9667	0.9483	0.0137	0.0017	0.0082	0.0105	0.0136	0.0091
House	R 0.9552	0.9591	0.9252	0.0129	0.0098	0.0139	0.0118	0.0086	0.0136
	G 0.9405	0.9445	0.8951	0.0135	0.0061	0.0102	0.0107	0.0059	0.0109
	B 0.9728	0.9691	0.9456	0.0109	0.0090	0.0090	0.0136	0.0128	0.0112
Lake	R 0.9574	0.9557	0.9440	0.0105	0.0120	0.0156	0.0131	0.0132	0.0121
	G 0.9718	0.9666	0.9534	0.0140	0.0110	0.0129	0.0131	0.0119	0.0104
	B 0.9713	0.9697	0.9534	0.0117	0.0097	0.0117	0.0118	0.0148	0.0080
Splash	R 0.9938	0.9953	0.9898	0.0108	0.0077	0.0105	0.0103	0.0099	0.0090
	G 0.9812	0.9872	0.9713	0.0105	0.0054	0.0137	0.0114	0.0110	0.0129
	B 0.9826	0.9792	0.9653	0.0112	0.0029	0.0097	0.0137	0.0127	0.0115
San Diego	R 0.8539	0.8395	0.7770	0.0108	0.0072	0.0113	0.0132	0.0139	0.0092
	G 0.7933	0.7719	0.6943	0.0080	0.0098	0.0101	0.0108	0.0143	0.0086
	B 0.7930	0.7728	0.7055	0.0094	0.0069	0.0121	0.0118	0.0140	0.0096
Jetplane	R 0.9738	0.9593	0.9382	0.0132	0.0102	0.0112	0.0108	0.0126	0.0118
	G 0.9596	0.9691	0.9356	0.0137	0.0135	0.0115	0.0104	0.0117	0.0105
	B 0.9673	0.9431	0.9249	0.0121	0.0068	0.0139	0.0119	0.0110	0.0110
House (gray)	0.9503	0.9592	0.9172	0.0137	0.0086	0.0127	0.0100	0.0076	0.0104

It is evident that the correlation value of the original image is close to 1, while the horizontal, vertical, and diagonal correlations of the encrypted image are close to 0 [36]. These values indicate that the correlation between adjacent pixels of the encrypted image is very weak.

Figure 11, Figure 12, and Figure 13, respectively, show the original image, the first round of encrypted image, and the second round of encrypted image in the horizontal, vertical, and diagonal directions of pixel correlation sex. It can be seen from Figure 11 that, since the pixels of the original image are highly correlated, most points in these three directions align with the 45° line. Meanwhile, Figure 12 and Figure 13 show that these points are distributed in the whole area, reflecting the weak pixel correlation in the encrypted image. Therefore, the algorithm proves that it is effective against attacks such as statistical attacks.

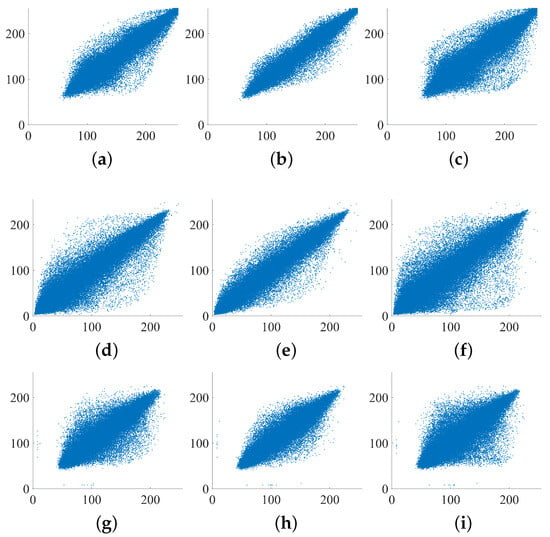
Figure 11. Correlation analysis of the original image: (a,d,g) correlation between pixels in the horizontal direction of the R, G, B channel of the original image; (b,e,h) correlation between pixels in the vertical direction of the R, G, B channel of the original image; (c,f,i) correlation between pixels in the diagonal direction of the R, G, B channel of the original image.

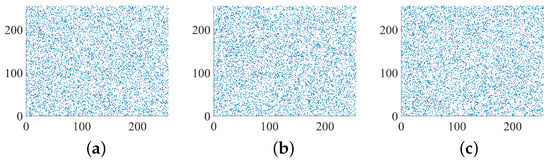
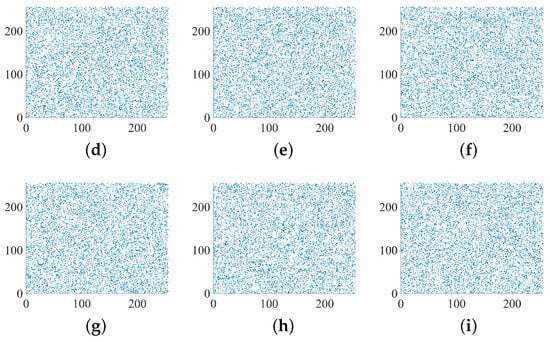
Figure 12. Correlation analysis of the first round of encrypted image: (a,d,g) correlation between pixels in the horizontal direction of the R, G, B channel of the first round of encrypted image; (b,e,h) correlation between pixels in the vertical direction of the R, G, B channel of the first round of encrypted image; (c,f,i) correlation between pixels in the diagonal direction of the R, G, B channel of the first round of encrypted image.

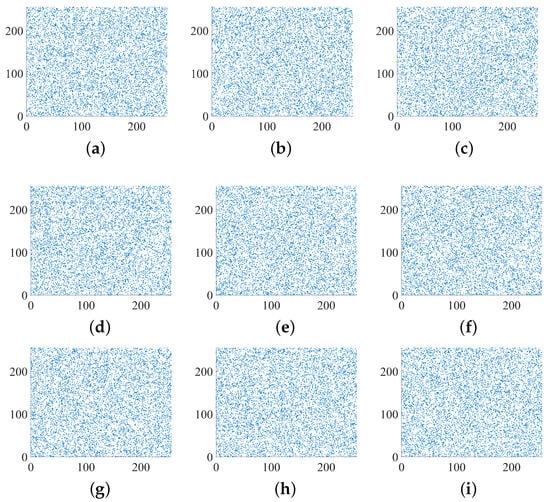
Figure 13. Correlation analysis of the second round of encrypted image: (a,d,g) correlation between pixels in the horizontal direction of the R, G, B channel of the second round of encrypted image; (b,e,h) correlation between pixels in the vertical direction of the R, G, B channel of the second round of encrypted image; (c,f,i) correlation between pixels in the diagonal direction of the R, G, B channel of the second round of encrypted image.

4.5. Entropy

To measure the expected value of a message and the unpredictability of information content, information entropy (IE) is usually taken to test the strength of a designed encryption algorithm [37], which is defined in Equation (14) for a received message m. The theoretical value of the information entropy is 8 [38].

$$\begin{array}{c}\hfill IE\left(m\right)=\sum _{j=0}^{2^L-1}p\left(m_j\right){\log }_2\left(\frac{1}{p\left(m_j\right)}\right)\end{array}$$

(14)

where L is the length of pixel value in binary form (for images in this experiment, L = 9), $p\left(m_j\right)$ denotes the probability of the occurrence of the symbol $m_j$, and $lo{g}_2$ represents the base 2 algorithm. Table 3 is a comparison of the information entropy of the original image and the encrypted image of the eight color images and a gray house image.

Table 3. Entropy of original image, the first round of encrypted image, and the second round of encrypted image.

Image	Result
	Original Image	First Round of Encrypted Image	Second Round of Encrypted Image
Mandrill	7.1073	7.9998	7.9998
Lena	7.7502	7.9998	7.9998
Peppers	7.6698	7.9997	7.9998
House	7.4858	7.9998	7.9998
Lake	7.7622	7.9997	7.9998
Splash	7.2428	7.9997	7.9997
San Diego	7.3311	7.9998	7.9998
Jetplane	6.6639	7.9997	7.9997
House (gray)	7.2334	7.9993	7.7993

4.6. MSE and PSNR Analysis

The most common metric for evaluating the effectiveness of lossy image compression codecs is PSNR. The correct determination of the spatial alignment and level offset between the encrypted picture sequence and the original image sequence is crucial to the PSNR calculation [39]. Given a noise-free m × n monochrome image I and its noisy approximation K, MSE and PSNR are defined as [40]

$$\begin{array}{cc}\hfill \mathrm{MSE}& =\frac{1}{mn}\sum _{i=1}^m\sum _{j=1}^m{[I(i,j)-K(i,j)]}^2\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill \mathrm{PSNR}& =10·{\log }_{10}\left(\frac{MA{X}_I^2}{MSE}\right)\hfill \end{array}$$

(16)

where $MA{X}_I$ is the maximum possible pixel value of the image. When samples are represented using linear PCM with B bits per sample, $MA{X}_I$ is $2^B-1$. In this paper, the pixels are represented using 8 bits per sample, and $MA{X}_I$ is 255.

Table 4 shows the comparison of MSE and PSNR. To reduce the probability of assaults, a lower PSNR value and a higher MSE value are preferred [2]. As a result, it is clear that the PSNR values computed for encrypted pictures using the proposed scheme are comparable to or better than those obtained from other schemes in the literature [41].

Table 4. MSE and PSNR comparison.

Image	MSE	PSNR
Mandrill	8773	8.6994
Lena	8923	8.6256
Peppers	10129	8.0751
House	9252	8.4686
Lake	10099	8.0880
Splash	11252	7.6183
San Diego	8480	8.8469
Jetplane	10360	7.9772
House (gray)	8955	8.6103
Ref. [41]	8353	8.9272
Ref. [42]	7274	9.55
Ref. [43]	8332	8.9331

4.7. Ablation Analysis

The ablation analysis shows the improvement in encryption due to two rounds of encryption. The experiment can be divided into four cases and the result is demonstrated in Table 5.

Table 5. Ablation analysis.

Method	Key Space	Entropy	CC				NPCR (%)				UACI (%)
			R	G	B	Cipher	R	G	B	Cipher	R	G	B	Cipher
Case 1	$>2^{1169}$	7.9997	0.0107	0.0118	0.0105	0.0079	99.6391	99.6391	99.6391	99.6391	33.4310	33.4089	33.4219	33.4206
Case 2	$>2^{1169}$	7.4858	0.0368	0.0446	0.0195	0.0079	99.3141	99.1238	99.2275	99.2218	22.0984	20.2759	27.1392	23.1712
Case 3	$>2^{1169}$	7.9998	0.0107	0.0111	0.0105	0.0069	99.5838	99.6136	99.6048	99.6007	33.4498	33.4860	33.4681	33.4680
Case 4	$>2^{1169}$	7.9998	0.0122	0.0099	0.0096	0.0067	99.6098	99.6238	99.6055	99.6131	33.4417	33.3564	33.2640	33.3541
Proposed	$>2^{2338}$	7.9998	0.0113	0.0092	0.0125	0.0072	99.6162	99.6086	99.6048	99.6099	33.4552	33.4399	33.4081	33.4344

Case 1: Proposed method without scrambling.

Case 2: Proposed method without diffusion.

Case 3: Proposed method without the first round of encryption.

Case 4: Proposed method without the second round of encryption.

It can be seen from the table that, when encryption is performed without diffusion operation, the pixel correlation of the scheme is substantially higher than the proposed scheme, and the UACI is likewise far away from the theoretical value. Without scrambling operations or without one of the rounds being used for encryption, these data are within a respectable range, but the primary benefit of the proposed scheme with two rounds of encryption is the extremely large key space.

4.8. Key Sensitivity Analysis

Key sensitivity analysis is a cryptographic evaluation method that assesses the significance and security of an algorithm [35]. It ensures that even a slight modification to the key will render the original flat image irrecoverable [2].

This encryption system demonstrates a high level of sensitivity to the key. By maintaining constant control variables and initial conditions, a small increment of ${10}^{-14}$ is added to the key within the scheme. Consequently, the encrypted image exhibits significant differences between the two variables over time, displaying pseudo-random characteristics. This observation suggests that the system’s key is highly sensitive to initial conditions. To illustrate this sensitivity, two similar images are encrypted using keys with minute differences. Figure 14 shows the waveform of $x_1$ and $x_1+\mathsf{\Delta }x$ over time and their difference. After performing the subtraction of the encrypted images, it is clearly seen from Figure 15 that the resulting images exhibit significant dissimilarities.

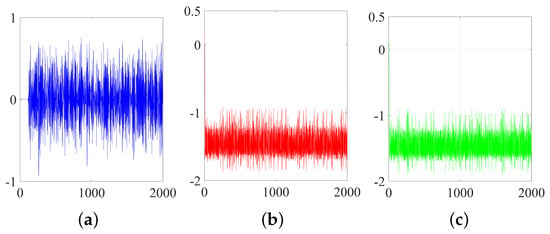
Figure 14. (a) The difference waveform of $x_1$ and $x_1+\mathsf{\Delta }x$ over time; (b) the values of $x_1+\mathsf{\Delta }x$ over time; (c) the values of $x_1$ over time.

Figure 15. Key sensitivity test: (a) the difference between the twice encrypted image of the R channel of images; (b) the difference between the twice encrypted image of the G channel of images; (c) the difference between the twice encrypted image of the R channel of images; (d) the difference between the twice encrypted images of three channels of images.

Key sensitivity analysis is usually performed based on the following two indicators: one is the number of pixels rate of change (NPCR), and the other is the uniform average intensity of change (UACI). These two indicators are defined as [44]

$$\begin{array}{cc}\hfill \mathrm{NPCR}& =\sum _{i=1}^N\sum _{j=1}^M\frac{D(i,j)}{M\times N}\times 100\%\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \mathrm{UACI}& =\sum _{i=1}^N\sum _{j=1}^M\frac{|C_1(i,j)-C_2(i,j)|}{T\times M\times N}\times 100\%\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill \mathrm{D}(\mathrm{i},\mathrm{j})& =\left\{\begin{array}{cc}0,\hfill & \mathrm{if}{C}_1(i,j)=C_2(i,j)\hfill \\ 1,\hfill & \mathrm{if}{C}_1(i,j)\ne C_2(i,j)\hfill \end{array}\right.\hfill \end{array}$$

(19)

where $C_1$ and $C_2$ are two encrypted images of size $M\times N$, and T denotes the largest allowed pixel intensity.

NPCR and UACI are theoretically 99.6043% and 33.4635% [45]. The data presented in Table 6 and Table 7 demonstrates that the test value of the algorithm exhibits a high degree of proximity to the ideal value, indicating a strong level of key sensitivity. In summary, this scheme has high key sensitivity.

Table 6. NPCR of three channels in key sensitivity analysis.

Image	NPCR (%)
	R	G	B
Mandrill	99.5930	99.6330	99.6113
Lena	99.5811	99.6162	99.6052
Peppers	99.6048	99.6021	99.6140
House	99.6162	99.6086	99.6048
Lake	99.6273	99.6307	99.6063
Splash	99.6078	99.5998	99.6201
San Diego	99.6117	99.6071	99.6025
Jetplane	99.6128	99.6227	99.6158
Lena (gray)		99.6017

Table 7. UACI of three channels in key sensitivity analysis.

Image	UACI (%)
	R	G	B
Mandrill	33.4605	33.4560	33.5050
Lena	33.3818	33.5105	33.4385
Peppers	33.4500	33.5263	33.5738
House	33.4552	33.4399	33.4081
Lake	33.5367	33.4740	33.3750
Splash	33.4298	33.4887	33.5137
San Diego	33.4646	33.4861	33.4083
Jetplane	33.5527	33.5670	33.5132
Lena (gray)		33.4496

4.9. Differential Attack

To avoid differential attacks, a secure cryptosystem should be sensitive to plaintext [46], indicating that even minor alterations in the pixel values of a regular image can result in significant modifications in the corresponding encrypted image [47]. Figure 16 shows the results of differential attack experiments.

Figure 16. Differential attack test: (a) the difference between the twice encrypted image of the R channel of images; (b) the difference between the twice encrypted image of the G channel of images; (c) the difference between the twice encrypted image of the R channel of images; (d) the difference between the twice encrypted images of three channels of images.

Table 8 and Table 9 show the NPCR and UACI of the differential attack. The test results indicate a strong correlation between the system’s value and the theoretical value, suggesting that the system is capable of effectively defending against differential attacks.

Table 8. NPCR of three channels in differential attack experiments.

Image	NPCR (%)
	R	G	B
Mandril	99.6174	99.6136	99.6025
Lena	99.6105	99.6212	99.6162
Peppers	99.6204	99.6208	99.6262
House	99.5785	99.6117	99.6040
Lake	99.5979	99.6178	99.6166
Splash	99.6227	99.6246	99.6002
San Diego	99.6059	99.6071	99.5972
Jetplane	99.6254	99.6002	99.6227
Lena (gray)		99.6249

Table 9. UACI of three channels in differential attack experiments.

Image	UACI (%)
	R	G	B
Mandrill	33.4335	33.4402	33.4821
Lena	33.4898	33.4291	33.4875
Peppers	33.4562	33.4732	33.5182
House	33.4944	33.4663	33.5236
Lake	33.4197	33.5304	33.4407
Splash	33.4215	33.5089	33.4760
San Diego	33.4363	33.4986	33.4557
Jetplane	33.5001	33.4588	33.5305
Lena (gray)		33.4892

4.10. Cropping Attack

A robust cryptographic system should have the capability to resist potential data loss during transmission and storage [48]. The receiver wants to recover the plain image as much as possible from some of the information received in this case [33]. Thus, the analysis of cropping attacks is a valuable approach to assessing the robustness of encryption schemes [49].

For evaluating and comparing the performance of different encryption algorithms in the face of cropping attacks, a series of experiments is conducted, and the following comparative illustrations are produced. As shown in Figure 17, the images decrypted from the cipher images with data loss rates of 6.25, 12.5%, 23.44%, 25%, 43.75%, and 50% are very similar to the original images and can still provide valuable information about the input images’ visual information.

Figure 17. Cropping attack test [50]: (a) cropped 6.25% of the encrypted image; (b) cropped 12.5% of the encrypted image; (c) cropped 23.44% of the encrypted image; (d) cropped 25% of the encrypted image; (e) cropped 43.75% of the encrypted image; (f) cropped 50% of the encrypted image; (g) decrypted image based on the cropped 6.25% of the encrypted image; (h) decrypted image based on the cropped 12.5% of the encrypted image; (i) decrypted image based on the cropped 23.44% of the encrypted image; (j) decrypted image based on the cropped 25% of the encrypted image; (k) decrypted image based on the cropped 43.75% of the encrypted image; (l) decrypted image based on the cropped 50% of the encrypted image.

4.11. Randomness Tests for the Encrypted Image

In order to guarantee the security of the encryption system, the image should contain properties for further measurable investigation to distinguish between different designs [51]. For the DIEHARD test, which focuses on several types of potential randomness in the sequence [52], the value of each pixel of the encrypted image is transformed into binary. The results of the DIEHARD test in Table 10 show that the proposed scheme exhibits highly random behavior.

Table 10. Result of DIEHARD tests suite.

Image	p-Value	Assessment
Birthday spacing	0.4381	PASSED
Overlapping permutation	0.8404	PASSED
Binary rank 32 × 32	0.4542	PASSED
Binary rank 6 × 8	0.5309	PASSED
Bitstream	0.6567	PASSED
OPSO	0.1355	PASSED
OQSO	0.4506	PASSED
DNA	0.7073	PASSED
Count the ones 01	0.9588	PASSED
Count the ones 02	0.7266	PASSED
Parking lot	0.6397	PASSED
2DS sphere	0.0297	PASSED
3DS spheres	0.6735	PASSED
Squeeze	0.9060	PASSED
Overlapping sum	0.1625	PASSED
Runs	0.7672	PASSED
Craps	0.1105	PASSED

4.12. Comparison with Existing Methods

This section compares the scheme with existing encryption schemes by comparing the key space, entropy, CC, NPCR, and UACI. CC is the average value of the correlation of adjacent pixels in the horizontal, vertical, and diagonal directions of the image, and the formula is as follows:

$$\begin{array}{c}\hfill CC=\frac{|C_h|+|C_v|+|C_d|}{3}\end{array}$$

(20)

where $C_h$, $C_v$, and $C_d$ are correlations of horizontal, vertical, and diagonal of encrypted images.

Table 11 shows the comparison of encrypted Lena images.

Table 11. Key space, entropy, CC, NPCR, and UACI comparison.

Method	Key Space	Entropy	CC				NPCR (%)				UACI (%)
			R	G	B	Cipher	R	G	B	Cipher	R	G	B	Cipher
Proposed	$>2^{2338}$	7.9998	0.0119	0.0096	0.0109	0.0070	99.5811	99.6162	99.6052	99.6062	33.3818	33.5105	33.4385	33.4623
Ref. [53]	$>2^{160}$	7.9992	0.0320	0.0099	0.0221	-	100	100	100	100	33.6313	33.4737	33.6520	33.5857
Ref. [2]	$2^{128}$	7.9998	0.0020	0.0007	0.0018	0.0015	100	100	100	100	33.4877	33.3697	33.4629	33.4400
Ref. [54]	$2^{233}$	7.9967	0.0043	0.0035	0.0020	-	99.5865	99.2172	99.8480	-	33.4835	33.4640	33.2689	-
Ref. [55]	$2^{626}$	7.9998	-	-	-	0.0026	99.6296	99.6174	99.6473	-	33.6027	33.4997	33.5516	-
Ref. [56]	-	7.9956	0.0004	0.0004	0.0004	-	99.6420	99.5960	99.5290	99.5890	32.7630	30.0490	27.5670	30.1260
Ref. [57]	$2^{170}$	7.9998	0.0021	0.0025	0.00040	0.0013	-	-	-	99.6166	-	-	-	33.4476
Ref. [58]	$2^{170}$	7.9994	0.0034	0.0002	0.0028	0.0013	99.6099	99.6093	99.6101	-	33.4650	33.4637	33.4641	-
Ref. [59]	$2^{711}$	7.9978	-	-	-	0.0042	-	-	-	99.6090	-	-	-	33.4500
Ref. [60]	$>2^{183}$	7.9994	0.0021	0.0009	0.0005	-	99.6089	99.6089	99.6085	-	33.4589	33.4598	33.4624	-
Ref. [61]	-	7.9998	-	-	-	0.0002	-	-	-	99.62	-	-	-	33.47
Ref. [62]	-	7.9997	-	-	-	0.0006	-	-	-	-	-	-	-	-
Ref. [41]	$2^{554}$	7.9989	0.0030	0.0015	0.0031	0.0036	99.6246	99.6246	99.6246	99.6246	33.0716	30.7640	27.8720	30.5681
Ref. [63]	$2^{418}$	7.9988	-	-	-	0.0022	-	-	-	99.6112	-	-	-	33.4254

5. Conclusions

The image encryption algorithm based on the novel eighth-order hyperchaotic system proposed in this paper performs a significant level of security in experiments. The algorithm effectively improves the randomness and unpredictability of encrypted images through multiple rounds of diffusion and scrambling operations. In contrast to the conventional chaotic system, the novel hyperchaotic system exhibits superior performance in terms of key space and resistance against attacks, while also demonstrating heightened sensitivity to keys. By comparing the results of other encryption algorithms, it can be seen that the key space of the proposed algorithm is significantly larger than those of other references; NPCR and UACI are closer to the theoretical values; and the pixel correlation is also lower than most references. Based on the aforementioned notable benefits, it is evident that the algorithm demonstrates exceptional performance in the encryption of images.