DADE-DQN: Dual Action and Dual Environment Deep Q-Network for Enhancing Stock Trading Strategy

Abstract

Deep reinforcement learning (DRL) has attracted strong interest since AlphaGo beat human professionals, and its applications in stock trading are widespread. In this paper, an enhanced stock trading strategy called Dual Action and Dual Environment Deep Q-Network (DADE-DQN) for profit and risk reduction is proposed. Our approach incorporates several key highlights. First, to achieve a better balance between exploration and exploitation, a dual-action selection and dual-environment mechanism are incorporated into our DQN framework. Second, our approach optimizes the utilization of storage transitions by utilizing independent replay memories and performing dual mini-batch updates, leading to faster convergence and more efficient learning. Third, a novel deep network structure that incorporates Long Short-Term Memory (LSTM) and attention mechanisms is introduced, thereby improving the network’s ability to capture essential features and patterns. In addition, an innovative feature selection method is presented to efficiently enhance the input data by utilizing mutual information to identify and eliminate irrelevant features. Evaluation on six datasets shows that our DADE-DQN algorithm outperforms multiple DRL-based strategies (TDQN, DQN-Pattern, DQN-Vanilla) and traditional strategies (B&H, S&H, MR, TF). For example, on the KS11 dataset, the DADE-DQN strategy has achieved an impressive cumulative return of 79.43% and a Sharpe ratio of 2.21, outperforming all other methods. These experimental results demonstrate the performance of our approach in enhancing stock trading strategies.

1. Introduction

The primary objective of investing in financial assets is usually to optimize returns while effectively managing risk. This objective revolves around striking a balance between risk and returns to achieve sustainable long-term investment returns. However, traditional methods typically involve human traders who analyze market data and trends, evaluate price fluctuations, and execute buy and sell trades based on their decisions. In contrast, algorithmic trading uses computer programs to automate decision making and trade execution. These programs operate using pre-defined algorithms and rules, eliminating the need for human intervention. Algorithmic trading mainly includes rule-based and machine learning (ML)-based approaches. Rule-based algorithmic trading involves several steps. These include analyzing and modeling the market and developing a set of rules based on market trends, price fluctuations, and other factors. Afterward, decisions and trading are carried out based on those rules. On the other hand, machine learning-based algorithmic trading involves training machine learning models to discover market patterns and then making decisions and trades based on those patterns.

However, rule-based algorithmic trading methods have been widely used to solve financial decision problems that consider the time series of financial assets as a sequence of random variables controlled by a stochastic process [1]. These methods often oversimplify real-world financial markets by assuming discrete time points, leading to suboptimal outcomes and potential financial losses. To overcome this limitation and develop models that can effectively capture the complex nature of financial markets without oversimplifying them is a huge mathematical and computational challenge.

AlphaGo’s success in competing against human professionals has sparked interest in reinforcement learning (RL) as a promising approach for statistical modeling and data processing in finance [2]. Significant progress has been made in several areas by combining RL with deep learning techniques. Notable examples include AlphaGo [3], which used RL and Monte Carlo tree search to defeat top Go players, as well as AlphaStar and OpenAI Five demonstrated extraordinary performance in StarCraft II and Dota 2 through DRL-based methods [4,5]. DRL involves an agent interacting with an unknown environment in a sequential manner, utilizing deep learning techniques to make decisions based on acquired information with the objective of maximizing cumulative rewards. RL techniques have demonstrated significant potential in addressing complex sequential decision problems.

Advances in DRL and massive financial datasets have motivated researchers to apply DRL algorithms to financial markets. The researchers focus on modeling and analyzing financial markets by adapting DRL techniques. Using historical asset prices as input, they design neural networks to optimize trading actions to maximize returns or Sharpe ratios. DRL has been successful in several financial areas, including optimal execution, portfolio optimization, and market making.

In this paper, a Dual Action and Dual Environment Deep Q-Network, named DADE-DQN, which is a trading strategy that extends and enhances the DQN algorithm, is proposed. First, to achieve a better balance between exploration and exploitation, a dual-action selection and dual-environment mechanism is added to the DQN framework. This enables agents to explore new actions while utilizing what they have learned. Second, for faster convergence and more efficient learning, our approach optimizes storage conversion by exploiting independent replay memories and performing dual mini-batch updates. Third, a novel deep network structure combining LSTM and attention mechanisms is introduced, which enhances the network’s ability to capture key features and patterns. In addition, a creative feature selection method is proposed to efficiently improve the input data by utilizing mutual information to identify and eliminate irrelevant features.

In summary, our study makes the following key contributions:

• A novel DRL model, Dual Action and Dual Environment Deep Q-Network, named DADE-DQN, is proposed. The proposed model incorporates dual action selection and dual environment mechanisms into the DQN framework to effectively balance exploration and exploitation.
• Optimized utilization of storage transitions by leveraging independent replay memory and performing dual mini-batch updates leads to faster convergence and more efficient learning.
• A novel deep network architecture of combining LSTM and attention mechanisms is introduced to capture important features and patterns in stock market data for improving the network’s ability.
• An innovative feature selection method is proposed to efficiently enhance input data by utilizing mutual information in order to identify and eliminate irrelevant features.
• Evaluations on six datasets show that the presented DADE-DQN algorithm demonstrates excellent performance compared to multiple DRL-based strategies such as TDQN, DQN-Pattern, DQN-Vanilla, and traditional strategies such as B&H, S&H, MR, and TF.

The rest of this paper is arranged as follows. Section 2 describes the related work. Section 3 generally formalizes the stock trading problem and describes the proposed approach in detail. The experimental results are shown and analyzed in Section 4. Section 5 presents the discussion. Section 6 presents the conclusions and future work.

2. Related Work

This section reviews two research areas: the improvement of DRL algorithms and DRL in financial trading.

2.1. Improvements in DRL Algorithms

Recent advancements in RL and deep learning have brought new ideas to various fields. In 2013, Mnih and Silver et al. introduced the deep Q-network (DQN) algorithm, which employed an empirical replay pool and a target network to stabilize the training process. They demonstrated that DQN achieved human-level performance in Atari games [6]. Since the proposal of DQN, several improved versions based on DQN have emerged, categorized into enhancements of training algorithms [7,8,9,10,11,12,13,14,15], introductions of new learning mechanisms [16,17], and improvements to neural network structures [18,19].

In terms of training algorithm improvements, Hasselt et al. proposed the double DQN algorithm, combining DQN with double Q-learning to address the issue of overestimating action value functions in Q-learning [7]. Lipton et al. introduced Bayes-by-Backprop Q-networks to improve the performance of DQNs in scenarios with sparse rewards and large action spaces, utilizing $ϵ$-greedy exploration [8]. Mossalam et al. developed the deep optimistic linear support learning algorithm, which combined an optimistic linear support framework with deep Q-learning to solve high-dimensional multi-objective decision problems with unknown relative importance among objectives [9]. Mahajan et al. proposed a symmetric DQN that explored symmetries in the environment and incorporates them into the function approximation process [10]. Taitler et al. introduced the Guided DQN algorithm to address the control strategy learning problem in air hockey hitting [11]. Levine et al. presented the least squares DQN, which combined DQN with linear least squares [12]. Leibfried et al. extended information-theoretical bounded rationality to high-dimensional state spaces and incorporated internal penalty signals in DQNs to mitigate cumulative reward overestimation and reduce sampling complexity [13]. Anschel et al. proposed the averaged DQN algorithm to alleviate the negative effects of variability and instability in DRL algorithms [14]. Hester et al. introduced Deep Q Learning from the Demonstrations algorithm, significantly accelerating the learning process by utilizing demonstration data [15].

Regarding the new learning mechanisms, Schaul et al. proposed prioritized experience replay, which utilized an importance sampling mechanism to alleviate bias introduced during the update process. This technique improved the performance of DQN and DDQN in Atari games [16]. Sorokin et al. introduced the attention mechanism deep recurrent Q network, which incorporated an attention mechanism into the DRQN structure. This addition not only enhanced computational speed but also improved the interpretability of modality [17].

Concerning improvements to neural network structures, Hausknecht et al. presented the deep recurrent Q-network algorithm to address partially observable states. This approach combined a long-short memory (LSTM) network with DQN, replacing the first fully connected layer of DQN with an LSTM layer [18]. Wang et al. proposed the dueling network architecture, where the convolutional layer in the Q network was split into two branches: one representing the scalar state value function and the other representing the state-action advantage function. These branches were then combined in the output module to obtain the Q value for each action [19].

2.2. DRL in Financial Trading

Given the abundance of financial data and advancements in machine learning technology, trading strategies have increasingly focused on RL as a prominent research direction [20,21]. Researchers have integrated RL with deep neural networks, enabling the development of DRL methods for learning trading strategies from historical data. These approaches can be classified into three categories: value-based [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38], policy-based [39,40,41,42,43,44], or actor–critic [45,46,47,48,49,50]. However, when it comes to generating trading strategies for single stock, the DRL algorithms primarily adopt value-based approaches. Table 1 shows a representative selection of modeling options in datasets, state and action spaces, reward functions, methods, and performance metrics used in the various articles on value-based RL. It is important to note that this list is not exhaustive but instead captures a significant portion of the diversity in the entire corpus. For instance, Chen et al. proposed a framework that combined DQN with Monte Carlo tree search to learn an optimal trading policy [24]. Jeong et al. introduced a novel approach using deep Q-learning for financial trading decisions, focusing on stock quantity prediction, strategy selection, and transfer learning across different markets [25]. Ma et al. developed a parallel multi-module DRL algorithm for stock trading, employing multiple neural networks and RL techniques to capture both current market data and long-term historical trends [29]. Li et al. utilized a combination of Convolutional Neural Networks (CNN) and LSTM networks with Double DQN and Dueling DQN algorithms to learn optimal dynamic trading strategies from stock data and candlestick charts [33]. Taghian et al. proposed a framework that integrated DQN with technical indicators to learn an optimal trading policy for individual assets [34]. Other studies have explored variations of DQN, such as Double DQN, and applied them to optimize parameters in automated trading systems [36]. Liu et al. introduced a new approach for algorithmic trading that employed DRL, combining financial data, news sentiment data, and technical indicator data. Their framework used an actor–critic method and a dueling network to extract temporal features and candlestick chart features for learning the optimal trading policy [35].

Table 1. Value-based RL algorithms for single-asset trading.

Article	Data Set	State Space	Action Space	Reward	Method	Performance
1-7 [22] (2018)	Artificial time series	prices	cash, buy, hold	return	DQN + CNN, LSTM, GRU, MLP	mean profit
1-7 [23] (2018)	foreign exchange	OHLCV, position	hold, buy, sell	log return	DRQN + LSTM	profit, return, ShR, SoR, WR, MDD etc.
1-7 [24] (2019)	SPY (S&P500 ETF)	adjusted closes	buy, sell, hold	return	DQN, DRQN + RNN	AmR
1-7 [25] (2019)	S&P500, KOSPI, HSI, EuroStoxx50	200-days prices	buy, sell, hold	return rate	DQN + MLP	profit, correlation
1-7 [26] (2019)	10 U.S. stocks	prices, volumes	buy, sell, hold	none	Dueling DQN, DDQN, DQN + MLP, CNN	profit
1-7 [27] (2020)	2 U.S indices, 2 Indian indices	closing prices	long, short, neutral	return	DQN	returns, MDD, ShR, Skewness, AR, Kurtosis etc.
1-7 [28] (2020)	Google	prices	buy, sell, hold	profit	Dueling DQN, DQN, DDQN + CNN	profit
1-7 [29] (2021)	Chinese stocks	OHLCV, technical indicators	buy, sell, hold	return	DDQN + DNN, LSTM	returns, ShR
1-7 [30] (2021)	Chinese stocks, U.S. stocks	OHLCV, action	long/buy, short/sell	return	DDQN + CNN	accuracy, profit, returns, MDD
1-7 [31] (2021)	30 stocks	OHLCV, position	buy, sell	return	DDQN + CNN	profit, ShR, MDD, MDDD, AR, SoR etc.
1-7 [32] (2021)	Indian market	prices, volume	buy, sell, hold	none	DQN, DDQN, Dueling DDQN + CNN	profit
1-7 [33] (2022)	S&P 500, Chinese stocks	technical indicators, candlestick charts	long, short, neural	ShR + PR	Dueling DQN, DDQN + CNN, BiLSTM	AR, ShR, MDD
1-7 [34] (2022)	AAPL, GOOGL, KSS, BTC/USD	OHLC	buy, sell, hold	customized	SARSA, DQN + MLP, CNN, GRU	AR, TR, VaR, ShR, MDD
1-7 [35] (2023)	Chinese stock, S&P 500 stocks	OHLCV, technical indicators, candlestick charts	buy, sell, hold	profit	Dueling DQN, DDQN + CNN, LSTM, BiLSTM	profit, AR, ShR, MDD, MDDD
1-7 [36] (2023)	BTC-USDT	OHLC	buy, sell, hold	ShR	Dueling DQN, DDQN + CNN	average return
1-7 [37] (2023)	Dow Jones, NASDAQ, General Electric, AAPLE	OHLCV	buy, sell, hold	ShR	SARSA + CNN	profit, AR, ShR
1-7 [38] (2023)	10 stocks (AAPL etc.)	close price	buy, sell, hold	profit	Mult-step DQN + LSTM	return, CR
1-7 Our	Six stock indices	OHLC, technical indicators	buy, sell, hold	ShR	DDQN + LSTM + attention mechanisms	CR, AR, ShR, MDD

In the stock market, stock price fluctuations are influenced by various factors, including price and liquidity indicators. To tackle the challenges of overfitting, computational complexity, and the impact of irrelevant variables, researchers employ feature factor filtering methods. For example, Nesselroade et al. provided a detailed explanation of the correlation coefficient, which was used to assess the correlation and strength of the relationship between two variables [51]. The Pearson coefficient was employed to analyze the degree of correlation between features and response variables. Cai et al. used the Pearson coefficient to identify influential factors by measuring the linear correlation between variables [52]. Li et al. proposed a method for stock price prediction that combined the Pearson correlation coefficient and Broad Learning System for multi-indicator feature selection [53]. These methods aim to select relevant factors and construct an initial indicator system for model training. Various techniques have been utilized, such as correlation coefficients, including the Pearson coefficient, to assess the strength of relationships between variables. However, mutual information has also been employed for feature selection to capture nonlinear relationships between features and response variables. Guo et al. utilized mutual information to capture the non-linear relationships between stocks, considering it a more effective measure than correlation coefficients in volatile stock markets [54]. Kong et al. conducted feature selection based on time series mutual information and minimum redundancy maximum correlation techniques to analyze micro-trading patterns specific to stocks prior to price increases [55]. Vasileios et al. combined proximal policy optimization with rule-based safety mechanisms to both maximize profit and loss returns and minimize trading risk.

Motivated by the previously mentioned literature review, this paper introduces a novel DRL model called DADE-DQN (Dual Action and Dual Environment Deep Q-Network). The model incorporates dual-action selection and dual-environment mechanisms into the DQN framework, effectively achieving a balance between exploration and utilization. Meanwhile, faster convergence and more efficient learning are achieved by employing independent replay memories and performing dual mini-batch updates to optimize the utilization of storage transitions. In addition, a novel deep network structure combining LSTM and attention mechanism is proposed to improve the performance of the network. By incorporating the attention mechanism, the agent can focus on crucial features and patterns in the stock market data. However, as the stock market is influenced by various factors, accurately representing the state in RL becomes challenging. To overcome this problem, a mutual information-based factor filtering approach is used to effectively remove irrelevant features and address issues such as overfitting and computational complexity associated with large datasets.

3. Materials and Methods

Driven by the progress of DQN, the DADE-DQN method was proposed to improve stock trading strategies using a dual-action, dual-environment deep Q-network approach The DQN algorithm has been widely utilized in optimizing trading strategies using stock states as inputs.

3.1. Materials

RL is a framework that involves an agent, a set of states S, and a set of actions A for each state [56]. The goal of reinforcement learning is to improve decision making by allowing the agent to learn from the consequences of its actions. Markov Decision Process (MDP) is a mathematical framework used to model decision-making problems in which an agent interacts with an environment to achieve certain goals. It is widely used in various fields, including finance and economics, to analyze and optimize decision-making processes. In the context of the financial market, both in a broad sense and specifically in the stock market, MDPs can be employed to understand and potentially improve decision-making strategies [57]. Figure 1 illustrates the agent’s interaction with the Markov decision process environment.

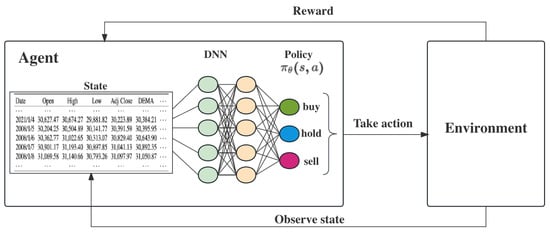
Figure 1. The interaction diagram of an agent with the Markov decision process environment. Different colored circles represent different neurons.

When an agent performs an action $a\in A$, it transitions from one state to another. Each action taken in a particular state provides the agent with a reward, denoted as $r_t$. The agent’s goal is to maximize its cumulative reward by considering the potential future rewards. This is achieved by adding the maximum achievable future reward to the reward obtained in the current state, thereby influencing the agent’s current action based on the potential future rewards. The potential future reward is calculated as the weighted sum of the expected values of rewards for all future steps starting from the current state. Mathematically, it can be represented as Equations (1) and (2).

$${\pi }^{*}=arg\underset{\pi }{max}\mathbb{E}[R\mid \pi ],$$

(1)

$$R=\sum _{t=0}^{\infty }{\gamma }^t{r}_t,$$

(2)

where ${\pi }^{*}$ represents the optimal policy, $\pi$ represents the current policy, $\gamma$ is the discount factor ($\gamma \in [0,1]$), $r_t$ represents immediate rewards at time step t, and R denotes the cumulative reward. The discount factor $\gamma$ determines the relative importance of future rewards in the overall cumulative reward calculation.

3.1.1. States

In the context of algorithmic trading, the RL environment can be considered as an abstraction that contains the trading mechanism and all relevant information that can influence the agent’s trading activity. At each time step t, the RL agent receives a set of information including RL status (current trading position, available cash, etc.), stock information (opening price, closing price, volume, etc.), technical indicators of the stock market (moving average convergence divergence, relative strength index, average direction index, etc.), macroeconomic information, news information, etc.

Therefore, it is important to select and properly process information from the environment. Many existing studies rely on the use of raw stock information as input to RL, which may not provide enough information for RL agents to make effective differentiation and informed decisions. In this paper, mutual information is used as a technique to select highly relevant features. The dimension of the state of the environment at time t is denoted as $m\times n$, where m corresponds to the different technical indicators obtained from the price information and n represents the time window length. It can be expressed as Equations (3) and (4).

$$s_t\triangleq [I_{t-n+1},I_{t-n+2},\cdots ,I_t],$$

(3)

$$I_t=[I_t^1,I_t^2,\cdots ,I_t^m],$$

(4)

where, $I_t^j$ denotes the ith normalized technical indicator on the tth day; n represents the number of days in the past.

3.1.2. Actions

At each time step t, the RL agent first obtains the environment state $s_t$. According to the RL policy $\pi \left(a_t\right|s_t)$, the agent selects an action $a_t$. The state–action value is referred to as the Q-value and represents the expected cumulative reward, expressed as Equation (5).

$$Q_{\pi }(s,a)={\mathbb{E}}_{\pi }\left[\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k+1}|s_t,a_t\right],$$

(5)

This Q-value represents the expected cumulative reward when taking action $a_t$ under state $s_t$ according to policy $\pi$. The optimal Q-value, denoted $Q^{*}(s,a)$, is determined by the optimal policy that maximizes the Q-value. The Bellman equation can be expressed as Equation (6):

$$Q^{*}(s,a)=\underset{\pi }{max}{Q}_{\pi }(s,a),$$

(6)

The optimal Q-value $Q^{*}(s,a)$ can be recursively can be expressed as Equation (7):

$$Q^{*}(s,a)=\underset{\pi }{max}\left[r_t+\gamma Q(s_{t+1},a^{\prime })\right],$$

(7)

where $a^{\prime }$ represents the action taken in the subsequent state $s_{t+1}$.

This paper assumes that the agent’s actions do not influence the financial market. Consequently, the action space can be expressed as Equation (8).

$$a_t^{*}=\left\{\begin{array}{cc}-1,\hfill & \mathrm{if}{Q}^{*}(s,a)=Q_t^{\mathrm{Sell}};\hfill \\ 0,\hfill & \mathrm{if}{Q}^{*}(s,a)=Q_t^{\mathrm{Hold}};\hfill \\ 1,\hfill & \mathrm{if}{Q}^{*}(s,a)=Q_t^{\mathrm{Buy}}.\hfill \end{array}\right.$$

(8)

where $Q_t^{\mathrm{Sell}}$, $Q_t^{\mathrm{Hold}}$, and $Q_t^{\mathrm{Buy}}$ is determined by the Q-network at each time step t.

To incorporate the position information ${\mathrm{POS}}_t$, the final action and updated position information are computed as Equations (9) and (10).

$$a_t=a_t^{*}·\left(a_t^{*}\oplus {\mathrm{POS}}_{t-1}\right),$$

(9)

where the symbol ⊕ indicates a process of element-wise multiplication followed by addition. This operation involves multiplying corresponding values of two elements and subsequently summing the products. In this context, it implies that each element of $a_t^{*}$ is individually multiplied by the corresponding element of ${\mathrm{POS}}_{t-1}$, and the resulting products are then aggregated to yield the ultimate value of $a_t$.

$${\mathrm{POS}}_t=a_t+{\mathrm{POS}}_{t-1},$$

(10)

The position information ${\mathrm{POS}}_t$ takes values from the set $\{-1,0,1\}$, where ${\mathrm{POS}}_0=0$ indicates no initial position. A positive value of ${\mathrm{POS}}_t$ (e.g., ${\mathrm{POS}}_t=1$) indicates a long position, while a negative value (e.g., ${\mathrm{POS}}_t=-1$) indicates a short position. In the action space $A=\{-1,0,1\}$, when $a_t^{*}=1$ and ${\mathrm{POS}}_{t-1}=0$, the agent establishes a long position. When $a_t^{*}=-1$ and ${\mathrm{POS}}_{t-1}=1$, it closes this long position. Similarly, when $a_t^{*}=-1$ and ${\mathrm{POS}}_{t-1}=0$, the agent opens a short position and closes this short position when $a_t^{*}=1$ and ${\mathrm{POS}}_{t-1}=-1$. These trading strategies are intuitive and realistic, allowing agents to behave more similarly to human traders.

3.1.3. Reward Function

The reward function is an important component of the RL algorithm that determines the reward assigned to each action taken by the agent. Its purpose is to maximize the cumulative reward over time. In this study, the short-term Sharpe Ratio (SSR) award is used to address this challenge [37]. The SSR reward function effectively contains information about the subsequent k days and also the agent’s location. Thus, it is an appropriate indicator of the actual reward in the RL context. Mathematically, the SSR reward function is defined as Equations (11)–(13).

$${\mathrm{SSR}}_t={\mathrm{POS}}_t\times R_t^{*},$$

(11)

$$R_t^{*}=\frac{\mathrm{mean}\left(R_t^k\right)}{\mathrm{std}\left(R_t^k\right)},$$

(12)

$$R_t^k=\left[\frac{p_{t+1}-p_t}{p_t},\frac{p_{t+2}-p_t}{p_t},\cdots ,\frac{p_{t+k}-p_t}{p_t}\right],$$

(13)

where $R_t^k$ represents the returns over the next k days, calculated as the percentage change in price ($p_t$) from time t to $t+k$.

3.2. Methods

3.2.1. Dual Action and Dual Environment Deep Q-Network (DADE-DQN)

In the financial market, achieving higher profits while minimizing risks is a difficult task for traders. Inspired by the DQN algorithm, a novel approach called Dual Action and Dual Environment Deep Q-Network (DADE-DQN) is proposed to address this challenge. DADE-DQN is an extension of the DQN algorithm specifically designed for the trading problem. Typically, DQN-based RL agents require a large number of training events to learn the optimal strategy and maximize the cumulative reward. However, in stock trading, this can lead to overfitting and poor performance on the test set due to high data noise, randomness, and limited real stock data. Our goal is to overcome overfitting and explore the best policy efficiently with limited data. The main features of the DADE-DQN algorithm are as follows:

Optimal and Exploit Replay Memory: The DADE-DQN algorithm utilizes two separate replay memories: an optimal replay memory (D) and an exploit replay memory ($D^{-}$). This separation allows for more effective learning by selectively replaying transitions based on their potential for exploration or exploitation.

Dual Action Selection: In DADE-DQN, the agent takes two different actions at the same time, obtaining two sets of transactions from the environment. This approach addresses the issue of limited data to a certain extent. During training, using these two sets of transactions, the maximum and minimum Q values corresponding to the actions generated by the Q network are optimized alternatively. This allows the RL agent to avoid selecting the worst action. The selection of the best action is based on maximizing the Q-value, while the selection of the exploited action is based on minimizing the Q-value. This dual action selection strategy enhances the agent’s ability to explore while using its knowledge to exploit the learned values.

Dual Minibatch Update: The DADE-DQN algorithm performs dual minibatch updates based on the selected actions. In one time interval, it samples transitions from the optimal replay memory (D) and uses the argmax action selection to update the Q value for the next state. In another time interval, it samples transitions from the exploitation replay memory ($D^{-}$) and updates the Q-values using argmin action selection. This dual minibatch update process facilitates more efficient learning and better utilization of the replay memories.

Novel Q-network: The efficacy of DRL algorithms relies largely on the structure of the value/policy network employed by agents. Therefore, a network structure is designed to approximate the action-value function of DADE-DQN. The network topology consists of four main layers: an input layer, an encoder layer, an attention layer, and an action layer, as shown in Figure 2. In recent years, attention mechanisms have shown good potential in computer vision (CV) and natural language processing (NLP) fields. In this paper, a hierarchical attention mechanism proposed by Yang et al. is used to design the proposed network [58].

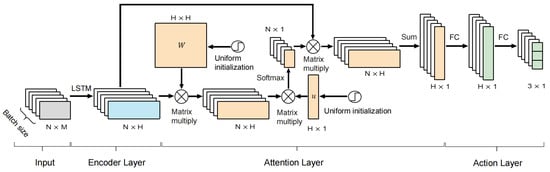
Figure 2. The Q-network structure of the proposed algorithm.

Input: As stated in Section 3.1.1, the input part contains M components, consisting of several technical indicators and the open, close, high, and low price of the previous N days as the state of the time step t. During the training process, a mini-batch is selected to train the network.

Encoder Layer: Initially, the input is passed through a LSTM network to obtain a hidden representation, denoted as $h_i$, which effectively captures the temporal information [59]. LSTM is a specialized type of recurrent neural network (RNN) that alleviates the vanishing gradient problem and facilitates the learning of long-term dependencies.

The following equations outline the fundamental operations, where ⊙ denotes the element-wise product (Hadamard product) as Equations (14)–(18).

$$i_t=\sigma (W_{xi}{x}_t+W_{hi}{h}_{t-1}+W_{ci}\odot c_{t-1}+b_i)$$

(14)

$$f_t=\sigma (W_{xf}{x}_t+W_{hf}{h}_{t-1}+W_{cf}\odot c_{t-1}+b_f)$$

(15)

$$c_t=f_t\odot c_{t-1}+i_t\odot tanh(W_{xc}{x}_t+W_{hc}{h}_{t-1}+b_c)$$

(16)

$$o_t=\sigma (W_{xo}{x}_t+W_{ho}{h}_{t-1}+W_{co}\odot c_t+b_o)$$

(17)

$$h_t=o_t\odot tanh\left(c_t\right)$$

(18)

The core of LSTM lies in the cell state, which can selectively add or remove information through specialized structures called gates. Gates, which include a sigmoid neural network layer and a point-wise product operation, regulate the flow of information. The sigmoid functions have output values between 0 and 1, where 1 represents “keep this information completely” and 0 represents “discard this information entirely”. LSTM cells contain three gates: the forget gate, input gate, and output gate, which together protect and manage the cell state. The forget gate $f_t$ uses the sigmoid neural network layer that uses the past cell output $h_{t-1}$ and the current cell input $x_t$ to determine which information should be discarded from the cell state $c_t$. The input gate $i_t$ works alongside a tanh layer to control the addition of new information. The tanh layer generates a vector $\widetilde{c_t}=\tan \mathrm{h}(W_{xc}{x}_t+W_{hc}{h}_{t-1}+b_c)$, which is then added to the cell state $c_t$. Subsequently, the sigmoid layer outputs a value between 0 and 1 for each element in $\widetilde{c_t}$, determining the extent to which the new information is assimilated. The output gate $o_t$ governs the amount of information that is filtered out from the current cell state.

Attention Layer: The hidden states from different days have different levels of importance to the agent. To address this problem, an attention mechanism is introduced to extract the weights assigned to each day and hidden state, thereby aggregating the representation of these summarized states. The hierarchical attention mechanism used in this study operates as Equations (19)–(21).

$$u_i=\tan \mathrm{h}(W{h}_i+b),$$

(19)

$${\alpha }_i=\frac{\exp \left(u_i^{T}u\right)}{{\sum }_i\exp \left(u_i^{T}u\right)},$$

(20)

$$v=\sum _i{\alpha }_i{h}_i,$$

(21)

In our implementation, the hidden representation $h_i$ is initially transformed by matrix W, which is uniformly initialized, resulting in $u_i$ as a weighted representation of $h_i$. The importance of the states is then measured based on the similarity between $u_i$ and a uniformly initialized vector u. A softmax function is applied to obtain normalized weights ${\alpha }_i$. Subsequently, the state v is computed as a weighted sum of the hidden representations. This process generates an attention value vector v, which encapsulates all the information related to the different days and hidden states in the hidden representation $h_i$. The matrix W and the vector v are learned together during the training process.

Action Layer: Finally, the attention value vector v is fed into an action network consisting of two fully connected layers to obtain the Q values of the three available actions.

3.2.2. Feature Selection Based on Mutual Information

In this section, mutual information is used to measure the statistical dependence or the amount of information shared between two random variables. Developed within the field of information theory by Claude Shannon, mutual information has become an important concept in various fields. The goal is to select several technical indicators as explanatory variables, with the closing price of the day serving as the response variable.

The feature selection process begins by pre-selecting several features from the library as potential explanatory variables. Then, univariate analysis is conducted to identify features with low variance and a significant number of missing values, which are excluded from further analysis. Subsequently, mutual information is employed to measure the interdependence between all remaining explanatory variables and the response variable, providing insights into the correlation between each explanatory variable and the closing price. Finally, a higher threshold is set to filter out the final technical factors. This threshold is used to select the characteristics that exhibit a high correlation with the closing price. Figure 3 illustrates the flow of feature selection.

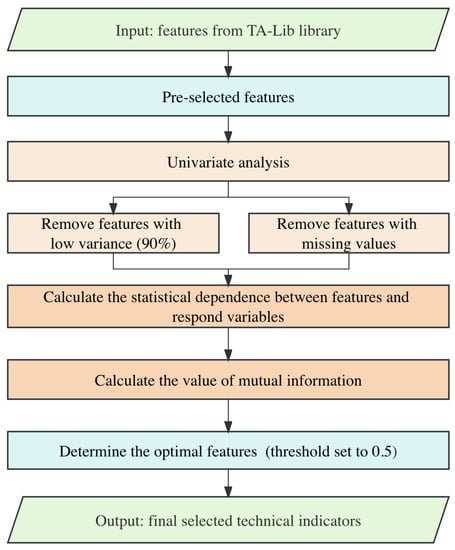
Figure 3. The flow of feature selection.

Mutual information quantifies the statistical dependence between two random variables. It is based on the concept of entropy, which measures the uncertainty or randomness of a random variable. The mutual information between two random variables, denoted as $I(X;Y)$, is calculated using the probabilities of their joint distribution $P(X,Y)$ and their individual marginal distributions $P\left(X\right)$ and $P\left(Y\right)$. The formula for calculating mutual information can be expressed as Equation (22).

$$I(X;Y)=\sum \sum P(X,Y)·log\left(\frac{P(X,Y)}{P\left(X\right)·P\left(Y\right)}\right),$$

(22)

where, $P(X,Y)$ represents the joint probability distribution of variables X and Y, while $P\left(X\right)$ and $P\left(Y\right)$ represent their respective marginal probability distributions. The resulting mutual information value, $I(X;Y)$, is always non-negative, with a higher value indicating a stronger dependency between the variables. A value of zero indicates that the variables are independent.

In specific cases, a sample threshold can be set for the mutual information. This threshold is used as a criterion for selecting the final technical factor features. Factors with mutual information values above the threshold were considered to have a strong dependence on the closing price and were included in the final set of selected features.

3.2.3. DADE-DQN Training

To summarize, Algorithm 1 provides the pseudo-code of the entire DADE-DQN algorithm, which is the basis of our proposed trading strategy. The strategy is updated based on further learning from daily observations during the trading process. This iterative process ensures the continuous learning and refinement of the trading strategy.

Algorithm 1 DADE-DQN algorithm

1: Initialize optimal replay memory D to capacity N.  2: Initialize exploit replay memory $D^{-}$ to capacity N.  3: Initialize the policy network with random weights $\theta$.  4: Initialize the target network with weights ${\theta }^{-}=\theta$.  5: for episode = 1, M do  6:       Acquire the initial state $s_1$ from the environment.  7:       for t = 1, T do  8:             Choose an optimal action $a_t^{+}=argma{x}_{a}Q(s_t,a)$.  9:             With probability ${ϵ}_t$ select a random action $a_t^{-}$ between actions except $a_t^{+}$; 10:             Otherwise, select $a_t^{-}=argmi{n}_{a}Q(s_t,a;\theta )$. 11:             Copy the environment ${\delta }^{-}=\delta$. 12:             Execute action $a_t^{+}$ in the environment $\delta$ and get reward $r_t^{+}$ and the new state $s_{t+1}$. 13:             Execute action $a_t^{-}$ in the environment ${\delta }^{-}$ and get reward $r_t^{-}$ and the new state $s_{t+1}$. 14:             Store transition $(s_t,a_t,r_t,s_{t+1})$ in D. 15:             Store transition $(s_t,a_t^{-},r_t^{-},s_{t+1})$ in $D^{-}$. 16:             if t % Interval = 0 and t % (2*Interval)! = 0 then 17:             Sample random minibatch of transitions $(s_i,a_i,r_i,s_{i+1})$ from D. 18:             Set $y_i=\left\{\begin{array}{cc}{r}_i\hfill & \mathrm{if}{s}_{i+1}\mathrm{is}\mathrm{terminal},\hfill \\ r_i+\gamma Q(s_{i+1},{\mathrm{argmax}}_{a}Q(s_{i+1},a;\theta );{\theta }^{-})\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$ 19:             Perform a gradient descent step on ${(y_i-Q(s_i,a_i;\theta ))}^2$ with respect to the parameters $\theta$. 20:             end if 21:             if t % Interval! = 0 and t % (2*Interval) = 0 then 22:             Sample random minibatch of transitions $(s_i,a_i^{-},r_i^{-},s_{i+1})$ from $D^{-}$. 23:             Set $y_i=\left\{\begin{array}{cc}{r}_i\hfill & \mathrm{if}{s}_{i+1}\mathrm{is}\mathrm{terminal},\hfill \\ r_i+\gamma Q(s_{i+1},{\mathrm{argmin}}_{a}Q(s_{i+1},a;\theta );{\theta }^{-})\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$ 24:             Perform a gradient descent step on ${(y_i-Q(s_i,a_i;\theta ))}^2$ with respect to the parameters $\theta$. 25:             end if 26:             Update the target network parameters ${\theta }^{-}=\theta$ every $T^{-}$ steps. 27:             Anneal the $ϵ$-greedy exploration parameter ${ϵ}_t$. 28:       end for 29: end for

4. Experiments and Results

In this section, the process of selecting the dataset and associated features is first investigated. Subsequently, the details of the experiment settings are discussed. Finally, the experimental results are examined and discussed. The effectiveness of the proposed model is assessed by evaluating its performance on six different stock index datasets.

4.1. Datasets

In order to fully assess the performance and robustness of our model, a range of indices from different regions and economic backgrounds were used in the experiments, including the NASDAQ Composite (IXIC), the S&P 500 (SP500), and the Dow Jones Industrial Average (DJI) in the U.S., as well as the CAC 40 (FCHI) in France, the Korea Composite Stock Price Index (KOSPI, KS11) in Korea, and the Nikkei 225 (N225) in Japan. The duration of the dataset spans from 1 January 2007, to 31 December 2022. The dataset was divided into a training set, covering 1 January 2007, to 31 December 2022, and a test set, covering 1 January 2007, to 31 December 2022. Figure 4 shows the price movement of the seven assets. The training period was the green line and the test period was the blue line.

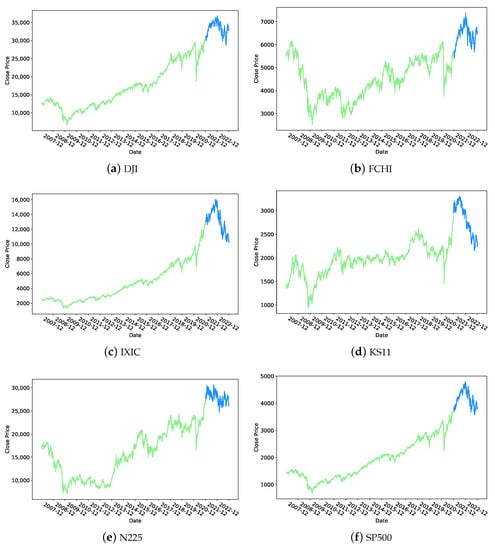
Figure 4. The price movement of the seven assets [from 1 January 2007 to 31 December 2022] [green parts: training set; blue parts: test set].

4.2. Feature Selection Results

To identify relevant explanatory variables, 57 features were selected from the TA-Lib software library, as shown in Table 2. Subsequently, a series of steps were performed to filter and refine these features. First, univariate analyses were first performed to exclude features with low variance (greater than 90%) and those with a significant number of missing values. Following this, mutual information scores were calculated to assess the interdependence between the explanatory and response variables, as demonstrated in Table 3.

Table 2. Description of exploited technical indicators.

Categories	Feature Name	Description
Overlapping Indicators	DEMA	Double Exponential Moving Average
	SMA_3	Simple Moving Average (3 days)
	SMA_5	Simple Moving Average (5 days)
	SMA_10	Simple Moving Average (10 days)
	BBANDS_UP	Bollinger BandsDEMA (UP)
	BBANDS_MIDDLE	Bollinger BandsDEMA (MIDDLE)
	BBANDS_LOW	Bollinger BandsDEMA (LOW)
	EMA	Exponential Moving Average
	HT_TRENDLINE	Hilbert Transform— Instantaneous Trendline
	KAMA	Kaufman Adaptive Moving Average
	MA	All Moving Average
	SAR	Parabolic SAR
Momentum Indicators	ADX	Average Directional Movement Index
	AROONOSC	Aroon Oscillator
	RSI	Relative Strength Index
	MFI	Money Flow Index
	MOM	Momentum
	WILLR	Williams’ %R
	TRIX	1-day Rate-Of-Change (ROC) of a Triple Smooth EMA
	PPO	Percentage Price Oscillator
	BOP	Balance Of Power
	DIF	Moving Average Convergence/Divergence
	DEM	Moving Average Convergence/Divergence
	HISTOGRAM	Moving Average Convergence/Divergence
	ROC	Rate of change: $(\left(\frac{Price}{prevPrice}\right)-1)*100$
	ADXR	Average Directional Movement Index Rating
	APO	Absolute Price Oscillator
	AROON_UP	Strength of the upward trend
	CCI	Commodity Channel Index
	PLUS_DI	Plus Directional Indicator
	CMO	Chande Momentum Oscillator
	ROCP	Rate of change Percentage: $\left(\frac{Price-prevPrice}{prevPrice}\right)$
	RR	Daily simple rate of return
	LOG_RR	Daily log returns
Volume Indicators	AD	Chaikin A/D Line
	ADOSC	Chaikin A/D Oscillator
	OBV	On Balance Volume
Volatility Indicators	NATR	Normalized Average True Range
	ATR	Average True Range
	TRANGE	True Range
Price Change Indicators	AVGPRICE	Average Price
	MEDPRICE	Median Price
	TYPPRICE	Typical Price
	WCLPRICE	Weighted Close Price
Periodic Indicators	HT_DCPERIOD	Hilbert Transform—Dominant Cycle Period
	HT_DCPHASE	Hilbert Transform—Dominant Cycle Phase
	INPHASE	Hilbert Transform—Phasor Components
	QUADRATURE	Hilbert Transform—Phasor Components
	SINE	Hilbert Transform—SineWave
	LEADSINE	Hilbert Transform—SineWave
	HT_TRENDMODE	Hilbert Transform—Trend vs. Cycle Mode
Statistical Indicators	BETA	Beta
	TSF	Time Series Forecast
Raw Data	Open	Open price
	Low	Low price
	High	High price
	Volume	Trading volume

Table 3. Mutual information scores for selected technical indicators.

Feature	DJI	FCHI	IXIC	KS11	N225	SP500
DEMA	4.1177	3.3413	4.3570	3.2748	3.7140	4.2179
SMA_3	3.7271	2.9425	3.9640	2.8457	3.2789	3.8332
SMA_5	3.3791	2.5757	3.6082	2.4649	2.9325	3.4812
SMA_10	3.0716	2.2392	3.3372	2.0869	2.5346	3.2159
BBANDS_UP	3.4327	2.6122	3.6738	2.5206	2.9584	3.5264
BBANDS_MIDDLE	3.3791	2.5757	3.6082	2.4649	2.9325	3.4812
BBANDS_LOW	3.3193	2.6309	3.5638	2.5015	2.9366	3.4449
EMA	3.6016	2.8031	3.8492	2.6916	3.1308	3.7237
HT_TRENDLINE	2.8111	1.8744	3.0767	1.6562	2.1876	2.9604
KAMA	2.8897	1.9904	3.1711	1.8767	2.3706	2.9943
MA	2.8822	1.9745	3.1665	1.7855	2.2974	2.9875
SAR	0.7567	0.0632	0.5591	0.4079	0.5781	0.7737
ADX	0.3911	0.1834	0.3769	0.2700	0.2881	0.3232
AROONOSC	0.3703	0.2319	0.3567	0.1856	0.3223	0.3511
RSI	0.3073	0.2390	0.2215	0.2921	0.2919	0.2406
MFI	0.2990	0.1842	0.4474	0.2264	0.3132	0.4289
MOM	0.2128	0.1223	0.3048	0.1262	0.1692	0.2085
WILLR	0.0960	0.1021	0.0693	0.0739	0.1003	0.0955
TRIX	0.9735	0.6552	1.0965	0.7253	0.8499	1.0828
PPO	0.4377	0.2552	0.4563	0.3123	0.3044	0.4465
DIF	0.6538	0.3573	0.8089	0.4175	0.4798	0.6663
DEM	0.6997	0.3663	0.8898	0.3949	0.5235	0.7089
HISTOGRAM	0.3269	0.1597	0.3312	0.1912	0.2279	0.2925
ROC	0.1774	0.1460	0.1774	0.1638	0.1606	0.1793
ADXR	0.5443	0.2849	0.5293	0.3817	0.4301	0.4915
APO	0.5044	0.2010	0.6402	0.2815	0.3118	0.5028
AROON_UP	0.0198	0.0257	0.0000	0.0315	0.0000	0.0000
CCI	0.0913	0.0527	0.0536	0.0708	0.0888	0.0466
PLUS_DI	0.2150	0.1669	0.1908	0.1680	0.1969	0.1760
CMO	0.3073	0.2390	0.2215	0.2921	0.2919	0.2406
ROCP	0.1774	0.1460	0.1774	0.1638	0.1606	0.1793
RR	0.0796	0.0450	0.0654	0.0617	0.0242	0.0942
LOG RR	0.0790	0.0454	0.0650	0.0617	0.0240	0.0944
AD	2.8611	1.8524	3.3141	1.7776	1.7214	3.0831
ADOSC	0.3156	0.1419	0.1676	0.1312	0.1273	0.1702
OBV	2.5657	1.3280	3.0720	1.4878	2.1969	2.7141
NATR	1.0036	0.7114	1.0310	0.6404	0.5802	1.0850
ATR	0.9430	0.4994	1.2376	0.4829	0.6761	0.9683
TRANGE	0.1966	0.0502	0.2877	0.1059	0.1375	0.1681
AVGPRICE	4.2120	3.5395	4.5136	3.4856	4.0977	4.3229
MEDPRICE	4.1514	3.4655	4.4266	3.4079	4.0328	4.2623
TYPPRICE	4.5448	3.8758	4.8251	3.8178	4.4584	4.6562
WCLPRICE	4.8117	4.1710	5.0773	4.1032	4.7400	4.9200
HT_DCPERIOD	0.3719	0.2053	0.2927	0.1784	0.2862	0.3396
HT_DCPHASE	0.1776	0.0672	0.1850	0.1042	0.1497	0.1745
INPHASE	0.1469	0.0158	0.2421	0.0666	0.1238	0.1734
QUADRATURE	0.1121	0.0049	0.1233	0.0300	0.0400	0.0777
SINE	0.1040	0.0198	0.0972	0.0390	0.1012	0.1004
LEADSINE	0.1470	0.0659	0.1672	0.0839	0.1157	0.1302
HT_TRENDMODE	0.0667	0.0400	0.0724	0.0275	0.0565	0.0610
BETA	0.0937	0.0701	0.0871	0.0761	0.0917	0.0834
TSF	3.2989	2.4815	3.5202	2.3681	2.8195	3.4074
Open	3.4958	2.8795	3.8893	2.8079	3.3896	3.6429
Low	4.1668	3.5306	4.4530	3.4674	4.0848	4.2808
High	4.2085	3.5045	4.5037	3.4317	4.0687	4.3466
Volume	0.7044	0.2008	0.3621	0.1448	0.4166	0.3471

To establish a strong relationship with the closing price, 24 features were selected based on a threshold of $0.5$. These selected features were detailed in Table 4. For each time step, the RL environment state was constructed by considering the closing prices and technical indicators from the previous n days. Consequently, the size of the environment state at time t could be represented as an $m\times n$ matrix, where $m=24$. This matrix included the opening price, closing price, high price, low price, and 20 different technical indicators based on price and volume. Further information regarding these indicators can be found in Table 4. In this context, the previous n days were represented by $n=10$, with more details in the experiment settings.

Table 4. Mutual information scores for selected technical indicators with a threshold of 0.5.

Feature	DJI	FCHI	IXIC	KS11	N225	SP500
DEMA	4.1177	3.3413	4.3570	3.2748	3.7140	4.2179
SMA_3	3.7271	2.9425	3.9640	2.8457	3.2789	3.8332
SMA_5	3.3791	2.5757	3.6082	2.4649	2.9325	3.4812
SMA_10	3.0716	2.2392	3.3372	2.0869	2.5346	3.2159
BBANDS_UP	3.4327	2.6122	3.6738	2.5206	2.9584	3.5264
BBANDS_MIDDLE	3.3791	2.5757	3.6082	2.4649	2.9325	3.4812
BBANDS_LOW	3.3193	2.6309	3.5638	2.5015	2.9366	3.4449
EMA	3.6016	2.8031	3.8492	2.6916	3.1308	3.7237
HT_TRENDLINE	2.8111	1.8744	3.0767	1.6562	2.1876	2.9604
KAMA	2.8897	1.9904	3.1711	1.8767	2.3706	2.9943
MA	2.8822	1.9745	3.1665	1.7855	2.2974	2.9875
TRIX	0.9735	0.6552	1.0965	0.7253	0.8499	1.0828
AD	2.8611	1.8524	3.3141	1.7776	1.7214	3.0831
OBV	2.5657	1.3280	3.0720	1.4878	2.1969	2.7141
NATR	1.0036	0.7114	1.0310	0.6404	0.5802	1.0850
AVGPRICE	4.2120	3.5395	4.5136	3.4856	4.0977	4.3229
MEDPRICE	4.1514	3.4655	4.4266	3.4079	4.0328	4.2623
TYPPRICE	4.5448	3.8758	4.8251	3.8178	4.4584	4.6562
WCLPRICE	4.8117	4.1710	5.0773	4.1032	4.7400	4.9200
TSF	3.2989	2.4815	3.5202	2.3681	2.8195	3.4074
Open	3.4958	2.8795	3.8893	2.8079	3.3896	3.6429
Low	4.1668	3.5306	4.4530	3.4674	4.0848	4.2808
High	4.2085	3.5045	4.5037	3.4317	4.0687	4.3466

4.3. Experiment Settings

To assess the performance of the DADE-DQN model with different window lengths, experiments were conducted using the DJI dataset. Figure 5 depicts the cumulative rewards curves obtained from training DADE-DQN with window lengths of 5, 10, 15, and 20, respectively. As can be seen in the figure, the training curve with a window length of 10 was balanced between stability and cumulative return. Furthermore, Table 5 presents the results of various performance metrics, including the cumulative return, annualized return, Sharpe ratio, and maximum drawdown, for window lengths of 5, 10, 15, and 20, respectively. Upon analyzing the table, it became apparent that a window length of 10 yields superior results compared to other window lengths. Consequently, the window length chosen for this study was 10.

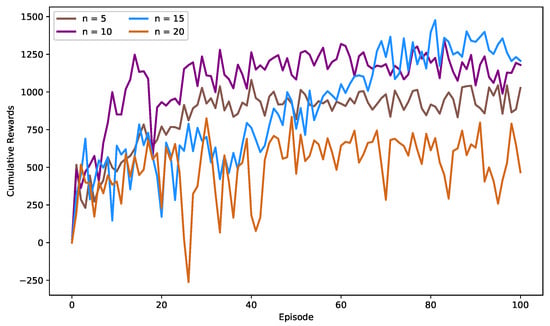
Figure 5. The cumulative rewards curve for DADE-DQN training with window lengths of 5, 10, 15, and 20 on the DJI dataset.

Table 5. Performance of DADE-DQN on DJI dataset with window lengths of 5, 10, 15 and 20.

Metrics	n = 5	n = 10	n = 15	n = 20
Cumulative return (%)	14.11	26.17	15.01	16.91
Annualized return (%)	11.08	18.24	11.91	13.34
Sharpe ratio	0.54	0.93	0.56	0.61
Maximum drawdown (%)	13.03	11.52	18.26	14.75

The implementation of the models was carried out using the PyTorch library in Python. The baseline methods were adopted from the code provided by Theate et al. [31] (Note: https://github.com/ThibautTheate/An-Application-of-Deep-Reinforcement-Learning-to-Algorithmic-Trading (accessed on 1 August 2023)) and Taghian et al. [34] (Note: https://github.com/MehranTaghian/DQN-Trading (accessed on 1 August 2023)) to build the algorithm.

The experimental setup involved several key components as follows:

• Preprocessing: Preprocessing was performed by normalizing each input variable to ensure consistent scaling and prevent gradient explosions. This normalization resulted in a mean of 0 and a standard deviation of 1 for the normalized data.
• Initialization: Xavier initialization was employed to enhance the convergence of the algorithm by setting the initial weights in a manner that maintained a constant variance of gradients across the deep neural network layers.
• Performance metrics: To accurately evaluate the performance of the trading strategies, four performance metrics were selected, namely cumulative return (CR), Sharpe ratio (SR), maximum drawdown (MDD), and annualized return (AR). These metrics provide a comprehensive and objective analysis of the strategy’s benefits and drawbacks in terms of profitability and risk management.
• Baseline methods: To objectively evaluate the advantages and disadvantages of the DADE-DQN algorithm, a comparison was made with traditional methods like buy and hold (B&H), sell and hold (S&H), mean reversion with moving averages (MR), and trend following with moving averages (TF) [60,61,62], as well as DRL methods including TDQN [31], DQN-Vanilla, and DQN-Pattern [34].

It was worth mentioning that tuning the hyperparameters of DRL algorithms was a complex and time-consuming task. In this study, the trial-and-error method was used to determine the hyperparameter values. Table 6 presents the hyperparameter values used in the DADE-DQN model.

Table 6. The hyperparameters values of DADE-DQN.

Hyperparameter	Value	Hyperparameter	Value
Input size	24	Window length (n)	10
Number of neurons in hidden layer	64	Number of LSTM layer	1
Output size	3	Attention weight	0.1
Activation function	Tanh	Learning rate ($\alpha$)	0.003
Discount factor ($\gamma$)	0.9	$ϵ$-greedy	0.9
Number of steps to update the target Q network parameters	10	Replay memory size	1000
Optimizer is Adam with L2Factor	0.000001	Episode	100
Initial capital	USD 500,000	Trading cost	0.001

Figure 6 illustrates the trend of the cumulative reward during the training process of the DADE-DQN model using SSR on six datasets. Figure 6 shows a gradual increase in the cumulative reward as the number of training episodes progresses, eventually reaching a state of convergence. The cumulative rewards served as a crucial performance metric to evaluate the effectiveness of the DADE-DQN algorithm, quantifying the total reward obtained by the model over multiple episodes of training and reflecting its ability to make profitable trading decisions. Initially, the cumulative reward exhibited fluctuations and variability as the model explores and learned from the environment. However, as training progresses, the DADE-DQN algorithm improved its policy and decision-making capabilities, resulting in a steady increase in cumulative rewards.

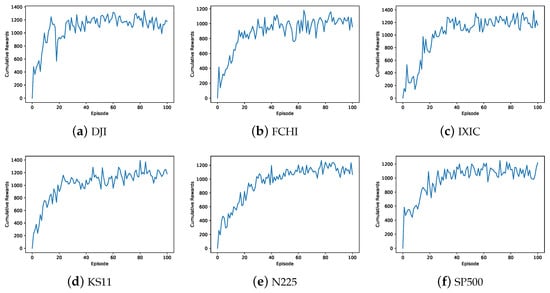
Figure 6. The trend of the cumulative reward during the training process of the DADE-DQN model using SSR on six datasets.

Therefore, the convergence of the cumulative rewards indicated that the DADE-DQN model learned an effective trading strategy and achieved a stable state. At this point, the model acquired sufficient knowledge from the training data and consistently generates profitable trading decisions. The convergence of cumulative returns meant that the DADE-DQN algorithm successfully captured the underlying patterns and dynamics of the financial markets and used historical price data, technical indicators, and environmental conditions to make informed trading choices that maximized cumulative returns.

4.4. Experimental Results

This section presented a comparison between the proposed DADE-DQN framework and seven baseline methods to evaluate its performance. The experimental results for the six stock index datasets are provided in Table 7. The trading performance was assessed using four performance metrics: cumulative return (CR), Sharpe ratio (SR), annualized return (AR), and maximum drawdown (MDD).

Table 7. Performances of various trading methods on six assets.

Assets	Metrics	B&H	S&H	MR	TF	TDQN	DQN-Pattern	DQN-Vanilla	DADE-DQN
DJI	CR[%]	8.10	−8.30	−0.28	−15.90	−7.97	5.31	20.47	26.17
	AR[%]	7.85	−3.98	1.42	−11.86	−2.96	5.65	14.99	18.24
	SR	0.33	−0.14	0.06	−0.53	−0.18	0.24	0.66	0.93
	MDD[%]	21.70	21.27	18.36	27.09	33.00	21.94	17.21	11.52
FCHI	CR[%]	17.10	−17.34	−20.00	10.05	15.08	−13.26	16.22	43.46
	AR[%]	14.70	−10.09	−15.26	9.54	8.40	−8.54	13.38	28.42
	SR	0.53	−0.26	−0.55	0.38	0.48	−0.34	0.50	1.18
	MDD[%]	22.42	32.93	25.14	23.63	28.05	30.83	22.42	20.70
IXIC	CR[%]	−17.50	17.30	12.03	-29.46	-33.00	-18.43	24.10	49.15
	AR[%]	−9.94	16.63	12.65	−23.51	−18.75	−10.12	18.29	32.22
	SR	−0.26	0.45	0.36	−0.65	−0.68	−0.26	0.62	0.99
	MDD[%]	35.40	25.48	21.64	38.13	38.63	36.40	25.24	16.35
KS11	CR[%]	−24.47	24.27	−3.87	1.06	−27.31	−25.03	23.11	79.43
	AR[%]	−20.40	18.04	−1.19	2.62	−15.93	−19.92	16.47	43.57
	SR	−0.78	0.88	−0.05	0.11	−0.89	−0.77	0.81	2.21
	MDD[%]	34.61	10.74	26.12	25.73	33.13	33.65	12.84	7.63
N225	CR[%]	−6.00	5.80	9.35	−22.16	−24.66	−4.01	−5.58	24.10
	AR[%]	−2.24	6.89	9.27	17.94	−13.50	−0.30	−1.55	18.25
	SR	−0.08	0.25	0.35	−0.68	−0.70	−0.01	−0.05	0.75
	MDD[%]	18.71	13.69	15.16	25.18	31.22	19.40	19.41	16.46
SP500	CR[%]	2.81	−3.01	35.33	−29.32	−44.34	2.92	22.45	42.37
	AR[%]	4.89	1.82	24.59	−25.19	−33.06	4.78	16.72	27.51
	SR	0.17	0.05	0.96	−0.92	−1.45	0.17	0.64	1.11
	MDD[%]	25.34	28.20	16.41	33.25	48.41	25.43	17.50	11.04

Table 7 shows the performance of various trading methods on six assets. Among the listed metrics, the DADE-DQN strategy achieved the best scores, indicating its promising performance. The DADE-DQN strategy achieved significantly higher cumulative returns compared to other strategies. Additionally, it almost demonstrated the smallest maximum drawdown, highlighting its strong profitability and risk aversion on the six datasets. For instance, on the IXIC dataset, the DADE-DQN strategy achieved a cumulative return of 49.15%, surpassing all other methods. It also demonstrated a Sharpe ratio of 0.99, indicating favorable risk-adjusted returns. Furthermore, the maximum drawdown of the DADE-DQN strategy on the IXIC dataset was 16.35%, which was the lowest among all the methods. Similar observations could be made for the other assets listed in the table. The DADE-DQN consistently outperformed the baseline methods with respect to cumulative return, Sharpe ratio, and annualized return, demonstrating its superior performance. These results validated the effectiveness of the proposed DADE-DQN framework in generating profitable trading strategies with reduced risk.

Figure 7 illustrates the cumulative return curves obtained by applying various trading strategies, including B&H, S&H, MR, TF, TDQN, DQN-Vanilla, DQN-Pattern, and the proposed DADE-DQN strategy. The figure clearly shows the superior performance of the DADE-DQN strategy compared to the other strategies. It exhibited a remarkable ability to mitigate the risk of significant losses while achieving excess returns. Moreover, the total assets under the DADE-DQN strategy exhibited a smoother upward trend compared to the benchmark strategy.

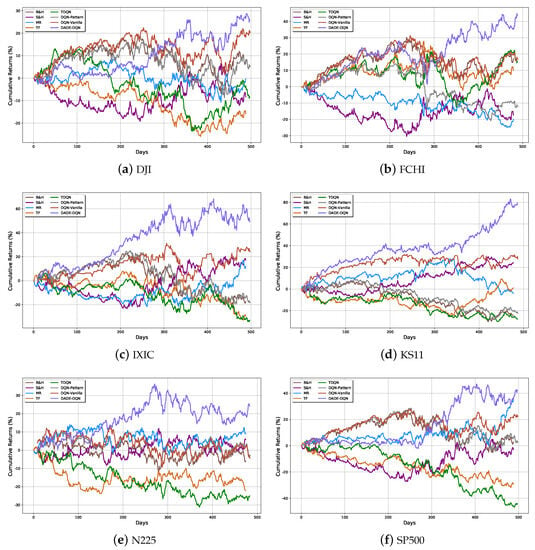
Figure 7. Performance of different models on six datasets.

The observed performance in Figure 7 aligns with the conclusions derived from the performance metrics in Table 7. The DADE-DQN strategy consistently outperformed the baseline methods across different assets, confirming its effectiveness in generating profitable trading strategies. It not only avoided the substantial risk of loss but also generated excess returns, surpassing the benchmark strategy and other comparative approaches. This result further confirmed the effectiveness of the DADE-DQN framework in generating profitable trading strategies. It successfully balanced risk and reward, providing investors with a more stable and profitable investment approach compared to traditional strategies and DRL methods.

Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 illustrates the trading signals generated by the DADE-DQN strategy for different assets. The figures showcase the strategy’s ability to accurately detect market trends and effectively adapt its position to mitigate risks, particularly during periods of significant market shocks. The trading signals provided by the DADE-DQN strategy demonstrated its capability to identify favorable market conditions and adjust positions accordingly. By leveraging its DRL framework to analyze historical price and technical indicator data, it could capture important market patterns and make informed decisions. During periods of severe market shocks, such as sudden downturns or volatility spikes, the DADE-DQN strategy demonstrated its adaptability by swiftly changing the direction of positions. This allowed it to hedge against potential risks and minimize losses.

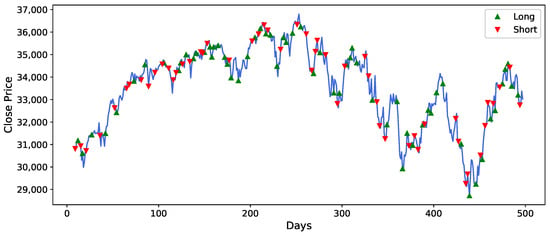
Figure 8. Trading signals of DJI based on DADE-DQN algorithm.

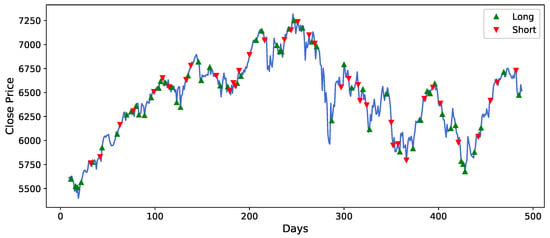
Figure 9. Trading signals of FCHI based on DADE-DQN algorithm.

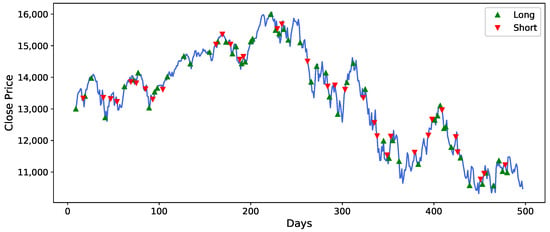
Figure 10. Trading signals of IXIC based on DADE-DQN algorithm.

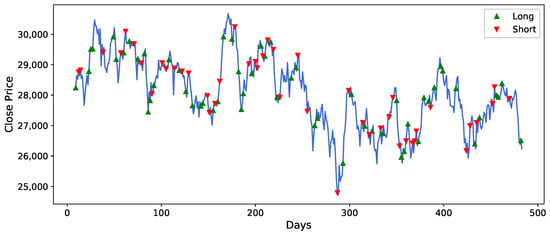
Figure 11. Trading signals of N225 based on DADE-DQN algorithm.

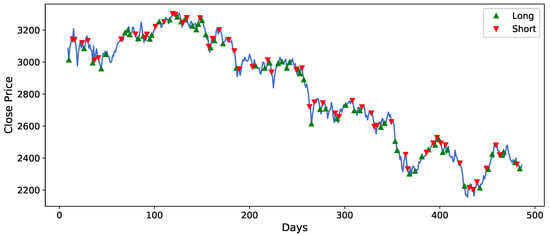
Figure 12. Trading signals of KS11 based on DADE-DQN algorithm.

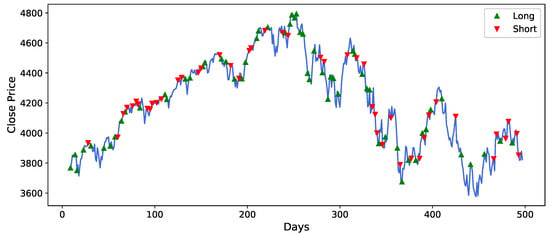
Figure 13. Trading signals of SP500 based on DADE-DQN algorithm.

5. Discussion

This study introduces the DADE-DQN algorithm, an extension of the DQN algorithm, aimed at enhancing stock trading strategies. Table 7 presents a comprehensive overview of performance across various trading methods for each of the six assets. Of significance, the DADE-DQN strategy consistently exhibits exceptional performance, underscoring its potential. Notably, it consistently achieves the highest cumulative returns when compared to all other methods. Additionally, its strong risk-management capabilities are evident through consistently low maximum drawdowns, emphasizing its capacity for balanced profitability and risk reduction across diverse datasets. These empirical findings have important implications for policymakers, traders, and finance experts.

Comparative analysis involving multiple DRL-based strategies (TDQN, DQN-Pattern, DQN-Vanilla) and traditional strategies (B&H, S&H, MR, TF) under identical conditions clearly establishes the superiority of the DADE-DQN algorithm. Across various trading objectives, the DADE-DQN algorithm consistently outperforms benchmark methods, achieving remarkable cumulative returns and Sharpe ratios. Notably, on the KS11 dataset, the DADE-DQN strategy stands out with an impressive cumulative return of 79.43% and a Sharpe ratio of 2.21, showcasing its ability to generate profitable trading strategies while effectively managing risk.

The compelling results validate the effectiveness of the proposed DADE-DQN framework in generating profitable trading strategies while mitigating risk. This conclusion is further supported by Figure 7, which presents cumulative return curves for different trading strategies, including DADE-DQN, across various assets. The visual representation unequivocally demonstrates the outstanding performance of the DADE-DQN strategy, consistently achieving excess returns while effectively controlling the risk of significant losses. Importantly, the cumulative return curve of the DADE-DQN strategy exhibits a smoother upward trend in comparison to benchmark strategies, highlighting its enhanced stability and profitability.

Moreover, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 provide detailed insights into the specific trading signals generated by the DADE-DQN strategy for different assets. These figures illustrate the strategy’s proficiency in identifying market trends and adeptly adjusting positions to manage risk, especially during periods of market turbulence. The trading signals capture favorable market conditions and dynamically adapt, showcasing the strategy’s versatility. Leveraging deep reinforcement learning, the strategy effectively analyzes historical price data and technical indicators, enabling it to identify crucial market patterns and make informed decisions. Importantly, in response to abrupt market changes, such as sudden declines or heightened volatility, the DADE-DQN strategy displays resilience by swiftly readjusting positions to mitigate risk. Hence, the robust performance of the DADE-DQN strategy, demonstrated in both backtesting and real-world application, highlights its potential to enhance stock trading strategies, offering investors stability and favorable returns.

In summary, the effectiveness of the DRL strategy in identifying market trends and dynamically adjusting positions to manage risk contributes to its overall profitability and establishes its role as a reliable trading strategy across diverse market scenarios. This underscores its potential to enhance stock trading strategies, providing investors with stability and favorable returns.

6. Conclusions and Future Work

Firstly, the primary value of this paper lies in the introduction of the DADE-DQN algorithm, an extension of the DQN algorithm, which presents a significant enhancement to stock trading strategies. The novel dual action selection and dual environment mechanism incorporated into the DADE-DQN algorithm effectively addresses the challenges posed by limited financial data and algorithmic stability. By striking a balance between exploration and exploitation, this mechanism elevates the performance of the algorithm, surpassing traditional methods. The incorporation of LSTM and attention mechanisms enriches the deep network architecture, enhancing its capacity to capture intricate patterns and important features within stock market data. Furthermore, the introduction of a feature selection method based on mutual information demonstrates innovation in enhancing model interpretability and efficiency.

Secondly, by moving forward, several avenues for improvement exist. While the DADE-DQN algorithm showcased promising results, we acknowledge the need for further refinement. In particular, our current trading strategy, involving all-or-nothing position adjustments, might expose traders to higher risks and transaction fees during actual trading. We also recognize the absence of consideration for the impact of trading actions on the environment and the issue of slippage, both of which are pertinent aspects of real-world trading scenarios.

Finally, future research endeavors should focus on developing more sophisticated trading position mechanisms that enhance control over risk exposure while targeting increased returns. Additionally, exploring action distribution strategies to address uncertainties and risks is an exciting avenue for investigation. By accounting for the environmental impact of trading actions and tackling the slippage problem, we can attain a more accurate representation of actual trading conditions. These advancements will contribute to more reliable and effective trading strategies, offering practical implications for financial professionals and decision-makers alike.