Framed Natural Mates of Framed Curves in Euclidean 3-Space

Abstract

In this study, we consider framed curves as regular or singular space curves with an adapted frame in Euclidean 3-space. We define framed natural mates of a framed curve that are tangent to the generalized principal normal of the framed curve. Subsequently, we present the relationships between a framed curve and its framed natural mates. In particular, we establish some necessary and sufficient conditions for the framed natural mates of specific framed curves, such as framed spherical curves, framed helices, framed slant helices, and framed rectifying curves. Finally, we support the concept with some examples.

1. Introduction

A regular space curve has no singular point in Euclidean space. In this case, the curvature and torsion functions of a regular space curve are well defined at every point. However, this situation is not applicable to all space curves, as some may have singular points. Therefore, the Frenet–Serret frame fails at singular points. Honda and Takahashi [1] introduced a framed curve, which is a regular curve or singular space curve with a moving frame in Euclidean space. Similar to curvature functions of a regular curve, they also defined the framed curvature functions, which are well defined even at singular points. Also, Fukunaga and Takahashi [2] studied the existence conditions of framed curves. Additionally, Wang et al. [3] proposed an adapted frame as an alternative to the moving frame of a framed curve in Euclidean space, with its elements referred to as the generalized tangent vector, generalized principal normal vector, and generalized binormal vector, respectively.

Naturally, the theory of framed curves, which includes regular curves as well, has captured the interest of researchers. As a result, concepts traditionally belonging to the category of regular curves (e.g., helix [4,5], slant helix [6,7], rectifying curve [8], Salkowski curve [9], etc.) have now been extended to the theory of framed curves. In this regard, recently, the concepts of framed helix [10], framed slant helix [11], framed clad helix [12], framed rectifying curve [3,13], framed normal curve [14], and framed Bertrand and Mannheim curves [15] have been introduced. References [16,17,18] are additional noteworthy studies that contribute to the theory of framed curves. Furthermore, a group of researchers, known as Li et al. and referenced in [19,20,21,22,23,24], conducted theoretical research and development on submanifold theory, soliton theory, etc. We can find more motivations from some papers [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51]. Their work has contributed to the advancement of related research topics.

Moreover, Legendre curves are a special case of framed curves. Therefore, References [52,53,54,55,56,57,58,59,60,61,62,63,64,65] are other notable studies that contribute to the field of framed curves, specifically in the category of frontal or front curves.

Additionally, in the category of curves associated with the Frenet–Serret elements of regular curves, the concept of the principal direction (binormal direction) curve was introduced. It is defined as the integral curve of the principal normal vector (binormal vector) of a regular Frenet curve by Choi et al. [66]. Moreover, the natural mate (resp. conjugate mate) is a regular curve that is tangent to the principal normal (resp. binormal) vector of the base regular curve. These curves were introduced as partner curves of any regular curve by Deshmukh et al. [67].

On the other hand, natural and conjugate mates correspond to principal direction and binormal direction curves from the algebraic viewpoint, respectively. But, since the integral curve is defined only for vector fields on a region that contains a curve (i.e., not along a curve), it is more suitable to use the terminology of natural and conjugate mate from a geometric viewpoint. In this sense, as a generalization of the concept of natural mates of a regular space curve, we introduce framed natural mates of the framed curve in Euclidean space by using the adapted frame in [3]. After, we give the necessary and sufficient conditions for framed natural mates of a framed curve when the frame curve is a framed helix, framed slant helix, framed rectifying curve, or framed spherical curve. Finally, the concept of framed natural mate with some examples is enriched.

2. Preliminary

Let ${\mathbb{R}}^3$ denote the Euclidean 3-space, that is, the 3-dimensional real vector space endowed with the standard inner product $⟨x,y⟩={\displaystyle \sum _{i=1}^3}{x}_i{y}_i,$ for all $x=(x_1,x_2,x_3),$ $y=(y_1,y_2,y_3)\in {\mathbb{R}}^3$. The norm of a vector $x\in {\mathbb{R}}^3$ is defined by $∥x∥=\sqrt{⟨x,x⟩}$. Also, the cross-product of vectors x and y is given by $x\wedge y=\left(x_2{y}_3-x_3{y}_2,-x_1{y}_3+x_3{y}_1,x_1{y}_2-x_2{y}_1\right)$.

Framed Curves in Euclidean 3-Space

Let $\mathsf{\gamma }$: $I\to {\mathbb{R}}^3$ be a space curve. If $\dot{\mathsf{\gamma }}\left(t_0\right)=\frac{d\mathsf{\gamma }}{dt}\left(t_0\right)=0$ at $t_0\in I$, then $t_0$ is called a singular point of $\mathsf{\gamma }$. It is easy to see that the Frenet frame of any space curve is not well defined at any singular of the curve. Now, let us give the following concept about framed curves, which is a regular curve with linear independent condition or singular space curve in ${\mathbb{R}}^3$ (see [1,2,3,10] for more detail and background).

Let us take the set ${\mathsf{\Delta }}_2=\left\{\mathit{u}=\left({\mathit{u}}_1,{\mathit{u}}_2\right)\in {\mathbb{S}}^2\times {\mathbb{S}}^2\left|⟨{\mathit{u}}_1,{\mathit{u}}_2⟩=0\right.\right\}$ as a 3-dimensional manifold.

Definition 1.

$\left(\mathsf{\gamma },{\mathsf{\mu }}_1,{\mathsf{\mu }}_2\right)$: $I\to {\mathbb{R}}^3\times {\mathsf{\Delta }}_2\subset {\mathbb{R}}^3\times {\mathbb{S}}^2\times {\mathbb{S}}^2$ is called a framed curve, if $⟨\dot{\mathsf{\gamma }}\left(t\right),{\mathsf{\mu }}_i\left(t\right)⟩=0$ for all $t\in I$. $\mathsf{\gamma }:I\to {\mathbb{R}}^3$ is also called a framed curve (or framed base curve) if there exists $\mathsf{\mu }=\left({\mathsf{\mu }}_1,{\mathsf{\mu }}_2\right)$: $I\to {\mathsf{\Delta }}_2$ such that $\left(\mathsf{\gamma },{\mathsf{\mu }}_1,{\mathsf{\mu }}_2\right)$ is a framed curve [1].

Now, unlike the Frenet frame, a well-defined moving frame can be constructed along the framed curve $\mathsf{\gamma }$, which may have singular points. Let $\left(\mathsf{\gamma },{\mathsf{\mu }}_1,{\mathsf{\mu }}_2\right)$ be a framed curve, and let $\mathsf{\vartheta }:I\to {\mathbb{S}}^2$ be a regular spherical curve such that $\mathsf{\vartheta }\left(t\right)={\mathsf{\mu }}_1\left(t\right)\wedge {\mathsf{\mu }}_2\left(t\right)$ for all $t\in I$. Hence, $\left\{{\mathsf{\mu }}_1,{\mathsf{\mu }}_2,\mathsf{\vartheta }\right\}$ is an orthonormal frame, which is a moving frame along the framed curve $\mathsf{\gamma }$ in ${\mathbb{R}}^3$. Then, the Frenet–Serret-type formulas are given by:

$$\begin{array}{ccc}\hfill {\dot{\mathsf{\mu }}}_1\left(t\right)& =& \mathfrak{l}\left(t\right){\mathsf{\mu }}_2\left(t\right)+\mathfrak{m}\left(t\right)\mathsf{\vartheta }\left(t\right),\hfill \\ \hfill {\dot{\mathsf{\mu }}}_2\left(t\right)& =& -\mathfrak{l}\left(t\right){\mathsf{\mu }}_1\left(t\right)+\mathfrak{n}\left(t\right)\mathsf{\vartheta }\left(t\right),\hfill \\ \hfill \dot{\mathsf{\vartheta }}\left(t\right)& =& -\mathfrak{m}\left(t\right){\mathsf{\mu }}_1\left(t\right)-\mathfrak{n}\left(t\right){\mathsf{\mu }}_2\left(t\right),\hfill \end{array}$$

and there exists a smooth function $\mathfrak{a}:I\to \mathbb{R}$ such that

$$\begin{array}{c}\hfill \dot{\mathsf{\gamma }}\left(t\right)=\mathfrak{a}\left(t\right)\mathsf{\vartheta }\left(t\right).\end{array}$$

(1)

Here, the quadruple smooth functions $\left(\mathfrak{l},\mathfrak{m},\mathfrak{n},\mathfrak{a}\right)=\left(⟨{\dot{\mathsf{\mu }}}_1,{\mathsf{\mu }}_2⟩,⟨{\dot{\mathsf{\mu }}}_1,\mathsf{\vartheta }⟩,⟨{\dot{\mathsf{\mu }}}_2,\mathsf{\vartheta }⟩,⟨\dot{\mathsf{\gamma }},\mathsf{\vartheta }⟩\right)$ are called the curvature of the framed curve $\mathsf{\gamma }$.

Remark 1.

It is clear that if $t_0\in I$ is a singular point of $\mathsf{\gamma }$, then $\mathfrak{a}\left(t_0\right)=0$. Moreover, since we suppose that $\mathsf{\vartheta }$ is a regular spherical curve (i.e., that $\dot{\mathsf{\vartheta }}\left(t\right)\ne 0$), then $\left(\mathfrak{m}\right(t),\mathfrak{n}(t\left)\right)\ne (0,0)$ for all $t\in I$.

Similar to Bishop frame [68] of regular curves, Wang et al. [3] give the following adapted frame, which is an alternative to the moving frame of the framed curve:

Let $\left({\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)\in {\mathsf{\Delta }}_2$ and $\theta :I\to \mathbb{R}$ be a smooth function such that

$$\left(\begin{array}{c}{\mathsf{\eta }}_1\left(t\right)\\ {\mathsf{\eta }}_2\left(t\right)\end{array}\right)=\left(\begin{array}{cc}cos\theta \left(t\right)& -sin\theta \left(t\right)\\ sin\theta \left(t\right)& cos\theta \left(t\right)\end{array}\right)\left(\begin{array}{c}{\mathsf{\mu }}_1\left(t\right)\\ {\mathsf{\mu }}_2\left(t\right)\end{array}\right).$$

It is easy to see that $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$: $I\to {\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ is also a framed curve and $\mathsf{\vartheta }={\mathsf{\mu }}_1\wedge {\mathsf{\mu }}_2={\mathsf{\eta }}_1\wedge {\mathsf{\eta }}_2$. Now, we assume that $\mathfrak{m}\left(t\right)=-\mathfrak{p}\left(t\right)cos\theta \left(t\right)$ and $\mathfrak{n}\left(t\right)=\mathfrak{p}\left(t\right)sin\theta \left(t\right)$ such that $\mathfrak{m}\left(t\right)sin\theta \left(t\right)+\mathfrak{n}\left(t\right)cos\theta \left(t\right)=0$, then we have an adapted frame $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right\}$ along the framed curve $\mathsf{\gamma }$ and the following Frenet–Serret-type formulas:

$$\begin{array}{c}\hfill \dot{\mathsf{\vartheta }}\left(t\right)=\mathfrak{p}\left(t\right){\mathsf{\eta }}_1\left(t\right),{\dot{\mathsf{\eta }}}_1\left(t\right)=-\mathfrak{p}\left(t\right)\mathsf{\vartheta }\left(t\right)+\mathfrak{q}\left(t\right){\mathsf{\eta }}_2\left(t\right),{\dot{\mathsf{\eta }}}_2\left(t\right)=-\mathfrak{q}\left(t\right){\mathsf{\eta }}_1\left(t\right),\end{array}$$

(2)

where

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\mathfrak{p}=⟨\dot{\mathsf{\vartheta }},{\mathsf{\eta }}_1⟩=∥\dot{\mathsf{\vartheta }}∥=\sqrt{{\mathfrak{m}}^2+{\mathfrak{n}}^2}>0\hfill \\ \mathfrak{q}=⟨{\dot{\mathsf{\eta }}}_1,{\mathsf{\eta }}_2⟩=\mathfrak{l}-\dot{\theta }=\mathfrak{l}+\left(\frac{{\mathfrak{m}}^2}{{\mathfrak{m}}^2+{\mathfrak{n}}^2}\right)\left(\frac{\mathfrak{n}}{\mathfrak{m}}\right)\dot{}\hfill \\ \mathfrak{a}=⟨\dot{\mathsf{\gamma }},\mathsf{\vartheta }⟩\hfill \end{array}\right.\end{array}$$

(3)

The triple smooth functions $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$ are called framed curvature with respect to the adapted frame $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right\}$ along the framed curve $\mathsf{\gamma }$. Moreover, the vectors $\mathsf{\vartheta }\left(t\right),{\mathsf{\eta }}_1\left(t\right),{\mathsf{\eta }}_2\left(t\right)$ are called the generalized tangent vector, the generalized principal normal vector, and the generalized binormal vector of the framed curve, respectively.

Proposition 1.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$: $I\to {\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ be a framed curve with framed curvature $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$. If the framed curve $\mathsf{\gamma }$ is a regular curve with curvature κ and torsion τ, then we have $\kappa =\frac{\mathfrak{p}}{\left|\mathfrak{a}\right|}$ and $\tau =\frac{\mathfrak{q}}{\mathfrak{a}}$ [3].

Now, we introduce the framed Darboux vector (framed centrode) and the framed co-Darboux vector (framed co-centrode) with respect to the adapted frame $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right\}$ of framed curve $\mathsf{\gamma }$, respectively.

Definition 2.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with adapted frame apparatus $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2,\right.$ $\left.\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)\right\}$. Then, the framed Darboux vector of the framed curve $\mathsf{\gamma }$ is defined by $\mathsf{\Omega }\left(t\right)=\mathfrak{q}\left(t\right)\mathsf{\vartheta }\left(t\right)+\mathfrak{p}\left(t\right){\mathsf{\eta }}_2\left(t\right)$, which satisfies the following equations:

$$\begin{array}{c}\hfill \dot{\mathsf{\vartheta }}\left(t\right)=\mathsf{\Omega }\left(t\right)\wedge \mathsf{\vartheta }\left(t\right),{\dot{\mathsf{\eta }}}_1\left(t\right)=\mathsf{\Omega }\left(t\right)\wedge {\mathsf{\eta }}_1\left(t\right),{\dot{\mathsf{\eta }}}_2\left(t\right)=\mathsf{\Omega }\left(t\right)\wedge {\mathsf{\eta }}_2\left(t\right).\end{array}$$

Moreover, we call that

$$\begin{array}{c}\hfill {\mathsf{\Omega }}_{\mathbf{0}}\left(t\right)=\frac{\mathfrak{q}\left(t\right)\mathsf{\vartheta }\left(t\right)+\mathfrak{p}\left(t\right){\mathsf{\eta }}_2\left(t\right)}{\sqrt{{\mathfrak{p}}^2\left(t\right)+{\mathfrak{q}}^2\left(t\right)}}\end{array}$$

(4)

is the unit framed Darboux vector of $\mathsf{\gamma }$.

Definition 3.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with adapted frame apparatus $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2,\right.$ $\left.\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)\right\}$. Then, the framed co-Darboux vector of the framed curve $\mathsf{\gamma }$ is defined by $\widehat{\mathsf{\Omega }}\left(t\right)=-\mathfrak{p}\left(t\right)\mathsf{\vartheta }\left(t\right)+\mathfrak{q}\left(t\right){\mathsf{\eta }}_2\left(t\right)$. Moreover, we call that

$$\begin{array}{c}\hfill {\widehat{\mathsf{\Omega }}}_{\mathbf{0}}\left(t\right)=\frac{-\mathfrak{p}\left(t\right)\mathsf{\vartheta }\left(t\right)+\mathfrak{q}\left(t\right){\mathsf{\eta }}_2\left(t\right)}{\sqrt{{\mathfrak{p}}^2\left(t\right)+{\mathfrak{q}}^2\left(t\right)}}\end{array}$$

(5)

is the unit framed co-Darboux vector of $\mathsf{\gamma }$. Also, it is easy to see that ${\widehat{\mathsf{\Omega }}}_{\mathbf{0}}=\frac{{\dot{\mathsf{\eta }}}_1}{∥{\dot{\mathsf{\eta }}}_1∥}$.

Now, we give the following framed versions (i.e., that generalized versions) of well-known definitions and characterizations for regular space curves.

Definition 4.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$. Then, $\mathsf{\gamma }$ is called a framed planar curve if it lies on a plane in ${\mathbb{R}}^3$ [1].

By using Proposition 3.3 in [1] with Equation (3), we give the following characterization of framed planar curves with respect to the adapted curvature.

Theorem 1.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with framed curvature $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$. Then, $\mathsf{\gamma }$ is a framed planar curve if and only if $\mathfrak{q}=0$.

Definition 5.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$. Then, $\mathsf{\gamma }$ is called a framed spherical curve if it lies on a sphere with a radius r in ${\mathbb{R}}^3$ [3].

We give Theorem 2 and Corollary 1 by using Proposition 2 and Corollary 1 in [3] with Equation (3).

Theorem 2.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with framed curvature $\left(\mathfrak{p},\mathfrak{q}=0,\mathfrak{a}\right)$. Then, $\mathsf{\gamma }$ is a framed spherical curve, which is a circle in ${\mathbb{R}}^3$ if and only if $\mathfrak{q}=0$ and $\frac{\mathfrak{p}}{\left|\mathfrak{a}\right|}$ is a constant such that $\mathfrak{a}\ne 0$.

Corollary 1.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with framed curvature $\left(\mathfrak{p},\mathfrak{q}=0,\mathfrak{a}\right)$. Then, $\mathsf{\gamma }$ is a framed spherical curve, which is a great circle in ${\mathbb{S}}^2\left(r\right)$ if and only if $\mathfrak{q}=0$ and $\frac{\mathfrak{p}}{\left|\mathfrak{a}\right|}=\frac{1}{r}$ such that $\mathfrak{a}\ne 0$.

Theorem 3.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with framed curvature $\left(\mathfrak{p},\mathfrak{q}\ne 0,\mathfrak{a}\right)$. Then, $\mathsf{\gamma }$ is a framed spherical curve in ${\mathbb{S}}^2\left(r\right)$ if and only if

$$\begin{array}{c}\hfill {\left(\frac{1}{\mathfrak{q}}\left(\frac{\mathfrak{a}}{\mathfrak{p}}\right)\dot{}\right)}^2+{\left(\frac{\mathfrak{a}}{\mathfrak{p}}\right)}^2=r^2,\end{array}$$

(6)

or equivalently,

$$\begin{array}{c}\hfill \left(\frac{1}{\mathfrak{q}}\left(\frac{\mathfrak{a}}{\mathfrak{p}}\right)\dot{}\right)\dot{}+\frac{\mathfrak{a}\mathfrak{q}}{\mathfrak{p}}=0.\end{array}$$

Ref. [14].

Definition 6.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with framed curvature $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$. Then, the framed harmonic curvature of $\mathsf{\gamma }$ is given by $\mathfrak{h}=\frac{\mathfrak{q}}{\mathfrak{p}}$ [11].

Definition 7.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with adapted frame $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right\}$. Then, $\mathsf{\gamma }$ is called a framed helix if its generalized tangent vector ν makes a constant angle with a fixed unit vector ζ [3,10].

Theorem 4.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with framed curvature $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$. Then, $\mathsf{\gamma }$ is a framed helix if and only if $\mathfrak{h}=cot\varphi$ such that ϕ is a constant angle [3].

Definition 8.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with adapted frame $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right\}$. Then, $\mathsf{\gamma }$ is called a framed slant helix if its generalized principal normal vector ${\mathsf{\eta }}_1$ makes a constant angle with a fixed unit vector ζ. That is, $⟨{\mathsf{\eta }}_1,\mathsf{\zeta }⟩=cos\varphi$, where $\varphi \ne \pi /2$ is a constant angle [11].

Theorem 5.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with framed curvature $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$. Then, $\mathsf{\gamma }$ is a framed slant helix if and only if

$$\begin{array}{c}\hfill \mathsf{\sigma }=\frac{{\mathfrak{p}}^2\left(\frac{\mathfrak{q}}{\mathfrak{p}}\right)\dot{}}{{\left({\mathfrak{p}}^2+{\mathfrak{q}}^2\right)}^{3/2}}=\frac{\dot{\mathfrak{h}}}{\mathfrak{p}{\left(1+{\mathfrak{h}}^2\right)}^{3/2}}\end{array}$$

is a constant function [11].

Definition 9.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with adapted frame $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right\}$. Then, $\mathsf{\gamma }$ is called a framed rectifying curve if its position vector satisfies

$$\begin{array}{c}\hfill \mathsf{\gamma }\left(t\right)={\lambda }_1\left(t\right)\mathsf{\vartheta }\left(t\right)+{\lambda }_2\left(t\right){\mathsf{\eta }}_2\left(t\right)\end{array}$$

for some smooth functions ${\lambda }_1\left(t\right),{\lambda }_2\left(t\right)$ [3].

Theorem 6.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with framed curvature $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$. Then, $\mathsf{\gamma }$ is a framed rectifying curve if and only if its framed harmonic curvature is given by

$$\begin{array}{c}\hfill \mathfrak{h}\left(t\right)=c_1\int \mathfrak{a}\left(t\right)dt+c_2\end{array}$$

for some constants $c_1\ne 0$, and $c_2$ [3].

3. Framed Natural Mates

In this section, we give the concept of framed natural mates of a framed curve as a regular or singular space curve. This concept is more general than the concept of a natural mate of a Frenet curve in [67].

Definition 10.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$: $I\to {\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ be a framed curve with an adapted frame $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right\}$. Then, a framed curve $\left({\mathsf{\gamma }}_{★},{{\mathsf{\eta }}_1}_{★},{\mathsf{\eta }}_{2★}\right)$: $I\to {\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with an adapted frame $\left\{{\mathsf{\vartheta }}_{★},{\mathsf{\eta }}_{1★},{\mathsf{\eta }}_{2★}\right\}$ is called a framed natural mate of $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$, if the generalized tangent vector ${\mathsf{\vartheta }}_{★}$ of ${\mathsf{\gamma }}_{★}$ is tangent to the generalized principal normal vector ${\mathsf{\eta }}_1$ of the framed curve $\mathsf{\gamma }$ (i.e., that ${\mathsf{\vartheta }}_{★}\left(t\right)={\mathsf{\eta }}_1\left(t\right)$ for all $t\in I$).

From now on, we call that the framed curve ${\mathsf{\gamma }}_{★}$ is a framed natural mate of the framed curve $\mathsf{\gamma }$, if $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ and $\left({\mathsf{\gamma }}_{★},{{\mathsf{\eta }}_1}_{★},{\mathsf{\eta }}_{2★}\right)$ are framed natural mates.

Theorem 7.

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ and $\left({\mathsf{\gamma }}_{★},{{\mathsf{\eta }}_1}_{★},{\mathsf{\eta }}_{2★}\right)$ be framed curves. Then, a framed natural mate ${\mathsf{\gamma }}_{★}$ of the framed curve $\mathsf{\gamma }$ is given by

$$\begin{array}{c}\hfill {\mathsf{\gamma }}_{★}\left(t\right)=\int {\mathfrak{a}}_{★}\left(t\right){\mathsf{\eta }}_1\left(t\right)dt\end{array}$$

(7)

with the following adapted frame apparatus

$$\begin{array}{c}\hfill {\mathsf{\vartheta }}_{★}={\mathsf{\eta }}_1,{\mathsf{\eta }}_{1★}={\widehat{\mathsf{\Omega }}}_{\mathbf{0}},{\mathsf{\eta }}_{2★}={\mathsf{\Omega }}_{\mathbf{0}},{\mathfrak{p}}_{★}=\sqrt{{\mathfrak{p}}^2+{\mathfrak{q}}^2},{\mathfrak{q}}_{★}=\frac{\dot{\mathfrak{h}}}{1+{\mathfrak{h}}^2}\end{array}$$

(8)

where ${\mathfrak{a}}_{★}:I\to \mathbb{R}$ is a smooth function.

Proof. 

Let $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ be a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with adapted frame apparatus $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2,\right.$ $\left.\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)\right\}$. Then, we see that $\left\{{\mathsf{\eta }}_1,{\widehat{\mathsf{\Omega }}}_{\mathbf{0}},{\mathsf{\Omega }}_{\mathbf{0}}\right\}$ is an orthonormal basis along the framed curve $\mathsf{\gamma }$ in ${\mathbb{R}}^3$, where ${\mathsf{\Omega }}_{\mathbf{0}},{\widehat{\mathsf{\Omega }}}_{\mathbf{0}}$ are given by (4) and (5), respectively. Moreover, by using Equation (2), we have the following equations:

$$\begin{array}{c}\hfill {\dot{\mathsf{\eta }}}_1={\mathfrak{p}}_{★}{\widehat{\mathsf{\Omega }}}_{\mathbf{0}},{\dot{\widehat{\mathsf{\Omega }}}}_0=-{\mathfrak{p}}_{★}{\mathsf{\eta }}_1+{\mathfrak{q}}_{★}{\mathsf{\Omega }}_{\mathbf{0}},{\dot{\mathsf{\Omega }}}_0=-{\mathfrak{q}}_{★}{\widehat{\mathsf{\Omega }}}_{\mathbf{0}},\end{array}$$

such that

$$\begin{array}{c}\hfill {\mathfrak{p}}_{★}=\sqrt{{\mathfrak{p}}^2+{\mathfrak{q}}^2},{\mathfrak{q}}_{★}=\frac{\dot{\mathfrak{h}}}{1+{\mathfrak{h}}^2}\end{array}$$

where $\mathfrak{h}$ is the framed harmonic curvature of $\mathsf{\gamma }$. In that case, from the Existence and Uniqueness Theorems of framed curves in [1], there exists a framed curve $\left({\mathsf{\gamma }}_{★},{{\mathsf{\eta }}_1}_{★},{\mathsf{\eta }}_{2★}\right)$ in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$ with the adapted frame apparatus $\left\{{\mathsf{\vartheta }}_{★},{\mathsf{\eta }}_{1★},{\mathsf{\eta }}_{2★},\left({\mathfrak{p}}_{★},{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)\right\}$ whose elements are determined by the Equation (8). Also, by using (1), we have ${\dot{\mathsf{\gamma }}}_{★}={\mathfrak{a}}_{★}{\mathsf{\vartheta }}_{★}.$ This equality leads to the framed curve ${\mathsf{\gamma }}_{★}$ being given by (7) such that ${\mathfrak{a}}_{★}$: $I\to \mathbb{R}$ is a smooth function. Finally, by Definition 10, it is nothing but a framed natural mate of $\mathsf{\gamma }$. □

Remark 2.

By Theorem 7, there exists a smooth function ${\mathfrak{a}}_{★}$: $I\to \mathbb{R}$ such that a framed natural mate of $\mathsf{\gamma }$ is given by (7). Hence, we see that each smooth function ${\mathfrak{a}}_{★}$ generates a different framed natural mate of $\mathsf{\gamma }$, and so a framed natural mate of a framed curve is not unique. Moreover, by Definition 1, it is easy to see that the framed natural mate of $\left(\mathsf{\gamma },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2\right)$ is given by $\left({\mathsf{\gamma }}_{★},{\widehat{\mathsf{\Omega }}}_{\mathbf{0}},{\mathsf{\Omega }}_{\mathbf{0}}\right)$, which is also a framed curve in ${\mathbb{R}}^3\times {\mathsf{\Delta }}_2$.

Remark 3.

Particularly, when framed curves $\mathsf{\gamma },{\mathsf{\gamma }}_{★}$ are regular curves and $\mathfrak{a}\left(t\right),{\mathfrak{a}}_{★}\left(t\right)$ are their speed functions, which are equal to 1, then the concept of framed natural mate coincides with the concept of Frenet natural mate [67] (also, the concept of principal normal direction curve of $\mathsf{\gamma }$ [66]). So, the concept of framed natural mate is a generalized version of [67].

Now, when $\mathsf{\gamma }$ is a framed helix or slant helix, it is easy to see that the following results by using Theorems 1, 4, and 5.

Corollary 2.

Let ${\mathsf{\gamma }}_{★}$ be a framed natural mate of the framed curve $\mathsf{\gamma }$ in ${\mathbb{R}}^3$. Then, $\mathsf{\gamma }$ is a framed helix if and only if ${\mathsf{\gamma }}_{★}$ is a framed planar curve.

Corollary 3.

Let ${\mathsf{\gamma }}_{★}$ be a framed natural mate of the framed curve $\mathsf{\gamma }$ in ${\mathbb{R}}^3$. Then, $\mathsf{\gamma }$ is a framed slant helix if and only if ${\mathsf{\gamma }}_{★}$ is a framed helix.

Now, we give the following relationship between framed curvatures of a framed rectifying curve and its framed natural mate.

Corollary 4.

Let $\mathsf{\gamma }$ and ${\mathsf{\gamma }}_{★}$ be framed natural mates in ${\mathbb{R}}^3$ with framed curvatures $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$ and $\left({\mathfrak{p}}_{★},{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)$, respectively. Then, $\mathsf{\gamma }$ is a framed rectifying curve if and only if the following equation holds:

$$\begin{array}{c}\hfill \lambda \mathfrak{a}{\mathfrak{p}}^2={\mathfrak{p}}_{★}^2{\mathfrak{q}}_{★}\end{array}$$

(9)

where λ is a nonzero constant.

Proof. 

Assume that $\mathsf{\gamma }$ is a framed rectifying curve in ${\mathbb{R}}^3$ with framed curvature $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$ and $\mathfrak{h}$ is its framed harmonic curvature. Then, by using Theorem 6, $\mathfrak{h}\left(t\right)=c_1\int \mathfrak{a}\left(t\right)dt+c_2$ for some constants $c_1\ne 0$ and $c_2$. Also, let ${\mathsf{\gamma }}_{★}$ be a framed natural mate of $\mathsf{\gamma }$ with a framed curvature $\left({\mathfrak{p}}_{★},{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)$. Then, by using (8), we have

$$\begin{array}{c}\hfill {\mathfrak{p}}_{★}^2={\mathfrak{p}}^2(1+{\mathfrak{h}}^2),{\mathfrak{q}}_{★}=\frac{c_1\mathfrak{a}}{1+{\mathfrak{h}}^2}.\end{array}$$

Thus, the last equations lead to easily (9). Conversely, let $\mathsf{\gamma }$ and ${\mathsf{\gamma }}_{★}$ be framed natural mates, which satisfy the Equation (9). Then, if (8) is taken into account with (9), $\dot{\mathfrak{h}}\left(t\right)=c_1\mathfrak{a}\left(t\right)$, where $c_1$ is a nonzero constant. Consequently, $\mathsf{\gamma }$ is a framed rectifying curve in ${\mathbb{R}}^3$ with respect to Theorem 6, □

Now, we give a relation with respect to the framed curvatures of a framed spherical curve and its framed natural mate.

Corollary 5.

Let $\mathsf{\gamma }$ and ${\mathsf{\gamma }}_{★}$ be framed natural mates in ${\mathbb{R}}^3$ with framed curvatures $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$ and $\left({\mathfrak{p}}_{★},{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)$, respectively. Then, $\mathsf{\gamma }$ is a framed spherical curve in ${\mathbb{S}}^2\left(r\right)$ if and only if the following equation holds:

$$\begin{array}{c}\hfill \frac{{\dot{\mathfrak{p}}}_{★}}{{\mathfrak{p}}_{★}}={\mathfrak{q}}_{★}\mathfrak{h}+\frac{\dot{\mathfrak{a}}}{\mathfrak{a}}\mp \frac{\mathfrak{q}}{\mathfrak{a}}\sqrt{r^2{\mathfrak{p}}^2-{\mathfrak{a}}^2}.\end{array}$$

(10)

Proof. 

Assume that $\mathsf{\gamma }$ is a framed spherical curve in ${\mathbb{S}}^2\left(r\right)$ with framed curvatures $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$. Then, by using Theorem 3, we have

$$\begin{array}{c}\hfill \left(\frac{\mathfrak{a}}{\mathfrak{p}}\right)\dot{}=\pm \frac{\mathfrak{q}}{\mathfrak{p}}\sqrt{r^2{\mathfrak{p}}^2-{\mathfrak{a}}^2}\end{array}$$

and so,

$$\begin{array}{c}\hfill \frac{\dot{\mathfrak{p}}}{\mathfrak{p}}=\frac{\dot{\mathfrak{a}}}{\mathfrak{a}}\mp \frac{\mathfrak{q}}{\mathfrak{a}}\sqrt{r^2{\mathfrak{p}}^2-{\mathfrak{a}}^2}.\end{array}$$

Moreover, after using Equation (8) and accordingly, the ratio of ${\dot{\mathfrak{p}}}_{★}$ over ${\mathfrak{p}}_{★}$ is

$$\begin{array}{c}\hfill \frac{{\dot{\mathfrak{p}}}_{★}}{{\mathfrak{p}}_{★}}=\frac{\dot{\mathfrak{p}}}{\mathfrak{p}}+\frac{\mathfrak{h}\dot{\mathfrak{h}}}{1+{\mathfrak{h}}^2}=\frac{\dot{\mathfrak{p}}}{\mathfrak{p}}+{\mathfrak{q}}_{★}\mathfrak{h}\end{array}$$

Thus, it is easy to see that Equation (10) from the last two equations. Conversely, let $\mathsf{\gamma }$ and ${\mathsf{\gamma }}_{★}$ be framed natural mates, which satisfy the Equation (10). Then, by taking into account the Equation (8), we obtain

$$\begin{array}{c}\hfill \frac{\dot{\mathfrak{p}}}{\mathfrak{p}}=\frac{{\dot{\mathfrak{p}}}_{★}}{{\mathfrak{p}}_{★}}-{\mathfrak{q}}_{★}\mathfrak{h}=\frac{\dot{\mathfrak{a}}}{\mathfrak{a}}\mp \frac{\mathfrak{q}}{\mathfrak{a}}\sqrt{r^2{\mathfrak{p}}^2-{\mathfrak{a}}^2}.\end{array}$$

This leads to the following equation

$$\begin{array}{c}\hfill \dot{\mathfrak{p}}\mathfrak{a}-\mathfrak{p}\dot{\mathfrak{a}}=\mp \mathfrak{p}\mathfrak{q}\sqrt{r^2{\mathfrak{p}}^2-{\mathfrak{a}}^2},\end{array}$$

and after suitable settings, we obtain

$$\begin{array}{c}\hfill \left(\frac{\mathfrak{a}}{\mathfrak{p}}\right)\dot{}=\pm \frac{\mathfrak{q}}{\mathfrak{p}}\sqrt{r^2{\mathfrak{p}}^2-{\mathfrak{a}}^2}\end{array}$$

(11)

As the first case, if $\mathfrak{q}=0$ in (11), then the proof is clear by Theorem 2. In the other case, if $\mathfrak{q}\ne 0$ in (11), then we reach

$$\begin{array}{c}\hfill {\left(\frac{1}{\mathfrak{q}}\left(\frac{\mathfrak{a}}{\mathfrak{p}}\right)\dot{}\right)}^2=r^2-{\left(\frac{\mathfrak{a}}{\mathfrak{p}}\right)}^2.\end{array}$$

Finally, the desired result is obtained by using Theorem 3. □

After that, let us concentrate on the results of some special framed natural mates of $\mathsf{\gamma }$.

Theorem 8.

Let $\mathsf{\gamma }$ and ${\mathsf{\gamma }}_{★}$ be framed natural mates in ${\mathbb{R}}^3$ with framed curvatures $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)$ and $\left({\mathfrak{p}}_{★},{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)$, respectively. If $\mathsf{\gamma }$ is a framed curve with framed curvature $\left(r,\mathfrak{q},\mathfrak{a}\right)$ such that r is a positive constant, then its framed natural mate ${\mathsf{\gamma }}_{★}$ is a framed spherical curve in ${\mathbb{S}}^2\left(\frac{{\mathfrak{a}}_{★}}{r}\right)$ such that ${\mathfrak{a}}_{★}$ is a positive constant. The converse is true only when ${\mathsf{\gamma }}_{★}$ is a framed spherical curve that is not a circle (i.e., that ${\mathfrak{q}}_{★}\ne 0$) and ${\mathfrak{a}}_{★}$ is a positive constant.

Proof. 

Suppose that the framed curvature of $\mathsf{\gamma }$ is $\left(r,\mathfrak{q},\mathfrak{a}\right)$ such that r is a positive constant. Then, for framed curvature functions of a framed natural mate ${\mathsf{\gamma }}_{★}$, we have

$$\begin{array}{c}\hfill {\mathfrak{p}}_{★}=\sqrt{r^2+{\mathfrak{q}}^2},{\mathfrak{q}}_{★}=\frac{r\dot{\mathfrak{q}}}{r^2+{\mathfrak{q}}^2}.\end{array}$$

(12)

As the first case, if $\mathfrak{q}=0$ in (12), then it is clear that ${\mathsf{\gamma }}_{★}$ is a framed circle with a radius $1/r$ by Theorem 2. In the other case, we suppose that $\mathfrak{q}\ne 0$ in (12) and ${\mathfrak{a}}_{★}=a_0$ is a positive constant, then by using (12), we obtain

$$\begin{array}{c}\hfill {\left(\frac{1}{{\mathfrak{q}}_{★}}\left(\frac{{\mathfrak{a}}_{★}}{{\mathfrak{p}}_{★}}\right)\dot{}\right)}^2+{\left(\frac{{\mathfrak{a}}_{★}}{{\mathfrak{p}}_{★}}\right)}^2=\frac{{a_0}^2}{r^2}.\end{array}$$

Thus, by using Theorem 3, ${\mathsf{\gamma }}_{★}$ is a framed spherical curve in ${\mathbb{S}}^2\left(\frac{{\mathfrak{a}}_0}{r}\right)$.

Conversely, we assume that ${\mathsf{\gamma }}_{★}$ is a framed spherical curve in ${\mathbb{S}}^2\left(\frac{{\mathfrak{a}}_0}{r}\right)$ such that ${\mathfrak{q}}_{★}\ne 0$, and ${\mathfrak{a}}_{★}=a_0$ is a positive constant. Then, by using Equation (6),

$$\begin{array}{c}\hfill \frac{{a_0}^2{\left({\dot{\mathfrak{p}}}_{★}\right)}^2}{{\mathfrak{q}}_{★}^2{\mathfrak{p}}_{★}^4}+\frac{{a_0}^2}{{\mathfrak{p}}_{★}^2}=\frac{{a_0}^2}{r^2},\end{array}$$

and after suitable settings and integration, without loss of generality, we obtain

$$\begin{array}{c}\hfill {\mathfrak{p}}_{★}=rsec\left(\int {\mathfrak{q}}_{★}dt\right).\end{array}$$

(13)

Now, if we choose as the framed harmonic curvature $\mathfrak{h}=tan\phi$ such that $\phi$ is a smooth function, then this choice leads to ${\mathfrak{q}}_{★}=\dot{\phi }$ by applying Equation (8). Thus, by taking into account (13), we obtain ${\mathfrak{p}}_{★}=rsec\phi$. Moreover, by applying Equation (8), ${\mathfrak{p}}_{★}=\mathfrak{p}\sqrt{1+{\mathfrak{h}}^2}=\mathfrak{p}sec\phi$. Hence, we conclude that $\mathfrak{p}=r$ by the last two equations of ${\mathfrak{p}}_{★}$. □

Let $\mathsf{\gamma }$ be a framed curve with framed curvature $\left(\mathfrak{p}=\lambda cos\varphi ,\mathfrak{q}=\lambda sin\varphi ,\mathfrak{a}\right)$ such that $\lambda$ is a positive constant and $\varphi$ is a smooth function. Then, by using Equation (8), we see that its framed natural mate ${\mathsf{\gamma }}_{★}$ has the framed curvature $\left({\mathfrak{p}}_{★}=\lambda ,{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)$. Now, let us give the following theorem for the converse of this statement.

Theorem 9.

Let ${\mathsf{\gamma }}_{★}$ be a framed natural mate of the framed curve $\mathsf{\gamma }$ in ${\mathbb{R}}^3$. If ${\mathsf{\gamma }}_{★}$ has the framed curvature $\left({\mathfrak{p}}_{★}=\lambda ,{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)$ such that λ is a positive constant, then the framed curvature of $\mathsf{\gamma }$ is given by:

$$\left(\mathfrak{p}=\lambda cos\left(\int {\mathfrak{q}}_{★}dt\right),\mathfrak{q}=\lambda sin\left(\int {\mathfrak{q}}_{★}dt\right),\mathfrak{a}\right).$$

Proof. 

Assume that the framed curvature of the framed natural mate ${\mathsf{\gamma }}_{★}$ is $\left({\mathfrak{p}}_{★}=\lambda ,{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)$ such that $\lambda$ is a positive constant. Then, by using (8), we have

$$\begin{array}{c}\hfill \mathfrak{p}=\sqrt{{\lambda }^2-{\mathfrak{q}}^2}.\end{array}$$

This leads to $\mathfrak{h}=\mathfrak{q}/\sqrt{{\lambda }^2-{\mathfrak{q}}^2}$ and again, by taking into account (8), we obtain

$$\begin{array}{c}\hfill {\mathfrak{q}}_{★}=\frac{\left(\frac{\mathfrak{q}}{\sqrt{{\lambda }^2-{\mathfrak{q}}^2}}\right)\dot{}}{1+\frac{{\mathfrak{q}}^2}{{\lambda }^2-{\mathfrak{q}}^2}}=\frac{\dot{\mathfrak{q}}}{\sqrt{{\lambda }^2-{\mathfrak{q}}^2}}=\frac{\left(\frac{\mathfrak{q}}{\lambda }\right)\dot{}}{\sqrt{1-{\left(\frac{\mathfrak{q}}{\lambda }\right)}^2}}.\end{array}$$

After integration, we obtain $\mathfrak{q}=\lambda sin\left(\int {\mathfrak{q}}_{★}dt\right)$ and so; it leads to the conclusion that $\mathfrak{p}=\lambda cos\left(\int {\mathfrak{q}}_{★}dt\right)$. □

By Theorem 9, we obtain the following results, which are answer to the question: “When does the framed curve $\mathsf{\gamma }$ become a framed spherical curve for its framed natural mate ${\mathsf{\gamma }}_{★}$ with a framed curvature $\left({\mathfrak{p}}_{★}=\lambda ,{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right).$”

Theorem 10.

Let $\mathsf{\gamma }$ and ${\mathsf{\gamma }}_{★}$ be framed natural mates with framed curvatures $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}=a_0\right)$ and $\left({\mathfrak{p}}_{★}=\lambda ,{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)$ such that $a_0$ and λ are some positive constants, respectively. Then, $\mathsf{\gamma }$ is a framed spherical curve in ${\mathbb{S}}^2\left(r\right)$ if and only if ${\mathsf{\gamma }}_{★}$ has the framed curvature $\left(\lambda ,\pm \frac{{\lambda }^2\sqrt{{\rho }^2-{\lambda }^2}cos\left(\lambda t\right)}{{\lambda }^2+({\rho }^2-{\lambda }^2){sin}^2\left(\lambda t\right)},{\mathfrak{a}}_{★}\right)$ for a positive constant $\rho \ge \lambda$.

Proof. 

Suppose that $\mathsf{\gamma }$ is a framed spherical curve with framed curvature $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}=a_0\right)$ in ${\mathbb{S}}^2\left(r\right)$ such that $a_0$ is a positive constant, and its framed natural mate ${\mathsf{\gamma }}_{★}$ has framed curvature $\left({\mathfrak{p}}_{★}=\lambda ,{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)$ such that $\lambda$ is a positive constant. Then, by using Theorems 3 and 9, we have

$$\begin{array}{c}\hfill \frac{{a_0}^2}{{\lambda }^4}{sec}^{2}f\left({\lambda }^2+{\dot{f}}^2{sec}^{2}f\right)=r^2\end{array}$$

where $f=\int {\mathfrak{q}}_{★}dt$, and so

$$\begin{array}{c}\hfill \frac{{\lambda }^4{r}^2}{{a_0}^2}{cos}^{2}f-{\lambda }^2={\dot{f}}^2{sec}^{2}f.\end{array}$$

We see that there exists a positive constant $\rho =\frac{{\lambda }^{2}r}{a_0}$ such that $\rho \ge \lambda$ by the last equation. Accordingly, after suitable settings, we have

$$\begin{array}{c}\hfill \frac{\lambda \dot{f}{sec}^{2}f}{\sqrt{{\rho }^2-{\lambda }^2{sec}^{2}f}}=\pm \lambda \end{array}$$

and next step, by applying integration, we obtain

$$\begin{array}{c}\hfill arcsin\left(\frac{\lambda tanf}{\sqrt{{\rho }^2-{\lambda }^2}}\right)=\pm \lambda t.\end{array}$$

This equation leads to the following equation

$$\begin{array}{c}\hfill f=arctan\left(\pm \frac{\sqrt{{\rho }^2-{\lambda }^2}}{\lambda }sin\left(\lambda t\right)\right)\end{array}$$

(14)

Finally, the desired result is obtained by ${\mathfrak{q}}_{★}=\dot{f}$.

Conversely, we suppose that $\mathsf{\gamma }$ has framed curvature $\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}=a_0\right)$ such that $a_0$ is a positive constant, and ${\mathsf{\gamma }}_{★}$ has framed curvature

$$\left({\mathfrak{p}}_{★}=\lambda ,{\mathfrak{q}}_{★}=\pm \frac{{\lambda }^2\sqrt{{\rho }^2-{\lambda }^2}cos\left(\lambda t\right)}{{\lambda }^2+({\rho }^2-{\lambda }^2){sin}^2\left(\lambda t\right)},{\mathfrak{a}}_{★}\right)$$

such that $\lambda$ is a positive constant. Now, if we take as $f=\int {\mathfrak{q}}_{★}dt$, then by using Theorem 9 and hypothesis, we have

$$\begin{array}{c}\hfill \mathfrak{p}=\lambda cosf,\mathfrak{q}=\lambda sinf,\mathfrak{a}=a_0.\end{array}$$

(15)

Moreover, by using hypothesis, f is given by (14). Now, we must check the Equation (6). After applying Equations (14) and (15) in Equation (6), we obtain the positive constant $\frac{{a_0}^2{\rho }^2}{{\lambda }^4}$. Consequently, $\mathsf{\gamma }$ is a framed spherical curve in ${\mathbb{S}}^2\left(\frac{a_0\rho }{{\lambda }^2}\right)$ by Theorem 3. □

Corollary 6.

Let $\mathsf{\gamma }$ be a framed curve and ${\mathsf{\gamma }}_{★}$ be its framed natural mate with framed curvature $\left({\mathfrak{p}}_{★}=\lambda ,{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)$ such that λ is a positive constant. Then, $\mathsf{\gamma }$ is a framed spherical curve, which is not a circle in ${\mathbb{S}}^2\left(r\right)$ if and only if ${\mathsf{\gamma }}_{★}$ has the framed curvature $\left({\mathfrak{p}}_{★}=\lambda ,{\mathfrak{q}}_{★}=\frac{-\dot{\mathfrak{a}}\pm \mathfrak{q}\sqrt{r^2{\mathfrak{p}}^2-{\mathfrak{a}}^2}}{\mathfrak{a}\mathfrak{h}},{\mathfrak{a}}_{★}\right)$ such that $\mathfrak{q}\ne 0$.

Proof. 

The proof is clear by using Corollary 5 and Theorem 10. □

4. Some Examples of Framed Natural Mates

By using the following Frenet-type method (cf. [10]), we can uniquely determine the adapted frame apparatus of any framed curves as regular or singular space curves in ${\mathbb{R}}^3$.

Let $\mathsf{\vartheta }:I\to {\mathbb{S}}^2$ be a regular spherical curve, and $\mathfrak{a}:I\to \mathbb{R}$ be a smooth function. Then, there exists a framed curve $\mathsf{\gamma }:I\to {\mathbb{R}}^3$ with the adapted frame

$$\begin{array}{c}\hfill \left\{\mathsf{\vartheta },{\mathsf{\eta }}_1=\frac{\dot{\mathsf{\vartheta }}}{∥\dot{\mathsf{\vartheta }}∥},{\mathsf{\eta }}_2=\mathsf{\vartheta }\wedge {\mathsf{\eta }}_1\right\}\end{array}$$

(16)

such that $\dot{\mathsf{\gamma }}=\mathfrak{a}\mathsf{\vartheta }$. Thus, the smooth function $\mathfrak{a}$ corresponds to the speed function of $\mathsf{\gamma }$.

Example 1.

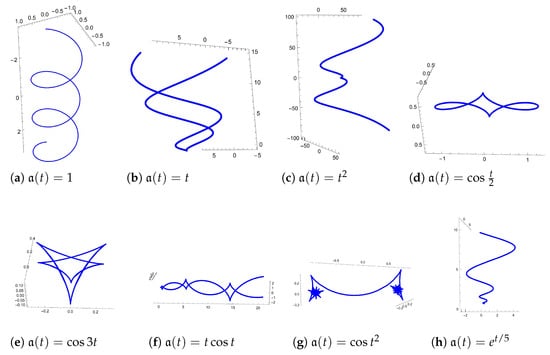
Let $\mathsf{\vartheta }$ be a small circle in ${\mathbb{S}}^2$ given by:

$$\begin{array}{c}\hfill \mathsf{\vartheta }\left(t\right)=\left(\frac{2\sqrt{2}}{3}cost,\frac{2\sqrt{2}}{3}sint,\frac{1}{3}\right).\end{array}$$

Then, by integrating (1) for any smooth function $\mathfrak{a}$, we obtain a family of framed helices $\mathsf{\gamma }$ with framed curvature $\left(\mathfrak{p}\left(t\right),\mathfrak{q}\left(t\right),\mathfrak{a}\left(t\right)\right)=\left(\frac{2\sqrt{2}}{3},\frac{1}{3},\mathfrak{a}\left(t\right)\right)$, which are generated by $\mathfrak{a}$ and $\mathsf{\vartheta }$. Moreover, by using (7) and (16), framed natural mates ${\mathsf{\gamma }}_{★}$ of $\mathsf{\gamma }$ are a family of framed planar curves with framed curvature $\left({\mathfrak{p}}_{★},{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)=\left(1,0,{\mathfrak{a}}_{★}\right)$ for any smooth function ${\mathfrak{a}}_{★}$. For example, if $\mathfrak{a}\left(t\right)=cos\left(3t\right)$, then the parametrization of framed helix $\mathsf{\gamma }$ is given by

$$\begin{array}{c}\hfill \mathsf{\gamma }\left(t\right)=\left(\frac{1}{12}\left(2\sqrt{2}sin\left(2t\right)+\sqrt{2}sin\left(4t\right)\right),\frac{1}{12}\left(2\sqrt{2}cos\left(2t\right)-\sqrt{2}cos\left(4t\right)+2\right),\frac{1}{9}sin\left(3t\right)\right)\end{array}$$

(see Figure 1e) and the framed natural mate ${\mathsf{\gamma }}_{★}$, which is a framed planar curve, is given by

$$\begin{array}{c}\hfill {\mathsf{\gamma }}_{★}\left(t\right)=\left(\frac{1}{8}(-2cos\left(2t\right)+cos\left(4t\right)-2),\frac{1}{8}(2sin\left(2t\right)+sin\left(4t\right)),0\right)\end{array}$$

such that ${\mathfrak{a}}_{★}\left(t\right)=cos\left(3t\right)$ (see Figure 2e).

Figure 1. Some framed helices with framed curvature $\left(\frac{2\sqrt{2}}{3},\frac{1}{3},\mathfrak{a}\left(t\right)\right)$.

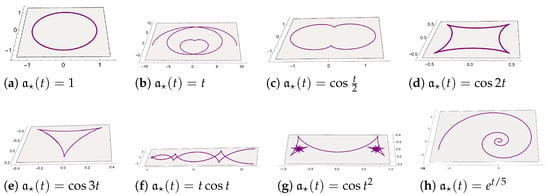
Figure 2. Some framed planar curves with framed curvature $\left(1,0,{\mathfrak{a}}_{★}\left(t\right)\right)$, which are framed natural mates of framed helices in Figure 1.

Example 2.

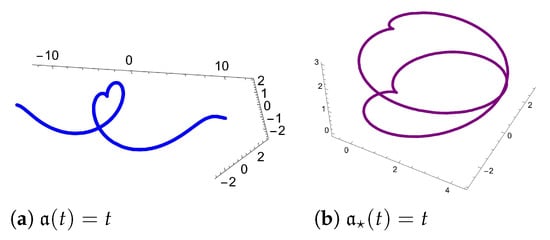
Let $\mathsf{\vartheta }$ be a unit speed spherical helix in ${\mathbb{S}}^2$ given by

$$\begin{array}{c}\hfill \mathsf{\vartheta }\left(t\right)=\left(\frac{32t^7-2352t^5+51450t^3-300125t}{51450\sqrt{35}},\frac{\left(16t^4-336t^2+735\right){\left(35-t^2\right)}^{3/2}}{25725\sqrt{35}},\frac{t}{6}\right)\end{array}$$

and $\mathfrak{a}\left(t\right)=t$, then the parametrization of framed slant helix $\mathsf{\gamma }$ is given by

$$\begin{array}{c}\hfill \mathsf{\gamma }\left(t\right)=\left(\frac{t^3\left(32t^6-3024t^4+92610t^2-900375\right)}{463050\sqrt{35}},\frac{{\left(35-t^2\right)}^{5/2}\left(-16t^4+112t^2+245\right)}{231525\sqrt{35}},\frac{t^3}{18}\right)\end{array}$$

with framed curvature $\left(\mathfrak{p}\left(t\right),\mathfrak{q}\left(t\right),\mathfrak{a}\left(t\right)\right)=\left(1,\frac{t}{\sqrt{35-t^2}},t\right)$ and $\mathsf{\sigma }=\frac{1}{\sqrt{35}}$ (see Figure 3a). Thus, for the choice ${\mathfrak{a}}_{★}\left(t\right)=t$, a framed natural mate, which is a framed helix of $\mathsf{\gamma }$ is given by

$$\begin{array}{c}\hfill {\mathsf{\gamma }}_{★}\left(t\right)=\left(\frac{t^2\left(t^2-35\right)\left(8t^4-280t^2+1225\right)}{14700\sqrt{35}},\frac{t^3\left(2t^2-35\right){\left(35-t^2\right)}^{3/2}}{3675\sqrt{35}},\frac{t^2}{12}\right)\end{array}$$

with framed curvature $\left({\mathfrak{p}}_{★},{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)=\left(\frac{\sqrt{35}}{\sqrt{35-t^2}},\frac{1}{\sqrt{35-t^2}},t\right)$ and ${\mathfrak{h}}_{★}\left(t\right)=\frac{1}{\sqrt{35}}$ (see Figure 3b).

Figure 3. (a) Framed slant helix $\mathsf{\gamma }$; (b) its framed natural mate ${\mathsf{\gamma }}_{★}$, which is a framed helix.

Example 3.

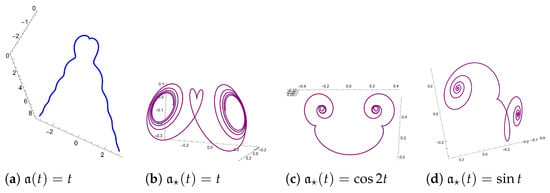
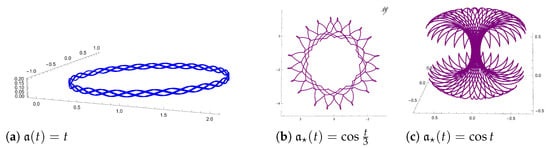
Let $\left\{\mathsf{\vartheta },{\mathsf{\eta }}_1,{\mathsf{\eta }}_2,\left(\mathfrak{p},\mathfrak{q},\mathfrak{a}\right)\right\}$ and $\left\{{\mathsf{\vartheta }}_{★},{\mathsf{\eta }}_{1★},{\mathsf{\eta }}_{2★},\left({\mathfrak{p}}_{★},{\mathfrak{q}}_{★},{\mathfrak{a}}_{★}\right)\right\}$ be adapted frame apparatus of $\mathsf{\gamma }$ and ${\mathsf{\gamma }}_{★}$, respectively. According to the Existence and Uniqueness Theorems of framed curves in [1], if the framed curvature of a framed curve is given, then we can draw a congruent graphic to the framed curve by applying numerical solution method to Frenet-type differential Equations (1)–(3) with the initial conditions. Also, the framed curvature of its framed natural mate is determined from by Theorem 7. Thus, the following graphics of the framed curve and its framed natural mate are obtained by using the “NDSolve” command in Mathematica [69].

Let $\mathsf{\gamma }$ be a framed curve with framed curvature $\left(\mathfrak{p}\left(t\right),\mathfrak{q}\left(t\right),\mathfrak{a}\left(t\right)\right)=\left(3,3t^2,2t\right)$. By using Theorem 6, $\mathsf{\gamma }$ is a framed rectifying curve (see Figure 4a). Thus, we obtain its framed natural mates, which has the framed curvature $\left({\mathfrak{p}}_{★}\left(t\right),{\mathfrak{q}}_{★}\left(t\right),{\mathfrak{a}}_{★}\left(t\right)\right)=\left(3\sqrt{1+t^4},\frac{2t}{1+t^4},{\mathfrak{a}}_{★}\left(t\right)\right)$ (see Figure 4b–d).

Figure 4. (a) Framed rectifying curve $\mathsf{\gamma }$; (b–d) its framed natural mates ${\mathsf{\gamma }}_{★}$, which are a spiral-type framed curve.

Finally, as an application of by Theorem 10, if we choose $\lambda =2,r=1,\mathfrak{a}\left(t\right)=\frac{1}{5}$ such that $\rho =20$. Then, $\mathsf{\gamma }$ is a framed spherical curve in ${\mathbb{S}}^2$ with framed curvature $\left(\mathfrak{p}\left(t\right),\mathfrak{q}\left(t\right),\mathfrak{a}\left(t\right)\right)=\left(\frac{2}{\sqrt{1+99{(sin2t)}^2}},\frac{6\sqrt{11}sin2t}{\sqrt{1+99{(sin2t)}^2}},\frac{1}{5}\right)$ (see Figure 5a). Thus, we obtain its framed natural mates, which has the framed curvature $\left({\mathfrak{p}}_{★}\left(t\right),{\mathfrak{q}}_{★}\left(t\right),{\mathfrak{a}}_{★}\left(t\right)\right)=\left(2,\frac{6\sqrt{11}sin2t}{\sqrt{1+99{(sin2t)}^2}},{\mathfrak{a}}_{★}\left(t\right)\right)$ (see Figure 5b,c).

Figure 5. (a) Framed spherical curve $\mathsf{\gamma }$; (b,c) its framed natural mates ${\mathsf{\gamma }}_{★}$.