On the P₃-Coloring of Bipartite Graphs

Abstract

The advancement in coloring schemes of graphs is expanding over time to solve emerging problems. Recently, a new form of coloring, namely $P_3$-coloring, was introduced. A simple graph is called a $P_3$-colorable graph if its vertices can be colored so that all the vertices in each $P_3$ path of the graph have different colors; this is called the $P_3$-coloring of the graph. The minimum number of colors required to form a $P_3$-coloring of a graph is called the $P_3$-chromatic number of the graph. The aim of this article is to determine the $P_3$-chromatic number of different well-known classes of bipartite graphs such as complete bipartite graphs, tree graphs, grid graphs, and some special types of bipartite graphs. Moreover, we have also presented some algorithms to produce a $P_3$-coloring of these classes with a minimum number of colors required.

1. Introduction

Graph theory deals with the study of graphs, which are mathematical structures representing a set of vertices or objects connected by any set of lines; these lines are called edges. The study of graphs is a very important tool for the applications of different subjects, such as chemistry, biochemistry, computer science, communication networks, operations research, and coding theory (see [1]). The history of graph theory dates back to the 18th century when Leonhard Euler solved the famous seven bridges of Konigsberg problem (see [2]). Then, in the 19th century, graph theory was developed by mathematicians James Joseph Sylvester and Arthur Cayley (see [3]). In the 20th century, graph theory found significant importance in different fields. One of the important problems in graph theory is graph coloring, which involves assigning colors to the vertices of the graph such that no two vertices which are adjacent have the same color. Graph coloring has numerous applications, such as map coloring (see [4]), scheduling (see [5,6]), resource allocation, and register allocation (see [7]).

Graph coloring is a fundamental concept in graph theory, a branch of mathematics that deals with the study of networks or graphs. The history of graph coloring can be traced back to the 19th century when the four color theorem was first proposed by Francis Guthrie. This theorem states that any map on a plane can be colored with just four colors in such a way that no two adjacent regions have the same color. The proof of this theorem took several decades and involved significant mathematical developments, including the use of computers to verify thousands of cases. In 1880, Tait proved in [8] that the four color theorem is equivalent to the conjecture saying that every cubic map has a proper edge coloring with three colors. Haken et al. introduced a new type of coloring, face and map coloring [9]. The four color theorem sparked great interest in graph coloring and led to further research and the development of various coloring techniques. There are different types of graph coloring, each serving a specific purpose. The most well-known type is vertex coloring, where the goal is to assign colors to the vertices of a graph in such a way that no two adjacent vertices share the same color [10,11]. Another type is edge coloring, which focuses on coloring the edges of a graph so that no two adjacent edges have the same color [10,11]. In [12], Zhou discussed edge coloring and its applications.

A detailed review on vertex coloring was given in [13,14]. Baber described list coloring in [15]. A detailed review about list coloring and some properties and algorithms of list coloring are included in [16,17]. Jenson et al. explained path coloring in [18]. Total coloring is also a type of graph coloring, and a complete review of it was provided in [19]; the algorithm of total coloring was constructed by Isobe in [20]. These various types of graph coloring have contributed to a wide range of applications and continue to be studied and refined by mathematicians and computer scientists. Moreover, there are also different types of vertex coloring and edge coloring, such as Equitable vertex coloring [21,22,23], Circular vertex coloring [24,25,26], Acyclic vertex coloring [27,28], Star vertex coloring [28,29], Circular edge coloring [30], Acyclic edge coloring [31,32,33], Baerge Fulkerson coloring [34], and Fan Raspand coloring [35]. In 2023, Naeem et al. introduced (see [36]) a new form of graph coloring, “$P_3$-coloring”, and they gave some general results about this coloring. In [36], the authors have also discussed $P_3$-coloring of some well-known families of graphs such as complete graphs, wheel graphs, star graphs, cycle graphs, prism graphs, ladder graphs, and path graphs.

Definition 1.

Let G be a simple graph and let ℓ$:V\left(G\right)\to \{c_1,c_2,\dots ,c_k\}$ be coloring of the vertices of G. If, for every $P_3$ path in G, the colors of its vertices are different, then ℓ is called $P_3$-coloring of G, that is, if $uvw$ is a $P_3$ path on G, then $\ell \left(u\right)\ne \ell \left(v\right)\ne \ell \left(w\right)\ne \ell \left(u\right)$.

Definition 2.

For a graph G, the minimum number of colors (or k in above definition) required to produce (or form) a $P_3$-coloring is called the $P_3$-chromatic number of G. It is denoted as ${\chi }_3\left(G\right)$. It is worth noticing that for all graphs G, we have ${\chi }_3\left(G\right)\ge 3$.

The following results are useful to prove some of our main Theorems in this article.

Theorem 1

([36], Corollary 3). Let $S_n$ be a star graph on n vertices; then ${\chi }_3\left(S_n\right)=n$, for all $n\ge 3$.

Theorem 2

([36], Theorem 1). Let G be a graph and H be a subgraph of G; then ${\chi }_3\left(G\right)\ge {\chi }_3\left(H\right)$.

The aim of this article is to discuss the $P_3$-coloring and $P_3$-chromatic number of bipartite graphs. Trees are one of the well-known types of bipartite graphs, and in Theorem 3, we have proved that ${\chi }_3$ of a tree graph is $\mathsf{\Delta }\left(T\right)+1$, where $\mathsf{\Delta }\left(T\right)$ is the maximum degree of the tree graph. Theorem 4 discusses the $P_3$-chromatic number of complete bipartite graphs. The mesh graph or the grid graphs are also bipartite graphs and the $P_3$-chromatic number of grid graphs is discussed in Theorem 5. Section 4 contains the main result of this article. In Theorem 6, we give the formula for the $P_3$-chromatic number of any bipartite graph having exactly one cycle. Moreover, we have also presented algorithms of these results, and using these algorithms, we can produce the $P_3$-coloring with a minimum number of colors.

2. $P_3$-Chromatic Number of Tree and Complete Bipartite Graphs

In graph theory, a tree is a simple graph in which any two vertices are connected by exactly one path, that is, a tree is a simple graph having no cycles. A tree graph is also a bipartite graph. A bipartite graph is a graph such that its vertices are partitioned into two sets of vertices in such a way that any edge of the graph connects only the vertices of one set to another. A complete bipartite graph is a special kind of bipartite graph such that $V\left(G\right)=V_1\cup V_2$. In this graph, every vertex of set $V_1$ is connected with every vertex of set $V_2$. It is denoted by $K_{m,n}$, where m and n are the number of vertices of the set $V_1$ and the set $V_2$, respectively.

In this section, we have determined the $P_3$-chromatic number of tree graphs and complete bipartite graphs. Let T be a tree graph and $\mathsf{\Delta }\left(T\right)$ be the maximum degree of T. We have the following useful notions about the coloring of a graph and its elements:

• A $P_3$ path has different colors if all the vertices in $P_3$ are of different colors.
• We say that a vertex u of the graph G is $P_3$ colored if all the $P_3$ paths containing u have different colors.

Theorem 3.

Let T be a tree graph on n vertices; then ${\chi }_3\left(T\right)=\mathsf{\Delta }\left(T\right)+1$.

Proof. 

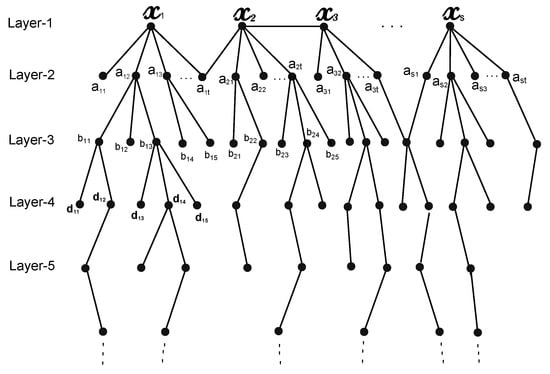
Let T be a tree graph on $n\ge 3$ vertices and let $\mathsf{\Delta }\left(T\right)$ be the maximum degree of T. Then, there exists a star subgraph $S_m$ of T with $\mathsf{\Delta }\left(T\right)+1$ vertices. By Theorem 1, we have ${\chi }_3\left(S_m\right)=m=\mathsf{\Delta }\left(T\right)+1$, and by Theorem 2, ${\chi }_3\left(T\right)\ge {\chi }_3\left(S_m\right)$. So, ${\chi }_3\left(T\right)\ge \mathsf{\Delta }\left(T\right)+1$. For the converse, we draw the tree graph as shown in Figure 1, where we consider all the vertices with degree $\mathsf{\Delta }\left(T\right)$ in the first layer.

Figure 1. Tree graph.

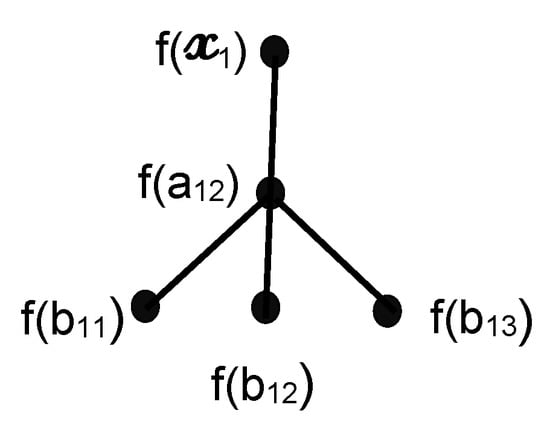
As we move down in the layers by following any path, the degree of the vertices is decreasing and the degree of the vertices in the last layer is 1. In a tree graph, the path between all the vertices is unique, and if there is a $P_3$ path between any two vertices, then it is also unique. To show that ${\chi }_3\left(T\right)\le \mathsf{\Delta }\left(T\right)+1$, we will show that $\mathsf{\Delta }\left(T\right)+1$ colors are enough to produce $P_3$-coloring of T. Let C be the set of colors and $\left|C\right|=\mathsf{\Delta }\left(T\right)+1$. We will produce a $P_3$ color function f from vertices of T to C. Notice that, in any coloring of a graph, if every vertex of the graph is $P_3$ colored, then such coloring is a $P_3$-coloring. Using this observation, firstly, we will show that $x_1$ is $P_3$ colored. So we start by assigning the color $f\left(x_1\right)$ to $x_1$ and the remaining $\mathsf{\Delta }\left(T\right)$ colors are assigned to the neighboring vertices of $x_1$. In this way, the $x_1$ vertex is $P_3$ colored. To explain this claim, consider the vertex $x_1$, as shown in Figure 1. The degree of $x_1$ is $\mathsf{\Delta }\left(T\right)$, and let $f\left(x_1\right)$ be the color of $x_1$. There exist three types of $P_3$ paths that contain $x_1$. The first type of $P_3$ path has $x_1$ as the middle vertex, the second type of $P_3$ path is the path whose one end point is $x_1$ and other is some $x_i$ (if possible), and the third type of path is the path with one end as $x_1$ and the other as the vertex $b_{1k}$; such a path has some $a_{1j}$ as the middle vertex. The first type of path whose middle vertex is $x_1$ is clearly of different colors under the assignment that we used. For the second type of path having $x_1$ as one end and the other as one of $x_i$ (if it exists), we will have $\mathsf{\Delta }\left(T\right)-1$ choices of colors from C because there cannot exist any cycle in a tree graph, so any such $x_i$ must be adjacent to exactly one neighbor of $x_1$. So, without any loss of generality, we can use the same color for such $x_i$ as the color of any neighbor of $x_1$ that is not adjacent to $x_i$. We shall always prefer the fewest colors for the $x_i$s (that is, if the set of colors has elements with increasing subscripts, then the first choice of color will be the color having the least subscripts). Now, for the third type of path (say $x_1{a}_{1j}{b}_{1k}$) having one end point as $x_1$ and the other as $b_{1k}$, we will assign different colors $f\left(b_{1k}\right)$ from C to these vertices $b_{1k}$, such as the colors $f\left(x_1\right)$ and $f\left(a_{1j}\right)$; see Figure 2. Because $d\left(a_{1j}\right)<d\left(x_1\right)$, we will have at least $\mathsf{\Delta }\left(T\right)-2$ choices for such a color scheme. So, this third type of path containing $x_1$ also has different colors. Thus, $x_1$ is a $P_3$ colored vertex.

Figure 2. Assignment of colors.

Now, to show that the vertices in the second layer are also $P_3$-colored with the set C, we observe that if there is a vertex such as $a_{11}$, then this vertex is already $P_3$ colored by the above coloring scheme. For the other types of vertices, such as $a_{12}$ in Figure 1, we proceed as follows. There are three possible $P_3$ paths that contain the vertex $a_{12}$. One path has $x_1$ as the middle vertex and $a_{12}$ as the end vertex (such as $a_{11}{x}_1{a}_{12}$). The second type of path is that which starts from $a_{12}$ and goes down to the descendant vertices (like $a_{12}{b}_{11}{d}_{11}$). The third type is the $P_3$ path that contains $a_{12}$ as the middle vertex (such as $b_{11}{a}_{12}{b}_{12}$ or $x_1{a}_{12}{b}_{11}$). The first and third types of these $P_3$ paths already have different colors. For the second type of $P_3$ path, which has a middle vertex from $b_{1k}$s such as $a_{12}{b}_{11}{d}_{11}$, we assign different colors from C to the vertices $d_{ik}$ so that none of these colors are equal to the assigned color of the middle vertex $b_{1k}$ and $f\left(a_{12}\right)$. Since $deg\left(b_{1k}\right)<deg\left(x_1\right)$, we have at least $\mathsf{\Delta }\left(T\right)-2$ choices of such colors. In this way, the third type of $P_3$ path has different colors. Thus, the vertex $a_{12}$ is $P_3$ colored.

So, we can use $\mathsf{\Delta }\left(T\right)+1$ or less colors for $P_3$-coloring of all the $P_3$ paths that contain $a_{12}$. Similarly, we can show that the vertex $a_{12}$ is $P_3$ colored. Now, for the vertices in the third and all lower layers, we can use same scheme of coloring using at most $\mathsf{\Delta }\left(T\right)+1$ colors. We will apply the same scheme for the rest of the vertices of the graph T. This shows that all the vertices of T can be $P_3$ colorable with at most $\mathsf{\Delta }\left(T\right)+1$ colors. Therefore, by the definition of $P_3$-chromatic number, ${\chi }_3\left(T\right)\le \mathsf{\Delta }\left(T\right)+1$. This concludes the proof. □

Algorithm to produce a $P_3$-coloring of tree graphs

Let T be a tree graph. Draw the tree graph shaped like a rooted tree such that all the vertices with maximum degree are in the first layer. Let C be a color class with colors $\left\{c_i\right|i=1,2,\dots ,\mathsf{\Delta }\left(T\right)+1\}$. So, $\left|C\right|=\mathsf{\Delta }\left(T\right)+1$. To understand the algorithm, we have labelled vertices of the k-th layer by $x_{{\alpha }_1{\alpha }_2\dots {\alpha }_k}^k$. It represents a complete tracing of the vertices, that is, this is a vertex in the k-th layer which is connected to a vertex in the first layer by the path $x_{{\alpha }_1}^1{x}_{{\alpha }_1{\alpha }_2}^2\dots x_{{\alpha }_1{\alpha }_2\dots {\alpha }_k}^k$. For example, the vertex $x_{{\alpha }_i{\alpha }_3}^2$ shows that it is the third vertex of the second layer and it is adjacent to the i-th vertex $x_{{\alpha }_i}^1$ of the first layer. Let $f:V\left(T\right)\to C$ be the coloring function defined by the following steps. Fix $f\left(x_{{\alpha }_1}^1\right)=c_1$.

Step 1:

If $x_{{\alpha }_i}^1,x_{{\alpha }_1{\alpha }_i}^2\in N\left(x_{{\alpha }_1}^1\right)$, then $f\left(x_{{\alpha }_i}^1\right)=c_i,\mathrm{for}i=2,3,\dots ,s$ and $f\left(x_{{\alpha }_1{\alpha }_i}^2\right)=c_j,\mathrm{for}j=s+1,s+2,\dots ,\mathsf{\Delta }\left(T\right)+1$. We shall prefer the fewest colors for $x_{{\alpha }_i}^1$s while selecting the color of these vertices.

Step 2:

Select a colored vertex, say $x_{{\alpha }_1{\alpha }_i}^2$, from the second layer having neighbor vertices in its lower layers and assign colors to these neighbor vertices in such way that the colors we are choosing are not assigned to $x_{{\alpha }_1{\alpha }_i}^2$ and to the neighbors of $x_{{\alpha }_1{\alpha }_i}^2$ in the upper layer.

Step 3:

Apply “Step 2” to the vertices of lower layers having $x_1^1$ as the top vertex.

Step 4:

Select a vertex, say $x_{{\alpha }_s}^1$, from first layer, which is already assigned a color, say $c_j$, then apply “Step 1” to $x_{{\alpha }_s}^1$ by setting $c_1=c_j$. Moreover, apply “Step 3” to $x_{{\alpha }_s}^1$.

Step 5:

Repeat “Step 4” until all the vertices have their colors.

Example 1.

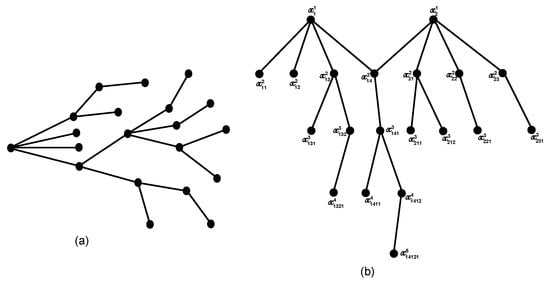
For a better understanding of this algorithm, we provide an example. Consider a tree graph T as shown in Figure 3a.

Figure 3. (a) A random tree graph. (b) Arrangement of the tree of part (a) according to the algorithm.

Arrange the graph in such a way that all the vertices with maximum degree are in the first layer (see Figure 3b), where we can see that $\mathsf{\Delta }\left(T\right)=4$. Consider the color class $C=\{c_1,c_2,c_3,c_4,c_5\}$. Fix $f\left(x_1^1\right)=c_1$.

Step 1:

The $N\left(x_1^1\right)=\{x_{11}^2,x_{12}^2,x_{13}^2,x_{14}^2\}$. So, we set $f\left(x_{11}^2\right)=c_2$, $f\left(x_{12}^2\right)=c_3$, $f\left(x_{13}^2\right)=c_4$, $f\left(x_{14}^2\right)=c_5$.

Step 2:

The assignment of colors to the neighbors of $x_{13}^2$ which are not yet assigned any color yet is $f\left(x_{131}^3\right)=c_2$, $f\left(x_{132}^3\right)=c_3$.

The assignment of colors to the neighbors of $x_{14}^2$ which are not yet assigned any color is $f\left(x_2^1\right)=c_2$, $f\left(x_{141}^3\right)=c_3$.

Step 3:

There is only one vertex $x_{1321}^4$ in the neighbor of $x_{132}^3$ which is not assigned any color, so we put $f\left(x_{1321}^4\right)=c_1$.

The assignment of colors to the neighbors of $x_{141}^3$ which are not yet assigned any color is $f\left(x_{1411}^4\right)=c_1$, $f\left(x_{1412}^4\right)=c_2$.

There is only one vertex $x_{14121}^5$ in the neighbor of $x_{1412}^4$ which is not assigned any color, so we put $f\left(x_{14121}^5\right)=c_1$.

Step 4:

The assignment of colors to the neighbors of $x_2^1$ which are not yet assigned any color is $f\left(x_{21}^2\right)=c_1$, $f\left(x_{22}^2\right)=c_3$, $f\left(x_{23}^2\right)=c_4$.

The assignment of colors to the neighbors of $x_{21}^2$ which are not yet assigned any color is $f\left(x_{211}^3\right)=c_3$, $f\left(x_{212}^3\right)=c_4$.

There is only one vertex $x_{221}^3$ in the neighbor of $x_{22}^2$ which is not assigned any color, so we put $f\left(x_{221}^3\right)=c_4$.

There is only one vertex $x_{231}^3$ in the neighbor of $x_{23}^2$ which is not assigned any color, so we put $f\left(x_{231}^3\right)=c_5$.

Step 5:

All the vertices are already colored; see Figure 4. This completes the example.

Figure 4. $P_3$-labelling of T.

The following Theorem 4 formulates the $P_3$-chromatic number of the complete bipartite graph.

Theorem 4.

Let $K_{m,n}$ be a complete bipartite graph; then ${\chi }_3\left(K_{m,n}\right)=m+n$.

Proof. 

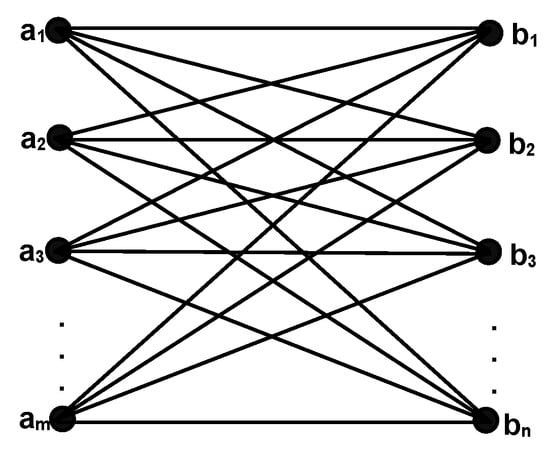
Let $K_{m,n}$ be a complete bipartite graph with two sets of vertices U and V, where U has m number of vertices and V has n number of vertices.

As the graph is complete bipartite, every vertex of set U is adjacent to each vertex of set V (see Figure 5). Now if we assign a color 0 to the vertex $a_1$, then for the vertex $a_1$ to be a $P_3$ colored vertex, we must assign n different colors to $b_i$s. Now, select any vertex $a_s$ different from $a_1$; then for this vertex to be a $P_3$ colored vertex, we cannot assign any color from the set $\{0,1,\dots n\}$. Because the path $a_1{b}_t{a}_s$ is the $P_3$ path containing $a_s$ for any arbitrary vertex $b_t$, we cannot assign the colors of $b_t$ and $a_1$ to $a_s$. So, we must use a different color for every vertex of $K_{m,n}$ for $P_3$-labelling. Therefore, the number of colors must be equal to the number of vertices of $K_{m,n}$ and the number of vertices of $K_{m,n}$ is $m+n$. Thus, ${\chi }_3\left(K_{m,n}\right)=m+n$. □

Figure 5. Complete bipartite graph $K_{m,n}$.

3. $P_3$-Chromatic Number of Grid Graph

In this section, we have computed the $P_3$ chromatic number of the grid graph. A grid graph is also one of the many well-known bipartite graphs. It is the Cartesian product $P_m\square P_n$ of path graphs with $m$ and $n$ vertices. The $m\times n$ grid graph is also denoted by $L(m,n)$. Grid graphs are also known as lattice graphs or rectangular graphs. In Theorem 5, the generalized form of the $P_3$-chromatic number of grid graph $(P_m\square P_n)$ is determined, where $m,n\ge 3$.

Theorem 5.

Let $P_m\square P_n$ be the grid graph; then ${\chi }_3(P_m\square P_n)=5$ for all $m,n\ge 3$.

Proof. 

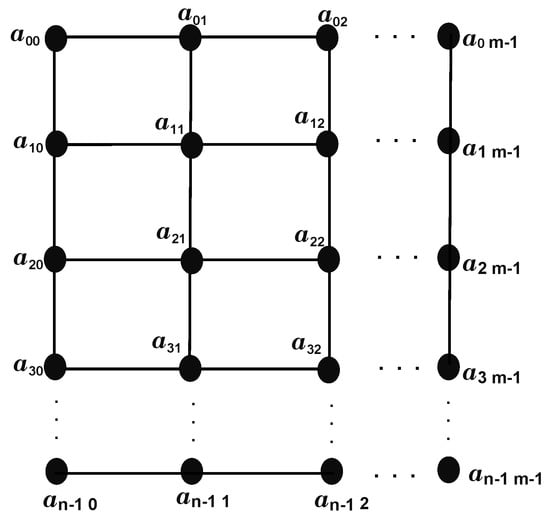
Let $P_m\square P_n$ be a grid graph with $m,n\ge 3$. From the definition of grid graph and from Figure 6, we can see that the star graph $S_5$ is a subgraph of $P_m\square P_n$. Then, by Theorem 1 and Theorem 2, $P_m\square P_n\ge 5$. This means that we need at least 5 colors for the $P_3$-coloring of $P_m\square P_n$.

Figure 6. The grid graph $P_m\square P_n$.

To prove the converse, we will define a $P_3$-labeling $f:V(P_m\square P_n)\to \{0,1,2,3,4\}$, where the set $\{0,1,2,3,4\}$ is the set of colors. Let $j\in \{0,\dots ,m-1\}$; then we define $f$ as follows.

$$f\left(a_{ij}\right)=2i+j(mod5),0\le i\le n-1,0\le j\le m-1.$$

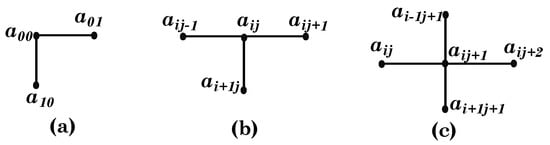
To show that $f$ is indeed a $P_3$-coloring, we must show that each vertex of $P_m\square P_n$ is $P_3$ colored. As the graph is symmetric, it is sufficient to show that the vertices on $P_3$ paths in Figure 7 have this property. Because every vertex in $P_m\square P_n$ lies on one of these type of figures, if the vertices of Figure 7 are $P_3$ colored, then with the same scheme, we can say that it would be true for all vertices of the grid graph.

Figure 7. Sub-graphs of $P_m\square P_n$. (a) Represent the corner subgraphs. (b) Represent subgraphs from sides. (c) Represent subgraphs from inside of $P_m\square P_n$.

Figure 7a represents the four subgraphs on corners of the grid graph, Figure 7b represents such subgraphs on the borderline of the grid graph, and Figure 7c represents all such internal subgraphs of the grid graph. In Figure 7a, there are five possible $P_3$ paths containing the vertex $a_{00}$, where $0\le i\le 2$ and $0\le j\le 2$. The paths are

$$a_{00}{a}_{01}{a}_{02},a_{00}{a}_{01}{a}_{11},a_{00}{a}_{10}{a}_{20},a_{00}{a}_{10}{a}_{11},a_{01}{a}_{00}{a}_{10}.$$

We shall discuss only one path from the above five paths to show that they are colored. Similarly, the other paths can be shown to be colored. Let us consider the path $a_{01}{a}_{00}{a}_{10}$; then $f\left(a_{01}\right)=1,f\left(a_{00}\right)=0,f\left(a_{10}\right)=2$.

Now, for $i=0$ and $j=1$, the sub-graph in Figure 7b shows that there are eight possible $P_3$ paths that contain the vertex $a_{01}$, and the list of such paths is

$$a_{00}{a}_{01}{a}_{02},a_{00}{a}_{01}{a}_{11},a_{02}{a}_{01}{a}_{11},a_{01}{a}_{02}{a}_{03},a_{01}{a}_{11}{a}_{12},a_{01}{a}_{11}{a}_{10},a_{01}{a}_{00}{a}_{10},a_{01}{a}_{02}{a}_{12}.$$

We shall discuss only one path from the above eight paths to show that they are colored. Similarly, the other paths can be shown to be colored. Let us consider the path $a_{00}{a}_{01}{a}_{02}$; then $f\left(a_{00}\right)=0,f\left(a_{01}\right)=1,f\left(a_{02}\right)=2$.

For $i=0$ and $1<j<m-2$, the sub-graph in Figure 7b shows that there are nine possible $P_3$ paths that contain the vertex $a_{ij}$, and these $P_3$ path are

$$a_{ij-1}{a}_{ij}{a}_{ij+1},a_{ij-1}{a}_{ij}{a}_{i+1j},a_{ij+1}{a}_{ij}{a}_{i+1j},a_{ij}{a}_{ij+1}{a}_{ij+2},a_{ij}{a}_{i+1j}{a}_{i+1j+1},a_{ij}{a}_{i+1j}{a}_{i+1j-1},$$

$$a_{ij}{a}_{ij-1}{a}_{ij-2},a_{ij}{a}_{ij-1}{a}_{i+1j-1},a_{ij}{a}_{ij+1}{a}_{i+1j+1}.$$

Similarly, as above, we shall discuss only one path from the above nine paths to show that they are colored. The other paths can be shown to be colored by following a similar technique. Note that this case also proves that the result is true under the condition on the subscripts $i$ and $j$ as follows.

For $i=0,n-1$ we have $1<j<m-2$, and for $j=0,m-1$ we have $1<i<n-2$.

We shall discuss only one possibility here; the proofs for others will follow similarly. Let us consider the path $a_{ij-1}{a}_{ij}{a}_{ij+1}$, then $f\left(a_{ij-1}\right)=2i+j-1,f\left(a_{ij}\right)=2i+j$, and $f\left(a_{ij+1}\right)=2i+j+1$.

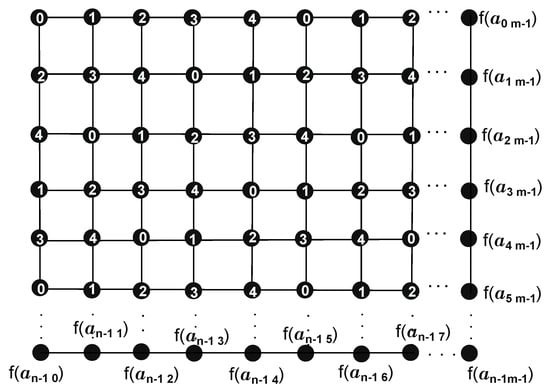
Thus, all the vertices on the four sides of the grid are $P_3$ colored. Figure 8 represents the $P_3$-coloring and algorithm under the function $f$.

Figure 8. $P_3$-labelling of $P_m\square P_n$.

Now, we can see from Figure 7c that the vertex $a_{ij}$, where $1\le i\le n-2,1\le j\le m-2$, is contained in the following eighteen $P_3$ paths:

$$\begin{array}{cccccccc}& \left(\mathrm{i}\right)a_{i-1j}{a}_{ij}{a}_{i+1j},\hfill & & \left(\mathrm{ii}\right)a_{ij-1}{a}_{ij}{a}_{ij+1},\hfill & & \left(\mathrm{iii}\right)a_{i-1j}{a}_{ij}{a}_{ij-1},\hfill & & \left(\mathrm{iv}\right)a_{i-1j}{a}_{ij}{a}_{ij+1},\hfill \\ & \left(\mathrm{v}\right)a_{ij-1}{a}_{ij}{a}_{i+1j},\hfill & & \left(\mathrm{vi}\right)a_{ij+1}{a}_{ij}{a}_{i+1j},\hfill & & \left(\mathrm{vii}\right)a_{ij}{a}_{i+1j}{a}_{i+2j},\hfill & & \left(\mathrm{viii}\right)a_{ij}{a}_{i-1j}{a}_{i-2j},\hfill \\ & \left(\mathrm{ix}\right)a_{ij}{a}_{ij+1}{a}_{ij+2},\hfill & & \left(\mathrm{x}\right)a_{ij}{a}_{ij-1}{a}_{ij-2},\hfill & & \left(\mathrm{xi}\right)a_{ij}{a}_{i+1j}{a}_{i+1j-1},\hfill & & \left(\mathrm{xii}\right)a_{ij}{a}_{i+1j}{a}_{i+1j+1},\hfill \\ & \left(\mathrm{xiii}\right)a_{ij}{a}_{ij+1}{a}_{i+1j+1},\hfill & & \left(\mathrm{xiv}\right)a_{ij}{a}_{ij-1}{a}_{i+1j-1},\hfill & & \left(\mathrm{xv}\right)a_{ij}{a}_{ij+1}{a}_{i-1j+1},\hfill & & \left(\mathrm{xvi}\right)a_{ij}{a}_{ij-1}{a}_{i-1j-1},\hfill \\ & \left(\mathrm{xvii}\right)a_{ij}{a}_{i-1j}{a}_{i-1j+1},\hfill & & \left(\mathrm{xviii}\right)a_{ij}{a}_{i-1j}{a}_{i-1j-1}.\hfill & & & \end{array}$$

We shall discuss one $P_3$ path from the above list. The computations for other paths will follow similarly. So, consider an arbitrary $P_3$ path from the above list, say $a_{ij}{a}_{ij+1}{a}_{ij+2}$; then

$$f\left(a_{ij}\right)=2i+j,f\left(a_{ij+1}\right)=2i+j+1\mathrm{and}f\left(a_{ij+2}\right)=2i+j+2.$$

This shows that all $P_3$ paths in this case are colored. Therefore, all the internal vertices of the grid graph are $P_3$ colored and this proves that $f$ is a $P_3$-coloring. Similarly, every vertex is $P_3$ colored in all the cases. So, ${\chi }_3(P_m\square P_n)=5$. □

4. $P_3$-Chromatic Number of Bipartite Graphs Having Exactly One Cycle

In this section, we have discussed the $P_3$ chromatic number for a special class of bipartite graphs consisting of one or more cycles under different conditions. Theorem 6 provides the $P_3$-chromatic number of bipartite graphs, which contains exactly one cycle. We have constructed an algorithm for Theorem 6 after its proof.

Theorem 6.

Let $G$ be a bipartite graph having exactly one cycle; then ${\chi }_3\left(G\right)=\mathsf{\Delta }\left(G\right)+1$.

Proof. 

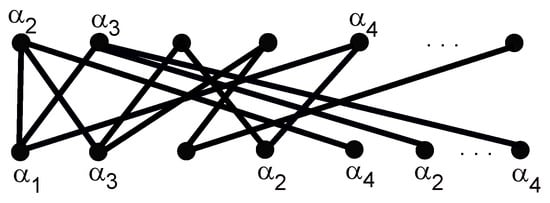
Let $G$ be a bipartite graph having exactly one cycle, with $U$ and $V$ being a vertex partition of $V\left(G\right)$. For simplicity, let $\mathsf{\Delta }\left(G\right)=deg\left(u_1\right)$. Then, it contains a star subgraph $S_m$, such that $m=\mathsf{\Delta }\left(G\right)+1$. By Theorem 1, we have ${\chi }_3\left(S_m\right)=\mathsf{\Delta }\left(G\right)+1$, and from Theorem 2, we obtain ${\chi }_3\left(G\right)\ge {\chi }_3\left(S_m\right)$. So,

$${\chi }_3\left(G\right)\ge \mathsf{\Delta }\left(G\right)+1$$

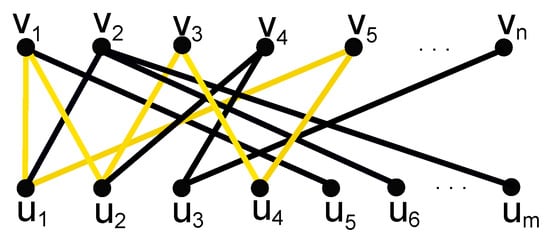
For the converse, we need to show that every vertex $G$ can be $P_3$ colored with a color class $C=\left\{{\alpha }_i\right|i=1,2,3,\dots ,\mathsf{\Delta }\left(G\right)+1\}$, that is, no vertices in any $P_3$ path have the same colors. For this, we will arrange(or draw) the graph in such a way that all the vertices having maximum degree are on the leftmost side of the graph and the degrees of the vertices are in decreasing order from left to right, as shown in Figure 9, where $deg\left(u_1\right)\ge deg\left(u_2\right)\ge deg\left(u_3\right)\ge \dots \ge deg\left(u_m\right)$, and the same for the $v_i$’s.

Figure 9. A bipartite graph $G$ with one cycle. Cycle is in color.

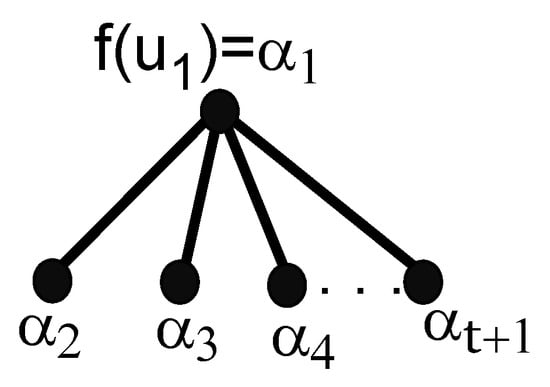
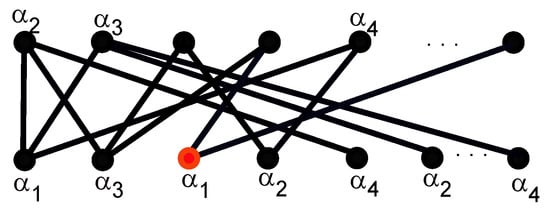
Now, consider the vertex $u_1$ of the graph $G$. The vertex $u_1$ is adjacent to $\mathsf{\Delta }\left(G\right)$ vertices of the set $V$. Therefore, we can assign $\mathsf{\Delta }\left(G\right)+1$ different colors to $u_1$ and to its $\mathsf{\Delta }\left(G\right)$ neighbors for the production of a $P_3$-coloring, as shown in Figure 10.

Figure 10. $P_3$-coloring at vertex $u_1$.

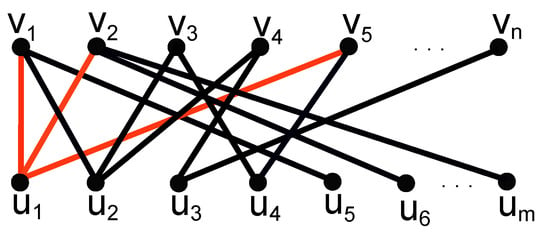
The graph $G$ is a bipartite graph that contains a cycle, so there will be vertices which are connected by more than one $P_3$ path. Moreover, there are two types of $P_3$ paths containing each vertex $x\in V\left(G\right)$. In one $P_3$ path, the vertex $x$ is a middle vertex (with end points from the opposite set of vertices $U$ or $V$), and in the second type of $P_3$ path, the vertex $x$ is one of the two end points (with the other end vertex from the same set $U$ or $V$). So, for the vertex $u_1$, there also exist two types of $P_3$ paths which contain $u_1$. The first type of $P_3$ paths would be the paths whose middle vertex is $u_1$ and end points must be some $v_i$s, for $i\in \{1,2,3,\dots ,\mathsf{\Delta }(G\left)\right\}$; these types of $P_3$ paths are highlighted in Figure 11.

Figure 11. $P_3$ paths whose middle vertex is $u_1$.

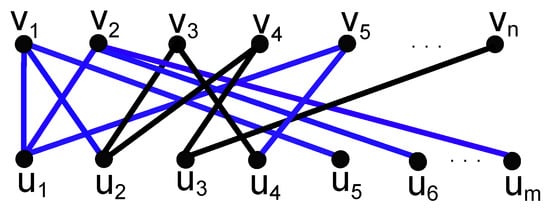
The second type of $P_3$ path that contains $u_1$ starts from $u_1$ and must end at some other $u_i$, where the number of such $u_i$s is at most $\mathsf{\Delta }\left(G\right)$; such types of $P_3$ paths are shown in Figure 12.

Figure 12. $P_3$ paths which start from $u_1$ and end at any other $u_i$.

The first type of $P_3$ path which contains $u_1$ as the middle vertex is already colored because its end points are $v_i$s, and such $v_i$s are neighbors of $u_1$. From Figure 10, it is clear that we have already assigned colors to $u_1$ and its neighbor vertices using the $C$ color class that has $\mathsf{\Delta }\left(G\right)+1$ colors. Now, for the second type of $P_3$ path containing $u_1$ that starts from $u_1$ and ends at some other $u_i$, the middle vertex of these types of $P_3$ paths must be some $v_i$. Such $v_i$s are already assigned colors, as shown in Figure 10. So, now we need to assign color only to $u_i$s, which are the end points of this second type of $P_3$ path.

To continue the procedure of producing a $P_3$-coloring, we will assign colors to these $u_i$s (from the same color class $C$) which are not assigned to $u_1$ and to the neighbors of these $u_i$s. As there exists only one cycle, in these types of paths, any $u_i$ can be adjacent to at most two neighbors of $u_1$. Therefore, we can use the colors of $v_j$s, say ${\alpha }_j$s, which are not adjacent to $u_i$, so in this way, we will have at least $\mathsf{\Delta }\left(G\right)-2$ and $\mathsf{\Delta }\left(G\right)-1$ choices of colors for each $u_i$ when $u_i$ is adjacent to two and one neighbors of $u_1$, respectively. Therefore, to produce a $P_3$-coloring at $u_1$ for the second type of $P_3$ paths, we can assign colors to such $u_i$s from left to right in decreasing order with respect to subscripts of colors, as shown in Figure 13. Thus, $u_1$ is $P_3$ colored.

Figure 13. $P_3$-coloring of all $P_3$ paths containing $u_1$.

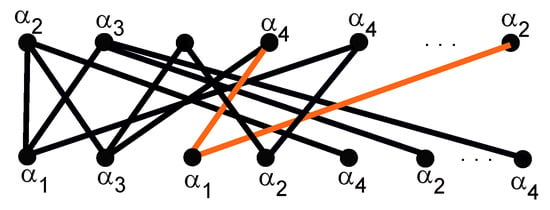
Now, consider any other $u_i$ (if it exists) that is not colored yet, say $u_{\ell }$. For example, in Figure 14, the vertex $u_3$ is such a vertex. We will show that $u_{\ell }$ is also $P_3$ colored. For this, firstly, we will assign ${\alpha }_1$ color to $u_{\ell }$, as shown in Figure 14; the vertex $u_3$ is assigned the color ${\alpha }_1$.

Figure 14. Assignment of color to $u_{\ell }$. Here, it is $u_3$.

We can use the color assigned to $u_1$ for $u_{\ell }$ because $u_{\ell }$ is not adjacent to $u_1$ and also $u_{\ell }$ is not contained in any $P_3$ path that contains $u_1$. The vertex $u_{\ell }$ is also contained in two types of $P_3$ paths. The first type of path is the path having a middle vertex as $u_{\ell }$. The degree of the vertex $u_{\ell }$ is less than or equal to $\mathsf{\Delta }\left(G\right)$, so for its coloring, we can use the same color class $C$; see Figure 15. We will assign those colors to neighbors $v_j$s of $u_{\ell }$ which are not used for $u_{\ell }$, not used for the $u_i$s, which are the end points of $P_3$ paths with $u_{\ell }$ as the second end point, and not used for the previous colored $v_i$s, which are the end points of $P_3$ paths with $v_j$s as the second end point (e.g., in Figure 15, we will not assign colors ${\alpha }_1$, ${\alpha }_3$, and ${\alpha }_2$ to $v_4$). We will have choices of colors from $C$ for $v_j$s because there is only one cycle, and the degree of the vertices $u_{\ell }$, $u_i$s, and $v_i$s (which are already assigned a color in some $P_3$ paths) is not more than $\mathsf{\Delta }\left(G\right)$.

Figure 15. $P_3$ coloring of paths having $u_3$ as middle vertex.

Now, consider the second type of $P_3$ path having $u_{\ell }$ as one end point and $u_i$ as the second end point (other than $u_{\ell }$). Note that some vertices of these types of paths may already be colored, while some may not be. The ones that are not yet assigned colors, such as $u_i$s, are not adjacent to any $v_i$ that is adjacent to any $u_k$ whose $P_3$-coloring is already completed. There will be choices (at least one) of colors for such vertices from color class $C$. For example, the second type of $P_3$ path for the vertex $u_3$ in Figure 15 is already colored. Similarly, for any $u_i$ that is not assigned color, we can use color class $C$. That $u_i$ must be contained in at most two types of $P_3$ paths with the same conditions. So, with the same technique, a $P_3$-coloring of all the $P_3$ paths which contain $u_i$s can be produced by using the same color class $C$. We will select the fewest colors (with respect to the order in the subscripts) when selecting the colors of vertices $u_i$s which are not used for vertices of any $P_3$ that contains the vertex $u_i$. We will apply this same scheme until all the $u_i$s are colored. After assigning colors to vertices $u_i$s, we shall have two cases:

(1)

All $v_p$s are colored.

(2)

Some $v_p$s are not colored. See Figure 15.

In the first case, the $P_3$-coloring of the graph is already completed. So, we will obtain our required result. But in the second case, we will consider the $u_i$ vertex that is already colored, but some $v_p$ that are adjacent to that $u_i$ are not colored yet. That $u_i$ must be contained in two types of $P_3$ paths. The first type of $P_3$ path has that $u_i$ as its middle vertex (and $v_p$ as one end point), and in the second type of $P_3$ path, that $u_i$ would be one end point of the paths, and the other end point would be any other $u_i$ (with $v_p$ as the middle vertex). For the first type of path, we need to color only $v_p$s because $u_i$ is already colored. As the degree of that $u_i$ must be less than or equal to $\mathsf{\Delta }\left(G\right)$, $u_i$ must be connected with at most $\mathsf{\Delta }\left(G\right)$ types of $v_p$s. So, we can use the colors from $C$ that are not used for the neighbors of that $v_p$ and also not used for the neighbors of the neighbors of $v_p$s. As the considered vertex $u_i$ is already colored, but some of its neighbors are not colored, it shows that this $u_i$ is the end point of any $P_3$ path whose other end point is some different $u_p$ who is already $P_3$ colored and this $u_i$ is assigned a color when we colored the second type of $P_3$ paths that contain the $u_p$ vertex as their one end point. So, it means we can use the colors of that $u_p$, say ${\alpha }_p$, for the $v_p$.

For example, the $v_3$ vertex is such a vertex in Figure 15, and it is assigned a color as shown in Figure 16, where $f\left(u_1\right)$ and $f\left(v_3\right)$ are the colors of vertices $u_1$ and $v_3$, respectively. By using this scheme, all the $v_p$s in this type of path would be colored by using same color class $C$. Then, we do not need to color the second type of $P_3$ path because that must already be colored, as here we assigned colors to $v_p$s and all the $u_i$s are already labelled. So, by using this technique, we can color all the remaining vertices of set $V$ by using at most $\mathsf{\Delta }\left(G\right)+1$ colors (see Figure 16). The process will end eventually since the graph is finite and the degree of vertices is non-increasing from left to right, with every vertex becoming $P_3$ colored in the process with at most $\mathsf{\Delta }\left(G\right)+1$ colors. Therefore, ${\chi }_3\left(G\right)\le \mathsf{\Delta }\left(G\right)+1$. We have already proved that ${\chi }_3\left(G\right)\ge \mathsf{\Delta }\left(G\right)+1$; therefore,

$${\chi }_3\left(G\right)=\mathsf{\Delta }\left(G\right)+1.$$

□

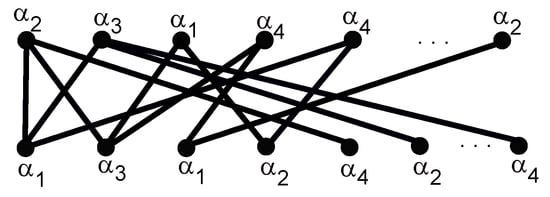
Figure 16. $f\left(u_1\right)=f\left(v_3\right)$.

Algorithm to produce a $P_3$-coloring of graphs for Theorem 6

Let $G$ be a bipartite graph having exactly one cycle and $V\left(G\right)=U\cup V$ be the vertex partition of $G$. Let $\mathsf{\Delta }\left(G\right)$ be the maximum degree of $G$. Arrange the bipartite graph such that $d\left(u_1\right)\ge d\left(u_2\right)\ge d\left(u_3\right)\ge \dots \ge d\left(u_m\right)$, $d\left(v_1\right)\ge d\left(v_2\right)\ge d\left(v_3\right)\ge \dots \ge d\left(v_n\right)$ from left to right. We define a $P_3$-coloring $f:V\left(G\right)\to C$, where $C=\left\{{\alpha }_i\right|i=1,2,\dots ,\mathsf{\Delta }\left(G\right)+1\}$. Let $d\left(u_1\right)=\mathsf{\Delta }\left(G\right)$ and fix $f\left(u_1\right)={\alpha }_1$.

Step 1:

If $v_j\in N\left(u_1\right)$ then $f\left(v_j\right)={\alpha }_i,i=2,3,\dots ,\mathsf{\Delta }\left(G\right)+1$.

Step 2:

Select the vertex $v_j\in N\left(u_1\right)$ that already has a color, say ${\alpha }_j$, and assign different colors to neighbors of $v_j$. Choose colors that are not used for other neighbors of $v_j$.

Step 3:

Select the immediate next vertex of set $U$ which is not colored yet, say $u_s$, and put $f\left(u_s\right)={\alpha }_1$. Then apply Step 1 and Step 2 to $u_s$.

Step 4:

Repeat Step 3 until all the $u_i$s are not colored.

Step 5:

Select the vertex from set $V$ which is not yet colored, say $v_t$. Assign the color ${\alpha }_t$ to the vertex $v_t$ where ${\alpha }_t$ is the color that is not assigned to neighbors of $v_t$ and neighbors of its neighbors.

Step 6:

Repeat Step 5 until all the $v_t$s are not colored.

Example 2.

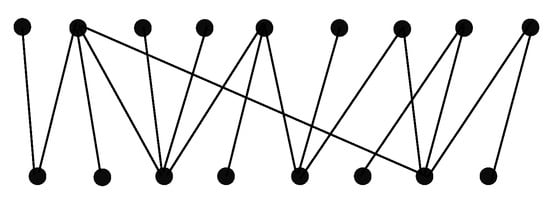
Consider the bipartite graph $G$ having exactly one cycle, as depicted in Figure 17.

Figure 17. A bipartite graph having exactly one cycle.

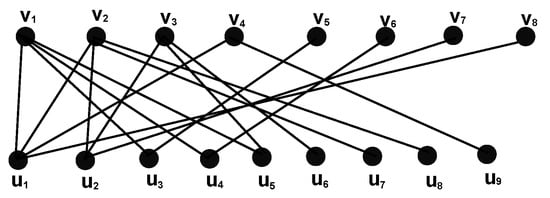
Arrange graph $G$ such that the degrees of the vertices are in decreasing order from left to right, as shown in Figure 18. We can see $\mathsf{\Delta }\left(G\right)=4$. So, $C=\left\{{\alpha }_i\right|i=1,2,3,4,5\}$. Fix $f\left(u_1\right)={\alpha }_1$.

Figure 18. Arrangement of the vertices of $G$ in non-increasing order from left to right.

Step 1:

We have $N\left(u_1\right)=\{v_1,v_2,v_4,v_8\}$. We consider the assignment of colors to the neighbors of $u_1$ as $f\left(v_1\right)={\alpha }_2$, $f\left(v_2\right)={\alpha }_3$, $f\left(v_4\right)={\alpha }_4$, $f\left(v_8\right)={\alpha }_5$.

Step 2:

The neighborhood of $v_1$ is $\{u_1,u_3,u_4,u_5\}$; therefore, we assign $f\left(u_3\right)={\alpha }_3$, $f\left(u_4\right)={\alpha }_4$, and $f\left(u_5\right)={\alpha }_5$.

The neighborhood of $v_2$ is $\{u_1,u_2,u_7,u_8\}$; therefore, we assign $f\left(u_2\right)={\alpha }_2$, $f\left(u_7\right)={\alpha }_4$, and $f\left(u_8\right)={\alpha }_5$.

The neighborhood of $v_4$ is $\{u_1,u_9\}$; therefore, we put $f\left(u_9\right)={\alpha }_2$.

Step 3:

Select the immediate next vertex $u_6$ of set $U$ which is not colored yet and assign $f\left(u_6\right)={\alpha }_1$. The vertex $v_3$ is the only neighbor of $u_6$, and we assign $f\left(v_3\right)={\alpha }_4$.

Step 4:

All the $u_i$s are already colored. So we move to Step 5.

Step 5:

The vertex $v_5$ from set $V$ is not colored yet. We assign $f\left(v_5\right)={\alpha }_1$.

Step 6:

Now, select vertex $v_6$ and assign $f\left(v_6\right)={\alpha }_1$. For the vertex $v_7$, we put $f\left(v_7\right)={\alpha }_1$.

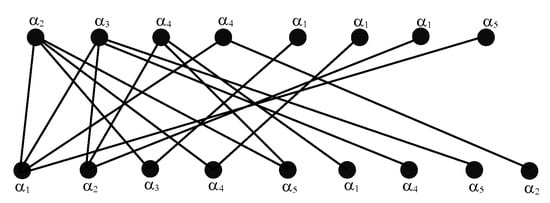
Thus, Figure 19 represents the final $P_3$-coloring of the graph.

Figure 19. $P_3$-labelling of $G$.

5. Conclusions

In this article, the main interest of the authors was to study a recently introduced coloring of graphs called $P_3$-coloring. This coloring arises as a natural generalization of the coloring of a graph. In this respect, we have determined the $P_3$-chromatic number of different families of bipartite graphs. We have formalized the $P_3$-chromatic number of tree graphs, grid graphs, complete bipartite graphs, and the class of bipartite graphs that have only one cycle. Moreover, we have also presented algorithms to produce a $P_3$-coloring of tree graphs, grid graphs, and the bipartite graphs that have exactly one cycle with the minimum number of colors. In the future, the authors are interested in extending this study and making some more significant advancements.