Cycle Existence for All Edges in Folded Hypercubes under Scope Faults

Abstract

The reliability of large-scale networks can be compromised by various factors such as natural disasters, human-induced incidents such as hacker attacks, bomb attacks, or even meteorite impacts, which can lead to failures in scope of processors or links. Therefore, ensuring fault tolerance in the interconnection network is vital to maintaining system reliability. The n-dimensional folded hypercube network structure, denoted as ${FQ}_n$, is constructed by adding an edge between every pair of vertices with complementary addresses from an n-dimensional hypercube, $Q_n$. Notably, ${FQ}_n$ exhibits distinct characteristics based on the dimensionality: it is bipartite for odd integers $n\ge 3$ and non-bipartite for even integers $n\ge 2$. Recently, in terms of the issue of how ${FQ}_n$ performs in communication under regional or widespread destruction, we mentioned that in ${FQ}_n$, even when a pair of adjacent vertices encounter errors, any fault-free edge can still be embedded in cycles of various lengths. Additionally, even when the smallest communication ring experiences errors, it is still possible to embed cycles of any length. The smallest communication ring in ${FQ}_n$ is observed to be the four-cycle ring. In order to further investigate the communication capabilities of ${FQ}_n$, we further discuss whether every fault-free edge will still be a part of every communication ring with different lengths when the smallest communication ring is compromised in ${FQ}_n$. In this study, we consider a fault-free edge $e=(u,v)$ and $F_4=\{f_1,f_2,f_3,f_4\}$ as the set of faulty extreme vertices for any four cycles in ${FQ}_n$. Our research focuses on investigating the cycle-embedding properties in ${FQ}_n-F_4$, where the fault-free edges play a significant role. The following properties are demonstrated: (1) For $n\ge 4$ in ${FQ}_n-F_4$, every even length cycle with a length ranging from $4 \mathrm{t}\mathrm{o} 2^n-4$ contains a fault-free edge e; (2) For every even $n\ge 4$ in ${FQ}_n-F_4$, every odd length cycle with a length ranging from $n+1\mathrm{t}\mathrm{o}{2}^n-5$ contains a fault-free edge $e$. These findings provide insights into the cycle-embedding capabilities of ${FQ}_n$, specifically in the context of fault tolerance when considering certain sets of faulty vertices.

1. Introduction

In multiprocessor systems, processors communicate with each other through an interconnection network. A wide variety of network topologies have been proposed, among which the n-dimensional hypercube ${(Q}_n)$ stands out due to its symmetry, recursive structure, regularity, strong connectivity, small diameter, low degree, and low edge complexity [1]. Currently, many transformed or expanded topological structures of $Q_n$ have been developed for research and exploration. The reason is that these topologies possess numerous excellent characteristics, such as regularity, symmetry, low degree, and a graph diameter that is almost only half of that of a hypercube. Therefore, each of them has its own research value. However, among the various topological structures with variations of $Q_n$, folded hypercubes $\left({FQ}_n\right)$ contain complement edges, which are obtained by adding an edge to each pair of vertices that are farthest apart in $Q_n$. Since ${FQ}_n$ have more edges than $Q_n$, ${FQ}_n$ can not be classified as hypercube-like structures and can not develop the generally fault-tolerant Hamiltonian property. Therefore, ${FQ}_n$ serve as the network topology for our study. Moreover, ${FQ}_n$ has been shown to improve the performance of $Q_n$ in multiple measurements [2]. Additionally, ${FQ}_n$ are distinguished from other recursive and bipartite graph structures. The uniqueness of ${FQ}_n$ lies in the fact that when their dimensions are odd, they are bipartite graphs, while they are not bipartite in even dimensions. Therefore, when investigating cycle embeddings, it is often necessary to separately consider odd-dimensional and even-dimensional aspects. Based on these superiorities make ${FQ}_n$ widely used in parallel computing systems.

In real-world networks, faults in edges and/or vertices are inevitable. Therefore, the evaluation of fault-tolerant problems in ${FQ}_n$ has been widely studied in the literature [3,4,5,6,7,8,9,10]. Recently, the issue of how ${FQ}_n$ performs in communication under adverse conditions such as natural disasters or human-inflicted damage, which can result in regional or widespread destruction, including earthquakes, meteorite impacts, or bombings, has been raised. For example, in our previous works, we mentioned that in ${FQ}_n$, even when a pair of adjacent vertices encounter errors, any fault-free edge can still be embedded in cycles of various lengths [10]. Additionally, even when the smallest communication ring experiences errors, it is still possible to embed cycles of any length [9]. The smallest communication ring in ${FQ}_n$ is observed to be the four-cycle ring. In order to further investigate the communication capabilities of ${FQ}_n$, we further discuss whether every fault-free edge will still be a part of every communication ring with different lengths when the smallest communication ring is compromised in ${FQ}_n$. This paper addresses this question by studying fault-free edges $e=(u,v)$ and the scope faulty set $F_4=\{f_1,f_2,f_3,f_4\}$ of faulty extreme vertices of any four-cycle ring in ${FQ}_n$. The main results obtained are: (1) for $n\ge 4$, every fault-free edge $e$ can lie on a cycle of every even length from 4 to $2^n-4$ in ${FQ}_n-F_4$; (2) for every even $n\ge 4$, every fault-free edge $e$ can lie on a cycle of every odd length from $n+1$ to $2^n-5$ in ${FQ}_n-F_4$.

The remainder of this paper is organized as follows: Section 2 furnishes an overview of the definitions and properties of ${FQ}_n$, while Section 3 presents the main results. Section 4 concludes this paper.

2. Preliminaries

The graph terminology used in this paper is based on the definitions provided in [11] when utilizing a graph $G$ to model the network. Let us take into account a graph $G=\left(V\right(G),E(G\left)\right)$ which is finite, where $V\left(G\right)$ and $E\left(G\right)$ denote the sets of vertices and edges of $G$, respectively.

Consider a graph $G=\left(V\right(G),E(G\left)\right)$ with sets $Fe$ and $Fv$ representing faulty edges and faulty vertices, respectively. Here, $Fe$ is a subset of $E\left(G\right)$ and $Fv$ is a subset of $V\left(G\right)$. The subgraph obtained after removing $Fe$ and $Fv$ from $G$ is denoted by $G-Fv-Fe$. Typically, removing a set of vertices also means removing all edges connected to the set of vertices. A path $P\left[v_0,v_m\right]=⟨v_0,v_1,\dots ,v_m⟩$ is a sequence of adjacent vertices where each vertex $v_0,v_1,\dots ,v_m$ is distinct. The path may include a subpath, represented as $⟨v_0,v_1,\dots ,v_i,P\left[v_i,v_j\right],v_j,v_{j+1},\dots ,v_m⟩$, where $P\left[v_i,v_j\right]=⟨v_i,v_{i+1},\dots ,v_{j-1},v_j⟩$. The length of the path $P\left[v_0,v_m\right]$ is denoted as $l\left(P\left[v_0,v_m\right]\right)$, which is equivalent to the number of edges in $P\left[v_0,v_m\right]$. A cycle in $G$ is a sequence of vertices $⟨v_0,v_1,\dots ,v_m,v_0⟩$ where $m\ge 2$, and all vertices $v_0,v_1,\dots ,v_m$ are distinct. Additionally, any two consecutive vertices in the cycle are adjacent.

Consider the graph $Q_n$, where n is a positive integer. This graph has $2^n$ vertices, each of which is labeled with an n-bit binary string, ranging from $\underset{n}{\underbrace{00\dots 0}n}$ to $\underset{n}{\underbrace{11\dots 1}}$n, denoted as $x_n{x}_{n-1}\dots x_i\dots x_1$ where $x_i$ is either 0 or 1 and $1\le i\le n$. The edges of $Q_n$ connect vertices that differ in exactly one bit position. In other words, an edge $(u,v)$ exists if and only if $u$ and $v$ have different labels in exactly one position $k$, where $1\le k\le n$, and $v$ is obtained from $u$ by flipping the bit in position $k$. We call this edge an edge of dimension $2^{n-1}$ edges, so the total number of edges is ${n\times 2}^{n-1}$.

Given two vertices $u=u_n{u}_{n-1}\dots u_i\dots u_1$ and $v=v_n{v}_{n-1}\dots v_1\dots v_1$, we define the Hamming distance $d_H(u,v)$ as the number of positions where their corresponding binary strings differ. We also define the complement of a vertex $u$, denoted by $\overline{u}$, as the vertex obtained by flipping all bits in $u$. Finally, we define the operation $u^{\left(k\right)}$ as the vertex obtained from u by flipping the $k$-th bit of $u$. In other words, if $v=u^{\left(k\right)}$, then $v_i=u_i$ for all $1\le i\le n$ and $i\ne k$, and $v_k=1-u_k$.

${FQ}_n$ is an extension of $Q_n$ where every pair of vertices that have the maximum distance between them in $Q_n$ are connected by a complementary edge. As a result, ${FQ}_n$ has $2^{n-1}$ complementary edges denoted by the set $E_c$. The set of regular edges in ${FQ}_n$ that belong to $Q_n$ are denoted by $E_r$. Specifically, $E_r$ is the union of $Q_n\prime s$ i-dimensional edge sets for $1\le i\le n$, that is $E_r=E_1\cup E_2\cup \dots \cup E_n$. Therefore, the set of edges in ${FQ}_n$ is given by ${E(FQ}_n)=E_r\cup E_c$ which contains all the edges $\mathrm{e}=(u,v)$ such that $d_H\left(u,v\right)=1$ or $d_H\left(u,v\right)=n$. Figure 1 illustrates instances of ${FQ}_2$ and ${FQ}_3$.

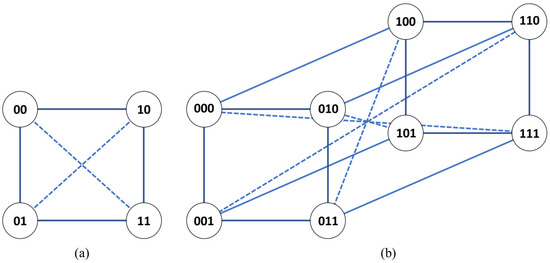
Figure 1. Graphs (a) ${FQ}_2$ and (b) ${FQ}_3$, complementary edge set $E_c$ is depicted as dashed lines.

Given a regular hypercube $Q_n$, we can divide it into two subcubes along dimension i, where $1\le i\le n$. These subcubes are denoted as $Q_{n-1}^{0i}={\ast }^{n-1}0 {\ast }^{i-1}$ and $Q_{n-1}^{1i}={\ast }^{n-1}1 {\ast }^{i-1}$, where the i-th bit of vertices in $Q_{n-1}^0$ and $Q_{n-1}^1$ are 0 and 1 respectively. To simplify notation, we can denote $Q_{n-1}^{0i}$ and $Q_{n-1}^{1i}$ as $Q_{n-1}^0$ and $Q_{n-1}^1$ respectively.

Definition 1 ([12]).

A partition of ${FQ}_n$ into two subcubes, $Q_{n-1}^0$ and $Q_{n-1}^1$, along a specific dimension i is called an i-partition, where $1\le i\le n$. Furthermore, all complementary edges in ${FQ}_n$ connect a vertex in $Q_{n-1}^0$ to a vertex in $Q_{n-1}^1$. To simplify, we use $Q_{n-1}^0$ and $Q_{n-1}^1$ as brief notations for $Q_{n-1}^{0i}$ and $Q_{n-1}^{1i}$, respectively.

According to Definition 1, we can partition the set of faulty vertices $F_v$ in ${FQ}_n$ into two subsets by executing an i-partition. This partition results in the formation of two $(n-1)$-cubes, denoted as $Q_{n-1}^0$ and $Q_{n-1}^0$. We can then define the subsets of $F_v$ within each $(n-1)$-cubes as $F_v^j=F_v\cap V\left(Q_{n-1}^j\right)$ for $j\in 0,1$. Finally, we can use ${|F}_v^j|$ to represent the cardinality of $F_v^j$ for each $j\in \{0,1\}$.

For the rest of this section, we will examine certain outcomes that have been documented in $Q_n$ or ${FQ}_n$, and which are beneficial to our primary argument.

Lemma 1 ([7]).

Assuming $\left|F_v\right|\le n-2$, it can be shown that for $n\ge 3$, any fault-free edge $e=(u,v)$ in ${FQ}_n-F_v$ can lie on a cycle of even length l within the range of $4{\le l\le 2}^n-2\left|F_v\right|$. Similarly, for every even $n\ge 2$ and $\left|F_v\right|\le n-2$, every fault-free edge $e=(u,v)$ in ${FQ}_n-F_v$ can also be a part of a cycle of odd length l within the range of $n+1{\le l\le 2}^n-2\left|F_v\right|-1$.

The subsequent corollary can be obtained directly by referring to Lemma 1.

Corollary 1.

Suppose $\left|F_v\right|=4$. Then, for $n\ge 6$, any fault-free edge $e=(u,v)$ in ${FQ}_n-F_v$ can lie on a cycle with any even length l satisfying $4{\le l\le 2}^n-8$. Additionally, for every even $n\ge 6$, any fault-free edge $e=(u,v)$ in ${FQ}_n-F_v$ an also be a part of a cycle with any odd length l satisfying $n+1{\le l\le 2}^n-9$.

Lemma 2 ([9]).

Consider $Q_n$, where $n\ge 4$ and let $f_1$ and $f_2$ represent two adjacent faulty vertices. It is possible to find a path $P[x,y]$ of length $2^n-4$ within $Q_n-\{f_1,f_2\}$, where x and y are fault-free vertices belonging to the same partite set.

Lemma 3 ([13]).

Let $F_v$ represent faulty vertices and $F_e$ faulty edges in $Q_n$. For any two fault-free vertices x and y in $Q_n$, with $\left|F_e\right|+\left|F_v\right|\le n-2$ and $n\ge 3$, there exists a fault-free path $P[x,y]$ with length l such that $d_H\left(u,v\right)+2\le l\le 2^n-2\left|F_v\right|-1$, provided ${(l-d}_H\left(u,v\right))$ is divisible by 2.

Lemma 4 ([14]).

For any two vertices x and y in $Q_n$, where $n\ge 2$, there is a path $P[x,y]$ of length l, where $d_H\left(u,v\right)\le l\le 2^n-1$. Moreover, the difference ${(l-d}_H\left(u,v\right))$ is always a multiple of 2.

Lemma 5.

Suppose  $f_1$ and  $f_2$ are two adjacent faulty vertices in  $Q_n$, where  $n\ge 4$. Then, for any fault-free edge  $e=(u,v)$, it is possible for e to be a part of a cycle of length  $l=2^n-2$ in  $Q_n-\{f_1,f_2\}$.

Proof. 

We will prove the lemma by using mathematical induction on n. Let us consider the base case, where $n=4$. $Q_4$ has a symmetric structure, thus we can assume without any loss of generality that $f_1=0000$ and $f_2=0001$. In Table 1, every fault-free edge can be obtained in at least one of these cycles of length 14. The lemma is verified for $n=4$. Assuming that the lemma holds for all integers where $5\le n\le k-1$, where $k>4$, we aim to demonstrate that it also holds for $n=k$. We consider the case where $f_1$ and $f_2$ are adjacent in $Q_k$. Without loss of generality, we may assume that $(f_1,f_2)\in E_1$. Then, we can partition $Q_k$ into two subcubes $Q_{k-1}^0$ and $Q_{k-1}^1$ along dimension i, where $2\le i\le k$, such that $\{f_1,f_2\}\subseteq V\left(Q_{k-1}^0\right)$ or $\{f_1,f_2\}\subseteq V\left(Q_{k-1}^1\right)$. We can make the assumption that $i=k$ and $f_1,f_2\subseteq V\left(Q_{k-1}^0\right)$, without it affecting the general nature of the argument. Given that $e=(u,v)$ be any fault-free edge in $Q_k$, then we have the following subcases.  □

Table 1. Lemma 5 is being applied to the base case where n = 4.

Each Edge e is a Part of a Minimum of One Cycle with a Length of 14.
<0010; 0011; 1011; 1111; 0111; 0110; 0100; 0101; 1101; 1001; 1000; 1100; 1110; 1010; 0010>
<0101; 0111; 0011; 0010; 0110; 0100; 1100; 1000; 1010; 1110; 1111; 1011; 1001; 1101; 0101>
<0100; 0101; 0111; 0011; 0010; 0110; 1110; 1111; 1011; 1010; 1000; 1001; 1101; 1100; 0100>
<0100; 0101; 0111; 0011; 0010; 0110; 1110; 1111; 1101; 1001; 1011; 1010; 1000; 1100; 0100>

• Case 1. $u$ and $v$ are in different subcubes. Assuming $u\in V\left(Q_{k-1}^0\right)$ and $v\in V\left(Q_{k-1}^1\right)$, we can make the following argument without losing generality. Let $x$ be a neighbor of $u$ in $Q_{k-1}^0$ that is free of faults and is not one of $f_1$ or $f_2$. (Note that since $k\ge 5$, $x$ must have more than four neighbors in $Q_{k-1}^0$.) By the induction hypothesis, $(u,x)$ can lie on a fault-free cycle $C_0$ of length $2^{k-1}-2$ in $Q_{k-1}^0$, which can be represented as $⟨u,P_0\left[u,x\right],x,u⟩$. Observe that $x^{\left(k\right)}$ is the neighbor of $x$ in $Q_{k-1}^1$, and $d_H\left(x^{\left(k\right)},v\right)=1$. As per Lemma 4, there is a path $P_1\left[x^{\left(k\right)},v\right]$ of length $2^{k-1}-1$ in $Q_{k-1}^1$. Consequently, the cycle comprising of the sequence $⟨u,P_0\left[u,x\right],x,x^{\left(k\right)},P_1\left[x^{\left(k\right)},v\right],u,v⟩$ has a length of ${(2}^{k-1}-2)-1+2+{(2}^{k-1}-1)={(2}^k-2)$, and it contains the edge $e$ in $Q_k-\{f_1,f_2\}$ (Figure 2a).
  

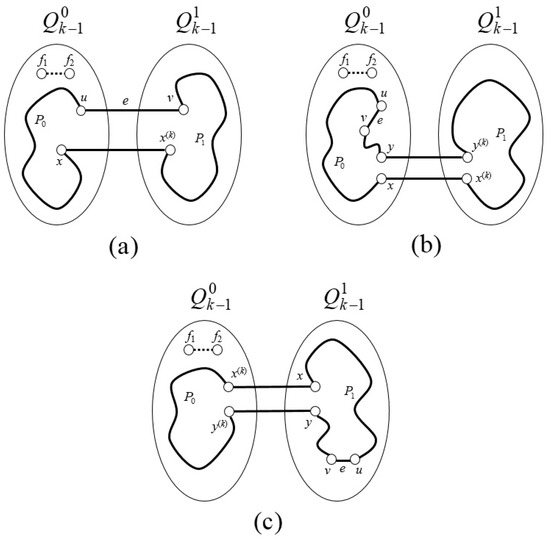  Figure 2. The proof of Case 1 (a) Case 2 (b) and Case 3 (c) in Lemma 5 are illustrated.
• Case 2. $u$ and $v$ both are in $Q_{k-1}^0$. Using the induction hypothesis, we assume that edge $e=(u,v)$ belongs to a fault-free cycle $C_0$ in $Q_{k-1}^0$ with length $2^{k-1}-2$. We consider another edge $(x,y)\ne (u,v)$ in $C_0$ and express $C_0$ as $⟨x,P_0\left[x,u\right],u,v,P_0\left[v,y\right],y,x⟩$. Since $x^{\left(k\right)}$ and $y^{\left(k\right)}$ belong to $Q_{k-1}^1$ and their Hamming distance is 1, Lemma 4 implies there exists a path $P_1\left[y^{\left(k\right)},x^{\left(k\right)}\right]$ with length $2^{k-1}-1$ in $Q_{k-1}^1$. Therefore, the cycle $⟨u,P_0\left[x,u\right],u,v,P_0\left[v,y\right],y,y^{\left(k\right)},P_1\left[y^{\left(k\right)},x^{\left(k\right)}\right],x^{\left(k\right)},x⟩$ has length $2^k-2$ and includes edge $e$ in $Q_k-\{f_1,f_2\}$ (Figure 2b).
• Case 3. $u$ and $v$ both are in $Q_{k-1}^1$. Given $d_H\left(u,v\right)=1$ in $Q_k$, by Lemma 4, we know that there exists a path $P_1\left[u,v\right]$ of length $2^{k-1}-1$ in $Q_{k-1}^1$. Since $k\ge 5$, the length of $P_1\left[u,v\right]$ is more than 15 in $Q_{k-1}^1$, so there must exist an edge $\left(x,y\right)\ne \left(u,v\right)$ in $P_1\left[u,v\right]$ such that ${\{y}^{\left(k\right)},x^{\left(k\right)}\}\bigcap \left\{f_1,f_2\right\}=\varnothing$ in $Q_{k-1}^0$. Since $d_H\left(x^{\left(k\right)},y^{\left(k\right)}\right)=1$ in $Q_{k-1}^0$, by induction hypothesis, $\left(x^{\left(k\right)},y^{\left(k\right)}\right)$ can lie on a fault-free cycle $C_0$ of length $2^{k-1}-2$ in $Q_{k-1}^0$. We can express $C_0$ as $⟨x^{\left(k\right)},P_0\left[x^{\left(k\right)},y^{\left(k\right)}\right],y^{\left(k\right)},x^{\left(k\right)}⟩$. Now, we can express $P_1\left[u,v\right]$ as $⟨u,P_1\left[u,x\right],x,y,P_1\left[y,v\right],v⟩$. Therefore, the cycle $⟨u,P_1\left[u,x\right],x,x^{\left(k\right)},P_0\left[x^{\left(k\right)},y^{\left(k\right)}\right],y^{\left(k\right)},y,P_1\left[y,v\right],v,u⟩$ has length $2^{k-1}-2-1+2+\left(2^{k-1}-1\right)=2^k-2$ and includes edge $e$ in $Q_k-\{f_1,f_2\}$ (Figure 2c).

We have completed the proof by combining the above cases. Thus, we have shown that the lemma holds for $n=k$. Q.E.D.

3. Every Cycle of ${\mathit{F}\mathit{Q}}_{\mathit{n}}-{\mathit{F}}_4$ Contains Any Edge

Let us assume that $e=(u,v)$ is an edge free from faults, and define the set $F_4$ as the collection of faulty extreme vertices, denoted by $f_1,f_2,f_3$ and $f_4$, that belong to any four-cycle ring in ${FQ}_n$. In this section, we will demonstrate the following results regarding $e$ in ${FQ}_n-F_4$: (1) For $n\ge 4$, $e$ can lie on a cycle of any even length between 4 and $2^n-4$, inclusive; (2) For every even $n\ge 4$, $e$ can lie on a cycle of any odd length between $n+1$ and $2^n-5$, inclusive.

Lemma 6.

When $n\ge 4$, any edge $e=(u,v)$ that is free of faults can lie on a cycle of even length l with ${4\le l\le 2}^n-4$ in ${FQ}_n-F_4$. The set $F_4$ represents the scope of faulty vertices at the extreme ends of any four-cycle ring in ${FQ}_n$.

Proof. 

The scenarios are evaluated separately for three cases of n: $n=4$, $n=5$, and $n\ge 6$.  □

• Case 1. For $n=4$. Since the structure of ${FQ}_4$ is symmetric. Without loss of generality, the scope faulty four-cycle F₄ can be categorized into two types: those that do not contain complement edges $F_4=\{0000,0001,0011,0010\}$ and those that contain complement edges $F_4=\{0000,1111,1110,0001\}$. With this assumption, we can observe that every fault-free edge $e$ in Table 2 and Table 3 can be found in at least one even cycle with a length between 4 to 12 in ${FQ}_4-\{0000;0001;0011;0010\}$ and ${FQ}_4-\{0000;1111;1110;0001\}$, respectively. Hence, the case $n=4$ satisfies the lemma.
  Table 2. The justification for Case 1 in Lemma 6, where $F_4=\{0000,0001,0011,0010\}$ .

  Cycle Length l	Edge e is Present in at Least One of the l Cycles Listed
  l = 4	<0101; 0111; 0110; 0100; 0101>
  	<1001; 1011; 1010; 1000; 1001>
  	<1101; 1111; 1110; 1100; 1101>
  	<1001; 1101; 1100; 1000; 1001>
  	<1011; 1111; 1110; 1010; 1011>
  	<0101; 1010; 1000; 0111; 0101>
  	<0100; 0110; 1001; 1011; 0100>
  	<0100; 1100; 1101; 0101; 0100>
  	<0111; 0110; 1110; 1111; 0111>
  l = 6	<0101; 1101; 1111; 1110; 1100; 0100; 0101>
  	<0111; 1111; 1011; 1010; 1110; 0110; 0111>
  	<0111; 0101; 0100; 0110; 1001; 1000; 0111>
  	<1011; 1001; 1000; 1010; 0101; 0100; 1011>
  	<1001; 1101; 1100; 1000; 1010; 1011; 1001>
  l = 8	<0101; 0100; 1100; 1000; 1001; 1011; 1111; 1101; 0101>
  	<0101; 0111; 0110; 0100; 1011; 1001; 1000; 1010; 0101>
  	<0110; 1001; 1101; 1100; 1110; 1010; 1000; 0111; 0110>
  	<0110; 1110; 1010; 1011; 1001; 1101; 1111; 0111; 0110>
  	<1111; 1110; 1100; 1101; 1001; 1000; 1010; 1011; 1111>
  l = 10	<0101; 0111; 0110; 0100; 1100; 1110; 1010; 1011; 1111; 1101; 0101>
  	<0101; 0100; 1011; 1001; 0110; 0111; 1000; 1100; 1110; 1010; 0101>
  	<1001; 1000; 1010; 1110; 0110; 0111; 1111; 1011; 0100; 0110; 1001>
  	<1001; 1101; 1100; 1110; 1111; 1011; 1010; 0101; 0100; 0110; 1001>
  l = 12	<0111; 0101; 0100; 0110; 1110; 1100; 1000; 1010; 1011; 1001; 1101; 1111; 0111>
  	<0101; 1010; 1011; 0100; 0110; 1001; 1000; 0111; 1111; 1110; 1100; 1101; 0101>
  	<0111; 0110; 0100; 1100; 1110; 1010; 1000; 1001; 1011; 1111; 1101; 0101; 0111>

  Table 3. The justification for Case 1 in Lemma 6, where $F_4=\{0000,1111,1110,0001\}$ .

  Cycle Length l	Edge e is Present in at Least One of the l Cycles Listed
  l = 4	<0011; 0111; 0110; 0010; 0011>
  	<0111; 0101; 0100; 0110; 0111>
  	<0101; 0100; 1100; 1101; 0101>
  	<1000; 1100; 1101; 1001; 1000>
  	<1001; 1011; 1010; 1000; 1001>
  	<0011; 1011; 1010; 0010; 0011>
  	<0101; 1010; 1011; 0100; 0101>
  	<0111; 1000; 1001; 0110; 0111>
  	<0011; 1100; 1101; 0010; 0011>
  l = 6	<0011; 1100; 1000; 1001; 1101; 0010; 0011>
  	<0010; 0110; 0111; 0011; 1011; 1010; 0010>
  	<0111; 0101; 0100; 0110; 1001; 1000; 0111>
  	<0101; 1010; 1000; 1001; 1011; 0100; 0101>
  	<0101; 1101; 1100; 0100; 0110; 0111; 0101>
  l = 8	<0011; 1100; 1000; 1010; 1011; 1001; 1101; 0010; 0011>
  	<0110; 0111; 0101; 0100; 1011; 1010; 1000; 1001; 0110>
  	<1100; 0100; 0110; 0010; 0011; 0111; 0101; 1101; 1100>
  	<1000; 0111; 0011; 1011; 1010; 0010; 0110; 1001; 1000>
  	<1010; 0101; 0111; 0110; 0100; 1011; 1001; 1000; 1010>
  l = 10	<0011; 1100; 1000; 1010; 1011; 1001; 1101; 0010; 0110; 0111; 0011>
  	<0100; 1011; 1001; 0110; 0010; 0011; 0111; 0101; 1101; 1100; 0100>
  	<0101; 1010; 1011; 1001; 1000; 0111; 0011; 0010; 0110; 0100; 0101>
  	<0111; 0110; 0010; 1010; 1000; 1100; 1101; 1001; 1011; 0011; 0111>
  l = 12	<0011; 1100; 1000; 1010; 1011; 1001; 1101; 0010; 0110; 0100; 0101; 0111; 0011>
  	<0100; 1100; 1101; 0101; 1010; 1011; 1001; 1000; 0111; 0011; 0010; 0110; 0100>
  	<0011; 0010; 0110; 1001; 1101; 1100; 1000; 1010; 1011; 0100; 0101; 0111; 0011>
  	<0011; 0111; 0101; 0100; 0110; 0010; 1010; 1000; 1100; 1101; 1001; 1011; 0011>
  	<0101; 0100; 0110; 0111; 0011; 0010; 1010; 1011; 1001; 1000; 1100; 1101; 0101>

• Case 2. For $n=5$. Assuming the symmetry of the structure of ${FQ}_5$, we can, without loss of generality, consider $F_4$ as either $\{f_1=0000,f_2=0001,f_3=0011,f_4=0010\}$ or $\{f_1=00000,f_2=00001,f_3=11110,f_4=11111\}$. By using Definition 1, we can apply the 2-partition on ${FQ}_5$ to generate two 4-dimensional subcubes, $Q_4^0$ and $Q_4^1$, such that $\{f_1,f_2\}\subseteq V\left(Q_4^0\right)$ and $\{f_3,f_4\}\subseteq V\left(Q_4^1\right)$. For any fault-free edge $e=(u,v)$ in ${FQ}_5$, we can investigate its distribution using the following scenarios.
  • Case 2.1. $e=(u,v)\in E\left(Q_4^0\right)$ or $e=(u,v)\in E\left(Q_4^1\right)$. Assuming no loss of generality, we can consider $e\in E\left(Q_4^0\right)$. In this case, we need to account for the fact that $e$ can be found in every even cycle of length l with $4\le l\le 28$ in ${FQ}_5-F_4$. Consequently, the following subcases emerge.
    • Case 2.1.1. Even length l with $4\le l\le 24$. By Lemma 3, since $d_H\left(u,v\right)=1$ and $\left|F_v^0\right|=2$, there exists a fault-free path $P_0[u,v]$ of every odd length 3, 5, 7, 9, and 11 in $Q_4^0-F_v^0$, respectively. Thus, $⟨u,P_0\left[u,v\right],u,v⟩$ can form the cycle $C_0$ of every even length l with $4\le l\le 12$ which obtains the edge $e$ in ${FQ}_5-F_4$. Without loss of generality, we may select a cycle $C_0$ with length 12 and let $(x,y)\ne (u,v)$ be any edge in $C_0$ such that $\{x^{\left(2\right)},y^{\left(2\right)}\}\cap \left\{f_3,f_4\right\}=\varnothing$ in $Q_4^1$. Then, $C_0$ can be expressed as $⟨u,P_0\left[u,x\right],x,y,P_0\left[y,v\right],v,u⟩$. Since $x^{\left(2\right)},y^{\left(2\right)}$ is fault-free in $Q_4^1$, $⟨u,P_0\left[u,x\right],x,x^{\left(2\right)},y^{\left(2\right)},y,P_0\left[y,v\right],v,u⟩$ forms a cycle of even leng $l=14$ which obtains the edge $e$ in ${FQ}_5-F_4$. Note that $d_H\left(x^{\left(2\right)},y^{\left(2\right)}\right)=1$, and $\left|F_v^1\right|=2$ in $Q_4^1$. By Lemma 3, there exists a fault-free path $P_1\left(x^{\left(2\right)},y^{\left(2\right)}\right)$ of every odd length 3, 5, 7, 9, and 11 in $Q_4^1-F_v^1$, respectively. Then, $⟨u,P_0\left[u,x\right],x,x^{\left(2\right)},P_1\left[x^{\left(2\right)},y^{\left(2\right)}\right],y^{\left(2\right)},y,P_0\left[y,v\right],v,u⟩$ forms a cycle of every even length l with $16\le l\le 24$ which obtains the edge $e$ in ${FQ}_5-F_4$.
    • Case 2.1.2. Even length l with $26\le l\le 28$. Given that $f_1$ and $f_2$ are adjacent faulty vertices and $e=\left(u,v\right)$ is a fault-free edge in $Q_4^0$, by Lemma 5, $e$ can be on a cycle $C_0$ of length 14 in $Q_4^0-\{f_1,f_2\}$. We select an edge $(x,y)\ne (u,v)$ from $C_0$ such that $\{x^{\left(2\right)},y^{\left(2\right)}\}\cap \left\{f_3,f_4\right\}=\varnothing$ in $Q_4^1$. Then, $C_0$ can be expressed as $⟨u,P_0\left[u,x\right],x,y,P_0\left[y,v\right],v,u⟩$. This gives rise to the following subcases.
      • Case 2.1.2.1. $l=26$. Lemma 3 guarantees that a fault-free path $P_1[x^{\left(2\right)},y^{\left(2\right)}]$ of odd length 11 exists in $Q_4^1-F_v^1$, where $d_H\left(x^{\left(2\right)},y^{\left(2\right)}\right)=1$ $\left|F_v^1\right|=2$. Therefore, the cycle $C_0$ can be expressed as $⟨u,P_0\left[u,x\right],x,x^{\left(2\right)},P_1\left[x^{\left(2\right)},y^{\left(2\right)}\right],y^{\left(2\right)},y,P_0\left[y,v\right],v,u⟩$, which has even length $l=\left(14-1\right)+2+11=26$, and includes the edge $e$ in ${FQ}_5-F_4$ (Figure 3a).
        

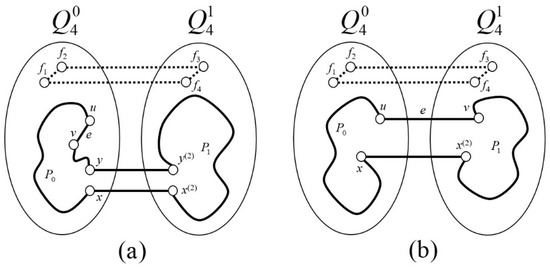        Figure 3. Figure showing the proof of subcases Case 2.1.2.1 (a) and Case 2.2.2.1 (b) in Lemma 6.
      • Case 2.1.2.2. $l=28$. Given that $f_3$ and $f_4$ are two adjacent faulty vertices and $(x^{\left(2\right)},y^{\left(2\right)})$ is a fault-free edge in $Q_4^1$, by Lemma 5, $(x^{\left(2\right)},y^{\left(2\right)})$ can be on a cycle $C_1$ of even length 14 in $Q_4^1-\{f_3,f_4\}$. We note that $C_1$ can be represented as $⟨x^{\left(2\right)},P_1\left[x^{\left(2\right)},y^{\left(2\right)}\right],y^{\left(2\right)},x^{\left(2\right)}⟩$. Hence, $⟨u,P_0\left[u,x\right],x,x^{\left(2\right)},P_1\left[x^{\left(2\right)},y^{\left(2\right)}\right],y^{\left(2\right)},y,P_0\left[y,v\right],v,u⟩$ forms a cycle of even length $l=\left(14-1\right)+2+(14-1)=28$, which obtains the edge $e$ in ${FQ}_5-F_4$.
  • Case 2.2. $e=\left(u,v\right)\in E_2$. Assuming without loss of generality, $u\in V\left(Q_4^0\right)$ and $v\in V\left(Q_4^1\right)$. We must then consider that $e$ can be obtained in any even cycle of length l with $4\le l\le 28$ in ${FQ}_5-F_4$. This gives rise to the following subcases.
    • Case 2.2.1. Even length l with $4\le l\le 24$. Let $x$ be a fault-free neighbor of $u$ in $V\left(Q_4^0\right)$ such that $x^{\left(2\right)}\notin \{f_3,f_4\}$ in $V\left(Q_4^1\right)$. This is possible as the neighbor of $u$ in $V\left(Q_4^0\right)$ are 4 vertices and at most one of them belongs to $f_1$ or $f_2$, by the hypercube structure. Therefore, there exists at least one vertex that meets this condition. Without loss of generality, assume $u\in V\left(Q_4^0\right)$ and $v\in V\left(Q_4^1\right)$. Note that $d_H\left(u,x\right)=1$ and $d_H\left(v,x^{\left(2\right)}\right)=1$ in $Q_4^0$ and $Q_4^1$, respectively. Thus, $⟨{u,v,x}^{\left(2\right)},x⟩$ forms a cycle of even length $l=24$ that contains the edge $e$ in ${FQ}_5-F_4$. Moreover, since $d_H\left(u,x\right)=1$ and $\left|F_v^0\right|=2$, by Lemma 3, there exists a fault-free path $P_0\left[u,x\right]$ of every odd length 3, 5, 7, 9, and 11 in $Q_4^0-F_v^0$, respectively. Therefore, $⟨u,P_0\left[u,x\right],x,x^{\left(2\right)},v,u⟩$ can form the cycle of every even length l with $6\le l\le 14$ that contains the edge $e$ in ${FQ}_5-F_4$. To construct every cycle of even length l with $16\le l\le 24$, we select a path $P_0\left[u,x\right]$ with length 11 in $Q_4^0$. Then, in $Q_4^1$, since $d_H\left(x^{\left(2\right)},v\right)=1$ and $\left|F_v^1\right|=2$, by Lemma 3, there exists a fault-free path $P_1\left[x^{\left(2\right)},v\right]$ of every odd length 3, 5, 7, 9, and 11 in $Q_4^1-F_v^1$, respectively. Therefore, $⟨u,P_0\left[u,x\right],x,x^{\left(2\right)},P_1\left[x^{\left(2\right)},v\right],v,u⟩$ forms a cycle of every even length l with $16\le l\le 24$ that contains the edge $e$ in ${FQ}_5-F_4$.
    • Case 2.2.2. Even length l with $26\le l\le 28$. Given that $f_1$ and $f_2$ are two adjacent faulty vertices and $(u,x)$ is an edge without faults in $Q_4^0$, according to Lemma 5, $(u,x)$ can exist on a cycle $C_0$ that has a length of 14 in $Q_4^0$ after removing vertices $f_1$ and $f_2$. The cycle $C_0$ can be expressed as $⟨u,P_0\left[u,x\right],x,u⟩$. Based on this, the following subcases arise.
      • Case 2.2.2.1. $l=26$. Given that $d_H\left(x^{\left(2\right)},v\right)=1$ and $\left|F_v^1\right|=2$, we can use Lemma 3 to conclude that there exists a fault-free path $P_1\left[x^{\left(2\right)},v\right]$ of odd length 11 in $Q_4^1-F_v^1$. Using this information, we can construct a cycle of even length $l=\left(14-1\right)+2+11=26$ by considering the path $⟨u,P_0\left[u,x\right],x,x^{\left(2\right)},P_1\left[x^{\left(2\right)},v\right],u⟩$ This cycle obtains the edge $e$ in ${FQ}_5-F_4$ (Figure 3b).
      • Case 2.2.2.2. $l=28$. According to Lemma 5, since $f_3$ and $f_4$ are two adjacent faulty vertices and $\left(x^{\left(2\right)},v\right)$ is a fault-free edge in $Q_4^1$, the edge $\left(x^{\left(2\right)},v\right)$ can lie on a cycle $C_1$ of even length 14 in $Q_4^1-\{f_3,f_4\}$. This cycle $C_1$ can be expressed as $⟨x^{\left(2\right)},P_1\left[x^{\left(2\right)},v\right],v,x^{\left(2\right)}⟩$. Therefore, $⟨u,P_0\left[u,x\right],x,x^{\left(2\right)},P_1\left[x^{\left(2\right)},v\right],v,u⟩$ forms a cycle of even length $l=\left(14-1\right)+2+(14-1)=28$ that includes the edge $e$ in ${FQ}_5-F_4$.
  • Case 2.3. $e=\left(u,v\right)\in E_c$. Assuming without loss of generality, $u$ is in $V\left(Q_4^0\right)$ and $v$ is in $V\left(Q_4^1\right)$. Next, we select a fault-free neighbor $x$ of $u$ in $V\left(Q_4^0\right)$ such that $\overline{x}$ is not equal to either $f_3$ or $f_4$ in $V\left(Q_4^1\right)$. It should be noted that the Hamming distance between $u$ and $x$ is one in $Q_4^0$, and the Hamming distance between $v$ and $\overline{x}$ is one in $Q_4^1$. Using this approach, an edge $e$ can lie on a cycle of every even length l with $4\le l\le 28$ in ${FQ}_5-F_4$ can be constructed similar to that in Case 2.2 of Lemma 6.
• Case 3. For $n\ge 6$. Suppose we have a fault-free edge $e=\left(u,v\right)$ in ${FQ}_n$. Our goal is to show that $e=\left(u,v\right)$ can lie on a cycle of every even length l with $4\le l\le 2^n-4$ in ${FQ}_n-F_4$. Since $n\ge 6$ and ${|F}_4|=4$, by using Corollary 1, we can conclude that $e=\left(u,v\right)$ can lie on a cycle of every even length l with $4\le l\le 2^n-8$ in ${FQ}_n-F_4$. However, we also need to show that $e=\left(u,v\right)$ can lie on a cycle of every even length l with $2^n-6\le l\le 2^n-4$ in ${FQ}_n-F_4$. Here, $F_4=\{f_1,f_2,f_3,f_4\}$ be the set of faulty extreme vertices, taken from any four cycles in ${FQ}_n$. As per Definition 1, since $n\ge 6$, the edges of the cycle $⟨f_1,f_2,f_3,f_4,f_1⟩$ are contained within two dimensions i and j, where $\{i,j\}\subseteq \{1,2,\dots ,n,c\}$ and $i\ne j$. As a result, a k-partition of ${FQ}_n$ exists such that one pair of adjacent vertices of the quadrilateral $F_4$ belongs to $Q_{n-1}^0$ and the other pair belongs to $Q_{n-1}^1$. Here, we can select $k=n,\{f_1,f_2\}\subseteq V\left(Q_{n-1}^0\right)$, and $\{f_3,f_4\}\subseteq V\left(Q_{n-1}^1\right)$, without any loss of generality. After partition, we can explore the distribution of the edge $e=\left(u,v\right)$ and show that it can lie on a cycle of every even length l with $2^n-6\le l\le 2^n-4$ in ${FQ}_n-F_4$.
  • Case 3.1. $e=\left(u,v\right)\in E\left(Q_{n-1}^0\right)$ or $e=\left(u,v\right)\in E\left(Q_{n-1}^1\right)$. Let us assume without loss of generality that $e\in E\left(Q_{n-1}^0\right)$. Since $f_1$ and $f_2$ are two adjacent faulty vertices and $e$ is a fault-free edge in $Q_{n-1}^0$, we can use Lemma 5 to show that edge $e$ can lie on a cycle $C_0$ of length $2^{n-1}-2$ in $Q_{n-1}^0$ that does not contain $\{f_1,f_2\}$. We can then select any edge $\left(x,y\right)\ne \left(u,v\right)$ in $C_0$ such that $\left\{x^{\left(n\right)},y^{\left(n\right)}\right\}\bigcap \left\{f_3,f_4\right\}=\varnothing$ in $Q_{n-1}^1$. Then, $C_0$ can be expressed as $⟨u,P_0\left[u,x\right],x,y,P_0\left[y,v\right],v,u⟩$. We can then consider the following subcases.
    • Case 3.1.1. $l=2^n-6$. Given that $d_H\left(x^{\left(n\right)},y^{\left(n\right)}\right)=1$ and $\left|F_v^1\right|=2$, we can use Lemma 3 to conclude that a fault-free path $P_1\left[x^{\left(n\right)},y^{\left(n\right)}\right]$ of odd length $2^{n-1}-5$ exists in $Q_{n-1}^1-F_v^1$. This path, combined with the paths $P_0\left[u,x\right]$ and $P_0\left[y,v\right]$ between vertices $u$ and $x$, and vertices $y$ and $v$ respectively, can be used to form a cycle of even length $l=\left(2^{n-1}-2\right)-1+2+\left(2^{n-1}-5\right)=2^n-6$. This cycle obtains the edge $e$ in ${FQ}_n-F_4$. The cycle is given by $⟨u,P_0\left[u,x\right],x,x^{\left(n\right)},P_1\left[x^{\left(n\right)},y^{\left(n\right)}\right],y^{\left(n\right)},y,P_0\left[y,v\right],u,v⟩$.
    • Case 3.1.2. $l=2^n-4$. Assuming $f_3$ and $f_4$ are two adjacent faulty vertices and $\left(x^{\left(n\right)},y^{\left(n\right)}\right)$ is a fault-free edge in $Q_{n-1}^1$, then by Lemma 5, we know that $\left(x^{\left(n\right)},y^{\left(n\right)}\right)$ can lie on a cycle $C_1$ of even length $2^{n-1}-2$ in $Q_{n-1}^1$ after removing faulty vertices $f_3$ and $f_4$. The cycle $C_1$ can be expressed as $⟨x^{\left(n\right)},P_1\left[x^{\left(n\right)},y^{\left(n\right)}\right],y^{\left(n\right)},x^{\left(n\right)}⟩$. Therefore, we can conclude that $⟨u,P_0\left[u,x\right],x,x^{\left(n\right)},P_1\left[x^{\left(n\right)},y^{\left(n\right)}\right],y^{\left(n\right)},y,P_0\left[y,v\right],u,v⟩$ is a cycle with even length $l=2^n-4$. This cycle includes the edge $e$ and can be found in ${FQ}_n-F_4$.
  • Case 3.2. $e=\left(u,v\right)\in E_n$. Assuming without loss of generality, $u\in V\left(Q_{n-1}^0\right)$ and $v\in V\left(Q_{n-1}^1\right)$, we can choose a fault-free neighbor $x$ of $u$ in $V\left(Q_{n-1}^0\right)$ such that $x^{\left(n\right)}\notin \{f_3,f_4\}$ in $V\left(Q_{n-1}^1\right)$. Since $f_1$ and $f_2$ are two adjacent faulty vertices and $\left(u,x\right)$ be a fault-free edge in $Q_{n-1}^0$, by applying Lemma 5, we know that $\left(u,x\right)$ can lie on a cycle $C_0$ of length $2^{n-1}-2$ in $Q_{n-1}^0$ after removing faulty vertices $f_1$ and $f_2$. The cycle $C_0$ can be expressed as $⟨u,P_0\left[u,x\right],x,u⟩$, which leads to the following subcases.
    • Case 3.2.1. $l=2^n-6$. Using Lemma 3, we can show that there exists a fault-free path $P_1\left[x^{\left(n\right)},v\right]$ of odd length $2^{n-1}-5$ in $Q_{n-1}^1-F_v^1$ since $d_H\left(x^{\left(n\right)},v\right)=1$ and $\left|F_v^1\right|=2$. Therefore, the cycle $⟨u,P_0\left[u,x\right],x,x^{\left(n\right)},P_1\left[x^{\left(n\right)},v\right],u⟩$ has an even length of $l=(2^{n-1}-2)-1+2+\left(2^{n-1}-5\right)=2^n-6$ and it contains the edge $e$ in ${FQ}_n-F_4$.
    • Case 3.2.2. $l=2^n-4$. Using Lemma 5, we know that since $f_3$ and $f_4$ are adjacent faulty vertices and $\left(x^{\left(n\right)},v\right)$ is a fault-free edge in $Q_{n-1}^1$, edge $\left(x^{\left(n\right)},v\right)$ can lie on a cycle $C_1$ of even length $2^{n-1}-2$ in $Q_{n-1}^1-\left\{f_3,f_4\right\}$. We can express $C_1$ as $⟨x^{\left(n\right)},P_1\left[x^{\left(n\right)},v\right],v,x^{\left(n\right)}⟩$. As a result, $⟨u,P_0\left[u,x\right],x,x^{\left(n\right)},P_1\left[x^{\left(n\right)},v\right],v,u⟩$ forms a cycle of even length $l=\left(2^{n-1}-2\right)-1+2+\left(2^{n-1}-2\right)-1=2^n-4$, which obtains the edge $e$ in ${FQ}_n-F_4$.
  • Case 3.3. $e=\left(u,v\right)\in E_c$. Assuming $u\in V\left(Q_{n-1}^0\right)$ and $v\in V\left(Q_{n-1}^1\right)$ without loss of generality, we can choose a fault-free neighbor $x$ of $u$ in $V\left(Q_{n-1}^0\right)$ such that $\overline{x}\notin \left\{f_3,f_4\right\}$. In $Q_{n-1}^0$ and $Q_{n-1}^1$, we have $d_H\left(u,x\right)=1$ and $d_H\left(v,\overline{x}\right)=1$, respectively. The process of constructing the edge $e$ lying on a cycle of every even length $l=2^n-6$ and $l=2^n-4$ in ${FQ}_n-F_4$ is similar to that described in Case 3.2 of Lemma 6.

The proof is completed by considering all the cases mentioned above. Q.E.D.

Lemma 7.

For every even $n\ge 4$, consider the set $F_4$ which consists of four faulty extreme vertices, namely $f_1$, $f_2$, $f_3$, and $f_4$, found within any four-cycle ring in ${FQ}_n$. If $e=\left(u,v\right)$ is a fault-free edge in ${FQ}_n-F_4$ then $e$ can belong to a cycle of every odd length l with $n+1\le l\le 2^n-5$.

Proof. 

We examine the scenarios for $n=4$ as well as every even $n\ge 6$.  □

• Case 1. For $n=4$. Since the structure of ${FQ}_4$ is symmetric. Without loss of generality, the scope faulty four-cycle F₄ can be categorized into two types: those that do not contain complement edges $F_4=\{0000,0001,0011,0010\}$ and those that contain complement edges $F_4=\{0000,1111,1110,0001\}$. Then, using Table 4 and Table 5, we can observe that every fault-free edge $e$ can be found in at least one cycle of odd length ranging from 5 to 11 in ${FQ}_4-\{0000,0001,0011,0010\}$ and ${FQ}_4-\{0000,1111,1110,0001\}$, respectively. Hence, the lemma holds for the case $n=4$.
  Table 4. The justification for Case 1 in Lemma 7, where $F_4=\{0000,0001,0011,0010\}$.

  Cycle Length l	Edge e is Present in at Least One of the l Cycles Listed
  l = 5	<0111; 1000; 1001; 1101; 1111; 0111>
  	<0101; 1010; 1011; 1111; 1101; 0101>
  	<0100; 1011; 1001; 1101; 1100; 0100>
  	<0110; 1001; 1000; 1100; 1110; 0110>
  	<1000; 1010; 1110; 1111; 0111; 1000>
  	<0110; 0111; 0101; 1101; 1001; 0110>
  	<0101; 0100; 0110; 1001; 1101; 0101>
  l = 7	<0101; 1010; 1011; 0100; 0110; 1001; 1101; 0101>
  	<0111; 1000; 1001; 1011; 1010; 1110; 1111; 0111>
  	<0100; 0101; 0111; 0110; 1110; 1111; 1011; 0100>
  	<0100; 1100; 1000; 1010; 1110; 1111; 1011; 0100>
  	<1111; 1101; 1100; 1110; 1010; 0101; 0111; 1111>
  l = 9	<0101; 1101; 1111; 0111; 1000; 1010; 1110; 1100; 0100; 0101>
  	<0101; 0111; 0110; 0100; 1011; 1001; 1000; 1100; 1101; 0101>
  	<0101; 1010; 1011; 1001; 1101; 1111; 1110; 0110; 0111; 0101>
  	<0110; 1001; 1101; 1111; 1011; 1010; 1000; 1100; 1110; 0110>
  l = 11	<0101; 1010; 1011; 0100; 0110; 1001; 1000; 1100; 1110; 1111; 1101; 0101>
  	<0100; 0101; 0111; 1000; 1001; 1101; 1111; 1011; 1010; 1110; 1100; 0100>
  	<0111; 0110; 0100; 0101; 1010; 1011; 1001; 1000; 1100; 1110; 1111; 0111>
  	<0110; 0111; 0101; 0100; 1011; 1010; 1000; 1001; 1101; 1100; 1110; 0110>

  Table 5. The justification for Case 1 in Lemma 7, where $F_4=\{0000,1111,1110,0001\}$.

  Cycle Length l	Edge e is Present in at Least One of the l Cycles Listed
  l = 5	<0011; 1100; 1000; 1001; 1011; 0011>
  	<0011; 0010; 1010; 1000; 0111; 0011>
  	<0010; 1101; 0101; 0100; 0110; 0010>
  	<0010; 1101; 0101; 0111; 0110; 0010>
  	<1100; 1101; 1001; 0110; 0100; 1100>
  	<1010; 1011; 0100; 0110; 0010; 1010>
  	<1010; 1011; 1001; 1101; 0101; 1010>
  l = 7	<0011; 1100; 1000; 1001; 1011; 1010; 0010; 0011>
  	<0100; 1011; 1001; 0110; 0111; 1000; 1100; 0100>
  	<0101; 1010; 1000; 1001; 1101; 1100; 0100; 0101>
  	<0010; 1101; 0101; 0100; 0110; 0111; 0011; 0010>
  	<1011; 0011; 0010; 0110; 0111; 0101; 1010; 1011>
  l = 9	<0011; 1100; 1101; 1001; 1011; 1010; 0010; 0110; 0111; 0011>
  	<0010; 1101; 1100; 1000; 1010; 0101; 0100; 1011; 0011; 0010>
  	<0100; 1001; 1000; 0111; 0101; 1101; 1100; 0011; 0010; 0110>
  	<0110; 0100; 1100; 1000; 1010; 0101; 0111; 0011; 0010; 0110>
  l = 11	<0011; 1100; 1101; 1001; 1000; 1010; 0010; 0110; 0100; 0101; 0111; 0011>
  	<0010; 1101; 1001; 0110; 0111; 1000; 1010; 0101; 0100; 1011; 0011; 0010>
  	<0101; 1101; 1001; 1011; 1010; 1000; 1100; 0011; 0010; 0110; 0100; 0101>
  	<0100; 1100; 1000; 1010; 1011; 1001; 1101; 0010; 0011; 0111; 0110; 0100>

• Case 2. For every even $n\ge 6$. Suppose that $e=\left(u,v\right)$ is an edge in ${FQ}_n$ that is free of faults. Our goal is to show that $e=\left(u,v\right)$ can lie on a cycle of every odd length l such that $n+1\le l\le 2^n-5$ in ${FQ}_n-F_4$. Here, $F_4=\{f_1$, $f_2$, $f_3$, $f_4$} be the set of faulty extreme vertices, taken from any four cycles in ${FQ}_n$. Note that ${|F}_4|=4$ for every even $n\ge 6$. Therefore, by Corollary 1, we know that $e=\left(u,v\right)$ can lie on a cycle of every odd length l with $n+1\le l\le 2^n-9$ in ${FQ}_n-F_4$. We also need to consider the case where $e=\left(u,v\right)$ can lie on a cycle of every odd length l such that $2^n-7\le l\le 2^n-5$ in ${FQ}_n-F_4$. For every even $n\ge 6$, the edges of the cycle $\{f_1$, $f_2$, $f_3$, $f_4,f_1$} are contained within two dimensions i and j, where $\left\{i,j\right\}\subseteq \{1,2,\dots ,n,c\}$ and $i\ne j$. According to Definition 1, a k-partition of ${FQ}_n$ exists such that one pair of adjacent vertices of the quadrilateral $F_4$ belongs to $Q_{n-1}^0$ and the other pair belongs to $Q_{n-1}^1$. Here, we can select $k=n,\{f_1,f_2\}\subseteq V\left(Q_{n-1}^0\right)$ and $\{f_3,f_4\}\subseteq V\left(Q_{n-1}^1\right)$. After partition, we can explore the distribution of the edge $e=\left(u,v\right)$ and show that it can lie on a cycle of every even length l with $2^n-7\le l\le 2^n-5$ in ${FQ}_n-F_4$.
  • Case 2.1. $e=\left(u,v\right)\in E\left(Q_{n-1}^0\right)$ or $e=\left(u,v\right)\in E\left(Q_{n-1}^1\right)$. It is permissible to assume that $e\in E\left(Q_{n-1}^0\right)$. This assumption results in the following subcases.
    • Case 2.1.1. $l=2^n-7$. According to Lemma 3, in $Q_{n-1}^0$, there exists a fault-free path $P_0\left[u,v\right]$ of odd length $2^{n-1}-5$ in $Q_{n-1}^0-F_v^1$, since ${|F}_v^0|=2$ and $d_H\left(u,v\right)=1$. Let $\left(x,y\right)$ be an edge in $P_0\left[u,v\right]$ such that $\left\{x^{\left(n\right)},\overline{y}\right\}\bigcap \left\{f_3,f_4\right\}=\varnothing$ in $Q_{n-1}^1$. Since $l(P_0\left[u,v\right]\ge 2^5-5=27)$ for every even $n\ge 6$, it is not difficult to find such an edge $\left(x,y\right)$. By Lemma 2, there exists a fault-free path $P_1\left[x^{\left(n\right)},\overline{y}\right]$ of even length $2^{n-1}-4$ in $Q_{n-1}^1-\left\{f_3,f_4\right\}$, since $f_3$ and $f_4$ are two adjacent faulty vertices and $d_H\left(x^{\left(n\right)},\overline{y}\right)=\mathrm{n}-2$ in $Q_{n-1}^1$. Note that $d_H\left(x^{\left(n\right)},\overline{y}\right)=\mathrm{n}-2$ is even for every even $n\ge 6$, which means that vertices $x^{\left(n\right)}$ and $\overline{y}$ are in the same partite set. Then, the cycle $⟨u,P_0\left[u,x\right],x,x^{\left(n\right)},P_1\left[x^{\left(n\right)},\overline{y}\right],\overline{y},y,P_0\left[y,v\right]v,u⟩$ forms a cycle of odd length $l={(2}^{n-1}-5)+2+{(2}^{n-1}-4)=2^n-7$, which obtains the edge $e$ in ${FQ}_n-F_4$ (Figure 4a).
      

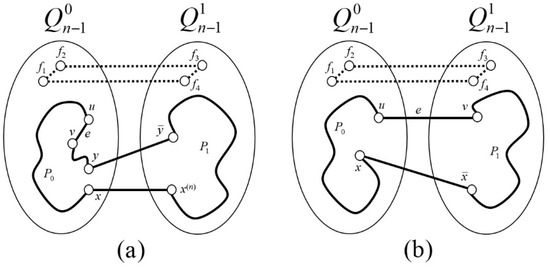      Figure 4. Figure showing the proof of subcases Case 2.1.1 (a) and Case 2.2.1 (b) in Lemma 7.
    • Case 2.1.2. $l=2^n-5$. Since $e=\left(u,v\right)$ is a fault-free edge in $Q_{n-1}^0$ and $f_1$ and $f_2$ are two adjacent faulty vertices, Lemma 5 implies that $\left(u,v\right)$ can lie on a cycle $C_0$ with even length $2^{n-1}-2$ in $Q_{n-1}^0-f_1,f_2$. Let $\left(x,y\right)\ne \left(u,v\right)$ be any edge in $C_0$ such that $\left\{x^{\left(n\right)},\overline{y}\right\}\bigcap \left\{f_3,f_4\right\}=\varnothing$ in $Q_{n-1}^1$. We can express $C_0$ as $⟨u,P_0\left[u,x\right],x,y,P_0\left[y,v\right],v,u⟩$. Since $f_3$ and $f_4$ are two adjacent faulty vertices and $d_H\left(x^{\left(n\right)},\overline{y}\right)=\mathrm{n}-2$ in $Q_{n-1}^1$, Lemma 2 implies that there exists a fault-free path $P_1\left[x^{\left(n\right)},\overline{y}\right]$ of even length $2^{n-1}-4$ in $Q_{n-1}^1-\left\{f_3,f_4\right\}$. Then, the cycle $⟨u,P_0\left[u,x\right],x,x^{\left(n\right)},P_1\left[x^{\left(n\right)},\overline{y}\right],\overline{y},y,P_0\left[y,v\right]v,u⟩$ has an odd length of $l={(2}^{n-1}-2)-1+2+{(2}^{n-1}-4)=2^n-5$, which contains the edge $e$ in ${FQ}_n-F_4$.
  • Case 2.2. $e=\left(u,v\right)\in E_n$. Assuming without loss of generality, we can take $u$ to be an element of $V\left(Q_{n-1}^0\right)$ and $v$ to be an element of $V\left(Q_{n-1}^1\right)$. We can then find a neighbor $x$ of $u$ in $V\left(Q_{n-1}^0\right)$ that is free from faults and satisfies the condition $\overline{x}\notin \{f_3,f_4\}$ in $V\left(Q_{n-1}^1\right)$. This gives rise to the following subcases.
    • Case 2.2.1. $l=2^n-7$. By utilizing Lemma 3, it can be observed that a fault-free path $P_0\left[u,x\right]$ of odd length $2^{n-1}-5$ exists in $Q_{n-1}^0-F_v^1$ since $F_v^0=2$ and $d_H\left(u,x\right)=1$ in $Q_{n-1}^0$. Moreover, as per Lemma 2, a fault-free path $P_1\left[\overline{x},v\right]$ of even length $2^{n-1}-4$ exists in $Q_{n-1}^1-\{f_3,f_4\}$ because $f_3$ and $f_4$ are two adjacent faulty vertices and $d_H\left(\overline{x},v\right)=n-2$ in $Q_{n-1}^1$. Therefore, the cycle $⟨u,P_0\left[u,x\right],x,\overline{x},P_1\left[\overline{x},v\right],v,u⟩$ of odd length $l={(2}^{n-1}-5)+2+{(2}^{n-1}-4)=2^n-7$ obtains the edge $e$ in ${FQ}_n-F_4$ (Figure 4b).
    • Case 2.2.2. $l=2^n-5$. Given that $f_1$ and $f_2$ are two adjacent faulty vertices, and $e=\left(u,x\right)$ is a fault-free edge in $Q_{n-1}^0$, we can apply Lemma 5 to conclude that $\left(u,x\right)$ can lie on a cycle $C_0$ of even length $2^{n-1}-2$ in $Q_{n-1}^0-\left\{f_1,f_2\right\}$. We can represent this cycle as $⟨u,P_0\left[u,x\right],x,u⟩$. Note that $f_3$ and $f_4$ are two adjacent faulty vertices and $d_H\left(\overline{x},v\right)=n-2$ in $Q_{n-1}^1$. By applying Lemma 2, we can find a fault-free path $P_1\left[\overline{x},v\right]$ of even length $2^{n-1}-4$ in $Q_{n-1}^1-\{f_3,f_4\}$. We can then construct a cycle $⟨u,P_0\left[u,x\right],x,\overline{x},P_1\left[\overline{x},v\right],v,u⟩$ of odd length $l={(2}^{n-1}-2)-1+2+{(2}^{n-1}-4)=2^n-5$ obtains the edge $e$ in ${FQ}_n-F_4$.
  • Case 2.3. $e=\left(u,v\right)\in E_c$. We can assume, without loss of generality, that $u$ is a vertex in $Q_{n-1}^0$ and $v$ is a vertex in $Q_{n-1}^1$. Let $x$ be a fault-free neighbor of $u$ in $Q_{n-1}^0$ such that $x^{\left(n\right)}\notin \{f_3,f_4\}$ in $Q_{n-1}^1$. Note that $d_H\left(u,x\right)=1$ and $d_H\left(x^{\left(n\right)},v\right)=n-2$ in $Q_{n-1}^0$ and $Q_{n-1}^1$, respectively. The construction of the edge $e$ lying on a cycle of odd length $l=2^n-7$ or $l=2^n-5$ in ${FQ}_n-F_4$ is similar to that described in Case 2.2 of Lemma 7.

The proof is completed by considering all the cases mentioned above. Q.E.D.

Applying Lemmas 6 and 7, we can derive the following theorem.

Theorem 1.

Suppose $e=\left(u,v\right)$ be any fault-free edge, and let $F_4$ enote the set which consists of four faulty extreme vertices, namely $f_1$, $f_2$, $f_3$, and $f_4$, found within any four-cycle ring in ${FQ}_n$. Then, for $n\ge 4$, every fault-free edge $e$ can lie on a cycle of even length from 4 to $2^n-4$ in ${FQ}_n-F_4$. Moreover, for every even $n\ge 4$, every fault-free edge $e$ can lie on a cycle of odd length from $n+1$ to $2^n-5$ in ${FQ}_n-F_4$.

4. Concluding Remarks

In a large network, processors or links can experience failures due to either natural calamities or human-induced factors, such as meteorite drops, earthquakes, hacker attacks, and bomb attacks, which can result in regional or scope damage and potentially paralyze the network. Therefore, analyzing the reliability of networks in the field of fault-tolerant embedding research has become an important research topic.

This paper addresses the reliability analysis problem in the context of the folded hypercube network ${FQ}_n$. Specifically, for any fault-free edge $e=\left(u,v\right)$ in ${FQ}_n$, we consider the set of faulty extreme vertices $F_4=\{f_1$, $f_2$, $f_3$, $f_4$} in any four-cycle ring of ${FQ}_n$. We show that, for $n\ge 4$, every fault-free edge $e$ can lie on a cycle of even length from 4 to $2^n-4$ in ${FQ}_n-F_4$. Furthermore, for every even $n\ge 4$, every fault-free edge $e$ can lie on a cycle of odd length from $n+1$ to $2^n-5$ in ${FQ}_n-F_4$. In future works, we will further investigate the problem of path embedding between any two vertices in ${FQ}_n-F_4$.